Determining both adhesion energy and residual stress by measuring the stiction shape of a microbeam

Abstract

The competition between the adhesive force and the beam restoring force determines the stiction shape of a microbeam. The presence of residual stress changes the beam stiffness and thus leads to the change of the beam restoring force. This study presents a model of incorporating the residual stress effect for the beam stiction. The previous models of arc-shape and S-shape correspond to the zero residual stress case, which also prescribes the stiction shape. When the residual stress becomes large, arc-shape and S-shape significantly deviate from the actual stiction shape of a slender beam. With the assumed stiction shape of arc-shape and S-shape, suspension length is the only parameter needed to characterize the stiction shape and suspension length can also be used to uniquely determine the adhesion energy. However, there are infinite combinations of residual stress and adhesion energy which can result in the same suspension length. Besides suspension length, the beam rise above the substrate can also be used as a parameter to characterize the stiction shape. This study presents a method of using these two parameters to uniquely determine the residual stress and adhesion energy as an inverse problem. A computation technique of using the stiction shape symmetry to significantly reduce the computation is also demonstrated.

Appendix: arc-shaped and S-shaped deflections

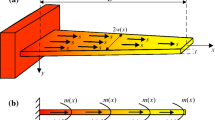
Figure 1b shows the arc-shape and S-shaped deflections and the coordinate system. When a beam is under stiction with no transverse and axial loads, the following governing equation holds:

$$\begin{aligned} w_{\xi \xi \xi \xi }=0. \end{aligned}$$

(18)

The solution to the above equation is

$$\begin{aligned} w(\xi )=A\xi ^3+B\xi ^2+C\xi +D. \end{aligned}$$

(19)

$A$, $B$, $C$ and $D$ are the four unknown constants to be determined by the boundary conditions.

For an arc-shaped beam, the following boundary conditions hold:

$$\begin{aligned} w(0)=0, \quad w_\xi (0)=0, \quad w(s_{arc})=h, \quad w_{\xi \xi }(s_{arc})=0. \end{aligned}$$

(20)

$w(\xi )$ of arc-shaped beam is then solved as follows

$$\begin{aligned} w(\xi )=-\frac{h}{2s_{arc}^3}\xi ^3 + \frac{3h}{2s_{arc}^2}\xi ^2. \end{aligned}$$

(21)

The (dimensional) suspension length of arc-shaped beam is given as follows (Mastrangelo and Hsu 1993b; Yang 2004)

$$\begin{aligned} S_{arc}^4=\frac{3}{8} \frac{E_1H^2T^3}{\gamma _s}=\frac{9E_1IH^2}{4B\gamma _s}. \end{aligned}$$

(22)

According to the nondimensionalization scheme of Eq. (4), we have $s_{arc}=\beta S_{arc}=\root 4 \of {9h^2/\alpha }$.

For an S-shaped beam, the following boundary conditions hold:

$$\begin{aligned} w(0)=0, \quad w_\xi (0)=0, \quad w(s_{c-c})=h, \quad w_\xi (s_{c-c})=0. \end{aligned}$$

(23)

$w(\xi )$ of S-shaped beam is solved as follows

$$\begin{aligned} w(\xi )=-\frac{2h}{s_{c-c}^3}\xi ^3 + \frac{3h}{s_{c-c}^2}\xi ^2. \end{aligned}$$

(24)

The (dimensional) suspension length of S-shaped beam is given by Yang (2004) as follows

$$\begin{aligned} S_{c-c}^4=\frac{3}{2}\frac{E_1H^2T^3}{\gamma _s}=\frac{9E_1IH^2}{B\gamma _s}. \end{aligned}$$

(25)

The dimensionless $s_{c-c}=\beta S_{c-c}=\root 4 \of {36h^2/\alpha _r}$ and $s_{arc}=\frac{\sqrt{2}}{2}s_{c-c}$. Equations (21) and (24) are also presented by de Boer et al. (1999). As the two coordinate systems in Fig. 1a and b are different, Eqs. (21) and (24) are the following forms in the coordinate system of Fig. 1a

$$\begin{aligned} w(\xi )=-\frac{h}{2s_{arc}^3}(\xi +l_1)^3 + \frac{3h}{2s_{arc}^2}(\xi +l_1)^2 \quad (arc-shape), \quad w(\xi )=-\frac{2h}{s_{c-c}^3}(\xi +l_1)^3 + \frac{3h}{s_{c-c}^2}(\xi +l_1)^2 \quad (S-shape). \end{aligned}$$

(26)