Abstract
Hard disk drives must be designed to be resistant to operational and non-operational shock (Jayson et al. in IEEE Trans Magn 38(5):2150–2152, 2002). Numerical and experimental results show that “lift-tab separation” and “dimple separation” are two possible failure modes of presently used head suspension assemblies (Murthy in Ph.D. thesis, Center for Magnetic Recording Research, University of California, San Diego, 2007). In addition, “dimple and tongue wear” at the interface of gimbal and dimple are areas of concern in the design and operation of high performance suspensions during shock. In this investigation, an improved numerical model for non-operational shock response of a load/unload hard disk drive is implemented by including design parameters of suspension such as dimple preload, suspension material, dimple height and the surface diameter of the dimple in the model. Results for dimple and lift-tab separation, as well as the maximum impact stress at the dimple region, as a function of preload and suspension design parameters, will be presented.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The shock response of a hard disk drive (HDD) is an important design consideration. A number of studies have been made in the past to study the non-operational shock response. Allen and Bogy (1996) investigated experimentally the effect of high shock amplitude and short shock duration on a hard disk drive and compared their results with a finite element model using ABAQUS. In their model, they considered the effect of both the suspension and the hard disk on the shock behavior and defined contact between slider and disk in terms of gap contact elements. Edwards (1999) developed a model of a 3½ inch hard disk drive using ANSYS. He studied the effect of different shock conditions on the dynamic response of the whole disk drive by varying the contact stiffness of the impact surface. Jayson et al. (2002, 2003) studied the shock response for both non-operational and operational HDDs corresponding to linear and rotary shock inputs using LS-Dyna and developed a correlation between rotary and linear shock test. Murthy et al. (2007) studied the dynamic response of small form factor disk drives with both “thin” and “thick” enclosures due to external vibrations and shock. They performed modal and vibration analysis on both models and investigated the relative on-track and off-track displacement amplitudes of a slider due to shock and vibration excitation. Gao et al. (2006) performed non-operational shock analysis using a multi-body dynamic analysis to determine the shock level which causes the slider to lift off from the disk. They derived the governing equation for the voice coil motor-head actuator assembly system using a Lagrangian formulation and obtained the shock response of the hard disk drive by including the constraint equations between the slider and the disk surface. Luo et al. (2007) found that the lift off height of the slider reaches a peak value as a function of pulse width. Shi et al. (2006) considered a head actuator arm model to analyze the deflection of the tip of the arm relative to the pivot for various input pulse shapes and correlated their experimental results with predictions from numerical simulations.
To improve the performance and to increase the areal storage density, load/unload (L/UL) drives are now widely used. Murthy (2007) studied the L/UL process and investigated the effect of shock input, as well as suspension and gimbal design on the head disk interface. Feliss et al. (2007) tested the shock and vibration response of microdrives during linear and rotary shock using a scanning Laser Doppler Vibrometer and compared their results with a finite element model for both non-operational and operational conditions. In a recent study, Shu et al. (2007) presented the relative displacement between the tip of the actuator arm and the pivot onto which the cantilever arm is fixed as a function of shock amplitude and duration. They verified their numerical simulation using a simplified single degree of freedom model and investigated the relationship between maximum relative displacement and frequency ratio.
In this study, we investigate the effect of dimple preload, suspension material and dimple design on dimple separation, lift-tab separation and dimple-gimbal contact.
2 Numerical model
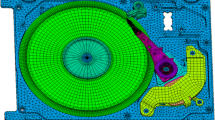
In this paper, a finite element model (Fig. 1) is used, consisting of the actuator arm, the suspension, the head gimbal assembly (HGA), the disk and the enclosure base of the HDD with a ramp attached. The geometry of the model was first created in Pro/E and then imported into HyperMesh for discretization and application of boundary conditions. The slider, the enclosure base of the disk and the ramp are modeled by constant stress solid elements while other components are simulated with Belytschko–Tsay shell elements. The contact pairs created between suspension and gimbal, slider and gimbal, as well as ramp and suspension, are calculated using the penalty method. After preprocessing in HyperMesh, the model is analyzed using LS-Dyna, a commercially available finite element transient solver. Finally, the results are displayed in HyperView.
A typical shock input is shown in Fig. 2. The shock is simulated as half-sine wave acceleration applied at the enclosure base of the hard disk drive. The dimple is semi-spherical in shape. The mesh over the area of dimple is highly refined to allow a detailed study of the contact process occurring at the dimple to tongue interface.
The contact force between the dimple and gimbal is obtained from the numerical model. The stress induced by the impact is an important factor for the reliability of the dimple to tongue interface. To better understand the effect of suspension designs on the maximum contact stress, we simplify the contact between dimple and gimbal as a contact between a deformable sphere and a rigid flat, respectively. The maximum contact stress is obtained from the Hertz solution (Johnson 1985)
where P is the contact force, and r is the radius of the area of contact given by
The equivalent radius R in Eq. 2 is defined by \( 1/R = 1/R_{1} + 1/R_{2} , \) and the equivalent Young’s modulus is given by \( 1/E^{*} = \left( {1 - v_{{_{1} }}^{2} } \right)/E_{1} + \left( {1 - v_{2}^{2} } \right)/E_{2} , \) where R 1 and R 2, E 1 and E 2, υ 1 and υ 2 are the radii, the Young’s moduli and the Poisson ratios of the dimple and gimbal, respectively.
3 Simulation result
3.1 The effect of dimple preload
Figures 3 and 4 show the effect of dimple preload on dimple separation and lift-tab separation, respectively, during a non-operational shock. Negative values in Fig. 3 represent the downward displacement of the gimbal. The dimple preload is modeled as a couple of force between dimple and gimbal. The magnitude of the dimple preload was varied between 1.76 and 3.53 mN. As the preload increases by a factor 2, the maximum dimple separation decreases by approximately 30%, and the maximum lift-tab separation is reduced by roughly 15%, i.e., an increase in dimple preload reduces both the dimple separation and the lift-tab separation during shock. An increased dimple preload could potentially limit further motion of the gimbal, thereby limiting the separation.
In a previous study (Murthy 2007), it was shown that both dimple separation and lift-tab separation increase with the shock level. Figures 5 and 6 show the maximum dimple separation and lift-tab separation with preloads of 1.73 and 3.53 mN, respectively, as a function of shock level. It is apparent that an increase in the preload reduces both dimple separation and lift-tab separation during the shock event.
3.2 Young’s modulus of suspension
Suspensions are made of stainless steel, with a Young’s modulus of approximately 200 GPa. To study the sensitivity of the shock response on the Young’s modulus of the suspension, we have evaluated the shock response as a function of Young’s modulus, keeping all other material properties, such as density and Poisson’s ratio, unchanged. The results for dimple separation, lift-tab separation and the maximum contact stress caused by the impact force as a function of the Young’s modulus are shown in Figs. 7 and 8, respectively.
The results show that an increase in the Young’s modulus of the suspension from 150 to 250 GPa leads to an approximately 24% decrease in the maximum lift-tab separation and an approximately 14% increase in the maximum contact stress. The head gimbal assembly becomes stiffer for an increasing modulus of elasticity.
3.3 The effect of dimple design
Figure 9 shows the parameters of the dimple design considered in our study, i.e., dimple surface diameter (d) and dimple height (h).
Simulation results for the maximum displacement of the suspension are shown in Figs. 10 and 12. The change of the maximum dimple separation and lift-tab separation as a function of dimple diameter is less than 1%. Thus, it is apparent that the dimple surface diameter has little effect on the dimple separation and lift-tab separation. An increasing dimple height, on the other hand, increases the lift-tab separation while reducing the dimple separation (Fig. 12).
The contact stresses for both cases changes significantly with the geometry of dimple (Figs. 11, 13). This is because the radius of the dimple increases with either an increase in the dimple surface diameter or a reduction of the dimple height. As the radius increases, the contact stress decreases. Therefore, an increase in the surface diameter causes a reduction of the maximum contact stress at the dimple area, while an increase in the dimple height leads to an increase of the contact stress.
4 Conclusion
This paper investigates the effect of suspension design parameters on dimple and lift-tab separation and the maximum impact stress in the dimple region. The following conclusions can be drawn from this investigation:
-
(1)
Increasing the dimple preload reduces both the dimple separation and the lift-tab separation during a shock. Therefore a high dimple preload (3.53 mN, based on the range of dimple preload investigated in the paper) is recommended to improve the shock performance of the suspension.
-
(2)
The maximum lift-tab separation decreases when the Young’s modulus of the suspension increases, while the maximum contact stress increases. Within the span of the Young’s moduli studied in this paper, the range between 200 and 250 GPa seems optimal to reduce the lift-tab separation while keeping the increase of the contact stress small.
-
(3)
The dimple surface diameter has little effect on the dimple separation and lift-tab separation. However, an increase in the diameter will reduce the impact stress. In order to minimize the contact stress, a large diameter (200 μm in our study) is recommended.
-
(4)
A decrease in the dimple height will reduce the stress at the dimple/gimbal interface while increasing the dimple separation. From our simulation results, a dimple height ranging from 43 to 53 μm is suggested.
References
Allen AM, Bogy DB (1996) Effects of shock on the head-disk interface. IEEE Trans Magn 32(5):3717–3719
Edwards JR (1999) Finite element analysis of the shock response and head slap behavior of a hard disk drive. IEEE Trans Magn 35(2):863–867
Feliss B, Murthy AN, Talke FE (2007) Microdrive operational and non-operational shock and vibration testing. Microsyst Technol 13(8–10):1015–1021
Gao F, Yap FF, Yan Y, Harmoko H (2006) Shock analysis of non-operating hard disk drives based on a multibody dynamic formulation. Microsyst Technol 12(3):247–257
Jayson EM, Murphy JM, Smith PW, Talke FE (2002) Shock and head slap simulations of operational and non-operational hard disk drives. IEEE Trans Magn 38(5):2150–2152
Jayson EM, Murphy J, Smith PW, Talke FE (2003) Head slap simulation for linear and rotary shock impulses. Tribol Int 36:311–316
Johnson KL (1985) Contact mechanics. Cambridge University Press, Cambridge
Luo J, Shu DW, Shi BJ, Gu B (2007) The pulse width effect on the shock response of the hard disk drive. Int J Impact Eng 34:1342–1349
Murthy AN (2007) Investigation of the effect of shock, vibration, surface texture and surface pattern on the dynamics of the head disk interface. Ph.D. thesis. Center for Magnetic Recording Research, University of California, San Diego
Murthy AN, Pfabe M, Xu J, Talke FE (2007) Dynamic response of 1-in form factor disk drives to external shock and vibration loads. Microsyst Technol 13(8–10):1031–1038
Shi BJ, Wang S, Shu DW, Luo J, Meng H, Ng QY, Zambri R (2006) Excitation pulse shape effects in drop test simulation of the actuator arm of a hard disk drive. Microsyst Technol 12(4):299–305
Shu DW, Shi BJ, Meng H, Yap FF, Jiang DZ, Ng Q, Zambri R, Lau JHT, Cheng CS (2007) Shock analysis of a head actuator assembly subjected to half-sine acceleration pulses. Int J Impact Eng 34:253–263
Acknowledgments
We would like to thank Dr. Hui Li from CMRR for his help and advice with this simulation. We would also like to acknowledge the interest of Mr. M. Hanya of NHK in this research project. In addition, we acknowledge helpful discussions with Dr. Bart Raeymaekers.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Zheng, H., Murthy, A.N., Fanslau, E.B. et al. Effect of suspension design on the non-operational shock response in a load/unload hard disk drive. Microsyst Technol 16, 267–271 (2010). https://doi.org/10.1007/s00542-009-0854-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00542-009-0854-x