1 Introduction

Reducing the flying height (FH) of sliders is a requirement to achieve higher recording densities in hard disk drives (HDD). With certain minimum thicknesses of slider and disk diamond-like-carbon (DLC) overcoats and lubricant films, there is a limit to how low the magnetic spacing can be for a reliable interface. However, the Wallace spacing loss equation indicates that the magnetic signal increases exponentially as a slider’s FH deceases. There are several contact interface designs under consideration for the planned magnetic recording density of 1 Tbit/in2 and beyond in HDD: “wear in”, “proximity”, and “full contact”. It is expected that all of these technologies, except possibly the last one, will rely on an air bearing to support most of the suspension load, while the trailing pad of the slider will be in contact with the disk at the beginning, frequently or continuously. In this sense, the sliders in those head disk interfaces are air bearing sliders with partial contact.

For a partial contact slider, the air shear and friction acting on the air bearing surface (ABS) may cause in-plane vibrations as well as a bouncing vibration of the slider on the disk. The slider’s bouncing vibration may cause an unacceptably large FH variation. The in-plane vibration may also cause a large off-track variance, which reduces the slider’s track following capability. In this paper, we develop a nonlinear dynamic model to numerically analyze the in-plane vibrations of partial contact sliders. In the model, the partial contact air bearing is obtained through the generalized Reynolds equation modified with the Fukui–Kaneko (FK) slip correction together with a recent slip correction for the contact condition. A six-degree-of-freedom (DOF) model of the slider’s motion is proposed to consider the slider’s vibrations in the vertical, pitch, roll, down-track, off-track and yaw directions, the last three of which contribute to the slider’s in-plane vibration. The adhesion, contact and friction between the slider and disk are also considered in this model. Realistic, measured disk track profiles are used in the simulations.

It is found that the in-plane vibrations of the partial contact slider with a micro-trailing pad are dominated by the suspension modes and not air bearing modes. Increasing the suspension damping is critical to minimizing the in-plane vibration amplitudes. The in-plane vibrations are forced vibrations under the slider–disk friction. The disk micro-waviness and roughness can excite the vertical bouncing of the slider, but it may not excite the in-plane vibration. Friction and contact pad size have important effects on the slider’s in-plane vibrations.

2 Air bearing, adhesion, contact and friction models for partial contact sliders

The generalized time-dependent Reynolds equation is used to model the air bearing between the partial contact slider and the disk. The Reynolds equation is often modified using the FK slip correction (Fukui and Kaneko 1988) to account for the rarefaction of the ultra thin air film within the slider/disk spacing. As indicated by Wu and Bogy (2003), the FK correction has an unbounded contact pressure singularity for the air bearing with contact. They proposed a new second order slip model without the pressure singularity, which predicts results not far from the FK correction when the modified inverse Knudsen number is small. For the contact region in an air bearing, Huang and Bogy (1998) adopted in their Monte Carlo method, a no-fly-zone condition, which assumes that air molecules cannot enter a gap smaller than themselves. Here, we combine the FK model and the new second order slip model. When the air film thickness is larger than 0.3 nm, close to the diameter of an oxygen or nitrogen atom, we use the FK model; when it is less than 0.3 nm, we use the new second order slip model to avoid the pressure singularity.

A brief analysis shows that the impact between the partial contact slider and the disk is quasi-static and can be modeled with an elastic contact model based on the static influence coefficient matrix. The CML slider dynamic simulation shows that the impact speed of the slider is on the order of 10−1 m/s. The sliding speed of the slider with respect to the disk, which is proportional to the disk rotation speed and the radial position of the slider, is on the order of 10 m/s. Both speeds are much less than the elastic wave speeds in the disk media. So the slider–disk impact is quasi-static, which means that the deformation is restricted to the vicinity of the contact area and can be obtained through use of static contact theory. Johnson (1985) described a contact model based on influence coefficients from an elasticity analysis of loading on an elastic half-space. This model can be incorporated with the approach that approximates the contact between two rough surfaces as that between a rigid flat surface and an equivalent elastic rough surface. We use this model instead of asperity-based contact models, such as that in the CEB model (Chang et al. 1987), because those models are only valid when bulk deformation and interactions between asperities are negligible. For a partial contact head disk interface (HDI), the flying height at some parts of the ABS might be negative, which means that the distance between those parts of the slider and the undeformed disk surface is less than zero. Under this condition, bulk deformation and interactions between asperities are not negligible.

The adhesion between the slider and the disk is calculated through the modified intermolecular force model (Chen and Bogy 2006), which does not suffer from an infinite repulsion pressure, when the slider and disk are in contact. The effect of the lubricant is included in the model through the choice of the value of the surface energy difference before and after contact. This model is used instead of the asperity-based adhesion models, such as the CEB model, also because of the non-negligible bulk deformation and interactions between asperities.

As to the friction between the slider and disk, we use Coulomb’s law, the product of the normal contract force and a friction coefficient. Asperity-based friction force models, such as the CEB friction force model, are valid for static friction with negligible bulk deformation and interactions between asperities. They may not be the best choice for the dynamic simulation of the partial contact HDI.

All of these models were implemented in the CML slider dynamic air bearing program. The ABS is discretized into small grids, which are approximately parallel to the disk surface with various spacings. The modified Reynolds equation is then discretized using Patankar’s control volume method, and the final discretization equations are solved using the alternating direction line sweep method combined with the full multi-grid algorithm. Then the modified intermolecular force model and the elastic contact model are applied to each grid.

3 Six-DOF slider dynamic model

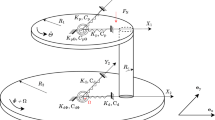
Suppose that the suspension with length, r rotates with an angular velocity, ω and an angular acceleration, a. The suspension is approximated here using six linear springs and six linear dampers in the x, y, z, roll, pitch and yaw directions. The x, y and z directions are shown in Fig. 1, where the xyz coordinate system is attached to the suspension. Let ϕ, θ and β indicate the roll, pitch and yaw angles of the slider’s motion. The position of the suspension load point on the slider’s upper surface is (x 0, y 0, z 0). Let (x c , y c , z c ) indicate the position of the slider’s mass center. If we have obtained the air bearing pressure, p, the adhesion and contact force and moment with respect to the mass center F d and M d , the air shear force and moment F a and M a , the slider–disk friction force and moment F f and M f , then the equations of motion of the slider’s mass center within the xyz coordinate system are,

$$ \begin{aligned} m\ddot{x}_{c} + c_{x} \dot{x}_{\text{o}} + k_{x} x_{\text{o}} & = F_{sx} + F_{fx} + m\omega^{2} r + 2m\omega \dot{y}_{c} \\ m\ddot{y}_{c} + c_{y} \dot{y}_{\text{o}} + k_{y} y_{\text{o}} & = F_{sy} + F_{fy} + mar + 2m\omega \dot{x}_{c} \\ m\ddot{z}_{c} + c_{z} \dot{z}_{\text{o}} + k_{z} z_{\text{o}} & = F_{ 0} + F_{d} + \iint {(p - p_{ 0} ){\text{d}}A}. \\ \end{aligned} $$
Fig. 1
figure 1

Suspension and slider coordinate systems

Full size image

The x′y′z′ coordinate system is attached to the slider’s mass center with x′, y′ and z′ along the slider’s length, width, and thickness directions, respectively. Suppose that the slider’s vibrations in the pitch, roll and yaw directions are very small, then the directions of the x′, y′ and z′ axes are very close to those of the x, y and z axes, respectively. Neglecting the second order terms and using Euler's equations for dynamics of a rigid body, we can approximate the slider’s equations of angular motion as,

$$ \begin{gathered} I_{\varphi } \ddot{\varphi } + c_{\varphi } \dot{\varphi } + k_{\varphi } \varphi + \dot{\theta }\dot{\beta }(I_{\beta } - I_{\theta } ) = M_{d\varphi } + M_{f\varphi } + M_{s\varphi } + \hfill \\ \quad \quad (k_{z} z_{0} + f_{0} )(y_{c} - y_{0} ) + \iint {(p - p_{0} )(y_{c} - y){\text{d}}A} + k_{y} y_{0} z_{c} \hfill \\ I_{\theta } \ddot{\theta } + c_{\theta } \dot{\theta } + k_{\theta } \theta + \dot{\beta }\dot{\phi }(I_{\varphi } - I_{\beta } ) = M_{f\theta } + M_{s\theta } + M_{d\theta } + \hfill \\ \quad \quad (k_{z} z_{\text{o}} + f_{0} )(x_{0} - x_{c} ) + \iint {(p - p_{s} )(x_{c} - x){\text{d}}A} + k_{\text{x}} x_{0} z_{\text{c}} \hfill \\ I_{\beta } \ddot{\beta } + c_{\beta } \dot{\beta } + k_{\beta } \beta + \dot{\phi }\dot{\theta }(I_{\theta } - I_{\varphi } ) = M_{f\beta } + M_{s\beta } + k_{x} x_{0} (y_{c} - y_{ 0} ) \hfill \\ \quad \quad \quad \quad + k_{y} y_{ 0} (x_{ 0} - x_{c} ) \hfill \\ \end{gathered} $$

where I ϕ , I β , and I θ , are the mass moments of inertia of the slider about the roll, pitch and yaw directions, respectively. The slider’s equations of motion show that the in-plane vibration is caused by the air shear and slider–disk friction acting on the ABS. The effect of the load offset, which corresponds the terms k y x 0(y c  − y 0) and k y y 0(x 0 − x c ), can be damped out. The in-plane displacements also have effects on the slider’s movement in pitch and roll directions.

The Newark Beta method is used in the CML dynamic program to solve the six equations of motion of the six-DOF slider. The in-plane vibrations of the slider include the slider’s vibration in the x, y and yaw directions. Let C denote the point at the trailing edge center, and let ψ denote the skew angle. Then the off-track and down-track displacements of the trailing edge center can be expressed as,

$$ \begin{aligned} {\hbox{off}{\hbox {-}}{\hbox {track}}} & = \cos \psi (\left\| {GC} \right\|\sin \beta + y_{c} ) + \sin \psi (\left\| {GC} \right\|\cos \beta + x_{c} ), \\ {\hbox{down}{\hbox {-}}{\hbox {track}}} & = \sin \psi (\left\| {GC} \right\|\sin \beta + y_{c} ) + \cos \psi (\left\| {GC} \right\|\cos \beta + x_{c} ). \\ \end{aligned} $$

4 Dynamic simulations of a micro-trailing pad slider

A micro-trailing pad slider is employed in the simulations. As was found in (Juang et al. 2006), in the contact regime, a slider with a minimized trailing pad incurs smaller short range attractive forces between the slider and disk as well as less contact force. It is a good candidate to be a partial contact slider with small bouncing vibrations and small contact and adhesion forces. The ABS design of the slider is shown in Fig. 2. The steady state minimum flying height of the slider on a flat disk surface is approximately 0.5 nm and the transducer flying height is 2.5 nm. The suspension stiffness parameters are listed in Table 1, which are obtained from the finite element analysis of a suspension model.

Fig. 2
figure 2

Air bearing surface design (unit: mm)

Full size image
Table 1 Suspension specifications
Full size table

4.1 Dynamic response to an initial excitation

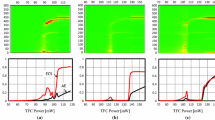
The dynamic response of the micro-trailing-pad partial contact slider to an initial excitation is analyzed first. The slider is loaded onto a flat disk surface from a 2 nm initial FH, steady state pitch and roll angles, zero in-plane displacements and zero yaw angle. Figure 3 shows the time histories of the slider’s minimum FH, pitch, roll, down-track, off-track displacements and contact force and the corresponding power spectra. It is seen that the minimum FH, pitch and roll have only small variations at the beginning. Then the initial excitation is damped out quickly and the slider achieves a steady state with a minimum FH close to 0.5 nm. The corresponding spectra plots show that the minimum FH and pitch vibration have frequency peaks around 8, 126 and 385 kHz with its harmonic frequency around 770 kHz. The roll vibration has two peaks around 8 and 133 kHz. The 1st pitch, roll and 2nd pitch modes of the air bearing are clearly shown. The down-track and off-track vibrations are dominated by only one frequency component around 8 kHz and they are damped out much more slowly than the vertical vibrations. The in-plane suspension force acting on the slider due to the slider’s in-plane displacement exerts a moment with respect to the slider’s mass center, since the load point is on the slider’s upper surface. This moment has components in the pitch and roll directions. So the slider’s pitch, roll and minimum flying height are affected by the slider’s in-plane vibration and they all have the 8 kHz frequency component. This frequency is clearly associated with a suspension mode. However, due to the simple spring-damper model of the suspension, the modes of the suspension cannot be fully shown in the slider’s in-plane vibration.

Fig. 3
figure 3

Dynamic response to an initial excitation of loading the slider from 2 nm onto a flat disk surface

Full size image

If no suspension damping is added in the simulation the slider’s dynamic response changes to that in Fig. 4. The vertical, pitch and roll vibration components with air bearing frequencies are still damped out quickly. However, the low-frequency components of the out-of-plane and in-plane vibrations cannot be damped out. The high damping ratio of the air bearing has no effect on the slider’s in-plane vibrations. This agrees with all of the simulation results with a full suspension model in (Yu et al. 2006), which have zero suspension damping. So the suspension damping is critical to the slider’s in-plane vibration.

Fig. 4
figure 4

Dynamic response to an initial excitation of loading the slider from 2 nm onto a flat disk surface with zero suspension damping in the simulation

Full size image

4.2 Effect of disk micro-waviness and roughness

As shown in (Chen and Bogy 2007), the disk micro-waviness and roughness, which move through the HDI as the disk rotates, can excite the slider’s vertical bouncing vibration. The effect of disk roughness on the slider’s in-plane vibration needs to be investigated. Figure 5 shows a measured track with RMS roughness of 0.2 nm and the power spectrum of the track profile with a speed of 24 m/s, which corresponds to 10,000 rpm. The power spectrum of the disk profile has peaks in a wide frequency range. Figure 6 shows the time history of the slider’s minimum FH, down-track and off-track displacements and contact force on this track and the corresponding power spectra. The slider’s vertical bouncing is excited and its two dominant frequencies are approximately 8 and 400 kHz with its harmonic frequency 800 kHz. The disk roughness moves into the HDI as the disk rotates, so the excitation never stops and the slider’s vertical bouncing vibration is continuous. The excited air bearing frequency is increased due to the slider–disk contact. The power spectra of shear forces in the X and Y directions show that all of the spectrum peaks are less than 0 dB. So the variation of shear force is extremely small. The contact force has frequency content similar to that of the minimum FH. The friction force, which is proportional to contact force, has the same frequency contents. Notice that in this case, the skew angle is zero, so the friction force is mainly along the slider’s length direction, i.e. down-track direction. Therefore, the off-track vibration does not contain the air bearing frequency component and the vibration amplitude is negligible. However, the down-track vibration does not contain the air bearing frequency components, either. This can be simply explained with the steady state response of a one-DOF forced spring mass system. The steady state vibration amplitude is,

$$ \frac{{F_{0} }}{K}/\sqrt {\left (1 - \frac{{f^{2} }}{{f_{n}^{2} }}\right)^{2} + \left (2\varsigma \frac{f}{{f_{n} }}\right)^{2} } , $$

where F 0 is the amplitude of the external force and f is its frequency; K, ζ and f n are the stiffness, damping factor and natural frequency of the system, respectively. Here we take K = 1.316 × 103 N/m, i.e. the X stiffness of the suspension; f n  = 8 kHz, the suspension frequency, and f = 400 kHz, an excited air bearing frequency. Even if we take the damping factor to be zero and the peak-to-peak amplitude of the contact force at 400 kHz to be 0.1 g, then F 0 = 0.1/2 × 0.3 × 9.8 mN =0.147 mN, and the steady state amplitude obtained is approximately 0.05 nm. This small vibration amplitude is still negligible compared with the down-track vibrations shown in Fig. 6. This calculation qualitatively agrees with the experimental analysis of (Kiely and Hsia 2006), in which one of the experimental cases showed that the air bearing pitch modes had amplitudes as large as 20.5 nm in vertical bouncing, but only 1 nm in the down-track vibration and 0.01 nm in the off-track vibration.

Fig. 5
figure 5

Measured track profile and its power spectrum at the disk velocity 24 m/s

Full size image
Fig. 6
figure 6

Time history of the slider on a smooth disk with RMS 0.2 nm and the corresponding power spectrum

Full size image

4.3 Effect of skew angle

It is expected that the component of the friction force along the off-track direction increases from zero and hence the off-track vibration increases, as the skew angle deviates from zero. But the effect of skew angle on slider dynamics interferes with other effects. In simulations, it is difficult to change the skew angle while keeping the slider’s air bearing and static flying height unchanged. Figure 7 shows the time histories of the minimum FH, off-track and down-track displacements of the same simulation case as in Fig. 6, except that the skew angle is changed from 0 to 6.65°. The in-plane vibration amplitudes are increased. This is partially caused by the increased vertical bouncing vibrations and the increased contact force variation, which is due to the change of skew angle. But the off-track vibration amplitude increases by three orders of magnitude. This is caused by the non-zero friction force in the slider’s width direction, due to the non-zero skew angle.

Fig. 7
figure 7

Time history of the slider with a skew angle of 6.65°

Full size image

4.4 Effect of friction

The effect of friction force on the slider’s motion can be analyzed with simulations using different friction coefficients, since Coulomb’s law is used for the friction force. Figure 8 shows the vertical bouncing, contact force, down-track and off-track vibrations of the slider on a smooth disk with friction coefficients 0, 0.3, 0.6, 1 and 2, respectively. Here the skew angle is 6.65°. When the friction coefficient is zero, the initial in-plane vibrations are totally damped out. The reason is that the air shear almost remains constant, and it cannot excite the in-plane vibrations. As shown in (Chen and Bogy 2007), the vertical bouncing vibration is almost not affected by the change of fiction coefficient. However, as the friction force increases, the in-plane vibration amplitudes increase. Here we can roughly conclude that the off-track vibration peak to peak amplitude is on the order of 10 nm and the down-track vibration peak-to-peak amplitude is on the order of 100 nm, when the contact force is less than 0.25 g and the friction coefficient is less than 0.3. So a small dynamic friction coefficient is important for small in-plane vibrations.

Fig. 8
figure 8figure 8

Time history of the slider on a smooth disk on a smooth disk with different friction coefficients

Full size image

4.5 Effect of the micro-trailing pad width

The micro-trailing pad of the slider used in the above simulations has a width of 100 μm. Figure 9 show the vertical bouncing, on-track and off-track vibrations of the slider with micro-trailing pad widths of 100, 80 and 60 μm, respectively. As discussed in (Chen and Bogy 2007), the slider’s vertical bouncing reduces as the pad’s width reduces. Here, the simulations of in-plane vibrations show that down-track and off-track vibrations also decrease. If we check the contact force, we can see that the variation of the contact force decreases as the micro-trailing pad width decreases. A smaller contact pad helps to decrease the vertical bouncing and the variation of contact force; then the variation of friction force and in-plane vibrations are also reduced. This result agrees with the experimental observations in (Xu et al. 2005). On the other hand, the width of the micro-trailing pad should also be large enough to embed the read/write transducer. So an optimized trailing pad size is important for reducing the vertical bouncing and the in-plane vibrations.

Fig. 9
figure 9

Time history of the slider with trailing pad width of 100, 80 and 60 μm

Full size image

5 Conclusions

A six-DOF slider dynamic simulator is developed to analyze the slider’s motion in the vertical, pitch, roll, yaw, length and width directions. The modified time-dependent Reynolds equation is used to model the air bearing and a new second order slip model is used for a bounded contact air bearing pressure. The simulator considers the air bearing shear acting on the ABS and the slider-disk contact and adhesion. Dynamic simulations of a partial contact slider with a micro-trailing pad are carried out. The simulation results show the following,

  1. 1.

    Within the HDI, the slider’s in-plane vibrations are forced vibrations by the air shear and slider–disk friction. The air shear remains almost constant and the in-plane vibration is mainly caused by the slider-disk friction.

  2. 2.

    The in-plane vibrations are dominated by the suspension modes. The air bearing modes and damping do not have much effect on the in-plane vibrations. The damping of the suspension is critical to the decrease of in-plane vibration amplitudes.

  3. 3.

    Disk surface micro-waviness and roughness excite the slider’s vertical bouncing. But the micro-waviness and roughness can not excite the slider’s in-plane vibrations.

  4. 4.

    The slider’s skew angle affects the slider’s off-track vibrations. The change of skew angle can cause a change in the order of magnitude of the off-track vibration amplitude. The skew angle also has an effect on the slider’s flying and contact attitude; accordingly, the vertical and in-plane vibrations are affected.

  5. 5.

    The slider–disk friction is critical to the in-plane vibration, although it does not affect the vertical bouncing. The smaller the slider–disk friction, the smaller the in-plane vibration amplitudes. The dynamic simulator roughly predicts that the off-track vibration peak to peak amplitude is on the order of 10 nm and the down-track vibration peak to peak amplitude is on the order of 100 nm when the contact force is less than 0.25 g and the friction coefficient is less than 0.3.

  6. 6.

    For the micro-trailing pad slider, the slider with a reduced trailing pad width incurs smaller contact force variation, smaller contact force and smaller slider–disk adhesion force. And the vertical and in-plane vibrations are also reduced.