1 Introduction

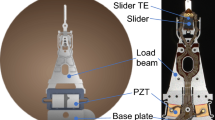
Lateral tape motion (LTM) is the in-plane motion of tape perpendicular to the tape transport direction. LTM is considered to be a disturbance to tape recording systems because it can cause read/write errors and limits the maximum track density that can be achieved. Figure 1a shows a typical tape head. The read/write elements are mounted in a slot in the air bearing surface and are encompassed by two servo heads, as indicated in Fig. 1b. The air bearing surface with the read/write elements is mounted on a bracket, which is connected to the voice coil motor (VCM). A leaf spring on top of the head provides stiffness and alignment to the assembly. The VCM enables motion of the tape head in the direction perpendicular to the tape transport direction for following the lateral displacement of the magnetic tape as it shuttles from the supply reel to the take-up reel.

Fig. 1
figure 1

a Tape head and b read/write elements

Full size image

The lateral position of the head is controlled in a feedback servo loop. Relative lateral displacement between the magnetic tape and the tape head generates a position error signal (PES) from the servo pattern on the tape (Barrett et al. 1998). The servo controller uses the PES to determine the required action of the VCM to avoid track misregistration. The open loop servo bandwidth of the VCM limits the servo controller, mainly due to mass of the actuator and available power. LTM at frequencies higher than the open loop bandwidth of the servo actuator is generally referred to as high-frequency LTM, which cannot be followed by the VCM. Currently, a state-of-the-art VCM has an open loop bandwidth on the order of 750–1,000 Hz.

In this paper, the mechanical design of a dual state actuator tape head is presented. The dual stage actuator design uses a VCM for low frequency track following. A micro-actuator based on a piezo crystal has been implemented for high-frequency track following.

2 Dual stage actuator head

The idea of a dual stage actuator was first introduced in hard disk drive (HDD) technology in 1981. Mori et al. (1991) implemented a piezo (PZT) based rotary micro-actuator at the suspension level. In this work, the VCM was used as a “coarse actuator”, operating primarily with large stroke at low frequencies, while the micro-actuator is used as a “fine actuator”, operating with a small stroke at frequencies higher than the bandwidth of the VCM.

Different types of micro-actuator designs have been proposed in the literature. Koganezawa et al. (1996) designed a micro-actuator that operates at the suspension level of a HDD using a flexural cross-shaped spring. Instead of using “stacked” PZT’s, they used shear-mode PZT crystals (Koganezawa et al. 1999). Evans and Griesbach (1999) presented a piezoelectric micro-actuator design that takes manufacturability and economical considerations into account. They modeled the dynamics of their design and presented two voltage drivers that can be used to drive the actuator. Nakamura et al. (2002) introduced a push–pull multi-layered piggyback PZT actuator that also operates at the suspension level. Their design features a large stroke, combined with a low voltage. While most dual stage designs are PZT-based, some researchers have attempted to manufacture electrostatic micro-actuators. Fan et al. (1995) implemented a milli-actuator, which is a micro-actuator that operates at the slider level instead of at the suspension level. A more in-depth analysis of the milli-actuator proposed by Fan et al., was presented by Hirano et al. (1998). Horsley et al. (1999) used parallel-plate capacitive electrodes to generate an electrostatic force, which was used to drive an actuator. In addition to the designs discussed above, the use of an electromagnetic micro-actuator was investigated by Tang et al. (1995).

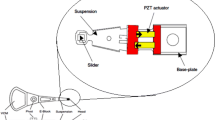
For the design of a dual stage actuator tape head, a similar approach to the one used in HDDs can be used. The main difference, however, is that the tape drive design requires a linear micro-actuator, while HDD designs are based on a rotary micro-actuator. The design presented here attempts to increase the open loop bandwidth of the track-following servo by introducing a secondary actuator stage using a stacked PZT. The micro-actuator serves as a fine-tuning mechanism that can follow high-frequency LTM (>1 kHz) with small stroke. Due to the limited stroke of the PZT, a division of actuation effort is maintained between the VCM and micro-actuator. The dual stage actuator tape head is designed such that the VCM follows the low frequency LTM (<1 kHz) while the micro-actuator follows the high-frequency LTM (>1 kHz). Figure 2 shows a schematic of the dual stage actuator tape head concept. The division of effort increases the overall open loop servo bandwidth. Increasing the open loop servo bandwidth enables an increase in track density, since track misregistration would be reduced.

Fig. 2
figure 2

Schematic of the dual stage actuator tape head concept

Full size image

3 Design

The designed stroke of the micro-actuator is determined by the high-frequency LTM that cannot be followed by the VCM. High-frequency LTM can be characterized by its 6σ-value (INSIC 2005), where σ denotes the standard deviation. Figure 3a shows a typical LTM signal measured from a state-of-the-art commercial tape drive, while Fig. 3b shows the 1-kHz high pass filtered LTM signal. The tape drive was operating at 4 m/s and at a nominal tape tension of 1 N.

Fig. 3
figure 3

a LTM signal and b 1-kHz high pass filtered LTM signal

Full size image

The LTM signal shown in Fig. 3a has been high pass filtered with cut-off frequencies ranging from 0 to 3 kHz. The results are summarized in Table 1.

Table 1 Lateral tape motion versus cut-off frequency
Full size table

It can be observed from Table 1 that 6σ of the high-frequency LTM (>1 kHz) is 1.08 μm. A VCM with a bandwidth of 1 kHz requires a micro-actuator stroke of approximately 1 μm in order to track-follow the LTM that cannot be followed by the VCM. The PZT used in the present design is a 2 mm × 2 mm × 2 mm stacked-type crystal, which gives a 1-μm displacement at 100 V. The constitutive equation that relates the strain ɛ of the PZT transducer to the applied electric field E is given by (Moheimani and Fleming 2006)

$$ \{ \varepsilon \} = [S^{E} ]\{ \sigma \} + [d]\{ E\} $$
(1)

ɛ is the strain tensor, S E is the compliance matrix at constant electric field strength (m2/N), σ is the stress tensor (N/m2), d is the matrix with piezoelectric constants of the PZT transducer (C/N) and E is the strength of the electric field (N/C).

The design of the dual stage actuator tape head is based on the commercial tape head shown in Fig. 1a. Figure 4 illustrates the mechanical design of the dual stage actuator tape head. Figure 4a shows an isometric view, while Fig. 4b shows a side view. All components of the tape head have been identified in the figure.

Fig. 4
figure 4

Mechanical design of dual stage actuator tape head a isometric view and b side view

Full size image

Two L-brackets encapsulate a PZT transducer and form the micro-actuator which drives the second stage of the dual stage actuator tape head. The L-brackets and PZT are attached to each other and to the tape head bracket on one side and the air bearing surface on the other side. The micro-actuator thus creates a relative motion between the tape head bracket and the air bearing surface. Two leaf springs were fixed to the top and the bottom of the air bearing surface, respectively, to provide alignment and stiffness. The leaf springs are very flexible to bend around axis 1 (see Fig. 4a), but inhibit bending in the other directions (2 and 3 in Fig. 4a). Therefore, undesirable motion of the air bearing surface such as warping and torsion motion is minimized.

4 Experimental analysis of the dual stage tape head

Figure 5 shows the experimental set-up to determine the dynamic behavior of the micro-actuator. A chirp signal (Proakis and Manolakis 1988) was injected into the micro-actuator, and the resulting displacement of the air bearing surface was determined with a laser Doppler vibrometer (LDV).

Fig. 5
figure 5

Experimental set-up to determine the frequency response function

Full size image

The ratio of output and input signal yields the frequency response function (FRF), which expresses the response of a dynamic system to a given input as a function of frequency. The coherence function was determined for the FRF and found to be equal to one over most of the frequency range. The coherence function describes the quality of the FRF as a function of the frequency.

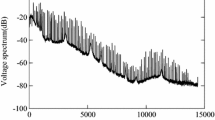
Figure 6 shows the FRF for the case that the PZT micro-actuator is excited. From Fig. 6 we observe that a resonance peak exists at 190 Hz, which is directly followed by an anti-resonance peak. This peak corresponds to the resonance frequency of the VCM. At 1.9 kHz another resonance peak, followed by an anti-resonance peak, is observed. This peak appears to correspond to the frequency where the VCM and micro-actuator are counter-acting each other. The resonance peaks at 3.6 and 5.1 kHz appear to be eigenfrequencies related to the piezo crystal.

Fig. 6
figure 6

Frequency response function

Full size image

5 Model

We have modeled the FRF using system identification techniques (de Callafon et al. 1999). We have fitted a 16th-order ARX model (Auto-Regressive with eXogeneous input) (van den Bosch and van der Klauw 1994) to the experimentally obtained FRF of the micro-actuator, shown in Fig. 6. A discrete-time model P(ω, θ) can be fitted by a least squares minimization (van den Bosch and van der Klauw 1994; Graham et al. 2006), where ω refers to the frequency domain and θ are the system identification parameters. The optimum set of parameters \( \hat{\theta } \) for a dataset of length N can be found as

$$ \hat{\theta } = \mathop {\min }\limits_{\theta } \sum\limits_{k = 1}^{N} {E_{i} (\omega_{k} ,\theta ) \times E_{i - 1} (\omega_{k} ,\theta )} $$
(2)

for which the curve fit error

$$ E_{i - 1} (\omega_{k} ,\theta ) = [P_{0} (\omega_{k} ) - P(\omega_{k} ,\theta )]W_{i - 1} (\omega_{k} ) $$
(3)

is being minimized. Here, E represents the error between the experimentally determined open loop frequency response P 0(ω k ) and the model P(ω k , θ), using a weighting function W i-1(ω k ). The results for both the amplitude and the phase of the system are displayed in Fig. 7. The experimental FRF is shown in solid line, while the model is shown in dashed line.

Fig. 7
figure 7

Frequency response function; experimental (solid line) and model (dashed line)

Full size image

To evaluate the quality of our model, a PES obtained from a state-of-the-art commercial tape drive was injected into the PZT micro-actuator and the response of the air bearing surface was measured with an LDV. Since the micro-actuator serves as a fine-tuning mechanism to follow LTM >1 kHz, we have first high pass filtered the PES at 1 kHz, before injecting it into the micro-actuator. Next, we have injected the same 1-kHz high pass filtered PES into our model and simulated the response of the system. Figure 8 shows both the experimentally obtained (solid line) and simulated response (dashed line) of the micro-actuator as a function of time.

Fig. 8
figure 8

PZT micro-actuator response; experimental (solid line) and model (dashed line)

Full size image

Comparing the experimentally obtained response with the simulated response, very good agreement is observed. In particular, a cross-correlation coefficient between both responses of r = 80% was calculated.

6 Conclusion

We have implemented a stacked PZT as a linear micro-actuator in the design of a dual-stage actuator tape head for high-bandwidth track following. The dual stage actuator tape head could give an increase in track density for future high-performance tape drives. The dynamics of the new actuator were found to be in good agreement with the experimental results.