Introduction

On December 22, 2018, parts of the southwestern flank of Anak Krakatau collapsed and triggered a tsunami, which killed over 400 people on both sides of the Sunda Strait (Grilli et al. 2019; Gouhier and Paris 2019; Williams et al. 2019). Although numerical simulations demonstrated the tsunami hazard associated with a potential lateral collapse of Anak Krakatau (Giachetti et al. 2012), there were no recognised precursors to the failure of the volcano’s flank in 2018, and tsunami waves struck the coastal population without warning. This event emphasises the significant tsunami hazard associated with volcanic sector collapses, as well as the challenges in both forecasting sector collapses and in developing mitigation strategies against resultant tsunami hazards. The scarps of volcanic sector collapses have been identified at more than 400 Quaternary volcanoes and at least 17 sector collapses have occurred since 1600, highlighting the commonness of these catastrophic events (Siebert et al. 1987, 2006). Historic volcanic sector collapses have had volumes between 0.02 and 4 km3 (Day 2015). However, hydroacoustic mapping offshore the Canary Islands has revealed several sector collapse deposits with volumes between 100 and 350 km3; while the Nuuanu landslide offshore Hawaii represents the largest known mass flow event on Earth, with a volume of ~ 5000 km3 (Masson et al. 2002; Hunt et al. 2013; Moore et al. 1989). Sector collapses of coastal or island volcanoes have the potential to trigger devastating tsunamis, which have caused more than 15,000 fatalities since the seventeenth century (Auker et al. 2013; Day 2015). The deadliest historic volcanic landslide-induced tsunamis affected the volcanoes Oshima-Oshima in 1741 (Japan; ~ 2000 casualties), Mt. Unzen in 1792 (Japan; ~ 14,500 casualties) and Ritter Island in 1888 (Papua New Guinea; > 1500 casualties; Day et al. 2015).

The generic numerical tsunami simulations by Giachetti et al. (2012) closely matched the tsunami waves generated by the catastrophic event of December 22, 2018 (Grilli et al. 2019), highlighting the great potential of numerical simulations in tsunami hazard assessment. However, the reliability of numerical simulations depends on the robustness of the input parameters and approximations made by the modelling algorithm. In the case of landslide-induced tsunamis, the most important emplacement parameters—the landslide volume and velocity—are poorly constrained for most tsunamigenic volcanic landslide events. Estimating landslide velocity based on post-slide information is generally difficult and has only been attempted for very few (non-volcanic) slide events (e.g. Grand Banks Slide; Fine et al. 2005). Most volume estimates of volcanic landslide deposits do not distinguish between the initial volcanic slide component (the primary volcanic lateral collapse), which is the most significant and efficient in terms of tsunami generation, and the secondary incorporation or failure of seafloor sediments, which may form a major component of the landslide deposits, but are likely to have less impact on the resulting tsunami (Watt et al. 2012; Karstens et al. 2019). Differentiation of those slide components and reconstructing the dynamics of a volcanic landslide event require detailed information about the internal structure of slide deposits and the failed volcanic edifice. Solely surface-data-based interpretations may significantly miscalculate slide volumes and fail to identify internal subunits indicating multiple slide phases (Karstens et al. 2019), while 2D seismic data are generally affected by method-inherent imaging limitations due to side reflections from transported blocks or complex internal architectures. Therefore, detailed subsurface information, capable of highlighting complex internal deposit structures, erosional features, and spatially variable characteristics, may only be derived from 3D seismic datasets, as shown for volcanic landslide deposits offshore Montserrat (Crutchley et al. 2013; Karstens et al. 2013) and Ritter Island (Karstens et al. 2019).

At Ritter Island, the combined analyses of a 3D seismic dataset with additional 2D seismic and sediment echosounder profiles, sediment samples, and seafloor imagery enabled the reconstruction of the 1888 collapse in great detail (Micallef et al. 2017; Karstens et al. 2019; Watt et al. 2019). The sector collapse of Ritter Island occurred in two phases. The first phase was characterised by deep-seated spreading within the volcanic edifice, which occurred, possibly episodically, over a long period. The spreading continued into the adjacent seafloor sediments, constituting up to 80% of the total sediment volume of ~ 13 km3 mobilised as part of the lateral collapse (Karstens et al. 2019). The second phase of the collapse includes the catastrophic volcanic-flank failure of March 13, 1888, when most of the previously ~ 800 m high volcanic cone slid into the Bismarck Sea, alongside a large proportion of the submarine edifice (Day et al. 2015). This event was highly energetic and most likely accompanied by a phreatomagmatic explosion triggered by the exposure of the hot core of the volcano with seawater and rapid decompression of the volcanic plumbing system (Karstens et al. 2019; Watt et al. 2019). The catastrophic phase of the Ritter Island sector collapse removed about 2.4 km3 of the volcanic cone and was, therefore, far more voluminous than other historic tsunamigenic sector collapse, such as those at Oshima-Oshima (~ 0.4 km3; Siebert et al. 1987), Mt. Unzen (0.34 km3; Siebert et al. 1987) and recently, Anak Krakatoa (~ 0.3 km3; Grilli et al. 2019). Nevertheless, it constitutes a relatively small component of the ~ 13 km3 total volume of the mass movement, which is dominated by material affected by the gradual, deep-seated deformation referred to above.

The 1888 Ritter Island sector collapse triggered a devastating tsunami with maximum tsunami heights of more than 20 m on the neighbouring islands of Sakar, Umboi, and New Britain and was noticed 600 km away from its source (Anonymous 1888; Steinhäuser 1892; Ward and Day 2003). There are detailed eyewitness accounts about the tsunami by German colonists from various settlements on New Guinea and New Britain, which deliver highly valuable far-field information about the propagation of the tsunami (cf. Ward and Day 2003). These eyewitness accounts in combination with the 3D seismic data represent a unique dataset that allow the reconstruction of the emplacement of the Ritter Island sector collapse deposits and the genesis of the corresponding tsunami.

Based on these constraints, the main aim of this paper is to perform coupled numerical landslide-tsunami simulations of the 1888 Ritter Island sector collapse and compare these model results with the historic tsunami observations to achieve a better understanding of tsunami genesis during the event. We use the numerical landslide-tsunami simulation code VolcFlow to perform simulations of various collapse scenarios along two seismically defined slide planes. The shallow slide plane includes solely the failed cone, which was removed during the second, catastrophic phase of Ritter Island’s collapse. In addition to the failed cone, the deep slide plane includes the deformed seafloor sediments in front of the western flank of Ritter, with a total volume of 7.3 km3. These two scenarios allow us to constrain the significance of the involvement of the deformed seafloor sediment in the lower part of the landslide in contributing to tsunami genesis. Furthermore, we evaluate the impact of a potential explosive eruption during the collapse on tsunami genesis. While explosive eruption may trigger tsunamis by a multitude of source mechanisms (the explosive energy of the eruption, caldera subsidence, pyroclastic density currents, subaereal and submarine mass movement), our simulations only attribute the effect of the explosive eruption energy and not the emplacement of potentially associated pyroclastic density currents. Finally, we will discuss the general implications of our simulations on sector collapse-induced tsunamis and discuss their implications for volcanogenic tsunami hazard assessment.

Geological background

Bismarck volcanic arc and Ritter Island

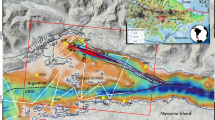
Ritter Island is part of the Bismarck volcanic arc, which is formed by the northward subduction of the Solomon Sea beneath the South Bismarck Sea micro plate and a complex zone of arc-continent collision to the west (Fig. 1b; Woodhead et al. 2010; Baldwin et al. 2012). Ritter Island is located at the boundary between these arc segments and Ritter’s volcanic products are mainly basaltic (Johnson 1977; Woodhead et al. 2010; Watt et al. 2019). The Bismarck volcanic arc is one of the most active volcanic regions worldwide and has hosted several volcanic sector collapses, remnants of which are exposed on the seafloor next to several islands (Silver et al. 2009). Several historic reports describe Ritter Island as a prominent landmark for sailors in the Bismarck Sea (Johnson 2013). These reports include apparent descriptions of Strombolian activity and lava flows reaching the sea in 1699 and 1793, steam and “smoke” in 1835, 1848 and 1887 as well as ash fall from an eruption potentially associated with Ritter in 1878 (Johnson 2013). In 1887, von Schleinitz (published in 1889) mapped Ritter Island and the surrounding islands just 1 year before its collapse and described the island as an almost perfect cone with smoke at its summit. There are no written eyewitness accounts of the catastrophic collapse (as opposed to the tsunami) of Ritter Island on March 13, 1888.

Fig. 1
figure 1

a Map showing the distribution of the deposits of the 1888 Ritter Island sector collapse. b Overview map of the Bismarck Sea and the Bismarck volcanic arc. c Map showing the proximal deposits of the 1888 Ritter Island sector collapse

Full size image

Historic eyewitness accounts of the 1888 Ritter Island tsunami

The arrival of the 1888 tsunami and the resulting destruction were noted in detail in two contemporary reports (Anonymous 1888; Steinhäuser 1892). It has not been possible to determine if the anonymous author made observations alongside Steinhäuser, or if this is an entirely independent source. From these reports, we have information for the three colonial settlements Finschhafen, Hatzfeldthafen and Kelana as well as the west coast of New Britain (Table 1; cf. Ward and Day 2003, for an earlier discussion of these reports). Finschhafen is located 120 km south of Ritter Island and was the main settlement in the region. On March 13, 1888, Steinhäuser (1892) noted a hollow, thunder-like noise before the water in the harbour retreated and then returned with violent force at Finschhafen. He noted three waves, that the time between the lowest wave trough to the highest peak was 4–5 min and that the currents remained strong for 20 min before they normalised 15 min after. The Anonymous source (1888) reported for Finschhafen a thunder-like noise at around 6:30 a.m. and that the sea retreated 5–6 foot (~ 2 m) and returned after 3–4 min and that the sea kept rising and falling in regular intervals until 10 a.m. Both reports note a fine ash fall. The west coast of New Britain lies about 20 km to the east of Ritter Island. The eyewitness accounts for New Britain reported that stripes of land were missing along the coastline, and that the jungle floor was covered with pumice and broken trees (Steinhäuser 1892). Observations at remaining trees indicated a more than 10-m high wave as evidenced by broken branches and fishes spiked on these (Steinhäuser 1892). The second source (Anonymous 1888) reported that the jungle was devastated over 1 km inland and that the wave was at least 12 m high, as indicated by measurements at coastal cliffs. The same anonymous source reported for Kalena (80 km southwest of Ritter Island) that the first of 20 tsunami waves arrived at 6:30 a.m. and inundated 8 m inland. The fourth wave inundated 10 m inland and at the morning of the following day, the entire coast was covered with pumice fragments. At Hatzfeldthafen, about 350 km west of Ritter Island, a shot-like sound was noticed about 6:00 a.m. and the first tsunami wave arrived ~ 6:40 a.m. It was 2 m higher than highest flood mark (Anonymous 1888). The wave retreated and the harbour became dry. Strong tsunami peaks and troughs alternated in intervals between 3 and 4 min until about 9 a.m. and the highest wave had a height of 8 m. There are no detailed reports for the islands Umboi and Sakar, which are closest to Ritter Island. On an expedition 1 year after the collapse, another anonymous source reported that several settlements on the east coast of Umboi were missing, that the settlement Lutherhafen on the northwest coast was abandoned and that hundreds of people lost their life according to a local chief (Anonymous 1890).

Table 1 Tsunami parameters from historic eyewitness accounts based on Anonymous (1888), Steinhäuser (1892) and Ward and Day (2003)
Full size table

3D seismic reconstruction of the 1888 Ritter Island sector collapse

The combination of 2D and 3D seismic data covering the western slope of the failed volcanic cone of Ritter Island and the neighbouring seafloor revealed compressional deformation, which stretches from the volcanic edifice more than 10 km to the west, manifesting as a complex pattern of thrusting and folding (Fig. 2, Karstens et al. 2019). The deformation affects sediments up to 500 m beneath the seafloor at the foot of Ritter Island and is limited by a shear zone rather than a sharp slide plane (Fig. 2). A toreva block, representing an intact remnant of the failed western flank of Ritter Island, also shows internal folding. The folding within the toreva block increases with depth, and thickened packages within the synforms of these folds indicate that the compressional deformation developed over a long period of cone growth and likely occurred episodically (Fig. 2; Karstens et al. 2019). This long-lasting gradual spreading along a deep shear surface defines the first phase of slope instability at Ritter. The second phase comprises the catastrophic collapse of the volcanic cone at March 13, 1888. This collapse occurred along a distinct slide plane, which defines most of the present-day morphology of the Ritter Island collapse scarp. The volcanic cone failed, disintegrated, and travelled west. It did not deposit any intact blocks within the area of the 3D seismic data (except the toreva block). This highlights the highly energetic character of the mobilized mass (Karstens et al. 2019). Watt et al. (2019) inferred that the failed mass must have disintegrated rapidly, and that this efficient fragmentation was likely facilitated by the bedded, clastic nature of the primary edifice. The flow formed a network of erosional channels initiating close to Ritter Island. These channels cut increasingly deep into the underlying compressionally deformed sediment packages and finally merge into one major channel meandering between two volcanic ridges west of Ritter Island (Fig. 2). These observations indicate that the hummocky seafloor topography west of Ritter Island is the result of an interplay between deformation and erosion (Karstens et al. 2019) and does not represent the blocky facies of a debris avalanche (e.g. as observed in the deposits of the 1980 Mt St. Helens collapse and many other debris avalanche deposits; Glicken 1996; Day et al. 2015). When the energetic flow passed the volcanic ridges west of Ritter Island, it travelled as debris flows and turbidites for another 70 km into the basin west of Sakar and Umboi (Fig. 1; Day et al. 2015; Watt et al. 2019). The seismic data do not conclusively show whether the collapse of 1888 solely occurred along the shallow failure plane or if it also involved additional movement along the deep-seated, episodically active shear zone (Karstens et al. 2019). The analysis of pumice fragments within the slide deposits associated with the 1888 collapse indicated that the catastrophic collapse was followed by a magmatic eruption that was most likely submarine (Watt et al. 2019). The timing of this eruption relative to the collapse is unconstrained, but it could potentially have occurred immediately after the collapse. This would be in agreement with reports of washed up pumice, and in this scenario, a submarine eruption may potentially have contributed to the generated tsunami. Regardless of the timing of this magmatic eruption, it is highly likely that a phreatic explosion accompanied the failure of Ritter’s cone, given that the volcano had been active recently and that the collapse cut the central conduit, thus exposing the hot, shallow feeder system to seawater. Explosive activity is potentially consistent with eyewitness accounts suggestive of ash fall and thunder-like noises, and although the precise nature and timing of explosive volcanism accompanying the sector collapse is somewhat uncertain, a volcanic explosion at least warrants consideration as a contributory source to the event’s tsunami. The 1888 Ritter Island sector collapse produced a very complex and spatially heterogeneous landslide, which transformed from a deep-seated deformation-dominated slope instability with pronounced basement incorporation into a highly energetic debris avalanche consisting mainly of scoriaceous cone material that eventually disintegrated entirely into debris flows and turbidites (Karstens et al. 2019; Watt et al. 2019).

Fig. 2
figure 2

a 3D view on the proximal deposits of the 1888 Ritter Island sector collapse. b Seismic profile covering the failed edifice of Ritter Island, the deformed seafloor sediments (yellow), and the volcanic ridge (red) to the west. c Seismic profile through the failed volcanic edifice and the post-1888 volcanic cone. d Seismic profile crossing the toreva block (yellow) and the scoria cone (red) at the toe of the western flank of Ritter Island

Full size image

Methods

Geophysical data

The simulations presented here are based on the interpretation of high-resolution 2D and P-Cable 3D seismic data acquired during expedition SO252 on board of R/V SONNE in late 2016. The P-Cable 3D seismic system consisted of 16 eight-channel streamers. The 250-m-long 2D seismic streamer had 160 channels with a group spacing of 1.56 m. We used two 105/105 cubic inch GI airguns in harmonic mode as the seismic source. The 3D seismic processing steps were source–receiver geometry corrections, bandpass frequency filtering, normal move-out correction, stacking, trace interpolation, and 3D time migration using a constant seismic velocity of 1500 m/s. The 60 km2 P-Cable 3D seismic cube has a lateral resolution of 3.25 m and vertical resolution of approximately 6 m at the seafloor. The 2D seismic processing steps were bandpass filtering, normal move-out correction, stacking, and 2D stolt-migration using a constant seismic velocity of 1500 m/s. In addition, we acquired bathymetric data using Kongsberg EM710 and EM122 multibeam echosounder systems, which were integrated into a bathymetric grid with a lateral resolution of 5 m. This grid was combined with GEBCO bathymetry and SRTM elevation datasets to create the regional grid required for the tsunami simulations.

Numerical landslide-tsunami simulations

VolcFlow

The tsunami genesis by landslides is controlled by the complex interaction between a sliding mass and a body of water. This process has been numerically implemented in a variety of ways, in most cases representing landslide motion either as the movement of blocks, or as Newtonian or non-Newtonian (Bingham rheology) flows (e.g., Løvholt et al. 2015; Smith et al. 2016). Based on the representation of landslide propagation, the initiation and propagation of the resulting tsunami may then be calculated using shallow water wave equations or Boussinesq models (Løvholt et al. 2015). In contrast to this approach, VolcFlow treats the sliding mass as a fluid and is able to couple the interaction between the slide and the water at each time step (details in Kelfoun et al. 2010). VolcFlow has been previously applied to volcanic-landslide tsunami simulations at various other locations, including La Reunion (Kelfoun et al. 2010), Kolumbo (Ulvrova et al. 2016) and Anak Krakatau (Giachetti et al. 2012). Both the Anak Krakatau and Kolumbo case studies produce simulated tsunami heights and propagation patterns that are in-line with historic observations (Ulvrova et al. 2016) or actual events (Anak Krakatau; Grilli et al. 2019), supporting the validity of this approach for simulating volcanogenic landslide tsunamis. VolcFlow models a landslide based on a depth-averaged approximation on a topography-linked coordinate system, using the general depth-averaged equations of mass (Eq. 1) and momentum (Eqs. 2, 3) conservation (Kelfoun and Druitt 2005; Kelfoun et al. 2010, 2011):

$$\frac{\partial h_{a}}{\partial t}\, + \, \frac{\partial}{\partial x}\left( {h_{{\text{a}}} u_{x} } \right) \, + \, \frac{\partial}{\partial y}\left( {h_{{\text{a}}} u_{y} } \right) \, = \, 0,$$
(1)
$$\frac{\partial}{\partial t}\left( {h_{{\text{a}}} u_{x} } \right) \, + \, \frac{\partial}{\partial x}\left( {h_{{\text{a}}} u_{x}^{2} } \right) \, + \, \frac{\partial}{\partial y}\left( {h_{{\text{a}}} u_{x} u_{y} } \right) \, = \, gh_{{\text{a}}} \sin \alpha_{x} - \, \frac{1}{2}k_{{\text{act/pass}}} \frac{\partial}{\partial x}\left( {gh_{{\text{a}}}^{2} \cos \alpha } \right) \, + \frac{T_{x}}{\rho},$$
(2)
$$\frac{\partial}{\partial t}\left( {h_{{\text{a}}} u_{y} } \right) \, + \, \frac{\partial}{\partial y}\left( {h_{{\text{a}}} u_{y}^{2} } \right) \,+ \,\frac{\partial}{\partial x}\left( {h_{{\text{a}}} u_{y} u_{x} } \right) \, = \, gh_{{\text{a}}} \sin \alpha_{y} - \, \frac{1}{2} k_{{\text{act/pass}}} \frac{\partial}{\partial y}\left( {gh_{{\text{a}}}^{2} \cos \alpha } \right) \, + \frac{T_{y}}{\rho},$$
(3)

where ha is the thickness of the flow, u = (ux, uy) is flow velocity, α is slope of the ground, T is retarding stress of the slide material, ρ is the density of the slide (2000 kg m−3), kact/pass is the earth pressure coefficient. The water displacement is modeled as well with equations of mass (Eq. 4) and momentum (Eqs. 5, 6) conservation (Kelfoun et al. 2010):

$$\frac{\partial h_{{\text{w}}}}{\partial t} \, + \, \frac{\partial}{\partial x}\left( {h_{{\text{w}}} v_{x} } \right) \, + \, \frac{\partial}{\partial y}\left( {h_{{\text{w}}} v_{y} } \right) \, = \, 0,$$
(4)
$$\frac{\partial}{\partial t}\left( {h_{{\text{w}}} v_{x} } \right) + \frac{\partial}{\partial x}\left( {h_{{\text{w}}} v_{x}^{2} } \right) + \frac{\partial}{\partial y}\left( {h_{{\text{w}}} v_{x} v_{y} } \right) \, = \, gh_{{\text{w}}} \sin \beta_{x} - \frac{1}{2}\frac{\partial}{\partial x}\left( {gh_{{\text{w}}}^{2} \cos \beta } \right) + \frac{S_{x}}{\rho_{\text{w}}} - 3\frac{\mu_{{\text{w}}}}{\rho_{{\text{w}}} h_{{\text{w}}}} v_{x},$$
(5)
$$\frac{\partial}{\partial t}\left( {h_{{\text{w}}} v_{y} } \right) + \frac{\partial}{\partial y}\left( {h_{{\text{w}}} v_{y}^{2} } \right) + \frac{\partial}{\partial x}\left( {h_{{\text{w}}} v_{y} v_{x} } \right) \, = \, gh_{{\text{w}}} \sin \beta_{y} - \frac{1}{2} \, \frac{\partial}{\partial y}\left( {gh_{{\text{w}}}^{2} \cos \beta } \right) + \frac{S_{y}}{\rho_{\text{w}}} - 3\frac{\mu_{{\text{w}}}}{\rho_{{\text{w}}} h_{{\text{w}}}} v_{y},$$
(6)

where μw is viscosity of water (1.14 × 10–3 Pa s), ρw is the density of water (1000 kg m−3), hw is the thickness of the water column, v = (vx, vy) is the water velocity, and β is the slope of the slide-water surface. The parameter S describes the drag between the water and the landslide and is defined following Tinti et al. (2006). The sudden elevation of the sea level Δz is then defined by an approximation that takes into account volume conservation in 3D (Kelfoun et al. 2010):

$$Dz \, = \, c \, \times \, \frac{V}{d^{2}} \times \, \exp ( - \ln (\pi) \, \times \, d/h_{{\text{w}}} ),$$
(7)

where V is the volume of displaced water and c is a parameter of mass conservation. The parameter d is the distance between the water surface and the volume change at the seafloor.

VolcFlow allows adjustment of the flow behaviour of the landslide mass by varying the rheological parameters collisional stress, density, and yield strength. There is no information about the rheological properties for any phase of the landslide formed by the 1888 Ritter Island sector collapse. Thus, we implemented rheological parameters tested by sensitivity analyses for previous landslide-tsunami case studies conducted with VolcFlow. To change the dynamic properties of the flow, we varied the yield strength between 10,000 and 100,000 Pa for our simulations, while the collisional stress (0.001 Pa s; e.g. Giachetti et al. 2012) and the density of the flow (2000 kg/m3; Kelfoun et al. 2010) were kept constant. The yield strength values are in the same order as used in the VolcFlow simulations for La Reunion (Kelfoun et al. 2010) and Anak Krakatau (Giachetti et al. 2012), which used yield strengths between 20,000 and 50,000 Pa and 5,000 and 10,000 Pa, respectively in their constant stress models. The deep slide plane simulations aim to test the effect of the deep-seated deformation with very limited lateral transport of material, which requires higher yield strengths than 50,000 Pa. At the same time, the geophysical observations indicate that sliding mass was channelized in between the volcanic ridges west of Ritter rather than travelling above these, which already occurred during simulations with 10,000 Pa. Therefore, we did not lower the yield strength below this value in any simulation. VolcFlow uses two surfaces, the pre-slide topography and the slide plane, as input parameters for the simulations (Fig. 3a). Based on previous interpretations (Karstens et al. 2019), we defined two slide scenarios using the present-day seafloor with the surficial exposed failure plane for our “shallow slide plane scenario” and the deep shear zone for our “deep slide plane scenario” (Fig. 3b, c). We reconstructed the pre-slide topography based on a combination of geophysical data and historic accounts about the shape and height of the island (comparable to the approaches by Johnson 1987; Ward and Day 2003; Day et al. 2015). For this purpose, we used a grid of the present day bathymetry and removed the slide scarp including the toreva block. We then extracted contour lines in 50 m intervals between 450 and 800 m below sea level and calculated fitted ellipsoids to fill the gaps within the slide scarp. For shallower depths, the ellipsoid fitting was not possible, because too much of the cone was missing. We then used the ellipsoid parameters of the 450 m below sea level contour line and extrapolated the ellipsoids for the contour lines from 400 m below sea level to 800 m above sea level using a constant slope angle (Fig. 3a).

Fig. 3
figure 3

a Reconstruction of the pre-slide topography of Ritter Island. Dashed rectangles show zoom-ins of an area that highlights the difference between the shallow and the deep slide plane. b The present day seafloor topography representing the shallow slide plane. c 3D seismic reconstruction of the deep slide plane. Dashed black line indicates the location of profiles (P1–P2) shown in d. d Profiles crossing the pre-slide topography, the shallow and deep slide planes at the same location

Full size image

To simulate the impact of a potential explosive eruption during the collapse of Ritter Island, we followed the approach of Ulvrova et al. (2014,2016), who simulated the tsunami wave of a submarine explosion by an initial water displacement η representing a crater-rim-shaped water undulation, which is defined as:

$$\eta = \eta_{0} \left( {2\left( {r/R} \right)^{2} - \, 1} \right)\quad if \, r \le R,$$
(8)
$$\eta = 0,\quad {\text{ if }}r > R,$$
(9)

where η0 is the initial height of the crater-shaped water wave, r is the horizontal distance from the explosion center and R is the radius of the initial water crater rim, which is assumed to be equal to the radius of the crater formed by the eruption (Ulvrova et al. 2014). η0 can be approximated using an equation by Le Mehaute and Wang (1996):

$$\eta_{0} = \, f \, E^{0.24} ,$$
(10)

where f is a scaling factor [0.014 for small explosions, which is the case for Ritter following Le Mehaute and Wang (1996) and Ulvrova et al. (2014)] and E is the explosion energy, which can be quantified following Sato and Taniguchi (1997):

$$E \, = \, 3.56 \, \times \, 10^{7} R^{3} .$$
(11)

In the case of Ritter, we assume a maximum crater radius of 750 m based on seismic data (Fig. 2c), which results in an initial height of the tsunami wave of ~ 107 m. The impact of an explosive eruption was integrated in the simulations by adding the initial water displacement η to the water wave field from the landslide-tsunami simulations at time steps, when the central conduit of Ritter Island becomes exposed to seawater (between 60 and 90 s).

In total, we performed 19 simulations with various grid sizes, extents and simulation durations. The first set of simulations aimed to limit the parameter space of the yield strength by comparing the flow behaviour with the geophysical observations of the 1888 Ritter Island landslide. For this purpose, we used a grid size of 100 m and calculated the distribution of the landslide deposits using yield strength values between 10,000 and 100,000 Pa for both slide planes (S1–S12 in Table 2).

Table 2 Simulation scenarios with applied parameters
Full size table

We ran simulations for the “shallow slide plane scenario” assuming that solely the catastrophic failure of the volcanic cone contributed to tsunami genesis and simulations for the “deep slide plane scenario”, which includes the deformation of the basin-filling sediments. The landslide volume of the “shallow slide plane scenario” is 2.59 km3, while the “deep slide plane scenario” has a volume of 7.34 km3. The volume of the “deep slide plane scenario” is smaller than the seismically constrained volume of 9.2–11.6 km3 (Karstens et al. 2019), whereas the volume simulated in the “shallow slide plane scenario” is very similar to the seismically constrained 2.4 km3. The smaller volume for the “deep slide plane scenario” is mainly the result of geometrically adjusting the deep slide plane to combine the seismically constrained, buried part and the bathymetrically constrained, exposed part of the slide plane as well as to extend the slide plane margins towards the seafloor. Based on the results of these simulations (Sect. 4.1), we limited the parameter space for both slide plane scenarios and performed six simulations (S13–S18 in Table 2) using a grid size of 200 m for a larger area (including the coast of New Guinea) to evaluate the effects of various input parameters and of an explosive eruption on tsunami genesis. Finally, we performed one simulation (S19) using a grid size of 200 m covering an even larger area of the Bismarck Sea including Hatzfeldthafen in the northwest and Finschhafen in the southwest to be able to compare eyewitness accounts from these locations to the simulation results.

Results

Landslide emplacement and deposit distribution

The landslide simulations for the “shallow slide plane scenario” resulted in the disintegration of Ritter Island’s volcanic cone (Fig. 4). The failed cone transformed into a flow, which travelled on top of the seafloor topography and was emplaced in the basin between Ritter Island and the volcanic ridges to the west, and beyond this constriction. Variation of the yield strength from 10,000 to 100,000 Pa shows that landslide mobility decreases as expected with increasing yield strength (Fig. 5a–d). For the simulations using yield strength values of 10,000 and 20,000 Pa, the landslide passes the volcanic ridges west of Ritter Island and enters the basin west of Umboi and Sakar, while the landslide remains in the basin between Ritter Island and the volcanic ridges for higher yield strength values. For the simulation using 100,000 Pa, the slide does not even pass the scoria cone at the foot of the western flank of Ritter Island. The landslide simulations for the “deep slide plane scenario” have similar results. Yield strength values of 10,000 and 20,000 Pa result in flows passing the volcanic ridges west of Ritter Island, while the slide mass remains in the basin east of the ridges for simulations with higher yield strength values (Fig. 5e–h). The simulations with the deeper slide plane generally result in the transport of more material over longer distances compared to the simulations with the shallow slide plane. The deposits within the basin between Ritter Island and the volcanic ridges are generally 100 m thicker for the deep slide plane than for the shallow slide plane, which reflects the depth and volume differences between both slide surfaces. At the same time, it indicates that the amount of deposited material within the proximal slide region is quite similar in both scenarios. The simulations for both slide plane scenarios show that the material transport is controlled by the constrictions formed by the volcanic ridges and cones west of Ritter Island. Seismic observations (Karstens et al. 2019) indicate that the material above the deep slide plane was deformed but remained broadly in situ across this proximal region, immediately west of Ritter Island. We infer that a high yield strength is thus appropriate to capture the distribution of mass for this portion of the landslide. For the shallow slide plane scenario, all field observations indicate that the 1888 Ritter cone collapse formed a highly mobile flow, reaching beyond the volcanic ridges, and a low yield strength value is thus appropriate for this scenario. Therefore, we reduced the parameter space for the yield strength to 10,000—50,000 Pa for the “shallow slide plane scenario” and 20,000–100,000 for the “deep slide plane scenario” for the tsunami analysis.

Fig. 4
figure 4

3D view of the simulated collapse of Ritter Island along the shallow slide plane

Full size image
Fig. 5
figure 5

Maps showing the landslide distribution of the 1888 Ritter Island sector collapse using the shallow (a–d) and the deep slide plane (e–h)

Full size image

Tsunami simulations

The landslide-tsunami simulations aimed to test the influence of various yield strength values, the depth of the slide plane (deep versus shallow scenario) and the timing of a potential explosive eruption on the development of the 1888 Ritter Island tsunami. The modelled tsunami waves generated at Ritter reach the coast of Sakar and Umboi within minutes and result in maximum tsunami heights of ~ 100 m on Sakar and ~ 70 m on Umboi in all simulations (Figs. 6a, 7). The tsunami reaches New Britain within 15 min and results in maximum tsunami heights of ~ 11 m for simulations using the deep slide plane (independent of the chosen yield strengths between 20,000 and 100,000 Pa) and more than 20 m for the shallow glide plane (for yield strengths of 20,000 and 50,000 Pa) (Fig. 6b). This difference is due to a single spike-like wave peak of the second wave crest in the simulations for the shallow slide plane. This spike is the only major difference between the simulations with the shallow slide plane and those with a deep slide plane and develops every time regardless of the chosen yield strength. However, the amplitude of the spike increases with increasing yield strength and it does not result in a significant increase of the maximum tsunami height at New Britain for the 10,000 Pa simulation. The tsunami height, arrival time and period appear to be generally independent of the chosen yield strength values at all three virtual tide gauge locations and for both slide plane scenarios. The addition of the wave generated by a submarine explosion slightly increases the maximum tsunami height at New Britain (less than 7%) and the heights of the second and third waves at Umboi and New Britain. The explosion is visible as an additional tsunami impulse radiating from the explosion point, and superimpose on the waves generated by the landslide (Fig. 7c).

Fig. 6
figure 6

a Simulation of the propagation of the 1888 Ritter Island tsunami. b Virtual tide gauges at New Britain, Kelana and Finschhafen for simulations with various yield strength values for the shallow and the deep slide planes

Full size image
Fig. 7
figure 7

a Virtual tide gauges at Sakar, Umboi and New Britain for simulations with an explosive eruptions after 60 s and 90 s as well as without an explosion. b Propagation of the 1888 Ritter Island tsunami without an explosive eruption. c Propagation of the 1888 Ritter Island tsunami with an explosive eruption after 90 s

Full size image

Based on these observations, we modelled the tsunami propagation for a larger area (including Hatzfeldthafen) using a yield strength value of 20,000 Pa, a failure on the shallow slide plane alone, and no explosion (Fig. 8). The tsunami from this simulation arrives at Kelana about 20 min after the collapse and had a maximum tsunami height of 5 m. The simulated leading wave arrives at Finschhafen about 30 min after the collapse, with oscillations between − 1.5 and 1.5 m. The simulated tsunami arrives at Hatzfeldthafen about 50 min after the collapse and has a maximum tsunami height of about 6 m. The simulated tsunami consists of two main waves followed by several smaller wave peaks, and the wave period increases with distance from Ritter. The maximum tsunami height reaches or exceeds 4 m for most of the coastline of northern New Guinea and locally reaches heights of more than 8 m (Fig. 8a). The simulations indicate a tsunami inundation of more than 1 km for the relatively flat north coast of Umboi and up to 500 m for the steeper coastlines of Sakar and western New Britain.

Fig. 8
figure 8

a Map showing the maximum tsunami height for simulation S19 of the 1888 Ritter Island tsunami. b–e Virtual tide gauges and the tsunami heights (pink squares) and arrival times (dashed lines) from historic eyewitness accounts

Full size image

Discussion

The effect of the slide parameters on tsunami genesis

Previous studies of tsunamis generated by submarine landslides (volcanic and sedimentary) indicated that landslide volume and emplacement velocity are the primary controls of tsunami magnitude (e.g., Løvholt et al. 2005). Tsunami genesis is also affected if the slide emplacement is subdivided into multiple, temporally separated slide stages, which may reduce the resulting tsunami magnitude significantly (Løvholt et al. 2005). Watt et al. (2012) have shown that the failure and incorporation of seafloor sediments, triggered by the emplacement of a primary volcanic landslide, is likely to be a relatively minor additional component to the magnitude of the associated tsunami. This is an important consideration, when reconstructing tsunami heights from landslide deposit volumes, because the final deposit may include a substantial proportion of incorporated material, distinct from the primary collapse. For the Ritter Island sector collapse, it is possible to constrain two scenarios for the tsunamigenic phase of the collapse, which differ by limiting the failure to the volcanic cone or by also including the deep-seated deformation of seafloor sediments that extends across the basin west of the volcano (and which comprises ~ 2/3 of the total slide volume). The seismic data from Ritter cannot reveal whether the catastrophic phase of collapse was strictly limited to the shallow slide plane (i.e. the volcanic cone) or included additional movement and deformation of the basin-filling sediments along the deeper plane as well (Karstens et al. 2019). In either case, a single tsunamigenic phase of movement is indicated by the observations of one wave train associated with the 1888 Ritter Island collapse (Day et al. 2015). The gentle folding of the confined package of basin-filling sediments above the deep slide plane suggests that the rate of movement was likely low, and did not result in substantial displacement of the overlying water column (since the mass was not evacuated above this basal plane). This implies that this phase of landslide movement, even if it accompanied the catastrophic stage of collapse, was likely much less important for tsunami generation compared to the disintegration of the volcanic cone along the shallow slide plane. The failure mass was affected by a complex transition from a debris avalanche, to debris flow and turbidites (Watt et al. 2019), and the proximal deformation along the deep-seated slide plane is fundamentally different (Karstens et al. 2019). The different styles and rates of movement cannot be captured in the tsunami simulations, because it is not possible to choose different parameters for the two parts of the failure mass. The combined slide emplacement, therefore, had to be approximated in the model by estimating bulk properties (yield strength and slide plane geometry for the sliding mass) that result in the closest match between calculated and observed landslide deposits. However, this inevitably simplifies the pattern of movement and mass distribution for the deep slide plane scenario.

The landslide simulations reveal that yield strength and the slide plane geometry have a strong impact on the mobility of the landslide (Fig. 5). For both slide planes, the simulated slide run-out varies between ~ 5 km (for a yield strength of 100,000 Pa) to over 25 km (for a yield strength of 10,000 Pa), while the deep slide plane simulations result in slightly longer run-out distances for equivalent yield strengths (Fig. 5). A high mobility is in agreement with the transport of the debris flows and turbidites in the distal parts of the slide from the cone collapse (shallow slide plane scenario). However, the primary goal of our simulations was to evaluate the range of possible tsunami generating scenarios at Ritter, rather than the simulation of mass distribution beyond the volcanic ridges. Therefore, we focused on simulations with bulk yield strength values of 20,000 and 50,000, representing intermediate values between a higher bulk yield strength, which appeared more plausible for simulating the whole slide mass in the “deep slide plane scenario”, and a lower bulk yield strength, which better represents the mass distribution originating solely from the failed cone in the “shallow slide plane scenario”. The tsunami simulations reveal that the deep and the shallow glide plane scenarios result in very similar tsunami heights. Lower yield strengths appear to produce slightly lower tsunami amplitudes, but this effect is not consistent (e.g. deep slide plane results for Finschhafen in Fig. 6b) and the impact of yield strength alone on tsunami genesis may generally be considered minor for our simulations (Fig. 6). This seems surprising at first glance, because landslide volume and emplacement velocity are normally considered the primary controls on landslide-induced tsunami genesis (Løvholt et al. 2005). However, the variation of yield strength and the slide plane geometry primarily affect the transport of material from the toe of the volcano towards and beyond the volcanic ridges west of Ritter Island. The collapse of the cone itself is the most significant component of tsunami generation within the model and triggers the primary tsunami impulse. The magnitude of the wave generated by the cone collapse is barely affected by the yield strength and the variations of the slide plane depth at the toe of the volcano across the range of modelled scenarios. VolcFlow treats the sliding mass as a liquid. This reduces the effect of the slide plane geometry on the interaction between the failing volcanic cone and the water column. While a flow-like behaviour is the most plausible emplacement scenario for the transport of the failed cone in the distal region beyond the volcanic ridges, it seems far more likely that the initial movement along the shallow glide plane occurred as a more intact mass, and that this initial stage, prior to disintegration, may be better represented as a block. Nonetheless, the tsunamis in our simulations are similar in amplitude to earlier simulations treating the collapsing cone as blocks (Ward and Day 2003).

Our simulations indicate that the total slide volume (i.e. the entire volume of material mobilised by the event, which may include more gradual deformation or secondary seafloor failures) and mobility are not always the primary controls of landslide-induced tsunami magnitude by volcanic sector collapses. In case of Ritter Island, the position and geometry of the slide plane leads to an almost vertical drop of the volcanic cone into the sea. This is the primary control on the main tsunami impulse and it is the volume of this particular component of the landslide, and its initial acceleration, that exerts the main control on tsunami magnitude in the modelled scenarios. This has implications for reconstructing tsunami heights of palaeo sector collapses as it adds a further complication to the already difficult task of differentiating between primary volcanic and secondary sedimentary slide volumes, and reconstructing the number of emplacement phases. The submarine mobility of the slide after it surpassed the toe of the volcano after the initial failure appears less important for cases like Ritter Island, and likely also for events such as the recent lateral collapse of Anak Krakatau. Our simulation results highlight the importance of constraints on the failure and emplacement characteristics of volcanic sector collapses, which can only be obtained by having internal structural information through seismic imaging as well as subaerial constraints of the slide plane geometry, especially for collapse events that span the subaerial-submarine boundary.

The effect of an explosive eruption on tsunami genesis

Explosive eruptions are considered the most common source mechanism for volcanogenic tsunamis (Paris et al. 2014; e.g. the tsunami associated with the 1650 Kolumbo eruption, Ulvrova et al. 2016) and represent a common process during volcanic sector collapses (e.g. Mt. St Helens, Glicken 1996; Anak Krakatau, Grilli et al. 2019; Wiliams et al. 2019). The analysis of pumice fragments entrapped in distal deposits of the 1888 Ritter Island collapse (Watt et al. 2019), the presence of a crater-like depression beneath the post-1888 cone (Fig. 2; Karstens et al. 2019) as well as historic eyewitness accounts that report a loud noise suggest that the 1888 Ritter Island sector collapse was also accompanied by an explosive eruption. The tsunami genesis by submarine eruptions is controlled by the displacement of the water column and the resulting tsunami is primarily dependent on the released energy, which can be approximated by the crater radius (Ulvrova et al. 2016). In case of Ritter, the seismic data constrain these parameters and yield a maximum height of the crater-mimicking initial tsunami wave of ~ 107 m. VolcFlow cannot incorporate representations of submarine explosive eruptions and thus we superimposed the initial tsunami impulse onto the tsunami wave field from the landslide simulations. This approach is a simplification, because it ignores the complex coupling between landslide emplacement and the eruption, which may have amplifying or weakening effects on the tsunami and the slide dynamics, but is nevertheless useful to make a first-order assessment of the potential tsunamigenic contribution of a shallow explosive eruption. Most crucially, our approach assumes that the two processes were closely spaced in time, such that both contributed constructively to simultaneous tsunami generation. This seems plausible as the eruption in this scenario is triggered by the exposure of the hot interior of the volcano by the removal of the overburden. In the case of Mt. St. Helens, the eruption followed unroofing almost simultaneously, although the collapse in that case was triggered by a very shallow intrusion of magma, and we cannot determine if a similar process was likely to have been involved in the Ritter collapse.

The simulations reveal that the tsunami phase, period and duration are only slightly affected by a potential eruption, regardless of its timing (Fig. 7). The tsunami signal of the explosive eruptions is clearly detectable in the modeled scenarios on the New Britain shoreline, where it affects the height of the second wave peak and increases the maximum wave height by less than 1 m (at the location of the virtual tide gauge offshore New Britain). Therefore, it is not possible to use the historic tsunami reports to confirm or rule out the existence or timing of an explosive eruption during the 1888 Ritter Island sector collapse. In summary, our simulations suggest that the effects of an explosive eruption on the resulting tsunami would have been only minor for the 1888 Ritter Island tsunami. This conclusion may not necessarily be transferable to other sector collapse events, and a stronger eruption during a less tsunamigenic sector collapse (e.g. a small volume cone failure) may be more important for the resulting tsunami than the landslide. Therefore, the effects of volcanic explosions should not be ignored in tsunami reconstructions and hazard assessment and require further exploration.

Comparison between simulation results and historic eyewitness accounts

The comparison between the modelled tsunami propagation and the historic eyewitness accounts requires caution as both have significant limitations. The numerical simulations were based on the assumptions and parameter uncertainties discussed above and the bathymetric data have comparably poor resolution in wide parts of the study area. This is especially the case for the Dampier Strait between Umboi, New Britain and New Guinea, where shallow water depths significantly decelerate the propagation of the tsunami wave (Fig. 6). The satellite-derived bathymetric data show several depressions in the Dampier Strait. If these are real (e.g. representing channels, rather than artefacts), tsunami propagation might have been substantially quicker and more efficient through the Dampier Strait. Bathymetry is a key parameter for the propagation of tsunami waves and the topography of the shelf may significantly affect local tsunami heights by focusing energies of superimposing waves, which has been shown for various tsunami events (e.g. the 1998 Papua New Guinea tsunami, Matsuyama et al. 1999; the 2004 Sumatra tsunami, Ioualalen et al. 2007). The single spike-like wave in our deep-slide plane simulations for the virtual tide gauge offshore New Britain is an example of the effect of wave superposition (Figs. 6b, 8c). The spike is not observed at any of the other virtual tide gauges and only for the deep slide plane simulations, highlighting the strong impact of wave superposition on local tsunami heights. Another limiting factor is the gridding of the data, which results in average depth values within a grid cell, which may be very different compared to the real topography at the observation points. Simulations for the 2004 Sumatra tsunami have shown that the grid size itself has an impact on the validity of the simulation results (Ioualalen et al. 2007). This effect appears to be less important for our simulations, which result in very similar results regardless of whether grid size values of 100 m or 200 m are chosen (at least at the locations of our virtual tide gauges). Also, the eyewitness accounts have limitations, as they may be incomplete, subjective, exaggerated, or derived from secondary sources. The approximations of the tsunami heights and arrival times should, therefore, be treated with caution.

Nonetheless, our simulations are in good agreement with the eyewitness accounts (Fig. 8). The simulated tsunami arrived after ~ 20 min in Kelana, after ~ 30 min in Finschhafen and after ~ 50 min in Hatzfeldthafen. The reports about the arrival times of the tsunami have to be treated with caution, because in 1888 the clocks at different locations were not necessarily synchronized, and a statement like “6:30 a.m.” may well be rounded by the eyewitness or the author of the historic report. Using Finschhafen as reference site, the differences of the observed and modelled tsunami arrival times for Kalena (tsunami arrival at the same time as Finschhafen; Anonymous 1888) and Hatzfeldthafen (about 10 min after Finschhafen; Anonymous 1888) are only 10 min off, which is surprisingly accurate, given the vague time information in the reports. The time between the reported shot-like noise and the arrival of the tsunami wave in Hatzfeldhafen was about 40 min (Anonymous 1888). Considering a distance of ~ 350 km between Hatzfeldthaven and Ritter Island, a speed of sound of 1236 km/h, and that the creation of the sound directly accompanied the collapse, the noise of an eruption would have reached Hatzfeldthafen after 17 min, while the simulations indicate a tsunami travel time of ~ 50 min (Fig. 8). The resulting time gap of 33 min is in broad agreement with the 40-min time gap from the historic reports (keeping in mind all previous mentioned uncertainties related to eyewitness accounts and numerical simulations).

Also, the simulated tsunami heights fit the reports well. The historical observations report a maximum tsunami height of 12–5 m for New Britain and 7–8 m for Hatzfeldthafen and a maximum sea-retreat of 1.5–1.8 m for Finschhafen. These accounts are in good agreement with the simulations resulting in a maximum tsunami height of 11–22 m for New Britain, 6 m for Hatzfeldthafen and a maximum sea retreat of 1.5 m for Finschhafen (Fig. 8). The 22 m maximum tsunami height at New Britain was only produced in the shallow slide plane simulations and was most likely the result of wave superposition at the location of the virtual tide gauge. At the same time, the tsunami height observations are not well constrained for New Britain as they rely on observations days after the collapse and their exact location is unknown (Steinhäuser et al. 1892). The observation that the first wave peak at Kelana was not the largest, as well as wave periods of 6–10 min, are in agreement with our simulation results. The comparison between the simulation results and the eyewitness accounts highlights that historic eyewitness accounts represent an important source for testing numerical simulations and thus provide important input for simulation-based tsunami hazard assessment.

Conclusions

3D seismically constrained numerical simulations of the 1888 Ritter Island sector collapse result in a tsunami wave field, which affects the Bismarck Sea and reaches New Britain and the north coast of New Guinea. Simulations using a shallow slide plane and simulations using a deep slide plane result in very similar tsunami wave fields, indicating that tsunami genesis was primarily controlled by the catastrophic collapse of the volcanic cone. The deeper-seated deformation or incorporation of seafloor sediments at the toe of the volcano had no significant effect on tsunami heights or waveforms in our simulations. The simulations indicate further that the mobility of the failed mass, which in our simulations is captured by a range of yield strength values, has a major impact on the distribution of the landslide mass and its deposits, but only a small impact on the tsunami heights. Additional simulations indicate that an explosive eruption, if it accompanied the Ritter Island collapse, is likely to have had only a minor impact on the resulting tsunami. These combined observations show that tsunami genesis during the Ritter Island sector collapse was primarily caused by the displacement of the water column by the collapsing cone, which spanned the subaerial-submarine boundary because of the failure plane geometry and had a high initial acceleration. Slide volume and velocity are generally considered the primary parameters of tsunami genesis. However, our simulations indicate that the total slide volume (as inferred from the final deposit, and, therefore, representing the total volume mobilised by the event) is not necessarily a scalable parameter for the resulting tsunami height and that the geometry of the slide plane and especially its position in relation to the sea surface play a very important role. Our tsunami simulation results are in good agreement with historic eyewitness accounts with regards to timing, height and waveform of the tsunami. This study highlights that numerical landslide-tsunami simulations are capable of adequately reproducing real landslide-induced tsunami events and represent a valuable tool for tsunami hazard assessment.