Crustal and uppermost mantle S-wave velocity below the East European Craton in northern Poland from the inversion of ambient-noise records

Abstract

The P-wave velocities (V_p) within the East European Craton in Poland are well known through several seismic experiments which permitted to build a high-resolution 3D model down to 60 km depth. However, these seismic data do not provide sufficient information about the S-wave velocities (V_s). For this reason, this paper presents the values of lithospheric V_s and P-wave-to-S-wave velocity ratios (V_p/V_s) calculated from the ambient noise recorded during 2014 at “13 BB star” seismic array (13 stations, 78 midpoints) located in northern Poland. The 3D V_p model in the area of the array consists of six sedimentary layers having total thickness within 3–7 km and V_p in the range 1.85.3 km/s, a three-layer crystalline crust of total thickness ~ 40 km and V_p within 6.15–7.15 km/s, and the uppermost mantle, where V_p is about 8.25 km/s. The V_s and V_p/V_s values are calculated by the inversion of the surface-wave dispersion curves extracted from the noise cross correlation between all the station pairs. Due to the strong velocity differences among the layers, several modes are recognized in the 0.021 Hz frequency band: therefore, multimodal Monte Carlo inversions are applied. The calculated V_s and V_p/V_s values in the sedimentary cover range within 0.992.66 km/s and 1.751.97 as expected. In the upper crust, the V_s value (3.48 ± 0.10 km/s) is very low compared to the starting value of 3.75 ± 0.10 km/s. Consequently, the V_p/V_s value is very large (1.81 ± 0.03). To explain that the calculated values are compared with the ones for other old cratonic areas.

Introduction

The East European Craton (EEC), mainly Archaean and Paleoproterozoic, occupies the northeastern half of Europe (e.g., Bogdanova et al. 2006). The separation from the southwestern Variscan Europe is marked by the Trans-European Suture Zone, which is a wide lithospheric boundary in Central and Western Europe (Fig. 1a). The analysis of the lithospheric S-wave velocity (V_s) from the recorded earthquakes shows that the Trans-European Suture Zone divides the high-velocity layers of the Precambrian EEC from the low-velocity ones of the Paleozoic Europe (Zielhuis and Nolet 1994; Pharaoh 1999; Winchester and PACE TMR Network Team 2002; Grad et al. 2002; Bogdanova et al. 2006; Wilde-Piórko et al. 2010). The southern edge of the EEC corresponds to the Teisseyre–Tornquist Zone (Fig. 1a), which is a system of deep seated faults extended from northeast to southeast of Poland, separating regions with high crustal P-wave velocity in the southwest beneath the EEC from areas with low V_p in the southeast under the Paleozoic Platform (Grad et al. 2005). The location within Europe of the described area is shown in Fig. 1b. In Poland, the thickness of the EEC sedimentary cover increases from 1 to 2 km in the northern part to 7–8 km in the edge of the craton (Fig. 1). The average V_p raises from ~ 2.5 km/s for sediments having thicknesses of 1 km, to ~ 4.3 km/s for layers 8 km thick (Grad et al. 2003). The underlying crystalline crust shows a characteristic three-layer structure for EEC: the upper crust (UC), the middle crust (MC), and the lower crust (LC) which lies on the uppermost mantle (UMM). The Moho shows a relatively flat topography, which is advantageous to study the lithospheric velocity structure (Grad et al. 2015).

Fig. 1

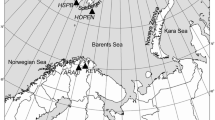
a Location of the “13 BB star” array (within red circle) on the background of the tectonic map of the pre-Permian Central Europe in the contact area of the East European Platform, the Variscides and the Alpine orogeny (Franke 2014). BT Baltic Terrane, EA Eastern Avalonia, FSS Fennoscandia–Sarmatia Suture, HCM Holy Cross Mountains, MB Małopolska Block, MLSZ Mid-Lithuanian Suture Zone, M Moldanubian Zone, MGCH Mid-German Crystalline High, MS Moravian–Silesian Zone, PB Polish Basin, PLT Polish–Latvian Terrane, PM Pomerania Massif, RH Rheno-Hercynian Zone, RG Rønne Graben, RFH Ringkobing-Fyn High, STZ Sorgenfrei–Tornquist Zone, ST Saxo-Thuringian Zone, TB Tepla–Barrandian Unit, TESZ Trans-European Suture Zone, TTZ Teisseyre–Tornquist Zone, USB Upper Silesian Block, VDF Variscan Deformation Front. The area of Bohemian Massif is highlighted in dark green. b Map of the Europe in which the red rectangle locates the area previously described. c Map of the “13 BB star” array on the background of the topographic map of northern Poland (distance scale = 20 km). The navy-blue circles show the planned locations of the 13 stations within the array, which has a symmetric geometry. The navy-blue dots represent the effective locations of the stations (A0, B1–B6, C1–C6). The distance scale is reported in the bottom right part of the figure

The geological surveys conducted in Poland across extended seismic refraction profiles provided significant data about the V_p down to the UMM, to a depth of about 60 km (Grad et al. 2016). However, they do not provide sufficient information about the V_s. The crustal S-waves (Sg) are frequently not recognizable, mainly because they show a low signal-to-noise ratio. The S-waves reflected from the Moho (SmS) are identified on several seismic sections as an envelope with high amplitude, rather than as clear separate arrivals (Środa and POLONAISE Profile P3 Working Group 1999). The only exception is the seismic P3 profile, which extends in northern Poland near the boundary of the EEC. In this case, notwithstanding the S-wave wavefield presents a lower amplitude than the P-wave velocity wavefield, the Sg arrivals are of good quality for some sections and the time uncertainty of the SmS travel-time curve is less than 1%. The V_p/V_s values reported for the model of Środa and POLONAISE Profile P3 Working Group (1999) are 1.67 in the UC, 1.73 in the MC, 1.77 in the LC, and again 1.73 in the UMM. These V_p/V_s values were used to define the expected velocity model (EVM) in the lithosphere, as their uncertainties are very small (± 0.03). Such small uncertainties are also reported by Zhu and Kanamori (2000) for the standard velocity model (SVM) having V_p/V_s equals to 1.73 in all the layers.

The purpose of the present paper is to estimate the V_s and V_p/V_s values down to 60 km depth below the EEC margin by the inversion of the surface-wave dispersion (SWD) curves for the velocity extracted from the Green’s function (GF) retrieved from the cross correlation (CC) of the noise wavefield. The study will examine whether several modes of the SWD curves are present for differences in velocity among the sedimentary cover, the UC, the MC, the LC, and the UMM. In such a case, the SWD curves will be inverted through the multimodal Monte Carlo algorithm described by Sambridge (1999). Then, the estimated V_s and V_p/V_s values will be compared with the starting values and the potential discrepancies related to the geological features of the investigated area. The analysed noise is recorded during 2014 at the “13 BB star” seismic array located in northern Poland. The spatial disposition of the 13 broadband stations is shown briefly in Fig. 1c, while the details are given in Grad et al. (2015) and Lepore et al. (2016).

P-wave velocity model below the array

The recently published high-resolution 3D seismic V_p model of Poland describes geometry and velocity down to 60 km depth (Grad et al. 2016). The model consists of six sedimentary layers—Tertiary–Quaternary (TQ), Cretaceous (Cr), Jurassic (Ju), Triassic (Tr), Permian (Pe), and Older Palaeozoic (OP)—which lie on the three layers of crystalline crust (UC, MC, and LC) that in turn are placed above the UMM (Grad and Polkowski 2012, 2016). The geometry of the uppermost part of the sediments, as well as the V_p for the stratigraphic successions from the TQ down to the OP, is fairly well known from the seismic boreholes. The V_p model for the crystalline crust and the UMM was built from 2D refraction profiles (Grad et al. 2016).

The construction of the 3D model in northern Poland is shown in Fig. 2. The geological surveys at 10,075 boreholes, out of more than 100,000 boreholes used for the whole territory of Poland, document the geometry of the stratigraphic successions from the TQ down to the crystalline basement (Fig. 2a). On the other hand, the seismic investigations at the 70 vertical boreholes (Fig. 2b), out of the 1188 deep boreholes used for the entire Polish territory, provide information about seismic velocities in the sediments (Polkowski and Grad 2015). For deeper layers, 2D velocity models from 6 seismic refraction profiles (Fig. 2c), out of the 32 deep profiles used for the construction of the model for the whole territory of Poland (Grad et al. 2015, 2016), supply information about depth and V_p in the basement beneath the sedimentary cover (Grad and Polkowski 2012, 2016), as well as about V_p in the crystalline crust and the UMM (Grad et al. 2016). The application of the 3D model in the lithosphere below the area of the array is presented in Fig. 2d. The open circles in Fig. 2b–d show the location of the stations of the array, while the small dark blue points in Fig. 2d indicate the location of the 78 midpoints among all the station pairs, connected with red lines.

Fig. 2

Boreholes and seismic profiles in the area of northern Poland from which the high-resolution 3D P-wave velocity model was created. Open circles show the location of the stations of the “13 BB star” array. a Boreholes used to determine the main geological features of the layers in the sedimentary cover. b Deep boreholes with VSP (vertical seismic profiling) used for the P-wave velocity. The isolines indicate the sedimentary thickness in km. c Seismic refraction profiles used to investigate the basement, the crystalline crust, and the uppermost mantle. d The 78 midpoints (blue dots) among all the station pairs, connected with red lines. Compiled from Grad et al. (1991, 1994, 1999, 2003, 2005, 2016), Janik et al. (2002), Guterch et al. (1994), Środa and POLONAISE Profile P3 Working Group (1999)

The 3D model calculation is illustrated in Fig. 3. The rectangular grid shown in each diagram is constituted by cells, whose dimensions in geographic coordinates are 0.02° in longitude, 0.01° in latitude, and 10 m in depth. For northern Poland, these dimensions correspond to the real size of 1112 m by 1281 m by 10 m from the sediments down to the UMM. Each cell of the grid was assigned to the right layer by gathering several maps for depth and thickness. For each layer below the area of the array, except for the UMM, the first diagram presents the thickness distribution ${h_j}\left( {x,y} \right)$ and the second one the velocity variation ${\text{A}}{{\text{V}}_i}\left( {x,y} \right)$. Therefore, the thickness and velocity values are reported for the six layers in the sedimentary cover (TQ, Cr, Ju, Tr, Pe, and OP) and the three layers in the crystalline crust (UC, MC, and LC). The last two diagrams of the figure show the depth distribution in the Moho discontinuity and the velocity variation in the UMM. The thickness varies by a few 100 m in the TQ, by 2.5 km in the Cr, Ju, Tr, and Pe, and by 8 km in the OP. The corresponding average V_p increases from 1.85 km/s in the TQ to 4.75 km/s in the OP. Moving to the crystalline crust, the UC, MC, and LC have an average thickness equal to 12 km and V_p varies within 5.8–6.5, 6.4–6.7, and 7.0–7.3 km/s, respectively. The Moho depth is in the range 36–46 km and the velocity in the UMM ranges within 8.1–8.4 km/s.

Fig. 3

Maps of thicknesses h (in km) and average P-wave velocities AV (in km/s) in Tertiary–Quaternary (TQ), Cretaceous (Cr), Jurassic (Ju), Triassic (Tr), Permian (Pe), Old Paleozoic (OP), upper crust (UC), middle crust (MC), and lower crust (LC). Maps of the depth for the Moho discontinuity (Moho) and of the average P-wave velocities in the uppermost mantle (UMM). Be aware of the different scales

All 1D P-wave velocity models below the 78 midpoints of the array (Fig. 2d), extracted from the 3D high-resolution model of Poland (Grad et al. 2016), are shown in Fig. 4. The depth range is from ± 100 m to ± 2 km in the sedimentary cover, ± 3 km in the basement, ± 2 km in the crystalline crust, and ± 5 km in the Moho. The range for V_p is ± 0.06 km/s on average in the sediments, ± 0.2 km/s in the UC, MC, and UMM, and only ± 0.04 km/s in the LC.

Fig. 4

1D P-wave velocity models below the 78 midpoints of the “13 BB star” array, extracted from the 3D high-resolution model of Poland (Grad et al. 2016)

Modal analysis of the dispersion curves

As reported in the literature, the surface-wave GF in a 1D-layered structure shows the presence of several modes (Aki and Richards 2002). They are extracted from the CC of ambient noise by the spectral analysis of all the arrivals in the GF (e.g., Yao et al. 2011). The extraction involves the GF retrieval from the CC traces obtained by the analysis of the ambient-noise waveform between the station pairs (see, for instance, Ma et al. 2016). The retrieval of the GF from the diffuse wavefields was widely studied in seismology (e.g., Shapiro and Campillo 2004). If the distribution of the noise sources is limited in space and the noise wavefield is strongly directional, some difficulties are encountered in retrieving the GF and extracting SWD curves at frequencies lower than 1 Hz especially for distant sources (Halliday and Curtis 2008). In such a case, the identification of the modes is challenging (Shapiro et al. 2001; Gouédard et al. 2008; Brooks et al. 2009; Yao et al. 2011; Kimman et al. 2012; Rivet et al. 2015; Ma et al. 2016): even though the fundamental and first modes are often recognised, higher modes are observed only for some datasets. The recognition of the fundamental mode is straightforward, since its scattering is predominantly in the forward direction and the overlapping with the higher modes is weak (e.g., Bensen et al. 2008). The first mode is also observed rather easily, while the second and the third ones only sometimes, due to the incomplete distribution of the noise sources (Harmon et al. 2007). In general, the retrieval of the modes becomes even more difficult at increasing distance from the source, since the wavefield energy decreases progressively (Kimman and Trampert 2010). Therefore, the estimation of the higher modes is much more reliable as the GF is retrieved from the CC traces between station pairs oriented along the main direction of the noise wavefield (Rivet et al. 2015). Nevertheless, since low-order modes explore the layers closer to the surface, whereas high-order ones probe the deeper layers, it is necessary the proper identification of all the modes and the multimodal inversion to describe correctly the lithospheric structure (Bergamo et al. 2011).

Examples of CC traces, evaluated by stacking the daily traces for January, April, and September (reference months) 2014, representing different seasons (winter, spring, autumn), are shown in Fig. 5 in time vs intra-station distance plots for the vertical component in the 0.1–1 and 0.02–0.1 Hz frequency bands. As a consequence of the symmetrical geometry of the array, the negative-time amplitudes of any trace and the positive-time ones of its reverse result equivalent. Therefore, only the positive-time part of the traces allowing the most proper recovery of the surface waves is displayed. In addition, to avoid the crowding of the traces, some of them pertaining to station pairs with similar intra-distances, as well as some others showing low resolution, were rejected: the remaining ones are shown in the time–distance plots. The four thick grey lines show some reference velocities for the surface waves in both frequency bands. For the 0.1–1 Hz band, the arrivals are located in correspondence of the lines. The fastest arrivals are observed at ~ 7 s in time, ~ 20 km in distance, and at ~ 39 s, ~ 117 km, so the average velocity is ~ 3 km/s. The second cluster of arrivals, at ~ 10 s, ~ 20 km, and at ~ 58.5 s, ~ 117 km, has an average velocity equal to ~ 2 km/s. The third group of arrivals is detected at ~ 13 s, ~ 20 km, and at ~ 78 s, ~ 117 km: accordingly, the average velocity is ~ 1.5 km/s. The slowest arrivals are seen at ~ 20 s, ~ 20 km and at ~ 117 s, ~ 117 km, with an average velocity equal to ~ 1 km/s. Regarding the 0.02–0.1 Hz band, the arrivals are located before the lines, and then they have a velocity higher than the preceding case. The fastest arrivals are observed at ~ 4.5 s in time, ~ 20 km distance, and at ~ 26 s, ~ 117 km, so the average velocity is ~ 4.5 km/s. The second cluster of arrivals, at ~ 7 s, ~ 20 km and at ~ 39 s, ~ 117 km, has an average velocity equal to ~ 3 km/s. The third group of arrivals is detected at ~ 10 s, ~ 20 km and at ~ 58.5 s, ~ 117 km: accordingly, the average velocity is ~ 2 km/s. The slowest arrivals are seen at ~ 13 s, ~ 20 km and at ~ 78 s, ~ 117 km, with an average velocity equal to ~ 1.5 km/s. Every surface-wave arrival was carefully recovered, so that it could not interfere with any other (Shapiro and Campillo 2004). The accuracy in identifying the arrivals was higher when the intra-station distance (20,120 km) is longer than three wavelengths: assuming an average surface-wave velocity of ~ 2 km/s, the wavelength is ~ 8 km at 0.1 Hz and ~ 16 km at 0.02 Hz (Bensen et al. 2007). Nevertheless, the scattering usually present in the surface waves, together with the strong directionality of the noise wavefield, can make challenging the recognition of the arrivals (Pedersen et al. 2007; Lepore et al. 2016). Similar to Brooks et al. (2009), the fundamental SWD mode and at least two higher order modes were identified in both the frequency bands.

Fig. 5

Cross-correlation traces of the ambient noise for the Z component, stacked for January, April, and September 2014, and evaluated within 0.1–1 Hz (top) and 0.02–0.1 Hz (bottom) frequency bands. Accordingly to the symmetrical geometry of the array, the negative-time amplitudes of any trace and the positive-time ones of its reverse result equivalent. Thus, only the positive-time part of the traces allowing the most proper recovery of the surface waves is shown. Furthermore, to avoid the crowding of the traces, some of them pertaining to station pairs with similar intra-distances, as well as some others showing low resolution and bad quality, were removed from the plots. The final plots contain only the selected traces. The four thick grey lines show some reference velocities helping in the recognition of the surface-wave arrivals in both bands

The extraction of the SWD curves was carried out considering the velocity and the time of each arrival as a function of frequency f:

$$v\left( f \right)=\frac{R}{{\tau \left( f \right)}}$$

where v(f) is the wave velocity, R the intra-station distance, and τ(f) the starting time of the arrival. The frequency bands chosen for the retrieval of the SWD curves, namely, 0.10–1.00 and 0.02–0.10 Hz, were divided, respectively, into 17 shorter bands of 0.1 Hz length overlapped by 0.05 Hz, and into 15 shorter bands of 0.01 Hz length overlapped by 0.005 Hz. Then, any surface-wave arrival was filtered between the limits of every short band: the times of all the peaks resulting from the filtering process were automatically picked and stored. After that, the matrix of the velocities was calculated from the corresponding one of the times, and the dispersion curves were calculated from the envelope of all frequency curves imposing that the velocity always decreases as the frequency increases. The described procedure of retrieving the dispersion modes, known as the multidimensional deconvolution of the CC traces (Wapenaar et al. 2011), is summarized in the flow chart presented in Fig. 6. As an example, the retrieval of the second mode for the C6–C4 station pair (intra-station distance ~ 105 km) in the 0.10–1.00 Hz frequency band is shown in Fig. 7 for each one of the shorter bands. Assuming 2 km/s as the maximum velocity for this mode (Brooks et al. 2009), the related arrival is identified in the CC trace as the first maximum after the time ~ 52.5 s. Consequently, the two grey lines define the time limits of the maximum, so that it does not interfere with the other maxima present in the trace. In the shorter bands 0.10–0.20, 0.15–0.25, and 0.20–0.30 Hz, no maxima are present between the two grey lines: thus, the velocity cannot be evaluated. From 0.25–0.35 to 0.50–0.60 Hz band, only one maximum is observed: according to the continuous decrease of velocity in the dispersion curve, only the first and the last time are accepted. Joining these two values makes the first part of the final dispersion curve (in blue) shown in Fig. 8 in the velocity vs frequency plot. From the 0.55–0.65 up to 0.90–1.00 Hz band, the arrival is split into two maxima (Fig. 7): in line with the cited criterion, only the initial four times of the second maximum are taken into account to define the second part of the final dispersion curve (in red, see Fig. 8). The blue and red dispersion curves, together with the final dispersion curve (in grey, thicker traced with the points highlighted by grey circles), are reported in Fig. 8. The procedure was repeated for all the station pairs and the reference months: the resultant dispersion curves are reported in the semi-log plot shown in Fig. 9 within the 0.02–1.00 Hz joined frequency band. Four modes are observed: the curves of the fundamental mode (mode 0) are coloured in purple, the ones for the first mode (mode 1) in yellow, those for the second mode (mode 2) in red, and those for the third mode (mode 3) in grey. The velocity ranges within 0.8–1.5 km/s in the mode 0, within 1.2–2.1 km/s in the mode 1, within 1.6–2.6 km/s in the mode 2, and within 2.0–4.0 km/s in the mode 3. Therefore, the sedimentary cover is examined by the mode 0, the upper crust by the mode 1, the middle crust by the mode 2, and the lower crust by the mode 3. Moreover, the velocity variations were the smallest for the modes 0 and 1, becoming larger for the mode 2 and even larger for the mode 3. Thus, the uncertainty in the vs was increasingly larger at increasing depth. Being 0.02 Hz the lowest frequency of the dispersion curves and 3 km/s the average velocity in the mode 3, a good resolution in the estimation of the vs was ensured down to the UMM. According to the directionality of the main noise source during the reference months, some dispersion curves (reported in black and thinner traced) can be considered less reliable than the others. From the analysis of the beam-power plots shown in Fig. 10, obtained using the procedure described in Lepore et al. (2016), it is found that the main noise source is in the North Sea (240°–245°) during January, in the eastern part of the Baltic Sea (15°–60°) during April and again in the North Sea (310°–360°) during September. It means, for instance, that the noise wavefield propagates almost perpendicularly in January for C1–B5 and B4–C4 station pairs, in April for C5–C4 and C6–C3 pairs, and in September for C4–B3 and C6–C5 pairs. Hence, the evaluation of the values of velocities or the trend of dispersion curves may result different from the corresponding ones for the other months. For this reason, those dispersion curves will not be taken into account in the final evaluation of the average vs and V_p/V_s values.

Fig. 6

Flow chart showing the steps of the multidimensional deconvolution of the cross-correlation traces, that is the procedure to calculate the surface-wave dispersion curves

Fig. 7

Drawing of the surface-wave dispersion curve for the C6–C4 station pair in January for the second mode, assuming 2 km/s as the maximum velocity. The related arrival is identified in the CC trace as the first maximum after the time ~ 52.5 s and the two grey lines define the time limits of this maximum, so that it does not interfere with the other maxima present in the trace. After having divided the whole band in 17 shorter bands of 0.1 Hz length overlapped by 0.05 Hz, the velocity was calculated for each maximum between the time limits defined by the two grey lines. The first maximum is marked with a blue star, while the second one with a red star. Note that the pattern changes from one to two maxima between 0.50–0.60 and 0.55–0.65 Hz

Fig. 8

Dispersion peaks for the C6–C4 station pair in the frequency range 0.1–1 Hz. The thin blue line shows the trend of the dispersion curve for the first peak; in the same way, the thin red line refers to the second peak. The thick grey line connects the points accepted for the surface-wave dispersion curve drawn in Fig. 7, highlighted with grey circles

Fig. 9

Plot of velocity (km/s) vs frequency (Hz) in semi-log scale for the surface-wave dispersion curves related to all the station pairs and to January, April, and September 2014, within the joined 0.02–1 Hz frequency band. The light grey thick line divides the two bands (see Fig. 5) used for evaluating each dispersion curve, which connects the individual points, as described in Fig. 8. The curves of the four modes are coloured as follows: purple, yellow, red, and dark grey. According to the directionality of the main noise source during 3 months, some dispersion curves (reported in black and thinner traced) can be considered less reliable than the others. For this reason, those dispersion curves will not be considered in the final evaluation of the average vs and V_p/V_s values

Fig. 10

Beampower for the “13 BB star” array stacked for the whole months of January, April, and September 2014. As reported in Lepore et al. (2016), dotted lines show the range of azimuth of the main source of the ambient noise: 240°–245° (North Sea) during January, 15°–60° (eastern part of Baltic Sea) during April, and 310°–360° (again in the North Sea) during September

Inversion of the dispersion curves

The evaluation of the 1D vs profiles from the joined SWD curves is a highly nonlinear inversion problem. The first step was the linearization of the inversion algorithm, determining the best velocity profile (i.e., best model) among the solutions obtained from all the possible linear combinations of the parameters. However, several problems arise in this approach. First, the reliability of the best model is strongly influenced by the accuracy of the starting model. Second, it is hard to understand whether the best model is placed on a local or a global minimum of the parameter space. Third, the speed of the convergence towards the best model is rather slow (Behr et al. 2010). To overcome these problems, iterative nonlinear inversions were added according to the multimodal Monte Carlo algorithm described by Sambridge (1999). It involves an iterative search technique to seek for the global minimum of the multidimensional error function (EF) in the parameter space without being influenced by the chosen starting model. The best model was identified by iterative inversions, comparing each SWD curve with a group of theoretical dispersion curves belonging to the same population of that SWD curve within a preset confidence limit (acceptable models, Maraschini and Foti 2010). The theoretical curves were generated from a set of representative models selected randomly, after having subdivided the solution space into Voronoi cells (Sambridge 1999). Therefore, the Monte Carlo method has some disadvantages such as the large computational cost, due to the huge number of models to be used, and the strong dependence on the choice of the confidence criterion which highly affects the uncertainties in the best model. Nevertheless, the method is fairly robust, so that the convergence towards the global minimum is guaranteed: as a fact, the value assumed by the EF in each iteration decreases progressively during the inversion (Shapiro and Ritzwoller 2002; Mordret et al. 2014).

The Monte Carlo multimodal algorithm was subdivided into four steps. First, the theoretical dispersion curve, TDC₁, was generated from the starting model, m₁, and then used in the simple linear inversion of the SWD curves. The resulting estimated model, m₂, was assumed as the basic reference model. In the second step, the TDC₂ produced from the m₂ model was employed in the simulated annealing (Lepore and Ghose 2015) inversion of the SWD curves, to create the m₃ best fit model. The third step consisted in building a Voronoi grid over the parameter space and then generating a set of acceptable models, m₄, from the m₃ model, on the basis of the Markov Chain algorithm, following all the new possible paths to the best model (Sambridge 1999). In the fourth step, the group of TDC₄, derived from the m₄ models, was used in the inversion of SWD curves by the genetic algorithm of Sambridge and Drijkoningen (1992) to obtain the representative m₅ models. Then, the best model, selected among the m₄ models as the one that minimizes the EF in the parameter space, was calculated by a weighted average over the m₅ models, using the inverse of the EF as the weighting factor. In particular, when these factors are not so different for several models, the weighted average represents the best choice for the selection of the best model. An accurate identification of the size of the parameter space through a careful definition of both the number of parameters and their range of variation is extremely important to reduce the computational time necessary to evaluate the best model (Shapiro and Ritzwoller 2002).

To perform 1D seismic investigations of the lithospheric structure, the V_p, thickness and density were considered as parameters in each layer, while V_p/V_s was allowed to vary of ± 15% around the value defined in the EVM and SVM starting models. The values of depth, V_p, and density were taken from the 3D model, while the starting vs values were calculated dividing V_p by V_p/V_s previously defined for both the starting models. To evaluate the SWD curves, CC was calculated separately for each month in the 0.1–1 and 0.02–0.1 Hz frequency bands, so allowing to highlight the variations of the quality in the retrieval of the SWD curves. The extraction of the SWD curves from the GF was performed in both bands, and then, the two sets of curves were joined in a single group, permitting a reliable estimation of the vs and V_p/V_s values down to the UMM, as reported by Pasyanos (2005). The SWD curves were inverted by the Monte Carlo multimodal inversion technique to obtain the 1D vs profiles as a function of depth along the Z component, separately for each reference month and station pair. Each inversion was carried out in the parameter space using 4000 acceptable models, 1000 Voronoi cells (0.2–18.0 m in depth), and 3000 representative models. On the basis of the range of the values assumed by the EF, the representative models were classified according to its level of reliability, associating the lowest value of the EF was with the most reliable model. To reduce the computational cost of the inversions, the discrepancy between the best model and the starting model was calculated using 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100 most reliable profiles. Observing that from 10 to 60 profiles the discrepancy gradually decreased reaching shortly afterwards a plateau, the 70 most reliable profiles were used to calculate the best model for the vs velocities and the V_p/V_s ratios separately for each reference month and station pair. Since the 78 midpoints (Fig. 2d) are very close each other, 2D maps were built for all the calculated vs and V_p/V_s values in every layer based on the EVM and SVM models. As an example, in Figs. 11 and 12, the maps based on the EVM are shown for vs and V_p/V_s values, respectively. In Table 1, all the values obtained for vs and V_p/V_s for the reference months and for the average over these months (indicated as average) are reported together with the values assumed by vs and V_p/V_s in the EVM and SVM models.

Fig. 11

Maps of all the values of the calculated S-wave velocity in ten-layer models below the 78 midpoints of the “13 BB star” array for January, April, and September 2014, as well as for the arithmetic average over the 3 months (indicated as average). In the right bottom corner, average values of vs are given. The maps were obtained using a boxcar filter having radius depending on the thickness of the layers: 2 km for the Tertiary and Quaternary, the Cretaceous and the Jurassic; 4 km for the Triassic and the Permian; 6 km for the Older Paleozoic; 20 km for the Upper Crust; 40 km for the Middle Crust; 60 km for the Lower Crust; 100 km for the Uppermost Mantle

Fig. 12

Maps of all the values of the calculated P-wave-to-S-wave velocity ratio in ten-layer models below the 78 midpoints of the “13 BB star” array for January, April, and September 2014, as well as for the arithmetic average over the 3 months (indicated as average). In the right bottom corner, average values of V_p/V_s are given. The maps were obtained using the boxcar filter described for Fig. 11

Table 1 Comparison of vs and V_p/V_s values for starting (orig) EVM and SVM with calculated (calc) values from the Monte Carlo inversions

Results and discussion

The vs maps in each of the ten layers are shown in Fig. 11. In the first three columns, the maps are given for the reference months, and in the fourth for the arithmetic average over the reference months (indicated as average). The maps were obtained using a boxcar filter having radius depending on the thickness of the layers: 2 km for the TQ, the Cr, and the Ju; 4 km for the Tr and the Pe; 6 km for the OP; 20 km for the UC; 40 km for the MC; 60 km for the LC; and 100 km for the UMM. Increasing filter radius is taken into account for longer wave periods at greater depths. In each map, the average vs values on all the midpoints are reported in the bottom right corner. Variations of the vs values in the ± 0.10 km/s error limits among the reference months are noticed in all the layers except MC and LC. As the average error on the starting vs values is 0.10 km/s, the average values in the sedimentary cover range within 0.99–2.66 km/s as expected according to the starting EVM model (Table 1). In the UC, the average vs value is much lower than the starting value (3.48 km/s instead of 3.75 km/s). In the MC and LC, the average values are very close to the starting values, while in the UMM, the average vs value is the same within the errors. The comparison between the starting and calculated vs values for the SVM model (Table 1) confirms what above-described for the EVM.

The V_p/V_s maps in each of the ten layers are shown in Fig. 12 for the reference months and for the average: they were obtained using the aforementioned boxcar filter. In each map, the average V_p/V_s values on all the midpoints are reported in the bottom right corner. Variations of the V_p/V_s values in the ± 0.03 error limits among the reference months are noticed in all the layers except Pe, MC, and LC. As the average error on the starting V_p/V_s values is 0.03, the average values in the sedimentary cover range within 1.8–1.9 as expected according to the starting EVM model (Table 1), except for Cr, Tr, and OP layers in which they are 1.97, 1.92, and 1.91, respectively. In the UC, the average V_p/V_s value is much larger than the starting value (1.81 instead of 1.67) as expected from the low vs value (3.48 km/s). In the MC, LC, and UMM, the average values are very close to the starting values. The same analysis can be performed comparing the starting and calculated V_p/V_s values for the SVM model (Table 1).

As an example of the comparison between the starting and the calculated vs values, the 1D vs profiles for the reference months are extracted from the maps in Fig. 11 in the midpoint of the C6C4 station pair and shown in Fig. 13 as coloured lines, together with the 70 most reliable vs profiles from the Monte Carlo inversions (thin grey lines) and the profile of the starting vs values for the EVM model (dotted black line). In January and September, the error on vs in the crust is lower than the error in the UMM, while the reverse is verified in April. This dissimilarity can be explained looking at the CC traces shown in Fig. 5. In both frequency bands, the best resolution to retrieve the surface-wave arrivals having velocities higher than 2.0 km/s is achieved in April, whereas the arrivals having velocities within 1.5–2.0 km/s are better retrieved in January and September. It means that the crust is more accurately analysed than the UMM in January and September when the noise source is in the North Sea, while the reverse occurs in April when the source is in the Baltic Sea (Fig. 10). Going back to Fig. 13, the discrepancy between the average and the starting values is generally small in the sedimentary cover except for the Cr and OP layers, then, it is larger in the UC, and again smaller in the MC, LC, and UMM. The low vs in the Cr and OP layers is ascribable to a resolution problem caused by the very small thickness of the two layers in comparison with the intra-station distance of the array. The calculated vs for each reference month is rather low in the UC, consistently with what found in the previous works about the study of the V_p distribution in the Polish Basin. This anomaly can be produced by the presence of sedimentary rocks down to about 20 km depth mixed together with intrusive ones (Grad et al. 2003; Środa et al. 2006).

Fig. 13

Average 1D S-wave velocity profiles in the midpoint of the C6–C4 station pair for January (cyan), April (green), and September (red) 2014. The thin grey lines represent the 70 most reliable profiles within the 3000 representative models resulting from the Monte Carlo inversion. The dotted black line marks the profile of the starting velocity values for the EVM model

The 1D profiles for the V_p/V_s ratios, obtained directly from the values in Table 1, are shown in Fig. 14 for January (blue line), April (green line), and September (red line) together with the 1D profiles for the EVM and SVM models (dotted black line). In the right diagram in Fig. 14, the 1D profile for the average from all the models (black line) is reported with the 1D profile for the SVM (dotted black line). The 1D profiles obtained using the EVM model show that the V_p/V_s ratio in the sedimentary cover ranges within 1.81.9 as expected, except for the Cr, Tr, and OP layers in which the average values are 1.97, 1.92, and 1.91, respectively. The 1D profiles obtained using the SVM model show that the V_p/V_s ratio in the sedimentary cover ranges within 1.71.8 as expected, except for the Cr and OP layers, where the average values are 1.86 and 1.88, respectively. In the UC, the average V_p/V_s ratio is rather large (1.81 for EVM and 1.86 for SVM) as expected from the low vs value (3.48 km/s for EVM and 3.40 km/s for SVM). In the MC, LC, and UMM, the calculated V_p/V_s values are very close to the starting values in both cases. The comparison of the average profiles in the right diagram confirms this description.

Fig. 14

Starting values of V_p/V_s for EVM and SVM (dotted black line), together with the average values of V_p/V_s for January (blue), April (green), and September (red), and final average model (black) of all V_p/V_s values

The very low average value of vs in the UC needs a deeper discussion. To that, the geophysical and tectonic characteristics in the area of the array, summarized in Fig. 15, were further investigated. The massifs present in northern Poland, metamorphosed in several phases mainly during the Gotian (< 1.7 Ga), are characterized by subdued magnetic anomalies (Fig. 15a). They are separated by Pre-Karelian metamorphic–magmatic Kaszuby belt, whose shape and location have been inferred from correlative strong positive magnetic anomaly (Królikowski and Wybraniec 1996). The magnetic modelling of northern Poland reveals a remarkably complex structure in the underlying crust including the presence of low-velocity layers (Bogdanova et al. 2006; Krzemiński et al. 2014). The tectonic sketch of the crystalline basement in northern Poland shows four massifs and zones (Fig. 15b), namely, Pomorze massif, Kaszuby zone, Karelian metamorphic–magmatic complexes, and Dobrzyń massif (Kubicki and Ryka 1982; Ryka 1984; Znosko 1998). Dobrzyń and Pomorze massifs are large granitoid structures of Pre-Karelian age (> 2.6 Ga). The presence of granitoid rocks of various kinds, forming flat-lying sheeted bodies in the upper and middle crust, is inferred to be responsible for low seismic velocities (Bogdanova et al. 2006). The low value of the vs velocity correlates well with the “cold” area of EEC, where the heat flow (Fig. 15c) is only about 40 mW/m² (Karwasiecka and Bruszewska 1997; Majorowicz et al. 2003). However, a high vs value would be expected in the case of low temperature: then, the low vs value must be attributed to the mineral composition of the basement. A low value of vs velocity leads into a large value of V_p/V_s ratio (1.80), in agreement with that found by Bogdanova et al. 2006 in northeastern Poland in the high-velocity body with V_p of ~ 6.5 km/s (Fig. 15d). Nevertheless, typical values of the ratio (1.67–1.71) were observed in the upper crust of northern Poland around that body (Czuba et al. 2002). Low values of V_p/V_s in the upper crust were found also in other regions of the EEC. In the upper crust of the Baltic Shield, V_p/V_s ranges within 1.70–1.71 (Grad and Luosto 1994; Grad et al. 1998; Uski et al. 2012); in the upper crust of the Ukrainian Shield, it varies within 1.65–1.71 (Grad and Tripolsky 1995). The exception in the Ukrainian Shield is the high-velocity (V_p = 6.7 km/s) Korosten Pluton which has generally higher values of V_p/V_s (1.77–1.84) in the upper crust (Thybo et al. 2003). The seismic velocity and density values in the Korosten Pluton suggest that it is composed of both rapakivi granites and anorthosites (Kozlovskaya et al. 2004). Values higher than 1.81 up to 1.89 for V_p/V_s were found in the crust of Bushveld Province, South Africa, the site of the world’s largest layered mafic intrusion (Delph and Porter 2015). However, those high values are not typical for the Precambrian cratons.

Fig. 15

Summary of geophysical and tectonic characteristics of the EEC basement in northern Poland beneath “13 BB star” array. a Magnetic anomaly map of Poland illuminated from SE (Wybraniec 1999). b Tectonic scheme of the crystalline basement of the EEC in northern Poland (Kubicki and Ryka 1982; Ryka 1984; Znosko 1998). Cn Ciechanów zone, Db Dobrzyń massif, Kb Kaszuby zone, Km Karelian metamorphic–magmatic complexes, Mc Mazury complex, Pm Pomorze massif. Small white dots are the midpoints of the array. c Heat flow map (Karwasiecka and Bruszewska 1997; Majorowicz et al. 2003); white dots show locations of wells with temperature logs. d Average map of V_p/V_s in the upper crust (crystalline basement). Thin lines in all maps show the tectonic borders of the basement as in b; small magenta dots are the midpoints of the array

Conclusions

To study the lithospheric structure down to 60 km depth below the East European Craton in northern Poland, the S-wave velocity, V_s, and the P-wave-to-S-wave velocity ratio, V_p/V_s, were calculated by inverting the surface-wave dispersion curves for the velocity evaluated in both 0.02–0.1 and 0.1–1 Hz frequency bands. The whole procedure allowed to estimate the vs and V_p/V_s values down to the uppermost mantle, solving the lack of information concerning the vs in the high-resolution 3D model of Poland assumed as the reference model for the V_p values. The dispersion curves were extracted from the arrivals identified on the cross-correlation traces retrieved from the ambient noise recorded during 2014 at the “13 BB star” array in northern Poland. At the most, four groups of arrivals were observed on the cross-correlation traces, whose velocities ranged within 0.8–4 km/s in the 0.02–1.00 Hz band: in this range, the fundamental and three higher modes were recognized in the dispersion curves. The velocity variations of the surface-wave velocity dispersion curves in the 0.02–1 Hz band were the smallest for the fundamental and first modes, then larger for the second mode and even larger for the third one. Based on the directionality of the main noise source during 2014, some dispersion curves were considered less reliable than others as, for instance, the ones pertaining to the station pairs oriented almost perpendicularly to the direction of the noise wavefield. The remaining dispersion curves were inverted using a Monte Carlo multimodal inversion algorithm to evaluate the 1D vs and V_p/V_s profiles, assuming the depth, P-wave velocity, V_p, density, and Poisson’s ratio in all the layers as known from the high-resolution 3D model of Poland. The starting values for the vs were evaluated dividing V_p by the V_p/V_s ratios, taken from the expected velocity model (from 1.9 down to 1.8 in the sedimentary cover, 1.67 in the upper crust (UC), 1.73 in the middle crust, 1.77 in the lower crust, and 1.73 in the uppermost mantle) and the standard velocity model (1.73 in all the layers). Once the representative models were classified according to the level of reliability, the weighted average over the 70 most reliable profiles was used to calculate the best model for the vs and V_p/V_s values beneath the array. As the average error on the starting vs values is 0.10 km/s, good agreement between the starting and the calculated models was found in all the layers except for the upper crust, in which the calculated value is 3.48 km/s instead of the starting value of 3.75 km/s. The very low average vs value in the upper crust is due to the presence of sedimentary rocks mixed together with granitoid intrusive ones and correlates well with the low value for the heat flow (40 mW/m²): as a consequence, the average V_p/V_s value is very large (1.81 instead of 1.67). The calculated ratio is coherent with the value (1.80) found within EEC in northeastern Poland in the high-velocity body having V_p ~ 6.5 km/s and with the values higher than 1.81 found in the crust of Bushveld Province, South Africa, the site of the world’s largest layered mafic intrusion.