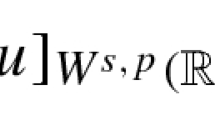Bourgain-Brezis-Mironescu formula for $W^{s,p}_q$-spaces in arbitrary domains

Abstract

Under certain restrictions on s, p, q, the Triebel-Lizorkin spaces can be viewed as generalised fractional Sobolev spaces $W^{s,p}_q$. In this article, we show that the Bourgain-Brezis-Mironescu formula holds for $W^{s,p}_q$-seminorms in arbitrary domain. This addresses an open question raised by Brazke-Schikorra-Yung (Calc Var Partial Differ Equ 62(2):41–33, (2023).

1 Introduction

Sobolev spaces arise naturally in the study of partial differential equations. They are defined in terms of weak derivatives. For an open set $\Omega \subseteq {\mathbb {R}}^N$, and $1\le p<\infty$, the Sobolev space $W^{1,p}(\Omega )$ is defined to be $\{f\in L^p(\Omega )\ |\ [f]_{W^{1,p}(\Omega )}<\infty \}$, where

$$\begin{aligned}{}[f]_{W^{1,p}(\Omega )}^p:= \int _{\Omega }|\nabla f(x)|^pdx. \end{aligned}$$

Some closely related spaces are Triebel-Lizorkin spaces $F^s_{p,q}(\Omega )$, which are defined to be $\{f|_{\Omega }\ |\ f\in F^s_{p,q}({\mathbb {R}}^N) \}$, and are equipped with the norm $[\cdot ]_{F^s_{p,q}({\mathbb {R}}^N)}$. We shall not define the norm $[\cdot ]_{F^s_{p,q}({\mathbb {R}}^N)}$ as it will not be necessary for the present article. Instead, we refer the reader, for definition and classical results regarding Triebel-Lizorkin spaces, to [59], or more modern references like [36, 56]. For $1\le p,q<\infty$, $\max \{0,\frac{N(q-p)}{pq}\}<s<1$, we have the characterisation (see Theorem 1.2 of [55])

$$\begin{aligned} F^s_{p,q}({\mathbb {R}}^N):= \left\{ f\in L^{\max \{p,q\}}({\mathbb {R}}^N)\ \Big |\ \Vert f\Vert _{L^p({\mathbb {R}}^N)}+[f]_{W^{s,p}_q({\mathbb {R}}^N)}<\infty \right\} , \end{aligned}$$

where

$$\begin{aligned}{}[f]_{W^{s,p}_q(\Omega )}:= \left( \int _{\Omega }\left( \int _{\Omega }\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}\right) ^\frac{1}{p}. \end{aligned}$$

(1)

In the special case of $p=q$, these spaces are related to the so-called fractional Sobolev spaces $W^{s,p}(\Omega )$, defined by

$$\begin{aligned} W^{s,p}(\Omega ):= \left\{ f\in L^p(\Omega )\ \Big |\ \Vert f\Vert _{L^p(\Omega )}+[f]_{W^{s,p}(\Omega )}<\infty \right\} , \end{aligned}$$

where $[f]_{W^{s,p}(\Omega )}:=[f]_{W^{s,p}_p(\Omega )}$. Of course, when $\Omega ={\mathbb {R}}^N$, or when $\Omega$ is fractional extension domain (see [25]), we have $W^{s,p}(\Omega )=F^s_{p,p}(\Omega )$.

Bourgain-Brezis-Mironescu [8] showed that for any smooth and bounded domain $\Omega$, $1\le p<\infty$, and any $f\in W^{1,p}(\Omega )$,

$$\begin{aligned} \lim _{s\rightarrow 1-}(1-s)[f]_{W^{s,p}(\Omega )}^p = K\Vert \nabla f\Vert _{L^p(\Omega )}^p. \end{aligned}$$

Conversely, for any $f\in L^p(\Omega )$, if we have

$$\begin{aligned} \lim _{s\rightarrow 1-}(1-s)[f]_{W^{s,p}(\Omega )}^p<\infty , \end{aligned}$$

then $f\in W^{1,p}(\Omega )$ if $p>1$ and $f\in BV(\Omega )$ if $p=1$. Later Dávila [23] extended this result and proved that for any $f\in BV(\Omega )$, $\lim _{s\rightarrow 1-}(1-s)[f]_{W^{s,1}(\Omega )}^p=K|\nabla f|(\Omega )$. This is commonly known as the Bourgain-Brezis-Mironescu formula (BBM formula for short). The subject was further developed in [9, 10, 18, 47, 48, 53]. The BBM formula has been generalised to Orlicz and generalised Orlicz setup in [1,2,3, 28, 31, 61], to variable exponent setup in [30, 39], to magnetic Sobolev spaces [29, 49, 50, 52, 57], to anisotropic setup [37, 45, 51], to Riemannian manifolds in [42], to metric spaces in [24, 35], to Banach function spaces in [22, 62]. Similar studies are possible in the context of Besov spaces also [41, 60]. More recent developments on this topic can be found in [14,15,16,17]. For further reading, we refer the reader to [4, 6, 7, 11, 19, 21, 26, 32,33,34, 38, 46, 54].

Our first interest lies in works regarding the domain. That is, how far the smooth-bounded condition, on the domain, can be relaxed. In this direction, we mention three works. The first is due to Lioni-Spector [43, 44]. They showed that for an arbitrary domain $\Omega$, and $f\in L^p(\Omega )$,

$$\begin{aligned} \lim _{\lambda \rightarrow 0+}\lim _{s\rightarrow 1-}{(1-s)}\int _{\Omega _\lambda }\int _{\Omega _\lambda }\frac{|f(x)-f(y)|^p}{|x-y|^{N+sp}}dydx=K[f]_{W^{1,p}(\Omega )}^p. \end{aligned}$$

where

$$\begin{aligned} \Omega _\lambda :=\{x\in \Omega \ |\ \text{ dist }(x,\partial \Omega )>\lambda \}\cap B(0,\lambda ^{-1}). \end{aligned}$$

(2)

The second result is due to the author with Bal-Roy [5], where it has been shown that the BBM-formula [8], holds if we take $\Omega$ to be a $W^{1,p}$-extension domain. The third result is due to Drelichman-Duran [27]. They showed that for $1<p<\infty$, and an arbitrary bounded domain $\Omega$, and any $\tau \in (0,1)$, we have

$$\begin{aligned} \lim _{s\rightarrow 1-}{(1-s)}\int _{\Omega }\int _{B(x,\tau \text{ dist }(x,\partial \Omega ))}\frac{|f(x)-f(y)|^p}{|x-y|^{N+sp}}dydx=K[f]_{W^{1,p}(\Omega )}^p. \end{aligned}$$

The second direction of work regarding the BBM-formula, that we are interested in, is its extension for Triebel-Lizorkin spaces. The first work in this direction was done by Brazke-Schikorra-Yung [12]. They explained via examining thoroughly various constants of embeddings that although $F^s_{p,p}=W^{s,p}$, when $s\in (0,1)$ and $F^s_{p,2}=W^{1,p}$ it makes sense for the scaled $W^{s,p}$ seminorm to converge to $W^{1,p}$-seminorm, even when $p\ne 2$. They posed the open problem (see [12, Question 1.12]) about the asymptotic constant in the identification of the $\Vert \cdot \Vert _{W^{s,p}_q}\approx \Vert \cdot \Vert _{F^s_{p,q}}$.

The current article addresses this question by showing the asymptotic behaviour (as $s\rightarrow 1-$) of $W^{s,p}_q$-seminorms. Similar studies has been done, when $1<q<p<\infty$, in [22] for ${\mathbb {R}}^N$, and in [62, Theorem 6.1] for a special class of bounded extension domains (called $(\varepsilon ,\infty )$-domains).

We concentrate our focus on the following seminorm (for some $\tau \in (0,1)$)

$$\begin{aligned}{}[f]_{{\tilde{W}}^{s,p}_q(\Omega )}:= \left( \int _{\Omega }\left( \int _{B(x,\tau \text{ dist }(x,\partial \Omega ))}\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}\right) ^\frac{1}{p}, \end{aligned}$$

(3)

as one can then extend the above question for arbitrary bounded domains, motivated by [27]. We go one step further and show that the boundedness of the domain is not necessary. Our main results are the following:

Theorem 1

Let $\Omega \subset {\mathbb {R}}^N$ be any open set $\tau \in (0,1)$. Assume one of the following conditions

• (1) $1\le q\le p<\infty$,

• (2) $1<p<q<\infty$ with $p\le N$ and $q <\frac{Np}{N-p}$,

• (3) $N<p<q<\infty$.

Then there is a constant $K=K(N,p,q)>0$ such that for any $f\in W^{1,p}(\Omega )$, we have,

$$\begin{aligned} \lim _{s\rightarrow 1-} (1-s)^\frac{p}{q}\int _{\Omega }\left( \int _{B(x,\tau \text{ dist }(x,\partial \Omega ))}\frac{|f(x)-f(y) |^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}dx = K\int _{\Omega }|\nabla f(x)|^pdx. \end{aligned}$$

(4)

Theorem 2

Let $\Omega \subset {\mathbb {R}}^N$ be an open set, $\tau \in (0,1)$ and $1\le p,q<\infty$. If $f\in L^p(\Omega )\cap L^q(\Omega )$ is such that

$$\begin{aligned} L^*_{p,q}(f):=\lim _{s\rightarrow 1-} \int _{\Omega }\left( (1-s)\int _{B(x,\tau \text{ dist }(x,\partial \Omega ))}\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}dx<\infty , \end{aligned}$$

then $f\in W^{1,p}(\Omega )$ when $p>1$, and $f\in BV(\Omega )$ when $p=1$.

Remark 3

Before proceeding further, let us discuss some difficulties that arise here, and strategies for overcoming them. The proof of the main results roughly follow the outline of [8]. However, there are certain obstacles to that path. The first obstacle arises when we want to apply dominated convergence theorem to interchange limit and integral. Similar difficulty was faced and overcome in [27], but we had to take a different route (see lemma 9) for this purpose. The introduction of the second exponent q forces us to deviate from the usual route again; The case $q\le p$ is rather easy to handle, for the case $p<q$, a careful use of Sobolev embedding is needed. To take into account the case where the domain $\Omega$ is unbounded, we need to restrict the seminorm further and define some new fractional Sobolev spaces (see eq. 5) and prove a version of the main result theorem 1 in that context (see theorem 14), and then finally derive the proof of the main results from there.

The article is organised as follows: In section 2, we list some preliminary results, already known in literature, which shall be useful for the proof of our main results. In section 3, we introduce a variant of fractional Sobolev spaces and prove some relevant embedding results. In section 4 we prove the main results in the context of these new spaces (see theorems 14 and 15). Finally in section 5, we prove theorems 1 and 2.

2 Preliminary results

For the sake of completeness, we first state the well-known Sobolev inequality (also known as (q, p)-Poincaré inequality):

Lemma 4

Let $1\le p,q\le \infty$, $\tau \in (0,1)$, and one of the following hold

• (1) $p<N$, and $q \le \frac{Np}{N-p}$,

• (2) $p=N$, and $q <\infty$

• (3) $p>N$.

Then there is a constants $C=C(p,q,N)>0$ such that the following holds for any $f\in W^{1,p}(B(0,\frac{t}{\tau }))$:

$$\begin{aligned} \frac{1}{t^N}\int _{B(0,t)}|f(y)|^qdy{} & {} \le C(N,p,q) t^q \left( \frac{1}{t^N}\int _{B(0,t)}|\nabla f (y)|^p dy\right) ^\frac{q}{p} \\{} & {} + C(N,p,q) \left( \frac{1}{t^N}\int _{B(0,t)}|f(y)|^p dy\right) ^\frac{q}{p}. \end{aligned}$$

The following lemma was established in [20] for $1<p<\infty$; the $p\ge 1$ case can be found in [58, Chapter-VI, Theorems 5 and 5’].

Lemma 5

Let $\Omega \subseteq {\mathbb {R}}^N$ be an open set with Lipschitz boundary and $1\le p<\infty$. Then for any $f\in W^{1,p}(\Omega )$ there is some ${\tilde{f}}\in W^{1,p}({\mathbb {R}}^N)$ such that ${\tilde{f}}|_{\Omega }=f$ and for some constant $C=C(N,\Omega ,p)$,

$$\begin{aligned} \Vert {\tilde{f}}\Vert _{W^{1,p}({\mathbb {R}}^N)}\le C\Vert f\Vert _{W^{1,p}(\Omega )}. \end{aligned}$$

The following result can be found in Proposition 9.3 and Remark 6 of [13].

Lemma 6

Let $\Omega \subseteq {\mathbb {R}}^N$ be open, $1\le p<\infty$, $\frac{1}{p}+\frac{1}{p'}=1$, and $f\in L^p(\Omega )$. Assume that there is constant $C>0$ such that for any $\varphi \in C_c^{\infty }(\Omega )$

$$\begin{aligned} \left| \int _{\Omega }f(x)\frac{\partial \varphi (x)}{\partial x_i}dx\right| \le C\Vert \varphi \Vert _{L^{p'}(\Omega )} \quad \text{ for } i=1,2,\cdots , N. \end{aligned}$$

Then $f\in W^{1,p}(\Omega )$ when $1<p$, and $f\in BV(\Omega )$ when $p=1$.

Next we list a special case of Proposition 2/(ii) of [59, Chapter 2.3.3], combined with the fact that $W^{1,p}({\mathbb {R}}^N)=F^1_{p,2}({\mathbb {R}}^N)$.

Lemma 7

Let $1\le p,q<\infty$, $s\in (0,1)$. Then

$$\begin{aligned} W^{1,p}({\mathbb {R}}^N)\subseteq F^s_{p,q}({\mathbb {R}}^N) = W^{s,p}_q({\mathbb {R}}^N). \end{aligned}$$

The following result is taken from Lemma 8 of [5].

Lemma 8

Let $\Omega \subseteq {\mathbb {R}}^N$ be open and $\lambda > 0$ be sufficiently small. Then there is a bounded open set $\Omega _\lambda ^*$ with smooth boundary such that $\Omega _\lambda \subseteq \Omega _\lambda ^* \subseteq \Omega$, where $\Omega _\lambda$ is as in (2).

The next result can be found in Theorem 2.1 of [40]. It will play a crucial in this article.

Lemma 9

Let $\Omega \subseteq {\mathbb {R}}^N$, $\{\Omega _i\}_{i\in {\mathbb {N}}}$ be such that $\Omega =\cup _i\Omega _i$, $F_n,F\in L^1(\Omega )$ for $n\in {\mathbb {N}}$ be such that for a.e. $x\in \Omega$, $F_n(x)\rightarrow F(x)$ as $n\rightarrow \infty$. Assume that

• (1)
  $$\begin{aligned} \quad \quad \limsup _{n\rightarrow \infty }\sup _{x\in \Omega _i}\left| F_n(x)-F(x) \right| <\infty \quad \text{ for } \text{ all } i\in {\mathbb {N}}, \end{aligned}$$
• (2)
  $$\begin{aligned} \quad \quad \liminf _{i\rightarrow \infty }\limsup _{n\rightarrow \infty }\int _{\Omega \setminus \Omega _i} F_n(x)dx=0. \end{aligned}$$

Then

$$\begin{aligned} \lim _{n\rightarrow \infty }\int _{\Omega }F_n(x)dx =\int _{\Omega }F(x). \end{aligned}$$

3 Fractional Sobolev space with restricted internal distance

Fix $R>0$ and $\tau \in (0,1)$ once and for all. Denote $\delta _{x,R,\tau }= \min \{R,\tau \text{ dist }(x,\partial \Omega )\}$. We shall often drop the R and $\tau$ in the above notation and write $\delta _x$ to denote $\delta _{x,R,\tau }$.

Remark 10

If the function $x\mapsto \text{ dist }(x,\partial \Omega )$ is bounded in $\Omega$, we can choose $R>0$ large enough, so that $\delta _x=\tau \text{ dist }(x,\partial \Omega )$. Then the particular case $p=q$ of theorems 14 and 15 are similar to the results proved in [27], but here $\Omega$ need not be a bounded domain; for example, it can be a cylindrical domain or any open subset of ${\mathbb {R}}^N\setminus {\mathbb {Z}}^N$.

Define, for any open set $\Omega \subseteq {\mathbb {R}}^N$, $1\le p,q<\infty$, $0<s<1$, ${\hat{W}}^{s,p}_q(\Omega ):=\{f\in L^p(\Omega )\ |\ [f]_{{\hat{W}}^{s,p}_q(\Omega )}<\infty \}$ where

$$\begin{aligned}{}[f]_{{\hat{W}}^{s,p}_q(\Omega )}^p:=\int _{x\in \Omega }\left( \int _{y\in B(x,\delta _x)}\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}dx. \end{aligned}$$

(5)

We shall need some embedding results for these new fractional Sobolev spaces for our purpose. As expected, the case $q\le p$ and $p<q$ are treated separately.

Lemma 11

Let $\Omega \subseteq {\mathbb {R}}^N$ be open and $1\le q\le p <\infty$. Assume either $D={\tilde{D}}= \Omega$ or, for some $\frac{1}{2R}>\alpha >0$, $D= \{x\in \Omega \ |\ \text{ dist }(x,\partial \Omega )<\alpha \}$ with ${\tilde{D}}=\{x\in \Omega \ |\ \text{ dist }(x,\partial \Omega )<2\alpha \text{ or } |x|> \frac{1}{2\alpha } \}$. Then there is a constant $C=C(p,q,R,\Omega ,N)$ such that for any f in $W^{1,p}(\Omega )$,

$$\begin{aligned} (1-s)^\frac{p}{q}\int _{x\in D}\left( \int _{y\in B(x,\delta _x)} \frac{| f(x)-f(y) |^q}{| x-y |^{N+sq}} dy\right) ^\frac{p}{q}dx \le C [f]_{W^{1,p}({\tilde{D}})}^p. \end{aligned}$$

(6)

Proof

We have

$$\begin{aligned} (1-s)^\frac{p}{q}\int _{x\in D}&\left( \int _{y\in B(x,\delta _x)} \frac{| f(x)-f(y) |^q}{| x-y |^{N+sq}} dy\right) ^\frac{p}{q}dx\\ =&(1-s)^\frac{p}{q}\int _{x\in D} \left( \int _{h\in B(0,\delta _x)} \frac{| f(x+h)-f(x) |^q}{| h |^{N+sq}} dh\right) ^\frac{p}{q}dx\\ =&(1-s)^\frac{p}{q}\int _{x\in D} \left( \int _{h\in B(0,\delta _x)} \frac{| f(x+h)-f(x) |^q}{| h |^p} \frac{dh}{|h|^{N+sq-q}}\right) ^\frac{p}{q}dx\\ \le&(1-s)^\frac{p}{q}\int _{x\in D}\left( \int _{h\in B(0,\delta _x)} \int _{0}^1|\nabla f(x+th)|^qdt \frac{dh}{|h|^{N+sq-q}}\right) ^\frac{p}{q}dx. \end{aligned}$$

The last inequality follows from the absolute continuity on lines of the $W^{1,p}$-functions. We now have, after a change of variable $y=x+th$, (using that $B(x,t\delta _x) \subset B(x,\delta _x)$)

$$\begin{aligned} (1-s)^\frac{p}{q}\int _{x\in D}&\left( \int _{y\in B(x,\delta _x)} \frac{| f(x)-f(y) |^q}{| x-y |^{N+sq}} dy\right) ^\frac{p}{q}dx\\ \le&(1-s)^\frac{p}{q}\int _{x\in D}\left( \int _{y\in B(x,\delta _x)} \int _{0}^1|\nabla f(y)|^qt^{sq-q}dt \frac{dy}{|x-y|^{N+sq-q}}\right) ^\frac{p}{q}dx\\ =&\frac{(1-s)^\frac{p}{q}}{(sq-q+1)^\frac{p}{q}}\int _{x\in D}\left( \int _{y\in B(x,\delta _x)} |\nabla f(y)|^q \frac{dy}{|x-y|^{N+sq-q}}\right) ^\frac{p}{q}dx. \end{aligned}$$

Note that in the above inequality, $\nabla f$ is required to be defined only inside ${\tilde{D}}$. So, we shall take a 0-extension of $\nabla f$ outside ${\tilde{D}}$. Since we have $\frac{p}{q}\ge 1$, we can use Young’s convolution inequality to get

$$\begin{aligned} (1-s)^\frac{p}{q}\int _{x\in D}&\left( \int _{y\in B(x,\delta _x)} \frac{| f(x)-f(y) |^q}{| x-y |^{N+sq}} dy\right) ^\frac{p}{q}dx\\ \le&\frac{(1-s)^\frac{p}{q}}{(sq-q+1)^\frac{p}{q}}\int _{x\in D}\left( \int _{y\in B(x,R)} |\nabla f(y)|^q \frac{dy}{|x-y|^{N+sq-q}}\right) ^\frac{p}{q}dx\\ \le&\frac{(1-s)^\frac{p}{q}}{(sq-q+1)^\frac{p}{q}}\int _{{x\in {\tilde{D}}}}|\nabla f(x)|^pdx\left( \int _{x\in B(0,R)} \frac{dx}{|x|^{N+sq-q}}\right) ^\frac{p}{q}\\ =&\frac{R^{p-sp}}{q^\frac{p}{q}}\int _{{x\in {\tilde{D}}}}|\nabla f(x)|^pdx. \end{aligned}$$

$\square$

Lemma 12

Let $\Omega \subseteq {\mathbb {R}}^N$ be open, $1<p<q<\infty$, and one of the following hold

• (1) $p<N$, and $q <\frac{Np}{N-p}$,

• (2) $N\le p$.

Assume either $D={\tilde{D}}= \Omega$ or, for some $\frac{1}{2R}>\alpha >0$, $D= \{x\in \Omega \ |\ \text{ dist }(x,\partial \Omega )<\alpha \}$ and ${\tilde{D}}=\{x\in \Omega \ |\ \text{ dist }(x,\partial \Omega )<2\alpha \text{ or } |x|> \frac{1}{2\alpha }\}$. Then there is a constant $C=C(N,R,p,q)>0$ such that for any $f\in W^{1,p}(\Omega )$, eq. (6) holds.

Proof

Note that

$$\begin{aligned} \int _{t=|h|}^{\delta _x}\frac{dt}{t^{N+sq+1}} =\frac{1}{N+sq}\left( \frac{1}{|h|^{N+sq}}-\frac{1}{\delta _x^{N+sq}}\right) , \end{aligned}$$

which gives

$$\begin{aligned} \frac{1}{|h|^{N+sq}} = (N+sq)\int _{t=|h|}^{\delta _x}\frac{dt}{t^{N+sq+1}}+\delta _x^{-N-sq}. \end{aligned}$$

So, we can write

$$\begin{aligned} C(p,q) \int _{x\in D}&\left( (1-s)\int _{h\in B(0,\delta _x)} \frac{| f(x+h)-f(x) |^q}{| h |^{N+sq}} dh\right) ^\frac{p}{q}dx\nonumber \\ \le&\int _{x\in D}\left( (N+sq)(1-s)\int _{h\in B(0,\delta _x)} \int _{t=|h|}^{\delta _x} \frac{| f(x+h)-f(x) |^q}{t^{N+sq+1}}dt dh\right) ^\frac{p}{q}dx\nonumber \\&+ \int _{x\in D}\left( (1-s)\int _{h\in B(0,\delta _x)} \frac{| f(x+h)-f(x) |^q}{\delta _x^{N+sq}} dh\right) ^\frac{p}{q}dx\nonumber \\ =&I_1+I_2. \end{aligned}$$

(7)

According to either $p<N$ or $p\ge N$, fix $\beta \in (0,1)$, depending on p, q, N, such that $(q,\beta p)$-type Poincaré inequality (lemma 4) is satisfied. We use this to estimate $I_1$ below. First, we change the order of integration between t and h, then apply lemma 4.

$$\begin{aligned} I_1=&\int _{x\in D}\left( (N+sq)(1-s)\int _{t=0}^{\delta _x} \frac{1}{t^{N+sq+1}} \int _{h\in B(0,t)} | f(x+h)-f(x) |^q dhdt \right) ^\frac{p}{q}dx\nonumber \\ \le&\int _{x\in D}\left( (N+sq)(1-s)\int _{t=0}^{\delta _x} \frac{1}{t^{sq+1-q}} \left( \frac{1}{t^N}\int _{h\in B(x,t)} |\nabla f(h)|^{\beta p}dh\right) ^\frac{q}{\beta p}dt \right) ^\frac{p}{q}dx\nonumber \\&+ \int _{x\in D}\left( (N+sq)(1-s)\int _{t=0}^{\delta _x} \frac{1}{t^{sq+1}} \left( \frac{1}{t^N}\int _{h\in B(0,t)} | f(x+h)-f(x) |^{\beta p} dh \right) ^\frac{q}{\beta p}dt \right) ^\frac{p}{q}dx\nonumber \\ =&\, I_{1,1}+I_{1,2}. \end{aligned}$$

(8)

As in the proof of the previous lemma, we shall take a 0-extension of $\nabla f$ outside ${\tilde{D}}$. Now using Hardy-Littelewood maximal inequality, we get

$$\begin{aligned} I_{1,1} \le&\, \int _{x\in D}(M |\nabla f(x)|^{\beta p})^\frac{1}{\beta }\left( (N+sq)(1-s)\int _{t=0}^{\delta _x} \frac{1}{t^{sq+1-q}} dt \right) ^\frac{p}{q}dx\nonumber \\ =&\, C(N,p,q,R)\int _{{x\in {\mathbb {R}}^N}}(M |\nabla f(x)|^{\beta p})^\frac{1}{\beta }dx\nonumber \\ \le&C(N,p,q,R)\int _{{x\in {\tilde{D}}}}|\nabla f(x)|^pdx. \end{aligned}$$

(9)

Again,

$$\begin{aligned} I_{1,2} \le&\int _{x\in D}\left( (N+sq)(1-s)\int _{t=0}^{\delta _x} \frac{1}{t^{sq+1-q}} \left( \frac{1}{t^N}\int _{h\in B(0,t)} \frac{| f(x+h)-f(x) |^{\beta p}}{|h|^{\beta p}} dh \right) ^\frac{q}{\beta p}dt \right) ^\frac{p}{q}dx\nonumber \\ \le&\int _{x\in D}\left( (N+sq)(1-s)\int _{t=0}^{\delta _x} \frac{1}{t^{sq+1-q}} \left( \int _{r=0}^1\frac{1}{t^N}\int _{h\in B(0,t)} |\nabla f(x+rh)|^{\beta p} dhdr \right) ^\frac{q}{\beta p}dt \right) ^\frac{p}{q}dx\nonumber \\ =&\int _{x\in D}\left( (N+sq)(1-s)\int _{t=0}^{\delta _x} \frac{1}{t^{sq+1-q}} \left( \int _{r=0}^1\frac{1}{(rt)^N}\int _{h\in B(x,rt)} |\nabla f(h)|^{\beta p} dhdr \right) ^\frac{q}{\beta p}dt \right) ^\frac{p}{q}dx\nonumber \\ \le&\int _{x\in {\mathbb {R}}^N}(M|\nabla f(x)|^{\beta p})^\frac{1}{\beta }\left( (N+sq)(1-s)\int _{t=0}^{R} \frac{1}{t^{sq+1-q}} \left( \int _{r=0}^1dr \right) ^\frac{q}{\beta p}dt \right) ^\frac{p}{q}dx\nonumber \\ \le&C(p,q,N,R) \int _{{x\in {\tilde{D}}}}|\nabla f(x)|^{p}dx. \end{aligned}$$

(10)

Combining eqs. (9) and (10), we get

$$\begin{aligned} I_1 \le C(p,q,N,R) \Vert \nabla f\Vert _{{L^p({\tilde{D}})}}^p. \end{aligned}$$

(11)

Again, we can estimate $I_2$, in similar way as above with $\delta _x$ in place of t. We have a better estimate this time. Also, we can apply (q, p)-Poincaré inequality this time.

$$\begin{aligned}&I_2 =\int _{x\in D}\left( (1-s)\int _{h\in B(0,\delta _x)} \frac{| f(x+h)-f(x) |^q}{\delta _x^{N+sq}} dh\right) ^\frac{p}{q}dx\nonumber \\&\quad \le \int _{x\in D}\left( \frac{(1-s)}{\delta _x^{sq}}\left( \delta _x^{p-N}\int _{h\in B(0,\delta _x)} |\nabla f(x+h)|^p dh + \delta _x^{-N}\right. \right. \nonumber \\&\quad \left. \left. \int _{h\in B(0,\delta _x)} | f(x+h)-f(x) |^p dh\right) ^\frac{q}{p}\right) ^\frac{p}{q}dx\nonumber \\&\quad \le \int _{x\in D}\frac{(1-s)^\frac{p}{q}}{\delta _x^{sp-p}}\left( \left( \delta _x^{-N}\int _{h\in B(0,\delta _x)} |\nabla f(x+h)|^p dh + \delta _x^{-N}\right. \right. \nonumber \\&\quad \left. \left. \int _{h\in B(0,\delta _x)} \frac{| f(x+h)-f(x) |^p}{|h|^p} dh\right) ^\frac{q}{p}\right) ^\frac{p}{q}dx\nonumber \\&\quad \le \int _{x\in D}\frac{(1-s)^\frac{p}{q}}{\delta _x^{sp-p}}\left( \delta _x^{-N}\int _{h\in B(0,\delta _x)} |\nabla f(x+h)|^p dh + \int _{r=0}^1\frac{1}{(r\delta _x)^N}\right. \nonumber \\&\quad \left. \int _{h\in B(0,r\delta _x)} |\nabla f(x+h)|^p dhdr\right) dx\nonumber \\&\quad \le (1-s)^\frac{p}{q}\int _{x\in D}\delta _x^{p-sp}|\nabla f(x)|^pdx. \end{aligned}$$

(12)

Combing eqs. (7), (11) and (12),

$$\begin{aligned} \int _{x\in D}\left( (1-s)\int _{h\in B(0,\delta _x)} \frac{| f(x+h)-f(x) |^q}{| h |^{N+sq}} dh\right) ^\frac{p}{q}dx \le C(N,p,q,R) \Vert \nabla f\Vert _{{L^p({\tilde{D}})}}^p. \end{aligned}$$

This proves the lemma. $\square$

4 BBM formula for ${\hat{W}}^{s,p}_q$-seminorms

First, we state the following result whose proof can be found in the proof of Theorem  of [8] as the quantity $\delta _x$ is bounded by R.

Lemma 13

Let $\Omega \subset {\mathbb {R}}^N$ be any open set, $1\le q<\infty$, $0<s<1$. Then for any $f\in C^2(\Omega )$, we have for all $x\in \Omega$,

$$\begin{aligned} \lim _{s\rightarrow 1-} (1-s)\int _{B(x,\delta _x)}\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy = K |\nabla f(x)|^q. \end{aligned}$$

(13)

We now prove the following BBM-type results which are closely related with theorems 1 and 2.

Theorem 14

Let $\Omega \subset {\mathbb {R}}^N$ be any open set. Assume one of the following conditions

• (1) $1\le q\le p<\infty$,

• (2) $1<p<q<\infty$ with $p\le N$ and $q <\frac{Np}{N-p}$,

• (3) $N<p<q<\infty$.

Then there is a constant $K=K(N,p,q)>0$ such that for any $f\in W^{1,p}(\Omega )$, we have for all $x\in \Omega$,

$$\begin{aligned} \lim _{s\rightarrow 1-} (1-s)^\frac{p}{q}\int _{\Omega }\left( \int _{B(x,\delta _x)}\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}dx = K\int _{\Omega }|\nabla f(x)|^pdx. \end{aligned}$$

(14)

Proof of Theorem 14

Step-1: We show that it is enough to prove eq. (14) for $f\in W^{1,p}(\Omega )\cap C^2(\Omega )$.

Let $f \in W^{1,p}(\Omega )$ and $\varepsilon >0$ be fixed. Since $C^2(\Omega )\cap W^{1,p}(\Omega )$ is dense in $W^{1,p}(\Omega )$, there exists $g \in C^2(\Omega )\cap W^{1,p}(\Omega )$ such that

$$\begin{aligned}{}[f-g]_{W^{1,p}(\Omega )} < \varepsilon . \end{aligned}$$

(15)

Since we have assumed that eq. (14) holds for functions in $C^2(\Omega )\cap W^{1,p}(\Omega )$, for $s>\frac{1}{2}$, we have

$$\begin{aligned} \left| (1-s)^\frac{1}{q}[g]_{s,p,q,\Omega ,R}-K^\frac{1}{p}[g]_{W^{1,p}(\Omega )} \right| <\varepsilon . \end{aligned}$$

(16)

Using triangle inequality, and then eq. (16) followed by eq. (15) and either lemma 11 or lemma 12, we get

$$\begin{aligned}&\left| (1-s)^\frac{1}{q}[f]_{s,p,q,\Omega ,R}-K^\frac{1}{p}[f]_{W^{1,p}(\Omega )} \right| \le (1-s)^\frac{1}{q}\left| [f]_{s,p,q,\Omega ,R} - [g]_{s,p,q,\Omega ,R} \right| \\&+\quad \left| (1-s)^\frac{1}{q}[g]_{s,p,\Omega ,R}-K^\frac{1}{q}[g]_{W^{1,p}(\Omega )} \right| + K^\frac{1}{q}\left| [g]_{W^{1,p}(\Omega )}-[f]_{W^{1,p}(\Omega )}\right| \\&\quad \le (1-s)^\frac{1}{q}[f-g]_{s,p,q,\Omega ,R} + \varepsilon + K^\frac{1}{p}[f-g]_{W^{1,p}(\Omega )}\\&\quad \le [f-g]_{W^{1,p}(\Omega )} +\varepsilon + K^\frac{1}{p}[f-g]_{W^{1,p}(\Omega )}\\&\quad \le C(K,q) \varepsilon . \end{aligned}$$

The proof of step-1 follows.

Step-2:

In view of the previous step, it is now enough to assume that $f\in C^2(\Omega )\cap W^{1,p}(\Omega )$ and prove eq. (14). Let us take an arbitrary sequence $s_n\in (0,1)$ such that $s_n\rightarrow 1-$ as $n\rightarrow \infty$. Set

$$\begin{aligned} F_n(x):=\left( (1-s_n)\int _{B(0,\delta _x)}\frac{|f(x+h)-f(x)|^p}{|h|^{N+s_np}}dh\right) ^\frac{p}{q}, \end{aligned}$$

and

$$\begin{aligned} F(x):=K|\nabla f(x)|^p. \end{aligned}$$

Also note that, lemma 13 implies that $F_n\rightarrow F$ pointwise a.e in $\Omega$. To complete the proof, it is enough to show that

$$\begin{aligned} \lim _{n\rightarrow \infty }\int _{\Omega }F_n(x)dx=\int _{\Omega }F(x)dx. \end{aligned}$$

We shall apply lemma 9 on $F_n$ to show that the interchange of limit and integral is valid.

For any $i\in {\mathbb {N}}$, consider the sets $\Omega _i:=\{x\in \Omega \ |\ \text{ dist }(x,\partial \Omega )>\frac{1}{i}\}\cap B(0,i)$. We need to verify the the hypotheses of lemma 9. First, note that for $x\in \Omega _i$, $h\in B(0,\delta _x)$, $t\in (0,1)$, we have

$$\begin{aligned} \text{ dist }(x+th,\partial \Omega ) > \text{ dist }(x,\partial \Omega ) -|h| \ge (1-\tau )\text{ dist }(x,\partial \Omega ). \end{aligned}$$

Thus $x+th\in \Omega _{i^2}$ for $i>\frac{1}{(1-\tau )}$. Thus, we have using triangle inequality and then mean value inequality,

$$\begin{aligned} |F_{n}(x)-F(x)|&=\left| \left( (1-s_n)\int _{B(0,\delta _x)}\frac{|f(x+h)-f(x)|^q}{|h|^{N+s_nq}}dh\right) ^\frac{p}{q}-K|\nabla f(x)|^p \right| \\&\le \sup _{y\in \Omega _{i^2}}|\nabla f(y)|^p\left( (1-s_n)\int _{B(0,R)}\frac{dh}{|h|^{N+s_nq-q}}\right) ^\frac{p}{q} +K|\nabla f(x)|^p\\&\le C(N,p,q,R)\sup _{y\in \Omega _{i^2}}|\nabla f(y)|^p. \end{aligned}$$

Since f is continuous in the closure of the bounded open set $\Omega _{i^2}$, we have the hypothesis (1) of lemma 9 satisfied for sufficiently large $i\in {\mathbb {N}}$.

Note that, to show that hypothesis (2) of lemma 9 is satisfied, it is enough to show that

$$\begin{aligned} \lim _{i\rightarrow \infty }\lim _{n\rightarrow \infty }\int _{\Omega \setminus \Omega _{2i}} F_n(x)dx=0. \end{aligned}$$

We start with an arbitrary $x\in \Omega \setminus \Omega _{2i}$, $h\in B(0,\delta _x)$ and $t\in (0,1)$. There can be two cases:

Case:1 $\delta _x=\text{ dist }(x,\partial \Omega )<\frac{1}{2i}$.

We have $\text{ dist }(x+th,\partial \Omega )\le |x+th-x|+\text{ dist }(x,\partial \Omega )<\frac{\tau }{2i}+\frac{1}{2i}<\frac{1}{i}$. Thus $x+th\in \Omega \setminus \Omega _i$.

Case:2 $|x|>2i$ and $\frac{1}{2i}<\delta _x=R<\text{ dist }(x,\partial \Omega )$. Moreover, we can assume $R<i$ without loss of generality.

We have $|x+th|\ge |x|-\tau R \ge 2i-\tau R\ge i$. Thus $x+th\in \Omega \setminus B(0,i)\subseteq \Omega \setminus \Omega _i$. Hence we always have

$$\begin{aligned} x+th\in \Omega \setminus \Omega _i \text{ whenever } x\in \Omega \setminus \Omega _{2i}. \end{aligned}$$

(17)

From eq. (17), we get

$$\begin{aligned} \lim _{i\rightarrow \infty }\lim _{n\rightarrow \infty }\int _{\Omega \setminus \Omega _{2i}} F_n(x)dx =\lim _{i\rightarrow \infty }\lim _{n\rightarrow \infty } \int _{x\in \Omega \setminus \Omega _{2i}}\left( (1-s_n)\int _{y\in B(x,\delta _x)} \frac{| f(x)-f(y) |^q}{| x-y |^{N+s_nq}} dy\right) ^\frac{p}{q}dx. \end{aligned}$$

Now we apply lemma 11 or lemma 12 with $D=\Omega \setminus \Omega _{2i}$ (so that ${\tilde{D}}=\Omega \setminus \Omega _{i}$) to get

$$\begin{aligned} \lim _{i\rightarrow \infty }\lim _{n\rightarrow \infty }\int _{\Omega \setminus \Omega _{2i}} F_n(x)dx\le & {} \lim _{i\rightarrow \infty }\lim _{n\rightarrow \infty } C(p,q,R,N)[f]_{W^{1,p}(\Omega \setminus \Omega _i)}^p \\= & {} \lim _{i\rightarrow \infty } C(p,q,R,N)[f]_{W^{1,p}(\Omega \setminus \Omega _i)}^p =0. \end{aligned}$$

Hence we can integrate eq. (13) and interchange the limit and the integral to get the result. $\square$

Theorem 15

Let $\Omega \subset {\mathbb {R}}^N$ be an open set. If $f\in L^p(\Omega )\cap L^p(\Omega )$ is such that

$$\begin{aligned} L_{p,q}(f):=\lim _{s\rightarrow 1-} \int _{\Omega }\left( (1-s)\int _{B(x,\delta _x)}\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}dx<\infty , \end{aligned}$$

then $f\in W^{1,p}(\Omega )$ when $p>1$, and $f\in BV(\Omega )$ when $p=1$.

Proof of Theorem 15

We divide the proof into two parts. First, we prove it for a particular case with a bit stronger assumptions, and then give the general proof.

Step-1: $\Omega$ is bounded with $\Omega \subseteq B(0,\lambda )$, and

$$\begin{aligned} {\tilde{L}}_{p,q}(f):=\lim _{s\rightarrow 1-} \int _{\Omega }\left( (1-s)\int _{\Omega }\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}dx <\infty . \end{aligned}$$

Extend f by 0, outside $\Omega$. From the proof of Theorem 2 and 3 in [8] we can see that for any $i=1,2,\cdots ,N$, and $\varphi \in C_c^{\infty }(\Omega )$,

$$\begin{aligned} \left| \int _{\Omega }f(x)\frac{\partial \varphi (x)}{\partial x_i} dx\right| \le C(\Omega ,N,p,q)(1-s)(J_{1,s}+J_{2,s}), \end{aligned}$$

(18)

where,

$$\begin{aligned} J_{1,s}= \int _{\Omega }\int _{\Omega }\frac{|f(x)-f(y)|}{|x-y|^{1+N+sq-q}}|\varphi (y)|dydx \end{aligned}$$

and

$$\begin{aligned} J_{2,s}=\int _{{\mathbb {R}}^N\setminus \Omega }\int _{\text{ supp }\varphi }\frac{|f(y)||\varphi (y)|}{|x-y|^{1+N+sq-q}}dydx. \end{aligned}$$

We estimate $J_{1,s}$ using Fubuni’s theorem to change the order of integration, then using Hölder’s inequality twice, first with respect to the measure $\frac{dx}{|x-y|^{N+sq-q}}$ and then with respect to dy. We get

$$\begin{aligned} J_{1,s}&\le \int _{\Omega }\left( \int _{\Omega }\frac{|f(x)-f(y)|^q}{|x-y|^{q+N+sq-q}}dx\right) ^\frac{1}{q} \left( \int _{\Omega }\frac{|\varphi (y)|^{q'}}{|x-y|^{N+sq-q}}dx\right) ^\frac{1}{q'}dy\\&\le \left( \int _{\Omega }\left( \int _{\Omega }\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dx\right) ^\frac{p}{q}dy\right) ^\frac{1}{p} \left( \int _{\Omega }\left( \int _{\Omega }\frac{|\varphi (y)|^{q'}}{|x-y|^{N+sq-q}}dx\right) ^\frac{p'}{q'}dy\right) ^\frac{1}{p'}\\&\le \left( \int _{\Omega }\left( \int _{\Omega }\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}dx\right) ^\frac{1}{p} \left( \int _{\Omega }|\varphi (y)|^{p'}\left( \int _{B(0,\lambda )}\frac{dx}{|x-y|^{N+sq-q}}\right) ^\frac{p'}{q'}dy\right) ^\frac{1}{p'}\\&= C(p,q,N,\lambda )(1-s)^\frac{-1}{q'} \left( \int _{\Omega }\left( \int _{\Omega }\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}dx\right) ^\frac{1}{p} \Vert \varphi \Vert _{L^{p'}(\Omega )} \end{aligned}$$

Now using the hypothesis of Step-1, we have

$$\begin{aligned} (1-s)J_{1,s} \le C(p,q,N,\lambda ) {\tilde{L}}_{p,q}(f) \Vert \varphi \Vert _{L^{p'}(\Omega )}. \end{aligned}$$

(19)

Using Hölder’s inequality, we estimate $J_{2,s}$ as in [8] to get

$$\begin{aligned} (1-s)J_{2,s} \le C(N,p,q,\lambda ) \Vert \varphi \Vert _{L^{p'}(\Omega )} \Vert f\Vert _{L^{p}(\Omega )} \end{aligned}$$

(20)

Using eqs. (18) to (20), we get

$$\begin{aligned} \left| \int _{\Omega }f(x)\frac{\partial \varphi (x)}{\partial x_i} \right| \le C(\Omega ,N,p,q,\lambda ,f)\Vert \varphi \Vert _{L^{p'}(\Omega )}, \end{aligned}$$

Hence by lemma 6, the result follows.

Step-2: We now prove the theorem in full generality.

For $1< p<\infty$, define $X^{1,p}(\Omega ):=W^{1,p}(\Omega )$, and $X^{1,1}(\Omega ):=BV(\Omega )$. Using lemma 8, choose an increasing sequence of bounded open sets $\{\Omega _n\}_n$ with smooth boundary such that $\cup _n\Omega _n=\Omega$, and $\text{ dist }(x,\partial \Omega )>\frac{1}{n}$, for $x\in \Omega _n$. From the hypothesis, it follows that

$$\begin{aligned} \lim _{s\rightarrow 1-} \int _{x\in \Omega _n}\left( (1-s)\int _{y\in \Omega _n\cap B(x,\delta _x)}\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}dx<\infty . \end{aligned}$$

We also have, for $s>\frac{1}{2}$, and $R>\frac{1}{n}$,

$$\begin{aligned} \int _{\Omega _n}\left( \int _{\Omega _n\setminus B(x,\delta _x)}\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}dx&\le \int _{\Omega _n}\left( \int _{\Omega _n,\ |x-y|>\frac{1}{n}}\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}dx\\&\le n^{\frac{Np}{q}+sp}\int _{\Omega _n}\left( \int _{\Omega _n,\ |x-y|>\frac{1}{n}}|f(x)-f(y)|^qdy\right) ^\frac{p}{q}dx\\&\le C(n,N,p,q) \left[ \Vert f\Vert _{L^p(\Omega _n)}^p|\Omega _n|^\frac{p}{q} + \Vert f\Vert _{L^q(\Omega _n)}^p|\Omega _n|\right] . \end{aligned}$$

Since, we have $f\in L^p(\Omega )\cap L^p(\Omega )$ frfom the hypotheses, and $\Omega _n$ are bounded domains, we have

$$\begin{aligned} \lim _{s\rightarrow 1-} \int _{\Omega _n}\left( (1-s)\int _{\Omega _n}\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}dx<\infty . \end{aligned}$$

From Step-1, we can conclude that $f\in X^{1,p}(\Omega _n)$ for all n. Further the $X^{1,p}$-seminorms are uniformly bounded (independent of n) as can be seen from the following calculation, where we use theorem 14,

$$\begin{aligned} K[f]_{X^{1,p}(\Omega _n)}^p&= \lim _{s\rightarrow 1-} \int _{x\in \Omega _n}\left( (1-s)\int _{y\in B(x,\delta _{x,\Omega _n})}\frac{|f(x)-f(y)|^p}{|x-y|^{N+sp}}dy\right) ^\frac{p}{q}dx\\&\le \lim _{s\rightarrow 1-} \int _{x\in \Omega }\left( (1-s)\int _{y\in B(x,\delta _x)}\frac{|f(x)-f(y)|^p}{|x-y|^{N+sp}}dy\right) ^\frac{p}{q}dx\\&=L_{p,q}(f)<\infty . \end{aligned}$$

The proof follows from the observation that $K[f]_{X^{1,p}(\Omega )}^p =\sup _{n} K[f]_{X^{1,p}(\Omega _n)}^p$. $\square$

5 Proofs of Theorems 1 and 2

Note that theorem 2 is a straightforward consequence of theorem 15, as $L_{p,q}(f)\le L^*_{p,q}(f)$. theorem 1 is also a consequence of theorem 14, but it requires a bit more work. To complete the proof of theorem 1, we only need the following lemma:

Lemma 16

Let $\Omega \subseteq {\mathbb {R}}^N$ be an open set, $1\le p <\infty$, $\tau \in (0,1)$, $f\in W^{1,p}(\Omega )$ and $R>0$. Assume one of the following conditions

• (1) $1\le q\le \frac{Np}{N-p}$ with $p< N$,

• (2) $1\le q<\infty$ with $p\ge N$.

Then eq. (14) implies eq. (4).

In order to prove this, we first prove a bit more general result.

Proposition 17

Let $\Omega \subseteq {\mathbb {R}}^N$ be an open set, $1\le p,q<\infty$, $\tau \in (0,1)$, $f\in L^p(\Omega )\cap L^q(\Omega )$ and $R>0$. Additionally, in the case $p<q$, assume that for some $s_0\in (0,1)$,

$$\begin{aligned} \int _{\Omega }\left( \int _{R\le |h|\le \tau \text{ dist }(x,\partial \Omega )}\frac{|f(x+h)-f(x)|^q}{|h|^{N+s_0q}}dh\right) ^\frac{p}{q}dx<\infty . \end{aligned}$$

(21)

Then eq. (14) implies eq. (4).

Proof of Proposition 17

Note that, since

$$\begin{aligned} \int _{\Omega }\left( \int _{B(x,\delta _x)}\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}dx \le \int _{\Omega }\left( \int _{B(x,\tau \text{ dist }(x,\partial \Omega ))}\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}dx, \end{aligned}$$

from eq. (14) we have

$$\begin{aligned} \lim _{s\rightarrow 1-} (1-s)^\frac{p}{q}\int _{\Omega }\left( \int _{B(x,\tau \text{ dist }(x,\partial \Omega ))}\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}dx \ge K\int _{\Omega }|\nabla f(x)|^pdx. \end{aligned}$$

We focus on the reverse inequality. Observe that for $x,y\in \Omega$, $\delta _x< |x-y|\le \tau \text{ dist }(x,\partial \Omega )$ implies $R< |x-y|\le \tau \text{ dist }(x,\partial \Omega )$. Hence we can write, using triangle inequality for $L^p$-norms,

$$\begin{aligned}&\left( \int _{\Omega }\left( \int _{B(x,\tau \text{ dist }(x,\partial \Omega ))}\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}dx\right) ^\frac{1}{p} \\&\quad = \left( \int _{\Omega }\left( \int _{B(x,\delta _x)}\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy + \int _{\delta _x\le |x-y|\le \tau \text{ dist }(x,\partial \Omega )}\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}dx\right) ^\frac{1}{p} \\&\quad \le \left( \int _{\Omega }\left( \int _{B(x,\delta _x)}\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}dx\right) ^\frac{1}{p} \\&\qquad + \left( \int _{\Omega }\left( \int _{R\le |x-y|\le \tau \text{ dist }(x,\partial \Omega )}\frac{|f(x)-f(y)|^q}{|x-y|^{N+sq}}dy\right) ^\frac{p}{q}dx\right) ^\frac{1}{p}\\&\quad =:I_1^\frac{1}{p}+I_2^\frac{1}{p}. \end{aligned}$$

In order to complete the proof, in view of eq. (14), we need to show that $I_2$ is bounded as $s\rightarrow 1-$. We estimate $I_2$ in two separate cases.

Case-1: $1\le q\le p<\infty$.

Using Minkowsky’s integral inequality and taking the 0-extension of f outside $\Omega$, we have

$$\begin{aligned} I_2^\frac{q}{p}&\le \left( \int _{\Omega }\left( \int _{R\le |h|\le \tau \text{ dist }(x,\partial \Omega )}\frac{|f(x+h)-f(x)|^q}{|h|^{N+sq}}dh\right) ^\frac{p}{q}dx\right) ^\frac{q}{p}\\&\le \int _{{\mathbb {R}}^N}\left( \int _{\Omega }\frac{|f(x+h)-f(x)|^p}{|h|^{\frac{Np}{q}+sp}}\chi _{B(0,\tau \text{ dist }(x,\partial \Omega ))\setminus B(0,R)}(h)dx\right) ^\frac{q}{p}dh\\&\le \int _{|h|\ge R}\frac{1}{|h|^{N+sq}} \left( \int _{\Omega }|f(x+h)-f(x)|^pdx\right) ^\frac{q}{p}dh\\&\le C(p,q) \int _{|h|\ge R}\frac{1}{|h|^{N+sq}} \left( \int _{\Omega }|f(x)|^pdx\right) ^\frac{q}{p}dh\\&\le C(p,q,R,N) \Vert f\Vert _{L^p(\Omega )}^q. \end{aligned}$$

Hence the proof follows in this case.

Case-2: $1\le p\le q<\infty$.

From eq. (21) we get that there is some $\lambda _f>0$ such that for $s\in (s_0,1)$,

$$\begin{aligned} I_2&\le \int _{\Omega }\left( \int _{R\le |h|\le \tau \text{ dist }(x,\partial \Omega )}\frac{|f(x+h)-f(x)|^q}{|h|^{N+s_0q}}dh\right) ^\frac{p}{q}dx\\&\le 2\int _{\Omega \cap B(0,\lambda _f)}\left( \int _{R\le |h|\le \tau \text{ dist }(x,\partial \Omega )}\frac{|f(x+h)-f(x)|^q}{|h|^{N+s_0q}}dh\right) ^\frac{p}{q}dx. \end{aligned}$$

Using Hölder’s inequality, we get

$$\begin{aligned} I_2 \le 2\lambda _f^{N(1-\frac{p}{q})}\left( \int _{\Omega \cap B(0,\lambda _f)}\int _{R\le |h|\le \tau \text{ dist }(x,\partial \Omega )}\frac{|f(x+h)-f(x)|^q}{|h|^{N+s_0q}}dhdx\right) ^\frac{p}{q}. \end{aligned}$$

Now we can proceed as in Case-1 to show that

$$\begin{aligned} I_2 \le C(N,p,q,R,f) \Vert f\Vert _{L^q(\Omega )}^p. \end{aligned}$$

This completes the proof. $\square$

Now we can prove lemma 16 and thereby complete the proof of theorem 1.

Proof of lemma 16

By the standard embedding theorems, we already know that $f\in L^q(\Omega )$. In order to prove the statement, we need to show that when $p<q$, eq. (21) holds. Let $\Omega _1$ be a smooth domain such that

$$\begin{aligned} \{x\in \Omega \ |\ \text{ dist }(x,\partial \Omega )>R\} \subseteq \Omega _1\subseteq \Omega . \end{aligned}$$

Clearly $\Omega _1$ is a $W^{1,p}$-extension domain (by lemma 5). Let ${\tilde{f}}\in W^{1,p}({\mathbb {R}}^N)$ be an extension of $f|_{\Omega _1}$, that is

$$\begin{aligned} \Vert {\tilde{f}}\Vert _{W^{1,p}({\mathbb {R}}^N)} \le C(p,q,N,\Omega ) \Vert f\Vert _{W^{1,p}(\Omega _1)} \le C(p,q,N,\Omega ) \Vert f\Vert _{W^{1,p}(\Omega )}<\infty . \end{aligned}$$

This, along with lemma 7

$$\begin{aligned}&\int _{\Omega }\left( \int _{R\le |h|\le \tau \text{ dist }(x,\partial \Omega )}\frac{|f(x+h)-f(x)|^q}{|h|^{N+sq}}dh\right) ^\frac{p}{q}dx \\&\quad = \int _{\Omega _1}\left( \int _{R\le |h|\le \tau \text{ dist }(x,\partial \Omega )}\frac{|f(x+h)-f(x)|^q}{|h|^{N+sq}}dh\right) ^\frac{p}{q}dx\\&\quad \le \int _{{\mathbb {R}}^N}\left( \int _{{\mathbb {R}}^N}\frac{|{\tilde{f}}(x+h)-{\tilde{f}}(x)|^q}{|h|^{N+sq}}dh\right) ^\frac{p}{q}dx\\&\quad <\infty . \end{aligned}$$

$\square$