Linear inverse problems with Hessian–Schatten total variation

Abstract

In this paper, we characterize the class of extremal points of the unit ball of the Hessian–Schatten total variation (HTV) functional. The underlying motivation for our work stems from a general representer theorem that characterizes the solution set of regularized linear inverse problems in terms of the extremal points of the regularization ball. Our analysis is mainly based on studying the class of continuous and piecewise linear (CPWL) functions. In particular, we show that in dimension $d=2$, CPWL functions are dense in the unit ball of the HTV functional. Moreover, we prove that a CPWL function is extremal if and only if its Hessian is minimally supported. For the converse, we prove that the density result (which we have only proven for dimension $d=2$) implies that the closure of the CPWL extreme points contains all extremal points.

1 Introduction

Broadly speaking, the goal of an inverse problem is to reconstruct an unknown signal of interest from a collection of (possibly noisy) observations. Linear inverse problems, in particular, are prevalent in various areas of signal processing, such as denoising, impainting, and image reconstruction. They are defined via the specification of three principal components: (i) a hypothesis space ${\mathcal {F}}$ from which we aim to reconstruct the unknown signal $f^*\in {\mathcal {F}}$; (ii) a linear forward operator $\varvec{\nu }:{\mathcal {F}}\rightarrow {\mathbb {R}}^M$ that models the data acquisition process; and, (iii) the observed data that is stored in an array ${\varvec{y}}\in {\mathbb {R}}^M$ with the implicit assumption that ${\varvec{y}}\approx \varvec{\nu }(f^*)$. The task is then to (approximately) reconstruct the unknown signal $f^*$ from the observed data ${\varvec{y}}$. From a variational perspective, the problem can be formulated as a minimization of the form

$$\begin{aligned} f^* \in \mathop {{{\,\mathrm{arg\,min}\,}}}\limits _{f\in {\mathcal {F}}} \left( E\left( \varvec{\nu }(f),{\varvec{y}}\right) + \lambda {\mathcal {R}}(f)\right) , \end{aligned}$$

(1)

where $E:{\mathbb {R}}^M\times {\mathbb {R}}^M\rightarrow {\mathbb {R}}$ is a convex loss function that measures the data discrepancy, ${\mathcal {R}}:{\mathcal {F}}\rightarrow {\mathbb {R}}$ is the regularization functional that enforces prior knowledge on the reconstructed signal, and $\lambda >0$ is a tunable parameter that adjusts the two terms.

The use of regularization for solving inverse problems dates back to the 1960 s, when Tikhonov proposed a quadratic ($\ell _2$-type) functional for solving finite-dimensional problems [46]. More recently, Tikhonov regularization has been outperformed by $\ell _1$-type functionals in various settings [28, 45]. This is largely due to the sparsity-promoting effect of the latter, in the sense that the solution of an $\ell _1$-regularized inverse problem can be typically written as the linear combination of a few predefined elements, known as atoms [17, 27]. Sparsity is a pivotal concept in modern signal processing and constitutes the core of many celebrated methods. The most notable example is the framework of compressed sensing [19, 26, 29], which has brought lots of attention in the past decades.

In general, regularization enhances the stability of the problem and alleviates its inherent ill-posedness, especially when the hypothesis space is much larger than M. While this can happen in the discrete setting (e.g. when ${\mathcal {F}}={\mathbb {R}}^d$ with $d\gg M$), it is inevitable in the continuum where ${\mathcal {F}}$ is an infinite-dimensional space of functions. Since naturally occurring signals and images are usually indexed over the whole continuum, studying continuous-domain problems is, therefore, undeniably important. It thus comes with no surprise to see the rich literature on this class of optimization problems. Among the classical examples are the smoothing splines for interpolation [39, 43] and the celebrated framework of learning over reproducing kernel Hilbert spaces [42, 50]. Remarkably, the latter laid the foundation of numerous kernel-based machine learning schemes such as support-vector machines [31]. The key theoretical result of these frameworks is a “representer theorem” that provides a parametric form for their optimal solutions. While these examples formulate optimization problems over Hilbert spaces, the representer theorem has been recently extended to cover generic convex optimization problems over Banach spaces [12, 15, 47, 49]. In simple terms, these abstract results characterize the solution set of (1) in terms of the extreme points of the unit ball of the regularization functional $B_{{\mathcal {R}}}=\{f\in {\mathcal {F}}: {\mathcal {R}}(f)\le 1\}$. Hence, the original problem can be translated in finding the extreme points of the unit ball $B_{{\mathcal {R}}}$.

In parallel, Osher–Rudin–Fatemi’s total-variation has been systematically explored in the context of image restoration and denoising [20, 32, 40]. The total-variation of a differentiable function $f:\Omega \rightarrow {\mathbb {R}}$ can be computed as

$$\begin{aligned} \textrm{TV}(f) = \int _{\Omega } \Vert \varvec{\nabla } f ({\varvec{x}})\Vert _{\ell _2} \textrm{d}{\varvec{x}}. \end{aligned}$$

(2)

The notion can be extended to cover non-differentiable functions using the theory of functions with bounded variation [2, 21]. In this case, the representer theorem states that the solution can be written as the linear combination of some indicator functions [15]. This adequately explains the so called “stair-case effect” of TV regularization. Subsequently, higher-order generalizations of TV regularization have been proposed by Bredies et al. [13, 14, 16]. Particularly, the second-order TV has been used in various applications [9, 33, 34]. By analogy with (2), the second-order TV is defined over the space of functions with bounded Hessian [25]. In particular, it can be computed for twice-differentiable functions $f:\Omega \rightarrow {\mathbb {R}}$ as

$$\begin{aligned} \textrm{TV}^{(2)}(f) = \int _{\Omega } \Vert \nabla ^2 f({\varvec{x}})\Vert _F \textrm{d}{\varvec{x}}, \end{aligned}$$

(3)

where $\Vert \mathbf{\,\cdot \,}\Vert _F$ denotes the Frobenius norm of a matrix. Lefkimiatis et al. generalized the notion by replacing the Frobenius norm with any Schatten-p norm for $p\in [1,+\infty ]$ [35, 36]. While this had been only defined for twice-differentiable functions, it has been recently extended to the space of functions with bounded Hessian [6]. The extended seminorm—the Hessian–Schatten total variation (HTV)—has also been used for learning continuous and piecewise linear (CPWL) mappings [18, 38]. The motivation and importance of the latter stems from the following observations:

• (1) The CPWL family plays a significant role in deep learning. Indeed, it is known that the input–output mapping of any deep neural networks (DNN) with rectified linear unit (ReLU) activation functions is a CPWL function [37]. Conversely, any CPWL mapping can be exactly represented by a DNN with ReLU activation functions [4]. These results provide a one-to-one correspondence between the CPWL family and the input–output mappings of commonly used DNNs.

• (2) For one-dimensional problems (i.e., when $\Omega \subseteq {\mathbb {R}}$), the HTV seminorm coincides with the second-order TV. Remarkably, the representer theorem in this case states that the optimal solution can be achieved by a linear spline; that is, a univariate CPWL function. The latter suggests the use of $\textrm{TV}^{(2)}$ regularization for learning univariate functions [5, 8, 11, 23, 41, 48].

• (3) It is known from the literature on low-rank matrix recovery that the Schatten-1 norm (also known as the nuclear norm) promotes low rank matrices [22]. Hence, by using the $\textrm{HTV}$ seminorm with $p=1$, one expects to obtain a mapping whose Hessian has low rank at most points, with the extreme case being the CPWL family whose Hessian is zero almost everywhere.

The aim of this paper is to identify the solution set of linear inverse problems with HTV regularization. Motivated by recent general representer theorems (see, [12, 47], we focus on the characterization of the extreme points of the unit ball of the HTV functional. After recalling some preliminary concepts (Sect. 2), we study the HTV seminorm and its associated native space from a mathematical perspective (Sect. 3). Next, we prove our main theoretical result on density of CPWL functions in the unit ball of the HTV seminorm (Theorem 21) in Sect. 4. Finally, we invoke a variant of the Krein–Milman theorem to characterize the extreme points of the unit ball of the HTV seminorm (Sect. 5).

2 Preliminaries

Throughout the paper, we shall use fairly standard notations for various objects, such as function spaces and sets. For example, ${\mathcal {L}}^n$ and ${\mathcal {H}}^k$ denote the Lebesgue and k-dimensional Hausdorff measures on ${\mathbb {R}}^n$, respectively. Below, we recall some of the concepts that are foundational for this paper.

2.1 Schatten norms

Definition 1

(Schatten norm) Let $p\in [1,+\infty ]$. If $M\in {\mathbb {R}}^{n\times n}$ and $s_1(M),\dots , s_n(M)\ge 0$ denote the singular values of M (counted with their multiplicity), we define the Schatten p-norm of M by

$$\begin{aligned} |M|_p\mathrel {\mathop :}=\Vert (s_1(M),\dots ,s_n(M))\Vert _{\ell ^p}. \end{aligned}$$

We recall that the scalar product between $M,N\in {\mathbb {R}}^{n\times n}$ is defined by

$$\begin{aligned} M\,\cdot \, N\mathrel {\mathop :}={\textrm{tr}}(M^t N)=\sum _{i,j=1,\dots ,n} M_{i,j}N_{i,j} \end{aligned}$$

and induces the Hilbert–Schmidt norm. Next, we enumerate several properties of the Schatten norms that shall be used throughout the paper. We refer to standard books on matrix analysis (such as [10]) for the proof of these results.

Proposition 2

The family of Schatten norms satisfies the following properties.

• (1) If $M\in {\mathbb {R}}^{n\times n}$ is symmetric, then its singular values $s_1(M),\dots ,s_n(M)$ are equal to $|\lambda _1(M)|,\dots ,|\lambda _n(M)|$, where $\lambda _1(M),\dots ,\lambda _n(M)$ denote the eigenvalues of M (counted with their multiplicity). Hence $|M|_p=\Vert (\lambda _1(M),\dots ,\lambda _n(M))\Vert _{\ell ^p}$.

• (2) If $M\in {\mathbb {R}}^{n\times n}$ and $N\in O({\mathbb {R}}^n)$, then $|M N|_p=|N M|_p=|M|_p$.

• (3) If $M,N\in {\mathbb {R}}^{n\times n}$, then $|M N|_p\le |M|_p |N|_p$.

• (4) If $M\in {\mathbb {R}}^{n\times n}$, then $|M|_p=\sup _N M\,\cdot \, N$, where the supremum is taken among all $N\in {\mathbb {R}}^{n\times n}$ with $|N|_{p^*}\le 1$, for $p^*$ the conjugate exponent of p.

• (5) If M has rank 1, then $|M|_p$ coincides with the Hilbert–Schmidt norm of M for every $p\in [1,+\infty ]$.

• (6) If $p\in (1,+\infty )$, then the Schatten p-norm is strictly convex [7, Corollary 1].

• (7) If $M\in {\mathbb {R}}^{n\times n}$, then $|M|_p\le C|M|_q$, where $C=C(n,p,q)$ depends only on n, p and q.

Definition 3

($L^r$-Schatten p-norm) Let $p,r\in [1,+\infty ]$ and let $M\in (L^r({\mathbb {R}}^n))^{n\times n}$. We define the $L^r$-Schatten p-norm of M as

$$\begin{aligned} \Vert M\Vert _{p,r}\mathrel {\mathop :}=\Vert |M|_p\Vert _{L^r({\mathbb {R}}^n)}. \end{aligned}$$

An analogous definition can be given when the reference measure for the $L^r$ space is not the Lebesgue measure.

2.2 Poincaré inequalities

We recall that for a Borel set $A\subseteq {\mathbb {R}}^n$ with ${\mathcal {L}}^n(A)>0$ and $f\in L^1(A)$, then

Definition 4

Let $A\subseteq {\mathbb {R}}^n$ be an open domain. We say that A supports Poincaré inequalities if for every $q\in [1,n)$ there exists a constant $C=C(A,q)$ depending on A and q such that

where $1/{q^*}=1/q-1/n$.

We recall that any ball in ${\mathbb {R}}^n$ supports Poincaré inequalities [30, Theorem 4.9].

Remark 5

Let A be a bounded open domain supporting Poincaré inequalities. We recall the following fact: if $f\in W^{1,1}_{{\textrm{loc}}}(A)$ is such that $\int _A|\nabla f|^q{\textrm{d}}{\mathcal {L}}^n<+\infty$, then $f\in L^{q^*}(A)$, where $1/q^*=1/q-1/n$. To show this, apply a Poincaré inequality to $f_m\mathrel {\mathop :}=(f\wedge m)\vee -m\in W^{1,q}(A)$, with $\int _A|\nabla f_m|^q{\textrm{d}}{\mathcal {L}}^n\le \int _A|\nabla f|^q{\textrm{d}}{\mathcal {L}}^n$, and deduce that, for a constant , it holds

Now, if $B\subseteq A$ is a ball with ${{\bar{B}}}\subseteq A$, we have that $\Vert f_m\Vert _{L^1(B)}\le \Vert f\Vert _{L^1(B)}<+\infty$ and $\Vert f_m-c_m\Vert _{L^1(B)}$ is bounded in m, so that $\sup _m|c_m|<\infty$. We also have that $\Vert f_m-c_m\Vert _{L^{q^*}(A)}$ is uniformly bounded. Thus, we infer that $\Vert f_m\Vert _{L^{q^*}(A)}$ is bounded in m, whence $f\in {L^{q^*}(A)}$.$\square$

2.3 Distributions

We denote, as usual, ${\mathcal {D}}(\Omega )=C^\infty _{{\textrm{c}}}(\Omega )$ the space of test functions and ${\mathcal {D}}'(\Omega )$ its dual, i.e. the space of distributions [44]. If $T\in {\mathcal {D}}'(\Omega )$, we denote with $\nabla ^2 T$ the distributional Hessian of T, i.e. the matrix of distributions $\{\partial ^2_{i,j} T\}_{i,j\in 1,\dots ,n}$ where $(\partial ^2_{i,j} T )(f)\mathrel {\mathop :}=T(\partial _i\partial _j f)$ for every $f\in {\mathcal {D}}(\Omega )$. In a natural way, if $F\in {\mathcal {D}}(\Omega )^{n\times n}$, we denote

$$\begin{aligned} \nabla ^2 T(F)\mathrel {\mathop :}=\sum _{i,j=1\dots ,n} \partial ^2_{i,j}T(F_{i,j}). \end{aligned}$$

Remark 6

Let T be a distribution on $\Omega$ such that for every $i=1,\dots ,n$, $\partial _i T$ is a Radon measure. Then T is induced by a ${\textrm{BV}}_{{\textrm{loc}}}(\Omega )$ function.

The proof of this fact is classical. Here, we sketch it for the reader’s convenience.

We let $\{\rho _k\}_k$ be a sequence of Friedrich mollifiers. Let $B\subseteq \Omega$ be a ball such that ${{\bar{B}}}\subseteq \Omega$, so that, if k is big enough (that we will implicitly assume in what follows), we have a well defined distribution $\rho _k*T$ on B, which is induced by a $C^\infty ({{\bar{B}}})$ function, say $t_k$. It is immediate to show that for every $i=1,\dots ,n$, $\int _B|\partial _i t_k|{\textrm{d}}{\mathcal {L}}^n$ are uniformly bounded in k, as T has derivatives that are Radon measures. Therefore, using a Poincaré inequality on B, we have that for some $q^*>1$, $\Vert t_k-c_k\Vert _{L^{q^*}(B)}$ is uniformly bounded in k, where . Hence, up to non-relabelled subsequences, $t_k-c_k$ converges to an $L^{q^*}(B)$ function f in the weak topology of $L^{q^*}(B)$ and then in the weak topology of ${\mathcal {D}}'(B)$. Also, $t_k$ converges in the topology of ${\mathcal {D}}'(B)$ to T. Hence $c_k=t_k-(t_k-c_k)$ converges in the weak topology of ${\mathcal {D}}'(B)$ to $T-f\in {\mathcal {D}}'(B)$. This forces $\{c_k\}_k\subseteq {\mathbb {R}}$ to be bounded, so that also $t_k$ was bounded in $L^{q^*}(B)$ and hence T is induced by an $L^{q^*}(B)$ function on B. A partition of unity argument shows that T is induced by an $L^1_{{\textrm{loc}}}(\Omega )$ function, whence the conclusion.$\square$

3 Hessian–Schatten total variation

In this section, we fix $\Omega \subseteq {\mathbb {R}}^n$ to be an open set and $p\in [1,+\infty ]$. We let $p^*$ denote the conjugate exponent of p. First, we recall the definition of the HTV seminorm, presented in [6], in the spirit of the classical theory of functions of bounded variation. Next, we review some known results for the space of functions with bounded Hessian (see, [25]), proposing at the same time a few refinements and/or extensions.

3.1 Definitions and basic properties

Definition 7

(Hessian–Schatten total variation) Let $f\in L^1_{{\textrm{loc}}}(\Omega )$. For every $A\subseteq \Omega$ open we define the Hessian–Schatten total variation of f as

$$\begin{aligned} | {\textrm{D}}^2_p f|(A)\mathrel {\mathop :}=\sup _F \int _A \sum _{i,j=1,\dots ,n} f \partial _i\partial _j F_{i,j}{\textrm{d}}{\mathcal {L}}^n, \end{aligned}$$

(4)

where the supremum runs among all $F\in C_{{\textrm{c}}}^\infty (A)^{n\times n}$ with $\Vert F\Vert _{p^*,\infty }\le 1$. We say that f has bounded p-Hessian–Schatten variation in $\Omega$ if $| {\textrm{D}}^2_p f|(\Omega )<\infty$.

Remark 8

If f has bounded p-Hessian–Schatten variation in $\Omega$, then the set function defined in (4) is the restriction to open sets of a finite Borel measure, that we still call $| {\textrm{D}}^2_p f|$. This can be proved with a classical argument, building upon [24] (see also [2, Theorem 1.53]).

By its very definition, the p-Hessian–Schatten variation is lower semicontinuous with respect to $L^1_{{\textrm{loc}}}$ convergence.$\square$

For any couple $p,q\in [1,+\infty ]$, f has bounded p-Hessian–Schatten variation if and only if f has bounded q-Hessian–Schatten variation and moreover

$$\begin{aligned} C^{-1}| {\textrm{D}}^2_p f| \le | {\textrm{D}}^2_q f| \le C| {\textrm{D}}^2_p f| \end{aligned}$$

for some constant $C=C(p,q)$ depending only on p and q. Hence, the induced topology is independent of the choice of p. For this reason, in what follows, we will often implicitly take $p=1$ (omitting thus to write p), and we will stress p when this choice plays a role.

We prove now that having bounded Hessian–Schatten variation measure is equivalent to membership in $W^{1,1}_{{\textrm{loc}}}$ with gradient with bounded total variation. Also, we compare the Hessian–Schatten variation measure to the total variation measure of the gradient. This will be a key observation, as it will allow us to use the classical theory of functions of bounded variation, see e.g. [2].

Proposition 9

Let $f\in L^1_{{\textrm{loc}}}(\Omega )$. Then the following are equivalent:

• (1) f has bounded Hessian–Schatten variation in $\Omega$,

• (2) $f\in W^{1,1}_{{\textrm{loc}}}(\Omega )$ and $\nabla f\in {\textrm{BV}}_{{\textrm{loc}}}(\Omega )$ with $| {\textrm{D}}\nabla f|(\Omega )<\infty$.

If this is the case, then, as measures,

(5)

In particular, there exists a constant $C=C(n,p)$ depending only on n and p such that

as measures.

Proof

We divide the proof in two steps.

Step 1. We prove $1\Rightarrow 2$. Let $T\in {\mathcal {D}}'(\Omega )$ denote the distribution induced by $f\in L^1_{{\textrm{loc}}}(\Omega )$. For $i=1,\dots ,n$, define $S_i\mathrel {\mathop :}=\partial _i T\in {\mathcal {D}}'(\Omega )$. By the fact that f has bounded Hessian–Schatten variation in $\Omega$, we can apply Riesz Theorem and deduce that for every $j=1,\dots ,n$, $\partial _j S_i$ is induced by a finite measure on $\Omega$. Indeed, if $\varphi \in C_c^\infty (\Omega )$, it holds

$$\begin{aligned} \partial _j S_i(\varphi )=\int _\Omega f \partial _j\partial _i\varphi \le C\Vert \varphi \Vert _{\infty }, \end{aligned}$$

where C is independent of $\varphi$. Then, by Remark 6, $S_i$ is induced by an $L^1_{{\textrm{loc}}}(\Omega )$ function, which proves the claim.

Step 2. We prove $2\Rightarrow 1$ and (5). First, we can write ${\textrm{D}}\nabla f=M \mu$, where $|M(x)|_p=1$ for $\mu$-a.e. $x\in \Omega$. Namely,

This decomposition depends on p, but we will not make this dependence explicit.

Let $A\subseteq \Omega$ be open and let $F\in C_{{\textrm{c}}}^\infty (A)^{n\times n}$ with $\Vert F\Vert _{p^*,\infty }\le 1$. Then

$$\begin{aligned} \int _A \sum _{i,j} f\partial _i\partial _j F_{i,j}=\int _A \sum _{i,j} M_{i,j} F_{i,j}{\textrm{d}}\mu \le \mu (A), \end{aligned}$$

so that f has bounded p-Hessian–Schatten variation and $|{\textrm{D}}_p^2 f| \le \mu$ as measures on $\Omega$.

We show now that $\mu (\Omega )\le |{\textrm{D}}_p^2 f|(\Omega )$. Fix now $\varepsilon >0$. By Lusin’s Theorem, we can find a compact set $K\subseteq \Omega$ such that $\mu (\Omega \setminus K)<\varepsilon$ and the restriction of M to K is continuous. Since

$$\begin{aligned} \sup _{|N|_{p^*}\le 1}M(x)\,\cdot \,N=1\qquad \text {for every } x\in K, \end{aligned}$$

by the continuity of M we can find a Borel function N with finitely many values such that $|N(x)|_{p^*}\le 1$ for every $x\in \Omega$ and $M\,\cdot \, N\ge 1-\varepsilon$ on K. Now we take $\psi \in C^\infty _{{\textrm{c}}}(\Omega )$ with $\Vert \psi \Vert _{\infty }\le 1$ and we let $\{\rho _k\}_k$ be a sequence of Friedrich mollifiers. We consider (if k is big enough) $\psi (\rho _k*N)\in C_{{\textrm{c}}}^\infty (\Omega )$, which satisfies $\Vert \psi (\rho _k*N)\Vert _{p^*,\infty }\le 1$ on $\Omega$ (by convexity of the Schatten $p^*$-norm). Therefore,

We let $k\rightarrow \infty$, taking into account that $x\mapsto N(x)$ is continuous on K and we recall that $\psi$ was arbitrary to infer that

As $\varepsilon >0$ was arbitrary, the proof is concluded as we have shown that $|{\textrm{D}}^2_p f|=\mu$. $\square$

Remark 10

One may wonder what happens if, instead of defining the Hessian–Schatten total variation only on $L^1_{{\textrm{loc}}}$ functions, we define it on the bigger space of distributions, extending, in a natural way, (4) to distributions, i.e. interpreting the right hand side as $\sup _F \sum _{i,j=1}^n\partial _i\partial _j T(F_{i,j})=\sup _F \sum _{i,j=1}^n T(\partial _i\partial _jF_{i,j})$.

It turns out that the difference is immaterial: distributions with bounded Hessian–Schatten total variation are induced by $L^1_{{{\textrm{loc}}}}$ functions, and, of course, the two definitions of p-Hessian–Schatten total variation coincide. This is proved exactly as in Step 1 of the proof of Proposition 9, using Remark 6 once more.$\square$

The following proposition is basically taken from [25] and is a density (in energy) result akin to Meyers–Serrin Theorem.

Proposition 11

Let $f\in L^1_{{\textrm{loc}}}(\Omega )$. Then, for every $A\subseteq \Omega$ open, it holds

where the infimum is taken among all sequences $\{f_k\}_k\subseteq C^\infty (A)$ such that $f_k\rightarrow f$ in $L^1_{{\textrm{loc}}}(A)$. If moreover $f\in L^1(A)$, the convergence in $L^1_{{\textrm{loc}}}(A)$ above can be replaced by convergence in $L^1(A)$.

Proof

The $(\le )$ inequality is trivial by lower semicontinuity. The proof of the opposite inequality is due to a Meyers–Serrin argument, and can be obtained adapting [25, Proposition 1.4] (we know that $f\in W^{1,1}_{{\textrm{loc}}}(\Omega )$ thanks to Proposition 9). Notice that in the proof of [25] Hilbert–Schmidt norms instead of Schatten norms are used. The proof can be adapted with no effort to any norm. Alternatively, one may notice that the result with Hilbert–Schmidt norms implies the result for any other matrix norm, thanks to the Reshetnyak continuity Theorem (see e.g. [2, Theorem 2.39]), taking into account that ${\textrm{D}}\nabla f_k\rightarrow {\textrm{D}}\nabla f$ in the weak* topology and (5). $\square$

Now we show that Hessian–Schatten total variations decrease under the effect of convolutions, that is a a well-known property in the ${\textrm{BV}}$ context.

Lemma 12

Let $f\in L^1_{{\textrm{loc}}}(\Omega )$ with bounded Hessian–Schatten variation in $\Omega$. Let also $A\subseteq {\mathbb {R}}^n$ open and $\varepsilon >0$ with $B_\varepsilon (A)\subseteq \Omega$. Then, if $\rho \in C_{{\textrm{c}}}({\mathbb {R}}^n)$ is a convolution kernel with ${\textrm{supp}\,}\rho \subseteq B_\varepsilon (0)$, it holds

Proof

Let $F\in C_{{\textrm{c}}}^\infty (A)^{n\times n}$ with $\Vert F\Vert _{p^*,\infty }\le 1$. We compute

$$\begin{aligned} \int _A \sum _{i,j} (\rho *f)\partial _i\partial _j F_{i,j}=\int _A \sum _{i,j} f\partial _i\partial _j (\check{\rho }*F_{i,j}), \end{aligned}$$

(6)

where $\check{\rho }(x)\mathrel {\mathop :}=\rho (-x)$. Notice that, defining the action of the mollification component-wise, $\check{\rho }*F\in C_{{\textrm{c}}}^\infty (\Omega )$ (by the assumption on the support of $\rho$) with (by duality)

$$\begin{aligned} |(\check{\rho }*F)(x)|_p=\sup _M M\,\cdot \,(\check{\rho }*F)(x)=\sup _M (\check{\rho }*(M\,\cdot \, F))(x)\le (\check{\rho }*1) (x)\le 1, \end{aligned}$$

where the supremum is taken among all $M\in {\mathbb {R}}^{n\times n}$ with $|M|_{p^*}\le 1$. Here we used that $|F|_{p^*}(x)\le 1$ for every $x\in \Omega$. Hence $\Vert (\check{\rho }*F)\Vert _{p^*,\infty }\le 1$. Also, $\check{\rho }*F$ is supported in $B_\varepsilon (A)$, so that the right hand side of (6) is bounded by $|{\textrm{D}}^2_p f|(B_\varepsilon (A))$ and the proof is concluded as F was arbitrary. $\square$

In the following proposition we obtain an analogue of the classical Sobolev embedding Theorems tailored for our situation. Recall Definition 4.

Proposition 13

(Sobolev embedding) Let $f\in L^1_{{\textrm{loc}}}(\Omega )$ with bounded Hessian–Schatten variation in $\Omega$. Then

$$\begin{aligned}&f\in L^{n/(n-2)}_{{{\textrm{loc}}}}(\Omega )\cap W_{{\textrm{loc}}}^{1,n/(n-1)}(\Omega )\qquad{} & {} \text {if }n\ge 3,\\&f\in L^\infty _{{{\textrm{loc}}}}(\Omega )\cap W^{1,2}_{{\textrm{loc}}}(\Omega )\qquad{} & {} \text {if }n= 2,\\&f\in L^\infty _{{{\textrm{loc}}}}(\Omega )\cap W^{1,\infty }_{{\textrm{loc}}}(\Omega )\qquad{} & {} \text {if }n= 1 \end{aligned}$$

and, if $n=2$, f has a continuous representative.

More explicitly, for every bounded domain $A\subseteq \Omega$ that supports Poincaré inequalities and $r\in [1,+\infty )$, there an affine map $g=g(A,f)$ such that, setting ${{\tilde{f}}}\mathrel {\mathop :}=f-g$, it holds that

$$\begin{aligned}&\Vert {{\tilde{f}}}\Vert _{L^{n/(n-2)}(A)}+\Vert \nabla {{\tilde{f}}}\Vert _{L^{n/(n-1)}(A)}\le C(A)|{\textrm{D}}^2 f|(A)\qquad{} & {} \text {if }n\ge 3, \end{aligned}$$

(7)

$$\begin{aligned}&\Vert {{\tilde{f}}}\Vert _{L^r(A)}+\Vert \nabla {{\tilde{f}}}\Vert _{L^2(A)}\le C(A,r)|{\textrm{D}}^2 f|(A)\qquad{} & {} \text {if }n= 2, \end{aligned}$$

(8)

$$\begin{aligned}&\Vert {{\tilde{f}}}\Vert _{L^\infty (A)}+\Vert \nabla {{\tilde{f}}}\Vert _{L^\infty (A)}\le C(A)|{\textrm{D}}^2 f|(A)\qquad{} & {} \text {if }n= 1. \end{aligned}$$

(9)

Proof

The case $n=1$ is readily proved by direct computation (as, if a domain of ${\mathbb {R}}$ supports Poincaré inequality has to be an interval) so that in the following we assume $n\ge 2$. Also, recall that Proposition 9 states that $f\in W^{1,1}_{{\textrm{loc}}}(\Omega )$ with $\nabla f\in {\textrm{BV}}_{{\textrm{loc}}}(\Omega )$. Therefore we can apply [25, Proposition 3.1] to have continuity of f in the case $n=2$, which also implies $L^\infty _{{\textrm{loc}}}(\Omega )$ membership.

As balls satisfy Poincaré inequalities, it is enough to establish the estimates of the second part of the claim to conclude. Fix then A and r as in the second part of the statement.

Let now $\{f_k\}_k$ be given by Proposition 11 for f on A. Iterating Poincaré inequalities, taking into account Remark 5, we obtain affine maps $g_k$ so that, setting ${{\tilde{f}}}_k\mathrel {\mathop :}=f_k-g_k$, $\tilde{f_k}$ satisfies (7) or (8), depending on n. Arguing as for Remark 5, we see that $g_k$ is bounded in $L^1(B)$ for any ball $B\subseteq A$. This implies that $g_k$ and $\nabla g_k$ are bounded in $L^\infty (A)$. Therefore, up to extracting a further non relabelled subsequence, ${{\tilde{f}}}_k$ converges in $L_{{\textrm{loc}}}^1(A)$ to $f-g$, for an affine function g. Lower semicontinuity of the norms at the left hand sides of (7) or (8) allows us to conclude the proof. $\square$

Remark 14

(Linear extension domains) Let $n=2$, we keep the same notation as for Proposition 13. Assume also that A has the following property: there exists an open set $V\subseteq {\mathbb {R}}^2$ with ${{\bar{A}}}\subseteq V$ and a bounded linear map $E:W^{1,2}(A)\rightarrow W^{1,2}(V)$ satisfying, for every u with bounded Hessian–Schatten variation (hence $u\in W^{1,2}(A)$ by Proposition 13):

• (1) $E u=u$ a.e. on A,

• (2) Eu is supported in V,

• (3) $|{\textrm{D}}^2 E u|(V)\le C|{\textrm{D}}^2 u|(A)$ for some constant C.

Then we show that (8) can be improved to

$$\begin{aligned} \Vert {{\tilde{f}}}\Vert _{L^\infty (A)}+\Vert \nabla {{\tilde{f}}}\Vert _{L^2(A)}\le C|{\textrm{D}}_p^2 f|(A), \end{aligned}$$

where we possibly modified the constant C.

First, by (8) it holds that $\Vert {{\tilde{f}}}\Vert _{W^{1,2}(A)}\le C|{\textrm{D}}^2 f|(A)$. Now take $\psi \in C_c^\infty ({\mathbb {R}}^2)$ with support contained in V and such that $\psi =1$ on A. Then we have

$$\begin{aligned} |{\textrm{D}}^2 (\psi E{{\tilde{f}}})|(V)\le C\big (|{\textrm{D}}^2 (E{{\tilde{f}}})|(V)+\Vert E{{\tilde{f}}}\Vert _{W^{1,2}(V)} \big )\le C|{\textrm{D}}^2 {{\tilde{f}}}|(A). \end{aligned}$$

Then we use the continuous representative of $\psi E{{\tilde{f}}}$ as in [25, Proposition 3.1] and, from its very definition, the claim follows.

It is easy to see that $(0,1)^2$ is suitable for the above argument, see Lemma 17 below and its proof.$\square$

The strict convexity of the Schatten p-norm, for $p\in (1,+\infty )$ has, as a consequence, the following rigidity result.

Lemma 15

(Rigidity) Let $f,g\in L^1_{{\textrm{loc}}}(\Omega )$ with bounded Hessian–Schatten variation and assume that

$$\begin{aligned} |{\textrm{D}}^2_p (f+g)|(\Omega )= |{\textrm{D}}^2_p f|(\Omega )+ |{\textrm{D}}^2_p g|(\Omega ). \end{aligned}$$

Then

$$\begin{aligned} |{\textrm{D}}^2_p (f+g)|= |{\textrm{D}}^2_p f|+ |{\textrm{D}}^2_p g| \end{aligned}$$

as measures on $\Omega$. If moreover, $p\in (1,+\infty )$, then

$$\begin{aligned} {\textrm{D}}\nabla f=\rho _f {\textrm{D}}\nabla (f+g)\qquad \text {and}\qquad {\textrm{D}}\nabla g=\rho _g {\textrm{D}}\nabla (f+g) \end{aligned}$$

for a (unique) couple $\rho _f,\rho _g\in L^\infty (|{\textrm{D}}\nabla (f+g)|)$ such that $0\le \rho _f,\rho _g\le 1$ $|{\textrm{D}}\nabla (f+g)|$-a.e. and satisfying $\rho _f+\rho _g=1$ $|{\textrm{D}}\nabla (f+g)|$-a.e. In particular, for every $q\in [1,+\infty ]$,

$$\begin{aligned} |{\textrm{D}}^2_q (f+g)|= |{\textrm{D}}^2_q f|+ |{\textrm{D}}^2_q g| \end{aligned}$$

as measures on $\Omega$.

Proof

The first claim follows from the triangle inequality and the equality in the assumption. Now assume $p\in (1,+\infty )$. Take then $\rho _f$ and $\rho _g$, the Radon–Nikodym derivatives:

$$\begin{aligned} |{\textrm{D}}^2_p f|=\rho _f |{\textrm{D}}^2_p (f+g)|\qquad \text {and}\qquad |{\textrm{D}}^2_p g|=\rho _g |{\textrm{D}}^2_p (f+g)| \end{aligned}$$

as measures on $\Omega$, where $\rho _f+\rho _g=1 \ |{\textrm{D}}^2_p (f+g)|$-a.e. We can apply Proposition 9 and write the polar decompositions ${\textrm{D}}\nabla f=M_p|{\textrm{D}}_p^2 f|$, ${\textrm{D}}\nabla g=N_p|{\textrm{D}}_p^2 g|$ and ${\textrm{D}}\nabla (f+g)=O_p|{\textrm{D}}\nabla (f+g)|$ where $|M_p|_p,|N_p|_p,|O_p|_p$ are identically equal to 1. Therefore ${\textrm{D}}\nabla f=M_p\rho _f|{\textrm{D}}_p^2 (f+g)|$, ${\textrm{D}}\nabla g=N_p\rho _g|{\textrm{D}}_p^2 (f+g)|$ and ${\textrm{D}}\nabla (f+g)=O_p|{\textrm{D}}_p^2 (f+g)|$ and by linearity we obtain that

$$\begin{aligned} M_p\rho _f|{\textrm{D}}_p^2 (f+g)|+N_p\rho _g|{\textrm{D}}_p^2 (f+g)|=O_p|{\textrm{D}}_p^2 (f+g)| \end{aligned}$$

which implies that $\rho _f M_p+\rho _g N_p=O_p\ |{\textrm{D}}_p^2 (f+g)|$-a.e. Taking p-Schatten norms,

$$\begin{aligned} 1=|O_p|_p=|\rho _f M_p+\rho _g N_p|_p\le \rho _f| M_p|_p+\rho _g| N_p|_p=1\qquad |{\textrm{D}}_p^2 (f+g)|\text {-a.e.} \end{aligned}$$

which implies the claim by strict convexity. The last assertion is due to Proposition 9. $\square$

3.2 Boundary extension

[25, Theorem 2.2] provides us with an extension operator for bounded domains with $C^2$ boundary. However, we need the result for parallelepipeds. This can be obtained following [25, Remark 2.1]. However, we sketch the argument as we are going also to need a slightly more refined result compared to the one stated in [25]. This extension result (namely, its corollary Proposition 18) will play a key role in the proof of Theorem 21 below.

Lemma 16

Let $\Omega =(a_0,a_1)\times \Omega '$ be a parallelepiped in ${\mathbb {R}}^n$ and let $f\in L^1_{{\textrm{loc}}}(\Omega )$ with bounded Hessian–Schatten variation in $\Omega$. Then, if we set

$$\begin{aligned} {\tilde{\Omega }}\mathrel {\mathop :}=(a_0-(a_1-a_0)/2,a_1)\times \Omega ', \end{aligned}$$

there exists ${\tilde{f}}\in L^1_{{\textrm{loc}}}({\tilde{\Omega }})$ with bounded Hessian–Schatten variation in ${{\tilde{\Omega }}}$ such that ${\tilde{f}}=f$ a.e. on $\Omega$,

$$\begin{aligned} |{\textrm{D}}^2 {\tilde{f}}|(\{a_0\}\times \Omega ')=0 \end{aligned}$$

(10)

and

$$\begin{aligned} |{\textrm{D}}^2{\tilde{f}}|({\tilde{\Omega }})\le C |{\textrm{D}}^2{f}|(\Omega ), \end{aligned}$$

(11)

where C is a scale invariant constant that depends only on $\Omega$ (and ${\tilde{\Omega }}$) but not on f.

Proof

Up to a linear change of coordinates, we can assume that $\Omega =(0,1)^n$. Set $\Omega _1=\Omega$ and $\Omega _2=(-1/2,0)\times (0,1)^{n-1} = M(\Omega )$, for $M(x,y)\mathrel {\mathop :}=(-x/2,y)$, where we use coordinates ${\mathbb {R}}\times {\mathbb {R}}^{n-1}\ni (x,y)$ for ${\mathbb {R}}^n$. Set also

$$\begin{aligned} {\tilde{f}}(x,y)\mathrel {\mathop :}={\left\{ \begin{array}{ll} f(x,y)\qquad &{}\text {if }(x,y)\in \Omega _1,\\ 3 f(-x,y)-2 f(-2x,y)\qquad &{}\text {if }(x,y)\in \Omega _2. \end{array}\right. } \end{aligned}$$

An application of the theory of traces ( [2, Theorem 3.87 and Corollary 3.89]) together with Proposition 9 yields that $|{\textrm{D}}\nabla {{\tilde{f}}}|(\partial \Omega _1\cap \partial \Omega _2)=0$, hence (10). Then, we compute

$$\begin{aligned} |{\textrm{D}}^2{{\tilde{f}}}|(\Omega _1\cup \Omega _2\cup (\partial \Omega _1\cap \partial \Omega _2))= |{\textrm{D}}^2{{\tilde{f}}}|(\Omega _1)+|{\textrm{D}}^2{{\tilde{f}}}|(\Omega _2)\le C |{\textrm{D}}^2 f|(\Omega _1), \end{aligned}$$

where C is a constant, so that (11) follows. $\square$

Lemma 17

Let $\Omega =(0,1)^n$ and let $f\in L_{{\textrm{loc}}}^1(\Omega )$ with bounded Hessian–Schatten variation in $\Omega$. Then there exist a neighbourhood ${\tilde{\Omega }}$ of ${\bar{\Omega }}$ and ${\tilde{f}}\in L_{{\textrm{loc}}}^1({\tilde{\Omega }})$ with bounded Hessian–Schatten variation in ${{\tilde{\Omega }}}$ such that ${{\tilde{f}}}=f$ a.e. on $\Omega$,

$$\begin{aligned} |{\textrm{D}}^2 {{\tilde{f}}}|(\partial \Omega )=0 \end{aligned}$$

(12)

and

$$\begin{aligned} |{\textrm{D}}^2 {{\tilde{f}}}|({\tilde{\Omega }})\le C |{\textrm{D}}^2 f|(\Omega ), \end{aligned}$$

(13)

where C is a scale invariant constant that depends only on $\Omega$ (and ${\tilde{\Omega }}$) but not on f.

Proof

Apply several times (a suitable variant) of Lemma 16, extending $\Omega$ along each side. Notice that at each step, we are extending a parallelepiped which contains $\Omega$. $\square$

Proposition 18

Let $\Omega =(0,1)^n$ and let $f\in L_{{\textrm{loc}}}^1(\Omega )$ with bounded Hessian–Schatten variation in $\Omega$. Then there exists a sequence $\{f_k\}_k\subseteq C^\infty ({\tilde{\Omega }})$, where ${\tilde{\Omega }}$ is a neighbourhood of ${\bar{\Omega }}$ such that

$$\begin{aligned} \begin{aligned} f_k&\rightarrow f\qquad \text {in }L^1(\Omega )\\ |{\textrm{D}}^2_p f_k|(\Omega )&\rightarrow | {\textrm{D}}^2_p f|(\Omega ) \end{aligned} \end{aligned}$$

(14)

for any $p\in [1,+\infty ]$.

Proof

Take ${\tilde{f}}$ as in Lemma 17 and, if $\{\rho _k\}_k$ is a sequence of Friedrich mollifiers, set $f_k\mathrel {\mathop :}={\tilde{f}}*\rho _k$. The claim follows from lower semicontinuity and Lemma 12. $\square$

4 A density result for CPWL functions

In this section, we study the density of CPWL functions in the unit ball of the HTV functional. As usual, we let $\Omega \subseteq {\mathbb {R}}^n$ open and $p\in [1,+\infty ]$.

4.1 Definitions and the main result

Definition 19

We say that $f\in C(\Omega )$ belongs to $\textrm{CPWL}(\Omega )$ if there exists a decomposition $\{P_k\}_k$ of ${\mathbb {R}}^n$ in n-dimensional convex polytopes (with convex polytope we mean the closed convex hull of finitely many points), intersecting only at their boundaries (their intersection being either empty or a common face) such that for every k, $f_{|P_k\cap \Omega }$ is affine and such that for every ball B, only finitely many $P_k$ intersect B.

Notice that $\textrm{CPWL}$ functions defined on bounded sets have automatically finite Hessian–Schatten variation, by Proposition 9.

In the particular case $n=2$, we can and will assume that the convex polytopes $\{P_k\}_k$ as in the definition of $\textrm{CPWL}$ function are triangles.

Remark 20

Let $f\in \textrm{CPWL}(\Omega )$, where $\Omega \subseteq {\mathbb {R}}^n$ is open. Notice that $\nabla f$ is constant on each $P_k$, call this constant $a_k$.

Thanks to Proposition 9, we can deal with $|{\textrm{D}}_p^2f|$ and $|{\textrm{D}}\nabla f|$ exploiting the theory of vector valued functions of bounded variation [2]. In particular, $|{\textrm{D}}\nabla f|$ will charge only 1-codimensional faces of $P_k$. Then, take a non degenerate face $\sigma =P_k\cap P_{k'}$ for $k\ne k'$ (i.e. $\sigma$ is the common face of $P_k$ and $P_{k'}$). Then the Gauss–Green Theorem gives , where $\nu$ is the unit normal to $\sigma$ going from $P_k$ to $P_{k'}$ (hence $(a_k-a_{k'})\perp \sigma$). Then,

(15)

where, as usual, $|a_{k'}-a_{k}|$ denotes the Euclidean norm. Let us remark that (15) has also been shown in [6], directly relying on Definition 7, which paved the way of developing numerical schemes for learning CPWL functions [18, 38]. Since has rank one -a.e.  we obtain also

(we recall that the matrix norm $|\,\cdot \,|$ without any subscript denotes the Hilbert–Schmidt norm). It follows from (5) that $|{\textrm{D}}_p^2 f|=|{\textrm{D}}\nabla f|$ for every $p\in [1,+\infty ]$, in particular, $|{\textrm{D}}_p^2 f|$ is independent of p.

Notice also that the rank one structure of ${\textrm{D}}\nabla f$ is a particular case of the celebrated Alberti’s theorem [1], for vector-valued $\mathrm BV$ functions. According to this theorem the rank one structure holds for the singular part of the distributional derivative. $\square$

The following theorem on the density of CPWL functions is the main theoretical result of this paper. Its proof is deferred to Sect. 4.2. In view of it, notice that by Lemma 17 together with Proposition 13, if $f\in L^1_{{\textrm{loc}}}((0,1)^2)$ has bounded Hessian–Schatten variation in $(0,1)^2$, then $f\in L^\infty ((0,1)^2)$. Also, notice that the statement of the theorem is for $p=1$ only. This will be discussed in the forthcoming Remark 22.

Theorem 21

Let $n=2$, let $\Omega =(0,1)^2$ and let $p=1$. Then $\mathrm CPWL(\Omega )$ functions are dense in energy $|{\textrm{D}}_1^2\,\cdot \,|(\Omega )$ in

$$\begin{aligned} \left\{ f\in L^1_{{\textrm{loc}}}(\Omega ): f\text { has bounded Hessian--Schatten variation}\right\} \end{aligned}$$

with respect to the $L^\infty (\Omega )$ topology. Namely, for any $f\in L^1_{{\textrm{loc}}}(\Omega )$ with bounded Hessian–Schatten variation in $\Omega$ there exist $f_k\in \textrm{CPWL}(\Omega )$ convergent in $L^\infty (\Omega )$ to f with $|{\textrm{D}}^2_1 f_k|(\Omega )$ convergent to $|{\textrm{D}}^2_1 f|(\Omega )$.

Remark 22

Theorem 21 shows in particular density in energy $|{\textrm{D}}^2_1\,\cdot \,|(\Omega )$ of $\textrm{CPWL}(\Omega )$ functions with respect to the $L^1_{{\textrm{loc}}}(\Omega )$ convergence. Notice that this conclusion is false if we take instead the $|{\textrm{D}}\nabla \,\cdot \,|(\Omega )$ seminorm, and this provides one more theoretical justification of the relevance of the Schatten 1-norm.

We now justify this claim. By Remark 20, it is easy to realize that the two seminorms above coincide for $\textrm{CPWL}(\Omega )$ functions, but are, in general, different for arbitrary functions. For example, take $f((x,y))\mathrel {\mathop :}=\frac{x^2+y^2}{2}$. Then $|{\textrm{D}}^2_1 f|=2{\mathcal {L}}^2$, whereas $|{\textrm{D}}\nabla f|=\sqrt{2}{\mathcal {L}}^2$. Now assume by contradiction that there exists a sequence $\{f_k\}_k\subseteq \textrm{CPWL}(\Omega )$ such that $f_k\rightarrow f$ in $L^1_{{\textrm{loc}}}(\Omega )$ and $|{\textrm{D}}\nabla f_k|(\Omega )\rightarrow |{\textrm{D}}\nabla f|(\Omega )$. Then

$$\begin{aligned} \liminf _k|{\textrm{D}}\nabla f_k|(\Omega )=\liminf _k|{\textrm{D}}^2_1 f_k|(\Omega )\ge |{\textrm{D}}^2_1 f|(\Omega )>|{\textrm{D}}\nabla f|(\Omega ), \end{aligned}$$

which is absurd. This also gives the same conclusion for $|{\textrm{D}}_p^2\,\cdot \,|$, in the case $p\in (1,+\infty ]$. $\square$

We conjecture that the result of Theorem 21 can be extended to arbitrary dimensions (i.e. $\Omega =(0,1)^n\subseteq {\mathbb {R}}^n$). Notice that, in the general case $n\ge 3$, the natural choice for the topology is $L^1(\Omega )$ (or $L^{n/(n-2)}(\Omega )$), as any $f\in L^1_{{\textrm{loc}}}(\Omega )$ with bounded Hessian–Schatten variation in $\Omega$ belongs to $L^{n/(n-2)}(\Omega )$, see the discussion right before Theorem 21.

Conjecture 1

The density result of Theorem 21 remains valid when the input domain is chosen to be any n-dimensional hypercube, $\Omega =(0,1)^n$, provided that the $L^\infty (\Omega )$ topology is replaced by the $L^1(\Omega )$ topology.¹

4.2 Proof of Theorem 21

This whole section is devoted to the proof of Theorem 21. Remarkably, our proof is constructive and provides an effective algorithm to build such approximating sequence.

Take $f\in L^1_{{\textrm{loc}}}(\Omega )$ with finite Hessian–Schatten variation. We remark again that indeed $f\in L^\infty (\Omega )$. We notice that we can assume with no loss of generality that f is the restriction to $\Omega$ of a $C_{{\textrm{c}}}^\infty ({\mathbb {R}}^2)$ function. This is due to Proposition 18 (and its proof), a cut off argument and and a diagonal argument. Still, we only have to bound Hessian–Schatten variations only on $\Omega$.

We want to find a sequence $\{f_j\}_j\subseteq \textrm{CPWL}(\Omega )$ such that $f_j\rightarrow f$ in $L^\infty (\Omega )$ and $\limsup _{j} |{\textrm{D}}^2_1 f_j|(\Omega )\le |{\textrm{D}}^2_1 f|(\Omega )$. This will suffice, by lower semicontinuity.

Overview. As the proof is rather long and involved, it is divided in ten steps. We start with an overview, to explain the strategy of the proof and the main constructions that will be detailed in the following steps.

Our approximating sequence as above will be obtained as a sequence of affine interpolation of f on a suitable sequence of triangulations of $\Omega$. In other words (Step 1), we fix $\varepsilon \in (0,1)$ and we build a triangulation such that, if g is the affine interpolation of f obtained using that triangulation, then g is $\varepsilon$-close to f and the Hessian–Schatten total variation of g is $\varepsilon$-close to the one of f. The construction of the triangulation is carried out in two main parts and the building blocks are two successive choice of grids (grids are rigorously defined in Step 2).

In the first part, we consider $G^N$, the dyadic subdivision of $\Omega$ in $2^{2N}$ squares of sidelength $2^{-N}$ which will be called $\{Q_k^N\}_k$ (Step 3). The choice of N is fixed almost at the beginning of the proof (Step 5), and depends morally on the modulus of continuity of the Hessian of f: the guiding principle here is item (a) below.

• (a) On each of the squares $Q_k^N$, the Hessian of f, read in suitable coordinates (these coordinates depending on k), will be close enough to a diagonal matrix $D^N_k$. See Step 4.

Having fixed the parameter N, we suppress the superscript N for the sake of readability.

In the second part we want to further refine the grid, arguing on each of the squares $Q_k$ separately, namely we are going to build, for each $Q_k$, a second grid $G^K_k$ (Step 6). Here a second parameter K enters into play (once that N has been fixed). The guiding principles, in this refining procedures, are in item (b) and item (c) below.

• (b) On $Q_k$, we would like the grid $G_k^K$ to follow the coordinates that induce the matrix $D_k$, i.e. reading the Hessian of f in the system of coordinates given by $G_k^K$, we want to recover a matrix that is very close to $D_k$. This is because, if we interpolate on a grid (actually, we have to interpolate on a triangulation induced in the most natural way by the grid), the optimal result, in terms of lowest Hessian–Schatten total variation, is obtained when the sides of the grid are oriented as just described (see the computations in Step 10).

The issue now is that different squares $Q_k$ have different associated systems of coordinates, so we will have to carefully merge the triangulations to take into account of the different rotations. Hence what follows.

• (c) We want all the triangulations obtained starting from $\{G_k^K\}_k$ to merge in a controlled way at the boundaries of the squares $\{Q_k\}_k$, in particular, we want that all the angles in the merged triangulations are bounded from below independently of K, so that letting $K\rightarrow \infty$ will not cause any problem. The reason is that, with such property of the triangulations, we can control the Hessian–Schatten variation on the merging regions in a way that does not deteriorate as $K\rightarrow \infty$ (see the computations in Step 9).

Notice that we still have to discuss the width of the grid $G_k^K$, which will be called $h_k^K$. In order to obtain such properties, we consider a grid $G_k^K$ that is almost the one as in item (b) above (i.e. the one inducing the matrix $D_k$), but is slightly tilted (in a quantitatively controlled way) so that the smallest angle it forms with the x-axis has a non null rational tangent. We centre the grid $G_k^K$ at a vertex of $Q_k$ (say the top left one) and we show that it is possible to choose widths $\{h_k^K\}_k$ (with $h_k^K\rightarrow 0$ as $K\rightarrow \infty$) in such a way that the intersections of the grid $G_k^K$ with the sides of the square $Q_k$ match the intersections of the grid $G_h^K$ with the sides of the square $Q_h$, whenever $Q_k$ and $Q_h$ are neighbouring squares and moreover the vertices of $Q_k$ are also vertices of the grid $G_k^K$. This is possible thanks to the slight tilt that we made to the grid, see Step 6.

We conclude then by obtaining a triangulation of $Q_k$ starting from the grid $G_k^K$ (Step 7). In the region of $Q_k$ that is close to the boundary (this region shrinks as $K\rightarrow \infty$) we adopt a careful self-similar construction, taking into account the choice of the widths $\{h_k^K\}_k$, in order to ensure the compatibility condition of item (c) above. In the remaining part of $G_k^K$, we build the triangulation in the most natural way, i.e. considering also the diagonals of the squares, in order to have a triangulation that is close to the one looked for in item (b) above.

Then, if K is taken large enough, the interpolation along the just built triangulation satisfies the requests made at the beginning of the proof and this is shown in Step 8. Notice that the bulk of the proof is to show that the Hessian–Schatten total variation of the interpolating function g is close to the one of f, as trivially g is close to f if K is large enough (as $h_k^K\rightarrow 0$ when $K\rightarrow \infty$).

Step 1. Fix now $\varepsilon >0$ arbitrarily. The proof will be concluded if we find $g\in \textrm{CPWL}(\Omega )$ with $\Vert f-g\Vert _{L^\infty (\Omega )}\le \varepsilon$ and $|{\textrm{D}}^2_1 g|(\Omega )\le |{\textrm{D}}^2_1 f|(\Omega )+C_f\varepsilon$, where $C_f$ is a constant that depends only on f (via its derivatives, even of second and third order) that still has to be determined. In what follows we will allow $C_f$ to vary from line to line.

Step 2. We add a bit of notation. Let $v,w\in S^1$ with $v\perp w$, $s\in {\mathbb {R}}^2$ and $h\in (0,\infty )$. We call G(v, w, s, h) the grid of ${\mathbb {R}}^2$

$$\begin{aligned} G(v,w,s,h)\mathrel {\mathop :}=\left\{ s+t v+ z h w: t\in {\mathbb {R}},z\in {\mathbb {Z}}\right\} \cup \left\{ s+z h v+ t w: t\in {\mathbb {R}},z\in {\mathbb {Z}}\right\} . \end{aligned}$$

The grid consist in boundaries of squares (open or closed) that are called squares of the grid. Vertices of squares of the grid are called vertices of the grid and the same for edges. Notice that G(v, w, s, h) contains a square with vertex s and whose squares have sides of length h and are parallel either to v or to w.

Step 3. For $N\in {\mathbb {N}}$, we consider the grid

$$\begin{aligned} G^N\mathrel {\mathop :}=G((1,0),(0,1),0,2^{-N}) \end{aligned}$$

and we let $Q_k^N$ denote the closed squares of this grid that are contained in ${{\bar{\Omega }}}$. Here $k=1,\dots ,2^{2 N}$.

Step 4. For every N we find two collections of matrices $\{D_k^N\}_k$ and $\{U^N_k\}_k$ satisfying the following properties, for every k:

• (1) $D_k^N$ is diagonal.

• (2) $U^N_k\in O({\mathbb {Q}}^2)$ is a rotation matrix of angle $\theta _k\in (0,\pi /2)$, $\theta _k\ne \{\pi /4\}$.

• (3) It holds that

  $$\begin{aligned} \lim _{N\rightarrow \infty }\sup _k \sup _{x\in Q^N_k}| (U_k^N)^t\nabla ^2 f(x) U_k^N -D_k^N|_1\rightarrow 0. \end{aligned}$$

To build such sequences, first build $\{ D_k^N\}_k$ and $\{{{\tilde{U}}}^N_k\}_k$ with $D_k^N$ diagonal and ${{\tilde{U}}}^N_k\in O({\mathbb {R}}^2)$ such that

$$\begin{aligned} ({{\tilde{U}}}^N_k)^t\nabla ^2 f(x_k^N){{\tilde{U}}}^N_k= D_k^N, \end{aligned}$$

(16)

where $x_k^N$ is the centre of the square $Q^N_k$. We can do this thanks to the symmetry of Hessians of smooth functions.

We denote $R_\theta$ the rotation matrix of angle $\theta$. We set ${{\hat{U}}}^N_k\mathrel {\mathop :}={{\tilde{U}}}_k^N A_k$, where $A_k$ is a matrix of the type

$$\begin{aligned} \begin{pmatrix} 0&{}\pm 1\\ \pm 1&{}0 \end{pmatrix}\qquad \text {or}\qquad \begin{pmatrix} \pm 1&{}0\\ 0&{}\pm 1 \end{pmatrix} \end{aligned}$$

defined in such a way that ${{\hat{U}}}^N_k=R_{{\hat{\theta }}_k}$, for some ${\hat{\theta }}_k\in [0,\pi /2)$. Notice that (16) still holds for ${{\hat{U}}}^N_k$ in place of ${{\tilde{U}}}^N_k$.

Now notice that points with rational coordinates are dense in $S^1\subseteq {\mathbb {R}}^2$, as a consequence of the well known fact that the inverse of the stereographic projection maps ${\mathbb {Q}}$ into ${\mathbb {Q}}^2$. Therefore we can find $\theta _k\in (0,\pi /2)$, $\theta _k\ne \pi /4$ so close to ${\hat{\theta }}_k$ so that $|R_{\theta _k}-R_{{\hat{\theta }}_k}|_1\le N^{-1}$ and such that $R_{\theta _k}\in {\mathbb {Q}}^{2\times 2}$. Then, set $U_k^N\mathrel {\mathop :}=R_{\theta _k}$. Items (1) and (2) hold by the construction above, whereas item (3) can be proved taking into account also the smoothness of f.

We write

$$\begin{aligned} U^N_k= \begin{pmatrix} |&{}|\\ v_k^N&{}w_k^N\\ |&{}| \end{pmatrix}. \end{aligned}$$

Notice that $v_k^N\perp w_k^N$ and $v_k^N,w_k^N\in S^1$. Also, $\theta _k$ is the angle formed by the x-axis with $v_k^N$ so that by (2).

Step 5. By item (3) of Step 4, we take N big enough so that

$$\begin{aligned} \sup _k \sup _{x\in Q^N_k}| (U_k^N)^t\nabla ^2 f(x) U_k^N -D_k^N| \le \varepsilon . \end{aligned}$$

(17)

We suppress the dependence on N in what follows as from now N will be fixed. Also, we can, and will, assume $2^{-N}\le \varepsilon$.

Step 6. We consider grids on $Q_k$, for every k and depending on $K\in {\mathbb {N}}$, free parameter. We recall that $Q_k$ has been defined in Step 3. These grids will be called

$$\begin{aligned} G^K_k\mathrel {\mathop :}=G(v_k,w_k,s_k,h_k^K), \end{aligned}$$

where $h_k^K$ will be determined in this step and $s_k$ is any of the vertices of $Q_k$ (the choice of the vertex will not affect the grid).

For every k, we write

$$\begin{aligned} {\mathbb {Q}}\ni \tan (\theta _k)=\frac{q_k}{p_k}, \end{aligned}$$

where $\textrm{MCD} (p_k,q_k)=1$. We can do this as we chose $\theta _k\in (0,\pi /2)$, $\theta _k\ne \pi /4$ satisfying $R_{\theta _k}\in {\mathbb {Q}}^{2\times 2}$, notice also that our choice implies, in particular, $q_k\ne 0$. We define also

$$\begin{aligned} h_k^K\mathrel {\mathop :}=\frac{1}{2^N} \frac{1}{2^K}\frac{1}{ \sqrt{p_k^2+q_k^2}\prod _{h\ne k}q_h}. \end{aligned}$$

Notice that

$$\begin{aligned} U_k=\frac{1}{\sqrt{p_k^2+q_k^2}} \begin{pmatrix} p_k&{}-q_k\\ q_k&{}p_k \end{pmatrix}, \end{aligned}$$

and, as $U_k$ is an orthogonal matrix, we have that

$$\begin{aligned} {\sqrt{p_k^2+q_k^2}}U_k^{-1}= \begin{pmatrix} p_k&{}q_k\\ -q_k&{}p_k \end{pmatrix}\in {\mathbb {Z}}^{2\times 2}. \end{aligned}$$

This ensures that the vertices of $Q_k$ are also vertices of $G_k^K$. Now notice that lines in $G_k^K$ parallel to $v_k$ intersect the horizontal edges of $Q_k$ in points spaced and also lines in $G_k^K$ parallel to $w_k$ intersect the vertical edges of $Q_k$ in points spaced . We now compute

$$\begin{aligned} \frac{h_k^K}{\sin (\theta _k)}={h_k^K}{\sqrt{1+\cot ^2(\theta _k)}}=\frac{1}{2^N 2^K \sqrt{p_k^2+q_k^2}\prod _{h\ne k}q_h}\sqrt{1+\frac{p_k^2}{q_k^2}}=\frac{1}{2^N}\frac{1}{ 2^K}\frac{1}{\prod _h q_h} \end{aligned}$$

and we notice that this quantity depends only on K (and on N) but not on k.

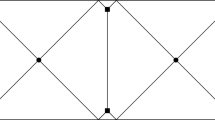
Step 7. Now we want to build a triangulation for the square $Q_k$, such triangulation will depend on the free parameter K and will be called $\Gamma _k^K$. We will then glue all the triangulations $\{\Gamma _k^K\}_k$ to obtain $\Gamma ^K$, a triangulation for ${{\bar{\Omega }}}$. We call edges and vertices of triangulation the edges and vertices of its triangles. We refer to Fig. 1 for an illustration of the proposed triangulation.

Fig. 1

An illustration of the proposed triangulation in the square $Q_k$

Fix for the moment k. By symmetry, we can reduce ourselves to the case of $\theta _k\in (\pi /4,\pi /2)$. Indeed, if $\theta _k\in (0,\pi /4)$, consider ${\mathcal {S}}$ to be the reflection against the axis passing through the top left and bottom right vertex of $Q_k$, let $v_k'\mathrel {\mathop :}=-{\mathcal {S}} v_k$ and $w_k'\mathrel {\mathop :}={\mathcal {S}} w_k$, build the triangulation $(\Gamma _k^K)'$ according to $v_k'$ and $w_k'$ and finally set $\Gamma _k^K\mathrel {\mathop :}={\mathcal {S}}(\Gamma _k^K)'$.

Our building block for the triangulation is the triangle ${\mathcal {T}}^0_u$, which corresponds to the starting case $K=0$. The triangle ${\mathcal {T}}^0_u$ will be then suitably rotated to obtain also the triangles ${\mathcal {T}}^0_r$, ${\mathcal {T}}^0_d$, ${\mathcal {T}}^0_l$. Then, with a suitable rescaling, we will obtain the corresponding elements for the successive steps K, i.e. ${\mathcal {T}}^K_u$, ${\mathcal {T}}^K_r$, ${\mathcal {T}}^K_d$, ${\mathcal {T}}^K_l$. We denote A, B, C, D the vertices of the square $Q_k$, with A corresponding to the top left vertex and the other named clockwise. Let M, N, O, P denote the midpoints of ${\overline{AB}},{\overline{BC}},{\overline{CD}},{\overline{DA}}$ respectively. Then ${\mathcal {T}}^0_u=ABE$ is the right triangle with hypotenuse ${\overline{AB}}$ and such that its angle in A is $\pi /2-\theta _k$ and such that E lies inside $Q_k$. We notice that E is a vertex of $G_k^0$ by what proved in Step 6. Now we consider the intersections of lines of $G_k^0$ parallel to $v_k$ with the hypotenuse of ${\mathcal {T}}_u^0$ (these are not, in general, vertices of $G_k^0$) and the vertices of $G_k^0$ that lie on the short sides of ${\mathcal {T}}_u^0$ (it may be useful to recall that, by construction, the short sides of ${\mathcal {T}}_u^0$ are along $G^0_k$). Then we triangulate ${\mathcal {T}}^0_u$ in such a way that the vertices of the triangulation on the sides ${\mathcal {T}}^0_u$ are exactly at the points just considered. Any finite triangulation is possible, but it has to be fixed. Now we rotate a copy of ${\mathcal {T}}^0_u$ (together with its triangulation) clockwise by $\pi /2$ and we translate it so that the point corresponding to A moves to B. We thus obtain a triangulated triangle ${\mathcal {T}}^0_r=BCF$. By construction, the triangulation on ${\mathcal {T}}^0_r$ has the following property: its vertices on the hypotenuse of ${\mathcal {T}}^0_u$ correspond to the intersection points of lines of $G_k^0$ parallel to $w_k$ with the hypotenuse and its vertices on the short sides are exactly the vertices of $G_k^0$ on the short sides. Then we continue in this fashion to obtain four triangulated triangles, ${\mathcal {T}}^0_u,{\mathcal {T}}^0_r,{\mathcal {T}}^0_d,{\mathcal {T}}^0_l$, as in the left side of Fig. 1 (we shaded ${\mathcal {T}}^0_u$). Notice that ${\mathcal {T}}^0_u\cup {\mathcal {T}}^0_r\cup {\mathcal {T}}^0_d\cup {\mathcal {T}}^0_l$, together with its triangulation is invariant by rotations of $\pi /2$ with centre the centre of $Q_k$. Notice also that $Q_k{\setminus } \big ({\mathcal {T}}^0_u\cup {\mathcal {T}}^0_r\cup {\mathcal {T}}^0_d\cup {\mathcal {T}}^0_l\big )$ is formed by a square which is itself a union of squares, each with sides parallel to $v_k$ or $w_k$ and of length $h_k^0$. We triangulate $Q_k{\setminus } \big ({\mathcal {T}}^0_u\cup {\mathcal {T}}^0_r\cup {\mathcal {T}}^0_d\cup {\mathcal {T}}^0_l\big )$ in the standard way, where by standard way we mean the triangulation obtained considering the grid $G^K_k$ (now $K=0$) and, for every square of the grid, the diagonal with direction $(v_k-w_k)/\sqrt{2}$. This is step 0 and this triangulation will be called $\Gamma _k^0$.

We show now how to build the triangulation at step $K+1$, $\Gamma _k^{K+1}$ starting from the one at step K, $\Gamma _k^K$, see the right side of Fig. 1 (we shaded ${\mathcal {T}}^{1}_u$). At step K we will have ${\mathcal {T}}^K_u,{\mathcal {T}}^K_r,{\mathcal {T}}^K_d,{\mathcal {T}}^K_l$. Now ${\mathcal {T}}^{K+1}_u$ will be union of two copies of ${\mathcal {T}}^{K}_u$ scaled by a factor 1/2 but not rotated nor reflected, but translated so that the vertices corresponding to A will correspond to A and M respectively. Also the triangulation of ${\mathcal {T}}^{K}_u$ is scaled and maintained. We do the same for ${\mathcal {T}}^{K}_r,{\mathcal {T}}^{K}_d,{\mathcal {T}}^{K}_l$, so that ${\mathcal {T}}^{K+1}_u\cup {\mathcal {T}}^{K+1}_r\cup {\mathcal {T}}^{K+1}_d\cup {\mathcal {T}}^{K+1}_l$ together with its triangulation is invariant by rotations of $\pi /2$ with centre the centre of $Q_k$.

We triangulate $Q_k{\setminus } \big ({\mathcal {T}}^{K+1}_u\cup {\mathcal {T}}^{K+1}_r\cup {\mathcal {T}}^{K+1}_d\cup {\mathcal {T}}^{K+1}_l\big )$ using the standard triangulation, with respect to $G_k^{K+1}$. We remark that $Q_k{\setminus } \big ({\mathcal {T}}^{K+1}_u\cup {\mathcal {T}}^{K+1}_r\cup {\mathcal {T}}^{K+1}_d\cup {\mathcal {T}}^{K+1}_l\big )$ is formed by union of squares, each with sides parallel to $v_k$ or $w_k$ and of length $h_k^{K+1}$. Notice that if $\sigma$ is a segment that is part of the boundary of one of ${\mathcal {T}}^{K+1}_u,{\mathcal {T}}^{K+1}_r,{\mathcal {T}}^{K+1}_d,{\mathcal {T}}^{K+1}_l$ and $\sigma$ is not contained in the boundary of $Q_k$, then the vertices of the triangulations on $\sigma$ coincide exactly with vertices of $G^{K+1}_k$ on $\sigma$, so that we have a well defined triangulation, of $Q_k$ that we call $\Gamma _k^{K+1}$.

Now we define $\Gamma ^{K}$ as the triangulation of ${{\bar{\Omega }}}$ obtained by considering all the triangulations in $\{\Gamma _k^{K}\}_k$. Notice that, by Step 6, the triangulations in $\{\Gamma _k^{K}\}_k$ can be joined, as their vertices on the boundaries of $\{Q_k\}_k$ match. Notice that for every K, ${\mathcal {T}}^{K}_u\cup {\mathcal {T}}^{K}_r\cup {\mathcal {T}}^{K}_d\cup {\mathcal {T}}^{K}_l$ is contained in a $2^{-N}2^{-K}$ neighbourhood of the lines of $G^N$, and this neighbourhood (in $\Omega$) has vanishing area as $K\rightarrow \infty$. Therefore, squares of the grid that are triangulated by $\Gamma ^K$ in the standard way and such that also their eight neighbours are triangulated in the standard way by $\Gamma ^K$ eventually cover monotonically $\Omega$, up to the axes of the grid $G^N$. Notice also that triangles in $\Gamma ^K$ have edges of length smaller that $2^{-N} 2^{-K}$.

We add here this crucial remark on which we will heavily rely in the sequel and which will be the occasion to introduce the angle ${{\bar{\theta }}}$. There exists an angle, ${{\bar{\theta }}}>0$, such that every angle in the triangles of $\Gamma ^K$ is bounded from below by ${\bar{\theta }}$, uniformly in K (${\bar{\theta }}$ depends on the choice of the various triangulations of ${\mathcal {T}}_u^0$, that, in turn, depend on N, so that ${\bar{\theta }}$ depends only on N and f). This property is ensured by the self-similarity construction, that provides at each step K two families of triangles, those arising from self-similarity and those arising from the bisection of a (tilted) square with sides parallel to those of $Q_k$, as in Fig. 1.

Step 8. For every K, we set $g^K$ as the $\mathrm CPWL$ interpolant of f according to $\Gamma ^K$. Recall that $\mathrm CPWL$ functions on $\Omega$ have finite Hessian–Schatten total variation. We can compute $|{\textrm{D}}^2_1 g^K|=|{\textrm{D}}\nabla g^K|$ explicitly, that will be concentrated on jump points of the $\nabla g^K$, i.e. on the edges of the triangulation $\Gamma ^K$ (Remark 20).

The computations of Step 9 below ensure that $\{g^K\}_K$ are equi-Lipschitz functions, so that it is clear that as $K\rightarrow \infty$ it holds that $\Vert f-g^K\Vert _{L^\infty (\Omega )}\rightarrow 0$. We claim that $\limsup _{K\rightarrow \infty }|{\textrm{D}}^2_1 g^K|(\Omega )\le |{\textrm{D}}^2 f|(\Omega )+C_f\varepsilon$. Let $U^\delta$ denote the open $\delta$ neighbourhood of $G^N$, intersected with $\Omega$.

Recall the definition of ${\bar{\theta }}$ given at the end of Step 7. Some of our estimates depend on ${\bar{\theta }}$ (see, in particular, the first item below and Step 9) whose value essentially depends on N. Since N has been fixed, depending on $\varepsilon$ and the modulus of continuity of $\nabla ^2 f$, we may absorb the ${\bar{\theta }}$ dependence into the f dependence.

The claim, hence the conclusion, will be a consequence of these two following facts, stated for T closed triangle in $\Gamma ^K$, say $T\in Q_{ k}$:

• (1) it holds

  $$\begin{aligned} |{\textrm{D}}^2_1 g^K|(T\cap \Omega )\le C_f{\mathcal {L}}^2(T); \end{aligned}$$

• (2) whenever T does not intersect $U^{2\cdot 2^{-N} 2^{-K}}$, then

  $$\begin{aligned} \frac{1}{2} |{\textrm{D}}^2_1 g^K|(T)\le (|D_{ k}|_1+C_f\varepsilon ){\mathcal {L}}^2(T). \end{aligned}$$

  We recall that $D_{ k}$ is the diagonal matrix introduced in Step 4 for the closed square $Q_{ k}$.

Notice that in the first item we have a constant $C_f$ which depends on f, and hence we have to take K big enough so that the contributions of these terms are small enough.

Recall that in our estimates we allow $C_f$ to vary line to line.

We defer the proof of items 1 and 2 to Step 9 and Step 10 respectively, now let us show how to conclude the proof using these facts. Fix for the moment K and k. Now consider $\{T_i\}_i$, the (finite) collection (depending on K and k, but we will not make such dependence explicit) of all the closed triangles in the triangulation $\Gamma ^K$ that are contained in ${\bar{Q}}_k$. Notice that

• i) The interiors of $\{T_i\}_i$ are pairwise disjoint.

• ii) If $\sigma$ is an edge of $\Gamma ^K$ that lies on the boundary of $Q_k$, then there exists exactly one element of $\{T_i\}_i$ having $\sigma$ as edge. This is due to the fact that we are taking triangles contained in ${{\bar{Q}}}_k$

• iii) If $\sigma$ is an edge of $\Gamma ^K$ that does not lie on the boundary of $Q_k$, then there exist exactly two elements of $\{T_i\}_i$ having $\sigma$ as edge.

We order the collection $\{T_i\}_i$ in such a way that $T_1,\dots , T_{I}$ are contained in $U^{4\cdot 2^{-N}2^{-K}}$ and $T_{I+1},\dots$ do not intersect $U^{2\cdot 2^{-N}2^{-K}}$ (if there is a triangle $T_i$ contained in $U^{4\cdot 2^{-N}2^{-K}}$ and not intersecting $U^{2\cdot 2^{-N}2^{-K}}$, we agree that it belongs to the first set of triangles $T_1,\dots , T_{I}$, even though this choice makes no difference in the end). We explain the motivation for this distinction. The triangles $T_1,\dots , T_{I}$ are the ones contained a small neighbourhood of the grid $G^N$ (the measure of such neighbourhood vanishes as $K\rightarrow \infty$) so that their contribution to the Hessian–Schatten variation vanishes as $K\rightarrow \infty$. The remaining triangles, $T_{I+1},\dots$ are far enough from the grid $G^N$: this ensures that they (as well as their neighbours) belong to the region that has been triangulated in the standard way, hence their contribution to the Hessian–Schatten variation remains manageable. Notice also that this distinction covers any possible case, as the lengths of the edges of the triangles in $\{T_i\}_i$ are bounded from above by $2^{-N}2^{-K}$, hence any of these triangles that intersects $U^{2\cdot 2^{-N}2^{-K}}$ is contained in $U^{4\cdot 2^{-N}2^{-K}}$. We compute, using items 1 and 2, recalling iii) above for what concerns the factor 1/2 in the first line,

$$\begin{aligned} |{\textrm{D}}^2_1 g^K|(\Omega \cap {\bar{Q}}_k)&\le \sum _{i\le I} |{\textrm{D}}^2_1 g^K|(T_i)+\frac{1}{2}\sum _{i> I} |{\textrm{D}}^2_1 g^K|(T_i) \\&\le \sum _{i\le I} C_{f}{\mathcal {L}}^2(T_i)+\sum _{i> I}(|D_{ k}|_1+C_f\varepsilon ) {\mathcal {L}}^2(T_i) \\&\le C_{f}{\mathcal {L}}^2(U^{4\cdot 2^{-N}2^{-K}}\cap Q_{k})+(|D_{ k}|_1+C_f\varepsilon ) {\mathcal {L}}^2(Q_k). \end{aligned}$$

Therefore, repeating the procedure for every k,

$$\begin{aligned} |{\textrm{D}}^2_1 g^K|(\Omega )&\le \sum _k |{\textrm{D}}^2_1 g^K|(\Omega \cap {\bar{Q}}_k)\\ {}&\le \sum _kC_{f}{\mathcal {L}}^2(U^{4\cdot 2^{-N}2^{-K}}\cap Q_k)+C_f\varepsilon \sum _k {\mathcal {L}}^2(Q_k)+ \sum _k |D_k|_1 {\mathcal {L}}^2(Q_k)\\ {}&\le C_{f}{\mathcal {L}}^2(U^{4\cdot 2^{-N}2^{-K}})+ C_f\varepsilon {\mathcal {L}}^2(\Omega )+\sum _k |D_k|_1 {\mathcal {L}}^2(Q_k). \end{aligned}$$

Fix now K big enough so that $C_{f}{\mathcal {L}}^2(U^{4\cdot 2^{-N}2^{-K}})\le \varepsilon$, we have

$$\begin{aligned} |{\textrm{D}}^2_1 g^K|(\Omega )\le C_f\varepsilon +\sum _k |D_k|_1 {\mathcal {L}}^2(Q_k). \end{aligned}$$

Now we compute, for every k, taking into account (17),

$$\begin{aligned} |D_k|_1{\mathcal {L}}^2(Q_k)&= \int _{Q_k} |D_k|_1\le \int _{Q_k} \big (| (U_k^N)^t\nabla ^2 f(x) U_k^N|_1+\varepsilon \big )= \int _{Q_k} \big (| \nabla ^2 f(x) |_1+\varepsilon \big )\\ {}&=|{\textrm{D}}^2_1 f|(Q_k)+\varepsilon {\mathcal {L}}^2(Q_k) \end{aligned}$$

so that we can continue our previous computation to see that

$$\begin{aligned} |{\textrm{D}}^2_1 g^K|(\Omega )&\le C_f\varepsilon +\sum _k |D_k|_1 {\mathcal {L}}^2(Q_k)\le C_f\varepsilon +\sum _k |{\textrm{D}}^2 f|(Q_k)+\sum _k\varepsilon {\mathcal {L}}^2(Q_k) \\&=C_f\varepsilon +|{\textrm{D}}^2_1 f|(\Omega )+\varepsilon {\mathcal {L}}^2(\Omega )\le C_f\varepsilon +|{\textrm{D}}^2_1 f|(\Omega ) \end{aligned}$$

thus concluding the proof.

Step 9. We prove item 1 of Step 8. For definiteness, assume that K is fixed. We will heavily use Remark 20 with no reference.

Say $T=ABC\subseteq Q_k$. It is enough to show that $|{\textrm{D}}^2_1 g^K|({\overline{AB}})\le C_f{\mathcal {L}}^2(T)$, under the assumption that ${\overline{AB}}$ does not lie in the boundary of $\Omega$, so that there exists another triangle $T'=ABC'$ of $\Gamma ^K$ (possibly inside an adjacent cube to $Q_k$, recall also that the mesh size parameter K is independent of k), so that T and $T'$ have disjoint interiors.

Call $a=\nabla g^K$ on T and $a'=\nabla g^K$ on $T'$. Then,

$$\begin{aligned}&{\left\{ \begin{array}{ll} a\,\cdot \,(B-C)=f(B)-f(C)\\ a\,\cdot \,(A-C)=f(A)-f(C) \end{array}\right. }{} & {} \qquad \text {and}\qquad {\left\{ \begin{array}{ll} a'\,\cdot \,(B-C')=f(B)-f(C')\\ a'\,\cdot \,(A-C')=f(A)-f(C'). \end{array}\right. } \end{aligned}$$

The mean value theorem gives

$$\begin{aligned}&\begin{pmatrix} (B-C)^t\\ (A-C)^t \end{pmatrix} a{} & {} = \begin{pmatrix} \nabla f(C)(B-C)+\frac{1}{2}(B-C)^t\nabla ^2 f(\xi _1)(B-C)\\ \nabla f(C)(A-C)+\frac{1}{2}(A-C)^t\nabla ^2 f(\xi _2)(A-C) \end{pmatrix}, \end{aligned}$$

(18)

where $\xi _1,\xi _2\in T$. Now notice that as the angles of ABC are bounded below by ${\bar{\theta }}$, the matrix

$$\begin{aligned} \begin{pmatrix} (B-C)^t\\ (A-C)^t \end{pmatrix} \end{aligned}$$

is invertible and its inverse has norm bounded above by $\frac{c_{{\bar{\theta }}}}{|{\overline{AB}}|}$, for a suitable constant $c_{{\bar{\theta }}}$. Also, possibly choosing a larger constant $c_{{\bar{\theta }}}$, the bound from below of the angles yields that $|{\overline{BC}}| \le c_{{\bar{\theta }}}|{\overline{AB}}|$ and $|{\overline{AC}}| \le c_{{\bar{\theta }}}|{\overline{AB}}|$. Similar considerations hold for the triangle $T'$. As $c_{{\bar{\theta }}}$ depends only on ${\bar{\theta }}$, we will absorb this dependence into the f dependence, as announced above.

We rewrite then (18) as

$$\begin{aligned} a=\nabla f(C)+\frac{1}{2} \begin{pmatrix} (B-C)^t\\ (A-C)^t \end{pmatrix}^{-1} \begin{pmatrix} (B-C)^t\nabla ^2 f(\xi _1)(B-C)\\ (A-C)^t\nabla ^2 f(\xi _2)(A-C) \end{pmatrix}. \end{aligned}$$

Similarly,

$$\begin{aligned} a'=\nabla f(C')+\frac{1}{2} \begin{pmatrix} (B-C')^t\\ (A-C')^t \end{pmatrix}^{-1} \begin{pmatrix} (B-C')^t\nabla ^2 f(\eta _1)(B-C')\\ (A-C')^t\nabla ^2 f(\eta _2)(A-C') \end{pmatrix}, \end{aligned}$$

for $\eta _1,\eta _2\in T'$. Hence

$$\begin{aligned} |{\textrm{D}}^2_1 g^K|({\overline{AB}})=|a-a'||{\overline{AB}}| \le \bigg ( |\nabla f(C)-\nabla f(C')|+\frac{C_{f}}{|{\overline{AB}}|}|{\overline{AB}}|^2\bigg )|{\overline{AB}}|. \end{aligned}$$

Now, $|\nabla f(C)-\nabla f(C')| \le \max |\nabla f| (|{\overline{AC}}|+|\overline{AC'}|)$ so that

$$\begin{aligned} |{\textrm{D}}^2_1 g^K|({\overline{AB}})\le C_{f}|{\overline{AB}}|^2 \end{aligned}$$

and the right hand side is bounded above by $C_{f}{\mathcal {L}}^2(T)$ as the angles of T are bounded below by ${\bar{\theta }}$.

Step 10. We prove item 2 of Step 8. For definiteness, assume that K and k are fixed, for $T\subseteq Q_k$. We will heavily use Remark 20 with no reference again. Notice that T lies in a closed square of $G_k^K$ and this square, together with the other squares of $G_k^K$ intersecting it (at the boundary), is triangulated in the standard way, by the assumption that T does not intersect $U^{2\cdot 2^{-N}2^{-K}}$. Notice that the square mentioned before is divided by $\Gamma ^K$ into two triangles. For definiteness, assume that T is the one whose barycentre has smaller y coordinate, the other case being similar. Also, for definiteness, assume that $\theta _k \in (\pi /4,\pi /2)$, the case $\theta _k\in (0,\pi /4)$ being similar.

Call $T=ACD$, such that the angles are named clockwise and the angle at D is of $\pi /2$. Call B the other vertex of the square of the grid in which T lies. Call E the vertex of $\Gamma ^K$ such that $C=(B+E)/{2}$. Call $a=\nabla g^K$ on T, $a'=\nabla g^K$ on ACB and $a''=\nabla g^K$ on CDE. Finally, call $F\mathrel {\mathop :}=(B+D)/{2}$ and $\ell =|{\overline{AD}}|$. We refer to Fig. 2 for an illustration on the introduced notations.

Fig. 2

An illustration of the notations introduced in the Step 10 of the proof

We first estimate $|{\textrm{D}}^2_1 g^K|({\overline{AC}})$:

$$\begin{aligned} |{\textrm{D}}^2_1 g^K|({\overline{AC}})= |a-a'|{\mathcal {H}}^1({\overline{AC}})=\sqrt{2}\ell |a-a'|. \end{aligned}$$

Now we compute

$$\begin{aligned} (g^K(D)-g^K(F))-(g^K(F)-g^K(B))&=f(D)+f(B)-f(A)-f(C)\\ {}&=(f(D)-f(A))-(f(C)-f(B)). \end{aligned}$$

Now,

$$\begin{aligned} \big |f(D)-f(A)-\big (-\ell \partial _{w_k} f(A)+\frac{\ell ^2}{2}\partial ^2_{w_k,w_k}f(A)\big )\big |&\le \frac{\ell ^3}{6} \Vert \partial _{w_k,w_k,w_k}^3 f\Vert _\infty ,\\ \big |f(C)-f(B)-\big (-\ell \partial _{w_k} f(B)+\frac{\ell ^2}{2}\partial ^2_{w_k,w_k}f(B)\big )\big |&\le \frac{\ell ^3}{6} \Vert \partial _{w_k,w_k,w_k}^3 f\Vert _\infty . \end{aligned}$$

and

$$\begin{aligned} |\partial ^2_{w_k,w_k}f(B)-\partial ^2_{w_k,w_k}f(A)|&\le \ell \Vert \partial _{v_k,w_k,w_k}^3 f\Vert _\infty ,\\ |\partial _{w_k}f(B)-\partial _{w_k}f(A)-\ell \partial ^2_{v_k,w_k}f(A)|&\le \frac{\ell ^2}{2} \Vert \partial _{v_k,v_k,w_k}^3 f\Vert _\infty . \end{aligned}$$

Then we can compute

$$\begin{aligned} |a-a'|= \frac{\sqrt{2}}{\ell }\big |(g^K(D)-g^K(F))-(g^K(F)-g^K(B))\big | \le \frac{\sqrt{2}}{\ell }\big (\ell ^2|\partial ^2_{v_k,w_k}f(A)|+C_f\ell ^3\big ). \end{aligned}$$

All in all, recalling $2^{-N}\le \varepsilon$,

$$\begin{aligned} |{\textrm{D}}^2_1 g^K|({\overline{AC}})\le 2 \ell ^2\big (|\partial ^2_{v_k,w_k}f(A)|+C_f \varepsilon \big ). \end{aligned}$$

Now

$$\begin{aligned} \partial ^2_{v_k,w_k}f(A)=w_k^t\nabla ^2 f(A)v_k=(0,1)^t U_k^t\nabla ^2 f(A) U_k(1,0) \end{aligned}$$

so that, by (17),

$$\begin{aligned} |\partial ^2_{v_k,w_k}f(A)| \le |(0,1)^tD_k (1,0)|+ |(0,1)^t (U_k^t\nabla ^2 f(A) U_k-D_k)(1,0)| \le C_f\varepsilon \end{aligned}$$

and this gives

$$\begin{aligned} |{\textrm{D}}^2_1 g^K|({\overline{AC}})\le \ell ^2 C_f\varepsilon . \end{aligned}$$

We turn to $|{\textrm{D}}^2_1 g^k|({\overline{CD}})$:

$$\begin{aligned} |{\textrm{D}}^2_1 g^K|({\overline{CD}})=|a-a''|{\mathcal {H}}^1({\overline{CD}})=\ell |a-a''|. \end{aligned}$$

Now we compute

$$\begin{aligned} (g^K(E)-g^K(C))-(g^K(D)-g^K(A))=(f(E)-f(C))+(f(A)-f(D)). \end{aligned}$$

Now

$$\begin{aligned} \big |f(E)-f(C)-\big (-\ell \partial _{w_k} f(C)+\frac{\ell ^2}{2}\partial ^2_{w_k,w_k}f(C)\big )\big |&\le \frac{\ell ^3}{6} \Vert \partial _{w_k,w_k,w_k}^3 f\Vert _\infty ,\\ \big |f(A)-f(D)-\big (\ell \partial _{w_k} f(D)+\frac{\ell ^2}{2}\partial ^2_{w_k,w_k}f(D)\big )\big |&\le \frac{\ell ^3}{6} \Vert \partial _{w_k,w_k,w_k}^3 f\Vert _\infty . \end{aligned}$$

and

$$\begin{aligned} |\partial _{w_k} f(C)-\partial _{w_k} f(D)-\ell \partial ^2_{v_k,w_k}f(D)| \le \frac{\ell ^2}{2}\Vert \partial ^3_{v_k,v_k,w_k}f\Vert _\infty . \end{aligned}$$

Then we can compute

$$\begin{aligned} |a-a''|&= \frac{1}{\ell }\big |(g^K(E)-g^K(C))-(g^K(D)-g^K(A))\big |\\ {}&\le \frac{1}{\ell } \big ( \frac{\ell ^2}{2}|\partial ^2_{w_k,w_k}f(C)|+\frac{\ell ^2}{2}|\partial ^2_{w_k,w_k}f(D)|+\ell ^2|\partial ^2_{v_k,w_k}f(D)|+C_f\ell ^3\big ). \end{aligned}$$

All in all, recalling again $2^{-N}\le \varepsilon$,

$$\begin{aligned} |{\textrm{D}}^2_1 g^K|({\overline{CD}})\le \ell ^2(\frac{1}{2}|\partial ^2_{w_k,w_k}f(C)|+\frac{1}{2}|\partial ^2_{w_k,w_k}f(D)|+|\partial ^2_{v_k,w_k}f(D)|+C_f\varepsilon ). \end{aligned}$$

As before, $|\partial ^2_{v_k,w_k}f(D)| \le C_f\varepsilon$. Also, with similar computations as before,

$$\begin{aligned} |\partial ^2_{w_k,w_k}f(C)|{} & {} \le |(0,1)^tD_k (0,1)|+ |(0,1)^t (U_k^t\nabla ^2 f(D) U_k-D_k)(0,1)| \\{} & {} \le |(0,1)^tD_k (0,1)|+ C_f\varepsilon , \end{aligned}$$

and similarly

$$\begin{aligned} |\partial ^2_{w_k,w_k}f(D)|{} & {} \le |(0,1)^tD_k (0,1)|+ |(0,1)^t (U_k^t\nabla ^2 f(D) U_k-D_k)(0,1)|\\{} & {} \le |(0,1)^tD_k (0,1)|+ C_f\varepsilon . \end{aligned}$$

Therefore,

$$\begin{aligned} |{\textrm{D}}^2_1 g^K|({\overline{CD}})\le \ell ^2\big ( |(0,1)^tD_k (0,1)|+C_f\varepsilon \big ). \end{aligned}$$

With similar computations we arrive at

$$\begin{aligned} |{\textrm{D}}^2_1 g^K|({\overline{AD}})\le \ell ^2\big ( |(1,0)^tD_k (1,0)|+C_f\varepsilon \big ). \end{aligned}$$

Summing all the three contributions,

$$\begin{aligned} |{\textrm{D}}^2_1 g^K|(T)&=|{\textrm{D}}^2_1 g^K|({\overline{AC}})+|{\textrm{D}}^2_1 g^K|({\overline{CD}})+|{\textrm{D}}^2_1 g^K|({\overline{AD}})\\ {}&\le \ell ^2 C_f\varepsilon +\ell ^2\big ( |(0,1)^tD_k (0,1)|+C_f\varepsilon \big )+\ell ^2\big ( |(1,0)^tD_k (1,0)|+C_f\varepsilon \big ) \\ {}&\le \ell ^2 (C_f\varepsilon + |(0,1)^tD_k (0,1)|+ |(1,0)^tD_k (1,0)|) \\ {}&=2{\mathcal {L}}^2(T) (C_f\varepsilon +|D_k|_1) \end{aligned}$$

which concludes the proof. $\square$

5 Extremal points of the unit ball

Let $\Omega \mathrel {\mathop :}=(0,1)^n\subseteq {\mathbb {R}}^n$. In this section, we investigate the extremal points of the set

$$\begin{aligned} \{f\in L^1_{{\textrm{loc}}}(\Omega ):|{\textrm{D}}^2 f|(\Omega )\le 1\}. \end{aligned}$$

Notice that elements of the set above are indeed in $L^1(\Omega )$, by Proposition 13, as cubes support Poincaré inequalities. In order to carry out our investigation, we will consider a suitable quotient space. We describe now our working setting.

We consider the Banach space $L^1(\Omega )$, endowed with the standard $L^1$ norm. We let ${\mathcal {A}}\subseteq L^1(\Omega )$ denote the (closed) subspace of affine functions. Therefore, ${L^1(\Omega )}/{{\mathcal {A}}}$, endowed with the quotient norm, is still a Banach space. We call $\pi :L^1(\Omega )\rightarrow {L^1(\Omega )}/{{\mathcal {A}}}$ the canonical projection. We define

$$\begin{aligned} {\mathcal {B}}\mathrel {\mathop :}=\left\{ g\in \displaystyle {L^1(\Omega )}/{{\mathcal {A}}}: |{\textrm{D}}^2 g|(\Omega )\le 1\right\} , \end{aligned}$$

where we notice that the $|{\textrm{D}}^2 \,\cdot \,|(\Omega )$ seminorm factorizes to the quotient, so that ${\mathcal {B}}=\pi (\{f\in L^1(\Omega ):|{\textrm{D}}^2 f |(\Omega )\le 1\})$. We endow ${\mathcal {B}}$ with the subspace topology, hence, in the end, its topology is the one induced by the $L^1$ topology. Also, by Proposition 13 and standard functional analytic arguments (in particular, the Rellich–Kondrachov Theorem), we can prove that the convex set ${\mathcal {B}}$ is compact. We will then be able to apply the Krein–Milman Theorem, for ${\mathcal {M}}\subseteq {\mathcal {B}}$:

$$\begin{aligned} {\mathcal {B}}={\overline{\textrm{co}}}({\mathcal {M}})\text { if and only if }\textrm{ext}({\mathcal {B}})\subseteq {\overline{{\mathcal {M}}}}. \end{aligned}$$

(KM)

We set

$$\begin{aligned} {\mathcal {E}}\mathrel {\mathop :}=\pi (\textrm{CPWL}(\Omega ))\cap \textrm{ext}({\mathcal {B}})\subseteq {\mathcal {S}}, \end{aligned}$$

where

$$\begin{aligned} {\mathcal {S}}\mathrel {\mathop :}=\left\{ g\in \displaystyle {L^1(\Omega )}/{{\mathcal {A}}}: |{\textrm{D}}^2 g|(\Omega )= 1\right\} . \end{aligned}$$

Thus, ${\mathcal {B}}$ corresponds to the unit ball with respect to the $|{\textrm{D}}^2 \,\cdot \, |(\Omega )$ norm whereas ${\mathcal {S}}$ to the unit spere with respect to the same norm.

Even though we do not have an explicit characterization of extremal points of ${\mathcal {B}}$, it is easy to establish whether a function $g\in \pi (\textrm{CPWL}(\Omega ))$ is extremal or not.

Proposition 23

(CPWL Extreme Points) A function $g\in \pi (\textrm{CPWL}(\Omega ))\cap {\mathcal {S}}$ belongs to ${\mathcal {E}}$ if and only if $h\in \textrm{span}(g)$ for all $h\in {\mathcal {B}}$ with ${\textrm{supp}\,}(|{\textrm{D}}^2\,h|)\subseteq {\textrm{supp}\,}(|{\textrm{D}}^2\,g|)$.

Proof

The “only if” implication follows easily from Proposition 15.

We prove now the converse implication via a perturbation argument, recall Remark 20: we will use the same notation.

Let $g\in {\mathcal {E}}$ and let $h\in {\mathcal {B}}$ with ${\textrm{supp}\,}(|{\textrm{D}}^2\,h|)\subseteq {\textrm{supp}\,}(|{\textrm{D}}^2\,g|)$. We have to prove that $h\in \textrm{span}(g)$. Assume by contradiction that $h\notin \textrm{span}(g)$. We call now $\{P^g_k\}_k$ (resp. $\{P^h_k\}_k$) the triangles associated to g (resp. h) and $\{a_k^g\}_k$ (resp. $\{a_k^h\}_k$) the values associated to $\nabla g$ (resp. $\nabla h$). As we are assuming ${\textrm{supp}\,}(|{\textrm{D}}^2\,h|)\subseteq {\textrm{supp}\,}(|{\textrm{D}}^2\,g|)$, we can and will assume that $\{P^g_k\}_k$ and $\{P^h_k\}_k$ have the same cardinality and $P^g_k=P_k^h$ for every k, so that we will drop the superscripts g and h on these triangles. Also, we assume that for every k, $P_k\subseteq {\bar{\Omega }}$. Call

$$\begin{aligned} \delta \mathrel {\mathop :}=\min \left\{ | a^g_k-a^g_\ell |: {\mathcal {H}}^1(\partial P_k\cap \partial P_\ell )>0,\ a^g_k\ne a^g_\ell \right\} \end{aligned}$$

and

$$\begin{aligned} \Delta \mathrel {\mathop :}=\max \left\{ | a^h_k-a^h_\ell |: {\mathcal {H}}^1(\partial P_k\cap \partial P_\ell )>0\right\} \end{aligned}$$

and set finally $\varepsilon \mathrel {\mathop :}={\delta }/{\Delta }$ (if $\Delta =0$, then $h=0$ and hence there is nothing to prove). Now we write

$$\begin{aligned} g_1\mathrel {\mathop :}=\frac{g+\varepsilon h}{|{\textrm{D}}^2 (g+\varepsilon h)|(\Omega )}\qquad \text {and}\qquad g_2\mathrel {\mathop :}=\frac{g-\varepsilon h}{|{\textrm{D}}^2 (g-\varepsilon h)|(\Omega )}, \end{aligned}$$

notice that $g_1,g_2\in {\mathcal {S}}$ are well defined as we are assuming $h\notin \textrm{span}(g)$. Clearly $g=c_1 g_1+c_2 g_2$, where

$$\begin{aligned}c_1\mathrel {\mathop :}=\frac{|{\textrm{D}}^2 (g+\varepsilon h)|(\Omega )}{2} \qquad \text {and}\qquad c_2\mathrel {\mathop :}=\frac{|{\textrm{D}}^2 (g-\varepsilon h)|(\Omega )}{2}.\end{aligned}$$

If we show that $c_1+c_2=1$, then we have concluded the proof, as this will show that g was not extremal (recall we are assuming that $h\notin \textrm{span}(g)$) and hence a contradiction.

We prove now the claim. We compute

$$\begin{aligned} |{\textrm{D}}^2(g+\varepsilon h)|(\Omega )&=\sum _{k<\ell }| (a^g_k+\varepsilon a_k^h) - (a_\ell ^g+\varepsilon a_\ell ^h)|{\mathcal {H}}^1(\partial P_k\cap \partial P_\ell )\\ {}&=\sum _{k<\ell } | (a^g_k-a_\ell ^g)+\varepsilon (a_k^h- a_\ell ^h)|{\mathcal {H}}^1(\partial P_k\cap \partial P_\ell ) \end{aligned}$$

and similarly we compute $|{\textrm{D}}^2 (g-\varepsilon h)|$. Notice now that for every $k,\ell$ satisfying ${\mathcal {H}}^1(\partial P_k\cap \partial P_\ell )>0$, there exists $\lambda _{k,\ell }$ with $\varepsilon |\lambda _{k,\ell }| \le 1$ such that $a_k^h-a_\ell ^h=\lambda _{k,\ell } (a_k^g-a_\ell ^g)$. This follows from Remark 20 and the fact that $a_k^g=a_\ell ^g$ implies $a_k^h=a_\ell ^h$. Therefore,

$$\begin{aligned}&|{\textrm{D}}^2(g+\varepsilon h)|(\Omega )+|{\textrm{D}}^2(g-\varepsilon h)|(\Omega )\\&\quad =\sum _{k<\ell }\big (| (a^g_k-a_\ell ^g)+\varepsilon (a_k^h- a_\ell ^h)| +| (a^g_k-a_\ell ^g)-\varepsilon (a_k^h- a_\ell ^h)|\big ){\mathcal {H}}^1(\partial P_k\cap \partial P_\ell )\\&\quad =\sum _{k<\ell }\big ( |a_k^g-a_\ell ^g| (1+\varepsilon \lambda _{k,\ell })+ |a_k^g-a_\ell ^g| (1-\varepsilon \lambda _{k,\ell })\big ) {\mathcal {H}}^1(\partial P_k\cap \partial P_\ell )\\&\quad =2\sum _{k<\ell } |a_k^g-a_\ell ^g| {\mathcal {H}}^1(\partial P_k\cap \partial P_\ell )=2|{\textrm{D}}^2 g|(\Omega )=2, \end{aligned}$$

which concludes the proof. $\square$

Proposition 24

It holds that

$$\begin{aligned} {\textrm{co}({\mathcal {E}})}=\pi (\textrm{CPWL}(\Omega ))\cap {\mathcal {B}}. \end{aligned}$$

Proof

Being the inclusion $\subseteq$ trivial by convexity, we focus on the opposite inclusion. We will heavily rely on Remark 20. Take $g\in \pi (\textrm{CPWL}(\Omega ))\cap {\mathcal {B}}$, $g\ne 0$. Now consider the set

$$\begin{aligned} T\mathrel {\mathop :}=\left\{ h\in {\mathcal {E}}\cap {\mathcal {S}}:{\textrm{supp}\,}(|{\textrm{D}}^2 h|)\subseteq {\textrm{supp}\,}(|{\textrm{D}}^2 g|)\right\} , \end{aligned}$$

and notice that by Proposition 23 and the fact that $g\in \textrm{CPWL}(\Omega )$, then T is finite (we will show that $T\ne \emptyset$ in Step 1). Also notice that $h\in T$ if and only if $-h\in T$, so that we write $T=\{\pm t_1,\dots ,\pm t_\ell \}$. We aim at showing that $g\in \textrm{co}(T)$, this will conclude the proof.

Step 1. We claim that $T\ne \emptyset$. First, if $g\in {\mathbb {R}}{\mathcal {E}}$, then the whole proof is concluded, as $g/|{\textrm{D}}^2\,g|(\Omega )\in T$ so that $g\in \textrm{co}(T)$. Otherwise, thanks to Proposition 23, we can take $h_1\in {\mathcal {B}}$ with ${\textrm{supp}\,}(|{\textrm{D}}^2 h_1|)\subseteq {\textrm{supp}\,}(|{\textrm{D}}^2 g|)$ but $h_1\notin \textrm{span}(g)$. Notice that this forces $h_1\in \pi (\textrm{CPWL}(\Omega ))$. We can then take $\lambda _1\in {\mathbb {R}}$ such that

$$\begin{aligned} 0< {\mathcal {H}}^1({\textrm{supp}\,}(|{\textrm{D}}^2(g-\lambda _1 h_1)|))\le {\mathcal {H}}^1({\textrm{supp}\,}(|{\textrm{D}}^2 g|))-\Lambda , \end{aligned}$$

where

$$\begin{aligned} \Lambda :=\min \{{\mathcal {H}}^1(\partial P_k\cap \partial P_\ell ): {\mathcal {H}}^1(\partial P_k\cap \partial P_\ell )>0,\,\, k\ne \ell \} \end{aligned}$$

and we are using the same notation as for Proposition 23 (here the finitely many triangles are relative to g). If $g-\lambda _1 h_1\in {\mathbb {R}}{\mathcal {E}}$ then we have concluded the proof of this step. Otherwise, take $h_2\in {\mathcal {B}}$ with ${\textrm{supp}\,}(|{\textrm{D}}^2 h_2|) \subseteq {\textrm{supp}\,}(|{\textrm{D}}^2 (g-\lambda _1 h_1)|)$ but $h_2\notin \textrm{span}(g-\lambda _1 h_1)$. Take then $\lambda _2\in {\mathbb {R}}$ such that

$$\begin{aligned} 0< & {} {\mathcal {H}}^1({\textrm{supp}\,}(|{\textrm{D}}^2(g-\lambda _1 h_1-\lambda _2 h_2)|))\le {\mathcal {H}}^1({\textrm{supp}\,}(|{\textrm{D}}^2 (g-\lambda _1 h_1)|))\\{} & {} -\Lambda \le {\mathcal {H}}^1({\textrm{supp}\,}(|{\textrm{D}}^2 g|))-2\Lambda . \end{aligned}$$

If $g-\lambda _1 h_1-\lambda _2 h_2\in {\mathbb {R}}{\mathcal {E}}$, then the proof of this step is concluded. Otherwise we continue in this way, but, by the uniform decay posed on Hessian–Schatten total variations, this process must stop, and this forces eventually $g-\lambda _1 h_1-\lambda _2 h_2-\ldots - \lambda _s h_s\in {\mathbb {R}}{\mathcal {E}}$.

Step 2. We claim that $g\in \textrm{span}(T)$. The proof of this fact is identical to the one of Step 1, but we take $h_i\in T$ instead of $h_i\in {\mathcal {B}}$. The possibility of doing so is ensured by Step 1 (applied to $g,g-\lambda _1 h_1,\ldots$) and process would stop when $g-\lambda _1 g_1-\lambda _2 h_2- \ldots - \lambda _s h_s=0$.

Step 3. We consider the finite dimensional vector subspace ${\mathcal {V}}\mathrel {\mathop :}=\textrm{span}(T)\subseteq {L^1(\Omega )}/{{\mathcal {A}}}$, endowed with the subspace topology. Consider also ${\mathcal {B}}\cap {\mathcal {V}}$, compact and convex, notice that $g\in {\mathcal {B}}\cap {\mathcal {V}}$, by Step 2. We claim that $\textrm{ext}({\mathcal {B}}\cap {\mathcal {V}})\subseteq T$. This will conclude the proof by the Krein–Milman Theorem, as in (KM), with T in place of ${\mathcal {M}}$ and ${\mathcal {B}}\cap {\mathcal {V}}$ in place of ${\mathcal {B}}$. We are using that T is closed and that $\textrm{co}(T)=\overline{\textrm{co}}(T)$ as T is finite. Take $h\in \textrm{ext}({\mathcal {B}}\cap {\mathcal {V}})$, write then $h=\lambda _1 t_1+\cdots +\lambda _\ell t_\ell$. Then there exists $j\in \{1,\dots ,\ell \}$ such that ${\textrm{supp}\,}(|{\textrm{D}}^2 t_j|)\subseteq {\textrm{supp}\,}(|{\textrm{D}}^2 h|)$, as ${\textrm{supp}\,}(|{\textrm{D}}^2 h|)\subseteq {\textrm{supp}\,}(|{\textrm{D}}^2 g|)$ and by Step 1 applied to h instead of g. The same perturbation argument of Proposition 23 shows that, in order for h to be extremal in ${\mathcal {B}}\cap {\mathcal {V}}$, we must have $h=\pm t_j$, which concludes the proof. $\square$

Theorem 25

(Density of $\textrm{CPWL}$ extreme points) If $n=2$, then $\textrm{ext}({\mathcal {B}})\subseteq {\overline{{\mathcal {E}}}}$. In particular, the extreme points of

$$\begin{aligned} \{f\in L^1_{{\textrm{loc}}}(\Omega ):|{\textrm{D}}^2 f|(\Omega )\le 1\} \end{aligned}$$

are contained in $\pi ^{-1}(\overline{{\mathcal {E}}})$ (recall that the closure is taken with respect to the quotient topology of $\displaystyle {L^1(\Omega )}/{{\mathcal {A}}}$). If Conjecture 1 holds, this is true for any number n of space dimensions.

Proof

By Proposition 24,

$$\begin{aligned} {\textrm{co}({\mathcal {E}})}=\pi (\textrm{CPWL}(\Omega ))\cap {\mathcal {B}}, \end{aligned}$$

so that the density Theorem 21 gives

$$\begin{aligned} {\overline{\textrm{co}}}({\mathcal {E}})=\overline{\pi (\textrm{CPWL}(\Omega ))\cap {\mathcal {B}}}={\mathcal {B}}. \end{aligned}$$

Then the claim follows from the Krein–Milman Theorem as recalled in (KM). $\square$