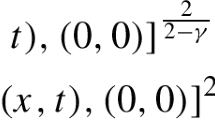The evolution Navier–Stokes equations in a cube under Navier boundary conditions: rarefaction and uniqueness of global solutions

Abstract

We study the evolution Navier–Stokes equations in a cube under Navier boundary conditions. For the related stationary Stokes problem, we determine explicitly all the eigenvectors, eigenvalues and the corresponding Weyl asymptotic. We introduce the notion of rarefaction, namely families of eigenvectors that weakly interact with each other through the nonlinearity. By combining the spectral analysis with rarefaction, we expand the solutions in Fourier series, making explicit some of their properties. We then suggest several new points of view in order to explain the striking difference in uniqueness results between 2D and 3D. First, we construct examples of solutions for which the nonlinearity plays a minor role, both in 2D and 3D. Second, we show that, if a solution is rarefied, then its energy is decreasing: hence, rarefaction may be seen as an almost two dimensional assumption. Finally, by exploiting the explicit form of the eigenvectors we provide a numerical explanation of the difficulty in using energy methods for general solutions of the 3D equations.

1 Introduction

The Navier–Stokes equations

$$\begin{aligned} u_t-\mu \Delta u+(u\cdot \nabla )u+\nabla p=f\,\quad \nabla \cdot u=0\, \end{aligned}$$

(1.1)

model the motion of an incompressible viscous fluid: $u\in {\mathbb {R}}^d$ ($d=2,3$) is its velocity, $p\in {\mathbb {R}}$ its pressure, $\mu >0$ is the kinematic viscosity, $f\in {\mathbb {R}}^d$ is an external force. The equations (1.1) are complemented with an initial condition at $t=0$ and, in bounded domains $\Omega \subset {\mathbb {R}}^d$, with some boundary conditions on $\partial \Omega$, the most common being the homogeneous Dirichlet conditions $u=0$. These no-slip conditions are physically reasonable if the flow is somehow “regular”. But, in some situations, they are no longer suitable to describe the behaviour of the fluid at the boundary and slip boundary conditions appear more realistic. In 1827, Navier [31] proposed boundary conditions with friction, in which there is a stagnant layer of fluid close to the boundary allowing the flow to slip tangentially. Denoting by

$$\begin{aligned} \textbf{D}u=\frac{\ \nabla u+\nabla ^\top u\ }{2} \end{aligned}$$

the strain tensor, Navier claims that, instead of being zero, the tangential component of the fluid velocity at the boundary is proportional to the rate of strain at the surface, that is,

$$\begin{aligned} (\textbf{D}u,\nu )\cdot \tau +\alpha u\cdot \tau =0\quad \text{ on } \partial \Omega , \end{aligned}$$

where $\alpha \ge 0$ is a friction coefficient depending on the fluid viscosity and the roughness of the boundary. Both the Dirichlet ($\beta =1$, infinite friction) and Navier ($0\le \beta <1$, finite friction) boundary conditions may be written in the general form

$$\begin{aligned} u\cdot \nu =\big [\beta u+(1-\beta )(\textbf{D}u,\nu )\big ]\cdot \tau =0\quad \text{ on } \partial \Omega \qquad (\beta \in [0,1])\,, \end{aligned}$$

(1.2)

where $\nu$ is the outward normal vector to $\partial \Omega$ while $\tau$ is tangential. The boundary conditions (1.2) with $\beta <1$ are appropriate in several physically relevant situations [5, 15, 32, 36] and have been studied by many authors. The first contribution is due to Solonnikov-Scadilov [37]. Concerning regularity results, see the works by Beir$\tilde{\textrm{a}}$o da Veiga [6], Amrouche–Rejaiba [2], Acevedo–Amrouche–Conca–Ghosh [1], Berselli [8]. Moreover, Mulone–Salemi [29, 30] studied periodic motions while Clopeau–Mikelic–Robert [10] and Iftimie–Sueur [21] studied the inviscid limit of (1.1) under conditions (1.2). Let us also mention the survey paper by Berselli [7] where one can find further references and more physical applications.

In the present paper, we consider the zero-friction case $\beta =0$ so that (1.2) becomes

$$\begin{aligned} u\cdot \nu =(\textbf{D}u,\nu )\cdot \tau =0\quad \text{ on } \partial \Omega \end{aligned}$$

(1.3)

and we restrict our attention to the cubic 3D domain

$$\begin{aligned} \Omega :=(0,\pi )^3, \end{aligned}$$

in which some regularity results for (1.1) can be found in [11]. It is known [8] that for flat boundaries, (1.3) become mixed Dirichlet–Neumann boundary conditions. Let $T>0$ and $Q_T:= \Omega \times (0,T)$; if we consider (1.1) in the cube $\Omega$ and we complement them with (1.3), we obtain the problem

$$\begin{aligned} \left\{ \begin{array}{ll} u_t-\mu \Delta u+(u\cdot \nabla )u+\nabla p=f\quad &{}\text{ in } Q_T,\\ \nabla \cdot u=0\quad &{}\text{ in } Q_T,\\ u_1=\partial _xu_2=\partial _xu_3=0\quad &{}\text{ on } \{0,\pi \}\times (0,\pi )\times (0,\pi )\times (0,T),\\ u_2=\partial _yu_1=\partial _yu_3=0\quad &{}\text{ on } (0,\pi )\times \{0,\pi \}\times (0,\pi )\times (0,T),\\ u_3=\partial _zu_1=\partial _zu_2=0\quad &{}\text{ on } (0,\pi )\times (0,\pi )\times \{0,\pi \}\times (0,T), \end{array}\right. \end{aligned}$$

(1.4)

where the pressure p is defined up to an additive constant so that one can fix its mean value, for instance

$$\begin{aligned} \int _\Omega p(t)=0\qquad \forall t\ge 0. \end{aligned}$$

(1.5)

To (1.4) we associate an initial condition such as

$$\begin{aligned} u(x,y,z,0)=u_0(x,y,z)\quad \text{ in } \Omega . \end{aligned}$$

(1.6)

Besides the above mentioned physical explanation, the initial-boundary value problem (1.4)–(1.6) has a deep mathematical interest since its solutions can be seen as the restrictions to the cube $\Omega$ of some particular space-periodic solutions of (1.1) over the entire space ${\mathbb {R}}^3$. The matching between two adjacent cubes is smooth and the extended solution satisfies

$$\begin{aligned} u(x+h\pi ,y+k\pi ,z+l\pi ,t)=u(x,y,z,t)\qquad \forall (x,y,z)\in {\mathbb {R}}^3\,,\quad \forall (h,k,l)\in {\mathbb {Z}}^3\,,\quad \forall t\ge 0\,, \end{aligned}$$

see [3, 11] for the details.

The first step for a rigorous analysis of (1.4) is the study of the associated (stationary) Stokes eigenvalue problem which, so far, has been considered in full detail only in special domains [9, 33,34,35] and the growth of the eigenvalues has been estimated through Weyl-type bounds [4, 19, 27, 43]. None of these works considers conditions (1.3) and, only recently, the problem under Navier boundary conditions was tackled in [3, 12]. In Sect. 2.2 we take advantage of the cubic shape of the domain and of the Navier boundary conditions (1.3) in order to determine explicitly all the Stokes eigenvectors. Since the eigenvalues may have large multiplicity, we introduce a criterion for choosing the associated eigenvectors in such a way that, not only they are $L^2(\Omega )$-orthonormal, but they also have nice forms when transformed through the nonlinearity in (1.1). We also show that the set of eigenvectors generates the solenoidal subspace of the Helmholtz–Weyl decomposition [16, 42] and we derive an asymptotic Weyl-type formula [40, 41] for the spectrum, see Sect. 2.3. We then take advantage of the specific form of (1.4) and, in Sect. 2.4, we determine the role of the nonlinearity $(u\cdot \nabla )u$ in the pattern of energy transfer. It turns out that for some eigenvectors the energy increases/decreases/vanishes and moves upward/downward in the spectrum. By exploiting this behaviour we introduce the notion of rarefaction, namely families of eigenvectors weakly interacting with each other through the nonlinearity.

The pioneering works by Leray [24, 25] emphasized that, while for planar flows a solution of (1.1) which is smooth on some interval of time remains smooth for all subsequent times, in the 3D space it is not clear whether a locally smooth solution of (1.1) can develop a singularity at later time. The possible loss of regularity of the solutions is considered the main cause for the lack of global uniqueness results in 3D. Our purpose is to give new points of view on the differences between the 2D and 3D cases.

In Sect. 3.1 we recall the main differences between the 2D and 3D Navier–Stokes equations (1.1), adapted to (1.4)–(1.6), see Propositions 3.2 and 3.3. With the spectral analysis at hand we improve 2D uniqueness results in situations where the nonlinearity is ruled out and explicit solutions can be determined, see Proposition 3.4.

In Sect. 3.2 we introduce the Fourier decomposition of the solutions of (1.4) and we highlight additional differences between 2D and 3D. We show that some 3D rarefied solutions of (1.4)–(1.6) may also be explicitly determined for a suitable class of forces, in particular yielding global smooth (and unique) solutions, see Theorem 3.6 and Corollary 3.7. The class of forces is not “topologically” characterized as (e.g.) for the density result by Fursikov [13], because our purpose is different: we aim to emphasize the relationship between the regularity of the initial datum and the asymptotic growth of the sequence of eigenvalues appearing in the Fourier series.

It is well-known that in 3D one obtains local uniqueness of the solution of (1.1) by using the energy (the squared Dirichlet norm of the solution): the solution is uniquely extended until the energy remains bounded. Global uniqueness is guaranteed in any 2D bounded domain and, in Theorem 3.5, we prove that this also occurs in $\Omega$ if the solution is rarefied or “almost” rarefied. Thanks to the knowledge of the spectrum some energy bounds become simpler and we show that, if a solution is rarefied, then its energy is decreasing. This result is complemented in Sect. 3.3, with a numerical explanation of the difficulty in bounding the energy for general solutions of the 3D equations.

This paper is organized as follows. In Sect. 2 we determine the spectrum of the Stokes eigenvalue problem and we define rarefaction. In Sect. 3 we explain the connection between rarefaction, the asymptotic growth of the eigenvalues involved in the Fourier expansion and uniqueness of global solutions. Section 4 is devoted to the proofs of the main results, with a distinction between propositions and theorems.

2 Spectral analysis

2.1 The Helmholtz–Weyl decomposition

We recall here the spaces appearing in the Helmholtz–Weyl [16, 42] orthogonal decomposition of $L^2(\Omega )$:

$$\begin{aligned}{} & {} H:=\{v\in L^2(\Omega );\, \nabla \cdot v=0 \text{ in } \Omega ,\, v\cdot \nu =0 \text{ on } \partial \Omega \}\,,\\{} & {} \qquad G:=\{v\in L^2(\Omega );\, \exists g\in H^1(\Omega ),\, v=\nabla g\}\,, \end{aligned}$$

in which, with an abuse of notation, we denote by $v\cdot \nu$ the normal trace of v, which belongs to $H^{-1/2}(\partial \Omega )$ because $\nabla \cdot v\in L^2(\Omega )$. It is known that

$$\begin{aligned} L^2(\Omega )=H\oplus G\,\qquad H\perp G\, \end{aligned}$$

(2.1)

where orthogonality is intended with respect to the scalar product in $L^2(\Omega )$. The space G is made of weakly irrotational (conservative) vector fields, namely

$$\begin{aligned} G=\{w\in L^2(\Omega ):\ \textrm{curl}\, w=0 \text{ in } \text{ distributional } \text{ sense }\}\,. \end{aligned}$$

In the sequel, we use the notation

$$\begin{aligned} \forall v,w\in L^2(\Omega )\qquad \qquad v=w+G\quad \begin{array}{c} \tiny {\text {notation}}\\ \Longleftrightarrow \\ \ \end{array} \quad v-w\in G\,, \end{aligned}$$

which means that v and w have the same projection onto H. In order to determine the components of a vector field $\Phi \in L^2(\Omega )$ following (2.1), one proceeds as follows. Let $\varphi \in H^1(\Omega )$ be a (scalar) weak solution of the Neumann problem

$$\begin{aligned} \Delta \varphi =\nabla \cdot \Phi \quad \text{ in } \Omega \,,\qquad \partial _\nu \varphi =\Phi \cdot \nu \quad \text{ on } \partial \Omega \,. \end{aligned}$$

(2.2)

Since the compatibility condition is satisfied, such $\varphi$ exists and is unique, up to the addition of constants. Then notice that $\nabla \cdot (\Phi -\nabla \varphi )=0$ in $\Omega$ and $(\Phi -\nabla \varphi )\cdot \nu =0$ on $\partial \Omega$. Therefore $(\Phi -\nabla \varphi )\in H$ and we can write

$$\begin{aligned} \Phi =(\Phi -\nabla \varphi )+\nabla \varphi =(\Phi -\nabla \varphi )+G\,. \end{aligned}$$

(2.3)

In all the cases that we will consider, we obtain this decomposition directly from the following statement.

Proposition 2.1

Assume that $\Phi \in C^1({\overline{\Omega }})$ satisfies $\Phi \cdot \nu =0$ on $\partial \Omega$. Then, $\int _\Omega \nabla \cdot \Phi =0$ and $\Phi$ can be written as in (2.3), with $\varphi$ being a solution of the Neumann problem for the scalar Poisson equation (2.2).

The important part of the dynamics of (1.1) is described by its projection onto H, where we need more regularity. This is why we also introduce the space

$$\begin{aligned} U:=H\cap H^1(\Omega )\,. \end{aligned}$$

From [23] we know that H is a closed subspace of $L^2(\Omega )$; therefore, U is a closed subspace of $H^1(\Omega )$ which, however, does not coincide with the closure of $\{u\in C^\infty _c(\Omega );\, \nabla \cdot u=0 \text{ in } \Omega \}$ with respect to the Dirichlet norm, see the space V in (4.6), the difference being the possible non-annihilation of the tangential components of the vector fields on $\partial \Omega$. We endow H and U, respectively, with the scalar products and norms

$$\begin{aligned} (v,w)_\Omega := & {} \int _\Omega v\cdot w\,,\quad \Vert v\Vert ^2_{L^2(\Omega )}:=\int _\Omega |v|^2\,,\quad \nonumber \\ (\nabla v,\nabla w)_\Omega := & {} \int _\Omega \nabla v:\nabla w\,,\quad \Vert \nabla v\Vert ^2_{L^2(\Omega )}:=\int _\Omega |\nabla v|^2\,, \end{aligned}$$

(2.4)

where $\nabla v:\nabla w$ is the Euclidean scalar product between Jacobian matrices. It is straightforward that

$$\begin{aligned}{} & {} \int _\Omega (u\cdot \nabla )v\cdot w=-\int _\Omega (u\cdot \nabla )w\cdot v\quad \forall u,v,w\in U\,, \nonumber \\{} & {} \qquad \int _\Omega (u\cdot \nabla )v\cdot v=0\quad \forall u,v\in U\,. \end{aligned}$$

(2.5)

We conclude this section by emphasizing a first important advantage of dealing with the cubic domain $\Omega$, whose boundary consists of six (flat) faces. In Sect. 4.1 we prove

Proposition 2.2

If $\Omega =(0,\pi )^3$ then

$$\begin{aligned} \int _\Omega \nabla v:\nabla w =2\int _{\Omega }{\textbf{D}}v:{\textbf{D}}w \quad \forall v,w\in U. \end{aligned}$$

In the next subsection we study the spectrum of the Stokes operator. Combined with Proposition 2.2 this analysis will justify the choice of the second norm in (2.4).

2.2 Explicit eigenvectors of the Stokes operator in the cube

In order to obtain the Fourier decomposition of the solutions of (1.4) we analyze here the associated Stokes eigenvalue problem

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta v=\lambda v\quad &{} \text{ in } \Omega ,\\ \nabla \cdot v=0\quad &{} \text{ in } \Omega ,\\ v_1=\partial _xv_2=\partial _xv_3=0\quad &{} \text{ on } \{0,\pi \}\times (0,\pi )\times (0,\pi ),\\ v_2=\partial _yv_1=\partial _yv_3=0\quad &{} \text{ on } (0,\pi )\times \{0,\pi \}\times (0,\pi ),\\ v_3=\partial _zv_1=\partial _zv_2=0\quad &{} \text{ on } (0,\pi )\times (0,\pi )\times \{0,\pi \}. \end{array}\right. \end{aligned}$$

(2.6)

In general domains $\Omega$ the eigenvectors v of (2.6) are defined up to the addition of a gradient but, in a cube there is no such indeterminacy. Here and in the sequel, we denote by $\Delta$ both the Laplacian and the Stokes operator (its projection onto H), without distinguishing the notations. Thanks to Proposition 2.2, the problem (2.6) in weak form reads

$$\begin{aligned} (\nabla v,\nabla w)_\Omega =\lambda (v,w)_\Omega \qquad \forall w\in U. \end{aligned}$$

(2.7)

We introduce five families of linearly independent eigenvectors of (2.6). For $m,n,p\in {\mathbb {N}}_+$ we define

$$\begin{aligned}{} & {} X_{0,n,p}(y,z):=\frac{2}{\sqrt{\pi ^3(n^2+p^2)}} \left( \begin{array}{c} 0\\ p\sin (ny)\cos (pz)\\ -n\cos (ny)\sin (pz) \end{array}\right) , \end{aligned}$$

(2.8)

$$\begin{aligned}{} & {} Y_{m,0,p}(x,z):=\frac{2}{\sqrt{\pi ^3(m^2+p^2)}} \left( \begin{array}{c} -p\sin (mx)\cos (pz)\\ 0\\ m\cos (mx)\sin (pz) \end{array}\right) , \end{aligned}$$

(2.9)

$$\begin{aligned}{} & {} Z_{m,n,0}(x,y):=\frac{2}{\sqrt{\pi ^3(m^2+n^2)}} \left( \begin{array}{c} n\sin (mx)\cos (ny)\\ -m\cos (mx)\sin (ny)\\ 0 \end{array}\right) , \end{aligned}$$

(2.10)

$$\begin{aligned}{} & {} V_{m,n,p}(x,y,z):=\frac{2\sqrt{2} \, \cos (mx)}{\sqrt{\pi ^3(n^2+p^2)}} \left( \begin{array}{c} 0\\ p\sin (ny)\cos (pz)\\ -n\cos (ny)\sin (pz) \end{array}\right) , \end{aligned}$$

(2.11)

$$\begin{aligned}{} & {} W_{m,n,p}(x,y,z) :=\frac{2\sqrt{2} }{\sqrt{\pi ^3(m^2+n^2+p^2)(n^2+p^2)}}\nonumber \\{} & {} \qquad \qquad \qquad \qquad \qquad \times \left( \begin{array}{c} (n^2+p^2)\sin (mx)\cos (ny)\cos (pz)\\ -mn\cos (mx)\sin (ny)\cos (pz)\\ -mp\cos (mx)\cos (ny)\sin (pz) \end{array}\right) . \end{aligned}$$

(2.12)

The vectors (2.8)–(2.9)–(2.10) are not deductible from (2.11)–(2.12) when $mnp=0$ since there is an additional normalization factor $\sqrt{2}$ (reminiscent of the coefficient $a_0/2$ in the Fourier series $a_0/2+\sum _na_n\cos (ns)+b_n\sin (ns)$). With a slight abuse of language, in the sequel we call m, n, p the frequencies of the eigenvectors.

In Sect. 4.1 we prove the following statement.

Proposition 2.3

All the eigenvalues of (2.6) have finite multiplicity and can be ordered in a non-decreasing divergent sequence, in which the eigenvalues are repeated according to their multiplicity. For $m,n,p\in {\mathbb {N}}_+$ the eigenvectors in (2.8)–(2.9)–(2.10)–(2.11)–(2.12) are a basis, orthogonal in U and orthonormal in H.

This result deserves several comments. The eigenvectors

$$\begin{aligned} H_{m,n,p}(x,y,z)\!= & {} \!\frac{2\sqrt{2} \cos (ny)}{\sqrt{\pi ^3(m^2+p^2)}} \begin{pmatrix} -p\sin (mx)\cos (pz)\\ 0 \\ m\cos (mx)\sin (pz) \end{pmatrix} \!,\ \\ K_{m,n,p}(x,y,z)\!= & {} \!\frac{2\sqrt{2} \cos (pz)}{\sqrt{\pi ^3(m^2+n^2)}} \begin{pmatrix} n\sin (mx)\cos (ny)\\ -m\cos (mx)\sin (ny)\\ 0 \end{pmatrix} \end{aligned}$$

seem to be missing in the above families but, in fact, they are linear combinations of $V_{m,n,p}$ and $W_{m,n,p}$:

$$\begin{aligned} \begin{aligned}&H_{m,n,p}=-\dfrac{p\sqrt{(m^2+n^2+p^2)(n^2+p^2)}W_{m,n,p}+nm\sqrt{n^2+p^2}V_{m,n,p}}{(n^2+p^2)\sqrt{m^2+p^2}}\\&K_{m,n,p}=\dfrac{n\sqrt{(m^2+n^2+p^2)(n^2+p^2)}W_{m,n,p}-mp\sqrt{n^2+p^2}V_{m,n,p}}{(n^2+p^2)\sqrt{m^2+n^2}}. \end{aligned} \end{aligned}$$

We consider $W_{m,n,p}$ (instead of $H_{m,n,p}$ or $K_{m,n,p}$), because it is $L^2(\Omega )$-orthogonal to all the eigenvectors in (2.8)–(2.9)–(2.10)–(2.11). On the contrary, the eigenvectors $H_{m,n,p}$ and $K_{m,n,p}$ are not orthogonal since

$$\begin{aligned} \int _\Omega V_{m,n,p}\cdot H_{m,n,p}=\frac{-m\, n}{\sqrt{(m^2+p^2)(n^2+p^2)}}\,. \end{aligned}$$

A further reason to focus on the eigenvectors $V_{m,n,p}$ and $W_{m,n,p}$ is the validity of a surprising formula such as (2.18) below, which allows to simplify several computations.

For any $m\in {\mathbb {N}}_+$, the eigenvalue $\lambda =3m^2$ has at least multiplicity 2 and is associated to the vectors (2.11) and (2.12) with $p=n=m$. If only two of the indexes are equal, say $p=m\ne n$, then the eigenvalue is $\lambda =2m^2+n^2$ and the possible permutations of the indexes (m, m, n) (with a repetition) are 3, giving multiplicity 6 after permutation of variables. If the indexes are all different, the possible orderings of (m, n, p) are 6 which, combined with the permutations of variables, gives multiplicity 12. We summarize all these properties within the following statement.

Proposition 2.4

For $m,n,p\in {\mathbb {N}}_+$ all the eigenvalues of (2.6) have multiplicity given by one or a combination of the next five cases:

• (i) $\lambda =m^2+n^2$ with $m\ne n$ has multiplicity 6 and the corresponding linearly independent eigenvectors may be $X_{0,m,n}$, $Y_{n,0,m}$, $Z_{m,n,0}$, $X_{0,n,m}$, $Y_{m,0,n}$, $Z_{n,m,0}$;

• (ii) $\lambda =2m^2$ has multiplicity 3 and the corresponding linearly independent eigenvectors may be $X_{0,m,m}$, $Y_{m,0,m}$, $Z_{m,m,0}$;

• (iii) $\lambda =m^2+n^2+p^2$ with $m\ne n,p$ and $n\ne p$, has multiplicity 12 and the corresponding linearly independent eigenvectors may be $V_{m,n,p}$, $W_{m,n,p}$ with all the possible 6 orderings of the indexes m, n, p;

• (iv) $\lambda =2m^2+n^2$ with $m\ne n$ has multiplicity 6 and the corresponding linearly independent eigenvectors may be $V_{m,m,n}$, $W_{m,m,n}$, $V_{m,n,m}$, $W_{m,n,m}$, $V_{n,m,m}$, $W_{n,m,m}$;

• (v) $\lambda =3m^2$ has multiplicity 2 and the corresponding linearly independent eigenvectors may be $V_{m,m,m}$, $W_{m,m,m}$;

• (vi) if $\lambda$ satisfies at the same time two or more of the above conditions, its multiplicity is obtained by adding the corresponding multiplicities.

The large multiplicities in Proposition 2.4 suggest to introduce a notation clarifying the difference between the eigenvalues $\lambda _k$ and the values of the eigenvalues $\lambda _j^0$. The eigenvalues $\lambda _k$ are ordered along a non-decreasing sequence containing the same eigenvalue repeated following its multiplicity. The values of the eigenvalues $\lambda _j^0$ are ordered along a strictly increasing sequence that contains no information on the multiplicity.

Remark 2.5

From Proposition 2.4 (ii), we infer that the least eigenvalue of (2.6) is $\lambda _1=2$, with multiplicity 3. This shows the validity of the Poincaré inequality

$$\begin{aligned} 2\Vert v\Vert _{L^2(\Omega )}^2\le \Vert \nabla v\Vert _{L^2(\Omega )}^2\qquad \forall v\in U\,. \end{aligned}$$

On the other hand, in the (2D) square $(0,\pi )^2$ the least eigenvalue $\lambda _1$ of the Stokes operator under Navier boundary conditions (S-Nbc) is simple and $\lambda _1=2$, see [3]. In smooth planar domains, Kelliher [22] shows that the k-th eigenvalue $\lambda _k$ of (S-Nbc) is strictly smaller than the k-th eigenvalue $\tau _k$ of the Stokes problem under Dirichlet boundary conditions (S-Dbc):

$$\begin{aligned} \lambda _k<\tau _k\quad \forall k\in {\mathbb {N}}_+. \end{aligned}$$

(2.13)

Although $\Omega =(0,\pi )^3$ is not smooth, it is natural to conjecture that (2.13) remains true also in 3D domains.

In general domains, Proposition 2.2 and Remark 2.5 may not hold, modifying the weak formulation (2.7) of the Stokes eigenvalue problem (2.6). Indeed, [12, Corollary 1] states the following.

Proposition 2.6

Let $\Omega \subset {\mathbb {R}}^3$ be a bounded piecewise $C^{1,1}$ domain with connected boundary. Then, one of the following facts holds:

• if $\Omega$ is not axisymmetric, then the least eigenvalue of (2.6) is strictly positive: $\lambda _1>0$;

• if $\Omega$ is monoaxially symmetric, then the least eigenvalue of (2.6) is $\lambda _1=0$ and is simple;

• if $\Omega$ is a ball, then the least eigenvalue of (2.6) is $\lambda _1=0$ and has multiplicity 3.

In fact, the assumption of connectedness of $\Omega$ was forgotten in [12]; without this assumption, also a spherical annulus is a domain in which $\lambda _1=0$ has multiplicity 3. Moreover, a global $C^{1,1}$-regularity of the boundary was required but the proof therein also works under the slightly weaker assumption of piecewise $C^{1,1}$-regularity. Since $\Omega =(0,\pi )^3$ is not axisymmetric, we have that $\lambda _1>0$ and the Poincaré inequality holds. Therefore, Propositions 2.2 and 2.6 justify the choice of $\Vert \nabla \cdot \Vert _{L^2(\Omega )}$ as a norm over the space U.

2.3 The Weyl asymptotic formula

From Proposition 2.4, we see that all the eigenvalues of (2.6) have at least multiplicity 2, with cases of large multiplicities. In Table 1 we report the first 23 (distinct) values $\lambda _j^0$ of the eigenvalues of (2.6), with the corresponding multiplicity $M(\lambda _j^0)$ and the counting number $N(\lambda ^0_j)$, representing the number of eigenvalues, repeated according to their multiplicity, less than or equal to $\lambda ^0_j$.

Table 1 The least 23 values $\lambda _j^0$ of the eigenvalues of (2.6), with their multiplicity and counting number

Let us now order the eigenvectors of (2.6). The most natural way is to follow the increasing eigenvalues so that we just need to introduce a criterion for multiple eigenvalues.

Criterion 2.7

For equal eigenvalues, we follow the order (2.8)–(2.9)–(2.10)–(2.11)–(2.12). Within the same family, for instance (2.8), the order follows the increasing triples of indexes and $X_{0,n,p}$ comes before $X_{0,p,n}$ if $n<p$.

As an example, consider the eigenvalue $\lambda =26$ for which Criterion 2.7 gives the order

$$\begin{aligned} \begin{array}{c} X_{0,1,5},\ X_{0,5,1},\ Y_{1,0,5},\ Y_{5,0,1},\ Z_{1,5,0},\ Z_{5,1,0},\\ V_{1,3,4},\ V_{1,4,3},\ V_{3,1,4},\ V_{3,4,1},\ V_{4,1,3},\ V_{4,3,1},\ W_{1,3,4},\ W_{1,4,3},\ W_{3,1,4},\ W_{3,4,1},\ W_{4,1,3},\ W_{4,3,1}. \end{array} \end{aligned}$$

In Table 2 we report the first 15 eigenvalues $\lambda _k$ of (2.6), writing the corresponding eigenfunctions $\Psi _k$ ordered following Criterion 2.7.

Table 2 The first 15 eigenvalues $\lambda _k$ and eigenfunctions of (2.6)

Inspired by the Weyl formula for the Dirichlet–Laplacian [40, 41], Métivier [27] found an asymptotic law for the eigenvalues of (S-Dbc). If $\omega _d$ denotes the volume of the unit ball in ${\mathbb {R}}^d$, in the hypercube $\Omega =(0,\pi )^d$ the Métivier formula reads

$$\begin{aligned} \tau _k\sim \dfrac{4}{\big (\omega _d(d-1)\big )^{2/d}}k^{2/d}\qquad \text {as }\,\,k\rightarrow \infty . \end{aligned}$$

For (S-Nbc) in $\Omega =(0,\pi )^3$, see (2.6), Proposition 2.4 shows that the asymptotic behaviour of the eigenvalues is strictly related to the so-called Gauss circle problem. In the next statement, proved in Sect. 4.2, we compare $\lambda _k$ and $\tau _k$, providing an asymptotic law for the eigenvalues of (2.6).

Theorem 2.8

Let $\{\lambda _k\}_{k\in {\mathbb {N}}_+}$ and $\{\tau _k\}_{k\in {\mathbb {N}}_+}$ be the non-decreasing sequences of eigenvalues of, respectively, (S-Nbc) and (S-Dbc) in $\Omega =(0,\pi )^d$ with $d\in \{2,3\}$. Then

$$\begin{aligned} \lambda _k\le \tau _k \quad \forall k\in {\mathbb {N}}_+\qquad \text{ and }\qquad \lambda _k\sim \tau _k\sim \dfrac{4}{(\omega _d(d-1))^{2/d}} k^{2/d} \qquad \text {as }\,\,k\rightarrow \infty . \end{aligned}$$

(2.14)

In spite of the inequality in (2.14), the asymptotic in (2.14) coincide. In Table 3 we report the least 72 values, repeated according to their multiplicity, of $\lambda _k$ and $\tau _k$ in the cube $(0,\pi )^3$. The eigenvalues $\lambda _k$ are computed by using Proposition 2.4, while we refer to [26] for the numerical computation of the eigenvalues $\tau _k$. In Fig. 1 we plot graph of the eigenvalues of Table 3 in dependence of k, illustrating the validity of the inequality in (2.14) and suggesting a strict inequality as (2.13) which, however, is beyond the scopes of the present paper and requires delicate tools, see [22].

Table 3 The least 72 eigenvalues $\lambda _k$ and $\tau _k$ repeated with their multiplicity

Fig. 1

The eigenvalues from Table 3: $\lambda _k$ (black dots) and $\tau _k$ (gray dots), in dependence of k

2.4 Transformations of eigenvectors and rarefaction

For $u,v\in U$, we define the two operators

$$\begin{aligned} u\mapsto {\mathcal {N}}(u)=(u\cdot \nabla )u\qquad \text{ and }\qquad (u,v)\mapsto {\mathcal {B}}(u,v)=(u\cdot \nabla )v+(v\cdot \nabla )u\,. \end{aligned}$$

Clearly, ${\mathcal {N}}$ is nonlinear (somehow quadratic) while ${\mathcal {B}}$ is bilinear: they satisfy

$$\begin{aligned} {\mathcal {B}}(u,u)=2{\mathcal {N}}(u)\qquad {\mathcal {B}}(u,v)={\mathcal {B}}(v,u)\qquad \forall u,v\in U. \end{aligned}$$

We analyze here how these operators transform the eigenvectors of (2.6). We introduce the notations

$$\begin{aligned} \xi :=(x,y,z)\,,\quad \Psi _k:=\Psi _{m_k,n_k,p_k}(\xi )\,,\quad \lambda _k:=m_k^2+n_k^2+p_k^2\quad m_k,n_k,p_k\in {\mathbb {N}}\qquad \end{aligned}$$

(2.15)

in which $\xi$ represents the group of space variables and $\Psi _k$ a generic eigenvector of (2.6) (chosen among those in (2.8)–(2.9)–(2.10)–(2.11)–(2.12)) corresponding to the eigenvalue $\lambda _k=m_k^2+n_k^2+p_k^2$. It can be $m_kn_kp_k=0$, e.g. for $\Psi _{0,n_k,p_k}=X_{0,n_k,p_k}$. A family of eigenvectors $\{\Psi _k\}$ as in (2.15) will always be ordered following Criterion 2.7 so that

$$\begin{aligned}{} & {} k\mapsto \lambda _k=m_k^2+n_k^2+p_k^2\quad \text{ is } \text{ non-decreasing } \text{ but }\\{} & {} \quad k\mapsto m_k,\ k\mapsto n_k,\ k\mapsto p_k\quad \text{ may } \text{ not } \text{ be } \text{ monotone. } \end{aligned}$$

For any integer $\ell \ge 2$, any $A_1,...,A_\ell \in {\mathbb {R}}$ (possibly depending on t), any eigenvectors $\Psi _1,...,\Psi _\ell$ of (2.6), we have

$$\begin{aligned} \begin{array}{c} \displaystyle {\mathcal {N}}\Big (\sum _{k=1}^\ell A_k\Psi _k\Big )={\mathcal {N}}\bigg (\sum _{k=1}^{\ell -1} A_k\Psi _k\bigg )+A_\ell ^2{\mathcal {N}}(\Psi _\ell )+A_\ell \sum _{k=1}^{\ell -1} A_k{\mathcal {B}}(\Psi _k,\Psi _\ell )\,,\\ \displaystyle {\mathcal {N}}\bigg (\sum _{k=1}^\ell A_k\Psi _k\bigg )=\sum _{k=1}^\ell A_k^2{\mathcal {N}}(\Psi _k)+\sum _{1\le k<j}^\ell A_kA_j{\mathcal {B}}(\Psi _k,\Psi _j)\,. \end{array} \end{aligned}$$

(2.16)

The second formula in (2.16) shows that, in order to compute ${\mathcal {N}}(\cdot )$ for a linear combination of $\ell$ eigenvectors, one needs to compute ${\mathcal {N}}(\cdot )$ for $\ell$ eigenvectors and ${\mathcal {B}}(\cdot ,\cdot )$ for $(\ell ^2-\ell )/2$ couples of eigenvectors. Therefore, the number of computations increases quadratically with respect to the number of eigenvectors.

We now compute explicitly the solenoidal part of the transformation through ${\mathcal {N}}(\cdot )$ of the eigenvectors of (2.6); as expected, this strongly depends on the particular eigenvector considered. The following statement is proved in Sect. 4.1.

Proposition 2.9

For $m,n,p\in {\mathbb {N}}_+$ we have

$$\begin{aligned} {\mathcal {N}}(X_{0,n,p})=G\,,\qquad {\mathcal {N}}(Y_{m,0,p})=G\,,\qquad {\mathcal {N}}(Z_{m,n,0})=G\,, \end{aligned}$$

(2.17)

and these are the only eigenvectors $\Psi$ of (2.6) satisfying ${\mathcal {N}}(\Psi )=G$. Moreover, for $m,n,p\in {\mathbb {N}}_+$, one has

$$\begin{aligned} {\mathcal {N}}(V_{m,n,p})= & {} -{\mathcal {N}}(W_{m,n,p})+G\nonumber \\= & {} \tfrac{mn^2p}{(n^2+p^2)\sqrt{\pi ^3(m^2+p^2)}}\, Y_{2m,0,2p}-\tfrac{mnp^2}{(n^2+p^2)\sqrt{\pi ^3(m^2+n^2)}}\, Z_{2m,2n,0}+G.\qquad \end{aligned}$$

(2.18)

The formulas (2.17) express the fact that, up to neglecting the G-part, the nonlinear transformation of the eigenvectors $X_{0,n,p}$, $Y_{m,0,p}$, $Z_{m,n,0}$ annihilates the norms. On the contrary, formulas (2.18) show that, after neglecting the G-part, the $L^2(\Omega )$-squared-norm of the nonlinear transformation of the eigenvectors $V_{m,n,p}$ and $W_{m,n,p}$ is given by

$$\begin{aligned} \frac{m^2n^2p^2}{\pi ^3(n^2+p^2)^2}\left( \frac{n^2}{m^2+p^2}+\frac{p^2}{m^2+n^2}\right) \end{aligned}$$

and, hence, up to neglecting the G-part, the nonlinear transformation of the eigenvectors $V_{m,n,p}$ and $W_{m,n,p}$ can either increment or decrement the norms, but it never annihilates them. The simplicity and elegance of (2.18) are the main reasons for the choice of the eigenvectors (2.11) and (2.12), as a completion of (2.8)–(2.9)–(2.10) within the orthonormal basis in H.

Then we consider the nonlinearity ${\mathcal {B}}$ and we define the trilinear forms

$$\begin{aligned}{} & {} {{\textbf{B}}}_\Omega (\Psi _i,\Psi _j,\Psi _k):=\int _\Omega {\mathcal {B}}(\Psi _i,\Psi _j)\Psi _k\,,\nonumber \\{} & {} \qquad {{\textbf{N}}}_\Omega (\Psi _i,\Psi _k):=\int _\Omega {\mathcal {N}}(\Psi _i)\Psi _k=\frac{{{\textbf{B}}}_\Omega (\Psi _i,\Psi _i,\Psi _k)}{2} \end{aligned}$$

(2.19)

that enable us to introduce the notion of rarefied sequences of eigenvectors.

Definition 2.10

Following (2.15), a sequence $S=\{\Psi _k\}_{k\in {\mathbb {N}}_+}$ of eigenvectors of (2.6) is called rarefied if

$$\begin{aligned} {{\textbf{B}}}_\Omega (\Psi _i,\Psi _j,\Psi _k)=0\qquad \forall \Psi _i,\Psi _j,\Psi _k\in S; \end{aligned}$$

(2.20)

Similarly, for $T>0$, we say that $g\in L^2(Q_T)$ is rarefied if there exist a rarefied sequence of eigenvectors $\{\Psi _k\}_{k\in {\mathbb {N}}_+}$ and a sequence $\{\alpha _k\}_{k\in {\mathbb {N}}_+}\subset L^2(0,T)$ such that

$$\begin{aligned} g(\xi ,t)=\sum _{k=1}^\infty \alpha _k(t)\Psi _k(\xi )\,. \end{aligned}$$

The family $S=\{\Psi _k\}$ may also be finite, in which case the series reduces to a finite sum and most of what follows becomes trivial. The second part of Definition 2.10 states that rarefied functions in $L^2(Q_T)$ are associated with a Fourier series which runs on a rarefied sequence of eigenvectors.

Our next result, proved in Sect. 4.3, fully characterizes rarefied sequences of eigenvectors.

Theorem 2.11

A sequence of eigenvectors $S=\{\Psi _k\}_{k\in {\mathbb {N}}_+}$ of (2.6) is rarefied if and only if, for any choice of the indexes $i,j,k\in {\mathbb {N}}_+$, at least one of the three following couples of conditions holds

$$\begin{aligned} m_i+m_j\ne m_k\ne |m_i-m_j|\,\text{ or }\, n_i+n_j\ne n_k\ne |n_i-n_j|\,\text{ or }\, p_i+p_j\ne p_k\ne |p_i-p_j|.\, \end{aligned}$$

(2.21)

Two remarks are in order.

Remark 2.12

The condition (2.21) includes the possibility that some integers are zero. For the triad $\{X_{0,n_i,p_i}, Y_{m_j,0,p_j}, Z_{m_k,n_k,0}\}$, (2.21) reduces to

$$\begin{aligned} m_k\ne m_j\quad \text{ or }\quad n_k\ne n_i\quad \text{ or }\quad p_i\ne p_j. \end{aligned}$$

For the triad $\{X_{0,n_i,p_i}, X_{0,n_j,p_j}, X_{0,n_k,p_k}\}$ (with $m_k=m_j=m_i=0$) and similar ones, the first couple of conditions is false (because $0=0$), hence (2.21) reduces to

$$\begin{aligned} n_i+n_j\ne n_k\ne |n_i-n_j|\quad \text{ or }\quad p_i+p_j\ne p_k\ne |p_i-p_j|. \end{aligned}$$

Moreover, (2.21) is fulfilled by triads such as $\{X_{0,n_i,p_i},X_{0,n_j,p_j},Y_{m_k,0,p_k}\}$ or $\{X_{0,n_i,p_i},X_{0,n_j,p_j},W_{m_k,n_k,p_k}\}$, and similar triads, since $m_k\ne 0$ ensures the first condition in (2.21).

Remark 2.13

The word “rarefied” seems to express the fact that only “few” eigenvectors are involved, but this is not the case, there are also “weakly rarefied sequences”. The simplest example is obtained through the odd integers (but not the even!): consider all the eigenvectors (2.12) with odd m-frequency (whose differences and sums are even) so that the first condition in (2.21) is satisfied. For this sequence, following the proof of Theorem 2.8, we still find a counting number of the order $\frac{\pi }{6} \lambda _k^{3/2}$ as $k\rightarrow \infty$, implying that $\lambda _k\sim (\frac{6}{\pi }k)^{2/3}$ which is the same order as (2.14) but with a different coefficient.

3 Rarefied global smooth solutions

3.1 A comparison between 2D and 3D

The eigenvectors in Proposition 2.3 have different dimensions both in the domain and in the range. We classify them according to the next definition.

Definition 3.1

Let $A,B\in \{2,3\}$. We say that a vector field $\Phi (\cdot )$, possibly depending on t, is AD-BD if $\Phi :[0,\pi ]^A\rightarrow {\mathbb {R}}^B$ and there exists a vector $\Phi _0\in {\mathbb {R}}^B$ such that $\Phi =\Phi _0+G$.

By Definition 3.1, the eigenvectors $X_{0,n,p}$ in (2.8) are 2D-2D and the associated eigenvalue is $\lambda =n^2+p^2$ (and, similarly, for $Y_{m,0,p}$ in (2.9) and $Z_{m,n,0}$ in (2.10)). By counting the number of indexes and variables permutations, we see that it has multiplicity 6 if $n\ne p$ and multiplicity 3 if $n=p$. The eigenvectors $V_{m,n,p}$ in (2.11) are 3D-2D and are associated with the eigenvalue $\lambda =m^2+n^2+p^2$. The eigenvectors $W_{m,n,p}$ in (2.12) are 3D-3D and are associated with the eigenvalue $\lambda =m^2+n^2+p^2$.

For $T>0$, we put $Q_T:=(0,T)\times \Omega$. In the sequel, for simplicity, we assume that

$$\begin{aligned} f\in L^2(Q_T)\quad \text{ for } \text{ some }\quad T>0. \end{aligned}$$

(3.1)

In a smooth planar bounded domain $\omega \subset {\mathbb {R}}^2$, the initial value problem for (1.1) under Navier boundary conditions admits a unique global weak solution u: this is a consequence of the fact that $u\in L^4\big ((0,T)\times \omega \big )$, see e.g. [14, 23, 38] for similar results under Dirichlet boundary conditions. Assuming $f\in L^2\big ((0,T)\times \omega \big )$ and $u_0\in U$, the regularity of u is ensured under no further restrictions on f and $u_0$. If we embed the square $(0,\pi )^2$ into the cube $(0,\pi )^3$ and we combine these results with [11, Theorem 1], we deduce

Proposition 3.2

Let $T>0$. Let $f\in L^2(Q_T)$ and $u_0\in H$ be 2D-2D vector fields of the same kind, e.g. $f=(f_1(x,y,t),f_2(x,y,t),0)$ and $u_0=(u_{01}(x,y),u_{02}(x,y),0)$. Then there exists a unique weak global solution (u, p) of (1.4)–(1.6); such solution is 2D-2D and satisfies $u\in C^0([0,T];H)$. Moreover, if $u_0\in U$, then $u\in C^0([0,T];U)$.

Proposition 3.2 is well-known under Dirichlet boundary conditions in general domains, see e.g. [23]. In view of Proposition 2.2, the very same proof works under Navier boundary conditions.

In the 3D case much less is known. In the next proposition we state a classical result of global existence of a weak solution and local uniqueness of smooth solutions, adapted to (1.4)–(1.6) in [11].

Proposition 3.3

Let $T>0$. Assume (3.1) and let $u_0\in H$, then:

• (1.4)–(1.6) admits a (global) weak solution $u\in L^\infty (0,T;H)\cap L^2(0,T;U)$;

• if $u_0\in U$, then there exist $K,T^*>0$ satisfying

$$\begin{aligned} 0<\frac{K\mu ^5}{\bigg (\mu \Vert \nabla u_0\Vert ^2_{L^2(\Omega )}+\Vert f\Vert ^2_{L^2(Q_T)}\bigg )^2}\le T^*\le T \end{aligned}$$

such that the weak solution u of (1.4) is unique in $[0,T^*)$ and

$$\begin{aligned} u\in L^\infty (0,T^*;U)\qquad u_t, \Delta u, \nabla p\in L^2(Q_{T^*}). \end{aligned}$$

(3.2)

In fact, (3.2) may be slightly improved by stating that $u\in C^0([0,T^*);U)$. Hence, if $f\in L^2(Q_T)$ and $u_0\in U$, Proposition 3.3 merely ensures that $u\in C^0([0,T^*);U)$ for some $T^*\le T$. If $T^*<T$, then the U-norm of the solution u(t) may blow up before time $t=T$ and global uniqueness of the solution may then fail. We point out that other assumptions on f yield similar results, see [23, 38]. In [11] (and in Proposition 3.3) we assumed $f\in L^2(Q_T)$ following [17, Theorem 2’], where an analogous regularity result is obtained under Dirichlet boundary conditions.

The proof of the uniqueness result in Proposition 3.2 fails in 3D because there is no $L^4$-integrability (in time and space) of the solution and one can merely derive local regularity (and uniqueness) results, see [14, 17, 18]. We now show that, by combining the spectral analysis with rarefaction, see Sect. 2, this lack of regularity is not the only possible explanation of the failure of the proof.

A first combination is the possibility to improve Proposition 3.2 in some particular situations. There are examples for which the nonlinearity plays no role, as in the next statement, where explicit solutions can be determined.

Proposition 3.4

Let $m,n\ge 1$ and $Z_{m,n,0}$ be as in (2.10). Let $u_0(\xi )=\gamma Z_{m,n,0}(\xi )$ for some $\gamma \in {\mathbb {R}}$ and let $f(\xi ,t)=\alpha (t)Z_{m,n,0}(\xi )$ for some $\alpha \in L^2({\mathbb {R}}_+)$. Then the unique solution (u, p) of (1.4)–(1.5)–(1.6) is globally defined in ${\mathbb {R}}_+$ and is explicitly given by

$$\begin{aligned} u(\xi ,t)= & {} \left( \gamma +\int _0^t\alpha (s)e^{\mu (m^2+n^2)s}\, ds\right) e^{-\mu (m^2+n^2)t}\, Z_{m,n,0}(\xi )\,, \nonumber \\ p(\xi ,t)= & {} \left( \gamma +\int _0^t\alpha (s)e^{\mu (m^2+n^2)s}\, ds\right) ^2e^{-2\mu (m^2+n^2)t}\nonumber \\{} & {} \left( \dfrac{1}{\pi ^3}-\frac{2n^2\sin ^2(mx)+2m^2\sin ^2(ny)}{\pi ^3(m^2+n^2)}\right) \,. \end{aligned}$$

(3.3)

Proposition 3.4 describes the behaviour of a linear Stokes equation and it has a simple physical interpretation. Imagine that a fluid is initially moving in the cube $\Omega$ with a planar velocity $u_0$ proportional to $Z_{m,n,0}$. Also imagine that an external force f (such as the wind) acts in the very same direction $Z_{m,n,0}$. Then, according to (3.3), the resulting variable-in-time velocity u(t) will also be proportional to $Z_{m,n,0}$, with exponential decay as $t\rightarrow \infty$ when $f\equiv 0$. With an artificial construction, in Sect. 3.2 we will show that some 3D-3D rarefied solutions of (1.4) also solve some simplified problems.

The second combination concerns the energy method. If $u_0\in U$, Proposition 3.3 allows us to define the energy function

$$\begin{aligned} E(t)=\frac{\Vert u(t)\Vert _U^2}{2}=\frac{\Vert \nabla u(t)\Vert _{L^2(\Omega )}^2}{2},\qquad E\in C^0[0,T^*)\, \end{aligned}$$

(3.4)

and, if $T^*=T$, then the solution is global. In order to prove Proposition 3.3, it is crucial to use both the energy (3.4) and the map

$$\begin{aligned} I_u(t):=\int _\Omega \big (u(t)\cdot \nabla \big )u(t)\cdot \Delta u(t)\,\quad \text {for a.e. } t\in (0,T^*), \end{aligned}$$

(3.5)

when u satisfies (3.2). It is known that the solution can be extended until $I_u(t)$ remains “small” in a suitable sense. In the 2D square $(0,\pi )^2$, it is a simple exercise to show that $I_u(t)\equiv 0$ for any (possibly constant) $u\in U$ satisfying (1.3), see e.g. [39, Lemma 3.1], and not only for solutions of (1.1). In the 3D cube, (3.5) does not vanish even if u solves (1.4). However, if u is rarefied then $I_u(t)\equiv 0$, see Theorem 3.5 (a) below, so that rarefaction may be seen as an almost two dimensional assumption. In completely different contexts, Iftimie [20] and Miller [28] show the importance of almost two dimensional solutions of (1.1) for uniqueness statements.

Finally, a further combination of the spectral analysis with rarefaction enables us to introduce the Fourier decomposition of the solutions of (1.4), making more explicit some differences between the 2D and 3D cases, see next section.

3.2 Rarefaction and uniqueness

We order all the ($L^2(\Omega )$-normalized) eigenvectors of (2.6), as given in Proposition 2.3, along a sequence $\{\Psi _k\}_{k\in {\mathbb {N}}_+}$ in such a way that the corresponding sequence of eigenvalues $\{\lambda _k\}_{k\in {\mathbb {N}}_+}$ is non-decreasing and follows Criterion 2.7, see also Table 2. If (3.1) holds, then there exists a sequence of time-dependent Fourier coefficients $\alpha _k=\alpha _k(t)$ such that

$$\begin{aligned}{} & {} f(\xi ,t)=\sum _{k=1}^\infty \alpha _k(t)\Psi _k(\xi )\,,\qquad \Vert f(t)\Vert _{L^2(\Omega )}^2=\sum _{k=1}^\infty \alpha _k(t)^2 \,,\nonumber \\{} & {} \Vert f\Vert _{L^2(Q_T)}^2=\sum _{k=1}^\infty \Vert \alpha _k\Vert ^2_{L^2(0,T)}<\infty \,; \end{aligned}$$

since we consider all the eigenvectors $\{\Psi _k\}$, it may be $\alpha _k(t)\equiv 0$ for some k. Similarly, the u-part of the solution of (1.4)–(1.6) may be written as

$$\begin{aligned} \begin{array}{cc} \displaystyle u(\xi ,t)=\sum _{k=1}^\infty A_k(t)\Psi _k(\xi )\quad \text{ with }\,\Vert \nabla u\Vert _{L^\infty (0,T;L^2(\Omega ))}^2 =\sup _{(0,T)}\sum _{k=1}^\infty \lambda _k A_k(t)^2\,,\\ \displaystyle u(\xi ,0)=u_0(\xi )=\sum _{k=1}^\infty \gamma _k\Psi _k(\xi )\quad \text{ with }\quad \{\gamma _k\}\in \ell ^2\,, \end{array} \end{aligned}$$

(3.6)

and, again, it may be $A_k(t)\equiv 0$ for some k. Then, the Fourier coefficients $A_k$ of u satisfy the infinite-dimensional nonlinear system

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\dot{A}}_k(t)+\mu \lambda _kA_k(t)\\ +\mathop {\sum }\limits _{\begin{array}{c} i=1 \\ i\ne k \end{array}}^\infty {{\textbf{N}}}_\Omega (\Psi _i,\Psi _k) A_i(t)^2+ \sum \limits _{1=i<j}^\infty {{\textbf{B}}}_\Omega (\Psi _i,\Psi _j,\Psi _k)A_i(t)A_j(t)=\alpha _k(t)\\ A_k(0)=\gamma _k\,, \end{array}\right. \end{aligned}$$

(3.7)

for a.e. $t\in [0,T]$ and for all integers $i,j,k\ge 1$, where ${{\textbf{B}}}_\Omega$ and ${{\textbf{N}}}_\Omega$ are defined in (2.19). The system (3.7) is obtained by multiplying the equation in (1.4) by $\Psi _k(\xi )$, by using (2.16) and by integrating over $\Omega$.

The annihilation of (3.5) is a sufficient condition for the smooth extension of solutions to the whole interval [0, T] and, hence, uniqueness. But the annihilation of (3.5) is not necessary for a solution $u\in C^0([0,T^*);U)$ to become a function in $L^\infty (0,T;U)$. A slightly weaker sufficient condition for the extension is the existence of $\varepsilon \in (0,\mu ]$ and $C_\varepsilon , C^\varepsilon >0$ such that

$$\begin{aligned} J_u(t){} & {} := \int _0^tI_u(s)ds\le \varepsilon \!\int _0^t\!\Vert \Delta u(s)\Vert _{L^2(\Omega )}^2ds+C_\varepsilon \!\int _0^t\!\Vert \nabla u(s)\Vert _{L^2(\Omega )}^2ds + C^\varepsilon \quad \forall t\!\le \! T^*.\nonumber \\ \end{aligned}$$

(3.8)

Although (3.8) is still a very restrictive sufficient condition for solutions u to be global (and unique), in the next result we show that it is satisfied if the solution is “almost” rarefied, see Sect. 4.4 for the proof.

Theorem 3.5

Let $T>0$, assume (3.1) and $u_0\in U$. Let $T^*\le T$ be as in Proposition 3.3. If the corresponding solution u of (1.4)–(1.6) is rarefied in $(0,T^*)$ then:

• (a) $I_u(t)\equiv 0$ and $T^*=T$ so that u is global and $u\in L^\infty (0,T;U)$ is the unique solution;

• (b) for any eigenvector $X_{0,n_\aleph ,p_\aleph }$ of the kind (2.8) there exists $A_\aleph \in L^\infty (0,T^*)$ such that the vector $w(\xi ,t)=u(\xi ,t)+A_\aleph (t)X_{0,n_\aleph ,p_\aleph }(\xi )$ satisfies $J_w(t)\le 0$ for all $t\le T^*$, thereby also satisfying (3.8);

• (c) for any finite linear combination of eigenvectors $\Psi _h^\aleph$ ($h=1,\dots , n$) of (2.6), with coefficients $A_h^\aleph \in L^\infty (0,T^*)$, the vector

$$\begin{aligned} w(\xi ,t)=u(\xi ,t)+\sum _{h=1}^nA_h^\aleph (t)\Psi _h^\aleph (\xi ) \end{aligned}$$

satisfies (3.8).

Statements (b) and (c) show that “almost”rarefied functions satisfying (3.2), not necessarily solving a given equation, maintain (3.8) in $[0,T^*]$. In statement (b), instead of $X_{0,n_\aleph ,p_\aleph }$ one may add a different eigenvector among (2.9)–(2.10)–(2.11)–(2.12), at the price of more computations, see Remark 4.4 below.

A necessary condition for a solution u of (1.4)–(1.6) to be rarefied is that $u_0$ is rarefied. Theorem 3.5 raises the natural “converse” question whether rarefied initial data are also sufficient to have rarefied solution. We do not have a full answer to this query, but we now show that if rarefaction is “strengthened” with some further conditions, then many external forces f yield a rarefied (smooth, global, unique) solution of (1.4)–(1.6). In what follows, we denote by

$$\begin{aligned}&{\mathcal {L}}_r(W_{m_k,n_k,p_k})\quad a\ linear\ combination\ (possibly \ infinite)\\&\quad of\,\, a\,\, family\, \{W_{m_k,n_k,p_k}\}\, of\,\, rarefied\,\, eigenvectors \end{aligned}$$

and the notation $u={\mathcal {L}}_r(W_{m_k,n_k,p_k})$ means that there exists a sequence of rarefied eigenvectors $\{W_{m_k,n_k,p_k}\}$ (ordered following Criterion 2.7) and a sequence of coefficients $\{A_k\}$ (possibly depending on time) such that $u=\sum _kA_kW_{m_k,n_k,p_k}$. The possibility to transform the PDEs (1.4)–(1.6) into the explicit system of ODEs (3.7) enables us to find a connection between the initial regularity and the asymptotic growth of the eigenvalues involved in rarefied solution, as in the next statement proved in Sect. 4.5.

Theorem 3.6

Let $T>0$ and fix any $\varepsilon >0$. In any of the three cases:

• (i) $u_0\in U\cap H^{\frac{3}{2}+\varepsilon }(\Omega )$ with $u_0= {\mathcal {L}}_r(W_{m_k,n_k,p_k})$,

• (ii) $u_0\in U\cap H^{1+\varepsilon }(\Omega )$ with $u_0= {\mathcal {L}}_r(W_{m_k,n_k,n_k})$, namely $p_k=n_k$,

• (iii) $u_0\in U$ with $u_0= {\mathcal {L}}_r(W_{m_k,n_k,p_k})$ and $\lambda _k:=m_k^2+n_k^2+p_k^2$ be such that $\liminf \limits _{k\rightarrow \infty }\frac{\lambda _k}{k^{1+\varepsilon }}>0,$

there exists an uncountable family of 3D-3D forces $f\in L^2(Q_T)$ such that the resulting solution (u, p) of (1.4)–(1.6) is global with the u-component 3D-3D, $u\in L^\infty (0,T;U)$ and $u={\mathcal {L}}_r(W_{m_k,n_k,p_k})$, for the same family of $\{W_{m_k,n_k,p_k}\}$ as $u_0$.

The reason why in Theorem 3.6 we consider three items with a different regularity of $u_0$ is related to the asymptotics associated with the involved eigenvalues. The faster is the asymptotics, the lower is the regularity needed for $u_0$, see Lemma 4.6 below. In item (i) we have $\lambda _k=m_k^2+n_k^2+p_k^2$, which does not ensure an asymptotic behaviour faster than $k^{2/3}$, see Remark 2.13: in this case we need $u_0\in H^{\frac{3}{2}+\varepsilon }(\Omega )$. In item (ii) we have $\lambda _k=m_k^2+2n_k^2$, which does not ensure an asymptotic behaviour faster than k: in this case we only need $u_0\in H^{1+\varepsilon }(\Omega )$. In item (iii) we assume a priori the asymptotic behaviour of the involved eigenvalues in order to get rid of the additional regularity of $u_0$. Therefore, the main interest of Theorem 3.6 is not its statement, but the connection between rarefaction and three different combinations of initial regularity with the asymptotic growth of $k\mapsto \lambda _k$.

The proof of Theorem 3.6 is obtained by constructing explicit rarefied solutions of (1.4)–(1.6), expanded in Fourier series, starting from a rarefied initial datum. With u at hand, we find the corresponding forcing term by setting $f=u_t-\mu \Delta u+(u\cdot \nabla )u+G$: hence, the Fourier series of f “compensates the gaps” left open by the rarefied solution in the equation (1.4). The proofs work precisely because u is rarefied and f is chosen “compatible” with $u_0$. It is fairly simple to find some $u\in L^\infty (0,T;U)$ such that $u_t-\mu \Delta u+(u\cdot \nabla )u\not \in L^2(Q_T)$. In this case, one has that $f\not \in L^2(Q_T)$. The main difficulty in proving Theorem 3.6 is precisely to ensure that the resulting force satisfies $f\in L^2(Q_T)$. In the same spirit, further global uniqueness results with different choices of rarefied eigenvectors may be obtained.

As an example and a direct consequence of Theorem 3.6 (iii) we may combine rarefaction with isofrequency, namely we require that the flow is governed by the same spatial frequencies in any direction. In this case $\lambda _k=3m_k^2\ge 3k^2$, thereby satisfying the required lower bound for the liminf.

Corollary 3.7

Let $T>0$ and $u_0\in U$ with $u_0={\mathcal {L}}_r(W_{m_k,m_k,m_k})$. There exists an uncountable family of 3D-3D forces $f\in L^2(Q_T)$ such that the resulting solution (u, p) of (1.4)–(1.6) is global with the u-component 3D-3D, $u\in L^\infty (0,T;U)$ and $u= {\mathcal {L}}_r(W_{m_k,m_k,m_k})$, for the same family $\{W_{m_k,m_k,m_k}\}$ as $u_0$.

The difference in (2.14) between $d=2$ and $d=3$, and the large multiplicity of eigenvalues (see [3] for the planar case) may suggest that the asymptotic growth of the eigenvalues has a role in the differences for (1.1) in 2D and 3D. The above results show that the rarefaction and a precise spectral analysis may partially explain these differences.

3.3 Numerical hints to explain the failure of energy methods in 3D

We analyse here the variation of the energy E defined in (3.4). With some additional regularity, E is differentiable and in Sect. 4.1 we prove

Proposition 3.8

Assume that $f\equiv 0$ and $u_0\in U\cap H^2(\Omega ){\setminus }\{0\}$. Let $u=u(t)$ be the local solution of (1.4)–(1.6), see Proposition 3.3. Let $I_{u_0}=I_u(0)$ be as in (3.5).

If $I_{u_0}=0$, then ${\dot{E}}(0)<0$; in particular, this happens if $u_0$ is rarefied.

If $I_{u_0}>0$, then there exists ${\overline{\gamma }}={\overline{\gamma }}(u_0)>0$ such that the energy $E_\gamma$ associated to the initial datum $v_0:=\gamma u_0$ satisfies

$$\begin{aligned} {\dot{E}}_\gamma (0)<0 \text{ if } \gamma <{\overline{\gamma }},\quad {\dot{E}}_{{\overline{\gamma }}}(0)=0,\quad {\dot{E}}_\gamma (0)>0 \text{ if } \gamma >{\overline{\gamma }}. \end{aligned}$$

If $I_{u_0}<0$, a similar result holds with ${\overline{\gamma }}={\overline{\gamma }}(u_0)<0$ and reversed signs for ${\dot{E}}_\gamma (0)$.

Whence, contrary to the 2D square $(0,\pi )^2$, the energy may be initially increasing. In this section we use Proposition 3.8 in order to attempt an explanation why the proofs of Propositions 3.2 and 3.4 cannot be extended to a full 3D situation. For simplicity we take

$$\begin{aligned} \mu =1,\quad f\equiv 0,\quad u(\xi ,0)=u_0(\xi )=\gamma V_{m,n,p}(\xi )\quad \text{ in } \Omega \qquad (\gamma \in {\mathbb {R}}\setminus \{0\}). \end{aligned}$$

(3.9)

A straightforward consequence of Proposition 3.3 and [14, Theorem 6.1] reads

Proposition 3.9

Assume (3.9) for some $m,n,p\in {\mathbb {N}}_+$ and $\gamma \in {\mathbb {R}}\setminus \{0\}$. Then:

• (1.4)–(1.6) admits a global weak solution $u\in L^\infty ({\mathbb {R}}_+;H)\cap L^2({\mathbb {R}}_+;U)$;

• there exist $K,T=T(\gamma )>0$ satisfying

  $$\begin{aligned} 0<\frac{K}{(m^2+n^2+p^2)^2\, \gamma ^4}\le T\le +\infty \end{aligned}$$

  such that the weak solution u of (1.4) is unique in [0, T) and $u\in L^\infty (0,T;U)$ with $u_t, \Delta u, \nabla p\in L^2(Q_{T})$;

• there exists ${\overline{\gamma }}>0$ such that if $|\gamma |<{\overline{\gamma }}$, then $T(\gamma )=+\infty$.

We now complement Proposition 3.9 with some numerics. We assume (3.9) and we perform the first steps of a Galerkin scheme, by projecting (1.4)–(1.6) on finite dimensional subspaces, thereby obtaining systems of ODEs. The solution of (1.4)–(1.6) can be written as a Fourier series in the form (3.6). For the first order Galerkin approximation, we consider $\overline{u}(\xi ,t)=A_1(t)V_{m,n,p}(\xi )$; by projecting onto the one-dimensional space spanned by $V_{m,n,p}$ we obtain the single ODE:

$$\begin{aligned} {\dot{A}}_1(t)=-(m^2+n^2+p^2) A_1(t), \quad A_1(0)=\gamma . \end{aligned}$$

As for the 2D-2D case, see Proposition 3.4, the nonlinearity plays no role and $A_1(t)=\gamma e^{-(m^2+n^2+p^2)t}$.

Then we project over a suitable three-dimensional space. Proposition 2.9 suggests to consider the Galerkin approximation given by

$$\begin{aligned} {\overline{u}}(\xi ,t)= A_1(t)V_{m,n,p}(\xi )+A_2(t)Y_{2m,0,2p}(\xi )+A_3(t)Z_{2m,2n,0}(\xi ), \end{aligned}$$

where the three components are, respectively, associated with the eigenvalues

$$\begin{aligned} \lambda _1:=m^2+n^2+p^2,\quad \lambda _2:=4(m^2+p^2),\quad \lambda _3:=4(m^2+n^2); \end{aligned}$$

note that ${\overline{u}}$ is not rarefied. Thanks to (2.16) and (2.17) we compute

$$\begin{aligned} \begin{aligned} {\mathcal {N}}(\overline{u})=&A_1^2(t){\mathcal {N}}(V_{m,n,p})+A_1(t)A_2(t){\mathcal {B}}(V_{m,n,p},Y_{2m,0,2p})\\&+A_1(t)A_3(t){\mathcal {B}}(V_{m,n,p},Z_{2m,2n,0})+A_2(t)A_3(t){\mathcal {B}}(Y_{2m,0,2p},Z_{2m,2n,0})+G. \end{aligned} \end{aligned}$$

With some computations we find

$$\begin{aligned} \begin{aligned}&{(2.5)}\quad \quad \Rightarrow \quad {{\textbf{N}}}_\Omega (V_{m,n,p},V_{m,n,p})=0,\\&{(2.5)+(2.18)}\quad \Rightarrow \quad {{\textbf{N}}}_\Omega (V_{m,n,p},Y_{2m,0,2p})\\&=-{{\textbf{B}}}_\Omega (V_{m,n,p},Y_{2m,0,2p},V_{m,n,p})=\tfrac{mn^2p}{(n^2+p^2)\sqrt{\pi ^3(m^2+p^2)}}=:K_1,\\&{(2.5)+(2.18)}\quad \Rightarrow \quad {{\textbf{B}}}_\Omega (V_{m,n,p},Z_{2m,2n,0},V_{m,n,p})\\&=-{{\textbf{N}}}_\Omega (V_{m,n,p},Z_{2m,2n,0})=\tfrac{mnp^2}{(n^2+p^2)\sqrt{\pi ^3(m^2+n^2)}}=:K_2. \end{aligned} \end{aligned}$$

Moreover,

$$\begin{aligned} \begin{aligned}&{{\textbf{B}}}_\Omega (V_{m,n,p},Y_{2m,0,2p},Y_{2m,0,2p})={{\textbf{B}}}_\Omega (V_{m,n,p},Y_{2m,0,2p},Z_{2m,2n,0})=0,\\&{{\textbf{B}}}_\Omega (V_{m,n,p},Z_{2m,2n,0},Y_{2m,0,2p})={{\textbf{B}}}_\Omega (V_{m,n,p},Z_{2m,2n,0},Z_{2m,2n,0})=0,\\&{{\textbf{B}}}_\Omega (Y_{2m,0,2p},Z_{2m,0,2p},V_{m,n,p})={{\textbf{B}}}_\Omega (Y_{2m,0,2p},Z_{2m,0,2p},Y_{2m,0,2p})\\&={{\textbf{B}}}_\Omega (Y_{2m,0,2p},Z_{2m,0,2p},Z_{2m,2n,0})=0, \end{aligned} \end{aligned}$$

since all these triads satisfy (2.21). Then, according to (3.9), we obtain the $3\times 3$ system of ODEs

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{A}}_1(t)=-\lambda _1 A_1(t)+K_1A_1(t)A_2(t)-K_2A_1(t)A_3(t)\quad t\in \big (0, T\big )\\ {\dot{A}}_2(t)=-\lambda _2 A_2(t)-K_1A_1(t)^2\qquad t\in \big (0, T\big )\\ {\dot{A}}_3(t)=-\lambda _3 A_3(t)+K_2 A_1(t)^2\qquad t\in \big (0, T\big )\\ A_1(0)=\gamma \qquad A_2(0)=A_3(0)=0, \end{array}\right. } \end{aligned}$$

(3.10)

where $T=T(\gamma )$ may be infinite. The energy (3.4) of the solution of (3.10) is given by

$$\begin{aligned} E_3^\gamma (t)=\frac{1}{2} \sum _{i=1}^{3}\lambda _iA_i(t)^2\ \Longrightarrow \ {\dot{E}}_3^\gamma (t)=\sum _{i=1}^{3}\lambda _iA_i(t){\dot{A}}_i(t)\ \Longrightarrow \ {\dot{E}}_3^\gamma (0)=-\lambda _1^2\gamma ^2;\qquad \quad \end{aligned}$$

(3.11)

hence, except for the case $\gamma =0$ which yields a zero solution of (3.10), the energy is initially decreasing. Note also that $E_3^\gamma (t)\equiv E_3^{-\gamma }(t)$.

In some cases, we have that $E_3^\gamma (t)$ is bounded and decays exponentially as $t\rightarrow +\infty$, which ensures that the local solution of (3.10) can be extended for all $t>0$. In Sect. 4.1 we prove

Proposition 3.10

Let $\lambda =\min \{\lambda _2,\lambda _3\}$ and let $\gamma \ne 0$. Assume that one of the following couples of inequalities holds:

$$\begin{aligned} n^2>3(m^2+p^2)\quad \text{ and }\quad \frac{n^2(n^2-3m^2-3p^2)}{m^2+p^2}\ge \frac{p^2(3m^2+3n^2-p^2)}{m^2+n^2}, \end{aligned}$$

(3.12)

$$\begin{aligned} p^2>3(m^2+n^2)\quad \text{ and }\quad \frac{p^2(p^2-3m^2-3n^2)}{m^2+n^2}\ge \frac{n^2(3m^2+3p^2-n^2)}{m^2+p^2}\,. \end{aligned}$$

(3.13)

Then $E_3^\gamma (t)\le E_3^\gamma (0)e^{-2\lambda t}$ for all $t\ge 0$.

In particular, Proposition 3.10 implies that $t\mapsto E_3^\gamma (t)$ attains its maximum at $t=0$ for any $\gamma \ne 0$. But, as we now show numerically, this may be no longer true if both (3.12) and (3.13) fail. Fix $m=n=p=1$; although this is an isofrequency case, we numerically obtain that $t\mapsto E_3^\gamma (t)$ is not globally decreasing for all $\gamma \ne 0$. In Fig. 2 we display the obtained graphs of $t\mapsto E_3^\gamma (t)$ for some values of $\gamma$.

Fig. 2

For $m=n=p=1$, graphs of $t\mapsto E_3^\gamma (t)$. From left to right: $\gamma =10,\, 100,\, 150,\, 300$

Above a critical ${{\overline{\gamma }}}>0$, the maximum energy is no longer attained at $t=0$. As $\gamma$ grows the maximum energy increases, while the corresponding maximum point $t_M$ decreases towards zero, see Table 4, as expected from Proposition 3.9. This gives the flavour of the difficulty to obtain global solutions under large initial data.

Table 4 For $m\!=\!n\!=\!p\!=\!1\!$ and some $\gamma \!>\!0$: values of $E^\gamma _3(0)$, maximum energy, $t_M$ achieving the maximum

We performed numerical experiments also for other triads (m, n, p) violating both (3.12) and (3.13), finding the same qualitative behaviour as in Fig. 2 and Table 4. Whether (3.12) and (3.13) are also necessary conditions for Proposition 3.10 to hold for any $\gamma \ne 0$ is an open question that will be addressed in a future work.

4 Proofs of the results

4.1 Proofs of the propositions

Proof of Proposition 2.2

Using the definition of the strain tensor, we write

$$\begin{aligned} \begin{aligned} 4\int _\Omega {\textbf{D}}v:{\textbf{D}}w&=\int _\Omega \nabla v:\nabla w+\int _\Omega \nabla ^\top v:\nabla ^\top w+\int _\Omega \nabla ^\top v:\nabla w+\int _\Omega \nabla v:\nabla ^\top w\\&=2\int _\Omega \nabla v:\nabla w+\int _\Omega \nabla ^\top v:\nabla w+\int _\Omega \nabla v:\nabla ^\top w\qquad \forall v,w\in U. \end{aligned} \end{aligned}$$

We observe that

$$\begin{aligned} \int _\Omega \nabla ^\top v:\nabla w=-\int _\Omega \nabla \cdot (\nabla ^\top v)\cdot w+\int _{\partial \Omega } \nabla ^\top v\cdot w\cdot \nu \\ =-\int _\Omega \nabla (\nabla \cdot v)\cdot w=0\qquad \forall v,w\in U; \end{aligned}$$

indeed, v is solenoidal and, focusing on the boundary face $\partial \Omega ^x_\pi :=\{\pi \}\times (0,\pi )^2$ with $\nu =(1,0,0)$ (similarly the other faces), we have

$$\begin{aligned} \int _{\partial \Omega ^x_\pi }\nabla ^\top v\cdot w\cdot \nu =\int _{\partial \Omega ^x_\pi }\partial _xv_1w_1+\partial _yv_1w_2+\partial _zv_1w_3=0\qquad \forall v,w\in U, \end{aligned}$$

being $v_1=0$ on $\partial \Omega ^x_\pi$. The same arguments can be repeated for the term $\int _\Omega \nabla v:\nabla ^\top w$. $\square$

Proof of Proposition 2.3

Since U is a Hilbert space and the Stokes operator is linear, compact, self-adjoint and positive (by Proposition 2.2 and Remark 2.5), the first statement follows.

It is straightforward to show that the eigenvectors in (2.8)–(2.9)–(2.10)–(2.11)–(2.12) are normal in $L^2(\Omega )$ (in H) and are linearly independent. In order to show that they generate U, we observe that any linear combination of the eigenvectors in (2.8)–(2.9)–(2.10)–(2.11)–(2.12) can be written as

$$\begin{aligned} v(x,y,z)=\left( \begin{array}{c} a\sin (mx)\cos (ny)\cos (pz)\\ b\cos (mx)\sin (ny)\cos (pz)\\ c\cos (mx)\cos (ny)\sin (pz) \end{array}\right) , \end{aligned}$$

(4.1)

for some $a,b,c\in {\mathbb {R}}$ and $m,n,p\in {\mathbb {N}}$, with the possibility that at most one among m, n, p is zero. Then

$$\begin{aligned} \nabla \cdot v=0\ \Longleftrightarrow \ am+bn+cp=0 \end{aligned}$$

(4.2)

and we need to show that the set of eigenvectors

$$\begin{aligned} {\mathcal {S}}:=\bigg \{v \text { in }(4.1):\,\,am+bn+cp=0\bigg \} \end{aligned}$$

generates U. In view of the boundary conditions in (2.6), each scalar component $v_i$ ($i=1,2,3$) of an eigenvector v satisfies homogeneous Dirichlet boundary conditions on two opposite faces of $\Omega$ and homogeneous Neumann boundary conditions on the remaining four faces. By separating variables, we then find that (e.g.) $v_1(x,y,z)=\sin (mx)\cos (ny)\cos (pz)$ are all the possible eigenfunctions of this scalar eigenvalue problem for $-\Delta$. By adding the solenoidal constraint (4.2), we find the set ${\mathcal {S}}$. $\square$

Proof of Proposition 2.9

The equality (2.17) follows from the identity

$$\begin{aligned} {\mathcal {N}}(Z_{m,n,0})=\frac{2mn}{\pi ^3(m^2+n^2)}\begin{pmatrix} n\sin (2mx)\\ m\sin (2ny)\\ 0 \end{pmatrix} =\nabla \left( \frac{2n^2\sin ^2(mx)+2m^2\sin ^2(ny)}{\pi ^3(m^2+n^2)}\right) \qquad \end{aligned}$$

(4.3)

and, similarly with obvious changes, for ${\mathcal {N}}(Y_{m,0,p})$ and ${\mathcal {N}}(X_{0,n,p})$.

Conversely, let $\Psi$ be an eigenvector of (2.6) satisfying ${\mathcal {N}}(\Psi )=G$. By (4.1) we know that $\Psi$ has the form

$$\begin{aligned} \Psi (\xi )=\left( \begin{array}{c} \Phi _1(\xi )\\ \Phi _2(\xi )\\ \Phi _3(\xi ) \end{array}\right) = \left( \begin{array}{c} a\sin (mx)\cos (ny)\cos (pz)\\ b\cos (mx)\sin (ny)\cos (pz)\\ c\cos (mx)\cos (ny)\sin (pz) \end{array}\right) \end{aligned}$$

for some $m,n,p\in {\mathbb {N}}$ and some $a,b,c\in {\mathbb {R}}$ satisfying (4.2). By the just proved (2.17), we may restrict our attention to the case $m,n,p\in {\mathbb {N}}_+$. Recalling the definition of ${\mathcal {N}}$ in Sect. 2.4, we have

$$\begin{aligned} {\mathcal {N}}(\Psi )=\begin{pmatrix} \Phi _1\partial _x\Phi _1+\Phi _2\partial _y\Phi _1+\Phi _3\partial _z\Phi _1 \\ \Phi _1\partial _x\Phi _2+\Phi _2\partial _y\Phi _2+\Phi _3\partial _z\Phi _2 \\ \Phi _1\partial _x\Phi _3+\Phi _2\partial _y\Phi _3+\Phi _3\partial _z\Phi _3 \end{pmatrix}\,. \end{aligned}$$

By imposing the irrotational properties

$$\begin{aligned} \partial _y{\mathcal {N}}(\Psi )_1=\partial _x{\mathcal {N}}(\Psi )_2\,,\quad \partial _z{\mathcal {N}}(\Psi )_1=\partial _x{\mathcal {N}}(\Psi )_3\,,\quad \partial _y{\mathcal {N}}(\Psi )_3=\partial _z{\mathcal {N}}(\Psi )_2\,, \end{aligned}$$

and after some tedious computations we reach, among others, the conditions $acn=bcm=abp$ (we use that $mnp\ne 0$). But this is impossible in view of (4.2). Hence, if $mnp\in {\mathbb {N}}_+$, it cannot be ${\mathcal {N}}(\Psi )\in G$, proving the statement following (2.17).

The proofs of identities such as (2.17) can also be obtained by showing that the curl of the considered vector is null. In particular, by computing the curl of the differences, one can check that (2.18) holds. $\square$

Proof of Proposition 3.4

The proof is obtained by combining two facts. First notice that u in (3.3) satisfies

$$\begin{aligned} u_t(\xi ,t)-\mu \Delta u(\xi ,t)=u_t(\xi ,t)+\mu (m^2+n^2)u(\xi ,t)=\alpha (t)Z_{m,n,0}(\xi )=f(\xi ,t)\,, \end{aligned}$$

since $Z_{m,n,0}$ is an eigenfunction of (2.6) with eigenvalue $\lambda =m^2+n^2$. Then notice that, for u and p as in (3.3), we have ${\mathcal {N}}\big (u(t)\big )=-\nabla p(t)$, see (4.3). Moreover, u and p satisfy (1.4)–(1.5). $\square$

Proof of Proposition 3.8

We differentiate E in (3.4) and obtain

$$\begin{aligned} {\dot{E}}(t)= & {} \int _\Omega \nabla u(t):\nabla u_t(t)=-\int _\Omega \Delta u(t)\, u_t(t)=\int _\Omega \!\big (u(t)\cdot \nabla \big )u(t)\cdot \Delta u(t)\\{} & {} \quad -\mu \Vert \Delta u(t)\Vert _{L^2(\Omega )}^2 \quad \text {for a.e. }t\in [0,T^*), \end{aligned}$$

where we used (1.4). In particular, we infer that

$$\begin{aligned} {\dot{E}}(0)=I_{u_0}-\mu \Vert \Delta u_0\Vert _{L^2(\Omega )}^2. \end{aligned}$$

Hence, if $I_{u_0}=0$ then ${\dot{E}}(0)<0$. Moreover,

$$\begin{aligned} {\dot{E}}_\gamma (0)=\gamma ^3J_{u_0}-\gamma ^2\mu \Vert \Delta u_0\Vert _{L^2(\Omega )}^2 \end{aligned}$$

and the remaining results follow by taking $\overline{\gamma }=\frac{\mu \Vert \Delta u_0\Vert _{L^2(\Omega )}^2}{I_{u_0}}$. $\square$

Proof of Proposition 3.10

We rewrite (3.10)$_2$ and (3.10)$_3$ as

$$\begin{aligned} \frac{d}{dt}\big (e^{\lambda _2t}A_2(t)\big )=-K_1e^{\lambda _2t}A_1(t)^2\ \Longrightarrow \ A_2(t) =-K_1\int _{0}^{t}e^{\lambda _2(\tau -t)}A_1(\tau )^2d\tau \,, \end{aligned}$$

(4.4)

$$\begin{aligned} \frac{d}{dt}\big (e^{\lambda _3t}A_3(t)\big )=K_2e^{\lambda _3t}A_1(t)^2\ \Longrightarrow \ A_3(t) =K_2\int _{0}^{t}e^{\lambda _3(\tau -t)}A_1(\tau )^2d\tau \,, \end{aligned}$$

(4.5)

where we used the null initial conditions in (3.10)$_4$.

By multiplying (3.10)$_i$ by $\lambda _iA_i(t)$ ($i=1,2,3$) and adding the equations we obtain

$$\begin{aligned} \sum _{i=1}^3\big [\lambda _i{\dot{A}}_i(t)A_i(t)+\lambda _i^2A_i(t)^2] =\big [K_1(\lambda _1-\lambda _2)A_2(t)+K_2(\lambda _3-\lambda _1)A_3(t)\big ]A_1(t)^2 \end{aligned}$$

which, by recalling (3.11), implies (replacing t by z)

$$\begin{aligned} {\dot{E}}_3^\gamma (z)+2\lambda E_3^\gamma (z)\le \big [K_1(\lambda _1-\lambda _2)A_2(z)+K_2(\lambda _3-\lambda _1)A_3(z)\big ]A_1(z)^2\,. \end{aligned}$$

Indeed, in both cases (3.12) and (3.13) we have $\min \{\lambda _1,\lambda _2,\lambda _3\}=\min \{\lambda _2,\lambda _3\}=\lambda$. Recalling (4.4)–(4.5), multiplying this inequality by $e^{2\lambda z}$, and integrating over (0, t), yields

$$\begin{aligned}{} & {} e^{2\lambda t}E_3^\gamma (t)-E_3^\gamma (0) \le \\{} & {} \int _0^te^{2\lambda z}A_1(z)^2\bigg [\int _{0}^{z}\Big [K_1^2(\lambda _2-\lambda _1)e^{\lambda _2(\tau -z)}+K_2^2(\lambda _3-\lambda _1)e^{\lambda _3(\tau -z)}\Big ] A_1(\tau )^2d\tau \bigg ]\, dz\,. \end{aligned}$$

By replacing the values of the $\lambda _i$’s ($i=1,2,3$) and of the $K_i$’s ($i=1,2$), the function G inside the inner squared bracket reads

$$\begin{aligned} G(\tau )=\frac{m^2n^2p^2}{\pi ^3(n^2+p^2)^2}\left[ \frac{n^2(3m^2+3p^2-n^2)}{m^2+p^2}e^{\lambda _2(\tau -z)}+ \frac{p^2(3m^2+3n^2-p^2)}{m^2+n^2}e^{\lambda _3(\tau -z)}\right] . \end{aligned}$$

If (3.12)$_1$ holds, then $n>p$ and, hence,

$$\begin{aligned} e^{\lambda _2(\tau -z)}=e^{4(m^2+p^2)(\tau -z)}>e^{4(m^2+n^2)(\tau -z)}=e^{\lambda _3(\tau -z)}\qquad \forall \tau \in [0,z)\,. \end{aligned}$$

Using also (3.12)$_2$, we infer that $G(\tau )<0$ for all $\tau \in [0,z)$.

If (3.13) holds, we argue similarly by reversing the inequalities and we find again that $G(\tau )<0$ for all $\tau \in [0,z)$. Hence, for both (3.12)–(3.13) we obtain $e^{2\lambda t}E_3^\gamma (t)-E_3^\gamma (0) \le 0$, proving the statement. $\square$

4.2 Proof of Theorem 2.8

Consider the usual functional space for the Stokes problem under Dirichlet boundary conditions, i.e.

$$\begin{aligned} V:=\{v\in H^1_0(\Omega );\, \nabla \cdot v=0 \text{ in } \Omega \}. \end{aligned}$$

(4.6)

By Proposition 2.2, in $\Omega =(0,\pi )^d$ for $d\in \{2,3\}$, the norms $\Vert {\textbf{D}}\cdot \Vert _{L^2(\Omega )}$ and $\Vert \nabla \cdot \Vert _{L^2(\Omega )}$ are equivalent; hence, we may characterize variationally the eigenvalues of the Stokes problems under Navier and Dirichlet boundary conditions as

$$\begin{aligned} \lambda _k=\inf _{\begin{array}{c} W_k\subset U\\ \dim W_k=k \end{array}}\quad \sup _{\begin{array}{c} u\in W_k\setminus \{0\} \end{array}}\frac{\Vert \nabla u\Vert ^2_{L^2(\Omega )}}{\Vert u\Vert ^2_{L^2(\Omega )}}\quad \text {and}\qquad \tau _k=\inf _{\begin{array}{c} W_k\subset V\\ \dim W_k=k \end{array}}\quad \sup _{\begin{array}{c} u\in W_k\setminus \{0\} \end{array}}\frac{\Vert \nabla u\Vert ^2_{L^2(\Omega )}}{\Vert u\Vert ^2_{L^2(\Omega )}}. \end{aligned}$$

Since $V\subset U$, we obtain the inequality in (2.14).

For the asymptotic law in (2.14), we first consider the case $d=2$. From [3, (13)] we know that the $L^2-$normalized eigenfunctions of (2.6) in the square $(0,\pi )^2$ are given by

$$\begin{aligned} \frac{2}{\pi \sqrt{m^2+n^2}} \left( \begin{array}{c} -n\sin (mx)\cos (ny)\\ m\cos (mx)\sin (ny) \end{array}\right) \qquad (m,n\in {\mathbb {N}}_+). \end{aligned}$$

The associated eigenvalues are $\lambda =m^2+n^2$ and the counting function $N(\lambda _k)$ coincides with the number of lattice points $(m,n)\in {\mathbb {N}}_+^2$ belonging to the set

$$\begin{aligned} C_{\lambda _k}:=\{(x,y)\in {\mathbb {R}}^2:\, x^2+y^2\le \lambda _k,\, x>0,\, y>0\}. \end{aligned}$$

This number is approximated by the area of $C_{\lambda _k}$, at least for large k; not only we have to take one fourth of the lattice points inside the circle of radius $\sqrt{\lambda _k}$, but we also need to subtract the number of points on the axis that, however, has a lower order growth with respect to k. Hence, we have

$$\begin{aligned} N(\lambda _k)\sim |C_{\lambda _k}|=\dfrac{\pi }{4}\lambda _k\qquad \text{ as } k\rightarrow \infty \,. \end{aligned}$$

(4.7)

We then notice that $N(\lambda _k)\ge k$, with equality only if $\lambda _k$ is such that $\lambda _k<\lambda _{k+1}$ (that is, when the k-th eigenvalue is simple or the last of a family of multiple eigenvalues). Similarly, $N(\lambda _k)\le k-1+M(\lambda _k)$, with equality only if $\lambda _k$ is simple. Since $M(\lambda _k)\sim |\partial C_{\lambda _k}|=o(|C_{\lambda _k}|)$, by combining these two inequalities, we obtain that $N(\lambda _k)\sim k$ as $k\rightarrow \infty$. In turn, combined with (4.7), this proves the asymptotic in (2.14) for $d=2$ and $\omega _2=\pi$.

If $d=3$, then the counting function $N(\lambda _k)$ equals 3 times the number of lattice points in $C_{\lambda _k}$ plus 2 times the number of lattice points $(m,n,p)\in {\mathbb {N}}_+^3$ inside the set

$$\begin{aligned} S_{\lambda _k}:=\{(x,y,z)\in {\mathbb {R}}^3:\, x^2+y^2+z^2\le \lambda _k,\, x>0,\, y>0,\, z>0\}; \end{aligned}$$

indeed for each lattice point $(m,n,p)\in {\mathbb {N}}_+^3$ we have the two linear independent eigenvectors $V_{m,n,p}$ and $W_{m,n,p}$, see Proposition 2.4. Similarly to (4.7), we then get

$$\begin{aligned} N(\lambda _k)\sim 2|S_{\lambda _k}|+3|C_{\lambda _k}|=2\dfrac{\pi }{6}\lambda _k^{3/2}+\dfrac{3\pi }{4}\lambda _k\sim \dfrac{\pi }{3}\lambda _k^{3/2} \qquad \text{ as } k\rightarrow \infty \,. \end{aligned}$$

We have again that $k\le N(\lambda _k)\le k-1+M(\lambda _k)$ and $M(\lambda _k)\sim 2|\partial S_{\lambda _k}|=o(|S_{\lambda _k}|)$ so that $N(\lambda _k)\sim k$ as $k\rightarrow \infty$. We then conclude as for $d=2$, thereby proving the asymptotic in (2.14) with $d=3$ and $\omega _3=4\pi /3$.

4.3 Proof of Theorem 2.11

In the sequel, we apply the following conventions.

Criterion 4.1

When some of the indexes of the eigenvectors in (2.8)–(2.9)–(2.10)–(2.11)–(2.12) are zeros or negative integers

$$\begin{aligned} \begin{aligned}&V_{0,a,b}=\sqrt{2}X_{0,a,b}\,,\qquad W_{a,0,b}=-\sqrt{2}Y_{a,0,b}\,,\qquad W_{a,b,0}=\sqrt{2}Z_{a,b,0}\qquad \qquad \forall a,b\in {\mathbb {Z}}\setminus \{0\}\\&X_{0,0,a}=X_{0,a,0}=Y_{a,0,0}=Y_{0,0,a}=Z_{a,0,0}=Z_{0,a,0}=V_{a,b,0}=V_{a,0,b}=\\&V_{a,0,0}=V_{0,0,a}=V_{0,a,0}=W_{0,a,b}=W_{a,0,0}=W_{0,0,a}=W_{0,a,0}\equiv (0,0,0)\qquad \forall a,b\in {\mathbb {Z}}\\&X_{0,-n,-p}=X_{0,n,p}\qquad \quad X_{0,-n,p}=X_{0,n,-p}=-X_{0,n,p}\qquad \quad \forall m,n,p\in {\mathbb {N}}_+\\ {}&Y_{-m,0,-p}=Y_{m,0,p}\qquad \quad Y_{-m,0,p}=Y_{m,0,-p}=-Y_{m,0,p}\qquad \quad \forall m,n,p\in {\mathbb {N}}_+\\ {}&Z_{-m,-n,0}=Z_{m,n,0}\qquad \quad Z_{-m,n,0}=Z_{m,-n,0}=-Z_{m,n,0}\qquad \quad \forall m,n,p\in {\mathbb {N}}_+\\&V_{\pm m,-n,-p}=V_{\pm m,n,p}=V_{ m,n,p}\qquad \quad V_{\pm m,-n,p}=V_{\pm m,n,-p}=-V_{ m,n,p}\qquad \quad \forall m,n,p\in {\mathbb {N}}_+\\ {}&W_{\pm m,- n,- p}=W_{\pm m,n,p}=\mp W_{m,n,p}\qquad W_{\pm m,- n,p}=W_{\pm m,n,-p}=\pm W_{m,n,p}\qquad \forall m,n,p\in {\mathbb {N}}_+. \end{aligned} \end{aligned}$$

For the proof of Theorem 2.11, we need the following technical result which explains how the bilinear operator ${\mathcal {B}}$ acts on the frequencies of couples of eigenvectors.

Lemma 4.2

Following notation (2.15), let $\Psi _i$ and $\Psi _j$ be two eigenvectors chosen among (2.8)–(2.9)–(2.10)–(2.11)–(2.12), possibly belonging to the same family. Then ${\mathcal {B}}(\Psi _i,\Psi _j)$ is a linear combination of eigenvectors in (2.8)–(2.9)–(2.10)–(2.11)–(2.12), having frequencies given either by the sum or the difference between the frequencies of $\Psi _i$ and $\Psi _j$, adopting Criterion 4.1.

Proof

We point out that, adopting the convention of Criterion 4.1, there is the possibility that the linear combination of eigenvectors includes some trivial eigenvector, but not all. Since the computations are quite unpleasant we prove the lemma only for two particular couples of $\Psi _i$ and $\Psi _j$.

We consider first the case $\Psi _i=Y_{m_i,0,p_i}$, $\Psi _j=Z_{m_j,n_j,0}$. We have

$$\begin{aligned} \begin{aligned}&{\mathcal {B}}\big (Y_{m_i,0,p_i},Z_{m_j,n_j,0}\big )= \dfrac{-4}{\pi ^3\sqrt{(m_i^2+p_i^2)(m_j^2+n_j^2)}}\times \\ {}&\begin{pmatrix} n_jp_i\cos (n_jy)\cos (p_iz)(m_i\cos (m_ix)\sin (m_jx)+m_j\cos (m_jx)\sin (m_ix))\\ m_j^2p_i\cos (p_iz)\sin (m_j y)\sin (m_ix)\sin (n_jy)\\ m_i^2n_j\cos (n_j x)\sin (m_j x) \sin (m_i x)\sin (p_iz) \end{pmatrix} \end{aligned} \end{aligned}$$

and, hence, that ${\mathcal {B}}\big (Y_{m_i,0,p_i},Z_{m_j,n_j,0}\big )\cdot \nu =0$ on $\partial \Omega$. We then compute

$$\begin{aligned} \nabla \cdot {\mathcal {B}}\big (Y_{m_i,0,p_i},Z_{m_j,n_j,0}\big )=\dfrac{-8m_jm_in_jp_i}{\pi ^3\sqrt{(m_i^2+p_i^2)(m_j^2+n_j^2)}} \cos (m_ix)\cos (m_jx)\cos (n_jy)\cos (p_iz) \end{aligned}$$

and, following Proposition 2.1,

$$\begin{aligned} \varphi= & {} \dfrac{4m_jm_in_jp_i}{\pi ^3\sqrt{(m_i^2+p_i^2)(m_j^2+n_j^2)}}\times \\{} & {} \quad \times \bigg [\dfrac{\cos [(m_i+m_j)x]}{(m_i+m_j)^2+n_j^2+p_i^2}+\dfrac{\cos [(m_i-m_j)x]}{(m_i-m_j)^2+n_j^2+p_i^2}\bigg ]\cos (n_jy)\cos (p_iz). \end{aligned}$$

Computing ${\mathcal {B}}\big (Y_{m_i,0,p_i},Z_{m_j,n_j,0}\big )-\nabla \varphi$, by (2.3) we obtain

$$\begin{aligned}&\quad {\mathcal {B}}\big (Y_{m_i,0,p_i},Z_{m_j,n_j,0}\big )=G+\tfrac{1 }{\sqrt{2\pi ^3(m_i^2+p_i^2)(m_j^2+n_j^2)(n_j^2+p_i^2)}}\times \\ \times \bigg \{&(m_j^2p_i^2-m_i^2n_j^2)V_{m_i+m_j,n_j,p_i}-\dfrac{n_jp_i(m_i+m_j)(m_i^2+m_j^2+n_j^2+p_i^2)}{\sqrt{(m_i+m_j)^2+n_j^2+p_i^2}}W_{m_i+m_j,n_j,p_i}\\ -&(m_j^2p_i^2-m_i^2n_j^2) V_{m_i-m_j,n_j,p_i}+\dfrac{n_jp_i(m_i-m_j)(m_i^2+m_j^2+n_j^2+p_i^2)}{\sqrt{(m_i-m_j)^2+n_j^2+p_i^2}} W_{m_i-m_j,n_j,p_i}\bigg \}. \end{aligned}$$

Similarly, we compute the bilinear form when two eigenvectors belong to the same family. If $\Psi _i=V_{m_i,n_i,p_i}$ and $\Psi _j=V_{m_j,n_j,p_j}$, we obtain

$$\begin{aligned}&{\mathcal {B}}(V_{m_i,n_i,p_i},V_{m_j,n_j,p_j})\\&= \tfrac{n_ip_j-p_in_j}{2\sqrt{2\pi ^3(n_i^2+p_i^2)(n_j^2+p_j^2)}}\\&\quad \bigg [\tfrac{(n_i^2-n_j^2+p_i^2-p_j^2)V_{m_i+m_j,n_i+n_j,p_i+p_j}}{\sqrt{(n_i+n_j)^2+(p_i+p_j)^2}}+ \tfrac{2(m_i+m_j)(n_ip_j-n_jp_i)W_{m_i+m_j,n_i+n_j,p_i+p_j}}{\sqrt{[(m_i+m_j)^2+(n_i+n_j)^2 +(p_i+p_j)^2][(n_i+n_j)^2+(p_i+p_j)^2]}}\\&\quad -\tfrac{(n_i^2-n_j^2+p_i^2-p_j^2)V_{m_i+m_j,n_i-n_j,p_i-p_j}}{\sqrt{(n_i-n_j)^2+(p_i-p_j)^2}} +\tfrac{2(m_i+m_j)(n_ip_j-n_jp_i)W_{m_i+m_j,n_i-n_j,p_i-p_j}}{\sqrt{[(m_i+m_j)^2+(n_i-n_j)^2 +(p_i-p_j)^2][(n_i-n_j)^2+(p_i-p_j)^2]}}\\&\quad -\tfrac{(n_i^2-n_j^2+p_i^2-p_j^2)V_{m_i-m_j,n_i-n_j,p_i-p_j}}{\sqrt{(n_i-n_j)^2+(p_i-p_j)^2}} +\tfrac{2(m_i-m_j)(n_ip_j-n_jp_i)W_{m_i-m_j,n_i-n_j,p_i-p_j}}{\sqrt{[(m_i-m_j)^2+(n_i-n_j)^2 +(p_i-p_j)^2][(n_i-n_j)^2+(p_i-p_j)^2]}}\\&\quad +\tfrac{(n_i^2-n_j^2+p_i^2-p_j^2)V_{m_i-m_j,n_i+n_j,p_i+p_j}}{\sqrt{(n_i+n_j)^2+(p_i+p_j)^2}} +\tfrac{2(m_i-m_j)(n_ip_j-n_jp_i)W_{m_i-m_j,n_i+n_j,p_i+p_j}}{\sqrt{[(m_i-m_j)^2+(n_i+n_j)^2 +(p_i+p_j)^2][(n_i+n_j)^2+(p_i+p_j)^2]}}\bigg ]\\&\quad -\tfrac{n_ip_j+p_in_j}{2\sqrt{2\pi ^3(n_i^2+p_i^2)(n_j^2+p_j^2)}}\\&\quad \bigg [\tfrac{(n_i^2-n_j^2 +p_i^2-p_j^2)V_{m_i+m_j,n_i-n_j,p_i+p_j}}{\sqrt{(n_i-n_j)^2+(p_i+p_j)^2}} +\tfrac{2(m_i+m_j)(n_ip_j+n_jp_i)W_{m_i+m_j,n_i-n_j,p_i+p_j}}{\sqrt{[(m_i+m_j)^2+(n_i-n_j)^2 +(p_i+p_j)^2][(n_i-n_j)^2+(p_i+p_j)^2]}}\\&\quad -\tfrac{(n_i^2-n_j^2+p_i^2-p_j^2)V_{m_i+m_j,n_i+n_j,p_i-p_j}}{\sqrt{(n_i+n_j)^2+(p_i-p_j)^2}} +\tfrac{2(m_i+m_j)(n_ip_j+n_jp_i)W_{m_i+m_j,n_i+n_j,p_i-p_j}}{\sqrt{[(m_i+m_j)^2+(n_i+n_j)^2 +(p_i-p_j)^2][(n_i+n_j)^2+(p_i-p_j)^2]}}\\&\quad -\tfrac{(n_i^2-n_j^2+p_i^2-p_j^2)V_{m_i-m_j,n_i+n_j,p_i-p_j}}{\sqrt{(n_i+n_j)^2+(p_i-p_j)^2}} +\tfrac{2(m_i-m_j)(n_ip_j+n_jp_i)W_{m_i-m_j,n_i+n_j,p_i-p_j}}{\sqrt{[(m_i-m_j)^2+(n_i+n_j)^2 +(p_i-p_j)^2][(n_i+n_j)^2+(p_i-p_j)^2]}}\\&\quad +\tfrac{(n_i^2-n_j^2+p_i^2-p_j^2)V_{m_i-m_j,n_i-n_j,p_i+p_j}}{\sqrt{(n_i-n_j)^2+(p_i+p_j)^2}} +\tfrac{2(m_i-m_j)(n_ip_j+n_jp_i)W_{m_i-m_j,n_i-n_j,p_i+p_j}}{\sqrt{[(m_i-m_j)^2+(n_i-n_j)^2 +(p_i+p_j)^2][(n_i-n_j)^2+(p_i+p_j)^2]}}\bigg ]+G. \end{aligned}$$

All the other couples of eigenvectors give analogous results by proceeding in a similar way. $\square$

Recalling (2.19), by Lemma 4.2 and condition (2.21) we see that $\Psi _k=\Psi _{m_k,n_k,p_k}$ and ${\mathcal {B}}(\Psi _i,\Psi _j)$ have different frequencies, so that they are $L^2(\Omega )$-orthogonal. This proves the implication (2.21) $\Rightarrow$ (2.20).

On the other hand, from Lemma 4.2 we also know that ${\mathcal {B}}(\Psi _i,\Psi _j)$ is a linear combination of eigenvectors, not all trivial. The only cases in which ${{\textbf{B}}}_\Omega (\Psi _i,\Psi _j,\Psi _k)\ne 0$ occurs (denial of (2.20)) is when $\Psi _k$ is one of the eigenvectors generated by ${\mathcal {B}}(\Psi _i,\Psi _j)$, i.e. $\Psi _{m_k,n_k,p_k}$ must satisfy

$$\begin{aligned}{} & {} m_k=|m_i-m_j| \text{ or } m_k= m_i+m_j\quad \text{ and }\\{} & {} n_k=|n_i-n_j| \text{ or } n_k= n_i+n_j\quad \text{ and }\\{} & {} p_k=|p_i-p_j| \text{ or } p_k= p_i+p_j, \end{aligned}$$

that is the denial of (2.21).

4.4 Proof of Theorem 3.5

For some $f\in L^2(Q_T)$ and $u_0\in U$, let $T^*\le T$ be as in Proposition 3.3 and let $u=u(t)$ be the unique local solution of (1.4)–(1.6) in $(0,T^*)$, which then satisfies (3.2). Using the simplified notation (2.15), we write it in the form

$$\begin{aligned} u(\xi ,t)=\sum _{k=1}^\infty A_k(t)\, \Psi _{k}(\xi )\,,\qquad u(\xi ,0)=u_0(\xi )=\sum _{k=1}^\infty A_k(0)\, \Psi _{k}(\xi )\in U\,. \end{aligned}$$

If u is rarefied then

$$\begin{aligned} {{\textbf{B}}}_\Omega (\Psi _i,\Psi _j,\Delta \Psi _k)=-\lambda _k{{\textbf{B}}}_\Omega (\Psi _i,\Psi _j,\Psi _k)=0\qquad \forall i,j,k, \end{aligned}$$

where $\lambda _k$ is the eigenvalue associated with $\Psi _k$. Therefore,

$$\begin{aligned} \int _\Omega \big (u(t)\cdot \nabla \big )u(t)\cdot \Delta u(t)=-\sum _{k=1}^\infty \lambda _kA_k(t)\int _\Omega \big (u(t)\cdot \nabla \big )u(t)\cdot \Psi _k\equiv 0\,, \end{aligned}$$

(4.8)

implying that $I_u(t)\equiv 0$. Thanks to (3.2), we may test (1.4) by $-\Delta u$ and, through the Young inequality, we infer

$$\begin{aligned} \begin{aligned}&\dfrac{1}{2}\dfrac{d}{dt}\Vert \nabla u(t)\Vert ^2_{L^2(\Omega )}+\mu \Vert \Delta u(t)\Vert ^2_{L^2(\Omega )} = \int _\Omega (u(t)\cdot \nabla )u(t)\cdot \Delta u(t) -\int _{\Omega }f(t)\cdot \Delta u(t)\\&\text{ by } (4.8) =-\int _{\Omega }f(t)\cdot \Delta u(t)\\&\qquad \qquad \ \le \mu \Vert \Delta u(t)\Vert ^2_{L^2(\Omega )}+\frac{1}{4\mu }\Vert f(t)\Vert ^2_{L^2(\Omega )}\,\quad \text{ for } \text{ a.e. } t\in (0,T^*)\,. \end{aligned} \end{aligned}$$

(4.9)

After integration over (0, t), we obtain for almost every $t\in (0,T^*)$

$$\begin{aligned} \Vert \nabla u(t)\Vert ^2_{L^2(\Omega )}\le \Vert \nabla u_0\Vert ^2_{L^2(\Omega )}+ \frac{1}{2\mu }\int _0^T\Vert f(s)\Vert ^2_{L^2(\Omega )}\,ds=:\Gamma (T,f,u_0)<\infty . \end{aligned}$$

(4.10)

Since the upper bound (4.10) is uniform ($\Gamma$ is independent of $T^*$), if it was $T^*<T$ we could extend the solution beyond $T^*$; hence, $T^*=T$. Statement (a) is so proved.

To prove (b) we need a preliminary technical lemma on the forms ${{\textbf{N}}}_\Omega (\cdot ,\cdot )$ and ${{\textbf{B}}}_\Omega (\cdot ,\cdot ,\cdot )$.

Lemma 4.3

The following results hold:

$$\begin{aligned} \begin{aligned}&{{\textbf{N}}}_\Omega (V_{m_\aleph ,n_\aleph ,p_\aleph },Y_{m_k,0,p_k})=-{{\textbf{N}}}_\Omega (W_{m_\aleph ,n_\aleph ,p_\aleph },Y_{m_k,0,p_k})\ne 0\qquad \text {if }m_k=2m_\aleph , p_k=2p_\aleph ,\\&{{\textbf{N}}}_\Omega (V_{m_\aleph ,n_\aleph ,p_\aleph },Z_{m_k,n_k,0})=-{{\textbf{N}}}_\Omega (W_{m_\aleph ,n_\aleph ,p_\aleph },Z_{m_k,n_k,0})\ne 0\qquad \!\text {if }m_k=2m_\aleph , n_k=2n_\aleph ,\\&{{\textbf{N}}}_\Omega (V_{m_k,n_k,p_k},Y_{m_\aleph ,0,p_\aleph })=-{{\textbf{N}}}_\Omega (W_{m_k,n_k,p_k},Y_{m_\aleph ,0,p_\aleph })\ne 0\qquad \text {if }m_k=m_\aleph /2, p_k=p_\aleph /2,\\&{{\textbf{N}}}_\Omega (V_{m_k,n_k,p_k},Z_{m_\aleph ,n_\aleph ,0})=-{{\textbf{N}}}_\Omega (W_{m_k,n_k,p_k},Z_{m_\aleph ,n_\aleph ,0})\ne 0\qquad \text {if }m_k=m_\aleph /2, n_k=n_\aleph /2,\\&{{\textbf{N}}}_\Omega (\Psi _{\aleph },\Psi _{k})={{\textbf{N}}}_\Omega (\Psi _k,\Psi _{\aleph })=0\qquad \quad \text {for any other }\Psi _{\aleph },\Psi _{k}\text { as in} (2.15). \end{aligned} \end{aligned}$$

Moreover, ${{\textbf{B}}}_\Omega (\Psi _{k},\Psi _{\aleph },\Psi _\aleph )=-{{\textbf{N}}}_\Omega (\Psi _{\aleph },\Psi _{k})$ for any $\Psi _{\aleph },\Psi _{k}$ as in (2.15).

Proof

Recalling (2.19) and Proposition 2.9 we find:

$$\begin{aligned} \begin{aligned}&{{\textbf{N}}}_\Omega (\Psi _{\aleph },\Psi _{k})=\frac{m_\aleph n_\aleph p_\aleph }{(n_\aleph ^2+p_\aleph ^2)\sqrt{\pi ^3}}{\left\{ \begin{array}{ll} \tfrac{n_\aleph }{\sqrt{m_\aleph ^2+p_\aleph ^2}}\quad \quad &{}\text {if }\Psi _\aleph =V_{m_\aleph ,n_\aleph ,p_\aleph }\text { and } \Psi _k=Y_{2m_\aleph ,0,2p_\aleph }\\ -\tfrac{p_\aleph }{\sqrt{m_\aleph ^2+n_\aleph ^2}}\quad \quad &{}\text {if } \Psi _\aleph =V_{m_\aleph ,n_\aleph ,p_\aleph }\text { and }\Psi _k=Z_{2m_\aleph ,2n_\aleph ,0}\\ -\tfrac{n_\aleph }{\sqrt{m_\aleph ^2+p_\aleph ^2}}\quad \quad &{}\text {if }\Psi _\aleph =W_{m_\aleph ,n_\aleph ,p_\aleph }\text { and } \Psi _k=Y_{2m_\aleph ,0,2p_\aleph }\\ \tfrac{p_\aleph }{\sqrt{m_\aleph ^2+n_\aleph ^2}}\quad \quad &{}\text {if } \Psi _\aleph =W_{m_\aleph ,n_\aleph ,p_\aleph }\text { and } \Psi _k=Z_{2m_\aleph ,2n_\aleph ,0}\\ 0\quad \quad \text {otherwise}, \end{array}\right. } \end{aligned} \\ \begin{aligned}&{{\textbf{N}}}_\Omega (\Psi _{k},\Psi _{\aleph })=\frac{2m_\aleph }{\sqrt{\pi ^3}}{\left\{ \begin{array}{ll} \tfrac{n_k^2p_\aleph }{(4n_k^2+p_\aleph ^2)\sqrt{m_\aleph ^2+p_\aleph ^2}}\quad \quad &{}\text {if }\Psi _k=V_{\frac{m_\aleph }{2},n_k,\frac{p_\aleph }{2}}\text { and } \Psi _\aleph =Y_{m_\aleph ,0,p_\aleph }\\ -\tfrac{n_k^2p_\aleph }{(4n_k^2+p_\aleph ^2)\sqrt{m_\aleph ^2+p_\aleph ^2}}\quad \quad &{}\text {if } \Psi _k=W_{\frac{m_\aleph }{2},n_k,\frac{p_\aleph }{2}}\text { and }\Psi _\aleph =Y_{m_\aleph ,0,p_\aleph }\\ -\tfrac{p_k^2 n_\aleph }{(n_\aleph ^2+4p_k^2)\sqrt{m_\aleph ^2+n_\aleph ^2}}\quad \quad &{}\text {if}\, \Psi _k=V_{\frac{m_\aleph }{2},\frac{n_\aleph }{2},p_k}\text { and } \Psi _\aleph =Z_{m_\aleph ,n_\aleph ,0}\\ \tfrac{p_k^2 n_\aleph }{(n_\aleph ^2+4p_k^2)\sqrt{m_\aleph ^2+n_\aleph ^2}}\quad \quad &{}\text {if } \Psi _k=W_{\frac{m_\aleph }{2},\frac{n_\aleph }{2},p_k}\text { and } \Psi _\aleph =Z_{m_\aleph ,n_\aleph ,0}\\ 0\quad \quad \text {otherwise}. \end{array}\right. } \end{aligned} \end{aligned}$$

Moreover, by (2.5) and (2.19),

$$\begin{aligned} {{\textbf{B}}}_\Omega (\Psi _{k},\Psi _{\aleph },\Psi _\aleph )=\int _{\Omega }(\Psi _{\aleph }\cdot \nabla )\Psi _{k}\cdot \Psi _{\aleph }=-\int _{\Omega }(\Psi _{\aleph }\cdot \nabla )\Psi _{\aleph }\cdot \Psi _{k} =-{{\textbf{N}}}_\Omega (\Psi _{\aleph },\Psi _{k}) \end{aligned}$$

and the proof is complete. $\square$

We now prove statement (b) in a slightly more general form that allows to extend the result to different choices of the additional eigenvector, not necessarily $\Psi _\aleph =X_{0,n_\aleph ,p_\aleph }$, see Remark 4.4 below. We consider

$$\begin{aligned} w(\xi ,t)=u(\xi ,t)+A_\aleph (t)\, \Psi _{\aleph }(\xi )=\sum _{k=1}^\infty A_k(t)\, \Psi _{k}(\xi )+A_\aleph (t)\, \Psi _{\aleph }(\xi ), \end{aligned}$$

for some $\Psi _\aleph (\xi )$ as in (2.15). Two cases may occur.

If the family $\{\Psi _k\}_{k\in {\mathbb {N}}_+}\cup \{\Psi _{\aleph }\}$ is also rarefied, one can take any $A_\aleph \in L^\infty (0,T^*)$ and obtain the result as a direct consequence of statement (a).

If the family $\{\Psi _k\}_{k\in {\mathbb {N}}_+}\cup \{\Psi _{\aleph }\}$ fails to be rarefied, we determine $A_\aleph \in L^\infty (0,T^*)$ as follows. By (3.2) we have that $w\in L^\infty (0,T^*;U)$ and, through (2.16), this allows to compute

$$\begin{aligned} \begin{aligned}&\big (w(t)\cdot \nabla \big )w(t)\!=\!\sum _{k=1}^\infty A_k(t)^2{\mathcal {N}}(\Psi _{k})\!\\&\quad +\!\sum _{1\le k<j}^\infty A_k(t)A_j(t){\mathcal {B}}(\Psi _{k},\Psi _{j})\!+\!A_\aleph (t)^2{\mathcal {N}}(\Psi _{\aleph })\!+\!\sum _{k=1}^\infty A_k(t)A_\aleph (t){\mathcal {B}}(\Psi _{k},\Psi _{\aleph }),\\&\Delta w(t)=-\sum _{k=1}^\infty \lambda _k A_k(t)\, \Psi _{k}(\xi )-\lambda _\aleph A_\aleph (t)\, \Psi _{\aleph }(\xi ). \end{aligned} \end{aligned}$$

Hence, if we put

$$\begin{aligned} \begin{aligned}&\vartheta (t):=-\lambda _\aleph \sum _{k=1}^\infty A_k(t){{\textbf{B}}}_\Omega (\Psi _{k},\Psi _{\aleph },\Psi _\aleph )-\sum _{k=1}^{\infty }\lambda _kA_k(t){{\textbf{N}}}_\Omega (\Psi _\aleph ,\Psi _k),\\&\omega (t):=\lambda _\aleph \sum _{k=1}^{\infty }A_k(t)^2{{\textbf{N}}}_\Omega (\Psi _k,\Psi _\aleph ),\\&\zeta (t):=\lambda _\aleph \sum _{1\le k<j}^\infty A_k(t)A_j(t){{\textbf{B}}}_\Omega (\Psi _{k},\Psi _{j},\Psi _{\aleph })+ \sum _{k,j=1}^\infty \lambda _jA_k(t) A_j(t){{\textbf{B}}}_\Omega (\Psi _{k},\Psi _{\aleph },\Psi _{j}), \end{aligned} \end{aligned}$$

we obtain

$$\begin{aligned} I_w(t)=\vartheta (t)A_\aleph (t)^2-\big [\omega (t)+\zeta (t)\big ]A_\aleph (t)\,. \end{aligned}$$

(4.11)

If $\Psi _\aleph =X_{0,n_\aleph ,p_\aleph }$ by Lemma 4.3, we have $\vartheta (t)\equiv 0$, $\omega (t)\equiv 0$ and $J_w(t)=-\int _0^tA_\aleph (s)\zeta (s)ds$; by choosing (e.g.) $A_\aleph (t)=\zeta (t)$ we obtain $J_w(t)\le 0$ for all $t\le T^*$, proving statement (b). Note that other choices are possible, for instance $A_\aleph (t)=\zeta (t)^3$, and many others.

Remark 4.4

Slightly more difficult is the choice of $A_\aleph$ for eigenvectors $\Psi _\aleph$ among (2.9)–(2.10)–(2.11)–(2.12), see Lemma 4.3. If $\vartheta (t)<0$, one can take $A_\aleph (t)>0$ so large that (4.11) becomes pointwise negative. If $\vartheta (t)>0$ or $\vartheta$ changes sign, one can take $A_\aleph (t)=\varepsilon [\omega (t)+\zeta (t)]$ for $\varepsilon >0$ sufficiently small.

Let us now prove statement (c). We denote by

$$\begin{aligned} z(\xi , t):=\sum _{h=1}^n A^\aleph _h(t)\Psi ^\aleph _h(\xi ), \end{aligned}$$

the finite linear combination of eigenvectors to be added to u. Again, $w=u+z\in L^\infty (0,T^*;V)$, see (3.2). By taking into account Item (a), we compute

$$\begin{aligned} \begin{aligned}&\int _\Omega \big (w(t)\cdot \nabla \big ) w(t)\cdot \Delta w(t)=\int _\Omega \Big [\big (u(t)\cdot \nabla \big ) u(t)\cdot \Delta z(t)\\&\quad +\big (z(t)\cdot \nabla \big ) z(t)\cdot \Delta u(t)+\big (z(t)\cdot \nabla \big ) z(t)\cdot \Delta z(t)\\&\quad +\big [\big (z(t)\cdot \nabla \big ) u(t)+\big (u(t)\cdot \nabla \big ) z(t)\big ]\cdot \Delta u(t)+\big [\big (z(t)\cdot \nabla \big ) u(t)+\big (u(t)\cdot \nabla \big ) z(t)\big ]\cdot \Delta z(t)\Big ] \end{aligned} \end{aligned}$$

and we bound all the terms by using the Poincaré, Hölder and Young inequalities and by exploiting the fact that $z\in L^\infty (0,T^*;C^\infty ({{\overline{\Omega }}}))$ (this is why a finite sum for z is assumed):

$$\begin{aligned} \begin{aligned}&\left| \int _\Omega \big (u(t)\cdot \nabla \big ) u(t)\cdot \Delta z(t)\right| \le C\Vert \nabla u(t)\Vert ^2_{L^{2}(\Omega )},\qquad \left| \int _\Omega \big (z(t)\cdot \nabla \big ) z(t)\cdot \Delta z(t)\right| \le C,\quad \\&\left| \int _\Omega \big [\big (z(t)\cdot \nabla \big ) u(t)+\big (u(t)\cdot \nabla \big ) z(t)\big ]\cdot \Delta u(t)\right| \le \tfrac{C^2}{2\varepsilon }\Vert \nabla u(t)\Vert ^2_{L^2(\Omega )}+\tfrac{\varepsilon }{2}\Vert \Delta u(t)\Vert ^2_{L^2(\Omega )},\\&\left| \int _\Omega \big [\big (z(t)\cdot \nabla \big ) u(t)+\big (u(t)\cdot \nabla \big ) z(t)\big ]\cdot \Delta z(t)\right| \le \tfrac{\varepsilon }{2} +\tfrac{C^2}{2\varepsilon }\Vert \nabla u(t)\Vert ^2_{L^2(\Omega )},\\&\left| \int _\Omega \big (z(t)\cdot \nabla \big ) z(t)\cdot \Delta u(t)\right| \le \tfrac{C^2}{2\varepsilon }+ \tfrac{\varepsilon }{2}\Vert \Delta u(t)\Vert ^2_{L^2(\Omega )}, \end{aligned} \end{aligned}$$

for some constants $C,\varepsilon >0$ (that may vary from line to line) accounting for $A^\aleph _h\in L^\infty (0,T^*)$ in various forms. By collecting terms we obtain (3.8), thereby proving statement (c).

4.5 Proof of Theorem 3.6

We start by proving some technical results that are needed in the proof of Theorem 3.6.

Lemma 4.5

Let $T, \mu , \lambda >0$; let $\alpha \in L^2(0,T)$ and $\gamma \in {\mathbb {R}}$. Then the function

$$\begin{aligned} A(t):=e^{-\mu \lambda t}\bigg [\int _0^t\alpha (\tau )e^{\mu \lambda \tau }d\tau +\gamma \bigg ]\qquad \forall t\in [ 0,T] \end{aligned}$$

(4.12)

satisfies $A\in H^1(0,T)$ and

$$\begin{aligned} \Vert A\Vert _{L^p(0,T)}\le \frac{|\gamma |}{(\mu \lambda p)^{1/p}}+{\left\{ \begin{array}{ll} \dfrac{\Vert \alpha \Vert _{L^p(0,T)}}{\mu \lambda }\quad \quad p\in [1,2],\quad \\ \dfrac{\Vert \alpha \Vert _{L^2(0,T)}}{\sqrt{2\frac{p-1}{p}}\,(\mu \lambda )^{\frac{1}{2}+\frac{1}{p}}}\quad p\in [2,\infty ]. \end{array}\right. } \end{aligned}$$

(4.13)

In particular,

$$\begin{aligned} \Vert A\Vert _{L^\infty (0,T)}\le \dfrac{\Vert \alpha \Vert _{L^2(0,T)}}{\sqrt{2\mu \lambda }}+|\gamma |\,,\qquad \Vert A\Vert _{L^2(0,T)}\le \dfrac{\Vert \alpha \Vert _{L^2(0,T)}}{\mu \lambda }+\frac{|\gamma |}{\sqrt{2\mu \lambda }}\,. \end{aligned}$$

(4.14)

Proof

From (4.12) the function A(t) is an exponential multiplied by a primitive of an $L^2(0,T)$-function so that $A\in H^1(0,T)\subset C^0[0,T]$.

In order to prove (4.13), we treat the integral to be computed as a convolution, distinguishing two cases due to the assumption $\alpha \in L^2(0,T)$. Let $p\in [1,2]$, $p'=\tfrac{p}{p-1}\in [2,\infty ]$ and $a(t):=\int _0^t\alpha (\tau )e^{-\mu \lambda (t-\tau )}d\tau$ so that $A(t)=a(t)+\gamma e^{-\mu \lambda t}$. The first step is to use the triangle inequality:

$$\begin{aligned} \Vert A\Vert _{L^p(0,T)}\le & {} \Vert a\Vert _{L^p(0,T)}+|\gamma |\left[ \int _0^Te^{-\mu \lambda p t}dt \right] ^{1/p} \nonumber \\\le & {} \Vert a\Vert _{L^p(0,T)}+\frac{|\gamma |}{(\mu \lambda p)^{1/p}}. \end{aligned}$$

(4.15)

By applying the Hölder inequality, we get

$$\begin{aligned} \begin{aligned} |a(t)|^p&= \bigg |\int _0^t e^{-\frac{\mu \lambda }{p'} (t-\tau )}e^{-\frac{\mu \lambda }{p} (t-\tau )}\alpha (\tau )d\tau \bigg |^p\\&\le \bigg [\int _0^te^{-\mu \lambda (t-\tau )}d\tau \bigg ]^{p-1} \int _0^te^{-\mu \lambda (t-\tau )}|\alpha (\tau )|^pd\tau \\&\le \dfrac{1}{(\mu \lambda )^{p-1}}\int _0^te^{-\mu \lambda (t-\tau )}|\alpha (\tau )|^pd\tau \,. \end{aligned} \end{aligned}$$

Hence, integrating and applying the Fubini Theorem, we obtain

$$\begin{aligned}{} & {} \int _0^T\! |a(t)|^pdt\le \dfrac{1}{(\mu \lambda )^{p-1}}\int _0^T\!\int _0^te^{-\mu \lambda (t-\tau )}|\alpha (\tau )|^pd\tau \, dt \\{} & {} = \dfrac{1}{(\mu \lambda )^{p-1}}\int _0^T\!|\alpha (\tau )|^p \int _\tau ^T\!e^{-\mu \lambda (t-\tau )}dt\, d\tau \le \dfrac{\Vert \alpha \Vert ^p_{L^p(0,T)}}{(\mu \lambda )^{p}}. \end{aligned}$$

By (4.15) this implies

$$\begin{aligned} \Vert A\Vert _{L^p(0,T)}\le \dfrac{\Vert \alpha \Vert _{L^p(0,T)}}{\mu \lambda }+\frac{|\gamma |}{(\mu \lambda p)^{1/p}}. \end{aligned}$$

(4.16)

Let $p\in [2,\infty ]$, $p'=\tfrac{p}{p-1}\in [1,2]$ then we consider

$$\begin{aligned} \begin{aligned} |a(t)|^p&\le \bigg [\int _0^t e^{-\frac{\mu \lambda }{p'} (t-\tau )}|\alpha (\tau )|^{\frac{p-2}{p}}\,e^{-\frac{\mu \lambda }{p} (t-\tau )}|\alpha (\tau )|^{\frac{2}{p}}d\tau \bigg ]^p\\ {}&\le \bigg [\int _0^te^{-\mu \lambda (t-\tau )}|\alpha (\tau )|^{\frac{p-2}{p-1}}d\tau \bigg ]^{p-1} \int _0^te^{-\mu \lambda (t-\tau )}|\alpha (\tau )|^2d\tau \\&\le \Vert e^{-\mu \lambda (t-\tau )}\Vert ^{p-1}_{L^{\frac{2(p-1)}{p}}(0,t)}\Vert \alpha \Vert ^{p-2}_{L^{2}(0,T)}\int _0^te^{-\mu \lambda (t-\tau )}|\alpha (\tau )|^2d\tau \, \\&\le \dfrac{\Vert \alpha \Vert ^{p-2}_{L^{2}(0,T)}}{\big (\frac{p-1}{p}2\mu \lambda \big )^{\frac{p}{2}}}\int _0^te^{-\mu \lambda (t-\tau )}|\alpha (\tau )|^2d\tau \,. \end{aligned} \end{aligned}$$

Hence, integrating and applying the Fubini Theorem as before, we obtain

$$\begin{aligned} \int _0^T\! |a(t)|^pdt\le \dfrac{\Vert \alpha \Vert ^{p-2}_{L^{2}(0,T)}}{\big (2\,\frac{p-1}{p}\,\mu \lambda \big )^{\frac{p}{2}}}\dfrac{\Vert \alpha \Vert ^{2}_{L^{2}(0,T)}}{\mu \lambda }\le \dfrac{\Vert \alpha \Vert ^p_{L^2(0,T)}}{\big (2\,\frac{p-1}{p}\big )^{\frac{p}{2}}(\mu \lambda )^{\frac{p}{2}+1}}, \end{aligned}$$

implying through (4.15)

$$\begin{aligned} \Vert A\Vert _{L^p(0,T)}\le \dfrac{\Vert \alpha \Vert _{L^2(0,T)}}{\sqrt{2\frac{p-1}{p}}\,(\mu \lambda )^{\frac{1}{2}+\frac{1}{p}}}+\frac{|\gamma |}{(\mu \lambda p)^{1/p}}. \end{aligned}$$

This proves (4.13). $\square$

Note that (4.16) holds for any $p\in [1,\infty )$ for which $\alpha \in L^p(0,T)$. Hence, if $\alpha \in L^\infty (0,T)$ (which is not the assumption of Lemma 4.5!), then (4.14)$_1$ can be improved by letting $p\rightarrow \infty$ in (4.16), that is,

$$\begin{aligned} \Vert A\Vert _{L^\infty (0,T)}\le \dfrac{\Vert \alpha \Vert _{L^\infty (0,T)}}{\mu \lambda }+|\gamma |. \end{aligned}$$

In our proofs, only the bounds (4.14) in Lemma 4.5 are needed. However, because of their elegance and simplicity, we proved the more general bounds (4.13).

Then we prove a calculus statement that highlights the role of the Weyl formula (2.14).

Lemma 4.6

Let $\varepsilon >0$, $\{\alpha _k\}_{k\in {\mathbb {N}}_+}\subset L^2(0,T)$, $\{\gamma _k\}_{k\in {\mathbb {N}}_+}\subset {\mathbb {R}}$ and $\{\lambda _k\}_{k\in {\mathbb {N}}_+}\subset {\mathbb {R}}_+$. If, for some $C,\eta >0$, we have that $\lambda _k\sim C k^\eta$ as $k\rightarrow \infty$, then the following implication holds

$$\begin{aligned} \sum _{k=1}^\infty \big (\lambda _k^{\frac{1}{\eta }-1+\varepsilon }\Vert \alpha _k\Vert ^2_{L^2(0,T)}+\lambda _k^{\frac{1}{\eta }+\varepsilon }\gamma _k^2\big )<\infty \quad \Longrightarrow \quad \sum _{k=1}^\infty \bigg (\dfrac{\Vert \alpha _k\Vert _{L^2(0,T)}}{\sqrt{\lambda _k}}+|\gamma _k|\bigg )<\infty . \end{aligned}$$

Proof

By applying the Hölder inequality, we get

$$\begin{aligned} \begin{aligned}&\sum _{k=1}^\infty \dfrac{\Vert \alpha _k\Vert _{L^2(0,T)}}{\sqrt{\lambda _k}} =\sum _{k=1}^\infty \lambda _k^{-\frac{1}{2}}\Vert \alpha _k\Vert _{L^2(0,T)}\tfrac{\lambda _k^{(\varepsilon +1/\eta )/2}}{\lambda _k^{(\varepsilon +1/\eta )/2}}\\&\le \left[ \sum _{k=1}^\infty \lambda _k^{\frac{1}{\eta }-1+\varepsilon }\Vert \alpha _k\Vert ^2_{L^2(0,T)}\right] ^{1/2} \left[ \sum _{k=1}^\infty \tfrac{1}{\lambda _k^{\varepsilon +\frac{1}{\eta }}}\right] ^{1/2}\!<\!\infty \\&\sum _{k=1}^\infty |\gamma _k| =\sum _{k=1}^\infty |\gamma _k|\tfrac{\lambda _k^{(\varepsilon +1/\eta )/2}}{\lambda _k^{(\varepsilon +1/\eta )/2}}\le \left[ \sum _{k=1}^\infty \lambda _k^{\frac{1}{\eta }+\varepsilon }\gamma _k^2\right] ^{1/2} \left[ \sum _{k=1}^\infty \tfrac{1}{\lambda _k^{\varepsilon +\frac{1}{\eta }}}\right] ^{1/2}\!<\!\infty , \end{aligned} \end{aligned}$$

since $\lambda _k^{\frac{1}{\eta }+\varepsilon }\sim C^{\frac{1}{\eta }+\varepsilon } k^{1+\varepsilon \eta }$ as $k\rightarrow \infty$ and the series of general term $k^{-1-\varepsilon \eta }$ is convergent. $\square$

In the next lemma we give bounds on the $L^2(\Omega )-$norm of some bilinear terms involved in the proofs. The norms are computed after neglecting the G-part.

Lemma 4.7

Let $\Psi _j$ and $\Psi _k$ be two eigenfunctions of (2.6) chosen among (2.8)–(2.9)–(2.10)–(2.11)–(2.12) corresponding, respectively, to the eigenvalues $\lambda _j$ and $\lambda _k$. There exists a constant $C>0$ (independent of $\lambda _j$ and $\lambda _k$) such that

$$\begin{aligned} \Vert {\mathcal {N}}(\Psi _k)\Vert ^2_{L^2(\Omega )}\le C\lambda _k,\qquad \Vert {\mathcal {B}}(\Psi _j,\Psi _k)\Vert _{L^2(\Omega )}^2\le C(\lambda _j+\lambda _k). \end{aligned}$$

(4.17)

Proof

Let $\Psi _k$ be an $L^2(\Omega )$-normalized eigenfunction of the kind (2.8)–(2.9)–(2.10)–(2.11)–(2.12) associated with some eigenvalue $\lambda _k>0$. By its explicit form, there exists $\Gamma >0$ (independent of $\lambda _k$) such that

$$\begin{aligned} \Vert \Psi _k\Vert _{L^\infty (\Omega )}\le \Gamma \,. \end{aligned}$$

Then we bound

$$\begin{aligned} \Vert {\mathcal {N}}(\Psi _k)\Vert ^2_{L^2(\Omega )}=\Vert (\Psi _k\cdot \nabla )\Psi _k\Vert ^2_{L^2(\Omega )}\le \Vert \Psi _k\Vert ^2_{L^\infty (\Omega )}\Vert \nabla \Psi _k\Vert _{L^2(\Omega )}^2\le \Gamma ^2\, \lambda _k, \end{aligned}$$

since $\Vert \nabla \Psi _k\Vert _{L^2(\Omega )}^2=\lambda _k$; this proves the first of (4.17) with $C=\Gamma ^2$. Moreover,

$$\begin{aligned} \begin{aligned} \Vert {\mathcal {B}}(\Psi _k,\Psi _j)\Vert ^2_{L^2(\Omega )}&=\Vert (\Psi _k\cdot \nabla )\Psi _j+(\Psi _j\cdot \nabla )\Psi _k\Vert ^2_{L^2(\Omega )}\\&\le 2\big (\Vert \Psi _k\Vert ^2_{L^\infty (\Omega )}\Vert \nabla \Psi _j\Vert _{L^2(\Omega )}^2+\Vert \Psi _j\Vert ^2_{L^\infty (\Omega )}\Vert \nabla \Psi _k\Vert _{L^2(\Omega )}^2\big )\\&\le 2C(\lambda _k+\lambda _j), \end{aligned} \end{aligned}$$

proving the second inequality in (4.17). $\square$

We are now ready to start the proof of Theorem 3.6. Let $\varepsilon >0$ and let $u_0\in U$ be such that $u_0={\mathcal {L}}_r(W_{m_k,n_k,p_k})$. For each k, $\lambda _k=m_k^2+n_k^2+p_k^2$ is the eigenvalue of (2.6) associated with $W_{m_k,n_k,p_k}$. Then there exists a sequence $\{\gamma _k\}_{k\in {\mathbb {N}}_+}\subset {\mathbb {R}}$ satisfying

$$\begin{aligned} \sum _{k=1}^\infty \lambda _k^{\frac{3}{2}+\varepsilon }\gamma _k^2<\infty \end{aligned}$$

(4.18)

and a rarefied sequence $\{W_{m_k,n_k,p_k}\}_{k\in {\mathbb {N}}_+}$ of eigenvectors of the kind (2.12) such that

$$\begin{aligned} u_0(\xi )=\sum _{k=1}^\infty \gamma _k\, W_{m_k,n_k,p_k}(\xi )\,. \end{aligned}$$

(4.19)

We claim that for any sequence $\{\alpha _k(t)\}_{k\in {\mathbb {N}}_+}\subset L^2(0,T)$ satisfying

$$\begin{aligned} \sum _{k=1}^\infty \lambda _k^{\frac{1}{2}+\varepsilon }\Vert \alpha _k\Vert ^2_{L^2(0,T)}<\infty \end{aligned}$$

(4.20)

there exists a 3D-3D force $f\in L^2(Q_T)$ yielding global uniqueness. This would prove Item (i) in Theorem 3.6, since there is an uncountable family of such sequences $\{\alpha _k(t)\}_{k\in {\mathbb {N}}_+}$. We prove this claim in two steps.

Step 1: Construction of f. For any $k\in {\mathbb {N}}_+$, we consider the linear ODE problem

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{A}}_k(t)+\mu (\underbrace{m^2_k+n_k^2+p_k^2}_{\lambda _k})A_k(t)=\alpha _k(t)\qquad \forall k\in {\mathbb {N}}_+,\quad \forall t\in (0,T)\\ A_k(0)=\gamma _k, \end{array}\right. } \end{aligned}$$

(4.21)

whose solution is given by (4.12) with $A_k$, $\lambda _k$, $\alpha _k$ and $\gamma _k$ replacing A, $\lambda$, $\alpha$ and $\gamma$. Then we set

$$\begin{aligned} f(\xi ,t)= & {} \sum _{k=1}^\infty \!\alpha _k(t)W_{m_k,n_k,p_k}(\xi )+\sum _{k=1}^\infty \! A_k(t)^2{\mathcal {N}}(W_{m_k,n_k,p_k})\nonumber \\{} & {} \quad +\sum _{1\le k<j}^\infty \! A_k(t)A_j(t){\mathcal {B}}(W_{m_k,n_k,p_k},W_{m_j,n_j,p_j}) \end{aligned}$$

(4.22)

and we show that the (rarefied) function

$$\begin{aligned} u(\xi ,t)=\sum _{k=1}^\infty A_k(t)\, W_{m_k,n_k,p_k}(\xi ) \end{aligned}$$

(4.23)

is the u-component of the solution (u, p) of (1.4) satisfying $u(\xi ,0)=u_0(\xi )$ as given in (4.19). By (3.6) and (4.14) we know that

$$\begin{aligned} \Vert u\Vert _{L^\infty (0,T;U)}^2{} & {} =\sup _{(0,T)}\sum _{k=1}^\infty \lambda _k A_k(t)^2\le \sum _{k=1}^\infty \lambda _k \Vert A_k\Vert _{L^\infty (0,T)}^2\nonumber \\{} & {} \le \frac{1}{\mu }\sum _{k=1}^\infty \left( \Vert \alpha _k\Vert _{L^2(0,T)}^2+2\mu \lambda _k\gamma _k^2\right) <\infty \end{aligned}$$

(4.24)

in view of (4.18) and (4.20). Furthermore, u in (4.23) satisfies

$$\begin{aligned} u_t(\xi ,t)-\mu \Delta u(\xi ,t) = \sum _{k=1}^\infty \Big ( {\dot{A}}_k(t)+\mu \lambda _kA_k(t)\Big )W_{m_k,n_k,p_k}(\xi ) =\sum _{k=1}^\infty \alpha _k(t)W_{m_k,n_k,p_k}(\xi ) \end{aligned}$$

since $W_{m_k,n_k,p_k}$ is an eigenfunction of (2.6) associated with the eigenvalue $\lambda _k$ and $A_k$ satisfies (4.21). By (2.16) we also infer that

$$\begin{aligned} \begin{aligned} (u\cdot \nabla )u&= {\mathcal {N}}\bigg (\sum _{k=1}^\infty A_k(t) W_{m_k,n_k,p_k}\bigg ) =\sum _{k=1}^\infty A_k(t)^2{\mathcal {N}}(W_{m_k,n_k,p_k})\\&\quad +\sum _{1\le k<j}^\infty A_k(t)A_j(t){\mathcal {B}}(W_{m_k,n_k,p_k},W_{m_j,n_j,p_j}). \end{aligned} \end{aligned}$$

Hence, f in (4.22) can be written as $f=u_t-\mu \Delta u+ (u\cdot \nabla )u$ and $u= {\mathcal {L}}_r(W_{m_k,n_k,p_k})$ in (4.23) is the u-component of the solution (u, p) of (1.4)–(1.6).

Step 2: Regularity of f. To complete the proof of Item (i), we need to prove the regularity of f in (4.22). Since $\{\alpha _k\}_{k\in {\mathbb {N}}_+}$ satisfies (4.20), we infer that the first term in (4.22) satisfies

$$\begin{aligned} \sum _{k=1}^\infty \alpha _kW_{m_k,n_k,p_k}\in L^2(Q_T)\,. \end{aligned}$$

(4.25)

In order to bound the $L^2(Q_T)$-norm of the second term in (4.22), we observe that

$$\begin{aligned} \left\| \sum _{k=1}^\infty A_k^2{\mathcal {N}}(W_{m_k,n_k,p_k})\right\| _{L^2(Q_T)}^2= & {} \int _0^T\int _{\Omega }\bigg (\sum _{k=1}^\infty A_k(t)^2{\mathcal {N}}(W_{m_k,n_k,p_k})\bigg )^2\nonumber \\ \text {by the H}\ddot{\textrm{o}}\text {lder inequality }\le & {} T\sup _{(0,T)}\int _\Omega \bigg (\sum _{k=1}^\infty A_k(t)^2\, \big |{\mathcal {N}}(W_{m_k,n_k,p_k})\big |\bigg )^2\nonumber \\ \text {by the Minkowski inequality }\le & {} T\sup _{(0,T)}\bigg (\sum _{k=1}^\infty A_k(t)^2\, \Vert {\mathcal {N}}(W_{m_k,n_k,p_k})\Vert _{L^2(\Omega )}\bigg )^2\nonumber \\ \text{ by } (4.17)\le & {} CT\bigg (\sup _{(0,T)}\sum _{k=1}^\infty A_k(t)^2\, \sqrt{\lambda _{k}}\bigg )^2<\infty , \end{aligned}$$

(4.26)

in view of (4.24) and because $\lambda _k\ge 2$ for all k, see Remark 2.5. Hence, the second term in (4.22) is in $L^2(Q_T)$. We now bound the $L^2(Q_T)$-norm of the (most delicate) third term in (4.22):

$$\begin{aligned}{} & {} \left\| \sum _{1\le k<j}^\infty A_kA_j{\mathcal {B}}(W_{m_k,n_k,p_k},W_{m_j,n_j,p_j})\right\| _{L^2(Q_T)}^2\nonumber \\{} & {} \le \bigg (\sum _{1\le k<j}^\infty \left\| A_kA_j{\mathcal {B}}(W_{m_k,n_k,p_k},W_{m_j,n_j,p_j})\right\| _{L^2(Q_T)}\bigg )^2\nonumber \\{} & {} = \bigg (\sum _{1\le k<j}^\infty \left\| A_kA_j\right\| _{L^2(0,T)}\left\| {\mathcal {B}}(W_{m_k,n_k,p_k},W_{m_j,n_j,p_j})\right\| _{L^2(\Omega )}\bigg )^2\nonumber \\{} & {} \le C\bigg (\sum _{j=2}^\infty \Vert A_j\Vert _{L^2(0,T)}\sqrt{\lambda _{j}}\sum _{k=1}^{j-1}\Vert A_k\Vert _{L^\infty (0,T)}\bigg )^2\nonumber \\{} & {} \le \dfrac{{\overline{C}}}{\mu } \bigg [\sum _{k=1}^{\infty }\bigg (\dfrac{\Vert \alpha _k\Vert _{L^2(0,T)}}{\sqrt{\mu \lambda _{k}}}+|\gamma _k|\bigg )\bigg ]^4<\infty . \end{aligned}$$

(4.27)

This bound is obtained by applying the Minkowski inequality, the Hölder inequality, (4.17) (recalling that $k<j$, hence $\lambda _{k}\le \lambda _j$) and Lemma 4.6 with $\eta =2/3$; the choice of $\eta$ is justified by the Weyl asymptotic for $\lambda _k=m_k^2+n_k^2+p_k^2$, see Theorem 2.8 in dimension $d=3$. The three bounds (4.25)–(4.26)–(4.27) show that (4.22) belongs to $L^2(Q_T)$, which completes the proof of Theorem 3.6 (i).

In order to prove Theorem 3.6 (ii), the assumptions (4.18) and (4.20) should be replaced by

$$\begin{aligned} \begin{aligned}&\sum _{k=1}^\infty \lambda _k^{1+\varepsilon }\gamma _k^2<\infty ,\qquad \sum _{k=1}^\infty \lambda _k^{\varepsilon }\Vert \alpha _k\Vert ^2_{L^2(0,T)}<\infty . \end{aligned} \end{aligned}$$

We recall that the eigenvalues associated to $W_{m_k,n_k,n_k}$ are $\lambda _k=m_k^2+2n_k^2=O(k)$ as $k\rightarrow +\infty$, see Theorem 2.8 (and its proof) for $d=2$. Hence, the proof of Theorem 3.6 (ii) is the same as (i) until the estimate (4.26). The only difference is the estimate (4.27), that can be obtained applying Lemma 4.6 with $\eta =1$.

In Theorem 3.6 (iii) the assumptions (4.18) and (4.20) should be replaced by

$$\begin{aligned} \begin{aligned}&\sum _{k=1}^\infty \lambda _k\gamma _k^2<\infty ,\qquad \quad \sum _{k=1}^\infty \Vert \alpha _k\Vert ^2_{L^2(0,T)}<\infty \end{aligned} \end{aligned}$$

and the proof is the same until the estimate (4.26). Here (4.27) is obtained applying Lemma 4.6 with

$$\begin{aligned} \varepsilon _1=\frac{\varepsilon }{\varepsilon +1}, \qquad \eta \ge \frac{1}{1-\varepsilon _1}=1+\varepsilon . \end{aligned}$$