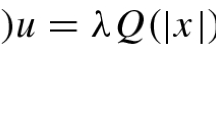A planar Schrödinger–Newton system with Trudinger–Moser critical growth

Abstract

In this paper, we focus on the existence of positive solutions to the following planar Schrödinger–Newton system with general critical exponential growth

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta {u}+u+\phi u =f(u)&{} \text{ in }\,\,\mathbb {R}^2, \\ \Delta {\phi }=u^2 &{} \text{ in }\,\, \mathbb {R}^2, \end{array} \right. \end{aligned}$$

where $f\in C^1(\mathbb {R},\mathbb {R})$. We apply a variational approach developed in [36] to study the above problem in the Sobolev space $H^1(\mathbb {R}^2)$. The analysis developed in this paper also allows to investigate the relation between a Riesz-type of Schrödinger–Newton systems and a logarithmic-type of Schrödinger–Poisson systems. Furthermore, this approach can overcome some difficulties resulting from either the nonlocal term with sign-changing and unbounded logarithmic integral kernel, or the critical nonlinearity, or the lack of monotonicity of $\frac{f(t)}{t^3}$. We emphasize that it seems much difficult to use the variational framework developed in the existed literature to study the above problem.

1 Introduction and results

1.1 Overview

Consider the following nonlinear Schrödinger–Newton system

$$\begin{aligned} \left\{ \begin{array}{ll}\displaystyle i\hbar \frac{\partial \psi }{\partial t}=\frac{\hbar ^2}{2m}\Delta \psi +W(x)\psi +\lambda \phi \psi -f(\psi )\,\,&{}\text{ in }\,\,\mathbb {R}^d\times \mathbb {R},\\ \Delta \phi =|\psi |^2&{}\text{ in }\,\,\mathbb {R}^d\times \mathbb {R}, \end{array} \right. \end{aligned}$$

(1.1)

where $\lambda \in \mathbb {R}$, i is the imaginary unit, $\hbar$ is the Planck constant. For $d=3$, $m>0$ stands for the mass of the particle, $\psi :\mathbb {R}^3\times [0,T]\rightarrow \mathbb {C}$ is a wave function, W is a real external potential and such a system often appears in quantum mechanics models and semiconductor theory (see [33]) and also arises, for example, as a model of the interaction of a charged particle with the electrostatic field (see [7]). It is well known that $\psi (x,t)=u(x)e^{-\frac{iEt}{\hbar }},x\in \mathbb {R}^d,t\in \mathbb {R}$ is a standing wave solution of (1.1) if and only if $u:\,\mathbb {R}^d\rightarrow \mathbb {R}$ satisfies

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle -\frac{\hbar ^2}{2m}\Delta {u}+ (W(x)-E)u+\lambda \phi u =f(u) &{} \text{ in }\,\, \mathbb {R}^d,\\ \Delta {\phi }= u^2 &{} \text{ in }\,\, \mathbb {R}^d. \end{array} \right. \end{aligned}$$

(1.2)

The second equation in system (1.2) can be solved by

$$\begin{aligned} \phi (x) =\Gamma _d(x) *u^2(x)=\int _{\mathbb {R}^d}\Gamma _d(x-y)u^2(y)\textrm{d}y, \end{aligned}$$

where $\Gamma _d$ is the Newtonian kernel in dimension d, which is expressed by

$$\begin{aligned} \Gamma _d(x)=\left\{ \begin{array}{ll} \frac{1}{2\pi }\ln |x|,&{} d=2,\\ \frac{1}{d(2-d)\omega _d}|x|^{2-d}, &{} d\ge 3. \end{array} \right. \end{aligned}$$

Here $\omega _d$ is the volume of the unit d-ball. Under such a formal inversion of the second equation in (1.2), we obtain the following non-local equation

$$\begin{aligned} -\Delta {u}+ V(x)u+\lambda (\Gamma _{d}*|u|)u =f(u)\quad \text{ in }\,\, \mathbb {R}^d, \end{aligned}$$

(1.3)

where $V=W-E$. The cases $\lambda > 0$ and $\lambda <0$ denote respectively two very different physical situations(see [22]). In particular, when $\lambda >0$, (1.3) stands for one attractive case of a Newton-Poisson coupling for gravitational mean-field models. When $\lambda <0$, (1.3) represents one d-dimensional case of repulsive electrostatic forces. Problem (1.3) is variational formally, and its associated energy functional is given by

$$\begin{aligned} I_d(u)= & {} \frac{1}{2} \int _{\mathbb {R}^{d}}\left( |\nabla u|^{2}+V(x) u^{2}\right) \textrm{d} x +\frac{\lambda }{4} \int _{\mathbb {R}^{d}} \int _{\mathbb {R}^{d}} \Gamma _{d}\left( |x-y|\right) u^{2}(x) u^{2}(y) \textrm{d} x \textrm{d} y\\{} & {} -\int _{\mathbb {R}^{d}}F(u) \textrm{d} x. \end{aligned}$$

In the case $d=3$, $I_d$ is well defined and of $C^1$ class in $H^1(\mathbb {R}^d)$ when $V\in L^\infty (\mathbb {R}^d)$. In the literature, by exploring the variational methods and topological methods, the existence, nonexistence, multiplicity and concentration of solutions to (1.3) have been investigated when f and V satisfy various assumptions, see e.g. [5, 7, 26, 28, 34, 38, 41] and so on.

Throughout this paper, we assume $\frac{\lambda }{2\pi }=1$, and consider the following Schrödinger–Newton equation

$$\begin{aligned} -\Delta {u}+V(x)u+(\ln (|\cdot |)*|u|^2)u =f(u)\quad \text{ in }\,\, \mathbb {R}^2, \end{aligned}$$

(1.4)

whose formal energy functional can be given by

$$\begin{aligned} I(u)=\frac{1}{2} \int _{\mathbb {R}^{2}}\left( |\nabla u|^{2}+V(x) u^{2}\right) \textrm{d} x +\frac{1}{4} \int _{\mathbb {R}^{4}} \ln \left( |x-y|\right) u^{2}(x) u^{2}(y) \textrm{d} x \textrm{d} y -\int _{\mathbb {R}^{2}}F(u) \textrm{d} x. \end{aligned}$$

Since $\tilde{\Gamma }(x):=\ln |x|$ is sign-changing and presents singularities at zero and infinity, compared with the higher dimensional case $d\ge 3$, the associated energy functional with (1.4) seems much more delicate. In particular, functional I is not well-defined on $H^1(\mathbb {R}^2)$ because of the appearance of the singular convolution term

$$\begin{aligned} \int _{\mathbb {R}^{2}} \int _{\mathbb {R}^{2}} \ln (|x-y|) u^{2}(x) u^{2}(y) \textrm{d} x \textrm{d} y, \end{aligned}$$

which is not well defined for all $u\in H^1(\mathbb {R}^2)$. Therefore, the approaches dealing with higher dimensional cases seem difficult to be adapted to the case $d=2$. So the rigorous study of the planar Schrödinger–Newton system had remained open for a long time. Recall that Choquard, Stubbe and Vuffray [19] proved the existence of a unique positive radially symmetric solution to (1.4) with $V(x)\equiv 1$ and $f(x,u)=0$ by applying a shooting method. To consider problem (1.4) with $d=2$ and $V(x)\equiv 1$, Stubbe [39] introduced the following weighted Sobolev space

$$\begin{aligned} X:= \left\{ u\in H^1(\mathbb {R}^2):\int _{\mathbb {R}^2}\ln (1+|x|)|u(x)|^{2}\textrm{d}x<+\infty \right\} , \end{aligned}$$

endowed with the norm

$$\begin{aligned} \Vert u\Vert _{X}^{2}=\int _{\mathbb {R}^{2}}\left( |\nabla u|^{2}+|u|^{2}\right) \textrm{d}x +\int _{\mathbb {R}^{2}} \ln (1+|x|)|u(x)|^{2} \textrm{d}x, \end{aligned}$$

which yields that the associated energy functional is well-defined and continuously differentiable on the space X. More precisely, thanks to the Hardy–Littlewood–Sobolev inequality [29], for any $u\in X$,

$$\begin{aligned} \int _{\mathbb {R}^{2}} \int _{\mathbb {R}^{2}} \ln (|x-y|) u^{2}(x) u^{2}(y) \textrm{d} x \textrm{d} y \end{aligned}$$

can be controlled by

$$\begin{aligned} \int _{\mathbb {R}^{2}} \ln (1+|x|) u^{2}(x) \textrm{d} x. \end{aligned}$$

Consequently, within the underlying space X above, Cingolani and Weth [20] studied problem (1.4) with $f(u)=|u|^{p-2}u, p\ge 4$ and obtained the existence and multiplicity of solutions. In studying planar Schrödinger–Newton systems in the underlying space X, one of main obstacles is that the norm $\Vert \cdot \Vert _X$ lacks translation invariance. This makes problems tough in verifying the compactness via the concentration-compactness principle. In [20, Lemma 2.1], it is shown that this difficulty can be overcome via a symmetric bilinear form

$$\begin{aligned} \int _{\mathbb {R}^{2}} \int _{\mathbb {R}^{2}} \ln \left( 1+|x-y|\right) u(x) v(y) \textrm{d} x \textrm{d} y. \end{aligned}$$

In a similar fashion, a sequence of higher energy solutions was obtained in [20] for $p\ge 4$ in a periodic setting, where the corresponding energy functional is invariant under $\mathbb {Z}^2$-translations. Later, Du and Weth [23] extended the above results to the case $p\in (2,4)$. Under the above variational framework in [20, 39], Chen and Tang in [16] considered the planar Schrödinger–Newton system in the axially symmetric setting. By using Jeanjean’s monotonicity trick [27] and a Nehari-Pohozaev manifold argument, they proved that there exists at least a ground state solution to (1.4). For some other related works to the two dimensional case, see [6, 9, 13, 17, 18, 21, 42] and the references therein. In all the results mentioned above for the planar Schrödinger–Newton system, it is obvious that the weighted function space X plays a fundamental role in ensuring that the energy functional is well defined and continuously differentiable.

Different from the variational frameworks above, the authors in [36] introduce a novel variational approach to study problem (1.4) by considering a perturbation problem defined in $H^1(\mathbb {R}^2)$. We aim to use a variational approach established in [36] to problem (1.4) involving the critical exponential growth in the sense of Trudinger–Moser, see [37, 40]. We now recall a notion of criticality which is totally different from the Sobolev type.

• ($f_0$) there exists $\theta _0>0$ such that

  $$\begin{aligned} \lim \limits _{|t|\rightarrow \infty }\frac{f(t)}{e^{\theta t^2}}=0,\quad \forall \theta >\theta _0,\quad \quad \lim \limits _{|t|\rightarrow \infty }\frac{f(t)}{e^{\theta t^2}}=+\infty ,\quad \forall \theta <\theta _0, \end{aligned}$$

which was introduced by Adimurthi and Yadava [2] and see also de Figueiredo, Miyagaki and Ruf [24]. We stress that Alves and Figueiredo [4] investigated the existence of positive ground state solutions for (1.4) when $V(x)\equiv 1$ and f satisfies ($f_0$) and the following conditions:

• ($f_1$) $f\in C(\mathbb {R},\mathbb {R})$ and $f(t)=o(t)$ as $t\rightarrow 0$.

• ($f_2$) $\frac{f(t)}{t^3}$ is increasing in $(0,\infty )$;

• ($f_3$) there exists $\mu >2$ such that $0<\mu F(t)\le f(t)t$ for all $t>0$, where $F(t)=\int _{0}^tF(s)\textrm{d}s$;

• ($f_4$) there exist constants $p>4$ and $\lambda _0> c_p$ for some positive constant $c_p$ depending on p.

And later, Chen and Tang [17] studied the existence of nontrivial solutions to (1.4) when f(u) is replaced by $f(x,u)\in C(\mathbb {R}^2\times \mathbb {R},\mathbb {R})$ which is required to satisfy the following conditions:

• ($F_1$) $f(x,t)=o(t)$ as $t\rightarrow 0$ uniformly for $x\in \mathbb {R}^2$; $f(x,t)=f(x_1,x_2,t)=f(|x_1|,|x_2|,t)$ for all $(x,t)\in \mathbb {R}^2\times \mathbb {R}$.

• ($F_2$) $f(x,t)t>0$ for all $(x,t)\in \mathbb {R}^2\times (\mathbb {R}\setminus \{0\})$ and there exist $M_0>0$ and $t_0>0$ such that

  $$\begin{aligned} F(x,t)\le M_0|f(x,t)|,\quad \forall x\in \mathbb {R}^2,\,\, |t|\ge t_0, \end{aligned}$$

  where $F(x,t)=\int _{0}^tF(x,s)\textrm{d}s$.

• ($F_3$) $\liminf _{t\rightarrow \infty }\frac{t^2F(x,t)}{e^{\theta _0 t^2}}\ge \kappa >\frac{2}{\theta _0^2\rho ^2}$, where $\rho \in (0,1/2)$ such that $\rho ^2\max _{|x|\le \rho } V(x)\le 1$.

• ($F_4$) For all $x\in \mathbb {R}^2$, the mapping $(0,\infty )\ni t\mapsto \displaystyle \frac{f(x,t)-V(x)t}{t^3}$ is non-decreasing.

1.2 Main result

Since we study the planar Schrödinger–Newton system with critical exponential nonlinearities in the sense of Trudinger–Moser, we first recall the 2D-Pohozaev–Trudinger–Moser inequality, which was established by Cao [12], see also [1, 11, 14, 15]. This result is crucial in estimating the subcritical or critical nonlinearity of Trudinger–Moser type.

Lemma 1.1

[12] If $\theta >0$ and $u\in H^1(\mathbb {R}^2)$, then

$$\begin{aligned} \int _{\mathbb {R}^2}\left( e^{\theta u^2}-1\right) \textrm{d}x<\infty . \end{aligned}$$

If, moreover, $u\in H^1(\mathbb {R}^2),\Vert \nabla u\Vert _2^2\le 1, \Vert u\Vert _2^2<M<\infty$ and $\theta <4\pi$, then there exists a constant $C_{M,\theta }$ which depends only on $M,\theta$ such that

$$\begin{aligned} \int _{\mathbb {R}^2}\left( e^{\theta u^2}-1\right) \textrm{d}x\le C_{M,\theta }. \end{aligned}$$

For this purpose, we make the following assumptions on the nonlinearity $f \in C^1(\mathbb {R},\mathbb {R})$.

• ($f_5$) $f(t)t>0$ for all $t\in \mathbb {R}\setminus \{0\}$, and there exist $M_0>0$ and $t_0>0$ such that

  $$\begin{aligned} F(t)\le M_0|f(t)|,\quad \forall |t|\ge t_0, \end{aligned}$$

  where $F(t)=\int _{0}^{t}f(s)\textrm{d}s$.

• ($f_6$) $\liminf _{t\rightarrow \infty }\frac{t^2F(t)}{e^{\theta _0 t^2}}\ge \kappa >\frac{1}{4\sqrt{\theta _0\pi }\rho ^2}$ for $\rho \in (0,1/2)$, where $\theta _0$ is given in ($f_0$).

• ($f_7$) The function $\frac{f(t)t-F(t)}{t^3}$ is nondecreasing in $(0,+\infty )$.

Remark 1.2

It follows from conditions ($f_1$), ($f_5$) and ($f_7$) that $0<3F(s)\le f(s)s$ for $s>0$.

Since we aim at finding positive solutions of equation (1.4), we always assume $f(s)\equiv 0$ for $s\le 0$, throughout this paper.

Our main results states as follows.

Theorem 1.3

Assume that hypotheses ($f_0$)–($f_1$) and ($f_5$)–($f_7$) hold. Then equation (1.4) with $V(x)\equiv 1$ has at least a positive solution $u\in H^1(\mathbb {R}^2)$ satisfying

$$\begin{aligned} \left| \int _{\mathbb {R}^2}\int _{\mathbb {R}^2}\ln |x-y|u^2(x)u^2(y)\textrm{d}x\textrm{d}y\right| <+\infty . \end{aligned}$$

(1.5)

Remark 1.4

Observe from [4] that the monotonicity condition ($f_2$) is often used to guarantee the boundedness of the Palais–Smale sequence $\{u_n\}$. With the aid of ($f_4$), the authors in [4] established directly an upper estimate on the $H^1(\mathbb {R}^2)$-norm of Palais–Smale sequence $\{u_n\}$. Then thanks to the Trudinger–Moser inequality, the compactness is recovered. However, as a global condition, ($f_4$) requires f(t) to be super-cubic for all $t\ge 0$, which seems a little bit strict especially for $t>0$ small. Observe that condition ($f_4$) does not reveal the essential features of the exponential growth given in ($f_0$). As mentioned in [17], there exist many model nonlinearities without satisfying ($f_2$) or ($f_4$) which are required in [4].

Observe that Chen and Tang in [17] obtained the existence of nontrivial solutions under ($F_1$)-($F_4$) which are weaker than those in [4]. Moreover, the authors in [17] introduced conditions ($F_2$) and ($F_3$) to state an upper estimate for the minimax-level using the Moser type sequence, so that vanish does not occur for the Cerami sequence $\{u_n\}$. However, in order to prove that the weak limit function $\bar{u}$ of Cerami sequence $\{u_n\}$ is a solution of system (1.4), one need to show directly

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}\ln (|x-y|)u^2_n\textrm{d}yu_n\phi \textrm{d}x =\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}\ln (|x-y|)\bar{u}^2\textrm{d}y\bar{u}\phi \textrm{d}x,\quad \forall \phi \in C_0^\infty (\mathbb {R}^2) \end{aligned}$$

(1.6)

and

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\int _{\mathbb {R}^2}f(x,u_n)(u_n-\bar{u})dx=0 \end{aligned}$$

(1.7)

without ($f_2$) or ($f_4$), which seems tough to establish in the weight space X, even if $u_n\rightarrow \bar{u}$ in $L^s(\mathbb {R}^2)$ for $s\in [2,+\infty )$. And so, ($F_4$) in [17] was introduced to guarantee that the associated energy functional can be studied in Nehari-type manifold, and then use some energy estimate method together with Fatou’s lemma to recover compactness in space X. We emphasize that ($F_4$) in [17] plays an essential role in proving the existence of nontrivial solution.

In the present paper, we also need ($f_5$) and ($f_6$) to establish a similar upper estimate as [17] by using the Moser type sequence. However, ($f_7$) is weaker than ($F_4$), when we consider autonomous nonlinearity f. One can not restrict functional I on Nehari-type manifold to study directly, since ($f_7$) results in that I has no lower bound at Nehari-type manifold. It even seems difficult to find some suitable manifold in the weighted space X to use constraint variational approaches to obtain (1.6) and (1.7) under condition ($f_7$).

Remark 1.5

Very recently, Albuquerque et al., [3] investigated the existence of solutions to the planar non-autonomous Schrödinger–Poisson system

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta u+V(|x|) u+\gamma \phi K(|x|) u=\lambda Q(|x|) f(u), &{} x \in \mathbb {R}^{2}, \\ \Delta \phi =K(|x|) u^{2}, &{} x \in \mathbb {R}^{2}, \end{array}\right. } \end{aligned}$$

(1.8)

where $\gamma ,\lambda$ are positive parameters, V, K, Q are continuous potentials, which can be unbounded or vanishing at infinity. By assuming that the nonlinearity f(t) satisfies ($f_0$), ($f_2$) and

• ($\tilde{f}_1$) $f(s)=o\left( |s|^{\gamma -1}\right)$ as $s \rightarrow 0$, where

  $$\begin{aligned} \gamma :=\max \{2,2(2+2 b-a) /(a+2)\}=\left\{ \begin{array}{cl} 2 &{} \text{ if } -2<b \le a, \\ 2(2+2 b-a) /(a+2) &{} \text{ if } -2<a<b, \end{array}\right. \end{aligned}$$

• ($\tilde{f}_{2}$) there exists $\theta >\max \{\gamma , 4\}$ such that $0<\theta F(s) \le f(s) s$ for all $s \ge 0$,

• ($\tilde{f}_{3}$) there exists $q>\gamma$ such that $\liminf _{s \rightarrow 0^{+}} F(s) / s^{q}>0$,

under a similar variational framework as that in [20], they derived the existence of a ground state solution to system (1.8) for $\lambda$ large enough. Compared with [3], we use the different variational framework to weaken the conditions ($\tilde{f}_{2}$) and ($f_{2}$).

1.3 Main difficulty and strategy

In the present paper, we employ the variational framework established in [36] to study problem (1.4) in the standard Sobolev space $H^1(\mathbb {R}^2)$ by variational methods. In order to overcome the difficulty that the sign-changing property of the Newtonian kernel $\Gamma _d(x)=\frac{1}{2\pi }\ln |x|$ leads to failure in setting the variational framework in $H^1(\mathbb {R}^2)$, as in [36], we modified equation (1.4) as follows

$$\begin{aligned} -\Delta {u}+ u-\frac{1}{\alpha }(G_{\alpha }(|\cdot |)*u^2) u=f(u) \quad \text{ in }\,\, \mathbb {R}^2, \end{aligned}$$

(1.9)

where $\alpha \in (0,1)$ is a parameter and

$$\begin{aligned} \lim \limits _{\alpha \rightarrow 0^+}G_{\alpha }(x):=\lim \limits _{\alpha \rightarrow 0^+}\frac{|x|^{-\alpha }-1}{\alpha }=\ln |x| \end{aligned}$$

for $x\in \mathbb {R}^2\setminus \{0\}$. The corresponding energy functional to (1.9) is well defined in $H^1(\mathbb {R}^2)$ for fixed $\alpha \in (0,1)$, which enables us to use minimax methods to study the existence of positive solutions for (1.9). By passing to the limit, a convergence argument within $H^1(\mathbb {R}^2)$ allows us to get positive solutions of the original problem (1.4).

In the limit process above as $\alpha \rightarrow 0^+$, the main difficulties are two-fold. Firstly, there is the lack of compactness due to the effect of critical exponential nonlinearity and the appearance of singularity at $\alpha =0$. Secondly, the boundedness of the Palais–Smale sequences is not easy to get, since 4-Ambrosetti–Rabinowitz condition does not hold. Moreover, Jeanjean’s monotonicity trick [27] seems not to work at our problem, since the singularity at $\alpha =0$ leads to failure at giving a uniform upper bound to the corresponding minimax value as $\alpha \rightarrow 0^+$.

In order to overcome these obstacles, in the proof of Theorem 1.3 we firstly adopt the perturbation introduced in [36](see also [34, 35]) to obtain the boundedness of the Palais–Smale sequences. Secondly, we need to use Moser type sequence together with some refined analysis to establish an upper estimate as a threshold to recover compactness locally. Thirdly, we use the concentration-compactness principle to establish a compactness splitting lemma of critical exponential version, and then to prove the modified equation (1.9) has a positive mountain pass solution $u_\alpha$. Moreover, the mountain pass value $c_\alpha$ is uniformly bounded from below and above as $\alpha \rightarrow 0^+$. Lastly, it follows from the moving plane arguments that $u_\alpha$ is radially symmetric, and then one exponential decay of $u_\alpha$ at infinity can be obtained uniformly for $\alpha >0$ small. Therefore, the Lebesgue dominated convergence theorem enables us to get the Frechet derivative of the corresponding energy functional is weakly sequence continuous and then get compactness.

Among other things our results will give the following findings and consequences:

• We use a variational approach (see also [36]) to study system (1.4) directly in the usual Sobolev space $H^1(\mathbb {R}^2)$, which is totally different from the one established in [20, 39]. Compared with solutions obtained in the weighted space X in the literature, we obtain solution u of system (1.4) in $H^1(\mathbb {R}^2)$ directly. Moreover, in our arguments we can find a relation between a Riesz-type of Schrödinger–Newton systems and a logarithmic-type of Schrödinger–Poisson systems.

• As mention in Remark 1.4, it seems tough to prove (1.6) and (1.7) directly in the weighted space X in our setting. That is to say, it seems difficult to use the variational approach established in [20] to prove Theorem 1.3. Therefore, this shows that the variational approach established in [36] can also be used to deal with some cases in which the variational approach [20] seems not easy to be adopted for us.

This paper is organized as follows. Some preliminaries are given in Section 2, and Section 3 is devoted to the existence of mountain pass type solutions to the modified equation. Then in Section 4, we complete the proof of Theorem 1.3.

2 Preliminary results

Let us fix some notations. The letter C will be repeatedly used to denote various positive constants, whose exact values may be irrelevant. Denote infinitely small quantities o(1) and $o(\alpha )$ by $o(1)\rightarrow 0$ as $n\rightarrow \infty$ and $o(\alpha )\rightarrow 0$ as $\alpha \rightarrow 0^+$, respectively. For every $1\le s\le +\infty$, we denote by $\Vert \cdot \Vert _s$ the usual norm of the Lebesgue space $L^s(\mathbb {R}^2)$. The function space

$$\begin{aligned} H^1(\mathbb {R}^2):=\{u\in L^2(\mathbb {R}^2):|\nabla u|\in L^2(\mathbb {R}^2)\} \end{aligned}$$

is the usual Sobolev space endowed with the norm

$$\begin{aligned} \Vert u\Vert :=\left( \int _{\mathbb {R}^2}(|\nabla u|^2+u^2)\textrm{d}x\right) ^{\frac{1}{2}}. \end{aligned}$$

In what follows, we recall the Hardy–Littlewood–Sobolev inequality (see [29]), which will be frequently used throughout this paper.

Lemma 2.1

(Hardy–Littlewood–Sobolev inequality [29]) Let $s,r>1$ and $\alpha \in (0,d)$ with $1/s+\alpha /d+1/r=2$, $f\in L^s(\mathbb {R}^d)$ and $h\in L^r(\mathbb {R}^d)$. There exists a sharp constant $C_{s,d,\alpha ,r}$ independent of f, h, such that

$$\begin{aligned} \int _{\mathbb {R}^d}[\frac{1}{|x|^\alpha }*f(x)]h(x)\textrm{d}x\le C_{s,d,\alpha ,r}\Vert f\Vert _s\Vert h\Vert _r. \end{aligned}$$

If $r=s=\frac{2d}{2d-\alpha }$, then

$$\begin{aligned} C_{s,d,\alpha ,r}=C_{d,\alpha }=\pi ^{\alpha /2}\frac{\Gamma \left( \frac{d}{2}- \frac{\alpha }{2}\right) }{\Gamma (d-\frac{\alpha }{2})}\left\{ \frac{\Gamma \left( \frac{d}{2}\right) }{\Gamma (d)}\right\} ^{-1+\frac{\alpha }{d}}, \end{aligned}$$

and if $d=2,\alpha \in (0,1]$, then $C_{2,\alpha }\le 2\sqrt{\pi }$.

Lemma 2.2

(Moser-Trudinger inequality[1, 12]) For any $\beta \in (0, 4\pi )$ there exists $C=C_\beta > 0$ such that for every $u\in H^1(\mathbb {R}^2)$ satisfying $\int _{\mathbb {R}^2}|\nabla u|^2\le 1$, one has

$$\begin{aligned} \int _{\mathbb {R}^2}\min \{1,u^2\}e^{\beta |u|^2}\le C_{\beta }\int _{\mathbb {R}^2}|u|^2. \end{aligned}$$

We recall the following elementary lemma which is of use in doing energy estimate.

Lemma 2.3

[44, Lemma 2.1] For any $\beta \in (0,\infty )$, there exists $C_\beta >0$ such that

$$\begin{aligned} \frac{s^{-\alpha }-1}{\alpha }\le C_\beta s^{-\beta },\,\,s>0 \end{aligned}$$

holds for all $\alpha \in (0,\beta )$.

3 The modified problem

Since the fact that I is not well defined on $H^1(\mathbb {R}^2)$, we use the perturbation technique (see [36]) to overcome this difficulty by modifying Schrödinger–Newton systems. We state the following modified problem

$$\begin{aligned} -\Delta {u}+ u-\frac{1}{\alpha }(G_{\alpha }(x)*u^2) u=f(u), \quad x\in \mathbb {R}^2, \end{aligned}$$

(3.1)

where $\alpha \in (0,1)$ is a parameter and $G_{\alpha }(x)=\frac{|x|^{-\alpha }-1}{\alpha }$, $x\not =0$. Its associated functional is

$$\begin{aligned} I_{\alpha }(u)=\frac{1}{2}\Vert u\Vert ^2-\frac{1}{4}\int _{\mathbb {R}^2}(G_{\alpha }(x)*u^2) u^2\textrm{d}x -\int _{\mathbb {R}^2}F(u)\textrm{d}x,\quad u\in H^1(\mathbb {R}^2). \end{aligned}$$

By virtue of the definition of $G_{\alpha }$, it follows from the Hardy-Littleword-Sobolev inequality that for any given $\alpha$, the perturbation functional $I_{\alpha }$ is well-defined on $H^1(\mathbb {R}^2)$, of $C^1$-class and

$$\begin{aligned} I'_{\alpha }(u)v= \int _{\mathbb {R}^2}(\nabla u \nabla v+uv)\textrm{d}x -\int _{\mathbb {R}^2}(G_{\alpha }(x)*u^2)uv\textrm{d}x -\int _{\mathbb {R}^2}f(u)v \textrm{d}x \end{aligned}$$

for $u,v\in H^1(\mathbb {R}^2)$. Since the conditions of Theorem 1.3 do not include the well-known 4-Ambrosetti–Rabinowitz condition, the boundedness of the Palais–Smale sequence is not easy to get. In order to overcome this difficulty, we add another perturbation technique developed in [34, 35] to equation (3.1). We now give more details to describe such a technique. Set

$$\begin{aligned} \lambda \in \left( 0,\min \left\{ 1,\root 4 \of {\frac{\theta _0}{5\pi }}\right\} \right) ,\,\, r\in (4,+\infty ). \end{aligned}$$

Let us consider the following modified problem

$$\begin{aligned} -\Delta {u}+ u-(G_{\alpha }(x)*u^2) u +\lambda \left( \int _{\mathbb {R}^2}u^2\textrm{d}x\right) ^{\frac{1}{4}}u =f(u)+ \lambda |u|^{r-2}u, u\in H^1(\mathbb {R}^2). \end{aligned}$$

(3.2)

The associated functional with (3.2) is given by

$$\begin{aligned} I_{\alpha ,\lambda }(u)=\frac{1}{2}\Vert u\Vert ^2-\frac{1}{4}\int _{\mathbb {R}^2}(G_{\alpha }(x)*u^2) u^2\textrm{d}x+\frac{2\lambda }{5} \Vert u\Vert _2^{\frac{5}{2}} -\int _{\mathbb {R}^2}F(u)\textrm{d}x-\frac{\lambda }{r}\Vert u\Vert _r^r. \end{aligned}$$

It is not hard for fixed $\alpha >0$ to show that functional $I_{\alpha ,\lambda }$ is well-defined on $H^1(\mathbb {R}^2)$, of $C^1$-class and

$$\begin{aligned} I'_{\alpha ,\lambda }(u)v= I'_{\alpha }(u)v+ \lambda \Vert u\Vert _2^{\frac{1}{2}}\int _{\mathbb {R}^2}uv\textrm{d}x -\lambda \int _{\mathbb {R}^2}|u|^{r-2}uv\textrm{d}x \end{aligned}$$

for $u,v\in H^1(\mathbb {R}^2)$. For any critical point $u\in H^1(\mathbb {R}^2)$ of $I_{\alpha ,\lambda }$, the following Pohozaev identity holds

$$\begin{aligned} P_{\alpha ,\lambda }(u):=\Vert u\Vert _2^2+\frac{1}{\alpha }\Vert u\Vert _2^4-\frac{4-\alpha }{4\alpha } Q(u)+\lambda \Vert u\Vert _2^{\frac{5}{2}}- 2\int _{\mathbb {R}^2}\left( F(u)+\frac{\lambda }{r}|u|^r\right) \textrm{d}x=0, \end{aligned}$$

(3.3)

where $Q(u)=\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*u^2\right) u^2\textrm{d}x$.

Lemma 3.1

Suppose ($f_0$)–($f_1$) and ($f_5$)–($f_7$) hold, then

(i) there exist $\rho ,\delta _0>0$ (independent of $\alpha ,\lambda$) such that $I_{\alpha ,\lambda }|_{S_\rho }(u)\ge \delta _0$ for every $u\in S_\rho =\{u\in H^1(\mathbb {R}^2): \Vert u\Vert =\rho \}$;

(ii) there is $e\in H^1(\mathbb {R}^2)$ (independent of $\alpha ,\lambda$) with $\Vert e\Vert >\rho$ such that $I_{\alpha ,\lambda }(e)<0$.

Proof

(i) From ($f_0$)-($f_1$), we have for any $\varepsilon >0$, there exists $C_{\varepsilon } > 0$ such that

$$\begin{aligned} |F(t)|\le \varepsilon |t|^2+C_{\varepsilon }|t|^3(e^{\theta _0 t^2}-1). \end{aligned}$$

(3.4)

Take $u\in H^1(\mathbb {R}^2)$ and $\Vert u\Vert ^2<2\pi /\theta _0$. Obviously, $\int _{\mathbb {R}^2}|\nabla u|^2\textrm{d}x<2\pi /\theta _0$. So by Lemma 1.1, one has

$$\begin{aligned} \begin{aligned} \int _{\mathbb {R}^2} F(u)\textrm{d}x&\le \varepsilon \int _{\mathbb {R}^2}|u|^2\textrm{d}x +C_{\varepsilon }\int _{\mathbb {R}^2}|u|^3(e^{\theta _0 u^2}-1)\textrm{d}x\\&\le \varepsilon \Vert u\Vert ^2+ C_\varepsilon \left[ \int _{\mathbb {R}^2}(e^{2\theta _0u^2}-1)\right] ^{1/2}\Vert u\Vert _6^3\\&\le \varepsilon \Vert u\Vert ^2+ C_\varepsilon \Vert u\Vert ^3. \end{aligned} \end{aligned}$$

(3.5)

It follows from (3.5), Lemma 2.3, and Hardy–Littlewood–Sobolev’s inequality that

$$\begin{aligned} \begin{aligned}&I_{\alpha ,\lambda }(u)\\&\quad =\frac{1}{2}\Vert u\Vert ^2-\frac{1}{4}\int _{\mathbb {R}^2}\int _{\mathbb {R}^2} \frac{|x-y|^{-\alpha }-1}{\alpha }u^2(y)u^2(x)\textrm{d}y\textrm{d}x\\&\qquad -\int _{\mathbb {R}^2}F(u)\textrm{d}x+\frac{2\lambda }{5} \Vert u\Vert _2^{\frac{5}{2}}-\frac{\lambda }{r}\Vert u\Vert _r^r\\&\quad \ge \frac{1-2\varepsilon }{2}\Vert u\Vert ^2-\frac{1}{4}\int \int _{|x-y|\le 1} \frac{|x-y|^{-\alpha }-1}{\alpha }u^2(y)u^2(x)\textrm{d}y\textrm{d}x-C_\varepsilon \Vert u\Vert ^3-\frac{\lambda }{r}\Vert u\Vert _r^r\\&\quad \ge \frac{1-2\varepsilon }{2}\Vert u\Vert ^2-\frac{C}{4}\Vert u\Vert ^4-C_\varepsilon \Vert u\Vert ^3-C\frac{1}{r}\Vert u\Vert ^r. \end{aligned} \end{aligned}$$

(3.6)

Letting $\varepsilon \in (0,\frac{1}{2})$ and $\Vert u\Vert =\rho >0$ small enough, it is clear that there exists $\delta _0>0$ such that $I_{\alpha }(u)\ge \delta _0$ for every $u\in S_{\rho }$.

(ii) The proof is very similar to that of Lemma 3.3 in [36]. For the reader’s convenience, we give the details. Take $e_0\in C_0^\infty (\mathbb {R}^2)$ such that $e_0(x)\equiv 1$ for $x\in B_{\frac{1}{8}}(0)$, $e_0(x)\equiv 0$ for $x\in \mathbb {R}^2{\setminus }{B_{\frac{1}{4}}(0)}$ and $|\nabla e_0(x)|\le C$. Note that

$$\begin{aligned} \frac{s^{-\alpha }-1}{\alpha }\ge \ln \frac{1}{s},\quad \text {for}\, s\in (0,1]. \end{aligned}$$

It then follows from the definition of $I_{\alpha ,\lambda }$ that for $t>0$,

$$\begin{aligned} \begin{aligned}&I_{\alpha ,\lambda }(te_0)\\&\quad \le \frac{t^2}{2}\Vert e_0\Vert ^2+\frac{2t^{5/2}}{5} \Vert u\Vert _2^{\frac{5}{2}} -\frac{t^4}{4}\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}\frac{|x-y|^{-\alpha }-1}{\alpha }e^2_0(y)e^2_0(x)\textrm{d}y\textrm{d}x-\int _{\mathbb {R}^2}F(te_0)\textrm{d}x\\&\quad \le \frac{t^2}{2}\Vert e_0\Vert ^2 -\frac{t^4}{4}\int _{|x|\le \frac{1}{4}}\int _{|y|\le \frac{1}{4}}\frac{|x-y|^{-\alpha }-1}{\alpha }e^2_0(y)e^2_0(x)\textrm{d}y\textrm{d}x\\&\quad \le \frac{t^2}{2}\Vert e_0\Vert ^2 -\frac{t^4}{4}\int _{|x|\le \frac{1}{4}}\int _{|y|\le \frac{1}{4}}\ln \frac{1}{|x-y|}e^2_0(y)e^2_0(x)\textrm{d}y\textrm{d}x\\&\quad \le \frac{t^2}{2}\Vert e_0\Vert ^2 -\frac{t^4\ln 2}{4}\left( \int _{\mathbb {R}^2}e^2_0(x)\textrm{d}x\right) ^2, \end{aligned} \end{aligned}$$

(3.7)

which implies that there exists $t_0>0$ large enough such that $I_{\alpha ,\lambda }(t_0e_0)<0$. $\square$

Based on the mountain pass theorem without the Palais–Smale condition (see [43]), there exists a (PS)$_{c_{\alpha ,\lambda }}$ sequence $\{u_n\}\subset H^1(\mathbb {R}^2)$, that is,

$$\begin{aligned} I_{\alpha ,\lambda }(u_n)\rightarrow c_{\alpha ,\lambda }\quad \text {and}\quad I'_{\alpha ,\lambda }(u_n)\rightarrow 0. \end{aligned}$$

(3.8)

Here $c_{\alpha ,\lambda }$ is the mountain pass level characterized by

$$\begin{aligned} c_{\alpha ,\lambda }=\inf \limits _{\gamma \in \Gamma }\max \limits _{t\in [0,1]}I_{\alpha ,\lambda }(\gamma (t)) \end{aligned}$$

(3.9)

with

$$\begin{aligned} \Gamma :=\{\gamma \in C^1([0,1],H^1(\mathbb {R}^2)):\,\gamma (0)=0\quad \text {and}\quad I_{\alpha ,\lambda }(\gamma (1))<0\}. \end{aligned}$$

Remark 3.2

Observe from Lemma 3.1 that there exist two constants $a,b>0$ independently of $\alpha ,\lambda$ such that $a<c_{\alpha ,\lambda }<b$.

Lemma 3.3

Let $\{u_n\}\subset H^1(\mathbb {R}^2)$ be a (PS)$_{c_{\alpha ,\lambda }}$ sequence of $I_{\alpha ,\lambda }$ for fixed $\alpha ,\lambda \in (0,1)$, then $\{u_n\}$ is bounded in $H^1(\mathbb {R}^2)$.

Proof

Observe that there exists $\mathcal {C}_1,\mathcal {C}_2>0$ such that

$$\begin{aligned} \begin{aligned}&\mathcal {C}_1+\mathcal {C}_2\Vert u_n\Vert \\&\quad \ge I_{\alpha ,\lambda }(u_n)-\frac{1}{4}I'_{\alpha ,\lambda }(u_n)u_n\\&\quad =\frac{1}{4}\Vert u_n\Vert ^2 +\frac{3\lambda }{20}\Vert u_n\Vert _2^{\frac{5}{2}}+\int _{A_n\cup \{\mathbb {R}^2\setminus {A_n}\}}\left( \frac{1}{4}f(u_n)u_n-F(u_n)\right) \textrm{d}x +\frac{r-4}{4r}\lambda \int _{\mathbb {R}^2}|u_n|^{r}\textrm{d}x\\&\quad \ge \frac{1}{4}\Vert u_n\Vert ^2 +\frac{3\lambda }{20}\Vert u_n\Vert _2^{\frac{5}{2}}-\int _{A_n}\left( F(u_n)-\frac{1}{4}f(u_n)u_n\right) \textrm{d}x +\frac{r-4}{4r}\lambda \int _{\mathbb {R}^2}|u_n|^{r}\textrm{d}x, \end{aligned} \end{aligned}$$

(3.10)

where $A_n:=\{x|\,\frac{1}{4}f(u_n)u_n-F(u_n)\le 0\}$. Recalling ($f_1$) and ($f_5$), we can take $t^*=\max \{t_0, 4M_0\}$ so that there exists $C_{t^*}>0$ such that

$$\begin{aligned} \begin{aligned}&\int _{A_n}(F(u_n)-\frac{1}{4}f(u_n)u_n)\textrm{d}x\\&\quad =\int _{A_n\cap \{|u_n|\le 4t^*\}}\left( F(u_n)-\frac{1}{4}f(u_n)u_n\right) \textrm{d}x+\int _{A_n\cap \{|u_n|\ge 4t^*\}} \left( F(u_n)-\frac{1}{4}f(u_n)u_n\right) \textrm{d}x\\&\quad \le C_{t^*}\int _{A_n\cap \{|u_n|\le 4t^*\}}u_n^2\textrm{d}x+\int _{A_n\cap \{|u_n|\ge 4t^*\}}\left( M_0-\frac{1}{4} u_n\right) f(u_n)\textrm{d}x\\&\quad \le C_{t^*}\Vert u_n\Vert _2^2. \end{aligned} \end{aligned}$$

(3.11)

Since for any large $B_1>0$, there exists $B_2>0$ such that $\frac{3}{20}\Vert u_n\Vert _2^{\frac{5}{2}}\ge B_1\Vert u_n\Vert _2^2-B_2$. So combining (3.10) and (3.11) we have

$$\begin{aligned} \begin{aligned} \mathcal {C}_1+\mathcal {C}_2\Vert u_n\Vert +\lambda B_2 \ge&\frac{1}{8}\Vert u_n\Vert ^2+\int _{\mathbb {R}^2}\left[ (\lambda B_1-C_{t^*})|u_n|^2 +\frac{r-4}{4r}\lambda |u_n|^{r}\right] \textrm{d}x. \end{aligned} \end{aligned}$$

(3.12)

We can obtain

$$\begin{aligned} (\lambda B_1-C_{t^*})t^2 +\frac{r-4}{4r}\lambda t^{r}\ge 0 \end{aligned}$$

for $t\ge 0$, by letting $B_1$ can be chosen arbitrary large. Thus, it follows from (3.12) that $\Vert u_n\Vert \le C$ for some C independently of n. $\square$

Let us define Moser type functions $w_n(x)$ supported in $B_{\rho }(0)$ as follows:

$$\begin{aligned} \begin{aligned} w_n(x)=\frac{1}{\sqrt{2\pi }}\left\{ \begin{array}{ll} \sqrt{\log n},&{} 0\le |x|\le \rho /n,\\ \frac{\log (\rho /|x|)}{ \sqrt{\log n}}, &{} \rho /n\le |x|\le \rho ,\\ 0,&{}|x|\ge \rho , \end{array} \right. \end{aligned} \end{aligned}$$

where $\rho$ is given in ($f_6$). An estimation yields

$$\begin{aligned} \begin{aligned} \Vert w_n\Vert ^2&= \int _{B_\rho (0)}\left( |\nabla w_n|^2+w_n^2\right) \textrm{d}x\\&=1+\rho ^2\left( \frac{1}{4\log n}-\frac{1}{4n^2\log n}-\frac{1}{2n^2}\right) \\&=:1+\rho ^2\delta _n, \end{aligned} \end{aligned}$$

(3.13)

and

$$\begin{aligned} \begin{aligned} \frac{2\lambda }{5}\Vert w_n\Vert _2^{\frac{5}{2}}&=\frac{2\lambda }{5}\rho ^{5/2}\left( \frac{1}{4\log n}-\frac{1}{4n^2\log n}-\frac{1}{2n^2}\right) ^{5/4} =\frac{2\lambda }{5}\rho ^{5/2}\delta _n^{5/4}. \end{aligned} \end{aligned}$$

(3.14)

Moreover,

$$\begin{aligned} \begin{aligned} \frac{1}{4}\int _{\mathbb {R}^2}(G_{\alpha }(x)*w_n^2) w_n^2\textrm{d}x&=\frac{1}{4}\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}\frac{|x-y|^{-\alpha }-1}{\alpha } w_n^2(x)w_n^2(y)\textrm{d}x\textrm{d}y\\&=\frac{1}{4}\int _{B_\rho (0)}\int _{B_\rho (0)}\frac{|x-y|^{-\alpha }-1}{\alpha } w_n^2(x)w_n^2(y)\textrm{d}x\textrm{d}y\\&\ge 0. \end{aligned} \end{aligned}$$

(3.15)

Lemma 3.4

$\sup \limits _{\alpha \in (0,1),\lambda \in (0,\lambda ^*)}c_{\alpha ,\lambda } <\frac{2\pi }{\theta _0}$, where $\lambda ^*:=\min \bigg \{1,\root 4 \of {\frac{\theta _0}{5\pi }}\bigg \}$.

Proof

Recalling ($f_6$), for

$$\begin{aligned} \varepsilon \in \left( 0,\kappa -\frac{1}{4\rho ^2\sqrt{\pi \theta _0}}\right) , \end{aligned}$$

(3.16)

there exists $t_\varepsilon >0$ such that,

$$\begin{aligned} \begin{aligned} t^2 F(t)\ge (\kappa -\varepsilon )e^{\theta _0 t^2},\quad \text {for}\,\, t\ge t_\varepsilon . \end{aligned} \end{aligned}$$

(3.17)

We proceed the proof by considering three cases.

Case 1. $t\in \bigg [0,\sqrt{\frac{2\pi }{\theta _0}}\bigg ]$, then by (3.13)-(3.15), we have for large n

$$\begin{aligned} \begin{aligned}&I_{\alpha ,\lambda }(tw_n)\\&\quad \le \frac{t^2}{2}\Vert w_n\Vert ^2-\frac{t^4}{4}\int _{\mathbb {R}^2}\int _{\mathbb {R}^2} \frac{|x-y|^{-\alpha }-1}{\alpha }w_n^2(y)w_n^2(x)\textrm{d}y\textrm{d}x-\int _{\mathbb {R}^2}F(tw_n)\textrm{d}x+\frac{2}{5} \Vert tw_n\Vert _2^{\frac{5}{2}}\\&\quad \le \frac{t^2}{2}\Vert w_n\Vert ^2+\frac{2 t^{\frac{5}{2}}}{5} \Vert w_n\Vert _2^{\frac{5}{2}}\\&\quad \le \frac{2\pi }{\theta _0}\left[ \frac{1}{2}\Vert w_n\Vert ^2+\frac{2}{5}\sqrt{\frac{2\pi }{\theta _0}} \Vert w_n\Vert _2^{\frac{5}{2}}\right] \\&\quad < \frac{2\pi }{\theta _0}. \end{aligned} \end{aligned}$$

(3.18)

Case 2. $t\in \bigg [\sqrt{\frac{5\pi }{\theta _0}},+\infty \bigg )$. According to the definition of $w_n$, we have for large $n\in \mathbb {N}$, $tw_n(x)\ge t_\varepsilon$ for $x\in B_{\rho /n}$. From (3.13)–(3.17), we deduce that for large n,

$$\begin{aligned} \begin{aligned}&I_{\alpha ,\lambda }(tw_n)\\&\quad \le \frac{t^2}{2}\Vert w_n\Vert ^2-\frac{t^4}{4}\int _{\mathbb {R}^2}\int _{\mathbb {R}^2} \frac{|x-y|^{-\alpha }-1}{\alpha }w_n^2(y)w_n^2(x)\textrm{d}y\textrm{d}x-\int _{\mathbb {R}^2}F(tw_n)\textrm{d}x+\frac{2}{5} \Vert tw_n\Vert _2^{\frac{5}{2}}\\&\quad \le \frac{t^2}{2}\Vert w_n\Vert ^2+\frac{2 t^{\frac{5}{2}}}{5} \Vert w_n\Vert _2^{\frac{5}{2}}-\frac{2\pi ^2(\kappa -\varepsilon )\rho ^2}{n^2t^2\log n}e^{\frac{\theta _0 t^2\log n}{2\pi }}\\&\quad =\frac{1+\delta _n\rho ^2}{2}t^2+\frac{2}{5}t^{\frac{5}{2}}\rho ^{\frac{5}{2}}\delta _n^{\frac{5}{4}}-\frac{2\pi ^2(\kappa -\varepsilon )\rho ^2}{n^2t^2\log n}e^{\frac{\theta _0 t^2\log n}{2\pi }}\\&\quad <t^2+\frac{2}{5}\rho ^{\frac{5}{2}}t^{\frac{5}{2}}-\frac{2\pi ^2(\kappa -\varepsilon )\rho ^2}{n^2t^2\log n}e^{\frac{\theta _0 t^2\log n}{2\pi }}. \end{aligned} \end{aligned}$$

(3.19)

Define

$$\begin{aligned} g(n):=\frac{2\pi ^2(\kappa -\varepsilon )\rho ^2}{n^2t^2\log n}e^{\frac{\theta _0 t^2\log n}{2\pi }} =\frac{2\pi ^2(\kappa -\varepsilon )\rho ^2}{n^2t^2\log n} n^{\frac{\theta _0}{2\pi } t^2}, \end{aligned}$$

then

$$\begin{aligned} \begin{aligned} g(n)\ge \frac{2\pi ^2(\kappa -\varepsilon )\rho ^2}{4t^2\log 2} 2^{\frac{\theta _0}{2\pi } t^2} \end{aligned} \end{aligned}$$

(3.20)

for large n. It then follows from (3.19) and (3.20) that

$$\begin{aligned} \begin{aligned} I_{\alpha ,\lambda }(tw_n)&<t^2+\frac{2}{5}\rho ^{\frac{5}{2}}t^{\frac{5}{2}}-\frac{2\pi ^2(\kappa -\varepsilon )\rho ^2}{4t^2\log 2} 2^{\frac{\theta _0}{2\pi } t^2}\\&\rightarrow -\infty ,\,\,\text {as}\,\,t\rightarrow \infty , \end{aligned} \end{aligned}$$

(3.21)

which implies that

$$\begin{aligned} \begin{aligned}&I_{\alpha ,\lambda }(tw_n)<\frac{2\pi }{\theta _0}. \end{aligned} \end{aligned}$$

(3.22)

Case 3. $t\in \bigg [\sqrt{\frac{2\pi }{\theta _0}},\sqrt{\frac{5\pi }{\theta _0}}\bigg ]$. According to the definition of $w_n$, we have for large $n\in \mathbb {N}$, $tw_n(x)\ge t_\varepsilon$ for $x\in B_{\rho /n}$. Since $\lambda \in \bigg (0,\min \bigg \{1,\root 4 \of {\frac{\theta _0}{5\pi }}\bigg \}\bigg )$, it then follows from (3.13)-(3.17) that for large n

$$\begin{aligned} \begin{aligned}&I_{\alpha ,\lambda }(tw_n)\\&\quad \le \frac{t^2}{2}\Vert w_n\Vert ^2-\frac{t^4}{4}\int _{\mathbb {R}^2}\int _{\mathbb {R}^2} \frac{|x-y|^{-\alpha }-1}{\alpha }w_n^2(y)w_n^2(x)\textrm{d}y\textrm{d}x-\int _{\mathbb {R}^2}F(tw_n)\textrm{d}x+\frac{2\lambda }{5} \Vert tw_n\Vert _2^{\frac{5}{2}}\\&\quad<\frac{t^2}{2}\Vert w_n\Vert ^2+\frac{2\lambda t^{\frac{5}{2}}}{5} \Vert w_n\Vert _2^{\frac{5}{2}}-\frac{2\pi ^2(\kappa -\varepsilon )\rho ^2}{n^2t^2\log n}e^{\frac{\theta _0 t^2\log n}{2\pi }}\\&\quad<\frac{t^2}{2}\Vert w_n\Vert ^2+\frac{2\lambda t^{\frac{5}{2}}}{5} \Vert w_n\Vert _2^{\frac{5}{2}}-\frac{2\pi \theta _0(\kappa -\varepsilon )\rho ^2}{5n^2\log n}e^{\frac{\theta _0 t^2\log n}{2\pi }}\\&\quad <\frac{t^2}{2}\Vert w_n\Vert ^2+\frac{2 t^{2}}{5} \Vert w_n\Vert _2^{\frac{5}{2}}-\frac{2\pi \theta _0(\kappa -\varepsilon )\rho ^2}{5n^2\log n}e^{\frac{\theta _0 t^2\log n}{2\pi }}:=\psi _n(t). \end{aligned} \end{aligned}$$

(3.23)

Then there exists $t_n>0$ such that $\psi _n(t_n)=\max _{t>0}\psi _n(t)$ and

$$\begin{aligned} t_n^2=\frac{4\pi }{\theta _0}\left[ 1+\frac{\log \left( 1+\rho ^2\delta _n+\frac{4}{5}\rho ^{\frac{5}{2}}\delta _n^{\frac{5}{4}}\right) -\log \left( 2\pi \theta _0(\kappa -\varepsilon )\rho ^2\right) +2\log \sqrt{\frac{5\pi }{\theta _0}}}{2\log n}\right] . \end{aligned}$$

(3.24)

Obviously, we can easily see that $t_n\in \bigg [\sqrt{\frac{2\pi }{\theta _0}},\sqrt{\frac{5\pi }{\theta _0}}\bigg ]$ for large n. Then, by (3.23) and (3.24) we have

$$\begin{aligned} \begin{aligned} \psi _n(t)\le&\psi _n(t_n)\\ =&\left( \frac{1}{2}\Vert w_n\Vert ^2+\frac{2}{5} \Vert w_n\Vert _2^{\frac{5}{2}}\right) t_n^2-\frac{\pi \left( \Vert w_n\Vert ^2+\frac{4}{5} \Vert w_n\Vert _2^{\frac{5}{2}}\right) }{\theta _0\log n}\\ =&\frac{4\pi }{\theta _0}\left( \frac{1}{2}+\frac{\rho ^2\delta _n}{2}+\frac{2}{5} \rho ^{\frac{5}{2}}\delta _n^{\frac{5}{4}}\right) \left[ 1+\frac{\log \left( 1+\rho ^2\delta _n+\frac{4}{5}\rho ^{\frac{5}{2}}\delta _n^{\frac{5}{4}}\right) }{2\log n}\right. \\&\left. -\frac{\log \left( 2\theta _0(\kappa -\varepsilon )\rho ^2 \sqrt{\frac{5\pi }{\theta _0}}\right) }{2\log n}-\frac{1}{2\log n}\right] \\ \le&\frac{4\pi }{\theta _0}\left( \frac{1}{2}+\frac{\rho ^2\delta _n}{2}+\frac{2}{5} \rho ^{\frac{5}{2}}\delta _n^{\frac{5}{4}}\right) \left[ 1+\frac{\log \left( 1+\rho ^2\delta _n+\frac{4}{5}\rho ^{\frac{5}{2}}\delta _n^{\frac{5}{4}}\right) }{2\log n}-\frac{1}{2\log n}\right] ,\\ \end{aligned} \end{aligned}$$

(3.25)

which, together with the definition of $\delta _n$, implies that

$$\begin{aligned} \begin{aligned} \psi _n(t)\le&\frac{4\pi }{\theta _0}\left[ \frac{1}{2}+\frac{\rho ^2}{8\log n} +\frac{o(1)}{\log n}-\frac{1}{4\log n}\right] \\ <&\frac{2\pi }{\theta _0},\,\,\text {for}\,\, n\,\,\text {large}. \end{aligned} \end{aligned}$$

(3.26)

Combining (3.18), (3.22) and (3.26), we have $I_{\alpha ,\lambda }(tw_n)<\frac{2\pi }{\theta _0}$. It follows from (3.21) that, for fixed n large enough, there exists $t_0>0$ such that $I_{\alpha ,\lambda }(t_0w_n)<0$. Define $\gamma (t)=tt_0w_n$ for $t\in [0,1]$, then $\gamma \in \Gamma$. Therefore, the conclusion follows immediately. The proof is complete. $\square$

In the following, we establish a critical exponential version of splitting lemma to the Palais–Smale sequences of $I_{\alpha ,\lambda }$.

Lemma 3.5

Assume that $\{u_n\}$ is a bounded (PS)$_{c_{\alpha ,\lambda }}$ sequence of $I_{\alpha ,\lambda }$ for fixed $\alpha$ and $\lambda$. Then there exist $B\in \mathbb {R}$ and a number $k\in \mathbb {N}\cup \{0\}$, and a finite sequence

$$\begin{aligned} (u_0,w^1,...,w^k)\subset H^1(\mathbb {R}^2),\quad w^j>0,\quad \text {for}\,\, j=1,...,k\,(\text {if}\,\,k\ge 1) \end{aligned}$$

of critical points for the following functional

$$\begin{aligned} \begin{aligned} J_{B,\alpha ,\lambda }(u):=&\frac{1}{2}\Vert u\Vert ^2+\frac{B^2}{2\alpha }\int _{\mathbb {R}^2}u^2\textrm{d}x+\frac{\lambda B^{1/2}}{2}\int _{\mathbb {R}^2}u^2\textrm{d}x\\&-\int _{\mathbb {R}^2}F(u)\textrm{d}x- \frac{1}{4\alpha }\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*u^2\right) u^2\textrm{d}x-\frac{\lambda }{r}\Vert u\Vert _r^r. \end{aligned} \end{aligned}$$

and k sequences of points $\{y_n^j\}\subset \mathbb {R}^2$, $1\le j\le k$, such that

• (i) $|y_n^j|\rightarrow +\infty$, $|y_n^j-y_n^i|\rightarrow +\infty \quad$ if $i\ne j,n\rightarrow +\infty$,

• (ii) $\Vert u_n\Vert ^2=\Vert u_0\Vert ^2+\sum \limits _{j=1}^{k}\Vert w^{j}\Vert ^2+o(1)$,

• (iii) $c_{\alpha ,\lambda }+\frac{B^4}{4\alpha }+\frac{B^{5/2}\lambda }{10} = J_{B,\alpha ,\lambda }(u_0)+\sum \limits _{j=1}^{k}J_{B,\alpha ,\lambda }(w^j)$,

• (iv) $B^2=\Vert u_0\Vert _2^2+\sum \limits _{j=1}^{k}\Vert w^{j}\Vert _2^2$.

Otherwise, if $k=0$, then $u_n\rightarrow u_0$ in $H^1(\mathbb {R}^2)$.

Proof

Recall that $\{u_n\}$ is a bounded sequence in $H^1(\mathbb {R}^2)$, then, up to subsequence, there exist $u_0\in H^1(\mathbb {R}^2)$ and $B\in \mathbb {R}$ such that $u_n\rightharpoonup u_0$ weakly in $H^1(\mathbb {R}^2)$ and $\int _{\mathbb {R}^2}| u_n|^2\textrm{d}x\rightarrow B^2$ as $n\rightarrow \infty$. According to Remark 3.2, it follows from (3.10) and (3.11) that there exists $C_1>0$ such that

$$\begin{aligned} \begin{aligned} \int _{\tilde{A}_n}\left( \frac{1}{4}f(u_n)u_n-F(u_n)\right) \textrm{d}x\le C_1, \end{aligned} \end{aligned}$$

(3.27)

where $\tilde{A}_n:=\{x|\,\frac{1}{4}f(u_n)u_n-F(u_n)\ge 0\}$. Let $M>\max \{20M_0,t_0\}$, then from ($f_5$) and (3.27), we conclude that

$$\begin{aligned} \begin{aligned}&\frac{1}{5}\int _{|u_n|\ge M}f(u_n)u_n\textrm{d}x\\&\quad \le \int _{|u_n|\ge M}\frac{1}{4}f(u_n)u_n-M_0|f(u_n)|\textrm{d}x\\&\quad \le \int _{|u_n|\ge M}\frac{1}{4}f(u_n)u_n-F(u_n)\textrm{d}x\\&\quad \le \int _{\tilde{A}_n}\frac{1}{4}f(u_n)u_n-F(u_n)\textrm{d}x\\&\quad <C_1, \end{aligned} \end{aligned}$$

(3.28)

which implies by ($f_1$) that $f(u_n)u_n$ is bounded in $L^1(\mathbb {R}^2)$. So we can infer that $f(u_n)\rightarrow f(u_0)$ in $L^1(B_R(0))$ for any $R>0$ and then (see [24])

$$\begin{aligned} \begin{aligned}&\int _{\mathbb {R}^2}f(u_n)\varphi \textrm{d}x\rightarrow \int _{\mathbb {R}^2}f(u_0)\varphi \textrm{d}x,\,\,\varphi \in C_0^\infty (\mathbb {R}^2). \end{aligned} \end{aligned}$$

(3.29)

Then $J'_{B,\alpha ,\lambda }(u_0)=0$ for any fixed $\alpha ,\lambda$. Observe that

$$\begin{aligned} I_{\alpha ,\lambda }(u_n)=J_{B,\alpha ,\lambda }(u_n)-\frac{B^4}{4\alpha }-\frac{B^{5/2}\lambda }{10}+o(1), \end{aligned}$$

and so $J_{B,\alpha ,\lambda }(u_n)\rightarrow c_{\alpha ,\lambda }+\frac{B^4}{4\alpha }+\frac{B^{5/2}\lambda }{10}$ and $J'_{B,\alpha ,\lambda }(u_n)\rightarrow 0$ in $H^{-1}$ as $n\rightarrow \infty$. Moreover, $v_n^1\rightharpoonup 0$ in $H^1(\mathbb {R}^2)$ if we define $v_n^1:=u_n-u_0$. It follows from the Brezis-Lieb lemma [10] that

$$\begin{aligned} \begin{aligned}&\Vert u_n\Vert ^2=\Vert v_n^1\Vert ^2+\Vert u_0\Vert ^2+o(1),\\&\quad \int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*u_n^2\right) u_n^2\textrm{d}x= \int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*u_0^2\right) u_0^2\textrm{d}x+\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*(v_n^1)^2\right) (v_n^1)^2\textrm{d}x+o(1),\\ \end{aligned} \end{aligned}$$

(3.30)

where the second identity can be proved similarly as that of Lemma 2.2 in [25] and we omit it. Using ($f_0$) and ($f_5$), we can also verify

$$\begin{aligned} \begin{aligned} \int _{\mathbb {R}^2}F(u_n)\textrm{d}x=\int _{\mathbb {R}^2}F(u_0)\textrm{d}x+\int _{\mathbb {R}^2}F(v_n^1)\textrm{d}x+o(1).\\ \end{aligned} \end{aligned}$$

(3.31)

Combining (3.31) with (3.30), we immediately get

$$\begin{aligned} \begin{aligned}&J_{B,\alpha ,\lambda }(u_n)-J_{B,\alpha ,\lambda }(u_0)\\&\quad =\frac{1}{2}\Vert v_n^1\Vert ^2+\frac{B^2}{2\alpha }\int _{\mathbb {R}^2}|v_n^1|^2\textrm{d}x +\frac{\lambda B^{1/2}}{2}\int _{\mathbb {R}^2}|v_n^1|^2\textrm{d}x,\\&\qquad -\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*(v_n^1)^2\right) (v_n^1)^2\textrm{d}x-\frac{\lambda }{r}\Vert v_n^1\Vert _r^r-\int _{\mathbb {R}^2}F(v_n^1)\textrm{d}x+o(1)\\&\quad =J_{B,\alpha ,\lambda }(v^1_n)+o(1). \end{aligned} \end{aligned}$$

(3.32)

Recalling $J'_{B,\alpha ,\lambda }(u_0)=0$ whose corresponding Pohozaev identity is

$$\begin{aligned}{} & {} P_{B,\alpha ,\lambda }(u_0):=\left( 1+\frac{B^2}{\alpha }+\lambda B^{1/2}\right) \Vert u_0\Vert _2^2- \frac{4-\alpha }{4\alpha }\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*(u_0)^2\right) (u_0)^2\textrm{d}x\\{} & {} \qquad - 2\int _{\mathbb {R}^2}\left( F(u_0)+\frac{\lambda }{r}|u_0|^r\right) \textrm{d}x=0, \end{aligned}$$

we can define

$$\begin{aligned} \begin{aligned} \mathcal {B}_{B,\alpha ,\lambda }(u_0)&:=2J'_{B,\alpha ,\lambda }(u_0)u_0-P_{B,\alpha ,\lambda }(u_0)\\&=2\Vert \nabla u_0\Vert _2^2+\left( 1+\frac{B^2}{\alpha }+\lambda B^{1/2}\right) \Vert u_0\Vert _2^2-\frac{4+\alpha }{4\alpha }\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*u_0^2\right) u_0^2\textrm{d}x\\&-(2-\frac{2}{r})\lambda \Vert u_0\Vert _r^r+2\int _{\mathbb {R}^2}[F(u_0)-f(u_0)u_0]\textrm{d}x=0, \end{aligned} \end{aligned}$$

which yields that

$$\begin{aligned} \begin{aligned} 4J_{B,\alpha ,\lambda }(u_0)=&\,4J_{B,\alpha ,\lambda }(u_0)-\mathcal {B}_{B,\alpha ,\lambda }(u_0)\\ =&\left( 1+\frac{B^2}{\alpha }+\lambda B^{1/2}\right) \Vert u_0\Vert _2^2 +\frac{1}{4}\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*u_0^2\right) u_0^2\textrm{d}x\\&+ 2\int _{\mathbb {R}^2}[f(u_0)u_0-3F(u_0)]\textrm{d}x+\left( 2-\frac{6}{r}\right) \lambda \Vert u_0\Vert _r^r. \end{aligned} \end{aligned}$$

(3.33)

Consider sequence $\{v_n^1\}$. We claim that either

• (v1) $v_n^1\rightarrow 0$ in $H^1(\mathbb {R}^2)$ as $n\rightarrow \infty$, or

• (v2) there exist $m>0$ and $\{y^1_n\}\subset \mathbb {R}^2$ such that

  $$\begin{aligned} \liminf \limits _{n\rightarrow \infty }\int _{B_{1}(y_n^1)}|v_n^1|^2\textrm{d}x\ge m>0. \end{aligned}$$

  (3.34)

If (3.34) does not occur, then by Lions’ vanishing lemma (see [30, 31]), we have $v_n^1\rightarrow 0$ in $L^s(\mathbb {R}^2)$ for all $s>2$. And so, using the Hardy–Littlewood–Sobolev inequality, we have $\int _{\mathbb {R}^2}\big (\frac{1}{|x|^\alpha }*(v_n^1)^2\big )(v_n^1)^2\textrm{d}x=o(1)$. Moreover, arguing similarly as in [24], we have $\int _{\mathbb {R}^2}F(v_n^1)\textrm{d}x=o(1)$. Here we consider two cases:

Case 1. $u_0\equiv 0$. That is, $v_n^1\equiv u_n$. Combining (3.32) with (3.33) we have

$$\begin{aligned} \begin{aligned} J_{B,\alpha ,\lambda }(u_n)=&\frac{1}{2}\Vert u_n\Vert ^2+\frac{B^2}{2\alpha }\int _{\mathbb {R}^2}|u_n|^2\textrm{d}x+\frac{\lambda B^{1/2}}{2}\int _{\mathbb {R}^2}|u_n|^2\textrm{d}x+o(1)\\ \ge&\frac{1}{2}\Vert u_n\Vert ^2+\frac{B^4}{2\alpha } +\frac{\lambda B^{5/2}}{2}+o(1), \end{aligned} \end{aligned}$$

(3.35)

which implies by $c_{\alpha ,\lambda }<\frac{2\pi }{\theta _0}$ that $\sup _{n\in \mathbb {N}}\Vert u_n\Vert ^2<\frac{4\pi }{\theta _0}$. Then there exists $\varepsilon _0>0$ small such that

$$\begin{aligned} \Vert u_n\Vert ^2<\frac{4\pi }{\theta _0}(1-5\varepsilon _0), \end{aligned}$$

(3.36)

and then there exists $s\in (1,2)$ such that

$$\begin{aligned} (1+\varepsilon _0)(1-5\varepsilon _0)s<1. \end{aligned}$$

For any $\xi >0$, there exists $C_\xi >0$ such that

$$\begin{aligned} |f(t)|^s\le \xi |t|+C_\xi [e^{\theta _0(1+\varepsilon _0)t^2}-1],\,\, t\ge 0. \end{aligned}$$

(3.37)

From Lemma 1.1, (3.36) and (3.37), Hölder’s inequality, we deduce that

$$\begin{aligned} \begin{aligned} \int _{\mathbb {R}^2}f(u_n)u_n\textrm{d}x&\le \xi \Vert u_n\Vert ^2+ C_\xi \left( \int _{\mathbb {R}^2}|f(u_n)|^s\textrm{d}x\right) ^{1/s}\Vert u_n\Vert _{s'}\\&\le \xi \Vert u_n\Vert ^2+C_\xi \left( \int _{\mathbb {R}^2}[e^{\theta _0(1+\varepsilon _0)s|u_n|^2}-1]\textrm{d}x\right) ^{1/s}\Vert u_n\Vert _{s'}\\&\le \xi \Vert u_n\Vert ^2+C_\xi \left( \int _{\mathbb {R}^2}[e^{\Vert u_n\Vert ^2\theta _0(1+\varepsilon _0)s\frac{|u_n|^2}{\Vert u_n\Vert ^2}}-1]\textrm{d}x\right) ^{1/s}\Vert u_n\Vert _{s'}\\&\le \xi \Vert u_n\Vert ^2+C_\xi \Vert u_n\Vert _{s'}=o(1). \end{aligned} \end{aligned}$$

(3.38)

Here, $s'=\frac{s}{s-1}\in (2,+\infty )$. Thus,

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\int _{\mathbb {R}^2}f(u_n)u_n\textrm{d}x=0. \end{aligned}$$

(3.39)

From $J'_{\alpha ,B,\lambda }(u_n)u_n=o(1)$, we deduce that $u_n\rightarrow 0$ in $H^1(\mathbb {R}^2)$ which contradicts the fact that

$$\begin{aligned} J_{B,\alpha ,\lambda }(u_n)\rightarrow c_{\alpha ,\lambda }+\frac{B^4}{4\alpha }+\frac{B^{5/2}\lambda }{10} \end{aligned}$$

as $n\rightarrow \infty$. Thus (v2) holds true for $\{v^1_n\}$.

Case 2. $u_0\not \equiv 0$. That is, $\Vert u_0\Vert >0$. In order to prove that (v1) holds for $\{v_n^1\}$, and Lemma 3.5 holds with $k=0$, we only need to show that

$$\begin{aligned} \Vert u_n\Vert ^2\rightarrow \Vert u_0\Vert ^2\quad \text {as}\,\,n\rightarrow \infty . \end{aligned}$$

(3.40)

Indeed, by Fatou’s lemma, we have

$$\begin{aligned} \begin{aligned} I_{\alpha ,\lambda }(u_0)=&\frac{1}{2}\Vert u_0\Vert ^2+\frac{1}{4\alpha }\Vert u_0\Vert ^2_2+\frac{2\lambda }{5}\Vert u_0\Vert _2^4\\&-\frac{1}{4\alpha }\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*(u_0)^2\right) (u_0)^2\textrm{d}x -\int _{\mathbb {R}^2}(F(u_0)+\frac{\lambda }{r}|u_0|^r)\textrm{d}x\\ \le&\liminf _{n\rightarrow \infty }\left( \frac{1}{2}\Vert u_n\Vert ^2+\frac{1}{4\alpha }\Vert u_n\Vert ^2_2+\frac{2\lambda }{5}\Vert u_n\Vert _2^4\right. \\&\left. -\frac{1}{4\alpha }\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*(u_n)^2\right) (u_n)^2\textrm{d}x -\int _{\mathbb {R}^2}\left( F(u_n)+\frac{\lambda }{r}|u_n|^r\right) \textrm{d}x\right) \\ =&\liminf _{n\rightarrow \infty }I_{\alpha ,\lambda }(u_n)=c_{\alpha ,\lambda }. \end{aligned} \end{aligned}$$

(3.41)

If $I_{\alpha ,\lambda }(u_0)=c_{\alpha ,\lambda }$, by (3.41) we obtain immediately (3.40) holds true. Otherwise if $I_{\alpha ,\lambda }(u_0)<c_{\alpha ,\lambda }$, then we have

$$\begin{aligned} \begin{aligned}&\Vert u_0\Vert ^2+\frac{1}{2\alpha }\Vert u_0\Vert _2^4+\frac{4\lambda }{5}\Vert u_0\Vert _2^5\\&\quad <2c_{\alpha ,\lambda }+2\int _{\mathbb {R}^2}F(u_0)\textrm{d}x +\frac{1}{2\alpha }\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*u_0^2\right) u_0^2\textrm{d}x+ \frac{2\lambda }{r}\Vert u_0\Vert _r^r. \end{aligned} \end{aligned}$$

(3.42)

In view of the definition of $I_{\alpha ,\lambda }$, we also have

$$\begin{aligned} \begin{aligned}&\lim \limits _{n\rightarrow \infty }\left( \Vert u_n\Vert ^2+\frac{1}{2\alpha }\Vert u_n\Vert _2^4+\frac{4\lambda }{5}\Vert u_n\Vert _2^5\right) \\&\quad =2c_{\alpha ,\lambda }+2\int _{\mathbb {R}^2}F(u_0)\textrm{d}x +\frac{1}{2\alpha }\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*u_0^2\right) u_0^2\textrm{d}x+ \frac{2\lambda }{r}\Vert u_0\Vert ^r. \end{aligned} \end{aligned}$$

(3.43)

Take

$$\begin{aligned} w_n=\frac{u_n}{\left( \Vert u_n\Vert ^2+\frac{1}{2\alpha }\Vert u_n\Vert _2^4+\frac{4\lambda }{5}\Vert u_n\Vert _2^5\right) ^{1/2}} \end{aligned}$$

and

$$\begin{aligned} w_0=\frac{u_0}{\sqrt{2c_{\alpha ,\lambda }+2\int _{\mathbb {R}^2}F(u_0)\textrm{d}x +\frac{1}{2\alpha }\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*u_0^2\right) u_0^2\textrm{d}x+ \frac{2\lambda }{r}\Vert u_0\Vert _r^r}}. \end{aligned}$$

It then follows from (3.42) and (3.43) that $\Vert w_n\Vert \le 1$, $w_n\rightharpoonup w_0$, and $\Vert w_0\Vert <1$. Similarly to Lions [32], one has that

$$\begin{aligned} \sup \limits _{n\in \mathbb {N}}\left( \int _{\mathbb {R}^2}e^{4\pi p w_n^2}-1\right) \textrm{d}x<\infty \end{aligned}$$

(3.44)

for all

$$\begin{aligned} p<\bar{p}:=\frac{1}{A-\Vert w_0\Vert ^2}=2\frac{c_{\alpha ,\lambda }+\int _{\mathbb {R}^2}F(u_0)\textrm{d}x +\frac{1}{4\alpha }\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*u_0^2\right) u_0^2\textrm{d}x+ \frac{\lambda }{r}\Vert u_0\Vert ^r}{\Vert u_n\Vert ^2-\Vert u_0\Vert ^2}+o(1), \end{aligned}$$

where $A=\lim _{n\rightarrow \infty }\Vert w_n\Vert ^2$. Recalling (3.32) with (3.33), we have

$$\begin{aligned} \begin{aligned}&c_{\alpha ,\lambda }+\frac{B^4}{4\alpha }+\frac{B^{5/2}\lambda }{10}=J_{B,\alpha ,\lambda }(u_n)+o(1)\\&\quad =J_{B,\alpha ,\lambda }(u_0)+\frac{1}{2}\Vert v_n^1\Vert ^2+\frac{B^2}{2\alpha }\int _{\mathbb {R}^2}|v_n^1|^2\textrm{d}x +\frac{\lambda B^{1/2}}{2}\int _{\mathbb {R}^2}|v_n^1|^2\textrm{d}x+o(1)\\&\quad \ge \frac{1}{4}\left( \frac{B^2}{\alpha }+\lambda B^{1/2}\right) \Vert u_0\Vert _2^2+\frac{1}{2}\Vert v_n^1\Vert ^2+\frac{B^2}{2\alpha }\int _{\mathbb {R}^2}|v_n^1|^2\textrm{d}x +\frac{\lambda B^{1/2}}{2}\int _{\mathbb {R}^2}|v_n^1|^2\textrm{d}x+o(1)\\&\quad \ge \frac{1}{4}\left( \frac{B^2}{\alpha }+\lambda B^{1/2}\right) \Vert u_n\Vert _2^2+\frac{1}{2}\Vert v_n^1\Vert ^2+o(1),\\&\quad =\frac{1}{4}\left( \frac{B^4}{\alpha }+\lambda B^{5/2}\right) +\frac{1}{2}\Vert v_n^1\Vert ^2+o(1), \end{aligned} \end{aligned}$$

(3.45)

which implies by $c_{\alpha ,\lambda }<\frac{2\pi }{\theta _0}$ that $\sup _{n\in \mathbb {N}}\Vert v_n^1\Vert ^2<\frac{4\pi }{\theta _0}$. And so,

$$\begin{aligned} \frac{\theta _0}{2\pi }<\frac{2}{D-\Vert u_0\Vert ^2}=\lim _{n\rightarrow \infty }\frac{2}{\Vert v^1_n\Vert ^2}, \end{aligned}$$

where $D=\lim _{n\rightarrow \infty }\Vert u_n\Vert ^2$. Then recalling (3.43), we can always choose $q>1$ sufficiently close to 1 and $\varepsilon >0$ small such that

$$\begin{aligned} \begin{aligned}&q(\theta _0+\varepsilon ) \left( \Vert u_n\Vert ^2+\frac{1}{2\alpha }\Vert u_n\Vert _2^4+\frac{4\lambda }{5}\Vert u_n\Vert _2^5\right) \\&\quad \le 4\pi p<4\pi \frac{1}{A-\Vert w_0\Vert ^2}\\&\quad =8\pi \frac{c_{\alpha ,\lambda }+\int _{\mathbb {R}^2}F(u_0)\textrm{d}x +\frac{1}{4\alpha }\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*u_0^2\right) u_0^2\textrm{d}x+ \frac{\lambda }{r}\Vert u_0\Vert ^r}{\Vert u_n\Vert ^2-\Vert u_0\Vert ^2}+o(1) \end{aligned} \end{aligned}$$

for some p satisfying (3.44). Based on the above facts, using condition ($f_0$), we have

$$\begin{aligned} \int _{\mathbb {R}^2}|f(u_n)|^q\textrm{d}x\le C\Vert u_n\Vert _q^q+C \int _{\mathbb {R}^2}\left[ e^{q(\theta _0+\varepsilon ) \left( \Vert u_n\Vert ^2+\frac{1}{2\alpha }\Vert u_n\Vert _2^4+\frac{4\lambda }{5}\Vert u_n\Vert _2^5\right) w_n^2}-1\right] \textrm{d}x<C \end{aligned}$$

for some $C>0$ independently of n. In virtue of the above facts and (3.29), we have

$$\begin{aligned} \begin{aligned}&\bigg |\int _{\mathbb {R}^2}f(u_n)u_n-f(u_0)u_0\textrm{d}x\bigg |\\&\quad =\bigg |\int _{\mathbb {R}^2}f(u_n)(u_n-u_0)-(f(u_n)-f(u_0))u_0\textrm{d}x\bigg |\\&\quad \le \bigg (\int _{\mathbb {R}^2}|f(u_n)|^qdx\bigg )^{\frac{1}{q}}\bigg (\int _{\mathbb {R}^2}|u_n-u_0|^{\frac{q}{q-1}}dx\bigg )^{\frac{q-1}{q}} +\bigg |\int _{\mathbb {R}^2}(f(u_n)-f(u_0))u_0\textrm{d}x\bigg |\\&\quad \rightarrow 0,\quad \text {as}\,\,n\rightarrow \infty . \end{aligned} \end{aligned}$$

By the fact that $(J'_{B,\alpha ,\lambda }(u_n)-J'_{B,\alpha ,\lambda }(u_0))(u_n-u_0)=o(1)$, we have $\Vert u_n-u_0\Vert =o(1)$, which implies that $I_{\alpha ,\lambda }(u_0)=c_{\alpha ,\lambda }$. This is a contradiction. Hence, $\Vert v_n^1\Vert \rightarrow 0$ and (v1) holds for $\{v_n^1\}$, Lemma 3.5 holds with $k=0$.

If (v2) holds, namely, (3.34) is true, then there exists $w^1\in H^1(\mathbb {R}^2)\setminus \{0\}$ such that $v_n^1(\cdot +y_n^1)\rightharpoonup w^1$ in $H^1(\mathbb {R}^2)$ and $u_n(\cdot +y_n^1)\rightharpoonup w^1$ in $H^1(\mathbb {R}^2)$. Recalling the fact that $v_n^1\rightharpoonup 0$ in $H^1(\mathbb {R}^2)$, we find that $\{y_n^1\}$ must be unbounded. That is, $|y^1_n|\rightarrow +\infty$. Let us now show that ${J}'_{B,\alpha ,\lambda }(w^1)=0$. Indeed, it suffices to show that ${J}'_{B,\alpha ,\lambda }(u_n(\cdot +y_n^1))\varphi \rightarrow 0$ for fixed $\varphi \in C_0^{\infty }(\mathbb {R}^2)$. Since $J'_{B,\alpha ,\lambda }(u_n)\rightarrow 0$ in $H^{-1}$ as $n\rightarrow \infty$, and then ${J}'_{B,\alpha ,\lambda }(u_n)\varphi (\cdot -y_n^1)\rightarrow 0$ for any $\varphi \in C_0^\infty (\mathbb {R}^2)$. Thus, it follows that as $n\rightarrow \infty$,

$$\begin{aligned} \begin{aligned}&{J}'_{B,\alpha ,\lambda }(u_n(\cdot +y_n^1))\varphi \\&\quad =\int _{\mathbb {R}^2}[\nabla u_n(x+y_n^1)\nabla \varphi +u_n(x+y_n^1)\varphi ]\textrm{d}x +\left( \frac{B^2}{\alpha }+\lambda B^{1/2}\right) \int _{\mathbb {R}^2}u_n(x+y_n^1)\varphi \textrm{d}x\\&\,\,\,\,\,\,\,\,-\frac{1}{\alpha }\int _{\mathbb {R}^2}\left( \frac{1}{|x+y_n^1|^\alpha }*u_n^2\right) u_n(x+y_n^1)\varphi \textrm{d}x -\lambda \int _{\mathbb {R}^2}|u_n(\cdot +y_n^1)|^{r-2}u_n(\cdot +y_n^1)\varphi \textrm{d}x\\&\,\,\,\,\,\,\,\,-\int _{\mathbb {R}^2}f(u_n(\cdot +y_n^1))\varphi \textrm{d}x\rightarrow 0. \end{aligned} \end{aligned}$$

So, ${J}'_{B,\alpha ,\lambda }(w^1)=0$. Set

$$\begin{aligned} v_n^2(x)=v_n^1(x)-w^1(x-y_n^1), \end{aligned}$$

(3.46)

then using the fact that $v_n^1(\cdot +y_n^1)\rightharpoonup w^1$ in $H^1(\mathbb {R}^2)$, we have $v_n^2\rightharpoonup 0$ in $H^1(\mathbb {R}^2)$. Using again the Brezis-Lieb lemma that

$$\begin{aligned} \begin{aligned}&\Vert u_n\Vert ^2=\Vert w^1\Vert ^2+\Vert u_0\Vert ^2+\Vert v_n^2\Vert ^2+o(1),\\&\quad \int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*u_n^2\right) u_n^2\textrm{d}x= \int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*u_0^2\right) u_0^2\textrm{d}x+\int _{\mathbb {R}^2} \left( \frac{1}{|x|^\alpha }*(w^1)^2\right) (w^1)^2\textrm{d}x\\&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*(v_n^2)^2\right) (v_n^2)^2\textrm{d}x+o(1),\\&\quad \int _{\mathbb {R}^2}F(u_n)\textrm{d}x=\int _{\mathbb {R}^2}F(u_0)\textrm{d}x+\int _{\mathbb {R}^2}F(w^1)\textrm{d}x+\int _{\mathbb {R}^2}F(v_n^2)\textrm{d}x+o(1).\\ \end{aligned} \end{aligned}$$

(3.47)

By virtue of the above estimates, we deduce that

$$\begin{aligned} \begin{aligned} \quad&{J}_{B,\alpha ,\lambda }(v_n^2)={J}_{B,\alpha ,\lambda }(u_n)-J_{B,\alpha ,\lambda }(u_0)-{J}_{B,\alpha ,\lambda }(w^1)+o(1).\\ \end{aligned} \end{aligned}$$

(3.48)

Let us now study $\{v_n^2\}$. Since $\{v_n^2\}$ is bounded in $H^1(\mathbb {R}^2)$, one of (v1) and (v2) holds for $\{v_n^2\}$. The similar arguments used before imply that Lemma 3.5 holds with $k=1$ if $v_n^2\rightarrow 0$ in $H^1(\mathbb {R}^2)$. Otherwise, (v2) holds for $\{v_n^2\}$. We repeat the arguments above. Iterating this procedure, there exists sequence $\{y_n^j\}\subset \mathbb {R}^2$ such that $|y_n^j|\rightarrow +\infty$, $|y_n^j-y_n^i|\rightarrow +\infty$ if $i\ne j$ as $n\rightarrow +\infty$ and $v_n^j=v_n^{j-1}-w^{j-1}(x-y_n^{j-1})$ (like (3.46)) with $j\ge 2$ such that

$$\begin{aligned} v_n^j\rightharpoonup 0\quad \text{ in }\,\, H^1(\mathbb {R}^2),\quad \,\,J'_{B,\alpha ,\lambda }(w^j)=0. \end{aligned}$$

Moreover, by the properties of the weak convergence, we get

$$\begin{aligned} \begin{aligned}&(a)\quad \Vert u_n\Vert ^2-\Vert u_0\Vert ^2-\sum _{i=1}^{j-1}\Vert w^i\Vert ^2=\Vert u_n-u_0-\sum _{i=1}^{j}w^{i}(\cdot -y_n^{i})\Vert ^2+o(1),\\&(b)\quad c_{\alpha ,\lambda }+\frac{B^4}{4\alpha }= {J}_{\alpha , B,\lambda }(u_0)+\sum _{i=1}^{j-1} {J}_{\alpha , B,\lambda }(w^{i})+{J}_{\alpha , B,\lambda }(v_n^{j})+o(1),\\&(c)\quad B^2=\Vert u_0\Vert _2^2+\sum _{i=1}^{j-1}\Vert w^i\Vert _2^2+\Vert v_n^{j+1}\Vert _2^2+o(1). \end{aligned} \end{aligned}$$

(3.49)

Now, we claim that there exists $C>0$ such that $\Vert w^i\Vert ^2\ge C$, $i=1,2,...,k$. Without loss of generality, we can assume that $\Vert w^i\Vert ^2<\frac{2\pi }{\theta _0}$ for some i. Using (3.4), (3.5), $J'_{B,\alpha ,\lambda }(w^i)w^i=0$, the Hardy–Littlewood–Sobolev inequality, the Moser-Trudinger inequality and Lemma 2.3, one finds that for any $\varepsilon >0$, there exists $C_\varepsilon >0$ such that

$$\begin{aligned} \begin{aligned} \Vert w^i\Vert ^2&\le \int \int _{|x-y|\le 1}\frac{|x-y|^{-\alpha }-1}{\alpha }|w^i(x)|^2|w^i(y)|^2\textrm{d}x\textrm{d}y+C\Vert w^i\Vert ^3+C\Vert w^i\Vert _r^r\\&\le \int _{\mathbb {R}^2}\int _{\mathbb {R}^2}\frac{|w^i(x)|^2|w^i(y)|^2}{|x-y|}\textrm{d}x\textrm{d}y+C\Vert w^i\Vert ^3+C\Vert w^i\Vert ^r\\&\le C\Vert w^i\Vert ^4+C\Vert w^i\Vert ^3+C\Vert w^i\Vert ^r. \end{aligned} \end{aligned}$$

Hence, the claim is true. Recall that $\{u_n\}$ is bounded in $H^1(\mathbb {R}^2)$, from (3.49)(a) we deduce that the iteration must stop at some finite index k. And so $v_n^{k+1}\rightarrow 0$ in $H^1(\mathbb {R}^2)$ as $n\rightarrow \infty$. The proof is complete. $\square$

If $u\in H^1(\mathbb {R}^2)$ is a critical point of $I_{\alpha ,\lambda }$, we have

$$\begin{aligned} \begin{aligned} \mathcal {B}_{\alpha ,\lambda }(u):=&2\Vert \nabla u\Vert _2^2+\Vert u\Vert _2^2+\frac{1}{\alpha }\Vert u\Vert _2^4+\lambda \Vert u\Vert _2^{5/2} -\frac{4+\alpha }{4\alpha }\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*u^2\right) u^2\textrm{d}x\\&+2\int _{\mathbb {R}^2}[F(u)-f(u)u]\textrm{d}x -\left( 2-\frac{2}{r}\right) \lambda \Vert u\Vert _r^r=0, \end{aligned} \end{aligned}$$

since $\mathcal {B}_{\alpha ,\lambda }(u)=2I'_{\alpha ,\lambda }(u)u-P_{\alpha ,\lambda }(u)$. Here, $P_{\alpha ,\lambda }(u)$ is the associated Pohozaev functional with $I'_{\alpha ,\lambda }(u)=0$.

Lemma 3.6

If $u\in H^1(\mathbb {R}^2)\setminus \{0\}$ satisfies $\mathcal {B}_{\alpha ,\lambda }(u)=0$, then there exists $\gamma \in C([0,1], H^1(\mathbb {R}^2))$ such that $\gamma (0)=0, I_{\alpha ,\lambda }(\gamma (1))<0, u\in \gamma ([0,1]), 0 \not \in \gamma ((0, 1])$ and

$$\begin{aligned} \max \limits _{t\in [0,1]} I_{\alpha ,\lambda }(\gamma (t)) =I_{\alpha ,\lambda }(u). \end{aligned}$$

Proof

For $t\in (0,\infty )$, define $u_t:=t^2u(t\cdot )$, then we have

$$\begin{aligned} \begin{aligned} g(t):=I_{\alpha ,\lambda }(u_t)=&\frac{t^4}{2}\Vert \nabla u\Vert _2^2+\frac{t^2}{2}\Vert u\Vert _2^2+ \frac{t^4}{4\alpha }\Vert u\Vert _2^4-\frac{t^{4+\alpha }}{4\alpha }\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*u^2\right) u^2\textrm{d}x\\&+\frac{2\lambda }{5}t^{5/2} \Vert u\Vert _2^{5/2} -\frac{\lambda t^{2(r-1)}}{r}\Vert u\Vert _r^r-t^{-2}\int _{\mathbb {R}^2}F(t^2u)\textrm{d}x, \end{aligned} \end{aligned}$$

which implies that for $t>0$ large enough

$$\begin{aligned} I_{\alpha ,\lambda }(u_t)<0. \end{aligned}$$

That is, there exists $t_0>1$ such that $I_{\alpha ,\lambda }(u_{t_0})<0$. Take $\gamma (t):=t^2t_0^2u(tt_0\cdot )$ for $t\in (0,1]$ and $\gamma (0):=0$. Then $\gamma \in C([0,1], H^1(\mathbb {R}^2))$ and $u\in \gamma ([0,1])$. Moreover,

$$\begin{aligned} \begin{aligned} g'(t)=&t^3\bigg [2\Vert \nabla u\Vert _2^2+\frac{1}{t^2}\Vert u\Vert _2^2+ \frac{1}{\alpha }\Vert u\Vert _2^4-\frac{(4+\alpha )t^{\alpha }}{4\alpha }\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*u^2\right) u^2\textrm{d}x\\&+\lambda t^{\frac{-3}{2}} \Vert u\Vert _2^{5/2} -\frac{2\lambda (r-1) t^{2(r-3)}}{r}\Vert u\Vert _r^r-2\int _{\mathbb {R}^2}\frac{f(t^2u)t^2u-F(t^2u)}{t^6u^3}u^3\textrm{d}x\bigg ], \end{aligned} \end{aligned}$$

which implies by ($f_7$) that $t=1/t_0$ is the unique maximum point of $t\mapsto I_{\alpha ,\lambda }(\gamma (t))$. Namely, $\max \limits _{t\in [0,1]} I_{\alpha ,\lambda }(\gamma (t)) =I_{\alpha ,\lambda }(u)$. The proof is complete. $\square$

Lemma 3.7

Let $\{u_n\}\subset H^1(\mathbb {R}^2)$ be a (PS)$_{c_{\alpha ,\lambda }}$ sequence of $I_{\alpha ,\lambda }$ for fixed $\alpha ,\lambda$, then there exists $u_0\in H^1(\mathbb {R}^2){\setminus }\{0\}$ such that $I'_{\alpha ,\lambda }(u_0)=0$.

Proof

In view of Lemma 3.3, we know that $\Vert u_n\Vert \le C$ for some C (independent of n). So there is $u_0\in H^1(\mathbb {R}^2)$ such that $u_n\rightharpoonup u_0$ weakly in $H^1(\mathbb {R}^2)$. There also exists $B\in \mathbb {R}$ such that

$$\begin{aligned} \Vert u_n\Vert _2^2\rightarrow B^2,\quad \text {as}\,\,n\rightarrow \infty , \end{aligned}$$

(3.50)

from which we deduce that $J'_{B,\alpha ,\lambda }(u_n)\rightarrow 0$ in $H^{-1}$ and $J'_{B,\alpha ,\lambda }(u_0)=0$. In view of Lemma 3.5, for each nontrivial critical point $w^j(j=1,...,k)$ of $J_{B,\alpha ,\lambda }$, we have

$$\begin{aligned} \begin{aligned} \mathcal {B}_{B,\alpha ,\lambda }(w^j)=&2J'_{B,\alpha ,\lambda }(w^j)w^j-P_{B,\alpha ,\lambda }(w^j)\\ =&2\Vert \nabla w^j\Vert _2^2+\left( 1+\frac{B^2}{\alpha }+\lambda B^{1/2}\right) \Vert w^j\Vert _2^2 -\frac{4+\alpha }{4\alpha }\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*(w^j)^2\right) (w^j)^2\textrm{d}x\\&-\left( 2-\frac{2}{r}\right) \lambda \Vert w^j\Vert _r^r+2\int _{\mathbb {R}^2}[F(w^j)-f(w^j)w^j]\textrm{d}x=0. \end{aligned} \end{aligned}$$

(3.51)

Observe from (3.51) that

$$\begin{aligned} \begin{aligned} 2&\Vert \nabla w^j\Vert _2^2+\Vert w^j\Vert _2^2+\frac{1}{\alpha }\Vert w^j\Vert _2^4+\lambda \Vert w^j\Vert _2^{5/2}\\&\quad \le \frac{4+\alpha }{4\alpha }\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*(w^j)^2\right) (w^j)^2\textrm{d}x +\left( 2-\frac{2}{r}\right) \lambda \Vert w^j\Vert _r^r+2\int _{\mathbb {R}^2}[f(w^j)w^j-F(w^j)]\textrm{d}x. \end{aligned} \end{aligned}$$

(3.52)

From (3.52) and ($f_7$) we deduce that there exists $t_j\in (0,1]$ such that

$$\begin{aligned} \begin{aligned} 2&t_j^4\Vert \nabla w^j\Vert _2^2+t_j^2\Vert w^j\Vert _2^2+t_j^4\frac{1}{\alpha }\Vert w^j\Vert _2^4+\lambda t_j^{5/2}\Vert w^j\Vert _2^{5/2}\\&\quad =\frac{4+\alpha }{4\alpha }t_j^{4+\alpha }\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*|w^j|^2\right) |w^j|^2\textrm{d}x +\left( 2-\frac{2}{r}\right) \lambda t_j^{2(r-1)}\Vert w^j\Vert _r^r\\&\qquad +2t_j^{-2}\int _{\mathbb {R}^2}[f(t_j^2w^j)t_j^2w^j-F(t_j^2w^j)]\textrm{d}x, \end{aligned} \end{aligned}$$

(3.53)

which implies $\mathcal {B}_{\alpha ,\lambda }(w^j_{t_j})=0$, $w^j_{t_j}(x):=t_j^2w^j(t_jx)$. Then it follows from Lemma 3.6 that there exists $\gamma \in C([0,1], H^1(\mathbb {R}^2))$ such that $\gamma (0)=0, I_{\alpha ,\lambda }(\gamma (1))<0, w^j_{t_j}\in \gamma ([0,1]), 0 \not \in \gamma ((0, 1])$ and

$$\begin{aligned} \max \limits _{t\in [0,1]} I_{\alpha ,\lambda }(\gamma (t)) =I_{\alpha ,\lambda }(w^j_{t_j}). \end{aligned}$$

As a result, a direct calculation from (3.53) yields

$$\begin{aligned} \begin{aligned} J_{B,\alpha ,\lambda }(w^j)=&J_{B,\alpha ,\lambda }(w^j)-\frac{1}{4}\mathcal {B}_{B,\alpha ,\lambda }(w^j)\\ =&\frac{1}{4}\left( 1+\frac{B^2}{\alpha }+\lambda B^{1/2}\right) \Vert w^j\Vert _2^2+\frac{1}{16}\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*(w^j)^2\right) (w^j)^2\textrm{d}x\\&+\frac{1}{2}\left( 1-\frac{3}{r}\right) \lambda \Vert w^j\Vert _r^r+\frac{1}{2}\int _{\mathbb {R}^2}[f(w^j)w^j-3F(w^j)]\textrm{d}x\\ \ge&\frac{1}{4}\Vert w^j_{t_j}\Vert _2^2+\frac{3\lambda }{20}\Vert w^j_{t_j}\Vert _2^{5/2}+\frac{1}{16}\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*(w^j_{t_j})^2\right) (w^j_{t_j})^2\textrm{d}x\\&+\frac{1}{2}\left( 1-\frac{3}{r}\right) \lambda \Vert w^j_{t_j}\Vert _r^r\\&+\frac{1}{2}\int _{\mathbb {R}^2}[f(w^j_{t_j})w^j_{t_j}-3F(w^j_{t_j})]\textrm{d}x+\frac{B^2}{4\alpha }\Vert w^j\Vert _2^2+\frac{\lambda B^{1/2}}{10}\Vert w^j\Vert _2^{2}\\ =&I_{\alpha ,\lambda }(w^j_{t_j})-\frac{1}{4}\mathcal {B}_{\alpha ,\lambda }(w^j_{t_j})+\bigg (\frac{B^2}{4\alpha } +\frac{\lambda B^{1/2}}{10}\bigg )\Vert w^j\Vert _2^{2}\\ \ge&c_{\alpha ,\lambda }+\bigg (\frac{B^2}{4\alpha } +\frac{\lambda B^{1/2}}{10}\bigg )\Vert w^j\Vert _2^{2}. \end{aligned} \end{aligned}$$

(3.54)

Then from Lemma 3.5 and (3.33), we conclude that

$$\begin{aligned} \begin{aligned}&c_{\alpha ,\lambda }+\frac{B^4}{4\alpha }+\frac{B^{5/2}\lambda }{10}\\&\quad = J_{B,\alpha ,\lambda }(u_0)+\sum \limits _{j=1}^{k}J_{B,\alpha ,\lambda }(w^j)\\&\quad \ge kc_{\alpha ,\lambda }+\frac{B^2}{4\alpha }\int _{\mathbb {R}^2}|u_0|^2dx+\frac{\lambda B^{1/2}}{10}\Vert u_0\Vert _2^{2} +\bigg (\frac{B^2}{4\alpha }+\frac{\lambda B^{1/2}}{10}\bigg )\sum \limits _{j=1}^{k}\int _{\mathbb {R}^2}|w^j|^2dx\\&\quad \ge kc_{\alpha ,\lambda }+\frac{B^4}{4\alpha }+\frac{B^{5/2}\lambda }{10}, \end{aligned} \end{aligned}$$

(3.55)

where $w^j\not =0$ for $j=1,...,k$. Observe that $k>1$ is impossible.

Thus, $k=0$, we are done. Then it follows that $J_{B,\alpha ,\lambda }(u_0)=I_{\alpha }(u_0)+\frac{B^4}{4\alpha }+\frac{B^{5/2}\lambda }{10}$ and $u_n\rightarrow u_0$ strongly in $H^1(\mathbb {R}^2)$. Assume $k=1$ and $u_0\ne 0$, then the first inequality in (3.55) strictly holds. This yields a contradiction. If $k=1$ and $u_0=0$, then by conclusion (iii) of Lemma 3.5, we get $B=\Vert w^1\Vert _2^2$ and $I'_{\alpha ,\lambda }(w^1)=0$ in $H^1(\mathbb {R}^2)$. The proof is complete. $\square$

4 Proof of Theorem 1.3

In view of Lemma 3.1 and 3.7, there is at least a mountain pass type critical point $u_{\alpha ,\lambda }$ of $I_{\alpha ,\lambda }$ with $I_{\alpha ,\lambda }(u_{\alpha ,\lambda })=c_{\alpha ,\lambda }$. That is, $u_{\alpha ,\lambda }\in H^1(\mathbb {R}^2)$ is a weak positive solution of equation (3.2).

Choosing a sequence $\{\lambda _n\}\subset (0,1]$ satisfying $\lambda _n\rightarrow 0^+$, we find a sequence of nontrivial critical points $\{u_{\lambda _n}\}$(still denoted by $\{u_n\}$) of $I_{\alpha ,\lambda _n}$ with $I_{\alpha ,\lambda _n}(u_n)=c_{\alpha ,\lambda _n}$. We state the following lemma to ensure that $u_n$ converges strongly to some $u\in H^1(\mathbb {R}^2)$.

Lemma 4.1

For fixed $\alpha \in (0,1)$, sequence $\{u_n\}$ is bounded in $H^1(\mathbb {R}^2)$.

Proof

Multiplying $I_{\alpha ,\lambda _n}(u_n)$, $I'_{\alpha ,\lambda _n}(u_n)u_n=0$ and $P_{\alpha ,\lambda _n}(u_n)=0$ by 1,$-1/2$ and 1/4 respectively and adding them up, we get

$$\begin{aligned} \begin{aligned} I_{\alpha ,\lambda _n}(u_n)=&\frac{1}{4}\int _{\mathbb {R}^2}u_n^2\textrm{d}x+\frac{1}{16}Q(u_n)+\frac{3\lambda _n}{20}\Vert u_n\Vert _2^{\frac{5}{2}}\\&+\frac{1}{2}\int _{\mathbb {R}^2}[f(u_n)u_n-3F(u_n)]\textrm{d}x+\frac{(r-3)\lambda _n}{2r}\int _{\mathbb {R}^2}|u_n|^r\textrm{d}x, \end{aligned} \end{aligned}$$

(4.1)

which implies by Remark 1.2 that $\{u_n\}$ is bounded in $L^2(\mathbb {R}^2)$ uniformly for $\alpha , n$. Moreover, from (4.1), we have $\int _{\mathbb {R}^2}f(u_n)u_n\textrm{d}x\le C+3\int _{\mathbb {R}^2}F(u_n)\textrm{d}x$. Let $M>\max \{4M_0,t_0\}$, then from ($f_1$) and ($f_5$), we conclude that

$$\begin{aligned} \begin{aligned}&\int _{\mathbb {R}^2}f(u_n)u_n\textrm{d}x\le C+3\int _{\mathbb {R}^2}F(u_n)\textrm{d}x\\&\quad \le C+3\int _{\{|u_n|\le M\}}F(u_n)\textrm{d}x+3\int _{\{|u_n|\ge M\}}M_0f(u_n)\textrm{d}x\\&\quad \le C+3C\int _{\{|u_n|\le M\}}|u_n|^2\textrm{d}x+3\int _{\{|u_n|\ge M\}}\frac{1}{4}f(u_n)u_n\textrm{d}x, \end{aligned} \end{aligned}$$

(4.2)

which implies that $\{f(u_n)u_n\}$ and $\{F(u_n)\}$ are bounded in $L^1(\mathbb {R}^2)$. For $t>0$, letting $u_{nt}(x):=t^2u_{n}(tx)$, we deduce that

$$\begin{aligned} \begin{aligned}&I_{\alpha ,\lambda _n}(u_n)-I_{\alpha ,\lambda _n}(t^2u_{nt})\\&\quad =\frac{1-t^4}{2}\Vert \nabla u_n\Vert _2^2 +\frac{1-t^2}{2}\int _{\mathbb {R}^2}u_n^2\textrm{d}x+\lambda _n\frac{2(1-t^{5/2})}{5}\Vert u_n\Vert _2^{5/2}\\&\qquad +\frac{1-t^4}{4\alpha }\Vert u_n\Vert _2^4 +\frac{1-t^{4(1+\alpha )}}{4\alpha }Q(u_n)\\&\qquad +\int _{\mathbb {R}^2}\bigg [\frac{F(t^2u_n)}{t^2}-F(u_n)\bigg ]\textrm{d}x-\frac{(1-t^{2(r-1)})\lambda _n}{r}\Vert u_n\Vert _r^r\\&\quad =\frac{1-t^4}{4}[2I'_{\alpha ,\lambda _n}(u_n)u_n-P_{\alpha ,\lambda _n}(u_n)]+\left( \frac{3}{20}+\frac{t^4}{4}-\frac{2t^{5/2}}{5}\right) \lambda _n\Vert u_n\Vert _2^{5/2}\\&\qquad +\frac{(1-t^2)^2}{4}\int _{\mathbb {R}^2}u_n^2\textrm{d}x+\frac{8+\alpha -4t^{4(1+\alpha )}-(4+\alpha )t^4}{16\alpha }Q(u_n)\\&\qquad +\int _{\mathbb {R}^2}\bigg [\frac{1-t^4}{2}f(u_n)u_n+\frac{t^4-3}{2}F(u_n) +\frac{1}{t^2}F(t^2u_n)\bigg ]\textrm{d}x\\&\qquad +\bigg [\frac{(r-1)(1-t^4)}{2r}-\frac{(1-t^{2(r-1)})}{r}\bigg ]\lambda _n\Vert u_n\Vert _r^r. \end{aligned} \end{aligned}$$

(4.3)

We now show that $\{\Vert \nabla u_n\Vert _2\}$ is bounded. By contradiction, suppose that $\Vert \nabla u_n\Vert _2\rightarrow \infty$. Take $t_n=(\sqrt{M}/\Vert \nabla u_n\Vert _2)^{1/2}$ for some $M>0$ large, then $t_n\rightarrow 0$. Letting $t=t_n$ in (4.3), since $\{u_n\}$ is bounded in $L^2(\mathbb {R}^2)$, we have

$$\begin{aligned} \begin{aligned}&I_{\alpha ,\lambda _n}(u_n)-I_{\alpha ,\lambda _n}(t_n^2u_{nt_{n}})\\&\quad =\frac{1}{4}\int _{\mathbb {R}^2}u_n^2\textrm{d}x+\frac{8+\alpha }{16\alpha }Q(u_n)+\int _{\mathbb {R}^2}\bigg [\frac{1}{2}f(u_n)u_n-\frac{3}{2}F(u_n) +\frac{1}{t_n^2}F(t_n^2u_n)\bigg ]\textrm{d}x,\\&\qquad +\frac{r-3}{2r}\lambda _n\Vert u_n\Vert _r^r+o(1). \end{aligned} \end{aligned}$$

(4.4)

Therefore, it follows from (4.4), Lemma 2.3, the Hardy–Littlewood–Sobolev inequality, and the Gagliardo-Nirenberg inequality that

$$\begin{aligned} \begin{aligned} c_{\alpha ,\lambda _n}\ge&I_{\alpha ,\lambda _n}(t_n^2u_{nt_{n}})+\frac{1}{t_n^2}\int _{\mathbb {R}^2}F(t_n^2u_n)\textrm{d}x+o(1)\\ =&\frac{t_n^4}{2}\Vert \nabla u_n\Vert _2^2+\frac{t_n^4}{4\alpha }\Vert u_n\Vert _2^4-\frac{t_n^{4+\alpha }}{4\alpha }Q(u_n)\\&+\frac{t_n^2 }{2}\int _{\mathbb {R}^2} u_n^2\textrm{d}x+\lambda _n\frac{2t_n^{5/2}}{5}\Vert u_n\Vert _2^{5/2}-\frac{t_n^{2r-2}}{r}\lambda _n\Vert u_n\Vert _r^{r}+o(1)\\ \ge&\frac{t_n^4}{2}\Vert \nabla u_n\Vert _2^2+\frac{t_n^4}{4\alpha }\Vert u_n\Vert _2^4-\frac{t_n^{4}}{4\alpha }Q(u_n) +o(1)\\ \ge&\frac{t_n^4}{2}\Vert \nabla u_n\Vert _2^2-\frac{t_n^4}{4}\int \int _{|x-y|\le 1}\frac{|x-y|^{-\alpha }-1}{\alpha }u^2_n(x)u^2_n(y)\textrm{d}x\textrm{d}y+o(1)\\ \ge&\frac{M}{2}-\frac{t_n^4C}{4}\Vert u_n\Vert _2^3\Vert \nabla u_n\Vert _2+o(1)\\ \ge&\frac{M}{2}+o(1), \end{aligned} \end{aligned}$$

(4.5)

from which we obtain a contradiction by letting $M>0$ large enough. Hence, $\{u_n\}$ is bounded in $H^1(\mathbb {R}^2)$. $\square$

Remark 4.2

Observe from Lemma 4.1 that $\{u_n\}$ is bounded not only uniformly for n, but also uniformly for $\alpha$.

Let us assume that $c_{\alpha ,\lambda _n}\rightarrow c_\alpha$ as $n\rightarrow \infty$, then $I_{\alpha ,\lambda _n}(u_n)\rightarrow c_\alpha$ and $I'_{\alpha ,\lambda _n}(u_n)\rightarrow 0$ in $H^{-1}$. It is easy to see from Lemma 3.4 that $c_\alpha <\frac{2\pi }{\theta _0}$. From Lemma 4.1, we know that $\{u_n\}$ is bounded in $H^1(\mathbb {R}^2)$. Now we take advantage of Lemma 4.1 to get the profile decomposition of $\{u_n\}$. Thus, arguing similarly as in the proof of Lemma 3.5, we have the following lemma.

Lemma 4.3

Assume that $\{u_n\}$ is a bounded critical point sequence of $I_{\alpha ,\lambda _n}$ with energy level $c_\alpha$ for fixed $\alpha \in (0,1)$. Then there exist $\tilde{B}\in \mathbb {R}$ and a number $k\in \mathbb {N}\cup \{0\}$, and a finite sequence

$$\begin{aligned} (u_0,\tilde{w}^1,...,\tilde{w}^k)\subset H^1(\mathbb {R}^2),\quad \tilde{w}^j>0,\quad \text {for}\,\, j=1,...,k \,(\text {if}\,\,k\ge 1) \end{aligned}$$

of critical points for the following functional

$$\begin{aligned} \begin{aligned} J_{\tilde{B},\alpha }(u):=&\frac{1}{2}\Vert u\Vert ^2+\frac{\tilde{B}^2}{2\alpha }\int _{\mathbb {R}^2}|u_n|^2\textrm{d}x -\frac{1}{4\alpha }\int _{\mathbb {R}^2}\left( \frac{1}{|x|^\alpha }*u^2\right) u^2\textrm{d}x-\int _{\mathbb {R}^2}F(u)dx \end{aligned} \end{aligned}$$

(4.6)

and k sequences of points $\{\tilde{y}_n^j\}\subset \mathbb {R}^3$, $1\le j\le k$, such that

• (i) $|\tilde{y}_n^j|\rightarrow +\infty$, $|\tilde{y}_n^j-\tilde{y}_n^i|\rightarrow +\infty \quad$ if $i\ne j,n\rightarrow +\infty$,

• (ii) $\Vert u_n-u_0-\sum \limits _{j=1}^{k}\tilde{w}^{j}(\cdot -y_n^j)\Vert \rightarrow 0$, $c_{\alpha }+\frac{\tilde{B}^4}{4\alpha } = J_{\tilde{B},\alpha }(u_0)+\sum \limits _{j=1}^{k}J_{\tilde{B},\alpha }(w^j)$,

• (iii) $\tilde{B}^2=\Vert u_0\Vert _2^2+\sum \limits _{j=1}^{k}\Vert \tilde{w}^{j}\Vert _2^2$.

Otherwise, if $k=0$, then $u_n\rightarrow u_0$ in $H^1(\mathbb {R}^2)$.

Based on Lemma 4.3, we use the similar arguments as Lemma 3.7 to obtain $u_n\rightarrow u_\alpha$ in $H^1(\mathbb {R}^2)$ as $n\rightarrow \infty$. Moreover, $I'_\alpha (u_\alpha )=0$ and $I_\alpha (u_\alpha )=c_\alpha$, namely $u_\alpha$ is a nontrivial critical point of $I_\alpha$. Although we observe from Remark 4.2 that $\Vert u_\alpha \Vert$ is uniformly bounded for $\alpha$, it seems difficult to make use of Moser’s iteration arguments to prove that $u_\alpha$ is bounded in $L^\infty (\mathbb {R}^2)$ uniformly for $\alpha$, since nonlinearity f is of critical exponential growth in the sense of Trudinger–Moser. More precisely, the following estimate:

$$\begin{aligned} \sup _{\alpha \in (0,1)}\Vert \nabla u_\alpha \Vert _2^2<\frac{4\pi }{\theta _0} \end{aligned}$$

is not easy to get, so it seems difficult to use the Trudinger–Moser inequality to state a uniform estimate of $f(u_\alpha )$ as $\alpha \rightarrow 0^+$. For fixed $\alpha \in (0,1)$, arguing as Lemma 3.7 of [36], we can also obtain that there exist $C_\alpha ,c_\alpha$ such that

$$\begin{aligned} u_\alpha (x)\le C_\alpha \exp \left( -c_\alpha |x|\right) \quad \text {for} \,\,x\in \mathbb {R}^2. \end{aligned}$$

Thus, arguing similarly as Theorem 4.1 in [36], there exists $\alpha _1\in (0, 1)$ such that for $\alpha \in (0, \alpha _1)$, $u_\alpha$ is radially symmetric up to translation and strictly decreasing in the distance from the symmetry center.

We now state exponential decay estimate of $u_\alpha$ at infinity uniformly for $\alpha$.

Lemma 4.4

There exist $R,C>0$ (independent of $\alpha$) such that

$$\begin{aligned} u_\alpha (x)\le C\exp \left( -\frac{1}{2}|x|\right) \quad \text {for} \,\,|x|\ge R. \end{aligned}$$

Proof

Since $u_\alpha$ is a positive function, by equation (3.1) and Lemma 2.3 we obtain

$$\begin{aligned} \begin{aligned} -\Delta {u_\alpha }+ u_\alpha&\le \int _{|x-y|\le 1}\frac{|x-y|^{-\alpha }-1}{\alpha }u_\alpha ^2(y)\textrm{d}y u_\alpha (x)+f(u_\alpha )\\&\le C\int _{|x-y|\le 1}\frac{u_\alpha ^2(y)\textrm{d}y}{|x-y|}u_\alpha (x)+ f(u_\alpha ). \end{aligned} \end{aligned}$$

(4.7)

Using the similar arguments as Lemma 2.3 in [36], we have

$$\begin{aligned} \begin{aligned} \int _{|x-y|\le 1}\frac{u_\alpha ^2(y)}{|x-y|}\textrm{d}y\rightarrow 0,\quad \text {as}\,\,|x|\rightarrow +\infty , \end{aligned} \end{aligned}$$

uniformly for $\alpha \in (0,\alpha _1)$, which implies that there exists $R_1>0$ such that for $|x|\ge R_1$

$$\begin{aligned} \int _{|x-y|\le 1}\frac{u_\alpha ^2(y)}{|x-y|}\textrm{d}y\le \frac{1}{4C}. \end{aligned}$$

(4.8)

By recalling Radial Lemma A.IV in [8], there exists $C>0$ independent of $\alpha$ such that

$$\begin{aligned} |u_\alpha (x)|\le C|x|^{-1}\Vert u_\alpha \Vert \le C|x|^{-1}, \end{aligned}$$

which implies that

$$\begin{aligned} \lim \limits _{|x|\rightarrow \infty }|u_\alpha (x)|=0\quad \text {uniformly for}\,\, \alpha \in (0,\alpha _1). \end{aligned}$$

Thus, using assumption ($f_1$), we deduce that there exists $R_2>0$ such that

$$\begin{aligned} \begin{aligned} f(u_\alpha )\le \frac{1}{4}u_\alpha ,\quad |x|\ge R_2. \end{aligned} \end{aligned}$$

(4.9)

Combining (4.7)-(4.9), let $R=\max \{R_1,R_2\}$, then

$$\begin{aligned} \begin{aligned} -\Delta {u_\alpha }+ \frac{1}{4}u_\alpha \le 0,\quad |x|\ge R. \end{aligned} \end{aligned}$$

(4.10)

It follows from (4.10) and a comparison principle, there exists constant $M\ge \frac{C}{R}e^{R/2}$ such that

$$\begin{aligned} u_\alpha (x)\le M \exp \left( -\frac{1}{2}|x|\right) \quad \text {for}\,\, |x|\ge R. \end{aligned}$$

Here R, M are independent of $\alpha$. The proof is complete. $\square$

Up to a subsequence, we assume

$$\begin{aligned} \begin{aligned}&u_\alpha \rightharpoonup u_0 \quad \text {in}\,\, H^1(\mathbb {R}^2),\\&u_\alpha \rightarrow u_0 \quad \,\,a.e.\,\text {in}\,\, \mathbb {R}^2,\\&u_\alpha \rightarrow u_0\quad \text {in}\,\, L^s(\mathbb {R}^2)\quad \text {for}\,\,s\in (2,+\infty ) \end{aligned} \end{aligned}$$

as $\alpha \rightarrow 0^+$. For any $\varphi \in C_0^\infty (\mathbb {R}^2)$, we have

$$\begin{aligned} \begin{aligned} I'_\alpha (u_\alpha )\varphi =&\int _{\mathbb {R}^2} \nabla u_\alpha \nabla \varphi \textrm{d}x +\int _{\mathbb {R}^2} u_\alpha \varphi \textrm{d}x-\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}\frac{|x-y|^{-\alpha }-1}{\alpha }u_\alpha ^2(y)\textrm{d}y u_\alpha (x)\varphi \textrm{d}x\\&-\int _{\mathbb {R}^2}f(u_\alpha )\varphi \textrm{d}x. \end{aligned} \end{aligned}$$

(4.11)

Similarly to (3.29), we have

$$\begin{aligned} \begin{aligned} \int _{\mathbb {R}^2}f(u_\alpha )\varphi \textrm{d}x\rightarrow \int _{\mathbb {R}^2}f(u_0)\varphi \textrm{d}x,\quad \text {as}\,\,\alpha \rightarrow 0^+. \end{aligned} \end{aligned}$$

(4.12)

Then it follows from Lemma 2.3 that for any fixed $\varphi \in C_0^\infty (\mathbb {R}^2)$, we have

$$\begin{aligned} \begin{aligned} \bigg |\frac{|x-y|^{-\alpha }-1}{\alpha }1_{|x-y|\le 1}u_\alpha ^2(y) u_\alpha (x)\varphi (x)\bigg | \le \bigg |\frac{1}{|x-y|}u_\alpha ^2(y) u_\alpha (x)\varphi (x)\bigg |:=h_\alpha (x,y). \end{aligned} \end{aligned}$$

(4.13)

Since $\{h_\alpha \}$ has a strongly convergent subsequence in $L^1(\mathbb {R}^4)$, we use the Lebesgue dominated convergence theorem to (4.13) to get

$$\begin{aligned}{} & {} \int \int _{|x-y|\le 1}\frac{|x-y|^{-\alpha }-1}{\alpha }u_\alpha ^2(y)\textrm{d}y u_\alpha (x)\varphi (x) \textrm{d}x\rightarrow \nonumber \\{} & {} \quad -\int \int _{|x-y|\le 1}\ln (|x-y|)u_0^2(y)\textrm{d}yu_0(x)\varphi (x) \textrm{d}x. \end{aligned}$$

(4.14)

Similarly to the proof of Theorem 1.2 in [36], by Lemma 4.4 and the Lebesgue dominated convergence theorem, one has

$$\begin{aligned}{} & {} \int \int _{|x-y|\ge 1}\frac{|x-y|^{-\alpha }-1}{\alpha }u_\alpha ^2(y)\textrm{d}y u_\alpha (x)\varphi (x) \textrm{d}x\rightarrow \nonumber \\{} & {} \quad -\int \int _{|x-y|\ge 1}\ln |x-y|u_0^2(y)\textrm{d}yu_0(x)\varphi (x) \textrm{d}x. \end{aligned}$$

(4.15)

Moreover, by Fatou’s lemma, we have

$$\begin{aligned} \begin{aligned}&\bigg |\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}\ln |x-y|u_0^2(y)\textrm{d}y u_0^2(x)\textrm{d}x\bigg |\\&\quad \le \liminf \limits _{\alpha \rightarrow 0} \bigg (\int \int _{|x-y|\le 1}G_{\alpha }(x-y)u_\alpha ^2(y)\textrm{d}y u^2_\alpha (x) \textrm{d}x-\int \int _{|x-y|\ge 1} G_{\alpha }(x-y)u_\alpha ^2(y)\textrm{d}y u^2_\alpha (x) \textrm{d}x\bigg ). \end{aligned} \end{aligned}$$

(4.16)

Using Hardy–Littlewood–Sobolev’s inequality and Lemma 2.3, we have

$$\begin{aligned} \int \int _{|x-y|\le 1}G_{\alpha }(x-y)u_\alpha ^2(y)\textrm{d}y u^2_\alpha (x) \textrm{d}x<+\infty \end{aligned}$$

(4.17)

uniformly for $\alpha$. So by Remark 3.2, we further deduce that

$$\begin{aligned} \begin{aligned}&\int \int _{|x-y|\ge 1} G_{\alpha }(x-y)u_\alpha ^2(y)\textrm{d}y u^2_\alpha (x)\textrm{d}x\\&\quad \le I_\alpha (u_\alpha )+\int \int _{|x-y|\le 1}G_{\alpha }(x-y)u_\alpha ^2(y)\textrm{d}y u^2_\alpha (x) \textrm{d}x +\int _{\mathbb {R}^2}F(u_\alpha )\textrm{d}x-\frac{1}{2}\Vert u_\alpha \Vert ^2\\&\quad < +\infty \end{aligned} \end{aligned}$$

(4.18)

uniformly for $\alpha$. Together (4.16), (4.17) with (4.18), we have

$$\begin{aligned} \bigg |\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}\ln |x-y|u_0^2(y)\textrm{d}y u_0^2(x)\textrm{d}x\bigg |<+\infty . \end{aligned}$$

(4.19)

By virtue of (4.14), (4.15) and (4.19), by taking the limit in (4.11), we have $I'(u_0)=0$ with $I(u_0)<+\infty$, that is, $u_0\in H^1(\mathbb {R}^2)$ solves equation (1.4).

We now claim that $u_0\ne 0$ and $u_\alpha \rightarrow u_0$ in $H^1(\mathbb {R}^2)$. Assume on the contrary that $u_\alpha \rightharpoonup 0$ in $H^1(\mathbb {R}^2)$, and so $u_\alpha \rightarrow 0$ in $L^s(\mathbb {R}^2)$ for $s\in (2,+\infty )$. Similarly to (3.39), we can obtain $\int _{\mathbb {R}^2}f(u_\alpha )u_\alpha \textrm{d}x=o_\alpha (1)$. So by Lemma 2.3 and Hardy–Littlewood–Sobolev’s inequality, we have

$$\begin{aligned} \begin{aligned} I'_\alpha (u_\alpha )u_\alpha&=\Vert u_\alpha \Vert ^2-\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}G_{\alpha }(x-y)u_\alpha ^2(y)u^2_\alpha (x)\textrm{d}x\textrm{d}y -\int _{\mathbb {R}^2}f(u_\alpha )u_\alpha \textrm{d}x\\&\ge \Vert u_\alpha \Vert ^2-\int \int _{|x-y|\le 1}G_{\alpha }(x-y)u_\alpha ^2(y)u^2_\alpha (x)\textrm{d}x\textrm{d}y+o_\alpha (1)\\&\ge \Vert u_\alpha \Vert ^2-\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}\frac{1}{|x-y|}u_\alpha ^2(y)u^2_\alpha (x)\textrm{d}x\textrm{d}y+o_\alpha (1)\\&\ge \Vert u_\alpha \Vert ^2-\Vert u_\alpha \Vert _{\frac{8}{3}}^4+o_\alpha (1), \end{aligned} \end{aligned}$$

which means $u_\alpha \rightarrow 0$ in $H^1(\mathbb {R}^2)$. Then according to Remark 3.2,

$$\begin{aligned} \begin{aligned} a&\le I_\alpha (u_\alpha )\\&=\frac{1}{2}\Vert u_\alpha \Vert ^2-\frac{1}{4}\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}G_{\alpha }(x-y)u_\alpha ^2(y)u^2_\alpha (x)\textrm{d}x\textrm{d}y-\int _{\mathbb {R}^2}F(u_\alpha )\textrm{d}x\\&=-\frac{1}{4}\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}G_{\alpha }(x-y)u_\alpha ^2(y)u^2_\alpha (x)\textrm{d}x\textrm{d}y+o_\alpha (1)\\&=o_\alpha (1), \end{aligned} \end{aligned}$$

which yields a contradiction and the last identity uses the Lebesgue dominated convergence theorem with Lemma 4.4. Furthermore, similarly to (4.13), (4.15), by Lemma 4.4 and the Lebesgue dominated convergence theorem, we have

$$\begin{aligned} \int _{\mathbb {R}^2}\int _{\mathbb {R}^2}\frac{|x-y|^{-\alpha }-1}{\alpha }u_\alpha ^2(y) u^2_\alpha (x)\textrm{dydx}\rightarrow -\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}\ln |x-y|u_0^2(y)u_0^2(x)\textrm{dxdy}. \end{aligned}$$

Using the similar argument as Case 2 of Lemma 3.5, we conclude that $u_\alpha \rightarrow u_0$ in $H^1(\mathbb {R}^2)$ as $\alpha \rightarrow 0^+$. $\square$