Onset of pattern formation in thin ferromagnetic films with perpendicular anisotropy

Abstract

We consider the onset of pattern formation in an ultrathin ferromagnetic film of the form $\Omega _t:= \Omega \times [0,t]$ for $\Omega \Subset \mathbb {R}^2$ with preferred perpendicular magnetization direction. The relative micromagnetic energy is given by

$$\begin{aligned} \mathcal {E}[M]= \int _{\Omega _t} d^2 |\nabla M|^2+ Q \int _{\Omega _t} (M_1^2+M_2^2) + \int _{\mathbb {R}^3} |\mathcal {H}(M)|^2 - \int _{\mathbb {R}^3} |\mathcal {H}(e_3 \chi _{\Omega _t})|^2, \end{aligned}$$

describing the energy difference for a given magnetization $M: \mathbb {R}^3 \rightarrow \mathbb {R}^3$ with $|M| = \chi _{\Omega _t}$ and the uniform magnetization $e_3 \chi _{\Omega _t}$. For $t \ll d$, we derive the scaling of the minimal energy and a BV-bound in the critical regime, where the base area of the film has size of order $|\Omega |^{{\frac{1}{2}}} \sim (Q-1)^{{-\frac{1}{2}}} d e^{\frac{2\pi d}{t} \sqrt{Q-1}}$. We furthermore investigate the onset of non-trivial pattern formation in the critical regime depending on the size of the rescaled film.

1 Introduction and statement of results

1.1 Introduction

Ferromagnetic materials are a complex class of solids which are capable of forming a wide range of spatially ordered magnetization patterns. These patterns can be tuned by e.g. changing the crystaline structure of materials or applying external fields which has lead to a variety of applications, e.g. in data storage. The observed configurations can be understood as ground states of the underlying Landau–Lifshitz energy functional [6, 18, 22]. From the perspective of this variational principle, the formation of magnetic domains—large regions with uniform magnetization—has been studied in the physical literature [25, 30, 38], see also [22] for an overview as well as the mathematical literature (e.g. [8, 11, 14, 16, 20, 26, 36]). In the last years there has been increased interest in the study of extremely thin ferromagnetic films with thickness of only a few atomic layers. In such films due to surface effects magnetization in perpendicular direction to the film plane is energetically preferred [3, 29]. One feature of these films is that they exhibit the formation of so called bubble or stripe domain patterns and that the domain size grows exponentially in terms of the inverse of the film thickness as experimental and numerical observations suggest [13, 24, 37]. In [28], these scaling laws have been rigorously confirmed in a periodic setting by minimization of energy. In this paper we continue the work in [28] by investigating a ferromagnetic film of critical size, associated with the onset of pattern formation. We confirm the above mentioned scaling laws for the case of a finite film and furthermore derive conditions for the presence and absence of non-trivial patterns, depending on the film size.

The (relative) energy associated with the magnetization ${\widetilde{M}}: \mathbb {R}^3 \rightarrow \mathbb {R}^3$ on a ferromagnetic thin film of shape $\widetilde{\Omega }_t = \widetilde{\Omega } \times [0,t]$, $\widetilde{\Omega } \Subset \mathbb {R}^2$ bounded, in a partially non-dimensionalized setting is given by

$$\begin{aligned} \mathcal {E}[{\widetilde{M}}]= \int _{\widetilde{\Omega }_t} d^2 |\nabla {\widetilde{M}}|^2+ Q \int _{\widetilde{\Omega }_t} ({\widetilde{M}}_1^2+{\widetilde{M}}_2^2) + \int _{\mathbb {R}^3} |\mathcal {H}({\widetilde{M}})|^2 - \int _{\mathbb {R}^3} |\mathcal {H}(e_3 \chi _{{\widetilde{\Omega }_t}})|^2 \end{aligned}$$

(1)

with the assumption that $|{\widetilde{M}}| = 1$ in ${\widetilde{\Omega }_t}$ and ${\widetilde{M}} = 0$ else. The first three integrals on the right hand side of (1) are the micromagnetic energy associated with the magnetization $\widetilde{M}$ [30]. The first integral is the exchange energy and reflects the preference of neighboring spins to be aligned. The second integral incorporates the crystal lattice structure of the considered material which in our case energetically prefers a direction of the magnetization normal to the film plane and is called anisotropy energy. The third integral is the magnetostatic (stray field) energy where the stray field operator $\mathcal {H}: L^2(\mathbb {R}^3;\mathbb {R}^3) \rightarrow L^2(\mathbb {R}^3;\mathbb {R}^3)$ is the projection on rotation free vector fields, i.e.

$$\begin{aligned} \mathcal {H}({\widetilde{M}}) = - \nabla \Phi , \quad \text {where}\; \Phi \in H^1(\mathbb {R}^3)\, \text {solves} \; \Delta \Phi = \textrm{div}{\widetilde{M}}. \end{aligned}$$

(2)

The last integral in (1) is the micromagnetic energy of the uniform magnetization $e_3 \chi _{\widetilde{\Omega }_t}$. Hence, $\mathcal {E}[\widetilde{M}]$ is the relative energy of the magnetization $\widetilde{M}$ w.r.t. the energy of the uniform magnetization $e_3 \chi _{\widetilde{\Omega }_t}$. The parameter d is called exchange length and the dimensionless parameter $Q > 0$ is the quality factor. The parameters in (1), generally also depend on the temperature (cf. [39]). Other contributions to the energy such as the Dzyaloshinskii–Moriya interaction are not considered (e.g. [31, 32]).

A good way to understand the magnetostatic energy is from the perspective of electrostatics: In view of (2), the magnetostatic field is created by the distributional divergence of the magnetization in the same way as the electrostatic field is created by the electric charge density. With this analogy in mind, $\textrm{div}{\widetilde{M}}$ is denoted as magnetic charge density. The absolutely continuous part $(\textrm{div}{\widetilde{M}})_{ac}$ represents volume charges; any non-zero normal component ${{\widetilde{M}} \cdot n \mathcal {H}^2_{|\partial \widetilde{\Omega }_t}}$ at the boundary $\partial \widetilde{\Omega }_t$ with outer normal n represents surface charges.

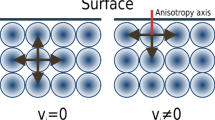
The local parts of the energy in (1), i.e. exchange and anisotropy energy, favor a uniform magnetization, at the same time a uniform magnetization leads to a high magnetostatic energy. The competition of local and nonlocal part of the energy hence leads to the formation of magnetostatic domains, i.e. extended regions of uniform magnetization which are separated by thin transition layers where the magnetization rotates rapidly (see Fig. 1). In the regime of thin films $t \ll d$ with sufficiently large lateral extension and for $Q > 1$, experimental findings [24] indicate the following scaling laws for the typical magnetic domain width and ground state energy

$$\begin{aligned} s&:= d \frac{e^{\frac{2\pi d}{t} \sqrt{Q-1}}}{\sqrt{Q-1}} \quad{} & {} \text {(scaling of typical domain width)}, \end{aligned}$$

(3)

$$\begin{aligned} \inf _{{\widetilde{M}}} \mathcal {E}[{\widetilde{M}}]&\sim d t^2 \frac{e^{\frac{2\pi d}{t} \sqrt{Q-1}}}{\sqrt{Q-1}} \quad{} & {} \text {(scaling of ground state energy).} \end{aligned}$$

(4)

For the above findings, it is assumed that the thin film is sufficiently large to allow for the formation of such domains. More precisely, the scaling laws should hold for $D \gg s$ where D is a suitable measure for the lateral extension of the ferromagnetic film, e.g. $D = |\textrm{diam}\widetilde{\Omega }|$ if $\widetilde{\Omega }$ is a disk. This suggests to consider three different regimes in dependence of the lateral size D of the film:

• (i) Supercritical regime $D \gg s$: The ferromagnetic film is large enough for magnetic domains to form and the scaling laws (3) and (4) are expected to hold.

• (ii) Subcritical regime $D \ll s$: The ferromagnetic film is too small for the formation of magnetic domains. The ground state of the system should then be attained by the uniform magnetization.

• (iii) Critical regime $D \sim s$: In this case, we expect a transition from the uniform magnetization to the emergence of non-trivial patterns. The critical regime is characterized by the situation when the rescaled set $\frac{1}{s} \widetilde{\Omega }$ has finite size.

The scaling laws (3)–(4) have been investigated numerically [13] and analytically [28] in a periodic setting with the periodicity representing the sample size. In particular, in [28, Thm. 2.6] it is shown that the scaling laws (3)–(4) hold in the supercritical regime (i). In the subcritical regime (ii), it is shown that the energy converges to a perimeter type energy [28, Thm. 2.5]. Furthermore, [28, Thm 2.7] gives a criterion for the related two-dimensional energy for the transition from the uniform states to non-trivial domain formation. In this work, we continue the investigation in [28] with an analysis of the behaviour of the system for fully three-dimensional magnetizations and at a domain size $D \sim s$ with critical scaling. The existence of lateral boundaries and related stray fields requires an adaption of some of the analysis. Before we describe our results in detail in Sect. 1.3 and give a comparision to the previous result in [28], we first non–dimensionalize our problem in Sect. 1.2.

Notation

We write $A \lesssim B$ if $A \le C B$ for some universal constant $C < \infty$. The notations $\gtrsim$ and $\sim$ are defined analogously. We write $A \ll B$ if $A/B \rightarrow 0$ in the considered limit. For two sets $E,F \subset \mathbb {R}^n$ we write $E \Subset F$ if E is compactly embedded in F. By $B_\delta (E):= \{ x \in \mathbb {R}^n: \textrm{dist}(x,E) < \delta \}$ we denote the $\delta$-neighborhood of the set E. For $\Omega \subset \mathbb {R}^n$ with non-zero interior we write $|\Omega |:= \mathcal {L}^n(\Omega )$ and $|\partial \Omega |:= \mathcal {H}^{n-1}(\partial \Omega )$. By $\chi _\Omega$ we denote the characteristic function of $\Omega$. The total variation of a function on the set $\Omega$ is written as $\Vert \nabla f\Vert _{\Omega }:= \int _\Omega |\nabla f|$. We denote points in $\mathbb {R}^3$ usually by $\overline{x} = (x,x_3) \in \mathbb {R}^3$. The magnetization $M: \mathbb {R}^3 \rightarrow \mathbb {R}^3$ is written in the form $M = (M',M_3)$. We write $M:= m \otimes \chi _{[0,t]}$ for the function $M(x,x_3) = m(x)\chi _{[0,t]}(x_3)$. For the two-dimensional Fourier transform we use the convention

$$\begin{aligned} {\widehat{f}}(\xi ) = \frac{1}{2\pi } \int _{\mathbb {R}^2} f(x) e^{-i\xi \cdot x} \, dx. \end{aligned}$$

Then Plancherel’s identity holds with prefactor 1, $\widehat{f*g} = 2\pi {\widehat{f}} {\widehat{g}}$ and $\widehat{\nabla f} = i \xi {\widehat{f}}$.

Fig. 1

Sketch of a stripe domain pattern structure in a thin ferromagnetic film

1.2 Non-dimensionalization and setting

We consider thin films where the thickness is much smaller than the exchange length, i.e. $t \ll d$, with $Q > 1$ fixed throughout the work. We rescale horizontal length scales according to the expected scaling of the domain width (3) and vertical lengths according to the film height t, i.e.

$$\begin{aligned} M(x,x_3) := \widetilde{M}(s x,t x_3) \quad \text {for}\quad (x,x_3) \in \mathbb {R}^2 \times \mathbb {R}. \end{aligned}$$

(5)

The rescaled magnetization then has support on the rescaled thin film

$$\begin{aligned} \Omega _1 := \Omega \times [0,1] \subset \mathbb {R}^3, \qquad \text {where}\; \Omega := \frac{1}{s} \widetilde{\Omega }. \end{aligned}$$

The admissible class of configurations in the rescaled setting takes the form

$$\begin{aligned} \mathcal {A}= \Big \{ M \in L^2(\mathbb {R}^3; \mathbb {R}^3) : M \in H^1(\Omega _1),\, |M| = 1\, \text {in}\, \Omega _1\, \text {and}\, M = 0\, \text {else} \Big \}. \end{aligned}$$

We note that the two local terms in the energy represent a vectorial Ginzburg–Landau type diffuse interface energy. By standard Modica–Mortola theory we expect diffuse interface layers of width of order $d/\sqrt{Q-1}$ between the magnetic domains. We hence introduce the non–dimensional parameter $\epsilon$ as the ratio between the typical width of transition layers and the typical domain width s, i.e.

$$\begin{aligned} \epsilon := {\frac{d}{s\sqrt{Q-1}}} \, {\mathop {=}\limits ^{(3)}} \, e^{- \frac{2\pi d}{t} \sqrt{Q-1}}. \end{aligned}$$

(6)

The thin film regime $t \ll d$ for $Q > 1$ then corresponds to $\epsilon \ll 1$. We rescale the energy according to the expected scaling of the ground state energy (4) and define

$$\begin{aligned} E_{\epsilon }[M] := \frac{\pi }{st^2} \mathcal {E}[\widetilde{M}] \quad \text {with}\quad M\, \text {defined by}\;(5). \end{aligned}$$

(7)

The rescaled energy can be expressed in terms of the two dimensionless parameters $\epsilon$ and Q. We suppress the dependence on Q in the notation since $Q > 1$ is assumed to be fixed. It is useful to keep the following parameter relations in mind:

Remark 1.1

(Parameter relations) We collect the relations of the dimensional parameters d, t and s in terms of the non-dimensional parameters $\epsilon \in (0,1)$ and $Q > 1$. By (6) we have $|\ln \epsilon | = \frac{2\pi d}{t} \sqrt{Q-1}$. By (3)–(6) we get $\frac{d}{s} = \epsilon \sqrt{Q-1}$. Hence,

$$\begin{aligned} \frac{d}{s} = \epsilon \sqrt{Q-1}, \quad \frac{s}{t} = \frac{|\ln \epsilon |}{2\pi (Q-1)\epsilon }, \quad \frac{d}{t} = \frac{|\ln \epsilon |}{2\pi \sqrt{Q-1}}. \end{aligned}$$

It is also convenient to introduce the aspect ratio $\omega$ by

$$\begin{aligned} \omega := \frac{t}{s} = 2\pi (Q-1) \frac{\epsilon }{|\ln \epsilon |}. \end{aligned}$$

(8)

In the considered thin film regime, variation of the magnetization in thickness direction is strongly penalized by the exchange energy. We hence expect the magnetization of low-energy configurations to be almost constant in height direction. This suggests to define a corresponding magnetization, averaged over the film height, by

(9)

In fact, for magnetizations $(m \otimes \chi _{[0,1]})(x,x_3):= m(x)\chi _{[0,1]}(x_3)$ with $m \in \overline{\mathcal {A}}$ where

$$\begin{aligned} \overline{\mathcal {A}} := \big \{ m \in L^2(\mathbb {R}^2;\mathbb {R}^3) : m \in H^1(\Omega ),\, |m| = 1\, \text {in}\, \Omega \, \text {and}\, m = 0\, \text {else} \big \} \end{aligned}$$

the rescaled energy (7) can be simplified (see Lemma 2.4) and we get

$$\begin{aligned} E_\epsilon [m \otimes \chi _{[0,1]}] = F_\epsilon [m] {+ G_\epsilon [m \otimes \chi _{[0,1]}]} \end{aligned}$$

for some remainder $G_\epsilon \ge 0$ (cf. Lemma 2.4) and with the two-dimensional energy

$$\begin{aligned} F_\epsilon [m] := L_\epsilon [m] - N[m], \end{aligned}$$

(10)

where

$$\begin{aligned} L_\epsilon [m]&:= |\ln \epsilon | \int _\Omega \frac{\epsilon }{2} |\nabla m|^2 + \frac{1}{2\epsilon } (1-m_3^2)^2 \, dx, \nonumber \\ N[m]&:= \frac{1}{8} \int \!\!\!\!\int _{\Omega \times \Omega } \frac{1}{|x-y|^3}|m_3(x) - m_3(y)|^2 \, dx dy. \end{aligned}$$

(11)

1.3 Statement of results

As discussed in the introduction, we expect that the transition from the uniform state to the formation of magnetic domains occurs in the critical regime depending on the lateral size of the rescaled film. This expectation is confirmed by our first theorem:

Theorem 1.2

(Onset of domain formation) Let $\Omega \Subset \mathbb {R}^2$ be convex. Then there is a universal constant $\epsilon _0 > 0$ such that for $\epsilon \in (0,\epsilon _0)$ we have

• (i) (Films with small diameter) If $\textrm{diam}\Omega < {\frac{4}{\pi e} (1 - \frac{4}{|\ln \epsilon |}})$, then

  $$\begin{aligned} \inf _{M \in \mathcal {A}, M = \overline{M}} E_\epsilon [M] = 0. \end{aligned}$$

  (12)

  Furthermore, the only two minimizers in (12) are given by $M = \pm e_3 \chi _{\Omega _1}$.

• (ii) (Minimal energy for large films) There are universal constants $0< c, C, R < \infty$ such that for $\Omega ^{(R)}:= \{ x \in \Omega : \textrm{dist}(x,\Omega ^c) \ge R \}$ we have

  $$\begin{aligned} - \frac{1}{ 2}\pi ^2 e |\Omega | {- C |\partial \Omega |} \le \inf _{M \in \mathcal {A}} E_\epsilon [M] \le - c |\Omega ^{(R)}|. \end{aligned}$$

Theorem 1.2 characterizes the onset of domain formation in dependence of the size $\textrm{diam}\Omega$ of the rescaled ferromagnetic film. In particular, statement (i) shows that for samples where the rescaled film has a small diameter, the energy is minimized by the uniform magnetization in the class of magnetizations which are constant in thickness direction of the film. We note that magnetizations of the form $M = \pm \chi _{\Omega _t} e_3$ are critical points of $E_\epsilon [m]$ within this class of configurations for any $\Omega \subset \mathbb {R}^2$ and any $\epsilon > 0$ (see Lemma 2.7). For general magnetizations a related estimate holds true up to a small error (see Lemma 2.6).

Statement (ii) shows that the uniform magnetization is not optimal if the rescaled film size is sufficiently large such that $|\Omega ^{(R)}| \ne 0$. Furthermore, this statement confirms the scaling law (4) for the ground state energy, formulated in the rescaled variables if the film is sufficiently regular in the sense that $|\Omega | \sim |\Omega ^{(R)}|$. We note that the ground state energy is negative since (1) is the relative energy w.r.t. the energy of the uniform magnetization.

The next theorem is concerned with the average size of the ferromagnetic domains in terms of the rescaled variables. These statements are formulated in terms of the total interfacial length $\Vert \nabla \overline{M}_3\Vert _{\Omega _1}$ between the domains with the understanding that $|\Omega |/\Vert \nabla \overline{M}_3\Vert _{\Omega _1}$ is a measure for the typical domain width:

Theorem 1.3

(BV bounds and compactness) With the assumptions of Theorem 1.2 and with the averaged magnetization $\overline{M}$ defined in (9) we have

• (i) (BV estimate)

  $$\begin{aligned} \left| \ln \left( \frac{\Vert \nabla \overline{M}_3\Vert _{\Omega _1}}{\pi ^2 e^2|\Omega |} \right) \right| \Vert \nabla \overline{M}_3\Vert _{\Omega _1} \le E_\epsilon [\overline{M}] + \frac{\pi ^2 e }{ 2} |\Omega | \quad \forall M \in \mathcal {A}. \end{aligned}$$

• (ii) (BV estimate for low energy configurations) For any $\alpha > 0$ there are constants $c_\alpha , C_\alpha > 0$ such that for any $M \in \mathcal {A}$ with $E_\epsilon [M] < - \alpha |\Omega |$ we have

  $$\begin{aligned} c_\alpha |\Omega | \le \Vert \nabla \overline{M}_3\Vert _{\Omega _1} \le C_\alpha |\Omega |. \end{aligned}$$

• (iii) (Compactness) For any family $M_\epsilon \in \mathcal {A}$ with $\limsup _{\epsilon \rightarrow 0} E_\epsilon [M_\epsilon ] < \infty$ there is $m \in BV(\mathbb {R}^2, \pm e_1)$ with $|M| = 1$ in $\Omega$ and $M = 0$ else such that for a subsequence $\epsilon \rightarrow 0$ and with $(m \otimes \chi _{[0,1]})(x,x_3):= m(x)\chi _{[0,1]}(x_3)$ we have

  $$\begin{aligned} M_\epsilon \rightarrow m \otimes \chi _{[0,1]} \quad \text {in}\; L^1(\Omega _1). \end{aligned}$$

Statement (i) provides a sharp bound for the BV-norm in terms of the energy. Statement (ii) shows that for configurations with small relative energy the total length of the interfaces is of order 1 which thus gives a rigorous justification for the scaling law (3). Finally, (iii) gives a corresponding compactness result which is a direct consequence of the BV-bounds. The statements are formulated in terms of the size of the rescaled film and give a precise understanding of the system near the transition between trivial and non–trivial states.

For the corresponding two-dimensional energy [cf (10)], an analogous criterion to Theorem 1.2(i) for the transition from the uniform states to the non–trivial domain formation has been given in [28, Thm 2.7] in the periodic setting. We extend this statement to the full three-dimensional model and also give an estimate for the precise constant for the phase transition. We also extend the estimate of the scaling of the ground state energy to the critical regime in Theorem 1.2(ii). Similarly, the compactness statement Theorem 1.3 is an extension of Theorem [28, Thm 2.7] to the three-dimensional energy $E_\epsilon$ and to the case of a finite domain. The two estimates on the BV-norm in terms of the domain size are new estimates for the finite domain case.

Without the nonlocal term, by standard Modica–Mortola theory, the first two terms on the right hand side of (10) would $\Gamma$-converge to the BV norm of $m_3$. The second term is nonlocal and is the homogeneous $H^{\frac{1}{2}}$-norm of $m_3$. Note that the BV-norm has the same scaling as the $H^{\frac{1}{2}}$-norm which is a major difficulty in the proof of the results and which explains the appearance of logarithms in Theorem 1.3. In the proof we will show that the leading order contributions of these two terms cancel in the limit $\epsilon \rightarrow 0$ and that the bound on the ground state energy is derived from the remaining term. We use similar arguments as in [28], some arguments, however, have to be adjusted: For the stray field estimates we partially rely on kernel estimates instead of Fourier estimates for the stray field equation. In the proof of Lemma 2.5, we need the assumption that the domain is convex to get the optimal leading order constant. In fact, for general domains the minimal energy can get negative and its lower bound cannot be controlled solely by the area of the domain even if the curvature of the domain boundary is uniformly bounded as illustrated in Fig. 2.

Fig. 2

For thin films $\Omega _\alpha \times [0,1]$ with nonconvex footprint $\Omega _\alpha \subset \mathbb {R}^2$ as illustrated, there are magnetizations with $E_\epsilon [m_\alpha ] \rightarrow - \infty$ for any fixed $\epsilon$ as $\alpha \rightarrow 0$, while the total area and the maximal curvature of the boundary stay approximately constant

Other related models Sharp interface versions of the energy (1) have been considered by different authors. In these models, compared to the energy (10), the local part of the energy is replaced by the perimeter term. At the same time, the $H^{\frac{1}{2}}$-norm is replaced by a regularized version of this norm with an $\epsilon$-dependent high frequency cut–off. This is reminiscent of the results of Bourgain et al. [5] and Dávila [15] which show the convergence of a class of nonlocal perimeter functionals towards the BV-norm. For a two-dimensional model of this, Muratov and Simon [35] have shown a $\Gamma$-convergence result, among other results. For a different approximation of the nonlocal term, a corresponding $\Gamma$-convergence result has been given by Cesaroni and Novaga [7]. A corresponding $\Gamma$-convergence result in arbitrary dimensions and for a more general class of approximations of the nonlocal energy has been shown in [27] by Shi and the second author. These results can be seen as second order extensions of the result in [15]. In these papers, there is a frequency cut-off for the nonlocal energy at high frequencies. The arguments in these papers strongly rely on the sharp interface structure of the considered models and this high frequency cut-off. The arguments hence cannot be used for our model. We also note that thin-film micromagnetics models in the case when the magnetization is assumed to be in-plane have been considered in different works such as [16, 17]. In these models, the main contribution of the nonlocal energy is due to in-plane divergence of the magnetization whereas in our case the main contribution is created by the out-of plane component of the magnetization. We also note the upcoming paper [19].

More generally, pattern formation has also been investigated in related models which include a competition between a local isoperimetric term and an opposing nonlocal term such as e.g. the Ohta–Kawasaki energy [1, 2, 9, 10, 21], liquid drop models [12, 23, 33], Ginzburg–Landau with dipolar interaction [34] or elastic materials (these references are certainly not complete). The methods used are typically specific for the model at hand. In particular, in the above models the nonlocal term does not have the same scaling as the perimeter contrary to the problem considered here.

2 Proofs

2.1 Dimensional reduction

In this section, we show that the two-dimensional energy (10) is a good approximation for the initial energy in the considered regime of thin films. Due to the specific geometry of our sample, it is useful to differentiate between directions within the film plane and normal directions. We hence consistently write $(x,x_3) \in \mathbb {R}^2 \times \mathbb {R}$ for points in $\mathbb {R}^3$. We first note that the stray field operator (2) is the orthogonal projection onto gradient fields:

Lemma 2.1

(Stray field) For any $M \in L^2(\mathbb {R}^3; \mathbb {R}^3)$ we have

$$\begin{aligned} \mathcal {H}(M)(x,x_3) = \nabla {(K * \textrm{div}M)(x,x_3)} \end{aligned}$$

(13)

for the stray field operator $\mathcal {H}: L^2(\mathbb {R}^3; \mathbb {R}^3) \rightarrow L^2(\mathbb {R}^3; \mathbb {R}^3)$, defined in (2), where the kernel $K: \mathbb {R}^3 \rightarrow \mathbb {R}$ and its Fourier transform in x are given by

$$\begin{aligned} K(x,x_3) := \frac{1}{4\pi \sqrt{|x|^2 + x_3^2}}, \quad {\widehat{K}} (\xi ,x_3) = \frac{1}{4\pi |\xi |} e^{-|x_3| |\xi |}. \end{aligned}$$

(14)

Furthermore, $\mathcal {H}$ is linear, ${\mathcal {H}\circ \mathcal {H}= \mathcal {H}}$ and

• (i) $\displaystyle \int _{\mathbb {R}^3} \mathcal {H}[M] \cdot \big ( \mathcal {H}[\widetilde{M}] - \widetilde{M} \big ) = 0\quad \forall \widetilde{M} \in H^1(\mathbb {R}^3; \mathbb {R}^3).$

• (ii) $\displaystyle \int _{\mathbb {R}^3} |\mathcal {H}[M]|^2$ $\displaystyle \le \int _{\mathbb {R}^3} |M|^2$.

Proof

The kernel K is just the Newton kernel in $\mathbb {R}^3$ which justifies (13). A standard integral formula [40, eq 6.554.1] then yields

$$\begin{aligned} {\widehat{K}}(\xi ) = \frac{1}{2\pi } \int _{\mathbb {R}^2} \frac{e^{-i\xi \cdot x}}{4\pi \sqrt{|x|^2 + x_3^2}} \, dx = \int _0^\infty \frac{J_0(|\xi | r)}{4\pi \sqrt{r^2 + x_3^2}} \, r\,dr = \frac{1}{4\pi } \frac{1}{|\xi |} e^{-|x_3| |\xi |}, \end{aligned}$$

where $J_0$ is the Bessel function of first kind. Multiple integration by parts yields

$$\begin{aligned} \int _{\mathbb {R}^3} \mathcal {H}(M) \cdot \mathcal {H}(\widetilde{M}) = - \int _{\mathbb {R}^3} {\Phi } \cdot \Delta {\widetilde{\Phi }} = \int _{\mathbb {R}^3} {\Phi } \cdot \textrm{div}\widetilde{M} = \int _{\mathbb {R}^3} \mathcal {H}(M) \cdot \widetilde{M}, \end{aligned}$$

where $\Phi$ and $\widetilde{\Phi }$ are the stray field potentials associated with M, $\widetilde{M}$ as defined in (2). Estimate (ii) follows from (i) and an application of Cauchy–Schwarz. $\square$

The following result is an adaptation of [28, Theorem 5.2] to the case of finite films. The different geometry requires some adaptions to the proof due to the possibility of surface charges at the lateral boundary. This is reflected on the right hand side of (15) which incorporates the lateral sample boundary $\partial \Omega \times [0,t]$.

Theorem 2.2

(Reduction of stray field) Let $\widetilde{\Omega } \Subset \mathbb {R}^2$ with finite perimeter and let $\widetilde{\Omega }_t:= \widetilde{\Omega } \times [0,t]$. Let $M = (M',M_3) \in \mathcal {A}$ and let $\overline{M}$ be given by (9). Then

$$\begin{aligned} \left| \int _{ \mathbb {R}^3} |\mathcal {H}[M]|^2 \, dx - \int _{ \mathbb {R}^3} |\mathcal {H}[\overline{M}]|^2 \, dx \right| \le 3 t^2 \int _{\widetilde{\Omega }_t}|\nabla M|^2 \, dx + t |B_{t}(\partial \widetilde{\Omega }) \cap \widetilde{\Omega }|. \end{aligned}$$

(15)

Proof

Let I be the left hand side of (15). We write $M = \overline{M} + U$. Since $\mathcal {H}$ is a linear operator and applying Lemma 2.1 we have

$$\begin{aligned} {I} \le \int _{\mathbb {R}^3} |\mathcal {H}(U)|^2 + 2 \left| \int _{\widetilde{\Omega }_t} \mathcal {H}(\overline{M}) \cdot \mathcal {H}(U) \right| \le \int _{\widetilde{\Omega }_t} |U|^2 + 2 \left| \int _{\widetilde{\Omega }_t} \mathcal {H}(\overline{M}) \cdot U \right| . \end{aligned}$$

(16)

Since $\overline{U} = 0$, Poincaré’s inequality yields

$$\begin{aligned} \int _{\widetilde{\Omega }_t} |U|^2 \le t^2 \int _{\widetilde{\Omega }_t} |\partial _3 M|^2. \end{aligned}$$

For $\delta > 0$, we choose a cut-off function $\zeta _\delta \in H^1(\mathbb {R}^2)$ by $\zeta _\delta (x) := \min \{ 1, \frac{1}{\delta } \textrm{dist}(x,\partial \widetilde{\Omega }) \}$ for $x \in \widetilde{\Omega }$ and $\zeta _\delta = 0$ else. Then we have $0 \le \zeta _\delta \le 1$, $\zeta _\delta = 0$ in $\widetilde{\Omega }^c$ and $\zeta = 1$ in $\widetilde{\Omega } \backslash {\widetilde{\Gamma }_\delta }$ where ${\widetilde{\Gamma }_\delta }:= B_{\delta }(\partial \widetilde{\Omega }) \cap \widetilde{\Omega }$. We define $M_\delta := m_\delta \otimes \chi _{[0,t]}$ where $m_\delta (x) := \zeta _\delta (x) \overline{M}(x,\frac{1}{2})$. With the notation $\overline{\mathcal {H}}:= \mathcal {H}(\overline{M})$ and $\mathcal {H}_\delta := \mathcal {H}(M_\delta )$ we then have

$$\begin{aligned} I {\mathop {\le }\limits ^{(16)}} \int _{\widetilde{\Omega }_t} |U|^2 + 2 \int _{\widetilde{\Omega }_t} |(\overline{\mathcal {H}}- \mathcal {H}_\delta ) \cdot U| + 2 \left| \int _{\widetilde{\Omega }_t} \mathcal {H}_\delta \cdot U \right| . \end{aligned}$$

Since U has a vanishing average, i.e. $\overline{U} = 0$ and $M_\delta = \overline{M}_\delta$ we also have

$$\begin{aligned} \int _{\widetilde{\Omega }_t } \mathcal {H}_\delta \cdot U = \int _{\widetilde{\Omega }_t} (\mathcal {H}_\delta - M_{\delta ,3} e_3) \cdot U. \end{aligned}$$

By an application of Cauchy–Schwarz we hence arrive at

$$\begin{aligned} I \le 3 \int _{\widetilde{\Omega }_t} |U|^2 + \int _{\widetilde{\Omega }_t} |\overline{\mathcal {H}}- \mathcal {H}_\delta |^2 + \int _{\widetilde{\Omega }_t} |\mathcal {H}_\delta - M_{\delta ,3} e_3|^2. \end{aligned}$$

(17)

By Lemma 2.1, Jensen’s inequality and with the choice $\delta := t$ we get

$$\begin{aligned} \int _{\widetilde{\Omega }_t} |{\mathcal {H}_\delta } - {\overline{\mathcal {H}}}|^2&\le \int _{\widetilde{\Omega }_t} |M_\delta - \overline{M}|^2 \le \delta |{\widetilde{\Gamma }_\delta }| = t |{\widetilde{\Gamma }_\delta }|, \end{aligned}$$

(18)

$$\begin{aligned} t^2 \int _{\widetilde{\Omega }_t} |\nabla ' M_\delta |^2&\le t^2 \left( \frac{t|{\widetilde{\Gamma }_\delta }|}{{t^2}} + \int _{\widetilde{\Omega }_t} |\nabla ' \overline{M}|^2 \right) = t |{\widetilde{\Gamma }_\delta }| + t^2 \int _{\widetilde{\Omega }_t} |\nabla ' M|^2. \end{aligned}$$

(19)

By the stray field formula from Lemma 2.1 we have

$$\begin{aligned} \mathcal {H}_\delta = \nabla \int _{\mathbb {R}^2} \left( \int _0^t K(x-{y},x_3-{z}) \, d{z} \right) (\nabla ' \cdot m_\delta '({y}) + \partial _3 m_{\delta ,3}({y})) \, d{y}. \end{aligned}$$

We apply the Fourier transform in x. Also integrating by parts we then get

$$\begin{aligned} \widehat{\mathcal {H}'_\delta }&= {2\pi } \int _0^t \widehat{K}(\xi ,x_3-{z}) d{z} \, {\xi (\xi \cdot \widehat{m_{\delta }'}(\xi ))} - {2\pi } \int _0^t \partial _3 \widehat{K}(\xi ,x_3-{z}) d{z} \, {i \xi \widehat{m_{\delta ,3}}(\xi )}, \\ \widehat{\mathcal {H}_{\delta ,3}}&= - {2\pi } \int _0^t \partial _3 \widehat{K}(\xi ,x_3-{z}) d{z} \, {i \xi \cdot \widehat{m_{\delta }'}(\xi )} + {2\pi } \int _0^t \partial _3^2 \widehat{K}(\xi ,x_3-{z}) d{z} \, \widehat{m_{\delta ,3}}(\xi ). \end{aligned}$$

The antiderivative and derivative of ${{\widehat{K}}} = \frac{1}{4\pi |\xi |} e^{-|\xi ||x_3|}$ in $x_3$ are given by

$$\begin{aligned} \int {{\widehat{K}}} dx_3 = \frac{\textrm{sign}x_3}{4\pi |\xi |^2} ( 1 - e^{-|\xi | |x_3|}) + c \quad \text {and} \quad \partial _3 {{\widehat{K}}} = -\frac{\textrm{sign}x_3}{4\pi } e^{-|\xi | |x_3|}. \end{aligned}$$

(20)

Using (20) the Fourier multipliers associated with $\mathcal {H}_d - M_\delta e_3$ are given by

$$\begin{aligned} \mu _1(\xi ,x_3)&:= {2}\pi |\xi |^2 \int _0^t \widehat{K}(\xi ,x_3-{z}) \, d{z} = \frac{1}{2} \big ( e^{-|\xi | (t - x_3)} + e^{-|\xi | x_3} - 2 \big ), \\ \mu _2(\xi ,x_3)&:= - {2}\pi |\xi | \int _0^t \partial _3 {\widehat{K}}(\xi ,x_3-{z}) \, d{z} = \frac{1}{2} \big ( e^{-|\xi | x_3} - e^{-|\xi | (t-x_3)} \big ), \\ \mu _3(\xi ,x_3)&:= {2}\pi \int _0^t \partial _3^2 {\widehat{K}} (\xi ,x_3-{z}) \, d{z} {-1} = \frac{1}{2} \big ( e^{-|\xi | (t-x_3)} + e^{-|\xi | x_3} \big ) {-1} \end{aligned}$$

for $x_3 \in (0,t)$. Hence, for $x_3 \in (0,t)$ we have

$$\begin{aligned} \widehat{\mathcal {H}'_\delta }(\xi ,x_3)&= \tfrac{\xi }{|\xi |} (\tfrac{\xi }{|\xi |} \cdot \widehat{m_{\delta }'}(\xi )) \mu _1(\xi ,x_3) + i \tfrac{\xi }{|\xi |} \widehat{m_{\delta ,3}}(\xi ) \mu _2(\xi ,x_3), \\ (\widehat{\mathcal {H}_{\delta ,3}} - {\widehat{M}}_{\delta ,3})(\xi ,x_3)&= i \tfrac{\xi }{|\xi |} \cdot \widehat{m_{\delta }'}(\xi ) \mu _2(\xi ,x_3) + \widehat{m_{\delta ,3}}(\xi ) \mu _3(\xi ,x_3). \end{aligned}$$

By Taylor expansion we have $|{\mu _i(\xi ,x_3)}| \le |\xi | t$ for $i=1,2,3$ and $|x_3| \le t$. Plancherel’s identity hence yields

$$\begin{aligned} \int _{\widetilde{\Omega }_t} |\mathcal {H}_\delta - M_{\delta ,3} e_3|^2 \le \sum _{i=1}^3 \int _0^t \int _{\mathbb {R}^2} |\mu _i|^2 |\widehat{m_\delta }(\xi )|^2 \, d\xi dx_3 \le 3 t^2 \int _0^t \int _{\mathbb {R}^2} |\xi |^2 |\widehat{m_\delta }(\xi )|^2 \, d\xi dx_3. \end{aligned}$$

Since $m_\delta = 0$ on $\partial \widetilde{\Omega }$ we have $m_\delta \in H^1(\mathbb {R}^2;\mathbb {R}^3)$ and

$$\begin{aligned} \int _0^t \int _{\mathbb {R}^2} |\xi |^2 |\widehat{{m_{\delta }}}|^2 \, d\xi dx_3 = \int _0^t \int _{\mathbb {R}^2} |\nabla ' {m_{\delta }}|^2\, dx dx_3 = \int _{\widetilde{\Omega }_t} |\nabla ' {M_{\delta }}|^2 \, dx dx_3. \end{aligned}$$

(21)

The proof is concluded by combining (17), (18), (19) and (21). $\square$

We next state the kernels for the stray field in thin-films (see also [20]).

Theorem 2.3

(Representation of stray field) Let $M = (M',M_3) \in H^1(\mathbb {R}^3;\mathbb {R}^3)$ with $\textrm{spt}M \subset \mathbb {R}^2 \times [0,t]$ and let $\overline{M}$ be given by (9). Then

$$\begin{aligned} \displaystyle \int _{ \mathbb {R}^3} |\mathcal {H}[\overline{M}]|^2 \, dx = \int _{ \mathbb {R}^3} |\mathcal {H}[\overline{M_3}e_3]|^2\, dx + \int _{ \mathbb {R}^3} |\mathcal {H}[\overline{M'}]|^2 \, dx. \end{aligned}$$

(22)

Furthermore, we have the representations

$$\begin{aligned} \int _{\mathbb {R}^3} |\mathcal {H}[\overline{M_3}e_3]|^2 \, dx&= t \int _{\mathbb {R}^2} {\overline{M}_3}^2 \, dx - \frac{t^2}{8\pi } \int \!\!\!\!\int _{\mathbb {R}^4} \Gamma \left( \tfrac{1}{t} |x-x'|\right) \frac{|{\overline{M}_3}(x) - {\overline{M}_3}(x')|^2}{|x-x'|^3} \, dx dx' \nonumber \\ \int _{\mathbb {R}^3} |\mathcal {H}[\overline{M'}]|^2 \, dx&= \frac{t^2}{4\pi } \int \!\!\!\!\int _{\mathbb {R}^4} \Theta \left( \tfrac{1}{t} |x-x'|\right) \frac{\textrm{div}\overline{M}'(x) \textrm{div}\overline{M}'(x')}{|x-x'|} \, dx dx', \end{aligned}$$

(23)

where the monotonically increasing functions $\Gamma$, $\Theta : [0,\infty ) \rightarrow \mathbb {R}$ are given by

$$\begin{aligned} \Gamma (\alpha ) := 2 \alpha ^2 \left( 1 - \frac{\alpha }{\sqrt{1+ \alpha ^2}} \right) , \quad \Theta (\alpha ) := 2 \left( \alpha \textrm{arsinh}\left( \frac{1}{\alpha }\right) + \alpha ^2 - {\alpha }\sqrt{1 + \alpha ^2} \right) . \end{aligned}$$

(24)

In particular, $\Gamma (0) = \Theta (0) = 0$ and $\Gamma (\alpha ), \Theta (\alpha ) \rightarrow 1$ for $\alpha \rightarrow \infty$ and $1 - \Gamma (\alpha ) \le \frac{C}{\alpha ^2}$.

Proof

To prove (22) we write $\overline{M} = \overline{M_3}e_3 + \overline{M'}$ and expand the expression $\mathcal {H}(\overline{M_3}e_3 + \overline{M'})$. The assertion then follows from

$$\begin{aligned} \int _{\mathbb {R}^3} \mathcal {H}(\overline{M_3} e_3) \cdot \mathcal {H}(\overline{M}') \, dx = 0. \end{aligned}$$

(25)

The identity (25) holds in view of the following symmetries: The surface charge density $\partial _3 \overline{M_3}$ is antisymmetric w.r.t. the plane $\{ x_3 = \frac{t}{2} \}$, while the charge density $\nabla ' \overline{M'}$ is symmetric w.r.t. the same plane. These symmetry properties carry over to the created stray fields.

The proof of the representation formulas is based on the real space representation (26) of the stray field in Lemma 2.1. In particular, we have

$$\begin{aligned} \int _{\mathbb {R}^3}|\mathcal {H}[\overline{M}]|^2\, dx = \int \!\!\!\!\int _{\mathbb {R}^6} K(x-x',x_3-{z}) \textrm{div}\overline{M}(x) \textrm{div}\overline{M}(x') \, dx_3 d{z} dx dx'. \end{aligned}$$

(26)

We apply this formula separately for $M_3 e_3$ and $M'$. Integrating by parts two times in $x_3$ in the formula (26) yields

$$\begin{aligned} \int _{\mathbb {R}^3} |\mathcal {H}[\overline{M_3}e_3]|^2 \, dx&= \int \!\!\!\!\int _{\mathbb {R}^4} \left( \int \!\!\!\!\int _{[0,t]^2} \partial _3^2 K(x-x',x_3-{z}) dx_3 d{z} \right) {\overline{M}_3}(x) {\overline{M}_3}(x') \, dx dx' \nonumber \\&=: \int \!\!\!\!\int _{\mathbb {R}^4} G_t(x-x') {\overline{M}_3}(x) {\overline{M}_3}(x') \, dx dx', \end{aligned}$$

(27)

where

$$\begin{aligned} G_t(x)&= \int _0^t \Big [ \partial _3 K(x,x_3-{z}) \Big ]_{x_3=0}^{x_3=t} \, d{z} = 2 \big ( K(x,0) - K(x,t) \big ) \\&{}{\mathop {=}\limits ^{(14)}} \frac{1}{2\pi |x|} \left( 1 - \frac{1}{\sqrt{1+ \left( \frac{t}{|x|}\right) ^2}} \right) {\mathop {=}\limits ^{(24)}} \frac{t^2}{4\pi |x|^3} \Gamma \left( \frac{|x|}{t}\right) . \end{aligned}$$

We write the right hand side of (27) as a difference operator, i.e.

$$\begin{aligned} \int _{\mathbb {R}^3} |\mathcal {H}[\overline{M_3}e_3]|^2 dx = \int \!\!\!\!\int _{\mathbb {R}^4} \left( G_t(x-x') |{\overline{M}_3}(x)|^2 - \frac{1}{2} G_t(x-x') |{\overline{M}_3}(x) - {\overline{M}_3}(x')|^2 \right) . \end{aligned}$$

The proof of the first assertion is concluded by an application of Fubini and with

$$\begin{aligned} \int _{\mathbb {R}^2} G_t({x}) \, d{x} = \int _0^\infty 1 - \frac{\rho }{\sqrt{t^2 + \rho ^2}} \, d\rho = \left[ \rho - \sqrt{t^2 + \rho ^2} \right] _0^\infty = t. \end{aligned}$$

For the proof of the second identity we note that for

$$\begin{aligned} \Psi (x,x_3) := {\frac{|x|}{4\pi } \left( \frac{x_3}{|x|}\textrm{arsinh}\left( \frac{x_3}{x}\right) - \left( 1 + \frac{x_3^2}{|x|^2}\right) ^{1/2}\right) }, \end{aligned}$$

we have $\partial _3 \Psi (x,x_3) = - \frac{1}{4\pi }\textrm{arsinh}\left( \frac{x_3}{|x|}\right)$ and $\partial _3^2 \Psi (x,x_3) = K(x,x_3)$. Hence, analogously to the calculation before, we compute

$$\begin{aligned} \int \!\!\!\!\int _{[0,t]^2} K(x,x_3-x_3') \, dx_3dx_3'&= 2 \Big [ \Psi (x,{t}) - \Psi (x,{0}) \Big ] \\&= \frac{|x|}{2\pi } \left[ \frac{t}{|x|} \textrm{arsinh}\left( \frac{t}{|x|}\right) + 1 - \sqrt{1 + \frac{t^2}{|x|^2}} \right] \\&= \frac{t^2}{4\pi |x|} \Theta \left( \frac{|x|}{t}\right) . \end{aligned}$$

A straightforward calculation shows that both $\Gamma$ and $\Theta$ are monotonically increasing with $\Gamma (0) = \Theta (0)= 0$ and $\Gamma (s), \Theta (s) \rightarrow 1$ for $s \rightarrow \infty$ and that the estimate $1 - \Gamma (\alpha ) \le C/\alpha ^2$ holds. $\square$

Combining the previous formulas for the stray field we obtain an asymptotic representation of the energy:

Lemma 2.4

(Representation for $E_\epsilon$) Let $\Omega \Subset \mathbb {R}^2$ be a set of finite perimeter. Let $M = (M',M_3) \in \mathcal {A}$ and let $\overline{M} = m \otimes \chi _{[0,1]}$ be given by (9). Then

$$\begin{aligned} E_\epsilon [M] = {F_\epsilon [m] + G_\epsilon [M] + \gamma _0 R_\epsilon [M],} \end{aligned}$$

(28)

where $F_\epsilon$ is defined in (10) and $G_\epsilon [M] \ge 0$ is given by

$$\begin{aligned} G_\epsilon [M]&:= \epsilon |\ln \epsilon | \int _{\Omega _1} \Big ( |\nabla ' M|^2 - |\nabla ' \overline{M}|^2 \Big ) + \frac{|\ln \epsilon |^3}{\epsilon (Q-1)^2(2\pi )^2}\int _{\Omega _1}|\partial _3 M|^2 \\&\quad + \frac{1}{8} \int \!\!\!\!\int _{\Omega \times \Omega } \left( 1- \Gamma (\tfrac{1}{\omega }|x-x'|)\right) \frac{|m_3(x) - m_3(x')|^2}{|x-x'|^3} \, dx d x' \\&\quad + \frac{1}{4} \int \!\!\!\!\int _{\Omega ^c \times \Omega } \Gamma \left( \tfrac{1}{\omega }|x-x'|\right) \frac{1 - m_3(x')^2}{|x-x'|^3} \, dx d x' \\&\quad + \frac{1}{4} \int \!\!\!\!\int _{{\mathbb {R}^2 \times \mathbb {R}^2}} \Theta \left( \tfrac{1}{\omega }|x-x'|\right) \textrm{div}m'(x) \textrm{div}m'(x') \, dx dx'. \end{aligned}$$

Finally, the remainder term is estimated by

$$\begin{aligned} {|R_\epsilon [M]| \le \frac{6 \pi ^2 (Q-1) \epsilon }{|\ln \epsilon |} \Vert \nabla ' M\Vert _{L^2({\Omega _1})}^2 + \frac{3 |\ln \epsilon |}{2(Q-1)\epsilon } \big ( \Vert \partial _3 M\Vert _{L^2({\Omega _1})}^2 + |B_{\omega }(\partial \Omega ) \cap \Omega | \big )} \end{aligned}$$

and the parameter $\gamma _0$ is defined by

$$\begin{aligned} {\gamma _0 := 1 \quad \text {if}\, M \ne \overline{M} \quad \text {and}\quad \gamma _0 := 0 \quad \text {else.}} \end{aligned}$$

(29)

Proof

Let $\widetilde{\Omega } = s \Omega$, $\widetilde{\Omega }_t:= \widetilde{\Omega } \times [0,t]$ and $\widetilde{M}(sx,tx_3):= M(x,t)$. By Theorem 2.2 and Theorem 2.3 we have

$$\begin{aligned}&\left| \int _{ \mathbb {R}^3} |\mathcal {H}[\widetilde{M}]|^2 \!-\! \int _{ \mathbb {R}^3} |\mathcal {H}[\overline{\widetilde{M}_3}e_3]|^2 \!-\! \int _{ \mathbb {R}^3} |\mathcal {H}[\overline{\widetilde{M}'}]|^2 \right| \!\le \! \gamma _0 \left( 3 t^2 \int _{\widetilde{\Omega }_t}|\nabla \widetilde{M}|^2 + t |B_{t}(\partial \widetilde{\Omega }) \cap \Omega | \right) , \end{aligned}$$

where $\gamma _0$ is defined in (29). Using Theorem 2.3, we note that

$$\begin{aligned}&\int \!\!\!\!\int _{\mathbb {R}^2 \times \mathbb {R}^2} |\mathcal {H}(\widetilde{M}_3 e_3)|^2 - \int \!\!\!\!\int _{\mathbb {R}^2 \times \mathbb {R}^2} |\mathcal {H}(\chi _{\widetilde{\Omega }} e_3)|^2 \\&\quad {\mathop {=}\limits ^{(23)}} t \int _{\widetilde{\Omega }} (\widetilde{M}_3^2 - 1) {-} \frac{t^2}{8\pi } \int \!\!\!\!\int _{\mathbb {R}^4} \Gamma \left( \tfrac{1}{t} |x-x'|\right) \frac{|{\overline{M}_3}(x) - {\overline{M}_3}(x')|^2 - |\chi _{\widetilde{\Omega }}(x) - \chi _{\widetilde{\Omega }}(x')|^2}{|x-x'|^3}\\&\quad = - t \int _{\widetilde{\Omega }} (1 - \widetilde{M}_3^2) {-} \frac{t^2}{8\pi } \int \!\!\!\!\int _{\widetilde{\Omega } \times \widetilde{\Omega }} \Gamma \left( \tfrac{1}{t} |x-x'|\right) \frac{|{\overline{M}_3}(x) - {\overline{M}_3}(x')|^2}{|x-x'|^3} \\&\qquad + \frac{t^2}{4\pi } \int \!\!\!\!\int _{\widetilde{\Omega } \times \widetilde{\Omega }^c} \Gamma \left( \tfrac{1}{t} |x-x'|\right) \frac{1 - {\overline{M}_3}(x)^2}{|x-x'|^3}. \end{aligned}$$

We similarly use Theorem 2.3 for the stray field term related to tangential charges.

We also rescale length and use the notations from the statement of the lemma. We also use the fact that $|m| = \chi _\Omega$. With $\Omega _1:= \Omega \times [0,1]$ we then obtain

$$\begin{aligned} {|\mathcal {E}[\widetilde{M}] - \mathcal {F}[m] - \mathcal {G}[\widetilde{M}]| \le 3 \gamma _0 \left( t^3 \int _{\Omega _1} |\nabla ' M|^2 + t s^2 \int _{\Omega _1} |\partial _3 M|^2 + t s^2 |B_{\omega }(\partial \Omega ) \cap \Omega | \right) .} \end{aligned}$$

where with $(..):= (\tfrac{s}{t} |x-x'|)$ we have

$$\begin{aligned} \mathcal {F}[m]&:= \int _{\Omega } t d^2 |\nabla m|^2 + s^2 t(Q-1) (1- m_3^2) \, dx - \frac{s t^2}{8\pi } \int \!\!\!\!\int _{\Omega \times \Omega } \Gamma (..) \frac{|m_3(x) - m_3(x')|^2}{|x-x'|^3} \\ \mathcal {G}[M]&:= t d^2 \left( \int _{\Omega _1} |\nabla ' M|^2 - |\nabla \overline{M}|^2 \right) + \frac{s^2 d^2}{t} \int _{\Omega _1} |\partial _3 M|^2 \\&\quad + \frac{s t^2}{4\pi } \left( \int \!\!\!\!\int _{\Omega ^c \times \Omega } \Gamma (..) \, \frac{1 - m_3(x')^2}{|x-x'|^3} + \int \!\!\!\!\int _{{\mathbb {R}^2 \times \mathbb {R}^2}} \Theta (..) \, \frac{\textrm{div}m'(x) \textrm{div}m'(x')}{|x-x'|} \right) . \end{aligned}$$

We recall that $E_\epsilon = \frac{\pi }{st^2}\mathcal {E}$ so that every prefactor needs to be multiplied with $\frac{\pi }{st^2}$. Using the identities from Remark 1.1, we compute $\frac{\pi t}{s} = 2\pi ^2 (Q-1)$ and $\frac{\pi s}{t} = \frac{1}{2(Q-1)}$. We also compute $\frac{\pi d^2}{st} = \frac{1}{2} \epsilon |\ln \epsilon |$, $\frac{\pi (Q-1)s}{t} = \frac{|\ln \epsilon |}{2\epsilon }$ and $\frac{s d^2}{t^3} = \frac{|\ln \epsilon |^3}{\epsilon (2\pi )^3}$. This yields the representation formula. We finally note that from the representation in Theorem 2.3 it follows that the integral in $G_\epsilon$ which contains $\Theta$ is nonnegative. Since $0 \le \Gamma \le 1$ and $m_3 \le 1$ it then follows that $G_\epsilon \ge 0$. $\square$

2.2 Lower bound and compactness

In this section, we give a lower bound for both $F_\epsilon$ and $E_\epsilon$. We first derive an adaption of [28, Lem. 6] to the case of finite domains:

Lemma 2.5

(Interpolation inequality) Let $\Omega {\Subset \mathbb {R}^2}$ be convex with $\delta := |\textrm{diam}\Omega |$. Let $f \in H^1(\Omega )$. Then for any $0 < r \le R$ we have

$$\begin{aligned}&{\frac{1}{8}} \int _{\Omega } \int _{\Omega } \frac{1}{|x-y|^3}|f(x) - f(y)|^2 \, dx dy \nonumber \\&\quad \le {\frac{\pi r}{8}} \int _{\Omega }|\nabla f|^2 \, dx + \ln \frac{R}{r} \Vert f\Vert _{L^\infty } \Vert \nabla f\Vert _{\Omega } + \frac{\pi {\alpha _0} }{{2}R} \min \Big \{ \delta \Vert f\Vert _{L^\infty } \Vert \nabla f\Vert _{\Omega }, 2 |\Omega | \Vert f\Vert _{L^\infty }^2 \Big \}, \end{aligned}$$

(30)

where ${\alpha _0} = 0$ if $R > \delta$ and ${\alpha _0} = 1$ else.

Proof

Let X be the left hand side of (30). Without loss of generality, we may assume that f is not constant. We show that for $0 < r \le R$ and $\Omega _z:= \Omega - z$ we have

$$\begin{aligned}&\int _{B_r} \int _{\Omega \cap \Omega _z} \frac{|f(x+z)-f(x)|^2}{|z|^3} \, dx dz \le \pi r\int _{\Omega } |\nabla f|^2 \, dx, \end{aligned}$$

(31)

$$\begin{aligned}&\int _{B_R \setminus B_r} \int _{\Omega \cap \Omega _z} \frac{|f(x+z)-f(x)|^2}{|z|^3} dx dz \le 8 \ln \left( \frac{R}{r} \right) \Vert f\Vert _{L^\infty } \Vert \nabla f\Vert _{\Omega }, \end{aligned}$$

(32)

$$\begin{aligned}&\int _{B_R^c} \int _{\Omega \cap \Omega _z} \frac{|f(x+z)-f(x)|^2}{|z|^3} dx dz \le \frac{4\pi }{R} \min \Big \{ \delta \Vert f\Vert _{L^\infty } \Vert \nabla f\Vert _{\Omega }, 2 |\Omega | \Vert f\Vert _{L^\infty }^2 \Big \}. \end{aligned}$$

(33)

The assertion of the lemma follows by adding (31)–(33). The proof of these estimates follows similarly as in [28]. For the convenience of the reader we sketch some details: We note that for convex sets $\Omega$ and for $p \ge 1$ we have

$$\begin{aligned} \int _{\Omega \cap \Omega _z} |f(x+z) - f(x)|^p \, dx \le \int _{\Omega }|\nabla f(x) \cdot z|^p \, dx \quad \forall z \in \mathbb {R}^2. \end{aligned}$$

(34)

Indeed, by the Fundamental Theorem of Calculus and Jensen’s inequality,

$$\begin{aligned}&\int _{\Omega \cap \Omega _z} |f(x+z) - f(x)|^p \, dx = \int _{\Omega \cap \Omega _z} \left| \int _0^1 \nabla f(x+tz) \cdot z \, dt \right| ^p \, dx \\&\quad \le \int _0^1 \int _{\Omega \cap \Omega _z} |\nabla f(x+tz) \cdot z|^p \,dx dt \le \int _{\Omega }|\nabla f(x) \cdot z|^p \, dx \quad \forall z \in \mathbb {R}^2, \end{aligned}$$

noting that $x + [0,1]z \in \Omega$ for $x \in \Omega \cap \Omega _z$ since $\Omega$ is convex. The estimates (31) and (32) then follow analogously as in [28].

For the proof of (33) we estimate

$$\begin{aligned} \int _{B_R^c} \int _{\Omega \cap \Omega _z} \frac{|f(x+z)-f(x)|^2}{|z|^3} dx dz \le 2\Vert f\Vert _{L^\infty } \int _{B_R^c} \frac{1}{|z|^3} \int _{\Omega \cap \Omega _z} |f(x+z)-f(x)| dx dz. \end{aligned}$$

The estimate then follows by noting that (34) with $p=1$ entails

$$\begin{aligned} \int _{\Omega \cap \Omega _z}|f(x + z) - f(x)| dx \le \min \left\{ \delta \int _{\mathbb {R}^2} |\nabla f \cdot z| dx, 2 |\Omega | \Vert f\Vert _{L^\infty } \right\} \end{aligned}$$

and integrating in z. $\square$

Theorems 1.2 and 1.3 are a consequence of the following lemmas and propositions:

Lemma 2.6

(Small diameter) Let $\Omega \Subset \mathbb {R}^2$ be convex. Then there is $\epsilon _0 \in (0,1)$ such that for $\epsilon \in (0,\epsilon _0)$ the following holds: If the diameter of the set $\Omega$ is bounded by

$$\begin{aligned} \textrm{diam}\Omega < \frac{{4}}{{\pi }e} \left( 1 - \frac{{4}}{|\ln \epsilon |} \right) \end{aligned}$$

(35)

then for some constant $c = c(Q)$ and with $\gamma _0$ defined in (29), the following holds

• (i) $\displaystyle \inf _{M \in \mathcal {A}, M = \overline{M}} E_\epsilon [M] = \inf _{m \in \overline{\mathcal {A}}} F_\epsilon [m] = 0$,

• (ii) $\displaystyle - c {\gamma _0} |\partial \Omega | \le \inf _{M \in \mathcal {A}} E_\epsilon [M] \le 0$.

The infimum in (i) is only achieved by either one of the configurations $\pm e_3 \chi _\Omega \in \overline{\mathcal {A}}$ for $F_\epsilon$ and $(\pm e_3 \chi _\Omega ) \otimes \chi _{[0,t]}$ for $E_\epsilon$.

Proof

We first note that $F_\epsilon [\pm e_3 \chi _{\Omega }] = 0$ and $E_\epsilon [\pm e_3 \chi _{\Omega _1}] = 0$. For the lower bounds we apply Lemma 2.4. Also using the convexity of $\Omega$ we have

$$\begin{aligned} \frac{|\ln \epsilon |}{\epsilon }|B_\omega (\partial \Omega ) \cap \Omega |&\le \frac{|\ln \epsilon | \omega }{\epsilon }|\partial \Omega | \ {\mathop {\le }\limits ^{(8)}} 2\pi (Q-1) |\partial \Omega | = c |\partial \Omega |, \\ G_\epsilon [M] - |R_\epsilon [M]|&\ge - \frac{{2}\epsilon }{|\ln \epsilon |} \Vert \nabla m\Vert _{L^2({\Omega })}^2 - c {\gamma _0} |\partial \Omega | {+ \frac{c|\ln \epsilon |^3}{\epsilon }\Vert \partial _3 M\Vert _{L^2({\Omega _1})}^2} \end{aligned}$$

for $\epsilon$ sufficiently small and with $m(x):= \overline{M}(x,\frac{1}{2})$. We hence have

$$\begin{aligned} E_\epsilon [M] + c {\gamma _0} |\partial \Omega |&{\mathop {\ge }\limits ^{(28)}} F_\epsilon [m] - \frac{{2}\epsilon }{|\ln \epsilon |}\Vert \nabla m\Vert _{L^2({\Omega })}^2 {+ \frac{c|\ln \epsilon |^3}{\epsilon }\Vert \partial _3 M\Vert _{L^2({\Omega _1})}^2}\nonumber \\&\ge L_\epsilon [m] - N[m] - \frac{{2}\epsilon }{|\ln \epsilon |} \Vert \nabla m\Vert _{L^2({\Omega })}^2 =: X. \end{aligned}$$

(36)

With the pointwise estimate $\frac{\epsilon }{2} |\nabla m|^2 + \frac{1}{2\epsilon } (1-m_3^2) \ge |\nabla m_3|$ we get

$$\begin{aligned}&L_\epsilon [m] {- \frac{{2}\epsilon }{|\ln \epsilon |} \Vert \nabla m\Vert _{L^2}^2} = |\ln \epsilon | \left( \frac{\epsilon }{2} \Vert \nabla m\Vert _{L^2}^2 + \frac{1}{2\epsilon } \Vert 1-m_3^2\Vert _{L^{1}}^2 \right) {- \frac{{2}\epsilon }{|\ln \epsilon |} \Vert \nabla m\Vert _{L^2}^2} \nonumber \\&\quad \ge {\frac{\epsilon }{2} \left( 1 - \frac{{4}}{|\ln \epsilon |} \right) } \Vert \nabla m\Vert _{L^2({\Omega })}^2 + (|\ln \epsilon | - 1) \Vert \nabla m_3\Vert _{\Omega }. \end{aligned}$$

(37)

To estimate the nonlocal term, we apply Lemma 2.5 with

$$\begin{aligned} r = {\frac{4\epsilon }{\pi } \left( 1 - \frac{4}{|\ln \epsilon |} \right) }, \quad R := \delta \end{aligned}$$

noting that $r \approx \epsilon \le R$ for $\epsilon$ sufficiently small. This yields

$$\begin{aligned} N[m]&\le \frac{\epsilon }{2} \left( 1 - \frac{{4}}{|\ln \epsilon |} \right) \Vert \nabla m\Vert _{L^2({\Omega })}^2 + \left( |\ln \epsilon | - \ln \left( \frac{{4}}{{\pi }\delta } \left( 1 - \frac{{4}}{|\ln \epsilon |} \right) \right) \right) \Vert \nabla m_3\Vert _{\Omega }. \end{aligned}$$

(38)

By inserting (37) and (38) into (36) we obtain the estimate

$$\begin{aligned} X&\ge \left[ \ln \left( \frac{{4}}{{\pi }\delta } \left( 1 - \frac{{4}}{|\ln \epsilon |} \right) \right) -1 \right] \Vert \nabla m_3\Vert _{\Omega }&= \ln \left( \frac{{4}}{{\pi }\delta e} \left( 1 - \frac{{4}}{|\ln \epsilon |} \right) \right) \Vert \nabla m_3\Vert _{\Omega } {\mathop {>}\limits ^{(35)}} 0 \end{aligned}$$

which yields both assertions (i) and (ii). $\square$

The configurations in Lemma 2.6(i) are critical:

Lemma 2.7

(Criticality) The configurations $M = \pm \chi _{\Omega _t} e_3$ are critical for the energy $E_\epsilon$ for all $\epsilon > 0$ within the class of configurations of form $m \otimes \chi _{(0,t)}$ with $m \in \overline{\mathcal {A}}$.

Proof

Indeed, within this class of configurations the tangent space at $m \otimes \chi _{[0,t]}$ is given by functions of the form $\varphi \otimes \chi _{\Omega _t}$ with $\varphi \in H^1(\mathbb {R}^2;\mathbb {R}^3)$ satisfying $\varphi \cdot m = 0$ and $\textrm{spt}\,\varphi \subset \overline{\Omega }$. For such test functions, the Euler–Lagrange equation then states that

$$\begin{aligned} dt \int _\Omega \nabla m \cdot \nabla \varphi - Qt \int _\Omega m \cdot \left( \begin{array}{c} 0 \\ \varphi _3 \end{array}\right) + \int _\Omega \left( \int _0^t \mathcal {H}(M) \, dx_3 \right) \cdot \varphi \, dx' = 0, \end{aligned}$$

(39)

using the dimensional formulation (cf. (1)) and Lemma 2.1(i). If $M = \pm e_3 \chi _{\Omega _t}$, i.e. $m = \pm e_3 \chi _\Omega$ then $\nabla m = 0$ in $\Omega$ and the first integral above vanishes. Furthermore, $\varphi \cdot e_3 = 0$ implies $\varphi _3 = 0$ so that the second integral vanishes. Finally, the magnetic charges $\textrm{div}(M)$ are antisymmetric w.r.t to the plane $\{ x_3 = \frac{t}{2} \}$. By Lemma 2.1, the tangential component $\mathcal {H}'(M)$ of the stray field has the same symmetry and hence

$$\begin{aligned} \int _0^t \mathcal {H}'[M] \, dx_3 = 0 \quad \text {for all}\quad x' \in \mathbb {R}^2. \end{aligned}$$

Equation (39) hence holds for all magnetizations of form $\pm \chi _{\Omega _t} e_3$. $\square$

The next lemma is concerned with energy bounds from below:

Proposition 2.8

(Lower bound) Let $\Omega \Subset \mathbb {R}^2$ be convex and $\epsilon \in (0, \frac{1}{4})$. Then

$$\begin{aligned} E_\epsilon [M] \ge \left| \ln \left( \frac{4\Vert \nabla \overline{M}_3\Vert _{\Omega _1}}{\pi ^2 e^2|\Omega |} \right) \right| \Vert \nabla \overline{M}_3\Vert _{\Omega _1} - \frac{\pi ^2 e }{ 2} |\Omega | - C {\gamma _0} |\partial \Omega |, \end{aligned}$$

(40)

where C is the constant from Lemma 2.6 and $\gamma _0$ is given in (29). If the configuration $M \in \mathcal {A}$ satisfies $E_\epsilon [M] \le - \alpha |\Omega |$ for some $\alpha > 0$ then for constants $C_\alpha , c_\alpha$ depending on $\alpha$ (with Notation (11)) we have

• (i) $c_\alpha |\Omega | \le \Vert \nabla \overline{M}_{ 3}\Vert _{\Omega _1} \le C_\alpha |\Omega |$,

• (ii) $\displaystyle 0 \le \frac{\epsilon }{2} \Vert \nabla \overline{M}\Vert _{L^2({\Omega _1})}^2 + \frac{1}{2\epsilon } \Vert 1 - \overline{M}_3^2\Vert _{L^{1}(\Omega _1)} - \Vert \nabla \overline{M}_{ 3}\Vert _{\Omega _1} \le \frac{C_\alpha }{|\ln \epsilon |} |\Omega |$,

• (iii) $\displaystyle c_\alpha |\Omega | |\ln \epsilon | \le L_\epsilon [\overline{M}],N[\overline{M}] \le C_\alpha |\Omega | |\ln \epsilon |$.

• (iv) $\displaystyle \Vert \partial _3 M_3\Vert _{L^2({\Omega _1})}^2 \displaystyle \le \frac{\epsilon }{|\ln \epsilon |^3} \Big ( E_\epsilon [\overline{M}] + C \Big )$.

For $m \in \overline{\mathcal {A}}$ the corresponding statement to (40) holds with $E_\epsilon [M] + c \gamma _0 |\partial \Omega |$ replaced by $F_\epsilon$. If $F_\epsilon [m] \le -\alpha |\Omega |$, then (i)–(iii) hold with $\overline{M}$ replaced by m.

Proof

We write $m:= \overline{M}(\cdot ,\frac{1}{2})$. For the proof of (40) it is enough to estimate X, defined in (36). We first apply Lemma 2.5 with $f = m_3$ and with the choice

$$\begin{aligned} r := \frac{{4}\epsilon }{\pi } \left( 1 - \frac{{4}}{|\ln \epsilon |} \right) , \quad R := \frac{\pi |\Omega |}{\Vert \nabla m_3\Vert _{\Omega }}. \end{aligned}$$

(41)

Since $\ln \frac{1}{y} = - \ln y$ and $1 = - \ln \frac{1}{e}$ and for $\epsilon \in (0,1)$ we obtain

$$\begin{aligned}&N[m] \le \frac{\epsilon }{2} \left( 1 - \frac{ 4}{|\ln \epsilon |} \right) \Vert \nabla m\Vert _{L^2({\Omega })}^2 + \left( \ln \frac{{\pi }R}{{4}\epsilon \left( 1 - \frac{{4}\epsilon }{|\ln \epsilon |}\right) } \right) \Vert \nabla m_3\Vert _{\Omega } + {\frac{\pi |\Omega |}{R}} \nonumber \\&\quad {\mathop {=}\limits ^{(41)}} \frac{\epsilon }{2} \left( 1 - \frac{ 4}{|\ln \epsilon |} \right) \Vert \nabla m\Vert _{L^2({\Omega })}^2 + \left( |\ln \epsilon | -\ln \frac{{4 \left( 1 - \frac{{4}\epsilon }{|\ln \epsilon |}\right) }{\Vert \nabla m_3\Vert _{\Omega }}}{e {\pi ^2} |\Omega |} \right) \Vert \nabla m_3\Vert _{\Omega }. \end{aligned}$$

(42)

Inserting (37) and (42) into (36), applying the identity $1 = - \ln \frac{1}{e}$ once more we get

$$\begin{aligned} X&{\mathop {\ge }\limits ^{(37)}} \ln \left( \frac{{4 \left( 1 - \frac{{4}\epsilon }{|\ln \epsilon |}\right) }{\Vert \nabla m_3\Vert _{\Omega }}}{e^2 {\pi ^2} |\Omega |} \right) \Vert \nabla m_3\Vert _{\Omega } \ge \ln \left( \frac{{2}{\Vert \nabla m_3\Vert _{\Omega }}}{e^2 {\pi ^2} |\Omega |} \right) \Vert \nabla m_3\Vert _{\Omega }. \end{aligned}$$

(43)

Minimizing the right hand side of (43) over all values ${s}:= \Vert \nabla m_3\Vert _{\Omega } \ge 0$ yields the lower bound $- \frac{\pi ^2 e }{ 2} |\Omega |$ and hence (40). The estimate (i) follows directly from (40). Keeping the nonnegative term $\frac{\epsilon }{2} \Vert \nabla \overline{M}\Vert _{L^2({\Omega _1})}^2 + \frac{1}{2\epsilon } \Vert 1 - \overline{M}_3^2\Vert _{L^{1}(\Omega _1)} - \Vert \nabla \overline{M}\Vert _{\Omega _1}$ in the estimate (37) yields (ii). Estimate (iii) follows from (i) and (ii). Assertion (iv) follows by keeping the nonnegative term $\Vert \partial _3 M_3\Vert _{L^2({\Omega _1})}^2$ in estimate (36). $\square$

The compactness follows directly from the BV-bound in Lemma 2.8:

Proposition 2.9

(Compactness) Let $\Omega {\Subset } \mathbb {R}^2$ be convex. Then

• (i) For any sequence $m_\epsilon \in \overline{\mathcal {A}}$ with $\limsup _{\epsilon \rightarrow 0} F_\epsilon [m_\epsilon ] < \infty$ there is $m \in BV(\Omega , \pm e_1)$ with $|m| = \chi _{\Omega }$ and a subsequence with $m_\epsilon \rightarrow m$ in  $L^1(\Omega )$ for $\epsilon \rightarrow 0$.

• (ii) The assertion of Theorem 1.3(iii) holds.

Proof

By Lemma 2.8(i) we have $\Vert \nabla m_{\epsilon ,3}\Vert _{\Omega } \le C$. This shows that $m_{\epsilon ,3} \rightarrow m_3$ in $L^1(\mathbb {R}^2)$ for some $m_{\epsilon ,3} \in L^1(\mathbb {R}^2)$ and for a subsequence by the compact embedding of $BV(\Omega )$ into $L^1(\Omega )$. From Proposition 2.8(iii) we also get

$$\begin{aligned} \Vert m_{1,\epsilon }\Vert _{L^2({\Omega })}^2 + \Vert m_{2,\epsilon }\Vert _{L^2({\Omega })}^2 \le \epsilon L_\epsilon [m_\epsilon ] {\mathop {\le }\limits ^{Prop. 2.8(iii)}}C \epsilon |\ln \epsilon | \rightarrow 0. \end{aligned}$$

Altogether this implies the assertion (i). Similarly, the corresponding compactness holds for $\overline{M}$ which again follows from Proposition 2.8. This shows (ii). $\square$

2.3 Proof of upper bound

We recall the family of asymptotically one-dimensional profiles from [28]:

Lemma 2.10

[28, Lem. 4.2] For $0< \epsilon < 1$, let $\xi _{\epsilon } \in C^1(\mathbb {R})$ be given by

$$\begin{aligned} \xi _{\epsilon }(\rho ) := \sin \left( \frac{\pi }{2} \frac{\arcsin ( \tanh ( \rho / \epsilon ) )}{\arcsin \left( \tanh \left( \epsilon ^{-\frac{1}{2}}\right) \right) } \right) \quad \text {for}\quad |\rho | < \epsilon ^{\frac{1}{2}} \end{aligned}$$

and $\xi _\epsilon (\rho ):= \textrm{sign}(\rho )$ for $|\rho | \ge \epsilon ^{\frac{1}{2}}$. Then, for universal $C,c_1,a > 0$, we have

• (i) $\displaystyle \frac{1}{2} \int _\mathbb {R}\frac{\epsilon |\xi _\epsilon '|^2}{1-\xi _\epsilon ^2} + \frac{1}{\epsilon } \big ( 1-\xi _\epsilon ^2 \big ) \, d\rho \le 2 + C e^{-a \epsilon ^{-1/2}}$,

• (ii) $\displaystyle \frac{1}{8} \int _{-H}^{H} \int _{-H}^H \frac{|\xi _\epsilon (\rho )- \xi _\epsilon (\rho ')|^2}{|\rho -\rho '|^2} d\rho d\rho ' \ge \ln \left( \frac{c_1 H}{\epsilon } \right) \quad \text {for }H \ge 2\epsilon$,

• (iii) $\displaystyle \int _{-H}^{H} \int _{-H}^H \frac{|\xi _\epsilon (\rho )- \xi _\epsilon (\rho ')|^2}{|\rho -\rho '|} + \frac{1}{H} |\xi _\epsilon (\rho )- \xi _\epsilon (\rho ')|^2 \, d\rho d\rho ' \le C H$.

Proof

(i) and (ii) follow from [28, Lem. 4.2] with the special choice of a transition layer with support of size $2\epsilon ^{\frac{1}{2}}$. (iii) follows from a straightforward estimate. $\square$

For the special case $\lambda = 0$, the $\Gamma$-convergence and in particular the construction of a recovery sequence is a classical result, relying on the optimal one-dimensional transition profiles to smooth out the jump discontinuity in the limit configuration [4]. As it turns out, this construction also works for $\lambda >0$, where $F_{\epsilon , \lambda }$ is nonlocal. We will use a similar construction based on the nearly optimal profile $\xi _\epsilon$ from Lemma 2.10. As the calculations for the local part of the energy are well-known, our focus is on the contribution of the homogeneous $H^{1/2}$-norm. We define the finite range version of the energy $F_\epsilon$ by

$$\begin{aligned} F_{\epsilon ,R}[m]&= |\ln \epsilon | \int _{\Omega } \frac{\epsilon |\nabla m|^2}{2} + \frac{1-m_3^2}{2\epsilon } dx - \frac{1}{8} \int \!\!\!\!\int _{|x-y| \le R} \frac{|m_3(x) - m_3({y})|^2}{|x-{y}|^3} dx dy \end{aligned}$$

(44)

noting that for all $m \in \overline{\mathcal {A}}$ we have

$$\begin{aligned} F_\epsilon [m] \le F_{\epsilon ,R}[m]. \end{aligned}$$

For the upper bound construction of the energy, we will use a matrix of disk–shaped domains. The choice of the shape of these domains is motivated by convenience but other domain shapes would yield an upper bound estimate as well. We next give an upper bound construction for the disk:

Lemma 2.11

(Upper bound for disk) There is a universal constant $C > 0$ such that if $R_0 > C$ and $B_{2R_0} \subset \Omega \subset \mathbb {R}^2$ then there is a sequence $m_\epsilon \in \overline{\mathcal {A}}$ such that

$$\begin{aligned} m_\epsilon = -e_3 \quad \text {in}\; B_{{{R_0}}-\epsilon ^{1/2}}, \qquad m_\epsilon = -e_3 \quad \text {in}\; \Omega \backslash B_{{{R_0}} + \epsilon ^{1/2}} \end{aligned}$$

(45)

and for $\epsilon > 0$ sufficiently small we have

$$\begin{aligned} F_{\epsilon ,{{R_0}}}[m_\epsilon ] \le - C {|\partial B_{{R_0}}|}. \end{aligned}$$

(46)

Proof

We proceed similarly as in the construction of [28, Lem. 4.3], however with a slightly more careful estimate since we need to capture the sign of the leading order term of the energy. We write $d(x):= {{R_0}} - |x|$ for the signed distance function for $\partial B_{{R_0}}$. For $x \in \mathcal {S}_\epsilon := B_{{{R_0}}+\epsilon ^{1/2}} \backslash B_{{{R_0}}-\epsilon ^{1/2}}$ we set

$$\begin{aligned} m_{\epsilon }(x) := \xi _\epsilon (d(x)) e_3 + \sqrt{1-\xi _\epsilon ^2(d(x))} \frac{x^\perp }{|x|}, \end{aligned}$$

where $\xi _\epsilon$ is given in Lemma 2.10. We also set $m_\epsilon = e_3$ in $B_{{{R_0}}-\epsilon ^{1/2}}$ and $m_\epsilon = -e_3$ in $\Omega \backslash B_{{{R_0}} + \epsilon ^{1/2}}$. Then $m_\epsilon \in \overline{\mathcal {A}}$ and $m_\epsilon$ satisfies (45). In order to show (46), we use the coarea formula to integrate on the level sets of d. This yields

$$\begin{aligned} L_\epsilon [m_\epsilon ]&:= |\ln \epsilon | \int _{\Omega } \left( \frac{\epsilon }{2}|\nabla m_\epsilon |^2 + \frac{1}{2\epsilon }(1-{m_{\epsilon ,3}^2} ) \right) dx\nonumber \\&= |\ln \epsilon | \int _{-\epsilon ^{\frac{1}{2}}}^{\epsilon ^{\frac{1}{2}}} \left( \frac{\epsilon |\xi '_\epsilon (\rho )|^2}{2(1-\xi _\epsilon ^2(\rho ))} + \frac{1}{2\epsilon }(1-\xi _\epsilon ^2(\rho ))\right) 2\pi ({{R_0}} + \rho )) \, d\rho \nonumber \\&\le 2|\partial B_{{R_0}}| |\ln \epsilon | + \mathcal {O}(\epsilon ^{1/2}), \end{aligned}$$

(47)

where we used Lemma 2.10(i) in the last line. For $\ell < {\frac{1}{8}} \pi {{R_0}}$ and $H < {\frac{1}{8}} {{R_0}}$ to be chosen later, let $Q:= (-\ell , \ell ) \times (-H,H)$. We define the diffeomorphism $\Phi : Q \rightarrow \Phi (Q) {\subset B_H(\partial B_{{R_0}})}$ by $\Phi (s,\rho ) = ({{R_0}} + \rho ) \nu (s)$ with $\nu (s):= (\cos \frac{s}{2\pi {{R_0}}}, \sin \frac{s}{2\pi {{R_0}}})$, i.e. s is the geodesic distance on $\partial {B_{{R_0}}}$ from $e_1$ and $\rho$ is the distance to $\partial {B_{{R_0}}}$. By rotational symmetry we have

$$\begin{aligned} N[m_{\epsilon }]\,&{{\mathop {\ge }\limits ^{(11)}} \frac{|\partial B_{{R_0}}|}{8} \int _{\mathbb {R}^2} \int _{{{R_0}}-H}^{{{R_0}}+H} \frac{|m_{\epsilon ,3}(\rho ' e_1) - m_{\epsilon ,3}(y)|^2}{|\rho ' e_1-y|^3} \, d\rho ' dy} \\&\ge \frac{|\partial {B_{{R_0}}}|}{8} \int \!\!\!\!\int _{(-H, H)^2} \left( \int _{-\ell }^\ell \frac{|\xi _{\epsilon }(\rho ') - \xi _{\epsilon }(\rho )|^2}{|\Phi (0,\rho )-\Phi (s,\rho ')|^3} \, ds \right) \left( 1\!+\!\frac{\rho '}{{R_0}} \right) {\left( 1\!+\!\frac{\rho }{{R_0}} \right) } \, d\rho d\rho '. \end{aligned}$$

We consider $X:= |{(0,\rho ) - (s,\rho ')}|$ and $Y:= |\Phi (0,\rho )-\Phi (s,\rho ')|$. We have $\partial _s \Phi (s,\rho ) = (1+\frac{\rho }{{R_0}}) \tau (s)$ and $\partial _\rho \Phi (s,\rho ) = \nu (s)$. Since $D\Phi (0,0) = \textrm{Id}$ and $\Vert D^2\Phi \Vert _{L^\infty ({Q})} \le \frac{2}{{R_0}}$ we have $|X-Y| \le \frac{X^2}{{R_0}}$ for $|\rho | < {{R_0}}$. In particular, $Y \sim X$ for $X \le \frac{{R_0}}{2}$. Therefore,

$$\begin{aligned}&\int _{-\ell }^\ell \left| \frac{1}{X^3} - \frac{1}{Y^3} \right| ds = \int _{-\ell }^\ell \left| \frac{(X-Y) (X^2 + Y^2)}{X^3Y^3} \right| ds \le \frac{C}{{{R_0}}} \int _{-\ell }^\ell \frac{1}{X^2} \, ds \\&\quad = \frac{C}{{R_0}} \int _{-\ell }^\ell \frac{1}{s^2 + |\rho -\rho '|^2} \, ds = \frac{C}{{{R_0}}|\rho - \rho '|} \arctan \left( \frac{\ell }{|\rho - \rho '|} \right) \le \frac{C}{{{R_0}}|\rho - \rho '|} \end{aligned}$$

for $(0,\rho ), (s,\rho ') \in Q$. By integration and using Taylor’s formula we also have

$$\begin{aligned} {\int _{-\ell }^\ell \frac{1}{X^3} \, ds}&= \int _{-\ell }^\ell \frac{1}{\big (s^2 + |\rho -\rho '|^2\big )^{3/2}} \, ds = \frac{2}{|\rho - \rho '|^2} \left( 1 + \frac{|\rho - \rho '|^2}{\ell ^2}\right) ^{-\frac{1}{2}} \\&\ge \frac{2}{|\rho - \rho '|^2} - \frac{1}{\ell ^2}. \end{aligned}$$

With these estimates we arrive at

$$\begin{aligned} N[m_\epsilon ]&\ge \frac{|\partial {B_{{R_0}}}|}{ 8} \int \!\!\!\!\int _{(-H, H)^2} \left( \frac{2}{|\rho - \rho '|^2} - \frac{C}{{{R_0}}|\rho - \rho '|} - \frac{1}{\ell ^2}\right) |\xi _{\epsilon }(\rho ') - \xi _{\epsilon }(\rho )|^2 \\&\quad {\left( 1+\frac{\rho }{{R_0}} \right) } \left( 1+\frac{\rho '}{{R_0}} \right) \, d\rho d\rho ' \\&= \frac{|\partial {B_{{R_0}}}|}{{8}} \int \!\!\!\!\int _{(-H, H)^2} \left( \frac{2}{|\rho - \rho '|^2} - \frac{C}{{{R_0}}|\rho - \rho '|} - \frac{1}{\ell ^2} \right) |\xi _{\epsilon }(\rho ') - \xi _{\epsilon }(\rho )|^2 \, d\rho d\rho ', \end{aligned}$$

where the identity in the second line above follows from symmetry. An application of Lemma 2.10(ii)–(iii) then yields

$$\begin{aligned} N[m_\epsilon ]&\ge 2|\partial {B_{{R_0}}}| |\ln \epsilon | + 2 |\partial {B_{{R_0}}}| \left( \ln (c_1 H) - \frac{C H}{{R_0}} - \frac{C H^2}{\ell ^2} \right) \nonumber \\&=: 2 |\partial {B_{{R_0}}}| |\ln \epsilon | + C_1|\partial {B_{{R_0}}}|. \end{aligned}$$

(48)

For ${{R_0}}$ sufficiently large we can hence find H and $\ell$ with $1 \ll H \ll \ell \ll {{R_0}}$ such that $C_1 > 0$. Adding equations (47) and (48) then yields the asserted inequality. In particular, since $H \le {{R_0}}$ the bound holds for the finite range energy $F_{\epsilon ,{{R_0}}}$. $\square$

Proposition 2.12

(Upper bound) There is a universal constant $R > 0$ such that for any $\Omega \Subset \mathbb {R}^2$ there are sequences $m_\epsilon \in \overline{\mathcal {A}}$ and $M_\epsilon := m_\epsilon \otimes \chi _{[0,t]} \in \mathcal {A}$ such that

$$\begin{aligned} \max \Big \{ E_\epsilon [M_\epsilon ], F_\epsilon [m_\epsilon ] \Big \} \le - C |{\Omega ^{(R)}}| \end{aligned}$$

for $\epsilon$ sufficiently small and where $\Omega ^{(R)}:= \{ x \in \Omega : \textrm{dist}(x, \Omega ^c) \ge R \}$.

Proof

Let $R_0$ be the constant from Lemma 2.11 and let $R:= (\lambda +2) R_0$ for some $\lambda > 0$ to be fixed later. Then the family of balls $\mathcal {U}\,= \{ B_{10R_0}(x): x \in \Omega ^{(R)} \}$ is an open covering of $\Omega ^{(R)}$. By Vitali’s theorem and since $\Omega \Subset \mathbb {R}^2$ there is a finite subcovering $\{ B_{10R_0}(x_i): i = 1, \ldots , N \}$ such that the balls $\widetilde{B}_i:= B_{2R_0}(x_i)$ are pairwise disjoint. For ${\widehat{B}}_i:= B_{R_0}(x_i)$ we have $\sum _{i=1}^N |{\widehat{B}}_i| \sim N \sim |\Omega ^{(R)}|$ and $\sum _{i=1}^N |\partial {\widehat{B}}_i| \sim N \sim |\Omega ^{(R)}|$. Furthermore, $\textrm{dist}(\widetilde{B}_i, \Omega ^c) \ge \lambda R_0$ and $\textrm{dist}({\widehat{B}}_i, {\widehat{B}}_j) \ge R_0$ if $i \ne j$.

For $x \in \widetilde{B}_i$ we define $m_\epsilon := m_\epsilon ^{(i)}: B_i \rightarrow \mathbb {S}^1$ as in Lemma 2.11 (with $R = R_0$) and $m_\epsilon := e_3$ for $x \not \in \bigcup _i {\widehat{B}}_i$. We next apply Lemma 2.11. Since the domain constructions on the single balls have distance $\ge 2R_0$ we do not need to take the interaction energy between the balls for the finite range energy $F_{\epsilon , R}$ into account, cf. (44). Hence,

$$\begin{aligned} F_\epsilon [m_\epsilon ] \le \sum _{i=1}^N F_{\epsilon ,{R}}[m_\epsilon ^{(i)}] \le - \sum _{i=1}^N C |\partial \widetilde{B}_i| \le - C_1 |\Omega ^{(R)}| \end{aligned}$$

(49)

for some universal constant $C_1$ (only depending on $R_0$). This yields the estimate for $F_\epsilon$. For $M_\epsilon := m_\epsilon \otimes \chi _{[0,t]}$ we have $\textrm{div}' M_\epsilon ' = 0$ and $M_\epsilon = \overline{M}_\epsilon$. By Lemma 2.4 we get

$$\begin{aligned} E_\epsilon [M_\epsilon ]&{\mathop {=}\limits ^{(28)}} F_\epsilon [m_\epsilon ] + {\frac{1}{4}} \int \!\!\!\!\int _{\Omega ^c \times \Omega } \frac{\Gamma \left( \frac{1}{\omega }|x-x'|\right) }{|x-x'|^3} \big ( 1 - m_{\epsilon ,3}(x)^2 \big ) \, dx dx' \\&\quad + {\frac{1}{8}} \int \!\!\!\!\int _{\Omega \times \Omega } \frac{1 - \Gamma \left( \frac{1}{\omega }|x-x'|\right) }{|x-x'|^3} |m_{\epsilon ,3}(x) - m_{\epsilon ,3}(x')|^2 \, dx dx'\\&=: F_\epsilon [m_\epsilon ] + X_1 + X_2. \end{aligned}$$

By construction we have $m_{\epsilon ,3} = 1$ in $\Omega \backslash \bigcup _{i=1}^N \widetilde{B}_i$ and $\textrm{dist}(\widetilde{B}_i,\Omega ^c) \ge \lambda R_0$ for all $i = 1, \ldots , N$. Also using that $N \le C |\Omega ^{(R)}|$ and $\Vert \Gamma \Vert _{L^\infty }$, $\Vert m_{\epsilon ,3}\Vert _{L^\infty }$ $\le 1$ we hence get

$$\begin{aligned} X_1&\le C \int _{\bigcup _{i=1}^N \widetilde{B}_i} \int _{\Omega ^c} \frac{1}{|x-x'|^3} \le C N \int _{\mathbb {R}^2 \backslash B_{\lambda R_0}} \frac{1}{|x|^3} \le \frac{C}{\lambda R_0} |\Omega ^{(R)}| \le \frac{C_1}{2} |\Omega ^{(R)}| \end{aligned}$$

for $\lambda = \lambda (C_1)$ sufficiently large and with the same constant $C_1$ as in (49). We next write $X_2 =: X_2^{1} + X_2^{(2)} + X_2^{(3)}$ corresponding to integration over the subdomains of $(x,x') \in \Omega \times \Omega$ with $|x-x'| \le \beta _\epsilon \epsilon$, $\beta _\epsilon \epsilon \le |x-x'| \le 1$ and $|x-x'| > 1$ with $\beta _\epsilon := |\ln \epsilon |^{-\frac{1}{4}}$. By (31) we have

$$\begin{aligned} X_2^{(1)} {\mathop {\le }\limits ^{(31)}} C \epsilon \beta _\epsilon \int _{\Omega } |\nabla m_{\epsilon ,3}|^2 \, dx {\mathop {\le }\limits ^{(47)}} \frac{C}{|\ln \epsilon |^{\frac{1}{4}}} \rightarrow 0. \end{aligned}$$

For the estimate of $X_2^{(2)}$ we note that $1-\Gamma (\alpha ) \le C/\alpha ^2$ and hence $1 - \Gamma (\frac{|x-x'|}{\omega }) \le C\omega ^2/(\beta _\epsilon ^2\epsilon ^2)$ for $|x-x'| \ge \beta _\epsilon \epsilon$. From (32) we hence get

$$\begin{aligned} X_2^{(2)} {\mathop {\le }\limits ^{(32)}} \frac{C \omega ^2}{\beta _\epsilon ^2 \epsilon ^2} |\ln (\beta _\epsilon \epsilon )| \Vert \nabla m_{\epsilon ,3}\Vert _{\Omega } \le \frac{C}{|\ln \epsilon |^{\frac{1}{2}}} \rightarrow 0, \end{aligned}$$

since $\omega \le C\epsilon /|\ln \epsilon |$ (cf. (8)) and $|\ln (\beta _\epsilon \epsilon )| \le C |\ln \epsilon |$. We habe also used that $\Vert \nabla m\Vert _{\Omega } \le C$ by (47) and with the pointwise estimate $\frac{\epsilon }{2} |\nabla m|^2 + \frac{1}{2\epsilon } (1-m_3^2) \ge |\nabla m_3|$. By dominated convergence, using that $|x'-x| \ge 1$ and since $\Gamma (\frac{1}{\omega }|x-x'|) \rightarrow 1$ pointwise it follows easily that $X_2^{(3)} \rightarrow 0$ concluding the proof. $\square$