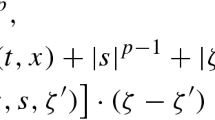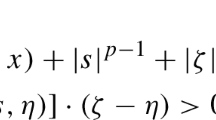$\mathcal {A}$-caloric approximation and partial regularity for parabolic systems with Orlicz growth

Abstract

We prove a new $\mathcal {A}$-caloric approximation lemma compatible with an Orlicz setting. With this result, we establish a partial regularity result for parabolic systems of the type

$$\begin{aligned} u_{t}- {{\,\textrm{div}\,}}a(Du)=0. \end{aligned}$$

Here the growth of a is bounded by the derivative of an N-function ${\varphi }$. The primary assumption for ${\varphi }$ is that $t{\varphi }''(t)$ and ${\varphi }'(t)$ are uniformly comparable on $(0,\infty )$.

1 Introduction

In this paper, we establish a partial regularity result for weak solutions to parabolic systems with general growth. By partial regularity, we mean Hölder continuity for the spatial gradient outside a closed set with zero measure. Let $\Omega \subset \mathbb {R}^{n}$ be an open bounded set, $n\ge 2$, $T>0$, and $N\ge 1$; we consider weak solutions $u:\Omega _{T}\rightarrow \mathbb {R}^{N}$, where $\Omega _{T}= \Omega \times (-T, 0)$, to the following homogeneous parabolic system

$$\begin{aligned} u_{t}- {{\,\textrm{div}\,}}a(Du)=0 \quad \text{ in } \Omega _{T}, \end{aligned}$$

(1.1)

where the $C^{1}$-vector field $a:\mathbb {R}^{Nn}\rightarrow \mathbb {R}^{Nn}$ satisfies ellipticity and growth conditions in terms of Orlicz functions. The precise structural assumptions on the vector field a will be presented later, but the principal prototype we have in mind is the parabolic ${\varphi }$-Laplacian system

$$\begin{aligned} u_{t}- {{\,\textrm{div}\,}}\left( \frac{{\varphi }'(\mu +|Du|)}{\mu +|Du|} Du\right) =0, \end{aligned}$$

(1.2)

where $\mu > 0$ and ${\varphi }$ is an Orlicz function (see Sect. 2). In the model case, with ${\varphi }(s)=\frac{1}{p}s^{p}$ for some $p>1$, (1.2) gives the more familiar non-degenerate evolutionary p-Laplacian system:

$$\begin{aligned} u_{t}- {{\,\textrm{div}\,}}\left( (\mu +|Du|)^{p-2} Du\right) =0. \end{aligned}$$

(1.3)

Hence system (1.2) (and consequently (1.1)) can be seen as a generalization of the p-Laplacian parabolic system (1.3). In particular, in addition to not requiring the system (1.1) to have the standard p-growth, we do not assume an Uhlenbeck structure as in (1.2).

The literature is rich with regularity results for parabolic systems with standard p-growth. In the paper by DiBenedetto and Friedman [14], everywhere regularity is proved. In this paper, the system has an Uhlenbeck structure: $a(\xi )=|\xi |^{p-2}\xi$ and $p>\frac{2n}{n+2}$. Using a combination of the Moser and De Giorgi iteration schemes, the solution’s spatial gradient is shown to be bounded and Hölder continuous on its domain. In [15], the authors extended their result to allow nonlinear forcing and introduced the intrinsic scaling which accommodates the singular ($p<2$) or degenerate ($p>2$) behavior of a in a natural way. (For a comprehensive introduction and collection of results on the subject, we refer the reader to DiBenedetto’s book [13].) It is well-known that, without special structural assumptions, solutions to systems can only be expected to possess partial regularity, that is regularity on an open set of full measure. Giaquinta and Giusti [28] provided the first result in this direction. Adapting a blow-up argument, successfully used for elliptic systems, they showed partial Hölder continuity for the weak solution, u, of nondegenerate systems with p-growth ($p\ge 2$). By again adapting techniques for elliptic systems, Giaquinta and Struwe proved higher integrability and partial Hölder continuity for a solution’s spatial gradient, Du, provided a has quadratic growth. For a general nonlinear $a(z,u,\xi )$ with quadratic growth, partial regularity for the spatial gradient remained an open problem until the work of Duzaar and Mingione [25]. In this transformative paper, the authors introduced the, now well-known, $\mathcal {A}$-caloric approximation approach to regularity theory for parabolic systems. Generalizations to problems with superquadratic or subquadratic growth were provided by Duzaar, Mingione, and Steffen [26] and Scheven [41]. Utilizing intrinsic scaling and p-caloric approximation, along with $\mathcal {A}$-caloric approximation, Bögelein, Duzaar, and Mingione [5] extended these results to p-growth systems, of the form (1.1), that are potentially degenerate ($p>2$) or singular $\frac{2n}{n+2}<p<2$. Without any attempt for completeness, we also mention to the papers [1, 5, 6, 27, 39] where the partial Hölder continuity, either for the solution’s spatial gradient or the solution itself, is established.

The main goal of this paper is to extend some of these partial regularity results into the Orlicz-growth setting. In the papers cited above, the superquadratic $p\ge 2$ and subquadratic $p<2$ cases require different techniques. Working in an Orlicz setting, we provide a unified treatment for both system classes.

There is a long history of interest in partial differential equations with nonstandard growth. Early existence results for both elliptic and parabolic problems were established by Donaldson [23, 24] (see also [43]). For elliptic equations and scalar-valued variational problems with (p, q)-growth, Marcellini [35, 36] developed an approximation and Moser iteration technique to prove everywhere regularity. For elliptic systems with an Uhlenbeck structure, Marcellini and Papi [38] extended this strategy to even allow problems oscillating between linear and exponential growth (see also [37]). Under general growth conditions, additional results for elliptic systems can be found, for example, in [7, 10,11,12, 16, 18, 21, 22] and the references therein. Regarding regularity for parabolic systems with general growth, much less work is available in the literature. Assuming an Uhlenbeck structure, the iteration strategies developed in [14, 15] have been adapted to problems with form (1.1). Assuming $t{\varphi }'(t)$ and ${\varphi }(t)$ are comparable on $(0,\infty )$, Lieberman [34] proved that a weak solution u to (1.2) has a Hölder continuous spatial gradient Du, provided Du is already known to be bounded. In [44], You removed the boundedness assumption, but under stricter growth assumptions. More recently, the boundedness of |Du| has been established under more general conditions. In [19], Diening, Scharle, and Schwarzacher assume $t{\varphi }''(t)$ and ${\varphi }'(t)$ to be comparable, while in [32], only a doubling property is needed to obtain the boundedness of u. For additional regularity and higher integrability results, where an Uhlenbeck or similar structure is assumed, we also mention [2, 3, 8, 20]. Without such a structural assumption, higher integrability was established by Hästö and Ok in [31]. As far as the authors are aware, the current paper is the first to establish the partial Hölder continuity of a weak solution’s spatial gradient.

We now list the specific assumptions needed (see also Sect. 2).

Assumption 1.1

Let ${\varphi }\in C^{1}([0, \infty ))\cap C^{2}(0, \infty )$ be an N-function satisfying

$$\begin{aligned} 0<p_{0}-1 \le \inf _{t>0} \frac{t {\varphi }''(t)}{{\varphi }'(t)}\le \sup _{t>0} \frac{t {\varphi }''(t)}{{\varphi }'(t)}\le p_{1}-1, \end{aligned}$$

with $\frac{2n}{n+2}<p_{0}\le p_{1}$. Without loss of generality we can assume that $p_{0}<2<p_{1}$.

With this ${\varphi }$, we consider (1.1) under the following hypotheses on the $C^1$-vector field $a: \mathbb {R}^{Nn}\rightarrow \mathbb {R}^{Nn}$:

$(a_{1})$:

There exists $L>0$ such that

$$\begin{aligned}&|a(\xi )|\le L {\varphi }'(1+|\xi |) \end{aligned}$$

holds for every $\xi \in \mathbb {R}^{Nn}$;

$(a_{2})$:

There exists $\nu >0$ such that

$$\begin{aligned} Da(\xi )(\eta ,\eta )\ge \nu {\varphi }''(1+|\xi |)|\eta |^2 \end{aligned}$$

holds for any $\xi , \eta \in \mathbb {R}^{Nn}$;

$(a_{3})$:

For every $\xi \in \mathbb {R}^{Nn}$

$$\begin{aligned} |Da(\xi )|\le L{\varphi }''(1+|\xi |); \end{aligned}$$

$(a_{4})$:

There exists a nondecreasing and concave function $\omega : [0, \infty ) \rightarrow [0, 1]$ with $\omega (0)=0$ such that

$$\begin{aligned} |Da(\xi )-Da(\eta )|\le L\omega \left( \frac{|\xi -\eta |}{1+|\xi |+|\eta |}\right) {\varphi }''(1+|\xi |+|\eta |) \end{aligned}$$

for every $\xi ,\eta \in \mathbb {R}^{Nn}$.

While it ensures $t{\varphi }''(t)$ is comparable ${\varphi }'(t)$ for $t>0$, Assumption 1.1 does not imply ${\varphi }$ has p-growth. It does imply ${\varphi }$ and ${\varphi }^*$ have the doubling property (2.1). Similar assumptions also appear in several of the works cited above.

The notion of weak solution adopted in the present paper is the following: $u\in C^0(-T,0, L^{2}(\Omega , \mathbb {R}^{N}))\cap L^{1}(-T,0, W^{1, 1}(\Omega ,\mathbb {R}^N))$ with ${\varphi }(|Du|)\in L^{1}(-T,0, L^{1}(\Omega ))$ is a weak solution to (1.1) if it holds

$$\begin{aligned} \int _{\Omega _T} u\cdot \eta _{t} - a( Du)\cdot D\eta \,dx\,dt =0, \end{aligned}$$

for all $\eta \in C^{\infty }_{c}(\Omega _T, \mathbb {R}^{N})$. Here $Du:(-T,0)\times \Omega \rightarrow \mathbb {R}^{Nn}$ denotes the spatial gradient of u.

We can now state our regularity result.

Theorem 1.2

Let $u\in C^0(-T,0; L^{2}(\Omega , \mathbb {R}^{N}))\cap L^{1}(-T,0; W^{1, 1}(\Omega ,\mathbb {R}^N))$ with ${\varphi }(|Du|)\in L^1(-T,0;L^1(\Omega ))$ be a weak solution to (1.1) in $\Omega _T$ under hypotheses $(a_{1})$-$(a_{4})$ and Assumption 1.1. Then for every $\alpha \in (0,1)$ there exists an open subset $\Omega _0\subseteq \Omega _T$ such that

$$\begin{aligned} V(Du)\in C_{loc}^{0,\frac{\alpha }{2},\alpha }(\Omega _0,\mathbb {R}^{Nn}) \qquad \hbox { and }\qquad |\Omega _T\setminus \Omega _0|=0, \end{aligned}$$

where $V(\xi )=\sqrt{\frac{{\varphi }'(1+|\xi |)}{1+|\xi |}}\xi$. Moreover, the singular set $\Omega _T\setminus \Omega _0\subseteq \Sigma _1\cup \Sigma _2$, where

$$\begin{aligned}&\Sigma _1=\left\{ z_0\in \Omega _T : \liminf _{\rho \rightarrow 0}int_{\mathcal {Q}_\rho (z_0)}|V(Du)-(V(Du))_{z_0,\rho }|^2dz>0\right\} ,\\&\Sigma _2=\left\{ z_0\in \Omega _T : \limsup _{\rho \rightarrow 0}|(Du)_{z_0,\rho }|=+\infty \right\} , \end{aligned}$$

denoting the mean value of a function over the parabolic cylinder $\mathcal {Q}_\rho (z_0)=\mathcal {B}_\rho (x_0)\times (t_0-\rho ^2,t_0)$ by $(\cdot )_{z_0,\rho }$.

Here $z_0=(x_0,t_{0})\in \Omega \times (-T,0)$ and $\mathcal {B}_\rho (x_0)$ is the ball in $\mathbb {R}^n$ with radius $\rho$ centered at $x_0$. Note that the Hölder continuity of V(Du) implies the Hölder continuity of Du with a different exponent depending on ${\varphi }$.

The proof of Theorem 1.2 relies on a decay estimate for certain excess functionals, which measure in a suitable way the oscillations of the solutions. More precisely, for $z_{0}\in \Omega _{T}$, $r>0$, $a\ge 0$, and an affine map $\ell : \mathbb {R}^{n}\rightarrow \mathbb {R}^{N}$, we define the excess functional by

$$\begin{aligned} \Psi _{a}(z_{0}, r, \ell )= int_{\mathcal {Q}_{r}(z_{0})} \left( \left| \frac{u-\ell }{r}\right| ^{2} + {\varphi }_{a} \left( \left| \frac{u-\ell }{r}\right| \right) \right) \, dz. \end{aligned}$$

Here ${\varphi }_a$ interpolates in a certain sense between $t^2$, when $t\le a$, and ${\varphi }$, when $t\ge a$. (The precise definition of the function ${\varphi }_a$ is given in Sect. 2.)

In order to achieve the decay estimate, we first derive the Caccioppoli inequality which is compatible with (1.1) (see Theorem 4.1). This, in particular, allows us to control the spatial oscillations of u and oscillations in Du via the excess functional. Though u need not be differentiable, if $\Psi _a$ is sufficiently small, then a family of smooth approximations to a spatial linearization of u, centered at $z_0$, can be produced. These 1st-order surrogates for u are, in fact, solutions to a constant coefficient parabolic system. Moreover, their approximation to u improves as $r\rightarrow 0^+$ providing a decay estimate for the $\Psi _a$, which implies the oscillations in V(Du) decrease as $r\rightarrow 0^+$. The rate of decrease is fast enough to deliver the regularity of V(Du) through Campanato’s characterization of Hölder continuity.

The outline of the proof of Theorem 1.2 follows the approach developed in [26, 41]. The cornerstone to the strategy is the $\mathcal {A}$-caloric approximation theorem, which provides the family of approximations to u. The generalization of this theorem to something suitable for the Orlicz setting was a significant obstacle and is the paper’s principal novelty. Our proof for this result does not require Assumption 1.1. In fact, ${\varphi }$ is only assumed to be an N-function with super $\frac{2n}{n+2}$-growth and a doubling property near zero. Thus ${\varphi }$ may have exponential or even super-exponential growth. A key difference between the p-growth and Orlicz settings is that for $L^p$-spaces one has

$$\begin{aligned} L^p(\mathcal {Q}_\rho )=L^p(-\rho ^2,0;L^p(\mathcal {B}_\rho )), \end{aligned}$$

but for the Orlicz spaces $L^{{\varphi }}$ one only has

$$\begin{aligned} L^{{\varphi }}(\mathcal {Q}_\rho )\subseteq L^{{\varphi }}(-\rho ^2,0;L^{{\varphi }}(\mathcal {B}_\rho )). \end{aligned}$$

In fact, equality holds if and only if ${\varphi }(t)$ is comparable to $t^p$ (see the remarks following Proposition 1.3 in [24]). With standard growth, the proofs for the $\mathcal {A}$-caloric approximation theorem can take advantage of Simon’s compactness result [42] in $L^p(-\rho ^2,0;L^p(\mathcal {B}_\rho ))$ to directly obtain convergence in $L^p(\mathcal {Q}_\rho )$. This, however, is not possible in the Orlicz setting. While we use Simon’s result for convergence in $L^2$, upgrading to convergence in $L^{{\varphi }}(\mathcal {Q}_\rho )$ involves a combination of approximations via convolution, sophisticated pointwise estimates, and integral bounds for the non-centered Hardy-Littlewood maximal function. With this new $\mathcal {A}$-caloric approximation, we prove a decay estimate for the excess function. Employing a standard iteration argument, we are able to identify the singular set with points where either the excess cannot be made sufficiently small, $\Sigma _1$, or the mean $(Du)_{z_0,\rho }$ is not bounded, $\Sigma _2$. Finally, to prove that the singular set is negligible, we use a Poincaré-Sobolev-type inequality for solutions to (1.1) which bounds the excess of u in terms of its spatial gradient Du. The proof for this inequality is rather complicated and relies on a Gagliardo-Nirenberg inequality from [31].

The paper is organized as follows: after collecting the basic terminology and other preliminaries in Sect. 2, we present the $\mathcal {A}$-caloric approximation in Sect. 3. In Sect. 4, the proofs of the Caccioppoli inequalities in the parabolic setting. We detail the Poincaré-Sobolev-type inequalities in Sect. 5 and the linearization in Sect. 6. We finally establish the decay estimates and the main theorem in the last two sections.

2 Notation and preliminary results

Let $\Omega \subset \mathbb {R}^{n}$ be a bounded domain; in the following $\Omega _{T}$ will denote the parabolic cylinder $\Omega \times (-T, 0)$, where $T>0$. If $z\in \Omega _{T}$, we denote $z=(x,t)$ with $x\in \Omega$ and $t\in (-T, 0)$. In what follows C will be often a general positive constant, possibly varying from line to line, but depending on only the structural parameters $n,N,L/\nu ,p_0,p_1$, with $1<p_0,p_1<\infty$ identified in Assumption 1.1 above. The notation $Du(x,t)\equiv D_{x} u(x,t)$ denotes the differentiation with respect to the spatial variable x, and $u_{t}$ stands for the differentiation with respect to the time variable.

With $x_{0}\in \mathbb {R}^{n}$, we set

$$\begin{aligned} \mathcal {B}_{r}(x_{0}):=\{x\in \mathbb {R}^{n} : |x-x_{0}|<r\} \end{aligned}$$

the open ball of $\mathbb {R}^{n}$ with radius $r>0$ and center $x_{0}$. When dealing with parabolic regularity, the geometry of cylinders plays an important role. We denote the general cylinder with spatial radius $\rho$ and time length $\tau$ centered at $z_0 =(x_0,t_0)$ by

$$\begin{aligned} \mathcal {Q}_{\rho ,\tau }(z_0)=\mathcal {B}_\rho (x_0)\times (t_0-\tau ,t_0), \end{aligned}$$

and we define the standard parabolic cylinder by

$$\begin{aligned} \mathcal {Q}_{\rho }(z_0)=\mathcal {Q}_{\rho ,\rho ^2}(z_0)=\mathcal {B}_\rho (x_{0})\times (t_{0}-\rho ^{2}, t_{0}). \end{aligned}$$

Given a cylinder $\mathcal {Q}=\mathcal {B}\times (s,t)$, its parabolic boundary is

$$\begin{aligned} \partial _{\mathcal {P}}\!\mathcal {Q}:=(\mathcal {B}\times \{s\})\cup (\partial \!\mathcal {B}\times [s,t]). \end{aligned}$$

The integral averages of a function u on $\mathcal {Q}\subset \mathbb {R}^{n+1}$ are given by

$$\begin{aligned} (u)_{\mathcal {Q}}(t)=int_{\mathcal {Q}} u(x, t) dx, \ \ \ (u)_{\mathcal {Q}}=int_{\mathcal {Q}} u(x,t)\,dz. \end{aligned}$$

We will denote the average $(u)_{\mathcal {Q}_\rho (z_0)}$ by $(u)_{z_0,\rho }$. The parabolic metric is defined as usual by

$$\begin{aligned} dist_{\mathcal {P}}(z, z_{0}):= \sqrt{|x-x_{0}|^{2}+|t-t_{0}|} \end{aligned}$$

whenever $z=(x,t),z_{0}=(x_{0},t_{0})\in \mathbb {R}^{n+1}$.

We recall that a strongly elliptic bilinear form $\mathcal {A}$ on $\mathbb {R}^{Nn}$ with ellipticity constant $\nu >0$ and upper bound $L>0$ means that

$$\begin{aligned} \nu |\xi |^2 \le \mathcal {A}(\xi , \xi ), \quad \mathcal {A}(\xi , \tilde{\xi }) \le L|\xi ||\tilde{\xi }| \quad \forall \xi ,\tilde{\xi }\in \mathbb {R}^{Nn}. \end{aligned}$$

Definition 2.1

We shall say that a function $h\in L^{2}(t_0-\rho ^2,t_0; W^{1, 2}(\mathcal {B}_{\rho }(x_0), \mathbb {R}^{N}))$ is $\mathcal {A}$-caloric on $\mathcal {Q}_{\rho }(z_0)$ if it satisfies

$$\begin{aligned} \int _{\mathcal {Q}_{\rho }(z_0)} h\cdot \eta _{t} - \mathcal {A}(Dh, D\eta )\, dz=0, \quad \text{ for } \text{ all } \eta \in C^{\infty }_{c}(\mathcal {Q}_{\rho }(z_0), \mathbb {R}^{N}). \end{aligned}$$

Remark 2.1

In the following we shall often write $u_t$ even if a weak solution of a parabolic system may not be differentiable in the time variable. The arguments can be made rigorous by the use of a smoothing procedure in time, as for instance via Steklov averages. However, since this argument is by now quite standard, we shall abuse the notation $u_t$ proceeding formally, without further explanation.

2.1 N-functions

We begin recalling the notion of N-functions (see [40]).

We write $f\sim g$, and we say that f and g are equivalent, if there exist constants $c_{1}, c_{2} >0$ such that $c_{1}g(t) \le f(t) \le c_{2}g(t)$ for any $t\ge 0$. Similarly the symbol $\lesssim$ stands for $\le$ up to a constant.

Definition 2.2

A real convex function $\varphi : [0, \infty )\rightarrow [0, \infty )$ is said to be an N-function if $\varphi (0)=0$ and there exists a right continuous nondecreasing derivative ${\varphi }'$ satisfying $\varphi '(0)=0$, $\varphi '(t)>0$ for $t>0$ and $\displaystyle {\lim _{t\rightarrow \infty } \varphi '(t)=\infty }$.

An N-function ${\varphi }$ satisfies the $\Delta _{2}$-condition, and we write ${\varphi }\in \Delta _{2}$, if there exists a constant $c>0$ such that

$$\begin{aligned} \varphi (2t)\le c\,\varphi (t) \quad \text{ for } \text{ all } t\ge 0. \end{aligned}$$

(2.1)

The smallest possible constant will be denoted by $\Delta _{2}({\varphi })$. Combining ${\varphi }(t)\le {\varphi }(2t)$ together with the $\Delta _{2}$-condition we get ${\varphi }(2t)\sim {\varphi }(t)$.

The conjugate function ${\varphi }^{*}:[0, +\infty ) \rightarrow [0, +\infty )$ of an N-function ${\varphi }$ is defined by

$$\begin{aligned} {\varphi }^{*}(t) := \sup _{s\ge 0}\, [s t -{\varphi }(s)] \quad \text{ for } \text{ all } t\ge 0. \end{aligned}$$

It holds that ${\varphi }^{*}$ itself is an N-function. If ${\varphi }$ and ${\varphi }^{*}$ both satisfy the $\Delta _{2}$-condition, then we will write that $\Delta _{2}({\varphi }, {\varphi }^{*}):=\max \{\Delta _2({\varphi }),\Delta _2({\varphi }^*)\}<\infty$. Assume that $\Delta _{2}({\varphi }, {\varphi }^{*})<\infty$; then for all $\delta >0$ there exists $c_{\delta }$ depending only on $\Delta _{2}(\varphi , \varphi ^{*})$ such that for all $s, t\ge 0$ it holds the Young’s inequality

$$\begin{aligned}&t\, s\le \delta \, \varphi (t)+c_{\delta } \, \varphi ^{*}(s). \end{aligned}$$

In most parts of the paper we will assume that ${\varphi }$ satisfies Assumption 1.1.

Remark 2.2

We remark that the lower bound on $p_0$ appearing in Assumption 1.1 is absolutely natural to prove regularity in such a context: one need only to consider the power case ${\varphi }(t)=t^{p}$ (see [13]).

Under Assumption 1.1 on ${\varphi }$ it follows from [12, Proposition 2.1] that $\Delta _2({\varphi },{\varphi }*)<\infty$ and

$$\begin{aligned} p_{0}\le \inf _{t>0} \frac{t{\varphi }'(t)}{{\varphi }(t)}\le \sup _{t>0} \frac{t{\varphi }'(t)}{{\varphi }(t)}\le p_{1}. \end{aligned}$$

Moreover the following inequalities hold for every $t\ge 0$:

$$\begin{aligned} \begin{aligned}&s^{p_{1}} {\varphi }(t) \le {\varphi }(st) \le s^{p_{0}} {\varphi }(t) \quad \text{ if } 0< s \le 1, \\&s^{p_{0}} {\varphi }(t) \le {\varphi }(st) \le s^{p_{1}} {\varphi }(t) \quad \text{ if } s \ge 1, \end{aligned} \end{aligned}$$

(2.2)

as well

$$\begin{aligned} \begin{aligned}&s^{\frac{p_0}{p_0-1}} {\varphi }^*(t) \le {\varphi }^*(st) \le s^{\frac{p_{1}}{p_1-1}} {\varphi }^*(t) \quad \text{ if } 0< s \le 1, \\&s^{\frac{p_{1}}{p_1-1}} {\varphi }^*(t) \le {\varphi }^*(st) \le s^{\frac{p_{0}}{p_0-1}} {\varphi }^*(t) \quad \text{ if } s \ge 1, \end{aligned} \end{aligned}$$

(2.3)

and also

$$\begin{aligned} \begin{aligned}&s^{p_{1}-1} {\varphi }'(t) \le {\varphi }'(st) \le s^{p_{0}-1} {\varphi }'(t) \quad \text{ if } 0< s \le 1, \\&s^{p_{0}-1} {\varphi }'(t) \le {\varphi }'(st) \le s^{p_{1}-1} {\varphi }'(t) \quad \text{ if } s \ge 1. \end{aligned} \end{aligned}$$

(2.4)

In particular, for $t>0$ we have

$$\begin{aligned} {\varphi }(t)\sim t{\varphi }'(t), \quad {\varphi }'(t)\sim t{\varphi }''(t), \quad {\varphi }^{*}({\varphi }'(t)) \sim {\varphi }(t), \quad {\varphi }^{-1}(t)({\varphi }^{*})^{-1}(t)\sim t. \end{aligned}$$

(2.5)

Now, we consider a family of N-functions $\{\varphi _{a}\}_{a\ge 0}$ setting, for $t\ge 0$,

$$\begin{aligned} \varphi _{a}(t):=\int _{0}^{t} \varphi '_{a}(s) \, ds \quad \text{ with } \quad \varphi '_{a}(t):= \varphi '(a+t) \frac{t}{a+t}. \end{aligned}$$

The following lemma can be found in [16, Lemma 27].

Lemma 2.1

Let ${\varphi }$ be an N-function with ${\varphi }\in \Delta _2$ together with its conjugate. Then for all $a\ge 0$ the function $\varphi _a$ is an N-function and $\{\varphi _{a}\}_{a\ge 0}$ and $\{(\varphi _{a})^{*}\}_{a\ge 0}\sim \{\varphi ^*_{\varphi '(a)}\}_{a\ge 0}$ satisfy the $\Delta _{2}$-condition uniformly in $a\ge 0$.

Let us observe that by the previous lemma $\varphi _{a}(t)\sim t\varphi '_{a}(t)$. Moreover, for $t\ge a$ we have $\varphi _{a}(t)\sim \varphi (t)$, while Assumption 1.1 provides

$$\begin{aligned} C^{-1}{\varphi }''(a)t^2\le {\varphi }_a(t) \le C{\varphi }''(a)t^2, \quad \hbox { for } 0\le t\le a, \end{aligned}$$

(2.6)

since ${\varphi }'\sim t{\varphi }''$. The constant C depends on only $p_0$ and $p_1$. This implies also that, for all $s\in [0,1]$, $a\ge 0$ and $t\in [0,a]$,

$$\begin{aligned} \varphi _{a}(st)\le C^2s^{2} \varphi _{a}(t). \end{aligned}$$

(2.7)

Finally, allowing Assumption 1.1, the following relations hold uniformly with respect to $a\ge 0$

$$\begin{aligned} \begin{aligned}&{\varphi }_{a}(t)\sim {\varphi }''(a+t) t^{2} \sim \frac{{\varphi }(a+t)}{(a+t)^{2}}t^{2} \sim \frac{{\varphi }'(a+t)}{a+t}t^{2}, \\&{\varphi }(a+t)\sim {\varphi }_{a}(t) + {\varphi }(a). \end{aligned} \end{aligned}$$

(2.8)

Remark 2.3

It is easy to check that if ${\varphi }$ satisfies Assumption 1.1, the same is true for ${\varphi }_a$, uniformly with respect to $a\ge 0$ (with the same $p_0$ and $p_1$). This in particular means that

$$\begin{aligned} \sup _{a\ge 0}\Delta _2({\varphi }_a)\le 2^{p_1} \end{aligned}$$

(2.9)

and

$$\begin{aligned} t^{p_0}{\varphi }_a(1)\le {\varphi }_a(t)\le t^{p_1}{\varphi }_a(1), \quad \hbox { for } t\ge a\ge 1, \end{aligned}$$

thanks to (2.2) for ${\varphi }_a$.

Next result is a slight generalization of [16, Lemma 20].

Lemma 2.2

Let $\varphi$ be an N-function with $\Delta _{2}(\varphi ,\varphi ^*)<\infty$; then, uniformly in $\xi _{1}, \xi _{2} \in \mathbb {R}^{Nn}$ with $|\xi _{1}|+|\xi _{2}|>0$, and in $\mu \ge 0$, it holds

$$\begin{aligned} \frac{\varphi '(\mu +|\xi _{1}|+|\xi _{2}|)}{\mu +|\xi _{1}|+|\xi _{2}|} \sim \int _{0}^{1} \frac{\varphi '(\mu +|\xi _{\theta }|)}{\mu +|\xi _{\theta }|} d\theta , \end{aligned}$$

where $\xi _{\theta }= \xi _{1} + \theta (\xi _{2}-\xi _{1})$ with $\theta \in [0,1]$.

Remark 2.4

We now state the following two consequences of our structure assumptions for further reference. First, we note that the ellipticity condition $(a_2)$ and Assumption 1.1 together with Lemma 2.2 and (2.8) imply

$$\begin{aligned} (a(\xi )-a(\xi _0))\cdot (\xi -\xi _0)\ge c {\varphi }_{1+|\xi _0|}(|\xi -\xi _0|), \end{aligned}$$

for every $\xi ,\xi _0\in \mathbb {R}^{Nn}$, where $c=c(p_0,p_1,\nu )$.

In a similar way, the growth condition $(a_3)$ and Assumption 1.1 imply

$$\begin{aligned} |a(\xi )-a(\xi _0)|\le c {\varphi }'_{1+|\xi _0|}(|\xi -\xi _0|), \end{aligned}$$

for every $\xi ,\xi _0\in \mathbb {R}^{Nn}$, where $c=c(p_0,p_1,L)$.

The following results deal with the change of shift of N-functions $\varphi _{a}$. The first one is proved in [17, Corollary 26].

Lemma 2.3

Let ${\varphi }$ be a N-function satisfying $\Delta _2({\varphi },{\varphi }^*)<+\infty$. Then for each $\delta >0$, there exists $c_\delta (\Delta _2({\varphi },{\varphi }^*)) > 0$ such that for all $a,b\in \mathbb {R}^d$ and $t\ge 0$

$$\begin{aligned} {\varphi }_{|a|}(t)\le c_\delta {\varphi }_{|b|}(t) + \delta {\varphi }_{|a|}(|a-b|). \end{aligned}$$

Lemma 2.4

Let ${\varphi }$ be a N-function satisfying Assumption 1.1; let $M\ge 1$ and $1\le a,b\le M$ be given. Then

$$\begin{aligned} {\varphi }_a(t)\le 4^{p_1+1}M^{p_1+2}{\varphi }_b(t), \quad \text { for all }t\ge 0. \end{aligned}$$

Proof

From the definition and the fact that $t/2{\varphi }'(t/2)\le {\varphi }(t)\le t{\varphi }'(t)$,

$$\begin{aligned} {\varphi }'_a(s)={\varphi }'_b(s)\left[ \frac{{\varphi }'(a+s)}{{\varphi }'(b+s)}\left( \frac{s+b}{s+a}\right) \right] \le {\varphi }'_b(s)\left[ \frac{{\varphi }(2(a+s))}{{\varphi }(b+s)} \left( \frac{s+b}{s+a}\right) ^2\right] . \end{aligned}$$

If $s\le M$, then, using (2.2), we have

$$\begin{aligned} \frac{{\varphi }(2(a+s))}{{\varphi }(b+s)}\left( \frac{s+b}{s+a}\right) ^2 \le \frac{{\varphi }(4M)}{{\varphi }(1)}M^2 \le 4^{p_1}M^{p_1+2}. \end{aligned}$$

Otherwise, $1\le a,b\le M< s$ and

$$\begin{aligned} \frac{{\varphi }(2(a+s))}{{\varphi }(b+s)}\left( \frac{s+b}{s+a}\right) ^2 \le 4\frac{{\varphi }(4s)}{{\varphi }(s)}\le 4^{p_1+1}. \end{aligned}$$

Thus

$$\begin{aligned} {\varphi }_a(t)=\int _0^t{\varphi }_a'(s)\, d s \le \left( 4^{p_1}M^{p_1+2}+4^{p_1+1}\right) \int _0^t{\varphi }_b'(s)\, d s \le 4^{p_1+1}M^{p_1+2}{\varphi }_b(t). \end{aligned}$$

$\square$

We will use the function $V:\mathbb {R}^{Nn}\rightarrow \mathbb {R}^{Nn}$ defined by

$$\begin{aligned} V(\xi ) = \sqrt{\frac{{\varphi }'(1+|\xi |)}{1+|\xi |}}\xi . \end{aligned}$$

The monotonicity property of ${\varphi }$ ensures that

$$\begin{aligned} |V(\xi _{1})-V(\xi _{2})|^{2}\sim {\varphi }_{1+|\xi _{1}|}(|\xi _{1}-\xi _{2}|) \quad \text{ for } \text{ any } \xi _{1}, \xi _{2} \in \mathbb {R}^{Nn}; \end{aligned}$$

(2.10)

see [16] for further properties about the V-function.

Let ${\varphi }$ be an N-function that satisfies the $\Delta _{2}$-condition. The set of functions $L^{{\varphi }}(\Omega , \mathbb {R}^{N})$ is defined by

$$\begin{aligned} L^{{\varphi }}(\Omega , \mathbb {R}^{N})= \left\{ u: \Omega \rightarrow \mathbb {R}^{N} \text{ measurable } : \, \int _{\Omega } {\varphi }(|u|)\, dx <\infty \right\} . \end{aligned}$$

The Luxembourg norm is defined as follows:

$$\begin{aligned} \Vert u\Vert _{L^\varphi (\Omega , \mathbb {R}^{N})}=\inf \left\{ \lambda >0 : \int _{\Omega } \varphi \left( \frac{|u(x)|}{\lambda } \right) \,dx\le 1\right\} . \end{aligned}$$

With this norm $L^\varphi (\Omega , \mathbb {R}^{N})$ is a Banach space.

By $W^{1, {\varphi }}(\Omega , \mathbb {R}^{N})$ we denote the classical Orlicz-Sobolev space, that is $u\in W^{1, {\varphi }}(\Omega , \mathbb {R}^{N})$ whenever $u, Du \in L^{{\varphi }}(\Omega , \mathbb {R}^{N})$. Furthermore, by $W^{1,{\varphi }}_{0}(\Omega , \mathbb {R}^{N})$ we mean the closure of $C^{\infty }_{c}(\Omega , \mathbb {R}^{N})$ functions with respect to the norm

$$\begin{aligned} \Vert u\Vert _{W^{1, {\varphi }}(\Omega , \mathbb {R}^{N})}=\Vert u\Vert _{L^{{\varphi }}(\Omega , \mathbb {R}^{N})}+\Vert Du\Vert _{L^{{\varphi }}(\Omega , \mathbb {R}^{N})}. \end{aligned}$$

For a function $u\in L^\varphi (\mathcal {Q}_\rho (z_0), \mathbb {R}^{N})$, using the decomposition

$$\begin{aligned} \mathcal {Q}_\rho ^{\le }(z_0)=\{z\in \mathcal {Q}_\rho (z_0) : |u(z)|\le a\}\quad \hbox { and } \quad \mathcal {Q}_\rho ^{>}(z_0)=\{z\in \mathcal {Q}_\rho (z_0) : |u(z)|> a\}, \end{aligned}$$

as well as (2.6) and Remark 2.3, we easily get the following lemma.

Lemma 2.5

Let ${\varphi }$ be a N-function satisfying Assumption 1.1 and let $u\in L^{{\varphi }}(\mathcal {Q}_\rho (z_0),\mathbb {R}^N)$, $a\ge 1$. Then

• (a)
  $$\begin{aligned} int_{\mathcal {Q}_\rho (z_0)}{\varphi }_a(|u|)\, dz \le C{\varphi }''(a)int_{\mathcal {Q}_\rho (z_0)}|u|^2\, dz+{\varphi }_a(1)int_{\mathcal {Q}_\rho (z_0)}|u|^{p_1}\, dz; \end{aligned}$$

• (b) for each $0\le s\le p_0<2$,

  $$\begin{aligned} int_{\mathcal {Q}_\rho (z_0)}|u|^s\, dz \le \left( \frac{C}{{\varphi }''(a)}int_{\mathcal {Q}_\rho (z_0)}{\varphi }_a(|u|)\, dz\right) ^\frac{s}{2} +\frac{1}{{\varphi }_a(1)}int_{\mathcal {Q}_\rho (z_0)}{\varphi }_a(|u|)\, dz. \end{aligned}$$

Here C only depends on $p_0,p_1$.

2.2 Affine functions

Let $z_{0}\in \mathbb {R}^{n+1}$ and $\rho >0$. Given $u\in L^{2}(\mathcal {Q}_{\rho }(z_{0}), \mathbb {R}^{N})$, we denote by $\ell _{z_{0}, \rho }:\mathbb {R}^{n}\rightarrow \mathbb {R}^{N}$ the unique affine function minimizing the functional

$$\begin{aligned} \ell (x)\mapsto int_{\mathcal {Q}_{\rho }(z_{0})} |u(x,t)-\ell (x)|^2\, dz \end{aligned}$$

amongst all affine functions $\ell : \mathbb {R}^{n}\rightarrow \mathbb {R}^{N}$. It is well known (see [5]) that

$$\begin{aligned} \ell _{z_{0}, \rho }(x)= (u)_{z_{0}, \rho } + P_{z_{0}, \rho }(x-x_{0}), \end{aligned}$$

(2.11)

where

$$\begin{aligned} P_{z_{0}, \rho }= \frac{n+2}{\rho ^{2}} int_{\mathcal {Q}_{\rho }(z_{0})} u(x,t)\otimes (x-x_{0})\, dz. \end{aligned}$$

(2.12)

The following lemma ensures that $\ell _{z_0,\rho }$ is an almost minimizer of the functional $\displaystyle {\ell \mapsto int_{\mathcal {Q}_{\rho }(z_{0})} {\varphi }\left( \frac{|u-\ell |}{r}\right) \, dz}$ amongst the affine functions $\ell : \mathbb {R}^{n}\rightarrow \mathbb {R}^{N}$.

Lemma 2.6

Let ${\varphi }$ be an N-function satisfying the $\Delta _2$-property and let $u\in L^{{\varphi }}(\mathcal {Q}_{\rho }(z_{0}), \mathbb {R}^{N})$. Let $r>0$, then there exists a constant $\kappa _0= \kappa _0(n,\Delta _2({\varphi }))>0$ such that

$$\begin{aligned} int_{\mathcal {Q}_{\rho }(z_{0})} {\varphi }\left( \frac{|u-\ell _{z_0,\rho }|}{r}\right) \, dz\le \kappa _0 int_{\mathcal {Q}_{\rho }(z_{0})} {\varphi }\left( \frac{|u-\ell |}{r}\right) \, dz, \end{aligned}$$

for every affine function $\ell : \mathbb {R}^{n}\rightarrow \mathbb {R}^{N}$.

Proof

Assume $z_{0}=(0,0)$ and denote $\ell _{z_0,\rho }$, $\mathcal {Q}_\rho (z_0)$, and $(u)_{z_0,\rho }$ by $\ell _{\rho }$, $\mathcal {Q}_\rho$, and $(u)_{\rho }$, respectively. Let us consider a generic affine function $\ell (x)=\zeta +Ax$, then, for $x\in \mathcal {B}_\rho$,

$$\begin{aligned} |\ell -\ell _\rho |=|(u)_\rho -\zeta + (D\ell _\rho -A)x|\le |(u)_\rho -\zeta |+\rho |D\ell _\rho -A|. \end{aligned}$$

Now we have

$$\begin{aligned} |(u)_\rho -\zeta |=\left| int_{\mathcal {Q}_\rho }(u-\zeta )\,dz\right| =\left| int_{\mathcal {Q}_\rho }(u-\zeta -Ax)\,dz\right| \le int_{\mathcal {Q}_\rho }|u-\ell |\,dz, \end{aligned}$$

and, using (2.12),

$$\begin{aligned}{} & {} |D\ell _\rho -A|=\frac{n+2}{\rho ^2}\left| int_{\mathcal {Q}_\rho }(u-Ax)\otimes x\,dz\right| =\frac{n+2}{\rho ^2}\left| int_{\mathcal {Q}_\rho }(u-\zeta -Ax)\otimes x\,dz\right| \nonumber \\{} & {} \le \frac{n+2}{\rho }int_{\mathcal {Q}_\rho }|u-\ell |\,dz. \end{aligned}$$

(2.13)

In conclusion

$$\begin{aligned} |\ell -\ell _\rho |\le (n+3)int_{\mathcal {Q}_\rho }|u-\ell |\,dz. \end{aligned}$$

(2.14)

Recalling that, by the convexity and the $\Delta _2$-condition, ${\varphi }(s+t)\sim {\varphi }(s)+ {\varphi }(t)$ for any $s, t\ge 0$, we have

$$\begin{aligned} int_{\mathcal {Q}_{\rho }} {\varphi }\left( \frac{|u-\ell _{\rho }|}{r}\right) \, dz \le \frac{\Delta _2({\varphi })}{2}int_{\mathcal {Q}_{\rho }} {\varphi }\left( \frac{|u-\ell |}{r}\right) \, dz + \frac{\Delta _2({\varphi })}{2}int_{\mathcal {Q}_{\rho }}{\varphi }\left( \frac{|\ell -\ell _{\rho }|}{r}\right) \, dz. \end{aligned}$$

Hence, using (2.14), the fact that ${\varphi }$ is increasing together with Jensen’s inequality, we can infer that

$$\begin{aligned} int_{\mathcal {Q}_{r}} {\varphi }\left( \frac{|\ell - \ell _{\rho }|}{r}\right) \, dz \lesssim int_{\mathcal {Q}_{\rho }} {\varphi }\left( \frac{|u-\ell |}{r}\right) \, dz. \end{aligned}$$

$\square$

An analogous reasoning leads to another basic inequality.

Remark 2.5

For an N-function ${\varphi }$ satisfying the $\Delta _2$-condition, we have

$$\begin{aligned} int_{\mathcal {Q}_{\rho }(z_{0})} {\varphi }\left( \frac{|u-(u)_{z_{0}, \rho }|}{r}\right) \,dz \le \Delta _2({\varphi }) \,int_{\mathcal {Q}_{\rho }(z_{0})} {\varphi }\left( \frac{|u-u_{0}|}{r}\right) \, dz, \end{aligned}$$

for any $u_0\in \mathbb {R}^N$ and for any $r>0$.

Finally, we can show that $\ell _{z_0,\rho }$ is an almost minimizer of the functional $\displaystyle \ell \mapsto int_{\mathcal {Q}_{\rho }(z_{0})} {\varphi }_{1+|D\ell |}\left( \frac{|u-\ell |}{\rho }\right) \, dz$ amongst the affine functions $\ell : \mathbb {R}^{n}\rightarrow \mathbb {R}^{N}$.

Lemma 2.7

Let ${\varphi }$ be an N-function satisfying $\Delta _2({\varphi },{\varphi }^*)<+\infty$, and let $u\in L^{{\varphi }}(\mathcal {Q}_{\rho }(z_{0}), \mathbb {R}^{N})$. There exists a constant $\kappa _1= \kappa _1(n,\Delta _2({\varphi },{\varphi }^*))>0$ such that

$$\begin{aligned} int_{\mathcal {Q}_{\rho }(z_{0})} {\varphi }_{1+|D\ell _{z_0,\rho }|}\left( \frac{|u-\ell _{z_0,\rho }|}{\rho }\right) \, dz\le \kappa _1 int_{\mathcal {Q}_{\rho }(z_{0})} {\varphi }_{1+|D\ell |}\left( \frac{|u-\ell |}{\rho }\right) \, dz, \end{aligned}$$

for every affine function $\ell : \mathbb {R}^{n}\rightarrow \mathbb {R}^{N}$.

Proof

From Lemma 2.1, Lemma 2.6, and Lemma 2.3 we obtain

$$\begin{aligned} \begin{aligned} int_{\mathcal {Q}_{\rho }(z_{0})} {\varphi }_{1+|D\ell _{z_0,\rho }|}\left( \frac{|u-\ell _{z_0,\rho }|}{\rho }\right) \, dz&\le \kappa _0\, int_{\mathcal {Q}_{\rho }(z_{0})} {\varphi }_{1+|D\ell _{z_0,\rho }|}\left( \frac{|u-\ell |}{\rho }\right) \, dz\\&\le c_\delta int_{\mathcal {Q}_{\rho }(z_{0})} {\varphi }_{1+|D\ell |}\left( \frac{|u-\ell |}{\rho }\right) \, dz +\delta {\varphi }_{1+|D\ell |}(|D\ell -D\ell _{z_0,\rho }|),\\ \end{aligned} \end{aligned}$$

using also the fact that ${\varphi }_{1+|a|}(|a-b|)\sim {\varphi }_{1+|b|}(|a-b|)$. Moreover, from (2.13) we infer

$$\begin{aligned} |D\ell _{z_0,\rho }-D\ell |\le (n+2)int_{\mathcal {Q}_\rho (z_0)}\frac{|u-\ell |}{\rho }\,dz. \end{aligned}$$

Inserting this above, applying the $\Delta _2$-condition, and Jensen’s inequality conclude the proof. $\square$

In the same way you obtain the following fact.

Remark 2.6

For an N-function ${\varphi }$ satisfying $\Delta _2({\varphi },{\varphi }^*)<\infty$, we have

$$\begin{aligned} int_{\mathcal {Q}_{\rho }(z_{0})} {\varphi }_{1+|(Du)_{z_0,\rho }|} \left( |Du-(Du)_{z_0,\rho }|\right) \,dz\le \kappa _2 \,int_{\mathcal {Q}_{\rho }(z_{0})} {\varphi }_{1+|A|}\left( |Du-A|\right) \, dz, \end{aligned}$$

for any $A\in \mathbb {R}^{Nn}$, where $\kappa _2= \kappa _2(n,\Delta _2({\varphi },{\varphi }^*))>0$.

We conclude the section with an excess-decay-estimate for weak solutions to linear parabolic systems with constant coefficients [9, Lemma 5.1]. This can be achieved along the lines of the classical proof with very minor changes, so we will consider only the main points of the proof referring for the rest to [9].

Lemma 2.8

($\mathcal {A}$-Caloric $\psi$-Excess Estimate) Suppose that $h\in L^1(t_0-R^2,t_0;W^{1,1}(\mathcal {B}_R(x_0);\mathbb {R}^{N}))$ is $\mathcal {A}$-caloric, and let $\psi :[0,\infty )\rightarrow [0,\infty )$ be an increasing function. Then $h\in C^\infty (\mathcal {Q}_R(z_0);\mathbb {R}^{N})$ and the following excess estimate holds: for each $0<\rho <R$, $\gamma >0$, and $0<\theta <1/4$, we have

$$\begin{aligned} int_{\mathcal {Q}_{\theta \rho }(z_0)}\psi \left( \left| \frac{\gamma (h-\ell ^{(h)}_{z_0,\theta \rho })}{\theta \rho }\right| \right) dz \le \psi \left( C\theta {int}_{Q_\rho (z_0)}\left| \frac{\gamma (h-\ell ^{(h)}_{z_0,\rho })}{\rho }\right| \,dz\right) \end{aligned}$$

where $\ell ^{(h)}_r(x):=(h)_{z_0,r}+(Dh)_{z_0,r}(x-x_0)$ and C depends on only $n,N,L/\nu$.

Proof

It is only necessary to prove the estimate, since the smoothness of h is already contained in [9]. As argued in [4, Remark 3.2 and Lemma 3.3], we may use (5.9) and (5.12) in [9] to show that there exists $C'=C'(n,L/\nu )<\infty$ such that

$$\begin{aligned} \sup _{\mathcal {Q}_{\rho /2}(z_0)} |D^2w| \le C'int_{\mathcal {Q}_\rho (z_0)}\left| \frac{w}{\rho ^2}\right| \, d z \quad \text { and }\quad \sup _{\mathcal {Q}_{\rho /2}(z_0)} |D^3w| \le C'int_{\mathcal {Q}_\rho (z_0)}\left| \frac{w}{\rho ^3}\right| \, d z,\nonumber \\ \end{aligned}$$

(2.15)

for any $\mathcal {A}$-caloric map $w\in C^\infty (\mathcal {Q}_R(z_0);\mathbb {R}^{N})$. Define $w_r= h-\ell ^{(h)}_{z_0,r}$. Then $w_r$ is $\mathcal {A}$-caloric and $w_r\in C^\infty (\mathcal {Q}_R(z_0);\mathbb {R}^N)$, for each $0<r<R$. Let $0<\theta <\frac{1}{4}$ and $0<\rho \le R$ be given. Using (2.15), the fact that $\mathcal {Q}_r(z_0)$ is a standard parabolic cylinder, and the fact that every derivative of h is still $\mathcal {A}$-caloric, for each $(x,t)\in \mathcal {Q}_{\theta \rho }(z_0)$, we have

$$\begin{aligned} |w_{\theta \rho }(x,t)| \le&\theta \rho \sup _{\mathcal {Q}_{\theta \rho }(z_0)}|Dh-(Dh)_{z_0,\theta \rho }|+\theta ^2\rho ^2\sup _{\mathcal {Q}_{\theta \rho }(z_0)}|\partial _th|\\ \le&\theta ^2\rho ^2\left( \sup _{\mathcal {Q}_{\theta \rho }(z_0)}|D^2h|+\theta \rho \sup _{\mathcal {Q}_{\theta \rho }(z_0)}|\partial _t Dh|+\sup _{\mathcal {Q}_{\theta \rho }(z_0)}|\partial _t h| \right) \\ \le&C''\theta ^2\rho ^2\left( \sup _{\mathcal {Q}_{\rho /2}(z_0)} |D^2w_\rho |+\theta \rho \sup _{\mathcal {Q}_{\rho /2}(z_0)}|D^3w_\rho |\right) \\ \le&C\theta ^2int_{\mathcal {Q}_{\rho }(z_0)}|w_\rho |\, d z. \end{aligned}$$

Here, $C''$ and C depend on only n, N, and $L/\nu$. The result follows from this and the definition of $w_\rho$. $\square$

3 ${\mathcal {A}}$-caloric approximation

To prove the partial regularity for non-degenerate parabolic systems with ${\varphi }$-growth, we shall compare the solution of our parabolic system with the solution of a linear parabolic system with constant coefficients. The comparison will be achieved by a generalization of the ${\mathcal {A}}$-caloric approximation lemma in Orlicz spaces. We emphasize that the approximation lemma requires no upper bound on the growth of ${\varphi }$.

Recall that a function $f:[0,+\infty )\rightarrow [0,+\infty )$ is said to be almost increasing if there exists $\Lambda \ge 1$ such that $f(t)\le \Lambda f(s)$ for every $0\le t<s<+\infty$. We will consider the following assumptions for the N-function ${\varphi }$, more general with respect to Assumption 1.1:

(H1):

There exists a $\displaystyle {p_0>\frac{2n}{n+2}}$ such that $\displaystyle {\frac{{\varphi }(t)}{t^{p_0}}}$ is almost increasing,

(H2):

${\varphi }$ has a uniform doubling property near zero; i.e. $\displaystyle {\limsup _{t\rightarrow 0^+} \frac{{\varphi }(2t)}{{\varphi }(t)}=\Delta _0({\varphi })<\infty }$.

In general, an N-function might not satisfy assumption (H2). For example, with

$$\begin{aligned} \ell _k(t)=\frac{1}{k!}+\frac{2^{k}(k-1)}{k!}(t-2^{-k}), \quad \text { for }k\in \mathbb {N}, \end{aligned}$$

the N-function

$$\begin{aligned} {\varphi }(t)=\left\{ \begin{array}{ll} 0, &{} t=0,\\ \ell _{k+1}(t), &{} k\in \mathbb {N}\setminus \{1\}\text { and }2^{-k-1}\le t<2^{-k}\\ 8t^2, &{} 2^{-2}\le t, \end{array}\right. \end{aligned}$$

is not uniformly doubling near zero since $(k+1)\ell _{k+1}(2^{-k-1})=\ell _k(2^{-k})$. For any N-function and $a>0$, however, (H2) is satisfied by the shifted function ${\varphi }_a(t)$. In fact,

$$\begin{aligned} \frac{{\varphi }_a(2t)}{{\varphi }_a(t)}\le \frac{4{\varphi }'(2a)}{{\varphi }'(a)}, \quad \text { for all }0<t\le \frac{a}{2}. \end{aligned}$$

3.1 Additional notation and supporting results

For this section, we introduce some additional notation. There are also several supporting results used in the proof of the approximation lemma.

First, we require a compactness principle of Simon.

Theorem 3.1

([42, Theorem 6]) Suppose that $X\subseteq B\subseteq Y$ are Banach spaces with a compact embedding $X\rightarrow B$. Given $1<q\le \infty$, assume

• F is bounded in $L^q(0,T;B)\cap L^1_{loc}(0,T;X)$,

• for all $0<t_1<t_2<T$, $\Vert f(\cdot +h)-f(\cdot )\Vert _{L^p(t_1,t_2;Y)}\rightarrow 0$ as $h\rightarrow 0$, uniformly for $f\in F$.

Then F is relatively compact in $L^p(0,T;B)$ for all $1\le p<q$.

We also need to work with the Orlicz norm: given a measurable $E\subseteq \mathbb {R}^n$,

$$\begin{aligned} \Vert f\Vert _{L^*_{{\varphi }}(E)}=\sup \left\{ \int _Ef(y)g(y) dy :\int _E{\varphi }^*(|g(y)|) dy\le 1\right\} . \end{aligned}$$

It can be verified [33] that the Orlicz space

$$\begin{aligned} L^*_{{\varphi }}(E)=\{f\in L^1(E): \Vert f\Vert _{L^*_{{\varphi }}(E)}<\infty \} \end{aligned}$$

is a Banach space. The Orlicz norm is equivalent to the Luxemborg norm ( [33], p. 80). Moreover, as established in [33, Lemma 9.2 and p. 75], given $\{f_k\}_{k=1}^\infty \subseteq L^*_{{\varphi }}(E)$ and $f\in L^*_{{\varphi }}(E)$,

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert f_k-f\Vert _{L^*_{{\varphi }}(E)}= 0 \Longrightarrow \lim _{k\rightarrow \infty }\int _E{\varphi }(\lambda |f_k(x)-f(x)|)d x=0, \quad \text { for all }\lambda >0.\nonumber \\ \end{aligned}$$

(3.1)

We will also need the following

Definition 3.1

Given an open set $E\subseteq \mathbb {R}^n$ and $f\in L^1_{loc}(E)$, the (non-centered) Hardy-Littlewood maximal operator is $M(f):E\rightarrow [0,\infty ]$

$$\begin{aligned} Mf(x)=\sup _{\mathcal {B}\ni x}int_{\mathcal {B}\cap E}|f(y)|dy. \end{aligned}$$

Here the supremum is taken over all balls containing x.

It is well-known that the maximal operator is bounded on $L^p$, for $p>1$. From [30, Corollary 4.3.3], we have

Corollary 3.1

Let an open set $E\subseteq \mathbb {R}^n$ and an N-function ${\varphi }$ be given. If $p>1$ and $\displaystyle {\frac{{\varphi }(t)}{t^{p}}}$ is almost increasing, then there exists a $\beta >0$ such that

$$\begin{aligned} {\varphi }(\beta Mf(x))^\frac{1}{p}\lesssim M\left( {\varphi }(f)^\frac{1}{p}\right) (x) \end{aligned}$$

for every ball $\mathcal {B}$, $x\in \mathcal {B}\cap E$, and $f\in L^{{\varphi }}(E)$ satisfying $\displaystyle {\int _E{\varphi }(f)dx\le 1}$.

Finally, as explained in the proof of the ${\mathcal {A}}$-caloric excess estimate (Lemma 2.8), we may use the regularity provided in (5.9) and (5.12) in [9] to show there is a $C=C(L/\nu )<\infty$ such that

$$\begin{aligned} \sup _{\mathcal {Q}_{\tau R}(z_0)}\left( |Dw|^2+|w|^2\right) \le C int_{\mathcal {Q}_R(z_0)}|w|^2dz, \end{aligned}$$

(3.2)

for any $\frac{3}{4}\le R\le 1$, $\frac{1}{2}\le \tau \le \frac{3}{4}$, and ${\mathcal {A}}$-caloric map $w\in L^1(t_0-R^2,0;W^{1,2}(\mathcal {B}_R(x_0);\mathbb {R}^N))$.

3.2 The ${\mathcal {A}}$-Caloric approximation lemma

With the preliminaries above, we can state and prove the main result for this section.

Theorem 3.2

Suppose that (H1) and (H2) are satisfied. Let $\varepsilon ,\nu >0$ and $\nu<L<\infty$ be given. There exists $\delta _0\le 1$, $\delta _0$ depending on $n,N,p_0,\Delta _0(\varphi ), \nu ,L,\varepsilon$, and $1\le K_{{\varphi }}$ with the following property: for any ${\gamma \in (0,1/\sqrt{\omega _n}\,]}$ (with $\omega _n$ being the measure of the unit sphere in $\mathbb {R}^n$), any bilinear form ${\mathcal {A}}$ satisfying

$$\begin{aligned} {\mathcal {A}}(\xi ,\xi )\ge \nu |\xi |^2 \quad \text { and }\quad |{\mathcal {A}}(\xi ,\eta )|\le L|\xi ||\eta |, \end{aligned}$$

and any approximately ${\mathcal {A}}$-caloric map $v\in L^\infty (t_0-\rho ^2,t_0;L^2(\mathcal {B}_\rho (x_0);\mathbb {R}^N))\cap L^1(t_0-\rho ^2,t_0;W^{1,1}(\mathcal {B}_\rho (x_0);\mathbb {R}^N))$ satisfying:

• ${\varphi }(|Dv|)\in L^1(t_0-\rho ^2,t_0;L^1(\mathcal {B}_\rho (x_0)))$,

• for some $0<\delta \le \delta _0$,

  $$\begin{aligned} \left| int_{\mathcal {Q}_\rho (z_0)}\left( v\cdot \partial _t\eta -{\mathcal {A}}(Dv,D\eta )\right) dz\right| \le \delta \sup _{\mathcal {Q}_\rho (z_0)}|D\eta |,\,\text { for all }\eta \in C^\infty _c(\mathcal {Q}_\rho (z_0);\mathbb {R}^N),\nonumber \\ \end{aligned}$$

  (3.3)

• and

  $$\begin{aligned} \sup _{t_0-\rho ^2<t<t_0}int_{B_\rho }\left| \frac{v}{\rho }\right| ^2d x +int_{\mathcal {Q}_\rho (z_0)}\left( {\varphi }\left( \left| \frac{v}{\rho }\right| \right) +{\varphi }(|Dv|)\right) d z\le \gamma ^2, \end{aligned}$$

  (3.4)

then there exists an ${\mathcal {A}}$-caloric map $h\in L^2(t_0-\rho ^2/4,t_0;W^{1,2}(\mathcal {B}_{\rho /2}(x_0);\mathbb {R}^N))$ such that

$$\begin{aligned} int_{\mathcal {Q}_{\rho /2(z_0)}}\left( \left| \frac{\gamma h}{\rho /2}\right| ^2 +{\varphi }\left( \left| \frac{\gamma h}{\rho /2}\right| \right) +{\varphi }(|\gamma Dh|)\right) d z \le 2^{n+2}K_{{\varphi }}\gamma ^2, \end{aligned}$$

and

$$\begin{aligned} int_{\mathcal {Q}_{\rho /2(z_0)}}\left( \left| \frac{v-\gamma h}{\rho /2}\right| ^2 +{\varphi }\left( \left| \frac{v-\gamma h}{\rho /2}\right| \right) \right) d z \le \varepsilon \gamma ^2. \end{aligned}$$

The constant $K_{{\varphi }}$ is defined in (3.12) and depends only on ${\varphi }$ and $C(L/\nu )$ in (3.2).

Proof

We translate and rescale to $z_0=(0,0)$ and $\rho =1$. Assuming the alternative, there exists an $\varepsilon _0>0$, sequences ${\gamma _k\in (0,1/\sqrt{\omega _n}\,]}$, bilinear forms ${\mathcal {A}}_k$, and maps $v_k\in L^\infty (-1,0;L^2(\mathcal {B}_1;\mathbb {R}^N))\cap L^1(-1,0;W^{1,1}(\mathcal {B}_1;\mathbb {R}^N))$, such that for each $k\in \mathbb {N}$, the following holds:

• (i) ${\varphi }(|Dv_k|)\in L^1(-1,0;L^1(\mathcal {B}_1))$,

• (ii) $\displaystyle {int_{\mathcal {Q}_1}\left( v_k\cdot \partial _t\eta -{\mathcal {A}}_k(Dv_k,D\eta )\right) d z \le \frac{1}{k}\displaystyle {\sup _{\mathcal {Q}_1}}|D\eta |,\,}$ for all $\eta \in C^\infty _0(\mathcal {Q}_1;\mathbb {R}^N)$,

• (iii) $\displaystyle {\sup _{t\in (-1,0)}int_{\mathcal {B}_1}|v_k|^2 d x +int_{\mathcal {Q}_1}\left( {\varphi }(|v_k|)+{\varphi }(|Dv_k|)\right) d z\le \gamma _k^2}$,

• (iv) for any ${\mathcal {A}}_k$-caloric map $h\in C^\infty (\mathcal {Q}_{1/2};\mathbb {R}^N)$ satisfying

  $$\begin{aligned} int_{\mathcal {Q}_{1/2}}\left( 4|\gamma _k h|^2+{\varphi }(2|\gamma _kh|) +{\varphi }(|\gamma _kDh|)\right) d z \le 2^{n+2}K_{{\varphi }}\gamma _k^2, \end{aligned}$$

  we find

  $$\begin{aligned} int_{\mathcal {Q}_{1/2}}\left( 4|v_k-\gamma _kh|^2+{\varphi }(2|v_k-\gamma _kh|)\right) d z >\varepsilon _0\gamma _k^2. \end{aligned}$$

By (iii) the sequence $\{{\varphi }(|Dv_k|)\}_{k=1}^\infty$ is bounded in $L^1(-1,0;L^1(\mathcal {B}_1;\mathbb {R}^N))$. Assumption (H1) implies the existence of a constant C such that

$$\begin{aligned} \Vert v_k\Vert _{L^{p_0}(\mathcal {Q}_1)} +\Vert Dv_k\Vert _{L^{p_0}(\mathcal {Q}_1)}\le C. \end{aligned}$$

It follows that, for a non-relabeled sequence, there exists a bilinear form ${\mathcal {A}}$ and a map $v\in L^2(\mathcal {Q}_1)\cap L^{p_0}(\mathcal {Q}_1)$ such that $Dv\in L^{p_0}(\mathcal {Q}_1)$ and

$$\begin{aligned} \left\{ \begin{array}{ll} v_k\rightharpoonup v &{} \text { in }L^2(\mathcal {Q}_1;\mathbb {R}^N),\\ Dv_k\rightharpoonup Dv &{} \text { in }L^{p_0}(\mathcal {Q}_1;\mathbb {R}^{Nn}),\\ {\mathcal {A}}_k\rightarrow {\mathcal {A}} &{} \text { in bilinear forms on}\, \mathbb {R}^{Nn},\\ \gamma _k\rightarrow \gamma \in {[0,1/\sqrt{\omega _n}]}. \end{array}\right. \end{aligned}$$

The convexity of ${{\varphi }}$ implies

$$\begin{aligned} int_{\mathcal {Q}_1}\left( |v|^2+{{\varphi }}(|v|)+{{\varphi }}(|Dv|)\right) d z\le \gamma ^2. \end{aligned}$$

(3.5)

Moreover, with the same argument used in [41], we conclude that v is ${\mathcal {A}}$-caloric and $v\in C^\infty (\mathcal {Q}_1;\mathbb {R}^N)$. From (3.2),

$$\begin{aligned} \sup _{\mathcal {Q}_{3/4}}{\left( |v|^2+|Dv|^2\right) } \le C(L/\nu )int_{\mathcal {Q}_1}|v|^2 dz \le C(L/\nu ){\gamma ^2}. \end{aligned}$$

(3.6)

As demonstrated in [41], given $\ell >\frac{n+2}{2}$, for any $-1<t_1<t_2<-h$,

$$\begin{aligned}&\Vert v_k(\cdot ,s)-v_k(\cdot ,s+h)\Vert _{W^{-\ell ,2}(\mathcal {B}_1)} \le C\left( h^\frac{p_0-1}{p_0}+\frac{1}{k}\right) , \quad \text{ for } s\in (t_1,t_2) \\&\Longrightarrow \int _{t_1}^{t_2}\Vert v_k(\cdot ,s)-v_k(\cdot ,s+h)\Vert ^p_{W^{-\ell ,2}(\mathcal {B}_1)} ds \le C\left( h^\frac{p(p_0-1)}{p_0}+\frac{1}{k^p}\right) , \end{aligned}$$

for any $p\ge 1$.

Moreover, the sequence $\{v_k\}_{k=1}^\infty$ is uniformly bounded in $L^\infty (-1,0;L^2(\mathcal {B}_1;\mathbb {R}^N))\cap L^1_{loc}(-1,0;W^{1,p_0}(\mathcal {B}_1;\mathbb {R}^N))$. With $X=W^{1,p_0}(\mathcal {B}_1;\mathbb {R}^N)$, $B=L^2(\mathcal {B}_1;\mathbb {R}^N)$, and $Y=W^{-\ell ,2}(\mathcal {B}_1;\mathbb {R}^N)$, Theorem 3.1 yields the strong convergence (for a non-relabeled subsequence)

$$\begin{aligned} v_k\rightarrow v\quad \text { in }L^p(-1,0;L^2(\mathcal {B}_1;\mathbb {R}^N)), \end{aligned}$$

(3.7)

for any $p\ge 1$. This entails also that $v_k\rightarrow v$ in $L^p(-1,0;L^1(\mathcal {B}_1;\mathbb {R}^N))$ for any $p\ge 1$, so $\Vert v_k-v\Vert _{L^1(B_1;\mathbb {R}^n)}\rightarrow 0$ for almost every $-1<t<0$.

Claim: $\displaystyle {\lim _{k\rightarrow \infty }\int _{\mathcal {Q}_{3/4}}{{\varphi }}(\lambda |v_k-v|) \,d z=0}$, for all $\lambda >0$.

First, we observe that $v_k(\cdot ,t)$ and $v(\cdot ,t)$ belong to $W^{1,1}(\mathcal {B}_1,\mathbb {R}^N)$, for almost every time $t\in (-1,0)$. We may therefore extend them to the whole of $\mathbb {R}^n$ in such a way that their extensions $\widetilde{v}_k(\cdot ,t)$ and $\widetilde{v}(\cdot ,t)$ belong to $W^{1,1}(\mathbb {R}^n,\mathbb {R}^N)$, and

$$\begin{aligned} \Vert \widetilde{v}_k(\cdot ,t)-\widetilde{v}(\cdot ,t)\Vert _{W^{1,1}(\mathbb {R}^n,\mathbb {R}^N)}\le C\Vert {v_k}(\cdot ,t)-v(\cdot ,t)\Vert _{W^{1,1}(\mathcal {B}_1,\mathbb {R}^N)}, \quad \text{ for } \text{ a.e. } t\in (-1, 0), \end{aligned}$$

where the constant C depends only on $\mathcal {B}_1$. Let $\sigma$ be the standard mollifier and $\sigma _{\varepsilon }(x)=\frac{1}{\varepsilon ^n}\sigma \left( \frac{|x|}{\varepsilon }\right)$.

On account of (3.1), it is enough to verify

$$\begin{aligned} \lim _{k\rightarrow \infty }\sup _{g}\int _{\mathcal {Q}_{3/4}}|v_k-v|\,g \,dz=0 \end{aligned}$$

where the supremum is taken over all $g\in L^1(\mathcal {Q}_{3/4})$ such that $\Vert {\varphi }^*(|g|)\Vert _{L^1(\mathcal {Q}_{3/4})}\le 1$. Fix $g\in L^1(\mathcal {Q}_{3/4})$ satisfying $\Vert {\varphi }^*(|g|)\Vert _{L^1(\mathcal {Q}_{3/4})}\le 1$. With $0<\varepsilon <1$ given, for each $-1<t<0$, we let $\widetilde{v}_k*\sigma _{\varepsilon }$ and $\widetilde{v}*\sigma _{\varepsilon }$ denote the mollifications of the extended maps $\widetilde{v}_k$ and $\widetilde{v}$ in the spatial direction. We have

$$\begin{aligned}&\left| \int _{\mathcal {Q}_{3/4}}|v_k(z)-v(z)|g(z)dz\right| \nonumber \\&\le \int _{\mathcal {Q}_{3/4}}|\widetilde{v}_k(x,t)-\widetilde{v}(x,t)||g(x,t)|dxdt \nonumber \\&\le \left[ \int _{\mathcal {Q}_{3/4}}|(\widetilde{v}_k*\sigma _{\varepsilon })(x,t)-\widetilde{v}_k(x,t)||g(x,t)|dxdt\right. \nonumber \\&\quad +\int _{\mathcal {Q}_{3/4}}|(\widetilde{v}_k -\widetilde{v})*\sigma _{\varepsilon }(x,t)||g(x,t)|dxdt \nonumber \\&\qquad \left. +\int _{\mathcal {Q}_{3/4}}|(\widetilde{v}*\sigma _{\varepsilon })(x,t)-v(x,t)||g(x,t)|dxdt\right] \nonumber \\&=: [I_{1,k}+I_{2,k}+I_{3,k}]. \end{aligned}$$

(3.8)

First, we examine $I_{2,k}$. Given $-1<t<0$, we use Young’s convolution inequality to write

$$\begin{aligned} \begin{aligned} \sup _{k\in \mathbb {N}} \Vert (\widetilde{v}_k-\widetilde{v})*\sigma _{\varepsilon }(\cdot ,t)\Vert _{L^\infty (\mathcal {B}_{3/4})} \le&\sup _{k\in \mathbb {N}} \Vert \widetilde{v}_k(\cdot ,t)-\widetilde{v}(\cdot ,t)\Vert _{L^1(\mathcal {B}_{3/4};\mathbb {R}^N)} \Vert \sigma _{\varepsilon }\Vert _{L^\infty (\mathcal {B}_{3/4})}\\ \le&\sup _{k\in \mathbb {N}} \left( \Vert \widetilde{v}_k(\cdot ,t)\Vert _{L^1(\mathcal {B}_{3/4};\mathbb {R}^N)} +\Vert \widetilde{v}(\cdot ,t)\Vert _{L^1(\mathcal {B}_{3/4};\mathbb {R}^N)}\right) \Vert \sigma _{\varepsilon }\Vert _{L^\infty (\mathcal {B}_{3/4})}\\ \le&C\sup _{k\in \mathbb {N}} \left( \Vert v_k(\cdot ,t)\Vert _{L^2(\mathcal {B}_1;\mathbb {R}^N)} +\Vert v(\cdot ,t)\Vert _{L^2(\mathcal {B}_1;\mathbb {R}^N)}\right) \Vert \sigma _{\varepsilon }\Vert _{L^\infty (\mathbb {R}^n)}\\ \le&C\Vert \sigma _{\varepsilon }\Vert _{L^\infty (\mathbb {R}^n)}. \end{aligned} \end{aligned}$$

(3.9)

For the last two inequalities, we used (iii). On the other hand, by Young’s inequality and by the convexity of ${\varphi }^*$, for any $\alpha \in (0,1)$, we have

$$\begin{aligned} \begin{aligned} \int _{\mathcal {Q}_{3/4}}|(\widetilde{v}_k-\widetilde{v})*\sigma _{\varepsilon }(x,t)||g(x,t)|dxdt \le&\int _{\mathcal {Q}_{3/4}}{\varphi }\left( \frac{|(\widetilde{v}_k-\widetilde{v})*\sigma _{\varepsilon }(x,t)|}{\alpha }\right) dxdt +\alpha \int _{\mathcal {Q}_{3/4}}{\varphi }^*(|g|)dxdt\\ \le&\int _{\mathcal {Q}_{3/4}}{\varphi }\left( \frac{|(\widetilde{v}_k-\widetilde{v})*\sigma _{\varepsilon }(x,t)|}{\alpha }\right) dxdt+\alpha . \end{aligned} \end{aligned}$$

Since

$$\begin{aligned} \lim _{k\rightarrow \infty }|(\widetilde{v}_k-\widetilde{v})*\sigma _{\varepsilon }(x,t)|\rightarrow 0 \quad \text { for a.e. }(x,t)\in \mathcal {Q}_{3/4}, \end{aligned}$$

thanks to (3.9) we may use the dominated convergence theorem to conclude that $\displaystyle {\lim _{k\rightarrow \infty }\sup _{g}I_{2,k}\le \alpha }$.

Now, we turn to bounding $I_{1,k}$ and $I_{3,k}$. The arguments for each term are similar, so we focus on $I_{1,k}$. We will use some results contained in [30]. As provided in [30] (p. 135), the following pointwise estimate holds for functions in $W^{1,1}_{loc}(\mathbb {R}^n,\mathbb {R}^N)$:

$$\begin{aligned} |\widetilde{v}_k(x,\cdot )-(\widetilde{v}_k*\sigma _{\varepsilon })(x,\cdot )|\le \varepsilon \int _0^1(|D \widetilde{v}_k|*\sigma _{\varepsilon \tau })(x,\cdot )\,d\tau , \end{aligned}$$

almost everywhere in $\mathcal {B}_{3/4}$. Let $\beta >0$ be the constant from Corollary 3.1. Combining the bound above with [30, Lemma 4.4.6], for each $-1<t<0$, we obtain

$$\begin{aligned} |\widetilde{v}_k(x,t)-(\widetilde{v}_k*\sigma _{\varepsilon })(x,t)|\le \frac{2\varepsilon }{\beta } M(\beta |D \widetilde{v}_k|(\cdot ,t))(x), \quad \text { for a.e. }x\in \mathcal {B}_{3/4}. \end{aligned}$$

Here M is the (non-centered Hardy-Littlewood) maximal function defined earlier. Observing that, for almost every $t\in (-1,0)$, we have

$$\begin{aligned} M(\beta |D\widetilde{v}_k(\cdot ,t)|)(x)&=\sup _{\mathcal {B}\ni x}\frac{\beta }{|\mathcal {B}|}\int _{\mathcal {B}\cap \mathcal {B}_1} |D\widetilde{v}_k(y,t)|\,dy\\&\le \sup _{\mathcal {Q}\ni (x,t)}\frac{\beta }{|\mathcal {Q}|}\int _{\mathcal {Q}\cap \mathcal {Q}_1} |D\widetilde{v}_k(y,s)|\,dy\,ds=M(\beta |D\widetilde{v}_k|)(x,t), \end{aligned}$$

we deduce that

$$\begin{aligned} |\widetilde{v}_k(z)-(\widetilde{v}_k*\sigma _{\varepsilon })(z)| \le \frac{2\varepsilon }{\beta } M(\beta |D\widetilde{v}_k|)(z), \quad \text { for a.e. }z\in \mathcal {Q}_{3/4}. \end{aligned}$$

Incorporating this into the definition of $I_{1,k}$ and applying Young’s inequality, we may write

$$\begin{aligned} I_{1,k} \le&\frac{2\varepsilon }{\beta }\int _{Q_{3/4}}M(\beta |D\widetilde{v}_k|)(z)|g(z)|dz\\ \le&\frac{2\varepsilon }{\beta }\left[ \int _{Q_{3/4}}{\varphi }(M(\beta |D\widetilde{v}_k|)(z))dz +\int _{Q_{3/4}}{\varphi }^*(|g(z)|)dz\right] \\ \le&\frac{2\varepsilon }{\beta }\left[ \int _{Q_{3/4}}{\varphi }(M(\beta |D\widetilde{v}_k|)(z))dz +1\right] , \end{aligned}$$

where we have used $\Vert {\varphi }^*(|g|)\Vert _{L^1(Q_{3/4})}\le 1$ in the last inequality. Recalling that $\displaystyle {\int _{\mathcal {Q}_1}{\varphi }(|D v_k|)\,dz\le 1}$ and that $\displaystyle {\frac{{\varphi }(t)}{t^{p_0}}}$ is almost increasing, we can use Corollary 3.1 to infer

$$\begin{aligned} {\varphi }(\beta M(|D v_k|)(z))^\frac{1}{p_0} \lesssim M\left( {\varphi }(|Dv_k|)^{\frac{1}{p_0}}\right) (z), \end{aligned}$$

almost everywhere in $\mathcal {Q}_1$. Thus

$$\begin{aligned} \int _{\mathcal {Q}_{3/4}}{\varphi }(\beta M(|D v_k|))\,dz\lesssim \int _{\mathcal {Q}_1}\left( M\left( {\varphi }(|D v_k|)^{\frac{1}{p_0}}\right) \right) ^{p_0}dz\lesssim \int _{\mathcal {Q}_1}{\varphi }(|D v_k|)\,dz\le 1, \end{aligned}$$

since M is bounded in $L^{p_0}$. We conclude that $I_{1,k}\lesssim \varepsilon /\beta$. A similar argument shows $I_{3,k}\lesssim \varepsilon /\beta$, as well.

Returning to (3.8), we have shown

$$\begin{aligned} \lim _{k\rightarrow \infty }\sup _{g}\int _{Q_{3/4}}|v_k(z)-v(z)|g(z)dz\lesssim \frac{\varepsilon }{\beta }+\alpha , \end{aligned}$$

with the supremum being taken over all $g\in L^1(Q_{3/4})$ satisfying $\Vert {\varphi }^*(|g|)\Vert _{L^1(Q_{3/4})}\le 1$. Here $\beta$ is independent of k. Since $\varepsilon ,\alpha >0$ were both arbitrary, the claim is proved.

Next, we produce a sequence $\{h_k\}_{k=1}^{\infty }\in C^\infty (\mathcal {Q}_{1/2};\mathbb {R}^N)$ of ${\mathcal {A}}$-caloric maps that will contradict (iv) for k sufficiently large.

Case 1: $\gamma _k\rightarrow 0$: In this case, clearly $v=0$, $v_k\rightarrow 0$ strongly in $L^2(\mathcal {Q}_1)$ and $\displaystyle {\int _{\mathcal {Q}_1}{\varphi }(2|v_k|) d z\rightarrow 0}$. Thus, we obtain a contradiction to (iv) with $h\equiv 0$.

Case 2: $\gamma _k\rightarrow \gamma \in {(0,1/\sqrt{\omega _n}]}$: For each $k\in \mathbb {N}$, let $h_k$ be the unique solution to

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle {\int _{\mathcal {Q}_{3/4}}\left( h_k\cdot \partial _t\eta -{\mathcal {A}}_k(Dh_k,D\eta )\right) d z=0} \quad \text { for all }\eta \in C^\infty _c(\mathcal {Q}_{3/4};\mathbb {R}^N)\\ h_k=\gamma _k^{-1}v\quad \text { on }\partial _{{\mathcal {P}}}\mathcal {Q}_{3/4}. \end{array}\right. \end{aligned}$$

Since $v\in C^\infty (\overline{\mathcal {Q}}_{3/4};\mathbb {R}^N)$ and $\gamma _k\rightarrow \gamma >0$, so is each $h_k$. As shown in [5] and [41], we have

$$\begin{aligned} \lim _{k\rightarrow \infty }\int _{\mathcal {Q}_{3/4}} \left( |v-\gamma _k h_k|^2+|Dv-\gamma _k Dh_k|^2\right) d z=0. \end{aligned}$$

Thus

$$\begin{aligned} \gamma _k h_k\rightarrow v\text { and }\gamma _k Dh_k\rightarrow Dv \quad \text { in }L^2(\mathcal {Q}_{3/4}). \end{aligned}$$

(3.10)

This implies convergence in measure for both sequences. Moreover, after taking a non-relabeled subsequence if necessary, the bounds in (3.2) and  (3.6) imply

$$\begin{aligned} \sup _{\mathcal {Q}_{1/2}}\left( |\gamma _kh_k|+|\gamma _kDh_k|\right) \le 2^{n+1}C(L/\nu ). \end{aligned}$$

Thus, since $\sup _{k\in \mathbb {N}}\Vert \gamma _kh_k-v\Vert _{L^\infty (Q_{1/2})}+\Vert \gamma _kDh_k-Dv\Vert _{L^\infty (Q_{1/2})}\le 2^{n+3}C(L/\nu )$,

$$\begin{aligned} \lim _{k\rightarrow \infty }\int _{\mathcal {Q}_{1/2}} \left( {{\varphi }}(\lambda |\gamma _k h_k-v|)+{{\varphi }}(\lambda |\gamma _k Dh_k-Dv|)\right) d z=0, \quad \text { for all }\lambda >0. \end{aligned}$$

(3.11)

To finish the proof, define

$$\begin{aligned} K_{{\varphi }}=8+\sup \left\{ \frac{{\varphi }(4t)}{{\varphi }(t)}:0<t\le 2^{n+2}C(L/\nu )\right\} . \end{aligned}$$

(3.12)

Note that $K_{{\varphi }}$ must be finite due to assumption (H2). Using  (3.5) and the convexity of ${\varphi }$,

$$\begin{aligned} \lim _{k\rightarrow \infty }&int_{\mathcal {Q}_{1/2}}\left( 4|\gamma _kh_k|^2+{{\varphi }}(2|\gamma _kh_k|)+{{\varphi }}(|\gamma _kDh_k|)\right) dz\\&\le \frac{1}{2}\lim _{k\rightarrow \infty }int_{\mathcal {Q}_{1/2}} \left( 16|\gamma _kh_k-v|^2+{{\varphi }}(4|\gamma _kh_k-v|)+{{\varphi }}(2|\gamma _kDh_k-Dv|)\right) d z\\&\quad +\frac{1}{2}int_{\mathcal {Q}_{1/2}}\left( 16|v|^2+{{\varphi }}(4|v|)+{{\varphi }}(2|Dv|)\right) d z\\&\le 2^{n+1}K_{{\varphi }}int_{\mathcal {Q}_1} \left( |v|^2+{{\varphi }}(|v|)+{{\varphi }}(|Dv|)\right) d z\\&\le 2^{n+1}K_{{\varphi }}\gamma ^2. \end{aligned}$$

Since $\gamma >0$, for k sufficiently large, we have $\gamma <2\gamma _k$, and the ${\mathcal {A}}_k$-caloric map $h_k$ satisfies

$$\begin{aligned} int_{\mathcal {Q}_{1/2}} \left( 4|\gamma _kh_k|^2+{{\varphi }}(2|\gamma _kh_k|)+{{\varphi }}(|\gamma _kDh_k|)\right) d z < 2^{n+2}K_{{\varphi }}\gamma _k^2. \end{aligned}$$

Similarly, using the convergences provided by the claim, (3.7), (3.10), and (3.11) we conclude that

$$\begin{aligned} \lim _{k\rightarrow \infty }&int_{\mathcal {Q}_{1/2}}\left( 4|v_k-\gamma _kh_k|^2+{{\varphi }}(2|v_k-\gamma _kh_k|)\right) d z=0, \end{aligned}$$

which provides the contradiction to (iv). $\square$

Remark 3.1

For the shifted function ${\varphi }_a$,

$$\begin{aligned} K_{{\varphi }_a}\le 8+\max \left\{ \left( \frac{4{\varphi }'(2a)}{{\varphi }'(a)}\right) ^2, \frac{{\varphi }_a(2^{n+4}C(L/\nu ))}{{\varphi }_a(a/4)}\right\} . \end{aligned}$$

If the function ${\varphi }$ is doubling, then $K_{{\varphi }}=8+\Delta _2({\varphi })^2$.

4 Caccioppoli type inequality

Let us prove the following Caccioppoli inequality for standard parabolic cylinders.

Theorem 4.1

Let $u\in C^0(-T,0; L^2(\Omega ,\mathbb {R}^N))\cap L^1(-T,0; W^{1,1}(\Omega ,\mathbb {R}^N))$ be a weak solution to (1.1) satisfying ${\varphi }(|Du|)\in L^1(-T,0; L^1(\Omega ))$. Under hypotheses $(a_{1})$-$(a_{4})$ and Assumption 1.1, given a standard cylinder $\mathcal {Q}_{R}(z_0)\subset \Omega _T$, with center $z_0=(x_0,t_0)$, and any affine map $\ell : \mathbb {R}^{n}\rightarrow \mathbb {R}^{N}$ and $0<r<R$, we have

$$\begin{aligned} \begin{aligned} \sup _{t_0-{r^2}<s<t_0}\ {}&\int _{\mathcal {B}_{r}(x_0)}\left| {u(x,s)-\ell (x)}\right| ^2dx+\int _{\mathcal {Q}_{r}(z_0)}{\varphi }_{1+|D\ell |}(|Du-D\ell |)dz\\ \le c_0&\int _{\mathcal {Q}_{R}(z_0)}\left[ {\varphi }_{1+|D\ell |}\left( \left| \frac{u-\ell }{R-r}\right| \right) +\left| \frac{u-\ell }{R-r}\right| ^2\right] dz, \end{aligned} \end{aligned}$$

where $c_0$ depends only on $n, N, L,\nu , p_0,p_1$.

Proof

For notational brevity, we put $M=1+|D\ell |$. Without loss of generality we may assume $z_0 =(0,0)$. For a generic radius $\rho$, we denote $\mathcal {Q}_\rho (z_0)=\mathcal {Q}_\rho$ and $\mathcal {B}_\rho (x_0)=\mathcal {B}_\rho$. Let us consider the function $\eta (x,t)=\chi ^{p_1}(x)\zeta ^2(t)(u(x,t)-\ell (x))$ as a test function in (1.1), where $\chi$ is a standard cutoff function between $\mathcal {B}_{r}$ and $\mathcal {B}_R$, and $\zeta \in C^0(\mathbb {R})$ is defined by

$$\begin{aligned} \left\{ \begin{array}{ll} \zeta (t)=0, &{} t\in (-\infty ,-{R^2})\\ \zeta _t(t)=\frac{1}{R^2-r^2}, &{}t\in (-{R^2},-{r^2})\\ \zeta (t)=1, &{}t\in (-{r^2},s)\\ \zeta _t(t)=-\frac{1}{\varepsilon },&{} t\in (s, s+\varepsilon )\\ \zeta (t)=0, &{}t\in (s+\varepsilon ,+\infty ) \end{array} \right. \end{aligned}$$

for $-r^{2}<s<0$ and $0< \varepsilon \le |s|$. We have

$$\begin{aligned}{} & {} \int _{\mathcal {Q}_R}\chi ^{p_1}\zeta ^2 a(Du)\cdot (Du-D\ell )\,dz\\ {}{} & {} =-p_1\int _{\mathcal {Q}_R}\chi ^{p_1-1}\zeta ^2a(Du)\cdot \left[ D\chi \otimes (u-\ell )\right] \,dz+\int _{\mathcal {Q}_R}u\cdot \eta _t\,dz. \end{aligned}$$

Noting that $\displaystyle {\int _{\mathcal {Q}_R}a(D\ell )\cdot D\eta \,dz =0}$ and $\displaystyle {\int _{\mathcal {Q}_R}\ell \cdot \eta _t \,dz=0}$, we obtain

$$\begin{aligned} \begin{aligned} I:=&\int _{\mathcal {Q}_R}\chi ^{p_1}\zeta ^2(a(Du)-a(D\ell ))\cdot (Du-D\ell )\,dz\\ =&-p_1\int _{\mathcal {Q}_R}\chi ^{p_1-1}\zeta ^2(a(Du)-a(D\ell ))\cdot \left[ D\chi \otimes (u-\ell )\right] \,dz\\ {}&+\int _{\mathcal {Q}_R}(u-\ell )\cdot \eta _t\,dz=:I\!I+I\!I\!I \end{aligned} \end{aligned}$$

(4.1)

The left hand side can be estimated thanks to Remark 2.4, leading to

$$\begin{aligned} I\ge c\int _{\mathcal {Q}_R}\chi ^{p_1}\zeta ^2{\varphi }_{M}(|Du-D\ell |)\,dz \end{aligned}$$

(4.2)

and

$$\begin{aligned} |I\!I|\le c\int _{\mathcal {Q}_R}\chi ^{p_1-1}\zeta ^2{\varphi }'_{M}(|Du-D\ell |)|D\chi ||u-\ell |\,dz. \end{aligned}$$

Using Young’s inequality and (2.3) together with (2.5), we derive the following bound for $I\!I$:

$$\begin{aligned} \begin{aligned} |I\!I|&\le c\, \delta \int _{\mathcal {Q}_R}\zeta ^2{\varphi }_{M}^*\left( {\varphi }'_{M}(|Du-D\ell |)\chi ^{p_1-1}\right) \,dz+c(\delta )\int _{\mathcal {Q}_R}\zeta ^2{\varphi }_{M}(|u-\ell ||D\chi |)\,dz\\&\le c\,\delta \int _{\mathcal {Q}_R}\chi ^{p_1}\zeta ^2{\varphi }_{M}(|Du-D\ell |)\,dz+c(\delta )\int _{\mathcal {Q}_R}\zeta ^2{\varphi }_{M}\left( \frac{|u-\ell |}{R-r}\right) \,dz. \end{aligned} \end{aligned}$$

(4.3)

Choosing $\delta$ sufficiently small, we can absorb the first integral of the right hand side into the left. Finally, expanding the derivative $\eta _t$, we may write (recalling Remark 2.1)

$$\begin{aligned} \begin{aligned} I\!I\!I&=2\int _{\mathcal {Q}_R}\chi ^{p_1}\zeta \zeta _t|u-\ell |^2dz+\int _{\mathcal {Q}_R}\chi ^{p_1}\zeta ^2(u-\ell )\cdot (u-\ell )_t\,dz\\&=2\int _{\mathcal {Q}_R}\chi ^{p_1}\zeta \zeta _t|u-\ell |^2dz+\frac{1}{2}\int _{\mathcal {Q}_R}\chi ^{p_1}\zeta ^2\frac{\partial }{\partial t}|u-\ell |^2\,dz. \end{aligned} \end{aligned}$$

So, an integration by parts yields

$$\begin{aligned} I\!I\!I=\int _{\mathcal {Q}_R}\chi ^{p_1}\zeta \zeta _t|u-\ell |^2dz. \end{aligned}$$

Exploiting the definition of $\zeta$, we obtain

$$\begin{aligned} \begin{aligned} I\!I\!I&=\frac{1}{R^2-r^2}\int _{-{R^2}}^{-{r^2}}\int _{\mathcal {B}_R}|u-\ell |^2\chi ^{p_1}\zeta \, dx\,dt-\frac{1}{\varepsilon }\int _s^{s+\varepsilon }\int _{\mathcal {B}_R}|u-\ell |^2\chi ^{p_1}\zeta \,dx\,dt\\&\le \int _{\mathcal {Q}_R}\left| \frac{u-\ell }{R-r}\right| ^2\,dz-\frac{1}{\varepsilon }\int _s^{s+\varepsilon }\int _{\mathcal {B}_R}|u-\ell |^2\chi ^{p_1}\zeta \,dx\,dt, \end{aligned} \end{aligned}$$

since $R^2-r^2\ge (R-r)^2$. Incorporating the above bound and the bounds for I and $I\!I$, in (4.2) and (4.3), into (4.1), we deduce that

$$\begin{aligned}{} & {} \frac{1}{\varepsilon }\int _s^{s+\varepsilon }\int _{\mathcal {B}_R}|u-\ell |^2\chi ^{p_1}\zeta \,dx\,dt+\int _{\mathcal {Q}_R}\chi ^{p_1}\zeta ^2{\varphi }_{M}(|Du-D\ell |)\,dz\le c\,\int _{\mathcal {Q}_R}\left| \frac{u-\ell }{R-r}\right| ^2\,dz\\{} & {} +c\,\int _{\mathcal {Q}_R}{\varphi }_{M}\left( \frac{|u-\ell |}{R-r}\right) \,dz. \end{aligned}$$

Recalling the definition of $\zeta$ and $\chi$, we may take the limit as $\varepsilon \rightarrow 0$ to get

$$\begin{aligned}{} & {} \int _{\mathcal {B}_{r}}|u(s,x)-\ell (x)|^2dx+\int _{-{r^2}}^s\int _{\mathcal {B}_{r}}{\varphi }_{M}(|Du-D\ell |)\,dz\\ {}{} & {} \le c\,\int _{\mathcal {Q}_{R}}\left| \frac{u-\ell }{R-r}\right| ^2\,dz+c\int _{\mathcal {Q}_R}{\varphi }_{M}\left( \frac{|u-\ell |}{R-r}\right) \,dz. \end{aligned}$$

We use the previous inequality twice: firstly, by dropping the second term in the left hand side, and taking the supremum over $s\in (-{r^2},0)$; secondly, by dropping the first term in the left hand side and letting s tend to 0. By summing up the two resulting contributions, this gives the result. $\square$

Finally, an application of the Caccioppoli inequality in Theorem 4.1 and (2.9) produces the following

Corollary 4.1

Let $u\in C^0(-T,0; L^2(\Omega ,\mathbb {R}^N))\cap L^1(-T,0; W^{1,1}(\Omega ,\mathbb {R}^N))$ be a weak solution to (1.1) satisfying ${\varphi }(|Du|)\in L^1(-T,0; L^1(\Omega ))$. Under hypotheses $(a_{1})$-$(a_{4})$ and Assumption 1.1, given any standard parabolic cylinder $\mathcal {Q}_{\rho }(z_0)\subset \Omega _T$, with center in $z_0=(x_0,t_0)$, and any affine map $\ell : \mathbb {R}^{n}\rightarrow \mathbb {R}^{N}$, we have

$$\begin{aligned} \begin{aligned} \sup _{t_0-(\frac{\rho }{2})^2<s<t_0}\&int_{\mathcal {B}_{\frac{\rho }{2}}(x_0)}\left| \frac{u(x,s)-\ell (x)}{{\rho }}\right| ^2dx+int_{\mathcal {Q}_{\frac{\rho }{2}}(z_0)}{\varphi }_{1+|D\ell |}(|Du-D\ell |)dz\\ \le&c_02^{n+p_1+2}int_{\mathcal {Q}_{\rho }(z_0)}\left[ {\varphi }_{1+|D\ell |}\left( \left| \frac{u-\ell }{\rho }\right| \right) +\left| \frac{u-\ell }{\rho }\right| ^2\right] dz, \end{aligned} \end{aligned}$$

where $c_0$ depends only on $n, N, L,\nu , p_0,p_1$.

5 Poincaré type inequalities

We begin this section providing a Poincaré type inequality valid for solutions to certain parabolic-like systems. The proof follows the same lines as [5, Lemma 3.1].

Lemma 5.1

Let $\psi$ be an N-function satisfying $\Delta _2(\psi ,\psi ^*)<\infty$. With $t_1<t_2$ and $U\subseteq \mathbb {R}^n$, suppose that $\xi \in L^1(U\times (t_1,t_2),\mathbb {R}^{Nn})$ and $w\in C^0(t_1,t_2, L^{2}(U, \mathbb {R}^{N}))\cap L^{1}(t_1,t_2, W^{1, 1}(U,\mathbb {R}^N))$ satisfy $\psi (|Dw|)\in L^{1}(t_1,t_2, L^{1}(U))$ and

$$\begin{aligned} \int _{U\times (t_1,t_2)} (w\cdot \zeta _t-\xi \cdot D\zeta )\, dz=0, \quad \text { for any }\zeta \in C^\infty _c(U\times (t_1,t_2),\mathbb {R}^N). \end{aligned}$$

(5.1)

Then for any parabolic cylinder $\mathcal {Q}_\rho (z_0)\subset U\times (t_1,t_2)$, we have

$$\begin{aligned} int_{\mathcal {Q}_\rho (z_0)}\psi \left( \left| \frac{w-(w)_{z_0,\rho }}{\rho }\right| \right) \, dz\le c_1\left[ int_{\mathcal {Q}_\rho (z_0)}\psi (|Dw|) \,dz+\psi \left( int_{\mathcal {Q}_\rho (z_0)}|\xi |\,dz\right) \right] \end{aligned}$$

with $c_1$ depending only on n, N,  and $\Delta _2(\psi ,\psi ^*)$.

Proof

We fix a nonnegative symmetric weight function $\eta \in C^\infty _c(\mathcal {B}_\rho (x_0))$ such that

$$\begin{aligned} \eta \ge 0, \quad int_{\mathcal {B}_{\rho }(x_{0})} \eta \, dx=1 \quad \text{ and } \quad \Vert \eta \Vert _{\infty }+ \rho \Vert D\eta \Vert _{\infty } \le c_{\eta }, \end{aligned}$$

(5.2)

and, for $t\in \left( t_0-{\rho ^2},t_0 \right)$ we denote

$$\begin{aligned} (w)_\eta (t)=int_{\mathcal {B}_\rho (x_0)}w(x,t)\eta (x)\,dx, \end{aligned}$$

as well as

$$\begin{aligned} (w)_\eta =int_{\mathcal {Q}_\rho (z_0)}w(x,t)\eta (x)\,dz. \end{aligned}$$

By the triangle inequality and the $\Delta _2$-condition we have

$$\begin{aligned}&int_{\mathcal {Q}_\rho (z_0)}\psi \left( \left| \frac{w-(w)_{z_0,\rho }}{\rho }\right| \right) dz\\&\quad \le c\left[ int_{\mathcal {Q}_\rho (z_0)}\psi \left( \left| \frac{w-(w)_\eta (t)}{\rho }\right| \right) dz\right. \\&\quad \left. +int_{t_0-{\rho ^2}}^{t_0}\psi \left( \left| \frac{(w)_\eta (t)-(w)_\eta }{\rho }\right| \right) dt + \psi \left( \left| \frac{(w)_\eta -(w)_{z_0,\rho }}{\rho }\right| \right) \right] \\&\quad =:c\,(I+I\!I+I\!I\!I), \end{aligned}$$

with the obvious meaning of I,$I\!I$, and $I\!I\!I$. Since $\Delta _2(\psi ,\psi ^*)<\infty$, we may bound I by applying Poincaré’s inequality for vanishing $\eta$-mean value (see [16, Theorem 7]) slicewise with respect to x: for a.e. $t\in (t_0-{\rho ^2},t_0)$,

$$\begin{aligned} I\le c(n,\Delta _2(\psi ,\psi ^*))int_{\mathcal {Q}_\rho (z_0)}\psi (|Dw|)dz. \end{aligned}$$

To bound $I\!I\!I$, we use Jensen’s inequality followed by the triangle inequality and $\Delta _2$-condition to infer

$$\begin{aligned}{} & {} I\!I\!I\le {int}_{\mathcal {Q}_\rho (z_0)}\psi \left( \left| \frac{w-(w)_\eta }{\rho }\right| \right) \,dz \le c\,\left[ int_{\mathcal {Q}_\rho (z_0)}\psi \left( \left| \frac{w-(w)_\eta (t)}{\rho }\right| \right) dz\right. \\{} & {} \left. +int_{t_0-{\rho ^2}}^{t_0}\psi \left( \left| \frac{(w)_\eta (t)-(w)_\eta }{\rho }\right| \right) dt\right] \\{} & {} =c(I+I\!I). \end{aligned}$$

So it remains to estimate $I\!I$. For this, we recall that w is a weak solution of the parabolic system (5.1). Even if the solution w, need not be differentiable in the time variable, with Steklov averages, we may rewrite (5.1) as

$$\begin{aligned} \int _U\left( w_t\cdot \zeta +\xi \cdot D\zeta \right) \,dx=0 \quad \text { for all }\zeta \in C^\infty _c(U,\mathbb {R}^N) \text { and for a.e. }t\in (t_0-\rho ^2,t_0). \end{aligned}$$

For $i=1,\dots ,N$, let $e_i\in \mathbb {R}^N$ denote the unit vector in the i-th coordinate direction. With $(t,\tau )\subset (t_0-{\rho ^2},t_0)$, we use (5.1) and (5.2), with $\zeta =\eta e_i\in C^\infty _c(U;\mathbb {R}^N)$, to write

$$\begin{aligned} |\left[ (w)_\eta (t)-(w)_\eta (\tau )\right] \cdot e_i|&=\left| \int _t^\tau \partial _s\left[ (w)_\eta (s)\right] \cdot e_i\,ds\right| =\left| \int _t^\tau {int}_{\mathcal {B}_\rho (x_0)}w_s \cdot (\eta e_i) \,dx\,ds\right| \\&=\left| \int _t^\tau {int}_{\mathcal {B}_\rho (x_0)}\xi \cdot (D\eta e_i)\,dx\,ds\right| \le \Vert D\eta \Vert _\infty \int _t^\tau {int}_{\mathcal {B}_\rho (x_0)}|\xi |dx\,ds\\&\le \frac{c}{\rho }\int _t^\tau {int}_{\mathcal {B}_\rho (x_0)}|\xi |dx\,ds\le c\,{\rho }int_{\mathcal {Q}_\rho (z_0)}|\xi |dz. \end{aligned}$$

Summing over each component, we conclude that

$$\begin{aligned} I\!I\le c\,\psi \left( int_{\mathcal {Q}_\rho (z_0)}|\xi |dz\right) . \end{aligned}$$

Combining these estimates we obtain the desired Poincaré type inequality. $\square$

Remark 5.1

Suppose that $\mathcal {A}$ is a bilinear form on $\mathbb {R}^{Nn}$ and there is $\Lambda <\infty$ such that $|\mathcal {A}(\eta _1,\eta _2)|\le \Lambda |\eta _1||\eta _2|$, for all $\eta _1,\eta _2\in \mathbb {R}^{Nn}$. If $h\in C^\infty (\mathcal {Q}_\rho (z_0);\mathbb {R}^N)$ is $\mathcal {A}$-caloric, then we may identify a $\xi \in C^\infty (\mathcal {Q}_\rho (z_0);\mathbb {R}^{Nn})$ so that, at each $z\in \mathcal {Q}_\rho (z_0)$, we have $\mathcal {A}(Dh(z),\eta )=\xi (z)\cdot \eta$, for all $\eta \in \mathbb {R}^{Nn}$. Then $|\xi |\le \Lambda |Dh|$ and Lemma 5.1 and Jensen’s inequality imply

$$\begin{aligned} int_{\mathcal {Q}_\rho (z_0)}\psi \left( \left| \frac{h-(h)_{z_0,\rho }}{\rho }\right| \right) \, dz\le c^*_1int_{\mathcal {Q}_\rho (z_0)}\psi (|Dh|) \,dz, \end{aligned}$$

with $\psi$ an N-function satisfying $\Delta _2(\psi ,\psi ^*)<\infty$ and $c^*_1$ depending on $n,N,\Lambda ,$ and $\Delta _2(\psi ,\psi ^*)$.

The following Poincaré type inequality for weak solutions of (1.1) is a consequence of the previous lemma.

Theorem 5.1

Under the assumptions $(a_{1})$-$(a_{4})$ and Assumption 1.1, suppose $u\in C^0(-T,0; L^2(\Omega ,\mathbb {R}^N))\cap L^1(-T,0; W^{1,1}(\Omega ,\mathbb {R}^N))$ is a weak solution to (1.1) such that ${\varphi }(|Du|)\in L^1(-T,0;L^1(\Omega ))$. Let $\mathcal {Q}_\rho (z_0)\subset \Omega _T$ be a standard parabolic cylinder. Then, for any N-function $\psi$ satisfying $\Delta _2(\psi ,\psi ^*)<\infty$ and any $A\in \mathbb {R}^{Nn}$, we have

$$\begin{aligned}&int_{\mathcal {Q}_\rho (z_0)}\psi \left( \left| \frac{u-(u)_{z_0,\rho }-A(x-x_0)}{\rho }\right| \right) dz\\&\le c_2\left[ int_{\mathcal {Q}_\rho (z_0)}\psi (|Du-A|)\, dz +\psi \left( int_{\mathcal {Q}_\rho (z_0)}{\varphi }'_{1+|A|}(|Du-A|)\right) \, dz \right] \end{aligned}$$

with $c_2$ depending on $n,N,p_0,p_1,\nu ,L,$ and $\Delta _2(\psi ,\psi ^*)$.

Proof

Without loss of generality we can assume that $z_0=(0,0)$. Exploiting  (1.1) and using the fact that $\displaystyle {\int _{\Omega _T}Ax\cdot \zeta _t\,dz=0}$ and $\displaystyle {\int _{\Omega _T}a(A)\cdot D\zeta \,dz = 0}$ for any function $\zeta \in C^\infty _c(\Omega _T , \mathbb {R}^N)$, we have

$$\begin{aligned} \int _{\Omega _T} \left[ (u-Ax)\cdot \zeta _t-(a(Du)-a(A))\cdot D\zeta \right] \,dz=0. \end{aligned}$$

Therefore, we can apply the Lemma 5.1 with $w=u-Ax$ and $\xi =a(Du)-a(A)$. As Ax has zero-mean on $\mathcal {Q}_\rho$, we obtain:

$$\begin{aligned}&int_{\mathcal {Q}_\rho (z_0)}\psi \left( \left| \frac{u-(u)_\rho -Ax}{\rho }\right| \right) dz\le c_1\left[ int_{\mathcal {Q}_\rho (z_0)}\psi (|Du-A|)dz\right. \\&\quad \left. +\psi \left( int_{\mathcal {Q}_\rho (z_0)}|a(Du)-a(A)|\,dz\right) \right] . \end{aligned}$$

By means of Remark 2.4, we can estimate the right-hand side of the above inequality, and we get

$$\begin{aligned}&int_{\mathcal {Q}_\rho (z_0)}\psi \left( \left| \frac{u-(u)_\rho -Ax}{\rho }\right| \right) dz\le c_2 \left[ int_{\mathcal {Q}_\rho (z_0)}\psi (|Du-A|)dz\right. \\&\quad \left. +\psi \left( int_{\mathcal {Q}_\rho (z_0)}{\varphi }'_{1+|A|}(|Du-A|)\,dz\right) \right] . \end{aligned}$$

$\square$

We conclude this section by proving a weird Sobolev-Poincaré inequality for solutions of (1.1). The proof follows the same lines as [31, Lemma 3.4]. A special application of the inequality is required for Theorem 5.3, which we ultimately use to establish the main regularity result in Theorem 1.2.

Theorem 5.2

Under the assumptions $(a_{1})$-$(a_{4})$ and Assumption 1.1, suppose $u\in C^0(-T,0; L^2(\Omega ,\mathbb {R}^N))\cap L^1(-T,0; W^{1,1}(\Omega ,\mathbb {R}^N))$ is a weak solution to (1.1) such that ${\varphi }(|Du|)\in L^1(-T,0;L^1(\Omega ))$. Let $\mathcal {Q}_{\rho }(z_0)\subseteq \Omega _T$ be a standard parabolic cylinder and $\psi$ be an N-function satisfying Assumption 1.1 (for some exponents $1<q_0\le q_1$). Then, for any $A\in \mathbb {R}^{Nn}$, any $\theta _0>0$ satisfying

$$\begin{aligned} \theta _0q_0 \in (1,n)\qquad \text { and }\qquad \frac{nq_1}{nq_1+2q_0}\le \theta _0\le 1, \end{aligned}$$

(5.3)

and each $\frac{\rho }{2}\le r<R\le \rho$, we have

$$\begin{aligned}{} & {} int_{\mathcal {Q}_r(z_0)}\psi \left( \left| \frac{u-(u)_{z_0,r}-A(x-x_0)}{r}\right| \right) dz\nonumber \\{} & {} \qquad \le c_3\psi \left( T(r,R)^{1/2}\right) ^{1-\theta _0}\left[ int_{\mathcal {Q}_r(z_0)}\psi (|Du-A|)^{\theta _0}dz+\psi \left( int_{\mathcal {Q}_r(z_0)}{\varphi }'_{1+|A|}(|Du-A|)dz\right) ^{\theta _0}\right] ,\nonumber \\ \end{aligned}$$

(5.4)

with $c_3<\infty$ depending on $n,N,p_0,p_1, q_0,q_1,\nu ,L$. Here

$$\begin{aligned} T(r,R)=int_{\mathcal {Q}_R(z_0)}\left[ \left| \frac{u-(u)_{z_0,R}-A(x-x_0)}{R-r}\right| ^2 +{\varphi }_{1+|A|}\left( \left| \frac{u-(u)_{z_0,R}-A(x-x_0)}{R-r}\right| \right) \right] dz. \end{aligned}$$

Proof

Without loss of generality we can assume that $z_0=(0,0)$. Suppose $\theta _0>0$ satisfies (5.3). We use the Gagliardo-Nirenberg inequality (see [31, Lemma 2.13] with $(\psi ,\gamma ,\theta ,p,q_1,q_2)=(\psi ^{\frac{1}{q_0}},q_0,\theta _0, \theta _0q_0,\frac{q_1}{q_0},2)$) to get

$$\begin{aligned} int_{\mathcal {B}_r}\psi \left( \left| \frac{f}{r}\right| \right) dx\le c \left( int_{\mathcal {B}_r}\left[ \psi (|Df|)^{\theta _0}+\psi \left( \left| \frac{f}{r}\right| \right) ^{\theta _0}\right] dx\right) \psi \left( \left( int_{\mathcal {B}_r}\left| \frac{f}{r}\right| ^2dx\right) ^{\frac{1}{2}}\right) ^{1-\theta _0}. \end{aligned}$$

With $f=u-(u)_r-Ax$, we apply the previous inequality to each time slice:

$$\begin{aligned} \begin{aligned}&int_{\mathcal {Q}_r}\psi \left( \left| \frac{u-(u)_r-Ax}{r}\right| \right) dz\\&\le c\left[ int_{\mathcal {Q}_r}\left[ \psi (|Du-A|)^{\theta _0}+\psi \left( \left| \frac{u-(u)_r-Ax}{r}\right| \right) ^{\theta _0}\right] dz \right] \times \\ {}&\psi \left( \left( \sup _{-{r^2}<t<0}int_{\mathcal {B}_r}\left| \frac{u-(u)_r-Ax}{r}\right| ^2dx\right) ^{\frac{1}{2}}\right) ^{1-\theta _0}. \end{aligned} \end{aligned}$$

Observe that $\psi ^{\theta _0}$ satisfies Assumption 1.1 with exponents $1<\theta _0q_0\le \theta _0q_1$. It follows that $\Delta _2\left( \psi ^{\theta _0},\left( \psi ^{\theta _0}\right) ^*\right) \le \max \left\{ 2^{\theta _0q_1},2^\frac{\theta _0q_0}{\theta _0q_0-1}\right\} <\infty$. We may therefore use the Poincaré type inequality in Theorem 5.1, with $\psi$ replaced with $\psi ^{\theta _0}$, to bound the second term in the right hand side. Thus,

$$\begin{aligned} \begin{aligned}&int_{\mathcal {Q}_r}\psi \left( \left| \frac{u-(u)_r-Ax}{r}\right| \right) dz\\&\le c \left[ int_{\mathcal {Q}_r}\psi (|Du-A|)^{\theta _0}dz+\psi \left( int_{\mathcal {Q}_r} {\varphi }'_{1+|A|}(|Du-A|)dz\right) ^{\theta _0}\right] \times \\&\psi \left( \left( \sup _{-{r^2}<t<0}int_{\mathcal {B}_r}\left| \frac{u-(u)_r-Ax}{r}\right| ^2dx\right) ^{\frac{1}{2}}\right) ^{1-\theta _0}. \end{aligned} \end{aligned}$$

Now, to estimate the sup-term, we apply the Caccioppoli inequality on the cylinders $\mathcal {Q}_r$ and $\mathcal {Q}_R$ (see Theorem 4.1). Since $R\le 2r$,

$$\begin{aligned}{} & {} \sup _{-{r^2}<t<0}int_{\mathcal {B}_r}\left| \frac{u-(u)_r-Ax}{r}\right| ^2dx \le \frac{c_0}{r^{n+2}}\left[ \int _{\mathcal {Q}_R}{\varphi }_{1+|A|}\left( \left| \frac{u-(u)_r-Ax}{R-r}\right| \right) \right. \\{} & {} \quad \left. + \left| \frac{u-(u)_r-Ax}{R-r}\right| ^2dz\right] \\{} & {} \le c_0 2^{n+2}\left[ int_{\mathcal {Q}_R}{\varphi }_{1+|A|}\left( \left| \frac{u-(u)_r-Ax}{R-r}\right| \right) + \left| \frac{u-(u)_r-Ax}{R-r}\right| ^2dz\right] . \end{aligned}$$

To replace $(u)_r$ with $(u)_R$, we note that

$$\begin{aligned} |(u)_r-(u)_R|=\left| int_{\mathcal {Q}_r}[u-(u)_R-Ax]\,dz\right| \le 2^{n+2}int_{\mathcal {Q}_R}|u-(u)_R-Ax|\,dz. \end{aligned}$$

The result follows from Jensen’s inequality and the $\Delta _2$-condition. $\square$

To establish the main regularity result, Theorem 1.2, we will need the following inequality, which is proved using Theorem 5.2 with the special choice $t\mapsto \psi (t)=t^2$.

Theorem 5.3

Let $u\in C^0(-T,0; L^2(\Omega ,\mathbb {R}^N))\cap L^1(-T,0; W^{1,1}(\Omega ,\mathbb {R}^N))$ be a weak solution to (1.1) satisfying ${\varphi }(|Du|)\in L^1(-T,0;L^1(\Omega ))$. Under assumptions $(a_{1})$-$(a_{4})$ and Assumption 1.1, given any standard cylinder $\mathcal {Q}_{\rho }(z_0)\subseteq \Omega _T$, with center $z_0=(x_0,t_0)$, and any $A\in \mathbb {R}^{Nn}$, we have

$$\begin{aligned} \begin{aligned}&int_{\mathcal {Q}_{\rho /2}(z_0)} \left| \frac{u-(u)_{\rho /2}-A(x-x_0)}{\rho /2} \right| ^2 dz\\&\qquad \le c_4\left[ int_{\mathcal {Q}_{\rho }(z_0)}{\varphi }_{1+|A|}(|Du-A|)dz +\left( int_{\mathcal {Q}_{\rho }(z_0)}|Du-A|^{p_0}dz \right) ^{\frac{2}{p_0}}\right. \\&\qquad \qquad \qquad \left. + {\varphi }_{1+|A|}\left( int_{\mathcal {Q}_{\rho }(z_0)}{\varphi }'_{1+|A|}(|Du-A|)dz \right) +\left( int_{\mathcal {Q}_{\rho }(z_0)}{\varphi }'_{1+|A|}(|Du-A|)dz \right) ^{2}\right] , \end{aligned} \end{aligned}$$

where $c_4$ depends on $n,N,p_0,p_1,\nu ,$ and L.

Proof

As usual, we may assume $z_0=(0,0)$. Let $\frac{\rho }{2}\le r<R\le \rho$. For convenience, put $M=1+|A|$. We use Theorem 5.2 with the N-function $t\mapsto \psi (t)=t^2$, $q_0=q_1=2$, and $\theta _0=p_0/2$. Observe that, since $\frac{2n}{n+2}<p_0<2$,

$$\begin{aligned} \theta _0q_0=p_0\in (1,n)\qquad \text { and }\qquad \frac{n}{n+2} =\frac{nq_1}{nq_1+2q_0} <\theta _0\le 1. \end{aligned}$$

The inequality (5.4) becomes

$$\begin{aligned}{} & {} int_{\mathcal {Q}_r}\left| \frac{u-(u)_r-Ax}{r}\right| ^2 dz \le c_3\left( T(r,R)\right) ^{1-\frac{p_0}{2}}\times \nonumber \\ {}{} & {} \left[ int_{\mathcal {Q}_r}|Du-A|^{p_0}dz+\left( int_{\mathcal {Q}_r}{\varphi }'_{M}(|Du-A|)dz\right) ^{p_0}\right] , \end{aligned}$$

(5.5)

where

$$\begin{aligned} \begin{aligned} T(r,R)&= int_{\mathcal {Q}_R}\left| \frac{u-(u)_R-Ax}{R-r}\right| ^2 +{\varphi }_{M}\left( \left| \frac{u-(u)_R-Ax}{R-r}\right| \right) dz\\&\le \left( \frac{R}{R-r}\right) ^2int_{\mathcal {Q}_R} \left| \frac{u-(u)_R-Ax}{R}\right| ^2dz +\left( \frac{R}{R-r}\right) ^{p_1} int_{\mathcal {Q}_R}{\varphi }_{M}\left( \left| \frac{u-(u)_R-Ax}{R} \right| \right) dz\\&\le \left( \frac{R}{R-r}\right) ^{p_1}\left[ int_{\mathcal {Q}_R} \left| \frac{u-(u)_R-Ax}{R}\right| ^2dz +int_{\mathcal {Q}_R}{\varphi }_{M}\left( \left| \frac{u-(u)_R-Ax}{R} \right| \right) dz\right] . \end{aligned} \end{aligned}$$

Here, we have taken advantage of (2.2), $p_1>2$, and $\frac{R}{R-r}>1$. Now, we use Young’s inequality in (5.5), with $\frac{1}{\theta _0}=\frac{2}{p_0}$ and its conjugate $\frac{1}{1-\theta _0}=\frac{2}{2-p_0}$. This produces

$$\begin{aligned} \begin{aligned} int_{\mathcal {Q}_r}\left| \frac{u-(u)_r-Ax}{r}\right| ^2 dz \le&\frac{1}{2}int_{\mathcal {Q}_R} \left| \frac{u-(u)_R-Ax}{R}\right| ^2dz +\frac{1}{2}int_{\mathcal {Q}_R}{\varphi }_{M} \left( \left| \frac{u-(u)_R-Ax}{R}\right| \right) dz\\&\qquad + c \left( \frac{R}{R-r}\right) ^{\frac{p_1(2-p_0)}{p_0}} \left[ int_{\mathcal {Q}_r}|Du-A|^{p_0}dz +\left( int_{\mathcal {Q}_r}{\varphi }'_{M}(|Du-A|)dz\right) ^{p_0} \right] ^{\frac{2}{p_0}}. \end{aligned} \end{aligned}$$

For the second term in the upper bound, we can use Theorem 5.1 with $\psi (t)={\varphi }_{M}(t)$. The previous inequality becomes

$$\begin{aligned} \begin{aligned}&int_{\mathcal {Q}_r}\left| \frac{u-(u)_r-Ax}{r}\right| ^2 dz\\&\le \frac{1}{2}int_{\mathcal {Q}_R} \left| \frac{u-(u)_R-Ax}{R}\right| ^2dz +cint_{\mathcal {Q}_R}{\varphi }_{M}(|Du-A|)dz +{\varphi }_{M}\left( int_{\mathcal {Q}_R}{\varphi }'_{M}(|Du-A|)dz\right) \\&\quad \quad + c \left( \frac{R}{R-r}\right) ^{\frac{p_1(2-p_0)}{p_0}} \left[ int_{\mathcal {Q}_r}|Du-A|^{p_0}dz +\left( int_{\mathcal {Q}_r}{\varphi }'_{M}(|Du-A|)dz\right) ^{p_0} \right] ^{\frac{2}{p_0}}. \end{aligned} \end{aligned}$$

Enlarging the domain of integration (recall that $\frac{\rho }{2}\le r<R\le \rho$), we get

$$\begin{aligned} \begin{aligned}&int_{\mathcal {Q}_r}\left| \frac{u-(u)_r-Ax}{r}\right| ^2 dz\\&\le \frac{1}{2}int_{\mathcal {Q}_R} \left| \frac{u-(u)_R-Ax}{R}\right| ^2dz +cint_{\mathcal {Q}_{\rho }}{\varphi }_{M}(|Du-A|)dz +{\varphi }_{M}\left( int_{\mathcal {Q}_{\rho }}{\varphi }'_{M}(|Du-A|)dz\right) \\&\quad \quad + c \left( \frac{\rho }{R-r}\right) ^{\frac{p_1(2-p_0)}{p_0}} \left[ int_{\mathcal {Q}_{\rho }}|Du-A|^{p_0}dz +\left( int_{\mathcal {Q}_{\rho }}{\varphi }'_{M}(|Du-A|)dz\right) ^{p_0} \right] ^{\frac{2}{p_0}}. \end{aligned} \end{aligned}$$

We are now in position to apply [29, Lemma 6.1] to conclude the proof. $\square$

6 Linearization

We now prove a lemma that facilitates the comparison of solutions to our system (1.1) to solutions for a linear system with constant coefficients.

Lemma 6.1

Suppose $u\in C^0(-T,0; L^2(\Omega ,\mathbb {R}^N))\cap L^1(-T,0; W^{1,1}(\Omega ,\mathbb {R}^N))$ is a weak solution to (1.1) that satisfies ${\varphi }(|Du|)\in L^1(-T,0; L^1(\Omega ))$. Let a generic parabolic cylinder $\mathcal {Q}_{\rho ,\tau }(z_0)\subset \Omega _T$, with center $z_0=(x_0,t_0)$, be given. Under the hypotheses $(a_{1})$-$(a_{4})$ and Assumption 1.1, given any affine map $\ell : \mathbb {R}^{n}\rightarrow \mathbb {R}^{N}$ and any map $\eta \in C^\infty _c(\mathcal {Q}_{\rho /2,\tau /4}(z_0),\mathbb {R}^N)$, we have

$$\begin{aligned}{} & {} \left| int_{\mathcal {Q}_{\rho /2,\tau /4}(z_{0})} (u-\ell )\cdot \eta _t- Da(D\ell )( Du-D\ell , D\eta ) \, dz \right| \\{} & {} \le c_5{\varphi }_{1+|D\ell |}(1) \left\{ \omega \left( S^{\frac{1}{2}}\right) ^{\frac{1}{2}}S^{\frac{1}{2}}+S\right\} \sup _{\mathcal {Q}_{\rho /2,\tau /4}(z_{0})}|D\eta | \end{aligned}$$

where $c_5$ depends only on $n, N, L,\nu , p_0,p_1$. Here

$$\begin{aligned} S=int_{\mathcal {Q}_{\rho /2,\tau /4}(z_0)} \frac{{\varphi }_{1+|D\ell |}(|Du-D\ell |)}{{\varphi }_{1+|D\ell |}(1)}\,dz. \end{aligned}$$

Proof

We may assume $z_0=(0,0)$. For convenience, we write $\mathcal {Q}_{\rho ,\tau }=\mathcal {Q}_{\rho ,\tau }(z_0)$ and $M=1+|D\ell |$. Let $\eta \in C^\infty _c(\mathcal {Q}_{\rho /2,\tau /4},\mathbb {R}^N)$ be given. We first note:

$$\begin{aligned} \begin{aligned}&int_{\mathcal {Q}_{\rho /2,\tau /4}} [(u-\ell )\cdot \eta _t-Da(D\ell )(Du-D\ell ,D\eta )]\,dz\\&= int_{\mathcal {Q}_{\rho /2,\tau /4}}[(u-\ell )\cdot \eta _t-a(Du)\cdot D\eta ]\,dz\\&\quad + int_{\mathcal {Q}_{\rho /2,\tau /4}}[(a(Du)-a(D\ell ))\cdot D\eta -Da(D\ell )(Du-D\ell ,D\eta )]\,dz =:I+I\!I. \end{aligned} \end{aligned}$$

Since u is a weak solution to (1.1) and $\displaystyle {int_{\mathcal {Q}_{\rho /2,\tau /4}}\ell \cdot \eta _t\,dz=0}$, we infer that $I=0$. On the other hand,

$$\begin{aligned} \begin{aligned} int_{\mathcal {Q}_{\rho /2,\tau /4}}(a(Du)-a(D\ell ))\cdot D\eta \,dz&=int_{\mathcal {Q}_{\rho /2,\tau /4}}\int _0^1\frac{d}{ds} \left[ a(D\ell +s(Du-D\ell ))\right] \cdot D\eta \,ds\,dz\\&=int_{\mathcal {Q}_{\rho /2,\tau /4}}\int _0^1Da(D\ell +s(Du-D\ell ))(Du-D\ell ,D\eta )\,ds\,dz, \end{aligned} \end{aligned}$$

so that

$$\begin{aligned} I\!I=int_{\mathcal {Q}_{\rho /2,\tau /4}}\int _0^1[Da(D\ell +s(Du-D\ell ))-Da(D\ell )](Du-D\ell ,D\eta )\,ds\,dz. \end{aligned}$$

Using the continuity assumption $(a_4)$,

$$\begin{aligned}{} & {} |I\!I| \le Lint_{\mathcal {Q}_{\rho /2,\tau /4}}\int _0^1 \omega \left( \frac{s|Du-D\ell |}{1+|D\ell +s(Du-D\ell )|+|D\ell |}\right) \\ {}{} & {} {\varphi }''(M+|D\ell +s(Du-D\ell )|)|Du-D\ell ||D\eta |\,ds\,dz\\{} & {} \le Lint_{\mathcal {Q}_{\rho /2,\tau /4}} \omega \left( |Du-D\ell |\right) |Du-D\ell ||D\eta |\int _0^1{\varphi }''(M+|D\ell +s(Du-D\ell )|)\,ds\,dz. \end{aligned}$$

As ${\varphi }'$ is nondecreasing, Assumption 1.1, Lemma 2.2, and (2.4) yield

$$\begin{aligned} \int _0^1{\varphi }''(M+|D\ell +s(Du-D\ell )|)\,ds \le c\,\frac{{\varphi }'(M+|Du|+|D\ell |)}{M+|Du|+|D\ell |} \le c\,\frac{{\varphi }'(M+|Du|)}{M+|Du|}. \end{aligned}$$

Thus,

$$\begin{aligned} |I\!I|\le c\sup _{\mathcal {Q}_{\rho /2,\tau /4}}\!\!\!\!|D\eta |\,int_{\mathcal {Q}_{\rho /2,\tau /4}} \omega \left( |Du-D\ell |\right) |Du-D\ell |\, \frac{{\varphi }'(M+|Du|)}{M+|Du|}\,dz. \end{aligned}$$

Now, we distinguish in $\mathcal {Q}_{\rho /2,\tau /4}$ the points where $|Du-D\ell |\le M$ from those where $|Du-D\ell |>M$. Denote by $\mathbb {X}$ the first set and by $\mathbb {Y}$ the second. On $\mathbb {X}$, we have $|Du|\le 2M$, so (2.4) implies ${\varphi }'(M+|Du|)\sim {\varphi }'(M)$. Thus

$$\begin{aligned} |Du-D\ell |\frac{{\varphi }'(M+|Du|)}{M+|Du|}&\le c\left( \frac{{\varphi }'(M)}{M}\right) ^\frac{1}{2} \left( |Du-D\ell |^2\frac{{\varphi }'(M+|Du-D\ell |)}{M+|Du-D\ell |}\right) ^\frac{1}{2} \\&\le c\left( \frac{{\varphi }'(M)}{M}\right) ^\frac{1}{2}{\varphi }_M(|Du-D\ell |)^\frac{1}{2}, \end{aligned}$$

where we have used (2.8). Moreover,

$$\begin{aligned} |Du-D\ell |&\le c\frac{M+|Du|}{{\varphi }'(M+|Du|)}\left( \frac{{\varphi }'(M)}{M}\right) ^\frac{1}{2}{\varphi }_M(|Du-D\ell |)^\frac{1}{2}\\&\le c\left( \frac{M}{{\varphi }'(M)}\right) ^\frac{1}{2}{\varphi }_M(|Du-D\ell |)^\frac{1}{2}. \end{aligned}$$

It follows that

$$\begin{aligned}&int_{\mathcal {Q}_{\rho /2,\tau /4}}\!\!\!\!\!\!\chi _{{\mathbb {X}}} \omega \left( |Du-D\ell |\right) |Du-D\ell |\, \frac{{\varphi }'(M+|Du|)}{M+|Du|}\,dz\\&\qquad \le c\left( \frac{{\varphi }'(M)}{M}\right) ^\frac{1}{2}int_{\mathcal {Q}_{\rho /2,\tau /4}} \omega \left( \left( \frac{M}{{\varphi }'(M)}\right) ^\frac{1}{2} {\varphi }_M(|Du-D\ell |)^\frac{1}{2}\right) {\varphi }_M(|Du-D\ell |)^\frac{1}{2}\,dz. \end{aligned}$$

Applying Hölder’s inequality and using the concavity of $\omega$ and the bound $\omega \le 1$, we continue with

$$\begin{aligned}&int_{\mathcal {Q}_{\rho /2,\tau /4}}\chi _{{\mathbb {X}}} \omega \left( |Du-D\ell |\right) |Du-D\ell |\,\frac{{\varphi }'(M+|Du|)}{M+|Du|}\,dz\\&\le c\left( \frac{{\varphi }'(M)}{M}\right) ^\frac{1}{2} \left( int_{\mathcal {Q}_{\rho /2,\tau /4}} \omega \left( \left( \frac{M}{{\varphi }'(M)}\right) ^\frac{1}{2} {\varphi }_M(|Du-D\ell |)^\frac{1}{2}\right) ^2\,dz\right) ^\frac{1}{2}\times \\&\qquad \left( int_{\mathcal {Q}_{\rho /2,\tau /4}}{\varphi }_M(|Du-D\ell |)\,dz\right) ^\frac{1}{2}\\&\le c\left( \frac{{\varphi }'(M)}{M}\right) ^\frac{1}{2} \omega \left( \left( \frac{M}{{\varphi }'(M)}\right) ^\frac{1}{2} \left( int_{\mathcal {Q}_{\rho /2,\tau /4}}{\varphi }_M(|Du-D\ell |)\,dz\right) ^\frac{1}{2}\right) ^{\frac{1}{2}}\times \\ {}&\qquad \left( int_{\mathcal {Q}_{\rho /2,\tau /4}}{\varphi }_M(|Du-D\ell |)\,dz\right) ^\frac{1}{2}\\&\le c\left( \frac{{\varphi }'(M)}{M}\right) ^\frac{1}{2} \omega \left( \left( \frac{M}{{\varphi }'(M)}\right) ^\frac{1}{2}S^\frac{1}{2}{\varphi }_M(1)^{\frac{1}{2}}\right) ^{\frac{1}{2}} S^\frac{1}{2}{\varphi }_M(1)^{\frac{1}{2}}. \end{aligned}$$

To complete the bound on $\mathbb {X}$, we use (2.4) and (2.8) to deduce that

$$\begin{aligned} \frac{{\varphi }'(M)}{M}\sim \frac{{\varphi }'(M+1)}{M+1}\sim {\varphi }_M(1). \end{aligned}$$

We conclude that

$$\begin{aligned} int_{\mathcal {Q}_{\rho /2,\tau /4}}\!\!\!\!\!\!\chi _{{\mathbb {X}}} \omega \left( |Du-D\ell |\right) |Du-D\ell |\, \frac{{\varphi }'(M+|Du|)}{M+|Du|}\,dz \le c{\varphi }_M(1)\omega \left( S^\frac{1}{2}\right) ^\frac{1}{2} S^\frac{1}{2}. \end{aligned}$$

(6.1)

Turning to the set $\mathbb {Y}$, we have $1\le M\le |Du-D\ell |\le |Du-D\ell |^2$. Recalling (2.4) and (2.8) once more, we have

$$\begin{aligned} |Du-D\ell |\frac{{\varphi }'(M+|Du|)}{M+|Du|} \le c|Du-D\ell |^2\frac{{\varphi }'(M+|Du-D\ell |)}{M+|Du-D\ell |} \le c{\varphi }_M(|Du-D\ell |). \end{aligned}$$

Thus

$$\begin{aligned}{} & {} int_{\mathcal {Q}_{\rho /2,\tau /4}}\!\!\!\!\!\!\chi _{{\mathbb {Y}}} \omega \left( |Du-D\ell |\right) |Du-D\ell |\, \frac{{\varphi }'(M+|Du|)}{M+|Du|}\,dz\nonumber \\ {}{} & {} \le cint_{\mathcal {Q}_{\rho /2,\tau /4}}{\varphi }_M(|Du-D\ell |)\,dz =c{\varphi }_M(1)S. \end{aligned}$$

(6.2)

Here, we have again used $\omega \le 1$. The lemma follows from summing (6.1) and (6.2). To verify the claim for the parameter dependencies of the constant $c_5$, we review the proof and note that only the hypothesis $(a_4)$, Assumption 1.1, and properties (2.4) and (2.8) were required. $\square$

7 Decay Estimates

For convenience, we recall the excess functional introduced in Section 1. Given $z_0\in \Omega _T$, $a\ge 0$, $r>0$, and an affine map $\ell :\mathbb {R}^{n}\rightarrow \mathbb {R}^{N}$, define

$$\begin{aligned} \Psi _a(z_0,r,\ell )=int_{\mathcal {Q}_r(z_0)}\left( \left| \frac{u-\ell }{r}\right| ^2+{\varphi }_a\left( \left| \frac{u-\ell }{r}\right| \right) \right) \, d z. \end{aligned}$$

In the following lemma we provide the decay of the excess $\Psi _{1+|D\ell _{z_0,\rho }|}(z_0,\rho ,\ell _{z_0,\rho })$. Recall that $\ell _{z_0,\rho }$ is defined in (2.11) and denotes the time-independent affine map closest to u with respect to the $L^2$-norm on $\mathcal {Q}_\rho (z_0)$.

Lemma 7.1

(Decay Estimate) Suppose that hypotheses $(a_{1})$-$(a_{4})$ and Assumption 1.1 hold and that $u\in C^0(-T,0; L^2(\Omega ,\mathbb {R}^N))\cap L^1(-T,0; W^{1,1}(\Omega ,\mathbb {R}^N))$ is a weak solution to (1.1) satisfying ${\varphi }(|Du|)\in L^1(-T,0; L^1(\Omega ))$. Let $M_0>0$ and $0<\alpha <1$ be given. There exist $0<\varepsilon ,\theta <1$ with the following property: if $z_0\in \Omega _T$ and $\rho >0$ are such that $\mathcal {Q}_\rho (z_0)\subseteq \Omega _T$,

$$\begin{aligned} |D\ell _{z_0,\rho }|\le M_0, \qquad \text { and }\qquad \Psi _{1+|D\ell _{z_0,\rho }|}(z_0,\rho ,\ell _{z_0,\rho })\le \varepsilon , \end{aligned}$$

then

$$\begin{aligned} \Psi _{1+|D\ell _{z_0,\theta \rho }|}(z_0,\theta \rho ,\ell _{z_0,\theta \rho }) \le \theta ^{2\alpha }\Psi _{1+|D\ell _{z_0,\rho }|}(z_0,\rho ,\ell _{z_0,\rho }) \end{aligned}$$

and

$$\begin{aligned} |D\ell _{z_0,\theta \rho }| \le |D\ell _{z_0,\rho }| +(n+2)\left( \frac{1}{\theta }\right) ^{n+3}\Psi _{1+|D\ell _\rho |}(z_0,\rho ,\ell _{z_0,\rho })^\frac{1}{2}. \end{aligned}$$

Proof

For each $0<r\le \rho$, we write $\ell _r=\ell _{z_0,r}$ and $\Psi _a(r)=\Psi _a(z_0,r,\ell _r)$. Define $v=u-\ell _\rho$ and $M=1+|D\ell _\rho |\le M_0+1$. Let $\mathcal {A}$ denote the bilinear form $Da(D\ell _{\rho })$. Thus

$$\begin{aligned} \mathcal {A}(\xi ,\xi )\ge \nu {\varphi }''(1+|D\ell _\rho |)|\xi |^2 \quad \text{ and } \quad |\mathcal {A}(\xi ,\eta )|\le L{\varphi }''(1+|D\ell _\rho |)|\xi ||\eta |. \end{aligned}$$

Let us recall that $\Delta _2({\varphi }_M)\le 2^{p_1}$; with $0<\alpha <1$ given, define

$$\begin{aligned} 0<\theta =\theta (M,\alpha ) =\min \left\{ \frac{1}{32}, \left( \frac{1}{1+c_{6,6}}\right) ^\frac{1}{2(1-\alpha )} \right\} , \end{aligned}$$

(7.1)

and suppose that

$$\begin{aligned}{} & {} \Psi _M(\rho )\le \varepsilon =\varepsilon (M)\nonumber \\{} & {} \quad \le \min \left\{ \frac{{\varphi }_M(1)}{c_{6,1}},\frac{\delta ^2}{c_{6,2}^2}, \frac{1}{{(\omega _n+1)}c_{6,3}c_{6,4}},\left( \frac{\theta ^{n+3}}{n+2}\right) ^2, \frac{(4\theta )^{n+p_1+4}}{c_{6,3}c_{6,5}\left( 2+\Delta _2({\varphi }_M)^3\right) }\right\} , \end{aligned}$$

(7.2)

where the precise values of the constants $c_{6,i}>1$ will be determined in the course of the proof. The constant $0<\delta <1$ is specified by Theorem 3.2, while the constant C appearing below may change from line to line but will depend on only $n,N,L/\nu ,p_0,p_1$.

As $\ell _\rho$ is independent of t, the map v is a weak solution to (1.1). Our first objective is to take advantage of the $\mathcal {A}$-caloric approximation lemma to produce an $\mathcal {A}$-caloric map close to v. With S defined in Lemma 6.1, the Caccioppoli inequality in Corollary 4.1 implies

$$\begin{aligned}{} & {} S=int_{Q_{\rho /2}}\frac{{\varphi }_M(|Du-D\ell _\rho |)}{{\varphi }_M(1)}\,dz\\ {}{} & {} \le \frac{c_02^{n+p_1+2}}{{\varphi }_M(1)} int_{Q_\rho }\left[ \left| \frac{v}{\rho }\right| ^2 +{\varphi }_M\left( \left| \frac{v}{\rho }\right| \right) \right] \,dz \le \frac{c_{6,1}}{{\varphi }_M(1)}\Psi _M(\rho )\le 1. \end{aligned}$$

Note that $c_{6,1}=c_02^{n+p_1+2}$. Now, Lemma 6.1 delivers the bound

$$\begin{aligned} \left| int_{\mathcal {Q}_{\rho /2}} \left( v\cdot \partial _t\eta -\mathcal {A}(Dv,D\eta )\right) \, dz\right|&\le c_5{\varphi }_M(1)\left\{ \omega \left( S^\frac{1}{2}\right) ^{\frac{1}{2}}S^\frac{1}{2}+S\right\} \sup _{Q_{\rho /2}}|D\eta |\\&\le 2c_5c_{6,1}^\frac{1}{2}{\varphi }_M(1)^\frac{1}{2}\Psi _M(\rho )^\frac{1}{2}\sup _{Q_{\rho /2}}|D\eta |\\&=c_{6,2}\Psi _M(\rho )^\frac{1}{2}\sup _{Q_{\rho /2}}|D\eta |\\&\le \delta \sup _{Q_{\rho /2}}|D\eta |. \end{aligned}$$

The smallness condition (7.2) was applied in the last inequality. This verifies the requirement in (3.3) of Theorem 3.2. For the other requirement in (3.4), we again use the Caccioppoli inequality:

$$\begin{aligned}&\sup _{t_0-\rho ^2/4<t<t_0}int_{\mathcal {B}_{\rho /2}} \left| \frac{v}{\rho /2}\right| ^2\,dx +int_{\mathcal {Q}_{\rho /2}} \left( {\varphi }_M\left( \left| \frac{v}{\rho /2}\right| \right) +{\varphi }_{M}(|Dv|)\right) \,dz\\&\qquad \qquad \qquad \qquad \le 4c_{6,1}\Psi _M(\rho )+\Delta _2({\varphi }_M)int_{\mathcal {Q}_{\rho /2}} {\varphi }_M\left( \left| \frac{v}{\rho }\right| \right) \,dz\\&\qquad \qquad \qquad \qquad \le c_02^{n+p_1+5}\Psi _M(\rho )= c_{6,3}\Psi _M(\rho )=:\gamma ^2\le {\min \{1/\omega _n,1\}}. \end{aligned}$$

With the hypotheses of Theorem 3.2 satisfied, taking into account Remarks 2.3 and 3.1 , we obtain an $\mathcal {A}$-caloric map $h\in C^\infty (\mathcal {Q}_{\rho /4};\mathbb {R}^{N})$ such that

$$\begin{aligned} int_{\mathcal {Q}_{\rho /4}}\left( \left| \frac{\gamma h}{\rho /4}\right| ^2 +{\varphi }_{M}\left( \left| \frac{\gamma h}{\rho /4}\right| \right) +{\varphi }_{M}(|\gamma Dh|)\right) \, d z \le 2^{n+2}K_{{\varphi }_M}\gamma ^2 \end{aligned}$$

(7.3)

and

$$\begin{aligned} int_{\mathcal {Q}_{\rho /4}}\left( \left| \frac{v-\gamma h}{\rho /4}\right| ^2 +{\varphi }_{M}\left( \left| \frac{v-\gamma h}{\rho /4}\right| \right) \right) \, d z \le \varepsilon \gamma ^2. \end{aligned}$$

Recall that $0<\theta <1/16$ by definition (7.1). As in Lemma 2.8, for $0<r\le \rho /4$, we define the affine map $\ell ^{(h)}_{r}(x)=(h)_{z_0,r}+(Dh)_{z_0,r}(x-x_0)$. We want to produce a bound for

$$\begin{aligned} int_{\mathcal {Q}_{\theta \rho }}\left| \frac{v-\gamma \ell ^{(h)}_{\theta \rho }}{\theta \rho }\right| ^2\, d z +int_{\mathcal {Q}_{\theta \rho }}{\varphi }_{M}\left( \left| \frac{v-\gamma \ell ^{(h)}_{\theta \rho }}{\theta \rho }\right| \right) \, d z =:I+I\!I. \end{aligned}$$

We will focus on $I\!I$. The argument for I is similar. We may write

$$\begin{aligned} I\!I&\le \Delta _2({\varphi }_M)int_{\mathcal {Q}_{\theta \rho }}{\varphi }_M\left( \left| \frac{v-\gamma h}{\theta \rho }\right| \right) +{\varphi }_{M}\left( \left| \frac{\gamma (h-\ell ^{(h)}_{z_0,\theta \rho })}{\theta \rho }\right| \right) \, d z\nonumber \\&\le \Delta _2({\varphi }_M)\left( \frac{1}{4\theta }\right) ^{p_1+n+2} int_{\mathcal {Q}_{\rho /4}}{\varphi }_{M}\left( \left| \frac{v-\gamma h}{\rho /4}\right| \right) \, d z +\Delta _2({\varphi }_M)int_{\mathcal {Q}_{\theta \rho }}{\varphi }_{M}\left( \left| \frac{\gamma (h-\ell ^{(h)}_{z_0,\theta \rho })}{\theta \rho }\right| \right) \, d z\nonumber \\&\le \Delta _2({\varphi }_M)\left( \frac{1}{4\theta }\right) ^{p_1+n+2}\varepsilon \gamma ^2 +\Delta _2({\varphi }_M)int_{\mathcal {Q}_{\theta \rho }}{\varphi }_{M}\left( \left| \frac{\gamma (h-\ell ^{(h)}_{z_0,\theta \rho })}{\theta \rho }\right| \right) \, d z. \end{aligned}$$

(7.4)

Observe that Lemma 2.5-(b) and (7.3) imply

$$\begin{aligned} int_{\mathcal {Q}_{\rho /4}} \left| \frac{\gamma (h-\ell ^{(h)}_{z_0,\rho /4})}{\rho /4}\right| ^2\, d z \le&6int_{\mathcal {Q}_{\rho /4}}\left| \frac{\gamma h}{\rho /4}\right| ^2\, d z +3\left( int_{\mathcal {Q}_{\rho /4}}|\gamma Dh|\right) ^2\, d z\\ \le&2^{n+5}K_{{\varphi }_M}\gamma ^2 \\&+\frac{C}{{\varphi }''(M)}int_{\mathcal {Q}_{\rho /4}} {\varphi }_{M}(|\gamma Dh|)\, d z+\frac{C}{{\varphi }_{M}(1)^2}\left( int_{\mathcal {Q}_{\rho /4}} {\varphi }_{M}(|\gamma Dh|)\, d z\right) ^2\\ \le&2^{n+5}K_{{\varphi }_M}\gamma ^2+C\left( \frac{1}{{\varphi }''(M)} +\frac{2^{n+2}K_{{\varphi }_M}\gamma ^2}{{\varphi }_M(1)^2}\right) 2^{n+2}K_{{\varphi }_M}\gamma ^2\\ \le&2^{2n+5}K^2_{{\varphi }_M}\left[ 1+C\left( \frac{1}{{\varphi }''(M)} +\frac{1}{{\varphi }_M(1)^2}\right) \right] \gamma ^2=c_{6,4}\gamma ^2\le 1. \end{aligned}$$

We may therefore use the inequality in Lemma 2.8, Remark 2.3, (2.7), and Jensen’s inequality to deduce that

$$\begin{aligned} int_{\mathcal {Q}_{\theta \rho }} {\varphi }_{M}\left( \left| \frac{\gamma (h-\ell ^{(h)}_{z_0,\theta \rho })}{\theta \rho }\right| \right) \, d z \le C\theta ^{2}int_{Q_{\rho /4}} {\varphi }_{M} \left( \left| \frac{\gamma (h-\ell ^{(h)}_{z_0,\rho /4})}{\rho /4}\right| \right) \, d z. \end{aligned}$$

(7.5)

On the other hand Jensen’s inequality and the $\Delta _2$-property imply

$$\begin{aligned} int_{\mathcal {Q}_{\rho /4}}{\varphi }_{M}\left( \left| \frac{\gamma (h-\ell ^{(h)}_{z_0,\rho /4})}{\rho /4}\right| \right) \, d z \le&\Delta _2({\varphi }_M)^2int_{\mathcal {Q}_{\rho /4}}\left( {\varphi }_{M}\left( \left| \frac{\gamma h}{\rho /4}\right| \right) +{\varphi }_{M}(|\gamma Dh|)\right) \, d z\nonumber \\ \le&2^{n+2}K_{{\varphi }_M}\Delta _2({\varphi }_M)^2\gamma ^2. \end{aligned}$$

(7.6)

With (7.5) and (7.6) we return to (7.4) to obtain

$$\begin{aligned} int_{\mathcal {Q}_{\theta \rho }}{\varphi }_M\left( \left| \frac{v-\gamma \ell ^{(h)}_{\theta \rho }}{\theta \rho }\right| \right) \,dz =II \le \Delta _2({\varphi }_M)^3\left[ \left( \frac{1}{4\theta }\right) ^{p_1+n+2}\varepsilon +C2^{n+2}K_{{\varphi }_M}\theta ^2\right] \gamma ^2. \end{aligned}$$

We similarly obtain

$$\begin{aligned} int_{\mathcal {Q}_{\theta \rho }}\left| \frac{v-\gamma \ell ^{(h)}_{\theta \rho }}{\theta \rho }\right| ^2\,dz =I \le \left[ 2\left( \frac{1}{4\theta }\right) ^{n+4}\varepsilon +Cc_{6,4}\theta ^2\right] \gamma ^2. \end{aligned}$$

Thus, since $\theta \le 1/4$,

$$\begin{aligned}&int_{\mathcal {Q}_{\theta \rho }}\left| \frac{v-\gamma \ell ^{(h)}_{z_0,\theta \rho }}{\theta \rho }\right| ^2 +{\varphi }_{M}\left( \left| \frac{v-\gamma \ell ^{(h)}_{z_0,\theta \rho }}{\theta \rho } \right| \right) \, d z \\&\le \left[ \left( \frac{1}{4\theta }\right) ^{n+p_1+2} \left( 2+\Delta _2({\varphi }_M)^3\right) \varepsilon +Cc_{6,4}\left( 1+\Delta _2({\varphi }_M)^3\right) \theta ^2\right] \gamma ^2. \end{aligned}$$

Let us point out that $1+|D\ell _{\theta \rho }|\le M+1$. Indeed, from (2.13) we obtain

$$\begin{aligned} \begin{aligned} |D\ell _{\theta \rho }|&\le |D\ell _\rho |+|D\ell _{\rho }- D\ell _{\theta \rho }|\\&\le M-1+(n+2) int_{\mathcal {Q}_{\theta \rho }} \left| \frac{u- \ell _{\rho }}{\theta \rho }\right| \, dz \le M-1+\left( \frac{n+2}{\theta ^{n+3}}\right) int_{\mathcal {Q}_{\rho }} \left| \frac{u- \ell _{\rho }}{\rho }\right| \, dz\\&\le M-1+\left( \frac{n+2}{\theta ^{n+3}}\right) \left( int_{\mathcal {Q}_{\rho }} \left| \frac{u- \ell _{\rho }}{\rho }\right| ^2\, dz\right) ^{\frac{1}{2}}\\&\le M-1+\left( \frac{n+2}{\theta ^{n+3}}\right) \Psi _{1+|D\ell _{\rho }|}(\rho )^{\frac{1}{2}}\\&\le M-1+\left( \frac{n+2}{\theta ^{n+3}}\right) \varepsilon ^{\frac{1}{2}} \le M \end{aligned} \end{aligned}$$

(7.7)

provided $\displaystyle {\varepsilon \le \left( \frac{\theta ^{n+3}}{n+2}\right) ^2}$.

Now, using Lemma 2.4 (with M replaced by $M+1$) and Lemma 2.6 (with $\ell =\ell _\rho -\gamma \ell ^{(h)}_{z_0,\theta \rho }$), and defining $c_{6,5}=\kappa _0\,4^{p_1+1}(M+1)^{p_1+2}$ ($\kappa _0$ from Lemma  2.6), we have

$$\begin{aligned} \Psi _{1+|D\ell _\theta \rho |}(z_0,\theta \rho , \ell _{\theta \rho }) =&int_{\mathcal {Q}_{\theta \rho }}\left( \left| \frac{u-\ell _{\theta \rho }}{\theta \rho }\right| ^2 +{\varphi }_{1+|D\ell _{\theta \rho }|}\left( \left| \frac{u-\ell _{\theta \rho }}{\theta \rho }\right| \right) \right) \, d z\\ \le&4^{p_1+1}(M+1)^{p_1+2} int_{\mathcal {Q}_{\theta \rho }}\left( \left| \frac{u-\ell _{\theta \rho }}{\theta \rho }\right| ^2 +{\varphi }_{M}\left( \left| \frac{u-\ell _{\theta \rho }}{\theta \rho }\right| \right) \right) \, d z\\ \le&c_{6,5}int_{\mathcal {Q}_{\theta \rho }}\left( \left| \frac{u-\ell _\rho -\gamma \ell ^{(h)}_{z_0,\theta \rho }}{\theta \rho }\right| ^2 +{\varphi }_{M}\left( \left| \frac{u-\ell _\rho -\gamma \ell ^{(h)}_{z_0,\theta \rho }}{\theta \rho } \right| \right) \right) \, d z\\ =&c_{6,5}int_{\mathcal {Q}_{\theta \rho }}\left( \left| \frac{v-\gamma \ell ^{(h)}_{z_0,\theta \rho }}{\theta \rho }\right| ^2 +{\varphi }_{M}\left( \left| \frac{v-\gamma \ell ^{(h)}_{z_0,\theta \rho }}{\theta \rho } \right| \right) \right) \, d z\\ \le&c_{6,3} \, c_{6,5} \left[ \left( \frac{1}{4\theta }\right) ^{n+p_1+2} \left( 2+\Delta _2({\varphi }_M)^3\right) \varepsilon +Cc_{6,4}\left( 1+\Delta _2({\varphi }_M)^3\right) \theta ^2\right] \Psi _M(\rho )\\ \le&\left[ \theta ^2+c_{6,6}\theta ^2\right] \Psi _{M}(\rho ), \end{aligned}$$

where $c_{6,6}=Cc_{6,3}c_{6,4}c_{6,5}(1+\Delta _2({\varphi }_M)^3)$. So, under the smallness assumption that $\Psi _{M}(\rho )\le \varepsilon$,

$$\begin{aligned} \Psi _{1+|D\ell _{\theta \rho }|}(z_0,\theta \rho ,\ell _{\theta \rho }) \le \theta ^{2\alpha }\Psi _{1+|D\ell _\rho |}(z_0,\rho ,\ell _\rho ). \end{aligned}$$

Combined with (7.7), we conclude that

$$\begin{aligned} |D\ell _{\theta \rho }| \le |D\ell _\rho | +(n+2)\left( \frac{1}{\theta }\right) ^{n+3}\Psi _{1+|D\ell _\rho |}(\rho )^\frac{1}{2}. \end{aligned}$$

$\square$

In the following lemma we will iterate the excess-decay estimate from the previous lemma.

Lemma 7.2

(Iteration Argument) Suppose that the assumptions, for u and ${\varphi }$, in Lemma 7.1 hold. Let $M_0>1$ and $0<\alpha <1$ be given. There exist $0<\varepsilon _0<\theta _0<1$ and $c_7=c_7(M_0,\theta _0,n,N,L/\nu ,p_0,p_1)$ with the following property: given a standard parabolic cylinder $\mathcal {Q}_{\rho _0}(z_0)\subseteq \Omega _T$, if

$$\begin{aligned} 1+|D\ell _{z_0,\rho _0}|\le M_0 \qquad \text { and }\qquad \Psi _{1+|D\ell _{z_0,\rho _0}|}(z_0,\rho ,\ell _{z_0,\rho _0})\le \varepsilon _0, \end{aligned}$$

then for each $j\in \mathbb {N}$, we have the following:

• (a) $\Psi _{1+|D\ell _{z_0,\theta _0^{j}\rho _0}|}(z_0,\theta _0^j\rho _0,\ell _{z_0,\theta _0^j\rho _0}) \le \theta _0^{2j\alpha }\Psi _{1+|D\ell _{z_0,\rho _0}|}(z_0,\rho _0,\ell _{z_0,\rho _0})$,

• (b) $|D\ell _{z_0,\theta _0^j\rho _0}|\le M_0-\theta _0^{j\alpha }$.

Moreover,

$$\begin{aligned}{} & {} int_{Q_r(z_0)} {\varphi }_{1+|(Du)_{z_0,r}|}(|Du-(Du)_{z_0,r}|)\, d z\nonumber \\ {}{} & {} \le c_7\left( \frac{r}{\rho _0}\right) ^{2\alpha } \Psi _{1+|D\ell _{z_0,\rho _0}|}(z_0,\rho _0,\ell _{z_0,\rho _0}), \quad \text { for all } 0<r\le \rho _0/2. \end{aligned}$$

(7.8)

Proof

Parts (a) and (b) follow from an induction argument. With $0<\alpha <1$, $\rho =\rho _0$, and $M_0$ fixed, let $0<\varepsilon ,\theta <1$ be provided by Lemma 7.1. Put

$$\begin{aligned} \theta _0:=\theta ,\quad \varepsilon _0:=\min \left\{ \varepsilon ,\frac{\theta _0^{2(n+3)}(1-\theta _0^\alpha )^2}{(n+2)^2}\right\} ,\quad \text { and }\quad \rho _j=\theta _0^{j}\rho _0,\quad \text { for each }j\in \mathbb {N}.\nonumber \\ \end{aligned}$$

(7.9)

Clearly $|D\ell _{z_0,\rho _0}|\le M_0$, and the base case, $j=1$, immediately follows from Lemma 7.1. With $j\in \mathbb {N}$ given, suppose that (a) and (b) are both true for all $k=1,\dots ,j$. We observe that (a) implies

$$\begin{aligned} \Psi _{1+|D\ell _{z_0,\rho _j}|}(z_0,\rho _j,\ell _{z_0,\rho _j}) \le \theta _0^{j\alpha }\Psi _{1+|D\ell _{z_0,\rho _0}|}(z_0,\rho _0,\ell _{z_0,\rho _0}) \le \varepsilon _0\le \varepsilon . \end{aligned}$$

By the inductive assumption,

$$\begin{aligned} |D\ell _{z_0,\rho _j}|\le M_0-\theta _0^{j\alpha }\le M_0. \end{aligned}$$

We may therefore use Lemma 7.1, with $\rho$ replaced with $\rho _j$ and the other parameters the same as in (7.9), to obtain

$$\begin{aligned} \Psi _{1+|D\ell _{z_0,\rho _{j+1}}|}(z_0,\rho _{j+1},\ell _{z_0,\rho _{j+1}}) \le&\theta _0^{2\alpha }\Psi _{1+|D\ell _{z_0,\rho _j}|}(z_0,\rho _j,\ell _{z_0,\rho _j})\\ \le&\theta _0^{2(j+1)\alpha }\Psi _{1+|D\ell _{z_0,\rho _0}|}(z_0,\rho _0,\ell _{z_0,\rho }). \end{aligned}$$

For part (b), we have

$$\begin{aligned} |D\ell _{z_0,\rho _{j+1}}| \le&|D\ell _{z_0,\rho _j}| +(n+2)\left( \frac{1}{\theta _0}\right) ^{n+3} \Psi _{1+|D\ell _{z_0,\rho _j}|}(z_0,\rho _j,\ell _{z_0,\rho _j})^\frac{1}{2}\\ \le&M_0-\theta _0^{j\alpha } +(n+2)\left( \frac{1}{\theta _0}\right) ^{n+3}\theta _0^{j\alpha }\varepsilon _0^\frac{1}{2} \le M_0-\theta _0^{j\alpha }+(1-\theta _0^\alpha )\theta _0^{j\alpha }\\ =&M_0-\theta ^{(j+1)\alpha }. \end{aligned}$$

By induction, we deduce (a) and (b) for all $j\in \mathbb {N}$.

It remains to verify (7.8). Given $0<r\le \rho _0/2$, we may select $j\in \mathbb {N}\cup \{0\}$ such that $\rho _{j+1}<2r\le \rho _j$. Using Remark 2.6 and Corollary 4.1, we have

$$\begin{aligned} int_{Q_r(z_0)}{\varphi }_{1+|(Du)_{z_0,r}|}(|Du-(Du)_{z_0,r}|)\, d z \le&\kappa _2\,int_{Q_r(z_0)} {\varphi }_{1+|D\ell _{z_0,\rho _{j}}|}(|Du-D\ell _{z_0,\rho _{j}}|)\, d z\\ \le&\frac{\kappa _2}{\theta _0^{n+2}}int_{Q_{\rho _j/2}(z_0)} {\varphi }_{1+|D\ell _{z_0,\rho _{j}}|}(|Du-D\ell _{z_0,\rho _{j}}|)\, d z\\ \le&c_02^{n+p_1+4}\left( \frac{\kappa _2}{\theta _0^{n+2}}\right) \Psi _{1+|D\ell _{z_0,\rho _j}|}(z_0,\rho _j,\ell _{z_0,\rho _j})\\ \le&c_02^{n+p_1+4}\left( \frac{\kappa _2}{\theta _0^{n+2}}\right) \theta _0^{2j\alpha } \Psi _{1+|D\ell _{z_0,\rho _0}|}(z_0,\rho _0,\ell _{z_0,\rho _0})\\ \le&c_7\left( \frac{r}{\rho _0}\right) ^{2\alpha } \Psi _{1+|D\ell _{z_0,\rho _0}|}(z_0,\rho _0,\ell _{z_0,\rho _0}). \end{aligned}$$

Since $\Delta _2({\varphi },{\varphi }^*)$ depends on only $p_1$ and $p_0$, the lemma is proved. $\square$

8 Partial regularity

We are now in position to prove the main result of the paper.

Proof of Theorem 1.2

Let $z_0\in \Omega _T$ be such that

$$\begin{aligned} \liminf _{\rho \rightarrow 0}int_{\mathcal {Q}_\rho (z_0)}|V(Du)-(V(Du))_{z_0,\rho }|^2dz=0, \end{aligned}$$

and

$$\begin{aligned} \limsup _{\rho \rightarrow 0}|(Du)_{z_0,\rho }|<+\infty . \end{aligned}$$

(8.1)

Using (2.10), we deduce that

$$\begin{aligned} \liminf _{\rho \rightarrow 0}int_{\mathcal {Q}_\rho (z_0)}{\varphi }_{1+|(Du)_{z_0,\rho }|}(|Du)-(Du)_{z_0,\rho }|)dz=0. \end{aligned}$$

Exploiting Lemma 2.7 and Poincaré’s inequality in Theorem 5.1, we get

$$\begin{aligned} \begin{aligned}&int_{\mathcal {Q}_\rho (z_0)}{\varphi }_{1+|D\ell _{z_0,\rho }|}\left( \left| \frac{u-\ell _{z_0,\rho }}{\rho }\right| \right) \,dz \\&\quad \le \kappa _1int_{\mathcal {Q}_\rho (z_0)}{\varphi }_{1+|(Du)_{z_0,\rho }|}\left( \left| \frac{u-(u)_{z_0,\rho }-(Du)_{z_0,\rho }(x-x_0)}{\rho }\right| \right) \,dz\\&\quad \le \kappa _1c_2\left[ int_{\mathcal {Q}_\rho (z_0)}{\varphi }_{1+|(Du)_{z_0,\rho }|}(|Du-(Du)_{z_0,\rho }|)\,dz \right. \\&\qquad \left. +{\varphi }_{1+|(Du)_{z_0,\rho }|}\left( int_{\mathcal {Q}_\rho (z_0)}{\varphi }'_{1+|(Du)_{z_0,\rho }|}(|Du-(Du)_{z_0,\rho }|)\,dz\right) \right] . \end{aligned} \end{aligned}$$

(8.2)

Thanks to (2.5) and Jensen’s inequality, we may write

$$\begin{aligned}{} & {} int_{\mathcal {Q}_\rho (z_0)}{\varphi }'_{1+|(Du)_{z_0,\rho }|}(|Du-(Du)_{z_0,\rho }|)\,dz\nonumber \\ {}{} & {} \lesssim ({\varphi }^*_{1+|(Du)_{z_0,\rho }|})^{-1}\left( int_{\mathcal {Q}_\rho (z_0)}{\varphi }_{1+|(Du)_{z_0,\rho }|}(|Du-(Du)_{z_0,\rho }|)\,dz\right) . \end{aligned}$$

(8.3)

On the other hand, Theorem 5.3 implies

$$\begin{aligned} \begin{aligned}&int_{\mathcal {Q}_\rho (z_0)}\left| \frac{u-\ell _{z_0,\rho }}{\rho }\right| ^2\,dz\\&\le int_{\mathcal {Q}_\rho (z_0)}\left| \frac{u-(u)_{z_0,\rho }-(Du)_{z_0,2\rho }(x-x_0)}{\rho }\right| ^2\,dz\\&\le c_4 \left[ int_{\mathcal {Q}_{2\rho }(z_0)}{\varphi }_{1+|(Du)_{z_0,2\rho }|}(|Du-(Du)_{z_0,2\rho }|)dz+\left( int_{\mathcal {Q}_{2\rho }(z_0)}|Du-(Du)_{z_0,2\rho }|^{p_0}dz\right) ^{\frac{2}{p_0}}\right. \\&\qquad +{\varphi }_{1+|(Du)_{z_0,2\rho }|}\left( int_{\mathcal {Q}_{2\rho }(z_0)}{\varphi }'_{1+|(Du)_{z_0,2\rho }|}(|Du-(Du)_{z_0,2\rho }|)dz\right) \\&\qquad \left. +\left( int_{\mathcal {Q}_{2\rho }(z_0)}{\varphi }'_{1+|(Du)_{z_0,2\rho }|}(|Du-(Du)_{z_0,2\rho }|)dz\right) ^{2}\right] . \end{aligned} \end{aligned}$$

(8.4)

We can use Lemma 2.5 to control the upper bound’s second integral:

$$\begin{aligned} \begin{aligned} int_{\mathcal {Q}_{2\rho }(z_0)}|Du-(Du)_{z_0,2\rho }|^{p_0}dz&\le C\left( \frac{1}{{\varphi }''(1+|(Du)_{z_0,2\rho }|)}int_{\mathcal {Q}_{2\rho }(z_0)}{\varphi }_{1+|(Du)_{z_0,2\rho }|}(|Du-(Du)_{z_0,2\rho }|)\,dz\right) ^{\frac{p_0}{2}}\\&+C\frac{1}{{\varphi }_{1+|(Du)_{z_0,2\rho }|}(1)}int_{\mathcal {Q}_{z_0,2\rho }}{\varphi }_{1+|(Du)_{z_0,2\rho }|}(|Du-(Du)_{z_0,2\rho }|)\,dz. \end{aligned} \end{aligned}$$

(8.5)

Finally, from (2.13)

$$\begin{aligned} \begin{aligned} |D\ell _{z_0,\rho }-(Du)_{z_0,\rho }|&\le (n+2)int_{\mathcal {Q}_\rho (z_0)}\left| \frac{u-(u)_{z_0,\rho }-(Du)_{z_0,\rho }(x-x_0)}{\rho }\right| \,dz\\&\lesssim ({\varphi }_{1+|(Du)_{z_0,\rho }|})^{-1}\left( int_{\mathcal {Q}_\rho (z_0)}{\varphi }_{1+|(Du)_{z_0,\rho }|}\left( \left| \frac{u-(u)_{z_0,\rho }-(Du)_{z_0,\rho }(x-x_0)}{\rho }\right| \right) \,dz\right) , \end{aligned} \end{aligned}$$

(8.6)

which in turn can be bounded via (8.2) and (8.3). Let $\varepsilon _0>0$ be as defined in (7.9). Keeping in mind the definition of $z_0$, the estimates (8.2), (8.4), and (8.6), supported by (8.1), (8.3), and (8.5), imply the existence of $M_0> 1$ and a radius $R_0>0$ such that $|D\ell _{z_0,R_0}|<M_0-1$ and $\Psi _{1+|D\ell _{z_0,R_0}|}(z_0,R_0,\ell _{z_0,R_0})<\varepsilon _0$. By the absolute continuity of the integrals, there exists $R_1<R_0$ such that, for any $z\in \mathcal {Q}_{R_1}(z_0)$ we have

$$\begin{aligned} 1+|D\ell _{z,R_0}|<M_0\ \ \ \ \ \ \hbox { and }\ \ \ \ \ \ \Psi _{1+|D\ell _{z,R_0}|}(z,R_0,\ell _{z,R_0})< {\varepsilon _0}. \end{aligned}$$

Applying Lemma 7.2 to each point $z\in \mathcal {Q}_{R_1}(z_0)$, we deduce that, for any $r\le R_0/2$,

$$\begin{aligned}{} & {} \int _{\mathcal {Q}_r(z)}|V(Du)-(V(Du))_{z,r}|^2dz\sim \int _{\mathcal {Q}_r(z)}{\varphi }_{1+|(Du)_{z,r}|}(|Du-(Du)_{z,r}|)dz\\ {}{} & {} \le C(M,\theta _0)\, \frac{r^{n+2+2\alpha }}{R_0^{2\alpha }}\varepsilon _0. \end{aligned}$$

This means that V(Du) belongs to the parabolic Campanato space ${{\mathcal {L}}}^{2,\frac{2\alpha }{n+2}}(\mathcal {Q}_{R_1}(z_0),\mathbb {R}^{Nn})$ and by the usual embedding we have $\displaystyle {V(Du)\in C^{0,\frac{\alpha }{2},\alpha }(\mathcal {Q}_{R_1}(z_0),\mathbb {R}^{Nn})}$. $\square$

Remark 8.1

Note, as indicated in Sect. 1, the Hölder continuity of V(Du) implies the Hölder continuity of Du with a different exponent depending on ${\varphi }$.