The generalized porous medium equation on graphs: existence and uniqueness of solutions with $\ell ^1$ data

Abstract

We study solutions of the generalized porous medium equation on infinite graphs. For nonnegative or nonpositive integrable data, we prove the existence and uniqueness of mild solutions on any graph. For changing sign integrable data, we show existence and uniqueness under extra assumptions such as local finiteness or a uniform lower bound on the node measure.

Appendices

Appendix A: Auxiliary results

In this appendix we collect several results which are used in various parts of the paper. The first result concerns the relationship between the Dirichlet Laplacian and restrictions of the formal Laplacian. For related material, see [43, 44].

Lemma A.1

Let $F=(X,w,k,\mu )$ be a graph, let A be a subset of X such that $\overset{\bullet }{\partial }A\ne \emptyset$ and let $F_{\text {dir}} =(A, w_{|A\times A}, k_{\mathrm{dir}}, \mu _{|A})$ be the Dirichlet subgraph associated to A. Define

$$\begin{aligned} \Delta _{|A} :\mathrm{dom}\left( \Delta _{|A} \right) \subseteq C(X) \rightarrow C(A) \end{aligned}$$

with

$$\begin{aligned}&\mathrm{dom}\left( \Delta _{|A} \right) :=\left\{ u \in C(X) \mid u\equiv 0 \text{ on } X\setminus A, \, \sum _{y \in A} w(x,y)\left| u(y)\right| < \infty \quad \forall x \in A \right\} ,\\&\Delta _{|A}u(x):=\Delta u(x) \quad \text{ for } \text{ every } x \in A. \end{aligned}$$

Then, we have the following commutative diagrams

where $\varvec{{\mathfrak {i}}}$ and $\varvec{\pi }$ are the canonical embedding and the canonical projection, respectively, as defined in (2.3). In particular, we have $\Delta _{\mathrm{dir}}\equiv \Delta _{|A}\varvec{{\mathfrak {i}}}$, $\Delta _{\mathrm{dir}}\varvec{\pi } \equiv \Delta _{|A}$ and

$$\begin{aligned}&\Delta _{\mathrm{dir}}v(x) = \Delta \varvec{{\mathfrak {i}}}v(x) \qquad \forall v \in \mathrm{dom}(\Delta _{\mathrm{dir}})\subseteq C(A),\; \forall x \in A,\\&\Delta _{\mathrm{dir}}\varvec{\pi }u(x)= \Delta u(x) \qquad \forall u \in \mathrm{dom}\left( \Delta _{|A}\right) \subseteq C(X),\; \forall x \in A. \end{aligned}$$

If every node in $\overset{\bullet }{\partial }A$ is connected to a finite number of nodes in A, then

$$\begin{aligned} \mathrm{dom}\left( \Delta _{|A}\right) = \mathrm{dom}\left( \Delta \right) \cap \left\{ u \in C(X) \mid u \equiv 0 \text{ on } X\setminus A \right\} \end{aligned}$$

and $\Delta _{|A} u$ can be uniquely extended to X for every $u \in \mathrm{dom}\left( \Delta _{|A}\right)$ in such a way that

$$\begin{aligned} \Delta _{|A} u(x)=\Delta u(x) \quad \forall \, x \in X, \end{aligned}$$

that is, $\Delta _{|A}$ is the restriction of $\Delta$ to the set of functions which vanish on $X\setminus A$.

Proof

Clearly, $\Delta _{|A}$ is well-defined and

$$\begin{aligned} \mathrm{dom}\left( \Delta _{|A}\right) \supseteq \mathrm{dom}\left( \Delta \right) \cap \left\{ u \in C(X) \mid u \equiv 0 \text{ on } X\setminus A \right\} . \end{aligned}$$

If every node in $\overset{\bullet }{\partial }A$ is connected to a finite number of nodes in A, then for every $u \in \mathrm{dom}\left( \Delta _{|A}\right)$ and $x \in X\setminus A$

$$\begin{aligned} \sum _{y \in X}w(x,y)\left| u(y)\right| =\sum _{y \in \mathring{\partial }A}w(x,y)\left| u(y)\right| < \infty . \end{aligned}$$

Therefore,

$$\begin{aligned} \mathrm{dom}\left( \Delta _{|A}\right) \subseteq \mathrm{dom}\left( \Delta \right) \cap \left\{ u \in C(X) \mid u \equiv 0 \text{ on } X\setminus A \right\} \end{aligned}$$

so that the two domains are equal as claimed. Furthermore, for every $u \in \mathrm{dom}\left( \Delta _{|A}\right)$, we can uniquely extend $\Delta _{|A} u$ to $X\setminus A$ so as to satisfy $\Delta _{|A} u=\Delta u$ by defining

$$\begin{aligned} \Delta _{|A} u(x) = -\frac{1}{\mu (x)} \sum _{y \in \mathring{\partial }A}w(x,y)u(y) \quad \text{ for } x \in X\setminus A. \end{aligned}$$

Observe now that

$$\begin{aligned} \mathrm{dom}\left( \Delta _{|A} \varvec{{\mathfrak {i}}}\right) =\left\{ v \in C(A) \mid \varvec{{\mathfrak {i}}} v \in \mathrm{dom}\left( \Delta _{|A}\right) \right\} \subseteq C(A) \end{aligned}$$

and if $v \in C(A)$, then

$$\begin{aligned} \sum _{y \in X}w(x,y)\left| \varvec{{\mathfrak {i}}}v(y)\right| = \sum _{y \in A}w(x,y)\left| v(y)\right| \quad \text{ for } \text{ every } x \in A. \end{aligned}$$

Therefore, it is immediate to check that $\mathrm{dom}\left( \Delta _{\mathrm{dir}}\right) = \mathrm{dom}\left( \Delta _{|A} \varvec{{\mathfrak {i}}}\right)$.

Finally, if $v \in \mathrm{dom}\left( \Delta _{\mathrm{dir}}\right)$, then for every $x \in A$ we have

$$\begin{aligned} \Delta _{\mathrm{dir}}v(x)&= \frac{1}{\mu _{|A}(x)}\sum _{y \in A} w_{|A\times A}(x,y)\left( v(x) - v(y)\right) +\frac{\kappa _{\mathrm{dir}}(x)}{\mu _{|A}(x)} v(x)\\&= \frac{1}{\mu _{|A}(x)}\sum _{y \in A} w_{|A\times A} (x,y)\left( v(x) - v(y)\right) + \frac{\kappa _{|A}(x) +b_{\mathrm{dir}}(x)}{\mu _{|A}(x)} v(x)\\&= \frac{1}{\mu (x)}\sum _{y \in A} w(x,y)\left( v(x) - v(y)\right) + \frac{\sum _{y \in \overset{\bullet }{\partial } A}w(x,y)}{\mu (x)}v(x) +\frac{\kappa (x)}{\mu (x)} v(x)\\&= \frac{1}{\mu (x)}\sum _{y \in X} w(x,y) \left( \varvec{{\mathfrak {i}}} v(x) -\varvec{{\mathfrak {i}}}v(y)\right) +\frac{\kappa (x)}{\mu (x)} \varvec{{\mathfrak {i}}}v(x)\\&= \Delta \varvec{{\mathfrak {i}}}v(x). \end{aligned}$$

This concludes the proof of diagram $D_1$. The proof of diagram $D_2$ is basically the same following suitable modifications. $\square$

The next theorem is a comparison principle for a nonlinear operator. This result generalizes [12,  Theorem 2, Section 23.1] and [43,  Theorem 8 and Proposition 3.1], see also the proof of Theorem 1.3.1 in [72]. In particular, we relax the assumptions on the function u by letting it not attain a minimum or maximum on X if the graph G does not have any infinite paths. We recall that for us a path is a walk without any repeated nodes.

Theorem A.2

(Comparison principle) Let $G=\left( X, w, \kappa , \mu \right)$ be a connected graph. Let $\lambda >0$ and $v \in \mathrm{dom}\left( \Delta \right)$. Assuming that $\psi :{\mathbb {R}}\rightarrow {\mathbb {R}}$ is strictly monotone increasing and $\psi (0)\le 0$ we consider three cases:

(Case 1) There exists $x_0 \in X$ such that u attains a minimum at $x_0$, i.e.,

$$\begin{aligned} v(x_{0})=\inf _{x\in X} \{v(x)\} > -\infty . \end{aligned}$$

(Case 2) G does not contain any infinite path.

(Case 3) G has an infinite path and for every infinite path $\{x_{n}\}$ we have $\sum _{x_{n}} \mu (x_{n})=\infty$ and there exists $p>0$ such that $\sum _{x_{n}}|v(x_{n})|^p\mu (x_{n})<\infty$ .

In all the three cases, if $\left( \Psi + \lambda \Delta \right) v \ge 0$, then $v \ge 0$.

Assuming instead $\psi (0)\ge 0$ and substituting $v(x_0)=\sup _{x\in X} \{v(x)\} <\infty$ for $v(x_0)=\inf _{x\in X} \{v(x)\} > -\infty$ in Case 1, if $\left( \Psi + \lambda \Delta \right) v \le 0$, then $v \le 0$. Moreover, in any case, if $v(x)=0$ for some $x\in X$, then $v\equiv 0$.

Proof

Let $v \in \mathrm{dom}\left( \Delta \right)$ be such that $\left( \Psi + \lambda \Delta \right) v \ge 0$ for $\psi (0)\le 0$ strictly monotone increasing. If $v\ge 0$, then there is nothing to prove. Hence, we assume that there exists $x_{0}\in X$ such that $v(x_{0}) <0$. We will show that this leads to a contradiction in all three cases.

Since $\psi (0)\le 0$ and $\psi$ is strictly monotone increasing,

$$\begin{aligned} \psi (v(x_{0}))+ \lambda \frac{\kappa (x_{0})}{\mu (x_{0})}v(x_{0}) < 0. \end{aligned}$$

(A.1)

Furthermore, as $\left( \Psi + \lambda \Delta \right) v(x_0) \ge 0$,

$$\begin{aligned} 0\le \psi (v(x_{0}))+\frac{\lambda }{\mu (x_{0})} \sum _{y\in X}w(x_{0},y)\left( v(x_{0})-v(y)\right) +\lambda \frac{\kappa (x_{0})}{\mu (x_{0})}v(x_{0}). \end{aligned}$$

(A.2)

Combining the above inequalities (A.1) and (A.2), we get

$$\begin{aligned} 0<-\left[ \psi (v(x_{0})) +\lambda \frac{\kappa (x_{0})}{\mu (x_{0})} v(x_{0}) \right] \le \frac{\lambda }{\mu (x_{0})}\sum _{y\in X} w(x_{0},y)\left( v(x_{0})-v(y)\right) \end{aligned}$$

and because $w(\cdot ,\cdot )\ge 0$ and G is connected, there exists $y=x_{1}\sim x_{0}$ such that $v(x_{1})< v(x_{0})$. In particular, $v(x_1)<0$.

Hence, we see that every node where v is negative is connected to a node where v is strictly smaller. This is the basic observation that will be used in all three cases.

(Case 1) From the discussion above, it is clear that v cannot achieve a negative minimum.

(Case 2) Iterating the procedure above, we find a sequence of distinct nodes $\{x_{k}\}_{k=0}^n$ such that $x_{0}\sim x_{1}\sim \cdots \sim x_{n}$ and

$$\begin{aligned} v(x_{n})< v(x_{n-1})< \ldots< v(x_{0}) <0. \end{aligned}$$

Since G does not have any infinite path this sequence must end which leads to a contradiction.

(Case 3) In this case, we can obtain an infinite sequence $\{v(x_{n})\}_n$ such that $\{x_{n}\}_n$ is an infinite path and

$$\begin{aligned} \ldots< v(x_{n})< v(x_{n-1})< \ldots< v(x_{0}) <0. \end{aligned}$$

It follows that $|v(x_{n})|>|v(x_{0})|>0$, for every n, and therefore

$$\begin{aligned} \sum _{{n}}|v(x_{n})|^p\mu (x_{n})>|v(x_{0})|^p\sum _{n}\mu (x_{n})=\infty \end{aligned}$$

for every $p>0$ which gives a contradiction.

Hence, we have established that $v \ge 0$ in all three cases. Now, if there exists $x_0 \in X$ such that $v(x_0)=0$, then

$$\begin{aligned} 0\le \Psi v(x_{0}) + \lambda \Delta v(x_{0}) =-\frac{\lambda }{\mu (x_{0})}\sum _{y\in X}w(x_{0},y)v(y) \le 0 \end{aligned}$$

and thus $v(y)=0$ for all $y\sim x_0$. Using induction and the assumption that G is connected we get $v\equiv 0$.

The proof that $\left( \Psi + \lambda \Delta \right) v \le 0$ implies $v \le 0$ when $\psi (0)\ge 0$ is completely analogous. $\square$

Remark 7

The above proof also shows that if v satisfies $\left( \Psi +\lambda \Delta \right) v \ge 0$, on any connected graph, $\psi (0)\le 0$ and $\min _{x \in X} v(x)\le 0$, then $v\equiv 0$.

Remark 8

A closer look at the proof shows that the conclusion of the theorem also holds for the operator

$$\begin{aligned} \sigma \Psi +\lambda \Delta \end{aligned}$$

where $\sigma \in C(X)$ is positive.

Corollary A.3

With the hypotheses of Theorem A.2, let $\psi (0)= 0$ for $\psi :{\mathbb {R}}\rightarrow {\mathbb {R}}$ is strictly monotone increasing. Let $v_1, v_2$ be solutions of

$$\begin{aligned} \left( \Psi + \lambda \Delta \right) v_k = g_k, \qquad \lambda >0 \text{ and } g_k \in C(X) \text{ for } k=1,2. \end{aligned}$$

If $g_1\ge g_2$, then $v_1 \ge v_2$.

Proof

Notice that, since $\psi$ is strictly increasing and $\psi (0)=0$, there exists a positive function $\sigma \in C(X)$ such that

$$\begin{aligned} \psi (v_1(x))-\psi (v_2(x))=\sigma (x) \psi (v_1(x)-v_2(x)) \end{aligned}$$

for all $x \in X$. Indeed, we can define

$$\begin{aligned} \sigma (x)= {\left\{ \begin{array}{ll} 1&{}\text {if } v_1(x)=v_2(x)\\ \frac{\psi (v_1(x))-\psi (v_2(x))}{\psi (v_1(x)-v_2(x))} &{}\text {otherwise}. \end{array}\right. } \end{aligned}$$

It follows that $v_1-v_2$ satisfies

$$\begin{aligned} \sigma \Psi (v_1-v_2) + \lambda \Delta (v_1-v_2)= g_1-g_2 \ge 0 \,\,\text { on } X \end{aligned}$$

and the conclusion follows from Remark 8. $\square$

Remark 9

As in Remark 7, the proof shows that if $v_k$ satisfy $\left( \Psi + \lambda \Delta \right) v_k = g_k$, $g_1\ge g_2$ and $\min _{x \in X}\{v_1(x)-v_2(x)\}\le 0$, then $v_1 \equiv v_2$ and $g_1 \equiv g_2$ on X

Finally, in the following two lemmas we discuss how to exhaust the graph via finite subgraphs which are nested and such that each subgraph is connected to the next subgraph. We note that as we do not assume local finiteness, we have to take a little bit of care in how we choose the exhaustion. Although this should certainly be well-known, for the convenience of the reader we include a short proof.

Let d denote the combinatorial graph metric, that is, the least number of edges in a path connecting two nodes. Fix a node $x_1 \in X$ and let $S_r=S_r(x_1)$ denote the sphere of radius $r = 0, 1, 2, \ldots$ about $x_0$, that is,

$$\begin{aligned} S_r =\{ x \in X \mid d(x,x_0)=r \}. \end{aligned}$$

For $x \in S_r$, we call $y \in X$ a forward neighbor of x if $y \sim x$ and $y \in S_{r+1}$. We will denote the set of forward neighbors of x via $N_+(x)$, i.e.,

$$\begin{aligned} N_+(x) = \{ y \sim x \mid d(y,x_0) =d(x,x_0)+1 \}. \end{aligned}$$

Fig. 4

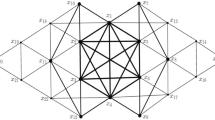
Exhaustion of a locally finite graph G by a chain of Dirichlet subgraphs $\{G_{\mathrm{dir},n}\}_n$. The figure is read from left to right, from top to bottom. The chain $\{G_{\mathrm{dir},n}\}_n$ is built starting from an inner node $x_0$ by applying the recursive procedure described in the proof of Lemma A.5. At each step $n=1,2,3,\ldots$, the interior nodes in $\mathring{X}_n$ are green while the inner boundary nodes in $\mathring{\partial }X_n$ are light green. The nodes belonging to the exterior boundary $\overset{\bullet }{\partial }X_n \subseteq X\setminus X_n$ are colored in light gray. We can visually see how every subgraph $G_{\mathrm{dir},n}$ is still “chained” to the supergraph G by the Dirichlet killing term $\kappa _{\mathrm{dir},n}$ which is depicted by red rings and red dashed lines. In particular, each $G_{\mathrm{dir},n}$ is a Dirichlet subgraph of $G_{\mathrm{dir},n+1}$

We now use the set of forward neighbors to inductively create our exhaustion sequence.

Lemma A.4

Let $G=(X,w,\kappa ,\mu )$ be a connected and infinite graph. Then there exists a sequence of connected and finite induced subgraphs $G_n=(X_n, w_n, \kappa _n, \mu _n)$ with $X_n\subset X_{n+1}$, $\bigcup _{n=1}^\infty X_n= X$ and

$$\begin{aligned} \{ x \in X_n \mid x\sim y \text{ for } \text{ some } y \in X_{n+1} \setminus X_n \}\ne \emptyset \end{aligned}$$

for all $n\in {\mathbb {N}}_0.$

Proof

We arrange the forward neighbors of each node in a sequence. Let $X_1 = \{x_0\}$. For $X_2$ choose the first forward neighbor of $x_0$ and add it to $X_0$, that is, $X_2=\{x_0, x_1 \}$ where $N_+(x_0)=\{x_1,x_2, \dots \}$. We note that $N_+(x_0) \ne \emptyset$ as the graph is infinite and connected.

Now, proceed inductively as follows: Given $X_n$ let $X_{n+1}$ consist of $X_n$ and, for every node x in $X_n$ we add to $X_n$ the first forward neighbor in $N_+(x)$ which is not included in $X_n$ to get $X_{n+1}$. Let $G_n$ denote the induced subgraph.

As we only add at most a single forward neighbor for each node at every step, it follows that each $X_n$ is finite with $|X_n| \le 2^{n}$. It is clear by construction that $G_n$ is connected. Furthermore, as the graph is infinite and connected, it follows that $\{ x \in X_n \mid x\sim y \text{ for } \text{ some } y \in X_{n+1}\setminus X_n \}\ne \emptyset$ for each $n \in {\mathbb {N}}$. Finally, to show that the union of the $X_n$ is the entire node set, let $x \in X$. Then, $x \in S_r$ for some r which means that there exists a sequence $\{y_k\}_{k=0}^r$ with $y_0=x_0$, $y_r=x$ and $y_k \in S_k$ such that $y_{k+1} \in N_{+}(y_k)$. As each node $y_k$ will then be included in some set of the exhaustion $X_n$, it follows that $x \in \bigcup _{n=1}^\infty X_n$. This completes the proof. $\square$

In the locally finite case, the above can be simplified by just using balls for our exhaustion sets. See Fig. 4 for a visual representation. In this case, it is also possible to exhaust in such a way that we have an inclusion between the interiors of the exhaustion sets.

Lemma A.5

Let $G=(X,w,\kappa ,\mu )$ be connected, infinite and locally finite. Then there exists a sequence of connected and finite induced subgraphs $G_n=(X_n, w_n, \kappa _n, \mu _n)$ with $\mathring{X}_n\subset \mathring{X}_{n+1}$, $X_n\subset X_{n+1}$, $\bigcup _{n=1}^\infty \mathring{X}_n= X$ and

$$\begin{aligned} \{ x \in X_n \mid x\sim y \text{ for } \text{ some } y \in X_{n+1}\setminus X_n \}\ne \emptyset \end{aligned}$$

for all $n\in {\mathbb {N}}$.

Proof

We modify the construction of the previous lemma: We take $X_1=\{x_0\}$ and, having constructed $X_n$, we add to it all forward neighbors of nodes in $X_n$ to get $X_{n+1}$. Thus, $X_{n+1}=B_n(x_0)=\{x \mid d(x,x_0)\le n\}.$ Since the graph is locally finite and connected it is clear that $\cup _n X_n=X$ and, since G is infinite, for every n at least one node in $X_n$ has a forward neighbor so that

$$\begin{aligned} \{ x \in X_n \mid x\sim y \text{ for } \text{ some } y \in X_{n+1} \setminus X_n \}\ne \emptyset . \end{aligned}$$

Finally, since a node $x_n$ in $X_n$ has no forward neighbors if and only if it belong to $\mathring{X}_n$ is follows that $\mathring{X}_n\subset \mathring{X}_{n+1}$. $\square$

Appendix B: Accretivity

In this appendix we prove that there exists a dense subset $\Omega$ of $\mathrm{dom}({\mathcal {L}})$ where ${\mathcal {L}}$ is accretive. This subset is of particular importance because every solution that is constructed while carrying out the proof of Theorem 1 belongs to $\Omega$.

From now on, if G is infinite, then we fix an exhaustion $\{X_n\}_{n=1}^\infty$ of X, i.e., a sequence of subsets $X_n$ of X such that $X_n \subseteq X_{n+1}$ and $X = \cup _{n=1}^\infty X_n$, where we additionally assume that each $X_n$ is finite. We denote by $\varvec{{\mathfrak {i}}}_{n,\infty }$ the canonical embedding and by $\varvec{\pi }_n$ the canonical projection for each $X_n$:

$$\begin{aligned}&\varvec{{\mathfrak {i}}}_{n,\infty } :C(X_n)\rightarrow C(X) \quad \varvec{{\mathfrak {i}}}_{n,\infty }u(x) :={\left\{ \begin{array}{ll} u(x) &{} \text{ if } x \in X_n,\\ 0 &{} \text{ if } x \in X\setminus X_n; \end{array}\right. }\\&\varvec{\pi }_n :C(X) \rightarrow C(X_n) \qquad \varvec{\pi }_nu(x) :=u(x) \text{ for } \text{ every } x \in X_n. \end{aligned}$$

We remark that, for the purpose of the results collected here, the exhaustion $\{X_n\}_{n=1}^\infty$ is not required to satisfy any additional properties other than that each $X_n$ is finite.

We recall that on a graph $G=(X,w,\kappa ,\mu )$ the operator ${\mathcal {L}} :\mathrm{dom}\left( {\mathcal {L}} \right) \subseteq \ell ^{1}\left( X,\mu \right) \rightarrow \ell ^{1}\left( X,\mu \right)$ is given by

$$\begin{aligned}&\mathrm{dom}\left( {\mathcal {L}} \right) :=\left\{ u \in \ell ^{1}\left( X,\mu \right) \mid \Phi u\in \mathrm{dom}\left( \Delta \right) , \Delta \Phi u \in \ell ^{1}\left( X,\mu \right) \right\} \\&{\mathcal {L}}u:=\Delta \Phi u. \end{aligned}$$

For a subset $\Omega \subseteq \mathrm{dom}\left( {\mathcal {L}} \right)$, we write ${\mathcal {L}}_{|\Omega }$ for the restriction of ${\mathcal {L}}$ to $\Omega$.

We first introduce a sequence of operators ${\mathcal {L}}_{n}$ whose purpose is to ‘nicely approximate’ the operator ${\mathcal {L}}$.

Definition B.1

(The operators ${\mathcal {L}}_n$) Let $G=(X,w,\kappa ,\mu )$ be a graph. We define

$$\begin{aligned} {\mathcal {L}}_{n}:\mathrm{dom}\left( {\mathcal {L}}_{n}\right) \subseteq \ell ^{1}\left( X,\mu \right) \rightarrow \ell ^{1}\left( X,\mu \right) \end{aligned}$$

by

$$\begin{aligned} \mathrm{dom}\left( {\mathcal {L}}_{n}\right) :=C_c(X), \quad {\mathcal {L}}_{n}u:=\varvec{{\mathfrak {i}}}_{n,\infty } \Delta _{\mathrm{dir},n}\Phi \varvec{\pi }_{n} u \end{aligned}$$

where $\Delta _{\mathrm{dir},n}$ is the graph Laplacian associated to the Dirichlet subgraph $G_{\mathrm{dir},n} \subseteq G$ on the node set $X_n$.

We are going to prove that ${\mathcal {L}}_{n}$ is accretive for every n. This result will be a consequence of the next proposition for finite graphs.

Proposition B.2

Let $G=(X,w,\kappa ,\mu )$ be a finite graph. Then,

$$\begin{aligned} \sum _{\begin{array}{c} x\in X:\\ u(x)\ne v(x) \end{array}} \left( \Delta \Phi u(x)-\Delta \Phi v(x)\right) \mathrm{sgn}(u(x)-v(x))\mu (x) \ge 0 \quad \forall \; u, v \in C(X). \end{aligned}$$

Proof

Define $h:=\Phi u-\Phi v \in C(X)$. Since $\phi$ is strictly monotone increasing and $\phi (0)=0$

$$\begin{aligned} \mathrm{sgn}( u(x)- v(x))= \mathrm{sgn} (\phi ( u(x))-\phi ( v(x)))=\mathrm{sgn}(h(x)) \end{aligned}$$

(B.1)

and, therefore,

$$\begin{aligned} (\phi (u(x))-\phi (v(x))) \mathrm{sgn}(u(x)-v(x)) =h(x) \mathrm{sgn}(h(x))= \left| h(x) \right| \ge 0 \quad \forall \, x \in X. \end{aligned}$$

(B.2)

By the linearity of $\Delta$ and (B.1) we get

$$\begin{aligned} \sum _{\begin{array}{c} x\in X:\\ u(x)\ne v(x) \end{array}} \left( \Delta \Phi u(x)-\Delta \Phi v(x)\right) \mathrm{sgn}(u(x)-v(x))\mu (x)=\sum _{x\in X} \Delta h(x)\mathrm{sgn}(h(x))\mu (x). \end{aligned}$$

Since G is finite, from the Green’s identity, see [37, 44], we get

$$\begin{aligned} \sum _{x\in X} \Delta h(x)\mathrm{sgn}(h(x))\mu (x)&= \frac{1}{2}\sum _{x,y \in X} w(x,y)\left( \mathrm{sgn}(h(x)) -\mathrm{sgn}(h(y)) \right) \left( h(x) - h(y)\right) \\&\quad + \sum _{x\in X} \kappa (x) h(x) \mathrm{sgn}(h(x)). \end{aligned}$$

Combining the above identity with (B.2), we obtain

$$\begin{aligned} \sum _{x\in X} \Delta h(x)\mathrm{sgn}(h(x))\mu (x)\ge \frac{1}{2} \sum _{x,y \in X} w(x,y)\left( \mathrm{sgn}(h(x)) -\mathrm{sgn}(h(y)) \right) \left( h(x) - h(y)\right) . \end{aligned}$$

Setting, for ease of notation,

$$\begin{aligned} \Gamma (x,y):=w(x,y)\left( \mathrm{sgn}(h(x)) -\mathrm{sgn}(h(y))\right) \left( h(x) - h(y)\right) \end{aligned}$$

we have:

• (i) If $\mathrm{sgn}(h(x))=0$, then $\Gamma (x,y)=w(x,y)|h(y)|\ge 0$;

• (ii) If $\mathrm{sgn}(h(y))=0$, then $\Gamma (x,y)=w(x,y)|h(x)|\ge 0$;

• (iii) If $\mathrm{sgn}(h(x))=\mathrm{sgn}(h(y))$, then $\Gamma (x,y)=0$;

• (iv) If $\mathrm{sgn}(h(y))=-\mathrm{sgn}(h(x))$, then $\Gamma (x,y)= 2w(x,y)\left( |h(x)| + |h(y)|\right) \ge 0$.

We obtain $\Gamma (x,y)\ge 0$ for every $x,y \in X$ and the required conclusion follows. $\square$

We next show that ${\mathcal {L}}$ is accretive on finite graphs.

Corollary B.3

Let $G=(X,w,\kappa ,\mu )$ be a finite graph. Then, ${\mathcal {L}}$ is accretive.

Proof

By condition (ii) in Definition 2.4, an operator ${\mathcal {L}}$ is accretive if $\langle {\mathcal {L}} u -{\mathcal {L}} v, u - v \rangle _+ \ge 0$ for every $u,v \in \mathrm{dom}\left( {\mathcal {L}}\right)$. From (2.5) in Remark 3, in the case of the $\ell ^1$-norm we have

$$\begin{aligned} \langle z, k \rangle _+&=\Vert k\Vert _1\left( \sum \limits _{\begin{array}{c} x\in X:\\ k(x)= 0 \end{array}}|z(x)|\mu (x) + \sum \limits _{\begin{array}{c} x\in X:\\ k(x)\ne 0 \end{array}} z(x)\mathrm{sgn}(k(x))\mu (x) \right) \\&\ge \Vert k\Vert _1\sum \limits _{\begin{array}{c} x\in X:\\ k(x)\ne 0 \end{array}} z(x) \mathrm{sgn}(k(x))\mu (x) \quad \forall \, z,k \in \ell ^1(X,\mu ). \end{aligned}$$

Therefore, to prove that ${\mathcal {L}}$ is accretive on $\ell ^1(X,\mu )$, it is sufficient to prove that

$$\begin{aligned} \sum _{\begin{array}{c} x\in X:\\ u(x)\ne v(x) \end{array}} \left( {\mathcal {L}} u(x)- {\mathcal {L}} v(x)\right) \mathrm{sgn}(u(x)-v(x))\mu (x) \ge 0 \quad \forall \; u, v \in \mathrm{dom}({\mathcal {L}}), \end{aligned}$$

(B.3)

that is,

$$\begin{aligned} \sum _{\begin{array}{c} x\in X:\\ u(x)\ne v(x) \end{array}} \left( \Delta \Phi u(x)-\Delta \Phi v(x)\right) \mathrm{sgn}(u(x)-v(x))\mu (x) \ge 0 \quad \forall \; u, v \in C(X). \end{aligned}$$

Since G is finite, we conclude the proof by Proposition B.2. $\square$

We next establish that the operators ${\mathcal {L}}_{n}$ are accretive.

Corollary B.4

Let $G=(X,w,\kappa ,\mu )$ be a graph. Then, ${\mathcal {L}}_{n}$ is accretive for every n.

Proof

By (B.3) in Corollary B.3, it suffices to show that

$$\begin{aligned} \sum _{\begin{array}{c} x\in X:\\ u(x)\ne v(x) \end{array}} \left( {\mathcal {L}}_{n}u(x)-{\mathcal {L}}_{n}v(x)\right) \mathrm{sgn}(u(x)-v(x)) \mu (x) \ge 0 \quad \forall \; u, v \in \mathrm{dom}({\mathcal {L}}_{n}), \end{aligned}$$

that is,

$$\begin{aligned}&\sum _{\begin{array}{c} x\in X:\\ u(x)\ne v(x) \end{array}} \left( \varvec{{\mathfrak {i}}}_{n,\infty } \Delta _{\mathrm{dir},n}\Phi \varvec{\pi }_{n} u(x) -\varvec{{\mathfrak {i}}}_{n,\infty } \Delta _{\mathrm{dir},n}\Phi \varvec{\pi }_{n} v(x)\right) \mathrm{sgn}(u(x)-v(x))\mu (x) \ge 0 \quad \forall \; u, v \in C_c(X). \end{aligned}$$

Let us observe that the left-hand side of the above is equal to

$$\begin{aligned} \sum _{\begin{array}{c} x\in X_n:\\ \varvec{\pi }_{n}u(x) \ne \varvec{\pi }_{n}v(x) \end{array}} \left( \Delta _{\mathrm{dir},n}\Phi \varvec{\pi }_{n} u(x)-\Delta _{\mathrm{dir},n}\Phi \varvec{\pi }_{n} v(x)\right) \mathrm{sgn}(\varvec{\pi }_{n}u(x) -\varvec{\pi }_{n}v(x))\mu (x). \end{aligned}$$

Since $\varvec{\pi }_{n} u, \varvec{\pi }_{n} v \in C(X_n)$ and $\Delta _{\mathrm{dir},n}$ is the graph Laplacian associated to the finite graph $G_{\mathrm{dir},n}$ with node set $X_n$, by Proposition B.2 we conclude that ${\mathcal {L}}_{n}$ is accretive. $\square$

The sequence of operators ${\mathcal {L}}_{n}$ defines a subset $\Omega$ of $\mathrm{dom}({\mathcal {L}})$. As we will see below, $\Omega$ is dense in $\mathrm{dom}({\mathcal {L}})$ and ${\mathcal {L}}$ restricted to $\Omega$ is accretive. Let us introduce the following notation for the support of a function: Given $u \in C(X)$ we let

$$\begin{aligned} \mathrm{supp}~u :=\{x\in X \mid u(x)\ne 0\}. \end{aligned}$$

We start by defining the subset of the domain of interest.

Definition B.5

(The set $\Omega$) Let $G=(X,w,\kappa ,\mu )$ be a graph. We define $\Omega \subseteq \mathrm{dom}({\mathcal {L}})$ by letting

$$\begin{aligned} \Omega :=\mathrm{dom}({\mathcal {L}}) = C(X) \end{aligned}$$

if G is finite and

$$\begin{aligned} \Omega :=\{u \in \mathrm{dom}({\mathcal {L}}) \mid \exists \, \{u_n\}_n \text{ s.t. } \mathrm{supp}~u_n \subseteq X_n,\; \lim _{n\rightarrow \infty }\Vert u_n -u \Vert =0,\; \lim _{n\rightarrow \infty }\Vert {\mathcal {L}}_{n}u_n -{\mathcal {L}}u \Vert =0 \} \end{aligned}$$

if G is infinite.

While the definition of $\Omega$ depends on the choice of the exhaustion, this set always contains all finitely supported functions as will be shown in Lemma B.7. In order to establish this, we first prove that the finitely supported functions are contained in the domain of ${\mathcal {L}}$.

Lemma B.6

Let $G=(X,w,\kappa ,\mu )$ be a graph. Then, $C_c(X) \subseteq \mathrm{dom}({\mathcal {L}})$.

Proof

Let $u \in C_c(X)$. Then, $u(x) = \sum _{j=1}^n \alpha _j \delta _{x_j}(x)$ where $\alpha _j \in {\mathbb {R}}$ and

$$\begin{aligned} \delta _{x_j}(x)={\left\{ \begin{array}{ll} 1 &{} \text{ if } x=x_j,\\ 0 &{}\text{ otherwise }. \end{array}\right. } \end{aligned}$$

Therefore, by linearity, $\Delta (C_c(X))\subseteq \ell ^1(X,\mu )$ if and only if $\Delta \delta _{z} \in \ell ^1(X,\mu )$ for every $z\in X$. Fix $z \in X$ and observe that

$$\begin{aligned} \sum _{x\in X}|\Delta \delta _{z}(x)|\mu (x)&\le \sum _{x\in X}\mathrm{Deg}(x)\delta _{z}(x)\mu (x) +\sum _{x\in X}\sum _{y\in X}w(x,y)|\delta _{z}(y)|\\&= \mathrm{Deg}(z)\mu (z) + \sum _{x\in X}w(x,z) < \infty \end{aligned}$$

so that $\Delta (C_c(X)) \subseteq \ell ^1(X,\mu )$. Since $\Phi u \in C_c(X)$ for every $u \in C_c(X)$, it follows that $\Phi u\in \mathrm{dom}(\Delta )$ and $\Delta \Phi u \in \ell ^1(X,\mu )$, that is, $u \in \mathrm{dom}({\mathcal {L}}$). $\square$

We now show that the set $\Omega$ contains the finitely supported functions.

Lemma B.7

Let $G=(X,w,\kappa ,\mu )$ be a graph. Then, $C_c(X) \subseteq \Omega$. In particular,

$$\begin{aligned} \overline{\Omega }=\overline{\mathrm{dom}({\mathcal {L}})}=\ell ^1(X,\mu ). \end{aligned}$$

Proof

Let us fix $u \in C_c(X)$. From Lemma B.6, we know that $u\in \mathrm{dom}({\mathcal {L}})$. Define

$$\begin{aligned} u_n(x):=\varvec{{\mathfrak {i}}}_{n,\infty } \varvec{\pi }_n u(x)= {\left\{ \begin{array}{ll} u(x) &{} \text{ if } x \in X_n,\\ 0 &{}\text{ otherwise }. \end{array}\right. } \end{aligned}$$

Clearly, $\mathrm{supp}~u_n \subseteq X_n$ and $\lim _{n\rightarrow \infty }\Vert u_n -u \Vert =0$. Since, $u\in C_c(X)$, there exists an $N>0$ such that $u(x)=0$ for every $x\in X\setminus X_N$. In particular, $\Phi u_n(x)=0$ for every $x\in X\setminus X_n$, $n\ge N$ and $\Phi u_n=\Phi u$ for every $n\ge N$.

By Lemma A.1, we have $\Phi u_n \in \mathrm{dom}(\Delta _{|X_n})$ for every $n\ge N$ and then

$$\begin{aligned} \Delta _{\mathrm{dir},n}\varvec{\pi }_n \Phi u_n (x) = \Delta \Phi u_n (x) = \Delta \Phi u (x) \quad \forall \; x\in X_n,\; n\ge N, \end{aligned}$$

that is,

$$\begin{aligned} \Delta _{\mathrm{dir},n}\varvec{\pi }_n \Phi u_n = \varvec{\pi }_n \Delta \Phi u \quad \forall \; n\ge N. \end{aligned}$$

Therefore, using the trivial fact that $\Phi \varvec{\pi }_n=\varvec{\pi }_n\Phi$,

$$\begin{aligned} {\mathcal {L}}_{n}u_n = \varvec{{\mathfrak {i}}}_{n,\infty } \Delta _{\mathrm{dir},n}\Phi \varvec{\pi }_n u_n =\varvec{{\mathfrak {i}}}_{n,\infty } \Delta _{\mathrm{dir},n}\varvec{\pi }_n \Phi u_n =\varvec{{\mathfrak {i}}}_{n,\infty } \varvec{\pi }_n\Delta \Phi u =\varvec{{\mathfrak {i}}}_{n,\infty } \varvec{\pi }_n{\mathcal {L}} u, \quad \forall \; n\ge N \end{aligned}$$

and, since ${\mathcal {L}}u \in \ell ^1(X,\mu )$, it follows that $\lim _{n\rightarrow \infty }\Vert {\mathcal {L}}_{n}u_n - {\mathcal {L}} u\Vert =0$ by dominated convergence. $\square$

To conclude this appendix, we prove that ${\mathcal {L}}_{|\Omega }$ is accretive.

Lemma B.8

Let $G=(X,w,\kappa ,\mu )$ be a graph. Then, ${\mathcal {L}}_{|\Omega }$ is accretive.

Proof

If G is finite, then $\Omega = \mathrm{dom}({\mathcal {L}})$ and ${\mathcal {L}}$ is accretive by Corollary B.3. If G is infinite, let $u,v \in \Omega$. Then, by the definition of $\Omega$, there exists $\{u_n\}_n, \{v_n\}_n$ such that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert u_n-u\Vert =\lim _{n\rightarrow \infty }\Vert v_n-v\Vert =0, \qquad \lim _{n\rightarrow \infty }\Vert {\mathcal {L}}_{n}u_n-{\mathcal {L}}u\Vert =\lim _{n\rightarrow \infty }\Vert {\mathcal {L}}_{n}v_n-{\mathcal {L}}v\Vert =0. \end{aligned}$$

By the accretivity of ${\mathcal {L}}_{n}$ established in Corollary B.4 above, it follows readily that

$$\begin{aligned}&\left\| (u - v) + \lambda \left( {\mathcal {L}}u -{\mathcal {L}}v\right) \right\| = \lim _{n\rightarrow \infty } \left\| (u_n - v_n) + \lambda \left( {\mathcal {L}}_{n}u_n - {\mathcal {L}}_{n}v_n\right) \right\| \\&\quad \ge \lim _{n\rightarrow \infty }\Vert u_n - v_n\Vert = \Vert u - v\Vert . \end{aligned}$$

This completes the proof. $\square$

Remark 10

One might be tempted to identify $\Omega$ with

$$\begin{aligned}&\Omega '=\{u\in \mathrm{dom}({\mathcal {L}})\mid \exists \, \{u_n\}_n \text{ s.t. } u_n\in C_c(X),\\&\quad \lim _{n\rightarrow \infty }\Vert u_n -u \Vert =0,\; \lim _{n\rightarrow \infty }\Vert {\mathcal {L}}_{\mathrm{min}} u_n -{\mathcal {L}}u \Vert =0 \} \end{aligned}$$

where ${\mathcal {L}}_{\mathrm{min}}$ is the minimal operator, that is, ${\mathcal {L}}_{\mathrm{min}}:={\mathcal {L}}_{|C_c(X)}$. It is possible to show that ${\mathcal {L}}$ is accretive on $\Omega '$ but unfortunately $\Omega$ is not equal to $\Omega '$. In particular, the solutions that are constructed in the proof of Theorem 1 may not belong to $\Omega '$. The main problem is that

$$\begin{aligned} | ({\text {id}} + \lambda \mathcal {L}_{{\text {min}}})u_n(x) - g(x)|={\left\{ \begin{array}{ll} 0 &{}\text{ if } x\in X_n,\\ \sum _{{y\in X_n}}w(x,y)u_n(y) + g(x) &{}\text{ if } x \in X\setminus X_n \end{array}\right. } \end{aligned}$$

with

$$\begin{aligned} | ({\text {id}} + \lambda \mathcal {L}_{{\text {min}}})u_n(x) - g(x)|={\left\{ \begin{array}{ll} 0 &{}\text{ if } x\in X_n,\\ \left| \lambda \sum _{{y\in X_n}}w(x,y)u_n(y) + g(x)\right| &{}\text{ if } x \in X\setminus X_n \end{array}\right. } \end{aligned}$$

and then $\Vert (\mathrm{id} + \lambda {\mathcal {L}}_{\mathrm{min}})u_n - g\Vert$ does not necessarily tend to 0. As a consequence, we cannot infer that $\lim _{n\rightarrow \infty }\Vert {\mathcal {L}}_{\mathrm{min}} u_n -{\mathcal {L}}u \Vert =0$.