Riesz transforms of a general Ornstein–Uhlenbeck semigroup

Abstract

We consider Riesz transforms of any order associated to an Ornstein–Uhlenbeck operator with covariance given by a real, symmetric and positive definite matrix, and with drift given by a real matrix whose eigenvalues have negative real parts. In this general Gaussian context, we prove that a Riesz transform is of weak type (1, 1) with respect to the invariant measure if and only if its order is at most 2.

1 Introduction

In this paper we are concerned with Riesz transforms of any order in a general Gaussian setting, in $\mathbb{R}^n$ with $n\ge 1$. An Ornstein-Uhlenbeck semigroup is determined by two $n\times n$ real matrices Q and B such that

• (h1) Q is symmetric and positive definite;

• (h2) all the eigenvalues of B have negative real parts.

Here Q and B indicate the covariance and the drift, respectively. We also introduce a family of covariance matrices

$$\begin{aligned} Q_t=\int _0^t e^{sB}\,Q\,e^{sB^*}\,ds, \qquad { t\in (0,+\infty ]}. \end{aligned}$$

(1.1)

Observe that these $Q_t$, including $Q_\infty$, are well defined, symmetric and positive definite. Then we define a family of normalized Gaussian measures in $\mathbb{R}^n$,

$$\begin{aligned} d\gamma _t (x)= (2\pi )^{-\frac{n}{2}}\, (\text {det} \, Q_t)^{-\frac{1}{2} }\, e^{-\frac{1}{2} \langle Q_t^{-1}x,x\rangle } \,dx \,,\qquad { t\in (0,+\infty ]}. \end{aligned}$$

On the space of bounded continuous functions in $\mathbb{R}^n$, the Ornstein–Uhlenbeck semigroup is explicitly given by Kolmogorov’s formula [8, 19]

$$\begin{aligned} {\mathscr {H}}_t f(x)= \int f(e^{tB}x-y)\,d\gamma _t (y)\,, \; \qquad x\in \mathbb{R}^n, \; \quad t>0, \end{aligned}$$

and generated by the Ornstein–Uhlenbeck operator, defined below. Notice that $d\gamma _\infty$ is the unique invariant probability measure with respect to the semigroup $\left( {\mathscr {H}}_t \right) _{t> 0}$; its density is proportional to $e^{-R(x)}$, where R(x) denotes the quadratic form

$$\begin{aligned} R(x) ={\frac{1}{2} \left\langle Q_\infty ^{-1}x ,x \right\rangle }, \qquad {x\in \mathbb{R}^n}. \end{aligned}$$

In this general Gaussian framework, the Ornstein–Uhlenbeck operator ${\mathscr {L}}$ is given for functions $f\in {\mathscr {S}} (\mathbb{R}^n)$ by

$$\begin{aligned} {\mathscr {L}} f(x)= \frac{1}{2}\, {{\,\mathrm{tr}\,}}\big ( Q\nabla ^2 f\big )(x)+ \langle Bx, \nabla f(x) \rangle \,,\qquad x\in \mathbb{R}^n, \end{aligned}$$

where $\nabla$ is the gradient and $\nabla ^2$ the Hessian. Notice that $-{\mathscr {L}}$ is elliptic. We write $D=(\partial _{x_1}, \ldots , \partial _{x_n})$ in $\mathbb{R}^n$ and let $\alpha =(\alpha _1,\ldots , \alpha _n) \in \mathbb{N}^n\setminus \{(0,\dots ,0) \}$ denote a multiindex, of length $|\alpha | = \sum _1^n \alpha _i$. Then we can define the Gaussian Riesz transforms as

$$\begin{aligned} R^{(\alpha )} = D^\alpha (-{\mathscr {L}})^{-|\alpha |/2} \ P_0^{\perp }, \end{aligned}$$

where $P_0^{\perp }$ is the orthogonal projection onto the orthogonal complement in $L^2(\gamma _\infty )$ of the eigenspace corresponding to the eigenvalue 0. Here the derivatives are taken in the sense of distributions. We will justify the introduction of negative powers of $-{\mathscr {L}}$ in Sect. 3.

When the order $|\alpha |$ of $R^{(\alpha )}$ equals 1 or 2, we shall denote by $R_j$ and $R_{ij}$ the corresponding Riesz transforms, that is, for $i,j\in \{1,\ldots , n\}$

$$\begin{aligned} R_j= {\partial _{ x_j}} (-{\mathscr {L}})^{-1/2} \ P_0^{\perp } \end{aligned}$$

and

$$\begin{aligned} R_{ij}= {\partial^2 _{ x_i x_j}} (-{\mathscr {L}})^{-1} \ P_0^{\perp } . \end{aligned}$$

There exists a vast literature concerning the $L^p$ boundedness of Riesz transforms in the Gaussian setting, in both the strong and the weak sense. We will only mention the results that are most significant for this work; here $1<p<\infty$.

In the standard case, when Q and $-B$ are the identity matrix, the strong type (p, p) of $R^{(\alpha )}$ has been proved with different techniques in [10, 13, 16, 22, 24, 29, 31]; for a recent account of this case we refer to [32, Chapter 9]. Other proofs, holding in the more general case $Q=I$ and B symmetric, may be found in [17, 18]. G. Mauceri and L. Noselli have shown more recently that the Riesz transforms of any order are bounded on $L^p(\gamma _\infty )$ in the general case (see [21, Proposition 2.3]). For some results in an infinite-dimensional framework, we refer to [7].

The problem of the weak type (1, 1) of $R^{(\alpha )}$ is more involved than in the Euclidean context, where it is well known that a Riesz transform of any order associated to the Laplacian is of weak type (1, 1). Indeed, in the standard Gaussian framework $Q=-B=I$, it is known that $R^{(\alpha )}$ is of weak type (1, 1) if and only if $|\alpha |\le 2$ (see [1, 2, 9, 11, 12, 14, 25,26,27,28, 30] for different proofs). In their paper [21], Mauceri and Noselli proved the weak type (1, 1) of the first-order Riesz transforms associated to an Ornstein–Uhlenbeck semigroup with covariance $Q=I$ and drift B satisfying a certain technical condition. To the best of our knowledge, no result beyond this is known about the weak type (1,1), neither for first-order Riesz transforms associated to more general semigroups nor for higher-order Riesz operators.

In this paper we continue the analysis started in [4] and [5] of a general Ornstein–Uhlenbeck semigroup, with real matrices Q and B satisfying only (h1) and (h2). Our main result will be the following extension of the result in the standard case.

Theorem 1.1

The Riesz transform $R^{(\alpha )}$ associated to the Ornstein–Uhlenbeck operator ${\mathscr {L}}$ is of weak type (1, 1) with respect to the invariant measure $d\gamma _\infty$ if and only if $|\alpha |\le 2$.

In particular, we shall prove the inequalities

$$\begin{aligned} \gamma _\infty \{x\in \mathbb{R}^n : R_j\, f(x)> C\lambda \} \le \frac{C}{\lambda }\,\Vert f\Vert _{L^1( \gamma _\infty )},\qquad { \lambda >0,} \end{aligned}$$

(1.2)

and

$$\begin{aligned} \gamma _\infty \{x\in \mathbb{R}^n : R_{ij}\,f(x)> C\lambda \} \le \frac{C}{\lambda }\,\Vert f\Vert _{L^1( \gamma _\infty )},\qquad { \lambda >0,} \end{aligned}$$

(1.3)

for all $i,\,j=1,\ldots ,n$ and all functions $f\in L^1 (\gamma _\infty )$, with $C=C(n,Q,B)>0$.

The plan of the paper is as follows. In Sect. 2, we introduce the Mehler kernel $K_t(x,u)$, which is the integral kernel of ${\mathscr {H}}_t$. Some estimates of this kernel are also given. As in [5], we introduce a system of polar coordinates which is essential in our approach, and we define suitable global and local regions. Section 3 deals with the definition of the negative powers of $-{\mathscr {L}}$.

Then in Sect. 4 we explicitly write the kernels of $R_{j}$ and $R_{ij}$ as integrals with respect to the parameter t, taken over $0<t<+\infty$. Section 5 contains bounds for those parts of these kernels which are given by integrals only over $t>1$. In Sect. 6, several technical simplifications reducing the complexity of the proof of Theorem 1.1 are discussed. After this preparatory work, the proof of the theorem, which is quite involved and requires several steps, begins. In Sect. 7, we consider those parts corresponding to $t>1$ of the kernels of $R_{j}$ and $R_{ij}$, and prove a weak type estimate. Section 8 is devoted to the proof of the weak bounds for the local parts of the operators. Finally, in Sect. 9 we conclude the proof of the sufficiency part of Theorem 1.1, by proving the weak type estimates for the global parts, with the integrals restricted to $0<t<1$. In Sect. 10, we establish the necessity statement in Theorem 1.1 by means of a counterexample.

In the following, the symbols $c>0$ and $C<\infty$ will denote various constants, not necessarily the same at different occurrences. All of them depend only on the dimension n and on Q and B. With $a, \,b > 0$ we write $a\lesssim b$ instead of $a \le C b$ and $a \gtrsim b$ instead of $a \ge c b$. The relation $a\simeq b$ means that both $a\lesssim b$ and $a \gtrsim b$ hold.

By $\mathbb{N}$ we denote the set of all nonnegative integers. If A is an $n\times n$ matrix, we write $\Vert A\Vert$ for its operator norm on $\mathbb{R}^n$ with the Euclidean norm $|\cdot |$. We let

$$\begin{aligned} |x|_Q = | Q_\infty ^{-1/2}x|, \end{aligned}$$

so that $R(x) = |x|_Q^2/2$. Observe that $|x|_Q$ is a norm on $\mathbb{R}^n$ and that $|x|_Q \simeq |x|$.

Integral kernels of operators are always meant in the sense of integration with respect to the measure $d\gamma _\infty$.

2 Notation and preliminaries

It follows from (1.1) that for $0<t<\infty$

$$\begin{aligned} Q_\infty -Q_t =\int _t^{\infty }e^{sB}Qe^{sB^*}ds. \end{aligned}$$

This difference and also

$$\begin{aligned} Q_t ^{-1} - Q_\infty ^{-1} = Q_t^{-1}( Q_\infty -Q_t )Q_\infty ^{-1} \end{aligned}$$

are symmetric and strictly positive-definite matrices.

It is shown in [5, formula (2.6)] that for bounded and continuous functions f

$$\begin{aligned} {\mathscr {H}}_t f(x)&= \int K_t (x,u)\, f(u)\, d\gamma _\infty (u), \qquad t>0, \end{aligned}$$

where the Mehler kernel $K_t$ is given by

$$\begin{aligned} K_t (x,u) = \Big ( \frac{\text {det} \, Q_\infty }{\text {det} \, Q_t} \Big )^{{1}/{2} } e^{ R(x)}\, \exp \left[ {-\frac{1}{2} \left\langle ( Q_t^{-1}-Q_\infty ^{-1})\, (u-D_t x) \,,\, u-D_t x\right\rangle }\right] \qquad ~ \end{aligned}$$

(2.1)

for $x,u\in \mathbb{R}^n$ and $t>0$. Here we use a one-parameter group of matrices

$$\begin{aligned} D_t = Q_\infty \, e^{-tB^*}\, Q_\infty ^{-1} , \qquad {t\in \mathbb{R}. } \end{aligned}$$

We recall from [5, Lemma 2.1] that $D_t$ may be expressed in various ways. Indeed, for $t>0$ one has

$$\begin{aligned} D_t&= (Q_t^{-1}-Q_\infty ^{-1} )^{-1}\, Q_t^{-1}\, e^{tB} \end{aligned}$$

(2.2)

and

$$\begin{aligned} D_t&= e^{tB} + Q_t\, e^{-tB^*}\,Q_\infty ^{-1}. \end{aligned}$$

(2.3)

We restate Lemma 3.1 in [5].

Lemma 2.1

For $s>0$ and for all $x\in \mathbb{R}^n$ the matrices $D_{s }$ and $D_{-s }= D_{s }^{-1}$ satisfy

$$\begin{aligned} e^{cs}|x| \lesssim |D_s\, x| \lesssim e^{Cs} |x|, \end{aligned}$$

and

$$\begin{aligned} e^{-Cs}|x| \lesssim |D_{-s}\, x| \lesssim e^{-cs} |x|. \end{aligned}$$

This also holds with $D_{s }$ replaced by $e^{-sB}$ or by $e^{-sB^*}$.

The following is part of [5, Lemma 3.2].

Lemma 2.2

For all $t>0$ one has

• (i) $\det { \, Q_t} \simeq (\min (1,t))^{n}$;

• (ii) $\Vert Q_t^{-1}\Vert \simeq (\min (1,t))^{-1}$;

• (iii) $\Vert Q_t^{-1}-Q_\infty ^{-1} \Vert \lesssim {t}^{-1}\,{e^{-ct}}$;

• (iv) $\Vert \left( Q_t^{-1}-Q_\infty ^{-1} \right) ^{-1/2}\Vert \lesssim {t^{1/2}}\, e^{Ct}$.

Lemma 4.1 in [5] says that for all $x \in \mathbb{R}^n$ and $s\in \mathbb{R}$ one has

$$\begin{aligned}&\frac{\partial }{\partial s}\, D_s\,x = -Q_\infty \, e^{-sB^*}B^*\,Q_\infty ^{-1} x; \end{aligned}$$

(2.4)

$$\begin{aligned}&\frac{\partial }{\partial s}\, R\big ( D_s\,x \big ) \simeq \big | D_s\, x\big |^2 . \end{aligned}$$

(2.5)

In (2.4) we can estimate $e^{-sB^*}$ by means of Lemma 2.1, to get

$$\begin{aligned} \left| \frac{\partial }{\partial s}\, D_s\,x \right| \simeq |x|, \qquad |s|\le 1. \end{aligned}$$

(2.6)

Integration of (2.5) leads to

$$\begin{aligned} |R(D_t \,x)-R(x)| \simeq |t|\, |x|^2, \qquad |t|\le 1, \end{aligned}$$

(2.7)

again because of Lemma 2.1.

Lemma 2.3

Let $0 \ne x \in \mathbb{R}^n$ and $|t| \le 1$. Then

$$\begin{aligned} |x- D_t \,x| \simeq |t|\, |x|. \end{aligned}$$

Proof

The upper estimate is an immediate consequence of (2.6). For the lower estimate, we write

$$\begin{aligned} |x- D_t\, x|&\simeq |x- D_t \,x|_Q \ge \big | |x|_Q -|D_t\, x|_Q \big | \nonumber \\&= \frac{\left| |x|_Q^2 -|D_t\, x|_Q^2 \right| }{ |x|_Q +|D_t \,x|_Q} \simeq \frac{|t|\, |x|^2}{|x|_Q} \simeq |t|\, |x|, \end{aligned}$$

(2.8)

where we used (2.7) to estimate the numerator and Lemma 2.1 for the denominator. $\square$

The following implication will be useful as well. Since $R(x) = |x|_Q^2/2$ and $|.|_Q$ is a norm,

$$\begin{aligned} R(x)>2R(y) \qquad \Rightarrow \qquad R(x-y)\simeq R(x). \end{aligned}$$

(2.9)

We finally give estimates of the kernel $K_t$, for small and large values of t. Combining (2.1) with Lemma 2.2 (iii) and (iv), we have

$$\begin{aligned} \frac{ e^{R( x)}}{t^{n/2}}\exp \left( -C\,\frac{|u-D_t \,x |^2}{t}\right) \lesssim K_t(x,u) \lesssim \frac{ e^{R( x)}}{t^{n/2}} \exp \left( -c\,\frac{|u-D_t\, x |^2}{t}\right) , \; \quad 0 < t\le 1. \end{aligned}$$

(2.10)

For $t\ge 1$, we can use the norm $|.|_Q$ to write [5, Lemma 3.4] slightly more precisely. The proof of [5, Lemma 3.3] shows that

$$\begin{aligned} \left\langle (Q_t^{-1}-Q_\infty ^{-1})\,D_t\, w, D_t\, w\right\rangle \ge |w|^2_Q \end{aligned}$$

for any $w \in \mathbb{R}^n$, and this leads to

$$\begin{aligned} e^{R(x)} \exp \Big [ -C \left| D_{-t}\,u- x\right| _Q^2 \Big ] \lesssim K_t (x,u) \lesssim e^{R(x)} \exp \Big [ -\frac{1}{2} \left| D_{-t}\,u- x\right| _Q^2 \Big ], \quad \, t\ge 1. \end{aligned}$$

(2.11)

For $\beta >0$, let $E_\beta$ be the ellipsoid

$$\begin{aligned} E_\beta =\{z\in \mathbb{R}^n:\, R(z)= \beta \} \,. \end{aligned}$$

As in [5, Subsection 4.1], we introduce polar coordinates $(s, {\tilde{x}})$ for any point $x\in \mathbb{R}^n,\,\, x\ne 0$, by writing

$$\begin{aligned} x=D_s\, {\tilde{x}} \end{aligned}$$

(2.12)

with ${\tilde{x}}\in E_\beta$ and $s\in \mathbb{R}$.

The Lebesgue measure in ${\mathbb{R}}^n$ is given in terms of $(s, {\tilde{x}})$ by

$$\begin{aligned} dx = e^{-s{{\,\mathrm{tr}\,}}B}\, \frac{ |Q^{1/2}\, Q_\infty ^{-1} {\tilde{x}} |^2}{2\,| Q_\infty ^{-1} {\tilde{x}} |}\, ds\, dS_\beta ( {\tilde{x}}) \simeq e^{-s{{\,\mathrm{tr}\,}}B}\, | {\tilde{x}}|\,ds\, dS_\beta ( {\tilde{x}}), \end{aligned}$$

(2.13)

where $dS_\beta$ denotes the area measure of $E_\beta$. We refer to [5, Proposition 4.2] for a proof.

For any $A>0$ we define global and local regions

$$\begin{aligned} G_A&=\left\{ (x,u)\in \mathbb{R}^n\times \mathbb{R}^n\,: \,|x-u|> \frac{A}{1+|x|} \right\} \end{aligned}$$

and

$$\begin{aligned} L_A&=\left\{ (x,u)\in \mathbb{R}^n\times \mathbb{R}^n\,: \,|x-u|\le \frac{A}{1+|x|} \right\} . \end{aligned}$$

3 On the definition of negative powers of $-{\mathscr {L}}$

We start recalling the definition of Riesz transforms introduced by Mauceri and Noselli in [21] in a nonsymmetric context. For any nonzero multiindex $\alpha \in {\mathbb{N}}^n$, the Riesz transform $R^{(\alpha )}$, of order $|\alpha |$, on $L^2(\gamma _\infty )$ is defined as

$$\begin{aligned} R^{(\alpha )} = D^\alpha {\mathscr {I}}_{|\alpha |/2}. \end{aligned}$$

Here the symbol ${\mathscr {I}}_a$ denotes for any $a>0$ a Gaussian Riesz potential given by

$$\begin{aligned} {\mathscr {I}}_a f(x)=\frac{1}{\Gamma (a)} \int _0^{+\infty } t^{a-1} {\mathscr {H}}_t \big ( P_0^{\perp } f \big )(x)\,dt, \qquad f\in L^2(\gamma _\infty ). \end{aligned}$$

(3.1)

Formally, ${\mathscr {I}}_a$ corresponds to the negative power $\big ( -{\mathscr {L}}\big )^{-a} \,P_0^{\perp }$. In fact, the definition of $\big ( -{\mathscr {L}}\big )^{-a}$ is the key point in order to define $R^{(\alpha )}$, since ${\mathscr {L}}$ is not self-adjoint in our general framework. Therefore, we shall now introduce in another way the Gaussian Riesz potentials, and prove the equivalence with (3.1) for $a > 0$.

In this section, we let $L^2(\gamma _\infty )$ consist of complex-valued funtions.

We first recall from [23] that the spectrum of $-{\mathscr {L}}$ is given by

$$\begin{aligned} \sigma (-{\mathscr {L}})= \left\{ \lambda =-\sum _{j=1}^r n_j \lambda _j\,:\, n_j\in {\mathbb{N}} \right\} , \end{aligned}$$

where $\lambda _1, \ldots , \lambda _r$ are the eigenvalues of the drift matrix B. In particular, 0 is an eigenvalue, and the corresponding eigenspace $\ker {\mathscr {L}}$ is one-dimensional and consists of all constant functions, as proved in [23, Sect. 3]. Any other point in the spectrum of $-{\mathscr {L}}$ belongs to a fixed cone $\{z \in \mathbb{C}: |\arg z| < \mu \}$ with $\mu < \pi /2$, since the same is true for the numbers $-\lambda _1, \ldots , -\lambda _r$.

We also recall that, given a linear operator L on some $L^2$ space, a number $\lambda \in \mathbb{C}$ is a generalized eigenvalue of L if there exists a nonzero $u \in L^2$ such that $(L - \lambda I)^k \,u=0$ for some positive integer k. Then u is called a generalized eigenfunction, and those u span the generalized eigenspace corresponding to $\lambda$.

It is known from [23, Sect. 3] that the Ornstein–Uhlenbeck operator ${\mathscr {L}}$ admits a complete system of generalized eigenfunctions, that is, the linear span of the generalized eigenfunctions is dense in $L^2(\gamma _\infty )$. Analogous $L^p$ results are obtained in [23, Theorem 3.1] but will not be used in our paper.

As will be shown in a forthcoming note by the authors [6], each generalized eigenfunction of $-{\mathscr {L}}$ with a nonzero eigenvalue is orthogonal to the space of constant functions, that is, to the kernel of $-{\mathscr {L}}$. Thus the orthogonal complement of $\ker {\mathscr {L}}$ in $L^2(\gamma _\infty )$ coincides with the closure of the subspace generated by all generalized eigenfunctions with a nonzero generalized eigenvalue. We denote this subspace by $L^2_0(\gamma _\infty )$, so that $P_0^{\perp }$ is the orthogonal projection onto $L^2_0(\gamma _\infty )$.

The restriction of $-{\mathscr {L}}$ to the generalized eigenspace corresponding to an eigenvalue $\lambda \ne 0$ has the form

$$\begin{aligned} -{\mathscr {L}}=\lambda (I+N), \end{aligned}$$

where N is a nilpotent operator.

Then for $a\in {\mathbb{R}}$ one would like to write the power $(-{\mathscr {L}})^{-a}$, restricted to the generalized eigenspace, as

$$\begin{aligned} \lambda ^{-a}\, (I+N)^{-a} = \lambda ^{-a}\, \sum _{j\ge 0}\frac{ (-a)_j}{j!}\, N^j, \end{aligned}$$

(3.2)

where the sum is finite and we use the Pochhammer symbol. But here $\lambda \in {\mathbb{C}}$, and for noninteger a it is not obvious how to choose the value of $\lambda ^{-a}$. For $a>0$ this can be done as follows. We define the argument $\arg \lambda$ to be in $(-\pi /2,\pi /2)$.

Proposition 3.1

Let $\lambda \ne 0$ be a generalized eigenvalue of $-{\mathscr {L}}$, and let $a>0$. Then the restriction to the corresponding generalized eigenspaces of $(-{\mathscr {L}})^{-a}$ defined by (3.1) is given by (3.2), where $\lambda ^{-a} = |\lambda |^{-a}\, e^{-ia\arg \lambda }$.

Proof

The restriction mentioned is

$$\begin{aligned} \frac{1}{\Gamma (a)} \int _0^{+\infty } t^{a-1} {\mathscr {H}}_t \,dt&=\frac{1}{\Gamma (a)} \int _0^{+\infty } t^{a-1} e^{-t\lambda (I+N)} \,dt \\&=\frac{1}{\Gamma (a)} \int _0^{+\infty } t^{a-1} e^{-t\lambda } \sum _{j\ge 0}\frac{ (-t\lambda )^j }{j!}\, N^j \,dt; \end{aligned}$$

the sum is again finite and the integral converges.

Here we make a complex change of variables, letting $\tau = t\lambda$. We arrive at a complex integral

$$\begin{aligned} \frac{1}{\Gamma (a)}\, \lambda ^{-a} \int _{R_\lambda } \tau ^{a-1} e^{-\tau } \sum _{j\ge 0}\frac{ (-\tau )^j }{j!}\, N^j \,d\tau , \end{aligned}$$

where $R_\lambda$ is the ray $t \, e^{i\arg \lambda }$, $t\in \mathbb{R}_+$, going from 0 to $\infty$; also $\tau ^{a-1} = |\tau |^{a-1}\, e^{i(a-1) \arg \lambda }$ and $\lambda ^{-a} = |\lambda |^{-a}\, e^{-ia \arg \lambda }$. It is not hard to see that we can move the integration to the positive real axis, getting

$$\begin{aligned} \frac{\lambda ^{-a}}{\Gamma (a)} \sum _{j\ge 0}\frac{ (-1 )^j }{j!} \,\int _0^\infty \tau ^{j+a-1}\, e^{-\tau }\,d\tau \, N^j&= \lambda ^{-a} \sum _{j\ge 0}\,\frac{ (-1 )^j }{j!}\, \frac{\Gamma (j+a)}{\Gamma (a)}\, N^j\\&= \lambda ^{-a} \sum _{j\ge 0} \,\frac{ (-a )_j }{j!}\, N^j\,, \end{aligned}$$

since $(-1)^j \, \Gamma (a+j) /\Gamma (a) =(-a)_j.$ This proves the proposition. $\square$

In [21, Lemma 2.2] it is proved that for each complex number a such that $\mathfrak {R}a > 0$ the Riesz potential $(-{\mathscr {L}})^{-a}P_0^{\perp }$ is bounded on $L^2_0(\gamma _\infty )$. Thus $(-{\mathscr {L}})^{-a}P_0^{\perp }$ is entirely determined by its restrictions to the generalized eigenspaces, given by (3.2). To summarize, this means that by using these restrictions and taking a limit, we get a definition of $(-{\mathscr {L}})^{-a}$ for $a > 0$, which is equivalent to (3.1).

Finally, let us comment on the fact that $-{\mathscr {L}}$ has real coefficients, although with $a>0$ (3.2) is not real for nonreal $\lambda$. But if $(-{\mathscr {L}} - \lambda I)^k \,u=0$, then $(-{\mathscr {L}} - {\bar{\lambda }} I)^k \,{\bar{u}}=0$. Thus for nonreal $\lambda$, the generalized eigenspaces come in isomorphic pairs, and the isomorphism is complex conjugation. Conjugating the relation $-{\mathscr {L}} u = \lambda (I+N) u$, we see that the restriction to the conjugate generalized eigenspace is given by ${\bar{\lambda }} (I+{\bar{N}})$. The restriction of $(-{\mathscr {L}})^{-a}$ to the sum of the two conjugate generalized eigenspaces is a real operator. Indeed, this sum is spanned by the functions $\mathfrak {R}u$ and $\mathfrak {I}u$, with u in the generalized eigenspace with eigenvalue $\lambda$. For these real functions, we can use the expression (3.2) for $(-{\mathscr {L}})^{-a}$ with $a>0$, since

$$\begin{aligned} (-{\mathscr {L}})^{-a} \,\mathfrak {R}u&= \frac{1}{2}\, \left[ (-{\mathscr {L}})^{-a}\, u + (-{\mathscr {L}})^{-a} \,{\bar{u}}\right] \\&= \frac{1}{2} \left[ \lambda ^{-a} \sum _{j\ge 0}\frac{ (-a)_j}{j!} N^j u + {\bar{\lambda }}^{-a} \sum _{j\ge 0}\frac{ ({-a})_j}{j!} {\bar{N}}^j\, {\bar{u}}\right] = \mathfrak {R}\left[ \lambda ^{-a} \sum _{j\ge 0}\frac{ (-a)_j}{j!} N^j \,u\right] , \end{aligned}$$

and similarly for $\mathfrak {I}u ={-i}(u - {\bar{u}})/2$. Thus we see that $(-{\mathscr {L}})^{-a}P_0^{\perp }$ is a real operator.

4 Riesz transforms

We start this section with some technical lemmata.

Lemma 4.1

For $i,j\in \{1,\ldots ,n\}$,  $x,\,u\in \mathbb{R}^n$ and $t>0$, one has

$$\begin{aligned} \partial _{x_j} K_t (x,u)&= K_t (x,u)\ P_j(t,x,u),\qquad {\text {where}} \end{aligned}$$

(4.1)

$$\begin{aligned} P_j(t,x,u)&= \langle Q_\infty ^{-1}x,\,e_j\rangle + { \left\langle Q_t^{-1}\, e^{tB}\, e_j \,,\, u-D_t\, x\right\rangle }; \nonumber \\ \partial _{u_j} K_t (x,u)&= - K_t (x,u)\,{\left\langle Q_t^{-1} e^{tB} \, ( D_{-t}\, u - x), \,e_j\right\rangle }; \end{aligned}$$

(4.2)

$$\begin{aligned} \partial ^2_{x_i x_j } K_t (x,u)&= K_t (x,u)\,\left( P_i (t,x,u) P_j(t,x,u)+ \Delta _{ij} (t)\right) , \qquad {\text {where}} \end{aligned}$$

(4.3)

$$\begin{aligned} \Delta _{i j} (t)&= \Delta _{ ji} (t)= \partial _{x_i} P_j(t,x,u) = -\langle e_j , e^{tB^*} Q_t^{-1}\, e^{tB}\, e_i\rangle ; \nonumber \\ \partial _{u_i} P_j(t,x,u)&= \langle Q_t^{-1}\, e^{tB}\, e_j,\, e_i \rangle . \end{aligned}$$

(4.4)

Proof

A direct computation, using (2.1) and (2.2), shows that

$$\begin{aligned} \partial _{x_j} K_t (x,u)&= K_t (x,u) \left[ \langle Q_\infty ^{-1}x, e_j\rangle + { \left\langle ( Q_t^{-1}-Q_\infty ^{-1}) \, D_t\, e_j \,,\, u-D_t \,x\right\rangle }\right] \\&= K_t (x,u) \left[ \langle Q_\infty ^{-1}x,e_j\rangle + { \left\langle Q_t^{-1} e^{tB}\, e_j \,,\, u-D_t\, x\right\rangle }\right] , \end{aligned}$$

yielding (4.1). An analogous argument leads to (4.2). Rewriting $P_j$ by means of (2.3), one obtains

$$\begin{aligned} P_j(t,x,u) = \langle e_j \,,\, e^{tB^*} Q_t^{-1} \,\big ( u - e^{tB} x \big ) \rangle , \end{aligned}$$

which implies (4.3) and (4.4). $\square$

The following lemma provides a different expression for $P_j$.

Lemma 4.2

One has

$$\begin{aligned} P_j(t,x,u) = \left\langle e_j , e^{tB^*} \ Q_t^{-1} e^{tB} \big ( D_{-t} \, u-x\big )\right\rangle + \left\langle e_j , Q_\infty ^{-1} D_{-t} \, u\right\rangle . \end{aligned}$$

Proof

From (2.3) and the expression for $P_j$ in (4.1), we get

$$\begin{aligned} P_j(t,x,u)&= \langle Q_\infty ^{-1}x,e_j\rangle + { \left\langle Q_t^{-1} e^{tB} e_j ,D_t \big ( D_{-t} \, u-x\big )\right\rangle }\\&= \langle Q_\infty ^{-1}x,e_j\rangle + { \left\langle Q_t^{-1} e^{tB} e_j , \big ( e^{tB} + Q_t e^{-tB^*}Q_\infty ^{-1} \big ) \big ( D_{-t} \, u-x\big )\right\rangle }\\&= \langle Q_\infty ^{-1}x,e_j\rangle + \left\langle Q_t^{-1} e^{tB} e_j , e^{tB} \big ( D_{-t}\, u-x\big )\right\rangle + \left\langle e_j , Q_\infty ^{-1} \big ( D_{-t}\, u-x\big )\right\rangle \\&=\left\langle e_j , e^{tB^*} \, Q_t^{-1} e^{tB} \big ( D_{-t} \, u-x\big )\right\rangle + \left\langle e_j , Q_\infty ^{-1} D_{-t} \, u\right\rangle . \end{aligned}$$

$\square$

As a consequence of (4.1), Lemma 2.2 and Lemma 4.2, one has for all $j\in \{1, \ldots ,n\}$

$$\begin{aligned} { |P_j (t,x,u)|\lesssim } {\left\{ \begin{array}{ll} |x| + { | u-D_t \,x |}/{t} &{}\text { if } 0 <t \le 1, \\ e^{-ct} | D_{-t} \, u-x| + |D_{-t} \, u | &{}\text { if } t\ge 1. \end{array}\right. } \end{aligned}$$

(4.5)

Moreover,

$$\begin{aligned} \big |\Delta _{ij} (t) \big | \lesssim {\big (\min (1,t)\big )}^{-1}\,{e^{-ct}}, \qquad t>0. \end{aligned}$$

(4.6)

With $i,j\in \{1,\ldots ,n \}$ we define the kernels

$$\begin{aligned} \mathscr {R}_j (x,u)=\frac{1}{\sqrt{\pi }}\int _0^{+\infty } t^{-1/2} \ \partial _{x_j} K_t (x,u) \ dt \end{aligned}$$

and

$$\begin{aligned} \mathscr {R}_{ij}(x,u)= \int _0^\infty {\partial ^2_{x_i x_j}} K_t (x,u)\, dt. \end{aligned}$$

These integrals are absolutely convergent for all $u \ne x$, as seen from (2.10), (4.5), (4.6) and Lemma 2.1. In order to distinguish between small and large values of t, we split the integrals as

$$\begin{aligned} \mathscr {R}_{j} (x,u) =\frac{1}{\sqrt{\pi }}\left( \int _0^{1}+\int _1^\infty \right) t^{-1/2} K_t (x,u) P_j(t,x,u) \, dt \,=:\, \mathscr {R}_{j,0} (x,u)+ \mathscr {R}_{j,\infty } (x,u), \end{aligned}$$

and

$$\begin{aligned} \mathscr {R}_{ij}(x,u)&=\left( \int _0^{1}+\int _1^\infty \right) K_t (x,u)\, \left( P_i (t,x,u) P_j(t,x,u)+ \Delta _{ij} (t)\right) \, dt \\&=: \mathscr {R}_{ij,0}(x,u)+\mathscr {R}_{ij,\infty }(x,u). \end{aligned}$$

The proof of the next proposition is straightforward and so omitted.

Proposition 4.3

The off-diagonal kernels of $R_j$ and $R_{ij}$ are $\mathscr {R}_j$ and $\mathscr {R}_{ij}$, in the sense that for $f\in {\mathscr {C}}_0^\infty (\mathbb{R}^n)$ and $x\not \in \text {supp} \ f$

$$\begin{aligned}R_j f(x)= \int \mathscr {R}_j (x,u) f(u)\, d\gamma _\infty (u)\end{aligned}$$

and

$$\begin{aligned} R_{ij} f(x)= \int \mathscr {R}_{ij}(x,u) f(u)\, d\gamma _\infty (u), \end{aligned}$$

where $i,j\in \{1,\ldots ,n\}$.

The following estimates for $\mathscr {R}_{j,0}$ and $\mathscr {R}_{ij,0}$ result from (2.10), (4.5) and (4.6)

$$\begin{aligned} \big | \mathscr {R}_{j,0} (x,u)\big |&\lesssim e^{R( x)} \int _0^{1} t^{-(n+1)/2} \exp \left( -c\,\frac{|u- D_t\, x |^2}{t}\right) \left( |x| + \frac{1}{\sqrt{t}} \right) \, dt, \end{aligned}$$

(4.7)

$$\begin{aligned} \big |\mathscr {R}_{ij,0}(x,u)\big |&\lesssim e^{R( x)} \int _0^{1} t^{-n/2} \exp \left( -c\,\frac{|u- D_t\, x |^2}{t}\right) \left( |x|^2 +\frac{1}{t} \right) \, dt, \end{aligned}$$

(4.8)

for all $(x,u)\in \mathbb{R}^n\times \mathbb{R}^n$ with $x\ne u$.

5 Some estimates for large t

In this section, we derive some estimates for $\mathscr {R}_{j,\infty }$ and $\mathscr {R}_{ij,\infty }$, after some preparations.

Lemma 5.1

For ${\sigma } \in \{1,2,3\}$ and $x,u\in \mathbb{R}^n$, one has

$$\begin{aligned} \int _1^{+\infty }\exp \Big ({-\frac{1}{4}\left| D_{-t}\,u- x \right| _Q^2 }\Big )\big | D_{-t} \, u\big |^\sigma \, dt \lesssim 1+|x|^{\sigma -1}. \end{aligned}$$

(5.1)

Proof

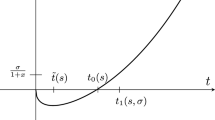
We can clearly assume that $u \ne 0$. Consider first the case when $R(x)\le 1$. Define $t_0 \in \mathbb{R}$ by $R(D_{-t_0}\,u) =2.$ If $t_0>1$, we split the integral at $t = t_0$.

For $1<t<t_0$, (2.5) yields

$$\begin{aligned} R( D_{-t}\,u)= R(D_{t_0-t}D_{-t_0}\, u)\ge R( D_{-t_0}\,u)=2\ge 2{R(x)}, \end{aligned}$$

whence by (2.9)

$$\begin{aligned} \big | D_{-t}\,u- x\big |_Q \simeq \big |D_{-t}\,u\big |_Q, \end{aligned}$$

and by Lemma 2.1

$$\begin{aligned} R( D_{-t}\,u) \gtrsim e^{c(t_0-t)}. \end{aligned}$$

Thus

$$\begin{aligned}&\int _1^{1\vee t_0} \exp \Big ( {-\frac{1}{4} \big |D_{-t}\,u- x\big |_Q^2 } \Big )\, \big | D_{-t} \, u \big |^\sigma dt\\&\quad \lesssim \int _1^{1\vee t_0} \exp \Big ( {-c\, \big |D_{-t}\,u\big |_Q^2 } \Big ) \ dt \\&\quad \lesssim \int _1^{1\vee t_0} \exp \Big ( {-c\, e^{c(t_0-t)} } \Big ) \ dt \lesssim 1.\end{aligned}$$

If $t\ge t_0$, then $R( D_{-t}\,u) \lesssim e^{c(t_0-t)}$, again because of Lemma 2.1, so that

$$\begin{aligned} \int _{1\vee t_0}^\infty \exp \Big ( {-\frac{1}{4} \big |D_{-t}\,u- x\big |_Q^2 } \Big )\, \big | D_{-t} \, u \big |^\sigma dt\lesssim \int _{1\vee t_0}^\infty e^{c\sigma (t_0-t)} \ dt \lesssim 1. \end{aligned}$$

This yields (5.1) in the case $R(x)\le 1$.

Next, assume $R(x) > 1$. Then the integral is split at the point $t_1$ defined by $R(D_{-t_1}\,u) =R(x)/2.$ For $1<t<t_1$ we write

$$\begin{aligned} \exp \Big ( {-\frac{1}{4}\, \big |D_{-t}\,u- x\big |_Q^2 } \Big )\, \big | D_{-t} \, u \big |^\sigma \lesssim&\,\exp \Big ( {-\frac{1}{4}\, \big |D_{-t}\,u- x\big |_Q^2 } \Big )\,\left( \big | D_{-t} \, u -x \big |^\sigma + |x|^\sigma \right) \nonumber \\ \lesssim&\, \exp \Big ( {-c \, \big |D_{-t}\,u- x\big |_Q^2 } \Big )\, (1+ |x|^\sigma ). \end{aligned}$$

(5.2)

Here we apply the polar coordinates (2.12) with $\beta = R(x)$, writing $x = {\tilde{x}}$ and $u = D_{s_u}\, {\tilde{u}}$, where $s_u\in \mathbb{R}$ and $R({\tilde{u}}) = R(x)$. Then for $1<t<t_1$

$$\begin{aligned} R( D_{-t}\,u) = R(D_{t_1-t} D_{-t_1}\, u) > R(D_{-t_1}\, u) = {R(x)}/2=\beta /2, \end{aligned}$$

and [5, Lemma 4.3 (ii)] applies, saying that

$$\begin{aligned} \big |D_{-t}\,u-x\big |= \big |D_{s_u-t}\,{\tilde{u}}-{\tilde{x}}\big | \gtrsim |x| \, |s_u-t|. \end{aligned}$$

We conclude from (5.2) that

$$\begin{aligned} \int _1^{1\vee t_1} \exp \Big ( {-\frac{1}{4}\, \big |D_{-t}\,u- x\big |_Q^2 } \Big )\, \big | D_{-t} \, u \big |^\sigma \, dt&\lesssim \int _\mathbb{R}\exp \left( - c \, |x|^2 \, |s_u-t|^2 \right) (1+ |x|^{\sigma })\,dt \\&\lesssim |x|^{\sigma -1}. \end{aligned}$$

For $t> 1\vee t_1$, we deduce from Lemma 2.1 that

$$\begin{aligned} |D_{-t}\, u|= |D_{t_1-t}\, D_{-t_1} \, u| \lesssim e^{c (t_1 - t)}\, |D_{-t_1}\,u|\lesssim e^{c (t_1 - t)}\,|x|. \end{aligned}$$

Moreover, we have $R(D_{-t}\,u)\le R(x)/{2}$ which implies $|D_{-t}\,u-x|\simeq |x|$ because of (2.9), so that

$$\begin{aligned} \int _{1\vee t_1}^{+\infty } \exp \Big ( {-\frac{1}{4} \big | D_{-t}\,u- x\big |^2 } \Big ) \big | D_{-t} \, u \big |^\sigma \, dt \lesssim \exp (-c |x|^2) \int _{1\vee t_1}^{+\infty } e^{c\sigma (t_1-t)} \, dt \, |x|^\sigma \lesssim 1. \end{aligned}$$

We have proved Lemma 5.1. $\square$

Proposition 5.2

Let $\sigma _1 \in \{0,1,2,3\}$ and $\sigma _2 \in \{1,2,3\}$. For all $x,u\in \mathbb{R}^n$ one has

$$\begin{aligned} \int _1^{+\infty } K_t (x,u)\,\big | D_{-t} \, u-x \big |^{\sigma _1} \, \big | D_{-t} \, u \big |^{\sigma _2} dt \lesssim e^{R(x)}\, (1+|x|^{\sigma _2-1})\,. \end{aligned}$$

Proof

We can delete the factor $\big | D_{-t} \, u-x \big |^{\sigma _1}$ in the integrand, by replacing the coefficient 1/2 of the exponential factor in $K_t$ by 1/4. Then this follows from Lemma 5.1. $\square$

Corollary 5.3

For all $x,u\in \mathbb{R}^n$ and for all $i,j,k\in \{1, \ldots , n\}$ the following estimates hold:

$$\begin{aligned}&\int _1^{+\infty } K_t (x,u)\big | P_j (t,x,u) \big | \, dt\lesssim e^{R(x)} \end{aligned}$$

(5.3)

$$\begin{aligned}&\int _1^{+\infty } K_t (x,u) \big | P_j (t,x,u) P_i (t,x,u) \big | \, dt\lesssim e^{R(x)}\,(1+|x|), \end{aligned}$$

(5.4)

$$\begin{aligned}&\int _1^{+\infty } K_t (x,u) \big | P_j (t,x,u) P_i (t,x,u) P_k (t,x,u) \big |\, dt\lesssim e^{R(x)}\, (1+|x|^2) \nonumber ,\\&\int _1^{+\infty } K_t (x,u) \big | \Delta _{j k} (t) \big | \, dt\lesssim e^{R(x)} , \nonumber \\&\int _1^{+\infty } K_t (x,u) \big | P_i (t,x,u) \Delta _{j k} (t) \big | \, dt\lesssim e^{R(x)}. \end{aligned}$$

(5.5)

Proof

It is enough to combine (2.11), Lemma 5.1 and Proposition 5.2 with (4.5) and (4.6). The quantities $\left| D_{-t}\,u- x\right|$ in the factors $P_j$ can be replaced by 1, because of the exponential factor in $K_t$. $\square$

Proposition 5.4

For all $(x,u)\in \mathbb{R}^n\times \mathbb{R}^n$ and all $i,j\in \{1, \ldots , n\}$,

$$\begin{aligned} \big | \mathscr {R}_{j,\infty } (x,u)\big | \lesssim e^{R( x)} \end{aligned}$$

(5.6)

and

$$\begin{aligned} \big |\mathscr {R}_{ij,\infty }(x,u)\big | \lesssim e^{R( x)} \,(1+|x|). \end{aligned}$$

(5.7)

Proof

The expressions for $\mathscr {R}_{j,\infty }$ and $\mathscr {R}_{ij,\infty }$ in Sect. 4 show that (5.6) follows from (5.3) and that (5.7) follows from (5.4) and (5.5). $\square$

Remark 5.5

If we use polar coordinates with $\beta < 2R(x)$, [5, Lemma 4.3 (i)] will imply that $\left| D_{-t}\,u- x \right| _Q \gtrsim |{\tilde{u}} - {\tilde{x}} |$. Then we can use a small part of the factor $\exp \left( -\frac{1}{2} \left| D_{-t}\,u- x \right| _Q^2 \right)$ in $K_t(x,u)$ to get an extra factor $\exp \left( -c\, |{\tilde{u}} - {\tilde{x}} |^2\right)$ in the right-hand sides of all the estimates in Lemma 5.1, Proposition 5.2, Corollary 5.3 and Proposition 5.4.

6 Some reductions and simplifications

This section is closely similar to Sect. 5 in [5].

When we prove (1.2) and (1.3), it is enough to take $f \ge 0$ satisfying $\Vert f\Vert _{L^1( \gamma _\infty )}=1$.

From now on, we also assume that $\lambda > 2$, since otherwise (1.2) and (1.3) are obvious.

The $d\gamma _\infty$ measure of the set of points x satisfying $R( x)> 2 \log \lambda$ is

$$\begin{aligned} \int _{ R(x)> 2 \log \lambda } \exp (-R(x) )\, dx\, \lesssim ( \log \lambda )^{(n-2)/2}\,\exp ({- 2 \log \lambda }) \lesssim \frac{1}{\lambda }, \end{aligned}$$

so this set can be neglected in (1.2) and (1.3).

Proposition 6.1

Let $x\in \mathbb{R}^n$ satisfy $R(x) < \frac{1}{2} \log \lambda$. Then for all $u\in \mathbb{R}^n$

$$\begin{aligned} | \mathscr {R}_{j,\infty } (x,u)|\lesssim { \lambda } \qquad \text { and } \qquad \big |\mathscr {R}_{ij,\infty }(x,u)\big | \lesssim { \lambda }. \end{aligned}$$

If also $(x,u) \in G_1$, the same estimates hold for $\mathscr {R}_{j,0}$ and $\mathscr {R}_{ij,0}$.

Proof

The first statement follows immediately from Proposition 5.4.

To deal with $\mathscr {R}_{j,0}$ and $\mathscr {R}_{ij,0}$, we recall from [5, formula (5.3)] that

$$\begin{aligned} t^2 \gtrsim \frac{1}{(1+|x|)^4}&\qquad \text {or} \qquad \frac{|u-D_{t}\, x|^2}{t} \gtrsim \frac{1}{(1+|x|)^2\,t} , \end{aligned}$$

(6.1)

if $(x,u) \in G_1$ and $0<t<1$.

From (4.7) and (4.8) we see that both $\big | \mathscr {R}_{j,0} (x,u)\big |$ and $\big | \mathscr {R}_{ij,0}(x,u)\big |$ can be estimated by a sum of expressions of type

$$\begin{aligned} e^{R(x)}\, (1+| x|)^p \int _0^{1} t^{-q} \exp \left( -c\,\frac{| u-D_t\,x|^2}{t}\right) \, dt, \end{aligned}$$

where $p,\, q \ge 0$. If here we integrate only over those $t\in (0,1)$ satisfying the first inequality in (6.1), we get at most

$$\begin{aligned} e^{R(x)}\, (1+| x|)^p \int _{c(1+|x|)^{-2}}^{1} t^{-q} \, dt \lesssim e^{R(x)}\, (1+| x|)^C. \end{aligned}$$

for some C. For the remaining t, the second inequality of (6.1) holds, and the corresponding part of the integral is no larger than

$$\begin{aligned} e^{R(x)}\, (1+| x|)^p \int _0^{1} t^{-q} \exp \Big (-\frac{c}{(1+|x|)^2\,t}\Big ) \, dt \lesssim e^{R(x)}\, (1+| x|)^C. \end{aligned}$$

Obviously $e^{R(x)}\, (1+| x|)^C \lesssim \lambda$ when $R(x) < \frac{1}{2} \log \lambda$, and the proposition is proved. $\square$

As a result of this section, we need only consider points x in the ellipsoidal annulus

$$\begin{aligned} {{\mathscr {E}}_\lambda }=\left\{ x \in \mathbb{R}^n:\, \frac{1}{2} \, \log \lambda \le R(x) \le 2 \log \lambda \, \right\} , \end{aligned}$$

when proving (1.2) and (1.3), except for $\mathscr {R}_{j,0}$ and $\mathscr {R}_{ij,0}$ in the local case.

7 The case of large t

Proposition 7.1

For all nonnegative functions $f\in L^1 (\gamma _\infty )$ such that $\Vert f\Vert _{L^1( \gamma _\infty )}=1$, all $i,\,j\in \{1, \ldots ,n\}$ and $\lambda >2$

$$\begin{aligned} \qquad \qquad \gamma _\infty \left\{ x : \int \mathscr {R}_{j,\infty } (x,u) f(u)\, d\gamma _\infty (u) > \lambda \right\} \lesssim \frac{1}{\lambda \sqrt{\log \lambda }}, \quad \end{aligned}$$

and

$$\begin{aligned} \gamma _\infty \left\{ x : \int \mathscr {R}_{ij,\infty }(x,u) f(u)\, d\gamma _\infty (u) > \lambda \right\} \lesssim \frac{1}{\lambda }. \end{aligned}$$

In particular, the operators with kernels $\mathscr {R}_{j,\infty }$ and $\mathscr {R}_{ij,\infty }$ are of weak type (1, 1) with respect to the invariant measure $d\gamma _\infty$.

Notice here that the estimate for $\mathscr {R}_{j,\infty }$ is sharpened by a logarithmic factor. A similar phenomenon occurs for the related maximal operator; see [5].

Proof

Having fixed $\lambda >2$, we use our polar coordinates with $\beta =\log \lambda$ and write $x=D_s\, {\tilde{x}}$ and $u=D_{s_u}\, {\tilde{u}}$, where ${\tilde{x}}, {\tilde{u}} \in E_\beta$. We restrict x to the annulus ${\mathscr {E}}_\lambda$, in view of Sect. 6. It is easily seen that this restriction is possible also with the logarithmic factor in the case of $\mathscr {R}_{j,\infty }$. Applying the estimates (5.6) and (5.7), we insert a factor $\exp \left( -c\, |{\tilde{u}} - {\tilde{x}} |^2\right)$, which is possible because of Remark 5.5. We also replace the factor $1+|x|$ in (5.7) by $\sqrt{\log \lambda }$ .

With $\sigma \in \{1,2\}$ we thus need to control the measure of the set

$$\begin{aligned} {\mathscr {A}}_\sigma (\lambda )=\left\{ x = D_s\,{\tilde{x}} \in {\mathscr {E}}_\lambda :\, e^{R(x)} \int \exp \big ( - c\, \big | {\tilde{x}}-{\tilde{u}}\big |^2\big )\, (\log \lambda )^{(\sigma -1)/2} \,f(u)\,d \gamma _\infty (u) > \lambda \right\} . \end{aligned}$$

The following lemma ends the proof of Proposition 7.1. $\square$

Lemma 7.2

Let $\sigma \in \{1,2\}$. The Gaussian measure of ${\mathscr {A}}_\sigma (\lambda )$ satisfies for $\lambda >2$

$$\begin{aligned} \gamma _\infty ( {\mathscr {A}}_\sigma (\lambda ))\lesssim \frac{1}{\lambda \left( {\log \lambda }\right) ^{(2-\sigma )/2}}. \end{aligned}$$

(7.1)

Proof

For $\sigma =1$, (7.1) has been proved in [5, Proposition 6.1], so we assume $\sigma =2$. In view of (2.5), the function

$$\begin{aligned} s\mapsto \exp \big ( R(D_s\, {\tilde{x}}) \big )\, \sqrt{\log \lambda } \int \exp \big ( - c\, \big | {\tilde{x}}-{\tilde{u}}\big |^2 \big ) \,f(u)\,d \gamma _\infty (u).\end{aligned}$$

is strictly increasing in s. We conclude that the inequality

$$\begin{aligned} \exp \big ( R(D_s\, {\tilde{x}}) \big )\,\sqrt{\log \lambda } \int \exp \big (- c\, \big | {\tilde{x}}-{\tilde{u}}\big |^2 \big )\, f(u)\,d \gamma _\infty (u)\, >\, \lambda \end{aligned}$$

(7.2)

holds if and only if $s> s_\lambda ({\tilde{x}})$ for some function ${\tilde{x}}\mapsto s_\lambda ({\tilde{x}}) \le \infty$, with equality for $s=s_\lambda ({\tilde{x}}) < \infty$. Notice also that if the point $x = D_s\, {\tilde{x}}$ is in ${\mathscr {A}}_2 (\lambda )$ and thus in ${\mathscr {E}}_\lambda$, then $|s|<C$ because of Lemma 2.1.

We use (2.13) to estimate the $d\gamma _\infty$ measure of ${\mathscr {A}}_2 (\lambda )$. Since s stays bounded and $|{\tilde{x}}|\simeq \sqrt{\log \lambda }$, we obtain

$$\begin{aligned} \gamma _\infty ({\mathscr {A}}_2(\lambda ))&=\int _{{\mathscr {A}}_2(\lambda )} e^{-R(x)}\, dx \\&\lesssim { \sqrt{\log \lambda }} \int _{E_{\log \lambda }} \int _{\begin{array}{c} s>s_\lambda ({\tilde{x}})\\ |s|<C \end{array}} e^{-R(D_s\, {\tilde{x}})} \,ds\, dS_{\log \lambda }({\tilde{x}})\\&\lesssim { \sqrt{\log \lambda }} \int _{E_{\log \lambda }} \int _{s_\lambda ({\tilde{x}})}^{+\infty } \exp \big ( -{R( D_{s_\lambda ({\tilde{x}})}\, {\tilde{x}})-c(s-s_\lambda ({\tilde{x}})})\log \lambda \big ) \,ds\, dS_{\log \lambda }({\tilde{x}}) , \end{aligned}$$

where the last inequality follows from (2.5), because $|D_s\, {\tilde{x}}|^2 \simeq \log \lambda$ for $|s|< C$. Now integrate in s, to get

$$\begin{aligned} \gamma _\infty ({\mathscr {A}}_2 (\lambda ))&\lesssim \frac{1}{\sqrt{\log \lambda }}\int _{E_{\log \lambda }} \exp \big (-R( D_{{s_\lambda ({\tilde{x}})}}\, {\tilde{x}}) \big )\,dS_{\log \lambda }({\tilde{x}}) . \end{aligned}$$

We combine this estimate with the case of equality in (7.2) and change the order of integration, concluding that

$$\begin{aligned} \gamma _\infty ({\mathscr {A}}_2 (\lambda )) \lesssim \frac{1}{\lambda } \int \int _{E_{\log \lambda }} \exp \big ( - c\, \big | {\tilde{x}}-{\tilde{u}}\big |^2 \big ) \, dS_{\log \lambda }({\tilde{x}})\,f(u)\,d \gamma _\infty (u) \lesssim \frac{1}{\lambda } \int f(u)\,d \gamma _\infty (u), \end{aligned}$$

which proves Lemma 7.2. $\square$

8 The local case

In this section we define and estimate the local parts of the Riesz operators of orders 1 and 2.

Let $\eta$ be a positive smooth function on $\mathbb{R}^n\times \mathbb{R}^n$, such that $\eta (x,u)=1$ if $(x,u)\in L_A$ and $\eta (x,u)=0$ if $(x,u)\notin L_{2A}$, for some $A\ge 1$. Here A will be determined later, in a way that depends only on n, Q and B. We can assume moreover that

$$\begin{aligned} \big | \nabla _x \,\eta (x,u)\big |+ \big | \nabla _u\, \eta (x,u)\big |\lesssim |x-u|^{-1}, \qquad x\ne u. \end{aligned}$$

(8.1)

We introduce the global and local parts of the first-order Riesz transform $R_j$ by

$$\begin{aligned} R_{j}^{\mathrm{{glob}}} f(x)=\int \mathscr {R}_{j} (x,u) \big (1-\eta (x,u)\big ) f(u) \,d\gamma _\infty (u), \qquad f\in {\mathscr {C}}^{\infty }_0(\mathbb{R}^n), \end{aligned}$$

and

$$\begin{aligned} R_{j}^{\mathrm{{loc}}} = R_j - R_{j}^{\mathrm{{glob}}}. \end{aligned}$$

The off-diagonal kernel of $R_{j}^{\mathrm{{loc}}}$ is ${\mathscr {R}}_{j}(x,u)\eta (x,u)$. For the second-order Riesz transforms, we simply repeat the above with the subscript j replaced by ij.

To prove the weak type (1, 1) of the operators $R_{j}^{\mathrm{{loc}}}$ and $R_{ij}^{\mathrm{{loc}}}$, we shall verify that their kernels $\mathscr {R}_{j} \eta$ and $\mathscr {R}_{ij} \eta$ satisfy the standard Calderón–Zygmund estimates.

We first need a lemma.

Lemma 8.1

Let $p,\, r\ge 0$ with $p+ r/2 > 1$, and $(x,u)\in L_{2A}$ with $x\ne u$. Then for $\delta >0$

$$\begin{aligned} \int _0^{1} t^{-p} \exp \left( -\delta \,\frac{|u- D_t \,x |^2}{t}\right) |x|^{r} \, dt\lesssim {C(\delta , p,r)}\,{|u-x|^{-2p-r+2}}, \end{aligned}$$

where the constant $C(\delta , p,r)$ may also depend on n, Q, B and A.

Proof

Write

$$\begin{aligned} |u- D_t\, x |^2 = |u-x|^2 + |x- D_t\, x|^2 + 2\langle u-x, x- D_t\, x \rangle . \end{aligned}$$

Since $|x- D_t \,x| \simeq t |x|$ and $(x,u)\in L_{2A}$, the absolute value of the last term here is no larger than CAt. It follows that

$$\begin{aligned} |u- D_t \,x |^2/t \ge |u-x|^2/t + c t |x|^2 - CA. \end{aligned}$$

We now apply this to the integral in the lemma, and estimate $\exp \left( -c\delta t |x|^2\right)$ by $C\delta ^{-r/2} t^{-r/2}\, |x|^{-r}$. The integral is thus controlled by

$$\begin{aligned} \delta ^{-r/2} \int _0^{1} t^{-p-r/2} \exp \left( -\delta \,\frac{|u- x |^2}{t}\right) \, dt, \end{aligned}$$

and the required estimate follows via the change of variables $s= {|u- x |^2}/t$. $\square$

Proposition 8.2

Let the function $\eta$ be as above. For all $(x,u)\in L_{2A}$, $x\ne u$, and all $j\in \{1, \ldots , n\}$, the following estimates hold:

• (i) $\big | \mathscr {R}_{j} (x,u) \ \eta (x,u)\big | \lesssim e^{R( x)}\,{|u-x|^{-n}}$;

• (ii) $\big |\nabla _x \big ( \mathscr {R}_{j} (x,u) \ \eta (x,u)\big )\big | \lesssim { e^{R( x)}\,}{|u-x|^{-(n+1)}}$;

• (iii) $\big |\nabla _u \big ( \mathscr {R}_{j} (x,u) \ \eta (x,u)\big )\big | \lesssim { e^{R( x)}\,}{|u-x|^{-(n+1)}}$,

with implicit constants depending on n, B, Q and A.

The same estimates hold for $\mathscr {R}_{ij},\;\; i,\,j\in \{1, \ldots , n\}$.

Proof

We start with $\mathscr {R}_{j}$.

(1) From (4.7) we obtain

$$\begin{aligned} \big | \mathscr {R}_{j,0} (x,u)\big |&\lesssim e^{R( x)} \int _0^{1} t^{-(n+1)/2} \ \exp \left( -c\,\frac{|u- D_t\, x |^2}{t}\right) \left( |x| + \frac{1}{\sqrt{t}} \right) \ dt \\&\lesssim { e^{R( x)}\, }{|u-x|^{-n}}, \end{aligned}$$

by Lemma 8.1. Further, (5.6) implies the desired estimate for $\mathscr {R}_{j,\infty }$, and (i) follows.

(2) As a consequence of (8.1), one has for $x\ne u$

$$\begin{aligned} \big | \partial _{x_\ell } \big ( \mathscr {R}_{j} (x,u) \ \eta (x,u)\big )\big |&\lesssim \big | \partial _{x_\ell }\, \mathscr {R}_{j} (x,u) \big | + |x-u|^{-1} \big | \mathscr {R}_{j} (x,u) \big |. \end{aligned}$$

Since item (1) above takes care of the last term here, it suffices to show that

$$\begin{aligned} \big | \partial _{x_\ell }\, \mathscr {R}_{j} (x,u) \big | \lesssim { e^{R( x)} }\,{|u-x|^{-(n+1)}}. \end{aligned}$$

(8.2)

For $\mathscr {R}_{j,0}$ we get from (4.1), (4.3), (4.5), (4.6), combined with (2.10)

$$\begin{aligned}&\left| \partial _{x_\ell }\, \mathscr {R}_{j,0} (x,u)\right| \lesssim \int _0^{1} t^{-1/2} K_t (x,u) \left| P_\ell (t,x,u) \, P_j(t,x,u) + \Delta _{j\ell } (t) \right| \, dt \\&\quad \lesssim \,e^{R( x)} \int _0^{1} t^{-(n+1)/2} \, \exp \left( -\frac{1}{2}\,\frac{|u-D_t \,x |^2}{t}\right) \left[ \left( |x| + \frac{ | u-D_t \,x |}{t}\right) ^2 +\frac{1}{t}\ \right] \, dt. \end{aligned}$$

In the last factor here, we can replace $|u-D_t \,x |$ by $\sqrt{t}$, reducing slightly the factor 1/2 in the exponential expression. This will be done repeatedly in the sequel. We arrive at

$$\begin{aligned} \big |\partial _{x_\ell }\, \mathscr {R}_{j,0} (x,u)\big | \lesssim e^{R( x)} \int _0^{1} t^{-(n+1)/2} \, \exp \left( -\frac{1}{4}\,\frac{|u-D_t\, x |^2}{t}\right) \left( |x|^2 + \frac{1}{ t}\right) \, dt, \end{aligned}$$

and Lemma 8.1 allows us to estimate this by ${ e^{R( x)} }\,{|u-x|^{-(n+1)}}$ as desired.

For $\mathscr {R}_{j,\infty }$ (5.4) and (5.5) imply that

$$\begin{aligned} \big | \partial _{x_\ell }\, \mathscr {R}_{j,\infty } (x,u)\big | \lesssim \int _1^{+\infty } K_t (x,u) \left| P_\ell (t,x,u) \, P_j(t,x,u) + \Delta _{j\ell } (t) \right| \, dt \lesssim e^{R( x)}\, (1+|x|). \end{aligned}$$

Here $1+|x| \lesssim |x-u|^{-1} \lesssim |x-u|^{-(n+1)}$, and (8.2) is verified, proving (ii) as well.

(3) As in item (2), it suffices to estimate $\left| \partial _{u_\ell }\, \mathscr {R}_{j} (x,u) \right|$. Because of (4.2), (4.4) and (4.5), we have

$$\begin{aligned} \big | \partial _{u_\ell }\, \mathscr {R}_{j,0}&(x,u)\big |\\&\lesssim \int _0^{1} t^{-1/2} K_t (x,u) \left| P_j(t,x,u) \, \left\langle Q_t^{-1}e^{tB} \, ( D_{-t}\,u- x), e_\ell \right\rangle + { \left\langle Q_t^{-1}e^{tB} e_j, e_\ell \right\rangle } \right| \, dt \\&\lesssim \int _0^{1} t^{-1/2} K_t (x,u) \left[ \left( |x| + \frac{ | u-D_t\, x |}{t}\right) \, \frac{ | D_{-t}\,u- x |}{t} +\frac{1}{t}\, \right] \, dt \\&\lesssim e^{R( x)}\, \int _0^{1} t^{-(n+1)/2} \ \exp \left( -c\,\frac{|u-D_t \, x |^2}{t}\right) \left( \frac{|x|}{\sqrt{t}}+ \frac{1}{t} \right) \, dt \\&\lesssim e^{R( x)}\, {|u- x|^{-(n+1)}}, \end{aligned}$$

where we proceeded much as in item (2). Similarly,

$$\begin{aligned} \big | \partial _{u_\ell }\,&\mathscr {R}_{j,\infty } (x,u)\big | \lesssim \int _1^{\infty } K_t (x,u)\, \Big ( |P_j(t,x,u)| \, \left| Q_t^{-1} e^{tB} \ (D_{-t}\, u- x)\right| + \left| Q_t^{-1} e^{tB} e_j \right| \Big ) \, dt \\&\lesssim \int _1^{\infty } K_t (x,u) \, \Big [\Big ( e^{-ct} \big | D_{-t} \, u-x \big |+\big | D_{-t} \, u \big |\Big ) \, e^{-ct} \, \big | D_{-t}\, u- x\big | + e^{-ct} \Big ] \, dt \\&\lesssim \int _1^{\infty } K_t (x,u)\, e^{-ct} \,\left[ \left| D_{-t} \, u-x \right| ^2+\left| D_{-t} \, u \right| \, \left| D_{-t}\, u- x\right| + 1 \right] \, dt \;\lesssim \; e^{R( x)}, \end{aligned}$$

as follows from Proposition 5.2.

Items (i), (ii) and (iii) are proved for $\mathscr {R}_j$, and we now turn to $\mathscr {R}_{ij}$.

(1’) For $(x,u) \in L_{2A}$, it results from (4.8) and Lemma 8.1 that

$$\begin{aligned} \big |\mathscr {R}_{ij,0}(x,u)\big |&\lesssim e^{R( x)} \int _0^{1} t^{-n/2} \, \exp \left( -c\,\frac{|u- D_t\, x |^2}{t}\right) \, \left( |x|^2 +\frac{1}{t} \right) \, dt \lesssim \frac{ e^{R( x)} }{|u-x|^n}. \end{aligned}$$

Since (5.7) gives the estimate for $\mathscr {R}_{ij,\infty }$, item (i) is verified.

(2’) As before, we need only consider the derivative $\partial _{x_\ell }\, \mathscr {R}_{ij}(x,u)$ in the local region. From (4.1) and (4.3), we have

$$\begin{aligned} \partial _{x_\ell }\, \mathscr {R}_{ij}(x,u)&= \int _0^{\infty } K_t (x,u) \Big [ P_\ell (t,x,u) \, \Big ( P_i (t,x,u) P_j(t,x,u)+\Delta _{ij} (t)\Big ) \\&\quad +\Delta _{{i \ell }} (t)\, P_j(t,x,u) +\Delta _{{j \ell }} (t)\, P_i(t,x,u) \Big ] \, dt. \end{aligned}$$

For $0<t<1$, we estimate the factors of type $P_i$ and $\Delta _{ij}$ here by means of (4.5) and (4.6). Then we use the exponential factor in $K_t$ to replace $|u-D_t\, x|$ by $\sqrt{t}$, and apply Lemma 8.1. The result will be

$$\begin{aligned} \big | \partial _{x_\ell }\, \mathscr {R}_{ij,0}(x,u)\big | \lesssim&\; e^{R( x)} \int _0^{1} t^{-n/2} \, \exp \left( -c\,\frac{|u- D_t\, x |^2}{t}\right) \left( |x|^3 +\frac{1}{{t\sqrt{t}}} \right) \, dt \\ \lesssim&\; {e^{R( x)} }\,{|u-x|^{-(n+1)}}. \end{aligned}$$

For $t>1$, we use (4.5) and (4.6), getting

$$\begin{aligned}&\big | \partial _{x_\ell }\, \mathscr {R}_{ij,\infty }(x,u)\big | \\&\lesssim \int _1^{\infty } K_t (x,u)\, \left( e^{-ct} \left| D_{-t} \,u- x\right| ^3 +\left| D_{-t}\, u\right| ^3 + e^{-ct}\left| D_{-t}\, u- x\right| + e^{-ct} \left| D_{-t}\, u\right| \right) \, dt \\&\lesssim e^{R( x)} \,|x-u|^{-2}, \end{aligned}$$

because of Lemma 5.2.

(3’) Applying (4.2) and (4.4), we have

$$\begin{aligned}&\partial _{u_\ell }\, \mathscr {R}_{ij}(x,u)\\&\quad = \int _0^{\infty } K_t (x,u) \Big [ - \left\langle Q_t^{-1}e^{tB} \ ( D_{-t}\,u- x), e_\ell \right\rangle \left( P_i (t,x,u) P_j(t,x,u)+\Delta _{j i} (t)\right) \\&\qquad + \left\langle Q_t^{-1}e^{tB} e_i, e_\ell \right\rangle P_j(t,x,u) + P_i (t,x,u) \left\langle Q_t^{-1}e^{tB} e_j, e_\ell \right\rangle \Big ] \, dt. \end{aligned}$$

Arguing as before, we conclude

$$\begin{aligned}&\left| \partial _{u_\ell }\, \mathscr {R}_{ij,0}(x,u)\right| \\&\quad \lesssim \int _0^{1} K_t (x,u) \left[ \frac{ | D_{-t}\,u- x |}{t} \left( \left( |x| + \frac{ | u-D_t \,x |}{t}\right) ^2 \, +\frac{1}{t}\right) + \frac{1}{t} \left( |x| + \frac{ | u-D_t\, x |}{t}\right) \right] \, dt \\&\quad \lesssim e^{R( x)}\, \int _0^{1} t^{-n/2} \, \exp \left( -c\,\frac{|u-D_t\, x |^2}{t}\right) \Big ( \frac{|x|^2}{\sqrt{t}}+ \frac{1}{t\sqrt{t}} \Big ) \, dt \\&\quad \lesssim e^{R( x)}\, {|u-x|^{-(n+1)}}. \end{aligned}$$

Further,

$$\begin{aligned} \big | \partial _{u_\ell }\, \mathscr {R}_{ij,\infty }&(x,u)\big | \\ \lesssim \int _1^{\infty }&K_t (x,u)\, e^{-ct} \big ( \left| D_{-t} \,u- x\right| ^3 +\left| D_{-t}\, u- x\right| \left| D_{-t}\, u\right| ^2 + 1 +\left| D_{-t}\, u- x\right| + \left| D_{-t}\, u\right| \big ) \, dt \\ \lesssim \,e^{R( x)}&\, |x-u|^{-1}, \end{aligned}$$

the last step from Proposition 5.2.

This completes the proof of Proposition 8.2. $\square$

We can now prove the weak type (1, 1) boundedness of the local parts of the Riesz transforms.

Proposition 8.3

For $i,\, j\in \{1, \ldots , n\}$, the operators ${R}^\mathrm{{loc}}_{j}$ and ${R}^\mathrm{{loc}}_{ij}$ are of weak type (1, 1) with respect to the invariant measure $d\gamma _\infty$.

Proof

This is now a straightforward consequence of [21, Proposition 2.3], [15, Proposition 3.4], our Proposition 8.2 and [15, Theorem 3.7]. $\square$

9 The global case for small t

In this section, we study the operators $R_{j,0}^\mathrm{{glob}}$ and $R_{ij,0}^\mathrm{{glob}}$, with kernels $\big (1-\eta ) \mathscr {R}_{j,0}$ and $\big (1-\eta )\mathscr {R}_{ij,0}$, respectively. The function $\eta$ was defined in the beginning of Sect. 8, depending on A. We have the following result.

Proposition 9.1

For $i,j\in \{1, \ldots , n\}$, the operators $R_{j,0}^\mathrm{{glob}}$ and $R_{ij,0}^\mathrm{{glob}}$ are of weak type (1, 1) with respect to the invariant measure $d\gamma _\infty$, provided A is chosen large enough.

The estimates (4.7) and (4.8) show that to prove this proposition, it suffices to verify the weak type (1, 1) boundedness of the operator with kernel $\int _0^{1} {\mathscr {K}}_t (x,u)\, dt \, \chi _{G_A} (x,u)$, where

$$\begin{aligned} {\mathscr {K}}_t (x,u) = e^{R( x)}\, t^{-n/2} \ \exp \left( -c\,\frac{|u- D_t \,x |^2}{t}\right) \, \left( |x|^2 + \frac{1}{ t} \right) . \end{aligned}$$

As is clear from Sect. 6, we need only consider the case $|x|\gtrsim 1.$ This assumption will be valid in the rest of this section.

The sets

$$\begin{aligned} I_m(x,u) =\left\{ t \in (0,1): \, 2^{m-1} \sqrt{t}< |u-D_t\, x |\le 2^{m} \sqrt{t} \,\right\} , \qquad m = 1,2,\dots , \end{aligned}$$

and

$$\begin{aligned} I_0(x,u) =\left\{ t \in (0,1): \, |u-D_t\, x |\le \sqrt{t} \,\right\} \end{aligned}$$

together form a partition of (0, 1). For $t \in I_m(x,u)$,

$$\begin{aligned} {\mathscr {K}}_t (x,u) \le e^{R( x)}\ t^{-n/2} \, \exp \left( -c\,2^{2m}\right) \, \left( |x|^2 + \frac{1}{ t} \right) . \end{aligned}$$

Let

$$\begin{aligned} {\mathscr {Q}}_m(x,u) = e^{R( x)} \int _{I_m(x,u)} t^{-n/2} \left( |x|^2 + \frac{1}{ t} \right) dt \, \chi _{G_A} (x,u), \qquad \; m = 0, 1,\dots . \end{aligned}$$

The operator we need to consider has kernel

$$\begin{aligned} \sum _{m=0}^\infty \, \exp \left( -c\,2^{2m}\right) \, {\mathscr {Q}}_m(x,u). \end{aligned}$$

(9.1)

Proposition 9.2

Let $m \in \{0, 1,\dots \}$. The operator whose kernel is $\mathscr {Q}_{m}$ is of weak type (1, 1) with respect to $d\gamma _\infty$, with a quasinorm bounded by $C\,2^{Cm}$ for some C.

This proposition implies Proposition 9.1, since the factors $\exp \left( -c\,2^{2m}\right)$ in (9.1) will allow us to sum over m in the space $L^{1,\infty }(\gamma _\infty )$. Before proving Proposition 9.2, we make some preparations.

From now on, we fix $m \in \{0,1,\dots \}$. If $t \in I_m(x,u)$, Lemma 2.3 implies

$$\begin{aligned} |u-x| \le |u - D_t\, x| + |D_t\, x - x| \lesssim 2^m\sqrt{t} + t|x|, \end{aligned}$$

(9.2)

and further

$$\begin{aligned} | R(D_t\, x) -R(u)| =\,\frac{1}{2}\, \big ( |D_t \,x|_Q+|u|_Q\big )\, \big | |D_t \,x|_Q - |u|_Q\big |&\lesssim \, (|x|+|u|)\,|D_t\, x - u|_Q \nonumber \\&\lesssim (|x|+|u|)\, 2^m\sqrt{t} \,. \end{aligned}$$

(9.3)

Lemma 9.3

Let $(x,u) \in G_A$. If A is chosen large enough, depending only on n, Q and B, then

$$\begin{aligned} I_m(x,u) \subset (2^{-2m}/|x|^2,\, 1), \qquad m = 0,1, \dots . \end{aligned}$$

Proof

If $t \in I_m(x,u)$ but $t \le 2^{-2m}/|x|^2$, the two terms to the right in (9.2) are both bounded by 1/|x|, so that $|x-u| < C/|x|$ for some C. Since we assume $|x|\gtrsim 1$, this will violate the hypothesis $(x,u) \in G_A$, if A is large. The lemma follows. $\square$

Lemma 9.4

Let $t \in I_m(x,u)$. If the constant $C_0 > 4$ is chosen large enough, depending only on n, Q and B, then $t > C_0\,2^{2m}/|x|^2$ implies

$$\begin{aligned} |u|&\simeq |x|, \end{aligned}$$

(9.4)

$$\begin{aligned} R(u) - R(x)&\simeq t|x|^2 \simeq |u-x|\,|x| \end{aligned}$$

(9.5)

and

$$\begin{aligned} t \simeq {|u-x|}/{|x|}. \end{aligned}$$

(9.6)

Proof

Because of our assumptions on t, (9.2) implies that $|u-x| \lesssim t|x| \lesssim |x|$, and so $|u| \lesssim |x|$. This proves one of the inequalities in both (9.4) and (9.6). Aiming at (9.5), we write

$$\begin{aligned} R(u) - R(x) = R(D_t \,x) - R(x) - (R(D_t\, x)- R(u)). \end{aligned}$$

From (2.7) it follows that

$$\begin{aligned} R(D_t \,x) - R(x) \simeq t|x|^2, \end{aligned}$$

and (9.3) and our assumptions lead to

$$\begin{aligned} | R(D_t\, x) -R(u)| \lesssim \,|x|\, 2^m\sqrt{t} \lesssim \, t|x|^2/\sqrt{C_0}\,. \end{aligned}$$

Thus we can choose $C_0>4$ so large that $| R(D_t \,x) - R(u)| < (R(D_t\, x) - R(x))/2$, and the first estimate in (9.5) follows. In particular, $R(u) > R(x)$, and so $|u|\gtrsim |x|$, which completes the proof of (9.4). We also obtain the remaining part of (9.6), by writing

$$\begin{aligned} t|x|^2 \simeq R(u) - R(x) = \frac{1}{2}\, (|u|_Q+ |x|_Q)\,(|u|_Q - |x|_Q) \lesssim |x|\,|u - x|_Q. \end{aligned}$$

Finally, the second estimate in (9.5) is a trivial consequence of (9.6).

The lemma is proved. $\square$

In view of the last two lemmas, we split $I_m(x,u)$ into

$$\begin{aligned} I_m^-(x,u) = I_m(x,u) \cap (2^{-2m}/|x|^2,\,1\wedge C_0\,2^{2m}/|x|^2 ) \end{aligned}$$

and

$$\begin{aligned} I_m^+(x,u) = I_m(x,u) \cap (1\wedge C_0\,2^{2m}/|x|^2,\, 1 ). \end{aligned}$$

Define for $m = 0,1,\dots$ and $|x|\gtrsim 1$

$$\begin{aligned} {\mathscr {Q}}_m^-(x,u) = e^{R( x)}\ \int _{I_m^-(x,u)} t^{-n/2} \, \left( |x|^2 + \frac{1}{ t} \right) \, dt \ \chi _{G_A} (x,u) \end{aligned}$$

and

$$\begin{aligned} {\mathscr {Q}}_m^+(x,u) = e^{R( x)}\ \int _{I_m^+(x,u)} t^{-n/2} \, \left( |x|^2 + \frac{1}{ t} \right) \, dt \ \chi _{G_A} (x,u), \end{aligned}$$

so that ${\mathscr {Q}}_m(x,u) = {\mathscr {Q}}_m^-(x,u) + {\mathscr {Q}}_m^+(x,u)$.

Lemma 9.5

The operator with kernel $\mathscr {Q}^{-}_{m}$ is of strong type (1, 1) with respect to $d\gamma _\infty$, with a norm bounded by $C\,2^{Cm}$.

Proof

For $t < C_0\,2^{2m}/|x|^2$, the estimate (9.2) implies

$$\begin{aligned} |u-x| \le 2\,C_0\, 2^{2m}/|x|, \end{aligned}$$

(9.7)

which leads to

$$\begin{aligned} {\mathscr {Q}}_m^-(x,u) \lesssim&\ e^{R( x)} \int _{2^{-2m}/|x|^2}^{C_0\,2^{2m}/|x|^2} t^{-n/2} \, \left( |x|^2 + \frac{1}{ t} \right) \, dt \ \chi _{\left\{ |u-x|\lesssim 2\,C_0\, 2^{2m}/|x| \right\} }\\ \lesssim&\ e^{R( x)}\,2^{Cm}\,|x|^{n}\, \chi _{\left\{ |u-x|\lesssim 2\,C_0\, 2^{2m}/|x| \right\} }, \end{aligned}$$

for some C.

Consider first the case $|x| \le C_0\,2^m$. Then ${\mathscr {Q}}_m^-(x,u) \lesssim e^{R( x)}\, 2^{Cm}$, and so

$$\begin{aligned} \int _{|x| \le C_0\,2^m} {\mathscr {Q}}_m^-(x,u)\, d\gamma _\infty (x) \lesssim 2^{Cm}. \end{aligned}$$

Since this is uniform in u, the strong type follows for $|x| < C_0\,2^m$.

To deal with points x with $|x| > C_0\,2^m$, we introduce dyadic rings

$$\begin{aligned} L_i = \{ x: C_0\,2^{m+i} < |x| \le C_0\,2^{m+i+1}\}, \qquad i = -1, 0, 1,\dots \,. \end{aligned}$$

If $x \in L_i$ with $i\ge 0$, it follows from (9.7) that

$$\begin{aligned} |u-x|< 2^{m-i+1} < C_0\, 2^{m-i-1}, \end{aligned}$$

the last step since $C_0 > 4$. The triangle inequality now shows that u is in the extended ring

$$\begin{aligned} L_i^{\prime} = L_{i-1} \cup L_i \cup L_{i+1}. \end{aligned}$$

With $0 \le f \in L^1(\gamma _\infty )$ we let $F(u) = e^{-R( u)}\,f(u)$, so that $\int f\,d\gamma _\infty = \int F\,du$. Then for $x \in L_i, \;\, i\ge 0$,

$$\begin{aligned} \int \mathscr {Q}^{-}_{m} (x,u)\, f(u)\, d\gamma _\infty (u)&\lesssim e^{R(x)}\, {2^{Cm}}\, 2^{n(m+i)} \int _{|u-x|\lesssim C_0\, 2^{m-i-1}} F(u)\, du\\&= e^{R(x)}\, {2^{Cm}} \, \Psi * F(x), \end{aligned}$$

where $\Psi$ is given by

$$\begin{aligned} \Psi (u)= 2^{n(m+i)} \, \chi _{B\left( 0,\, C_0 \, 2^{m-i-1} \right) }(u). \end{aligned}$$

Since $\int \Psi (u)\,du\lesssim 2^{Cm}$, we can integrate in x to get

$$\begin{aligned} \int _{L_i} d\gamma _\infty (x) \int \mathscr {Q}^{-}_{m} (x,u)\, f(u)\, d\gamma _\infty (u) \lesssim 2^{Cm} \int _{L_i} \Psi * F(x) \, dx \lesssim 2^{Cm} \int _{L_i^{\prime}} F(u) \, du. \end{aligned}$$

Summing over $i\ge 0$, we get

$$\begin{aligned} \int _{|x|> C_0 2^m} d\gamma _\infty (x) \int \mathscr {Q}^{-}_{m} (x,u)\, f(u)\, d\gamma _\infty (u) \lesssim 2^{Cm} \, \sum _{i =-1}^\infty \int _{L_i^{\prime}}\, F(u)\, d\gamma _\infty (u) \lesssim 2^{Cm} \, \int f\,d\gamma _\infty . \end{aligned}$$

The lemma follows. $\square$

Lemma 9.6

The operator with kernel $\mathscr {Q}^{+}_{m}$ is of weak type (1, 1) with respect to $d\gamma _\infty$, and its quasinorm is bounded by $C\,2^{Cm}$.

Proof

The support of the kernel ${\mathscr {Q}}_m^+$ is contained in the set

$$\begin{aligned} {\mathscr {C}}_m = \left\{ (x,u)\in G_A: \; I_m^+(x,u) \ne \emptyset \right\} . \end{aligned}$$

We first sharpen (9.6) by restricting t further. Because of (9.3), (9.4) and (9.6), any $t\in I_m^+(x,u)$ satisfies

$$\begin{aligned} \big |R(D_t \,x) -R(u)\big | \lesssim |x|\,2^m\,\sqrt{t} \lesssim 2^m\, \sqrt{{|x-u|}{|x|}}, \end{aligned}$$

(9.8)

and from (2.5) we know that

$$\begin{aligned} \partial _t R(D_t\, x) \simeq |x|^2. \end{aligned}$$

The size of this derivative shows that (9.8) can hold only for t in an interval of length at most $C\, 2^m\, \sqrt{|x-u|}/ |x|^{3/2}$, call it I. We obtain, using (9.6) again,

$$\begin{aligned} {\mathscr {Q}}_m^+(x,u) \lesssim&\ e^{R( x)}\, \int _{I\cap I_m^+(x,u)} \left( \frac{|x-u|}{|x|}\right) ^{-n/2} \left( |x|^2 + \frac{|x|}{|x-u|} \right) \, dt \, \chi _{{\mathscr {C}}_m}(x,u). \end{aligned}$$

The global condition implies $|x|/|x-u| \lesssim |x|^2$, so that

$$\begin{aligned} {\mathscr {Q}}_m^+(x,u) \lesssim \ e^{R( x)}\, 2^m\, |x|^{{(n+1)}/2}\, |x-u|^{{(1-n)}/2} \, \chi _{{\mathscr {C}}_m}(x,u) =: \mathscr {M}_{m} (x,u). \end{aligned}$$

It will be enough to prove Lemma 9.6 with ${\mathscr {Q}}_m^+$ replaced by the kernel $\mathscr {M}_{m}$ thus defined.

With $\lambda >2$ fixed, we assume $x \in {\mathscr {E}}_\lambda$. We use our polar coordinates with $\beta =(\log \lambda )/2$, writing

$$\begin{aligned} x=D_s \,{\tilde{x}} \qquad \text { and } \qquad u=D_{s_u}\, {\tilde{u}}, \end{aligned}$$

where ${\tilde{x}}, {\tilde{u}} \in E_\beta$ and $s\ge 0, \;\, s_u\in \mathbb{R}$. If $(x,u) \in {\mathscr {C}}_m$, we take $t \in I_m^+(x,u)$ and observe that $R(D_t \,x) > R(x)\ge \beta$. Then [5, Lemma 4.3 (i)] can be applied, giving

$$\begin{aligned} |{\tilde{u}}-{\tilde{x}}|\lesssim | u-D_t \,x| \le 2^m \sqrt{t} \simeq 2^m \sqrt{{|u-x|}/{|x|} }\,, \end{aligned}$$

(9.9)

the last step because of (9.6).

We shall cover the ellipsoid $E_\beta$ with little caps, and start with $E_1$. The small number $\delta > 0$ will be specified below, depending only on n, Q and B. Define for $e \in E_1$ the cap $\Omega _e^1 = E_1 \cap B(e,\delta ).$ We cover $E_1$ with caps $\Omega _e^1$ with e ranging over a finite subset of $E_1$, in such a way that the doubled caps ${\tilde{\Omega }}_e^1 = E_1 \cap B(e,2\delta )$ have C-bounded overlap.

Since $E_\beta = \sqrt{\beta }\, E_1$, we can scale these caps to get caps

$$\begin{aligned} \Omega _e^\beta = \sqrt{\beta }\, \Omega _e^1 = E_\beta \cap B\left( \sqrt{\beta }\,e, \sqrt{\beta }\,\delta \right) \end{aligned}$$

covering $E_\beta$. Similarly, ${\tilde{\Omega }}_e^\beta = \sqrt{\beta }\, {\tilde{\Omega }}_e^1$.

For each $x \in {\mathscr {E}}_\lambda$, the point ${\tilde{x}}$ will belong to some cap $\Omega _{e}^\beta$ of the covering. In the proof of Lemma 9.6 we need only consider those u for which ${\tilde{u}}$ is in the doubled cap ${\tilde{\Omega }}_{e}^\beta$. The reason is that if ${\tilde{u}} \notin {\tilde{\Omega }}_{e}^\beta$, then $|{\tilde{u}}-{\tilde{x}}| \gtrsim \sqrt{\beta }\, \delta \simeq |x|$, and [5, Lemma 4.3 (i)] implies $| u-D_t\, x| \gtrsim |x|$ and also $| u-x| \gtrsim |x|$. This and the definition of $I_m(x,u)$ lead to $|x| \lesssim 2^m \sqrt{t}$ and thus $1+|x| \lesssim 2^m$. It follows that

$$\begin{aligned} \mathscr {M}_{m} (x,u) \lesssim \, e^{R( x)}\, 2^m\, |x|^{{(n+1)}/2}\, |x-u|^{{(1-n)}/2} \lesssim \,e^{R(x)}\, 2^m\, |x| \lesssim \, e^{R(x)}\, 2^{(n+3)m}\, (1+ |x|)^{-n-1}. \end{aligned}$$

Since the last expression is independent of u and has integral

$$\begin{aligned} \int e^{R(x)}\, 2^{(n+3)m}\, (1+ |x|)^{-(n+1)} \,d\gamma _\infty (x) \lesssim 2^{Cm}, \end{aligned}$$

this part of the kernel $\mathscr {M}_m$ defines an operator which is of strong type (1, 1), with the desired bound.

Thus we fix a cap $\Omega _{e}^\beta$, assuming that ${\tilde{x}} \in \Omega _{e}^\beta$ and ${\tilde{u}} \in {\tilde{\Omega }}_{e}^\beta$. By means of a rotation, we may also assume that e is on the positive $x_1$ axis. Then we write ${\tilde{x}}$ as ${\tilde{x}}=({\tilde{x}}_1, {\tilde{x}}^{\prime}) \in \mathbb{R}\times \mathbb{R}^{n-1}$, and similarly ${\tilde{u}}=({\tilde{u}}_1, {\tilde{u}}^{\prime})$. If $\delta$ is chosen small enough, we will then have

$$\begin{aligned} |{\tilde{x}}-{\tilde{u}}| \simeq |{\tilde{x}}^{\prime} -{\tilde{u}}^{\prime}|, \end{aligned}$$

(9.10)

essentially because the $x_1$ axis is transversal to $E_\beta$ at the point of intersection $\sqrt{\beta }\,e$. Further, the area measure $dS_\beta$ of $E_\beta$ will satisfy

$$\begin{aligned} dS_\beta ({\tilde{u}}) \simeq d{\tilde{u}}^{\prime} \end{aligned}$$

(9.11)

in ${\tilde{\Omega }}_{e}^\beta$, again if $\delta$ is small.

We now recall Proposition 8 in [20]. This proposition is also applied in another framework in [3].

Proposition 9.7

[20] The operator

$$\begin{aligned} Tg(\xi )= e^{-2\xi _1} \int _{\begin{array}{c} \eta _1<\xi _1-1\\ |\xi^{\prime} -\eta^{\prime} |< \sqrt{\xi _1-\eta _1} \end{array}} (\xi _1-\eta _1)^{{(1-n)}/{2}} g(\eta )\, d\eta \end{aligned}$$

maps $L^1 (d\eta )$ boundedly into $L^{1,\infty }(e^{2\xi _1}\, d\xi )$. Here $\xi =(\xi _1,\, \xi^{\prime} )\in \mathbb{R}\times \mathbb{R}^{n-1}$ and similarly for $\eta$.

In order to apply this result, we define new variables $\xi =(\xi _1, \xi^{\prime} ) \in \mathbb{R}\times \mathbb{R}^{n-1}$ and analogously $\eta =(\eta _1, \eta^{\prime} )$, defined for $x \in {\mathscr {E}}_\lambda$ and $(x,u) \in {\mathscr {C}}_m$ satisfying ${\tilde{x}} \in \Omega _{e}^\beta$ and ${\tilde{u}} \in {\tilde{\Omega }}_{e}^\beta$, by

$$\begin{aligned} \xi _1= -\frac{1}{2}\, R(x), \qquad \eta _1= -\frac{1}{2}\, R(u) \end{aligned}$$

and

$$\begin{aligned} \xi^{\prime} = 2^{-m} \sqrt{ \log \lambda }\ {\tilde{x}}^{\prime} ,\qquad \eta^{\prime} = 2^{-m} \sqrt{\log \lambda } \ {\tilde{u}}^{\prime}. \end{aligned}$$

Lemma 9.4 implies that

$$\begin{aligned} |u-x| \simeq (\xi _1-\eta _1)/ |x| \simeq (\xi _1-\eta _1)/\sqrt{\log \lambda } . \end{aligned}$$

(9.12)

Then $\xi _1-\eta _1 \gtrsim A$ because of the global condition. Choosing A large enough, we will have

$$\begin{aligned} \xi _1-\eta _1 > 1. \end{aligned}$$

Applying (9.10), (9.9) and (9.12), we obtain

$$\begin{aligned} |\xi^{\prime} - \eta^{\prime} | = 2^{-m}\, \sqrt{\log \lambda } \,|{\tilde{u}}^{\prime} -{\tilde{x}}^{\prime}| \simeq 2^{-m}\, \sqrt{\log \lambda } \,|{\tilde{u}} -{\tilde{x}}| \lesssim \sqrt{ |x|\, |u-x|} \simeq \sqrt{\xi _1-\eta _1}. \end{aligned}$$

This allows us to estimate $\mathscr {M}_m$ in terms of the coordinates $\xi$ and $\eta$ :

$$\begin{aligned} \mathscr {M}_{m} (x,u) \lesssim e^{-2\xi _1} \, (\log \lambda )^{n/2}\,(\xi _1-\eta _1)^{(1-n)/2}\,\chi _{{\mathscr{C}}_m^{\prime}}, \end{aligned}$$

where

$$\begin{aligned} {\mathscr {C}}_m^{\prime} = \left\{ (\xi ,\eta ):\, \xi _1-\eta _1 > 1, \; |\xi^{\prime} - \eta^{\prime} | \le C\, \sqrt{\xi _1-\eta _1}\right\} \end{aligned}$$

for some C.

We must also express the Lebesgue measures dx and du in terms of $\xi$ and $\eta$, with x and u restricted as before. By (2.13),

$$\begin{aligned} dx \simeq e^{-s{{\,\mathrm{tr}\,}}B}\,|x| \,ds\,dS_\beta ({\tilde{x}}) \simeq \sqrt{\log \lambda }\;ds\,dS_\beta ({\tilde{x}}), \end{aligned}$$

the last step since $x \in {\mathscr {E}}_\lambda$ implies $s\lesssim 1$. Similarly, $du \simeq \sqrt{\log \lambda }\;ds_u\,dS_\beta ({\tilde{u}})$.

Because of (2.5), we can write $|{\partial \xi _1 }/{\partial s}| = \left| {\partial R(D_s \,{\tilde{x}})}/{\partial s}\right| /2 \simeq |D_s \,{\tilde{x}}|^2 = |x|^2 \simeq \log \lambda$, and if ${\tilde{x}}$ is kept fixed, we will have $ds \simeq (\log \lambda )^{-1}\,d\xi _1$. From (9.11) applied to x, we have $dS_\beta ({\tilde{x}}) \simeq d{\tilde{x}}^{\prime} = 2^{(n-1)m}\,(\log \lambda )^{(1-n)/2} \,d\xi^{\prime}$. Altogether, we get

$$\begin{aligned} dx \simeq 2^{(n-1)m}\,(\log \lambda )^{-n/2}\,d\xi \qquad \quad \mathrm {and} \qquad \quad du \simeq 2^{(n-1)m}\,(\log \lambda )^{-n/2}\,d\eta . \end{aligned}$$

(9.13)

Letting $g(\eta ) = e^{-R( u)}\,f(u)$, we can summarize the above and write

$$\begin{aligned} \int \mathscr {M}_{m} (x,u)\, f(u)\,d\gamma _{\infty }(u)&\lesssim 2^{Cm}\, e^{-2\xi _1} \int _{{\mathscr {C}}_m^{\prime}} (\xi _1-\eta _1)^{(1-n)/2}\,g(\eta )\,d\eta . \end{aligned}$$

Hence, the set of points x where

$$\begin{aligned} \int \mathscr {M}_{m} (x,u)\, f(u)\,d\gamma _{\infty }(u) > \lambda \end{aligned}$$

(9.14)

is, after the change of coordinates, contained in the set of $\xi$ for which

$$\begin{aligned} e^{-2\xi _1} \int _{\begin{array}{c} \eta _1<\xi _1-1\\ |\xi^{\prime} -\eta^{\prime} |<C \sqrt{\xi _1-\eta _1} \end{array}} (\xi _1-\eta _1)^{{(1-n)}/{2}}\, g(\eta )\, d\eta \gtrsim 2^{-Cm}\, \lambda . \end{aligned}$$

(9.15)

The integral here fits with that in Proposition 9.7, except for the factor C in the domain of integration. This factor can easily be eliminated by means of a scaling of the variables $\eta^{\prime}$. Thus Proposition 9.7 tells us that the level set defined by (9.14) has $e^{2\xi _1}\,d\xi$ measure at most $C\,2^{Cm}\,\lambda ^{-1}\int g(\eta )\,d\eta$. If we go back to the x coordinates, (9.13) implies that the $d\gamma _\infty$ measure of the same set is at most

$$\begin{aligned} C\,2^{Cm}\,(\log \lambda )^{-n/2}\,\lambda ^{-1}\int g(\eta )\,d\eta . \end{aligned}$$

But

$$\begin{aligned} \int g(\eta )\,d\eta \simeq 2^{(1-n)m}\,(\log \lambda )^{n/2} \int f(u)\,d\gamma _\infty (u), \end{aligned}$$

again by (9.13). Lemma 9.6 now follows. $\square$

Lemmata 9.5 and 9.6 together imply Proposition 9.2 and also Proposition 9.1.

10 A counterexample for $|\alpha |>2$

We prove the “only if” part of Theorem 1.1. Thus assuming $|\alpha |>2$, we will disprove the weak type (1, 1) of the Riesz transform $R^{(\alpha )}$.

The off-diagonal kernel of $R^{(\alpha )}$ is

$$\begin{aligned} \mathscr {R}_{\alpha } (x,u) =\frac{1}{\Gamma (|\alpha |/2)} \int _0^{+\infty } t^{(|\alpha |-2)/2}\, D^{\alpha }_x\, K_t (x,u) \, dt, \end{aligned}$$

(10.1)

$K_t$ being the Mehler kernel as in (2.1).

Repeated application of (4.1) in Lemma 4.1 implies that the derivative $D^{\alpha }_x\, K_t (x,u)$ is a sum of products of the form $K_t (x,u)\,P(t,x,u)\,Q(t)$, where P(t, x, u) is a product of factors of type $P_j(t,x,u)$, and Q(t) is a product of factors of type $\Delta _{ ij} (t)$. Since $\Delta _{ ij} (t)$ does not depend on x, there will be nothing more. More precisely, consider a term in this sum where the derivatives falling on $K_t (x,u)$ are given by a multiindex $\kappa$, with $\kappa \le \alpha$ in the sense of componentwise inequalities. Then $|\alpha | - |\kappa |$ differentiations must fall on the $P_j(t,x,u)$ factors, and necessarily $|\alpha | - |\kappa | \le |\kappa |$. This tells us that Q(t) must consist of $|\alpha | - |\kappa |$ factors and also that P(t, x, u) consists of $N := |\kappa | - (|\alpha | - |\kappa |)$ factors. It follows that $|\alpha | - |\kappa | =(|\alpha | - N)/2$. Thus we get products

$$\begin{aligned} K_t (x,u)\,P^{(N)}(t,x,u)\,Q^{((|\alpha | - N)/2)}(t), \end{aligned}$$

(10.2)

where the superscripts indicate the number of factors. Since $|\kappa |$ can be any integer satisfying $|\alpha |/2 \le |\kappa | \le |\alpha |$, we see that N runs over the set of integers in $[0, |\alpha |]$ congruent with $|\alpha |$ modulo 2.

With $\eta >0$ large, define

$$\begin{aligned} u_0=Q_\infty (\eta , \ldots , \eta )\in \mathbb{R}^n, \end{aligned}$$

where we mean the product of the matrix $Q_\infty$ and $(\eta , \ldots , \eta )$ written as a column vector.

Our f will be $\delta _{u_0}$, and we will verify that the $L^{1,\infty }(\gamma _\infty )$ quasinorm of $R^{(\alpha )}\, f$ tends to $+\infty$ with $\eta$. Since $\delta _{u_0}$ can be approximated by $L^1$ functions in a standard way, this will disprove the weak type (1, 1) estimate for $R^{(\alpha )}$. We have

$$\begin{aligned}R^{(\alpha )}\, f (x) =R^{(\alpha )}\, \delta _{u_0} (x) = \mathscr {R}_{\alpha } (x,u_0).\end{aligned}$$

For reasons that will become clear below, we fix a number $t_0 \in (0,1/2)$, independent of $\eta$ and so small that

$$\begin{aligned} \left\langle (1, 1,\dots ,1),\, e^{t_0 B}\,e_j\right\rangle > 1/2, \qquad j = 1,\dots , n. \end{aligned}$$

(10.3)

Define $x_0 = D_{-t_0}\, u_0$. We are going to evaluate $R^{(\alpha )}\, \delta _{u_0} (x)$ when x is in the ball $B\left( x_0,\sqrt{t}_0\right)$. Then we will have $|x| \simeq |x_0| \simeq |u_0| \simeq \eta$.

From (2.10) we get an estimate of $K_t(x,u_0)$ for $0<t<1$. There we want the exponent $|u_0-D_t\, x|^2/t$ to stay bounded when $x \in B\left( x_0,\sqrt{t_0}\right)$ and t is close to $t_0$. Write

$$\begin{aligned} u_0-D_t \,x = u_0-D_t \,x_0 + D_t\, (x_0 - x) = u_0 -D_{t-t_0}\, u_0 + D_t\, (x_0 - x), \end{aligned}$$

which we must then make smaller than constant times $\sqrt{t} \simeq \sqrt{t_0}$. Here

$$\begin{aligned} |u_0 -D_{t-t_0}\, u_0| \simeq |t-t_0| \,|u_0|, \end{aligned}$$

because of Lemma 2.3. Thus we take t with $|t-t_0| < \sqrt{t_0} /|u_0|$, which implies $t \simeq t_0$ for large enough $\eta$. Further, $|D_t\, (x_0 - x)|\simeq |x_0-x| < \sqrt{t_0}$. Then $|u_0-D_t \,x | \lesssim \sqrt{t}$, and it follows that

$$\begin{aligned} K_t(x,u_0) \simeq {e^{R(x)}}\,{t_0^{-n/2}} \qquad \mathrm {if}\qquad x \in B\big (x_0,\sqrt{t_0}\big ) \qquad \mathrm {and}\qquad |t-t_0| < \sqrt{t_0} /|u_0|. \end{aligned}$$

(10.4)

Lemma 4.1 says that

$$\begin{aligned} P_j(t,x,u_0)= \left\langle Q_\infty ^{-1}x,e_j\right\rangle + { \left\langle Q_t^{-1} e^{tB}\, e_j \,,\, u_0-D_t\, x\right\rangle }. \end{aligned}$$

(10.5)

The first summand here is for $x \in B\big (x_0,\sqrt{t}_0\big )$

$$\begin{aligned} \left\langle Q_\infty^{-1}x,e_j\right\rangle &= \left\langle Q_\infty^{-1} D_{-t_0}\,u_0,e_j\right\rangle + \left\langle Q_\infty^{-1}(x-x_0), e_j\right\rangle\\ &= \left\langle e^{t_0 B^*} Q_\infty^{-1} u_0, e_j\right\rangle +\mathcal{O}(|x-x_0|) \\ &= \left\langle (\eta, \eta,\dots, \eta), e^{t_0B}\,e_j\right\rangle + \mathcal{O}(\sqrt {t_0}),\end{aligned}$$

for large $\eta$, by the definition of $u_0$. Because of (10.3), this leads to

$$\begin{aligned} \langle Q_\infty ^{-1}x,e_j\rangle \simeq \eta \simeq |x|, \end{aligned}$$

(10.6)

and we observe that $\langle Q_\infty ^{-1}x,e_j\rangle$ does not depend on t.

Next, we rewrite the product (10.2) by using (10.5) to expand the factor $P^{(N)}$. We will then get a sum of terms like (10.2) but where $P^{(N)}$ is replaced by a product of powers of the two summands in (10.5). For $N = |\alpha |$ one of the terms in this sum will be

$$\begin{aligned} K_t (x,u_0)\, \prod _{j=1}^n\, \left\langle Q_\infty ^{-1}x,e_j\right\rangle ^{\alpha _j} \gtrsim K_t (x,u_0)\,|x|^{|\alpha | }, \end{aligned}$$

(10.7)

the inequality coming from (10.6). Since $N = |\alpha |$, the corresponding factor $Q^{((|\alpha | - N)/2)}(t)$ is 1. The positive quantity in (10.7) will give the divergence we need for the counterexample. We have to estimate the absolute values of all the other terms.

To do so, let $t \in (0,1)$. For the second summand in (10.5), we have

$$\begin{aligned} \left| \left\langle Q_t^{-1} e^{tB}\, e_j \,,\, u_0-D_t\, x\right\rangle \right| \lesssim \frac{|u_0-D_t\, x|}{t} , \end{aligned}$$

and by (4.6)

$$\begin{aligned} |\Delta _{ ij} (t)| \lesssim 1/t. \end{aligned}$$

Thus each of the terms we must estimate is controlled by an expression of type

$$\begin{aligned} K_t (x,u_0)\, |x|^{N_1}\, \left( \frac{|u_0-D_t \,x|}{t}\right) ^{N_2}\, \frac{1}{t^{(|\alpha |-N_1-N_2)/2}}, \end{aligned}$$

(10.8)

where $N_1$ and $N_2$ are nonnegative integers satisfying $N_1 + N_2 = N \le |\alpha |$ and $N_1 \le |\alpha |-1$. If instead of $K_t (x,u_0)$ we plug in here the upper bound in (2.10) and reduce slightly the coefficient c in the exponential, we can replace each factor $|u_0-D_t\, x|/t$ in (10.8) by $1/\sqrt{t}$. The quantity (10.8) is thus less than constant times

$$\begin{aligned} { e^{R( x)}}\,{t^{-n/2}}\, \exp \left( -c\,\frac{|u_0-D_t \,x |^2}{t}\right) |x|^{N_1}\,\frac{1}{t^{(|\alpha |-N_1)/2}}. \end{aligned}$$

(10.9)

We are now ready to estimate the integral in (10.1), at first taken only over the interval (0, 1). Here $u=u_0$ and $x \in B\left( x_0,\sqrt{t}_0\right)$. The positive term described in (10.7) will, because of (10.4), give a contribution which is larger than a constant c times

$$\begin{aligned}&|x|^{ |\alpha |}\, \int _0^{1} t^{(|\alpha |-2)/2} K_t (x,u) \, dt \ge \, \, |x|^{ |\alpha |}\, \int _{|t-t_0| < \sqrt{t}_0 /|u_0|} t^{(|\alpha |-2)/2} K_t (x,u) \, dt\nonumber \\&\quad \gtrsim \, |x|^{ |\alpha |}\, \,{e^{R(x)}}\,{t_0^{-n/2}}\, t_0^{(|\alpha |-1)/2} \, |u_0|^{-1} \, \simeq \, e^{R(x)}\, |x|^{ |\alpha |-1}, \end{aligned}$$

(10.10)

since $t_0 \simeq 1$ is fixed.

Next, we consider the expression in (10.9). The corresponding part of the integral in (10.1) will be at most a constant C times

$$\begin{aligned} {e^{R(x)}}\,|x|^{ N_1}\, \int _0^{1} t^{(N_1 - n-2)/2}\, \exp \left( -c\,\frac{|u_0-D_t \, x |^2}{t}\right) \, dt, \end{aligned}$$

In order to estimate this integral, we write, recalling that $D_t\,{x_0}\, = D_{t-t_0}\,u_0$,

$$\begin{aligned} |u_0-D_t\, x | \ge |u_0-D_{t-t_0}\,u_0| - |D_t \,(x-x_0)|. \end{aligned}$$

The first summand here satisfies for $0<t<1$, in view of Lemma 2.3,

$$\begin{aligned} |u_0-D_{t-t_0}\,u_0| \simeq |t - t_0|\, |u_0|, \end{aligned}$$

and the second summand is controlled by $\sqrt{t}_0$. Thus if $|t - t_0| > C/|u_0|$ for some large C, we will have

$$\begin{aligned} |u_0-D_t\, x | \ge |t - t_0|\, |u_0| \simeq 1 + |t - t_0|\, |u_0|, \end{aligned}$$

so that

$$\begin{aligned} \frac{|u_0-D_t \,x |^2}{t} \gtrsim \frac{1}{t} + \frac{ |t - t_0|^2\, |u_0|^2}{t}. \end{aligned}$$

This implies that

$$\begin{aligned}&{e^{R(x)}}\,|x|^{ N_1}\, \int _{\begin{array}{c} |t - t_0| > C/|u_0|\\ 0<t<1 \end{array}} t^{(N_1 -n-2)/2}\, \exp \left( -c\,\frac{|u_0-D_t\, x |^2}{t}\right) \, dt\\&\quad \lesssim \, \, {e^{R(x)}}\,|x|^{ N_1}\, \int _0^1 t^{(N_1-n-2)/2}\,\exp \left( -\frac{c}{t}\right) \, \exp \left( -c\,\frac{ |t - t_0|^2\, |u_0|^2}{t}\right) \, dt\\&\quad \lesssim \, \,{e^{R(x)}}\,|x|^{ N_1}\,\int _\mathbb{R}\exp {( -c\,|t - t_0|^2\, |u_0|^2})\, dt\\&\quad \lesssim \,\,{e^{R(x)}}\,|x|^{ N_1}\,\frac{1}{|u_0|} \, \simeq \, {e^{R(x)}}\,|x|^{ N_1-1}. \end{aligned}$$

What remains is

$$\begin{aligned} {e^{R(x)}}&\,|x|^{ N_1}\, \int _{ |t - t_0| < C/|u_0|}\, t^{(N_1-n-2)/2}\, \exp \left( -c\,\frac{|u_0-D_t x |^2}{t}\right) \, dt\\ \lesssim \,&\, {e^{R(x)}}\,|x|^{ N_1}\, t_0^{(N_1 -n-2)/2}\,|u_0|^{-1} \, \simeq \, {e^{R(x)}}\,|x|^{ N_1-1}. \end{aligned}$$

Since $N_1 < |\alpha |$, the last expression is less than ${e^{R(x)}}\,|x|^{|\alpha |-2 }$, and we see that for large $\eta$ the positive expression in (10.10) dominates over the effects of the other terms.

We finally treat the integral over $t>1$. For $x \in B\left( x_0,\sqrt{t_0}\right)$ and $t>1$, (2.11), (4.5) and (4.6) imply the following three estimates

$$\begin{aligned}&K_t (x,u_0) \lesssim e^{R(x)} \exp \Big [ -\frac{1}{2} \left| D_{-t}\,u_0- x\right| _Q^2 \Big ], \\&|P_j (t,x,u_0)|\lesssim e^{-ct}\, | D_{-t} \, u_0-x| + |D_{-t} \, u_0| \end{aligned}$$

and

$$\begin{aligned} |\Delta _{ij} (t)| \lesssim {e^{-ct}}. \end{aligned}$$

We can delete the factor $| D_{-t}\, u_0-x|$ from the second of these formulas, if we reduce slightly the coefficient 1/2 in the first formula. Further,

$$\begin{aligned} | D_{-t} \, u_0-x| \ge |D_{t_0-t} \,x_0 - x_0|-|x_0-x|. \end{aligned}$$

(10.11)

An argument like (2.8) now leads to $|D_{t_0-t} \,x_0 - x_0| \gtrsim |x|$, because here $t_0-t < -1/2$ and so (2.5) implies that $|x_0|_Q^2 -|D_{t_0-t} \,x_0|_Q^2 \simeq |x_0|_Q^2$. Since $|x_0-x|$ is much smaller than |x|, we conclude from (10.11) that $| D_{-t} \, u_0-x| \simeq |x|$. Moreover, $| D_{-t}\, u_0| \lesssim e^{-ct}\, |u_0| \simeq e^{-ct}\, |x|$ by Lemma 2.1. Estimating the products in (10.2), we arrive at

$$\begin{aligned} |D^\alpha _x\, K_t(x,u_0)| \lesssim e^{R(x)}\, \exp {(-c\,|x|^2)}\, e^{-ct}\, |x|^C, \qquad t>1. \end{aligned}$$

Hence,

$$\begin{aligned} \int _1^\infty t^{(|\alpha |-2)/2}\, |D^\alpha K_t(x,u_0)|\, dt \lesssim e^{R(x)}, \end{aligned}$$

and this is much smaller than the quantity in (10.10).

Summing up, we get an estimate for the integral in (10.1) saying that

$$\begin{aligned} \mathscr {R}_{\alpha } (x,u_0) \gtrsim e^{R(x)}\, |x|^{ |\alpha |-1}, \qquad x \in B\big (x_0, \sqrt{t}_0\big ). \end{aligned}$$

Let $\lambda = e^{R(x_0)}\, |x_0|^{ |\alpha |-1}$. The ball $B\big (x_0, \sqrt{t}_0\big )$ contains the set

$$\begin{aligned} V_{x_0} = \{x = D_s \, {\tilde{x}}: R( {\tilde{x}}) = R(x_0), \; \; |{\tilde{x}}-x_0|< c,\; \; 0<s<c/|x_0|^2\} \end{aligned}$$

for some c. Then $e^{R(x)} \simeq e^{R(x_0)}$ in $V_{x_0}$ as follows from (2.7), and so $\mathscr {R}_{\alpha } (x,u_0) \gtrsim \lambda$ in $V_{x_0}$. From (2.13) we see that the measure of $V_{x_0}$ is

$$\begin{aligned} \gamma _\infty (V_{x_0}) =&\int _0^{c/|x_0|^2} \int _{|{\tilde{x}}-x_0| < c} e^{-R(D_s \, {\tilde{x}})}\, e^{-s{{\,\mathrm{tr}\,}}B}\, \frac{ |Q^{1/2}\, Q_\infty ^{-1} {\tilde{x}} |^2}{2\,| Q_\infty ^{-1} {\tilde{x}} |}\, dS_\beta ( {\tilde{x}})\,ds\,\\ \simeq&\, e^{-R(x_0)} \int _0^{c/|x_0|^2} |x_0|\,ds \,\simeq \, e^{-R(x_0)} \,|x_0|^{-1}. \end{aligned}$$

We find that

$$\begin{aligned} \lambda \, \gamma _\infty (V_{x_0}) \gtrsim |x_0|^{ |\alpha |-2}. \end{aligned}$$

Since $|\alpha | > 2$, this expression tends to $+\infty$ with $\eta$, and so does the $L^{1,\infty }(\gamma _\infty )$ quasinorm of $R^{(\alpha )}\, f$.

Theorem 1.1 is completely proved.