Abstract
We consider Anzellotti-type almost minimizers for the thin obstacle (or Signorini) problem with zero thin obstacle and establish their \(C^{1,\beta }\) regularity on the either side of the thin manifold, the optimal growth away from the free boundary, the \(C^{1,\gamma }\) regularity of the regular part of the free boundary, as well as a structural theorem for the singular set. The analysis of the free boundary is based on a successful adaptation of energy methods such as a one-parameter family of Weiss-type monotonicity formulas, Almgren-type frequency formula, and the epiperimetric and logarithmic epiperimetric inequalities for the solutions of the thin obstacle problem.
Similar content being viewed by others
Notes
This can be seen on the explicit example \(u(x)={\text {Re}}(x_1+i|x_n|)^{3/2}\), which is a solution of the obstacle problem with \(\psi =0\) on
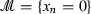 .
.Which follows from the inequality \( \int _{B_r(x_0)}|\nabla h|^2\le \int _{B_r(x_0)}|\nabla ( (1-\varepsilon )h+\varepsilon v)|^2\), \(\varepsilon \in (0,1)\) by a first variation argument.
We use the superscript A to distinguish this rescaling from the other rescalings, namely, homogeneous and almost homogeneous rescalings that we consider later.
References
Almgren, F.J., Jr.: Existence and regularity almost everywhere of solutions to elliptic variational problems with constraints. Mem. Am. Math. Soc. 4(165), viii+199 (1976). https://doi.org/10.1090/memo/0165
Almgren Jr., F.J.: Almgren’s big regularity paper, World Scientific Monograph Series in Mathematics, vol. 1, World Scientific Publishing Co., Inc., River Edge, NJ, (2000). Q-valued functions minimizing Dirichlet’s integral and the regularity of area-minimizing rectifiable currents up to codimension 2; With a preface by Jean E. Taylor and Vladimir Scheffer
Ambrosio, L.: Corso introduttivo alla teoria geometrica della misura ed alle superfici minime, Appunti dei Corsi Tenuti da Docenti della Scuola. [Notes of Courses Given by Teachers at the School], Scuola Normale Superiore, Pisa (1997) (Italian)
Anzellotti, G.: On the \(C^{1,\alpha }\)-regularity of \(\omega \)-minima of quadratic functionals. Boll. Un. Mat. Ital. C (6) 2(1), 195–212 (1983). (English, with Italian summary)
Athanasopoulos, I., Caffarelli, L.A.: Optimal regularity of lower dimensional obstacle problems, Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 310 (2004), no. Kraev. Zadachi Mat. Fiz. i Smezh. Vopr. Teor. Funkts. 35 [34], 49–66, 226, https://doi.org/10.1007/s10958-005-0496-1 (English, with English and Russian summaries); English transl., J. Math. Sci. (N.Y.) 132 (2006), no. 3, 274–284
Athanasopoulos, I., Caffarelli, L., Milakis, E.: On the regularity of the non-dynamic parabolic fractional obstacle problem. J. Differ. Equ. 265(6), 2614–2647 (2018). https://doi.org/10.1016/j.jde.2018.04.043
Athanasopoulos, I., Caffarelli, L.A., Salsa, S.: The structure of the free boundary for lower dimensional obstacle problems. Am. J. Math. 130(2), 485–498 (2008). https://doi.org/10.1353/ajm.2008.0016
Bombieri, E.: Regularity theory for almost minimal currents. Arch. Ration. Mech. Anal. 78(2), 99–130 (1982). https://doi.org/10.1007/BF00250836
Banerjee, A., Smit Vega Garcia, M., Zeller, A.K.: Higher regularity of the free boundary in the parabolic Signorini problem. Calc. Var. Partial Differ. Equ. 56(1), 7 (2017). https://doi.org/10.1007/s00526-016-1103-7
Caffarelli, L.A.: Further regularity for the Signorini problem. Comm. Partial Differ. Equ. 4(9), 1067–1075 (1979). https://doi.org/10.1080/03605307908820119
Caffarelli, L., Ros-Oton, X., Serra, J.: Obstacle problems for integro-differential operators: regularity of solutions and free boundaries. Invent. Math. 208(3), 1155–1211 (2017). https://doi.org/10.1007/s00222-016-0703-3
Caffarelli, L., Silvestre, L.: An extension problem related to the fractional Laplacian. Comm. Partial Differ. Equ. 32(7–9), 1245–1260 (2007). https://doi.org/10.1080/03605300600987306
Caffarelli, L.A., Salsa, S., Silvestre, L.: Regularity estimates for the solution and the free boundary of the obstacle problem for the fractional Laplacian. Invent. Math. 171(2), 425–461 (2008). https://doi.org/10.1007/s00222-007-0086-6
Colombo, M., Spolaor, L., Velichkov, B.: Direct epiperimetric inequalities for the thin obstacle problem and applications. Comm. Pure Appl. Math. 73(2), 384–420 (2020). https://doi.org/10.1002/cpa.21859
Danielli, D., Garofalo, N., Petrosyan, A., To, T.: Optimal regularity and the free boundary in the parabolic Signorini problem. Mem. Am. Math. Soc. 249, 1181 (2017). https://doi.org/10.1090/memo/1181
Danielli, D., Petrosyan, A., Pop, C.A.: Obstacle problems for nonlocal operators, New developments in the analysis of nonlocal operators. Contemp. Math. 723, 191–214 (2019). https://doi.org/10.1090/conm/723/14570
David, G., Engelstein, M., Toro, T.: Free boundary regularity for almost-minimizers. Adv. Math. 350, 1109–1192 (2019). https://doi.org/10.1016/j.aim.2019.04.059
David, G., Toro, T.: Regularity of almost minimizers with free boundary. Calc. Var. Partial Differ. Equ. 54(1), 455–524 (2015). https://doi.org/10.1007/s00526-014-0792-z
De Silva, D., Savin, O.: Boundary Harnack estimates in slit domains and applications to thin free boundary problems. Rev. Mat. Iberoam. 32(3), 891–912 (2016). https://doi.org/10.4171/RMI/902
De Silva, D., Savin, O.: Thin one-phase almost minimizers. Nonlinear Anal. 193, 111507 (2020). https://doi.org/10.1016/j.na.2019.04.006
De Silva, D., Savin, O.: Almost minimizers of the one-phase free boundary problem. Comm. Partial Differ. Equ. 45(8), 913–930 (2020). https://doi.org/10.1080/03605302.2020.1743718
de Queiroz, O.S., Tavares, L.S.: Almost minimizers for semilinear free boundary problems with variable coefficients. Math. Nachr. 291(10), 1486–1501 (2018). https://doi.org/10.1002/mana.201600103
Dolcini, A., Esposito, L., Fusco, N.: \(C^{0,\alpha }\) regularity of \(\omega \)-minima, language=English, with Italian summary. Boll. Un. Mat. Ital. A (7) 10(1), 113–125 (1996)
Duvaut, G., Lions, J.-L.: Inequalities in mechanics and physics. Springer-Verlag, Berlin-New York (1976). Translated from the French by C. W. John; Grundlehren der Mathematischen Wissenschaften, 219
Duzaar, F., Gastel, A., Grotowski, J.F.: Partial regularity for almost minimizers of quasi-convex integrals. SIAM J. Math. Anal. 32(3), 665–687 (2000). https://doi.org/10.1137/S0036141099374536
Esposito, L.: Leonetti, Francesco, Mingione, Giuseppe, Sharp regularity for functionals with \((p, q)\) growth. J. Differ. Equ. 204(1), 5–55 (2004). https://doi.org/10.1016/j.jde.2003.11.007
Esposito, L., Mingione, G.: A regularity theorem for \(\omega \)-minimizers of integral functionals, language=English, with English and Italian summaries. Rend. Mat. Appl. (7) 19(1), 17–44 (1999)
Fefferman, C.: Extension of \(C^{m,\omega }\)-smooth functions by linear operators. Rev. Mat. Iberoam. 25(1), 1–48 (2009). https://doi.org/10.4171/RMI/568
Focardi, M., Spadaro, E.: An epiperimetric inequality for the thin obstacle problem. Adv. Differ. Equ. 21(1–2), 153–200 (2016)
Focardi, M., Spadaro, E.: On the measure and the structure of the free boundary of the lower dimensional obstacle problem. Arch. Ration. Mech. Anal. 230(1), 125–184 (2018). https://doi.org/10.1007/s00205-018-1242-4
Focardi, M., Spadaro, E.: Correction to: on the measure and the structure of the free boundary of the lower dimensional obstacle problem. Arch. Ration. Mech. Anal. 230(2), 783–784 (2018). https://doi.org/10.1007/s00205-018-1273-x
Garofalo, N., Lin, F.-H.: Monotonicity properties of variational integrals, \(A_p\) weights and unique continuation. Indiana Univ. Math. J. 35(2), 245–268 (1986). https://doi.org/10.1512/iumj.1986.35.35015
Garofalo, N., Lin, F.-H.: Unique continuation for elliptic operators: a geometric-variational approach. Comm. Pure Appl. Math. 40(3), 347–366 (1987). https://doi.org/10.1002/cpa.3160400305
Garofalo, N., Petrosyan, A.: Some new monotonicity formulas and the singular set in the lower dimensional obstacle problem. Invent. Math. 177(2), 415–461 (2009). https://doi.org/10.1007/s00222-009-0188-4
Garofalo, N., Petrosyan, A., Smit Vega Garcia, M.: An epiperimetric inequality approach to the regularity of the free boundary in the Signorini problem with variable coefficients. J. Math. Pures Appl. (9) 105(6), 745–787 (2016). https://doi.org/10.1016/j.matpur.2015.11.013. (English, with English and French summaries)
Garofalo, N., Petrosyan, A., Pop, C.A., Smit Vega Garcia, M.: Regularity of the free boundary for the obstacle problem for the fractional Laplacian with drift. Ann. Inst. H. Poincaré Anal. Non Linéaire 34(3), 533–570 (2017). https://doi.org/10.1016/j.anihpc.2016.03.001
Garofalo, N., Smit Vega Garcia, M.: New monotonicity formulas and the optimal regularity in the Signorini problem with variable coefficients. Adv. Math. 262, 682–750 (2014). https://doi.org/10.1016/j.aim.2014.05.021
Giaquinta, M., Giusti, E.: On the regularity of the minima of variational integrals. Acta Math. 148, 31–46 (1982). https://doi.org/10.1007/BF02392725
Giaquinta, M., Giusti, E.: Quasiminima. Ann. Inst. H. Poincaré Anal. Non Linéaire 1(2), 79–107 (1984)
Giusti, E.: Direct Methods in the Calculus of Variations. World Scientific Publishing Co., Inc., River Edge, NJ (2003)
Han, Q., Lin, F.: Elliptic Partial Differential Equations, Courant Lecture Notes in Mathematics, 1, New York University, Courant Institute of Mathematical Sciences. New York. American Mathematical Society, Providence, RI (1997)
Jeon, S., Petrosyan, A.: Almost minimizers for certain fractional variational problems. Algebra i Analiz 32(4), 166–199 (2020)
Kinderlehrer, D.: The smoothness of the solution of the boundary obstacle problem. J. Math. Pures Appl. (9) 60(2), 193–212 (1981)
Koch, H., Petrosyan, A., Shi, W.: Higher regularity of the free boundary in the elliptic Signorini problem. Nonlinear Anal. 126, 3–44 (2015). https://doi.org/10.1016/j.na.2015.01.007
Koch, H., Rüland, A., Shi, W.: The variable coefficient thin obstacle problem: Carleman inequalities. Adv. Math. 301, 820–866 (2016). https://doi.org/10.1016/j.aim.2016.06.023
Koch, H., Rüland, A., Shi, W.: The variable coefficient thin obstacle problem: higher regularity. Adv. Differ. Equ. 22(11–12), 793–866 (2017)
Koch, H., Rüland, A., Shi, W.: The variable coefficient thin obstacle problem: optimal regularity and regularity of the regular free boundary. Ann. Inst. H. Poincaré Anal. Non Linéaire 34(4), 845–897 (2017). https://doi.org/10.1016/j.anihpc.2016.08.001
Mingione, G.: Regularity of minima: an invitation to the dark side of the calculus of variations. Appl. Math. 51(4), 355–426 (2006). https://doi.org/10.1007/s10778-006-0110-3
Petrosyan, A., Pop, C.A.: Optimal regularity of solutions to the obstacle problem for the fractional Laplacian with drift. J. Funct. Anal. 268(2), 417–472 (2015). https://doi.org/10.1016/j.jfa.2014.10.009
Petrosyan, A., Shahgholian, H., Uraltseva, N.: Regularity of Free Boundaries in Obstacle-type Problems, Graduate Studies in Mathematics, vol. 136. American Mathematical Society, Providence, RI (2012)
Petrosyan, A., Zeller, A.: Boundedness and continuity of the time derivative in the parabolic Signorini problem. Math. Res. Lett. 26(1), 281–292 (2019). https://doi.org/10.4310/MRL.2019.v26.n1.a13
Rüland, A., Shi, W.: Optimal regularity for the thin obstacle problem with \(C^{0,\alpha }\) coefficients. Calc. Var. Partial Differ. Equ. 56(5), 129 (2017). https://doi.org/10.1007/s00526-017-1230-9
Signorini, A.: Questioni di elasticità non linearizzata e semilinearizzata. Rend. Mat. e Appl. (5) 18, 95–139 (1959). (Italian)
Silvestre, L.: Regularity of the obstacle problem for a fractional power of the Laplace operator. Commun. Pure Appl. Math. 60(1), 67–112 (2007). https://doi.org/10.1002/cpa.20153
Ural’tseva, N.N.: Hölder continuity of gradients of solutions of parabolic equations with boundary conditions of Signorini type, language=Russian. Dokl. Akad. Nauk SSSR 280(3), 563–565 (1985)
Weiss, G.S.: Partial regularity for a minimum problem with free boundary. J. Geom. Anal. 9(2), 317–326 (1999). https://doi.org/10.1007/BF02921941
Weiss, G.S.: A homogeneity improvement approach to the obstacle problem. Invent. Math. 138(1), 23–50 (1999). https://doi.org/10.1007/s002220050340
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by L. Caffarelli.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A. Petrosyan supported in part by NSF Grant DMS-1800527.
Appendix A: Some examples of almost minimizers
Appendix A: Some examples of almost minimizers
Example A.1
If u is a minimizer of the functional
over the set  with strictly positive \(a\in C^{0,\alpha }({\overline{D}})\), \(0<\alpha \le 1\), then u is an almost minimizer for the Signorini problem with a gauge function \(\omega (r)=C r^\alpha \).
with strictly positive \(a\in C^{0,\alpha }({\overline{D}})\), \(0<\alpha \le 1\), then u is an almost minimizer for the Signorini problem with a gauge function \(\omega (r)=C r^\alpha \).
Proof
This is rather immediate. \(\square \)
Example A.2
Let u be a solution of the Signorini problem for the Laplacian with drift with the velocity field \(b\in L^p(B_1)\), \(p>n\):
even in \(x_n\)-variable. We understand this in the weak sense that u satisfies the variational inequality
for any competitor \(w\in {\mathfrak {K}}_{0,u}(B_1,B_1')\), i.e. \(w\in u+W^{1,2}_0(B_1)\) such that \(w\ge 0\) on \(B_1'\) in the sense of traces. Then u is an almost minimizer for the Signorini problem with \(\psi =0\) on  and a gauge function \(\omega (r)=Cr^{1-n/p}\).
and a gauge function \(\omega (r)=Cr^{1-n/p}\).
Proof
Let \(B_r(x_0)\Subset B_1\) and \(w\in {\mathfrak {K}}_{0,u}(B_r(x_0),B_1')\). Extending w as equal to u in \(B_1\setminus B_r(x_0)\), and applying the variational inequality for u, we obtain
Let v be the Signorini replacement of u on \(B_r(x_0)\). Then v satisfies the variational inequality
for all w as above. Now, taking \(w=u\pm (u-v)^+\) in (A.1) we will have
Next, taking \(w=v+(u-v)^+\) in (A.2), we have
Taking the difference, we then obtain
Similarly, taking \(w=v\pm (v-u)^+\) in (A.2) and \(w=u+(v-u)^+\) in (A.1) and subtracting the resulting inequalities, we obtain
Hence, combining the inequalities above, we arrive at
Then, applying Hölder’s inequality, we have for \(p>n\)
with \(p^*=2p/(p-2)\). Next, since \(v-u\in W^{1,2}_0(B_r(x_0))\), from the Sobolev’s inequality we have
and hence we can conclude that
with \(C=C_{n,p}\Vert b\Vert _{L^p(B_1)}^2\). This implies
where we have used Young’s inequality in the second line. Choosing \(\gamma =1-n/p\) we then deduce that for small enough \(0<r<r_0(n,p,\Vert b\Vert _{L^p(B_1)})\)
with \(C=C_{n,p}\Vert b\Vert _{L^p(B_1)}^2\). \(\square \)
Rights and permissions
About this article
Cite this article
Jeon, S., Petrosyan, A. Almost minimizers for the thin obstacle problem. Calc. Var. 60, 124 (2021). https://doi.org/10.1007/s00526-021-01986-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-021-01986-8



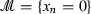 .
.