Brakke’s inequality for the thresholding scheme

Abstract

We continue our analysis of the thresholding scheme from the variational viewpoint and prove a conditional convergence result towards Brakke’s notion of mean curvature flow. Our proof is based on a localized version of the minimizing movements interpretation of Esedoğlu and the second author. We apply De Giorgi’s variational interpolation to the thresholding scheme and pass to the limit in the resulting energy-dissipation inequality. The result is conditional in the sense that we assume the time-integrated energies of the approximations to converge to those of the limit.

1 Introduction

The thresholding scheme is a time discretization for mean curvature flow. Its structural simplicity is intriguing to both applied and theoretical scientists. Merriman et al. [27] introduced the algorithm in 1992 to overcome the numerical difficulty of multiple scales in phase-field models. Their idea is based on an operator splitting for the Allen–Cahn equation, alternating between linear diffusion and thresholding. The latter replaces the fast reaction coming from the nonlinearity, i.e., the reaction-term, in the Allen–Cahn equation. We refer to Algorithm 1.1 below for a precise description of the scheme in the multi-phase setting. The convolution can be implemented efficiently on a uniform grid using the Fast Fourier Transform and the thresholding step is a simple pointwise operation. Because of its simplicity and efficiency, thresholding received a lot of attention in the last decades. Large-scale simulations [11,12,13] demonstrate the efficiency of a slight modification of the scheme. For applications in materials science and image segmentation it is desirable to design algorithms that are efficient enough to handle large numbers of phases but flexible enough to incorporate external forces, grain-dependent and even anisotropic surface energies. Not long ago, the natural extension to the multi-phase case [28] was generalized to arbitrary surface tensions by Esedoğlu and the second author [15]. In this paper, it was realized that thresholding preserves the gradient-flow structure of (multi-phase) mean-curvature flow in the sense that it can be viewed as a minimizing movements scheme for an energy that $\Gamma$-converges to the total interfacial area. This viewpoint allowed to incorporate a wide class of surface tensions including the well-known Read–Shockley formula for small-angle grain boundaries [31].

The development of thresholding schemes for anisotropic motions started with the work of Ishii et al. [19]. Efficient schemes were introduced by Bonnetier et al. [7], where the convolution kernels are explicit and well-behaved in Fourier space but not necessarily in real space. The recent work of Elsey and Esedoğlu [10] is inspired by the variational viewpoint [15] and shows that not all anisotropies can be obtained when structural features such as positivity of the kernel are required. However, variants of the scheme developed by Esedoğlu and Jacobs [14] share the same stability conditions even for more general kernels.

The rigorous asymptotic analysis of thresholding schemes started with the independent convergence proofs of Evans [16] and Barles and Georgelin [5] in the isotropic two-phase case. Since the scheme preserves the geometric comparison principle of mean curvature flow, they were able to prove convergence towards the viscosity solution of mean curvature flow. Recently, Swartz and Yip [32] proved convergence for a smooth evolution by establishing consistency and stability of the scheme, very much in the flavor of classical numerical analysis. They prove explicit bounds on the curvature and injectivity radius of the approximations and get a good understanding of the transition layer. However, also their result does not generalize to the multi-phase case immediately. In our previous work [22] we established the convergence of thresholding to a distributional formulation of multi-phase mean-curvature flow based on the assumption of convergence of the energies. In [25], Swartz and the first author applied these techniques to the case of volume-preserving mean-curvature flow and other variants.

Since the works [5, 16] are based on the comparison principle, the proofs do not apply in the multi-phase case. Our guiding principle in this work is instead the gradient-flow structure of (multi-phase) mean curvature flow. In general, a gradient-flow structure is given by an energy functional and a metric tensor, which endows the configuration space with a Riemannian structure that encodes the dissipation mechanism. A simple computation reveals this structure for mean curvature flow: If the hypersurface $\Sigma = \Sigma (t)$ evolves smoothly by its mean curvature (here and throughout we use the time scale such that $2V=H$) the change of area is given by

$$\begin{aligned} 2\frac{d}{dt} |\Sigma | = -\int _\Sigma 2V \cdot H = - \int _{\Sigma } |H|^2, \end{aligned}$$

(1)

where V denotes the normal velocity vector and H denotes the mean curvature vector of $\Sigma$. Although (1) does not characterize the mean curvature flow one can read off the metric tensor, the $L^2$-metric $\int _\Sigma |V|^2$ on the space of normal vector fields, when fixing the energy to be the surface area. However, some care needs to be taken when dealing with this metric as for example the geodesic distance vanishes identically [29]. The implicit time discretization developed by Almgren et al. [2] and Luckhaus and Sturzenhecker [26] makes use of this gradient-flow structure. In fact, it inspired De Giorgi to define a similar implicit time discretization for abstract gradient flows which he named “minimizing movements”. His abstract scheme consists of a family of minimization problems that mimic the principle of a gradient flow moving in direction of the steepest descent in an energy landscape. The configuration $\Sigma ^n$ at time step n is obtained from its predecessor $\Sigma ^{n-1}$ by minimizing $E(\Sigma ) + \frac{1}{2h}\hbox {dist}^2(\Sigma ,\Sigma ^{n-1}),$ where $\hbox {dist}$ denotes the geodesic distance induced by the Riemannian structure and $h>0$ denotes the time-step size. In the case of a Euclidean configuration space, the scheme boils down to the implicit Euler scheme. In its Riemannian version, it has been used for applications in partial differential equations and for instance allowed Jordan et al. [20] to interpret diffusion equations as gradient flows for the entropy w.r.t. the Wasserstein distance. In view of the degeneracy in the case of mean curvature flow it is evident that the scheme in [2, 26] uses a proxy for the geodesic distance. The replacement for the distance of two boundaries $\Sigma =\partial \Omega$ and $\tilde{\Sigma }=\partial \tilde{\Omega }$ is the (non-symmetric) quantity $4\int _{\Omega \Delta \tilde{\Omega }} d_{\tilde{\Omega }}\,dx$, where $d_{\tilde{\Omega }}$ denotes the (unsigned) distance to $\partial \tilde{\Omega }$. Chambolle [9] showed that the scheme [2, 26] which seems academic at a first glance can be implemented rather efficiently. Recently, Bellettini and Kholmatov [6] analyzed the scheme in the multi-phase case. However, neither a conditional convergence result to a distributional BV-solution, nor one to a Brakke flow are available yet.

Also Brakke’s pioneering work [8] is inspired by the gradient-flow structure of mean curvature flow. His definition is similar to the one of an abstract gradient flow and characterizes solutions by the optimal dissipation of energy. Brakke measures the dissipation of energy only in terms of the mean curvature. As (1) cannot characterize the solution, Brakke monitors localized versions of the surface area, which leads to a sensible notion of solution; we refer to Definition 2.1 for a precise definition in our context of sets of finite perimeter. Ilmanen [18] used a phase-field version of Huisken’s monotonicity formula [17] to prove the convergence of solutions to the scalar Allen–Cahn equation to Brakke’s mean curvature flow. Extending his proof to the multi-phase case is a challenging open problem. Only recently, Simon and the first author [24] proved a conditional convergence result for the vector-valued Allen–Cahn equation very much in the spirit of [22, 26]. However, an unconditional result is not yet available. Even the construction of non-trivial global solutions to multi-phase mean-curvature flow has only been achieved recently by Tonegawa and Kim [21].

In the present work we establish the convergence of the thresholding scheme to Brakke’s motion by mean curvature. As our previous result [22], also this one is only conditional in the sense that we assume the time-integrated energies to converge to those of the limit. Our proof is based on the observation that thresholding does not only have a global minimizing movements interpretation, but indeed solves a family of localized minimization problems. In Sect. 2 we state our main results, in particular Theorem 2.2. We use De Giorgi’s variational interpolation for these localized minimization problems to derive an exact energy-dissipation relation and pass to the limit in the inequality with help of our strengthened convergence. We first recall the known results from the abstract framework of gradient flows in metric spaces (cf. Chapter 3 in [4]). Then we pass to the limit $h\rightarrow 0$ in these terms with help of our strengthened convergence. It is worth pointing out that such a result is not known for the time discretization scheme [2, 26].

The starting point for our analysis of thresholding schemes is the minimizing movements interpretation of Esedoğlu and the second author [15]. Let us explain this interpretation with help of the example of the two-phase scheme. The combination $\chi ^n = \mathbf {1}_{\{ G_h*\chi ^{n-1} > \frac{1}{2}\}}$ of convolution and thresholding is equivalent to minimizing $E_h(\chi ) + \frac{1}{2h} \mathrm{d}_h^2(\chi ,\chi ^{n-1}),$ where $E_h$ is an approximation of the perimeter functional and $\mathrm{d}_h$ is a metric. The latter serves as a proxy for the induced distance, just like $4 \int _{\Omega \Delta \Omega ^{n-1}} d_{\Omega ^{n-1}} dx$ in the minimizing movements scheme of Almgren et al. [2], and Luckhaus and Sturzenhecker [26]. The $\Gamma$-convergence of similar functionals has been developed some time ago by Alberti and Bellettini [1] and more recently by Ambrosio et al. [3], and was proven for the functionals $E_h$ by Miranda et al. [30]. Esedoğlu and the second author found a simpler proof in the case of the energies $E_h$, which extends to the multi-phase case.

Let us recall the thresholding scheme and the basic notation.

Algorithm 1.1

Given the partition $\Omega _1^{n-1},\ldots ,\Omega _P^{n-1}$ at time $t=(n-1)h$, obtain the partition $\Omega _1^{n},\ldots ,\Omega _P^{n}$ at time $t=nh$ by the following two operations:

• 1. Convolution step: $\phi _i := G_h*\left( \sum _{j\ne i}\sigma _{ij} \mathbf {1}_{\Omega _j^{n-1}} \right) .$

• 2. Thresholding step: $\Omega _i^n := \left\{ \phi _i < \phi _j \text { for all } j\ne i\right\} .$

Here and throughout the paper

$$\begin{aligned} G_h(z) := \frac{1}{(2\pi h)^{d/2}} \exp \left( -\frac{|z|^2}{2h}\right) \end{aligned}$$

denotes the centered Gaussian of variance h, which we also think of as the heat kernel at time $\frac{h}{2}$. We assume the matrix of surface tensions $\sigma = (\sigma _{ij})_{i,j}$ to satisfy the obvious relations

$$\begin{aligned} \sigma _{ij} = \sigma _{ji} >0\quad \text {for}\quad i\ne j,\quad \sigma _{ii}=0 \end{aligned}$$

and the usual (strict) triangle inequality

$$\begin{aligned} \sigma _{ij} < \sigma _{ik}+\sigma _{kj}\quad \text {for all pairwise different}~i,j,k. \end{aligned}$$

Furthermore, we ask the matrix $\sigma$ to be conditionally negative definite

$$\begin{aligned} \sigma <0 \quad \text {as a bilinear form on}~ \left( 1,\ldots ,1\right) ^\perp . \end{aligned}$$

(2)

This condition can be simply spelled out as $\xi \cdot \sigma \xi \le -\underline{\sigma } |\xi |^2$ for all $\xi \in \mathbb {R}^P$ such that $\sum _{i=1}^P \xi _i=0$, where $\underline{\sigma }>0$ is a positive constant. The condition was introduced by Esedoğlu and the second author [15] and guarantees the dissipation of energy. Indeed, the conditional negativity (2) ensures that

$$\begin{aligned} \left| \xi \right| _\sigma ^2 := - \xi \cdot \sigma \xi = -\sum _{i,j} \sigma _{ij} \xi _i \xi _j, \quad \text {for}\quad \xi \in \mathbb {R}^P\quad \text {s.t.}~\sum _i \xi _i=0 \end{aligned}$$

defines a norm $\left| \mathop {\cdot } \right| _\sigma$ on the space $(1,\ldots ,1)^\perp$. In the isotropic case $\sigma _{ij}=1-\delta _{ij}$, a direct computation shows $|\xi |_\sigma = |\xi |$. For convenience we will work with periodic boundary conditions, i.e., on the flat torus ${[0,\Lambda )^d}$. We write $\int dx$ short for $\int _{{[0,\Lambda )^d}}dx$ and $\int dz$ short for $\int _{\mathbb {R}^d} dz$. Furthermore, $\chi ^n$ given by $\chi _i^n:= \mathbf {1}_{\Omega ^n}$, $i=1,\ldots ,P$, denotes the vector of characteristic functions of the phases $\Omega _i^n$ at time step n and we denote its piecewise constant interpolation by

$$\begin{aligned} \chi ^h(t) := \chi ^n = \left( \mathbf {1}_{\Omega _1^n},\ldots , \mathbf {1}_{\Omega _P^n} \right) \quad \text {for}\quad t\in [nh,(n+1)h). \end{aligned}$$

However, we will mostly use a nonlinear interpolation which will be introduced later. Selim Esedoğlu and the second author [15] showed that thresholding preserves the gradient-flow structure of (multi-phase) mean curvature flow in the sense that it can be viewed as a minimizing movements scheme

$$\begin{aligned} \chi ^n = \arg \min _u \left\{ E_h(u) + \frac{1}{2h} \mathrm{d}_h^2(u, \chi ^{n-1})\right\} , \end{aligned}$$

(3)

where the minimum runs over all measurable $u :{[0,\Lambda )^d}\rightarrow \mathbb {R}^P$ such that $0\le u_i\le 1$, $i=1,\ldots ,P$ and $\sum _i u_i = 1$ a.e. Here the dissipation functional

$$\begin{aligned} \frac{1}{2h}\mathrm{d}^2_h(u,\chi ):= & {} \frac{1}{\sqrt{h}}\int \left| G_{h/2}*\left( u-\chi \right) \right| _\sigma ^2 dx\nonumber \\= & {} -\frac{1}{\sqrt{h}}\int G_{h/2}*\left( u-\chi \right) \cdot \sigma \,G_{h/2}*\left( u-\chi \right) dx \end{aligned}$$

(4)

is, because of (2), the square of a metric and the energy

$$\begin{aligned} E_h(u) := \frac{1}{\sqrt{h}}\int u \cdot \sigma \, G_h*u \,dx \end{aligned}$$

(5)

is an approximation of the total interfacial area. Indeed, this functional $\Gamma$-converges to the energy

$$\begin{aligned} E(\chi ) := c_0 \sum _{i,j} \sigma _{ij} \int \frac{1}{2} \left( \left| \nabla \chi _i\right| +\left| \nabla \chi _j\right| -\left| \nabla (\chi _i+\chi _j)\right| \right) , \end{aligned}$$

defined for partitions $\chi :{[0,\Lambda )^d}\rightarrow \{0,1\}^P$ s.t. $\sum _i \chi _i =1$. Writing $\Omega _i = \{\chi _i=1\}$ and $\partial ^*\Omega _i$ for the reduced boundary of $\Omega _i$, the term

$$\begin{aligned} \int \frac{1}{2} \left( \left| \nabla \chi _i\right| +\left| \nabla \chi _j\right| -\left| \nabla (\chi _i+\chi _j)\right| \right) = \mathscr {H}^{d-1}(\partial ^*\Omega _i \cap \partial ^*\Omega _j) \end{aligned}$$

is the measure of the interface between Phases i and j, so that the energy E is indeed the total interfacial area

$$\begin{aligned} E(\chi ) =c_0 \sum _{i,j} \sigma _{ij} \mathscr {H}^{d-1}(\partial ^*\Omega _i \cap \partial ^*\Omega _j). \end{aligned}$$

The constant $c_0$ is given by the first moment of G, i.e.,

$$\begin{aligned} c_0 = \int _0^\infty \left| z\right| G(z) \,dz= \frac{1}{\sqrt{2\pi }}. \end{aligned}$$

An immediate consequence of the minimizing movements structure (3) of the scheme is the basic a priori estimate

$$\begin{aligned} \sup _N \left( E_h(\chi ^N) + h\sum _{n=1}^N\frac{\mathrm{d}_h^2(\chi ^n,\chi ^{n-1})}{2h^2} \right) \le E_0, \end{aligned}$$

(6)

which is however not sharp by a factor of 2. The above mentioned $\Gamma$-convergence is an immediate consequence of the pointwise convergence of these functionals and the monotonicity property

$$\begin{aligned} E_{N^2h}(u) \le E_h(u) \quad \text {for all}\quad u :{[0,\Lambda )^d}\rightarrow [0,1]^P \text { s.t.}~\sum _{i=1}^P u_i =1, h>0,\quad \text {and}\quad N\in \mathbb {N}, \end{aligned}$$

(7)

see [15, Lemma A.2].

We write $A \lesssim B$ to express that $A\le C B$ for a generic constant $C<\infty$ that only depends on the dimension d, on the size $\Lambda$ of the domain, and the matrix $\sigma$ of surface tensions. By $A=O(B)$ we mean the quantitative $|A|\lesssim B$ while $A=o(B)$ as $h\rightarrow 0$ means the qualitative $\frac{A}{B} \rightarrow 0$ as $h\rightarrow 0$.

2 Brakke’s inequality and main result

The main statement of this work is Theorem 2.2 below. Assuming there was no drop of energy as $h\rightarrow 0$, i.e.,

$$\begin{aligned} \int _0^T E_h(\chi ^h)\, dt \rightarrow \int _0^T E(\chi )\,dt, \end{aligned}$$

(8)

it states that the limit of the approximate solutions satisfies a BV-version of Brakke’s inequality [8].

Brakke’s inequality is a weak formulation of motion by mean curvature $2V=H$ and is motivated by the following characterization of the normal velocity. Given a smoothly evolving hypersurface $\partial \Omega (t)=\Sigma (t)$ with normal velocity vector V we have

$$\begin{aligned} \frac{d}{dt} \int _{\Sigma } \zeta = \int _\Sigma \left( -\zeta \, H \cdot V + V \cdot \nabla \zeta + \partial _t \zeta \right) \end{aligned}$$

(9)

for any smooth test function $\zeta \ge 0$. The converse is also true: Given a normal vector field $V:\Sigma \rightarrow \mathbb {R}^d$ such that (9) holds for any such test function $\zeta \ge 0$ then V is the normal velocity of $\Sigma$. In the pioneering work [8], Brakke uses this idea for his definition of the equation $2V=H$ to extend the concept of motion by mean curvature to general varifolds. We recall his definition in our more restrictive setting of finite perimeter sets, which in the smooth two-phase case simplifies to the inequality

$$\begin{aligned} 2 \frac{d}{dt} \int _{\Sigma } \zeta \le \int _\Sigma \left( -\zeta \, |H|^2 +H\cdot \nabla \zeta + 2\partial _t \zeta \right) . \end{aligned}$$

(10)

Definition 2.1

We say that the time-dependent partition $\chi :(0,T) \times {[0,\Lambda )^d}\rightarrow \{0,1\}^P \in BV$ with $\sum _i \chi _i =1$ a.e. moves by mean curvature with initial data $\chi ^0 :{[0,\Lambda )^d}\rightarrow \{0,1\}^P \in BV$ with $\sum _i \chi ^0_i =1$ a.e. if there exists a $\sum _{i,j}\sigma _{ij} \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) dt$-measurable normal vector field $H:(0,T)\times {[0,\Lambda )^d}\rightarrow \mathbb {R}^d$ with

$$\begin{aligned} \sum _{i,j} \sigma _{ij}\int _0^T\int |H|^2 \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) dt< \infty , \end{aligned}$$

which is the mean curvature vector of the partition in the sense that for all test vector fields $\xi \in C_c^\infty ((0,T)\times {[0,\Lambda )^d},\mathbb {R}^d)$

$$\begin{aligned} \sum _{i,j} \sigma _{ij}\int _0^T \int \left( \nabla \cdot \xi - \nu _i \cdot \nabla \xi \, \nu _i \right) \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) dt\nonumber \\ \quad = -\sum _{i,j} \sigma _{ij}\int _0^T\int H\cdot \xi \,\frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) dt, \end{aligned}$$

(11)

such that for any test function $\zeta \in C^\infty ([0,T]\times {[0,\Lambda )^d})$ with $\zeta \ge 0$ and $\zeta (\,\cdot \,,T)=0$ we have

$$\begin{aligned}&- 2\sum _{i,j} \sigma _{ij} \int \zeta (\,\cdot \,,0)\frac{1}{2}\left( \left| \nabla \chi _i^0\right| +\left| \nabla \chi _j^0\right| - \left| \nabla \left( \chi _i^0+\chi _j^0\right) \right| \right) \nonumber \\&\quad \le \sum _{i,j} \sigma _{ij}\int _0^T \int \left( - \zeta \, |H|^2 + H\cdot \nabla \zeta + 2\partial _t \zeta \right) \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) dt\nonumber \\ \end{aligned}$$

(12)

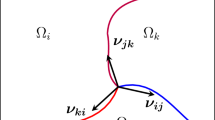
Here and throughout, $\nu _i$ denotes the measure theoretic normal of Phase i characterized by the equation $\nabla \chi _i = \nu _i \left| \nabla \chi _i\right|$.

Equation (11) encodes not only that H is the mean curvature vector along the smooth part of the surface cluster but furthermore enforces the Herring angle condition along triple junctions, which comes from the integration by parts rule for smooth hypersurfaces $\Sigma$ with boundary $\Gamma$:

$$\begin{aligned} \int _\Sigma \left( \nabla \cdot \xi -\nu \cdot \nabla \xi \, \nu \right) = \int _\Gamma \xi \cdot b - \int _\Sigma H\cdot \xi , \end{aligned}$$

where b denotes its conormal.

Equation (12) does not only encode the mean curvature flow equation via the optimal dissipation of energy but also the initial data $\chi ^0$ in a weak sense.

Theorem 2.2

(Brakke’s inequality) Given initial data $\chi ^0 :{[0,\Lambda )^d}\rightarrow \{0,1\}^P$ with $E(\chi ^0)< \infty$ and a finite time horizon $T<\infty$, for any sequence there exists a subsequence $h\downarrow 0$ such that the approximate solutions given by Algorithm 1.1 converge to a limit $\chi :(0,T)\times {[0,\Lambda )^d}\rightarrow \{0,1\}^P$ in $L^1$ and a.e. in space-time. Given the convergence assumption (8), $\chi$ evolves by mean curvature in the sense of Definition 2.1.

Remark 2.3

Let us comment on the result.

• (i) Given initial conditions $\chi ^0$ with $E(\chi ^0)<\infty$ the compactness in [22, Proposition 2.1] yields a subsequence such that $\chi ^h\rightarrow \chi$ in $L^1$ and a.e. for a partition $\chi$ with $\mathrm{ess\,sup}_t E(\chi (t)) \le E(\chi ^0)$.

• (ii) Theorem 2.2 is similar to our result in [22]. There we proved the convergence of thresholding towards a distributional formulation of (multi-phase) mean-curvature flow, the same notion as in [26]. Under the same assumption (8) as in the present work, for any $i=1,\ldots ,P$ we constructed a $|\nabla \chi _i|\,dt$-measurable function $\tilde{V}_i:(0,T) \times {[0,\Lambda )^d}\rightarrow \mathbb {R}$ with

  $$\begin{aligned} \int _0^T\int \tilde{V}_i^2 \left| \nabla \chi _i \right| dt < \infty , \end{aligned}$$

  which is the (scalar) normal velocity of the i-th phase in the sense that

  $$\begin{aligned} \int _0^T \int \partial _t \zeta \, \chi _i \, dx\,dt + \int \zeta (\,\cdot \,, 0)\, \chi _i^0 \,dx= - \int _0^T \int \zeta \, \tilde{V}_i \left| \nabla \chi _i\right| dt \end{aligned}$$

  for all $\zeta \in C^\infty ([0,T]\times {[0,\Lambda )^d})$ with $\zeta (\,\cdot \,,T)=0$, such that

  $$\begin{aligned} \sum _{i,j} \sigma _{ij}\int _0^T \int \left( \nabla \cdot \xi -\nu _i \cdot \nabla \xi \, \nu _i - 2\, \xi \cdot \nu _i \, \tilde{V}_i \right) \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) dt=0 \end{aligned}$$

  (13)

  for all $\xi \in C_0^\infty ((0,T)\times {[0,\Lambda )^d},\mathbb {R}^d)$. Without any regularity assumption, none of the two formulations is stronger in the sense that it implies the other. In case of a smooth evolution, either of the weak formulations implies the motion law in the classical sense and hence the other weak formulation. Nevertheless (13) requires more regularity as it is formulated for sets of finite perimeter, whereas Brakke’s inequality naturally extends to general varifolds. Finally, we note that our proof here is much softer than the result (13) proved in our earlier work [22]. In general, it is conceptually easier to derive Brakke’s inequality than the distributional formulation under the same assumptions.

Remark 2.4

We point out that under conditions as in Theorem 2.2 and similar methods we can derive yet another weak formulation of mean curvature flow, namely the optimal dissipation relation

$$\begin{aligned}&2\big ( E(\chi (T))-E(\chi (0)\big ) \nonumber \\&\quad \le \int _0^T -\frac{1}{2} \sum _{i,j} \sigma _{ij}\int \left( |H|^2 +|2V|^2 \right) \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) dt. \end{aligned}$$

(14)

We do so in a separate, self-contained way in [23]. Let us present a short alternative proof, which is however not as elementary; here will use one of the main results of our earlier work [22], cf. (15). Let us stress that for the proof of our theorem, however, we do not use this result.

Let us briefly explain how one can obtain the optimal dissipation relation (14), which is more in the spirit of De Giorgi’s abstract framework rather than Brakke’s weak solutions to mean curvature flow. We recommend the reader to at least take a glance at the outline of our proof of Brakke’s inequality in Sect. 3 before reading the following proof.

There are two main differences to the proof presented in the sequel. On the first sight (14) is easier to derive because it involves no localization. However, the metric term $\int |2V|^2 \left| \nabla \chi \right|$ is more difficult to understand than the term $\int |H|^2 \left| \nabla \chi \right|$ and (14) seems to rely more heavily on the convergence assumption (8). In fact, a term similar to this one caused the main difficulty in our earlier work [22]. There we proved that under the assumption of the convergence of the energies (8), what we will later call the first variation of the metric, converges:

$$\begin{aligned}&\lim _{h\rightarrow 0} \int _0^T \delta \Big (\frac{1}{2h} \mathrm{d}_h^2(\,\cdot \,,\chi ^{h}(t))\Big ) (\chi ^h(t+h),\xi ) \,dt \nonumber \\&\quad = \lim _{h\rightarrow 0} \int _0^T \int G_{h/2}*\frac{\chi ^h(t+h)-\chi ^h(t)}{h} \cdot \sigma \left( \sqrt{h}\, \xi \cdot \nabla \right) G_{h/2}*\chi ^h(t+h)\,dx\,dt\nonumber \\&\quad =- c_0 \int _0^T\sum _{i,j} \sigma _{ij} \int \xi \cdot \nu _i \, 2\tilde{V}_i \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) dt, \end{aligned}$$

(15)

where $\tilde{V}_i$ is the scalar normal velocity given by $\partial _t \chi _i = \tilde{V}_i \left| \nabla \chi _i\right| dt$. Indeed, (15) follows from [22, Prop. 4.1] followed by a localization argument and an application of De Giorgi’s Structure Result, which we presented there in the proof of Theorem 1.3, cf. [22, pp. 65–67].

In order to deduce (14) from (15)—as in our proof of Brakke’s inequality—we apply De Giorgi’s variational interpolations. Here we only need to consider the global minimization problem (3) and obtain similarly to Corollary 3.2 that

$$\begin{aligned} E_h(\chi ^h(T))+ \int _0^T \left( \frac{\mathrm{d}_h^2(\chi ^h(t+h),\chi ^h(t))}{2h^2} + \frac{1}{2} \big | \partial E_h \big |^2(u^h(t)) \right) \,dt \le E_h(\chi ^0), \end{aligned}$$

(16)

from which we want to deduce the optimal dissipation relation

$$\begin{aligned}&E(\chi (T)) + \frac{1}{2} \int _0^T \frac{c_0}{2} \sum _{i,j} \sigma _{ij} \int \left( |2V|^2 + |H|^2 \right) \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) dt\\&\quad \le E(\chi ^0), \end{aligned}$$

where we define $V=\tilde{V}_i \nu _i (=\tilde{V}_j \nu _j)$ on $\mathop {spt }\big ( \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) dt\big )$. The two inequalities are in the same form and the first left-hand side term as well as the right-hand side term converge because of (8). The $\liminf$-inequality

$$\begin{aligned} \int _0^T \frac{c_0}{2}\sum _{i,j} \sigma _{ij} \int |H|^2 \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) dt\\ \quad \le \liminf _{h\rightarrow 0} \int _0^T \big | \partial E_h \big |^2(u^h(t))\,dt \end{aligned}$$

for the local slope of $E_h$ will be derived in the present work, cf. Step 2 of the proof of Theorem 2.2, while the $\liminf$-inequality for the metric term

$$\begin{aligned} \int _0^T \frac{c_0}{2}\sum _{i,j} \sigma _{ij} \int |2V|^2 \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) dt \nonumber \\ \quad \le \liminf _{h\rightarrow 0} \int _0^T \frac{\mathrm{d}_h^2(\chi ^h(t+h),\chi ^h(t))}{h^2} \,dt \end{aligned}$$

(17)

can be derived as follows: By duality we have the general inequality

$$\begin{aligned} \frac{\mathrm{d}_h^2(u,\chi )}{2}&= \sqrt{h}\int \left| G_{h/2}*(u-\chi ) \right| _\sigma ^2 dx\nonumber \\&\ge \sup _{\xi } \Bigg ( 2 \sqrt{h}\int G_{h/2}*(u-\chi ) \cdot \sigma \left( \left( h\,\xi \cdot \nabla \right) G_{h/2}*u \right) dx\nonumber \\&\qquad \qquad \qquad - \sqrt{h}\int \left| \left( h\,\xi \cdot \nabla \right) G_{h/2}*u\right| _\sigma ^2dx \Bigg ), \end{aligned}$$

(18)

where the supremum runs over all smooth test vector fields $\xi$. Applied to $u=\chi ^h(t+h)$, $\chi =\chi ^h(t)$, divided by $h^2$ and integrated in time, this gives us a lower bound on the right-hand side of (17) and we only need to understand the limits of the two terms coming from the right-hand side of (18). This is precisely achieved by (15) and (36) in Lemma 3.6 below and we obtain

$$\begin{aligned}&\liminf _{h\rightarrow 0} \int _0^T \frac{\mathrm{d}_h^2(\chi ^h(t+h),\chi ^h(t))}{2h^2} \,dt\\&\quad \ge c_0 \int _0^T \sum _{ij} \sigma _{ij}\int \left( \left( \xi \cdot \nu _i \right) 2\tilde{V}_i - (\xi \cdot \nu _i )^2\right) \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) dt \end{aligned}$$

for all $\xi \in C_0^\infty ((0,T)\times {[0,\Lambda )^d},\mathbb {R}^d)$. Finally, taking the supremum over all such test vector fields $\xi$, we obtain (17).

3 De Giorgi’s variational interpolation and idea of proof

It is a well-appreciated fact that a classical gradient flow $\dot{u}(t) = - \nabla E(u(t))$ of a smooth energy functional E on a Riemannian manifold can be characterized by the optimal rate of dissipation of the energy E along the solution u:

$$\begin{aligned} \frac{d}{dt} E(u(t)) \le -\frac{1}{2} |\dot{u}(t)|^2 - \frac{1}{2} |\nabla E(u(t))|^2. \end{aligned}$$

(19)

This is the guiding principle in generalizing gradient flows to metric spaces where one replaces $|\dot{u}|$ by the metric derivative and $|\nabla E(u)|$ by some upper gradient, e.g. the local slope $|\partial E(u)|$, see (25) for a definition in our context.

As discussed in the introduction, mean curvature flow can be viewed as a gradient flow in the sense that for a smooth evolution $\Sigma =\Sigma (t)$ the energy, which in this case is the surface area $|\Sigma (t)|$, satisfies the inequality

$$\begin{aligned} 2 \frac{d}{dt} |\Sigma | = -\int _\Sigma 2V \cdot H \le -\frac{1}{2} \int _\Sigma |H|^2 - \frac{1}{2} \int _\Sigma |2V|^2, \end{aligned}$$

cf. Remark 2.3(ii). While in the abstract framework, the dissipation of the energy is measured w.r.t. both terms $|\dot{u}|^2 \hat{=} \int _\Sigma |2V|^2$ and $|\partial E(u)|^2 \hat{=} \int _\Sigma |H|^2$, Brakke measures the rate only in terms of the local slope $\int _\Sigma |H|^2$ but asks for the localized version (12), which due to (9) in the simple setting of a single surface evolving smoothly by its mean curvature is precisely (10) with equality.

The basis of this work is an approximate version of Brakke’s inequality, see Corollary 3.2 below. In view of the minimizing movements interpretation (3) it is feasible to obtain at least the global inequality

$$\begin{aligned} 2 \frac{d}{dt} |\Sigma | \le -\int _\Sigma |H|^2 \end{aligned}$$

using De Giorgi’s variational interpolation, but the localized inequality (12) would be still out of reach. The following lemma states that thresholding does not only solve the global minimization problem (3) but a whole family of local minimization problems, which will allow us to establish the family of localized inequalities (12).

Lemma 3.1

(Local minimality) Let $\chi ^n$ be obtained from $\chi ^{n-1}$ by one iteration of Algorithm 1.1 and $\zeta \ge 0$ an arbitrary test function. Then

$$\begin{aligned} \chi ^n = \arg \min _u \left\{ E_h(u,\chi ^{n-1};\zeta ) + \frac{1}{2h} \mathrm{d}_h^2(u,\chi ^{n-1};\zeta )\right\} , \end{aligned}$$

(20)

where the minimum runs over all $u:{[0,\Lambda )^d}\rightarrow [0,1]^P$ with $\sum _i u_i =1$ a.e. By $\mathrm{d}_h(u,\chi ;\zeta )$ we denote the localization of the metric $\mathrm{d}_h(u,\chi )$ given by

$$\begin{aligned} \frac{1}{2h} \mathrm{d}_h^2(u,\chi ;\zeta )&:= \frac{1}{\sqrt{h}}\int \zeta \left| G_{h/2} *\left( u-\chi \right) \right| ^2_\sigma dx, \end{aligned}$$

(21)

which is again a (semi-)metric on the space of all such u’s as above and in particular satisfies the triangle inequality. By $E_h(u,\chi ;\zeta )$ we denote the localized (approximate) energy incorporating the localization error in both energy and metric:

$$\begin{aligned} E_h(u,\chi ;\zeta ):= & {} \frac{1}{\sqrt{h}}\int \zeta \,u \cdot \sigma \,G_h*u\, dx + \frac{1}{\sqrt{h}}\int \left( u-\chi \right) \cdot \sigma \left[ \zeta ,G_h*\right] \chi \, dx\nonumber \\&- \frac{1}{\sqrt{h}}\int \left( u-\chi \right) \cdot \sigma \left[ \zeta ,G_{h/2}*\right] G_{h/2}*\left( u- \chi \right) dx. \end{aligned}$$

(22)

Here and throughout the paper

$$\begin{aligned} \left[ \zeta ,G_h*\right] u := \zeta \, G_h*u - G_h*\left( \zeta \,u\right) \approx -\nabla \zeta \cdot h\nabla G_h*u \end{aligned}$$

denotes the commutator of the multiplication with the (smooth) function $\zeta$ and the convolution with the kernel $G_h$, both of which act componentwise on the vector u.

Let us briefly comment on the structure of the localized energy $E_h$. First, by definition of $E_h$ we have

so that in particular we recover the minimizing movements interpretation (3) in the case $\zeta \equiv 1$. Second, with the localization $\zeta$, the first integral in the definition of $E_h$ is an approximation of the localized total interfacial energy $c_0 \sum _{i,j} \sigma _{ij}\int _{\Sigma _{ij}} \zeta$. We will see shortly that the second term gives rise to the transport term in Brakke’s inequality, while the last term, the commutator arising from the metric term, will be shown to be negligible in the limit $h\rightarrow 0$ for all quantities under consideration here.

Thanks to the local minimization property (20) of the thresholding scheme we can apply the abstract framework of De Giorgi, cf. Chapters 1–3 in [4], to this localized setting. As for any minimizing movements scheme, the comparison of $\chi ^n$ to the previous time step $\chi ^{n-1}$ in the minimization problem (20) yields an energy-dissipation inequality, cf. (6) above, which serves well as an a priori estimate, but which fails to be sharp by a factor of 2. To obtain a sharp inequality we follow the ideas of De Giorgi. We introduce his variational interpolation $u^h$ of $\chi ^n$ and $\chi ^{n-1}$: For $t\in (0,h]$ and $n\in \mathbb {N}$ we let

$$\begin{aligned} u^h( (n-1)h + t) := \arg \min _u \left\{ E_h(u,\chi ^{n-1};\zeta ) + \frac{1}{2t} \mathrm{d}_h^2(u,\chi ^{n-1};\zeta )\right\} . \end{aligned}$$

(23)

Note that a minimizer $u^h$ is not necessarily unique, but the functional value of $u^h(t)$ will vary continuously in t. Comparing $u^h(t)$ with $u^h(t+\delta t)$ in this minimization problem and taking the limit $\delta t \rightarrow 0$ while keeping h fixed, one obtains the sharp energy-dissipation inequality along this interpolation, the following approximate version of Brakke’s inequality (12).

It is worth pointing out that opposed to the special case $t=h$, we do not have an explicit formula for the interpolations $u^h$, and there is no guarantee for $u^h_i \in \{0,1\}$; indeed we expect that generically $u^h_i \in (0,1)$.

Corollary 3.2

(Approximate Brakke inequality) For any test function $\zeta \ge 0$, a time-step size $h>0$ and any $T=Nh$ we have

$$\begin{aligned}&E_h(\chi ^h(T),\chi ^h(T);\zeta )\nonumber \\&\quad + \int _0^T \Big (\frac{1}{2}\big | \partial E_h(\,\cdot \,, \chi ^{h}(t);\zeta ) \big |^2(\chi ^h(t+h)) + \frac{1}{2} \big | \partial E_h(\,\cdot \,, \chi ^h(t);\zeta ) \big |^2(u^h(t)) \Big )\,dt\nonumber \\&\quad + \int _0^T \frac{1}{h} \Big ( E_h(\chi ^h(t+h),\chi ^{h}(t);\zeta )-E_h(\chi ^h(t+h),\chi ^h(t+h);\zeta ) \Big ) \,dt \le E_h(\chi ^0,\chi ^0;\zeta ), \end{aligned}$$

(24)

where $\left| \partial E_h(\,\cdot \,,\chi ;\zeta ) \right| (u)$ is the “local slope” of $E_h(\,\cdot \,,\chi ;\zeta )$ at u defined by

$$\begin{aligned} \left| \partial E_h(\,\cdot \,,\chi ;\zeta ) \right| (u) := \limsup _{v\rightarrow u} \frac{\left( E_h(u,\chi ;\zeta ) - E_h(v,\chi ;\zeta )\right) _+}{\mathrm{d}_h(u,v;\zeta )}. \end{aligned}$$

(25)

The convergence $v\rightarrow u$ is in the sense of the metric $\mathrm{d}_h$.

Our goal is to derive Brakke’s inequality, which for a time-independent test function $\zeta =\zeta (x)$, and in the simpler two-phase case, reads

$$\begin{aligned} \int \zeta \left| \nabla \chi (T) \right| + \frac{1}{2} \int _0^{T} \int \zeta \, |H|^2 \left| \nabla \chi \right| dt -\frac{1}{2} \int _0^{T} \int H\cdot \nabla \zeta \left| \nabla \chi \right| dt \le \int \zeta \left| \nabla \chi (0) \right| \end{aligned}$$

(26)

from its approximate version (24), i.e., we want to relate the limits of the expressions in (24) to the terms appearing in (26). Recall that we work on the time scale such that $2V=H$, which causes the factor $\frac{1}{2}$ appearing in front of the shrinkage- and transport-terms.

While Corollary 3.2 is a mere application of the abstract theory in [4], we will now use the particular character of thresholding, i.e., the structure of the energy (22) and the metric term (21) in order to pass to the limit in the approximate Brakke inequality (24).

In order to obtain the $\liminf$-inequality for the local slope, which in the two-phase case reads

$$\begin{aligned} \frac{c_0}{2} \int _0^T \int \zeta |H|^2 \left| \nabla \chi \right| dt \le \liminf _{h\rightarrow 0}\frac{1}{2} \int _0^T\big | \partial E_h(\,\cdot \,, \chi ^h;\zeta ) \big |^2(u^h)\,dt, \end{aligned}$$

we need to estimate the local slope (25) from below. We will do so by probing the definition of the local slope with inner variations $u_s$ given by the transport equation

$$\begin{aligned} \partial _s u_s + \left( \xi \cdot \nabla \right) u_s = 0 \quad u_s|_{s=0}=u. \end{aligned}$$

(27)

As $s\rightarrow 0$, the numerator converges to the inner variation of $E_h$ given by

$$\begin{aligned} \delta E_h(\,\cdot \,, \chi ;\zeta )(u,\xi ) := \frac{d}{ds}\Big |_{s=0} E_h(u_s,\chi ;\zeta ) \end{aligned}$$

(28)

and the denominator yields the infinitesimal metric, i.e., the metric tensor. In the simpler two-phase case we simply obtain

$$\begin{aligned} \big | \partial E_h(\,\cdot \,, \chi ;\zeta ) \big |(u) \ge \frac{\delta E_h(\,\cdot \,,\chi ;\zeta )(u,\xi )}{\sqrt{2 \sqrt{h}\int \zeta \left( G_{h/2}*(\xi \cdot \nabla u) \right) ^2 dx}}. \end{aligned}$$

(29)

Then we will find that the localization $\zeta$ acts trivially on the numerator: As $h\rightarrow 0$, the first variation of the localized energy $\delta E_h(\,\cdot \,,\chi ;\zeta )(u,\xi )$ behaves like the first variation of the global energy in direction of the localized vector field $\zeta \xi$, i.e., $\delta E_h(\,\cdot \,)(u,\zeta \xi )$. This is consistent with the obvious fact that the localization acts trivially on the first variation of the total interfacial area.

Lemma 3.3

For any $u,\chi :{[0,\Lambda )^d}\rightarrow [0,1]^P$ with $\sum _i u_i=\sum _i \chi _i =1$ a.e. we have

$$\begin{aligned} \big | \delta E_h(\,\cdot \,,\chi ;\zeta )(u,\xi )-\delta E_h(\,\cdot \,)(u,\zeta \xi ) \big | \lesssim _{\zeta ,\xi } h^{1/4} \frac{\mathrm{d}_h(u,\chi )}{h}, \end{aligned}$$

where the implicit constant depends on the test fields $\zeta$ and $\xi$.

Note that the right-hand side can be controlled in our application after integration in time via the basic a priori estimate (6), or the corresponding estimate (37) below for the variational interpolations, respectively.

Taking the limit $h\rightarrow 0$, we will make use of our strengthened convergence in the form of Lemma 3.6 below for both terms, the numerator and the denominator. Then taking the supremum over all vector fields $\xi$ we obtain the $\liminf$-inequality

$$\begin{aligned} \frac{c_0}{2} \int _0^T \int \zeta H^2 \left| \nabla \chi \right| dt \le \liminf _{h\rightarrow 0}\frac{1}{2} \int _0^T\big | \partial E_h(\,\cdot \,, \chi ^h;\zeta ) \big |^2(u^h)\,dt. \end{aligned}$$

In the absence of the localization, i.e., if the test function $\zeta$ is constant, the last left-hand side term $h\sum _{n=1}^N \frac{1}{h}\left( E_h(\chi ^n,\chi ^{n-1};\zeta )-E_h(\chi ^n,\chi ^n;\zeta ) \right)$ in (24) vanishes. However, for a non-constant test function we have to pass to the limit in this extra term. Let us again restrict ourselves to the two-phase case for the following short discussion to see that formally, the behavior of this term is obvious. Expanding $\zeta$ (and ignoring the commutator in the metric term for a moment), the leading-order term of the increments on the left-hand side of (24) as $h\rightarrow 0$ is

$$\begin{aligned} \frac{1}{h}\left( E_h(\chi ^n,\chi ^{n-1};\zeta )-E_h(\chi ^n,\chi ^{n};\zeta )\right)\approx & {} \int \frac{\chi ^n-\chi ^{n-1}}{h} \frac{1}{\sqrt{h}}\left[ \zeta ,G_h*\right] (1-\chi ^{n-1})\, dx\nonumber \\\approx & {} \int \frac{\chi ^n-\chi ^{n-1}}{h} \,\nabla \zeta \cdot \sqrt{h}\nabla G_h *\chi ^{n-1}\, dx, \end{aligned}$$

(30)

which at least formally (and after integration in time) converges to $-c_0\int _0^T\int _\Sigma V \cdot \nabla \zeta$. Hence we expect to recover the transport term $-\frac{c_0}{2}\int _0^T\int _\Sigma H \cdot \nabla \zeta$ in Brakke’s inequality (12) by using the equation $2V=H$ once. The following lemma is the basis of the rigorous argument for this statement and applied to $u=\chi ^n$ and $\chi =\chi ^{n-1}$ allows us to replace the increments by the first variation of the metric term.

Lemma 3.4

For any $u,\chi :{[0,\Lambda )^d}\rightarrow [0,1]^P$ with $\sum _i u_i=\sum _i \chi _i =1$ a.e. we have

$$\begin{aligned}&\left| \frac{1}{h}\left( E_h(u,\chi ;\zeta )-E_h(u,u;\zeta )\right) + \frac{1}{2} \delta \left( \frac{1}{2h} \mathrm{d}_h^2(\,\cdot \,,\chi )\right) (u,\nabla \zeta ) \right| \\&\qquad \lesssim _{\zeta } h^{1/4} \frac{\mathrm{d}_h(u,\chi )}{h} + h\frac{\mathrm{d}_h^2(u,\chi )}{h^2} + h^{1/4} \left( E_h(u) + E_h(\chi ) \right) ^{1/2}, \end{aligned}$$

where the implicit constant in $\lesssim _{\zeta }$ depends on the test field $\zeta$.

Here again, in our application the right-hand side is indeed of lower order after integration in time by the simple a priori estimate (6). In the proof of the theorem we will apply the Euler–Lagrange equation

$$\begin{aligned} \delta \left( \frac{1}{2h} \mathrm{d}_h^2(\,\cdot \,,\chi )\right) (u,\xi ) =-\delta E_h(u,\xi ) \end{aligned}$$

(31)

of the global minimizing movements principle (3) to replace the first variation of the metric term by the first variation of the energy and finally use our strengthened convergence (8) in form of Lemma 3.6 to obtain the transport term as the tangential divergence of the gradient field $\nabla \zeta$, which in the simpler two-phase case reads

$$\begin{aligned} \frac{c_0}{2} \int _0^T \int \nabla ^2 \zeta :\left( Id-\nu \otimes \nu \right) \left| \nabla \chi \right| dt. \end{aligned}$$

We stress that we only use the convergence assumption (8) in order to guarantee that the two measures generated by the energy density $\frac{1}{\sqrt{h}}\left( 1-\chi ^h\right) G_h*\chi ^h$ and the measure generated by the trace of the second derivatives $\frac{1}{\sqrt{h}}\left( 1-\chi ^h\right) h \Delta G_h*\chi ^h$ agree. The following statement from [22] provides this identification under the convergence of the energies.

Proposition 3.5

(Lemma 2.8 and Proposition 3.5 in [22]) Given $u^h\rightarrow \chi$ and $E_h(u^h) \rightarrow E(\chi )$, for any test function $\zeta \in C^\infty ({[0,\Lambda )^d})$ it holds

$$\begin{aligned} \frac{1}{\sqrt{h}}\int \zeta \,u^h \cdot \sigma \, G_h *u^h \, dx \rightarrow c_0 \sum _{i,j} \sigma _{ij} \int \zeta \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) , \end{aligned}$$

(32)

and for any test matrix field $A \in C^\infty ({[0,\Lambda )^d},\mathbb {R}^{d\times d})$ we have

$$\begin{aligned}&\sum _{i,j} \sigma _{ij} \frac{1}{\sqrt{h}}\int A :u_i^h\, h\nabla ^2 G_h *u_j^h \, dx\nonumber \\&\quad \rightarrow c_0 \sum _{i,j} \sigma _{ij} \int \nu _i \cdot A \nu _i \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) . \end{aligned}$$

(33)

Let us point out the two consequences of Proposition 3.5, namely the convergence of the first variation of the energy and the infinitesimal metric, i.e., the metric tensor:

Lemma 3.6

Given $u:{[0,\Lambda )^d}\rightarrow [0,1]^P$ with $\sum _i u_i =1$ a.e. we have

$$\begin{aligned} \Big | \delta E_h(u,\xi ) - \frac{1}{\sqrt{h}}\int \nabla \xi \,:u\cdot \sigma \left( G_h \, Id - h \nabla ^2 G_h \right) *u \,dx\Big | \lesssim \sqrt{h}\Vert \nabla ^2 \xi \Vert _\infty E_h(u). \end{aligned}$$

(34)

In particular, if $u^h\rightarrow \chi$ in $L^1$ and $E_h(u^h) \rightarrow E(\chi )<\infty$, then

$$\begin{aligned} \lim _{h\rightarrow 0} \delta E_h(u^h,\xi )= & {} \delta E(\chi ,\xi )\nonumber \\= & {} c_0 \sum _{i,j} \sigma _{ij} \int \nabla \xi :(Id-\nu \otimes \nu ) \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) \nonumber \\ \end{aligned}$$

(35)

and

$$\begin{aligned}&\lim _{h\rightarrow 0} \sqrt{h}\int \zeta \left| G_{h/2} *\left( \left( \xi \cdot \nabla \right) u^h\right) \right| _\sigma ^2 dx\nonumber \\&\quad = c_0 \sum _{i,j} \sigma _{ij} \int \zeta \left( \xi \cdot \nu _i\right) ^2 \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) . \end{aligned}$$

(36)

The following quantitative closeness of the approximations to the piecewise constant interpolations in our metric $\mathrm{d}_h$, and the qualitative closeness measured in $L^1$ and measured in terms of their energies follows very easily.

Lemma 3.7

Given initial conditions $\chi ^0:{[0,\Lambda )^d}\rightarrow \{0,1\}^P$ with $\sum _i \chi ^0_i =1$ a.e. and finite energy $E_0:=E(\chi ^0)<\infty$, a time-step size $h>0$ and a finite time horizon $T=Nh$, if the test function $\zeta$ is strictly positive, then for the interpolation (23) we have

$$\begin{aligned} \limsup _{h\downarrow 0} \left( \sup _t E_h(u^h(t)) + \int _0^T \frac{\mathrm{d}_h^2(u^h(t),\chi ^{h}(t))}{2 h^2} dt \right) <\infty . \end{aligned}$$

(37)

Additionally, the interpolations $u^h$ converge to the same limit:

$$\begin{aligned} \lim _{h\rightarrow 0} u^h = \lim _{h\rightarrow 0} \chi ^h =\chi \quad \text {in }L^1. \end{aligned}$$

(38)

Moreover, if the energies of the piecewise constant interpolations converge, then so do those of the variational interpolations: Given the convergence assumption (8), we have

$$\begin{aligned} \int _0^T E_h(u^h)\,dt \rightarrow \int _0^T E(\chi )\,dt. \end{aligned}$$

(39)

4 Proofs

We first present the proofs of Lemma 3.1 and Corollary 3.2 which form the basis of our analysis. Then we turn to the problem specific statements which form the basis of the proof of Theorem 2.2. Finally we prove Theorem 2.2.

Proof of Lemma 3.1

Given initial conditions $\chi \in \{0,1\}^P$ with $\sum _i \chi _i =1$ and a time-step size $h>0$, one iteration of the thresholding scheme yields $\chi ^1_i = \mathbf {1}_{\{(\sigma G_h*\chi )_i = \min _j (\sigma G_h*\chi )_j\}}.$ Then $\chi ^1$ clearly minimizes

$$\begin{aligned} 2 u \cdot \sigma \, G_h*\chi \end{aligned}$$

among all $u\in [0,1]^P$ s.t. $\sum _{i} u_i =1$. This expression is equal to

$$\begin{aligned}&u \cdot \sigma \, G_h*u - (u-\chi ) \cdot \sigma \,G_h*(u -\chi ) + u\cdot \sigma \, G_h *\chi - \chi \cdot \sigma \, G_h *u +\chi \cdot \sigma \,G_h*\chi \\&\quad = u \cdot \sigma \, G_h*u - (u-\chi ) \cdot \sigma \,G_h*(u -\chi ) + (u-\chi )\cdot \sigma \, G_h *\chi - \chi \cdot \sigma \, G_h *(u-\chi )\\&\qquad \qquad \qquad \qquad \qquad \qquad \quad +\chi \cdot \sigma \,G_h*\chi , \end{aligned}$$

where the last right-hand side term is independent of u and thus irrelevant for the minimization. Multiplying with $\zeta \ge 0$ and integrating shows that $\chi ^1$ minimizes

$$\begin{aligned} \int \!\zeta \left[ u\cdot \sigma \,G_h*u - \left( u - \chi \right) \cdot \sigma \, G_h*\left( u -\chi \right) +(u-\chi ) \cdot \sigma \, G_h*\chi -\chi \cdot \sigma \, G_h*\left( u-\chi \right) \right] dx \\ \quad + \text {const.} \end{aligned}$$

Dividing by $\sqrt{h}$, recalling the definitions (21) and (22) of the localized distance and energy, and using the semi-group and symmetry properties of the kernel and the symmetry of $\sigma$ yield (20). $\square$

Corollary 3.2 is an immediate consequence of interpreting our problem from the point of view of gradient flows in metric spaces:

Given $\chi$ and $\zeta$, the Moreau–Yosida approximation $e_{h,t}$ of $E_h$ is defined by

$$\begin{aligned} e_{h,t}(\chi ;\zeta ) := \min _{u} \left\{ E_h(u,\chi ;\zeta ) + \frac{1}{2t} \mathrm{d}_h^2(u,\chi ;\zeta )\right\} \end{aligned}$$

and furthermore we recall the (not necessarily unique) variational interpolation $u^h(t)$ of $\chi$ and $\chi ^1:=u^h(h)$, cf. (23).

As t decreases we have a stronger penalization and thus we expect $u^h(t)$ to be “closer” to $\chi =u^h(0)$ than $\chi ^1=u^h(h)$ which justifies the name “interpolation”. Note that $E_h(u,\chi ;\zeta )$ and $\mathrm{d}_h(u,\chi ;\zeta )$ are, because of the smoothing property of the kernel $G_h$, weakly continuous in u and $\chi$.

The following general theorem monitors the evolution of the (approximate) energy along the interpolation $u^h(t)$ in terms of the distances at different time instances measured by the metric $\mathrm{d}_h$, and gives a lower bound in terms of the local slope $|\partial E_h|$ of $E_h$, cf. (25).

Because of the localization, our energy (22) depends on the configuration at the previous time step. However, we can apply the abstract framework (cf. Chapter 3 of [4]) to this case if we only follow one time step. Both h and $\zeta$ are fixed parameters when applying these results.

Theorem 4.1

(Theorem 3.1.4 and Lemma 3.1.3 in [4]) For every $\chi :{[0,\Lambda )^d}\rightarrow \{0,1\}^P$ with $\sum _i \chi _i =1$ a.e. we have

$$\begin{aligned}&\frac{t}{2} \left| \partial E_h(\,\cdot \,,\chi ;\zeta )\right| ^2 (u^h(t)) + \frac{1}{2} \int _0^t \left| \partial E_h(\,\cdot \,,\chi ;\zeta )\right| ^2(u^h(s))\, ds \nonumber \\&\quad \le \frac{1}{2t} \mathrm{d}_h^2(u^h(t),\chi ;\zeta ) + \int _0^t \frac{\mathrm{d}_h^2(u^h(s),\chi ;\zeta )}{2 s^2} ds = E_h(\chi ,\chi ;\zeta ) - E_h(u^h(t),\chi ;\zeta ). \end{aligned}$$

(40)

The idea behind Theorem 4.1 is rather simple: By testing the minimality of $u^h(t)$ against $u^h(s)$ and taking $s\uparrow t$ (and similarly with reversed roles for $s\downarrow t$) one obtains $\frac{d}{dt} e_{h,t}(\chi ;\zeta ) = - \frac{\mathrm{d}_h^2(u^h(t),\chi ;\zeta )}{2 t^2}$. Integrating this equation from $t=0$ to $t=h$ yields the equality between the energy difference and the metric term in (40). The first inequality between the local slope and the metric term comes from the general estimate $\left| \partial E_h(\,\cdot \,,\chi ;\zeta )\right| (u^h(t)) \le \frac{\mathrm{d}_h(u^h(t),\chi ;\zeta )}{t}$, which follows from the definition of the local slope and the triangle inequality.

Proof of Corollary 3.2

We apply (40) in Theorem 4.1 with $\chi =\chi ^{n-1}$ and $t=h$, and sum over $n=1,\ldots ,N$. $\square$

Now we turn to the more problem-specific statements, which use the special character of thresholding. Before giving the proofs of these statements, let us collect some useful basic facts on thresholding, the proofs of which we will present for the convenience of the reader.

Lemma 4.2

For any $h>0$ and $u,v:{[0,\Lambda )^d}\rightarrow [0,1]^P$ with $\sum _i u_i =\sum _i v_i =1$ the following statements hold.

• (i) The energy controls the BV-seminorm of the convolutions:

  $$\begin{aligned} \int \left| \nabla G_{h/2}*u\right| dx \lesssim E_h(u). \end{aligned}$$

• (ii) The energy controls the $L^1$-distance of u and its convolution:

  $$\begin{aligned} \int \left| G_h *u - u\right| dx \lesssim \sqrt{h}E_h(u). \end{aligned}$$

• (iii) The $L^2$-distance of u and v is controlled by a combination of their distance in our metric and their energies:

  $$\begin{aligned} \int \left| u-v\right| ^2dx \lesssim \frac{1}{\sqrt{h}} \mathrm{d}_h^2(u,v) + \sqrt{h}\left( E_h(u)+E_h(v)\right) . \end{aligned}$$

• (iv) For fixed $h>0$, the energy is Lipschitz continuous w.r.t. our metric:

  $$\begin{aligned} \left| E_h(u)-E_h(v) \right| ^2 \lesssim \frac{1}{\sqrt{h}} \frac{1}{2h}\mathrm{d}_h^2 (u,v). \end{aligned}$$

Proof of Lemma 4.2

Argument for (i). By $\int \nabla G(z)\,dz=0$ we obtain

$$\begin{aligned} \int \left| \nabla G_{h/2}*u\right| dx&=\int \bigg | \int \nabla G_{h/2}(z) \left( u(x)-u (x-z)\right) dz \bigg |dx\\&\le \iint |\nabla G_{h/2}(z)| \left| u(x)-u (x-z)\right| dz \,dx \end{aligned}$$

and by the pointwise estimates $|\nabla G_{h/2}(z)| \lesssim \frac{1}{\sqrt{h}}G_h(z)$ and

$$\begin{aligned} \left| u_i(x-z) -u_i(x)\right| \le (1-u_i)(x) \, u_i(x-z) + u_i(x)\,(1-u_i)(x-z), \end{aligned}$$

(41)

which because of $u_i\in [0,1]$ holds for any component of u, this yields indeed

$$\begin{aligned} \int \left| \nabla G_{h/2}*u_i\right| dx \lesssim \frac{2}{\sqrt{h}}\int (1-u_i) \, G_h*u_i\,dx \le \frac{1}{\min _{i\ne j} \sigma _{ij}} E_h(u^h). \end{aligned}$$

Argument for (ii). We simply observe that for all $i=1,\ldots ,P$

Argument for (iii). Since u and v are uniformly bounded

$$\begin{aligned} \int \left| u-v\right| ^2dx&= \int \big ((u-v)\cdot G_h*(u-v) -(u-v)\cdot (G_h*u - u) \\&\quad - (u-v) \cdot G_h*v-v)\big )\, dx\\&\lesssim \int (u-v)\cdot G_h*(u-v)\,dx + \int \left| G_h*u - u\right| \,dx + \int \left| G_h*v - v\right| \,dx\\&\lesssim \sqrt{h}\frac{1}{2h} \mathrm{d}_h^2(u,v) +\sqrt{h}E_h(u)+\sqrt{h}E_h(v), \end{aligned}$$

where in the last step we used that $\sigma$ is negative definite on $(1,\ldots ,1)^\perp$ and defines a norm on that space which is of course equivalent to the Euclidean norm, and for the last two terms we used Lemma 4.2, (ii).

Argument for (iv). Using the semigroup and symmetry properties of the kernel and the boundedness of u and v we obtain

$$\begin{aligned} E_h(u)-E_h(v)&= \frac{1}{\sqrt{h}}\int \left( G_{h/2} *u\cdot \sigma \, G_{h/2}*( u-v) + G_{h/2} *(u-v) \cdot \sigma \, G_{h/2}*v\right) dx\\&\lesssim \frac{1}{\sqrt{h}}\int \left| G_{h/2}*(u-v) \right| _\sigma dx \lesssim \frac{1}{\sqrt{h}}\left( \int \left| G_{h/2}*(u-v) \right| ^2_\sigma dx \right) ^{1/2}\\&= \left( \frac{1}{\sqrt{h}}\frac{1}{2h} \mathrm{d}_h^2(u,v)\right) ^{1/2}, \end{aligned}$$

which, since we may interchange the roles of u and v, concludes the proof. $\square$

Proof of Lemma 3.3

Step 1: We have the identity

$$\begin{aligned} \delta E_h(\,\cdot \, , \chi ; \zeta ) (u,\xi ) - \delta E_h( u,\zeta \, \xi ) = -\frac{2}{\sqrt{h}}\int G_{h/2}*\left( u-\chi \right) \cdot \sigma \, \left[ \zeta ,G_{h/2}*\right] \left( \left( \xi \cdot \nabla \right) u \right) dx. \end{aligned}$$

Indeed, using (27) we may compute the first variation of the localized energy $E_h(u,\chi ;\zeta )$, cf. (22):

$$\begin{aligned} \delta E_h(\,\cdot \, , \chi ; \zeta ) (u,\xi )&=\frac{d}{ds}\Big |_{s=0}E_h (u_s,\chi ;\zeta ) \nonumber \\&= \frac{1}{\sqrt{h}}\! \int \!\!- \zeta \left( \xi \cdot \nabla \right) u \cdot \sigma \, G_h*u - \zeta \, u\cdot \sigma \, G_h *\left( \left( \xi \cdot \nabla \right) u\right) \nonumber \\&\quad - \left( \xi \cdot \nabla \right) u \cdot \sigma \left[ \zeta , G_h*\right] u + \left( \xi \cdot \nabla \right) u \cdot \sigma \left[ \zeta ,G_h*\right] \left( u-\chi \right) \nonumber \\&\quad + \left( \xi \cdot \nabla \right) u \left[ \zeta , G_{h/2}*\right] \! G_{h/2} *( u-\chi ) - \left( \xi \cdot \nabla \right) u \cdot \sigma \,G_{h/2} \nonumber \\&\quad *\!\left[ \zeta , G_{h/2}*\right] \! \left( u-\chi \right) dx. \end{aligned}$$

(42)

The fourth term in the sum comes from replacing $\chi$ by u in the third term, while for the last term we used the antisymmetry $\int u \left[ \zeta , G_{h/2}*\right] v \,dx= - \int v \left[ \zeta , G_{h/2}*\right] u \,dx$ (and the symmetry of $\sigma$). Note that due to the symmetry of G and $\sigma$ there is a cancellation between the second and third term in this sum:

$$\begin{aligned} \int - \zeta \,u \cdot \sigma \, G_h *\left( \left( \xi \cdot \nabla \right) u\right) - \left( \xi \cdot \nabla \right) u \cdot \sigma \left[ \zeta , G_h*\right] u\, dx&= \int -\zeta \left( \xi \cdot \nabla \right) u \cdot \sigma \, G_h*u\, dx\\&=\int - u \cdot \sigma \,G_h*\left( \zeta \left( \xi \cdot \nabla \right) u \right) dx. \end{aligned}$$

A direct computation based on the semi-group property $G_h = G_{h/2}*G_{h/2}$ yields

$$\begin{aligned} \left[ \zeta , G_h*\right] v +\left[ \zeta , G_{h/2}*\right] G_{h/2}*v - G_{h/2}*\left[ \zeta , G_{h/2}*\right] v = 2 \left[ \zeta , G_{h/2}*\right] G_{h/2}*v \end{aligned}$$

(43)

so that the last three terms in the first variation of $E_h$ above can be combined using once more the antisymmetry of the commutator, and we get

$$\begin{aligned} \delta E_h(\,\cdot \, , \chi ; \zeta ) (u,\xi )&=\frac{1}{\sqrt{h}}\int - \zeta \left( \xi \cdot \nabla \right) u\cdot \sigma \, G_h*u - u\cdot \sigma \,G_h*\left( \zeta \left( \xi \cdot \nabla \right) u \right) dx\nonumber \\&\quad -\frac{2}{\sqrt{h}}\int G_{h/2}*\left( u-\chi \right) \cdot \sigma \, \left[ \zeta ,G_{h/2}*\right] \left( \left( \xi \cdot \nabla \right) u \right) dx. \end{aligned}$$

(44)

Note that the first right-hand side integral is exactly $\delta E_h(u,\zeta \,\xi )$, the first variation of the energy along the “localized” vector field $\zeta \,\xi$.

Step 2: We can estimate the right-hand side of Step 1 in the following way:

$$\begin{aligned}&\left| -\frac{2}{\sqrt{h}}\int G_{h/2}*\left( u-\chi \right) \cdot \sigma \, \left[ \zeta ,G_{h/2}*\right] \left( \left( \xi \cdot \nabla \right) u \right) dx\right| \\&\quad \lesssim \left( \Vert \nabla \zeta \Vert _\infty \Vert \xi \Vert _\infty + \Vert \zeta \Vert _\infty \Vert \nabla \xi \Vert _\infty \right) h^{1/4} \frac{\mathrm{d}_h(u,\chi )}{h}. \end{aligned}$$

Indeed, if we argue term by term in the sum over the phases, starting with Cauchy–Schwarz

$$\begin{aligned}&\left| -\frac{2}{\sqrt{h}}\int G_{h/2}*\left( u-\chi \right) _i \, \sigma _{ij} \left[ \zeta ,G_{h/2}*\right] \left( \left( \xi \cdot \nabla \right) u_j \right) dx\right| \\&\quad \le \frac{2\sigma _{ij}}{\sqrt{h}}\left( \int \left( G_{h/2}*\left( u-\chi \right) _i \right) ^2 dx\right) ^{1/2}\left( \int \big (\left[ \zeta ,G_{h/2}*\right] \left( \left( \xi \cdot \nabla \right) u_j\right) \big )^2dx \right) ^{1/2}, \end{aligned}$$

and since

$$\begin{aligned} \left( \int \left( G_{h/2}*\left( u-\chi \right) _i \right) ^2 dx\right) ^{1/2} \lesssim \left( \sqrt{h}\frac{1}{2h}\mathrm{d}_h^2(u,\chi )\right) ^{1/2} \end{aligned}$$

we see that we only need to show

$$\begin{aligned} \left\| \left[ \zeta , G_{h/2}*\right] \left( \left( \xi \cdot \nabla \right) u_i\right) \right\| _\infty \lesssim \Vert \nabla \zeta \Vert _\infty \Vert \xi \Vert _\infty + \Vert \zeta \Vert _\infty \Vert \nabla \cdot \xi \Vert _\infty . \end{aligned}$$

(45)

The latter is easy to see: Integrating by parts in z, we obtain

$$\begin{aligned}&\left( \left[ \zeta , G_{h/2}*\right] \left( \left( \xi \cdot \nabla \right) u_i\right) \right) (x)\\&\quad = \int G_{h/2} (z) \left( \zeta (x)-\zeta (x-z)\right) \xi (x-z)\cdot \nabla u_i(x-z)\,dz\\&\quad = \int \Big (\left( \zeta (x)-\zeta (x-z)\right) \left( \nabla G_{h/2} (z) \cdot \xi (x-z) -G_{h/2}(z) \nabla \cdot \xi (x-z)\right) \\&\qquad + G_{h/2}(z) \nabla \zeta (x-z)\cdot \xi (x-z) \Big )\, u_i(x-z)\,dz \end{aligned}$$

so that by $|u(x-z)| \le 1$, $|\zeta (x)-\zeta (x-z)|\le |z|\Vert \nabla \zeta \Vert _\infty$ we obtain

$$\begin{aligned}&\left| \left( \left[ \zeta , G_{h/2}*\right] \left( \left( \xi \cdot \nabla \right) u_i\right) \right) (x)\right| \\&\quad \lesssim \Vert \nabla \zeta \Vert _\infty \Vert \xi \Vert _\infty \int \left( |z|\left| \nabla G_{h/2}(z)\right| + G_{h/2}(z) \right) dz +2 \Vert \zeta \Vert _\infty \Vert \nabla \cdot \xi \Vert _\infty \int G_{h/2}(z)\,dz. \end{aligned}$$

Then (45) follows from the observation that both integrals on the right-hand side are uniformly bounded as $h\rightarrow 0$. $\square$

Proof of Lemma 3.4

Step 1: Expanding the commutator. We claim that we have the first- and second-order commutator estimates

$$\begin{aligned} \frac{1}{h} \left[ \zeta ,G_{h}*\right] v = \nabla G_{h} *\left( - \nabla \zeta \, v\right) + O\left( \Vert \nabla ^2 \zeta \Vert _\infty \Vert v\Vert _\infty \right) \end{aligned}$$

(46)

and

$$\begin{aligned} \frac{1}{h}\left[ \zeta , G_h*\right] v = \nabla G_h *\left( - \nabla \zeta \,v\right) + \frac{1}{2} \left( G_h\, Id + h\nabla ^2 G_h\right) *\left( \nabla ^2 \zeta \, v\right) + O\left( \sqrt{h}\Vert \nabla ^3\zeta \Vert _\infty \Vert v\Vert _\infty \right) . \end{aligned}$$

(47)

We only prove the finer second-order estimate (47): Expanding $\zeta$ to second order, we obtain

$$\begin{aligned} (\left[ \zeta , G_h*\right] v )(x)&=\int G_h(z) \left( \zeta (x)-\zeta (x-z)\right) v(x-z)\,dz\\&= \int G_h(z) \left( z\cdot \nabla \zeta (x-z) + \frac{1}{2} z\otimes z :\nabla ^2 \zeta (x-z) +O(|z|^3 \Vert \nabla ^3 \zeta \Vert _\infty )\right) \\&\qquad \times v(x-z)\,dz \end{aligned}$$

and after dividing by h, we recognize the terms appearing on the right-hand side of (47) via the trivial identities

$$\begin{aligned} \nabla G_h (z) = - G_h(z)\frac{z}{h} \quad \text {and} \quad \nabla ^2 G_h(z) = - G_h(z) \left( \frac{1}{h} Id - \frac{z}{h}\otimes \frac{z}{h}\right) . \end{aligned}$$

Step 2: We claim

$$\begin{aligned}&\frac{1}{h}\left( E_h(u,\chi ;\zeta )-E_h(u,u;\zeta )\right) +\frac{1}{2} \delta \Big ( \frac{1}{2h} \mathrm{d}_h^2(\,\cdot \,,\chi )\Big ) (u,\nabla \zeta )\nonumber \\&\quad = \frac{1}{\sqrt{h}}\int \left( G_{h/2} *(u-\chi ) \right) \cdot \sigma \left( \frac{1}{2} G_{h/2} \,Id + h \nabla ^2 G_{h/2}\right) *\left( u \nabla ^2 \zeta \right) dx \nonumber \\&\qquad + O\left( \Vert \nabla ^3 \zeta \Vert _\infty \int |u-\chi |\,dx\right) - \frac{1}{\sqrt{h}}\int \Delta \zeta \frac{1}{4} \left| G_{h/2} *\left( u-\chi \right) \right| _\sigma ^2dx\nonumber \\&\qquad + O\left( \Vert \nabla ^2 \zeta \Vert _\infty \frac{1}{\sqrt{h}}\int \left| G_{h/2}*(u-\chi )\right| dx\right) . \end{aligned}$$

(48)

We first note that by definition of the localized energy (22),

$$\begin{aligned}&\frac{1}{h} \left( E_h(u,\chi ;\zeta ) - E_h(u,u;\zeta )\right) \\&\quad =\frac{1}{\sqrt{h}}\int \left( u-\chi \right) \cdot \sigma \frac{1}{h}\left[ \zeta ,G_h*\right] \chi - \left( u-\chi \right) \cdot \sigma \frac{1}{h}\left[ \zeta ,G_{h/2}*\right] G_{h/2}*\left( u- \chi \right) dx. \end{aligned}$$

By the antisymmetry of the commutator (and the symmetry of $\sigma$), we may replace $\chi$ by u in the first right-hand side term:

$$\begin{aligned} \frac{1}{\sqrt{h}}\int \left( u-\chi \right) \cdot \sigma \frac{1}{h} \left[ \zeta ,G_h*\right] u- \left( u-\chi \right) \cdot \sigma \frac{1}{h}\left[ \zeta ,G_{h/2}*\right] G_{h/2}*\left( u- \chi \right) dx. \end{aligned}$$

Applying the commutator estimate (47) from Step 1 to the first term, we obtain the first-order term

$$\begin{aligned} \frac{1}{\sqrt{h}}\int \left( u-\chi \right) \cdot \sigma \nabla G_h*\left( -\nabla \zeta \,u \right) \, dx= \frac{1}{\sqrt{h}}\int \left( u-\chi \right) \cdot \sigma \,G_h *\left( -\left( \nabla \zeta \cdot \nabla \right) u -\Delta \zeta \,u\right) dx, \end{aligned}$$

in which we recognize the first variation of the (unlocalized) dissipation functional, cf. (4),

$$\begin{aligned} \delta \left( \frac{1}{2h} \mathrm{d}_h^2(\,\cdot \,,\chi ) \right) (u,\xi ) = -\frac{2}{\sqrt{h}}\int \left( u-\chi \right) \cdot \sigma \, G_h *\left( - \left( \xi \cdot \nabla \right) u \right) dx \end{aligned}$$

with $\nabla \zeta$ playing the role of $\xi$. Having this observation in mind we collect the terms accordingly:

$$\begin{aligned}&\frac{1}{h} \left( E_h(u,\chi ;\zeta ) - E_h(u,u;\zeta )\right) +\frac{1}{2}\delta \left( \frac{1}{2h} \mathrm{d}_h^2(\,\cdot \,,\chi ) \right) (u,\nabla \zeta )\nonumber \\&\quad = \frac{1}{\sqrt{h}}\int \left( u-\chi \right) \cdot \sigma \left( \frac{1}{h} \left[ \zeta ,G_h*\right] u + \nabla G_h *( u\,\nabla \zeta )\right) dx\nonumber \\&\qquad +\frac{1}{\sqrt{h}}\int \left( u-\chi \right) \cdot \sigma \left( \frac{1}{h} \left[ \zeta ,G_{h/2}*\right] G_{h/2} *(u-\chi ) - G_h*(u\,\Delta \zeta )\right) dx \end{aligned}$$

(49)

Taking into account all contributions from the commutator estimate (47), the first right-hand side integral is equal to

$$\begin{aligned}&\frac{1}{\sqrt{h}}\int \left( u-\chi \right) \cdot \sigma \left( \frac{1}{2}\left( G_h \,Id +h\nabla ^2 G_h\right) *\left( u\,\nabla ^2 \zeta \right) + O\left( \sqrt{h}\Vert \nabla ^3 \zeta \Vert _\infty \right) \right) dx\\&\quad =\frac{1}{\sqrt{h}}\int G_{h/2}*\left( u-\chi \right) \cdot \sigma \frac{1}{2}\left( G_{h/2} \,Id +h\nabla ^2 G_{h/2}\right) *\left( u\,\nabla ^2 \zeta \right) dx \\&\qquad + O\left( \Vert \nabla ^3 \zeta \Vert _\infty \int |u-\chi | \,dx\right) dx, \end{aligned}$$

where we used the semigroup and symmetry properties of the kernel $G_h$. Now we turn to the second right-hand side integral in (49). Using the antisymmetry of the commutator and the symmetry of $\sigma$ for the first term and the semigroup and symmetry properties of $G_h$ for the second term, we can rewrite this integral as

$$\begin{aligned}&-\frac{1}{\sqrt{h}}\int G_{h/2}*\left( u-\chi \right) \cdot \sigma \left( \frac{1}{h} \left[ \zeta ,G_{h/2}\right] *\left( u-\chi \right) + G_{h/2}*\left( u \,\Delta \zeta \right) \right) dx\\&\quad = - \frac{1}{\sqrt{h}}\int G_{h/2} *\left( u-\chi \right) \cdot \sigma \left( -\frac{1}{2} \nabla \zeta \cdot \nabla G_{h/2} *\left( u-\chi \right) + O(\Vert \nabla ^2\zeta \Vert _\infty )\right) dx \end{aligned}$$

where we used the second commutator estimate (46) from Step 1 and absorbed the last left-hand side term in the last right-hand side term. Now we may pull out a derivative and integrate by parts in the first right-hand side term:

$$\begin{aligned}&\frac{1}{\sqrt{h}}\int G_{h/2} *\left( u-\chi \right) \cdot \sigma \left( \frac{1}{2} \nabla \zeta \cdot \nabla G_{h/2} *\left( u-\chi \right) \right) \\&\quad = -\frac{1}{\sqrt{h}}\int \nabla \zeta \cdot \nabla \frac{1}{4}\left| G_{h/2} *\left( u-\chi \right) \right| _\sigma ^2 dx\\&\quad = \frac{1}{\sqrt{h}}\int \Delta \zeta \frac{1}{4} \left| G_{h/2} *\left( u-\chi \right) \right| _\sigma ^2 dx. \end{aligned}$$

Step 3: Conclusion. From Step 2 we obtain

$$\begin{aligned}&\left| \frac{1}{h}\left( E_h(u,\chi ;\zeta )-E_h(u,u;\zeta )\right) +\frac{1}{2} \delta \Big ( \frac{1}{2h} \mathrm{d}_h^2(\,\cdot \,,\chi )\Big ) (u,\nabla \zeta ) \right| \\&\quad \lesssim \Vert \nabla ^2 \zeta \Vert _\infty \left( \frac{1}{\sqrt{h}}\int \left| G_{h/2}*(u-\chi )\right| _\sigma dx+ \frac{1}{\sqrt{h}}\int \left| G_{h/2}*(u-\chi )\right| _\sigma ^2 dx \right) \\&\quad + \Vert \nabla ^3 \zeta \Vert _\infty \int \left| u-\chi \right| dx. \end{aligned}$$

By Jensen, we can manipulate the first right-hand side term

$$\begin{aligned} \frac{1}{\sqrt{h}}\int \left| G_{h/2}*(u-\chi )\right| _\sigma dx \lesssim \frac{1}{\sqrt{h}}\left( \int \left| G_{h/2}*(u-\chi )\right| _\sigma ^2 dx \right) ^{1/2} \lesssim h^{1/4} \frac{\mathrm{d}_h(u,\chi )}{h}, \end{aligned}$$

while the second right-hand side term is already of the desired form $h\frac{ \mathrm{d}_h^2(u,\chi )}{2h^2}$. By Jensen and Lemma 4.2(iii), the last right-hand side term is estimated by

$$\begin{aligned} \int \left| u-\chi \right| dx \lesssim \left( \int \left| u-\chi \right| ^2dx\right) ^{1/2} \le \left( \frac{1}{2\sqrt{h}} \mathrm{d}_h^2(u,\chi ) + 2\sqrt{h}\left( E_h(u) + E_h(\chi )\right) \right) ^{1/2}, \end{aligned}$$

which concludes the proof of Lemma 3.4. $\square$

Proof of Lemma 3.6

We first give the argument for (34). We can read off the first variation of $E_h$ from (42) by setting $\zeta =1$, which may be compactly rewritten as

$$\begin{aligned} \delta E_h(u,\xi ) = \frac{1}{\sqrt{h}}\int 2 \left( \nabla \cdot \xi \right) u\cdot \sigma \, G_h*u + u \cdot \sigma \left[ \xi \cdot ,\nabla G_h*\right] u - u \cdot \sigma \left[ \nabla \cdot \xi , G_h*\right] u \,dx. \end{aligned}$$

Componentwise in u, we expand the first commutator:

$$\begin{aligned} \left( \left[ \xi \cdot , \nabla G_h*\right] u_i\right) (x)&= \int \left( \xi (x)-\xi (x-z)\right) \cdot \nabla G_h(z) \,u_i(x-z)\,dz\\&= \nabla \xi (x) :\int - \frac{z}{\sqrt{h}}\otimes \frac{z}{\sqrt{h}} G_h(z)\, u_i(x-z)\,dz \\&\quad + O\left( \Vert \nabla ^2 \xi \Vert _\infty \big (\sqrt{h}\,k_h*u_i \big )(x) \right) , \end{aligned}$$

where we used the identity $\nabla G(z)=-G(z)z$ and where the kernel $k_h$ is given by the mask $k(z)=|z|^3 G(z)$ and can be controlled by a Gaussian with slightly larger variance $k(z) \lesssim G(z/2)$. Likewise, the second commutator can be estimated pointwise by

$$\begin{aligned} \left| \left[ \nabla \cdot \xi , G_h*\right] u _i\right| \lesssim \Vert \nabla ^2\xi \Vert _\infty \sqrt{h}\,\tilde{k}_h*u_i, \end{aligned}$$

where $\tilde{k}_h$ is given by the mask $\tilde{k}(z)=|z|\, G(z)\lesssim G(z/2)$. By the identity $G(z)\left( Id-z\otimes z\right) =-\nabla ^2 G(z)$ we indeed obtain (34) with an error of order $\Vert \nabla ^2 \xi \Vert _\infty \sqrt{h}\, E_{4h}(u)$, which by the monotonicity (7) of $E_h$ yields (34).

Since the second claim (35) now follows immediately from Proposition 3.5 we we turn to the third claim of the lemma, the convergence of the metric tensor (36). We plug the identity $\left( \xi \cdot \nabla \right) u^h = \nabla \cdot (\xi u^h) - \left( \nabla \cdot \xi \right) u^h$ into the quadratic term

$$\begin{aligned} \sqrt{h}\int \zeta \left| G_{h/2} *\left( \left( \xi \cdot \nabla \right) u^h\right) \right| _\sigma ^2 dx \end{aligned}$$

and expand the square. First we note that the only term that survives in the limit $h\rightarrow 0$ is

$$\begin{aligned} \sqrt{h}\int \zeta \left| G_{h/2}*\left( \nabla \cdot (\xi u^h)\right) \right| _\sigma ^2 dx = \sqrt{h}\int \zeta \left| \nabla G_{h/2}*\left( \xi \otimes u^h\right) \right| _\sigma ^2 dx. \end{aligned}$$

(50)

Indeed, we have

$$\begin{aligned} \sqrt{h}\int \zeta \left| G_{h/2}*\left( (\nabla \cdot \xi )\, u^h\right) \right| _\sigma ^2 dx \lesssim \sqrt{h}\Vert \nabla \xi \Vert _\infty ^2\Vert \zeta \Vert _\infty \end{aligned}$$

and the mixed term can be estimated by Young’s inequality and the boundedness of the leading-order term which we will show now. Using the antisymmetry of $\nabla G$ we have

$$\begin{aligned} \sqrt{h}\int \zeta \big |\nabla G_{h/2}*\big (\xi \otimes u^h \big ) \big |_\sigma ^2dx = \sqrt{h}\int u\cdot \sigma \left( \xi \cdot \nabla \right) G_{h/2}*\big (\zeta \,\nabla G_{h/2}*\big (\xi \, u^h \big ) \big )\,dx. \end{aligned}$$

We now want to commute the multiplication with $\xi$ and the outer convolution and afterwards the multiplication with $\zeta \,\xi$ and the inner convolution. For this we use the $L^\infty$-commutator estimate

$$\begin{aligned} \left\| \left[ \xi , \nabla G_h*\right] v \right\| _\infty \lesssim \Vert \nabla \xi \Vert _\infty \Vert v\Vert _\infty \end{aligned}$$

for the vector fields $\xi$ and $\zeta \xi$, which implies the $L^1$-estimate

$$\begin{aligned} \int \left| \nabla G_{h/2}*\left( \xi \, u^h_i \right) \right| dx \lesssim \Vert \nabla \xi \Vert _\infty + \Vert \xi \Vert _\infty \int \left| \nabla G_{h/2}*u^h_i\right| dx \lesssim \Vert \nabla \xi \Vert _\infty + \Vert \xi \Vert _\infty E_h(u^h), \end{aligned}$$

where we have used Lemma 4.2(i). Therefore, the left-hand side of (36) is to leading order given by

$$\begin{aligned} \frac{1}{\sqrt{h}}\int \zeta \left( \xi \otimes \xi \right) :u^h \cdot \sigma ( h\nabla ^2 G_h) *u^h\, dx \end{aligned}$$

and (36) follows from Proposition 3.5. $\square$

Proof of Lemma 3.7

In contrast to the piecewise constant interpolation $\chi ^h$, the variational interpolation $u^h$ is not given in an explicit form so we have to make do with the minimization problem (23). In particular, since in general $u^h$ may depend on the test function $\zeta$, we are tied to the local minimization problem (23). By (24) we have in particular

$$\begin{aligned}&E_h(u^h(\tilde{T}),u^h(\tilde{T});\zeta )+ \int _0^{\tilde{T}} \frac{\mathrm{d}_h^2(u^h,\chi ^h;\zeta )}{2h^2}dt \\&\quad \le E_h(\chi ^0,\chi ^0;\zeta )- \int _0^T \frac{1}{h} \Big ( E_h(\chi ^h(t+h),\chi ^{h}(t);\zeta ) -E_h(\chi ^h(t+h_,\chi ^h(t+h);\zeta ) \Big ) \,dt \end{aligned}$$

for any $\tilde{T}\in [Nh,(N+1)h)$, where $N \in \mathbb {N}$. The left-hand side is bounded from below by

$$\begin{aligned} \left( \inf \zeta \right) \left( E_h(u^h(\tilde{T})) + \int _0^{\tilde{T}} \frac{\mathrm{d}_h^2(u^h,\chi ^h)}{2h^2}dt \right) \end{aligned}$$

while the right-hand side can be controlled by first applying Lemma 3.4, then replacing the first variation of the metric term by the first variation of the energy via (31) and then estimating the first variation of the energy via (34) by $\Vert \nabla \xi \Vert _\infty E_h(u^h)$.

The convergence of $u^h$ to $\chi =\lim _h \chi ^h$ follows from the closeness of $u^h$ to $\chi$, which we have just shown, cf. (37) and Lemma 4.2(iii) and the convergence of the energies (39) follows immediately from (37) and Lemma 4.2(iv). $\square$

Proof of Theorem 2.2

Step 1: Time-freezing for $\zeta$. We claim that it is enough to prove

$$\begin{aligned}&\frac{c_0}{2}\sum _{i,j} \sigma _{ij}\int _0^{\tilde{T}} \int \left( \zeta \, |H|^2 - H\cdot \nabla \zeta \right) \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) dt\nonumber \\&\quad \le c_0\sum _{i,j} \sigma _{ij}\int \zeta \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) \Big |_{t=0} \nonumber \\&\qquad - c_0\sum _{i,j} \sigma _{ij} \int \zeta \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) \Big |_{t=\tilde{T}} \end{aligned}$$

(51)

for any time-independent, strictly positive test function $\zeta =\zeta (x)>0$ and a.e. $\tilde{T}$.

This is a standard approximation argument: In order to reduce (12) to (51) we fix a time-dependent test function $\zeta =\zeta (t,x)\ge 0$ and two time instances $0\le s< t$. It is no restriction to assume $s=0$. Writing $t=:\tilde{T}$ for the time horizon we take a regular partition $0=T_0< \cdots < T_M = \tilde{T}$ of the interval $(0,\tilde{T})$ of fineness $\tau =\tilde{T}/M$. We write $\zeta _M$ for the piecewise constant interpolation of $\zeta$ plus a small perturbation $\frac{1}{M}$ so that $\zeta _M \ge \frac{1}{M} >0$:

$$\begin{aligned} \zeta _M(t) := \zeta (T_{m-1}) + \frac{1}{M}\quad \text {if } t\in [T_{m-1},T_m). \end{aligned}$$

Writing $\partial ^{-\tau }\zeta _M (t) := \frac{1}{\tau }\left( \zeta _M(t) - \zeta _M(t-\tau )\right)$ for the discrete (backwards) time derivative we have

$$\begin{aligned} \zeta _M \rightarrow \zeta ,\quad \nabla \zeta _M \rightarrow \nabla \zeta \quad \text {and} \quad \partial ^{-\tau } \zeta _M \rightarrow \partial _t \zeta \quad \text {uniformly as } M\rightarrow \infty . \end{aligned}$$

(52)

Using (51) for $\zeta _M\ge \frac{1}{M} >0$ on each interval $[T_{m-1},T_m)$ and summing over m we obtain (12).

Step 2: A $\liminf$-inequality for the local slope. Given the convergence assumption (8), there exists a measurable normal vector field $H\in L^2(\sum _{i,j} \sigma _{ij}\frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) dt,\mathbb {R}^d)$ which is the mean curvature vector of the partition $\chi$ in the sense of (11), such that

$$\begin{aligned}&\frac{c_0}{2} \sum _{i,j} \sigma _{ij}\int _0^{\tilde{T}} \int \zeta \, |H|^2 \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) dt \nonumber \\&\quad \le \liminf _{h\rightarrow 0} \int _0^{\tilde{T}} \left( \frac{1}{2} \left| \partial E_h(\,\cdot \,, \chi ^h(t);\zeta ) \right| ^2(\chi ^h(t+h)) + \frac{1}{2}\left| \partial E_h(\,\cdot \,, \chi ^h(t);\zeta ) \right| ^2(u^h(t)) \right) dt. \end{aligned}$$

(53)

We give ourselves a test vector field $\xi$ and let the variations $u^h_s$ defined in (27) play the role of v in the definition of the local slope (25) so that we obtain the inequality

$$\begin{aligned} |\partial E_h(\,\cdot \,,\chi ^h;\zeta )|(u^h) \ge \limsup _{s\rightarrow 0} \frac{\left( E_h(u^h,\chi ^h;\zeta )-E_h(u^h_s,\chi ^h;\zeta )\right) _+}{\mathrm{d}_h(u^h_s,u^h;\zeta )}. \end{aligned}$$

As $s\rightarrow 0$ we expand the numerator in the following way

$$\begin{aligned} E_h(u^h_s,\chi ^h;\zeta ) = E_h(u^h,\chi ^h;\zeta ) + s \,\frac{d}{ds}\Big |_{s=0} E_h(u^h_s,\chi ^h;\zeta ) +o(s) \quad \text {as } s\rightarrow 0. \end{aligned}$$

For the denominator we have, cf. (4),

$$\begin{aligned} \frac{1}{2h}\mathrm{d}_h^2(u^h_s,u^h;\zeta ) = \frac{s^2}{\sqrt{h}}\int \zeta \left| G_{h/2}*\left( \left( \xi \cdot \nabla \right) u^h\right) \right| _\sigma ^2 dx + o(s^2) \quad \text {as } s\rightarrow 0. \end{aligned}$$

Taking the limit $s\rightarrow 0$ we obtain

$$\begin{aligned} |\partial E_h(\,\cdot \,,\chi ^h;\zeta )|(u^h) \ge \frac{\delta E_h(\,\cdot \,,\chi ^h;\zeta )(u^h,\xi )}{\sqrt{2\sqrt{h}\int \zeta \left| G_{h/2}*\left( \left( \xi \cdot \nabla \right) u^h\right) \right| _\sigma ^2 dx}}. \end{aligned}$$

(54)

Now we square both sides, apply Lemma 3.3 to the numerator and afterwards Lemma 3.6 to both numerator and denominator to obtain

$$\begin{aligned}&\liminf _{h\rightarrow 0}\int _0^{\tilde{T}} |\partial E_h(\,\cdot \,,\chi ^h;\zeta )|^2(u^h)\, dt\\&\quad \ge \frac{c_0}{2} \int _0^{\tilde{T}} \left( \sup _\xi \frac{ \int \nabla \left( \zeta \, \xi \right) :\left( Id - \nu _i \otimes \nu _i\right) \sum _{i,j} \sigma _{ij} \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) }{\sqrt{ \int \zeta \, |\xi |^2 \sum _{i,j} \sigma _{ij} \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) }} \right) ^2 dt. \end{aligned}$$

Here we have also used $\left( \xi \cdot \nu _i\right) ^2 \le |\xi |^2$ in the denominator. Applying this estimate for $u^h(t+h)=\chi ^h(t+h)$ and $\zeta =1$ furnishes the existence of the mean curvature vector

$$\begin{aligned} H\in L^2\left( \sum _{i,j}\sigma _{ij}\frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) dt, \mathbb {R}^d\right) . \end{aligned}$$

Turning back to the general case in which $u^h$ may be the variational interpolation or the piecewise constant interpolation, we see that H satisfies (53).

Step 3: Convergence of the transport term. Given the convergence assumption (8) we have

$$\begin{aligned}&\lim _{h\rightarrow 0} \int _0^{\tilde{T}} \frac{1}{h}\left( E_h(\chi ^h(t+h),\chi ^{h}(t);\zeta ) - E_h(\chi ^h(t+h),\chi ^h(t+h);\zeta ) \right) \\&\quad = \frac{c_0}{2} \sum _{i,j} \sigma _{ij} \int _0^T \int \nabla ^2 \zeta :\left( Id-\nu _i\otimes \nu _i\right) \frac{1}{2}\left( |\nabla \chi _i| +|\nabla \chi _j| - |\nabla (\chi _i+\chi _j)| \right) dt. \end{aligned}$$

Indeed, by Lemma 3.4, we may replace the increments on the left-hand side by the first variation of the metric term. Applying the Euler–Lagrange Eq. (31) and employing Lemma 3.6, we may pass to the limit in this term.

Step 4: Conclusion. Given a test function $\zeta =\zeta (x)>0$, we want to prove (51) for a.e. $\tilde{T}>0$. For simplicity, we may assume that $\tilde{T}=Nh$ is a multiple of the time step size h. Furthermore by (39) we may assume that $E_h(\chi ^h(\tilde{T}))\rightarrow E(\chi (\tilde{T}))$. Now Steps 2 and 3 allow us to pass to the limit in our approximate version of Brakke’s inequality (24), and we obtain (51). $\square$