Abstract
In branched transportation problems mass has to be transported from a given initial distribution to a given final distribution, where the cost of the transport is proportional to the transport distance, but subadditive in the transported mass. As a consequence, mass transport is cheaper the more mass is transported together, which leads to the emergence of hierarchically branching transport networks. We here consider transport costs that are piecewise affine in the transported mass with N affine segments, in which case the resulting network can be interpreted as a street network composed of N different types of streets. In two spatial dimensions we propose a phase field approximation of this street network using N phase fields and a function approximating the mass flux through the network. We prove the corresponding \(\Gamma \)-convergence and show some numerical simulation results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Branched transportation problems constitute a special class of optimal transport problems that have recently attracted lots of interest (see for instance [26, §4.4.2] and the references therein). Given two probability measures \(\mu _+\) and \(\mu _-\) on some domain \(\Omega \subset {\mathbf {R}}^n\), representing an initial and a final mass distribution, respectively, one seeks the most cost-efficient way to transport the mass from the initial to the final distribution. Unlike in classical optimal transport, the cost of a transportation scheme does not only depend on initial and final position of each mass particle, but also takes into account how many particles travel together. In fact, the transportation cost per transport distance is typically not proportional to the transported mass m, but rather a concave, nondecreasing function \(\tau :[0,\infty )\rightarrow [0,\infty )\), \(m\mapsto \tau (m)\). Therefore it is cheaper to transport mass in bulk rather than moving each mass particle separately. This automatically results in transportation paths that exhibit an interesting, hierarchically ramified structure (see Fig. 1). Well-known models (with parameters \(\alpha <1\), \(a,b>0\)) are obtained by the choices
There exist multiple equivalent formulations for branched transportation problems. One particular formulation models the mass flux \({{\mathcal {F}}}\) as an unknown vector-valued Radon measure that describes the transport from \(\mu _+\) to \(\mu _-\). The cost functional of the flux, which one seeks to minimize, is defined as
if \({{\,\mathrm{div}\,}}{{\mathcal {F}}}=\mu _+-\mu _-\) in the distributional sense (so that indeed \({{\mathcal {F}}}\) transports mass \(\mu _+\) to \(\mu _-\)) and  for some countably 1-rectifiable set \(S\subset {\mathbf {R}}^n\), an
for some countably 1-rectifiable set \(S\subset {\mathbf {R}}^n\), an  -measurable function \(\sigma :S\rightarrow {\mathbf {R}}^n\), and a diffuse part \({{\mathcal {F}}}^\perp \) (that is, \(|{{\mathcal {F}}}^\perp |(R)=0\) for any countably 1-rectifiable set \(R\subset {\mathbf {R}}^n\), for instance an absolutely continuous measure). Otherwise, \(E^{\mu _+,\mu _-}[{{\mathcal {F}}}]=\infty \).
-measurable function \(\sigma :S\rightarrow {\mathbf {R}}^n\), and a diffuse part \({{\mathcal {F}}}^\perp \) (that is, \(|{{\mathcal {F}}}^\perp |(R)=0\) for any countably 1-rectifiable set \(R\subset {\mathbf {R}}^n\), for instance an absolutely continuous measure). Otherwise, \(E^{\mu _+,\mu _-}[{{\mathcal {F}}}]=\infty \).
In this article we devise phase field approximations of the functional \(E^{\mu _+,\mu _-}\) in two space dimensions in the case of a piecewise affine transportation cost
with positive parameters \(\alpha _i,\beta _i\). In fact, for a positive phase field parameter \(\varepsilon \) we consider (a slightly improved but less intuitive version of) the phase field functional
if \({{\,\mathrm{div}\,}}\sigma =\mu _+^\varepsilon -\mu _-^\varepsilon \) and \(E_\varepsilon ^{\mu _+,\mu _-}[\sigma ,\varphi _1,\ldots ,\varphi _N]=\infty \) otherwise. Our main result Theorem 2.1 shows that \(E_\varepsilon ^{\mu _+,\mu _-}\) \(\Gamma \)-converges in a certain topology to \(E^{\mu _+,\mu _-}\) as \(\varepsilon \searrow 0\). Here the vector field \(\sigma \) approximates the mass flux \({{\mathcal {F}}}\), the auxiliary scalar phase fields \(\varphi _1,\ldots ,\varphi _N\) disappear in the limit, and \(\mu _+^\varepsilon ,\mu _-^\varepsilon \) are smoothed versions of \(\mu _+,\mu _-\). One motivation for our particular choice of \(\tau \) is that this allows a phase field version of the urban planning model, the other motivation is that any concave cost \(\tau \) can be approximated by a piecewise affine function. Those phase field approximations then allow to find numerical approximations of optimal mass fluxes.
1.1 Related work
Phase field approximations represent a widely used tool to approach solutions to optimization problems depending on lower-dimensional sets. The concept takes advantage of the definition of \(\Gamma \)-convergence [6, 7, 15] to approximate singular energies by smoother elliptic functionals such that the associated minimizers converge as well. The term phase field is due to Modica and Mortola [22] who study a rescaled version of the Cahn and Hilliard functional which models the phase transition between two immiscible liquids and which turns out to approximate the perimeter functional of a set. Subsequently a similar idea has been used by Ambrosio and Tortorelli in [3, 4] to obtain an approximation to the Mumford–Shah functional [23]. Later on these techniques have been used as well in fracture theory and optimal partitions problems [14, 19]. More recently such phase field approximations have also been applied to branched transportation problems and the Steiner minimal tree problem (to find the graph of smallest length connecting a given set of points) which both feature high combinatorial complexity [20]. For instance, in [24] the authors propose an approximation to the branched transport problem based on the Modica–Mortola functional in which the phase field is replaced by a vector-valued function satisfying a divergence constraint. Similarly, in [5] Santambrogio et al. study a variational approximation to the Steiner minimal tree problem in which the connectedness constraint of the graph is enforced trough the introduction of a geodesic distance depending on the phase field. Our phase field approximations can be viewed as a generalization of recent work by two of the authors [11, 12], in which essentially (1) for \(\tau (m)=\alpha m+\beta \) with \(\alpha ,\beta >0\) is approximated by an Ambrosio–Tortorelli-type functional defined as
if \({{\,\mathrm{div}\,}}\sigma =\rho _\varepsilon *(\mu _+-\mu _-)\) for a smoothing kernel \(\rho _\varepsilon \) and if \(\varphi \ge \frac{\alpha }{\sqrt{\beta }}\varepsilon \) almost everywhere, and \({\tilde{E}}_\varepsilon ^{\mu _+,\mu _-}[\sigma ,\varphi ]=\infty \) otherwise. The function \(1-\varphi \) may be regarded as a smooth version of the characteristic function of a 1-rectifiable set (the Steiner tree) whose total length is approximated by the Ambrosio–Tortorelli phase field term in parentheses. In addition, the first term in the integral forces this set to contain the support of a vector field \(\sigma \) which encodes the mass flux from \(\mu _+\) to \(\mu _-\).
1.2 Notation
Throughout, \(\Omega \subset {\mathbf {R}}^2\) is an open bounded domain with Lipschitz boundary. The spaces of scalar and \({\mathbf {R}}^n\)-valued continuous functions on the closure \({\overline{\Omega }}\) are denoted \({{\mathcal {C}}}({\overline{\Omega }})\) and \({{\mathcal {C}}}({\overline{\Omega }};{\mathbf {R}}^n)\) (for m times continuously differentiable functions we use \({{\mathcal {C}}}^m\)) and are equipped with the supremum norm \(\Vert \cdot \Vert _\infty \). Their topological duals are the spaces of scalar and \({\mathbf {R}}^n\)-valued Radon measures (regular countably additive measures) \({{\mathcal {M}}}({\overline{\Omega }})\) and \({{\mathcal {M}}}({\overline{\Omega }};{\mathbf {R}}^n)\), equipped with the total variation norm \(\Vert \cdot \Vert _{{\mathcal {M}}}\). Weak-* convergence in these spaces will be indicated by \({\mathop {\rightharpoonup }\limits ^{*}}\). The subset \({{\mathcal {P}}}({\overline{\Omega }})\subset {{\mathcal {M}}}({\overline{\Omega }})\) shall be the space of probability measures (nonnegative Radon measures with total variation 1). The total variation measure of some Radon measure \(\lambda \) will be denoted \(|\lambda |\), and its Radon–Nikodym derivative with respect to \(|\lambda |\) as \(\frac{\lambda }{|\lambda |}\). The restriction of \(\lambda \) to a measurable set A is abbreviated  . The pushforward of a measure \(\lambda \) under a measurable map T is denoted \({{T}_{\#}\lambda }\). The standard Lebesgue and Sobolev spaces are indicated by \(L^p(\Omega )\) and \(W^{k,p}(\Omega )\), respectively; if they map into \({\mathbf {R}}^n\) we write \(L^p(\Omega ;{\mathbf {R}}^n)\) and \(W^{k,p}(\Omega ;{\mathbf {R}}^n)\). The associated norms are indicated by \(\Vert \cdot \Vert _{L^p}\) and \(\Vert \cdot \Vert _{W^{k,p}}\). Finally, the n-dimensional Hausdorff measure is denoted \({\mathcal {H}}^n\).
. The pushforward of a measure \(\lambda \) under a measurable map T is denoted \({{T}_{\#}\lambda }\). The standard Lebesgue and Sobolev spaces are indicated by \(L^p(\Omega )\) and \(W^{k,p}(\Omega )\), respectively; if they map into \({\mathbf {R}}^n\) we write \(L^p(\Omega ;{\mathbf {R}}^n)\) and \(W^{k,p}(\Omega ;{\mathbf {R}}^n)\). The associated norms are indicated by \(\Vert \cdot \Vert _{L^p}\) and \(\Vert \cdot \Vert _{W^{k,p}}\). Finally, the n-dimensional Hausdorff measure is denoted \({\mathcal {H}}^n\).
Structure of the paper: In Sect. 2 we introduce the approximating energies and precisely state our results. Section 3 is devoted to the proof of the \(\Gamma \)-convergence result. Its first three subsections deal with the \(\Gamma {\mathrm{-}}\liminf \) inequality which is obtained via slicing, while the remaining two subsections prove an equicoercivity result and the \(\Gamma {\mathrm{-}}\limsup \) inequality. Finally, in Sect. 4 we introduce a numerical discretization and algorithmic scheme to perform some exemplary simulations of branched transportation networks.
2 Model summary and \(\Gamma \)-convergence result
Here we state in more detail the considered variational model for transportation networks and its phase field approximation as well as the \(\Gamma \)-convergence result.
2.1 Introduction of the energies
Before we state the original energy and its phase field approximation, let us briefly recall the objects representing the transportation networks.
Definition 1
(Divergence measure vector field and mass flux)
- 1.
A divergence measure vector field is a measure \({{\mathcal {F}}}\in {{\mathcal {M}}}({\overline{\Omega }};{\mathbf {R}}^2)\), whose weak divergence is a Radon measure, \({{\,\mathrm{div}\,}}{{\mathcal {F}}}\in {{\mathcal {M}}}({\overline{\Omega }})\), where the weak divergence is defined as
$$\begin{aligned} \int _{{\mathbf {R}}^2}\psi \,{\mathrm d}{{\,\mathrm{div}\,}}{{\mathcal {F}}}=-\int _{{\mathbf {R}}^2}\nabla \psi \cdot {\mathrm d}{{\mathcal {F}}}\qquad \text {for all }\psi \in {{\mathcal {C}}}^1({\mathbf {R}}^2)\text { with compact support.} \end{aligned}$$By [28], any divergence measure vector field \({{\mathcal {F}}}\) can be decomposed as

where \(S_{{\mathcal {F}}}\subset \Omega \) is countably 1-rectifiable, \(m_{{\mathcal {F}}}:S_{{\mathcal {F}}}\rightarrow [0,\infty )\) is
 -measurable,
\(\theta _{{\mathcal {F}}}:S_{{\mathcal {F}}}\rightarrow S^1\) is
-measurable,
\(\theta _{{\mathcal {F}}}:S_{{\mathcal {F}}}\rightarrow S^1\) is
 -measurable and orients the approximate tangent space of
\(S_{{\mathcal {F}}}\), and
\({{\mathcal {F}}}^\perp \) is
\({\mathcal {H}}^1\)-diffuse, that is,
\(|{{\mathcal {F}}}^\perp |(R)=0\) for any countably 1-rectifiable set
\(R\subset {\mathbf {R}}^2\) (similarly to the gradient of functions of bounded variation,
\({{\mathcal {F}}}^\perp \) could be decomposed into an absolutely continuous measure and a measure concentrated on a fractal set, often termed a Cantor measure).
-measurable and orients the approximate tangent space of
\(S_{{\mathcal {F}}}\), and
\({{\mathcal {F}}}^\perp \) is
\({\mathcal {H}}^1\)-diffuse, that is,
\(|{{\mathcal {F}}}^\perp |(R)=0\) for any countably 1-rectifiable set
\(R\subset {\mathbf {R}}^2\) (similarly to the gradient of functions of bounded variation,
\({{\mathcal {F}}}^\perp \) could be decomposed into an absolutely continuous measure and a measure concentrated on a fractal set, often termed a Cantor measure). - 2.
A divergence measure vector field \({{\mathcal {F}}}\) is polyhedral if it is a finite linear combination

of vector-valued line measures, where \(M\in {\mathbf {N}}\) and for \(i=1,\ldots ,M\) we have \(m_i\in {\mathbf {R}}\), \(e_i\subset {\mathbf {R}}^2\) a straight line segment, and \(\theta _i\) its unit tangent vector.
- 3.
Given \(\mu _+,\mu _-\in {{\mathcal {P}}}({\overline{\Omega }})\) with compact support in \(\Omega \), a mass flux between \(\mu _+\) and \(\mu _-\) is a divergence measure vector field \({{\mathcal {F}}}\) with \({{\,\mathrm{div}\,}}{{\mathcal {F}}}=\mu _+-\mu _-\). The set of mass fluxes between \(\mu _+\) and \(\mu _-\) is denoted
$$\begin{aligned} X^{\mu _+,\mu _-} =\{{{\mathcal {F}}}\in {{\mathcal {M}}}({\overline{\Omega }};{\mathbf {R}}^2)\,|\,{{\,\mathrm{div}\,}}{{\mathcal {F}}}=\mu _+-\mu _-\}{.} \end{aligned}$$
A mass flux between \(\mu _+\) and \(\mu _-\) can be interpreted as the material flow that transports the material from the initial mass distribution \(\mu _+\) to the final mass distribution \(\mu _-\). Next we specify the cost functional for branched transportation networks for which we will propose a phase field approximation.
Definition 2
(Cost functional)
- 1.
Given \(N\in {\mathbf {N}}\) and \(\alpha _0>\alpha _1>\cdots>\alpha _N>0\), \(0=\beta _0<\beta _1<\cdots<\beta _N<\infty \), we define the piecewise affine transport cost \(\tau :[0,\infty )\rightarrow [0,\infty )\),
$$\begin{aligned} \tau (m)=\min _{i=0,\ldots ,N}\{\alpha _im+\beta _i\}{.} \end{aligned}$$If \(\alpha _0=\infty \) we interpret \(\tau \) as
$$\begin{aligned} \tau (m)= {\left\{ \begin{array}{ll} 0&{}\text {if }m=0{,}\\ \min _{i=1,\ldots ,N}\{\alpha _im+\beta _i\}&{}\text {else.} \end{array}\right. } \end{aligned}$$ - 2.
We call \(\mu _+,\mu _-\in {{\mathcal {P}}}({\overline{\Omega }})\) an admissible source and sink if they have compact support in \(\Omega \) and in the case of \(\alpha _0=\infty \) can additionally be written as a finite linear combination of Dirac masses.
- 3.
Given admissible \(\mu _+,\mu _-\in {{\mathcal {P}}}({\overline{\Omega }})\), we define the cost functional \({\mathcal {E}}^{\mu _+,\mu _-}:X^{\mu _+,\mu _-}\rightarrow [0,\infty ]\),
$$\begin{aligned} {\mathcal {E}}^{\mu _+,\mu _-}[{{\mathcal {F}}}]= \int _{S_{{\mathcal {F}}}}\tau (m_{{\mathcal {F}}}(x))\,{\mathrm d}{\mathcal {H}}^1(x)+\tau '(0)|{{\mathcal {F}}}^\perp |({\overline{\Omega }}) \end{aligned}$$for \(\alpha _0<\infty \) (above, \(\tau '(0)=\alpha _0\) denotes the right derivative in 0) and otherwise
$$\begin{aligned} {\mathcal {E}}^{\mu _+,\mu _-}[{{\mathcal {F}}}]= {\left\{ \begin{array}{ll} \int _{S_{{\mathcal {F}}}}\tau (m_{{\mathcal {F}}}(x))\,{\mathrm d}{\mathcal {H}}^1(x)&{}\text {if }{{\mathcal {F}}}^\perp =0,\\ \infty &{}\text {else.} \end{array}\right. } \end{aligned}$$
Note that any nonnegative, concave, piecewise affine function \(\tau \) on \([0,\infty )\) can be represented in the form of Definition 2(1) (in particular, the opposite ordering of the \(\alpha _i\) and \(\beta _i\) is no restriction since \(\alpha \ge {\hat{\alpha }}\ \wedge \ \beta \ge {\hat{\beta }}\) would imply \(\min \{\alpha m+\beta ,{\hat{\alpha }} m+{\hat{\beta }}\}={\hat{\alpha }} m+{\hat{\beta }}\) for all \(m\ge 0\)).
The phase field functional approximating \({\mathcal {E}}^{\mu _+,\mu _-}\) will depend on a vector field \(\sigma \) approximating the mass flux and N Ambrosio–Tortorelli phase fields \(\varphi _1,\ldots ,\varphi _N\) that indicate which term in the definition of \(\tau \) is active.
Definition 3
(Phase field cost functional) Let \(\varepsilon >0\), \(p>1\), and \(\rho :{\mathbf {R}}^2\rightarrow [0,\infty )\) be a fixed smooth convolution kernel with support in the unit disk and \(\int _{{\mathbf {R}}^2}\rho \,{\mathrm d}x=1\).
- 1.
Given admissible source and sink \(\mu _+,\mu _-\in {{\mathcal {P}}}({\overline{\Omega }})\), the smoothed source and sink are
$$\begin{aligned} \mu _\pm ^\varepsilon =\rho _\varepsilon *\mu _\pm {,}\quad \text {where }\rho _\varepsilon =\tfrac{1}{\varepsilon ^2}\rho (\tfrac{\cdot }{\varepsilon }){.} \end{aligned}$$ - 2.
The set of admissible functions is
$$\begin{aligned}&X_\varepsilon ^{\mu _+,\mu _-} =\left\{ (\sigma ,\varphi _1,\ldots ,\varphi _N)\in L^{2}(\Omega ;{\mathbf {R}}^2)\times W^{1,2}(\Omega )^N\,\right| \\&\left. \,{{\,\mathrm{div}\,}}\sigma =\mu _+^\varepsilon -\mu _-^\varepsilon ,\,\varphi _1=\cdots =\varphi _N=1\text { on }\partial \Omega \right\} {.} \end{aligned}$$ - 3.
The phase field cost functional is given by \({\mathcal {E}}_\varepsilon ^{\mu _+,\mu _-}:X_\varepsilon ^{\mu _+,\mu _-}\rightarrow [0,\infty )\),
$$\begin{aligned} {\mathcal {E}}_\varepsilon ^{\mu _+,\mu _-}[\sigma ,\varphi _1,\ldots ,\varphi _N] =\int _\Omega \omega _\varepsilon \left( \alpha _0,\frac{\gamma _\varepsilon (x)}{\varepsilon },|\sigma (x)|\right) \,{\mathrm d}x +\sum _{i=1}^N\beta _i{\mathcal {L}}_\varepsilon [\varphi _i]{,} \end{aligned}$$where we abbreviated
$$\begin{aligned} {\mathcal {L}}_\varepsilon [\varphi ]&=\frac{1}{2}\int _\Omega \left[ \varepsilon |\nabla \varphi (x)|^2+\frac{(\varphi (x)-1)^2}{\varepsilon }\right] \,{\mathrm d}x{,}\\ \gamma _\varepsilon (x)&=\min _{i=1,\ldots ,N}\left\{ \varphi _i(x)^2+\alpha _i^2\varepsilon ^2/\beta _i\right\} {,}\\ \omega _\varepsilon \left( \alpha _0,\frac{\gamma _\varepsilon (x)}{\varepsilon },|\sigma (x)|\right)&=\left. {\left\{ \begin{array}{ll} \frac{\gamma _\varepsilon }{\varepsilon }\frac{|\sigma |^2}{2}&{}\text {if }|\sigma |\le \frac{\alpha _0}{\gamma _\varepsilon /\varepsilon }\\ \alpha _0(|\sigma |-\frac{\alpha _0}{2\gamma _\varepsilon /\varepsilon })&{}\text {if }|\sigma |>\frac{\alpha _0}{\gamma _\varepsilon /\varepsilon } \end{array}\right. }\right\} +\varepsilon ^p|\sigma (x)|^2&\text {for }\alpha _0<\infty {,}\\ \omega _\varepsilon \left( \alpha _0,\frac{\gamma _\varepsilon (x)}{\varepsilon },|\sigma (x)|\right)&=\frac{\gamma _\varepsilon }{\varepsilon }\frac{|\sigma |^2}{2}&\text {for }\alpha _0=\infty {.} \end{aligned}$$
Note that the pointwise minimum inside \(\gamma _\varepsilon \) is well-defined almost everywhere, since all elements of \(X_\varepsilon ^{\mu _+,\mu _-}\) are Lebesgue-measurable. Note also that for fixed phase fields \(\varphi _1,\ldots ,\varphi _N\) the phase field cost functional \({\mathcal {E}}_\varepsilon ^{\mu _+,\mu _-}\) is convex in \(\sigma \). This ensures the existence of minimizers for \({\mathcal {E}}_\varepsilon ^{\mu _+,\mu _-}\), which follows by a standard application of the direct method.
Proposition 2.1
(Existence of minimizers to the phase field functional) The phase field cost functional \({\mathcal {E}}_\varepsilon ^{\mu _+,\mu _-}\) has a minimizer \((\sigma ,\varphi _1,\ldots ,\varphi _N)\in X_\varepsilon ^{\mu _+,\mu _-}\).
Proof
The functional is bounded below by 0 and has a nonempty domain. Indeed, choose \({\hat{\varphi }}_1\equiv \cdots \equiv {\hat{\varphi }}_N\equiv 1\) and \({\hat{\sigma }}=\nabla \psi \), where \(\psi \) solves \(\Delta \psi =\mu _+^\varepsilon -\mu _-^\varepsilon \) in \(\Omega \) with Neumann boundary conditions \(\nabla \psi \cdot \nu _{\partial \Omega }=0\), \(\nu _{\partial \Omega }\) being the unit outward normal to \(\partial \Omega \). (Since \(\int _\Omega \mu _+^\varepsilon -\mu _-^\varepsilon \,{\mathrm d}x=0\), a solution \(\psi \) exists and lies in \(W^{2,2}(\Omega )\) by standard elliptic regularity.) Obviously, \(({\hat{\sigma }},{\hat{\varphi }}_1,\ldots ,{\hat{\varphi }}_N)\in X_\varepsilon ^{\mu _+,\mu _-}\) with \({\mathcal {E}}_\varepsilon ^{\mu _+,\mu _-}[{\hat{\sigma }},{\hat{\varphi }}_1,\ldots ,{\hat{\varphi }}_N]<\infty \).
\({\mathcal {E}}_\varepsilon ^{\mu _+,\mu _-}\) is coercive with respect to \(H=L^{2}(\Omega ;{\mathbf {R}}^2)\times W^{1,2}(\Omega )^N\), and \(X_\varepsilon ^{\mu _+,\mu _-}\) is closed with respect to weak convergence in H. Furthermore, the integrand of \({\mathcal {E}}_\varepsilon ^{\mu _+,\mu _-}\) is convex in \(\sigma (x)\) and the \(\nabla \varphi _i(x)\) as well as continuous in \(\sigma (x)\) and the \(\varphi _i(x)\), thus \({\mathcal {E}}_\varepsilon ^{\mu _+,\mu _-}\) is weakly sequentially lower semi-continuous by Ioffe’s theorem [1, Thm. 5.8] so that existence of minimizers follows by the direct method of the calculus of variations. \(\square \)
Remark 1
(Regularization of \(\sigma \)) Note that the phase field cost functional \({\mathcal {E}}_\varepsilon ^{\mu _+,\mu _-}\) is \(L^2(\Omega ;{\mathbf {R}}^2)\)-coercive in \(\sigma \), which is essential to have sequentially weak compactness of subsets of \(X_\varepsilon ^{\mu _+,\mu _-}\) with finite cost (and as a consequence existence of minimizers). For \(\alpha _0<\infty \) this is ensured by the regularization term \(\varepsilon ^p|\sigma |^2\) (which has no other purpose). Without it, the functional would only feature weak-\(*\) coercivity for \(\sigma \) in \({{\mathcal {M}}}({\overline{\Omega }};{\mathbf {R}}^2)\), however, the integral \(\int _\Omega \omega _\varepsilon \big (\alpha _0,\frac{\gamma _\varepsilon (x)}{\varepsilon },|\sigma (x)|\big )\,{\mathrm d}x\) with \(\gamma _\varepsilon \) Lebesgue-measurable would in general not be well-defined for \(\sigma \in {{\mathcal {M}}}({\overline{\Omega }};{\mathbf {R}}^2)\).
Remark 2
(Motivation of \(\omega _\varepsilon \left( \alpha _0,\frac{\gamma _\varepsilon (x)}{\varepsilon },|\sigma (x)|\right) \) via relaxation). Keeping the phase fields \(\varphi _1,\ldots ,\varphi _N\) fixed and ignoring the regularizing term \(\varepsilon ^p|\sigma |^2\), the integrand \(\omega _\varepsilon (\alpha _0,\frac{\gamma _\varepsilon }{\varepsilon },|\sigma |)\) is the convexification in \(\sigma \) of
which shows the intuition of the phase field functional much clearer. Indeed, the minimum over \(N+1\) terms parallels the minimum in the definition of \(\tau \), and the \(i^{\mathrm{th}}\) term for \(i=0,\ldots ,N\) describes (part of) the transportation cost \(\alpha _im+\beta _i\). However, since the above is not convex with respect to \(\sigma \), a functional with this integrand would not be weakly lower semi-continuous in \(\sigma \) and consequently possess no minimizers in general. Taking the lower semi-continuous envelope corresponds to replacing the above by \(\omega _\varepsilon (\alpha _0,\frac{\gamma _\varepsilon }{\varepsilon },|\sigma |)\) (note that this only ensures existence of minimizers, but will not change the \(\Gamma \)-limit of the phase field functional).
2.2 Statement of \(\Gamma \)-convergence and equi-coercivity
Let us extend both \({\mathcal {E}}^{\mu _+,\mu _-}\) and \({\mathcal {E}}_\varepsilon ^{\mu _+,\mu _-}\) to \({{\mathcal {M}}}({\overline{\Omega }};{\mathbf {R}}^2)\times L^1(\Omega )^N\) via
We have the following \(\Gamma \)-convergence result.
Theorem 2.1
(Convergence of phase field cost functional) For admissible \(\mu _+,\mu _-\in {{\mathcal {P}}}({\overline{\Omega }})\) we have
where the \(\Gamma \)-limit is with respect to weak-\(*\) convergence in \({{\mathcal {M}}}({\overline{\Omega }};{\mathbf {R}}^2)\) and strong convergence in \(L^1(\Omega )^N\).
The proof of this result is provided in the next section. Together with the following equicoercivity statement, whose proof is also deferred to the next section, we have that minimizers of the phase field cost functional \(E_\varepsilon ^{\mu _+,\mu _-}\) approximate minimizers of the original cost functional \(E^{\mu _+,\mu _-}\).
Theorem 2.2
(Equicoercivity) For \(\varepsilon \rightarrow 0\) let \((\sigma ^\varepsilon ,\varphi _1^\varepsilon ,\ldots ,\varphi _N^\varepsilon )\) be a sequence with uniformly bounded phase field cost functional \(E_\varepsilon ^{\mu _+,\mu _-}[\sigma ^\varepsilon ,\varphi _1^\varepsilon ,\ldots ,\varphi _N^\varepsilon ]<C<\infty \). Then, along a subsequence, \(\sigma ^\varepsilon {\mathop {\rightharpoonup }\limits ^{*}}\sigma \) in \({{\mathcal {M}}}({\overline{\Omega }};{\mathbf {R}}^2)\) for some \(\sigma \in {{\mathcal {M}}}({\overline{\Omega }};{\mathbf {R}}^2)\) and \(\varphi _i^\varepsilon \rightarrow 1\) in \(L^1(\Omega )\), \(i=1,\ldots ,N\).
As a consequence, if \(\mu _+,\mu _-\in {{\mathcal {P}}}({\overline{\Omega }})\) are admissible and such that there exists \({{\mathcal {F}}}\in X^{\mu _+,\mu _-}\) with \({\mathcal {E}}^{\mu _+,\mu _-}[{{\mathcal {F}}}]<\infty \), then any sequence of minimizers of \(E_\varepsilon ^{\mu _+,\mu _-}\) contains a subsequence converging to a minimizer of \(E^{\mu _+,\mu _-}\) as \(\varepsilon \rightarrow 0\).
Remark 3
(Phase field boundary conditions) Recall that we imposed boundary conditions \(\varphi _i=1\) on \(\partial \Omega \). Without those, the recovery sequence from the following section could easily be adapted such that all full phase field profiles near the boundary will be replaced by half, one-sided phase field profiles. It is straightforward to show that the resulting limit functional would become
where fluxes along the boundary are cheaper and thus preferred.
Remark 4
(Divergence measure vector fields and flat chains) Any divergence measure vector field can be identified with a flat 1-chain or a locally normal 1-current (see for instance [28, Sect. 5] or [8, Rem. 2.29(3)]; comprehensive references for flat chains and currents are [16, 30]). Furthermore, for a sequence \(\sigma ^j\), \(j\in {\mathbf {N}}\), of divergence measure vector fields with uniformly bounded \(\Vert {{\,\mathrm{div}\,}}\sigma ^j\Vert _{{\mathcal {M}}}\), weak-\(*\) convergence is equivalent to convergence of the corresponding flat 1-chains with respect to the flat norm [8, Rem. 2.29(4)]. Analogously, scalar Radon measures of finite total variation and bounded support can be identified with flat 0-chains or locally normal 0-currents [29, Thm. 2.2], and for a bounded sequence of compactly supported scalar measures, weak-\(*\) convergence is equivalent to convergence with respect to the flat norm of the corresponding flat 0-chains.
From the above it follows that in Theorems 2.1 and 2.2 we may replace weak-\(*\) convergence by convergence with respect to the flat norm. Indeed, for both results it suffices to consider sequences \((\sigma ^\varepsilon ,\varphi _1^\varepsilon ,\ldots ,\varphi _N^\varepsilon )\) with uniformly bounded cost \(E_\varepsilon ^{\mu _+,\mu _-}\). For those we have uniformly bounded \(\Vert \sigma ^\varepsilon \Vert _{{\mathcal {M}}}\) (by Theorem 2.2) as well as uniformly bounded \(\Vert {{\,\mathrm{div}\,}}\sigma ^\varepsilon \Vert _{{\mathcal {M}}}=\Vert \mu _+^\varepsilon -\mu _-^\varepsilon \Vert _{{\mathcal {M}}}\) so that weak-\(*\) and flat norm convergence are equivalent.
3 The \(\Gamma \)-limit of the phase field functional
In this section we prove the \(\Gamma \)-convergence result. As is canonical, we begin with the \(\liminf \)-inequality, after which we prove the \(\limsup \)-inequality as well as equicoercivity.
3.1 The \(\Gamma {\mathrm{-}}\liminf \) inequality for the dimension-reduced problem
Here we consider the energy reduced to codimension-1 slices of the domain \(\Omega \). In our particular case of a two-dimensional domain, each slice is just one-dimensional, which will simplify notation a little (the procedure would be the same for higher codimensions, though). The reduced functional depends on the (scalar) normal flux \(\vartheta \) through the slice as well as the scalar phase fields \(\varphi _1,\ldots ,\varphi _N\) restricted to the slice.
Definition 4
(Reduced functionals) Let \(I\subset {\mathbf {R}}\) be an open interval.
- 1.
The decomposition of a measure \(\vartheta \in {{\mathcal {M}}}({\overline{I}})\) into its atoms and the remainder is denoted

where \(S_\vartheta \subset {\overline{I}}\) is the set of atoms of \(\vartheta \), \(m_\vartheta :S_\vartheta \rightarrow {\mathbf {R}}\) is
 -measurable, and \(\vartheta ^\perp \) contains no atoms.
-measurable, and \(\vartheta ^\perp \) contains no atoms. - 2.
We define the reduced cost functional \({\mathcal {G}}[\cdot ;I]:{{\mathcal {M}}}({\overline{I}})\rightarrow [0,\infty )\),
$$\begin{aligned} {\mathcal {G}}[\vartheta ;I]=\sum _{x\in S_\vartheta \cap I}\tau (|m_\vartheta (x)|)+\tau '(0)|\vartheta ^\perp |(I)\, \end{aligned}$$for \(\alpha _0<\infty \) (above, \(\tau '(0)=\alpha _0\) denotes the right derivative in 0) and otherwise
$$\begin{aligned} {\mathcal {G}}[\vartheta ;I]= {\left\{ \begin{array}{ll} \sum _{x\in S_\vartheta \cap I}\tau (|m_\vartheta (x)|)&{}\text {if }\vartheta ^\perp =0,\\ \infty &{}\text {else.} \end{array}\right. } \end{aligned}$$Its extension to \({{\mathcal {M}}}({\overline{I}})\times L^1(I)^N\) is \({G}[\cdot ;I]:{{\mathcal {M}}}({\overline{I}})\times L^1(I)^N\rightarrow [0,\infty )\),
$$\begin{aligned} {G}[\vartheta ,\varphi _1,\ldots ,\varphi _N;I]= {\left\{ \begin{array}{ll} {\mathcal {G}}[\vartheta ;I]&{}\text {if }\varphi _1=\cdots =\varphi _N=1\text { almost everywhere,}\\ \infty &{}\text {else.} \end{array}\right. } \end{aligned}$$ - 3.
For any \((\vartheta ,\varphi _1,\ldots ,\varphi _N)\in L^2(I)\times W^{1,2}(I)^N\) we define the reduced phase field functional on I as
$$\begin{aligned} {\mathcal {G}}_\varepsilon [\vartheta ,\varphi _1,\ldots ,\varphi _N;I]&=\int _I\omega _\varepsilon \left( \alpha _0,\tfrac{\gamma _\varepsilon (x)}{\varepsilon },|\vartheta (x)|\right) \,{\mathrm d}x +\sum _{i=1}^N\beta _i{\mathcal {L}}_\varepsilon [\varphi _i;I]{,}\\ {\mathcal {L}}_\varepsilon [\varphi ;I]&=\frac{1}{2}\int _I\left[ \varepsilon |\varphi '(x)|^2+\frac{(\varphi (x)-1)^2}{\varepsilon }\right] \,{\mathrm d}x{,} \end{aligned}$$with \(\omega _\varepsilon \) and \(\gamma _\varepsilon \) from Definition 3. Likewise we define \({G}_\varepsilon [\cdot ;I]:{{\mathcal {M}}}({\overline{I}})\times L^1(I)^N\rightarrow [0,\infty )\),
$$\begin{aligned} {G}_\varepsilon [\vartheta ,\varphi _1,\ldots ,\varphi _N;I] = {\left\{ \begin{array}{ll} {\mathcal {G}}_\varepsilon [\vartheta ,\varphi _1,\ldots ,\varphi _N;I]&{}\text {if }(\vartheta ,\varphi _1,\ldots ,\varphi _N)\in L^2(I)\times W^{1,2}(I)^{N},\\ \infty &{}\text {else.} \end{array}\right. } \end{aligned}$$
For notational convenience, we next introduce the sets \(K_i^\varepsilon \) on which the pointwise minimum inside \({\mathcal {G}}_\varepsilon \) (or also \({\mathcal {E}}_\varepsilon ^{\mu _+,\mu _-}\)) is realized by the \(i^{\mathrm{th}}\) element.
Definition 5
(Cost domains) For given \((\vartheta ,\varphi _1,\ldots ,\varphi _N)\in L^2(I)\times W^{1,2}(I)^{N}\) we set
The sets are analogously defined for \((\sigma ,\varphi _1,\ldots ,\varphi _N)\in L^2(\Omega ;{\mathbf {R}}^2)\times W^{1,2}(\Omega )^N\), where we use the same notation (which case is referred to will be clear from the context).
We now show the following lower bound on the energy, from which the \(\Gamma {\mathrm{-}}\liminf \) inequality for the dimension-reduced situation will automatically follow.
Proposition 3.1
(Lower bound on reduced phase field functional) Let \(I=(a,b)\subset {\mathbf {R}}\) and \(0\le \delta \le \eta \le 1\). Let \(I_\eta \subset \{x\in I\,|\,\varphi _1(x),\ldots ,\varphi _N(x)\ge \eta \}\), and denote the collection of connected components of \(I{\setminus } I_\eta \) by \({\mathcal {C}}_\eta \). Furthermore define the subcollection of connected components \({\mathcal {C}}_\eta ^\ge =\{C\in {\mathcal {C}}_\eta \,|\,\inf _C\varphi _1,\ldots ,\inf _C\varphi _N\ge \delta \}\) and \(C^\ge =\bigcup _{C\in {\mathcal {C}}_\eta ^\ge }C\). Finally assume \(\varphi _i(a),\varphi _i(b)\ge \eta \) for all \(i=1,\ldots ,N\).
- 1.
If \(\alpha _0<\infty \) we have
$$\begin{aligned}&{\mathcal {G}}_\varepsilon [\vartheta ,\varphi _1,\ldots ,\varphi _N;I] \ge (\eta -\delta )^2\int _{I_\eta \cup C^\ge }\alpha _0|\vartheta |\,{\mathrm d}x\,\\&\quad +\,(\eta -\delta )^2\sum _{C\in {\mathcal {C}}_\eta {\setminus }{\mathcal {C}}_\eta ^\ge }\max \left\{ \beta _1,\tau \left( \int _C|\vartheta |\,{\mathrm d}x\right) \right\} \,-\,\alpha _0^2{\mathcal {H}}^1(I)\frac{\varepsilon }{\delta ^2}{.} \end{aligned}$$ - 2.
If \(\alpha _0=\infty \) we have
$$\begin{aligned}&{\mathcal {G}}_\varepsilon [\vartheta ,\varphi _1,\ldots ,\varphi _N;I] \ge \frac{\delta ^2}{2\varepsilon {\mathcal {H}}^1(I)}\left( \int _{I_\eta \cup C^\ge }|\vartheta |\,{\mathrm d}x\right) ^2\\&\quad +(\eta -\delta )^2\sum _{C\in {\mathcal {C}}_\eta {\setminus }{\mathcal {C}}_\eta ^\ge }\max \left\{ \beta _1,\tau \left( \int _C|\vartheta |\,{\mathrm d}x\right) \right\} \, -\,\alpha _1^2{\mathcal {H}}^1(I)\frac{\varepsilon }{\delta ^2}{.} \end{aligned}$$
Proof
1. (\(\alpha _0<\infty \)) We first show that without loss of generality we may assume
The motivation is that there may be regions in which a phase field \(\varphi _i\) is (still) small, but in which we actually have to pay \(\alpha _0|\vartheta |\). Thus, in those regions we would like \(\omega _\varepsilon (\alpha _0,\frac{\gamma _\varepsilon (x)}{\varepsilon },|\vartheta (x)|)\) to approximate \(\alpha _0|\vartheta (x)|\) sufficiently well, and the above condition on \(\vartheta \) ensures
We achieve (2) by modifying \(\vartheta \) while keeping the cost as well as \(\int _{I_\eta }|\vartheta |\,{\mathrm d}x\) and \(\int _C|\vartheta |\,{\mathrm d}x\) for all \(C\in {\mathcal {C}}_\eta \) the same so that the overall estimate of the proposition is not affected. The modification mimics the relaxation from Remark 2: the modified \(\vartheta \) oscillates between small and very large values. Indeed, for fixed \(C\in {\mathcal {C}}_\eta \cup \{I_\eta \}\) and \(x\in C\) set
where \(t_C\) is chosen such that \(\int _C|{\hat{\vartheta }}|\,{\mathrm d}x=\int _C|\vartheta |\,{\mathrm d}x\) (this is possible, since for \(t_C=\infty \) we have \(|{\hat{\vartheta }}|\ge |\vartheta |\) and for \(t_C=-\infty \) we have \(|{\hat{\vartheta }}|\le |\vartheta |\) everywhere on C). The cost did not change by this modification since
Note that the modification \({\hat{\vartheta }}\) has a different set \(K_0^\varepsilon ({\hat{\vartheta }},\varphi _1,\ldots ,\varphi _N;I)\) than the original \(\vartheta \). Indeed, by definition of \({\hat{\vartheta }}\) we have \(K_0^\varepsilon ({\hat{\vartheta }},\varphi _1,\ldots ,\varphi _N;I)\subset K_0^\varepsilon (\vartheta ,\varphi _1,\ldots ,\varphi _N;I)\) and \(|\vartheta (x)|\ge \frac{\alpha _0\varepsilon }{2\gamma _\varepsilon (x)}\frac{1}{1-(\eta -\delta )^2}\) on \(K_0^\varepsilon ({\hat{\vartheta }},\varphi _1,\ldots ,\varphi _N;I)\), as desired.
Let us now abbreviate \(m_0=\int _{(I_\eta \cup C^\ge ){\setminus } K_0^\varepsilon }|\vartheta |\,{\mathrm d}x\). Using the definition of \(\omega _\varepsilon \) as well as \(\gamma _\varepsilon \ge \delta ^2\) on \(I_\eta \cup C^\ge \) we compute
where we have employed (3) and Jensen’s inequality. Upon minimizing in \(m_0\), which yields the optimal value \(\alpha _0\varepsilon {\mathcal {H}}^1((I_\eta \cup C^\ge ){\setminus } K_0^\varepsilon )/\delta ^2\) for \(m_0\), we thus obtain
Next consider for each \(C\in {\mathcal {C}}_\eta {\setminus }{\mathcal {C}}_\eta ^\ge \) and \(i=1,\ldots ,N\) the subsets
and abbreviate \(m_A=\int _A|\vartheta |\,{\mathrm d}x\) for any \(A\subset I\). Using Young’s inequality, for \(i,j=1,\ldots ,N\) we have
Similarly, using Jensen’s inequality we have
where in the last step we optimized for \({\mathcal {H}}^1(C_i^<)\). Finally, if \(\inf _C\varphi _i\le \delta \) we have (using Young’s inequality)
where (c, d) and (e, f) denote the first and the last connected component of \(C{\setminus } C_i^<\).
Next, for \(C\in {\mathcal {C}}_\eta {\setminus }{\mathcal {C}}_\eta ^\ge \) define \(j(C)=\max \{j\in \{1,\ldots ,N\}\,|\,\inf _C\varphi _j<\delta \}\). Summarizing the previous estimates we obtain

Finally, we obtain the dTuesday, December 31, 2019 at 11:22 amesired estimate,
2. (\(\alpha _0=\infty \)) In this case the set \(K_0^\varepsilon \) is empty, and the cost functional reduces to
With Jensen’s inequality we thus compute
Furthermore, the same calculation as in the case \(\alpha _0<\infty \) yields
so that we obtain the desired estimate
\(\square \)
Corollary 3.1
(\(\Gamma {\mathrm{-}}\liminf \) inequality for reduced functionals) Let \(J\subset {\mathbf {R}}\) be open and bounded, \(\vartheta \in {{\mathcal {M}}}({\overline{J}})\), and \(\varphi _1,\ldots ,\varphi _N\in L^1(\Omega )\). Then
with respect to weak-\(*\) convergence in \({{\mathcal {M}}}({\overline{J}})\) and strong convergence in \(L^1(J)^N\).
Proof
Let \((\vartheta ^\varepsilon ,\varphi _1^\varepsilon ,\ldots ,\varphi _N^\varepsilon )\) be an arbitrary sequence converging to \((\vartheta ,\varphi _1,\ldots ,\varphi _N)\) in the considered topology as \(\varepsilon \rightarrow 0\), and assume without loss of generality that the limit inferior of \({G}_\varepsilon [\vartheta ^\varepsilon ,\varphi _1^\varepsilon ,\ldots ,\varphi _N^\varepsilon ;J]\) is actually a limit and is finite (else there is nothing to show). Further we may assume \({G}_\varepsilon [\vartheta ^\varepsilon ,\varphi _1^\varepsilon ,\ldots ,\varphi _N^\varepsilon ;J]={\mathcal {G}}_\varepsilon [\vartheta ^\varepsilon ,\varphi _1^\varepsilon ,\ldots ,\varphi _N^\varepsilon ;J]\) along the sequence.
It suffices to show the \(\liminf \)-inequality for each connected component \({\tilde{I}}=(a,b)\) of J separately. Due to \({\mathcal {G}}_\varepsilon [\vartheta ^\varepsilon ,\varphi _1^\varepsilon ,\ldots ,\varphi _N^\varepsilon ;{\tilde{I}}]\ge \frac{\beta _i}{2\varepsilon }\Vert \varphi _i^\varepsilon -1\Vert _{L^2}^2\) for \(i=1,\ldots ,N\) we must have \(\varphi _i^\varepsilon \rightarrow 1\) in \(L^2({\tilde{I}})\) and thus also in \(L^1({\tilde{I}})\) so that \(\varphi _i=1\). Even more, after passing to another subsequence, by Egorov’s theorem all \(\varphi _i^\varepsilon \) converge uniformly to 1 outside a set of arbitrarily small measure. In particular, for any \(\xi >0\) we can find an open interval \((a+\xi ,b-\xi )\subset I\subset {\tilde{I}}\) such that \(\varphi _i^\varepsilon \rightarrow 1\) uniformly on \(\partial I\), and for any \(\eta <1\) there is an open set \(I_\eta \subset I\) with \({\mathcal {H}}^1(I{\setminus } I_\eta )\le 1-\eta \) such that \(\varphi _i^\varepsilon \ge \eta \) on \(I_\eta \cup \partial I\) for all \(i=1,\ldots ,N\) and all \(\varepsilon \) small enough.
We now choose \(\delta =\varepsilon ^{1/3}\) and \(\eta =1-\varepsilon \) and denote by \({\mathcal {C}}_\eta (\varepsilon )\) and \({\mathcal {C}}_\eta ^\ge (\varepsilon )\) the collections of connected components of \(I{\setminus } I_\eta \) from Proposition 3.1 (which now depend on \(\varepsilon \)). Further we abbreviate \({\mathcal {C}}_\eta ^<(\varepsilon )={\mathcal {C}}_\eta (\varepsilon ){\setminus }{\mathcal {C}}_\eta ^\ge (\varepsilon )\). The bound of Proposition 3.1 implies that the number of elements in \({\mathcal {C}}_\eta ^<(\varepsilon )\) is bounded uniformly in \(\varepsilon \) and \(\eta \). Passing to another subsequence we may assume \({\mathcal {C}}_\eta ^<(\varepsilon )\) to contain K sets \(C_1(\varepsilon ),\ldots ,C_K(\varepsilon )\) whose midpoints converge to \(x_1,\ldots ,x_K\in {\overline{I}}\), respectively. Thus for an arbitrary \(\zeta >0\) we have that for all \(\varepsilon \) small enough each \(C\in {\mathcal {C}}_\eta ^<(\varepsilon )\) lies inside the closed \(\zeta \)-neighbourhood \(B_\zeta (\{x_1,\ldots ,x_K\})\) of \(\{x_1,\ldots ,x_K\}\).
Now for \(\alpha _0<\infty \) we obtain from Proposition 3.1
where in the second inequality we used
for all measurable \(A,B,C\subset I\) (due to the subadditivity of \(\tau \)) and in the third inequality we used \(\tau (m)\le \alpha _0m\) as well as the lower semi-continuity of the mass on an open set. Letting now \(\zeta \rightarrow 0\) (so that by the \(\sigma \)-continuity of \(\vartheta \) we have \(|\vartheta |(I{\setminus } B_\zeta (\{x_1,\ldots ,x_K\}))\rightarrow |\vartheta |(I{\setminus }\{x_1,\ldots ,x_K\})\)) we obtain
If on the other hand \(\alpha _0=\infty \) we obtain from Proposition 3.1
which implies \(|\vartheta |(I{\setminus }\{x_1,\ldots ,x_K\})=0\) and thus \(|\vartheta ^\perp |({\overline{I}})=0\) as well as \(S_\vartheta \cap {\overline{I}}\subset \{x_1,\ldots ,x_K\}\). Next note that for all \(i\in \{1,\ldots ,K\}\) with \(|m_\vartheta (x_i)|>0\) we have \(\int _{C_i(\varepsilon )}|\vartheta ^\varepsilon |\,{\mathrm d}x>0\) for all \(\varepsilon \) small enough. Indeed,
where \(\int _{B_\zeta (\{x_i\}){\setminus } C_i(\varepsilon )}|\vartheta ^\varepsilon |\,{\mathrm d}x\) decreases to zero by Proposition 3.1. Therefore, Proposition 3.1 implies
where in the second inequality we used \(\tau (m_1+m_2)\le \tau (m_1)+\alpha _1m_2\) for any \(m_1>0\), \(m_2\ge 0\) and in the third we optimized in \(\int _{B_\zeta (\{x_i\}){\setminus } C_i(\varepsilon )}|\vartheta ^\varepsilon |\,{\mathrm d}x\).
The proof is concluded by letting \(\xi \rightarrow 0\) and noting \(\liminf _{\xi \rightarrow 0}{\mathcal {G}}[\vartheta ;I]\ge {\mathcal {G}}[\vartheta ;{\tilde{I}}]\). \(\square \)
3.2 Slicing of vector-valued measures
We derive now some technical construction for divergence measure vector fields which are needed to reduce the \(\Gamma {\mathrm{-}}\liminf \) inequality to the lower-dimensional setting of the previous section. In particular, we will introduce slices of a divergence measure vector field, which in the language of geometric measure theory correspond to slices of currents. We will slice in the direction of a unitary vector \(\xi \in {\mathbf {S}}^{n-1}\) with orthogonal hyperplanes of the form
The orthogonal projection onto \(H_{\xi ,t}\) is denoted
The slicing will essentially be performed via disintegration. Let \(\sigma \) be a compactly supported divergence measure vector field. By the Disintegration Theorem [1, Thm. 2.28], for all \(\xi \in {\mathbf {S}}^{n-1}\) and almost all \(t\in {\mathbf {R}}\) there exists a unique measure \(\nu _{\xi ,t}\in {{\mathcal {M}}}(H_{\xi ,t})\) such that
We decompose \({{\pi _\xi }_{\#}|}\sigma \cdot \xi |\) into its absolutely continuous and singular part according to
for \({\mathrm d}t\) the Lebesgue measure on \({\mathbf {R}}\).
Lemma 3.1
For any \(\xi \in {\mathbf {S}}^{n-1}\) and any compactly supported divergence measure vector field \(\sigma \) we have \(\sigma _\xi ^\perp =0\), that is, the measure \({{\pi _\xi }_{\#}|\sigma \cdot \xi |}=\sigma _\xi (t)\,{\mathrm d}t\) is absolutely continuous with respect to the Lebesgue measure on \({\mathbf {R}}\). Moreover, for almost all \(t\in {\mathbf {R}}\) and any compactly supported \(\theta \in {{\mathcal {C}}}^\infty ({\mathbf {R}}^n)\) we have
Proof
Abbreviate \(H=\xi ^\perp =H_{\xi ,0}\) with corresponding orthogonal projection \(\pi _H\), let \(\phi \in {{\mathcal {C}}}^\infty (H)\) and \(\psi \in {{\mathcal {C}}}^\infty ({\mathbf {R}})\) be compactly supported, and define
Introducing \(\Psi (t)=\int _{-\infty }^t\psi (s)\,{\mathrm d}s\) we obtain via the chain and product rule
so that (denoting by \(\chi _A\) the characteristic function of a set A)
(Note that we could just as well have used \(\chi _{\{\xi \cdot x>s\}}\) instead of \(\chi _{\{\xi \cdot x\ge s\}}\), which would ultimately lead to integration domains \(\{\xi \cdot x\le t\}\) in (4); for almost all t this will be the same.) Applying the Fubini–Tonelli Theorem we obtain
where in the second step we just added \(0=\int _{{\mathbf {R}}^n}\nabla [\phi \circ \pi _H]\cdot {\mathrm d}\sigma +\int _{{\mathbf {R}}^n}\phi \circ \pi _H\,{\mathrm d}{{\,\mathrm{div}\,}}\sigma \) in the square brackets. On the other hand, using the disintegration of \(\sigma \cdot \xi \) we also have
Comparing both expressions for \(I(\phi ,\psi )\) we can identify
Since the right-hand side has no singular component with respect to the Lebesgue measure, we deduce \(\left[ \int _{H_{\xi ,s}}\phi (\pi _H(y))\,{\mathrm d}\nu _{\xi ,s}(y)\right] \sigma _\xi ^\perp (s)=0\). Now note that any compactly supported function in \({{\mathcal {C}}}^0({\mathbf {R}}^n)\) or \({{\mathcal {C}}}^1({\mathbf {R}}^n)\) can be arbitrarily well approximated (in the respective norm) by finite linear combinations of tensor products \((\phi \circ \pi _H)(\psi \circ \pi _\xi )\) with \(\phi \in {{\mathcal {C}}}^\infty (H)\) and \(\psi \in {{\mathcal {C}}}^\infty ({\mathbf {R}})\) with compact support. Thus, the above implies \(\int _{\mathbf {R}}\left[ \int _{H_{\xi ,s}}\theta (y)\,{\mathrm d}\nu _{\xi ,s}(y)\right] {\mathrm d}\sigma _\xi ^\perp (s)=0\) for any compactly supported \(\theta \in {{\mathcal {C}}}^0({\mathbf {R}}^n)\) so that
Summarizing, we have \(\sigma \cdot \xi =\sigma _\xi (s)\nu _{\xi ,s}\otimes {\mathrm d}s\) and
for all compactly supported \(\phi \in {{\mathcal {C}}}^\infty (H)\). Note that the right-hand side is left-continuous in s so that the left-hand side is as well. Consequently, \(\sigma _\xi (s)\nu _{\xi ,s}\) is left-continuous in s with respect to weak-* convergence. Now let \(\chi \in {{\mathcal {C}}}^\infty ({\mathbf {R}})\) with \(\chi =1\) on \((-\infty ,0]\), \(\chi =0\) on \([1,\infty )\), and \(0\le \chi \le 1\), and define for \(\rho >0\)
In the distributional sense we have
so that for any compactly supported \(\theta \in {{\mathcal {C}}}^\infty ({\mathbf {R}}^n)\) we have
Letting \(\rho \rightarrow 0\) and using the left-continuity of \(\sigma _\xi (s)\nu _{\xi ,s}\) in s we arrive at (4). \(\square \)
We now define the slice of a divergence measure vector field as the measure obtained via disintegration with respect to the one-dimensional Lebesgue measure.
Definition 6
(Sliced sets, functions, and measures) Let \(\xi \in {\mathbf {S}}^{n-1}\) and \(t\in {\mathbf {R}}\).
- 1.
For \(A\subset {\mathbf {R}}^n\) we define the sliced set \(A_{\xi ,t}=A\cap H_{\xi ,t}\).
- 2.
For \(f:A\rightarrow {\mathbf {R}}\) we define the sliced function \(f_{\xi ,t}:A_{\xi ,t}\rightarrow {\mathbf {R}}\), \(f_{\xi ,t}=f|_{A_{\xi ,t}}\). For \(f:A\rightarrow {\mathbf {R}}^n\) we define \(f_{\xi ,t}:A_{\xi ,t}\rightarrow {\mathbf {R}}^n\), \(f_{\xi ,t}=\xi \cdot f|_{A_{\xi ,t}}\).
- 3.
We define the sliced measure of a compactly supported divergence measure vector field \(\sigma \) as
$$\begin{aligned} \sigma _{\xi ,t}=\sigma _\xi (t)\;\nu _{\xi ,t}{.} \end{aligned}$$By Lemma 3.1 it holds \(\sigma \cdot \xi =\sigma _{\xi ,t}\otimes {\mathrm d}t\).
Remark 5
(Properties of sliced functions and measures)
- 1.
By Fubini’s theorem it follows that for any function f of Sobolev-type \(W^{m,p}\) the corresponding sliced function \(f_{\xi ,t}\) is well-defined and also of Sobolev-type \(W^{m,p}\) for almost all \((\xi ,t)\in {\mathbf {S}}^{n-1}\times {\mathbf {R}}\). For the same reason, strong convergence \(f_j\rightarrow _{j\rightarrow \infty } f\) in \(W^{m,p}\) implies strong convergence \((f_j)_{\xi ,t}\rightarrow f_{\xi ,t}\) in \(W^{m,p}\) on the sliced domain.
- 2.
The definitions of sliced functions and measures are consistent in the following sense. If we identify a Lebesgue function f with the measure \(\chi =f{\mathcal {L}}\) for \({\mathcal {L}}\) the Lebesgue measure, then the same identification holds between \(f_{\xi ,t}\) and \(\chi _{\xi ,t}\) for almost all \((\xi ,t)\in {\mathbf {S}}^{n-1}\times {\mathbf {R}}\).
- 3.
Let \(\sigma \) be a divergence measure vector field, then the properties [1, Thm. 2.28] of the disintegration \(\sigma \cdot \xi =\nu _{\xi ,t}\otimes {{\pi _\xi }_{\#}|}\sigma \cdot \xi |(t)=\nu _{\xi ,t}\otimes \sigma _\xi (t)\,{\mathrm d}t=\sigma _{\xi ,t}\otimes {\mathrm d}t\) immediately imply the following. The map \(t\mapsto \Vert \sigma _{\xi ,t}\Vert _{{{\mathcal {M}}}}\) is integrable and satisfies
$$\begin{aligned} \int _{{\mathbf {R}}}\Vert \sigma _{\xi ,t}\Vert _{{\mathcal {M}}}\,{\mathrm d}t = \int _{{\mathbf {R}}} \sigma _\xi (t)\,{\mathrm d}t =\Vert \sigma \cdot \xi \Vert _{{\mathcal {M}}}{.} \end{aligned}$$Furthermore, for any measurable function \(f:{\mathbf {R}}^n\rightarrow {\mathbf {R}}\), absolutely integrable with respect to \(|\sigma \cdot \xi |\), it holds
$$\begin{aligned} \int _{{\mathbf {R}}^n}f(x)\,{\mathrm d}\sigma \cdot \xi =\int _{\mathbf {R}}\int _{H_{\xi ,t}} f(x)\,{\mathrm d}\nu _{\xi ,t}(x)\,{\mathrm d}{{\pi _\xi }_{\#}|}\sigma \cdot \xi |(t) =\int _{\mathbf {R}}\int _{H_{\xi ,t}} f(x)\,{\mathrm d}\sigma _{\xi ,t}(x)\,{\mathrm d}t{.} \end{aligned}$$
We briefly relate our definition of sliced measures to other notions of slices from the literature.
Remark 6
(Notions of slices)
- 1.
Let \({\mathrm {Lip}}(A)\) denote the set of bounded Lipschitz functions on \(A\subset {\mathbf {R}}^n\). An alternative definition of the slice of a divergence measure vector field \(\sigma \) was introduced by Šilhavý [28] as the linear operator
$$\begin{aligned} \sigma _{\xi ,t}:{\mathrm {Lip}}(H_{\xi ,t})\rightarrow {\mathbf {R}},\quad \sigma _{\xi ,t}(\varphi |_{H_{\xi ,t}})=\lim _{\delta \searrow 0}\frac{1}{\delta }\int _{\{x\in {\mathbf {R}}^n\,|\,t-\delta<x\cdot \xi <t\}}\varphi \xi \cdot {\mathrm d}\sigma \end{aligned}$$(5)for all \(\varphi \in {\mathrm {Lip}}({\mathbf {R}}^n)\) (the right-hand side is well-defined and only depends on \(\varphi |_{H_{\xi ,t}}\) [28, Thm. 3.5 & Thm. 3.6]). This \(\sigma _{\xi ,t}\) equals the so-called normal trace of \(\sigma \) on \(H_{\xi ,t}\) (see [28] for its definition and properties). In general it is not a measure but continuous on \({\mathrm {Lip}}(H_{\xi ,t})\) in the sense
$$\begin{aligned} \sigma _{\xi ,t}(\varphi )\le (\Vert \sigma \Vert _{{\mathcal {M}}}+\Vert {{\,\mathrm{div}\,}}\sigma \Vert _{{\mathcal {M}}})\Vert \varphi \Vert _{W^{1,\infty }} \quad \text {for all }\varphi \in {\mathrm {Lip}}(H_{\xi ,t}){.} \end{aligned}$$ - 2.
Interpreting a divergence measure vector field as a 1-current or a flat 1-chain, Šilhavý’s definition of \(\sigma _{\xi ,t}\) is identical to the classical slice of \(\sigma \) on \(H_{\xi ,t}\) as for instance defined in [29] or [16, 4.3.1] (note that Šilhavý’s definition corresponds to [28, (3.8)], whose analogue for currents is [16, 4.3.2(5)]).
- 3.
Our notion of a sliced measure from Definition 6 is equivalent to both above-mentioned notions. Indeed, (4) implies

which shows that the sliced measure represents the normal flux through the hyperplane \(H_{\xi ,t}=\{x\cdot \xi =t\}\). This, however, is the same characterization as given in [28, (3.6)] and [16, 4.2.1] for both above notions of slices.
We conclude the section with several properties needed for the \(\Gamma {\mathrm{-}}\liminf \) inequality. The following result makes use of the Kantorovich–Rubinstein norm (see for instance [21, eq. (2) & (5)]; in geometric measure theory it is known as the flat norm) on \({{\mathcal {M}}}({\mathbf {R}}^n)\), defined by
For measures of uniformly bounded support and uniformly bounded mass it is known to metrize weak-\(*\) convergence (see for instance [8, Rem. 2.29(3)-(4)]). We will furthermore make use of the following fact. Let \(T_s:x\mapsto x-s\xi \) be the translation by s in direction \(-\xi \). It is straightforward to check that for any divergence measure vector field \(\mu \in {{\mathcal {M}}}({\mathbf {R}}^n;{\mathbf {R}}^n)\) we have
As a consequence, for any \(\mu \in {{\mathcal {M}}}(H_{\xi ,t})\) and \(\nu \in {{\mathcal {M}}}(H_{\xi ,t+s})\) we have
Indeed, let \(\delta >0\) arbitrary and \(\mu _1\in {{\mathcal {M}}}({\mathbf {R}}^n)\), \(\mu _2\in {{\mathcal {M}}}({\mathbf {R}}^n;{\mathbf {R}}^n)\) with \(\mu -\nu =\mu _1+{{\,\mathrm{div}\,}}\mu _2\) such that \(\Vert \mu -\nu \Vert _{\mathrm {KR}}\ge \Vert \mu _1\Vert _{{\mathcal {M}}}+\Vert \mu _2\Vert _{{\mathcal {M}}}-\delta \), then \({{\tilde{\mu }}}_1={{\pi _{H_{\xi ,t}}}_{\#}\mu _1}\) and \({{\tilde{\mu }}}_2={{\pi _{H_{\xi ,t}}}_{\#}(}\mu _2-\mu _2\cdot \xi \,\xi )\) satisfy \(\mu -{{T_s}_{\#}\nu }={{\tilde{\mu }}}_1+{{\,\mathrm{div}\,}}{{\tilde{\mu }}}_2\) and thus
Theorem 3.1
(Weak convergence of sliced measures) Let \(\sigma ^j{\mathop {\rightharpoonup }\limits ^{*}}\sigma \) as \(j\rightarrow \infty \) for a sequence \(\{\sigma ^j\}\) of divergence measure vector fields with uniformly bounded support and uniformly bounded \(\Vert {{\,\mathrm{div}\,}}\sigma ^j\Vert _{{\mathcal {M}}}\). Then there is a subsequence (still indexed by j) such that for almost all \((\xi ,t)\in {\mathbf {S}}^{n-1}\times {\mathbf {R}}\) we have
Proof
Consider the measures \(\nu ^j=|\sigma ^j|+|{{\,\mathrm{div}\,}}\sigma ^j|\). Since \(\Vert \nu ^j\Vert _{{\mathcal {M}}}\) is uniformly bounded, a subsequence converges weakly-\(*\) to some compactly supported nonnegative \(\nu \in {{\mathcal {M}}}({\mathbf {R}}^n)\) (the subsequence is still indexed by j). For \(I\subset {\mathbf {R}}\) introduce the notation \(H_{\xi ,I}=\bigcup _{t\in I}H_{\xi ,t}\). Then for almost all \(t\in {\mathbf {R}}\), \(\nu (H_{\xi ,[t-s,t+s]})\rightarrow 0\) as well as \((|\sigma |+|{{\,\mathrm{div}\,}}\sigma |)(H_{\xi ,[t-s,t+s]})\rightarrow 0\) as \(s\searrow 0\). For such a t we show convergence of \(\sigma _{\xi ,t}^j-\sigma _{\xi ,t}\) to zero in the Kantorovich–Rubinstein norm which implies weak-\(*\) convergence. To this end fix some arbitrary \(\delta >0\). Given \(\zeta >0\) let \(\rho _\zeta =\rho (\cdot /\zeta )/\zeta \) for a nonnegative smoothing kernel \(\rho \in {{\mathcal {C}}}^\infty ({\mathbf {R}})\) with support in \([-1,1]\) and \(\int _{\mathbf {R}}\rho \,{\mathrm d}t=1\). For any compactly supported divergence measure vector field \(\lambda \) we now define the convolved slice \(\lambda _{\xi ,\zeta ,t}\) by
where \(T_s:x\mapsto x-s\xi \) is the translation by s in direction \(-\xi \). By Remark 5(3) we have \(\sigma ^j_{\xi ,\zeta ,t}{\mathop {\rightharpoonup }\limits ^{*}}\sigma _{\xi ,\zeta ,t}\). Furthermore, there exist \(\zeta >0\) and \(J\in {\mathbf {N}}\) such that \(\Vert \sigma _{\xi ,t}-\sigma _{\xi ,\zeta ,t}\Vert _{\mathrm {KR}}\le \frac{\delta }{3}\) and \(\Vert \sigma _{\xi ,t}^j-\sigma ^j_{\xi ,\zeta ,t}\Vert _{\mathrm {KR}}\le \frac{\delta }{3}\) for all \(j\ge J\). Indeed, for a compactly supported divergence measure vector field \(\lambda \) we have

where in the equality we employed Remark 6(3). Thus, we can simply pick \(\zeta \) such that \(|\sigma |(H_{\xi ,[t-\zeta ,t+\zeta ]})+|{{\,\mathrm{div}\,}}\sigma |(H_{\xi ,[t-\zeta ,t+\zeta ]})\le \frac{\delta }{3}\) and \(\nu (H_{\xi ,[t-\zeta ,t+\zeta ]})\le \frac{\delta }{6}\), while we choose J such that \((\nu ^j-\nu )(H_{\xi ,[t-\zeta ,t+\zeta ]})\le \frac{\delta }{6}\) for all \(j>J\). Now let \({\bar{J}}\ge J\) such that \(\Vert \sigma ^j_{\xi ,\zeta ,t}-\sigma _{\xi ,\zeta ,t}\Vert _{\mathrm {KR}}\le \frac{\delta }{3}\) for all \(j\ge {\bar{J}}\), then we obtain
for all \(j>{\bar{J}}\). The arbitrariness of \(\delta \) concludes the proof. \(\square \)
Remark 7
(Flat convergence of sliced currents) The convergence from Theorem 3.1 is consistent with the following property of slices of 1-currents: If \(\sigma ^j\), \(j\in {\mathbf {N}}\), is a sequence of 1-currents of finite mass with \(\sigma ^j\rightarrow \sigma \) in the flat norm, then (potentially after choosing a subsequence) \(\sigma ^j_{\xi ,t}\rightarrow \sigma _{\xi ,t}\) in the flat norm for almost every \(\xi \in {\mathbf {S}}^{n-1}\), \(t\in {\mathbf {R}}\) (see [13, step 2 in proof of Prop. 2.5] or [29, Sect. 3]).
Remark 8
(Characterization of sliced measures)
- 1.
Let the compactly supported divergence measure vector field \(\sigma \) be countably 1-rectifiable, that is,
 for a countably 1-rectifiable set \(S\subset {\mathbf {R}}^n\) and
for a countably 1-rectifiable set \(S\subset {\mathbf {R}}^n\) and  -measurable functions \(m:S\rightarrow [0,\infty )\) and \(\theta :S\rightarrow {\mathbf {S}}^{n-1}\), tangent to S \({\mathcal {H}}^1\)-almost everywhere. Then the coarea formula for rectifiable sets [16, Thm. 3.2.22] implies
-measurable functions \(m:S\rightarrow [0,\infty )\) and \(\theta :S\rightarrow {\mathbf {S}}^{n-1}\), tangent to S \({\mathcal {H}}^1\)-almost everywhere. Then the coarea formula for rectifiable sets [16, Thm. 3.2.22] implies  so that $$\begin{aligned} \int _{{\mathbf {R}}^n}f\,{\mathrm d}\sigma \cdot \xi =\int _Sfm\theta \cdot \xi \,{\mathrm d}{\mathcal {H}}^1 =\int _{\mathbf {R}}\int _{S_{\xi ,t}}fm\mathop {\mathrm {sgn}}(\xi \cdot \theta )\,{\mathrm d}{\mathcal {H}}^0\,{\mathrm d}t \end{aligned}$$
so that $$\begin{aligned} \int _{{\mathbf {R}}^n}f\,{\mathrm d}\sigma \cdot \xi =\int _Sfm\theta \cdot \xi \,{\mathrm d}{\mathcal {H}}^1 =\int _{\mathbf {R}}\int _{S_{\xi ,t}}fm\mathop {\mathrm {sgn}}(\xi \cdot \theta )\,{\mathrm d}{\mathcal {H}}^0\,{\mathrm d}t \end{aligned}$$for any Borel function f. Hence, for almost all t,

The choice \(f=\frac{\tau (m)}{m}\mathop {\mathrm {sgn}}(\xi \cdot \theta )\) yields
$$\begin{aligned} \int _S\tau (m)|\theta \cdot \xi |\,{\mathrm d}{\mathcal {H}}^1=\int _{{\mathbf {R}}}\int _{S_{\xi ,t}}\tau (m)\,{\mathrm d}{\mathcal {H}}^0\,{\mathrm d}t{.} \end{aligned}$$ - 2.
Let the compactly supported divergence measure vector field \(\sigma \) be \({\mathcal {H}}^1\)-diffuse, that is, \(|\sigma |(R)=0\) for any countably 1-rectifiable set \(R\subset {\mathbf {R}}^n\). Then for almost all \((\xi ,t)\in {\mathbf {S}}^{n-1}\times {\mathbf {R}}\), \(\sigma _{\xi ,t}\) is \({\mathcal {H}}^0\)-diffuse, that is, it does not contain any atoms. Indeed, let \(\sigma _{\xi ,t}\) have an atom at \(x\in H_{\xi ,t}\), then
$$\begin{aligned} x\in \Theta (\sigma )=\left\{ x\in {\mathbf {R}}^n\,\big |\,\liminf _{\rho \searrow 0}|\sigma |(B_{\rho }(x))/\rho >0\right\} {,} \end{aligned}$$where \(B_{\rho }(x)\) denotes the open ball of radius \(\rho \) centred at x. This can be deduced as follows. Let \(\phi \in {{\mathcal {C}}}^\infty ({\mathbf {R}})\) be smooth and even with support in \((-1,1)\) and \(\phi (0)=\mathop {\mathrm {sgn}}(\sigma _{\xi ,t}(\{x\}))\). Further abbreviate \(K=\max _{x\in {\mathbf {R}}}|\phi '(x)|>0\) and \(\phi _\rho =\phi (|\cdot -x|/\rho )\) for any \(\rho >0\). Equation (4) now implies
$$\begin{aligned} \int _{H_{\xi ,t}}\phi _\rho \,{\mathrm d}\sigma _{\xi ,t} =\int _{\{\xi \cdot x<t\}}\phi _\rho \,{\mathrm d}{{\,\mathrm{div}\,}}\sigma +\int _{\{\xi \cdot x<t\}}\nabla \phi _\rho \cdot {\mathrm d}\sigma \le \int _{\{\xi \cdot x<t\}}\phi _\rho \,{\mathrm d}{{\,\mathrm{div}\,}}\sigma +K\frac{|\sigma |(B_\rho (x))}{\rho }{.} \end{aligned}$$
Taking on both sides the limit inferior as \(\rho \rightarrow 0\) we obtain \(|\sigma _{\xi ,t}|(\{x\})\le K\liminf _{\rho \searrow 0}|\sigma |(B_{\rho }(x))/\rho \), as desired.
As a result, for a given \(\xi \) the set of t such that \(\sigma _{\xi ,t}\) is not \({\mathcal {H}}^0\)-diffuse is a subset of \(\pi _\xi (\Theta )\). Thus it remains to show that for almost all \(\xi \in {\mathbf {S}}^{n-1}\) the set \(\pi _\xi (\Theta )\) is a Lebesgue-nullset. Writing
it actually suffices to show that \(\pi _\xi (\Theta _p)\) is a Lebesgue-nullset for any \(p\in {\mathbf {N}}\). Now by the properties of the 1-dimensional density of a measure [1, Thm. 2.56],
so that \(\Theta _p\) can be decomposed into a countably 1-rectifiable and a purely 1-unrectifiable set [1, p. 83],
(\(\Theta _p^u\) purely 1-unrectifiable means \({\mathcal {H}}^1(\Theta _p^u\cap f({\mathbf {R}}))=0\) for any Lipschitz \(f:{\mathbf {R}}\rightarrow {\mathbf {R}}^n\)). By the \({\mathcal {H}}^1\)-diffusivity assumption on \(\sigma \) we have (abbreviating the Lebesgue measure by \({\mathcal {L}}\))
and by a result due to Besicovitch [1, Thm. 2.65] we have
for almost all \(\xi \in {\mathbf {S}}^{n-1}\). Thus, for almost all \(\xi \in {\mathbf {S}}^{n-1}\) we have \({\mathcal {L}}(\pi _\xi (\Theta _p))=0\), as desired.
Remark 9
(Characterization of divergence measure vector fields) By a result due to Smirnov [27], any divergence measure vector field \(\sigma \) can be decomposed into simple oriented curves  with \(\gamma :[0,1]\rightarrow {\mathbf {R}}^n\) a Lipschitz curve and \({\mathrm d}s\) the Lebesgue measure, that is,
with \(\gamma :[0,1]\rightarrow {\mathbf {R}}^n\) a Lipschitz curve and \({\mathrm d}s\) the Lebesgue measure, that is,
with J the set of Lipschitz curves and \(\mu _\sigma \) a nonnegative Borel measure. The results of this section can alternatively be derived by resorting to this characterization, since the slice of a simple oriented curve \(\sigma _\gamma \) can be explicitly calculated.
3.3 The \(\Gamma {\mathrm{-}}\liminf \) inequality
We now prove the desired \(\liminf \)-inequality, which as already anticipated will be obtained by slicing.
Proposition 3.2
(\(\Gamma {\mathrm{-}}\liminf \) of phase field functional) Let \(\mu _+,\mu _-\in {{\mathcal {P}}}({\overline{\Omega }})\). We have
with respect to weak-\(*\) convergence in \({{\mathcal {M}}}({\overline{\Omega }};{\mathbf {R}}^2)\) and strong convergence in \(L^1(\Omega )^N\).
Proof
Let \((\sigma ^\varepsilon ,\varphi _1^\varepsilon ,\ldots ,\varphi _N^\varepsilon )\) converge to \((\sigma ,\varphi _1,\ldots ,\varphi _N)\) in the considered topology. We first extend \(\sigma ^\varepsilon \) and \(\sigma \) to \({\mathbf {R}}^2{\setminus }{\overline{\Omega }}\) by zero and \(\varphi _i^\varepsilon \) and \(\varphi _i\) to \({\mathbf {R}}^2{\setminus }\Omega \) by 1 for \(i=1,\ldots ,N\). The phase field cost functional and the cost functional are extended to \({\mathbf {R}}^2\) in the obvious way (their values do not change). Without loss of generality (potentially after extracting a subsequence) we may assume \(\lim _{\varepsilon \rightarrow 0}E_\varepsilon ^{\mu _+,\mu _-}[\sigma ^\varepsilon ,\varphi _1^\varepsilon ,\ldots ,\varphi _N^\varepsilon ]\) to exist and to be finite (else there is nothing to show). As a consequence we have \({{\,\mathrm{div}\,}}\sigma ^\varepsilon =\mu _+^\varepsilon -\mu _-^\varepsilon \) as well as \({{\,\mathrm{div}\,}}\sigma =\mu _+-\mu _-\) and \(\varphi _1\equiv \cdots \equiv \varphi _N\equiv 1\) (since the phase field cost functional is bounded below by \(\sum _{i=1}^N\frac{\beta _i}{2\varepsilon }\Vert \varphi _i^\varepsilon -1\Vert _{L^2}^2\)).
Now let \(A\subset {\mathbf {R}}^2\) open and bounded; the restriction of the phase field cost functional to a domain A will be denoted \({\mathcal {E}}_\varepsilon ^{\mu _+,\mu _-}[\cdot ;A]\). Choosing some \(\xi \in S^1\), by Fubini’s decomposition theorem we have
where \({\mathcal {G}}_\varepsilon \) is the dimension-reduced phase field energy from Definition 4 and for simplicity we identified the domain \(A_{\xi ,t}\) of the sliced functions with an open subset of the real line. Fatou’s lemma thus implies
By assumption, the left-hand side is finite so that the right-hand side integrand is finite for almost all \(t\in {\mathbf {R}}\) as well. Pick any such t and pass to a subsequence such that \(\liminf \) turns into \(\lim \). Indeed \(\sigma ^\varepsilon _{\xi ,t}{\mathop {\rightharpoonup }\limits ^{*}}\sigma _{\xi ,t}\) for every \(\xi \) and almost all t, due to \(\sigma ^\varepsilon {\mathop {\rightharpoonup }\limits ^{*}}\sigma \) and Theorem 3.1. Thus, Corollary 3.1 on the reduced dimension problem implies
for almost all \(t\in {\mathbf {R}}\) so that
For notational convenience let us now define the auxiliary function \(\kappa \), defined for open subsets \(A\subset {\mathbf {R}}^2\), as
Furthermore, introduce the nonnegative Borel measure
as well as the \(|\sigma |\)-measureable Borel functions
for some sequence \(\xi ^j\), \(j\in {\mathbf {N}}\), dense in \(S^1\).
Since \(\sigma \) is a divergence measure vector field, we have
for all \(j\in {\mathbf {N}}\) where we used Remark 8 in the last equality. By [6, Prop. 1.16] the above inequality implies
for any open \(A\subset {\mathbf {R}}^2\). In particular, choosing A as the 1-neighbourhood of \(\Omega \) we obtain
the desired result. \(\square \)
3.4 Equicoercivity
Proof of Theorem 2.2
Due to \(C>E_\varepsilon ^{\mu _+,\mu _-}[\sigma ^\varepsilon ,\varphi _1^\varepsilon ,\ldots ,\varphi _N^\varepsilon ]\ge \frac{\beta _i}{2\varepsilon }\Vert \varphi _i^\varepsilon -1\Vert _{L^2}^2\) for all \(i=1,\ldots ,N\), we have \(\varphi _i^\varepsilon \rightarrow 1\) in \(L^2(\Omega )\) and thus also in \(L^1(\Omega )\). Furthermore, we will show further below that \(\Vert \sigma ^\varepsilon \Vert _{L^1}=\Vert \sigma ^\varepsilon \Vert _{{\mathcal {M}}}\) is uniformly bounded, which by the Banach–Alaoglu theorem implies existence of a weakly-* converging subsequence (still denoted \(\sigma ^\varepsilon \)) with limit \(\sigma \in {{\mathcal {M}}}({\overline{\Omega }};{\mathbf {R}}^2)\). It is now a standard property of \(\Gamma \)-convergence that, due to the above equicoercivity, any sequence of minimizers of \(E_\varepsilon ^{\mu _+,\mu _-}\) contains a subsequence converging to a minimizer of \(E^{\mu _+,\mu _-}\).
To finish the proof we show uniform boundedness of \(\sigma ^\varepsilon \) in \({{\mathcal {M}}}({\overline{\Omega }};{\mathbf {R}}^2)\). Indeed, using \(\omega _\varepsilon (\alpha _0,\frac{\gamma _\varepsilon (x)}{\varepsilon },|\sigma (x)|)\ge \frac{\alpha _0}{2}|\sigma (x)|\) for \(x\in K_0^\varepsilon \) (remember that \(K_0^\varepsilon =\emptyset \) for \(\alpha _0=\infty \)) we obtain
(the first term is interpreted as zero for \(\alpha _0=\infty \)). Furthermore, by Hölder’s inequality we have
Choosing now some arbitrary \(\lambda \in (0,1)\) we can estimate
Summarizing, \(\Vert \sigma ^\varepsilon \Vert _{{\mathcal {M}}}\le \frac{C}{2\alpha _0}+\sum _{i=1}^N\sqrt{\frac{4C^2}{\alpha _i^2(1-\lambda )^2}+\frac{2\varepsilon C}{\lambda ^2}{\mathcal {H}}^2(\Omega )}\). \(\square \)
3.5 The \(\Gamma {\mathrm{-}}\limsup \) inequality
Proposition 3.3
(\(\Gamma {\mathrm{-}}\limsup \) of phase field functional) Let \(\mu _+,\mu _-\in {{\mathcal {P}}}({\overline{\Omega }})\) be an admissible source and sink. We have
with respect to weak-\(*\) convergence in \({{\mathcal {M}}}({\overline{\Omega }};{\mathbf {R}}^2)\) and strong convergence in \(L^1(\Omega )^N\).
Proof
Consider a mass flux \(\sigma \) between the measures \(\mu _+\) and \(\mu _-\). We will construct a recovery sequence \((\sigma ^\varepsilon , \varphi ^\varepsilon _1,\ldots , \varphi ^\varepsilon _N )\) such that \(\sigma ^\varepsilon {\mathop {\rightharpoonup }\limits ^{*}}\sigma \) and \(\varphi _1^\varepsilon \rightarrow 1,\ldots ,\varphi _N^\varepsilon \rightarrow 1\) in the desired topology as \(\varepsilon \rightarrow 0\) as well as \(\limsup _{\varepsilon \rightarrow 0} E_\varepsilon ^{\mu _+,\mu _-}[\sigma ^\varepsilon , \varphi ^\varepsilon _1,\ldots , \varphi ^\varepsilon _N]\le E^{\mu _+,\mu _-}[\sigma ,1,\ldots ,1]\). Without loss of generality we may restrict our attention to fluxes for which
since otherwise there is nothing to prove. By [8, Def. 2.2 & Prop. 2.32] there exists a sequence

of polyhedral divergence measure vector fields in \(\Omega \) such that
If \(\mu _+\) and \(\mu _-\) are finite linear combinations of Dirac masses (which we have assumed in the case \(\alpha _0=\infty \)), we may even choose \(\mu _\pm ^j=\mu _\pm \). We will construct the recovery sequence based on those polyhedral divergence measure vector fields. In the following we will use the notation
for the phase field cost functional without divergence constraints.
Step 1. Initial construction for a single polyhedral segment
In this step we approximate a single line element  of \(\sigma _j\) by a phase field version. To this end we fix j and \(0\le k\le M_j\) and drop these indices from now on in the notation for the sake of legibility. Without loss of generality we may assume \(\Sigma =[0,L]\times \{0\}\), \(m>0\), and \(\theta =e_1\) the standard Euclidean basis vector. Set
of \(\sigma _j\) by a phase field version. To this end we fix j and \(0\le k\le M_j\) and drop these indices from now on in the notation for the sake of legibility. Without loss of generality we may assume \(\Sigma =[0,L]\times \{0\}\), \(m>0\), and \(\theta =e_1\) the standard Euclidean basis vector. Set
to identify the phase field that will be active on \(\Sigma \) (\({\bar{\iota }}=0\) means that no phase field is active). We first specify (a preliminary version of) the vector field \(\sigma ^\varepsilon \). To this end let \(d_\Sigma \) denote the distance function associated with \(\Sigma \) and define the width
over which the vector field will be diffused. We now set
where \(\chi _A\) shall denote the characteristic function of a set A (see Fig. 2). Note that this vector field encodes a total mass flux of m that is evenly spread over the \(a_{{\bar{\iota }}}^\varepsilon \)-enlargement of \(\Sigma \). The corresponding active phase field will be zero in that region. Indeed, consider the auxiliary Cauchy problem
whose solution \(\phi _\varepsilon (t)=1-\exp \left( -\frac{t}{\varepsilon }\right) \) represents the well-known optimal Ambrosio–Tortorelli phase field profile. Then we set \({\overline{\varphi }}_i^\varepsilon =0\) for all \(i\ne {\bar{\iota }}\) and, if \({\bar{\iota }}\ne 0\),
Left: Sketch of the optimal profile of \(|{\overline{\sigma }}^\varepsilon |\) and a phase field \({\overline{\varphi }}_{{\bar{\iota }}}^\varepsilon \) for some \({\bar{\iota }}>0\) with \(m=2\), \(\varepsilon =0.1\), \(\alpha _{{\bar{\iota }}}=1\), \(\beta _{{\bar{\iota }}}=1\). Right: Sketch of the numerical solution to the 1D problem with the same parameters
Let us now evaluate the corresponding phase field cost. In the case \({\bar{\iota }}=0\) (which can only occur for \(\alpha _0<\infty \)) we obtain
where we abbreviated \(q=\min \{1,p-1\}>0\) and \(C(m,L)>0\) denotes a constant depending on m and L. In the case \({\bar{\iota }}\ne 0\) we have \(|{\overline{\sigma }}^\varepsilon |=\beta _{{\bar{\iota }}}/(\alpha _{{\bar{\iota }}}\varepsilon )\) as well as \({\overline{\gamma }}_\varepsilon =\alpha _{{\bar{\iota }}}^2\varepsilon ^2/\beta _{{\bar{\iota }}}\) on the support of \(|{\overline{\sigma }}^\varepsilon |\) so that
Furthermore we have \({\mathcal {L}}_{\varepsilon }({\overline{\varphi }}^\varepsilon _i)=0\) for \(i\ne {\bar{\iota }}\) and, employing the coarea formula,
Summarizing,
Step 2. Adapting sources and sinks of all polyhedral segments
The vector field constructions \({\overline{\sigma }}^\varepsilon _{k,j}\) from the previous step for each polyhedral segment \(\Sigma _{k,j}\) are not compatible with the divergence constraint associated with the measure \(\sigma ^j\), that is,
We remedy this by adapting the source and sink of each \({\overline{\sigma }}^\varepsilon _{k,j}\). Set
then all vector fields \({\overline{\sigma }}^\varepsilon _{k,j}\) have support in a band around \(\Sigma _{k,j}\) of width no larger than \(r(j)\varepsilon \). Without loss of generality we assume \(r(j)\ge 1\) (else we just increase it). Again we concentrate on a single segment with fixed j and k and drop these indices in the following (we will also write r instead of r(j)). Denote by \(s^+\) and \(s^-\) the starting and ending point of the segment \(\Sigma \) with respect to the orientation induced by \(\theta \). Consider the elliptic boundary value problems
where \(\delta _y\) denotes a Dirac mass centered at y, \(B_{r}(y)\) denotes the open ball of radius r around y, and \(\nu \) denotes the outer unit normal to \(\partial B_{r}(0)\). Note that the boundary value problems and their solutions \(u^+\) and \(u^-\) are independent of \(\varepsilon \) due to the definition of \({\overline{\sigma }}^\varepsilon \). Setting
(where we assume \(\varepsilon \) small enough such that \(B_{\varepsilon r}(s^+)\) and \(B_{\varepsilon r}(s^-)\) do not intersect) it is straightforward to check
Furthermore, to have at least one phase field zero on the new additional support \(B_{\varepsilon r}(s^+)\cup B_{\varepsilon r}(s^-)\) of the vector field we set
and \(\varphi _2^\varepsilon ={\overline{\varphi }}_2^\varepsilon ,\ldots ,\varphi _N^\varepsilon ={\overline{\varphi }}_N^\varepsilon \). Reintroducing now the indices k and j, we set
for \(i=1,\ldots ,N\). Obviously, we have, as desired,
Let us now estimate the costs. Let us assume that \(\varepsilon \) is small enough so that all balls \(B_{\varepsilon r(j)}(s^{\pm }_{k,j})\) are disjoint as are the supports \({{\,\mathrm{supp}\,}}{\tilde{\sigma }}_{k,j}^\varepsilon {\setminus }(B_{\varepsilon r(j)}(s^{+}_{k,j})\cup B_{\varepsilon r(j)}(s^{-}_{k,j}))\) for all k. An upper bound can then be achieved via
The last summand can be bounded above by
for some constant \(C>0\). For the second summand, note that \(({\tilde{\gamma }}_\varepsilon )_j\le \alpha _1^2\varepsilon ^2/\beta _1\) on \(B_{\varepsilon r(j)}(s^\pm _{k,j})\) due to \((\varphi _1^\varepsilon )_j=0\) there; furthermore,
Thus, if we set \(S^\pm =\{l\in \{1,\ldots ,M_j\}\,|\,s^\pm _{j,l}=s\}\) for fixed \(s=s^+_{k,j}\) or \(s=s^-_{k,j}\) we have
for some constant \(C(\sigma _j)>0\) depending on the polyhedral divergence measure vector field \(\sigma _j\) and the considered point s. In summary, we thus have
for some constant \(C(\sigma _j)\) depending on \(\sigma _j\).
Step 3. Correction of the global divergence
Recall that the vector field \(\sigma ^\varepsilon \) to be constructed has to satisfy \({{\,\mathrm{div}\,}}\sigma ^\varepsilon =\rho _\varepsilon *(\mu _+-\mu _-)\). In the case \(\alpha _0=\infty \) the vector field \({\tilde{\sigma }}_j^\varepsilon \) already has that property due to \(\mu _\pm ^j=\mu _\pm \) (thus we set \(\sigma _j^\varepsilon ={\tilde{\sigma }}_j^\varepsilon \)). However, if \(\alpha _0<\infty \) (so that admissible sources and sinks \(\mu _+\) and \(\mu _-\) do not have to be finite linear combinations of Dirac masses) we still need to adapt the vector field to achieve the correct divergence. To this end, let \(\lambda _\pm ^j\in {{\mathcal {M}}}(\{x\in \Omega \,|\,{\mathrm {dist}}(x,\partial \Omega )\ge \varepsilon ;{\mathbf {R}}^2)\) be the optimal Wasserstein-1 flux between \(\mu ^j_\pm \) and \(\mu _\pm \), that is, \(\lambda _j^\pm \) minimizes \(\Vert \lambda \Vert _{{\mathcal {M}}}\) among all vector-valued measures \(\lambda \) with \({{\,\mathrm{div}\,}}\lambda =\mu ^j_\pm -\mu _\pm \). Setting
we thus obtain \({{\,\mathrm{div}\,}}\sigma _j^\varepsilon =\rho _\varepsilon *(\mu _+-\mu _-)\), as desired. The additional cost can be estimated using the fact
as well as \(\Vert \rho _\varepsilon *\lambda _\pm ^j\Vert _{L^\infty }\le C\frac{\Vert \mu _+^j\Vert _{{\mathcal {M}}}+\Vert \mu _-^j\Vert _{{\mathcal {M}}}}{\varepsilon }\), where \(\Vert \mu _\pm ^j\Vert _{{\mathcal {M}}}\) is an upper bound for the total mass moved by \(\lambda _\pm ^j\) and the constant \(C>0\) depends on \(\rho \). With those ingredients we obtain
Now \(\Vert \rho _\varepsilon *(\lambda _+^j-\lambda _-^j)\Vert _{L^1}\le \Vert \lambda _+^j-\lambda _-^j\Vert _{{\mathcal {M}}}\le \Vert \lambda _+^j\Vert _{{\mathcal {M}}}+\Vert \lambda _-^j\Vert _{{\mathcal {M}}}=W_1(\mu _+^j,\mu _+)+W_1(\mu _-^j,\mu _-)=\kappa _j\) for a constant \(\kappa _j>0\) satisfying
since the Wasserstein-1 distance \(W_1(\cdot ,\cdot )\) metrizes weak-\(*\) convergence. Furthermore, in the previous steps we have already estimated \(\varepsilon ^p\Vert {\tilde{\sigma }}_j^\varepsilon \Vert _{L^2}^2\le C(\sigma _j)\varepsilon ^q\). Finally,
Summarizing,
for some constant \(C>0\) and \(C(\sigma _j)>0\) depending only on \(\sigma _j\).
Step 4. Extraction of a diagonal sequence
We will set \(\sigma ^\varepsilon =\sigma _j(\varepsilon )^\varepsilon \), \(\varphi _1^\varepsilon =(\varphi _1^\varepsilon )_{j(\varepsilon )},\ldots ,\varphi _N^\varepsilon =(\varphi _N^\varepsilon )_{j(\varepsilon )}\) for a suitable choice \(j(\varepsilon )\). Indeed, for a monotonic sequence \(\varepsilon _1,\varepsilon _2,\ldots \) approaching zero we set \(j(\varepsilon _1)=1\) and
Then \(j(\varepsilon _i)\rightarrow \infty \) and \(C(\sigma _{j(\varepsilon _i)})\varepsilon _i^q\rightarrow 0\) as \(i\rightarrow \infty \) so that
\(\square \)
4 Numerical experiments
Here we describe the discretization and numerical optimization for our experiments.
4.1 Discretization
Let \({\mathcal {T}}_h\) be a triangulation of the space \(\Omega \) of grid size h such that \(\overline{\Omega }=\bigcup _{T\in {\mathcal {T}}_h}{\overline{T}}\). Denoting by \({\mathbb {P}}^m\) the space of polynomials of degree m, we define the finite element spaces
and write the discretized phase field problem as
where all integrals are evaluated using midpoint quadrature.
4.2 Optimization
We perform an alternating minimization in \(\sigma \) and the different phase fields \(\varphi _1,\ldots ,\varphi _N\).
In each iteration, for fixed phase fields we perform a single Newton step in \(\sigma \) (which in the case \(\alpha _0=\infty \) returns the optimal \(\sigma \), since the energy is quadratic). In more detail, the optimality conditions for \(\sigma \) read
Letting \({\hat{\sigma }}\) and \({\hat{\lambda }}\) be the coefficients of \(\sigma \) and \(\lambda \) in some basis \(\{b_i^0\}_i\) of \(X_h^0\) and \(\{b_i^1\}_i\) of \(X_h^1\), respectively, these optimality conditions can be expressed as
where the finite element matrices and vectors are defined as
In each iteration of the alternating minimization scheme we now take one Newton step for \(0=R({\hat{\sigma }},{\hat{\lambda }})\).
To avoid minimization for phase field \(\varphi _i\) with the \(\min \)-function inside \(\gamma _\varepsilon \) we perform a heuristic operator splitting: in each iteration of the optimization we first identify at each location whether there is a diffuse flux \(\sigma \) without any active phase field or otherwise which term inside \(\gamma _\varepsilon =\min (\varphi _1^2+\alpha _1^2\varepsilon ^2/\beta _1,\ldots ,\varphi _N^2+\alpha _N^2\varepsilon ^2/\beta _N)\) is the minimizer, which is equivalent to specifying the regions
for \(i=1,\ldots ,N\). Afterwards we then optimize the energy \({\mathcal {E}}_\varepsilon \) separately for each phase field \(\varphi _i\in X_h^1\) assuming the regions \(R_i^\varepsilon \) fixed, that is, we minimize
where \(\chi _{R_i^\varepsilon }\) is the characteristic function of region \(R_i^\varepsilon \). Since the above is quadratic in \(\varphi _1,\ldots ,\varphi _N\), this amounts to solving a linear system.
Since in the above simple approach the regions \(R_i^\varepsilon \) and phase fields \(\varphi _i\) can move, but cannot nucleate within a different region, a suitable initial guess is crucial, for which we proceed as follows. We first generate some flux network \(\sigma ^0\) consistent with the given source and sink. This can for instance be done using the previously described algorithm for just a single phase field: in our simulations we simply ignore \(\varphi _2,\ldots ,\varphi _N\) and pretend only the phase field \(\varphi _1\) would exist (essentially this means we replace the cost function \(\tau \) by \(m\mapsto \alpha _1m+\beta _1\) for \(m>0\)). We then identify the total mass flowing through each branch of \(\sigma ^0\). To this end we convolve \(|\sigma ^0|\) with the characteristic function \(\chi _{B_r(0)}\) of a disc of radius r. If r is sufficiently large compared to the width of the support of \(\sigma ^0\), we obtain
where m(x) denotes the mass flux through the nearby branch of \(\sigma ^0\). Now we can compute the regions
and furthermore use \(\sigma ^0\) as initial guess of the vector field.
Optimal transportation networks for branched transportation from a single source to a number of identical sinks at the corners of regular polygons. Top: Ground truth. Middle: Support of mass flux \(\sigma \). Bottom: Phase field \(\varphi \). Parameters were \(\alpha _1=0.05\) (left), \(\alpha _1=1\) (right), and \(\beta _1=1\), \(\varepsilon =0.005\)
Numerically we found that a slight parameter change in our energy gives improved results since it leads to a flux \(\sigma \) that is less sensitive to changes in the active phase field. Indeed, if we assign a different phase field parameter \(\varepsilon _i=\beta _i\varepsilon /\alpha _i\) to each phase field \(\varphi _i\), Eq. (6) shows that the support width of \(\sigma \) becomes \(m\varepsilon \) and thus no longer depends on the phase field. Thus, in practice we usually work with the phase field cost
with \({\tilde{\gamma }}_\varepsilon (x)=\min _{i=1,\ldots ,N}\{\varphi _i(x)^2+\alpha _i^2\varepsilon \varepsilon _i/\beta _i\}=\min _{i=1,\ldots ,N}\{\varphi _i(x)^2+\alpha _i\varepsilon ^2\}\). The \(\Gamma \)-convergence result can readily be adapted to this case.
4.3 Experimental results
The algorithms were implemented in MATLAB\(^{{\textcircled {c}}}\); parameters reported refer to the rescaled cost (7). Figure 3 shows solutions for a source and a number of equal sinks arranged as a regular polygon with a single phase field (\(N=1\)). For small \(\alpha _1\) (left) the solution looks similar to the Steiner tree (which would correspond to \(\alpha _1=0\)), while the solutions become much more asymmetric for larger \(\alpha _1\) (right).
Figure 4 shows simulation results for 3 different linear segments in \(\tau \) and \(N=3\) (\(\alpha _0=\infty \)) or \(N=2\) (\(\alpha _0<\infty \)) phase fields. It is clear that different phase fields become active on the different network branches according to the mass flux through each branch. This can be interpreted as having streets of different qualities: the street \(\varphi _3\) or \(\varphi _2\) allows faster (cheaper) transport, but requires more maintenance than street \(\varphi _1\). If \(\alpha _0<\infty \) mass can also be transported off-road without a street network, thus having maintenance cost \(\beta _0=0\) but large transport expenses \(\alpha _0\). For \(\alpha _0<\infty \) it is also possible to have absolutely continuous sources and sinks, see Fig. 5.
References
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. Oxford Mathematical Monographs. Oxford University Press, New York (2000)
Ambrosio, L., Tilli, P.: Topics on Analysis in Metric Spaces. Oxford Lecture Series in Mathematics and Its Applications, vol. 25. Oxford University Press, Oxford (2004)
Ambrosio, L., Tortorelli, V.M.: On the approximation of free discontinuity problems. Boll. Un. Mat. Ital. B (7) 6(1), 105–123 (1992)
Ambrosio, L., Tortorelli, V.M.: Approximation of functionals depending on jumps by elliptic functionals via \(\Gamma \)-convergence. Commun. Pure Appl. Math. 43(8), 999–1036 (1990)
Bonnivard, M., Lemenant, A., Santambrogio, F.: Approximation of length minimization problems among compact connected sets. SIAM J. Math. Anal. 47(2), 1489–1529 (2015)
Braides, A.: Approximation of Free-Discontinuity Problems. Lecture Notes in Mathematics, vol. 1694. Springer, Berlin (1998)
Braides, A.: \(\Gamma \)-Convergence for Beginners. Oxford Lecture Series in Mathematics and Its Applications, vol. 22. Oxford University Press, Oxford (2002)
Brancolini, A., Wirth, B.: General transport problems with branched minimizers as functionals of 1-currents with prescribed boundary. Calc. Var. Part. Differ. Equ. 57, 82 (2018)
Buttazzo, G., Santambrogio, F.: A model for the optimal planning of an urban area. SIAM J. Math. Anal. 37(2), 514–530 (2005)
Buttazzo, G., Santambrogio, F.: A mass transportation model for the optimal planning of an urban region. SIAM Rev. 51(3), 593–610 (2009)
Chambolle, A., Ferrari, L., Merlet, B.: A phase-field approximation of the Steiner problem in dimension two. Adv. Calc. Var. 12, 157–179 (2017)
Chambolle, A., Ferrari, L.A.D., Merlet, B.: Variational approximation of size-mass energies for k-dimensional currents. ESAIM Control Optim. Calc. Var. 25, 43 (2019)
Colombo, M., De Rosa, A., Marchese, A., Stuvard, S.: On the lower semicontinuous envelope of functionals defined on polyhedral chains. Nonlinear Anal. 163, 201–215 (2017)
Conti, S., Focardi, M., Iurlano, F.: Phase field approximation of cohesive fracture models. Ann. Inst. H. Poincaré Anal. Non Linéaire 33(4), 1033–1067 (2016)
Dal Maso, G.: An Introduction to \(\Gamma \)-Convergence. Progress in Nonlinear Differential Equations and Their Applications, vol. 8. Birkhäuser Boston, Inc., Boston, MA (1993)
Federer, H.: Geometric Measure Theory. Die Grundlehren der mathematischen Wissenschaften, Band 153. Springer-Verlag, New York Inc., New York (1969)
Gilbert, E.N.: Minimum cost communication networks. Bell Syst. Tech. J. 46(9), 2209–2227 (1967)
Gilbert, E.N., Pollak, H.O.: Steiner minimal trees. SIAM J. Appl. Math. 16, 1–29 (1968)
Iurlano, F.: Fracture and plastic models as \(\Gamma \)-limits of damage models under different regimes. Adv. Calc. Var. 6(2), 165–189 (2013)
Karp, R.M.: Reducibility among combinatorial problems. In: Complexity of Computer Computations (Proceedings Symposium, IBM Thomas J. Watson Research Center, Yorktown Heights, N.Y., 1972), pp. 85–103. Plenum, New York (1972)
Lellmann, J., Lorenz, D.A., Schönlieb, C., Valkonen, T.: Imaging with Kantorovich–Rubinstein discrepancy. SIAM J. Imaging Sci. 7(4), 2833–2859 (2014)
Modica, L., Mortola, S.: Un esempio di \(\Gamma ^{-}\)-convergenza. Boll. Un. Mat. Ital. B (5) 14(1), 285–299 (1977)
Mumford, D., Shah, J.: Optimal approximation by piecewise smooth functions and associated variational problems. Commun. Pure Appl. Math. 42(5), 577–685 (1989)
Oudet, E., Santambrogio, F.: A Modica-Mortola approximation for branched transport and applications. Arch. Ration. Mech. Anal. 201(1), 115–142 (2011)
Paolini, E., Stepanov, E.: Existence and regularity results for the Steiner problem. Calc. Var. Partial Differ. Equ. 46(3–4), 837–860 (2013)
Santambrogio, F.: Optimal Transport for Applied Mathematicians. Progress in Nonlinear Differential Equations and Their Applications, vol. 87. Birkhäuser, Boston (2015)
Smirnov, S.K.: Decomposition of solenoidal vector charges into elementary solenoids, and the structure of normal one-dimensional flows. Algebra i Analiz 5(4), 206–238 (1993)
Šilhavý, M.: Divergence measure vectorfields: their structure and the divergence theorem. In: Mathematical Modelling of Bodies with Complicated Bulk and Boundary Behavior. Quad. Mat., vol. 20, pp. 217–237. Dept. Math., Seconda Univ. Napoli, Caserta (2007)
White, B.: Rectifiability of flat chains. Ann. Math. 150(1), 165–184 (1999)
Whitney, H.: Geometric Integration Theory. Princeton University Press, Princeton, NJ (1957)
Acknowledgements
Open Access funding provided by Projekt DEAL. The authors thank Antonin Chambolle and Bénoit Merlet for various discussions and suggestions. The work was supported by the Alfried Krupp Prize for Young University Teachers awarded by the Alfried Krupp von Bohlen und Halbach-Stiftung and by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) via Germany’s Excellence Strategy through the Clusters of Excellence “Cells-in-Motion” (EXC 1003) and “Mathematics Münster: Dynamics – Geometry – Structure” (EXC 2044) at the University of Münster.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by L. Ambrosio.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ferrari, L., Dirks, C. & Wirth, B. Phase field approximations of branched transportation problems. Calc. Var. 59, 37 (2020). https://doi.org/10.1007/s00526-019-1680-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-019-1680-3


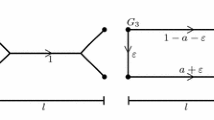



 -measurable,
-measurable,
 -measurable and orients the approximate tangent space of
-measurable and orients the approximate tangent space of


 -measurable, and
-measurable, and 
 for a countably 1-rectifiable set
for a countably 1-rectifiable set  -measurable functions
-measurable functions  so that
so that 



