Abstract
We consider a spectral optimal design problem involving the Neumann traces of the Dirichlet-Laplacian eigenfunctions on a smooth bounded open subset \(\Omega \) of  . The cost functional measures the amount of energy that Dirichlet eigenfunctions concentrate on the boundary and that can be recovered with a bounded density function. We first prove that, assuming a \(L^1\) constraint on densities, the so-called Rellich functions maximize this functional. Motivated by several issues in shape optimization or observation theory where it is relevant to deal with bounded densities, and noticing that the \(L^\infty \)-norm of Rellich functions may be large, depending on the shape of \(\Omega \), we analyze the effect of adding pointwise constraints when maximizing the same functional. We investigate the optimality of bang–bang functions and Rellich densities for this problem. We also deal with similar issues for a close problem, where the cost functional is replaced by a spectral approximation. Finally, this study is completed by the investigation of particular geometries and is illustrated by several numerical simulations.
. The cost functional measures the amount of energy that Dirichlet eigenfunctions concentrate on the boundary and that can be recovered with a bounded density function. We first prove that, assuming a \(L^1\) constraint on densities, the so-called Rellich functions maximize this functional. Motivated by several issues in shape optimization or observation theory where it is relevant to deal with bounded densities, and noticing that the \(L^\infty \)-norm of Rellich functions may be large, depending on the shape of \(\Omega \), we analyze the effect of adding pointwise constraints when maximizing the same functional. We investigate the optimality of bang–bang functions and Rellich densities for this problem. We also deal with similar issues for a close problem, where the cost functional is replaced by a spectral approximation. Finally, this study is completed by the investigation of particular geometries and is illustrated by several numerical simulations.









Similar content being viewed by others
Notes
In other words, the smallest radius of balls containing \(\Omega \).
The characteristic function \(\chi _\Gamma \) of the set \(\Gamma \) is the function equal to 1 in \(\Gamma \) and 0 elsewhere.
We also mention [30] for a review of Rellich-type identities and their use in free boundary problems theory.
Indeed, the outward unit normal \(\nu \) is defined almost everywhere, the eigenfunctions \(\phi _j\) belong to \(H^2(\Omega )\) and their Neumann trace \(\partial \phi _j/\partial \nu \) belongs to \(L^2(\partial \Omega )\) for any \(j\geqslant 1\). Hence \(a\left( \frac{\partial \phi _j}{\partial \nu }\right) ^2\in L^1(\partial \Omega )\) for every \(a\in L^\infty (\Omega )\).
In other words whenever \(-M\leqslant {\tilde{a}}_{x_0}\leqslant M\) a.e. in \(\partial \Omega \) since the function \({\tilde{a}}_{x_0}\) is constructed in such a way that \(\int _{\partial \Omega }{\tilde{a}}_{x_0}\, d\mathcal {H}^{n-1}=LM\mathcal {H}^{n-1}(\partial \Omega )\).
Roughly speaking, the authors highlighted in these articles the so-called spillover phenomenon, saying that the optimizer for N modes becomes the worst one when adding one mode and considering then \(N+1\) modes. Such a phenomenon can be interpreted in terms of \(L^\infty \) weak star convergence of the sequence of optimizers, as the number of modes increases.
Let
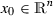 . The quantity \(\ell _{\partial \Omega }(x_0)\) is defined by \( \ell _{\partial \Omega }(x_0)=\max _{x\in \partial \Omega }\Vert x-x_0\Vert . \)
. The quantity \(\ell _{\partial \Omega }(x_0)\) is defined by \( \ell _{\partial \Omega }(x_0)=\max _{x\in \partial \Omega }\Vert x-x_0\Vert . \)Recall that one can endow \({\text {Diff}}^\alpha \) with its topology \(\tau \) inherited from the family of semi-norms defined by
$$\begin{aligned} p_\eta (T) = \sup _{x\in K, j\in \llbracket 1,\alpha \rrbracket ^n, |j|\leqslant \eta } | \partial ^j T(x) |. \end{aligned}$$for every \(\eta \in \{ 1,\ldots , \alpha \}\),
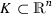 compact, and
compact, and  , making it a complete metric space.
, making it a complete metric space.Indeed, the proof rests upon the fact that Problem (\(\mathcal {P}_N\)) has necessarily a bang–bang solution whenever the set of solutions of the equation
$$\begin{aligned} \sum _{1\leqslant j \leqslant N}\frac{\beta _j^*}{\lambda _j}\left( \frac{\partial \phi _j}{\partial \nu } \right) ^2=\text {constant} \end{aligned}$$on \(\partial \Omega \) is either empty or discrete, for all choices of the family \((\beta _j^*)_{1\leqslant j\leqslant N}\) of nonnegative numbers such that \(\sum _{j=1}^N\beta _j^*=1\). When \(\Omega \) denotes the two-dimensional unit disk, one shows easily that such a property does not hold true since the squares of the eigenfunctions normal derivatives involve the square of cosine and sine functions, whose combination may be constant on intervals.
The basic idea behind this approach, inspired by barrier methods, is to interpret the discretized optimization problem as a bi-objective optimization problem with the two goals of minimizing the objective function and the constraint violation, see [50] for the complete description of the algorithm.
It means that every nontrivial rational linear combination of finitely many of its elements is different from zero.
Recall that a sequence of domains
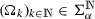 is said to compactly converge to \(\Omega \) if for every compact \(K\subset (\Omega \cup \overline{\Omega }^c)\), there exists
is said to compactly converge to \(\Omega \) if for every compact \(K\subset (\Omega \cup \overline{\Omega }^c)\), there exists 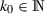 such that one has \(K\subset (\Omega _k\cup \overline{\Omega }_k^c)\) for every \(k\geqslant k_0\).
such that one has \(K\subset (\Omega _k\cup \overline{\Omega }_k^c)\) for every \(k\geqslant k_0\).Note that each eigenfunction \(\phi _j^k\) is supported by the bounded set \(\Omega _k\) which allows to apply the stanfdard elliptic regularity results.
Since \(\Omega \) is convex or has a \(\mathcal {C}^{1,1}\) boundary, the outward unit normal \(\nu \) is defined almost everywhere, the eigenfunctions \(\phi _j\) belong to \(H^2(\Omega )\) and their Neumann trace \(\partial \phi _j/\partial \nu \) belongs to \(L^2(\partial \Omega )\) for any \(j\geqslant 1\). Hence \(a\left( \frac{\partial \phi _j}{\partial \nu }\right) ^2\in L^1(\partial \Omega )\) for every \(a\in L^\infty (\partial \Omega )\).
The expression “density one” means that there exists
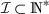 such that \(\# \{j\in \mathcal {I}\ \vert \ j\leqslant N\}/N\) converges to 1 as N tends to \(+\infty \).
such that \(\# \{j\in \mathcal {I}\ \vert \ j\leqslant N\}/N\) converges to 1 as N tends to \(+\infty \).We recall that an open smooth surface A in
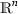 verifies a \(\delta \)-cone property if, for every \(x\in A\), there exists a normalized vector \(\xi _x\) such that \(C(y,\xi _x,\delta )\subset A\) for every \(y\in \overline{A}\cap B(x,\delta )\), where
verifies a \(\delta \)-cone property if, for every \(x\in A\), there exists a normalized vector \(\xi _x\) such that \(C(y,\xi _x,\delta )\subset A\) for every \(y\in \overline{A}\cap B(x,\delta )\), where  , see, e.g., [23].
, see, e.g., [23].In other words, the largest radius of balls contained in \(F_i\).
The isodiametric inequality states that, for every compact K of the Euclidean space
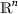 , there holds \(\vert K\vert \leqslant \vert B(0,{\text {diam}}(K)/2)\vert \). The same result holds, up to a multiplicative constant, for a compact stratified manifold endowed with the measure \(\mathcal {H}^{n-1}\) and the geodesic distance on each strata.
, there holds \(\vert K\vert \leqslant \vert B(0,{\text {diam}}(K)/2)\vert \). The same result holds, up to a multiplicative constant, for a compact stratified manifold endowed with the measure \(\mathcal {H}^{n-1}\) and the geodesic distance on each strata.It is well known that observability holds true in large time if \(\Gamma =\{x\in \partial \Omega \ \mid \ \langle x-x^0, \nu (x)\rangle >0\}\) for some \(x^0\in \Omega \) (proof by multipliers, see [25, 33]). Within the class of \(\mathcal {C}^\infty \) domains, observability holds true if \((\Gamma ,T)\) satisfies the Geometric Control Condition (GCC) (see [4]), and this sufficient condition is almost necessary. We refer to [48, 52] for an overview of boundary observability results for wave-like equations.
More precisely, y solves
$$\begin{aligned} \left\{ \begin{array}{ll} \partial _{tt}y(t,x) - \Delta y(t,x) = 0 &{} \forall (t,x)\in (0,T)\times \Omega , \\ \partial _\nu y(t,x) = 0 &{} \forall (t,x)\in (0,T)\times \partial \Omega , \\ y(0,x)=y^0(x), \; \partial _t y(0,x) = y^1(x) &{} \forall x\in \Omega , \\ \end{array} \right. \end{aligned}$$with \((y^0,y^1)\in H^1(\Omega ,\mathbb {C})\times L^2(\Omega ,\mathbb {C})\).
Here, the notation \(\langle \cdot ,\cdot \rangle _{H^{-1},H_0^1}\) stands for the standard duality bracket in \(H^{-1}\) and \(\langle \cdot ,\cdot \rangle _{L^2}\) for the usual inner product in \(L^2\).
There is however a small difficulty here in applying Danskin’s Theorem, due to the fact that the set [0, 1) is not compact. This difficulty is easily overcome by applying the slightly more general version [6, Theorem D2] of Danskin’s Theorem, noting that for \(a=1\) every \(s\in (0,1)\) realizes the infimum in the definition of K.
References
Afifi, L., Chafiai, A., El Jai, A.: Spatial compensation of boundary disturbances by boundary actuators. Appl. Math. Comput. Sci. 11(4), 899–920 (2001)
Arendt, W., Daners, D.: Uniform convergence for elliptic problems on varying domains. Math. Nachr. 280(1–2), 28–49 (2007)
Armaou, A., Demetriou, M.A.: Optimal actuator/sensor placement for linear parabolic pdes using spatial \(h^2\) norm. Chem. Eng. Sci. 61(22), 7351–7367 (2006)
Bardos, C., Lebeau, G., Rauch, J.: Sharp sufficient conditions for the observation, control, and stabilization of waves from the boundary. SIAM J. Control Optim. 30(5), 1024–1065 (1992)
Barnett, A., Hassell, A.: Estimates on neumann eigenfunctions at the boundary, and the “method of particular solutions” for computing them (2011). arXiv preprint arXiv:1107.2172
Bernhard, P., Rapaport, A.: On a theorem of danskin with an application to a theorem of von neumann-sion. Nonlinear Anal. Theory Methods Appl. 24(8), 1163–1181 (1995)
Bonnaillie-Noël, V., Léna, C.: Spectral minimal partitions of a sector. Discrete Contin. Dyn. Syst. Ser. B 19(1), 27–53 (2014)
Brezis, H.: Functional Analysis, Sobolev Spaces and Partial Differential Equations. Springer, Berlin (2010)
Bucur, D., Buttazzo, G.: Variational methods in shape optimization problems. In: Progress in Nonlinear Differential Equations and their Applications, vol. 65. Birkhäuser Boston, Inc., Boston, MA (2005)
Burq, N.: Quantum ergodicity of boundary values of eigenfunctions: a control theory approach. Can. Math. Bull. 48(1), 3–15 (2005)
Burq, N.: Large-time dynamics for the one-dimensional schrödinger equation. Proc. R. Soc. Edinb. Sect. A Math. 141(02), 227–251 (2011)
Burq, N., Tzvetkov, N.: Random data cauchy theory for supercritical wave equations I: local theory. Invent. Math. 173(3), 449–475 (2008)
Burq, N., Zworski, M.: Bouncing ball modes and quantum chaos. SIAM Rev. 47(1), 43–49 (2005)
Dardé, J., Hakula, H., Hyvönen, N., Staboulis, S., Somersalo, E.: Fine-tuning electrode information in electrical impedance tomography. Inverse Probl. Imaging 6, 399–421 (2012)
Delfour, M.C., Zolésio, J.-P.: Metrics, analysis, differential calculus, and optimization : shapes and geometries. In: Advances in Design and Control, 2nd edn, vol. 22. Society for Industrial and Applied Mathematics (SIAM), Philadelphia PA (2011)
Fourer, R., Gay, D.M., Kernighan, B.W.: A modeling language for mathematical programming. Manag. Sci. 36(5), 519–554 (1990)
Harris, T.J., Macgregor, J., Wright, J.: Optimal sensor location with an application to a packed bed tubular reactor. AIChE J. 26(6), 910–916 (1980)
Hassell, A., Zelditch, S.: Quantum ergodicity of boundary values of eigenfunctions. Commun. Math. Phys. 248(1), 119–168 (2004)
Hébrard, P., Henrot, A.: Optimal shape and position of the actuators for the stabilization of a string. Syst. Control Lett. 48(3), 199–209 (2003)
Hébrard, P., Henrot, A.: A spillover phenomenon in the optimal location of actuators. SIAM J. Control Optim. 44(1), 349–366 (2005)
Henrot, A.: Extremum Problems for Eigenvalues of Elliptic Operators. Frontiers in Mathematics. Birkhäuser Verlag, Basel (2006)
Henrot, A. (ed.): Shape Optimization and Spectral Theory. De Gruyter Open, Warsaw (2017)
Henrot, A., Pierre, M.: Variation et Optimisation de Formes: Une Analyse géométrique, vol. 48. Springer, Berlin (2006)
Hillairet, L., Judge, C.: Generic spectral simplicity of polygons. Proc. Am. Math. Soc. 137(6), 2139–2145 (2009)
Ho, L.F.: Observabilité frontière de l’équation des ondes. Compt. Rendus Acad. Sci. Sér. 1 Math. 302(12), 443–446 (1986)
Kato, T.: Perturbation Theory for Linear Operators. Springer, Berlin (2012)
Kawohl, B., Pironneau, O., Tartar, L., Zolésio, J.-P.: Optimal shape design. In: Lecture Notes in Mathematics, vol. 1740. Springer, Berlin; Centro Internazionale Matematico Estivo (C.I.M.E.), Florence, 2000. Lectures given at the Joint C.I.M./C.I.M.E. Summer School held in Tróia, June 1–6 (1998). Cellina, A., Ornelas, A. (eds.) Fondazione CIME/CIME Foundation Subseries
Lions, J.L.: Contrôlabilité exacte perturbations et stabilisation de systèmes distribués(tome 1, contrôlabilité exacte. tome 2, perturbations). Recherches en Mathematiques Appliquées (1988)
Lions, J.-L.: Exact controllability, stabilization and perturbations for distributed systems. SIAM Rev. 30(1), 1–68 (1988)
Liu, G.: Rellich type identities for eigenvalue problems and application to the pompeiu problem. J. Math. Anal. Appl. 330(2), 963–975 (2007)
Luke, Y.L.: Integrals of Bessel functions. McGraw-Hill, New York (1962)
Micheletti, A.M.: Metrica per famiglie di domini limitati e proprietà generiche degli autovalori. Ann. Scuola Norm. Sup. Pisa 3(26), 683–694 (1972)
Morawetz, C.S.: Notes on Time Decay and Scattering for Some Hyperbolic Problems, vol. 19. SIAM (1975)
Morrey, C.B.: On the analyticity of the solutions of analytic non-linear elliptic systems of partial differential equations: Part II. Analyticity at the boundary. Am. J. Math. 80, 219–237 (1958)
Morris, K.: Linear-quadratic optimal actuator location. IEEE Trans. Autom. Control 56(1), 113–124 (2011)
Ozawa, S.: Perturbation of domains and Green kernels of heat equations. Proc. Jpn. Acad. Ser. A Math. Sci. 54(10), 322–325 (1978)
Polak, E.: Optimization: Algorithms and Consistent Approximations, vol. 124. Springer, Berlin (2012)
Privat, Y., Sigalotti, M.: The squares of the Laplacian-Dirichlet eigenfunctions are generically linearly independent. ESAIM: Control Optim. Calc. Var. 16(03), 794–805 (2010)
Privat, Y., Trélat, E., Zuazua, E.: Optimal location of controllers for the one-dimensional wave equation. Ann. Inst. H. Poincaré Anal. Non Linéaire 30(6), 1097–1126 (2013)
Privat, Y., Trélat, E., Zuazua, E.: Optimal observation of the one-dimensional wave equation. J. Fourier Anal. Appl. 19(3), 514–544 (2013)
Privat, Y., Trélat, E., Zuazua, E.: Complexity and regularity of maximal energy domains for the wave equation with fixed initial data. Discrete Contin. Dyn. Syst. 35(12), 6133–6153 (2015)
Privat, Y., Trélat, E., Zuazua, E.: Optimal shape and location of sensors for parabolic equations with random initial data. Arch. Ration. Mech. Anal. 216(3), 921–981 (2015)
Privat, Y., Trélat, E., Zuazua, E.: Optimal observability of the multi-dimensional wave and Schrödinger equations in quantum ergodic domains. J. Eur. Math. Soc. (JEMS) 18(5), 1043–1111 (2016)
Privat, Y., Trélat, E., Zuazua, E.: Actuator design for parabolic distributed parameter systems with the moment method. SIAM J. Control Optim. 55(2), 1128–1152 (2017)
Rellich, F.: Darstellung der eigenwerte von \(\delta \)u+\(\lambda \)u= 0 durch ein randintegral. Math. Z. 46(1), 635–636 (1940)
Sarnak, P.: Recent progress on the quantum unique ergodicity conjecture. Bull. Am. Math. Soc. (N.S.) 48(2), 211–228 (2011)
Teytel, M.: How rare are multiple eigenvalues? Commun. Pure Appl. Math. 52(8), 917–934 (1999)
Tucsnak, M., Weiss, G.: Observation and Control for Operator Semigroups. Springer, Berlin (2009)
Uhlenbeck, K.: Generic properties of eigenfunctions. Am. J. Math. 98(4), 1059–1078 (1976)
Wächter, A., Biegler, L.T.: On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 106(1), 25–57 (2006)
Wouwer, A.V., Point, N., Porteman, S., Remy, M.: An approach to the selection of optimal sensor locations in distributed parameter systems. J. Process Control 10(4), 291–300 (2000)
Zuazua, E.: Controllability and observability of partial differential equations: some results and open problems. Handb. Differ. Equ. Evol. Equ. 3, 527–621 (2007)
Acknowledgements
Y. Privat was partially supported by the Project “Analysis and simulation of optimal shapes—application to lifesciences” of the Paris City Hall. The work of the third author has been partially funded by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 694126-DyCon), grant MTM2017-92996 of MINECO (Spain), ELKARTEK project KK-2018/00083 ROAD2DC of the Basque Government, ICON of the French ANR and “Nonlocal PDEs: Analysis, Control and Beyond”, AFOSR Grant FA9550-18-1-0242.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by L. Ambrosio.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix: Proofs of Propositions 4, 5 and 6
In what follows, we will assume that \(M=1\) for the sake of readability. The general result will be easily inferred by an immediate adaptation of the reasonings.
Proof of Proposition 4
This proof is inspired by [40, Proposition 1 and Theorem 1]. For this reason, we only provide a short sketch of proof, underlining the main steps.
Let us first solve the convexified optimal design problem (\(\mathcal {P}_\infty \)). According to the expression of \(J_\infty (a)\) given by (32), letting n and k going to \(+\infty \) yields
by using that \(\int _{\partial \Omega }a(x,y)\, d\mathcal {H}^{n-1}=2L\pi (\alpha +\beta )\) and as a consequence
Observe moreover that both components of the minimum above are equal at the optimum. To compute the optimal value for the convexified problem, we will use Theorem 3. Let us investigate the existence of Rellich-admissible functions. A simple computation shows that every Rellich-admissible function, whenever it exists, is necessarily constant on each side of \(\Omega \), namely on \(\Sigma _1\), \(\Sigma _2\), \(\Sigma _3\) and \(\Sigma _4\). Moreover, for a given \(x_0\) in \(\Omega \) and when x runs over \(\partial \Omega \), the quantity \(\langle x-x_0,\nu \rangle \) is successively equal to the distance of \(x_0\) to each side of \(\Omega \). Therefore, it is enough to investigate the case where \(x_0=(0,0)\) to determine the set of parameters L, \(\alpha \) and \(\beta \) for which there exists Rellich-admissible functions. In other words, this question comes to determine L, \(\alpha \) and \(\beta \) such that the function \(a^*\) defined by
belongs to \(\overline{\mathcal {U}}_{L,1}\).
It follows that there exists a Rellich-admissible function if, and only if \(|L|\leqslant L^c_{n}\) (defined in the statement of Proposition 4). Moreover, in this case, one has
Let us now investigate the converse case. Assume without loss of generality that \(\beta <\alpha \) and \(L\in (\frac{2\beta }{\alpha +\beta },1]\), the case \(L\in [-1,-\frac{2\beta }{\alpha +\beta })\) being treatable in a similar way. Then, one has
meaning that \(J_\infty (a)\leqslant \frac{4}{\pi \alpha }\) for every \(a\in \overline{\mathcal {U}}_{L,1}\), according to (45). The right-hand side in this inequality is in fact reached by every function a equal to 1 on \(\Sigma _1\cup \Sigma _3\), constant on each side \(\Sigma _2\) and \(\Sigma _3\), where each constant is chosen in such a way that a belongs to \(\overline{\mathcal {U}}_{L,1}\). Notice that such a choice is not unique, and easy computations yield that maximizers are given by
with \(u\in \left( 1-\left( \frac{\alpha }{L(\alpha +\beta )-\beta }-1\right) ,1+\left( \frac{\alpha }{L(\alpha +\beta )-\beta }-1\right) \right) \).
The rest of the proof is a direct adaptation of the results of [40, Theorem 1] and in particular of the fact that
Finally, the necessary and sufficient condition on L guaranteeing the existence of solutions for the initial optimal design problem follows by using the same Fourier series method as in the proof of [40, Theorem 1].
Proof of Proposition 5
The proof of this proposition is inspired by [19, Theorem 3.2] and [40, Theorem 1]. First, notice that for every a in \(\overline{\mathcal {U}}_{L,M}\), one has
and that \(J_\infty (L)=L\pi \), yielding that the optimal value for Problem (\(\mathcal {P}_\infty \)) is \(\pi L\). Moreover, the constant function equal to L belongs to \(\overline{\mathcal {U}}_{L,M}\) since \(M\geqslant 1\) and \(a\in \overline{\mathcal {U}}_{L,M}\) reaches \(\pi L\) if, and only if
or similarly

Considering the Fourier expansion \( a(\theta )=L+\sum _{j=1}^{+\infty } ( \alpha _j \cos (j\theta ) + \beta _j \sin (j\theta ) )\), the equality (48) holds if, and only if \(\alpha _{2j} = 0\), \(\forall j\geqslant 1\).
The no-gap property between the optimal values for Problem (\(\mathcal {P}_\infty ^\mathrm{bb}\)) and its convexified version (\(\mathcal {P}_\infty \)) is a consequence of Theorem 4.
Let us now investigate the no-gap property. Assume that \(a=2\chi _{\Gamma }-1\) solves (\(\mathcal {P}_\infty ^\mathrm{bb}\)) and consider \(a_e:\theta \mapsto \frac{a(\theta )+a(2\pi -\theta )}{2}\), its even part. First, \(a_e\) is still a solution of (\(\mathcal {P}_\infty \)) and \( a_e(\theta ) = L + \sum _{j=1}^{+\infty } \alpha _j \cos (j \theta ) \). Setting now \(\tilde{a}(\theta ) = \frac{a_e(\theta )+a_e(\pi -\theta )}{2}\), one has
Since \(\tilde{a}\) solves (\(\mathcal {P}_\infty \)), we have \(\alpha _{2j}=0\), for all \(j\geqslant 1\). Thus, \(\tilde{a}\) is necessarily constant equal to L. Finally since \(a\in \mathcal {U}_{L,M} \), hence the range of \(a_e\) is contained in \(\lbrace -1, 0, 1\rbrace \), and finally \(\tilde{a}\) in \(\lbrace -1,-1/2,0,1/2,1 \rbrace \). This yields that Problem (\(\mathcal {P}_\infty ^\mathrm{bb}\)) has no solution if \(L\notin \lbrace -1,-1/2,0,1/2,1 \rbrace \).
Conversely, if \(L\in \lbrace -1,-1/2,0,1/2,1 \rbrace \), a direct adaptation of the construction of solutions done in the proof of [40, Theorem 1] or [19, Lemma 3.1] yields the expected conclusion.
Proof of Proposition 6
Denote by \(\Sigma _1\), \( \Sigma _2\) and \(\Sigma _3\) the subsets of \(\partial \Omega \) defined by
Fixing  and letting k tend to \(+\infty \) shows that the sequence
and letting k tend to \(+\infty \) shows that the sequence  does not converge to a constant on \(\partial \Omega \). Therefore, \(\Omega \) does not satisfy the (QUEB) property.
does not converge to a constant on \(\partial \Omega \). Therefore, \(\Omega \) does not satisfy the (QUEB) property.
We do not know if \(\Omega \) satisfies the (WQEB) property. Anyway, we bypass this difficulty by showing a weaker version of this property. This is the purpose of the next two lemmas.
The results stated in the two next lemmas are inspired by [43, Proposition 4].
Lemma 4
For \(s\in (0,1)\), let us denote by \(F_s\) the function \([s,1]\ni x\mapsto \int _s^x \frac{du}{u^2\sqrt{u^2-s^2}}\). We have
where \(\mathcal {V}= \lbrace a\in L^\infty ([0,1])\ \mid \ \int _0^1 a(u)\, du = 1 \rbrace \).
Proof
Define the function \(K: \overline{\mathcal {U}}_{L,M}\ni a \mapsto \inf \limits _{s\in (0,1)} \; \frac{1}{F_s(1)}\int _0^1 \frac{a(u) \chi _{(s,1)}(u)}{u^2 \sqrt{u^2-s^2}} \, du \). Note that \( K(a=1) = 1\) by definition of \(F_s\) and that the infimum in the definition of K is reached for every \(s\in (0,1)\). As an infimum of linear functions, the function K is concave. Therefore, to prove the lemma, it is enough to show that the directional derivative of K at \(a=1\) in every admissible direction h satisfies the first-order necessary optimality conditions, namely that \(dK(a=1).h \leqslant 0\) for every function h defined on [0, 1] such that \(\int _0^1 h(u)du =0\).
According to Danskin’s theorem,Footnote 22 we have
By contradiction assume that there exists a function h such that
for every \(s\in (0,1)\). One has
leading to a contradiction. The conclusion follows. \(\square \)
Lemma 5
For every \(a\in \overline{\mathcal {U}}_{L,M}\), one has \( J_\infty (a) \leqslant \frac{L \mathcal {H}^{n-1}(\partial \Omega )}{|\Omega |}.\)
Proof
Let \(a\in \overline{\mathcal {U}}_{L,M}\). We will show the existence of a subsequence of  converging to \(\frac{1}{\theta _1 R^2} \int _{\partial \Omega } a(x)\, d\mathcal {H}^{n-1}=\frac{L \mathcal {H}^{n-1}(\partial \Omega )}{|\Omega |}\).
converging to \(\frac{1}{\theta _1 R^2} \int _{\partial \Omega } a(x)\, d\mathcal {H}^{n-1}=\frac{L \mathcal {H}^{n-1}(\partial \Omega )}{|\Omega |}\).
Since \(\frac{1}{\lambda _{n,k}} \left( \frac{\partial \varphi _{n,k}}{\partial \nu } \right) ^2 = \frac{2}{R^2 \theta _1} \sin \left( \frac{n\pi }{2\theta _1} (\theta + \theta _1)\right) \) on \(\Sigma _3\), the sequence  converges to \(\frac{1}{\theta _1 R^2} \int _{\Sigma _3} a(x)\, d\mathcal {H}^{n-1}\), according to the Riemann–Lebesgue Lemma.
converges to \(\frac{1}{\theta _1 R^2} \int _{\Sigma _3} a(x)\, d\mathcal {H}^{n-1}\), according to the Riemann–Lebesgue Lemma.
To conclude the proof, it is enough to prove the existence of a positive number \(\alpha \) such that, by keeping the ratio n / k constant equal to \(\alpha \), there holds
Setting \(\mu = \frac{n\pi }{2\theta _1}\) and introducing \(\Phi _{n,k}: [0,1]\ni u\mapsto \frac{ n^2 \pi ^2}{2 z_{n,k}^2 \theta _1^2} \left( \frac{J_\mu \left( z_{n,k}\frac{r}{R}\right) }{r J'_\mu (z_{n,k})} \right) ^2\), one has
Hence, we have to prove that for every \(\rho \in L^\infty ([-1,1],[-1,1])\), there exists \(\alpha >0\) such that for n and k chosen as previously,
According to [31, p. 257], one has \( \int _0^1 \Phi _{n,k}(u)\, du = \frac{n^2 \pi ^2}{n^2\pi ^2 - \theta _1}\). Then, taking the weak limit of the sequence of measures \(\Phi _{n,k}(u)\, du\) with a fixed ratio n / k, and making this ratio vary, we obtain the family of probability measures
parametrized by \(s\in (0,1)\).
To prove (49), let us argue by contradiction, by assuming that for every \(s \in (0,1)\), one has
We obtain a contradiction by using Lemma 4 and the expected conclusion follows. \(\square \)
In the next lemma, one computes the critical value \(L^c_{n}\) introduced in Theorem 3.
Lemma 6
Denote by \(L^c_{n}\) the critical value for the constraint parameter L, as introduced in Theorem 3. One has \(L^c_{n} = \frac{\theta _1 (1+\tan \theta _1)}{(1+\theta _1)\tan \theta _1}\).
Proof
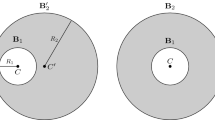
Following the proof of Theorem 3, the critical value \(L^c_{n}\) is given by (17). Therefore, the issue comes to determine the quantity \( \delta :=\min _{x_0\in \overline{\Omega }} \max _{x\in \partial \Omega } \langle x-x_0, \nu _x \rangle \). For the sake of simplicity, the notations we will use are summed-up on Fig. 10. Writing in polar coordinates \(x_0=(r_0,\theta _0)\), the quantity \(\langle x-x_0, \nu _x \rangle \) is equal to \(r_0\sin (\theta _1+\theta _0)\) on \(\Sigma _1\), \(r_0\sin (\theta _1-\theta _0)\) on \(\Sigma _2\) and \(R-r_0 \cos (\theta _0-\theta )\) on \(\Sigma _3\), where we denoted \(x=(R,\theta )\) in polar coordinates on \(\Sigma _3\).
As a consequence, one computes using symmetry arguments
and the maximum is reached provided that \(R-r_0\cos \theta _1= r_0 \sin \theta _1\). It follows that \( \delta = \frac{R\tan (\theta _1)}{1+\tan (\theta _1)}\), leading to the expected conclusion. \(\square \)
In the following lemma, we compute the optimal value of Problem (\(\mathcal {P}_\infty \)).
Lemma 7
Let \(L^c_{n} = \frac{\theta _1 (1+\tan \theta _1)}{(1+\theta _1)\tan \theta _1}\). We have
Proof
According to Lemma 5, one has \( J_\infty (a) \leqslant \frac{L \mathcal {H}^{n-1}(\partial \Omega )}{|\Omega |}\) and according to Lemma 6, the right-hand side in this inequality is reached by every Rellich-admissible function if \(|L|\leqslant L^c_{n}\).
Assume now that \(L>L^c_{n}\) (the case \(L<-L^c_n\) being exactly similar). Let us introduce \(a_c\), as the solution of the optimal design problem (\(\mathcal {P}_\infty \)) in the case where \(L=L^c_{n}\). One verifies that \(a_c=1\) on \(\Sigma _1\cup \Sigma _2\) and \(a_c = R-r_0\cos (\theta )\) on \(\Sigma _3\). Let \(a\in \overline{\mathcal {U}}_{L,M}\) and let us decompose a as \(a=a_c+h\), so that \( \int _{-\theta _1}^{\theta _1}a(R,\theta ) R d\theta = L\mathcal {H}^{n-1}(\partial \Omega ) - 2R\), \( \int _{-\theta _1}^{\theta _1}h(R,\theta ) R d\theta +\int _{\Sigma _1\cup \Sigma _2}h = (L-L^c_{n})\mathcal {H}^{n-1}(\partial \Omega )\) and \(h <0\) on \(\Sigma _1\cup \Sigma _2\).
Let us apply (2) with \(L=L^c_{n}\). One gets
Using this identity, we claim that  , where
, where
As a consequence and according to the Riemann–Lebesgue lemma, one has

Note that the right-hand side in the last inequality is reached by the function \(a^*\) equal to 1 on \(\Sigma _1\cup \Sigma _2\) and constant on \(\Sigma _3\), where the constant is chosen so that \(\int _{\partial \Omega }a^*\, d\mathcal {H}^{n-1}=L\mathcal {H}^{n-1}(\partial \Omega )\). We have then proved the expected result. \(\square \)
It remains now to prove the no-gap result between the optimal values for Problem (\(\mathcal {P}_\infty ^\mathrm{bb}\)) and its convexified version (\(\mathcal {P}_\infty \)) in the case where \(L\geqslant L^c_{n}\). Since every solution for the convexified problem (\(\mathcal {P}_\infty \)) is equal to 1 on \(\Sigma _1\cup \Sigma _2\), it is enough to exhibit a sequence  of elements in \(\mathcal {U}_{L,M}\) such that \(a_m =1\) on \(\Sigma _1\cup \Sigma _2\) and
of elements in \(\mathcal {U}_{L,M}\) such that \(a_m =1\) on \(\Sigma _1\cup \Sigma _2\) and

One refers to the proof of [40, Theorem 1] where the construction of such a sequence is explained.
Rights and permissions
About this article
Cite this article
Privat, Y., Trélat, E. & Zuazua, E. Spectral shape optimization for the Neumann traces of the Dirichlet-Laplacian eigenfunctions. Calc. Var. 58, 64 (2019). https://doi.org/10.1007/s00526-019-1522-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-019-1522-3




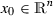 . The quantity
. The quantity 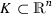 compact, and
compact, and  , making it a complete metric space.
, making it a complete metric space.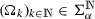 is said to compactly converge to
is said to compactly converge to 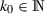 such that one has
such that one has 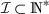 such that
such that 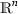 verifies a
verifies a  , see, e.g., [
, see, e.g., [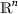 , there holds
, there holds 