Appendix
Here we collect together materials, mainly technical in nature, including background material, various technical computations, the proof of the \(\alpha \)-connection concentration compactness result used in Lemma 3.3, properties of the \({\widetilde{\triangledown }}\) Coulomb gauge, and the proof of the Morrey-type inequalities used in the proof of Proposition 4.3.
1.1 Background material
We state a variety of key polarization identities, which require elementary computation to show. For the following let \(\triangledown ,{\blacktriangledown }\in C^2 \left( {\mathcal {A}}_E(M) \right) \), and \(\Upsilon := \triangledown - {\blacktriangledown }\). We record Proposition 7.1 and in terms of more general formulas; not assuming \(M = {\mathbb {S}}^4\).
Proposition 7.1
We have that
$$\begin{aligned} \left( F_{\triangledown } - F_{{\blacktriangledown }} \right) _{ij\theta }^{\beta } = \left( {\blacktriangledown }_i \Upsilon _{j\theta }^{\beta } \right) - \left( {\blacktriangledown }_j \Upsilon _{i \theta }^{\beta } \right) + \Upsilon _{i \mu }^{\beta } \Upsilon _{j \theta }^{\mu } - \Upsilon _{j \mu }^{\beta } \Upsilon _{i \theta }^{\mu }. \end{aligned}$$
(7.1)
Proposition 7.2
We have that
$$\begin{aligned} -\left( D^*_{\triangledown } F_{\triangledown }- D_{{\blacktriangledown }}^* F_{{\blacktriangledown }} \right) _{i \theta }^{\beta }&= \left( {\blacktriangledown }_k {\blacktriangledown }_k \Upsilon _{i\theta }^{\beta } \right) - \left( {\blacktriangledown }_i {\blacktriangledown }_k \Upsilon _{k \theta }^{\beta } \right) - {{\,\mathrm{Rm}\,}}_{kik}^p \Upsilon _{p \theta }^{\beta } \\&\quad + 2\Upsilon _{k \mu }^{\beta } \left( F_{{\blacktriangledown }} \right) _{k i \theta }^{\mu } - 2\left( F_{{\blacktriangledown }} \right) _{ki \mu }^{\beta }\Upsilon _{k \theta }^{\mu } \\&\quad + \Upsilon _{i \zeta }^{\beta } \Upsilon _{k \mu }^{\zeta } \Upsilon _{k \theta }^{\mu } - 2 \Upsilon _{k \mu }^{\beta } \Upsilon _{i \zeta }^{\mu } \Upsilon _{k \theta }^{\zeta } + \Upsilon _{k \mu }^{\beta } \Upsilon _{k \zeta }^{\mu } \Upsilon _{i \theta }^{\zeta } \\&\quad + \left( {\blacktriangledown }_i \Upsilon _{k\mu }^{\beta } \right) \Upsilon _{k \theta }^{\mu } - \Upsilon _{k \mu }^{\beta } \left( {\blacktriangledown }_i \Upsilon _{k\theta }^{\mu } \right) \\&\quad + 2\Upsilon _{k \mu }^{\beta } \left( {\blacktriangledown }_k \Upsilon _{i \theta }^{\mu } \right) - 2\left( {\blacktriangledown }_k\Upsilon _{i \mu }^{\beta } \right) \Upsilon _{k \theta }^{\mu } \\&\quad + \left( {\blacktriangledown }_k \Upsilon _{k \mu }^{\beta } \right) \Upsilon _{i \theta }^{\mu } - \Upsilon _{i \mu }^{\beta } \left( {\blacktriangledown }_k\Upsilon _{k \theta }^{\mu } \right) . \end{aligned}$$
1.2 Various technical computations
Lemma 7.3
There is a constant \(C>0\) which is independent of \(\lambda \ge 1\) so that
$$\begin{aligned} \left| \left| \triangledown \log \chi _{\lambda } \right| \right| _{L^2} + \left| \left| \triangledown ^{(2)} \log \chi _{\lambda } \right| \right| _{L^2} \le {\left\{ \begin{array}{ll} C \log \lambda &{} \text { when } \lambda \in \left[ 1,e \right] \\ C \left( \log \lambda \right) ^{1/2} &{} \text { when } \lambda \in [e,\infty ) \\ \end{array}\right. }. \end{aligned}$$
(7.2)
Proof
To apply spherical coordinates we use the appropriate change of variables
$$\begin{aligned} \zeta _1 = r \sin \vartheta _1 \sin \vartheta _2 \cos \vartheta _3, \quad \zeta _2 = r \sin \vartheta _1 \sin \vartheta _2 \sin \vartheta _3, \quad \zeta _3 = r \sin \vartheta _1 \cos \vartheta _2, \quad \zeta _4 = r \cos \vartheta _4 \\ g_{rr} = 1, \quad g_{11} :=g_{\vartheta _1 \vartheta _1} = r^2, \quad g_{22}:=g_{\vartheta _2 \vartheta _2} = r^2 \sin ^2 \vartheta _1, \quad g_{33}:=g_{\vartheta _3 \vartheta _3} = r^2 \sin ^2 \vartheta _1 \sin ^2 \vartheta _2. \end{aligned}$$
Inserting these into the formula for the Levi Civita connection, we have
$$\begin{aligned} \Gamma _{ij}^r = 0 \, (i \ne j), \quad \Gamma _{11}^r = r, \quad \Gamma _{22}^r = r \sin ^2 \vartheta _1, \quad \Gamma _{33}^r = r \sin ^2 \vartheta _1 \sin ^2 \vartheta _2, \end{aligned}$$
(7.3)
Recalling the formula for \(\chi _{\lambda }(\zeta ) = \frac{1}{\lambda ^4} \left( \frac{1 + \left| \lambda \zeta \right| ^2}{\left| \zeta \right| ^2 + 1 } \right) ^4\) via (2.5), take \(r=\left| \zeta \right| \). Observe that
$$\begin{aligned} \triangledown \log \chi _{\lambda }&= \tfrac{\partial }{\partial r} \left[ \log \chi _{\lambda } \right] \quad \text {and} \quad \triangledown ^{(2)} \log \chi _{\lambda } = \tfrac{\partial ^2}{\partial r^2} \log \chi _{\lambda } - \left( \sum _{i=1}^3 \Gamma _{ii}^r \right) \tfrac{\partial }{\partial r} \left[ \log \chi _{\lambda } \right] . \end{aligned}$$
(7.4)
First we compute
$$\begin{aligned} \tfrac{\partial }{\partial r} \left[ \log \chi _{\lambda } \right]&= \tfrac{ 8r(\lambda ^2 -1)}{\left( 1+ \lambda ^2 r^2 \right) (1+r^2)}, \quad \tfrac{\partial ^2}{\partial r^2} \left[ \log \chi _{\lambda } \right] = - \tfrac{8 \left( \lambda ^2-1 \right) \left( 3 \lambda ^2 r^4 + \left( \lambda ^2+1 \right) r^2 -1 \right) }{\left( r^2+1 \right) ^2 \left( \lambda ^2 r^2 + 1 \right) ^2}. \end{aligned}$$
Thus we have that, for the first derivative of \(\log \chi _{\lambda }\),
$$\begin{aligned} \left| \left| \triangledown \log \chi _{\lambda } \right| \right| _{L^2}^2&= \left( \int _0^{2\pi } \int _0^{\pi } \int _0^{\pi } \, d \vartheta _1 \, d \vartheta _2 \, d \vartheta _3 \right) \left( \int _0^{\infty } \tfrac{r^3}{\left( 1+r^2 \right) ^2}\left( \tfrac{\partial }{\partial r}\left[ \log \chi _{\lambda } \right] \right) ^2 \, dr \right) \\&= 2 \pi ^3 \left( \int _0^{1/\lambda }+\int _{1/\lambda }^1 + \int _1^{\infty } \right) \tfrac{r^3}{\left( 1+r^2 \right) ^2}\left( \tfrac{\partial }{\partial r}\left[ \log \chi _{\lambda } \right] \right) ^2 \, dr \\&= 2^7 \pi ^3 \left( \lambda ^2-1 \right) ^1\left( \int _0^{1/\lambda } r^5 \, dr + \int _{1/\lambda }^1 \tfrac{r}{\lambda ^4} \, dr + \int _0^{1/\lambda } \tfrac{1}{\lambda ^4 r^{7}} \, dr \right) \\&= 2^7 \pi ^3 \left( \lambda ^2 - 1 \right) ^2 \left( \tfrac{1}{6 \lambda ^6} + \tfrac{1}{2\lambda ^4} - \tfrac{1}{2 \lambda ^6} + \tfrac{1}{6 \lambda ^4} \right) \\&= 2^7 \pi ^3 \left( \tfrac{\lambda - 1}{\lambda } \cdot \tfrac{\lambda + 1}{\lambda } \right) ^{2} \left( \tfrac{2}{3} - \tfrac{1}{3 \lambda ^2} \right) \\&= \tfrac{2^7}{3} \pi ^3 \left( \tfrac{\lambda - 1}{\lambda } \right) ^{2}\left( \tfrac{\lambda + 1}{\lambda } \right) ^{2}. \end{aligned}$$
Now we approach the second derivative of \(\log \chi _{\lambda }\). Utilizing (7.4) above, we note that
$$\begin{aligned} \left| \left| \triangledown ^{(2)} \log \chi _{\lambda } \right| \right| _{L^2}^2 \le \left| \left| \tfrac{\partial ^2}{\partial r^2} \left[ \log \chi _{\lambda } \right] \right| \right| _{L^2}^2 + \left| \left| \Gamma ^r \partial _r \log \chi _\lambda \right| \right| _{L^2}^2. \end{aligned}$$
(7.5)
In this case we have that
$$\begin{aligned}&\left| \left| \tfrac{\partial ^2}{\partial r^2} \left[ \log \chi _{\lambda } \right] \right| \right| _{L^2}^2 \\ \qquad \qquad&= \left( \int _0^{2\pi } \int _0^{\pi } \int _0^{\pi } \, d \vartheta _1 \, d \vartheta _2 \, d \vartheta _3 \right) \left( \int _0^{\infty } \tfrac{r^3}{\left( 1+r^2 \right) ^4}\left( \tfrac{\partial ^2}{\partial r^2}\left[ \log \chi _{\lambda } \right] \right) ^2 \, dr \right) \\ \qquad \qquad&= 2 \pi ^3 \left( \int _0^{1/\lambda } + \int _{1/\lambda }^1+\int _1^{\infty } \right) \tfrac{r^3}{\left( 1+r^2 \right) ^4}\left( \tfrac{\partial ^2}{\partial r^2}\left[ \log \chi _{\lambda } \right] \right) ^2 \, dr \\ \qquad \qquad&\le 2^7 \pi ^3 \left( \lambda ^2-1 \right) ^2 \int _0^{1/\lambda } \left( r^{11} 9 \lambda ^4 + r^9 \left( 6 \lambda ^4 + 6 \lambda ^2 \right) + r^7 \left( \lambda ^4 - 4 \lambda ^2 + 1 \right) \right. \\&\left. \qquad \qquad + r^5 \left( -2 \lambda ^2 - 2 \right) + r^3 \right) \, dr\\ \qquad \qquad&\qquad + 2^7 \pi ^3 \left( \lambda ^2-1 \right) ^2 \int _{1/\lambda }^1 \tfrac{1}{r^{8} \lambda ^8} \left( r^{11} 9 \lambda ^4 + r^9 \left( 6 \lambda ^4 + 6 \lambda ^2 \right) + r^7 \left( \lambda ^4 - 4 \lambda ^2 + 1 \right) \right. \\&\left. \qquad \qquad + r^5 \left( -2 \lambda ^2 - 2 \right) + r^3 \right) \, dr\\ \qquad \qquad&\qquad + 2^7 \pi ^3 \left( \lambda ^2-1 \right) ^2 \int _1^{\infty } \tfrac{1}{r^{24} \lambda ^8} \left( r^{11} 9 \lambda ^4 + r^9 \left( 6 \lambda ^4 + 6 \lambda ^2 \right) + r^7 \left( \lambda ^4 - 4 \lambda ^2 + 1 \right) \right. \\&\left. \qquad \qquad + r^5 \left( -2 \lambda ^2 - 2 \right) + r^3 \right) \, dr\\ \qquad \qquad&= 2^7 \pi ^3 \left( \tfrac{\lambda -1}{\lambda } \right) ^{2} \left( \tfrac{\lambda +1}{\lambda } \right) ^{2} \left( - \tfrac{2177}{720} \tfrac{1}{\lambda ^4} - \tfrac{209}{1260} \tfrac{1}{\lambda ^2} + \tfrac{1943}{336} \right) \\&= 2^7 \tfrac{1307}{504} \pi ^3 \left( \tfrac{\lambda -1}{\lambda } \right) ^{2} \left( \tfrac{\lambda +1}{\lambda } \right) ^{2}. \end{aligned}$$
For the second component of (7.5), we have
$$\begin{aligned} \int _0^{2\pi } \int _0^{\pi } \int _0^{\pi }&\int _0^{\infty } \tfrac{r^3}{\left( 1+r^2 \right) ^4}\left( \Gamma ^r \tfrac{\partial }{\partial r}\left[ \log \chi _{\lambda } \right] \right) ^2 \, dr \, d \vartheta _1 \, d \vartheta _2 \, d \vartheta _3 \\&= \left( \int _0^{2\pi } \int _0^{\pi } \int _0^{\pi } \left( 1+\sin ^2 \vartheta _1 + \sin ^2 \vartheta _1 \sin ^2 \vartheta _2 \right) ^2 \, d \vartheta _1 \, d \vartheta _2 \, d \vartheta _3 \right) \\&\qquad \times \left( \int _0^{\infty } \tfrac{64 \left( \lambda ^2 -1 \right) ^2 r^9}{\left( r^2+1 \right) ^6 \left( \lambda ^2 r^2+1 \right) ^2} \, dr \right) \\&= \tfrac{217 \pi ^2}{32} \left( \int _0^{\infty } \tfrac{64 \left( \lambda ^2 -1 \right) ^2 r^9}{\left( r^2+1 \right) ^6 \left( \lambda ^2 r^2+1 \right) ^2} \, dr \right) \\&\le 2 \cdot 217 \pi ^2 \left( \lambda ^2 -1 \right) ^2 \left( \int _0^{1/\lambda } r^9 \, dr + \int _{1/\lambda }^1 \tfrac{r^5}{\lambda ^4} \, dr + \int _1^{\infty } \tfrac{1}{\lambda ^4 r^7} \, dr \right) \\&= 2 \cdot 217 \pi ^2 \left( \tfrac{\lambda - 1}{\lambda } \right) ^2\left( \tfrac{\lambda + 1}{\lambda } \right) ^2 \left( \tfrac{1}{3} - \tfrac{1}{15 \lambda ^6} \right) \\&= \tfrac{2^3}{15} \cdot 217 \pi ^2 \left( \tfrac{\lambda - 1}{\lambda } \right) ^2\left( \tfrac{\lambda + 1}{\lambda } \right) ^2. \end{aligned}$$
Using (7.3) above we have that
$$\begin{aligned} \left| \Gamma ^r \partial _r \chi _{\lambda } \right| ^2 = r^2 \left( 1+\sin ^2 \vartheta _1+\sin ^2 \vartheta _1 \sin ^2 \vartheta _2 \right) ^2 \left| \tfrac{\partial }{\partial r} \chi _{\lambda } \right| ^2. \end{aligned}$$
With this we compute
$$\begin{aligned} \left| \left| \Gamma ^r \partial _r \chi _{\lambda } \right| \right| _{L^2}^2&= 2 \pi \left( \int _0^\pi \int _0^{\pi } \left( 1+\sin ^2 \vartheta _1 + \sin ^2 \vartheta _1 \sin ^2 \vartheta _2 \right) ^2 \, d\vartheta _1 \, d\vartheta _2 \right) \left( \int _0^{\infty } r^5 \left| \chi _{\lambda } \right| ^2 \, dr \right) \\&= \tfrac{\pi }{64} \int _0^{\pi }\left( -68 \cosh \left( 2 \vartheta _2 \right) + 3 \cosh (4 \vartheta _2) + 217 \right) \, d \vartheta _2 \left( \int _0^{\infty } r^5 \left| \chi _{\lambda } \right| ^2 \, dr \right) \\&= \tfrac{217 \pi ^2}{64} \int _0^{\infty } r^5 \left| \chi _{\lambda } \right| ^2 \, dr \\&= 217 \pi ^2 (\lambda ^2-1)^2 \left( \int _0^{\infty } \tfrac{r^7}{\left( 1+\lambda ^2 r^2 \right) ^2 \left( 1+r^2 \right) ^6} \, dr \right) \\&= 217 \pi ^2 (\lambda ^2-1)^2 \left( \int _0^{1/\lambda } r^7 \, dr + \tfrac{1}{\lambda ^4} \int _{1/\lambda }^1 r^3 \, dr + \tfrac{1}{\lambda ^4} \int _1^{\infty } r^{-9} \, dr \right) \\&=\tfrac{217}{8} \pi ^2 \left( \tfrac{\lambda -1}{\lambda } \right) ^2 \left( \tfrac{\lambda +1}{\lambda } \right) ^2 \left( \tfrac{3}{8} -\tfrac{1}{8 \lambda ^4} \right) \\&\le \tfrac{217}{2^7} \pi ^2 \left( \tfrac{\lambda -1}{\lambda } \right) ^2\left( \tfrac{\lambda +1}{\lambda } \right) ^2. \end{aligned}$$
To all of these estimates, we note that \(\left( \tfrac{\lambda + 1}{\lambda } \right) \le 1 + \tfrac{1}{\lambda } \le 2\). It is a standard fact that
$$\begin{aligned} \frac{\lambda - 1}{\lambda } \le {\left\{ \begin{array}{ll} \left( \log \lambda \right) \text { when }\lambda \in [1,\infty ), \\ \left( \log \lambda \right) ^{1/2} \text { when }\lambda \in [e,\infty ). \end{array}\right. } \end{aligned}$$
Applying these, we conclude (7.4). The result follows. \(\square \)
1.3
\(\varvec{\alpha }\)-connection concentration compactness result
Theorem 7.4
Let \(\left\{ \alpha _i \right\} \subset [1,2]\) with \(\lim _{i \rightarrow \infty } \alpha _i = \varvec{\alpha }\). Given corresponding Yang–Mills \(\alpha _i\)-energy minimizing connections \(\left\{ \triangledown ^{i} \right\} \), there exists sequences \(\left\{ \varphi _i \right\} \subset {{\,\mathrm{SO}\,}}(5,1)\) and \(\left\{ \sigma _i \right\} \subset S({\mathcal {G}}_{E})\) such that there is a subsequence \(\left\{ \sigma _{i_j} \left[ \widehat{\varphi _{i_j}}^* \triangledown ^{i_j} \right] \right\} \) which converges strongly in \(C^{\infty }\) to an antiself dual connection \(\triangledown ^{\infty }\).
Proof
First, assume that the pointwise curvature norms \(\left| F_{\triangledown ^{i}} \right| _{\mathring{g}}\) do not concentrate as \(i \rightarrow \infty \). If so, then the derivatives of curvature are also controlled via the \(\epsilon \)-regularity and derivative estimates results of [11] (Lemmata 3.5 and 3.6) (note that these results are for the Yang–Mills \(\alpha \)-flow, but for our purposes we can apply them assuming the stationary setting). Thus up to gauge transformation, the sequence \(\left\{ \sigma _{i_j} \left[ \widehat{\varphi _{i_j}}^* \triangledown ^{i_j} \right] \right\} \) converges to a minimal energy critical value of the Yang–Mills \(\varvec{\alpha }\)-energy, which implies antiself duality (cf. Proposition 1.1).
If the pointwise curvature norms concentrate as \(i \rightarrow \infty \), then we do a maximal blowup along the sequence, to identify a sequence of points \(\left\{ \zeta _{i'} \right\} \) with \(\zeta _{i'}\) admitting supremal pointwise curvature norm for all \(k \le i'\). There exists a further subsequence \(\left\{ \zeta _{i''} \right\} \) converging to \(\zeta _{\infty } \in {\mathbb {S}}^4\), so that
$$\begin{aligned} \lim _{i'' \rightarrow \infty }\left| F_{\triangledown ^{i''}}\left( \zeta _{i''} \right) \right| _{\mathring{g}} = \infty . \end{aligned}$$
Stereographically projecting \({\mathbb {S}}^4\) onto \({\mathbb {H}}^1\), with \(\zeta _{\infty }\) as the center point, we see that on \({\mathbb {H}}^1\), dilation centered at the origin is equivalent to performing a conformal automorphism on \({\mathbb {S}}^4\). We normalize the curvature via dilations in the blowup so that one has (identifying back to the corresponding setting on \({\mathbb {S}}^4\)),
$$\begin{aligned} \lim _{i'' \rightarrow \infty } \left| F_{\widehat{\varphi _{i''}}^* \triangledown ^{i''}} \left( \zeta _{i''} \right) \right| _{\mathring{g}} = 1. \end{aligned}$$
This modified sequence satisfies the initial case, above, namely that the pointwise norms do not concentrate, which concludes the result. \(\square \)
1.4 Poincaré Inequalities
In this section we will compute global and localized \({\widetilde{\triangledown }}\)-Poincaré inequalities which rely heavily on the strong structure of the \({\widetilde{\triangledown }}\) and its corresponding curvature. To do so, we first need to establish Lemma 3.4, namely, pointwise bounds on commutator type terms.
Proof of Lemma 3.4
Using the formula for \({\widetilde{F}}_{ij}\) written out in coordinates, identifying \({{\,\mathrm{Ad}\,}}E\) with \(\mathfrak {I}{\mathbb {H}}^1\) (as discussed in [15]), we see that on \({\mathbb {H}}^1\),
$$\begin{aligned} F_{{\widetilde{\triangledown }}} = \tfrac{2}{\left( 1 + \left| \zeta \right| ^2 \right) ^2} \left( \left( d\zeta ^{12} - d\zeta ^{34} \right) {\mathbf {i}} + \left( d\zeta ^{13} + d\zeta ^{24} \right) {\mathbf {j}} + \left( d\zeta ^{14} - d\zeta ^{23} \right) {\mathbf {k}} \right) , \end{aligned}$$
where here \(d\zeta ^{ij} := d \zeta ^i \wedge d \zeta ^j\). We aim to compute
$$\begin{aligned} \left\langle {\widetilde{F}}_{ij}, \left[ A_i, A_j \right] \right\rangle = {\widetilde{F}}_{ij}^{{\mathbf {i}}} \left[ A_i, A_j \right] ^{{\mathbf {i}}} + {\widetilde{F}}_{ij}^{{\mathbf {j}}} \left[ A_i, A_j \right] ^{{\mathbf {j}}}+ {\widetilde{F}}_{ij}^{{\mathbf {k}}} \left[ A_i, A_j \right] ^{{\mathbf {k}}}. \end{aligned}$$
Computing strictly in coordinates of \({\mathbb {H}}^1\), we compute the following:
$$\begin{aligned} \left[ A_i, A_j \right] ^{{\mathbf {i}}}&= 2 \left( A_i^{{\mathbf {j}}} A_j^{{\mathbf {k}}} - A_i^{{\mathbf {k}}} A_j^{{\mathbf {j}}} \right) . \end{aligned}$$
Then we have that
$$\begin{aligned} {\widetilde{F}}_{ij}^{{\mathbf {i}}} \left[ A_i,A_j \right] ^{{\mathbf {i}}} = \tfrac{4}{\left( 1+\left| \zeta \right| ^2 \right) ^2} \left( \left( A_1^{{\mathbf {j}}} A_2^{{\mathbf {j}} } - A_2^{{\mathbf {j}}} A_1^{{\mathbf {j}} } \right) - \left( A_3^{{\mathbf {j}}} A_4^{{\mathbf {j}} } - A_4^{{\mathbf {j}}} A_3^{{\mathbf {j}} } \right) \right) . \end{aligned}$$
We have that for \({\mathbf {l}},{\mathbf {m}} \in \mathfrak {I}{\mathbb {H}}\) then \(2 \left| A_i^{{\mathbf {l}}} A_j^{{\mathbf {m}}} \right| \le \left| A_i^{{\mathbf {l}}} \right| ^2 + \left| A_j^{{\mathbf {m}}} \right| ^2\), so we have
$$\begin{aligned}&\left| {\widetilde{F}}_{ij}^{{\mathbf {i}}} \left[ A_i,A_j \right] ^{{\mathbf {i}}} \right| \\&\quad \le \tfrac{2}{\left( 1 + \left| \zeta \right| ^2 \right) ^2} \left( \left| A_1^{{\mathbf {j}}} \right| ^2 + \left| A_1^{{\mathbf {k}}} \right| ^2 + \left| A_2^{{\mathbf {j}}} \right| ^2 + \left| A_2^{{\mathbf {k}}} \right| ^2 + \left| A_3^{{\mathbf {j}}} \right| ^2 + \left| A_3^{{\mathbf {k}}} \right| ^2 + \left| A_4^{{\mathbf {j}}} \right| ^2 + \left| A_4^{{\mathbf {k}}} \right| ^2 \right) . \end{aligned}$$
Consequently it follows that (applying the round metric)
$$\begin{aligned} \left| \left\langle {\widetilde{F}}_{ij}, \left[ A_i,A_j \right] \right\rangle _{\mathring{g}} \right|&\le \left| A \right| _{\mathring{g}}^2. \end{aligned}$$
The second inequality of (3.6) follows similarly (noting the contraction within the commutator adds an extra dimensional factor of 4). \(\square \)
Proposition 7.5
For \(R > 0\), \(\ell \in {\mathbb {N}}\), and \(A \in \left( \Lambda ^1 \left( B_R \right) \otimes {{\,\mathrm{Ad}\,}}E \right) \) where \(B_R \subset {\mathbb {S}}^4\) there exists \(C_P > 0\) such that
$$\begin{aligned} \int _{B_R} \left| A \right| ^{\ell }_{\mathring{g}} \, dV_{\mathring{g}}\le C_P R^{\ell } \int _{B_R} \left| {\widetilde{\triangledown }}A \right| ^{\ell }_{\mathring{g}} \, dV_{\mathring{g}}, \text { and } \int _{B_R} \left| {\widetilde{\triangledown }}A \right| ^{\ell }_{\mathring{g}} \, dV_{\mathring{g}} \le C_P R^{\ell } \int _{B_R} \left| {\widetilde{\triangledown }}^{(2)} A \right| ^{\ell }_{\mathring{g}} \, dV_{\mathring{g}}.\nonumber \\ \end{aligned}$$
(7.6)
Proof
We provide a proof by contradiction. If the inequality above were false, we can find a normalized sequence \(\left\{ A^i \right\} \) satisfying
$$\begin{aligned} \int _{B_R} \left| {\widetilde{\triangledown }}A^i \right| _{\mathring{g}}^{\ell } \, dV_{\mathring{g}} \rightarrow 0, \quad \int _{B_R} \left| A^i \right| ^{\ell }_{\mathring{g}} \, dV_{\mathring{g}} = 1. \end{aligned}$$
Via theorems of Rellich and Banach-Alaoglu, we choose a normalized subsequence \(\left\{ A^{i'} \right\} \) satisfying
$$\begin{aligned} A^{i'} \overset{L^p}{\rightarrow } A, \quad A^{i'} \overset{W^{1,p}}{\rightharpoonup } A \text { and so }{\widetilde{\triangledown }}A \equiv 0, \text { and } \left| \left| A \right| \right| _{L^{\ell }\left( \Lambda ^1 ( B_R) \otimes {{\,\mathrm{Ad}\,}}E \right) } \equiv 1. \end{aligned}$$
It follows from the Ambrose-Singer Theorem ( [2] Theorem 2) that this cannot hold. Implicitly the theorem relates the curvature of the connection to its holonomy. Thus, if one finds a local parallel section of \(\Lambda ^1 \left( B_R \right) \otimes {{\,\mathrm{Ad}\,}}E\) in a neighborhood of some point, the holonomy is reduced, which is a contradiction since \({\widetilde{\triangledown }}\) has full holonomy. This concludes the first inequality of (7.6).
For the second inequality of (7.6), we again perform a proof by contradiction and construct a normalizing sequence \(\left\{ A_j \right\} \), this time satisfying
$$\begin{aligned} \int _{B_R} \left| {\widetilde{\triangledown }}^{(2)} A_j \right| ^2_{\mathring{g}} \, dV_{\mathring{g}} \rightarrow 0, \quad \int _{B_R} \left| {\widetilde{\triangledown }}A \right| ^2_{\mathring{g}} \, dV_{\mathring{g}} = 1. \end{aligned}$$
Again by Rellich’s and Banach–Alaoglu’s theorems there is a further subsequence \(\left\{ A_{j'} \right\} \) such that
$$\begin{aligned} A_{j'} \overset{W^{1,2}}{\rightarrow } A, \quad A_{j'} \rightharpoonup A \text { and so } {\widetilde{\triangledown }}^{(2)} A \equiv 0, \text { and } \left| \left| {\widetilde{\triangledown }}A \right| \right| _{L^{\ell } \left( \left( \Lambda ^1 \left( B_R \right) \right) ^{\otimes 2} \otimes {{\,\mathrm{Ad}\,}}E \right) } \equiv 1. \end{aligned}$$
In particular \({\widetilde{\triangledown }}^{(2)} A \equiv 0\). Since this is true on the coordinate level, we also have
$$\begin{aligned} 0 = {\widetilde{\triangledown }}_i {\widetilde{\triangledown }}_j A_k - {\widetilde{\triangledown }}_j {\widetilde{\triangledown }}_i A_k = \left[ {\widetilde{\triangledown }}_i, {\widetilde{\triangledown }}_j \right] A_k. \end{aligned}$$
In particular, this implies that (using (3.4))
$$\begin{aligned} 0&= \left\langle \left[ {\widetilde{\triangledown }}_i, {\widetilde{\triangledown }}_j \right] A_i, A_j \right\rangle _{\mathring{g}} = -3 \left| A \right| _{\mathring{g}}^2 + \left\langle \left[ {\widetilde{F}}_{ij}, A_i \right] , A_j \right\rangle _{\mathring{g}} < 0, \end{aligned}$$
an obvious contradiction. \(\square \)
Note that Proposition 3.5 follows naturally from a simple covering argument over \({\mathbb {S}}^4\).
1.5 Properties of \({\widetilde{\triangledown }}\)-Coulomb gauge
Here we include a proof of Theorem 3.6, a global adaptation of Tao and Tian’s local result ( [17] Theorem 4.6) which in turn was inspired by Theorem 1.3 of [19]. Set \(K > 1\) to be an absolute constant we to be chosen later, and define two sets
$$\begin{aligned} {\mathcal {U}}_{\epsilon }&:= \left\{ \triangledown \in {\mathcal {A}}_E\left( {\mathbb {S}}^4 \right) : \inf _{\varsigma \in {\mathcal {G}}_E} \left| \left| F_{\varsigma \left[ \triangledown \right] } - F_{{\widetilde{\triangledown }}} \right| \right| _{L^2}\le \epsilon \right\} \\ {\mathcal {U}}_{\epsilon }^*&:= \left\{ \triangledown \in {\mathcal {U}}_{\epsilon }\left( {\mathbb {S}}^4 \right) : \left| \left| {\widetilde{\Pi }} \left[ \triangledown \right] - {\widetilde{\triangledown }} \right| \right| _{W^{1,2}}\le K \epsilon \right\} . \end{aligned}$$
Our goal is to show \({\mathcal {U}}^*_{\epsilon } \equiv {\mathcal {U}}_{\epsilon }\), thus establishing Theorem 3.6. The preliminary step needed in the proof is a bootstrap estimate. Throughout the proof, we warn the reader to be cautious of the meaning of the tensor \(\Upsilon \), as it changes throughout the argument (it will either be \(\triangledown - {\widetilde{\triangledown }}\) or \({\widetilde{\Pi }}\left[ \triangledown \right] - {\widetilde{\triangledown }}\)).
Lemma 7.6
(Bootstrap estimate) For any \(\triangledown \in {\mathcal {U}}_{\epsilon }^*\), the following estimate may be bootstrapped
$$\begin{aligned} \left| \left| {\widetilde{\Pi }} \left[ \triangledown \right] - {\widetilde{\triangledown }} \right| \right| _{L^{2}} \le K \epsilon , \end{aligned}$$
to instead obtain
$$\begin{aligned} \left| \left| {\widetilde{\Pi }} \left[ \triangledown \right] - {\widetilde{\triangledown }} \right| \right| _{L^{2}} \le K \tfrac{\epsilon }{2}, \end{aligned}$$
additionally, (3.9) holds.
Proof
Set \(\Upsilon :={\widetilde{\Pi }}\left[ \triangledown \right] - {\widetilde{\triangledown }}\). Via Proposition 3.5 and Proposition 7.1,
$$\begin{aligned} \left| \left| \Upsilon \right| \right| _{L^{2}}&\le C\left| \left| D_{{\widetilde{\triangledown }}} \Upsilon \right| \right| _{L^{2}} \\&= C \left| \left| F_{{\widetilde{\Pi }}\left[ \triangledown \right] } - F_{{\widetilde{\triangledown }}} + \left[ \Upsilon ,\Upsilon \right] \right| \right| _{L^{2}} \\&\le C \left| \left| F_{{\widetilde{\Pi }}\left[ \triangledown \right] } - F_{{\widetilde{\triangledown }}} \right| \right| _{L^{2}}+ C \left| \left| \Upsilon \right| \right| ^2_{L^{2}} \\&\le C \epsilon + C \left| \left| \Upsilon \right| \right| ^2_{L^{2}}. \end{aligned}$$
Applying the estimates yields the desired results. \(\square \)
Now take \(\triangledown \in {\mathcal {U}}_{\epsilon }\) and consider the one-parameter family of connections for \(s \in \left[ 0,1 \right] \) by
$$\begin{aligned} \triangledown _s \left( x \right) :={\widetilde{\triangledown }}\left( x \right) + s \left( \triangledown - {\widetilde{\triangledown }} \right) \left( sx \right) . \end{aligned}$$
One can see that for \(s = 0\), \(\triangledown _0 \equiv {\widetilde{\triangledown }}\) and \(\triangledown _1 \equiv \triangledown \). We next verify this entire family lies inside of \({\mathcal {U}}_{\epsilon }\).
Proposition 7.7
Using the notation above \(\triangledown _s \in {\mathcal {U}}_{\epsilon }\).
Proof
Take \(\Upsilon _s := \triangledown _s - {\widetilde{\triangledown }}\) and observe that
$$\begin{aligned} \left[ F_{\triangledown _s} - F_{{\widetilde{\triangledown }}} \right| _{x}&= \left[ D_{{\widetilde{\triangledown }}} \left( \Upsilon _s \right) + \left[ \Upsilon _s, \Upsilon _s \right] \right| _{x}\\&= s\left[ D_{{\widetilde{\triangledown }}} \left( \Upsilon \right) + \left[ \Upsilon , \Upsilon \right] \right| _{sx}\\&= s \left[ F_{\triangledown } - F_{{\widetilde{\triangledown }}} \right| _{sx}. \end{aligned}$$
Consequently \(\left| \left| F_{\triangledown _s} - F_{{\widetilde{\triangledown }}} \right| \right| _{L^{2}} = s\left| \left| F_{\triangledown } - F_{{\widetilde{\triangledown }}} \right| \right| _{L^{2}} \le \tfrac{s \epsilon }{2}\) as desired. \(\square \)
Proposition 7.8
Let \(X \in \left( 0,\infty \right) \), \(p \in \left( 2,4 \right) \) and let \(\triangledown \in {\mathcal {U}}_{\epsilon }\) be such that
$$\begin{aligned} \left| \left| \triangledown - {\widetilde{\triangledown }} \right| \right| _{W^{1,p}} \le X. \end{aligned}$$
(7.7)
Then there exists a quantity \(\delta _X > 0\) depending only on \(X, {\mathcal {G}}_{E}, p, \epsilon \), such that
$$\begin{aligned} \left\{ \triangledown + A \in {\mathcal {U}}_{\epsilon } : \left| \left| A \right| \right| _{W^{1,p}} \le \delta _X \right\} \subset {\mathcal {U}}_{\epsilon }^*. \end{aligned}$$
Proof
Fix p (all constants are allowed to depend on p), and let \(C_X \ge 0\) denote a constant dependent on X, which can be updated as necessary. As in [17], the argument consists of three steps.
Step 1. Estimation of the \({\widetilde{\triangledown }}\)-Coulomb gauge in smooth norms Note that via Proposition 7.1 combined with Hölder’s inequality, there exists a constant \(C_X \ge 0\) such that
$$\begin{aligned} \left| \left| F_{\triangledown } - F_{{\widetilde{\triangledown }}} \right| \right| _{L^p} \le C_X. \end{aligned}$$
This constant \(C_X\) can be updated as necessary to bound above
$$\begin{aligned} \left| \left| F_{{\widetilde{\Pi }}\left[ \triangledown \right] } - F_{{\widetilde{\triangledown }}} \right| \right| _{L^p} \le C_X. \end{aligned}$$
Manipulating as in the lemma above,
$$\begin{aligned} \left| \left| {\widetilde{\Pi }} \left[ \triangledown \right] - {\widetilde{\triangledown }} \right| \right| _{W^{1,p}}&\le \left| \left| F_{{\widetilde{\Pi }} \left[ \triangledown \right] } - F_{{\widetilde{\triangledown }}} \right| \right| _{L^p} + C \left| \left| \left( {\widetilde{\Pi }} \left[ \triangledown \right] - {\widetilde{\triangledown }} \right) \wedge \left( {\widetilde{\Pi }} \left[ \triangledown \right] - {\widetilde{\triangledown }} \right) \right| \right| _{W^{1,p}} \le C_X. \end{aligned}$$
Let \(\varsigma \) denote the gauge transformation such that \(\varsigma \left[ \triangledown \right] = {\widetilde{\Pi }} \left[ \triangledown \right] = \partial + \Sigma \). Then
$$\begin{aligned} \Sigma _{i \theta }^{\beta } := \left( \varsigma ^{-1} \right) _{\delta }^{\beta } \left( \partial _i \varsigma _{\theta }^{\delta } \right) + \left( \varsigma ^{-1} \right) _{\delta }^{\beta } \Gamma _{i \gamma }^{\delta } \varsigma _{\theta }^{\gamma }. \end{aligned}$$
Remanipulating, and setting \(\Upsilon := \varsigma \left[ \triangledown \right] - {\widetilde{\triangledown }}\) and \(\text {Y} := \triangledown - {\widetilde{\triangledown }}\) yields
$$\begin{aligned} \left( \partial _i \varsigma _{\theta }^{\rho } \right)&= \varsigma _{\beta }^{\rho }\Sigma _{i \theta }^{\beta } - \Gamma _{i \gamma }^{\rho } \varsigma _{\theta }^{\gamma } \\ \left( {\widetilde{\triangledown }}_i \varsigma _{\theta }^{\rho } \right)&= \varsigma _{\beta }^{\rho }\Sigma _{i \theta }^{\beta } - \Gamma _{i \gamma }^{\rho } \varsigma _{\theta }^{\gamma } - \varsigma _{\mu }^{\rho } {\widetilde{\Gamma }}_{i \theta }^{\mu }+ {\widetilde{\Gamma }}_{i \mu }^{\rho } \varsigma _{\theta }^{\mu } = \varsigma _{\beta }^{\rho }\Upsilon _{i \theta }^{\beta } - \text {Y}_{i \mu }^{\rho } \varsigma _{\theta }^{\mu }. \end{aligned}$$
Now we note that
$$\begin{aligned} {\widetilde{\triangledown }}_j {\widetilde{\triangledown }}_i \varsigma _{\theta }^{\rho }&= \left( {\widetilde{\triangledown }}_j \varsigma _{\beta }^{\rho } \right) \Upsilon _{i \theta }^{\beta } +\varsigma _{\beta }^{\rho } \left( {\widetilde{\triangledown }}_j \Upsilon _{i \theta }^{\beta } \right) - \left( {\widetilde{\triangledown }}_j \text {Y}_{i \mu }^{\rho } \right) \varsigma _{\theta }^{\mu } - \text {Y}_{i \mu }^{\rho } \left( {\widetilde{\triangledown }}_j \varsigma _{\theta }^{\mu } \right) \\&= \left( \varsigma _{\gamma }^{\rho } \Upsilon _{j \beta }^{\gamma }- \text {Y}_{j \gamma }^{\rho } \varsigma _{\beta }^{\gamma } \right) \Upsilon _{i \theta }^{\beta } +\varsigma _{\beta }^{\rho } \left( {\widetilde{\triangledown }}_j \Upsilon _{i \theta }^{\beta } \right) - \left( {\widetilde{\triangledown }}_j \text {Y}_{i \mu }^{\rho } \right) \varsigma _{\theta }^{\mu } \\&\quad - \text {Y}_{i \mu }^{\rho } \left( \varsigma _{\zeta }^{\mu } \Upsilon _{j \theta }^{\zeta } - \text {Y}_{j \zeta }^{\mu } \varsigma _{\theta }^{\zeta } \right) . \end{aligned}$$
We thus have that
$$\begin{aligned} \left| {\widetilde{\triangledown }}^{(2)} \varsigma \right| _{\mathring{g}}&\le \left| \varsigma \right| _{\mathring{g}} \left( \left| \Upsilon \right| _{\mathring{g}} + \left| \text {Y} \right| _{\mathring{g}} \left| \Upsilon \right| _{\mathring{g}} \right) + \left| \varsigma \right| _{\mathring{g}} \left( \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}} + \left| {\widetilde{\triangledown }}\text {Y} \right| _{\mathring{g}} \right) \\&\le C \left| \varsigma \right| _{\mathring{g}} \left( \left| \Upsilon \right| _{\mathring{g}} + \left| \Upsilon \right| ^2_{\mathring{g}} + \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}} + \left| \text {Y} \right| ^2_{\mathring{g}}\left| {\widetilde{\triangledown }}\text {Y} \right| _{\mathring{g}} \right) . \end{aligned}$$
Consequently we have
$$\begin{aligned} \left| \varsigma \right| _{\mathring{g}} + \left| {\widetilde{\triangledown }}\varsigma \right| _{\mathring{g}} + \left| {\widetilde{\triangledown }}^{(2)} \varsigma \right| _{\mathring{g}} \le C \left| \varsigma \right| _{\mathring{g}} \left( \left| \Upsilon \right| _{\mathring{g}} + \left| \Upsilon \right| _{\mathring{g}}^2 + \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}} + \left| \text {Y} \right| _{\mathring{g}} + \left| \text {Y} \right| _{\mathring{g}}^2+ \left| {\widetilde{\triangledown }}\text {Y} \right| _{\mathring{g}} \right) . \end{aligned}$$
Combining these all together we conclude that \(\left| \left| \varsigma \right| \right| _{W^{2,p}} \le C_X\), concluding the first step.
Step 2. Pass to the \({\widetilde{\triangledown }}\)-Coulomb gauge As a consequence of Step 1, it follows that the action of a \({\widetilde{\triangledown }}\)-Coulomb gauge transformation is uniformly continuous in the sense of the \(W^{2,p}\)-topology in a small neighborhood of \(\triangledown \). Furthermore, since both \({\mathcal {U}}_{\epsilon }\) and \({\mathcal {U}}_{\epsilon }^*\) are in fact invariant under gauge transformation (the \({\widetilde{\triangledown }}\)-projection always overrides any gauge action) we can prove Proposition 7.8 specifically in the setting \(\triangledown = {\widetilde{\Pi }} \left[ \triangledown \right] \).
Step 3. Apply perturbation theory to the Coulomb gauge Fix the perturbation parameter A as in Proposition 7.8. To show \(\triangledown + A \in {\mathcal {U}}_{\epsilon }^*\), we must construct a gauge transformation \(\varsigma \) satisfying
$$\begin{aligned} D_{{\widetilde{\triangledown }}}^* \left( \varsigma \left[ \triangledown + A \right] - {\widetilde{\triangledown }} \right) = 0. \end{aligned}$$
(7.8)
To do so, we give a perturbative argument. Set \(\varsigma := e^{\sigma }\), recall the formula (2.1) of a gauge action on a connection. We have that \(\varsigma \left[ \triangledown + A \right] - {\widetilde{\triangledown }}\) is given by
$$\begin{aligned} \left( \varsigma \left[ \triangledown + A \right] - {\widetilde{\triangledown }} \right) _{i \theta }^{\beta }&= \left( \varsigma ^{-1} \right) _{\delta }^{\beta } \left( \partial _i \varsigma _{\theta }^{\delta } \right) + \left( \varsigma ^{-1} \right) _{\delta }^{\beta } \left[ \Gamma - A \right] _{i \gamma }^{\delta } \varsigma _{\theta }^{\gamma } - {\widetilde{\Gamma }}_{i \theta }^{\beta } \\&= \left( \varsigma ^{-1} \right) _{\delta }^{\beta } \left( {\widetilde{\triangledown }}_i \varsigma _{\theta }^{\delta } \right) -\left( \varsigma ^{-1} \right) _{\delta }^{\beta } {\widetilde{\Gamma }}_{i \tau }^{\delta } \varsigma _{\theta }^{\tau } + \left( \varsigma ^{-1} \right) _{\delta }^{\beta } \left[ \Gamma + A \right] _{i \gamma }^{\delta } \varsigma ^{\gamma }_{\theta } \\&= \left( \varsigma ^{-1} \right) _{\delta }^{\beta } \left( {\widetilde{\triangledown }}_i \varsigma _{\theta }^{\delta } \right) + \left( \varsigma ^{-1} \right) _{\delta }^{\beta } \left( \Upsilon + A \right) _{i \gamma }^{\delta } \varsigma _{\theta }^{\gamma }. \end{aligned}$$
Converting this to be in terms of \(\sigma \) (and simultaneously defining our term \({\mathcal {W}}\)) we have
$$\begin{aligned} {\mathcal {W}} \left( \sigma , \triangledown + A \right)&= \left( \varsigma \left[ \triangledown + A \right] - {\widetilde{\triangledown }} \right) _{i \theta }^{\beta } - {\widetilde{\triangledown }}_i \sigma _{\theta }^{\beta }\nonumber \\&= \left( e^{-\sigma } \right) _{\delta }^{\beta } \left( \Upsilon + A \right) _{i \gamma }^{\delta } \left( e^\sigma \right) _{\theta }^{\gamma } \nonumber \\&= \left( {{\,\mathrm{Id}\,}}^{\beta }_{\delta } - \sigma _{\delta }^{\beta } + \cdots \right) \left( \Upsilon + A \right) _{i \gamma }^{\delta } \left( {{\,\mathrm{Id}\,}}^{\beta }_{\delta } + \sigma _{\delta }^{\beta } + \cdots \right) \nonumber \\&= \left( \Upsilon + A \right) _{i\theta }^{\beta } - \sigma _{\delta }^{\beta }\left( \Upsilon + A \right) _{i\theta }^{\delta } + \left( \Upsilon + A \right) _{i\delta }^{\beta }\sigma _{\theta }^{\delta } + \sigma _{\zeta }^{\beta } \left( \Upsilon + A \right) _{i\delta }^{\zeta }\sigma _{\theta }^{\delta } + \cdots . \end{aligned}$$
(7.9)
Expanding out \(0 = D^*_{{\widetilde{\triangledown }}}\left( {\mathcal {W}}\left( \sigma ,\triangledown +A \right) + \triangledown \sigma \right) \) gives
$$\begin{aligned} 0&=- {\widetilde{\triangledown }}_i \left[ \left( \varsigma ^{-1} \right) _{\gamma }^{\beta } \left( \partial _i \varsigma _{\theta }^{\gamma } \right) + \left( \varsigma ^{-1} \right) _{\delta }^{\beta } \left( \Gamma + A \right) _{i \gamma }^{\delta } \left( \varsigma _{\theta }^{\gamma } \right) \right] \\&=- {\widetilde{\triangledown }}_i \left[ \left( \varsigma ^{-1} \right) _{\gamma }^{\beta } \left( {\widetilde{\triangledown }}_i \varsigma _{\theta }^{\gamma } - {\widetilde{\Gamma }}_{i \zeta }^{\gamma } \varsigma ^{\zeta }_{\theta } + \varsigma ^{\gamma }_{\zeta } {\widetilde{\Gamma }}_{i \theta }^{\zeta } \right) + \left( \varsigma ^{-1} \right) _{\delta }^{\beta } \left( \Gamma + A \right) _{i \gamma }^{\delta } \left( \varsigma _{\theta }^{\gamma } \right) \right] \\&= - \left( \varsigma ^{-1} \right) _{\gamma }^{\beta } {\widetilde{\vartriangle }} \varsigma _{\theta }^{\gamma } + \left( \varsigma ^{-1} \right) _{\omega }^{\beta }\left( {\widetilde{\triangledown }}_i \varsigma _{\delta }^{\omega } \right) \left( \varsigma ^{-1} \right) _{\gamma }^{\delta } \left( {\widetilde{\triangledown }}_i \varsigma _{\theta }^{\gamma } \right) + \left( \varsigma ^{-1} \right) _{\gamma }^{\beta } {\widetilde{\Gamma }}_{i \zeta }^{\gamma } \left( {\widetilde{\triangledown }}_i \varsigma _{\theta }^{\zeta } \right) \\&\qquad - \left( \varsigma ^{-1} \right) _{\gamma }^{\beta } \left( {\widetilde{\triangledown }}_i \varsigma _{\zeta }^{\gamma } \right) {\widetilde{\Gamma }}_{i \theta }^{\zeta }\\&\qquad + \left( \varsigma ^{-1} \right) _{\mu }^{\beta }\left( {\widetilde{\triangledown }}_i \varsigma ^{\mu }_{\nu } \right) \left( \varsigma ^{-1} \right) _{\delta }^{\nu }\left( \Gamma + A \right) _{i \gamma }^{\delta } \varsigma _{\theta }^{\gamma } - \left( \varsigma ^{-1} \right) _{\delta }^{\beta } {\widetilde{\triangledown }}_i \left( \Gamma + A \right) _{i \gamma }^{\delta } \varsigma _{\theta }^{\gamma } \\&\qquad - \left( \varsigma ^{-1} \right) _{\delta }^{\beta }\left( \Gamma + A \right) _{i \gamma }^{\delta }\left( {\widetilde{\triangledown }}_i \varsigma _{\theta }^{\gamma } \right) . \end{aligned}$$
Inserting the fact that \(\varsigma \equiv e^\sigma \), we have that
$$\begin{aligned} 0&= - {\widetilde{\vartriangle }} \sigma _{\theta }^{\beta } +\left( {\widetilde{\triangledown }}_i \sigma _{\delta }^{\beta } \right) \left( {\widetilde{\triangledown }}_i \sigma _{\theta }^{\delta } \right) + \left( \exp (-\sigma ) \right) _{\gamma }^{\beta } {\widetilde{\Gamma }}_{i \zeta }^{\gamma } (e^\sigma )^{\zeta }_{\omega } \left( {\widetilde{\triangledown }}_i \sigma _{\theta }^{\omega } \right) -\left( {\widetilde{\triangledown }}_i \sigma _{\zeta }^{\beta } \right) {\widetilde{\Gamma }}_{i \theta }^{\zeta } \\&\qquad + \left( {\widetilde{\triangledown }}_i \sigma ^{\mu }_{\beta } \right) \left( e^{-\sigma } \right) _{\delta }^{\nu }\left( \Gamma + A \right) _{i \gamma }^{\delta } \left( e^\sigma \right) _{\theta }^{\gamma } - \left( e^{-\sigma } \right) _{\delta }^{\beta } {\widetilde{\triangledown }}_i \left( \Gamma + A \right) _{i \gamma }^{\delta } \left( e^{\sigma } \right) _{\theta }^{\gamma }\\&\qquad - \left( e^{-\sigma } \right) _{\delta }^{\beta }\left( \Gamma + A \right) _{i \gamma }^{\delta } \left( e^\sigma \right) ^{\gamma }_{\zeta }\left( {\widetilde{\triangledown }}_i \sigma _{\theta }^{\zeta } \right) \\&= - {\widetilde{\vartriangle }} \sigma _{\theta }^{\beta } +\left( {\widetilde{\triangledown }}_i \sigma _{\delta }^{\beta } \right) \left( {\widetilde{\triangledown }}_i \sigma _{\theta }^{\delta } \right) + \left( {\widetilde{\triangledown }}_i \sigma ^{\mu }_{\beta } \right) \left[ \left( e^{-\sigma } \right) _{\delta }^{\nu }\left( \Gamma + A \right) _{i \gamma }^{\delta } \left( e^\sigma \right) _{\theta }^{\gamma } - {\widetilde{\Gamma }}_{i \theta }^{\mu } \right] \\&\qquad - \left( e^{-\sigma } \right) _{\delta }^{\beta } {\widetilde{\triangledown }}_i \left( \Upsilon + A \right) _{i \gamma }^{\delta } \left( e^\sigma \right) _{\theta }^{\gamma } - \left( e^{-\sigma } \right) _{\delta }^{\beta } A_{i \gamma }^{\delta } \left( e^\sigma \right) ^{\gamma }_{\zeta }\left( {\widetilde{\triangledown }}_i \sigma _{\theta }^{\zeta } \right) . \end{aligned}$$
Therefore we have that,
$$\begin{aligned} {\widetilde{\vartriangle }} \sigma _{\theta }^{\beta }&= \left( {\widetilde{\triangledown }}_i \sigma _{\delta }^{\beta } \right) \left( {\widetilde{\triangledown }}_i \sigma _{\theta }^{\delta } \right) + \left( {\widetilde{\triangledown }}_i \sigma _{\nu }^{\beta } \right) \left[ \left( e^{-\sigma } \right) _{\delta }^{\nu }\left( \Upsilon + A \right) _{i \gamma }^{\delta } \left( e^{\sigma } \right) _{\theta }^{\gamma } + \left( e^{-\sigma } \right) _{\delta }^{\nu } {\widetilde{\Gamma }}_{i \gamma }^{\delta } \left( e^\sigma \right) _{\theta }^{\gamma } - {\widetilde{\Gamma }}_{i \theta }^{\nu } \right] \nonumber \\&\qquad - \left( e^{-\sigma } \right) _{\delta }^{\beta } {\widetilde{\triangledown }}_i A_{i \gamma }^{\delta } \left( e^{\sigma } \right) _{\theta }^{\gamma } - \left( e^{-\sigma } \right) _{\delta }^{\beta }\left( \Upsilon + A \right) _{i \gamma }^{\delta } \left( e^\sigma \right) ^{\gamma }_{\zeta }\left( {\widetilde{\triangledown }}_i \sigma _{\theta }^{\zeta } \right) . \end{aligned}$$
(7.10)
By combining (7.9) and (7.8), and noting that here, \(D^*_{{\widetilde{\triangledown }}} \left[ {\mathcal {W}} \left( \sigma ^{(j)},\triangledown + A \right) \right] \) is precisely the right hand side of (7.10), we conclude
$$\begin{aligned} {\widetilde{\vartriangle }} \sigma = D_{{\widetilde{\triangledown }}}^* \left[ {\mathcal {W}} \left( \sigma , \triangledown + A \right) \right] . \end{aligned}$$
Consider the following iteration scheme, with initial condition \(\sigma ^{(0)} \equiv 0\),
$$\begin{aligned} {\widetilde{\vartriangle }} \sigma ^{(\ell +1)}&:= D_{{\widetilde{\triangledown }}}^* \left[ {\mathcal {W}} \left( \sigma ^{(\ell )}, \triangledown + A \right) \right] . \end{aligned}$$
Note \(\sigma ^{(\ell +1)}\) is uniquely defined by standard elliptic regularity. We will derive bounds on \(\sigma ^{(\ell +1)}\). First, based off of the system above, we have
$$\begin{aligned} \left| \left| \sigma ^{(\ell +1)} \right| \right| _{W^{2,p}} \le C \left| \left| D_{{\widetilde{\triangledown }}}^* \left[ {\mathcal {W}}\left( \sigma ^{(\ell )}, \triangledown + A \right) \right] \right| \right| _{W^{2,p}} + C \left| \left| {\mathcal {W}}\left( \sigma ^{(\ell )},{\widetilde{\triangledown }}+ A \right) \right| \right| _{W^{1,p}} \end{aligned}$$
We estimate each term on the right hand side. For both terms, we apply the exponential power series expansion for some \(C > 0\) depending on \({\widetilde{\triangledown }}\). First by (7.9),
$$\begin{aligned} \left| {\mathcal {W}} \left( \sigma ^{(\ell )},{\widetilde{\triangledown }}+ A \right) \right| _{\mathring{g}} \le C \left| A \right| _{\mathring{g}} \left( 1 + \left| \sigma ^{(\ell )} \right| _{\mathring{g}} \right) . \end{aligned}$$
From this we can deduce, using Hölder’s inequality, that
$$\begin{aligned} \left| \left| {\mathcal {W}} \left( \sigma ^{(\ell )},{\widetilde{\triangledown }}+ A \right) \right| \right| _{W^{1,p}} \le C \left( \left| \left| \sigma ^{(\ell )} \right| \right| ^2_{W^{2,p}} + \left| \left| A \right| \right| _{W^{1,p}} \right) . \end{aligned}$$
Using (7.10) above, we see that
$$\begin{aligned}&\left| D_{{\widetilde{\triangledown }}}^* \left[ {\mathcal {W}}\left( \sigma ^{(\ell )}, \triangledown + A \right) \right] \right| _{\mathring{g}} \le C \left( \left| {\widetilde{\triangledown }}\sigma ^{(\ell )} \right| _{\mathring{g}}^2 + \left( 1 + \left| \sigma ^{(\ell )} \right| _{\mathring{g}} \right) \right. \\&\left. \quad \times \left( \left| {\widetilde{\triangledown }}\sigma ^{(\ell )} \right| _{\mathring{g}} \left( \left| \Upsilon + A \right| _{\mathring{g}} + 1 \right) + \left| {\widetilde{\triangledown }}A \right| _{\mathring{g}} \right) \right) . \end{aligned}$$
Therefore we can expand out with Holder’s inequality, noting that \(\triangledown \in {\mathcal {U}}_{\epsilon }^*\) and conclude that
$$\begin{aligned} \left| \left| D^*_{{\widetilde{\triangledown }}}{\mathcal {W}}\left( \sigma ^{(\ell )}, \triangledown + A \right) \right| \right| _{W^{1,p}} \le C \left| \left| \sigma ^{(\ell )} \right| \right| _{W^{2,p}}^2 + K \epsilon \left| \left| \sigma ^{(\ell )} \right| \right| _{W^{2,p}} + \left| \left| A \right| \right| _{W^{2,p}}. \end{aligned}$$
Thus, as long as \(\delta _X\) is sufficiently small, we can obtain inductively that
$$\begin{aligned} \left| \left| \sigma ^{(\ell )} \right| \right| _{W^{2,p}} \le C \delta _X. \end{aligned}$$
We adapt this iteration scheme to conclude that \(\sigma ^{(\ell )}\) converges in \(W^{2,p}\) to a solution \(\sigma \) satisfying
$$\begin{aligned} \left| \left| \sigma \right| \right| _{W^{2,p}} \le C \delta _X. \end{aligned}$$
As a result of standard Sobolev embeddings, \(\sigma \) has some Hölder regularity, which, when elliptic regularity is applied, can be bootstrapped to conclude that \(\sigma \) is in fact smooth. If we exponentiate \(\sigma \) and apply Hölder’s inequality we obtain a smooth \({\widetilde{\triangledown }}\)-Coulomb gauge \(\varsigma \left[ \triangledown + A \right] \) satisfying
$$\begin{aligned} \left| \left| \varsigma - {{\,\mathrm{Id}\,}} \right| \right| _{W^{2,p}} , \left| \left| \varsigma ^{-1} - {{\,\mathrm{Id}\,}} \right| \right| _{W^{2,p}} \le C \delta _X. \end{aligned}$$
As a consequence of the gauge transformation action and (7.7) of the assumptions on A,
$$\begin{aligned} \left| \left| \varsigma \left[ \triangledown + A \right] - \triangledown \right| \right| _{W^{1,p}} \le C_X \delta _X. \end{aligned}$$
therefore since \(p \in \left( 2,4 \right) \) we have
$$\begin{aligned} \left| \left| \varsigma \left[ \triangledown + A \right] - \triangledown \right| \right| _{W^{1,2}} \le C_X \delta _X. \end{aligned}$$
If \(\delta _X\) is sufficiently small, as a consequence of our bootstrapping estimate of Lemma 7.6 we have
$$\begin{aligned} \left| \left| \varsigma \left[ \triangledown + A \right] - {\widetilde{\triangledown }} \right| \right| _{W^{1,2} } \le K \epsilon . \end{aligned}$$
which is precisely the desired result. \(\square \)
1.6 Morrey-type Inequalities
Let \(R > 0\) and \(\eta \in C^{\infty }\) be a nonnegative function, where
$$\begin{aligned}\eta (x) = {\left\{ \begin{array}{ll} 1 &{} \text { when } x \in B_{R/2}, \\ 0 &{} \text { when } x \notin B_{R}. \end{array}\right. } \end{aligned}$$
Remark 7.9
(More notational conventions) We will be using an unusual convention when working with cutoff functions in this argument. Our notation simply notifies the reader that some power of the cutoff is present. Ultimately this makes the proof easier to read; the choice of power of the cutoff is not necessary to the argument, but it is clear it is finite. Take
$$\begin{aligned} d V_{\mathring{g},\eta } := \eta ^K d V_{\mathring{g}}, \text { where } K \in {\mathbb {N}} \text { is sufficiently large}. \end{aligned}$$
Refer to Remark 4.2 regarding our notation for scaling coefficients.
Lemma 7.10
Given the assumptions of Proposition 4.3, (4.2), and (4.10) there exists \(\beta >0\) such that
$$\begin{aligned} \left| \left| {\widetilde{\triangledown }}\Upsilon \right| \right| _{{\mathcal {M}}_{\beta }^{1,2}} \le C \left( \left( \alpha - 1 \right) + \delta \right) . \end{aligned}$$
Proof
We will check the Morrey inequalities for \({\widetilde{\triangledown }}\Upsilon \) and \({\widetilde{\triangledown }}^{(2)} \Upsilon \) separately. We also point out that due to the estimate (3.2) of Proposition 3.1 combined with Lemma 7.3 give that
$$\begin{aligned} \left( \alpha - 1 \right) \left| \left| \triangledown \log \chi _{\lambda } \right| \right| _{L^2}^{\mu } + \left( \alpha - 1 \right) \left| \left| \triangledown ^{(2)} \log \chi _{\lambda } \right| \right| _{L^2}^{\mu } \le C \delta \quad \mu \in \left\{ 1,2 \right\} . \end{aligned}$$
We show below that \({\widetilde{\triangledown }}\Upsilon \in {\mathcal {M}}_{2}^2\) and \({\widetilde{\triangledown }}^{(2)} \Upsilon \in {\mathcal {M}}_{\beta }^2\) to conclude \({\widetilde{\triangledown }}\Upsilon \in {\mathcal {M}}^{1,2}_{\beta }\) with necessary bounds.
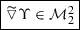 For this, we simply have the following by applying Hölder’s inequality followed by applying our global estimates on \({\widetilde{\triangledown }}^{(k)} \Upsilon \) for \(k \in \left\{ 0,1,2 \right\} \),
For this, we simply have the following by applying Hölder’s inequality followed by applying our global estimates on \({\widetilde{\triangledown }}^{(k)} \Upsilon \) for \(k \in \left\{ 0,1,2 \right\} \),
$$\begin{aligned} \int _{B_R} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }&\le \left( \int _{B_R} d V_{\mathring{g},\eta } \right) ^{1/2} \left( \int _{B_R} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^4 \, d V_{\mathring{g},\eta } \right) ^{1/2} \\&\le \left( \int _{B_R} d V_{\mathring{g},\eta } \right) ^{1/2} \left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^4 \, dV_{\mathring{g}} \right) ^{1/2}\\&\le C_S \left( \delta + \left( \alpha - 1 \right) \right) R^2. \end{aligned}$$
Therefore \({\widetilde{\triangledown }}\Upsilon \in {\mathcal {M}}_2^{2}\).
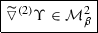 We perform a hole-filling argument. To begin,
We perform a hole-filling argument. To begin,
$$\begin{aligned} \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\le & {} \left[ C \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}} \left| \triangledown \eta \right| _{\mathring{g}} \, d V_{\mathring{g},\eta } \right] _{T_1} \nonumber \\&\quad + \left[ - \int _{{\mathbb {S}}^4} \left\langle {\widetilde{\triangledown }}\Upsilon , {\widetilde{\vartriangle }} {\widetilde{\triangledown }}\Upsilon \right\rangle _{\mathring{g}} \, d V_{\mathring{g},\eta } \right] _{T_2}. \end{aligned}$$
(7.11)
For the first term we have that, using a weighted Young’s inequality for \(\nu >0\) to be chosen and applying the local Poincaré inequality (Proposition 7.5)
$$\begin{aligned} T_1&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \tfrac{C}{\nu R^2} \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}}\\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C_P \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}}. \end{aligned}$$
We next manipulate \(T_2\), commuting derivatives and applying (4.7),
$$\begin{aligned} T_{2}&= -\int _{{\mathbb {S}}^4} \left\langle {\widetilde{\triangledown }}\Upsilon ,{\widetilde{\vartriangle }} {\widetilde{\triangledown }}\Upsilon \right\rangle _{\mathring{g}} \, d V_{\mathring{g},\eta }\\&= \left[ - \int _{{\mathbb {S}}^4} \left\langle {\widetilde{\triangledown }}_i \Upsilon _j, {\widetilde{\triangledown }}_k \left[ {\widetilde{\triangledown }}_k, {\widetilde{\triangledown }}_i \right] \Upsilon _j \right\rangle _{\mathring{g}} d V_{\mathring{g},\eta } \right] _{T_{21}} \\&\quad + \left[ - \int _{{\mathbb {S}}^4} \left\langle {\widetilde{\triangledown }}_i \Upsilon _j, \left[ {\widetilde{\triangledown }}_k, {\widetilde{\triangledown }}_i \right] {\widetilde{\triangledown }}_k \Upsilon _j \right\rangle _{\mathring{g}} d V_{\mathring{g},\eta } \right] _{T_{22}} + \left[ -\int _{{\mathbb {S}}^4} \left\langle {\widetilde{\triangledown }}\Upsilon ,{\widetilde{\triangledown }}{\widetilde{\vartriangle }} \Upsilon \right\rangle _{\mathring{g}} \, d V_{\mathring{g},\eta } \right] _{T_{23}}. \end{aligned}$$
Note that the estimates of \(T_{21}\) and \(T_{22}\) follow in suit with the manipulations of (4.6), and thus we conclude that
$$\begin{aligned} T_{21} + T_{22}&\le 11 \int _{B_R} \left| {\widetilde{\triangledown }} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}, \eta } + 8\int _{B_R} \left| \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}, \eta } \\&\le C_P \left( R^4 \int _{B_R} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}}+ R^2 \left( \left( \alpha - 1 \right) + \delta \right) \right) \le C \left( \left( \alpha - 1 \right) + \delta \right) R^2. \end{aligned}$$
Now we approach \(T_{23}\). Applying (4.7) coming from the \(\alpha \)-critical equation,
$$\begin{aligned} T_{23}&=\left[ - \int _{{\mathbb {S}}^4} \left\langle {\widetilde{\triangledown }}\Upsilon , 3 {\widetilde{\triangledown }}\Upsilon \right\rangle _{\mathring{g}} \, d V_{\mathring{g},\eta }- \int _{{\mathbb {S}}^4} \left\langle {\widetilde{\triangledown }}\Upsilon , \left[ {\widetilde{F}}, {\widetilde{\triangledown }}\Upsilon \right] \right\rangle _{\mathring{g}} \, d V_{\mathring{g},\eta } \right] _{T_{231}} \\&\qquad + \left[ \int _{{\mathbb {S}}^4} \left( {\widetilde{\triangledown }}\Upsilon \right) ^{*3} \, d V_{\mathring{g},\eta } \right] _{T_{232}} + \left[ \int _{{\mathbb {S}}^4} {\widetilde{\triangledown }}^{(2)} \Upsilon *{\widetilde{\triangledown }}\Upsilon *\Upsilon \, d V_{\mathring{g},\eta } \right] _{T_{233}}\\&\qquad + \left[ - \int _{{\mathbb {S}}^4} \left\langle {\widetilde{\triangledown }}\Upsilon , {\widetilde{\triangledown }}\Theta _1 \right\rangle _{\mathring{g}} \, d V_{\mathring{g},\eta } \right] _{T_{234}} + \left[ - \int _{{\mathbb {S}}^4} \left\langle {\widetilde{\triangledown }}\Upsilon , {\widetilde{\triangledown }}\Theta _2 \right\rangle _{\mathring{g}} \, d V_{\mathring{g},\eta } \right] _{T_{235}}. \end{aligned}$$
For the first term, note that using (3.6) once more,
$$\begin{aligned} T_{231}&\le \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\le C \left( \left( \alpha - 1 \right) + \delta \right) R^2. \end{aligned}$$
Next we have that, applying Hölder’s inequality, then global Sobolev embedding \(W^{1,2} \hookrightarrow L^4\), and localized Poincaré inequality and finally incorporating the global \(L^2\)-estimate for \({\widetilde{\triangledown }}^{(2)} \Upsilon \).
$$\begin{aligned} T_{232}&\le \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^3 \, d V_{\mathring{g},\eta }\\&\le \left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^4 \, d V_{\mathring{g},\eta } \right) ^{1/2} \left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta } \right) ^{1/2} \\&\le C_S \delta \left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\left[ \eta {\widetilde{\triangledown }}\Upsilon \right] \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta } \right) \\&\le C \delta \left( \int _{B_R} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} + \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\eta \right| _{\mathring{g}}^2 \left| {\widetilde{\triangledown }}\Upsilon \right| ^2 \, d V_{\mathring{g},\eta } \right) \\&\le C \delta \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C \delta \left( \int _{B_R} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} + \tfrac{1}{R^2} \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} \right) \\&\le C \delta \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C_P \delta \left( R^2 \int _{B_R} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} + \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} \right) \\&\le C \delta \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C \delta \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} + C \left( \left( \alpha - 1 \right) + \delta \right) R^2. \end{aligned}$$
Next, applying a weighted Young’s inequality, Hölder’s inequality, applying the global \(L^4\)-bound on \(\Upsilon \), and Sobolev embedding \(L^4 \hookrightarrow W^{1,2}\) and then applying the localized Poincaré inequality,
$$\begin{aligned} T_{233}&\le C \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}} \left| \Upsilon \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }\\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \tfrac{C}{\nu }\int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \left| \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C\left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^4 \, d V_{\mathring{g},\eta } \right) ^{1/2}\left( \int _{{\mathbb {S}}^4} \left| \Upsilon \right| _{\mathring{g}}^4 \, d V_{\mathring{g},\eta } \right) ^{1/2}\\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C_S \delta \left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\left[ \eta {\widetilde{\triangledown }}\Upsilon \right] \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta } \right) \\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C \delta \left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\right. \\&\left. \quad + \tfrac{1}{R^2} \int _{B_R \backslash B/2} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta } \right) \\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C_S \delta \left( R^2 \int _{B_R} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} + \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\right. \\&\left. \quad + \int _{B_R \backslash B/2} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} \right) \\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C_S \left( \delta + \left( \alpha - 1 \right) \right) R^2 + C \delta \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\\&\quad + C \int _{B_R \backslash B/2} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}}. \end{aligned}$$
We now approach the first term with \(\alpha \) dependence,
$$\begin{aligned} T_{234}&= \left[ \int _{{\mathbb {S}}^4} \left\langle {\widetilde{\vartriangle }} \Upsilon , \Theta _1 \right\rangle _{\mathring{g}} \, d V_{\mathring{g},\eta } \right] _{T_{2341}}+ \left[ \int _{{\mathbb {S}}^4} {\widetilde{\triangledown }}\Upsilon *\Theta _1 *\triangledown \eta \, d V_{\mathring{g},\eta } \right] _{T_{2342}}. \end{aligned}$$
We compute these separately. We have that
$$\begin{aligned} T_{2341}&\le \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| \left| \Theta _1 \right| \, d V_{\mathring{g},\eta }\nonumber \\&\le C \left( \alpha - 1 \right) \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C \left( \alpha - 1 \right) \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}} \left| \Upsilon \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }\nonumber \\&\qquad + C \left( \alpha - 1 \right) \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}} \left| \Upsilon \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }+ C \left( \alpha - 1 \right) \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}} \left| \Upsilon \right| _{\mathring{g}}^3 \, d V_{\mathring{g},\eta }. \end{aligned}$$
(7.12)
The first term can be absorbed, and the second is precisely \(T_{233}\). For the third term of (7.12) we apply a weighted Young’s inequality, localized Poincaré inequality twice, and the global estimate to \({\widetilde{\triangledown }}^{(2)} \Upsilon \).
$$\begin{aligned} \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}} \left| \Upsilon \right| \, d V_{\mathring{g},\eta }&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \tfrac{C}{\nu } \int _{{\mathbb {S}}^4} \left| \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C\int _{B_R} \left| \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}}\\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C_P \left( R^4 \int _{B_R} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}}+ R^2 \delta \right) \\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C R^2 \left( (\alpha - 1) + \delta \right) . \end{aligned}$$
For the last integral in (7.12) we have
$$\begin{aligned}&\int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}} \left| \Upsilon \right| ^3_{\mathring{g}} \, d V_{\mathring{g},\eta }\\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \tfrac{C}{\nu } \left( \int _{{\mathbb {S}}^4} \left| \Upsilon \right| _{\mathring{g}}^6 \, d V_{\mathring{g},\eta } \right) ^{1/3}\left( \int _{{\mathbb {S}}^4} \left| \Upsilon \right| _{\mathring{g}}^6 \, d V_{\mathring{g},\eta } \right) ^{2/3} \\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C \left( \left( \alpha - 1 \right) + \delta \right) \left( \int _{{\mathbb {S}}^4} \left| \Upsilon \right| _{\mathring{g}}^6 \, d V_{\mathring{g},\eta } \right) ^{1/3} \\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C_S \left( \left( \alpha - 1 \right) + \delta \right) \left( \int _{{\mathbb {S}}^4} \left| \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\left[ \eta \Upsilon \right] \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\right. \\&\left. \qquad + \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \left[ \eta \Upsilon \right] \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta } \right) \\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C \left( \left( \alpha - 1 \right) + \delta \right) \left( \int _{{\mathbb {S}}^4} \left| \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\right. \\&\left. \qquad + \int _{{\mathbb {S}}^4} \left| \Upsilon \right| _{\mathring{g}}^2 \left| \triangledown \eta \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta } \right) \\&\qquad + C \left( \left( \alpha - 1 \right) + \delta \right) \left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \left| \triangledown \eta \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\right. \\&\left. \qquad + \int _{{\mathbb {S}}^4} \left| \Upsilon \right| _{\mathring{g}}^2 \left| \triangledown ^{(2)} \eta \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta } \right) \\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C \left( \left( \alpha - 1 \right) + \delta \right) \left( \int _{B_R} \left| \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} + \int _{B_R} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} \right. \\&\left. \qquad + \tfrac{1}{R^2}\int _{B_R \backslash B_{R/2}} \left| \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} \right) \\&\qquad + C \left( \left( \alpha - 1 \right) + \delta \right) \left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \tfrac{1}{R^2}\int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} \right. \\&\left. \qquad + \tfrac{1}{R^4}\int _{B_R \backslash B_{R/2}} \left| \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} \right) \\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C_P \left( \left( \alpha - 1 \right) + \delta \right) \left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\right. \\&\left. \qquad + \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} \right) . \end{aligned}$$
We now address the next term
$$\begin{aligned} T_{2342}&= \int _{{\mathbb {S}}^4} {\widetilde{\triangledown }}\Upsilon *\Theta _1 *\triangledown \eta \, d V_{\mathring{g},\eta }\nonumber \\&\le C \left( \alpha - 1 \right) \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}} \left| \triangledown \eta \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }+ C \left( \alpha - 1 \right) \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \left| \Upsilon \right| _{\mathring{g}} \left| \triangledown \eta \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }\nonumber \\&\qquad + C \left( \alpha - 1 \right) \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}} \left| \Upsilon \right| _{\mathring{g}} \left| \triangledown \eta \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }+C \left( \alpha - 1 \right) \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}} \left| \Upsilon \right| ^3_{\mathring{g}} \left| \triangledown \eta \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }. \end{aligned}$$
(7.13)
The first term is exactly \(T_1\), so we can apply the same estimate. Now we approach the second term of (7.13), applying Young’s inequality, Hölder’s inequality, a global Sobolev embedding of \(W^{1,2} \hookrightarrow L^4\), and localized Poincaré inequalities, and global \(L^2\) control of \({\widetilde{\triangledown }}^{(2)} \Upsilon \),
$$\begin{aligned} \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \left| \Upsilon \right| _{\mathring{g}} \left| \triangledown \eta \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }&\le C \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^4 \, d V_{\mathring{g},\eta }+ \tfrac{C}{R^2} \int _{B_R \backslash B_{R/2}} \left| \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} \\&\le C \left( \delta + \left( \alpha - 1 \right) \right) \left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^4 \, d V_{\mathring{g},\eta } \right) ^{1/2} \\&\qquad + R^2 C_P \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}^{(2)}\Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} \\&\le C_S \left( \left( \alpha - 1 \right) + \delta \right) \left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\right. \\&\left. \qquad + \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\left[ \eta {\widetilde{\triangledown }}\Upsilon \right] \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta } \right) + C R^2 \left( \left( \alpha - 1 \right) + \delta \right) \\&\le C \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} + C_P \left( \left( \alpha - 1 \right) + \delta \right) \\&\qquad \times \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C R^2 \left( \left( \alpha - 1 \right) + \delta \right) . \end{aligned}$$
For the third term, applying weighted Young’s Inequality in preparation for an application of Poincaré inequality, then a Holder’s inequality followed by applying global \(L^4\) control of \(\Upsilon \),
$$\begin{aligned} \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}} \left| \Upsilon \right| _{\mathring{g}} \left| \triangledown \eta \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }&\le \tfrac{\nu }{C_P R^2}\int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} + \tfrac{C C_P}{\nu } \int _{B_R \backslash B_{R/2}} \left| \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} \\&\le \nu \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} \\&\qquad + C\left( \int _{{\mathbb {S}}^4} \, dV_{\mathring{g}} \right) ^{1/2} \left( \int _{B_R \backslash B_{R/2}} \left| \Upsilon \right| _{\mathring{g}}^4 \, d V_{\mathring{g},\eta } \right) ^{1/2}\\&\le \nu \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} + C \delta R^2. \end{aligned}$$
For the fourth integral we apply weighted Young’s inequality followed by localized Poincaré inequality and Hölder’s inequality, using the global Sobolev embedding \( W^{2,2}\hookrightarrow L^8\) and applying localized Poincaré,
$$\begin{aligned} \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}} \left| \Upsilon \right| _{\mathring{g}}^3 \left| \triangledown \eta \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }&\le \tfrac{1}{R^2} \int _{B_R \backslash B_{R/2}} \left| \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} + \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \left| \Upsilon \right| _{\mathring{g}}^4 \, d V_{\mathring{g},\eta }\\&\le C_P R^2 \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} \\&\qquad + C\left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^4 \, d V_{\mathring{g},\eta } \right) ^{1/2} \left( \int _{{\mathbb {S}}^4} \left| \Upsilon \right| _{\mathring{g}}^8 \, d V_{\mathring{g},\eta } \right) ^{1/2} \\&\le C \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} \\&\qquad + C_S \delta \left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\left[ \eta {\widetilde{\triangledown }}\Upsilon \right] \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta } \right) \\&\le C_P \delta \left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} \right) \\&\qquad + C R^2 \left( \left( \alpha - 1 \right) + \delta \right) . \end{aligned}$$
Next we have that
$$\begin{aligned} T_{235}&= \left[ \int _{{\mathbb {S}}^4} \left\langle \vartriangle \Upsilon , \Theta _2 \right\rangle _{\mathring{g}} \, d V_{\mathring{g},\eta } \right] _{T_{2351}} + \left[ \int _{{\mathbb {S}}^4} \triangledown \Upsilon *\Theta _2 *\triangledown \eta \, d V_{\mathring{g},\eta } \right] _{T_{2352}}. \end{aligned}$$
Then we expand out
$$\begin{aligned} T_{2351}&\le C(\alpha -1) \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}} \left| \Theta _2 \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }\nonumber \\&\le C(\alpha -1)\int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}\left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}} \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }\nonumber \\&\qquad + C(\alpha -1)\int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}} \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }\nonumber \\&\qquad + C(\alpha -1)\int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}} \left| \Upsilon \right| ^2 \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }. \end{aligned}$$
(7.14)
For the first term of (7.14), applying a weighted Young’s inequality and Hölder’s inequality, followed by global Sobolev embedding \(W^{1,2} \hookrightarrow L^4\),
$$\begin{aligned} C\left( \alpha - 1 \right)&\int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}} \left| {\widetilde{\triangledown }}\Upsilon \right| \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }\\&\qquad \le \left( \alpha - 1 \right) \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \tfrac{C \left( \alpha - 1 \right) }{\nu }\int _{{\mathbb {S}}^4} \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}}^2 \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\\&\qquad \le \left( \alpha - 1 \right) \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\\&\qquad + C \left( \alpha - 1 \right) \left( \int _{{\mathbb {S}}^4} \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}}^4 \, d V_{\mathring{g},\eta } \right) ^{1/2} \left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^4 \, d V_{\mathring{g},\eta } \right) ^{1/2}\\&\qquad \le \left( \alpha - 1 \right) \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C_S \delta \left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\right. \\&\left. \qquad + \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\left[ \eta {\widetilde{\triangledown }}\Upsilon \right] \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta } \right) \\&\qquad \le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+C_P \delta \left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\right. \\&\left. \qquad + \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} + R^2 \left( \alpha -1 + \delta \right) \right) . \end{aligned}$$
Next we have that, for the second term of (7.14), using weighted Young’s inequality followed by Holder’s inequality and applying the global bounds to \(\log \chi _{\lambda }\) type terms,
$$\begin{aligned} C\left( \alpha - 1 \right) \int _{{\mathbb {S}}^4}&\left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}} \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }\\&\le \left( \alpha - 1 \right) \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \tfrac{C}{\nu }\left( \alpha - 1 \right) \int _{{\mathbb {S}}^4} \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\\&\le \left( \alpha - 1 \right) \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\\&\qquad + C \left( \alpha - 1 \right) \left( \int _{{\mathbb {S}}^4}\left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}}^4 \, d V_{\mathring{g},\eta } \right) ^{1/2}\left( \int _{{\mathbb {S}}^4} \, d V_{\mathring{g},\eta } \right) ^{1/2}\\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ C R^2 \delta . \end{aligned}$$
Lastly for the third term of (7.14), we apply a weighted Young’s inequality, Hölder’s inequality, a global Sobolev embedding and then localized Poincaré to the remaining pieces,
$$\begin{aligned} C\left( \alpha - 1 \right) \int _{{\mathbb {S}}^4}&\left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}} \left| \Upsilon \right| ^2 \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }\\&\le \left( \alpha - 1 \right) \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \left( \alpha - 1 \right) \tfrac{C}{\nu }\int _{{\mathbb {S}}^4} \left| \Upsilon \right| _{\mathring{g}}^4 \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\\&\le \left( \alpha - 1 \right) \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\\&\qquad + \left( \alpha - 1 \right) C \left( \int _{{\mathbb {S}}^4} \left| \Upsilon \right| _{\mathring{g}}^8 \, d V_{\mathring{g},\eta } \right) ^{1/2}\left( \int _{{\mathbb {S}}^4} \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}}^4 \, d V_{\mathring{g},\eta } \right) ^{1/2} \\&\le \left( \alpha - 1 \right) \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\\&\qquad + C_S \delta \left( \int _{{\mathbb {S}}^4} \left| \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\left[ \eta \Upsilon \right] \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \left[ \eta \Upsilon \right] \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta } \right) ^2\\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\\&\qquad + C_P \delta ^2 \left( \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} + \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ R^2 \left( \alpha - 1 + \delta \right) \right) . \end{aligned}$$
We next expand out
$$\begin{aligned} T_{2352}&\le C \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}} \left| \Theta _2 \right| _{\mathring{g}} \left| \triangledown \eta \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }\nonumber \\&\le C \left( \alpha -1 \right) \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}} \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}} \left| \triangledown \eta \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }\nonumber \\&\qquad + C \left( \alpha -1 \right) \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}} \left| \triangledown \eta \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }\nonumber \\&\qquad + C \left( \alpha -1 \right) \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}} \left| \Upsilon \right| _{\mathring{g}}^2 \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}} \left| \triangledown \eta \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }. \end{aligned}$$
(7.15)
For the first term of (7.15), applying a weighted Young’s inequality in preparation for a Poincaré inequality, then Hölder’s inequality and applying the global bounds of \(\log \chi _{\lambda }\) type terms,
$$\begin{aligned} C \left( \alpha -1 \right)&\int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}} \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}} \left| \triangledown \eta \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }\\&\le \tfrac{\nu }{C_P R^2} \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} + \left( \alpha -1 \right) \tfrac{C C_P}{\nu } \int _{{\mathbb {S}}^4} \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} \\&\le \nu \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} + C\left( \alpha -1 \right) \left( \int _{{\mathbb {S}}^4} \, d V_{\mathring{g},\eta } \right) ^{1/2} \left( \int _{{\mathbb {S}}^4} \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}}^4 \, d V_{\mathring{g},\eta } \right) ^{1/2} \\&\le \nu \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} + C_{S} \delta R^2. \end{aligned}$$
For the second term of (7.15) we apply Hölder’s inequality twice followed by global \(L^4\) bounds of \(\triangledown \log \chi _{\lambda }\), a global Sobolev embedding \(W^{1,2} \hookrightarrow L^4\) and the localized Poincaré inequality
$$\begin{aligned} C \left( \alpha -1 \right)&\int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}} \left| \triangledown \eta \right| _{\mathring{g}} \, d V_{\mathring{g},\eta }\\&\le \tfrac{C}{R} \left( \alpha -1 \right) \left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^4 \, d V_{\mathring{g},\eta } \right) ^{1/2} \left( \int _{{\mathbb {S}}^4} \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta } \right) ^{1/2}\\&\le \tfrac{C}{R} \left( \alpha -1 \right) \left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^4 \,d V_{\mathring{g},\eta } \right) ^{1/2} \left( \int _{B_R} \, dV_{\mathring{g}} \right) ^{1/4}\left( \int _{{\mathbb {S}}^4} \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}}^4 \, d V_{\mathring{g},\eta } \right) ^{1/4}\\&\le C_S \delta \left( \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+\int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\left[ \eta \Upsilon \right] \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta } \right) \\&\le C_P \left( \delta + \left( \alpha - 1 \right) \right) R^2 + C_P \delta \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}}. \end{aligned}$$
For the third term of (7.15), applying weighted Young’s inequality (‘preparing’ for the application of the Poincaré inequality with our choice of weight), then Poincaré inequality and Hölder’s inequality, then applying Sobolev embedding \(W^{2,2} \hookrightarrow L^8\) and Poincaré inequalities once more
$$\begin{aligned} C \left( \alpha - 1 \right) \int _{{\mathbb {S}}^4}&\left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}} \left| \Upsilon \right| _{\mathring{g}}^2 \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}} \left| \triangledown \eta \right| _{\mathring{g}}\, d V_{\mathring{g},\eta }\\&\le \tfrac{\nu }{C_P R^2} \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \tfrac{C \left( \alpha - 1 \right) C_P}{\nu }\int _{{\mathbb {S}}^4} \left| \Upsilon \right| _{\mathring{g}}^4 \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\\&\qquad + C \left( \alpha - 1 \right) \left( \int _{{\mathbb {S}}^4} \left| \Upsilon \right| _{\mathring{g}}^8 \, d V_{\mathring{g},\eta } \right) ^{1/2}\left( \int _{{\mathbb {S}}^4} \left| \triangledown \log \chi _{\lambda } \right| _{\mathring{g}}^4 \, d V_{\mathring{g},\eta } \right) ^{1/2} \\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\\&\qquad + C_S \delta \left( \int _{{\mathbb {S}}^4} \left| \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}\left[ \eta \Upsilon \right] \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \left[ \eta \Upsilon \right] \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta } \right) ^2\\&\le \nu \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }\\&\qquad + C_P \delta \left( \int _{B_R \backslash B_{R/2}} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} + \int _{{\mathbb {S}}^4} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, d V_{\mathring{g},\eta }+ R^2 \left( \left( \alpha - 1 \right) + \delta \right) \right) . \end{aligned}$$
Take \(\nu \le \tfrac{1}{10}\) so that the terms scaled by \(\nu \) may be absorbed into the left hand side of (7.11). Furthermore, choose \(\delta \), \(\alpha \) sufficiently small so that remaining terms may be absorbed over,
$$\begin{aligned} \int _{B_{\frac{R}{2}}} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} \le C \left( \int _{B_R \backslash B_{\frac{R}{2}}} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} + R^2 \left( \left( \alpha - 1 \right) + \delta \right) \right) . \end{aligned}$$
(7.16)
Define
$$\begin{aligned} f (R) := \int _{B_R \backslash B_{\frac{R}{2}}} \left| {\widetilde{\triangledown }}^{(2)} \Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} + R^2 \left( \left( \alpha - 1 \right) + \delta \right) . \end{aligned}$$
Remanipulating (7.16) above, we have that \(f \left( \tfrac{R}{2} \right) \le \tfrac{C}{C + 1} f(R)\), and therefore for all \(k\ge 1\),
$$\begin{aligned} f\left( \tfrac{R}{2^k} \right) \le \left( \tfrac{C}{C+1} \right) ^k \left( \int _{B_R} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} + R^2 \left( \left( \alpha - 1 \right) + \delta \right) \right) \le \left( \tfrac{C}{C+1} \right) ^k C \left( \left( \alpha -1 \right) + \delta \right) . \end{aligned}$$
This implies that there exists some \(\beta > 0\) such that
$$\begin{aligned} \int _{B_R} \left| {\widetilde{\triangledown }}\Upsilon \right| _{\mathring{g}}^2 \, dV_{\mathring{g}} \le C \left( \alpha - 1 + \delta \right) R^{2 \beta }, \end{aligned}$$
which yields the desired Morrey bound. \(\square \)
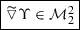 For this, we simply have the following by applying Hölder’s inequality followed by applying our global estimates on \({\widetilde{\triangledown }}^{(k)} \Upsilon \) for \(k \in \left\{ 0,1,2 \right\} \),
For this, we simply have the following by applying Hölder’s inequality followed by applying our global estimates on \({\widetilde{\triangledown }}^{(k)} \Upsilon \) for \(k \in \left\{ 0,1,2 \right\} \),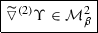 We perform a hole-filling argument. To begin,
We perform a hole-filling argument. To begin,