$\Gamma$-Convergence of variational functionals with boundary terms in Stein manifolds

Abstract

Let $\Omega$ be an open subset of a Stein manifold $\Sigma$ and let M be its boundary. It is well known that M inherits a natural contact structure. In this paper we consider a family of variational functionals $F_\varepsilon$ defined by the sum of two terms: a Dirichlet-type energy associated with a sub-Riemannian structure in $\Omega$ and a potential term on the boundary M. We prove that the functionals $F_\varepsilon$ $\Gamma$-converge to the intrinsic perimeter in M associated with its contact structure. Similar results have been obtained in the Euclidean space by Alberti, Bouchitté, Seppecher. We stress that already in the Euclidean setting the situation is not covered by the classical Modica–Mortola theorem because of the presence of the boundary term. We recall also that Modica–Mortola type results (without a boundary term) have been proved in the Euclidean space for sub-Riemannian energies by Monti and Serra Cassano.

Appendix: Densities and measures

In this Appendix we prove Theorem 5.6, which was a crucial ingredient in the proof of the liminf inequality. In order to do that, we need some preliminaries on densities and measures.

As in Theorem 5.3, let $(W_1^{0},\ldots ,W^{0}_{2n})$ be an orthonormal symplectic basis of $\ker \theta ({\bar{p}})$, and let $(W_1^{{\mathbb {H}}},\ldots ,W^{{\mathbb {H}}}_{2n})$ be the canonical orthonormal symplectic basis of $\ker \theta _0$ ($\theta _0$ being the canonical contact form of ${{\mathbb {H}}}^{n}$). Let now $\mathcal U\subset M$ and, for ${\bar{p}}\in \mathcal U$, let $\Psi : \mathcal U\rightarrow {{\mathbb {H}}}^{n}$ be the contact diffeomorphism constructed in Theorem 5.3. In $\Psi (\mathcal U)$, consider now the vector fields $\Psi _*W_i^0$, $i=1,\ldots ,2n$. Notice that

$$\begin{aligned} \mathrm {span}\; \{\Psi _*W_1^0,\ldots , \Psi _*W_{2n}^0\} = \ker \theta _0 = \mathrm {span}\; \{{W}^{{\mathbb {H}}}_1,\ldots ,{W}^{{\mathbb {H}}}_{2n} \}. \end{aligned}$$

Remember that $\Psi ({\bar{p}}) =0$. By the same theorem, $\Psi _*W_i^0(0)= W^{{\mathbb {H}}}_i(0)$ for $i=1,\ldots ,2n$. We denote by $d_c^\Psi$ the Carnot–Carathéodory distance in $\Psi (\mathcal U)$ associated with the Riemannian metric $(\Psi ^{-1})^*g$, and by $d^{{\mathbb {H}}}_c$ the standard Carnot–Carathéodory distance in ${{\mathbb {H}}}^{n}$. We denote also by $\overline{B}_\Psi$ and $\overline{B}_{{\mathbb {H}}}$ the closed balls associated with $d_c^\Psi$ and $d^{{\mathbb {H}}}_c$, respectively.

It is easy to see that for $p,q\in \mathcal U$

$$\begin{aligned} d_c (p,q) = d_c^\Psi (\Psi (p),\Psi (q)). \end{aligned}$$

In the sequel, $B^\Psi$ will be the open balls with respect to $d_c^\Psi$.

Lemma 7.1

For z in a neighborhood of $0\in {\mathbb {H}}^n$, the following estimates hold:

$$\begin{aligned} d_{{\mathbb {H}}}(z,0)\le & {} d_c^\Psi (z,0)(1+ Cd_c^\Psi (z,0)^{1/2}); \end{aligned}$$

(7.1)

$$\begin{aligned} d_c^\Psi (z,0)\le & {} d_{{\mathbb {H}}} (z,0)(1+ Cd_{{\mathbb {H}}}(z,0)^{1/2}). \end{aligned}$$

(7.2)

Proof

We denote by $\mathcal W_\Psi$ and $\mathcal W_{{\mathbb {H}}}$ the $(2n\times 2n)$-matrices whose columns are $\Psi _*{W}_1^0,\ldots , \Psi _*{W}_{2n}^0$ and ${W}^{{\mathbb {H}}}_1,\ldots ,{W}^{{\mathbb {H}}}_{2n}$, respectively. If we set

$$\begin{aligned} \mathcal A := (a_{ij})_{i,j =1,\ldots , 2n} := \mathcal W_{{\mathbb {H}}}^{-1} \mathcal W_\Psi , \end{aligned}$$

we obtain that $\mathcal A$ transforms the coordinates with respect to $(\Psi _*{W}_1^0,\ldots ,\Psi _*{W}_{2n}^0)$ of a generic point in $\ker \theta _0$ into its coordinates with respect to $({W}^{{\mathbb {H}}}_1,\ldots ,{W}^{{\mathbb {H}}}_{2n} )$. If we denote by z a generic point of $\Psi (\mathcal U)$, by Theorem 5.3,

$$\begin{aligned} \mathcal A(z) = \mathrm {Id} + O(|z|)\qquad \text{ as } z\rightarrow 0. \end{aligned}$$

Let now $z\in K\subset \subset \Psi (\mathcal U)$ be fixed, and let $\gamma : [0,1]\rightarrow {{\mathbb {H}}}^{n}$ a (smooth) $d_c^\Psi$-geodesic connecting 0 and z. If $t\in [0,1]$, we can write

$$\begin{aligned} \gamma '(t) = \sum _i \gamma _i (t) (\Psi _*W_i^0)(\gamma (t)) \quad \text{ and }\quad d_c^\Psi (z,0) = \int _0^1 \big (\sum _i \gamma _i^2(t)\big )^{1/2}\, dt. \end{aligned}$$

Thus, if $t\in [0,1]$, we have

$$\begin{aligned} \gamma '(t) = \sum _i \big \{\sum _j a_{i,j}(\gamma (t))\gamma _j(t)\big \} W^{{\mathbb {H}}}_i(\gamma (t)), \end{aligned}$$

and hence

$$\begin{aligned}\begin{aligned} d_{{\mathbb {H}}}(z,0)&\le \int _0^1 \Big ( \sum _i \big \{\sum _j a_{i,j}(\gamma (t))\gamma _j(t)\big \}^2\Big )^{1/2}\; dt\\&= \int _0^1 \Big ( \sum _i \big \{\sum _j (\delta _{i,j}+ O(|\gamma (t)|) )\gamma _j(t)\big \}^2\Big )^{1/2}\; dt \\ {}&= \int _0^1 \Big ( \sum _i \big \{\gamma _i(t) + O(|\gamma (t)|^2)\big \}^2\Big )^{1/2}\; dt\\&\le \int _0^1 \Big ( \sum _i \gamma _i(t)^2\Big )^{1/2}\; dt +\int _0^1 O(|\gamma (t)|^{3/2})\, dt\\&= d_c^\Psi (z,0)+\int _0^1 O(|\gamma (t)|^{3/2})\, dt. \end{aligned} \end{aligned}$$

On the other hand, since the Euclidean distance may be locally bounded by $d_c^\Psi$,

$$\begin{aligned}\begin{aligned} |\gamma (t)| \le C_1 d_c^\Psi (\gamma (t),0) \le C d_c^\Psi (z,0), \end{aligned} \end{aligned}$$

so that (7.1) follows. We can carry out the same argument interchanging the roles of $d_{{\mathbb {H}}}$ and $d_c^\Psi$, and we get (7.2). $\square$

To keep our paper as self-contained as possible, we gather here few more or less known results about Hausdorff measures in metric spaces. This part is taken almost verbatim from [24].

We recall first the definition of a centered density for an outer measure $\mu$ on X from Definition 5.5. In Euclidean spaces (and more generally in Carnot groups) we can replace in this definition the diameter $\mathrm {diam}\,\overline{B}(x,r)$ by 2r. This “elementary” statement fails to be true in general metric spaces, but still holds in contact manifolds endowed with their Carnot–Carathéodory distance. This will follow from the following results.

Lemma 7.2

Let M be a $(2n+1)$-dimensional contact manifold endowed with the contact form $\theta$, with the volume form $v_\theta := \theta \wedge (d\theta )^n$, and the Riemannian metric g on $\ker \theta$ as introduced in Propositions 2.9 and 2.12. We denote by $d_c$ the associated Carnot–Carathéodory distance. Let ${\bar{p}}\in M$ be a fixed point. We have:

• (i) if $c_0$ is the volume of the unit ball in ${{\mathbb {H}}}^{n}$ for the Carnot–Carathéodory distance associated with the canonical basis $(W_1^{{\mathbb {H}}},\ldots ,W^{{\mathbb {H}}}_{2n})$ of ${{\mathbb {H}}}^{n}$ (see Theorem 5.3), then

  $$\begin{aligned}\lim _{r\rightarrow 0}\dfrac{ v_\theta (\overline{B}(x,r))}{r^{2n+2}} = c_0;\end{aligned}$$

• (ii) Moreover,

  $$\begin{aligned} \lim _{r\rightarrow 0} \dfrac{\mathrm {diam}\,\overline{B}(x,r)}{2r} = 1. \end{aligned}$$

Proof

Take a ball $\overline{B}_r:=\overline{B}({\bar{p}},r)\subset M$ with $r>0$ sufficiently small. For sake of simplicity, in Lemma 7.1, put $\phi (t):= t(1+C\sqrt{t})$. Obviously, $\phi (r) = r + o(r)$ and $\phi ^{-1}(s) = s + o(s)$ as $s\rightarrow 0$.

By (7.1) and (7.2)

$$\begin{aligned} \begin{aligned} \overline{B}_{{\mathbb {H}}}(0, \phi ^{-1}(r))&\subset \Psi (\overline{B}_r) = B^\Psi (0,r) \subset \overline{B}_{{\mathbb {H}}}(0, \phi (r)). \end{aligned} \end{aligned}$$

(7.3)

We recall now that for $\rho >0$

$$\begin{aligned} c_0\rho ^{2n+2} =\mathcal L^{2n+1} (\overline{B}_{{\mathbb {H}}}(0,\rho )) = \int _{\overline{B}_{{\mathbb {H}}}} dv_{\theta _0}, \end{aligned}$$

and that

$$\begin{aligned}\begin{aligned} v_\theta (\overline{B}_r)&= \int _{\overline{B}_r} \theta \wedge (d\theta )^n = \int _{\Psi (\overline{B}_r)} (\Psi ^{-1})^*(\theta \wedge (d\theta )^n)\\&= \int _{\Psi (\overline{B}_r)} (\Psi ^{-1})^*\theta \wedge (d(\Psi ^{-1})^*(\theta )^n) = \int _{\Psi (\overline{B}_r)} \theta _0\wedge (d\theta _0)^n\\&= \int _{ B^\Psi (0,r)} dv_{\theta _0} = v_{\theta _0}( B^\Psi (0,r)), \end{aligned}\end{aligned}$$

so that

$$\begin{aligned}\begin{aligned} c_0 (\phi ^{-1}(r))^{2n+2} \le v_\theta (\overline{B}_r) \le c_0 \phi (r)^{2n+2}. \end{aligned} \end{aligned}$$

Then (i) follows straightforwardly.

Let us prove (ii). If $r>0$ By [22], Proposition 2.4, there exist $z_r,\zeta _r\in \overline{B}_{{\mathbb {H}}}(0, \phi ^{-1}(r))$ such that $d_{{\mathbb {H}}}(z_r,\zeta _r)= 2\phi ^{-1}(r)$. Arguing as above, if $\gamma :[0,1]\rightarrow {{\mathbb {H}}}^{n}$ is a $d_c^\Psi$-geodesic connecting $z_r$ and $\zeta _r$, then

$$\begin{aligned} d_{{\mathbb {H}}}(z_r,\zeta _r) \le d_c^\Psi (z_r,\zeta _r)+\int _0^1 O(|\gamma (t)|^{3/2})\, dt. \end{aligned}$$

On the other hand, $\gamma (t)\in \overline{B}_{{\mathbb {H}}}(0, 3 \phi ^{-1}(r))$, and hence, if $r>0$ is sufficiently small,

$$\begin{aligned} O(|\gamma (t)|^{3/2}) \le C_1 |\gamma (t)|^{3/2} \le C_2 d_{{\mathbb {H}}}(0,\gamma (t))^{3/2} \le C(\phi ^{-1}(r))^{3/2}= Cr^{3/2}(1+o(1)) , \end{aligned}$$

so that

$$\begin{aligned} 2\phi ^{-1}(r) =d_{{\mathbb {H}}}(z_r,\zeta _r) \le d_c^\Psi (z_r,\zeta _r) + Cr^{3/2}(1+o(1)). \end{aligned}$$

Therefore

$$\begin{aligned} d_c^\Psi (z_r,\zeta _r) \ge 2r (1+o(1)). \end{aligned}$$

By (7.3), $z_r,\zeta _r\in B^\Psi _r$, so that

$$\begin{aligned} \Psi (z_r), \Psi (\zeta _r) \in \overline{B}_r. \end{aligned}$$

Hence

$$\begin{aligned} \begin{aligned} 1 \ge \dfrac{\mathrm {diam}\,(\overline{B}_r) }{2r} \ge \dfrac{d_c(\Psi (z_r), \Phi (\zeta _r))}{2r} = \dfrac{d_c^\Phi (z_r,\zeta _r)}{2r} \ge 1 + o(1), \end{aligned} \end{aligned}$$

and (ii) follows. $\square$

Lemma 7.2 immediately yields the following equivalent definition of densities in contact manifolds:

Corollary 7.3

Let M be $(2n+1)$-dimensional contact manifold endowed with a contact form $\theta$ and a Riemannian metric g on the fibers of $\theta$ as introduced in Propositions 2.9 and 2.12. We denote by $d_c$ the associated Carnot–Carathéodory distance. Let $\mu$ be an outer measure on M. Then

$$\begin{aligned} \Theta ^{*\,m}(\mu ,x):=\limsup _{r\rightarrow 0}\frac{{\mathcal {\mu }}(\overline{B}(x,r))}{\alpha _m\, r^m }\, \end{aligned}$$

and

$$\begin{aligned} \Theta ^m_*(\mu ,x):=\liminf _{r\rightarrow 0}\frac{{\mathcal {\mu }}(\overline{B}(x,r))}{\alpha _m\, r^m}\,. \end{aligned}$$

Remark 7.4

In Corollary 7.3 we can replace closed balls $\overline{B}(x,r)$ by open balls B(x, r) (see [9], Remark 2.4.2).

Keeping in mind Corollary 7.3 and Remark 7.4, the following result can be proved by the same arguments used in the proof of Theorem 3.1 in [24].

Proposition 7.5

Let M be $(2n+1)$-dimensional contact manifold endowed with a contact form $\theta$ and a Riemannian metric g on the fibers of $\theta$ as introduced in Propositions 2.9 and 2.12. We denote by $d_c$ the associated Carnot–Carathéodory distance. Let $\mu$ be a $\sigma$-finite regular Borel measure on M. Then the map

$$\begin{aligned} \Theta ^{*\,m}(\mu ,\cdot ): X\rightarrow [0,+\infty ] \end{aligned}$$

is Borel measurable.

We give now the following:

Definition 7.6

Let $A\subset X$, $m \in [0,\infty )$, $\delta \in (0,\infty )$, and let $\beta _m$ be the constant (5.4).

(i):

The m-dimensional Hausdorff measure ${\mathcal {H}}^m$ is defined as

$$\begin{aligned} {\mathcal {H}}^m(A):=\lim _{\delta \rightarrow 0}{\mathcal {H}}_{\delta }^m(A) \end{aligned}$$

where

$$\begin{aligned} {\mathcal {H}}_{\delta }^m(A)=\inf \left\{ \sum _i \beta _m \mathrm {diam}\,(E_i)^m:\;A\subset \bigcup _i E_i,\quad \mathrm {diam}\,(E_i)\le \delta \right\} . \end{aligned}$$

(ii):

The m-dimensional spherical Hausdorff measure ${\mathcal {S}}^m$ is defined as

$$\begin{aligned} {\mathcal {S}}^m(A):=\lim _{\delta \rightarrow 0}{\mathcal {S}}_{\delta }^m(A) \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} {\mathcal {S}}_{\delta }^m(A)=\inf \Big \{\sum _i \beta _m&\mathrm {diam}\,(B(x_i,r_i))^m:\, A\subset \bigcup _i B(x_i,r_i),\\&\mathrm {diam}\,(B(x_i,r_i))\le \delta \Big \} \end{aligned} \end{aligned}$$

(iii):

The m-dimensional centered Hausdorff measure ${\mathcal {C}}^m$ is defined as

$$\begin{aligned} {\mathcal {C}}^m(A):=\,\sup _{E\subseteq A}{\mathcal {C}}_0^m(E)\,. \end{aligned}$$

where ${\mathcal {C}}_0^m(E):=\lim _{\delta \rightarrow 0^+}{\mathcal {C}}_{\delta }^m(E)$, and, in turn, ${\mathcal {C}}_{\delta }^m(E)=\,0\text { if } E=\,\emptyset$ and for $E\ne \emptyset$,

$$\begin{aligned} \begin{aligned} {\mathcal {C}}_{\delta }^m(E)=\inf \Big \{\sum _i \beta _m&\mathrm {diam}\,(B(x_i,r_i))^m:\, E\subset \bigcup _i B(x_i,r_i),\\&\, x_i\in E,\quad \mathrm {diam}\,(B(x_i,r_i))\le \delta \Big \}. \end{aligned} \end{aligned}$$

Notice that the set function ${\mathcal {C}}_0^m$ is not necessarily monotone (see [43, Sect. 4]) while ${\mathcal {C}}^m$ is monotone.

For reader’s convenience we collect a few results about the measures ${\mathcal {C}}^m$. Most of these results are taken from [15] and [24].

Let

$$\begin{aligned} \mathrm {dist}(E,F):=\,\inf \left\{ d(x,y):\,x\in E,\,y\in F\right\} \end{aligned}$$

denote the distance between E and F. Recall that an outer measure $\mu$ on X is said to be metric if

$$\begin{aligned} \mu (A\cup B)=\,\mu (A)+\,\mu (B)\qquad \text { whenever }\mathrm {dist}(A,B)>\,0\,. \end{aligned}$$

Being obtained by Carathëodory’s construction, ${\mathcal {H}}^m$ and ${\mathcal {S}}^m$ are metric (outer) measures (see [17, 2.10.1] or [31, Theorem 4.2]). Also the measures ${\mathcal {C}}^m$ are metric measures in any metric space, but this fact is not as immediate as for ${\mathcal {H}}^m$ and ${\mathcal {S}}^m$.

Lemma 7.7

([15], Proposition 4.1) ${\mathcal {C}}^m$ is a Borel regular outer measure.

Remark 7.8

The measures ${\mathcal {H}}^m$, ${\mathcal {S}}^m$ and ${\mathcal {C}}^m$ are all equivalent measures. Indeed, it is well known that (see, for instance, [17, 2.10.2])

$$\begin{aligned} {\mathcal {H}}^m\le \,{\mathcal {S}}^m\le \,2^m\,{\mathcal {H}}^m\, \end{aligned}$$

and, by definition,

$$\begin{aligned} {\mathcal {H}}^m\le \,{\mathcal {S}}^m\le \,{\mathcal {C}}^m\,. \end{aligned}$$

The opposite inequality between ${\mathcal {H}}^m$ (or ${\mathcal {S}}^m$) and ${\mathcal {C}}^m$ is less immediate: it was proved in [43, Lemma 3.3] for the case $X={\mathbb {R}}^n$. See also [44], but for a differently defined centered Hausdorff-type measure. The comparison in a general metric space is contained in [15].

Lemma 7.9

([15], Proposition 4.2) ${\mathcal {H}}^m\le \,{\mathcal {C}}^m\le \,2^m\,{\mathcal {H}}^m \,.$

By Lemma 7.9, it follows in particular that the metric dimensions induced by ${\mathcal {H}} ^m$ or ${\mathcal {S}}^m$ or ${\mathcal {C}}^m$ are the same.

The estimates needed to relate the m-dimensional density $\Theta ^{*\,m}(\mu ,\cdot )$ with the centered Hausdorff measure ${\mathcal {C}}^m$ are the following ones.

Theorem 7.10

([15], Theorem 4.15) Let (X, d) be a separable metric space, let $\mu$ be a finite Borel outer measure in X and let $B\subset X$ be a Borel set. Then

• (i)
  $$\begin{aligned} \mu (B)\le \,\sup _{x\in B}\Theta ^{*\,m}(\mu ,x)\,{\mathcal {C}}^m(B), \end{aligned}$$

  except when the product is $\infty \cdot 0$;

• (ii)
  $$\begin{aligned} \inf _{x\in B}\Theta ^{*\,m}(\mu ,x)\,{\mathcal {C}}^m(B)\le \,\mu (B)\,. \end{aligned}$$

By easy modifications of the proof of Theorem 7.10, one gets the following density estimates involving $\Theta ^{*\,m}(\mu ,x)$ and ${\mathcal {C}}^m$. These estimates are analogous to Federer’s ones involving $\Theta _F^{*\,m}(\mu ,x)$ and ${\mathcal {S}}^m$ (see [17]).

Theorem 7.11

Let (X, d) be a separable metric space, let $\mu$ be an outer measure in X and $t>\,0$.

• (i) If $\mu$ is Borel regular and

  

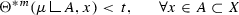
  then

  $$\begin{aligned} \mu (A)\le \, t\;{\mathcal {C}}^m(A)\,. \end{aligned}$$

• (ii) If $V\subset X$ is an open set and

  $$\begin{aligned} \Theta ^{*\,m}(\mu ,x)>\,t,\qquad \forall x\in B\subset V \end{aligned}$$

  then

  $$\begin{aligned} \mu (V)\ge \, t\;{\mathcal {C}}^m(B)\,. \end{aligned}$$

Remark 7.12

If $\mu$ is supposed to be a Radon measure, approximating from above by open sets, we can strengthen the conclusion in Theorem 7.11 (ii) getting the inequality $\mu (B)\ge \,t\;{\mathcal {C}}^m(B)$.

Using Lemma 7.2 (i.e. relying on the equivalence of the two notions of density) and Proposition 7.5, the following result can be proved following step by step the proof of Theorem 3.1 in [24].

Theorem 7.13

Let M be $(2n+1)$-dimensional contact manifold endowed with a contact form $\theta$ and a Riemannian metric g on the fibers of $\theta$ as introduced in Propositions 2.9 and 2.12. We denote by $d_c$ the associated Carnot–Carathéodory distance. Let $\mu$ be a $\sigma$-finite regular Borel measure on M, and let $A\subset X$ be a Borel set. If ${\mathcal {C}}^m(A)<\,\infty$ and is absolutely continuous with respect to , then for each Borel set $B\subset A$,

$$\begin{aligned} \mu (B)=\,\int _B \Theta ^{*\,m}(\mu ,x)\,d{\mathcal {C}}^m(x). \end{aligned}$$

Remark 7.14

Since ${\mathcal {C}}^m$ and ${\mathcal {S}}^m$ are equivalent, then ${\mathcal {C}}^m(A)<\,\infty$ if and only if ${\mathcal {S}}^m(A)<\,\infty$ and is absolutely continuous with respect to ${\mathcal {C}}^m$ if and only if is absolutely continuous with respect to ${\mathcal {S}}^m$.

Now we can give the proof of Theorem 5.6.

Proof of Theorem 5.6

Since $|\mathbf{W}^{0}\chi _E|$ is supported on $\partial ^*E$, without loss of generality we may assume that (5.5) holds for all $x\in \partial E$.

Suppose first

(7.4)

and denote by $A\subset \partial E$ the set of points where (5.5) holds, so that $\mathcal H^{2n+1}(\partial E{\setminus }A)=0$. We remind also that , by [6], Lemma 5.2. Thus, if $B\subset \partial E$ is a Borel set, we can apply Theorem 7.13 to get

Let us drop now the assumption (7.4). We can write

with

(see [42] Theorem 6.10), i.e. there exists $K \subset M$ such that

Set now

$$\begin{aligned} S_0:= \{x\in M\; ; \; \Theta ^{*2n+1}( \mu _s , x) = 0\}. \end{aligned}$$

Notice that $S_0$ is a Borel set, since $\Theta ^{* 2n+1} (\mu _s,\cdot )$ is a Borel function.

If $x\in S_0$, then

$$\begin{aligned}\begin{aligned} \Theta ^{*2n+1}&(|\mathbf{W}^{0}\chi _E|,x)\le \Theta ^{*2n+1} (\mu ,x)\\&\le \Theta ^{*2n+1} (\mu _s,x) + \Theta ^{*2n+1} ( \mu _{ac},x)\\&= \Theta ^{*2n+1} ( \mu _{ac},x). \end{aligned} \end{aligned}$$

Thus, as above, we can apply Theorem 7.13 to get for any Borel set B

$$\begin{aligned} |\mathbf{W}^{0}\chi _E|(B\cap S_0)\le \mu _{ac} (B\cap S_0)\le \mu (B\cap S_0)\le \mu (B). \end{aligned}$$

To complete the proof of (5.6), we shall prove that

(7.5)

that yields

$$\begin{aligned} |\mathbf{W}^{0}\chi _E|(S_0^c) = 0, \end{aligned}$$

by [6], Lemma 5.2 (here $S_0^c$ denotes the complement of $S_0$).

In order to prove (7.5), we can write

$$\begin{aligned} S_0^c = \cup _{n=1}^\infty \{x\in M\; ; \; \Theta ^{*2n+1} (\mu _s,x) > \tfrac{1}{n}\}:= \cup _{n=1}^\infty T_n. \end{aligned}$$

Then

(7.6)

since

On the other hand

(7.7)

The set $\partial E\cap S_0^c\cap K^c\cap T_n$ is a Borel set, so that, by Federer’s differentiation theorem (see, e.g., [9] Theorem 2.4.3)

(7.8)

Combining (7.6), (7.7) and (7.8) we obtain eventually (7.5). This completes the proof of the theorem. $\square$