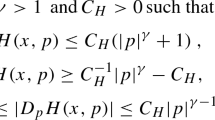Abstract
We are concerned with the well-posedness of Neumann boundary value problems for nonlocal Hamilton–Jacobi equations related to jump processes in general smooth domains. We consider a nonlocal diffusive term of censored type of order strictly less than 1 and Hamiltonians both in coercive form and in noncoercive Bellman form, whose growth in the gradient make them the leading term in the equation. We prove a comparison principle for bounded sub-and supersolutions in the context of viscosity solutions with generalized boundary conditions, and consequently by Perron’s method we get the existence and uniqueness of continuous solutions. We give some applications in the evolutive setting, proving the large time behaviour of the associated evolutive problem under suitable assumptions on the data.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The aim of this work is the analysis of the well-posedness of Neumann boundary value problems for partial-integro differential equations (PIDEs in short) of Hamilton–Jacobi type, where the nonlocal terms are singular integrals related to the infinitesimal generator of discontinuous jump processes. To be more specific, we consider the following
where \(H:\bar{\Omega } \times \mathbb {R}^N \mapsto \mathbb {R}\) is a continuous function, \(\Omega \subset \mathbb {R}^N\) is an open (smooth enough) domain, n(x) is the exterior unit normal vector to \(\partial \Omega \) at \(x \in \partial \Omega \) and \(\mathcal {I}[u]\) is an integro-differential operator of censored type and of order strictly less than 1 [see (1.2) for the definition].
In the probabilistic approach to PDEs, Neumann boundary conditions are associated to stochastic processes being reflected on the boundary. The underlying idea is to force the stochastic process to remain inside the domain of the equation. Classically, this is obtained essentially by a reflection on the boundary (see the method developed by Sznitman and Lions [25] in the continuous setting). A key result in the classical setting is that, for a PDE with Neumann boundary conditions, there is a unique underlying reflection process and any consistent approximation will converge to it (see [25] and Barles and Lions [10]).
When dealing with discontinuous jump processes, the underlying idea is the same but the situation is different. This is essentially due to the fact that the jump process may exit the domain without having first hit the boundary. The consequence is that Neumann boundary conditions can be obtained in many ways, depending on the kind of reflection we impose on the outside jumps. Moreover, the choice of a reflection on the boundary changes the equation inside the domain.
The starting point of our work is the paper [6] where Barles, Chasseigne, Georgeline and Jakobsen studied problems as in (1.1) in the case of linear equations (that is, without the Hamiltonian H) and when the domain \(\Omega \) is the half space. In [6] different models of reflection are presented, among which two types of reflections are particularly relevant for possible extensions in a more general setting. The first is the normal projection, close to the approach of Lions-Sznitman in [25], where outside jumps are immediately projected to the boundary by killing their normal component. This model has been thoroughly investigated in the paper [7] for fully non-linear equations set in general domains.
The second, the censored model, is the one we consider in our paper. In this case, any outside jump of the underlying process is cancelled (censored) and the process is restarted (resurrected) at the origin of that jump.
In particular, in the present work, we consider the boundary value problem (1.1) where \(\mathcal {I}[u]\) is an integro-differential operator of censored type and of order strictly less than 1 defined as
where \(\mu _x\) is a singular non-negative Radon measure representing the intensity of the jumps from x to \(x+z\) and satisfying the following integrability condition
and j(x, z) is a jump function (see assumptions (M), (J0), (J1) in the following section for details). A meaningful example is
where g, f are bounded and Lipschitz functions. Note that \(\mathcal {I}\) has to be interpreted as a principal value (P.V.) integral. We remark that the domain of integration is restricted to the z such that \(x+j(x,z) \in \bar{\Omega }\), avoiding thus any outside jump. Note also that, as a consequence of the fact that censored type processes are not allowed to jump outside \(\bar{\Omega }\), we don’t need any conditions on \(\Omega ^c\) in the boundary value problem (1.1).
We follow the PIDE analytical approach developed in [6], in the sense that we directly work with the infinitesimal generator and not yet with the processes themselves. For more details and probabilistic references on censored processes, we refer to e.g. [14, 21, 22, 24] and to the introduction of [6]. We just mention that the underlying processes in this paper are related to the censored stable processes of Bogdan et al. [14] and the reflected \(\sigma \)-stable process of Guan and Ma [22].
We stress that the boundary value problem (1.1) is interpreted in the sense of viscosity solutions, meaning that the Neumann boundary condition could also be not attained (and in this case the equation holds up to the boundary).
In the case of linear PIDES, as considered in [6], the kind of singularity of \(\mu \) influences the nature of the boundary value problem (1.1), in the sense that the Neumann boundary condition is attained only if the measure is singular enough. In particular in [6] it is shown that, when the singularity is of order strictly less than 1 as in (1.3), the equation holds up to the boundary and the process never reaches the boundary. On the other hand, when the singularity of the measure is strong, i.e. when \(\mu \) is of the type (1.3) with \(\sigma \in [1,2)\), the situation is far more complicated, mainly due to the “ugly” dependence in x of the operator in (1.2) and to the interplay between the singularity of the measure and the geometry of the boundary. In [6] this difficulty is tackled by considering solutions which are in some sense Hölder continuous up to the boundary and the comparison principle is established only in this class. Though the result could not be optimal, it is consistent with the “natural” Neumann boundary condition for the reflected \(\sigma \)-stable process (proved by Guann and Ma [22] through the variational formulation and Green type formulas) which in the case of the half space reads
This allows the normal derivative to growth less than \(|x_N|^{\sigma -2}\) and then suggests that it is appropriate to look for solutions which are \(\beta \)-Hölder continuous, with \(\beta >\sigma -1\), as assumed in [6]. We remark that the previous argument suggests also that, on the contrary, in the case \(\sigma <1\) there is no need to assume any further regularity.
The situation is different when dealing with nonlinear equations as (1.1), which we consider in this paper. Indeed, the presence of the Hamiltonian term H in (1.1) entails further difficulties even in the case of measures of order strictly less than 1 [e.g. as in (1.3)]. This is due to the fact that the nonlinear term H could force the process to hit the boundary and, consequently, the Neumann boundary condition to be attained.
In order to deal with this difficulty, we consider a class of Hamiltonians with a gradient growth stronger than the diffusive term in the nonlocal operator (1.2). The first example are Hamiltonians H with superfractional coercive growth in the gradient variable, namely
where \(m>\sigma \), \(\sigma \in (0,1)\), \(a, f \, : \bar{\Omega } \mapsto \mathbb {R}\) are bounded and continuous functions and \(a(x) \ge a_0>0\) for some fixed constant \(a_0\). We remark that the positivity of a and the condition \(m>\sigma \) make the first-order term the leading term in the equation. We also observe that we have no other additional restriction to m (in particular, we can deal with Hamiltonians as in (1.5) with \(m < 1\)), allowing the study of Hamiltonians which are concave in Du.
The second main example are Hamiltonians H of Bellman type, which arises in the study of Hamilton–Jacobi equations associated to optimal exit time problems, such as
where \(\mathcal {A}\) is a compact metric space (the control space) and b, l are continuous and bounded functions (we refer the reader to [2, 20] for some connections between this type of equations and control problems). Note that the diffusive term of \(\mathcal {I}\) defined in (1.2) is of weaker order than the first-order term when we assume \(\sigma < 1\). We also observe that, as in [13, 28], the well-posedness of (1.1) with Hamiltonians as in (1.6) is based on a careful study of the effects of the drift b at each point of \(\partial \Omega \times (0,+\infty )\). Note that the drift b is not allowed to be parallel to the boundary for all controls, differently from the local case. This assumption on b makes the Hamiltonian the leading order term in the equation and thus allows us to control the growth of the nonlocal term.
The main result of our paper is the comparison principle between bounded sub and super-viscosity solutions to (1.1), see Theorem 3.1. We remark that the proof of this result is not standard even in the case \(\sigma <1\) in the half space. The difficulties are mainly due to the fact that operators as in (1.2) behave badly in x. The main idea which is behind the proof is to localize the argument on points which have the same distance from the boundary and this is carried out through the use of a non-standard non regular test function. The main assumption which allows us to localize on equidistant points is the superfractional growth of the Hamiltonian term, see in particular the proof of Propositions 5.1 and 5.6 (more precisely, Lemmas 5.2, 5.7) for Bellman and coercive Hamiltonians respectively.
After the localization procedure, the rest of the proof in the case of the half space is simple, whereas in the case of general domains, further technical difficulties arise form the way the x-depending set of integration of \(\mathcal {I}\) interferes with the geometry of the boundary. To face these extra technical difficulties, we rectify the boundary relying on the smoothness of \(\Omega \). This is done in Lemma 4.1 which is a key result used in the proof of Theorem 3.1, which we prove before Theorem 3.1 in Sect. 4.
The first main application of our result is the proof of existence and uniqueness for (1.1), by standard Perron’s method (Corollary 3.2).
Then, in Sect. 6, we present some applications of our results to the evolutive setting. In particular, we prove the well-posedness of the Cauchy problem associated to (1.1) and we study two different kind of asymptotic behaviour under suitable assumptions on the data. We refer to Sect. 6 for precise assumptions, statement of the results and proofs.
Finally, we remark that in [13] Dirichlet boundary value problems associated to nonlocal Hamilton–Jacobi parabolic equations are studied. The main interest of [13] is to prove the well-posedness in the context of loss of the boundary condition, that is, in the case of Hamiltonians with dominating gradient terms, as the ones considered in the present paper. However, the nonlocal operators treated in [13] are very different from the censored operators (1.2) that we study here, since they are defined in all the space (and can therefore be seen as generalizations of the fractional laplacian). Moreover, differently from (1.1), in [13] also boundary conditions outside the domain are requested. This is strongly connected to the fact that here we consider Neumann boundary value problems with censored operators, that is, roughly speaking, we do not allow the process to jump outside the domain and therefore, no conditions outside is needed.
1.1 Organization of the paper
In Sect. 2 we state the assumptions on the nonlocal operator and the Hamiltonian and we give the definition of solution to problem (1.1). In Sect. 3 we state the main results, that is the uniqueness and existence for problem (1.1) for a Hamiltonian either coercive or of Bellman type (Theorem 3.1 and Corollary 3.2). In Sect. 4 we prove Lemma 4.1 and in Sect. 5 we prove Theorem 3.1. In Sect. 6 we treat the associated evolutive problem, studying uniqueness, existence and asymptotic behaviour of the associated evolutive problem for large time. Finally, in the “Appendix” we prove some lemmas used in the proof of Theorem 3.1.
2 Assumptions and definition of solutions
We consider \(\Omega \subset \mathbb {R}^N\) such that
This means that for any \(\hat{s} \in \partial \Omega \) there exists \(r=r(\hat{s})\) and a \(W^{2,\infty }\)-diffeomorphism \(\psi : B_r(\hat{s}) \mapsto \mathbb {R}^N\) satisfying \( \psi _N(s)=d(s) \, \text{ for } \text{ any } s \in B_r(\hat{s}), \) where d is the signed distance from the boundary of \(\Omega \).
Remark 1
By assumption (O), there exists a neighbourhood of the boundary of \(\Omega \) where the distance from the boundary d is smooth. Unless otherwise specified, throughout the paper we denote by d a function which coincides with the signed distance from the boundary of \(\partial \Omega \) in this neighbourhood and is bounded in all the domain. We recall that by n(x) we denote the exterior unit normal vector to \(\partial \Omega \) and we write \(n(x)=-Dd(x)\) in the neighbourhood of the boundary where d is smooth.
We consider non-negative Radon measures with density \(\frac{d\mu _x}{dz}\) satisfying
-
(M)
there exists \(C_\mu , D_\mu >0, \sigma \in (0,1)\) such that for any \(x,y \in \bar{\Omega }, z \in \mathbb {R}^N\)
$$\begin{aligned} \frac{d\mu _x}{dz}\le C_\mu |z|^{-(N+\sigma )}, \quad \left| \frac{d\mu _x}{dz}-\frac{d\mu _y}{dz}\right| \le D_\mu |x-y||z|^{-(N+\sigma )}. \end{aligned}$$
For example, (M) is satisfied by
where \(\sigma \in (0,1)\), \(g\, : \, \mathbb {R}^N \times \mathbb {R}^N \mapsto \mathbb {R}\) is a non-negative bounded function such that \(g(\cdot ,z)\) is Lipschitz uniformly with respect to z.
Concerning the jump function j we assume
-
(J0)
for any \(x \in \bar{\Omega }\), \( j(x,\cdot )\in C^1({\mathbb {R}}^N), \) \(j(x,\cdot )\) is invertible, \( j^{-1}(x,\cdot ) \in C^{1}(\mathbb {R}^N)\) and there exists a constant \(A_j\) such that
$$\begin{aligned} |Dj^{-1}(x,\cdot )|\le A_j \quad \forall x \in \bar{\Omega }; \end{aligned}$$ -
(J1)
there exist \(\tilde{C}_j,C_j, D_j>0\) such that for any \(x, y \in \bar{\Omega }, z \in \mathbb {R}^N \), it holds
$$\begin{aligned} \tilde{C}_j|z|\le |j(x,z)|\le C_j|z|, \quad |j(x,z)-j(y,z)|\le D_j|z||x-y|. \end{aligned}$$
For example (J0), (J1) are satisfied for
where \(f \, : \mathbb {R}^N \mapsto \mathbb {R}\) is Lipschitz and bounded.
2.1 Hamiltonian of Bellman type
Let \(\mathcal {A}\) be a compact metric space, \(b\, : \, \bar{\Omega } \times \mathcal {A} \rightarrow \mathbb {R}^N\) and \(f\, : \, \bar{\Omega } \times \mathcal {A}\rightarrow \mathbb {R}\) be continuous and bounded functions. We say that H is of Bellman type if for \(x \in \bar{\Omega }, p \in \mathbb {R}^N, H(x,p)\) can be written as
and satisfies the assumptions below. We assume also:
-
(C)
Uniform continuity of the cost l:
There exists a modulus of continuity \(\omega _l\) such that
$$\begin{aligned} |l(x,\alpha )-l(y,\alpha )|\le \omega _l(|x-y|) \quad \forall \alpha \in \mathcal {A}, \forall x, y \in \bar{\Omega }; \end{aligned}$$ -
(L)
Uniform Lipschitz continuity of the drift b:
$$\begin{aligned} (\exists C>0)\, (\forall \alpha \in \mathcal {A}) \, (\forall x,y \in \bar{\Omega }) \, \, :\, \, |b(x, \alpha )-b(y,\alpha )| \le C|x-y|. \end{aligned}$$
We introduce the following notation
Roughly speaking, \(\Gamma _{{\mathrm{in}}}\) and \(\Gamma _{{\mathrm{out}}}\) can be respectively understood as the set of points where the drift term pushes inside and outside \(\Omega \) the trajectories.
In order to avoid two completely different drifts behaviour for arbitrarily closed points, we assume that each of these subsets is uniformly away from the others, as encoded in the following assumption (B). For example, if \(\partial \Omega \) is connected, then it consists in one piece belonging to one of \(\Gamma _{{\mathrm{in}}}\), \(\Gamma _{{\mathrm{out}}}\) and \(\Gamma \); otherwise, we are able to deal with boundary with several components of different types, precisely each one belonging to one between \(\Gamma _{{\mathrm{in}}}\), \(\Gamma _{{\mathrm{out}}}, \Gamma \).
The assumptions we do on these subsets are the following
Remark 2
Note that the strict sign in the definition of \(\Gamma _{{\mathrm{in}}}, \Gamma _{{\mathrm{out}}} \) and \(\Gamma \) is fundamental, since it makes the Hamiltonian the leading order term in the equation, allowing us to control the growth of the nonlocal term, which is of order strictly less than 1.
Remark 3
In order to treat the points of \(\Gamma _{{\mathrm{in}}}\), we use the existence of a blow-up supersolution exploding on the boundary. We follow the same approach of [6], where the existence of a blow-up supersolution is proved for censored type operators (of order strictly less than 1) when the measure of integration satisfies specific assumptions (in particular does not depend on x and there exists at least one point where it is strictly positive). In this particular case it is shown in [6] that the integral term computed on the blow-up supersolution does not explode at the boundary. This is not true anymore when considering more general measures as we consider in (M). In order to solve this difficulty, we assume the strict sign in the behaviour of the drift term on \(\Gamma _{{\mathrm{in}}}\), which allows us to control the growth on the boundary of the integral term computed on this blow-up supersolution. We refer to the proof of Proposition 5.1 and in particular to Lemma 5.5 for further details.
2.2 Coercive Hamiltonian and examples
We consider superfractional coercive Hamiltonians:
-
(H1)
Let \(\sigma \) be as in (M). There exists \(m> \sigma , c_0>0,D>0\) such that for all \(x \in \bar{\Omega },p \in \mathbb {R}^N\)
$$\begin{aligned} H(x,p) \ge c_0 |p|^m -D. \end{aligned}$$
We distinguish the case of sub or superlinear coercivity:
Sublinear coercivity: We say that H is sublinearly coercive if it satisfies (H1) for \(m \le 1\) and the following continuity condition holds:
-
(Ha)
There exists a constant \(C>0\) and modulus of continuity \(\omega _1\) such that, for all \(x,y,q,p \in \mathbb {R}^N\), we have
$$\begin{aligned} H(y,p)-H(x,q) \le \omega _1(|x-y|)(1+|p|)+ C(|p-q|). \end{aligned}$$
Superlinear coercivity: We say that H is superlinearly coercive if:
-
(Hb)
There exists \(m> 1\),\(A, \bar{C}>0\) such that for all \(\mu \in (0,1), x,y,p \in \mathbb {R}^N\), we have
$$\begin{aligned} H(x,p)-\mu H(x,\mu ^{-1}p) \le (1-\mu )\left( \bar{C}(1-m)|p|^m +A\right) ; \end{aligned}$$ -
(Hc)
If m is as in assumption (Hb), there exist \(C>0\) and a modulus of continuity \(\omega _1\) such that, for all \(x,y, q,p \in \mathbb {R}^N\)
$$\begin{aligned} H(y,p)-H(x,q) \le \omega _1(|x-y|)(1+|p|^m\vee |q|^m)+ C|p-q|(|p|^{m-1}\vee |q|^{m-1}). \end{aligned}$$
Remark 4
Note that condition (Hb) implies (H1) for \(m>1\).
As it is classical in viscosity solution’s theory, the comparison principle allows the application of Perron’s method to conclude the existence of solutions. To this end, we introduce the following assumption, which will allows us to build sub and supersolutions:
-
(E)
There exists \(H_R>0\) such that for any \(p \in \mathbb {R}^N, |p|\le R\)
$$\begin{aligned}||H(\cdot ,p)||_\infty \le H_R. \end{aligned}$$
As a model example for sublinearly coercive Hamiltonians, we consider
with \(m\le 1, a_1\ge a_0>0\) for all \(x \in \Omega , l<m\) and \(a_1, a_2, f\, : \, \bar{\Omega } \mapsto \mathbb {R}\) are continuous and bounded functions and \(a_1,a_2\) are also Lipschitz continuous.
As a model example for superlinearly coercive Hamiltonian, we consider
with \(m>1, l \le m, b\) bounded and continuous and \(a_1,a_2, f\) as before.
These Hamiltonians are coercive in p and in the case \(m>1\) we can include transport terms with a Lipschitz continuous vector field \(b\,: \, \bar{\Omega } \mapsto \mathbb {R}^N\). The above assumptions are easily checkable in both cases.
2.3 Notion of viscosity solutions
We recall now the definition of solution to problem (1.1). We use the following notation:
where
The \(\mathcal {I}^\xi \)-term is well-defined for any bounded function \(\phi \). The \(\mathcal {I}_\xi \)-term is well-defined for \(\phi \in C^1\) thanks to (M0).
We also denote
Following the approach of [6], we give the definition of viscosity solution to (1.1). Let \(C_j\) be defined as in (J1).
Definition 2.1
-
(i)
A bounded usc function u is a viscosity subsolution to (1.1) if, for any test-function \(\phi \in C^1(\mathbb {R}^N) \) and maximum point x of \(u-\phi \) in \(\bar{B}_{C_j\xi }(x)\cap \bar{\Omega }\)
$$\begin{aligned}&F(x, u(x), D\phi (x), \mathcal {I}_\xi [\phi ]+\mathcal {I}^\xi [u]) \le 0 \quad x \in \Omega \\&\min \left\{ F(x,u(x), D\phi (x), \mathcal {I}_\xi [\phi ]+\mathcal {I}^\xi [u]),\frac{\partial \phi }{\partial n}\right\} \le 0 \quad x \in \partial \Omega . \end{aligned}$$ -
(ii)
A bounded lsc function v is a viscosity supersolution to (1.1) if, for any test-function \(\phi \in C^1(\mathbb {R}^N) \) and minimum point x of \(v-\phi \) in \(\bar{B}_{C_j\xi }(x)\cap \bar{\Omega },\)
$$\begin{aligned}&F(x, v(x), D\phi (x), \mathcal {I}_\xi [\phi ]+\mathcal {I}^\xi [v]) \ge 0 \quad x \in \Omega \\&\max \left\{ F(x,v(x), D\phi (x), \mathcal {I}_\xi [\phi ]+\mathcal {I}^\xi [v], \frac{\partial \phi }{\partial n}\right\} \ge 0 \quad x \in \partial \Omega . \end{aligned}$$ -
(iii)
A viscosity solution is both a sub- and a supersolution.
3 Main results
The main result of this part is the following comparison principle for the problem (1.1).
Theorem 3.1
(Comparison) Let \(\Omega \) be an open subset of \(\mathbb {R}^N\) satisfying (O). Assume (M), (J0), (J1). Let H be a Hamiltonian of Bellman type as in (2.2) satisfying (C), (L), (B) or a coercive Hamiltonian satisfying (H1), (Ha) or (H1), (Hb), (Hc). Let u be a bounded usc subsolution of (1.1) and v a bounded lsc supersolution of (1.1). Then \(u \le v\) in \(\bar{\Omega }\).
Once the comparison holds, we use the Perron’s method for integro-differential equations (see [1, 8, 19, 23, 26] for an introduction on the method) to get as a corollary existence and uniqueness for the problem (1.1) either when H is of Bellman type either for H coercive.
Corollary 3.2
(Existence and Uniqueness) Let \(\Omega \) be an open subset of \(\mathbb {R}^N\) satisfying (O). Assume (M), (J0), (J1)- Let H be either a Hamiltonian of Bellman type as in (2.2) satisfying (C), (L), (B) or a coercive Hamiltonian satisfying (H1), (Ha) or (H1), (Hb), (Hc). Assume (E). Then, there exists a unique bounded viscosity solution to problem (1.1).
4 A preliminary key lemma
We prove the following Lemma 4.1, which is a key result used in the proof of Theorem 3.1. Roughly speaking, it deals with the difficulties arising from the way the geometry of the boundary interferes with the singularity of the nonlocal terms. The scope is to estimate the nonlocal terms defined in (4.1) on points near the boundary and equidistant from it. The approach of the proof is essentially based on a rectification of the boundary, relying on its regularity.
Remark 5
In the case of domains with flat boundary, we do not need Lemma 4.1 in the proof of Theorem 3.1 since the estimation of the nonlocal terms can be carried out more easily. We refer to Remark 7, step 4 of the proof of Theorem 3.1.
For any \(\hat{s} \in \partial \Omega \), let \(r=r(\hat{s})\) and \(\psi : B_r(\hat{s}) \mapsto \mathbb {R}^N\) a \(W^{2,\infty }\)-diffeomorphism as defined in assumption (O). For \(s_1, s_2 \in B_{\frac{r}{2}}(\hat{s})\cap \bar{\Omega }\), let
where \( J_{s}=\{z \in {\mathbb {R}}^N \, |\, s+j(s,z) \in \bar{\Omega }\}, \) j satisfies assumptions (J0),(J1), \(\sigma \in (0,1)\) and \(0<\delta _0<rC_j^{-1}/2\), where \(C_j\) is the constant defined in (J1).
Lemma 4.1
Let \(\mathcal {I}[J_{\cdot }/J_{\cdot }]\) as in (4.1) and assume j satisfies (J0), (J1). Let \(\hat{s} \in \partial \Omega \), r given as above and \(s_1, s_2\) satisfying
Then there exists a positive constant C such that
Proof
Step 1. Rectification of the boundary.
We observe that since \(s_1,s_2 \in B_{\frac{r}{2}}(\hat{s})\cap \bar{\Omega }, \delta _0<rC_j^{-1}/2\) and by (J1), we have for any \(|z|\le \delta _0\)
By assumption (O), we describe the domain of integration of \(\mathcal {I}[J_{s_1}/J_{s_2}]\) through the diffeomorphism \(\psi \) as follows
We observe that by assumption (O) and (4.2), we have
We proceed performing a change of variable in order to write the set of integration in terms of \(\psi _N(s_1)\). In other words, we write
that is, \( j(s_1,z)=\psi ^{-1}\left( \psi (s_1)+w\right) -s_1. \) By (4.8), we write (4.5) as follows
Moreover, by (J1), (O) and since \(\psi \in W^{2,\infty }\), we get
Similarly one can prove an analogous upper bound for |w|, getting
for some constants \(\hat{C},\tilde{C}\) depending on the Lipschitz constants of \(\psi , \psi ^{-1}\) and on \(\tilde{C}_j, C_j\) of (J1).
In the following step, we rewrite the set of integration of \(\mathcal {I}[J_{s_1}/ J_{s_2}]\) in a different way using the change of variable (4.8) and the previous estimates.
Step 2. Rewriting the set of integration. By (4.8) and if \(\psi _N(s_2+j(s_2,z))\le 0\), we have
For convenience of notation, let for the moment
Note that \( s(0)+\zeta (0)=s_1+j(s_1,z)\), \(s(1)+\zeta (1)=s_2+j(s_2,z). \) Then, since \(\psi \in W^{2,\infty }\) and by (4.12) we write
where
From now on we denote by C any positive constant which may change from line to line. By definition of \(\zeta (t)\)
Then, by (4.14), (J1) and (4.10) we get
Now we analyse \(A_2\). Note that by (4.13) and (4.7)
Moreover, since \(\psi \in W^{2,\infty }\), by (J1) and (4.10)
Then we have \( A_2\le C|w||s_1-s_2|. \) We denote \( a=\psi _N(s_1) \) and observe \( a\ge 0. \) By (4.9) and the previous arguments, we get
Then, we perform the change of variable in \(\mathcal {I}[J_{s_1}/J_{s_2}]\) by (J0), (J1) and using that \(\psi \in W^{2,\infty }\) and by (4.15) and (4.11), we get
where
and \(\bar{C}, \tilde{C}, C\) are positive constants, which we suppose \(\bar{C}=\tilde{C}=C=1\), by no loss of generality and for simplicity of exposition.
Step 3. Estimate on \(\tilde{D}\). We introduce the following notation:
Note that by the second assumption in (4.2), \(|s_1-s_2|\le r\). Without loss of generality we can suppose \(r\le \frac{1}{2}\), so that we have \(|s_1-s_2|\le 1/2\). Then
Note that, if \(w \in \tilde{D}\), then
We identify two cases, depending on the sign of \(-a+|s_1-s_2||w'|\) and we denote
and
Observe that, if \(w\in \tilde{D} \cap D_2\), then \( -a+|s_1-s_2||w'|< 0 \) and (4.19) implies \( w_N < 0 \) and in particular \( -a\le w_N\le -\beta a+\beta |s_1-s_2||w'|< 0. \) Otherwise, if \(w \in \tilde{D}\cap D_1\), then \( -a+|s_1-s_2||w'|\ge 0 \) and \(w_N\) can assume both negative and positive values. In particular (4.19) implies \( -a\le w_N\le -da +d|s_1-s_2||w'|. \) Note also that \(-da +d|s_1-s_2||w'|\ge 0\).
By all the previous observations, we write
where
For \(\mathcal {F}_1\), we use that \( \frac{1}{|w'|^2+|w_N|^2}\le \frac{1}{|w'|^2} \) and by Fubini’s Theorem, we integrate in the N-variable and we get
By the first of (4.17) and (4.18) and since \(da \ge 0\), we have \( -da +d|s_1-s_2||w'|+a=-da|s_1-s_2|+d|s_1-s_2||w'|\le 2|s_1-s_2||w'|. \) Therefore
From now on we denote by C any positive constant which may change from line to line. Note that, since \(w' \in \mathbb {R}^{N-1}\) and \(\sigma <1\), we have
Then by the previous observations, we get
Now we analyse \(\mathcal {F}_2\). For simplicity of notation, we denote
and then, by Fubini’s Theorem, we have
We split the domain as follows
We estimate the first term by
where in the first inequality we used that \( -\beta a+\beta |s_1-s_2||w'|+a\le 2|w'||s_1-s_2|, \) since \(\beta \le 1\) and \(a\le |w'|\), and in the second inequality we used (4.23).
Take now the second term in (4.26). Note that, if \(a > |w'|\), by (4.17) and (4.18), we have \( -\beta a+\beta |s_1-s_2||w'|\le -\beta a d^{-1}\le -a4^{-1}\le 0. \) By all the previous observations, since the function \( w_N \mapsto \frac{1}{\left( |w'|+w_N^2\right) ^{\frac{N+\sigma -1}{2}}} \) is increasing on the negative half line, we have
Then
and coupling (4.28) and (4.29), we get
Then coupling (4.25), (4.26), (4.27) and (4.30), we obtain
and we conclude the proof by coupling (4.16), (4.20), (4.24) and (4.31). \(\square \)
5 Proof of the comparison principle
We prove Theorem 3.1 and we split the proof into two parts, depending whether H is of Bellman type or coercive.
5.1 Hamiltonians of Bellman type
The proof of Theorem 3.1 follows mainly by the following proposition, which we prove first. At the end of the proof of Proposition 5.1, we will prove Theorem 3.1.
Proposition 5.1
Let \(\Omega \) be an open subset of \(\mathbb {R}^N\) satisfying (O). Let \(\mathcal {I}\) as in (1.2) and assume \(\mu \) satisfies (M), j satisfies (J0), (J1). Let H be a Hamiltonian of Bellman type as in (2.2) satisfying (C), (L), (B) and let u, v be respectively bounded sub and supersolutions to (1.1). Then the function
satisfies, in the viscosity sense, the equation
where B is a positive constant depending on the data.
Proof
Let \(x_0\in \bar{\Omega }\) and \(\phi \in C^1(\mathbb {R}^N)\) such that \(\omega -\phi \) has a maximum point at \(x_0\) in \(\bar{B}_{C_j \xi }(x_0) \cap \bar{\Omega }\) for some \(0<\xi <1\). Note that the restriction \(\xi <1\) is only for simplicity of exposition. We can suppose that \(x_0\) is a strict maximum point by considering \(\tilde{\phi }=\phi (x)+ k|x-x_0|^2\) for k sufficiently large. In particular, note that we have the following property
From now on, we consider the test function \(\tilde{\phi }\) and we still denote it by \(\phi \), with some abuse of notation. We observe that if \(x_0 \in \Omega \) the proof is rather standard, since in this case the maximum points (x, y) of \(u-v-\phi \) converge as \(\varepsilon \rightarrow 0\) to \((x_0,x_0)\) and hence they are bounded away from the boundary for \(\varepsilon \) small enough. This last property implies that we can directly use the equations and then proceed as in the following case.
Let \(\Gamma _{{\mathrm{in}}}, \Gamma _{{\mathrm{out}}}, \Gamma \) be defined respectively in (2.3), (2.4) and (2.5) and recall they satisfy (B). We suppose \(x_0 \in \partial \Omega \) and we split the proof depending if
-
(a)
\( x_0\in \Gamma _{{\mathrm{in}}}; \)
-
(b)
\(x_0 \in \Gamma _{{\mathrm{out}}};\)
-
(c)
\(x_0\in \Gamma .\)
In case (a) we use the existence of the blow-up supersolution which explodes at the boundary and allows us to keep the maximum points far from the boundary. Since the proof in this case is inspired by a similar approach used in [6], we give the details at the end of the proof of (b) and (c) in Remark 9. Now we treat case (b) and (c). Since the proofs are similar, we treat them at the same time.
We suppose that
and prove that the F-viscosity inequality of Definition 2.1 hold for \(\omega \).
Step 1. Localising on equidistant points (that is, \(d(x)=d(y)\) ). Let \(\varepsilon >0\) and d be a function as in Remark 1. We double the variable by introducing the function for \(\varepsilon , \delta >0\)
where \(\chi _\varepsilon : \, \mathbb {R}\rightarrow \mathbb {R}\) (and similarly \(\chi _\delta \)) is defined as follows
and \(K>0\) is a constant large enough such that
where \(\gamma , C_2>0\) depend on \(x_0\) and are precisely defined in Lemma 6.10 in the “Appendix” (for \(\hat{s}=x_0\)). Let
and denote by \((\bar{x}, \bar{y})\) the maximum point of \(\Phi \) in \(\bar{B}_{2C_j\xi '}(x_0)\cap \bar{\Omega } \times \bar{B}_{2C_j\xi '}(x_0)\cap \bar{\Omega }\) for \(0<\xi '<\frac{\xi }{2}\). We observe that \((\bar{x}, \bar{y})\) depends now also on \(\delta \) and we omit the dependence.
Now consider
where
where d is the signed distance from the boundary (see Remark 1), \(\chi _\varepsilon \) is defined as in (5.4) and K is as in (5.5). Note that the test function in (5.8) is not differentiable on the points such that \(d(x)=d(y)\). By upper-continuity, \(\Psi \) in (5.7) attains its maximum over
at a point (x, y). By classical arguments in viscosity solution theory, we get as \(\varepsilon \rightarrow 0\)
and \( u(x)-v(y)-\tilde{\psi }(x,y)\rightarrow u(x_0)-v(x_0)-\phi (x_0). \) Note also that by the second of (5.9), it directly follows
We prove the following key lemma.
Lemma 5.2
Under the above notation, we have
-
(i)
\(\bar{x} \rightarrow x, \, \,\bar{y} \rightarrow y, \,\, u(\bar{x})\rightarrow u(x), \,\, v(\bar{y}) \rightarrow v(y)\,\, \text{ as } \delta \rightarrow 0;\)
-
(ii)
\(d(x)=d(y)\);
Proof
Note that (i) follows by classical argument in viscosity solution theory. We remark that the proof of (ii) is slightly different in case (b) and case (c). We argue by contradiction and we suppose that \(d(x)\ne d(y)\). First we prove that the F-viscosity inequalities for u and v of Definition 2.1 hold. Suppose that \(x \in \partial \Omega \), then \(d(x)=0\) and \(d(y)\ne 0\). We denote
and we write
Note that
Note that by (5.9), we can suppose that x, y are close to the boundary, by taking \(\varepsilon \) small enough. By the Taylor’s formula for the distance function, we have for \(\varepsilon \) small enough
and then
By (5.11), (5.13), (5.14) and (5.9), we have
Note that, from (5.2), for \(\varepsilon \) small enough we have also
By (5.12), (5.16), (5.15) and since \(K\ge 0\), we conclude for \(\varepsilon \) small enough
Then, since u is a viscosity subsolution and the function \(u(\cdot )-v(y)-\psi (\cdot ,y)\) has a local maximum at x, the F-viscosity inequality of Definition 2.1 (i) holds. A similar argument can be carried out for v. From now on, we treat separately Case (b) (\(x_0\in \Gamma _{{\mathrm{out}}}\)) and Case (c) (\(x_0\in \Gamma \)).
Case (b) In this case \(x_0\in \Gamma _{{\mathrm{out}}}\), where \(\Gamma _{{\mathrm{out}}}\) is defined in (2.4). Suppose \(d(x)>d(y)\). Then, by Definition 2.1 (i) and by (5.17), we have
Note that
where \(\hat{p}\) is defined in (5.11) and
We apply Lemma 6.10, (6.17) with \(\hat{s}=x_0\), \(p=\varepsilon ^{-1}\chi '_\varepsilon (|x-y|)\hat{p}+q\) and \(\lambda =\varepsilon ^{-1}K\) and by the definition (5.5) of K, we get for \(\varepsilon \) small
where by C, here and in the following, we denote any positive constant independent of \(\varepsilon \) which may change from line to line. To estimate the nonlocal terms we use the following lemma, which we prove in the “Appendix”.
Lemma 5.3
Let \(\mathcal {I}^\xi , \mathcal {I}_\xi \) be as in (2.7), (2.6) and assume the first of (M) and (J1). Under the above notation, for any \(\xi >0\), there exist a positive constants \(C_1\) independents of \(\varepsilon \) such that
-
(i)
\(-\mathcal {I}_\xi [\psi (\cdot , y)](x)-\mathcal {I}^\xi [u](x) \ge -\varepsilon ^{-1}C_1\xi ^{1-\sigma }-C_1\xi ^{-\sigma };\)
-
(ii)
\(-\mathcal {I}_\xi [\psi (x, \cdot )](y)-\mathcal {I}^\xi [v](y) \le \varepsilon ^{-1}C_1\xi ^{1-\sigma }+C_1\xi ^{-\sigma }.\)
Then, by (5.20), by Lemma 5.3 (i) with \(\xi '=\varepsilon \) and by the boundedness of u, we write (5.18) as follows
and we reach a contradiction for \(\varepsilon \) small enough, since C is independent of \(\varepsilon \) and \(\sigma <1\).
Now suppose \(d(x) <d(y)\). In this case we use the following F-viscosity inequality for the supersolution v
We have
where \(\hat{p}\) is defined in (5.11) and q is defined in (5.19). Then , for \(\varepsilon \) small enough, we apply Lemma 6.10, (6.18) with \(\hat{s}=x_0\), \(p=\varepsilon ^{-1}\chi '_\varepsilon (|x-y|)\hat{p} -q\) and \(\lambda =\varepsilon ^{-1}K\) and by (5.5) we get
We proceed as in the previous case, we apply Lemma 5.3 (ii) with \(\xi =\varepsilon \) and by (5.22) and the boundedness of v , we get
and we reach a contradiction for \(\varepsilon \) small enough as above.
Case (c) In this case \(x_0\in \Gamma \), where \(\Gamma \) is defined in (2.5). If \(d(x)>d(y)\) the proof is the same. If \(d(x)<d(y)\) we write again Eq. (5.18) and since
where \(\hat{p}\) is defined in (5.11), we apply Lemma 6.10 (6.20) with \(\hat{s}=x_0\), \(p=\varepsilon ^{-1}\chi '_\varepsilon (|x-y|)\hat{p}+q\) and \(\lambda =\varepsilon ^{-1}K\), for \(\varepsilon \) enough small, and we conclude as above. \(\square \)
Step 2. Writing the viscosity inequalities.
By (5.9) and Lemma 5.2 (i), from now on we consider \(\delta , \varepsilon \) small enough so that
Now we prove that the F-viscosity inequalities for u and v hold. We take \(\bar{x} \in \partial \Omega \) and we show that the boundary conditions do not hold, so the F-viscosity inequalities hold as in Definition 2.1. We proceed exactly as in Step 1, Lemma 5.2, so we omit the details. We recall that for all \(\delta >0\)
and we note only that since \(d(\bar{x})=0\), we have for \(\varepsilon , \delta \) small enough
where \(o_{\delta ,\varepsilon }(1)\) means that \(\lim _{\delta \rightarrow 0}o_{\delta ,\varepsilon }(1)=o_\varepsilon (1)\). Then we have
Since \(\tilde{\phi } \in C^1\), by (J1) and the first of (M), we have
where \(C_j\) is as in (J1) and \(o_{\xi '}(1)\) is independent of \(\delta \). The same holds for \(-\mathcal {I}_{\xi '}[-\tilde{\phi }(\bar{x},\cdot )](\bar{y})\).
Note that
where
For \(\delta , \varepsilon \) small enough, we suppose that \(\bar{x},\bar{y}\) belong to the neighbourhood of the boundary where the distance is smooth. By (5.24) and the smoothness of the distance function we have
By the definition of H and (5.29), we have
where \(B=\sup _{{x\in \bar{\Omega }, \alpha \in \mathcal {A}}}b(x,\alpha )\). Moreover by (C), (L), we have
and since
we get
where \(C>0\) is a constant depending on B, K and \(||D\phi ||_{L^\infty (B_{C_j}(x_0))}\). By coupling (5.30), (5.32), (5.10) and (i) of Lemma 5.2, we get
where \(o_{\delta , \varepsilon }(1)\) means \(\lim _{\delta \rightarrow 0} o_{\delta , \varepsilon }(1)=o_{\varepsilon }(1)\). Plugging (5.33) and (5.26) into (5.25), we get
Step 3. Sending \(\delta \rightarrow 0\). We want to send first \(\delta \rightarrow 0\) in (5.34) and we observe that the nonlocal terms are uniformly bounded in \(\delta \). Consider \(\mathcal {I}^{\xi '}[u](\bar{x})\), observing that the same argument works similarly for \(\mathcal {I}^{\xi '}[v](\bar{y})\). Note that by (5.23) and (J1), if \(|z|< 1\), then \(\bar{x}+j(\bar{x},z) \in B_{2C_j\xi '}(x_0)\). Since \((\bar{x},\bar{y})\) is a maximum point on \(\bar{B}_{2C_j\xi '}(x_0)\cap \bar{\Omega } \times \bar{B}_{2C_j\xi '}(x_0)\cap \bar{\Omega }\) of \(\Phi \) defined in (5.6), we have for \(\delta , \varepsilon \) small
Note that \(\chi _\delta \) is Lipschitz with Lipschitz constant independent of \(\delta \) thanks to (5.24). Then, by the definition of \(\tilde{\phi }\), since \(\chi _\varepsilon , \chi _\delta , \phi \) are Lipschitz and by (J1), we have
which, by the first of (M), gives the uniform boundedness in \(\delta \) of \(\mathcal {I}^{\xi '}[u](\bar{x})\) when \(|z|<1\). When \(|z|\ge 1\), the claim simply follows by the boundedness of u and the first of (M).
Then, we send \(\delta \rightarrow 0\) in (5.34) and, by the semicontinuity and boundedness of u and v and Lemma 5.2 (i), apply Fatou’s Lemma and we get
In the next step, we estimate the nonlocal terms by bounds independent of the parameter \(\xi '\) small. Indeed, at the end of the proof, we will send first \(\xi '\rightarrow 0\) and then \(\varepsilon \rightarrow 0\). Note also that now, thanks to Lemma 5.2 (ii), we have that \(d(x)=d(y)\).
Step 4. Estimate of the nonlocal terms. We prove the following lemma.
Lemma 5.4
Under the above notation, we have
where \(\mathcal {K}^\xi , \mathcal {P}_\xi \) are as in (5.47) and (5.48) and \(C>0\) is independent of all the parameters.
Remark 6
In the proof of Lemma 5.4, we deeply rely on the assumption \(\sigma \in (0,1)\).
Proof
For simplicity of exposition, we first conclude the proof when the measure \(\mu \) in the nonlocal terms has no dependence on x, i.e. \(\mu _x\equiv \mu \). We refer to Remark 8 for details in the case of x-dependence. We write
where \( J_x=\{z\in \mathbb {R}^n \, | \, x+j(x,z) \in \bar{\Omega }\}\) and
Consider \(\mathcal {T}^{\xi '}[J_x\cap J_y]\). Recall that \((\bar{x},\bar{y})\) satisfy for any \( x',y' \in \bar{B}_{2C_j\xi '}(x_0)\cap \bar{\Omega } \times \bar{B}_{2C_j\xi '}(x_0)\cap \bar{\Omega }\)
Letting \(\delta \rightarrow 0\) in (5.42), by (i) of Lemma 5.2, the definition of \(\tilde{\phi }\) and the semicontinuity of u, v, we get for any \( x',y' \in \bar{B}_{2C_j\xi '}(x_0)\cap \bar{\Omega } \times \bar{B}_{2C_j\xi '}(x_0)\cap \bar{\Omega }\)
If \(|z|< 1\), then by (5.23) and (J1), \(x+j(x,z),y+j(y,z) \in B_{2C_j\xi '}(x_0)\). Then we write (5.43) for \(x'=x+j(x,z), y'=y+j(y,z)\) and we have
Note that by the Lipschitz continuity of \(\chi _\varepsilon \), (J1) and (5.9), we have
where \(D_j\) is defined in (J1) and then
Then by (5.45) and the first of (M), we get
where \(o_{\varepsilon }(1)\) is independent of \(\xi '\) and
and
by (J1), the first of (M) and the Lipschitz character of \(\phi \).
Now we consider the term \(\mathcal {I}^{\xi '}[J_x/J_y]\), defined in (5.40), observing that the same argument works similarly for \(\mathcal {I}^{\xi '}[J_y/J_x]\). Take \(0<\delta _0<1\) enough small (note that \(\delta _0\) will be defined more precisely at the end of the proof of Lemma 5.38). We split the domain of integration in \(\{z\, : \, |z|\ge \delta _0\}\) and \(\{z\, : \, \xi ' \le |z|\le \delta _0\}\). We write
where
By the boundedness of u, we have
and since \(|J_x/J_y|\rightarrow 0\) as \(\varepsilon \rightarrow 0, \) by the first of (M) and the Dominated Convergence theorem, we get
where \(o_\varepsilon (1)\) is independent of \(\xi '\). For \(\mathcal {I}^{\xi '}[B_{\delta _0}]\) we use again the maximum point inequality (5.43) with \(x'=x+j(x,z), y'=y\) and since \(\phi \in C^1\) and by (J1), the first of (M), we get
where we remark that \(C>0\) is independent of all the parameters. We couple (5.39), (5.46), (5.49), (5.50), (5.51) and (5.52) with (5.39) and we get
where for all \(x,y \in \mathbb {R}^N\), we denote
Now we estimate the term in (5.54) by Lemma 4.1. Let \(r:=r(x_0)\), where \(r(x_0)\) is defined in assumption (O) for \(\hat{s}=x_0\). Take \(rC_j^{-1}/2>\delta _0\). Note that, by (5.23), (x, y) satisfy (4.2) for \(\hat{s}=x_0\) and \(r=r(x_0)\). Then we apply Lemma 4.1 by taking \(\{s_1,s_2\}=\{x,y\},\hat{s}=x_0\) in order to estimate \(\mathcal {I}^{\xi '}[J_{x}/J_{y}],\mathcal {I}^{\xi '}[J_{y}/J_{x}]\) defined in (5.54) and we get
Then the claim of the lemma follows by plugging (5.55) into (5.53). \(\square \)
Note that Lemma 4.1 is not necessary when dealing with domains with flat boundary. In the following remark we consider the case when \(\Omega \) is the half space and we show how the estimate of the nonlocal terms can be carried out more easily without Lemma 4.1.
Remark 7
Take \( \Omega := \{(x_1, \cdots , x_N=(x',x_N) \in \mathbb {R}^N\, : \, x_N >0\}. \) For simplicity, we suppose that \( j(x,z)=z \text{ if } x+z\in \bar{\Omega }. \) Note that (i),(ii) of Lemma 5.2 read
Consider the nonlocal terms in (5.25) and restrict ourselves to a subsequence such that \(\bar{x}_N \ge \bar{y}_N\) (if \(\bar{x}_N \le \bar{y}_N\) the argument is similar). Then we can write
where in the last line we used the same notation as in the previous step, see in particular (5.40), (5.41). The term \(\mathcal {T}^{\xi '}[J_{\bar{x}}\cap J_{\bar{y}}]\) is treated exactly as in the non flat case (see the previous step). On the contrary, note that in this case the estimate of the term \(\mathcal {I}^{\xi '}[J_{\bar{x}}/J_{\bar{y}}]\) is easier, since by (5.56) \( |J_{\bar{x}}/J_{\bar{y}}|\rightarrow 0\) as \( \delta \rightarrow 0 \) and then by the Dominated Convergence Theorem, we have \( \mathcal {I}^{\xi '}[J_{\bar{x}}/J_{\bar{y}}]\rightarrow 0 \) as \( \delta \rightarrow 0. \)
Step 5. Sending the other parameters to their limits. We couple (5.37) with (5.38) and we get
where \(C>0\) is independent of the parameters. Then, we first send \(\xi ' \rightarrow 0\) by the Dominated Convergence Theorem and we get
where C is a constant independent of \(\xi \). Moreover, since \(\phi \) is \(C^1\), by the first of (M), the Dominated Convergence Theorem and since \(x,y \rightarrow x_0\) as \(\varepsilon \rightarrow 0\), we have
and by the boundedness and semicontinuity of u, v and Lemma 5.2 (i), we apply Fatou’s lemma for each \(\xi >0\) fixed and we get
and, by the previous estimates, we conclude by sending \(\varepsilon \rightarrow 0\) in (5.57). \(\square \)
Remark 8
We give some details of the analysis of the nonlocal terms in step 4 when the measure \(\mu \) depends on x. We write (5.39) with
For \(\mathcal {I}^{\xi '}[J_x/J_y]\) and \(\mathcal {I}^{\xi '}[J_y/J_x]\) we proceed as above (Step 4), noting that the x-dependence plays no role by the first of (M). For the \(\mathcal {T}\)-term, we write
where
For \(\mathcal {T}^{\xi '}_1[J_x\cap J_y]\), we proceed as above (in Step 3, for \(\mathcal {T}^{\xi '}[J_x\cap J_y]\) defined in (5.41)) and we prove (5.46). Now consider \(\mathcal {T}^{\xi '}_2[J_x\cap J_y]\) and denote
where
For \(\mathcal {T}^{\xi '}_2[B_\xi ]\) we use the maximum point inequality (5.43) and we write for \(|z|\le \xi \)
Then by the Lipschitz continuity of \(\chi _\varepsilon \) and \(\phi \), (J1), (M) and (5.9) we get
where we observe \(o_\varepsilon (1)\) is independent of \(\xi '\) and from now on may change from line to line in the following. For \(\mathcal {T}^{\xi '}_2[B_{\xi }^c]\), by the boundedness of u, (M), (5.9), we get
Then, by (5.59) and (5.60), we get
where \(o_\varepsilon (1)\) is independent of \(\xi '\). From now on the proof is the same as above.
Remark 9
We give the details of the proof of Proposition 5.1 in case (a), when \(x_0\in \Gamma _{{\mathrm{in}}}\) is a strict maximum point of \(\omega -\phi =u-v-\phi \) in \(\bar{B}_{Cj\xi }(x_0)\cap \bar{\Omega }\), for \(\phi \in C^1({{\mathbb {R}}^N})\) and some \(0<\xi <1\).
The strategy of the proof relies on the existence of a blow-up supersolution exploding on the boundary, which allows us to keep the maximum points away from the boundary. The existence of such a supersolution is stated in the following lemma, whose proof is given in the “Appendix”.
Lemma 5.5
For any \(\bar{x} \in \Gamma _{{\mathrm{in}}}\), there exists \(r=r(\bar{x})>0\) and a positive function \(U_{r} \in C^2(B_{r}(\bar{x})\cap \Omega )\) satisfying for any \(\xi \) small enough (with respect to r, that is, \(\xi <C_j^{-1}\frac{r}{2}\))
-
(i)
\( -b(x,\alpha )\cdot DU_r -\mathcal {I}_\xi [U_r](x)\ge 0 \quad \text{ in } B_{\frac{r}{2}}(\bar{x})\cap \Omega , \quad \forall \alpha \in \mathcal {A}; \)
-
(ii)
\( U_r(x)\ge \frac{1}{\omega _{r}(d(x))} \quad \text{ in } B_{r}(\bar{x}) \cap \Omega , \) for some function \(\omega _{r}\) which is non-negative, continuous, strictly increasing in a neighbourhood of 0 and satisfies \(\omega _r(0)=0\).
Proof of case (a)
Let \(r=r(x_0)\) be defined in Lemma 5.5 for \(\bar{x}=x_0\). We localize the argument in a ball of radius r around \(x_0\) and we use the existence of the blow-up function \(U_r\) defined in Lemma 5.5 for \(\bar{x}=x_0\). Let \(0<\xi '<\min \{\xi , C_j^{-1}\frac{r}{4}\}\) and \(\varepsilon >0\). We double the variable and we consider (x, y) maximum point on \(\bar{B}_{C_j \xi '}(x_0)\cap \bar{\Omega } \times \bar{B}_{C_j\xi '}(x_0)\cap \bar{\Omega }\) of the function \( \Phi (x,y)= u(x)-v(y)-\tilde{\phi }(x,y), \) where
Note that, by (ii) of Lemma 5.5, we have that \((x,y)\in \bar{B}_{C_j\xi '}(x_0)\cap \Omega \times \bar{B}_{C_j\xi '}(x_0)\cap \Omega \); moreover, again by (ii) of Lemma 5.5, we have for k small enough
where \( L=||u||_{L^\infty (\bar{B}_{C_j}(x_0)\cap \bar{\Omega })}+||v||_{L^\infty (\bar{B}_{C_j}(x_0)\cap \bar{\Omega })}+||\phi ||_{L^\infty (\bar{B}_{C_j}(x_0)\cap \bar{\Omega })}+1. \) Note that the existence of the blow-up function plays its mayor role here to get (5.62). This estimate tells us, roughly speaking, that the maximum points are away from the boundary. For fixed k, a standard argument shows that
By the previous estimate on x, y and extracting subsequences if necessary, we can assume, without loss of generality, that as \(\varepsilon , k \rightarrow 0\)
Thanks to (5.64), we can take \(\varepsilon ,k\) small enough so that \(x,y \in B_{\frac{r}{4}}(x_0)\cap \Omega \). We proceed as in Step 2 in the above proof, we write the viscosity inequalities (5.25) and, using that \(\tilde{\phi } \in C^1\), (J1) and the first of (M), we get
where \(\lim _{\xi '\rightarrow 0} o_{\xi '}(1)=0\) for each k fixed and \(o_{\xi '}(1)\) is independent of \(\delta \). First we analyse the term \(\mathcal {I}^{\xi '}[u](x)-\mathcal {I}^{\xi '}[v](y)\). For simplicity of exposition, we conclude the proof in the case the measure \(\mu \) in the nonlocal terms has no dependence on x, i.e. \(\mu _x\equiv \mu \). The result can be easily extended in the case of x-dependence analogously as already shown in Remark 8 for case (b) and (c). We use the same notation of Proposition 5.1, see (5.40), (5.41) and we write
As in the proof of Proposition 5.1, the term \(\mathcal {T}^{\xi '}[J_x\cap J_y]\) can be estimated as follows
where we use the notation (5.47), (5.48) of Proposition 5.1. Note that \(o_{\varepsilon }(1)\) is independent of \(\xi '\). Since \(U_r\) is Lipschitz, by (J1) and the first of (M), we have \( \mathcal {I}_{\xi '}[U_r](x), \mathcal {I}_{\xi '}[U_r](y)\le o_{\xi '}(1), \) and then
where \(o_\varepsilon (1)\) is independent of \(\xi '\). Now we estimate the terms \(\mathcal {I}^{\xi '}[J_x/J_y]\) and \(\mathcal {I}^{\xi '}[J_y/J_x]\). Thanks to (5.62), in this case the estimate is easier than in the cases (b) and (c) treated above. Take for example \(\mathcal {I}^{\xi '}[J_x/J_y]\) (the argument being analogous for \(\mathcal {I}^{\xi '}[J_y/J_x]\)) and note that by (5.62) the integral is independent of \(\xi '\) as soon as \(\xi '<\bar{\delta }\) where \(\bar{\delta }\) is defined in (5.62). Then by the boundedness of u, we have
and since \( |J_x/J_y|\rightarrow 0 \text{ as } \varepsilon \rightarrow 0, \) by the first of (M), the Dominated Convergence theorem, we get
where \(o_\varepsilon (1)\) is independent of \(\xi '\). Then plugging (5.68) and (5.67) into (5.66) and then coupling it with (5.65), we get
where \(o_\varepsilon (1)\) is independent of \(\xi '\). Now, by (i) of Lemma 5.5, we estimate the integral terms of the left hand side of (5.69) together with the first order terms involving \(U_r\) in \(H(y,-D[\tilde{\phi }(x,\cdot )](y))-H(x,D[\tilde{\phi }(\cdot ,y)](x)\) and we get
Then, plugging (5.70) into (5.69), we get
where \(o_\varepsilon (1)\) is independent of \(\xi '\). The rest of the proof is the same as in the previous cases, by sending first \(\xi '\rightarrow 0\), then \(\varepsilon \rightarrow 0\) and finally \(k \rightarrow 0\). For the details we refer to the end of the proof of Proposition 5.1. \(\square \)
Now we prove Theorem 3.1 for H of Bellman type.
Proof of Theorem 3.1
By contradiction, we suppose that \( M=\sup _\Omega \{u-v\}>0. \) Denote \( \omega (x)=u(x)-v(x) \) and for \(\nu >0\), consider \( \Phi (x)=\omega (x)-\psi (R^{-1}|x|)+\nu d(x), \) where \(\psi \) is a smooth function such that
and d is the signed distance from the boundary (see Remark 1). Note that \(\sup \Phi \rightarrow M\) as \(R \rightarrow \infty \) and \(\nu \rightarrow 0\). Since \(\Phi \le -1/2\) for |x| large and \(\nu \) small enough and \(M>0\), the function \(\Phi \) achieves its positive maximum \(\sup \Phi >\frac{M}{2}\) at a point x for R big and \(\nu \) small enough. We give the details in the case where all maximum points x are located on the boundary. We have
where with \(o_{R,\nu }(1)\) we mean that \(o_{R,\nu }(1)\rightarrow 0\) if \( R\rightarrow \infty , \nu \rightarrow 0\).
We use \(\phi (\cdot ):=\psi (R^{-1}|\cdot |)-\nu d(\cdot )\) as a test function at x. Note that, if \(x \in \partial \Omega \) and for \(\nu > R^{-1}||\psi '||_{L^{\infty }}\), we have \( \frac{\partial \phi }{\partial n}\ge -R^{-1}||\psi '||_{L^{\infty }}+\nu >0. \) Then, by Proposition 5.1, we get
By Lemma 6.11 (see the “Appendix”), \( \mathcal {I}[\phi ](\cdot ), |D\phi (\cdot )| \le o_{\nu ,R}(1) \) and by (5.73), we get
and by letting \(R \rightarrow \infty \), \(\nu \rightarrow 0\), we get a contradiction since \(M>0\). \(\square \)
5.2 Coercive Hamiltonians
We proceed analogously as for Hamiltonians of Bellman type and we prove Proposition 5.6. Once proved Proposition 5.6, the proof of Theorem 3.1 for H coercive follows by standard arguments as already showed for Hamiltonians of Bellman type. We sketch first the proof of Theorem 3.1 and then we prove Proposition 5.6.
Proof of Theorem 3.1
We just observe that we proceed again by contradiction, supposing that \( M=\sup _\Omega \{u-v\}>0. \) We fix \(0<\mu <1\) and define for \( x \in \Omega \) \( \omega _\mu (x)=\mu u(x)-v(x). \) We proceed as in the Bellman case and we use Proposition 5.6 to get
Then, by letting \(R \rightarrow \infty \), \(\nu \rightarrow 0\) and finally \(\mu \rightarrow 1\), we get a contradiction since \(M>0\) and we conclude the proof.
Proposition 5.6
Let \(\mathcal {I}\) as in (1.2) and assume (M), (J0), (J1). Let H be a coercive Hamiltonian satisfying (H1), (Ha) or (H1), (Hb), (Hc) and let u, v be respectively bounded sub and supersolutions to (1.1). Let \(\mu \in (0,1)\) if H is superlinearly coercive, \(\mu =1\) is H is sublinearly coercive. Then the function \( \omega (x):=\mu u(x)-v(x) \) satisfies, in the viscosity sense, the equation
where \(A, C_{m,\mu }\) are positive constants which depend on the data. Precisely, if \(\mu =1\), \(C_{m,\mu }=\tilde{C}\) where \(\tilde{C}\) is defined in (Hb) and, if \(\mu \in (0,1)\), \(C_{m,\mu }=\bar{C}^{1-m}C^m2^{m-1}m^{-m}(1-\mu )^{1-m}\)
Proof
We give the details when H has superlinear form i.e. when \(m>1>\sigma \), since the proof in the sublinear case is similar with easier computations. Since the proof is similar to that of Proposition 5.1, we focus only on the main differences.
We start by noting that if u is a subsolution of (1.1), then \( \bar{u}=\mu u \) is a viscosity subsolution to
Let \(x_0\in \bar{\Omega }\) and \(\phi \) a smooth function such that \(\omega -\phi \) has a strict maximum point in \(\bar{B}_{C_j\xi }(x_0)\cap \bar{\Omega }\) at \(x_0\) for some \(0<\xi <1\). We suppose that \(x_0 \in \partial \Omega \), since the other case being similar and even simpler.
Step 1. Localising on equidistant points (i.e. \(d(x)=d(y)\) ). We double the variable and consider the function
where \(\tilde{\phi }\) is as in (5.3) with \(K=2\). Let \((\bar{x}, \bar{y})\) be a maximum point of \(\Phi \) over the set \( A:=\bar{B}_{2C_j\xi '}(x_0)\cap \bar{\Omega }\times \bar{B}_{2C_j\xi '}(x_0)\cap \bar{\Omega }, \) for \(0<\xi '<\frac{\xi }{2}\). Let \(\Psi =\bar{u}(x)-v(y)-\psi (x,y)\), where \(\psi \) is defined as in (5.8) with \(K=2\) and let (x, y) be a point of maximum of \(\Psi \) over A. By classical argument, we have as \(\varepsilon \rightarrow 0\)
We have the following lemma.
Lemma 5.7
Under the above notation, we have
-
(i)
\(\bar{x} \rightarrow x, \, \,\bar{y} \rightarrow y, \,\, u(\bar{x})\rightarrow u(x), \,\, v(\bar{y}) \rightarrow v(y)\,\, \text{ as } \delta \rightarrow 0,\)
-
(ii)
\(d(x)=d(y).\)
Proof
The proof is very similar to that of Lemma 5.2. We give a sketch of the proof of (ii). We suppose that \( \frac{\partial \phi }{\partial n}(x_0)>0, \) then for \(\varepsilon \) small enough \( \frac{\partial \psi }{\partial n}((x+y)/2)>\frac{1}{2}\frac{\partial \phi }{\partial n}(x_0)>0. \) We assume that \( d(x) > d(y). \) Then for \(0<\mu <1\), we have
Note that
where \(C>0\) is a constant independent of \(\varepsilon \). For the integral terms in (5.78) we proceed as in Proposition 5.1 by using Lemma 5.3. For the Hamiltonian terms we use assumption (H1) together with (5.79) and we get
which is a contradiction for \(\varepsilon \) small, since \(\sigma < m\). \(\square \)
Step 2. Writing the viscosity inequalities. We write the viscosity inequalities for u and v
where we estimated the \(\mathcal {I}_{\xi '}[\phi ]\) terms by \(o_{\xi '}(1)\) (independent of \(\delta \)) as in (5.26). Denote
We recall that
where
By the smoothness of the distance function
and
Thanks to (Hb) and (Hc), we get for \(\varepsilon \) small
Note that, by (5.77) and (iii) of Lemma 5.7, we can take \(\epsilon =\epsilon (\mu ), \delta =\delta (\mu )\) small enough so that
and we can write
where \(o_{\delta , \varepsilon }(1)\) means that \(\lim _{\delta \rightarrow 0} o_{\delta ,\varepsilon }(1)=o_{\varepsilon }(1)\). Note that the infimum in the previous expression is attained and therefore
where \(C_{m,\mu }=\bar{C}^{1-m}C^m2^{m-1}m^{-m}(1-\mu )^{1-m}.\) Then we couple (5.86), (5.81) and (5.80), we let \(\delta \rightarrow 0\) and we get
Step 3. Estimate of the nonlocal terms. In order to estimate the nonlocal terms we use the following lemma. We omit the proof since it is exactly the same as that of Lemma 5.4. We remark that in the proof we deeply rely on the assumption \(\sigma \in (0,1)\).
Lemma 5.8
Under the above notation, we have
where \(C>0\) is independent of all the parameters.
Then the rest of the proof easily follows as in Proposition 5.1, step 5. \(\square \)
6 Applications to evolutive problems: existence, uniqueness and asymptotic behavior
In this section we present some applications of our results proved in the previous sections for the stationary case to the evolutive setting and we consider the associated Cauchy problem
where \(\Omega \subset \mathbb {R}^N\) satisfies assumption (O), \(u_0\in C(\Omega )\), \(\mathcal {I}[u]\) is an integro-partial differential operator of censored type and of order strictly less than 1, defined as
where \(\mu _x\) is a singular non-negative Radon measure satisfying (M), and j(x, z) is a jump function satisfying (J0), (J1) (see Sect. 2) . The main example are measures \(\mu _x\) with density \(\frac{d\mu _x}{dz}=g(x,z)|z|^{-(N+\sigma )}\) with \(\sigma <1\) and g a non-negative bounded function Lipschitz in x uniformly with respect to z. Note that the operator (6.2) is the natural extension to the evolutive case of the nonlocal operator considered in the stationary case and defined in (1.2). Moreover \(H\, : \, \bar{\Omega } \times [0,+\infty )\times {\mathbb {R}}\times \mathbb {R}^N \mapsto \mathbb {R}\) is a continuous function whose growth in the gradient makes it the leading order term in the equation, and can be coercive or of Bellman type. We refer to the following section for the precise assumptions on the Hamiltonian. The well-posedness of problems as (6.1) follows from analogous arguments used for the stationary problem with some standard adaptations. We refer to Theorems 6.1 and 6.3 for further details and proofs of uniqueness and existence.
We study two different kind of asymptotic behaviour of the solutions of (6.1). First we consider a Hamiltonian either of Bellman type either coercive under assumptions ensuring uniqueness of the solution of the associated stationary problem. We prove, by classical methods based on the weak-relaxed semilimits, the convergence as \(t \rightarrow + \infty \) of the solution of (6.1) to the unique solution of the associated stationary problem. On the other hand, when the associated stationary problem has not unique solution, we consider a Hamiltonian with superfractional coercive growth and we study the so-called ergodic large time behaviour, proving that the solution of (6.1) approaches a solution of the so-called ergodic problem as \(t \rightarrow + \infty \). We follow the methods of [9], which rely on the Hölder regularity in \(\Omega \) of the subsolutions of the associated ergodic problem and on a Strong Maximum Principle. We recall also [5], where analogous methods were applied to uniformly elliptic integro-differential equations. We refer to Sect. 6.4 for more details.
6.1 Assumptions
We are going to consider the finite time horizon problem associated to (6.1)
The definition of viscosity solutions to (6.3) (and then to (6.1)) is the natural extension of Definition 2.1 to the corresponding Cauchy problem.
We assume the following condition.
- (H’):
-
For all \(R>0\), there exists \(\gamma _R\ge -K\) such that for all \(x \in \bar{\Omega }, u, v \in \mathbb {R},|u|,|v|\le R, 0\le t \le R\) and \(p\in \mathbb {R}^n\), we have
$$\begin{aligned} H(x,t, u,p)-H(x,t, v,p)\ge \gamma _R(u-v). \end{aligned}$$
Remark 10
Note that in the comparison principle (Theorem 6.1), assumption (H’) is assumed mainly for simplicity of exposition and can be relaxed assuming only \(\gamma _R \ge 1\). Indeed if \(\gamma _R<1\) we perform the change \(\tilde{u}=ue^{-(\gamma _R-1)t}\) (analogously for the supersolution) and prove Theorem 6.1 for \(\tilde{u}\) and \(\tilde{v}\).
As it is classical in viscosity solutions theory, the comparison principle allows the application of Perron’s method to conclude the existence. To this end, we introduce the following assumption, which will allows us to build sub and supersolutions:
- (E’):
-
For all \(T>0, R>0\) there exists a constant \(H_R>0\) such that
$$\begin{aligned} ||H(x,t, r, p)||_\infty \le H_R \, \, \forall x \in \Omega , t \in [0,T], r, p \in \mathbb {R}, |r|, |p| \le R. \end{aligned}$$
We consider Hamiltonian either of Bellman type either coercive.
We say that the Hamiltonian H is of Bellman type if for \(t \in [0,+\infty ), x \in \bar{\Omega }, p \in \mathbb {R}^N, H(x,t, r,p)\) can be written as
where \(b, \lambda \, : \, \bar{\Omega } \times [0,+\infty )\times \mathcal {A} \rightarrow \mathbb {R}^N\) and \(l\, : \, \bar{\Omega }\times [0,+\infty ) \times \mathcal {A}\rightarrow \mathbb {R},\) are continuous and bounded functions and satisfy the following properties.
- (C’):
-
Uniform continuity of l and \(\lambda \):
There exist modulus of continuity \(\omega _l, \omega _\lambda \) such that such that \(\forall \alpha \in \mathcal {A}, \forall x, y \in \bar{\Omega }, t,s\in [0,+\infty )\)
$$\begin{aligned}&|l(x,t,\alpha )-l(y,s,\alpha )|\le \omega _l(|x-y|+|t-s|);\\&|\lambda (x,t,\alpha )-\lambda (y,s,\alpha )|\le \omega _\lambda (|x-y|+|t-s|); \end{aligned}$$ - (L’):
-
Uniform Lipschitz continuity of the drift b: There exists \(C>0\) such that \(\forall \alpha \in \mathcal {A} \, \forall (x,s), (y,t) \in \bar{\Omega }\times [0+\infty )\)
$$\begin{aligned} |b(x,s, \alpha )-b(y,t,\alpha )| \le C(|x-y|+|s-t|). \end{aligned}$$
Remark 11
Note that assumption (L’) may seem unusual since it requires also the uniform Lipschitz continuity of the drift b in the time variable. This is due to the fact that in the proof of the comparison principle (Theorem 6.1) we need to double also the time variable in the test function, which as a consequence will have the same dependence on x and t, which we estimate by assumption (L’). We refer to Remark 12.
We assume that the components of the boundary are of three different types whose definition is analogous to that of \(\Gamma _{{\mathrm{in}}}, \Gamma _{{\mathrm{out}}}, \Gamma \) defined in (2.3), (2.4), (2.5) in the stationary case, with the only difference that now they are part of the parabolic boundary. For simplicity of exposition, we do not repeat the definition. For the sake of simplicity and for the rest of the paper, we adopt the following notation.
- (B’):
-
Assumption (B) where \(\Gamma _{{\mathrm{in}}}, \Gamma _{{\mathrm{out}}}, \Gamma \) are considered as parts of the parabolic boundary.
In the case of coercive Hamiltonians, we restrict the time dependence of H by the assumption:
- (H0’):
-
There exists \(H_0 \, : \, \bar{\Omega }\times \mathbb {R} \times \mathbb {R}^N \rightarrow \mathbb {R}\) continuous and \(f\, : \, \bar{\Omega } \times [0,\infty ) \rightarrow \mathbb {R}\) uniformly continuous and bounded such that for all \(x \in \bar{\Omega }, r \in \mathbb {R}, p \in \mathbb {R}^N\)
$$\begin{aligned} H(x,t,r,p)=H_0(x,r,p)-f(x,t). \end{aligned}$$
We assume that the Hamiltonian satisfies in x uniformly in t and uniformly on compact sets in r the assumptions made in the stationary case, namely, (H1), (Ha) (sublinear coercivity) or (H1), (Hb), (Hc) (superlinear coercivity). For the sake of brevity and simplicity of exposition, we omit to repeat them and for the rest of the paper we adopt the following notation.
- (He’):
-
The Hamiltonian satisfies (H1), (Ha) in x uniformly in t and uniformly on compact sets in r. In this case we say the Hamiltonian satisfies (H1’), (Ha’).
- (He”):
-
The Hamiltonian satisfies (H1), (Hb), (Hc) in x uniformly in t and uniformly on compact sets in r. In this case we say the Hamiltonian satisfies (H1”), (Hb”), (Hc”).
6.2 Existence and uniqueness
In the following theorem we state the comparison principle for the problem (6.1).
Theorem 6.1
Let \(\Omega \) be an open subset of \(\mathbb {R}^N\) satisfying (O), \(u_0\in C(\bar{\Omega })\). Assume (M), (J0), (J1). Let H be a Hamiltonian either of Bellman type as in (6.4) satisfying (C’), (L’), (B’) or a coercive Hamiltonian satisfying (H0’) and either (He’) or (He”). Assume also (H’). Let \(u, v \in L^{\infty }(\bar{\Omega }\times [0,T])\) for all \(T>0\) be respectively a bounded usc sub and bounded lsc supersolution of (6.1). Then
The proof is based on the following proposition, which is the analogous for the evolutive case to Propositions 5.1 and 5.6. The proof is also similar with some adaptation to the evolutive setting. Note that Proposition 6.2 is used also later in the proof of Proposition 6.5.
Proposition 6.2
Let \(\mathcal {I}\) as in (6.2) and assume (M),(J0), (J1). Let H be an Hamiltonian either in Bellman form as in (6.4) satisfying (C’), (L’), (B’) or a coercive Hamiltonian satisfying (H0’) and either (He’) or (He”). Assume also (H’). Let \(u,v \in L^{\infty }(\bar{\Omega }\times [0,T])\) for any \(T>0\) be respectively usc sub and lsc supersolutions to
Take \(\mu =1\) if H has Bellman form and if H is sublinearly coercive, \(\mu \in (0,1)\) if H is superlinearly coercive. Then, the function
satisfies, in the viscosity sense, the equation
where, for \(R=||\mu u||_\infty + ||v||_\infty \), \(\gamma _R\) is the constant of (H’), \(A_R>0\) is defined in \((He'')\)-\((Hb'')\) and \(C_{m,\mu ,R}>0\) is such that \(C_{m,\mu ,R}=:C_{\mu ,m}=(1-\mu )^{1-m}\) if \(\mu \in (0,1)\) and \(C_{m,\mu ,R}=\tilde{C}_R\) if \(\mu =1\) and H is sublinearly coercive, where \(\tilde{C}_R\) is defined in \((He')\)-\((Ha')\).
Remark 12
We omit the proof of Theorem 6.1, since it follows closely the arguments presented in Propositions 5.1 and 5.6 for the stationary case adapted by standard arguments to the evolution setting. We only remark that, since the strategy of the proof of Proposition 5.1 relies on an asymmetric use of the viscosity inequalities satisfied by the sub- and supersolution (see in particular in Step 1), the standard approach by the Ishi’s Lemma for evolutive equation is not applicable. Then, we need to double also the time variable in the test function, which as a consequence will have the same dependence on x and t. Because of this, in particular in order to estimate the Hamiltonian terms in the viscosity inequalities satisfied by u and v (in the Bellman case), we need the uniform continuity also with respect to time as stated in assumption (L’).
For both the coercive and Bellman case, the application of Perron’s method on a sequence of finite-time horizon problems with the form (6.3) with \(T \rightarrow +\infty \) and the strong comparison principle allows us to get the existence of a solution which is defined for all time. Note that, in order to apply Perron’s method, we ask the initial datum to be bounded, i.e. \(u_0\in C_b(\Omega )\).
Moreover, in order to have the uniform boundedness in T of the solutions of (6.1), we suppose the following assumption.
- (H”):
-
There exists \(\gamma _0>0\) such that \(\gamma _R\ge \gamma _0 \) for all \(R>0\) where \(\gamma _R\) is defined in (H’).
Theorem 6.3
Let \(\Omega \) be an open subset of \(\mathbb {R}^N\) satisfying \((O), u_0\in C_b(\mathbb {R}^N)\). Assume (M), (J0), (J1). Let H be a Hamiltonian either of Bellman type as in (6.4) satisfying (C’), (L’), (B’) or a coercive Hamiltonian satisfying (H0’) and either (He’) or (He”). Assume also (H’), (E’). Then, there exists a unique bounded viscosity solution to problem (6.1) in \(C(\bar{\Omega }\times [0,+\infty ))\cap L^{\infty }(\bar{\Omega } \times [0,T])\). In addition, if (H”) holds, then the unique solution \(u \in C(\bar{\Omega }\times [0,+\infty ))\cap L^{\infty }(\bar{\Omega } \times [0,T])\) for all \(T>0\) is uniformly bounded in \(\bar{\Omega } \times [0,+\infty )\).
6.3 Large time behaviour I: convergence in the classical sense
We address the question of the asymptotic behaviour as \(t\rightarrow \infty \) of the solution of (6.1), under assumption (H”), which ensures existence and uniqueness for the associated stationary problem. The main result is the following theorem.
Theorem 6.4
Let \(\Omega \) be an open subset of \(\mathbb {R}^N\) satisfying \((O), u_0 \in C_b(\Omega )\). Assume (M), (J0), (J1). Let H be a Hamiltonian either of Bellman type as in (6.4) satisfying (C’), (L’), (B’) or a coercive Hamiltonian satisfying (H0’) and either (He’) or (He”). Assume (H”), (E’). Assume also that there exists a continuous function \(\bar{H}\, : \, \bar{\Omega } \times \mathbb {R} \times \mathbb {R}^N \rightarrow \mathbb {R}\) satisfying
as \(t \rightarrow \infty \). Then, there exists a unique bounded viscosity solution u for the following problem
Moreover, the unique viscosity solution u of (6.1) converges uniformly on compact sets in \(\bar{\Omega }\) to \(u_\infty \), the unique viscosity solution of the problem (6.5).
For the existence and uniqueness for the problem (6.5) we refer to Theorem 3.1 and Corollary 3.2. We omit the proof of Theorem 6.4 since it is rather classical and follows the same arguments used in [13], where the same kind of results have been given in the case of the Dirichlet problem for nonlocal equations (fractional Laplacian) with Hamiltonians both coercive both of Bellman type.
6.4 Large time behavior II: convergence to the ergodic problem
In this subsection we prove large time behaviour for the problem
where \(\Omega \) is a bounded open subset of \(\mathbb {R}^N\) satisfying (O), \(u_0 \in C(\Omega )\) and H is a Hamiltonian in superfractional coercive form, that is, \(m>1\) in (H1’).
Existence and uniqueness for the problem (6.6) follow from Theorem 6.3. Note that H does not depend on u, so it does not satisfy (H’).
The main result of this section is Theorem 6.9, namely the convergence as \(t \rightarrow + \infty \) of the solution of (6.6) to a solution of the ergodic problem, which we solve in Proposition 6.8. The proof of Theorem 6.9 strongly relies on the Hölder regularity up to the boundary for subsolutions of (6.6) and on the control of their oscillation. This result was proved in the stationary setting by Barles, Ley, Koike, Topp in [9], Corollary 2.14 (see also Barles and Topp [12]), in the case of censored operators and coercive Hamiltonians with \(m > 1\). We recall this result in Proposition 6.7. For the evolutive problem we refer to the proof of Theorem 4.5 of [9], where first Lipschitz regularity in time is proved and then Corollary 2.14 is used to conclude the regularity in time and space.
We remark that, differently from [11], where the Lipschitz regularity of the solutions is used to linearise the equations in order to apply the Strong Maximum Principle, our proof relies mainly on the use of a Strong Maximum Principle à la Coville [17, 18] (see also Ciomaga [16]). This means that it relies mainly on a topological property of the support of the measure defining the nonlocal operator. Note that in this final part we assume \(\Omega \) bounded for technical reasons related to the proof of the Strong maximum principle, we refer to the proof of Proposition 6.5.
6.4.1 A strong maximum principle
We need some notation for the statement of the Strong Maximum Principle. Let \(\mu , j\) be as in the definition of the nonlocal operator \(\mathcal {I}\), that is, satisfying (M), (J0), (J1) and denote by \(\text{ supp }\mu \) the support of the measure \(\mu \). For \(x \in \mathbb {R}^n\) we define inductively
and
The Strong Maximum Principle presented in this paragraph relies in the non locality of the operator under the ”iterative covering property”
The most basic example is the case where \(j(x,z)=z\) and there exists \(r>0\) such that \( B_r\subset \text{ supp }\{\mu \}. \) For further details and examples we refer to [9].
The following proposition states the Strong Maximum Principle.
Proposition 6.5
Let \(\Omega \subset \mathbb {R}^N\) be a bounded domain satisfying (O). Let H be a coercive Hamiltonian satisfying (H0’) and (He”) with \(m>1\). Assume (M), (J0), (J1), (E’) and (6.7). Let u, v be respectively a bounded sub and supersolution of (6.6), such that there exists \((x_0,t_0) \in \bar{\Omega } \times (0,+\infty )\) satisfying
Then, the function \(u-v\) is constant in \(\bar{\Omega } \times [0,t_0]\). Moreover we have
The proof of Proposition 6.5 uses the following lemma, which is a consequence of the comparison principle, see [11], Theorem 4.1.
Lemma 6.6
Let assumptions of Proposition 6.5 hold. Let u, v be bounded sub and supersolution to Eq. (6.6) and for \(t \in [0,+\infty )\) define
Then, for all \(0\le s \le t\), we have \(k(t) \le k(s)\).
We prove the strong maximum principle. We essentially follow the argument of [9], Proposition 4.1, with some changes due to presence of the Neumann boundary condition. We give a sketch of the proof, focusing on the main differences.
Proof of Proposition 6.5
We divide the proof into several steps.
Step 1. Preliminaries. We want to prove that \( (u-v)(x,t)=k(0) \) for each \((x,t) \in \bar{\Omega } \times [0,t_0]\). Since \(k(t_0)\) is a global maximum value of k in \([0,+\infty )\), by Lemma 6.6 we have \(k(t)=k(0)\) for all \(t \in [0,t_0]\). Then, we have just to prove that
for each \(\tau \in (0,t_0)\). By upper-semicontinuity, we derive the result up to \(\tau =0\) and \(\tau =t_0\). Fix \(\tau \in (0,t_0)\) and define the set
We observe that by the upper-semicontinuity of \(u-v\), \(\mathcal {B}_\tau \) is non-empty. Then, the claim of the proposition follows once proved that \(\mathcal {B}_\tau =\bar{\Omega }\).
Step 2. Localization on time \(\tau \). For \(\eta >0\), define the function
and note that for each \((x,t) \in \bar{\Omega } \times (0,+\infty )\) and for \(\tilde{x} \in \mathcal {B}_\tau \) where \(\mathcal {B}_\tau \) is defined in (6.8), we have \( \Phi (x,t) \le k(t)-\eta (t-\tau )^2\le k(\tau )=(u-v)(\tilde{x},\tau )=\bar{W}(\tilde{x},\tau ). \) Then the supremum of \(\Phi \) in \(\bar{\Omega }\times (0,+\infty ) \) is achieved and
Step 3. Localization around a point in \(\mathcal {B}_\tau \). From now on we fix \( x_\tau \in \mathcal {B}_\tau , \) where \(\mathcal {B}_\tau \) is defined in (6.8). We define for \(\varepsilon , \alpha >0\)
where d is the signed distance from the boundary (see Remark 1) and \(K>0\) satisfies \( K>||D^2d||_\infty +1. \) Note that \( \psi _{\varepsilon ,\alpha }(x_\tau )=-\alpha d(x_\tau ). \) Moreover for each \(\varepsilon >0\) the first derivatives of \(\psi _{\varepsilon ,\alpha }\) are bounded, depending on \(\varepsilon \) and \(\alpha \).
For \(0<\mu <1\) we denote \( \omega _\mu =\mu u-v \) and we consider
By the upper-semicontinuity of \(\Phi _\mu \), there exists \((x_\mu , t_\mu ) \in \bar{\Omega }\times [0,t_0+1]\) such that
Since \(\Phi _\mu \rightarrow \Phi \) locally uniformly on \(\bar{\Omega }\times [0,+\infty )\) as \(\mu \rightarrow 1\), we get up to subsequences
Not also that for any \(\alpha \) bounded
Indeed, by using the maximum point inequality for \(\Phi _\mu \), we have
where we used the definition of \(k(\tau )\). Since \(t_\mu \in [0,t_0+1]\) for all \(\mu \) close to 1, we have \( (u-v)(x_\mu ,t_\mu )\le k(t_\mu )\le k(\tau ). \) Coupling the previous inequality with (6.10) we get \( \psi _{\varepsilon ,\alpha }(x_\mu )+\alpha d(x_\tau )\le u(x_\tau ,\tau )-u(x_\mu ,t_\mu ). \) Then, by the boundedness of u and of d, for \(\alpha \) small, we deduce that \( |x_\mu -x_\tau |\le C\varepsilon \) for some \(C>0\) independent on \(\mu \), which implies (6.9).
Step 4. Writing the viscosity inequality for \(\omega _\mu \). Denote
We test \(\omega _\mu \) with the function \(\phi \) in \((x_\mu ,t_\mu )\). We suppose \(x_\mu \in \partial \Omega \), since the other case being analogous and even simpler. By the Taylor’s formula for the distance function, we have
and then
Take \(\mu , \varepsilon \) small enough so that
By (6.11), by the definition of K and (6.12), we have
Then, the rest of the proof follows exactly as in [9], Proposition 4.1, by writing the viscosity inequality for \(\omega _\mu \), letting first \(\mu \rightarrow 1\), then \(\varepsilon \rightarrow 0\) and using the iterative covering property (6.7). We give some details for completeness of exposition. By Proposition 6.2, we get for \(\xi >0\)
where \(C_{\mu ,m}\) and \(A_R\) are defined in Proposition 6.2.
Since
for some \(C'>0\), we get
We recall that \(t_\mu \rightarrow \tau \) as \(\mu \rightarrow 1\) and we observe that by the smoothness of \(\psi _{\varepsilon ,\alpha }\) the term in parenthesis in (6.13) remain bounded as \(\mu \rightarrow 1\). Moreover, by the Dominated Convergence Theorem, we get
where we recall that \(\bar{x}\) is the limit of \(x_\mu \) as \(\mu \rightarrow 1\).
Then
and letting \(\varepsilon \rightarrow 0\) and recalling that \(\bar{x} \rightarrow x_\tau \) as \(\varepsilon \rightarrow 0\) and \((u-v)(x_\tau ,\tau )=k(\tau )\) we finally conclude
Since \(\xi >0\) is arbitrary, we get that
Therefore we can proceed in the same way as above, and conclude by induction that
Then we conclude the proof by the upper-semicontinuity of \(u-v\) and applying the iterative convering property (6.7). \(\square \)
6.4.2 The ergodic problem
Roughly speaking, solving the ergodic problem means pass to the limit as \(\delta \rightarrow 0\) in the stationary problem
whose existence and uniqueness for \(\delta >0\) holds by Theorem 3.1.
We solve the ergodic problem in Proposition 6.8. Note that we need the compactness of the family of solutions \(\{u_\delta \}\), which relies mainly on the regularity result for subsolutions of (6.14) which we recall in the following proposition. We remark that the Hölder regularity for subsolution of the first equation of (6.14) up to the boundary was proved in [9], Theorem 5.5. Note that here the Neumann boundary conditions play no role, since the regularity inside the domain follows by [9], Theorem 5, and the extension up to the boundary is carried out similarly to [9], applying the method used by Barles [3] (see also [15]).
Proposition 6.7
Let assumptions of Proposition 6.5 hold. Then any bounded viscosity subsolution \(u \, : \, \mathbb {R}^N \rightarrow \mathbb {R}\) to (6.14) is Hölder continuous in \(\bar{\Omega }\) with Hölder exponent \(\gamma _0=\frac{m-\sigma }{m}\) and Hölder seminorm depending on \(\Omega \), the data and \(\text{ osc }_{\Omega }(u)\) and not on \(\delta \). Moreover, there exists \(K>0\) such that for any bounded viscosity subsolution of (6.14) we have
Proposition 6.8
Under the assumptions of Proposition 6.5, there exists a unique constant \(\lambda \in \mathbb {R}\) for which the stationary ergodic problem
has a solution \(w \in C^{\frac{m-\sigma }{m}}(\bar{\Omega })\). Moreover w is the unique solution of (6.16) up to an additive constant.
Proof
A key ingredient is Proposition 6.7, which gives the compactness of the family of solutions of the approximating Eq. (6.14). Once we have the compactness, the proof follows standard arguments which we do not repeat. The uniqueness follows by the comparison principle for (6.6) and the application of the strong maximum principle for the problem (6.6) (Proposition 6.5). \(\square \)
6.4.3 Convergence as \(t\rightarrow + \infty \)
Theorem 6.9
Let assumptions of Proposition 6.5 hold. Let u be the unique solution to problem (6.6). Then, there exists a pair \((w,\lambda )\) solution to (6.16) such that
uniformly on \(\bar{\Omega }.\)
We omit the details of the proof since we follow closely the arguments given in [9] (see also [4, 13] for the local framework and [27] for the nonlocal one).
We just observe that again a crucial ingredient of the proof is the Hölder regularity of the solutions of (6.6). The proof is carried out as in Theorem 4.5 of [9], by first proving Lipschitz regularity in time and then applying Proposition 6.7 to conclude the regularity in time and space. Once established the regularity, the proof follows by the application of the strong maximum principle proved in Proposition 6.5.
References
Alvarez, O., Tourin, A.: Viscosity solutions of nonlinear integro-differential equations. Ann. l’I.H.P. Anal. Non Linéaire 13(3), 293–317 (1996)
Bardi, M., Capuzzo-Dolcetta, I.: Optimal Control and Viscosity Solutions of Hamilton–Jacobi–Bellman Equations. Birkhäuser Boston Inc, Boston, MA (1997)
Barles, G.: A short proof of the \(C^{0,\alpha }\)-regularity of viscosity subsolutions for superquadratic viscous Hamilton–Jacobi equations and applications. Nonlinear Anal. 73, 31–47 (2010)
Barles, G., Chasseigne, E., Ciomaga, A., Imbert, C.: Lipschitz regularity of solutions for mixed integro-differential equations. J. Differ. Equ. 252(11), 6012–6060 (2012)
Barles, G., Chasseigne, E., Ciomaga, A., Imbert, C.: Large time behaviour of periodic viscosity solutions for uniformly elliptic integro-differential equations. Calc. Var. Partial Differ. Equ. 50(1–2), 283–304 (2014)
Barles, G., Chasseigne, E., Georgeline, C., Jakobsen, E.R.: On Neumann type problems for non-local equations set in a half space. Trans. Am. Math. Soc. 366(9), 4873–4917 (2014)
Barles, G., Georgeline, C., Jakobsen, E.R.: On Neumann and oblique derivatives boundary conditions for second-order elliptic integro-differential equations. J. Differ. Equ. 256(4), 1368–1394 (2014)
Barles, G., Imbert, C.: Second-order elliptic integro-differential equations: viscosity solutions’ theory revisited. Ann. l’I.H.P. Anal. Non Linéaire 25(3), 567–585 (2008)
Barles, G., Koike, S., Ley, O., Topp, E.: Regularity results and large time behaviour for integro-differential equations with coercive Hamiltonians. Calc. Var. 54(1), 539–572 (2015)
Barles, G., Lions, P.L.: Remarques sur les problèmes de réflexion oblique. C. R. Acad. Sci.Paris Série I Math. 320(1), 69–74 (1995)
Barles, G., Souganidis, P.: Space–time periodic solutions and long-time behaviour of solutions of quasilinear parabolic equations. SIAM J. Math. Anal. (electronic) 32(6), 1311–1323 (2001)
Barles, G., Topp, E.: Lipschitz regularity for censored sub diffusive integro-differential equations with superfractional gradient terms. Nonlinear Anal. Theory Methods Appl. 131, 3–31 (2016). (Elsevier)
Barles, G., Topp, E.: Existence, Uniqueness and Asymptotic Behaviour for Nonlocal Parabolic Problems with Dominating Gradient Terms. arXiv:1404.7804 (Preprint 2014)
Bogdan, K., Burdzy, K., Chen, Z.-Q.: Censored stable processes. Prob. Theory Relat. Fields 127(1), 89–152 (2003)
Capuzzo-Dolcetta, I., Leoni, F., Porretta, A.: Hölder estimates in space–time for viscosity solutions of Hamilton–Jacobi equations. CPAM 63(5), 590–629 (2010)
Ciomaga, A.: On the strong maximum principle for second-order nonlinear parabolic integro-differential equations. Adv. Differ. Equ. 17(7–8), 635–671 (2012)
Coville, J.: Maximum principles, sliding techniques and applications to nonlocal equations. Electron. J. Differ. Equ. 68, 1–23 (2007)
Coville, J.: Remarks on the strong maximum principle for nonlocal operators. Electron. J. Differ. Equ. 66, 1–10 (2008)
Crandall, M., Ishii, H., Lions, P.-L.: User’s guide to viscosity solutions of second order partial differential equations. Bull. Am. Math. Soc. 27(1), 1–67 (1992)
Fleming, W.H., Soner, H.M.: Controlled Markov Processes and Viscosity Solutions. Springer, New York (2006)
Freidlin, M.: Functional Integration and Partial Differential Equations. Annals of Mathematics Studies, vol. 109. Princeton University Press, Princeton (1985)
Guan, Q.Y., Ma, Z.M.: Reflected symmetric \(\alpha \)-stable process and regional fractional Laplacian. Probab. Theory Relat. Fields 134(4), 649–694 (2006)
Ishii, H.: Perron’s method for Hamilton–Jacobi equations. Duke Math. J. 55(3), 369–384 (1987)
Jacob, N.: Pseudo Differential Operators and Markov Process, vol. III. Markov Process and Applications. Imperial College Press, London (2005). xxviii-474
Lions, P.-L., Sznitman, A.-S.: Stochastic differential equations with reflecting boundary conditions. Commun. Pure Appl. Math. 37(4), 511–537 (1984)
Sayah, A.: Équations d’Hamilton–Jacobi du premier ordre avec termes intégro-différentiels. II. Existence de solutions de viscosité. Commun. Partial Differ. Equ. 16(6–7), 1075–1093 (1991)
Tchamba, T.T.: Large time behaviour of solutions of viscous Hamilton–Jacobi equations with superquadratic Hamiltonian. Asymptot. Anal. 66, 161–186 (2019)
Topp, E.: Existence and uniqueness for integro-differential equations with dominating drift terms. Commun. Partial Differ. Equ. 39(8), 1523–1554 (2014)
Acknowledgements
Open access funding provided by University of Graz. This work has been carried out during the permanence of the author at the Laboratoire de Mathématiques de Tours, which the author wants to thank for the warm welcome. In particular the author wants to express her deepest gratitude to Prof. Guy Barles, for proposing the problem and for the important support given. Without him, this work would not have been carried out. The author kindly thanks also the anonymous referees, whose comments and suggestions were precious in the improving of the final presentation of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Y. Giga.
This work was partially supported by the ERC advanced Grant 668998 (OCLOC) under the EU’s H2020 research programme.
Appendix
Appendix
First we prove some lemmas used in the proof of Theorem 3.1, that is, the following Lemmas 6.10, 5.3 and 6.11. In Sect. 6.6 we prove the existence of the blow-up supersolution, stated in Remark 9, Lemma 5.5.
1.1 Some lemmas used in the proof of Theorem 3.1
Lemma 6.10
Let H be a Hamiltonian of Bellman type. For all \(\hat{s}\in \partial \Omega \), there exists \(r=r(\hat{s})>0\) and \(\gamma ,C_2>0\) constants such that for all \(s \in \bar{B}_r(\hat{s}), \lambda \in \mathbb {R}, p \in \mathbb {R}^N\), it holds:
-
(i)
if \(\hat{s} \in \Gamma _{{\mathrm{out}}}\)
$$\begin{aligned} H(s,p-|\lambda | n(s))\ge & {} \gamma |\lambda |-C_2|p|-C_2; \end{aligned}$$(6.17)$$\begin{aligned} H(s,p+|\lambda | n(s))\le & {} -\gamma |\lambda |+C_2|p|+C_2; \end{aligned}$$(6.18) -
(ii)
if \(\hat{s} \in \Gamma \), then
$$\begin{aligned} H(s,p-|\lambda | n(s))\ge & {} \gamma |\lambda |-C_2|p|-C_2; \end{aligned}$$(6.19)$$\begin{aligned} H(s,p+|\lambda | n(s))\ge & {} \gamma |\lambda |-C_2|p|-C_2. \end{aligned}$$(6.20)
Proof of Proposition 6.5
First we prove (i). Since \(\hat{s} \in \Gamma _{{\mathrm{out}}}\), for \(\alpha \in \mathcal {A}\), there exists \(r_1,\gamma _1 >0\) small enough such that \( b(s,\alpha )\cdot n(s)\ge \gamma _1 \) for any \(s \in \bar{\Omega } \cap B_{r_1}(\hat{s})\). Then, by the boundedness of b and l, we get for some \(C_1>0\)
for any \(s \in \bar{\Omega } \cap B_{r_1}(\hat{s})\). To prove (6.18), we approximate the supremum in the Hamiltonian by a sequence \(\tilde{\alpha }\in \mathcal {A}\). In particular, we take \(\tilde{\alpha }\) such that
Since \(\hat{s}\in \Gamma _{{\mathrm{out}}}\) and using that \(\mathcal {A}\) is compact, there exist \(r_2, C>0\) small enough such that \( b(s,\tilde{\alpha })\cdot n(s)\ge \gamma _2\) for any \(s \in \bar{\Omega } \cap B_{r_2}(\hat{s}). \) Then by the boundedness of b and l we get
for any \(s \in \bar{\Omega } \cap B_{r_2}(\hat{s}).\) We conclude the proof of (6.17) and (6.18) by using (6.21) and (6.22) and by denoting \(r=\min \{r_1,r_2\}, \gamma =\min \{\gamma _1,\gamma _2\}\) and \(C_2=C_1+1\).
Now we prove (ii). Since \(\hat{s} \in \Gamma \), there exist \(r,\gamma >0\) such that \( b(s,\alpha _1)\cdot n(s)\ge \gamma \) and \( b(s,\alpha _2)\cdot n(s)\le -\gamma \) for any \(s \in \bar{\Omega } \cap B_r(\hat{s})\). Then we get
for any \( s \in \bar{\Omega } \cap B_r(\hat{s})\), proving (6.19). Analogously, we get
for any \( s \in \bar{\Omega } \cap B_r(\hat{s})\) and by denoting \(C_2=C_1+1\) we conclude (6.20). \(\square \)
Now we prove Lemma 5.3, whose statement is given in the proof of Theorem 3.1, Step 1.
Proof of Lemma 5.3
First we prove (i). Take \(-\mathcal {I}_\xi [\phi (\cdot , y)](x)\). By the definition of \(\tilde{\phi }\), since \(\chi _\varepsilon , \phi \) are Lipschitz and by (J1) we have
and by the first of (M) we have
Take now \(-\mathcal {I}_\xi [u](x)\). Note that by the boundedness of u we have
and then by the first of (M), we get for some \(C>0\)
Plugging together (6.23) and (6.24), we conclude (i) for some \(C_1>0\). Similarly we prove (ii).
We state Lemma 6.11 and we omit the proof since it follows by standard arguments.
Lemma 6.11
Let \(R,\nu >0\) and denote \(\psi _R(x)=\psi (R^{-1}|x|)\) where \(\psi \) is a smooth function such that
Let d denote the distance from the boundary of \(\Omega \) in a neighbourhood V of the boundary and extend it \(C^1\) and bounded in all the domain. Let \(\mathcal {I}\) as in (1.2) and assume (M) and (J1). Then the function \(\phi =\psi _R+\nu d\) satisfies
1.2 Blow-up supersolution
In this section we prove Lemma 5.5, used in the proof of Theorem 3.1 (see in particular Proposition 5.1, Remark 9).
We construct the function \(U_r\) as showed in the following and then we prove Lemma 6.12. Note that Lemma 5.5 follows as a consequence of Lemma 6.12 and we prove it after the statement of Lemma 6.12.
Let \(\bar{x} \in \Gamma _{{\mathrm{in}}}\) and \(r=r(\bar{x})\) be given as in assumption (O). We recall that by (O), there exists a \(W^{2,\infty }\)-diffeomorphism \( \psi :B_{r}(\bar{x}) \mapsto \mathbb {R}^N, \) satisfying
where d is the signed distance from the boundary of \(\Omega \).
We define \(U_r\)in a suitable neighbourhood of the point \(\bar{x}\), where we rectify the boundary and carry on the computations. In particular we define \(U_r\) as follows
where
Note that \(\bar{U}_{r} \in C^\infty (0,r)\) is (non-negative) monotone and decreasing.
Lemma 6.12
For any \(\bar{x} \in \Gamma _{{\mathrm{in}}}\), let \(r=r(\bar{x})\) be defined as in assumption (O). Let \(U_{r}\) be defined as in (6.28). Then we have for \(\xi \) small enough (with respect to r)
In particular there exists \(\tilde{r}(r, A,\sigma )=\tilde{r}\) such that \(\tilde{r}\le r\) and
Remark 13
Note that the strict positivity of the drift term on the points of \(\Gamma _{{\mathrm{in}}}\) is essential here to prove (6.30), since the drift term controls the integral term which explodes on the boundary, as (6.29) shows.
As a consequence of Lemma 6.12, we prove Lemma 5.5.
Proof of Lemma 5.5
Take \(\tilde{r}\) as defined in Lemma 6.12 and let \(U_{\tilde{r}}\) be defined as in (6.28) for \(r=\tilde{r}\). Then \(U_{\tilde{r}}\) is a non-negative decreasing function which trivially satisfies (ii) of Lemma 5.5 with \(\omega _{\tilde{r}}(s)=\frac{1}{\bar{U}_{\tilde{r}}(s)}\). Moreover, (i) Lemma 5.5 follows as a direct application of (6.30) of Lemma 6.12. \(\square \)
Now we prove Lemma 6.12.
Proof of Lemma 6.12
First we prove (6.29). Let \(\xi \le C_j^{-1}\frac{r}{2}\). Then, by (J1), for \( |z|\le \xi \) and \(x \in B_{\frac{r}{2}}(\bar{x})\), we have that \( x+j(x,z)\in B_{r}(\bar{x}). \) We describe the domain of integration of \(\mathcal {I}_{\xi }[U_r]\) through the diffeomorphism \(\psi \) as \( x+j(x,z)\in \bar{\Omega }=\psi _N(x+j(x,z)) \ge 0. \) By the definition of \(U_r\) and (6.27)
We write \( \mathcal {I}_{\xi }[U_r](x)= I^1+I^2, \) where
and
and since \( I^1\le 0, \) we get
We proceed performing a change of variable in order to write the set of integration in terms of \(\psi _N(x)\). In other words, we write
Then by (J0), (J1), the first of (M) and since \(\psi \) is \(W^{2,\infty }\), (6.31) becomes
for some \(\bar{C},C>0\). By the change of variable \(y=\frac{w}{\psi _N(x)}\), we get
Note that the integral in the right hand side is finite and does not depend on \(\xi \). For convenience of notation we denote \( A:=\bar{C}\int _{{0\ge y_N\ge -1}}\left| \ln \left( 1+y_N\right) \right| \frac{dy}{|y|^{N+\sigma }}. \) Then (6.32) becomes
which is exactly (6.29).
Now we prove (6.30). First note that, by the definition of \(U_r\), we have
Then, by (6.29) and (6.33), we have for all \(\alpha \in \mathcal {A}\)
Since we are in a neighbourhood of \(\Gamma _{{\mathrm{in}}}\), \(\sigma <1\) and \(\mathcal {A}\) is compact, there exists \(0<\tilde{r}<r\) (depending only on \(A, \sigma \) and r), such that if \(x\in B_{\frac{r}{2}}(\bar{x})\cap \Omega \)
Then (6.30) follows and we conclude the proof of the Lemma. \(\square \)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ghilli, D. On Neumann problems for nonlocal Hamilton–Jacobi equations with dominating gradient terms. Calc. Var. 56, 139 (2017). https://doi.org/10.1007/s00526-017-1225-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-017-1225-6