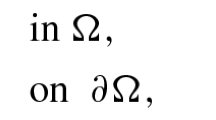On positive solutions for (p, q)-Laplace equations with two parameters

Abstract

We study the existence and non-existence of positive solutions for the (p, q)-Laplace equation $-\Delta _p u -\Delta _q u=\alpha |u|^{p-2}u+\beta |u|^{q-2}u$, where $p \ne q$, under the zero Dirichlet boundary condition in $\Omega$. The main result of our research is the construction of a continuous curve in $(\alpha ,\beta )$ plane, which becomes a threshold between the existence and non-existence of positive solutions. Furthermore, we provide the example of domains $\Omega$ for which the corresponding first Dirichlet eigenvalue of $-\Delta _p$ is not monotone w.r.t. $p > 1$.

Appendices

Appendix A: The Picone identity for the (p, q)-Laplacian

In this section we prove the variant of Picone’s-type identity (cf. [1]), which turns to be useful for problems with (p, q)-Laplacian.

First we prepare one auxiliary result. Denote

$$\begin{aligned} g(p,q;t):=\frac{(p-1) t^{p-2} + (q-1) t^{q-2}}{(p-1) \left( t^{p-1} + t^{q-1}\right) ^{\frac{p-2}{p-1}}}. \end{aligned}$$

(9.1)

Lemma 9

Let $1<q,p<\infty$. Then $\inf _{t>0} g(p,q; t) > 0$.

Proof

Let us denote $\widetilde{m} := \min \{p-1,q-1\}$. By standard calculations we get

$$\begin{aligned} g(p,q;t)&= \frac{(p-1) t^{p-2} + (q-1) t^{q-2}}{(p-1) (t^{p-1} + t^{q-1})^{\frac{p-2}{p-1}}} = \frac{\widetilde{m} t^{p-2}\left( \frac{p-1}{\widetilde{m}} + \frac{q-1}{\widetilde{m}} t^{q-p}\right) }{(p-1) t^{p-2} (1 + t^{q-p})^{\frac{p-2}{p-1}}} \\&\ge \frac{\widetilde{m} (1 + t^{q-p})}{(p-1) (1 + t^{q-p})^{\frac{p-2}{p-1}}} = \frac{\widetilde{m}}{p-1}(1 + t^{q-p})^{\frac{1}{p-1}} > \frac{\widetilde{m}}{p-1} > 0 \end{aligned}$$

for all $t > 0$, which completes the proof.

Proposition 8

Let $1<q<p<\infty$. Then there exists $\rho > 0$ such that for any differentiable functions $u > 0$ and $\varphi \ge 0$ in $\Omega$ it holds

$$\begin{aligned} (|\nabla u|^{p-2} + |\nabla u|^{q-2} ) \nabla u \nabla \left( \frac{\varphi ^p}{u^{p-1} + u^{q-1}} \right) \le \frac{|\nabla \varphi |^p + |\nabla (\varphi ^{p/q})|^q}{\rho }. \end{aligned}$$

(9.2)

Proof

First, by standard calculations we get

$$\begin{aligned}&|\nabla u|^{p-2} \nabla u \nabla \left( \frac{\varphi ^p}{u^{p-1} + u^{q-1}} \right) \nonumber \\&\quad = p |\nabla u|^{p-2} \nabla u \nabla \varphi \frac{\varphi ^{p-1}}{u^{p-1} + u^{q-1}} - |\nabla u|^{p} \varphi ^p \frac{(p-1) u^{p-2} + (q-1) u^{q-2}}{(u^{p-1} + u^{q-1})^2} \nonumber \\&\quad \le p |\nabla u|^{p-1} |\nabla \varphi | \frac{\varphi ^{p-1}}{u^{p-1} + u^{q-1}} - |\nabla u|^{p} \varphi ^p \frac{(p-1) u^{p-2} + (q-1) u^{q-2}}{(u^{p-1} + u^{q-1})^2} \end{aligned}$$

(9.3)

in $\Omega$. Applying to the first term Young’s inequality

$$\begin{aligned} ab =\frac{a}{\rho ^{\frac{p-1}{p}}}\,\rho ^{\frac{p-1}{p}} b \le \frac{|a|^p}{p\rho ^{p-1}} + \frac{\rho (p-1) |b|^{\frac{p}{p-1}}}{p} \end{aligned}$$

with $a= |\nabla \varphi |$, $b= |\nabla u|^{p-1} \frac{\varphi ^{p-1}}{u^{p-1} + u^{q-1}}$ and any $\rho >0$, we obtain

$$\begin{aligned} (9.3)&\le \frac{|\nabla \varphi |^p}{\rho ^{p-1}} + \frac{\rho (p-1) |\nabla u|^{p} \varphi ^p}{( u^{p-1} + u^{q-1} )^{\frac{p}{p-1}}} - |\nabla u|^{p} \varphi ^p \frac{(p-1) u^{p-2} + (q-1) u^{q-2}}{(u^{p-1} + u^{q-1})^2} \\&= \frac{|\nabla \varphi |^p}{\rho ^{p-1}} + \frac{\rho (p-1) |\nabla u|^{p} \varphi ^p}{( u^{p-1} + u^{q-1} )^{\frac{p}{p-1}}} \left[ 1 - \frac{(p-1) u^{p-2} + (q-1) u^{q-2}}{\rho (p-1) (u^{p-1} + u^{q-1})^{\frac{p-2}{p-1}}} \right] \\&= \frac{|\nabla \varphi |^p}{\rho ^{p-1}} + \frac{\rho (p-1) |\nabla u|^{p} \varphi ^p}{( u^{p-1} + u^{q-1} )^{\frac{p}{p-1}}} \left[ 1 - \frac{g(p,q;u)}{\rho }\right] \end{aligned}$$

in $\Omega$, where g(p, q; t) is defined by (9.1). Since Lemma 9 implies that $\inf _{t>0} g(p,q;t)$ is positive, we can choose $\rho _1 > 0$ small enough to satisfy $\inf _{t>0} g(p,q;t) \ge \rho _1$. This yields $[1-g(p,q;u)/\rho _1] \le 0$ in $\Omega$, and therefore

$$\begin{aligned} |\nabla u|^{p-2} \nabla u \nabla \left( \frac{\varphi ^p}{u^{p-1} + u^{q-1}} \right) \le \frac{|\nabla \varphi |^p}{\rho _1^{p-1}} \quad \mathrm{in}\ \Omega . \end{aligned}$$

(9.4)

Similarly, if we choose $\rho _2 > 0$ satisfying $\inf _{t>0} g(q,p;t) \ge \rho _2$, then for $\psi =\varphi ^{p/q}$ (note $p/q>1$ and $\varphi ^p=\psi ^q$) we obtain

$$\begin{aligned}&|\nabla u|^{q-2} \nabla u \nabla \left( \frac{\psi ^q}{u^{p-1} + u^{q-1}} \right) \nonumber \\&\quad \le \frac{|\nabla \psi |^q}{\rho _2^{q-1}} + \frac{\rho _2 (q-1) |\nabla u|^{q} \psi ^q}{( u^{p-1} + u^{q-1} )^{\frac{q}{q-1}}} \left[ 1 - \frac{g(q,p;u)}{\rho _2}\right] \le \frac{|\nabla \psi |^q}{\rho _2^{q-1}}. \end{aligned}$$

(9.5)

Combining now (9.4) with (9.5) and taking $\rho := \min \{ \rho _1^{p-1}, \rho _2^{q-1} \}$ we establish the formula (9.2).

Appendix B: Non-monotonicity of $\lambda _1(p)$ with respect to p

The main aim of this section is to provide sufficient conditions for $\lambda _1(p)$ to be a non-monotone function w.r.t. p.

Throughout this section, we write $\lambda _1(p, \Omega )$ to reflect the dependence of the first eigenvalue $\lambda _1(p)$ on the domain $\Omega$, on which it is defined.

By $B_R$ we denote an open ball in $\mathbb {R}^N$ of radius R. We don’t fix the center of $B_R$ and write $B_R \subset \Omega$ ($\Omega \subset B_R$) if such center exists.

Proposition 9

Assume that $r, R \in (1, e)$ and a domain $\Omega \subset \mathbb {R}^N$ $(N \ge 2)$ satisfy

$$\begin{aligned} \max \{1,e\ln R\}<r\le R<e \quad \mathrm{and} \quad B_{r} \subset \Omega \subset B_R. \end{aligned}$$

Then, the function $\lambda _1(p, \Omega )$ w.r.t. p has a maximum point $p^*>1$, and hence it is non-monotone.

In particular, if $\Omega =B_R$ with $R \in (1,e)$, then $\lambda _1(p,\Omega )$ is non-monotone w.r.t. p.

Proof

Note that $\lambda _1(p, \Omega )$ is a continuous function w.r.t. p (see [11, Theorem 2.1]). Hence, to prove that $\lambda _1(p, \Omega )$ possesses a maximum point $p^* > 1$ it is sufficient to show the existence of $p_0 > 1$ such that

$$\begin{aligned} \lambda _1(p_0, \Omega ) > \max \left\{ \lim _{p \rightarrow 1+0} \lambda _1(p, \Omega ), \lim _{p \rightarrow \infty } \lambda _1(p, \Omega )\right\} . \end{aligned}$$

(10.1)

First we find the corresponding limits. On the one hand, [11, Theorem 3.1] and [3, Corollary 5] yield that if there exists $r > 1$ such that $B_r \subset \Omega$, then

$$\begin{aligned} \lim _{p \rightarrow \infty } \lambda _1(p, \Omega ) = 0. \end{aligned}$$

(10.2)

On the other hand, it is proved in [15, Corollary 6] that

$$\begin{aligned} \lim _{p \rightarrow 1+0} \lambda _1(p, \Omega ) = h(\Omega ), \end{aligned}$$

(10.3)

where $h(\Omega )$ is the so-called Cheeger constant defined by

$$\begin{aligned} h(\Omega ) := \inf _{D \subset \Omega } \frac{|\partial D|}{|D|}. \end{aligned}$$

Here $|\partial D|$ and |D| are $(N-1)$- and N-dimensional Lebesgue measure of $\partial D$ and D, respectively. Note that Cheeger’s constant is known explicitly for some domains; for instance, $B_r$ has $h(B_r) = \frac{N}{r}$ (see [15]).

Now to get (10.1) we use the following estimation from [3, Theorem 2], which holds for any $\Omega \subset B_R$:

$$\begin{aligned} \lambda _1(p, \Omega ) \ge \frac{N p}{R^p}. \end{aligned}$$

(10.4)

Simple analysis of the function $y(p) = \frac{N p}{R^p}$ shows that if $R \in (1, e)$ then there exists a unique maximum point $p_0 = \frac{1}{\ln R} > 1$ of y(p), and $y(p_0) = \frac{N}{e \ln R}$.

Let us show now the existence of $r, R \in (1, e)$ such that for any $\Omega$ with $B_r \subset \Omega \subset B_R$ it holds $y(p_0) > h(\Omega )$. Then (10.2)–(10.4) will imply (10.1), which proves the assertion of the proposition.

From the monotonicity of Cheeger’s constant with respect to a domain (see [15, Remark 11]) it follows that $h(B_r) \ge h(\Omega )$, whenever $B_r \subset \Omega$. Therefore, it is enough to show that

$$\begin{aligned} y(p_0) = \frac{N}{e \ln R} > \frac{N}{r} = h(B_r) \end{aligned}$$

(10.5)

holds for some $r, R \in (1, e)$ with $r<R$. Inequality (10.5) is read as $r > e \ln R$. It is not hard to see that for any fixed $R \in (1, e)$ we have $\max \{1,e\ln R\}<R$, since the function $\ln t/t$ ($t>0$) has the maximum value 1 / e only at $t=e$.

Thus, for any $r, R \in (1, e)$ and $\Omega \in \mathbb {R}^N$ such that

$$\begin{aligned} \max \{1,e\ln R\}<r\le R<e \quad \mathrm{and} \quad B_{r} \subset \Omega \subset B_R, \end{aligned}$$

the inequality (10.1) is satisfied for some $p_0 > 1$, and this completes the proof.

Appendix C: Violation of the assumption (LI)

In this section we give a short one-dimensional example indicating that, in general, the first eigenvalues $\lambda _1(p, m_p)$ and $\lambda _1(q, m_q)$ of zero Dirichlet $-\Delta _p$ and $-\Delta _q$ on $\Omega$ with weights $m_p$ and $m_q$, respectively, can have the same eigenspace, that is, $\varphi _1(p, m_p) \equiv k \varphi _1(q, m_q)$ in $\Omega$ for some $k \ne 0$.

Let u be a positive $C^2$-solution of

$$\begin{aligned} \left\{ \begin{array}{ll} -u'' = |u|^{p-2}\, u &{}\quad \mathrm{in}\ (0, \pi ), \\ u(0) = u(\pi ) = 0,&{} \end{array} \right. \end{aligned}$$

where $p > 2$. Existence and regularity of such a solution is a classical example in various textbooks on nonlinear analysis (see, e.g., [9, Example 7.4.7, p. 485]).

It is easy to see, that u is also the first eigenfunction of zero Dirichlet $-\Delta$ on $(0, \pi )$ with the weight function $m_2(x) = |u(x)|^{p-2}$, with the corresponding eigenvalue $\lambda _1(2, m_2) =1$. Note that $m_2 > 0$ in $(0, \pi )$ and $m_2 \in L^{\infty }[0, \pi ]$, since $p > 2$.

At the same time, u becomes the first eigenfunction of $-\Delta _p$ on $(0, \pi )$ with weight $m_p(x) = (p-1) |u'(x)|^{p-2}$, with the eigenvalue $\lambda _1(p, m_p) =1$. Indeed,

$$\begin{aligned} \left\{ \begin{aligned} -(|u'|^{p-2} u')'&\equiv -(p-1)|u'|^{p-2} u'' \\&= (p-1) |u'|^{p-2} |u|^{p-2} u = m_p(x) |u|^{p-2} u \quad \mathrm{in}\ (0, \pi ), \\ u(0) = u(\pi )&= 0. \end{aligned} \right. \end{aligned}$$

Moreover, $m_p \in L^{\infty }[0, \pi ]$, since $p > 2$ and $u \in C^2[0, \pi ]$, and $m_p \ge 0$ in $[0, \pi ]$.

Therefore, $\lambda _1(2, m_2)$ and $\lambda _1(p, m_p)$ have the same eigenspace, i.e. (LI) is violated.