1 Introduction

Speed regulation of electric motors is a significant necessity in many industrial applications such as CNC, robotics, air conditioning, traction motors, and pumps. In all these applications, irrespective of any disturbance, the machine speed must be kept at the predefined value so that the system performs efficiently. Nowadays, direct current (DC) motors are the main horse power of several industrial plants [1]. Due to their attractive merits such as simple structure, low-cost installation, and high performance with a broad range of speed control characteristics, it is often to see these motors under service in robotics, 3D-printers, elevators, drones, cranes, electric vehicles, and other servo applications [2, 3]. To improve closed loop control precision and performance, advanced control algorithms are always welcome [4, 5].

Speed regulation of DC motors can be accomplished by controlling armature voltage or motor field current. However, in the permanent magnet DC (PMDC) motor case, the only alternative to achieve control requirements is to adjust armature voltage within the region below rated speed. For process control and industrial systems, there is enormous volume of control methodologies such as the classical ones pertaining to PID family and its cousins such as 2DOF/3DOF PID [6, 7], fractional order PID (FOPID) [8], fuzzy PID (FPID) [9], etc., whereas there are also other advanced algorithms based on optimal control [10], sliding mode [11], model predictive and adaptive control [12, 13], neural network [14], and H-∞ [15]. Design variations and modifications to PID, FOPID and FPID controllers are also noted in the literature to have augmented system performance [16,17,18,19]. Among the controllers above, classical PID variants are the ones that are still most implemented in practice, attributable to their ease of design, low computational cost and competing performance in most cases. However, for this type of controllers, the big stone to achieving high performance is their lack to manage nonlinearities.

To resolve this problem, several PID controllers added with nonlinear feature were also introduced [20,21,22]. More specifically, a sigmoidal function-based nonlinear PID controller was presented in [23, 24] to be used in robotic applications. Nonetheless, the performance of the above controllers was validated limited to simulation only and their practical feasibility was not checked.

In the present work, an exponential PI (EXP-PI) controller has been applied to speed regulation in PMDC motor. In the scheme that we introduce, the nonlinear gain in cascade with the linear fixed-gain PI controller is proposed to vary exponentially. To add more flexibility, the slope or sharpness of the exponential function along with its steady state or final value can be changed. An equivalent expression for the PI law is used as the anti-windup scheme to avoid integration overflow. Also, to reasonably set the controller parameters that offer good and stable performance in practice, a suitable cost function is defined and salp swarm algorithm (SSA) is invoked offline. Given this, no human interpterion is needed during the controller design stage. Several experimental results are presented to validate the potential of SSA tuned EXP-PI controller against changes in speed reference and external load disturbance. Moreover, comparisons with the results published recently are also presented.

The remainder of this paper is structured as follows. The PMDC motor model is provided in Sect. 2. Development of the EXP-PI concept is introduced in Sect. 3, and design of the controller is presented in Sect. 4. Section 5 is devoted to the stability of the proposed closed loop system. A study based on experimental findings is performed in Sect. 6 to indicate the credibility of our proposal. Finally, some conclusions are drawn in Sect. 7.

2 PMDC motor model

The standard equivalent circuit of a DC motor is comprised of a winding resistance \({R}_{a}\), a self-inductance \({L}_{a}\), and an induced or back electromotive force (emf) \(e\). The terminal equation is written as

$$v=e+{R}_{a}{i}_{a}+{L}_{a}\frac{d{i}_{a}}{dt},$$
(1)

where \(v\) is the applied armature voltage and \({i}_{a}\) is armature current. The expression for induced emf is derived as

$$e=K{\varnothing }_{f}{\omega }_{m},$$
(2)

In Eq. 2, \({\varnothing }_{f}\) is field flux per pole, \({\omega }_{m}\) is rotational speed and \(K\) is a constant based on the motor design. In PMDC motor, as the field flux is constant, the induced emf is rewritten as

$$e={K}_{b}{\omega }_{m},$$
(3)

where \({K}_{b}\) is the induced emf constant given by

$${K}_{b}=K{\varnothing }_{f}{\text{volt}}\cdot {\text{sec}}/{\text{rad}},$$
(4)

Thus, the electromagnetic torque or air gap torque is obtained by the ratio of armature power \({P}_{a}\) to \({\omega }_{m}\), given by

$${T}_{e}=\frac{{P}_{a}}{{\omega }_{m}}=\frac{{ei}_{a}}{{\omega }_{m}}={K}_{b}{i}_{a},$$
(5)

By modeling the load as a moment of inertia \(J\) with a viscous friction coefficient \(B\), then the acceleration torque \({T}_{a}\) driving the external load is calculated as

$$J\frac{{\text{d}}{\omega }_{m}}{{\text{d}}t}+B{\omega }_{m}={T}_{e}-{T}_{L}={T}_{a},$$
(6)

where \({T}_{a}\) stands for the load torque applied. Thus, the above equations form the dynamic model of the PMDC motor with load.

3 The EXP-PI controller structure

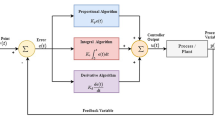
The concept behind using the Exp block before PI controller is presented in this section. In fact, this block functions as a variable gain \(k\), which is a nonlinear function of the error \(e\). When \(k=1\), the resulting controller is a classical PI controller with fixed gains. On the other hand, when \(k\) is a nonlinear function of the error, i.e., exponential function, the error signal is either amplified or attenuated using the nonlinear gain based on the magnitude of error. By acting on the error signal, the Exp block produces a nonlinear input signal for the PI controller as in Fig. 1.

Fig. 1
figure 1

The concept of EXP-PI controller

Full size image

As seen in Fig. 1, the Exp block receives the error signal and weighs it by \(\pm\, 1/\tau\) based on the error sign. Employing an exponential function performing as an activation function like in a neural network architecture, a nonlinear transformation is obtained. The nonlinear behavior of this controller lies in the nature of this function. There is also one gain, namely \(A\), to scale the output of Exp block and obtain \(\gamma \left(t\right)=k\cdot e\left(t\right)\), which is the nonlinearly transformed signal of \(e\). \(\gamma \left(t\right)\) is then fed to the PI controller block and eventually the control signal \({u}_{{\text{EXP}}-{\text{PI}}}\left(t\right)\) is generated from the EXP-PI controller output. Herein, the mathematical expression for the proposed nonlinear gain \(k\) based on exponential function can be given by

$$k=\left\{\begin{array}{cc}A\left(1-{\text{exp}}\left(-e\left(t\right)/\tau \right)\right)& e\left(t\right)>0\\ -A\left(1-{\text{exp}}\left(e\left(t\right)/\tau \right)\right)& e\left(t\right)\le 0\end{array}\right.,$$
(7)

where \(\pm A\) are the saturation limits of the function and \(\tau\) is added to have an adjustable slope or sharpness. As seen in Fig. 2, \(A\) is, in fact, a gain that scales the output of the function, whereas the slope of the function can be changed proportionally to \(\tau\).

Fig. 2
figure 2

Variation of the gain \(k\) as an exponential function of the error \(e\left(t\right)\) for different values of \(A\) and \(\tau\)

Full size image

Both \(A\) and \(\tau\) are considered in Eq. 7 to enable us have more degrees of freedom to design EXP-PI controller and accordingly have better system performance.

Using the nonlinear gains shown in Fig. 2, we let PI controller gains become adaptive. That is, it enables the controller to adapt its response to changeable conditions in the closed loop control system. When the error between the reference and actual values of the controlled variable is large, the gain amplifies the error to produce a large corrective control action so that the system output is driven to its reference hastily. As the time pasts and the error diminishes, the gain is decreased and thus excessive oscillations and unwanted overshoots in the response are prevented in this manner. As a result, the proposed controller is capable of accomplishing the two contradictory requirements of fast response (high initial gain) and non-oscillatory behavior (low gain), an ability that is not achievable at the same time by the classical fixed-gain PI controller. This conclusion is also valid when the system is exposed to disturbances whereby the nonlinear gain provides the system with remarkable disturbance rejection capacity.

In the EXP-PI controller, beside \({K}_{p}\) and \({K}_{i}\), \(A\) and \(\tau\) are also the important unknowns. All these gains need to be optimized properly to achieve improved performance. The best way to accomplish this task is to employ a suitable metaheuristic algorithm.

4 Improved speed servo system

In the current study, the performance assessment of the proposed concept is made by applying it to PI control scheme, which is more acceptable and effective in industrial applications. So, the new controller takes the name “Exponential PI (EXP-PI)”. In this controller, PI controller law is written as

$${u}_{{\text{EXP}}-{\text{PI}}}\left(t\right)={K}_{p}\gamma \left(t\right)+{K}_{i}{\int }_{0}^{t}\gamma \left(t\right){\text{d}}t,$$
(8)

Although Eq. 8 yields good control effort in simulation where the controller output is not bounded, it does not work satisfactorily in real-time experimentation because of the integration wind-up problem. To evade from this problem, we take the time derivative of two sides of Eq. 8 as

$$\frac{{u}_{{\text{EXP}}-{\text{PI}}}\left(k\right)-{u}_{{\text{EXP}}-{\text{PI}}}\left(k-1\right)}{T}={K}_{p}\frac{\gamma \left(k\right)-\gamma \left(k-1\right)}{T}+{K}_{i}\gamma \left(k\right),$$
(9)

where \(T\) is sample time with \(T>0\), \(\left(k\right)\) and \(\left(k-1\right)\) denote the current and previous sample time, respectively. Multiplying both sides of Eq. 9 by \(T\), we find:

$${u}_{{\text{EXP}}-{\text{PI}}}\left(k\right)-{u}_{{\text{EXP}}-{\text{PI}}}\left(k-1\right)={K}_{p}\left[\gamma \left(k\right)-\gamma \left(k-1\right)\right]+{K}_{i}T\gamma \left(k\right),$$
(10)

In Eq. 10, the difference between the \(\left(k\right)\) and \(\left(k-1\right)\) samples indicate a change for the given variable. So, Eq. 10 can be rewritten as

$${\Delta u}_{{\text{EXP}}-{\text{PI}}}\left(k\right)={K}_{p}\Delta \gamma \left(k\right)+{K}_{i}T\gamma \left(k\right),$$
(11)

Notice from Eq. 11 that the controller rule does not contain any integration term and thus eliminates the problem of excessive accumulation owing to the integral action. It generates the change of control action, not the actual value. So, to obtain the actual control action \({u}_{{\text{EXP}}-{\text{PI}}}\left(k\right)\), it requires to be accumulated by the previous control action as

$${u}_{{\text{EXP}}-{\text{PI}}}\left(k\right)={\Delta u}_{{\text{EXP}}-{\text{PI}}}\left(k\right)+{u}_{{\text{TSPI}}}\left(k-1\right),$$
(12)

Therefore, the EXP-PI controller has been provided the feature of anti-windup. In the next subsection, we explain a useful guideline to select controller gains properly so that the highest possible performance from the controller is achieved.

4.1 Designed cost function

It is noticeable from Eqs. 7 and 11 that the developed EXP-PI controller demands tuning the parameters \(A\) and \(\tau\) in addition to \({K}_{p}\) and \({K}_{i}\). As this is not an easy task, we address the problem by considering it from the viewpoint of optimization to evade from the risk of misleading performance owing to inappropriate parameter tuning based on trial-and-error.

To evaluate the fitness of each individual during optimization, we need to measure the quality of controlled responses quantitatively. Four commonly used error-based performance criteria to achieve this goal are integral squared error (ISE), integral absolute error (IAE), integral time-multiplied absolute error (ITAE) and integral time-multiplied squared error (ITSE). Among these, because ITAE and ITSE weight error with time, they consider errors at the start of the response less significantly than those occurring after a while. As such, they tend to produce systems with sluggish initial response. Squaring the error, ISE can eliminate large errors hastily, leading to a fast response, but with some considerable oscillation. As concerned to IAE, it yields less oscillation, but comparably slower response than ISE. As a result, to accomplish the two contradictory requirements of a fast response and no or mild overshoot, combination of ISE and IAE has been considered as a cost function in [25, 26] and also in the current paper. It can be also termed as figure of demerit (\({\text{FOD}}\)), which is expressed in Eq. 13.

$${\text{FOD}}={\omega }_{1}{\int }_{0}^{{t}_{s}}{e}_{s}^{2}{\text{d}}t+{\omega }_{2}{\int }_{0}^{{t}_{s}}\left|{e}_{s}\right|{\text{d}}t,$$
(13)

where \({e}_{s}\) is speed error, \({t}_{s}\) is the total simulation time in sec, \({\omega }_{i} \left(i=\mathrm{1,2}\right)\) is a weighting factor deciding the significance of each term in Eq. 13. It is found that good results are obtained when \({\omega }_{1}=0.01\) and \({\omega }_{2}=1\).

The two terms on the right-hand side of Eq. 13 are responsible for reducing the speed error as to enhance the speed response profile. Consequently, the optimization constraints in the current study are the EXP-PI controller gains. These are restricted to a particular range during the course of optimization. Thus, this paper considers to adjust the controller gains optimally by formulating it as an optimization problem as:

Minimize \({\text{FOD}}\), subject to:

$${{K}_{p}^{{\text{min}}}\le K}_{p}\le {K}_{p}^{{\text{max}}}, {{K}_{i}^{{\text{min}}}\le K}_{i}\le {K}_{i}^{{\text{max}}}, {A}^{{\text{min}}}\le A\le {A}^{{\text{max}}}, \,{\tau }^{{\text{min}}}\le \tau \le {\tau }^{{\text{max}}},$$
(14)

The superscripts \({\text{min}}\) and \({\text{max}}\) in Eq. 14 denote the minimum and maximum values of the tunable variables, which are set to 0 and 2 for \({K}_{p}\), \(A\), \(\tau\), and to 0 and 20 for \({K}_{i}\). To accomplish the optimization task, SSA has been applied as the recent and powerful optimizer.

4.2 Salp swarm algorithm

Salp swarm algorithm (SSA) is an optimization method recently introduced in [27]. The goal of SSA is to resolve optimization problems by mimicking the swarming behavior of salps living in oceans. Balanced exploration and exploitation propensities of this algorithm render it attractive for several applications needing for optimization. Compared to other existing algorithms, SSA is simple to code and uses relatively less computational resources. The algorithm is mainly guided by only one parameter whose value is reduced gradually during iterations to promote exploration for new areas in the initial stages and exploitation around a promising area in the final stages of optimization. Since its release, SSA has been found very prolific in diverse application areas such as classification [28], optimal conductor selection in a practical radial distribution system [29], optimization of power system stabilizer [30]/size of CMOS differential amplifier [31]/PV systems [32], optimal parameter identification of fuel cells [33], load frequency control [18, 19], economic load dispatch [34], etc. Good solution accuracy, fast convergence rate and low computation cost stressed in those researches are the attractive aspects of SSA, and the reasons why we prefer it to optimize the parameters of EXP-PI controller in the current study.

In SSA, the population is divided into two groups as leader and followers. The leader is the salp standing at the top of the chain, attacking in the direction of food source \(F\), while the remaining salps are all considered as followers. They form a salp chain as in Fig. 3 while navigating and foraging in deep oceans.

Fig. 3
figure 3

Chain of the salps

Full size image

For \(n\) salps (search agents) in a \(d\)-dimensional search space, the population of salps \(X\) can be generated by a \(n\times d\) matrix as:

$$X = \left[ {\begin{array}{*{20}l} {x_{1}^{1} } \hfill & {x_{1}^{2} } \hfill & \ldots \hfill & {x_{1}^{{d - 1}} } \hfill & {x_{1}^{d} } \hfill \\ {x_{2}^{1} } \hfill & {x_{2}^{2} } \hfill & \ldots \hfill & {x_{2}^{{d - 1}} } \hfill & {x_{2}^{d} } \hfill \\ \vdots \hfill & \vdots \hfill & {} \hfill & \vdots \hfill & \vdots \hfill \\ {x_{n}^{1} } \hfill & {x_{n}^{2} } \hfill & \ldots \hfill & {x_{n}^{{d - 1}} } \hfill & {x_{n}^{d} } \hfill \\ \end{array} } \right],$$
(15)

The following equation is used to update the position of the leader.

$${x}_{1}^{j}=\left\{\begin{array}{c}{F}^{j}+p\left({{\text{lb}}}^{j}+q\left({{\text{ub}}}^{j}-{{\text{lb}}}^{j}\right)\right),\quad r\ge 0.5\\ {F}^{j}-p\left({{\text{lb}}}^{j}+q\left({{\text{ub}}}^{j}-{{\text{lb}}}^{j}\right)\right),\quad r<0.5\end{array}\right.,$$
(16)

where \({x}_{1}^{j}\) and \({F}^{j}\) denote the position of the leader and food source in the \(j\) th dimension, respectively. \({{\text{lb}}}^{j}\) and \({{\text{ub}}}^{j}\) are the lower and upper bounds of the \(j\) th dimension for the problem. \(q\) and \(r\) are random numbers from the normal distribution 0–1. \(F\) is the best-obtained solution and it is the chain’s target. \(p\) is the main parameter of the algorithm defined in Eq. 17 [35].

$$p = 2e^{{ - \left( {4t/T} \right)2}}$$
(17)

where \(t\) and \(T\) stand for the current iteration and maximum iteration number, respectively. While \(t\) increases, the value of \(p\) is reduced to achieve an equilibrium between exploration and exploitation. That is, when \(p\) is high in the earlier iterations, Eq. 16 allows the search agents to move by large steps (exploration) whereas they are forced to move over a small range (exploitation) as the value of \(p\) reduces in the last iterations. As concerned to followers (\(i\ge 2\)), their position update rule is given by

$${x}_{i}^{j}=\frac{1}{2}\left({x}_{i}^{j}+{x}_{i-1}^{j}\right),$$
(18)

where \({x}_{i}^{j}\) is the location of the \(i\) th salp in the \(j\) th dimension. The pseudocode of SSA is provided in Algorithm 1.

Algorithm 1
figure a

Pseudocode of SSA

Full size image

4.3 Offline application of SSA to optimization of controller parameters

Using the drive system model and motor model in Section II, simulations are performed in a computer and the proposed EXP-PI controller parameters are obtained effectively by employing SSA. We do not explicitly know that the parameter values that we found are optimal, but we expect them as they are. The controller parameter values are then inserted into the DSP to make real-time implementations.

The EXP-PI controller has four tunable parameters; \(A\) and \(\tau\) for Exp block, and \({K}_{p}\) and \({K}_{i}\) for PI controller. Thus, each search agent in SSA is composed of these parameters. The SSA-based optimization process starts by initializing a number of salps randomly within their specified interval. For evaluation of cost function in Eq. 13, each candidate solution is used in the simulation model to obtain speed response from the controller. After assigning a fitness value, the salps are sent back to the optimization algorithm to evolve for the next iteration. Herein, for each cost evaluation, it is assumed that load torque and speed reference are changed from 0 to 1.2 Nm and from 0 to 2750 rpm, in steps of 0.2 Nm and 250 rpm, respectively (the upper limits are chosen based on the motor nameplate). Therefore, there are 84 different cases and the final cost is calculated as mean of these 84 costs. This is expressed mathematically by

$$J = \left( {\sum\limits_{{i = 1}}^{{{\text{NC}}}} {{\text{FOD}}_{i} } } \right)/{\text{NC,}}$$
(19)

where \({\text{NC}}\) is the number of cases equal to 84 and \(J\) is the mean cost for each search agent in SSA. By calculating the overall performance of solutions during optimization, their robustness against changeable system conditions is improved. In doing so, the requirement for resetting the controller parameters is alleviated when a change in load torque and/or speed reference occurs.

To provide more insights into the offline optimization of controller parameters and elucidate the above discourse further, the execution of SSA is depicted in detail in Fig. 4. Note that all these steps are implemented in a computer and the final solution returned by the algorithm including the best controller parameters are used and tested in experimental work.

Fig. 4
figure 4

Detailed execution of SSA during the optimization of controller parameters

Full size image

By following the above concept, SSA is run 50 times and the best controller parameters attained at the minimum value of \(J\) over 50 runs are provided in Table 1.

Table 1 Optimum values of EXP-PI controller parameters
Full size table

In the algorithm, the number of search agents is 50 while the maximum iteration number is set to 100. To show the convergence capacity of SSA, a few convergence graphs out of 50 runs with random initializations are saved and shown in Fig. 5. Note that the lower the value of \(J\), the better the controller parameters and the higher performance of the system we have. As seen, after a sharp drop in the initial stage of optimization, only small improvements on the solution quality are obtained because the best solution remains relatively constant around 48.8. Although the initial points are different, SSA is able to converge to a similar final solution within 40–50 iterations in each run. This outcome justifies that the selection of maximum iteration as 100 in the present research is sufficient for SSA to approach toward the global optimum solution.

Fig. 5
figure 5

SSA-based convergence trends of \(J\)

Full size image

5 Stability assessment

The stability analysis of control systems such as feedback loops is of primary importance to ensure that the system under control responds boundedly to any limited input [36, 37]. To address the stability concern, we consider the entire system as a linear time-invariant system. The open loop transfer function (TF) of the dynamical model for the DC motor is given in Eq. 20. The input and output of this function are voltage \(v\left(s\right)\) and angular speed \(\omega \left(s\right)\), respectively.

$${G}_{{\text{DCmotor}}}\left(s\right)=\frac{\omega \left(s\right)}{v\left(s\right)}=\frac{{k}_{t}}{\left({\text{Ls}}+R\right)\left(Js+B\right)+{k}_{t}{k}_{e}},$$
(20)

where \(J\) is the motor inertia, \(B\) is the viscous-friction coefficient of the rotor shaft, \(R\) is the armature resistance, \(L\) is the motor winding resistance, \({k}_{t}\) is the motor torque constant, which also equals to the motor back emf constant \({k}_{e}\). The following TF relating control input signal \({u}_{{\text{PI}}}\left(s\right)\) to processed speed error \(\widehat{e}\left(s\right)\) can be written for a classical PI controller.

$${G}_{{\text{PI}}}\left(s\right)=\frac{{u}_{{\text{PI}}}\left(s\right)}{\widehat{e}\left(s\right)}={K}_{p}+\frac{{K}_{i}}{s}=\frac{{K}_{p}s+{K}_{i}}{s},$$
(21)

As concerned to the exponential term that we use in front of the PI control scheme, for a step input, the speed error is positive (assuming no overshoot to simplify the analysis) and the nonlinear gain \(k\) in Eq. 7 becomes:

$$k=A\left(1-{\text{exp}}\left(-e\left(t\right)/\tau \right)\right),$$
(22)

For the Laplace transform of Eq. 22, we can arrive at:

$$G_{{{\text{EXP}}}} \left( s \right) = \frac{{u_{{{\text{EXP}}}} \left( s \right)}}{{e\left( s \right)}} = \frac{{A \cdot 1/\tau }}{{s + 1/\tau }} ,$$
(23)

Using the relevant motor and controller parameters, the TF block diagram of the entire PMDC motor speed servo system is demonstrated in Fig. 6.

Fig. 6
figure 6

TF block diagram of the entire PMDC motor speed servo system

Full size image

Consequently, the system has the following closed loop TF:

$$\frac{\omega \left(s\right)}{r\left(s\right)}=\frac{2.2114s+230.35}{9.57\cdot {10}^{-7}{s}^{4}+1.1117\cdot {10}^{-3}{s}^{3}+0.176{s}^{2}+9.6514s+230.35},$$
(24)

It is apparent from Eq. 24 that the studied system is a fourth order. It has a zero at \(-104.16\) and poles at \(\left\{-985.5, -102.12,-37.18\pm 3176i\right\}\). We see that all the poles have negative real parts and located far away from left to the imaginary axis in the complex plane. This finding completes the stability proof, assuring that our system is stable. The step response of the system represented by Eq. 24 is plotted in Fig. 7.

Fig. 7
figure 7

Step response of the system

Full size image

6 Experimental verification

In this section, the performance of the developed EXP-PI control scheme is evaluated on a DC motor drive system. The system block diagram is depicted in Fig. 8. It consists of a H-bridge converter to control the speed and rotation of motor, PMDC motor, permanent magnet DC generator (PMDG), DSP and other blocks that organize and synchronize the operation of the whole system. The EXP-PI controller works as the speed controller, whereas hysteresis current controller is used in the inner loop to regulate the motor armature current. PMDG is coupled with PMDC motor to apply external torque disturbances at the motor shaft, when required. As it is a PMDG, the output power and accordingly torque disturbance is speed-dependent. That is, the higher the speed, the greater the load torque.

Fig. 8
figure 8

The system block diagram

Full size image

The physical system showing the experimental prototype is given in Fig. 9. The PMDC motor model Sanyo Denki R730T-042EL7 is the motor to be controlled and the generator model Sanyo Denki T730B-569EL8N is used. The dc-link voltage is provided from Magna-Power DC power supply. In the converter, IGBTs of IXGH48N60C3D1 are adopted and the motor control algorithm is implemented in DSP of TMS320F28335 from Texas Instruments. The tested motor has a built-in tacho-generator with a voltage constant of 7.4 V/krpm, which is utilized to obtain speed responses. As there is no available torque sensor in our laboratory, we could not measure the load torque in experiments. Instead, motor armature current proportional to the applied load torque is measured with the Fluke 80i-110 s current probe. Both the speed and motor current are viewed and recorded by the Tektronix DPO 2024B oscilloscope.

Fig. 9
figure 9

The experimental system

Full size image

The PMDC motor nominal parameters are reported in Table 2.

Table 2 Sanyo Denki R730T-042EL7 motor nominal parameters
Full size table

In order to verify the feasibility and effectiveness of the EXP-PI controller, the PMDC motor was tested under two cases of experimentation such as speed regulation and torque disturbance rejection. In speed regulation test, constant/variable step speed references and reference trajectory are considered to be tracked. To show the contribution of our proposal, a comparison study with an anti-windup fixed-gain PI control scheme published previously [25] is also established. Symbiotic organisms search (SOS) algorithm was adopted in the respective paper to search for the PI controller parameters optimally, which yielded \({K}_{p}=0.265\) and \({K}_{p}=20\). All the results for the EXP-PI controller are obtained when the controller parameters remain fixed as in Table 1. This will also show us how robustly this controller performs.

6.1 Speed regulation performance

In the first test, speed control is performed when the step speed reference is \({n}^{*}=1500\) rpm and the PMDG terminals are open, generating no any torque. The resulting speed and current responses are displayed in Fig. 10. The desired speed and measured speed, \({n}^{*}\), \(n\), are shown with the red and turquoise traces, respectively, with a scaling factor of 270.27 rpm/div. The blue trace shows the motor armature current with a scaling factor of 5 A/div. This current scaling is used in all of the reported experiments below. Although the rise times of the speed responses seem similar for both controllers, the EXP-PI controller gives a better dynamic response with less overshoot and shorter settling time. This is attributed to the fact that the time required for the current to drop to its steady state value is shorter in the EXP-PI controller comparing with that in the PI controller. It should be also noticed that this response is comparable with that derived theoretically and displayed in Fig. 7

Fig. 10
figure 10

Experimental responses to a step speed reference of 1500 rpm a PI controller b EXP-PI controller

Full size image

In the following, the system transient and steady-state responses against step random changes in speed reference is analyzed. The speed reference is initially set to zero for the first 0.2. Afterward, it is set to 1000 rpm at \(t = 0.2\)s and 2000 rpm at \(t = 0.6\) s and 0 rpm at \(t = 1\) s and eventually 500 rpm at \(t = 1.4\) s. In this test, the PMDG terminals are closed, thus it applies torque disturbance proportional to the rotational speed. Critical observation of the responses in Fig. 11 reveals that both controllers is able to yield similar steady state performance because the motor speed in both cases tracks its reference tightly at steady state. Nonetheless, as concerned to the transient state, the EXP-PI controller performs better than the PI controller with respect to the overshoot generation and settling time. It is also noticeable in this figure that the motor current becomes different following each speed reference because of the load torque that changes all the time as the speed varies.

Fig. 11
figure 11

Experimental responses to random step speed references a PI controller b EXP-PI controller

Full size image

In the final speed regulation exercise, both controllers are used to track a desired trajectory. The reference trajectory considered for this test is \({n}^{*}=1500\times \left({\text{sin}}\left(t\right)+{\text{cos}}\left(0.5t\right)\right)\), and it is shown in Fig. 12. This signal has a period of \(T\cong 12.55\) s.

Fig. 12
figure 12

Desired trajectory

Full size image

Figure 13 depicts the actual trajectories and motor currents. As in the previous experiment, the PMDG terminals are closed. To display the measured speed adequately, the speed scaling factor has been changed to 675.67 rpm/div in this test. It is worth noting that during the experiment speed regulation with the PI controller was lost intermittently as seen in Fig. 13a. In such instants, PI controller could not perform stably and it yields a totally different response than the desired trajectory. As the controller is not capable of generating the reference current properly, the motor current is found to change abruptly within allowable limits. On the other hand, response in Fig. 13b clearly shows the capacity and potential of the EXP-PI controller in allowing the system to track the reference trajectory tightly. This claim can be confirmed by measuring the period of the speed response as \(T\cong 12.55\) s, which is equal to that in Fig. 12. Here, the motor current is controlled such in a way that the system tracks the desired trajectory.

Fig. 13
figure 13

Experimental responses to reference trajectory a PI controller b EXP-PI controller

Full size image

6.2 Torque disturbance rejection ability

In this test, the PMDG is allowed to introduce some torque disturbances at steady state by switching its terminals on and off, respectively, while the motor rotates at 2000 rpm. When the PMDG terminals are closed, the motor current rises up to 4 A as to compensate the increased load torque. As we can see in Fig. 14a, speed response obtained with the PI controller deviates notably from and settles again to its reference after a while following torque disturbances. However, the EXP-PI controller is found to achieve a far better disturbance rejection as in Fig. 14b, where the speed response is recovered quickly by rejecting torque disturbance very fast. This affirms that the EXP-PI controller has an outstanding robustness to abrupt load changes.

Fig. 14
figure 14

Experimental responses under load disturbance a PI controller b EXP-PI controller

Full size image

7 Conclusion

A fast step response without oscillations and good torque disturbance rejection are the main objectives to be met in a perfect control system. Satisfying one of these requirements undermines the performance of others when linear controllers are utilized. This paper presents a simple solution to this problem by introducing an exponential PI controller, taking advantages of a nonlinear gain that is a function of the error. The nonlinear characteristic of this gain comes from the exponential function designed. So, EXP-PI controller is simply obtained by adding an Exp block in front of the classical PI controller. The performance of the resulting controller is shown for speed regulation in PMDC motors. As optimizer, SSA is applied offline to search for optimal parameter values of the EXP-PI controller without human interpretation. Performance obtained is checked under several experiments where a comparison with a published PI control scheme is also presented. It is found that the EXP-PI controller enjoying the automatic adjustment of the gain performs satisfactorily in all the conditions of real-time implementation. Moreover, from the comparative results it is revealed that the EXP-PI controller achieves a more desirable level of performance in both speed reference tracking and disturbance attenuation. As a result, our proposal outshines its classical and published counterpart significantly without compromising on simplicity much.