Abstract
The main objective of this research study is to improve the performance of a standalone hybrid power system (SHPS) that consists of photovoltaic modules (PVMs), wind turbines (WTs), battery system (BS), and diesel engine (DE). The emphasis is on optimizing the system's design by incorporating demand response strategies (DRSs). Incorporating these strategies into the system can enhance system performance, stability, and profitability while also reducing the capacity of SHPS components and, consequently, lowering consumers' bills. To achieve this objective, the sizing model incorporates a novel indicator called the load variation factor (LVF). This paper assesses and contrasts various scenarios, including SHPS without DRS, with DRS, and with DRS but no DE. In this article, interruptible/curtailable (I/C) as one of the DRSs is incorporated into the model used for sizing issues. A newly developed optimization algorithm called the mountain gazelle optimizer (MGO) is utilized for the multi-objective design of the proposed SHPS. The utilization of MGO will facilitate achieving the lowest possible values for each of the following: cost of energy (COE), loss of power supply probability (LPSP), and carbon dioxide (CO2) emissions. This work introduces a mathematical model for the entire system, which is subsequently simulated using MATLAB software. The results reveal that among all the scenarios analysed, scenario iii — which has an LVF of 30% — is the most cost-effective. It has the lowest COE, at 0.2334 $/kWh, hence the lowest net present cost (NPC), at 6,836,445.5 $.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The surge in fossil fuel consumption and rapid economic expansion have exacerbated pollutant CO2 emissions. To combat this issue and preserve fossil fuels, renewable power sources (RPSs) offer a promising alternative. RPSs harness abundant and sustainable natural energy resources that do not deplete over time, providing a viable solution to reduce carbon emissions [1, 2]. As COP26 approaches, several countries have made new commitments, detailing their contributions to the global efforts towards achieving climate goals, particularly focusing on net zero emissions targets. As per this projection, the majority of the additional electricity production capacity by 2030 will be sourced from low-emission options. Energy from wind and solar is projected to be the main contributors, with a combined annual addition of almost 500 GW. As a result, coal utilization for power production is anticipated to decrease by 20% from its recent peak by the year 2030. With the successful implementation of all the announced pledges, global CO2 emissions attributed to energy are projected to decline by 40% by the year 2050 [3].
To ensure greater reliability, energy from wind and solar, which have a volatile nature, necessitates the integration of a unit for storing excess energy, such as a BS and/or a traditional power source, like a DE. Hybrid systems offer the flexibility to function either as grid-dependent or independent modes. In remote areas where the installation of electric utility becomes economically unviable due to escalating transmission line expenses, independent systems present a more favourable and optimal alternative [4]. One of the key difficulties faced in standalone hybrid power systems (SHPSs) is the task of obtaining the most efficient design. The major goal of optimal design is to reduce the expenses of producing electricity by SHPSs while ensuring a very reliable system and minimal pollutant emissions. Several assessment criteria are employed to determine the best size of SHPSs. Among the crucial indexes are reliability indexes such as loss of power supply probability (LPSP) and economic indicators like cost of energy (COE), along with environmental criteria such as CO2 emissions [5].
SHPSs often face challenges related to low load factors, which can lead to higher energy consumption from backup sources in order to satisfy overall demand, resulting in increased costs for the entire system. One of the solutions explored to address this issue is the implementation of suitable demand response strategies (DRSs). These strategies incentivize electricity consumers to decrease their consumption during system peak hours. This demand management approach helps utilize the available energy effectively without the need for additional generation [6]. DRSs can be classified into two primary categories based on the mechanism(s) behind changes in electrical load: incentive-based strategies (IBSs), which are system-led, and price-based strategies (PBS), which are market-led. Clients are offered “rewards” through IBSs when they reduce their energy consumption during peak times. Peak load management through PBSs is accomplished by implementing flexible electricity tariffs in order to smooth the load curve and relocate less essential loads from high-demand (peak) times to lower-demand (off-peak) times [7].
Lately, numerous optimization techniques have been utilized to address energy management challenges in SHPSs, aiming to achieve an optimal design. Several instances of these optimizers include the grey wolf optimizer [8], whale optimization algorithm [9], differential evolution [10], and harmony search algorithm [11]. Table 1 displays additional optimizers that have been employed to address the sizing issues of SHPSs integrating DRSs.
The key contributions of this study are summarized as follows:
-
Different configurations of SHPS are presented and their performance is assessed using commonly employed economic, technical, and environmental criteria.
-
Analysing different incentive payments to identify the maximum acceptable amount that would make the integration of DRS economically viable.
-
Applying a novel optimizer named “MGO,” designed to effectively address the sizing problem.
To provide an overview of the paper's structure, Sect. 2 discusses the modelling of the proposed SHPS, encompassing its components and power management strategy. Section 3 delves into the optimization problems. Section 4 is dedicated to presenting the results and subsequent discussions. Lastly, Sect. 5 concludes the paper.
2 Modelling of proposed SHPS
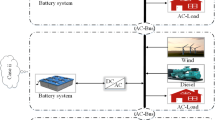
According to Fig. 1, the suggested SHPS comprises a PVM, WT, BS, DE, AC loads, and a bidirectional converter. The majority of SHPS commonly rely on renewable systems such as PVM and WT that produce power intermittently. To manage the intermittent nature of their generated power, these systems incorporate the BS as the primary backup to supply energy during periods of energy deficit. Additionally, a DE system serves as the final backup, providing additional power if the BS is unable to meet the load requirements. Figure 2 illustrates the concept of utilizing the BS as the primary backup due to its rapid response time and its relatively lower operational expenses when operating at low power levels [21].
Comparing the expenses associated with using BS versus DE [21]
2.1 PV modules
The electrical energy produced by solar modules can be affected in opposite ways by changes in ambient temperature and solar radiation. Higher ambient temperatures can decrease the output energy, while increased solar radiation can increase it. To calculate the amount of electrical energy that solar modules can generate (\({S}_{{\text{PVM}}}^{t}\)), the following formula can be used [22].
where \({N}_{{\text{PVM}}}\),\({\eta }_{{\text{PVM}}}\),\({S}_{R\_{\text{PVM}}}\),\({R}_{N}\),\({R}^{t}\),\({T}_{N}\),\({T}_{{\text{a}}}^{t}\), and \(\mu\) are the total number, efficiencies, capacity, radiation under standard conditions, radiation at time t, cell temperature at standard conditions, ambient temperature, and temperature coefficient of PVMs, respectively.
2.2 Wind turbine
The real output power (\({S}_{{\text{WT}}}^{t}\)) of a wind turbine can be determined by using the typical power curve characteristics of the turbine, as shown in the following calculation [23, 24].
where \({N}_{{\text{WT}}}\), \({\eta }_{{\text{WT}}}\), \({S}_{R\_{\text{WT}}}\), \({V}_{R}\), \({V}_{L}\) and \({V}_{H}\) denote the total number, efficiencies, rated power, rated speed, lowest and highest wind speed limitations of WT, respectively.
2.3 Diesel engine
A diesel engine is integrated into SHPS as a source of backup power to provide electricity when there is a shortage of power that cannot be met by the WTs, PVM, and BS. The fuel consumption rate of a DE (\({F}_{C\_{\text{DE}}}^{t}\)) in L/h can be determined on an hourly basis by using the following formula [25].
where \({S}_{{\text{DE}}}^{t}\) and \({S}_{R\_{\text{DE}}}\) indicate hourly generated power and rated power of DE, respectively, \({\gamma }_{1}\) and \({\gamma }_{2}\) signify fuel consumption coefficients that are approximately equal to 0.246 and 0.08415, respectively.
2.4 Battery
The purpose of BS is to retain any extra energy produced by available sustainable sources so that it can be utilized when required. If the amount of electricity provided by renewable sources exceeds the demand, the BS can be charged and used as a first backup for the SHPS, as shown by Eq. (4). On the other hand, if the demand for power is greater than what is being generated by renewable sources, the BS can be discharged to meet the demand as presented by Eq. (5) [26, 27].
where \({{\text{SOC}}}^{t}\), \({{\text{SOC}}}^{t-1}\), \({\beta }_{{\text{BS}}}\), and \({S}_{L}^{t}\) are BS's state of charge at a time \(t\), \(t-1\), self-discharge rate, and load demand, respectively, \({\eta }_{C}\), \({\eta }_{{\text{Ch}}}\) and \({\eta }_{{\text{DCh}}}\) denote converter, battery charging, and discharging efficiencies, respectively.
2.5 Bidirectional converter
A bidirectional converter has the ability to transfer power in both directions simultaneously. It can serve as a rectifier, allowing for the transfer of power from the AC bus to the DC bus while supplying DC power to the DC load and charging the BS. Alternatively, it can act as an inverter, providing an interface for power transfer from the DC bus to the AC load. Depending on the peak load requirement (\({S}_{L,P}\)), the capacity of the bidirectional converter (\({S}_{R\_C}\)) has been selected as follows [28]:
where \({\text{SF}}\) is the safety factor, and it's advised to have a converter capacity that's roughly 25–30% greater than the peak load.
2.6 Demand response strategy
The challenge of enhancing reliability without enlarging SHPS and incurring additional costs can be addressed by implementing DRSs. In this work, I/C strategy is applied, which is a form of IBSs, to decrease energy usage during peak hours. In this strategy, clients who plan to participate have already consented to the predetermined level of energy reduction and corresponding reward. During peak times, the amount of new load demand (\({S}_{L,{\text{new}}}^{t}\)) resulting from the I/C strategy implementation can be determined by considering the load variation factor (\({\text{LVF}}\)) as follows:
2.7 Power management strategy
During peak times, the load demand is adjusted to \({S}_{L,{\text{new}}}^{t}\) using Eq. (7) when DRS is implemented, while during all other periods, the load demand \({S}_{L}^{t}\) is met entirely. In this work, the primary source for supplying electricity to the load is by utilizing renewable systems (PVM and WT). As indicated by the flowchart in Fig. 3, if the available renewable systems are capable of fulfilling the load demand entirely, any surplus energy produced will be directed towards recharging the BS. Furthermore, any excess energy beyond the required charging level will be utilized in a dummy load. In the event that the renewable systems are unable to provide sufficient energy to meet the entire load demand, the BS will discharge power to meet the remaining load. When the combination of renewable systems and a BS cannot fully meet the electricity demand, a DE operation will be initiated to compensate for any energy deficit.
3 Optimization problem
3.1 Cost of energy
The cost of energy (\({\text{COE}}\)) is a commonly used criterion for evaluating the economic feasibility of SHPSs. It is calculated using the following formula [29]:
The annual total expense (\({\text{ATE}}\)) can be computed as follows:
where \({\text{ACE}},\)\({\text{ARE}}\),\({\text{AOME}},\)and \({\text{ADRSE}}\) denote the expenses annually of capital, replacement, operation and maintenance, and implementing the DRS, respectively.
where \({\text{CRF}}\), \({L}_{{\text{S}}},\)and \(i\) represent a factor affecting capital recovery, SHPS's lifespan, and interest rate, respectively.
The expense of implementing the DRS on an annual basis (\({\text{ADRSE}}\)) can be determined using the following formula [20]:
where \(p\) represents the incentive payment ($/kWh) made to clients for reducing their electricity consumption.
3.2 Loss of power supply probability
In simple terms, LPSP refers to the energy deficit in relation to the total amount of power required by the load during the entire operational time. LPSP values fall within the range of 0–1, where a value of zero indicates that the load demand has been completely supplied under all circumstances, while any nonzero value implies that the demand has not been entirely met. The LPSP is calculated by the relation as follows [30]:
3.3 Pollution (CO 2 ) emissions
One of the primary objectives of this research is to evaluate carbon emissions as an environmental criterion while designing SHPS. The amount of CO2 emitted by a DE (\({{\text{PE}}}_{{\text{DE}}}\)) is directly linked to its fuel consumption through the following relationship [31]:
, where \({F}_{{\text{E}}\_{\text{DE}}}\) denotes the emission factor of DE and has a value of 2.64 kg/L.
3.4 Objective function
The principal objective of the SHPS design, as stated in this research, is to diminish the \({\text{COE}}\), \({{\text{PE}}}_{{\text{DE}}},\) and \({\text{LPSP}}\), which can be established in the following manner:
3.5 Constraints
The SHPS components must adhere to specific constraints. First and foremost, as per Eq. (16), power balance must be maintained at all times. In this study, to avoid problems related to overcharging and undercharging, the BS's capabilities are restricted, as stated in Eq. (17). In this context, the maximum SOC (\({{\text{SOC}}}_{{\text{Max}}}\)) corresponds to the BS's complete capacity, while the minimum SOC (\({{\text{SOC}}}_{{\text{Min}}}\)) signifies the BS's inability to discharge completely. Another limitation presented in this research is the maximum allowable value of LPSP, which should not exceed 5%, as indicated in Eq. (18).
3.6 Mountain gazelle optimizer
The mountain gazelle optimizer is a recently developed meta-heuristic algorithm that takes its cues from the social interactions and hierarchical behaviour exhibited by wild mountain gazelles [32]. The MGO is mathematically formulated by incorporating the hierarchical and societal requirements exhibited by gazelles. This optimizer employs four major facets: bachelor male herds, maternity herds, solitary territorial males, and emigration, to explore and find food resources. Each gazelle (Xi) has the ability to join one of the three previously mentioned herds. The optimal global solution corresponds to the presence of a mature male gazelle within the territory of the herd. Figure 4 provides a depiction of the optimization process, illustrating the involvement of agents in the MGO. The algorithm introduced in this proposal includes exploitation and exploration stages, which involve the execution of four parallel processes. These processes are detailed below.
-
(i)
1st mechanism; territorial solitary males (\({M}_{{\text{TS}}}\))
MGO optimization procedure [32]
Highly territorial, mature male gazelles establish solitary territories. They engage in battle for territory or dominance over females. The model for their territory can be described as follows:
where \({M}_{g}\) represents the position vector of the best global solution, while \({R}_{i,1}\) and \({R}_{i,2}\) denote random integers either 1 or 2. The \({H}_{Y}\) vector represents the coefficient vector for the young male herd, calculated by Eq. (20). Additionally, the value of \(f\) is calculated utilizing Eq. (21), and \({C}_{R}\) is a coefficient vector that is randomly selected and updated following each iteration, calculated by Eq. (22).
where \({X}_{{\text{Ra}}}\) signifies a solution that is randomly selected from the range of \({\text{Ra}}\), \({M}_{{\text{pr}}}\) represents the average population, which is randomly generated (\(N/3\)). Here, \(N\) indicates population size. Moreover, \({R}_{1}\) and signify two random values that fall within the range of [0, 1].
where \({N}_{1}^{D}\) represents a random number sampled from a standard distribution. \(T\) stands for the maximum number of iterations and \(t\) refers to the current iteration.
In this context, \({R}_{3}\) and \({R}_{4}\) are random numbers chosen from the range [0, 1], while \({N}_{2}\), \({N}_{3},\)and \({N}_{4}\) represent random numbers generated from a normal distribution.
-
(ii)
2nd mechanism; maternity herds (\({H}_{{\text{M}}}\))
The presence of maternity herds is associated with the born of robust male gazelles. This behaviour can be represented and modelled as follows:
where \({R}_{i,3}\) and \({R}_{i,4}\) denote random integers either 1 or 2, while \({X}_{R}\) signifies the position vector randomly picked from the population.
-
(iii)
3rd mechanism; bachelor male herds (\({H}_{{\text{BM}}}\))
During their maturation, male gazelles actively seek out territories and female gazelles. In this pursuit, young male gazelles engage in conflicts with other males to assert control over the territory and female gazelles. This action can be represented and modelled by:
In this context, \({R}_{i,5}\) and \({R}_{i,6}\) are random integers that can take the values 2 or 1, while \({R}_{6}\) represents a uniform random number chosen from the range [0, 1].
-
(iv)
4th mechanism; emigration to explore and find food (\({E}_{{\text{EF}}}\))
Mountain gazelles exhibit foraging behaviour, and they are capable of travelling vast distances during emigration to access food sources. Additionally, they possess remarkable running speed and excellent jumping power. This action can be represented and modelled as:
In this context, \({\text{Ub}}\) and \({\text{Lb}}\) represent the upper and lower limits of the problem, respectively. Additionally, \({R}_{7}\) is a random integer that can take the values 0 or 1.
Each of the four processes,\({ M}_{{\text{TS}}}\), \({H}_{M}\), \({H}_{{\text{BM}}}\), and \({E}_{{\text{EF}}}\), are utilized to create new generations of mountain gazelles. At the end of each era, all-mountain gazelles are arranged in a rising pattern based on their performance. The top-performing gazelles are retained in the population for the subsequent generation, while the remaining gazelles are eliminated due to their perceived weakness.
Figure 5 depicts the flowchart of the MGO algorithm.
4 Simulation results and discussions
4.1 Study region
Ras Sudr is a town in Egypt's South Sinai Governorate that is located on the Gulf of Suez, was chosen as an actual case study of a SHPS. In the context of the case study, Fig. 6a displays the monthly variations in irradiance, ambient temperature, and speed of wind at a height of 50 m over the course of one year. Figure 6b shows the average monthly load demand over the same period [33]. Some of the SHPS component specifications are also presented in Table 2. In this research, the simulation software "MATLAB" was employed to create a model and enhance the size of a SHPS. The “MGO” optimization method was selected to address sizing challenges with a set of specific parameters, including 100 maximum iterations and 20 search agents.
4.2 An optimum design of scenario i
In this study's initial scenario, a combination system is created using renewable sources such as PVM and WT, along with backup units BS and DE, without considering DRS. By comparing the proposed scenarios listed in Table 3, it is clear that the system comprising 2000 PVMs, 20 WTs, 1980 batteries, and 100 kW DE has a COE of 0.2712 $/kWh, leading to an NPC of $7,942,540.6 and an LPSP of 0.012. Figure 7 demonstrates the convergence curves of various scenarios. At 406,923 kg, the highest annual carbon emissions are observed in this case. Figure 8 illustrates that sustainable sources account for 84% of the total energy supply, with PVMs contributing 39% and WTs providing 45%. The remaining 16% is covered by DE.
4.3 An optimum design of scenario ii
In this scenario, the system construction remains identical to the initial case, but with the implementation of DRS. To begin with, when LVF is set to 10%, the SHPS is comprised of 1690 PVMs, 19 WTs, 4580 batteries, and 75 kW DE. On the other hand, when LVF is increased to 30%, the hybrid system is made up of 1600 PVMs, 17 WTs, 4204 batteries, and 70 kW DE. The results indicate that scenario ii is financially more favourable compared to the case without DRS implementation. The results unambiguously show that as the LVF is raised from 10 to 30% while providing a 0.01 ($/kWh) incentive payment, SHPS becomes more cost-effective. At LVF = 10%, the COE amounts to 0.2422 $/kWh, leading to NPC of 7,093,224 and LPSP of 0.003. While, at LVF = 30%, the COE decreases to 0.2342, resulting in NPC of 6,860,664.7 and LPSP of 0.0023.
In the first scenario, the annual carbon emissions were at their highest. However, with LVF set at 10%, there was a notable reduction of 20%, bringing the emissions down to 325,687 kg. The most significant decrease occurred at LVF = 30%, where the emissions were further reduced to 307,914 kg, representing a 24% reduction compared to the initial scenario. If the LVF is 10%, renewable sources make up 85% of the overall energy supply, where PVMs contribute 37%, and WTs provide 48%. The remaining 15% is supplied by conventional energy (DE). On the other hand, when the LVF increases to 30%, renewable sources account for 84% of the total energy supply, with PVMs contributing 38% and WTs providing 46%. The remaining 16% is covered by conventional energy.
Table 4 clearly shows that increasing the incentive paid to the participants in the strategy will result in a corresponding increase in the SHPS cost. Based on the results, at LVF = 10%, incentive payments ranging from 0.01 to 0.07 $/kWh are considered acceptable for making the implementation of DRS cost-effective compared to the SHPS without DRS. On the other side, at LVF = 30%, the implementation of DRS is considered cost-effective compared to the SHPS without DRS, only when incentive payments fall within the range of 0.01–0.03 $/kWh, as highlighted by the bold values.
4.4 An optimum design of scenario iii
The final scenario in this work shares the same system configuration as the second one, except it does not include any conventional source (DE). The results indicate that if the LVF is set at 10%, the system will have 2850 PVMs, 21 WTs, and 6495 batteries, whereas if the LVF is raised from 10 to 30%, the hybrid power system will consist of 2850 PVMs, 18 WTs, and 6421 batteries. According to the results, scenario iii with LVF = 30% stands out as the most cost-effective among all cases, exhibiting the lowest COE at 0.2334 $/kWh, resulting in NPC of 6,836,445.5 $, and demonstrating LPSP of 0.0163. While, with LVF set at 10%, the COE amounts to 0.2418 $/kWh, leading to NPC of 7,082,116.6 $, and LPSP of 0.0184.
This scenario is environmentally friendly, as it does not include any traditional sources, resulting in zero carbon emissions. When the LVF is at 10%, the energy supply is divided, with 54% comes from PVMs and 46% from WTs. However, if the LVF is increased to 30%, the energy supply is divided differently, with PVMs contributing 59% and WTs providing the remaining 41%. According to the results, at LVF = 10%, the maximum acceptable incentive payment is 0.07 $/kWh, leading to a COE of 0.2705 $/kWh for making the implementation of DRS cost-effective. On the other hand, at LVF = 30%, the implementation of DRS is considered cost-effective only when the highest incentive payment allowed is 0.03 $/kWh, resulting in a COE of 0.2621 $/kWh, as highlighted by the bold values.
In this system configuration with LVF = 30%, Fig. 9 displays the hourly fluctuations of power produced for each component. The parameters include the energy supplied by PVMs (\({S}_{{\text{PVM}}}\)) and WTs (\({S}_{{\text{WT}}}\)), as well as the charging and discharging of energy in the BS (ECh and EDch). Lastly, it illustrates the SOC of the BS represented as a percentage of the battery bank's capacity (SOC %). Figure 10 depicts the results of the most cost-effective scenario (at LVF = 30%), specifically highlighting a particular day during the year (e.g., spanning from time 7656 to 7680). The daily load profile shows peak periods occurring between time 7670 and 7678. During these periods, a DRS is implemented, leading to a 30% reduction in the load. SDif represents the power gap between the energy needed for demand and the energy supplied by renewable sources. During the nighttime and early morning hours, no power is generated from PVMs. Consequently, the BS discharges to fulfil the power demand during these periods. When the sun comes up in the morning, the PVMs start generating more electricity, leading to the BS being charged by surplus energy.
5 Conclusion
This research paper focuses on the size optimization of different configurations under the influence of a DRS (I/C type). In a remote area of Egypt situated on the Gulf of Suez, SHPS comprising PVMs, WTs, BS, and conventional source of DE was utilized to provide power to the loads. The study employs the modern optimizer “MGO” to attain the technical, environmental, and economic goals of the SHPS. The results demonstrate that scenario iii (with LVF of 30%) is the most economically efficient one. It has the lowest COE of 0.2334 $/kWh and NPC of 6,836,445.5 $ among all the scenarios examined. This case leads to a 14% reduction in costs compared to the first scenario that was looked at. The last scenario is the most eco-friendly choice and avoids any carbon footprint (100% clean energy configuration). In this work, various incentive payment options are examined to determine the highest acceptable amount that would render the implementation of DRS economically viable. The results indicate that rewards between 0.01 and 0.07 $/kWh are deemed suitable for making the incorporation of DRS economically feasible compared to SHPS without DRS, when LVF is at 10%. However, when LVF is at 30%, DRS implementation is deemed cost-effective only if incentives fall within the range of 0.01–0.03 $/kWh. Future studies could incorporate various demand response strategies, along with an in-depth examination of their impact on hybrid system performance and a comprehensive analysis of their economic viability.
Data availability
All data generated or analysed during this study are included in this published article.
References
Choi YJ, Oh BC, Acquah MA, Kim DM, Kim SY (2021) Optimal operation of a hybrid power system as an Island microgrid in South-Korea. Sustainability 13(9):1–18. https://doi.org/10.3390/su13095022
Abd El Sattar M, Hafez WA, Elbaset AA, Alaboudy AHK (2020) Economic valuation of electrical wind energy in Egypt based on levelized cost of energy. Int J Renew Energy Res 10(4):1888–1891. https://doi.org/10.20508/ijrer.v10i4.11463.g8079
International Energy Agency. https://www.iea.org/reports/world-energy-outlook-2021/executive-summary. Accessed 31 Jul 2023
Haghighat A, Alberto S, Escandon A, Naja B, Shirazi A, Rinaldi F (2016) Techno-economic feasibility of photovoltaic, wind, diesel and hybrid electrification systems for off-grid rural electrification in Colombia. Renew Energy 97:293–305. https://doi.org/10.1016/j.renene.2016.05.086
Lian J, Zhang Y, Ma C, Yang Y, Chaima E (2019) A review on recent sizing methodologies of hybrid renewable energy systems. Energy Convers Manag 199:1–23. https://doi.org/10.1016/j.enconman.2019.112027
Akter H, Howlader HOR, Saber AY, Mandal P, Takahashi H, Senjyu T (2021) Optimal sizing of hybrid microgrid in a remote island considering advanced direct load control for demand response and low carbon emission. Energies 14(22):1–23. https://doi.org/10.3390/en14227599
Abdelsattar M, Hamdan I, Mesalam A, Fawzi A (2022) An overview of smart grid technology integration with hybrid energy systems based on demand response. In: 2022 23rd International Middle East power systems conference (MEPCON). IEEE, pp 1–6. Doi: https://doi.org/10.1109/MEPCON55441.2022.10021687.
Sharma S, Bhattacharjee S, Bhattacharya A (2016) Grey wolf optimisation for optimal sizing of battery energy storage device to minimise operation cost of microgrid. IET Gener Transm Distrib 10(3):625–637. https://doi.org/10.1049/iet-gtd.2015.0429
Yahiaoui A, Tlemçani A (2022) Superior performances strategies of different hybrid renewable energy systems configurations with energy storage units. Wind Eng 46(5):1471–1486. https://doi.org/10.1177/0309524X221084124
Kamal MM, Ashraf I, Fernandez E (2023) Optimal sizing of standalone rural microgrid for sustainable electrification with renewable energy resources. Sustain Cities Soc 88:1–21. https://doi.org/10.1016/j.scs.2022.104298
Güven AF, Yörükeren N, Samy MM (2022) Design optimization of a stand-alone green energy system of university campus based on Jaya-Harmony Search and Ant Colony optimization algorithms approaches. Energy 253:1–15. https://doi.org/10.1016/j.energy.2022.124089
Eltamaly AM, Alotaibi MA, Alolah AI, Ahmed MA (2021) A novel demand response strategy for sizing of hybrid energy system with smart grid concepts. IEEE Access 9:20277–20294. https://doi.org/10.1109/ACCESS.2021.3052128
Khezri R, Mahmoudi A, Haque MH (2020) Two-stage optimal sizing of standalone hybrid electricity systems with time-of-use incentive demand response. In: ECCE 2020—IEEE energy conversion congress exposition, pp 2759–2765. Doi: https://doi.org/10.1109/ECCE44975.2020.9236381.
Gamil MM, Senjyu T, Takahashi H, Hemeida AM, Krishna N, Lotfy ME (2021) Optimal multi-objective sizing of a residential microgrid in Egypt with different ToU demand response percentages. Sustain Cities Soc 75:1–16. https://doi.org/10.1016/j.scs.2021.103293
Gamil MM et al (2020) Optimal sizing of a real remote Japanese microgrid with sea water electrolysis plant under time-based demand response programs. Energies 13(14):1–22. https://doi.org/10.3390/en13143666
Eltamaly AM, Alotaibi MA, Elsheikh WA, Alolah AI, Ahmed MA (2022) Novel demand side-management strategy for smart grid concepts applications in hybrid renewable energy systems. In: Proccedings 2022 4th International youth conference radio electronics electrical power engineering REEPE 2022. Doi: https://doi.org/10.1109/REEPE53907.2022.9731431.
Javeed I, Khezri R, Mahmoudi A, Yazdani A, Shafiullah GM (2021) Optimal sizing of rooftop PV and battery storage for grid-connected houses considering flat and time-of-use electricity rates. Energies 14(12):1–19. https://doi.org/10.3390/en14123520
Li J, Zhao J, Chen Y, Mao L, Qu K, Li F (2023) Optimal sizing for a wind-photovoltaic-hydrogen hybrid system considering levelized cost of storage and source-load interaction. Int J Hydrog Energy 48(11):4129–4142
Sugimura M et al (2020) Optimal sizing and operation for microgrid with renewable energy considering two types demand response. J Renew Sustain Energy 12(6):1–12. https://doi.org/10.1063/5.0008065
Gharibi M, Askarzadeh A (2019) Size optimization of an off-grid hybrid system composed of photovoltaic and diesel generator subject to load variation factor. J Energy Storage 25:1–12. https://doi.org/10.1016/j.est.2019.100814
Zambrana V, Norman M (2018) System design and analysis of a renewable energy source powered microgrid. PhD Thesis, University Maryland, College Park. Doi: https://doi.org/10.13016/M2F47GX8G.
Mahmoud FS, Abdelhamid AM, Al Sumaiti A, El-Sayed AHM, Diab AAZ (2022) Sizing and design of a PV-wind-fuel cell storage system integrated into a grid considering the uncertainty of load demand using the marine predators algorithm. Mathematics 10(19):1–26. https://doi.org/10.3390/math10193708
Zhou J, Xu Z (2023) Optimal sizing design and integrated cost-benefit assessment of stand-alone microgrid system with different energy storage employing chameleon swarm algorithm: a rural case in Northeast China. Renew Energy 202:1110–1137. https://doi.org/10.1016/j.renene.2022.12.005
Diab AAZ, Sultan HM, Kuznetsov ON (2020) Optimal sizing of hybrid solar/wind/hydroelectric pumped storage energy system in Egypt based on different meta-heuristic techniques. Environ Sci Pollut Res 27(26):32318–32340. https://doi.org/10.1007/s11356-019-06566-0
Amara S, Toumi S, Ben Salah C, Saidi AS (2021) Improvement of techno-economic optimal sizing of a hybrid off-grid micro-grid system. Energy 233:1–20. https://doi.org/10.1016/j.energy.2021.121166
Mahmoud FS et al (2022) Optimal sizing of smart hybrid renewable energy system using different optimization algorithms. Energy Rep 8:4935–4956. https://doi.org/10.1016/j.egyr.2022.03.197
Abdelsattar M, Mesalam A, Fawzi A, Hamdan I (2024) optimizing grid-dependent hybrid renewable energy system with the African vultures optimization algorithm. SVU-Int J Eng Sci Appl 5:89–98. https://doi.org/10.21608/svusrc.2023.240888.1153
Demolli H, Dokuz AS, Ecemis A, Gokcek M (2021) Location-based optimal sizing of hybrid renewable energy systems using deterministic and heuristic algorithms. Int J Energy Res 45(11):16155–16175. https://doi.org/10.1002/er.6849
Islam MMM et al (2023) Techno-economic analysis of hybrid renewable energy system for healthcare centre in Northwest Bangladesh. Process Integr Optim Sustain 7:315–328. https://doi.org/10.1007/s41660-022-00294-8
Yazdani H, Baneshi M, Yaghoubi M (2023) Techno-economic and environmental design of hybrid energy systems using multi-objective optimization and multi-criteria decision making methods. Energy Convers Manag 282:1–20. https://doi.org/10.1016/j.enconman.2023.116873
Fodhil F, Hamidat A, Nadjemi O (2019) Potential, optimization and sensitivity analysis of photovoltaic-diesel-battery hybrid energy system for rural electrification in Algeria. Energy 169:613–624. https://doi.org/10.1016/j.energy.2018.12.049
Abdollahzadeh B, Gharehchopogh FS, Khodadadi N, Mirjalili S (2022) mountain gazelle optimizer: a new nature-inspired metaheuristic algorithm for global optimization problems. Adv Eng Softw 174:1–34. https://doi.org/10.1016/j.advengsoft.2022.103282
sNASA Power. https://power.larc.nasa.gov/data-access-viewer/. Accessed 31 Jul 2023
Zaki Diab AA, Sultan HM, Mohamed IS, Kuznetsov Oleg N, Do TD (2019) Application of different optimization algorithms for optimal sizing of PV/wind/diesel/battery storage stand-alone hybrid microgrid. IEEE Access 7:119223–119245. https://doi.org/10.1109/ACCESS.2019.2936656
Funding
Open access funding provided by The Science, Technology & Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB). Funding provided by the Science, Technology and Innovation Funding Authority (STDF) in cooperation with the Egyptian Knowledge Bank (EKB).
Author information
Authors and Affiliations
Contributions
MA, AM, AF, IH wrote the main manuscript text, prepared, and drown all figures. All authors reviewed and revised the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that, they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Abdelsattar, M., Mesalam, A., Fawzi, A. et al. Mountain gazelle optimizer for standalone hybrid power system design incorporating a type of incentive-based strategies. Neural Comput & Applic 36, 6839–6853 (2024). https://doi.org/10.1007/s00521-024-09433-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-024-09433-3