1 Introduction

In electrical power systems, the transformer is a critical component [1,2,3]. The transformer is represented by its steady-state model. The transformer model's parameters indicate its performance under various scenarios [4]. The proper estimation of transformer steady-state model parameters aids in the power transformer monitoring procedure. The requirement to improve the performance characteristics of transformers in both steady-state and transient circumstances necessitates the use of an accurate estimate process [5, 6]. The parameter estimation procedure is influenced by the presence of harmonics, saturation and transient circumstances in the transformer. To obtain an accurate calculation of the transformer parameters, real-time data were employed in conjunction with frequency response [7] or time-domain analysis [8,9,10,11]. By measuring the inrush current, the saturation of the transformer core was taken into account while estimating parameters [12]. The load terminal data, phase measurement unit (PMU), inrush current test, and open-circuit and short-circuit tests are all part of the real-time measurement process. In most circumstances, this technique necessitates turning off the transformer, which is regarded as an unrealistic approach.

Optimization approaches are one of the most preferred methods for resolving various electrical issues such as Electric machines, transformers, power lines, fuel cells and photovoltaic modules, batteries, management of a soft open point electrical distribution system, optimal power flow problem [13,14,15,16,17,18]. The optimization approaches evaluate the real and estimated value to reduce the variance between both cases [19,20,21]. The nameplate value is used as real value in several optimization algorithms [8, 11]. Coyote optimization algorithm (COA) [22], Jaya optimization algorithm (JOA) and particle swarm optimization (PSO) were used to estimate the parameters of equivalent circuit and motor design [14, 23]. Finally, the ideal estimated parameters are obtained by reducing the error between the reading values of power and voltage at various loading circumstances and the estimated values [5, 24,25,26,27].

In [28, 29], the chaotic optimization algorithm and gravitational search algorithms (GSA) are used to estimate the single-phase transformer parameters using the load test and nameplate data. By using short- and open-circuit tests, the bacterial foraging algorithm (BFA) is utilized to estimate the parameters data of three and single-phase transformer in [30]. Additionally, the artificial bee colony algorithm is used to estimate parameters of transformer in [31]. All these methods can be used with nameplate and load information while the transformer is in operation, eliminating the need to shut it down for testing.

Furthermore, these methods can be used to estimate the parameters of three-phase transformer like single-phase transformer parameters [32,33,34] and for the best design of a flux reversal high-speed three-phase machine [35]. References [36, 37] developed the coyote optimization algorithm (COA), a revolutionary metaheuristic optimization technique. COA has been used for a variety of purposes in the literature, including optimizing estimated parameters of fuel cell in [38] and estimating solar cell in [39]. TDO presents one of most recent optimization algorithms that were proposed by Dehghani et al. [40] to simulate the nature behavior of the Tasmanian devil during the portaging process. The Tasmanian devil insurance population is under constant observation, and imperfect detection and risk optimization has presented itself in [41].

PSO is a well-liked approach; however, because of its extremely basic features, applying it to a problem is not difficult. Similar to GA, one of PSO's biggest drawbacks is that, if its search range is too broad, it might easily fall into local search regions. Its convergence to a global optimum is therefore seldom certain. It is obvious that COA presently has major drawbacks that prevent convergence to the global optimum [42]. Despite these benefits, the Jaya algorithm has many drawbacks, such as unintended early convergence and the potential for getting stuck in local minima because of inadequate population [43].

Multiple approaches have been proposed in the literature to estimate transformers parameters without experimental work, using nameplate values used to determines the best values of transformer parameters to minimize absolute square error of computed and nameplate currents and voltages [22].

Despite the fact that metaheuristic methodologies can offer more reliable and accurate findings, the effectiveness of these methodologies is impacted by the depth of the search involved with the multimodal prospective of the electric transformer models and the reliance on adjusting algorithmic parameters, such as generation cycle and population size. Additionally, some algorithms include a number of particular control settings that significantly affect their performances and any inappropriate settings can raise the computational burden, and degrade the optimization accuracy with increasing the chance of getting trapped in local optima. Hence, there is still room for enhancement of the performance of the existing optimization schemes or developing new variants which can be supported by the perspective of the “no free lunch (NFL)” theory [44]. The relevant theory briefly implies that there is no single efficient algorithm that can address all optimization problems and outperform all the others. Therefore, the NFL theorem has prompted numerous researchers to enhance/modify the performance of current methods or develop new optimization schemes hoping to guarantee a strong performance while tackling various complicated optimization tasks. The aforementioned justifies why the Tasmanian devil optimization (TDO) [22] is presented as a promising alternative in this work to assess its efficacy in characterizing the parameters of electrical transformer at aiming to ensure a reliable operation for power system station.

Recently, the TDO was proposed by Dehghani et al. [40] to simulate the nature behavior of the Tasmanian devil during the food chasing process. The Tasmanian devil uses two distinct ways of feeding. The Tasmanian devil initially eats any carcass it comes upon. The second way is that it strikes the prey before eating it. The Tasmanian devil eating process was modeled to develop the TDO. The performance of TDO was assessed on 23 benchmark functions and the four-engineering design optimization. The results show the efficacy and efficiency of TDO through comparisons with some well-known state-of-the-art methods [40].

Despite the fact that TDO does not include any algorithm-specific controls, it still has two specific shortcomings. One is that there is not enough diversity in the population, which reduces the coverage of some promising areas and degrades the searching efficiency, and the other one is the lack for the leading strategy as the updating process is performed based on random searching which may lead to an imbalance among explorative and exploitative phases while increasing the chance of trapping in the local optima. Besides, no endeavors to adopt TDO for parameters estimation of electrical transformer have been purported in the literature.

This paper suggests an improved version of TDO using the Levy flight and spiralize learning strategies, named ITDO, for estimating transformer’ parameters precisely and reliably. In the ITDO, Levy flight strategy is integrated to scan the immediate areas of the promising solutions within the search space based on the Levy distribution perspective, thus maintaining the diversity of solutions. Furthermore, the spiralize learning strategy is promoted based on the logarithmic spiral conception to deepen the searching in the neighborhood of the promising solutions, thus emphasizing the exploitation ability. By this way, it is attempted to strike a good balance among the phases of explorative and exploitative abilities. The effectiveness of the ITDO algorithm is tested and examined through validating its performance on 33 benchmark problems which include classical test functions and CEC 2020 benchmarks with different landscape natures, where the comparisons were made with other optimization well-known methods [45, 46], including Harris hawk optimization (HHO) [47], sine–cosine algorithm (SCA) [48], Elman neural network for predicting the compressive and flexural strengths [49], jellyfish (JS) [34], grey wolf optimization (GWO) [50, 51], differential evolution (DE) [52, 53], particle swarm optimization (PSO) [54], double internal loop higher-order recurrent [55], adaptive control using a diagonal recurrent neural network [56], radial basis function network [57], adaptive dynamic programming for control and detection of Lyapunov stability [58], identification and adaptive predictive control using self-recurrent wavelet neural networks [59], neural network with external recurrence and Lyapunov stability analysis [60]. The statistical evaluations and nonparametric test using Wilcoxon test have ascertained the competitive and progressive performance of the ITDO when compared with other counterparts. On the other hand, the applicability of the ITDO is verified through characterizing the parameters of single-phase transformer.

The results revealed that the ITDO algorithm outperforms the other methods while achieving more accurate parameters of the electrical transformer model. The following are the primary characteristics of this work.

  1. 1.

    A newly developed ITDO approach based on the Levy flight and spiralize learning strategies, named ITDO, is presented to deal with the classical test functions, CEC 2020 benchmarks and electrical transformer model.

  2. 2.

    Levy flight is purported with the TDO to retain the solutions’ diversity, thus emphasizing the exploration searches, while spiralize learning strategy is integrated to deepen the neighborhood pattern while enhancing the exploitation propensities.

  3. 3.

    The efficacy of the suggested ITDO algorithm is verified through the comprehensive comparisons using eight state-of-the-art methods, where some performance indices include statistical tendency measures, convergence rate and descriptive analysis using box plot diagram, and Wilcoxon test has affirmed the great performance of the proposed variant.

  4. 4.

    The ITDO’ applicability is discovered by characterizing the accurate design parameters of the transformer equivalent circuit, and the reported outcomes proved the superiority of the ITDO as it highly achieves coincidence characteristics in terms of the efficiency and voltage regulation.

The sections of this study are organized as follows: Sect. 2 provides the statement for the function optimization and mathematical model of transformer characteristics. Section 3 presents the mathematical formulation of the original TDO and introduces the improved ITDO variant. Section 4 is to evaluate the performance of the ITDO on global optimization functions and extracting effective parameters of the transformer equivalent circuit. Finally, in Sect. 5, conclusions of this study are discussed.

2 Problem statements

This section describes the function optimization statement as well as the equivalent circuit of transformer with its optimization modeling.

2.1 Function optimization (FO)

FO is the process of finding the optimum solution for the candidate function of a several control variables over a certain search space. Several real-world situations may be formulated as FO problem using the following form [22]:

$$\begin{aligned} & {\text{Find}}\,x = \left( {x_1 ,x_2 , \ldots ,x_n } \right)^T \in R^n \,{\text{such}}\,{\text{that}} \\ & {\text{Min}}\,f{(}x{)} \\ & {\text{Subject}}\,{\text{to}}\,x_j^{\min_{j_j^{\max } } } \\ \end{aligned}$$
(1)

where x stands for the solution vector that involves \(n\) dimensions, \(R^n\) is the set of real numbers, f(x) indicates the goal function, and \(x_i^{\max }\) and \(x_i^{\min }\) define, respectively, the \(j{\text{th}}\) variable’ supper and the lower bounds.

2.2 Transformer equivalent circuit and optimization model

2.2.1 Mathematical model of transformer characteristics

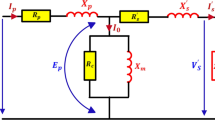
The current section discusses the mathematical representation of transformer models and the optimization of parameter estimation model. Figure 1 shows the per phase transformer's steady-state equivalent circuit [22].

Fig. 1
figure 1

Per phase equivalent circuit of transformer

Full size image

The following relationships can be found by applying Kirchhoff voltage and current rules to the transformer per phase equivalent circuit using Fig. 1:

$$\underline{E}_1 = \underline{V}_2^{\prime} + \underline{I}_2^{\prime} \underline{Z}_2^{\prime} .$$
(2)
$$\underline{V}_1 = \underline{E}_1 + \underline{I}_1 \underline{Z}_1$$
(3)
$$\underline{I}_1 = \underline{I}_o + \underline{I}_2^{\prime}$$
(4)
$$\underline{E}_1 = \underline{I}_o \underline{Z}_m$$
(5)

The primary current I1 and primary induced voltage E1 can be calculated using the four equations as follows:

$$\underline{I}_1 = \frac{{\underline{V}_1 + \underline{I}_2^{\prime} \underline{Z}_2^{\prime} }}{{\underline{Z}_1 + \underline{Z}_m }}$$
(6)
$$\underline{E}_1 = \underline{V}_1 - \underline{I}_1 \underline{Z}_1$$
(7)

The secondary referred voltage can be calculated from:

$$\underline V_2^{\prime} = \underline E_1 - \underline I_2^{\prime} \underline Z_2^{\prime}$$
(8)

As an equal value for the core magnetizing current value Im and the core active loss current value Im, the core current Io can be calculated as follows:

$$\underline{I}_o = \frac{{\underline{E}_1 }}{{\underline{Z}_m }} = \frac{{\underline{E}_1 }}{R_m } - j\frac{{\underline{E}_1 }}{X_m } = I_{e + h} - jI_m$$
(9)

The voltage regulation of the transformer is as follows:

$${\text{VR}} = \frac{{V_1 - V_2^{\prime} }}{V_1 }$$
(10)

The following formulas can be used to calculate the, the power input Pin, the power output Po, and primary power factor pf1:

$$P_{\text{o}} = real(V_2^{\prime} \times I_2^{{\prime} *} )$$
(11)
$$P_{{\text{in}}} = real(V_1 \times I_1^* )$$
(12)
$$pf_1 = \cos (angle(\underline{I}_1 ))$$
(13)

The transformer's efficiency can be estimated using the following formula:

$$\eta_{\text{r}} = \frac{{P_{\text{o}} }}{{P_{{\text{in}}} }}$$
(14)

The corresponding circuit parameters R2, R1, Rm, X2, X1 and Xm must be identified as precisely as feasible. Optimization methods are used to achieve this goal.

2.2.2 Optimization of parameter estimation model

Minimizing the difference between the estimated and manufacturer's values represents the objective or goal function regarding the parameter estimation issue of electric power transformer. In this sense, the estimated parameters, \(R_1 ,X_1 ,R_2 ,X_2 ,R_{e + h} ,X_m\), can affect Eqs. (2)–(14) that, in turn, affects efficiency, the primary current and the power factor of the load. Therefore, it is necessary to assess the estimated values with the manufacturer's data.

The fractional error of the transformer efficiency, primary current and primary power factor can be calculated from:

$$f_1 = \frac{e\eta_r - m\eta_r }{{m\eta_r }}$$
(15)
$$f_2 = \frac{eI_1 - mI_1 }{{mI_1 }}$$
(16)
$$f_3 = \frac{epf - mpf}{{mpf}}$$
(17)

In this case, achieving an accurate estimate requires minimizing the sum of relative error squares (SRRS) between the estimated and manufacturer's values. The following formula can be used to express the SRRS.

$${\text{SRRS}} = f_1^2 + f_2^2 + f_3^2$$
(18)

The following is the presentation of this work's objective function (OF):

$${\text{OF}} = {\text{min }}({\text{SRRS}})$$
(19)

Boundary restrictions on the control variables are subjected to Eq. (20) as follows:

$$\begin{aligned} R_1^{\min } & \le R_1 \le R_1^{\max } ,X_1^{\min } \le X_1 \le X_1^{\max } \\ R_2^{\min } & \le R_2 \le R_2^{\max } ,X_2^{\min } \le X_2 \le X_2^{\max } \\ R_m^{\min } & \le R_m \le R_m^{\max } ,X_m^{\min } \le X_m \le X_m^{\max } \\ \end{aligned}$$
(20)

3 The proposed methodology

The primary framework for the Tasmanian devil optimization (TDO) is presented in this section. Additionally, the proposed ITDO variant's structure is described.

3.1 The basics of TDO algorithm

In this section, the mathematical model regarding the Tasmanian devil optimization (TDO) is introduced [40]. TDO presents one of most recent optimization algorithms that were proposed by Dehghani et al. [40] to simulate the nature behavior of the Tasmanian devil during the portaging process. TDO was proposed based on Tasmanian devil behavior while searching for food source. It offers two strategies: attacking and eating live prey or carrion on dead animals. TDO is investigated on 23 benchmark function to evaluate its performance. For further analysis, it is applied for optimizing four engineering design tasks. Its performance is evaluated by comparisons with eight well-known optimization algorithms, where the simulation results have been affirmed its competitive performance. The main stages of TDO are described in detail as follows.

3.1.1 Initialization

TDO is like the other population-based algorithms that start its iterative process with some searcher agents named Tasmanian devils. In this regard, a population of agents is created randomly within the search space; each agent of a population represents a vector that contains several elements equal to the number variables. This initialization is expressed as follows.

$$X_{ij} = x_j^{\min } + rand.\left( {x_j^{\max } - x_j^{\min } } \right),\quad i = 1,2, \ldots ,M, j = 1,2, \ldots ,n$$
(21)

where \(rand\) denotes for a random value generated based on uniform distribution from the interval [0,1]. \(x_j^{\min }\) and \(x_j^{\max }\) stand for lower and maximum limits regarding the \(j{\text{th}}\) dimension search space. \(M\) and \(n\) define the size of Tasmanian devils and total number of variables. After the initialization, the quality of the candidate solution is evaluated by the objective function (OF). Based on the OF, the best objective function value is regarded as best member in the population. This best member is updated each iteration by Tasmanian devil feeding tactics. Any Tasmanian devil has the ability to consume carrion or seek food. In TDO, it is presumed that there is a 50% chance that one of these tactics will be chosen. According to this idea, just one of these two procedures is used to update each Tasmanian devil in TDO iteration.

3.1.2 Eating carrion: exploration stage

Sometimes, rather than going hunting, Tasmanian devils choose to eat local carrion. In the vicinity of the Tasmanian devil, there are other predatory creatures that seek enormous prey but are unable to consume it all. Additionally, these creatures might not be able to consume enough of their prey until the Tasmanian devil shows up. In this context, Tasmanian devil prefers to eat these carrions. The behavior of the Tasmanian devil when searching for carrion in its habitat is similar to the algorithm iterative process in a problem-solving environment. The Tasmanian devil tactic truly exemplifies the potential of TDO exploration in identifying the initial optimal location by scanning several regions of the search field. In terms of optimization viewpoint, for each Tasmanian devil, it is presumed that other population members' location within the search area corresponds to carrion locations. In this line, one of these situations is selected randomly as the target carrion for the \(i\mathrm{th}\) Tasmaniandevil as follows.

$$C_i = X_k , i = 1,2, \ldots ,M, k \in \left\{ {1,2, \ldots ,M{|}k \ne i} \right\}$$
(22)

where \({C}_{i}\) stands for the chosen carrion by \(i\mathrm{th}\) Tasmanian devil and \(k\) is randomly chosen from 1 to \(M\).

According to the selected carrion, the new location of the Tasmanian devil is determined as follows.

$$x_{i,j}^{{\text{new}}, S1} = \left\{ {\begin{array}{*{20}l} {x_{ij} + r \cdot \left( {c_{ij} - I \cdot x_{ij} } \right),} \hfill & {F_{C_i } < F_i } \hfill \\ {x_{ij} + r \cdot \left( {x_{ij} - c_{ij} } \right),} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(23)
$$X_i = \left\{ {\begin{array}{*{20}l} {X_i^{{\text{new}}, S1} ,} \hfill & {F_i^{{\text{new}}, S1} < F_i } \hfill \\ {X_i ,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(24)

Here, \({X}_{i}^{new, S1}\) defines the new position of the \(i\mathrm{th}\) Tasmanian devil using the first strategy, \({x}_{i,j}^{new, S1}\) is the element of the \(j\mathrm{th}\) dimension (variable), \({F}_{i}^{new, S1}\) defines the objective function value for the new status, \({F}_{{C}_{i}}\) denotes objective function for the chosen carrion, \(r\) stands for a random number within the range [0, 1], and \(I\) denotes a random integer number which can be 1 or 2.

3.1.3 Eating prey (exploitation phase)

In this stage, the Tasmanian devil is to hunt and eat prey, where this is carried out by two phases. In the first one, it is scanned the region to select the prey that can attack it. Then, in the second phase, after approaching the victim, the Tasmanian devil chases it, stops it and begins to eat. Therefore, the modeling of the first phase is expressed by Eqs. (25) to (27). In the second phase, the updating of the \(i\mathrm{th}\) Tasmanian devil is performed by considering the location of other population members as the prey’s position. Therefore, the \(k\mathrm{th}\) member is selected at random to represent prey position. The process of prey selection is expressed as follows.

$$P_i = X_k , i = 1,2, \ldots ,M, k \in \left\{ {1,2, \ldots ,M{|}k \ne i} \right\}$$
(25)

where \({P}_{i}\) stands for the chosen prey by \(i\mathrm{th}\) Tasmanian devil, \(k\) is chosen randomly from 1 to \(M\).

According to the selected prey, the second phase is carried out to obtain the new position of the Tasmanian devil as follows.

$$x_{i,j}^{{\text{new}}, S2} = \left\{ {\begin{array}{*{20}l} {x_{ij} + r \cdot \left( {p_{ij} - I \cdot x_{ij} } \right),} \hfill & {F_{P_i } < F_i } \hfill \\ {x_{ij} + r \cdot \left( {x_{ij} - p_{ij} } \right),} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(26)
$$X_i = \left\{ {\begin{array}{*{20}l} {X_i^{{\text{new}}, S2} ,} \hfill & {F_i^{{\text{new}}, S2} < F_i } \hfill \\ {X_i ,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(27)

Here, \(X_i^{{\text{new}},S2}\) defines the new position of the \(i{\text{th}}\) Tasmanian devil using the second strategy, \(x_{i,j}^{{\text{new}},S2}\) is the element of the \(j{\text{th}}\) dimension (variable), \(F_i^{{\text{new}},S2}\) defines the objective function value for the new status, and \(F_{P_i }\) denotes objective function for the chosen prey.

The Tasmanian devil chases its prey throughout the area of the attacked location to mimic this process of chasing. The Tasmanian devil uses Eqs. (28)–(30) to imitate the stage of prey pursuit. At this step, the Tasmanian devil location is regarded as the center of a neighborhood where the process of hunting prey takes place. The neighborhood radius indicates the area within which the Tasmanian devil follows its prey, and it is determined using (28). Thus, a new location according to the chasing process within this neighborhood is expressed by Eq. (29).

$$R = 0.01\left( {1 - t/T} \right),$$
(28)
$$x_{i,j}^{{\text{new}}} = x_{ij} + \left( {2r - 1} \right) \cdot R \cdot x_{ij}$$
(29)
$$X_i = \left\{ {\begin{array}{*{20}l} {X_i^{{\text{new}}} ,} \hfill & {F_i^{{\text{new}}} < F_i } \hfill \\ {X_i ,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(30)

where \(R\) defines the neighborhood radius of the attack location's point. \(t\) and \(T\) define the iteration counter and maximum size of iterations, respectively. \(X_i^{{\text{new}}}\) denotes the new position of the \(i{\text{th}}\) Tasmanian devil in vicinity of \(X_i\), \(x_{i,j}^{{\text{new}}}\) defines the \(j{\text{th}}\) element or variable of \(X_i^{{\text{new}}}\) and \(F_i^{{\text{new}}}\) denotes the new objective function value of \(X_i^{{\text{new}}}\). The flowchart of TDO is illustrated in Fig. 2.

Fig. 2
figure 2

Flowchart of TDO

Full size image

3.2 The proposed ITDO

For any optimization process, an adequate balance between the use of the search space's exploration and exploitation is required to reach a globally optimal solution. Exploration, also known as diversification, in the search space entails searching globally, whereas exploitation, also known as intensification, entails searching locally, based on the best solution available at the time. The algorithm's performance is negatively impacted by excessive exploration and exploitation since it increases the chances of trapping in the local optima and increases the convergence time. The conventional TDO employs a randomly generated position from the population as the prey’s position whether for the exploration or exploitation phase. This can increase the strength of the exploration capability of an algorithm but can weaken the exploitation capability of the algorithms by exhibiting slow convergence and sometimes leading to stagnation at local optima. To avoid this shortage, a novel improved Tasmanian devil optimization (ITDO) is presented based on two strategies. Two tactics are embedded in the conventional TDO to improvise its solution accuracy as well as convergence acceleration, which are (i) Levy flight strategy to offer further explorations and (ii) spiralize elite learning strategy to emphasize the exploitation ability.

3.2.1 Levy flight strategy

The Levy distribution (LD) was introduced by the French Levy [61] as a random flight process based on a probability distribution function. Due to be effective improvement on the algorithm design, it is flourished in some of the recently reported works [62,63,64]. The Levy flight step can strength the algorithm's capacity, where the Levy flights with tiny step widths can improve the exploitation ability while the Levy flights with huge step widths can raise the likelihood of avoiding the traps in local or misleading optimums. The mathematical definition of the Levy flight distribution can be expressed as follows [64].

$$L\left( {s, \gamma ,\mu } \right) = \left\{ {\begin{array}{*{20}l} {\sqrt {{\frac{y}{2\pi }}} e^{\left( {\frac{ - \gamma }{{2(s - \mu )}}} \right)} \left( {\frac{1}{{(s - \mu )^{3/2} }}} \right)} \hfill & {0 < \mu < s < \infty } \hfill \\ 0 \hfill & {s \le 0} \hfill \\ \end{array} } \right.$$
(31)

where \(s\) defines the samples, \(\gamma\) represents the scale parameter to control the distribution and \(\mu\) defines transmission factor. The Levy flight distribution is defined by the following.

$$F\left( k \right) = e^{\left( { - \alpha \left| k \right|^\beta } \right)} ,{ }\beta \in [0,{ }2]$$
(32)

where \(\beta\) defines a distribution index and \(\alpha\) denotes the scaling parameter. The step length, \(s\), is determined by the following expression [64].

$${\text{s}} = \left( {\frac{u}{{\left| v \right|^{\left( {1/\beta } \right)} }}} \right)$$
(33)

\(u\) and \(v\) are two parameters that have the Gaussian distributions as follows:

$$u\ N\left( {0,\sigma_u^2 } \right), v\ N\left( {0,\sigma_v^2 } \right)$$

where \(\sigma_u^2\) and \(\sigma_v^2\) define the standard deviations that are given as follows.

$$\sigma_u = \left\{ {\frac{{{\Gamma }\left( {1 + \beta } \right)\sin \left( {\frac{\pi \beta }{2}} \right)}}{{\beta .\Gamma \left( {\frac{1 + \beta }{2}} \right) \cdot { }2^{\frac{(\beta - 1)}{2}} }}} \right\}^{1/\beta } ,\quad \sigma_v = 1$$
(34)

where \(\Gamma \left( . \right)\) denotes the Gramma function.

In this step, the LF is used to update the solution obtained TDO to intensify the searching around best obtained solution so far (\(x_{{\text{best}}}\)) by the following equation.

$$x_i^{{\text{LF}}} = x_i + (2 \cdot rand - 1) \cdot levy(\beta ) \cdot (x_{{\text{best}}} - x_i )$$
(35)
$$x_i = \left\{ {\begin{array}{*{20}l} {x_i^{{\text{LF}}} } \hfill & {F\left( {x_i^{{\text{LF}}} } \right) < F(x_i )} \hfill \\ {x_i } \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(36)

where \(x_i^{{\text{LF}}}\) denotes the generated new position using the Levy flight process, \(x_i\) is the current solution and \(rand\) stands for random number from the interval [0, 1]. Equation (30) says that the current solution is substituted with updated one using Levy flight concept if it is better; otherwise, current one is continued.

3.2.2 Spiralize elite learning strategy

Since the original TDO performs the updating process by taking into account the positions of two randomly generated solutions which may lead to lose the promising regions, so it is vital to emphasize the exploitation ability by performing further searches around the best so far solution. In this context, the logarithmic spiral step (LSS) is introduced around the best solution. This step is performed such that it decreases gradually with the growth of iteration.

$${\text{LSS}} = Ae^{ - b \cdot t} {\text{cos}}(2c\pi t)$$
(37)
$$A = \left( {\frac{U_i - L_i }{2}} \right)*\left( {\frac{T - t}{T}} \right)^2 , U_i = \max \left( {X_i } \right), L_i = \min \left( {X_i } \right)$$
(38)
$$x_i^{{\text{LSS}}} = x_{{\text{best}}} + {\text{LSS}}$$
(39)

where \(x_i^{{\text{LSS}}}\) denotes the generated new position using the logarithmic spiral step, \(A\) define shrinking radius, \(b\) denotes a constant that determines the logarithmic spiral shape, the \(t\) is a parameter that determine how much the next position should be close to the best solution and \(c\) is the number of spirals. The flowchart of ITDO is shown in Fig. 3.

Fig. 3
figure 3

Block diagram for the main stages of the problem algorithm

Full size image

4 Experiment results and validations

To assess the effectiveness of ITDO, two validation analysis series are utilized, and they can be summed up as follows: The initial numerical verification is carried out on 10 classical benchmark problems and the latest IEEE CEC 2020 benchmark problems that encompass of unimodal, multimodal, hybrid and composition natures. The details regarding the studied functions are presented in Tables 9 and 10 in Appendix. These tables contain the function name, nature of the function, description, number of variables \((d)\), range of the variable (RV) and optimum solution (\(F_{{\text{opt}}}\)). A comprehensive comparisons between the proposed ITDO and some well-known algorithms including jellyfish (JS) [34], Harris hawk optimization (HHO) [47], grey wolf optimization (GWO) [51], sine–cosine algorithm (SCA) [48], DE [52], PSO [54], and original TDO [40]. Furthermore, to demonstrate its purported performance, ITDO is put up against some other competitors reported from the literature. The second task aims to gauge the performance of ITDO on the parameter’s estimation of the single-phase transformer.

All experiments are carried out on a Laptop with AMD Ryzen 5 5600u with Radeon Graphics 2.30 GHz CPU, 16 GB RAM under 64-bit Windows 10OS. MATLAB_R2020a is used for the implementation of the presented algorithms.

The parameter configurations for the employed algorithms are suggested as in their corresponding original works and they are listed in Table 1. For fair comparison, all parameters are considered the same. To ensure an equitable evaluation between the proposed ITDO algorithm and the compared ones (namely, DE, PSO, JS, HHO, GWO, SCA and the original TDO), they are executed with an identical maximum number of iterations for each run. Moreover, each algorithm underwent 20 independent runs to avoid the haphazard situation. The parameter settings for the implemented optimization methods were adopted from their respective original sources and are detailed in Table 1. Notably, common parameters such as the population size (M) for the presented optimizers were determined as 60 following a series of trials.

Table 1 Parameter’ settings for the implemented algorithms
Full size table

4.1 Simulation results on the basic and CEC 2020 benchmark functions

To analysis the performance of the ITDO, it is carried out on 33 benchmark functions which include 23 classical benchmark functions accompanied with unimodal, multimodal and fixed multimodal, and IEEE CEC2020 that includes 10 benchmark functions of hybrid optimization nature. In this regard, the performance of the ITDO is investigated using some of the well-known optimization algorithms. To diminish the chances of the outcome, the conducted algorithms are carried out for 20 independent runs with displaying some statistical measures such as the best (Min.), mean, median, worst (Max.) and standard deviation (SD) values of each problem. The results of the ITDO and the comparative algorithms are presented in Table 2, where the best or significant results are highlighted with bold font in terms of mean value recorded by each algorithm. Moreover, the experimental results are illustrated based on the number of occasions at which the method performs worse than/equal to/better than while taking into consideration the lowest mean values obtained for the benchmark problems. In light of this, it is indicated that the number of occasions satisfied by the suggested ITDO are 0/6/17, 0/4/19, 0/7/16, 2/7/14, 0/4/19, 0/3/20 and 0/9/14 against the competing optimization algorithms, i.e., DE, PSO, JS, HHO, GWO, SCA and TDO, respectively. In this sense, the HHO is better than ITDO for \(F_5\) and \(F_8\) while all competing optimization algorithms have same occasions for some benchmark problems. In summary, the ITDO has possessed progressive performance in comparison with other counterparts for most functions of the benchmark problems, which confirms its ability to deal with function optimization challenges.

Table 2 Results on the basic benchmark functions
Full size table

Next, the proposed ITDO and the compared algorithms were evaluated on the CEC2020 benchmark problems, one of the recent datasets in the field of numerical optimization. This dataset is made up of ten extremely difficult optimization issues and the characteristics of this dataset fall into four groups, unimodal, multimodal, hybrid and composite functions. The results of CEC 2020 benchmark functions are displayed in Table 3. To get the results more precisely and thoroughly, each algorithm is carried out for 20 independent runs, where the minimum value (described as Min.), average (described as mean), median (denoted as median), maximum (denoted as Max.) and standard deviation of (denoted as SD) are recorded. The significant optimization results in terms of mean values among the presented algorithms for each test function are marked in bold font. In this sense, the number of occasions that proposed algorithm performs worse than/equal to/better than the other counterparts are adopted to demonstrate the obtained results. In light of this, it is revealed that the number of occasions satisfied by the suggested ITDO are 1/0/9, 0/4/19, 0/0/10, 0/0/10, 0/0/10, 0/0/10 and 1/0/9 against the competing optimization algorithms, i.e., DE, PSO, JS, HHO, GWO, SCA and TDO, respectively. In this sense, the DE and TDO are better than ITDO for \(F_{10}\) and \(F_4\), respectively, and ITDO is better than the reset of competing optimization algorithms for all test functions. Based on the above analysis and results, ITDO has a promising with good comprehensive performance to the other advanced optimizers on most functions. This superior performance lies behind the inclusion of improvement strategies that support a positive influence on the original TDO.

Table 3 Results on CEC 2020 functions
Full size table

4.2 Convergence analysis

Convergence behavior is an essential criterion to assess the effectiveness of any optimization technique. In this sense, to justify concise information about the algorithm speed in finding more fitting results, the convergence rates for the implemented optimizers during the optimization process are depicted as in Fig. 4. For the comparison of convergence behavior among the 33 benchmark issues, 18 are chosen as an example, and their convergence curves are given in Fig. 4. As seen from the depicted curves, ITDO offers the best performance for most of the studied functions. ITDO exhibits a quicker convergence rate than the other ones and tries to converge to the optimum value with a significantly higher convergence rate. Furthermore, it is seen that ITDO virtually always comes in the first place in all assessments when compared with other methods. Taken together, the ITDO can significantly boost search effectiveness, solution accuracy and increase the speed of convergence. These characteristics affirm that the ITDO possesses a strong global search ability, results of newly embedded strategies, Levy flight and spiralize learning strategies. These strategies also try to strike an appropriate balance between exploration and exploitation. The description above demonstrates that ITDO efficiently solves optimization issues with an impressive convergence rate.

Fig. 4
figure 4

Convergence curves for the basic functions and CEC 2020 using the proposed ITDO and the compared ones

Full size image

4.3 Box plot analysis

A box plot displays another essential graphic criterion that shows the distribution of each algorithm's best results over the course of independent runs. In this regard, to justify concise information about the stability of the algorithm in finding more reliable results, box plot analysis is represented for the compared algorithms as provided in Fig. 5. In each figure, the box's length (interquartile range) determines the variance, where the shorter length denotes a smaller deviation between the findings achieved during independent runs. Additionally, when the plot is lower, the result is close to the ideal fitness, which is a good sign. The median of the findings across the independent runs is represented by the red line inside the box. Therefore, the depicted box plot reveals that the proposed ITDO has a compact and very consistent distribution with the global optimum value as it provides a narrower interquartile range for most of the studied benchmark suits. This simulation advocates the supremacy of the ITDO against most of the other counterparts.

Fig. 5
figure 5

Box plot analysis for the basic functions and CEC 2020 using the proposed ITDO and the compared ones

Full size image

4.4 Performance assessment by a pairwise Wilcoxon test

To analyze the achieved outcomes statistically, a nonparametric statistical hypothesis test, named Wilcoxon’s rank-sum test [65], is used to verify whether the two compared algorithms differ significantly from one another. Here, the null hypothesis is set up as follows. The two compared algorithms do not significantly differ from one another. When \(p\) is less than 0.05, it implies that the null hypothesis can be rejected with a level of significance of 5%. In this sense, Wilcoxon’s test is applied on the mean values of the benchmark functions achieved by the compared algorithms. The results obtained by the Wilcoxon’s test are recorded in Table 4 in terms of the sum of positive rank \((R^+ ),\) opposite rank (\(R^-\)) and \(p\) value. As illustrated in Table 4, ITDO outperforms all the compared algorithms as it provides a significance level less than 5% for most cases, which confirms the superiority of ITDO over the other counterparts.

Table 4 Wilcoxon test at 5% significant level on results of Tables 2 and 3
Full size table

Despite the fact that the competitive and progressive results have demonstrated the practicality and efficacy of the offered optimization approach for classical benchmark problems and complex CEC 2020 problems and parameter identification of electric transformer model, there are still some perspectives that are worth addressing in future studies. Firstly, the ITDO can be redesigned as a fusion strategy for dealing with more challenging optimization problems such as many-objective-constrained optimization with including some constraint handling insights, and bi-level optimization for estimating the contingencies in power transmission systems to exert its capability thoroughly. Secondly, extending the ITDO to deal with clean hydrogen production using optimized PV panel as an interesting perspective for sustainable energy. Thirdly, further investigation into the search performance of the ITDO is still warranted, and continuous experimentation on how to implement this proposal in various application situations is essential. It's essential to acknowledge that the ITDO cannot be considered the ultimate universal optimization tool, as no optimization framework can claim this status, as indicated by the NFL theorem. Furthermore, since the ITDO is crafted based on the principles of stochastic rule-based optimization, it might still grapple with challenges like stagnation or premature convergence when dealing with more complex and demanding datasets. Finally, we aspire for this study to serve as an inspiration for fellow researchers interested in exploring applications-oriented optimization methods. This work holds promise for future endeavors in the realm of real-world system applications.

4.5 Parameter estimation on the single-phase transformer

The effectiveness and efficiency of the proposed ITDO is confirmed verified by estimating the parameters of single-phase transformers with the following characteristics: 1 kVA, 230/230 V, 50 Hz. The testing of short circuit, open circuit, DC and load are performed to determine the equivalent circuit actual parameters.

Table 5 displays the recorded readings for the single-phase transformer under no load and during short-circuit tests. In this case, open- and short-circuit experimental tests were used to gather the transformer's actual data. The open-circuit test is conducted at nominal voltage, and the core resistance and magnetizing reactance, denoted by \(\le R_m\) and \(X_m\), respectively, are determined by measuring the measured current and power. Additionally, the primary and secondary resistances as well as the leakage reactances, denoted by \(R_1 ,{ }X_1\), and \(R_2 ,{ }X_2\) are determined using short-circuit test measurements (current, voltage and power).

Table 5 Experimental evaluations of (case study) single-phase transformer
Full size table

Toward the parameter’s estimation issue, the proposed ITDO algorithms as well as the compared algorithms are conducting to optimally obtain the equivalent circuit parameters. The achieved results by the competitive optimizers and the actual values are offered in Table 6. The calculated parameters are utilized to compute the transformer current, voltage regulation, power factor and efficiency under full-load conditions.

Table 6 Extracted parameters using the ITDO and compared algorithms for the single-phase transformer
Full size table

Moreover, the statistical results regarding the estimated parameters using the proposed algorithm and the compared ones are demonstrated in Table 7. The acquired findings demonstrate that the proposed ITDO produces the most accurate operational results. In this sense, the best mean values of the OF achieved are 4.4315E−28, 2.2795E−14, 5.8922E−13, 1.2087E−08, 1.6385E−08 and 7.7218E−08, for ITDO, JS, TDO, GWO, HHO and SCA, respectively. Also, the convergence assessment is presented to offer the performance of the algorithm during the iterative process. In this sense, the convergence behaviors of the implemented algorithms are depicted as in Fig. 6a. It is observed that ITDO converges quicker than the other counterparts and shows higher error improvement than the others.

Table 7 Statistical measures of ITDO and compared algorithms for the single-phase transformer
Full size table
Fig. 6
figure 6

Box plot and convergence curve analysis by competitively suggested and traditional optimizers

Full size image

To further validate the accurateness of the findings, the best extracted parameters of ITDO are presented for reconstructing the transforming characteristics at different loading percentage, voltage regulation, power factor and efficiency, as shown in Fig. 5a. The estimated results acquired by ITDO strongly match with the actual data, which emphasizes the accuracy of the estimated parameters. Moreover, to verify the robustness of the ITDO, 20 independent runs are carried out, and the mean of the OF is offered over the course of runs. Based on the exhibited behaviors, the ITDO acquires the highest stability than the others. As shown in Fig. 6b, while dealing with the single-phase transformer models, the suggested ITDO delivers exceptionally thin width for the inter quartile range as compared to the basic and advanced state of the art. Then, the box plots that are portrayed support the superiority of ITDO's over other algorithms.

Figure 7 compares the performance of a single-phase transformer for estimated parameters to the performance of the actual value. At varied loading percentages to the real performance, high similarity between estimated input power factor and efficiency is observed using JS; follow, ITDO; follow TDO and finally HHO. The voltage regulation computed using ITDO, on the other hand, is the closest to the real value. The suggested ITDO's estimated voltage regulation and efficiency are extremely near to the real values.

Fig. 7
figure 7

Performance of characteristic of 230/230 V, 1 kVA, 50 Hz single-phase transformer

Full size image

4.6 Computational complexity

Assessing an algorithm's computational complexity is an essential factor when evaluating its runtime performance. It offers insights into the behavior of the optimization algorithm and aids in identifying appropriate parameters and resources for effective execution. In this context, the focus of this study is to analyze the ITDO algorithm's computing complexity. The complexity of ITDO is impacted by different factors. The size of the population is one of these factors; a larger population necessitates more time for assessing and updating search agents. Another factor is the total number of decision variables; more decision variables result in a larger problem space and increase computational efforts. The maximum number of iterations has an impact on computation time because more iterations may lead to better responses but also take longer to get done. Furthermore, the complexity of the algorithm can be affected by the nature of the objective function (i.e., unimodal, multimodal, hybrid and compositional natures) and the mechanisms involved in the updating process. The goal of this work is to develop new optimization incorporating different updating mechanisms, which is an unconventional variant. In this regard, compromising on different updating mechanisms can demand more time than conventional ones that rely on a single updating scheme. Table 8 reports the computation time of the ITDO and the compared ones. From the obtained results, it can be noted that the ITDO provides less time for some of the competing algorithms as well as being slightly higher for some of the studied benchmark suites. However, the proposed optimization method surpasses the other competing methods in terms of producing superior outcomes for most of the studied problems. The goal is to achieve a balance between computation time and achieving the best outcomes.

Table 8 Comparative analysis of average computational time (in s)
Full size table

4.7 Advantages and limitations of the suggested algorithm

4.7.1 Advantages of the algorithm

  • Improved exploration: The algorithm embeds the Levy flight concept-based searching scheme into the TDO to detect new regions comprising the promising zones during the iterative process, enhancing the exploration tendency along the entire search space.

  • Guidance-based exploitation: The utilization of the spiralize elite learning strategy in the TDO assists in guiding the search toward better vicinities, leading to emphasize the intensification inclination while enhancing the accuracy of the search.

  • Rapid convergence: The ITDO algorithm can screen out promising solutions faster than conventional optimization methods due to its capacity to explore different trends in the search region more effectively while preventing it from getting stuck in local optima.

  • Robustness: The algorithm demonstrates superior performance compared to its counterparts on most of the studied problems by effectively balancing its exploitative and explorative characteristics

4.7.2 Limitations of the algorithm

  • Limited applicability: The suggested algorithm may be susceptible to worsening while tackling more complicated problems, such as the parametrized CEC 2021 benchmark problems, which consist of 8 variants of transformations such as rotation, bias and shift. More specifically, since ITDO is in its infancy with simple improvement strategies, degrading the exploration and convergence abilities of the algorithm can occur. So, the suggested algorithm can be further enhanced with other mutation strategies to deliver a more potent and reliable performance for solving complicated optimization tasks.

  • Limited savings: The suggested algorithm demands slightly more execution time than some of the compared algorithms for some of the studied problems due to the embedded efforts of the improvement strategies during the exploration and exploitation phases. So, the utilization of termination conditions with specified tolerance rather than performing the course of all iterations or using the number of function evaluations can be useful for saving computational efforts.

5 Conclusion

This paper presents an improved TDO based on Levy flight and spiralize learning strategies, termed ITDO, for estimating the equivalent circuit optimal parameters for the single-phase transformer. The ITDO embeds the Levy flight strategy to enrich the exploration scope within the search space while spiralize learning strategy is integrated to promote the vicinity searches around the promising areas. By these strategies, it attempts to enhance the original TDO's capability to strike a balance between diversification and identification abilities with higher processing efficiency. The effectiveness of the ITDO algorithm is examined through validating its performance on set of twenty-three standard functions and CEC 2020 suit of ten functions accompanied with different landscape natures. The comprehensive comparisons with other well-known optimization methods have proved the competitive performance of the proposed ITDO. Furthermore, the evaluations based on the statistical metrics, box plot analysis, convergence graphs and nonparametric Wilcoxon’s rank-sum test have confirmed the ITDO outperforms other algorithms in terms of reliability and accuracy of search operations. The results achieved by the Wilcoxon signed rank-sum test affirm that the ITDO exhibits amazing performance over its competitors as it achieves small \(p\) values (\(< 0.05\)), displaying a significant difference and promising performance. Afterward, the applicability of the ITDO is affirmed by estimating the parameters of the 1 kVA, 230/230 V, single-phase transformer. An extensive experimental result demonstrates that ITDO can provide competitive performance in terms of accuracy and reliability for estimating the transformer model parameters when compared with other well-established optimizers. The ITDO realizes steady, smooth and rapid convergence than the other counterparts. According to estimated parameters, ITDO highly provides coincidence characteristics with the actual data over the loading range, which affirms its ability and stability in estimating the parameters of single-phase transformer model. ITDO has a number of advantages that can be presented as follows. ITDO is characterized by its easy implementation and powerful exploitation and exploration abilities. Although ITDO is slightly slower than some of its competitors, it affirms the best results in most functions when compared to the others. Therefore, the following suggestions could be taken into consideration by researchers in the future. The integration/hybridization with a number of stochastic operators and chaos theory can accelerate the convergence performance of ITDO. ITDO can be applied to address constrained optimization problems, multi-/many-objective optimization tasks, real-world applications. Also, ITDO can be applied for several applications in power systems engineering such as the optimal power flow, reactive power compensation and combined AC/DC grids. Additionally, the integration of the ITDO with the long short-term memory (LSTM) and neural network models can be addressed to improve the accuracy of forecasting applications. Finally, we hope that the proposed work will serve as a source of inspiration for other researchers who are interested in solving real-world application-based optimization schemes.