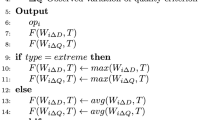1 Introduction

Markowitz [1] formulated the portfolio selection problem as a multi-objective optimisation problem (MOP), in which an investor aims to satisfy the conflicting objectives of maximising return while minimising risk. Since this seminal work, the portfolio optimisation problem has been expanded to include additional constraints and objectives to incorporate real-world considerations [2]. In addition, real-world portfolio management involves making a sequence of portfolio decisions over time and is thus more appropriately represented as a multi-period optimisation problem [3].

Adopting a multi-period perspective for the portfolio optimisation problem allows the optimisation framework to include intertemporal aspects of portfolio management. This includes trading costs [4], multi-period and time-varying forecasts, intertemporal hedging, and addressing other intertemporal constraints [5]. However, these advantages come with challenges. Firstly, Multiperiod Portfolio Optimisation (MPO) requires multi-period forecasts adding difficulty to the already challenging task of single-period forecasting. Secondly, MPO is computationally burdensome, especially when incorporating real-world considerations. Consequently, portfolio management in practice typically consists of repeatedly performing myopic single-period optimisations. This work addresses the second key problem—the computational intractability of a realistic multi-period portfolio management problem.

1.1 Background

Starting with Merton [6, 7], and others [8,9,10], MPO has been studied as a Markov decision problem (MDP) where optimal policies are found using dynamic programming (DP). Here, the portfolio optimisation problem is typically restricted to idealised settings that enable the construction and solution of the Bellman optimality equation. However, formulations relying on DP are typically unable to capture real-world market dynamics adequately and require several simplifications for the problem to be tractable. In particular, it is typical for the state-space to be limited to a few variables to avoid the curse of dimensionality and for the state transition function to be treated as known. In addition, the objective function is often chosen from a class of utility functions with convenient analytic properties. These utility functions typically render the problem as a single-objective optimisation problem where the risk-return trade-off is not explicit.Footnote 1 Furthermore, problems are restricted to one or two constraints of theoretical interest. Thus, studies investigating MPO through DP are largely theoretical, focusing on a qualitative understanding of normative investor behaviour.

Instead of DP, approximate policies can be determined by considering simpler (although sub-optimal) MO stochastic programming (SP) formulations that do not depend on Bellman optimality. SP is a highly flexible modelling framework for multi-period optimisation, capable of incorporating a diverse array of real-world considerations, including alternative risk measures, risks and uncertainty hedging, hard and soft constraints, and intermediate goals (including stochastic and irregular outflows) [2]. Moreover, SPs model uncertainty using scenarios, defined as sequences of states, and are not restricted to MDP formulations. However, an SP becomes computationally intractable as its specification grows more complex, necessitating approximate programs to find a policy. Common approximations include discretisation of the observed variables, aggregation of stages, reduction of the problem horizon, and replacing random quantities with their expectations [13]. When the expectations are unknown, they are replaced with forecasts sequentially updated at each timestep, more broadly referred to as a rolling horizon procedure or model predictive control (MPC), which is widely adopted in practice.

For example, Boyd et al. [2] present a convex optimisation framework for MPO suitable for MPC. They achieve this by extending the single-period mean-variance problem to multiple periods using additional risk and return objectives and constraints for each period. Competing objectives are linearly combined into a single function using trade-off parameters that reflect the relative importance of each objective (i.e. they “trade-off” different objectives). By varying the trade-off parameters and solving the optimisation problem, one can uncover the Pareto frontier or, in the finance jargon, the efficient frontierFootnote 2 [14, 15].

MO evolutionary algorithms (EAs) have been extensively applied in portfolio optimisation [16] and treat portfolio optimisation as a deterministic problem, where the objective function is known. However, in reality, portfolio optimisation more closely resembles a learning problem, where finding the Pareto frontier is akin to selecting hyper-parameters [2]. In particular, the risk and return terms of the objective function are estimated from the data. Objective values of optimised portfolios are considered in-sample (and hence highly inflated) estimates of their true performance [17], and there is also no guarantee that in-sample Pareto optimal solutions are optimal out-of-sample. Similar to hyper-parameter search in machine learning, the Pareto frontier is determined by estimating the performance of each trade-off parameter’s corresponding portfolios on separate out-of-sample data using a process known as backtesting. This process involves repeatedly solving an optimisation problem at each time step in the backtest period for each choice of trade-off parameters. MO EAs can be applied to improve the computational efficiency of the hyper-parameter selection process [18, 19].

1.2 Problem statement

In summary, despite being extensively investigated, crucial gaps remain in the portfolio optimisation literature. On the one hand, the multi-period nature of real-world portfolio management is largely unexplored in applications of MO EA. On the other hand, the MPO literature has largely ignored the MO aspects of portfolio optimisation. Both strands of literature give little consideration to the implications of formulating the portfolio optimisation problem stemming from the uncertainty of the data-generating process encountered in practice. In particular, the Pareto frontier must be determined on separate test data, which involves a computationally intensive hyper-parameter selection procedure.Footnote 3 To address these gaps, this study extends that of van Zyl et al. [19] by investigating MPO to answer the following research questions:

  1. 1.

    How can the computational burden of constructing the Pareto frontier in a realistic MPO problem be alleviated?

  2. 2.

    How can we improve the efficiency and performance of existing algorithms for hyper-parameter selection in the context of MO, MPO?

  3. 3.

    What is the impact of surrogate-assisted optimisation in MO, MPO, and can it be further enhanced?

Recognising that real-world portfolio management is a type of learning problem, Boyd et al. [2] and Nystrup et al. [18] adopt a hybrid approach, where the construction of the Pareto frontier is split into a convex portfolio optimisation problem and a hyper-parameter selection problem. Solving the portfolio optimisation problem determines the solution set, whilst solving the hyper-parameter selection problem determines the non-dominated solutions from the solution set. Since most real-world considerations can be incorporated in a convex specification of the portfolio optimisation problem [2], the computational intractability of evaluating all possible hyper-parameter combinations arises from the cost associated with performing multiple evaluations on test data (backtesting). A poor strategy for selecting candidate hyper-parameters can yield many dominated solutions, resulting in unnecessary computation. The key issue, therefore, is determining the efficient frontier with as few evaluations as possible.

1.3 Contributions

Nystrup et al. [18] shows that using the MO-CMA-ES EA for determining the efficient frontier improves upon the grid search procedure used by Boyd et al. [2]. Most recently, van Zyl et al. [19] compared several seminal MO EAs and proposed a surrogate-assisted procedure to enhance their performance, but their investigation is limited to the single-period case. The objectives of this work are to extend the aforementioned studies to the multi-period setting and to present a novel method that improves not only the efficiency of the algorithms but also the overall quality and performance of the solutions. To this end, the contributions of this study are:

  • An empirical performance comparison of several seminal MOP EA for both Single-period Portfolio Optimisation (SPO) and MPO,

  • The demonstration of the superior efficacy of surrogate-assisted optimisation to alleviate the computational burden of constructing the Pareto frontier for the MPO case,

  • And the presentation of a new algorithm, Pareto driven surrogate (ParDen-Sur), that improves upon the state-of-the-art surrogate-assisted portfolio optimisation

The presented method, ParDen-Sur, recognises several deficiencies in the originally developed ParDen algorithm [19] and contains several extensions to overcome these. Firstly, whilst ParDen only allows for generative models as surrogates, ParDen-Sur can also allow for the integration of discriminative models, allowing for a much broader range of models to be used as surrogates. Secondly, ParDen-Sur is especially cognisant of the limitations of adding additional free parameters to a surrogate-assisted algorithmic framework. To limit the number of free parameters and ensure the diversity of the population, ParDen-Sur introduces a reservoir sampling-based look-ahead mechanism that uses the surrogate model to iterate the EA forward several generations. Introducing a look-ahead procedure allows one to consider forgoing the acceptance sampling.Footnote 4 Lastly, ParDen-Sur uses a rank-based metric in the surrogate framework resulting in improved empirical performance. We argue that this is attributed to rankings being an easier learning target than accuracy but acknowledge that performance increases may arise from selective bias, which we investigate in future work.

2 Preliminaries

2.1 A convex optimisation framework for portfolio optimisation

The original mean-variance optimisation problem is a SPO specified by a bi-objective criterion, where risk is measured by the variance of the portfolio’s return [1]. These objectives are combined linearly into a single optimisation problem. Using the SP approach, Boyd et al. [2] extends Markowitz’s formulation by presenting a convex optimisation framework for MPO, which includes the single-period problem as a special case. Notably, trading and holding costs are treated as soft constraints selected to achieve some desired trading behaviour and are typically used as regularisation methods. The portfolio optimisation problem can be equivalently formulated by including the soft constraints as additional criteria in the objective function, with associated trade-off parameters:

$$\begin{aligned}&\text {maximise} \quad \sum _{\tau =t+1}^{t+H} {\textbf{w}}_{\tau }'\mathbf {\mu }_{\tau } - \frac{\gamma _{\text {risk}}}{2}{\textbf{w}}_{\tau }'\Sigma _{\tau } {\textbf{w}}_{\tau } \nonumber \\& - \gamma _{\text {trade}}\phi ^\text {trade}\left( {\textbf{w}}_{\tau } - {\textbf{w}}_{\tau -1}\right) \nonumber \\& - \gamma _{\text {hold}} \phi ^\text {hold}\left( {\textbf{w}}_{\tau }\right) \\&\text {subject to} \nonumber \\& {\textbf{w}}_{\tau }'{\textbf{1}} = 1, \nonumber \\& {\textbf{w}}_{\tau } - {\textbf{w}}_{\tau -1} \in {\mathcal {Z}}_{\tau }, \nonumber \\& {\textbf{w}}_{\tau } \in {\mathcal {W}}_{\tau } \nonumber \end{aligned}$$
(1)

where \(H \in {\mathbb {N}}\) represents the investment horizon, \({\textbf{w}}_{\tau }\) is a vector of portfolio weights at each period \(\tau = t, \dots , t+H\), \(\mathbf {\mu }_{\tau }\) and \(\Sigma _{\tau }\) are the return and risk forecasts, \({\mathcal {W}}_{\tau }\) and \({\mathcal {Z}}_{\tau }\) are convex sets representing the holding and trading constraints, respectively, and \(\gamma _{\text {risk}}\), \(\gamma _{\text {trade}}\), and \(\gamma _{\text {hold}}\) are the trade-off parameters for risk, trading costs, and holding costs, respectively. Note that setting \(H=1\) specifies the single-period problem.

The extended formulation of the mean-variance problem in Eq. 1 is analytically intractable. Computational methods determine the efficient frontier by repeatedly solving the optimisation problem for different trade-off parameters (\(\gamma _{\text {risk}}\), \(\gamma _{\text {trade}}\) and \(\gamma _{\text {hold}}\)). Given that SPO is a quadratic programming problem, it is reasonable to assume that a solver such as ECOS used in the study’s empirical evaluation will be polynomial of order \({\mathcal {O}}(n^3)\) where n is the number of assets [20]. Extending the single-period formulation to H periods increases the number of decision variables to Hn, resulting in the computational complexity further increasing to order \({\mathcal {O}}\left( (Hn)^3\right)\) [2]. The search for a Pareto frontier considers three trade-off parameters, so the aforementioned optimisation problem of order \({\mathcal {O}}\left( (Hn)^3\right)\) must search over a volume in three dimensions d resulting in an overall complexity \({\mathcal {O}}\left( d^3(Hn)^3\right)\). However, unlike Markowitz’s original formulation, not all selected trade-off parameters are non-dominated and associated with the Pareto optimal solutions. These dominated solutions result in excess computation.

2.2 Backtesting

When the data-generating process is unknown, the performance of a portfolio is evaluated on data not used during the portfolio optimisation process. The backtesting process consists of sequentially performing the optimisation in Eq. 1 to construct a portfolio \({\textbf{w}}_{t}\) at each time t, which earns a return \({\tilde{r}}_{\gamma , t+1}\) at time \(t+1\), for each hyper-parameter combination \(\gamma =\left( \gamma _{\text {risk}}, \gamma _{\text {trade}}, \gamma _{\text {hold}} \right)\) over a historical period \(t = 1, \dots , T-1\). The backtest performance of each hyper-parameter is summarised by its out-of-sample mean and standard deviation of returns \(({\tilde{\mu }}_{\gamma }, {\tilde{\sigma }}_{\gamma })\). A hyper-parameter combination \(\gamma\) is dominated by another \(\gamma '\) if \({\tilde{\mu }}_{\gamma } < {\tilde{\mu }}_{\gamma '}\) and \({\tilde{\sigma }}_{\gamma } > {\tilde{\sigma }}_{\gamma '}\). The backtesting procedure aims to find the set of non-dominated hyper-parameters in terms of out-of-sample performance.

2.3 Evolutionary algorithms

Numerous evolutionary MOP algorithms exist in the literature [21, 22]. Amongst these, certain algorithms are successful in applications across several different domains [23,24,25,26,27,28]. The use of evolutionary algorithms (EAs) for finding solutions to portfolio optimisation problems has been covered extensively in the portfolio optimisation literature [29,30,31] with the focus almost exclusively given to the single-period problem. The presented study aims to apply various representative EAs and demonstrate the utility of a surrogate-assisted evolutionary optimisation approach to solving portfolio optimisation problems described in this paper. To this end, this study implements the evolutionary MOP methods described below.

2.3.1 MO-CMA-ES

The Covariance Matrix Adaptation Evolution Strategy (CMA-ES) is an elitist evolutionary strategy for numerical optimisation. Multi-objective CMAES (MO-CMA-ES) maintains a population of individuals that adapt their search strategy as in the elitist CMA-ES. The elites are subjected to MO selection pressure. The selection pressure originates from non-dominated sorting using the crowding-distance first and hypervolume as the second criterion [25].

2.3.2 NSGA-II

The NSGA-II algorithm follows the form of a Genetic Algorithm (GA) with modified crossover and survival. The surviving individuals are chosen Pareto front-wise first. A situation arises where a front needs to be split since not all individuals can survive. When splitting the front, solutions are selected based on a Manhattan crowding distance in the objective space. However, the method seeks to hold onto the extreme points from each generation, and as a result, they are assigned a crowding distance of infinity. Furthermore, the method uses a binary tournament mating selection to increase selection pressure. Each individual is first compared by rank and then crowding distance [32].

2.3.3 R-NSGA-II

The R-NSGA-II algorithm follows NSGA-II with a modified survival selection mechanism. Unlike NSGA-II, solutions are selected based on rank in splitting the front. This rank is calculated based on the Euclidean distance to supplied reference points. The solution closest to a reference point is assigned a rank of one. The algorithm then selects the points with the highest rank to each reference point as offspring. After each reference point has selected the solution with the best rank for survival, all solutions within the epsilon distance of surviving solutions are “cleared”, meaning they cannot be selected for survival until all fronts have been processed. The cleared points are considered if more solutions still need to be selected-the free parameter epsilon with a smaller value results in a tighter set of solutions [32].

2.3.4 NSGA-III

The NSGA-III algorithm is based on reference directions instead of reference points. For the survival mechanism, the algorithm has a modified approach to dealing with the front splitting after non-dominated sorting. The algorithm fills up the under-represented reference direction first. If the reference direction does not have any solution assigned, the solution with the smallest perpendicular distance in the normalised objective space is assigned as the survivor. If additional solutions for a reference direction are required, these are assigned randomly. Consequently, when this algorithm converges, each reference direction attempts to find a suitable non-dominated solution [32].

2.3.5 R-NSGA-III

The R-NSGA-III algorithm follows the general NSGA-III procedure with a modified survival selection operator. First, non-dominated sorting is done as in NSGA-III. Solutions are associated with aspiration points based on perpendicular distance, and solutions from the underrepresented reference direction are chosen. For this reason, when this algorithm converges, each reference line seeks to find a good representative, non-dominated solution [32].

2.3.6 U-NSGA-III

The U-NSGA-III algorithm uses tournament pressure to improve the original NSGA-III approach that randomly selects parents for mating [32]. The advantages of tournament selection include promoting better convergence by favouring individuals with higher fitness and maintaining diversity within the population, which is essential for avoiding premature convergence. Additionally, the selection pressure can be controlled by adjusting the size of the tournament, allowing for a balance between exploration and exploitation. This feature makes the U-NSGA-III algorithm more versatile and adaptable for different problem sizes and complexities, improving the overall performance and reliability of the multi-objective optimisation process [33, 34].

2.4 Surrogate-assisted optimisation

Surrogate models are used in optimisation problems where the objective function is unknown and costly to evaluate. In the surrogate-assisted approach, objective values (outputs) are first evaluated for a sample of different decision variable choices (inputs). Then, a supervised learning algorithm (the surrogate) is trained on the input–output pairs to estimate the objective function. The surrogate model can then assist in numerically optimising the objective function. The surrogate model can also be sequentially improved by including input–output pairs for candidate solutions at each iteration as the optimisation algorithm proceeds [35]. This study’s unknown objective function is the out-of-sample performance over the hyper-parameter space of both SPO and MPO (Figs. 1, 2).

Fig. 1
figure 1

SPO versus MPO primary example: optimal frontiers

Full size image

3 Pareto Driven Surrogate

Surrogate methods have been extensively applied in single objective optimisation [36,37,38,39,40,41,42,43], whereas the applications of surrogate-assisted methods within a MO setting is substantially less common. In particular, the literature for data-driven evolutionary MO surrogate-assisted optimisation is especially sparse [44,45,46,47]. To this end, the presented Pareto driven surrogate (ParDen-Sur) framework is sufficiently general that it can be applied together with most evolutionary MO algorithms.

ParDen-Sur relies on the use of supervised learning models to act as a surrogate drop-in replacement \({\hat{f}}(\cdot )\) to evaluate a computationally resource-intensive real-world experiment or simulation \(f(\cdot )\). The core idea of ParDen-Sur is to limit the evaluation of candidates using the simulation \(f(\cdot )\) to only those that have a high probability of advancing the Pareto front (the non-dominated solution set \({\mathcal {P}}\)). The likelihood that a candidate would advance the Pareto front is determined by: i) whether the surrogate model predicts that the candidate advances the Pareto front and ii) the extent to which the surrogate is correct. In particular, ParDen-Sur attempts to estimate the probability that the surrogate is correct, which is used as a threshold within an acceptance sampling scheme, and to set the size of a reservoir sampling look-ahead scheme when selecting candidates.

To determine the extent to which the surrogate is correct, a mechanism is required for assessing the probability \(P\left[ (x_i, y_i) \in {\mathcal {P}} | {\hat{f}}\right]\) that a pretender \((x_i, y_i)\) will be in the current non-dominated set \({\mathcal {P}}\) given the surrogate’s prediction \({\hat{y}}_i = {\hat{f}}(\cdot )\). ParDen-Sur employs k-fold cross-validation \({\text {CV}}_k(\cdot )\) together with the non-dominating rank [48] of each candidate to estimate this probability as a non-dominated score (\({\text {NDScore}}\)).

Calculating an \({\text {NDScore}}\) requires fitting surrogates \({\hat{f}}_{_{X_T, Y_T}}(\cdot )\) to the training splits \((X_T, Y_T)\) with the MO \(Y_T\) as the target. For each point in a validation split \((X_V, Y_V)\), its non-dominating rank r in the split is calculated. The surrogates estimate the objective values on the validation split, \({\hat{Y}}_V={\hat{f}}_{_{X_T, Y_T}}(X_V)\), and their non-dominating ranks are calculated, producing predicted ranks \({\hat{r}}\). The performance of the predicted non-dominated ranks is evaluated using any error metric \({\mathcal {E}}({\hat{r}}, r)\), that is constrained to sum to one. Finally, the non-dominated score can be calculated by aggregating the errors calculated for the different splits: ParDen-Sur allows the use of any metric \({\mathcal {E}}({\hat{r}}, r)\) constrained to sum to one, to compare r with \({\hat{r}}\):

$${\text{NDScore(}} \cdot ) = \mathop {{\text{aggregation}}}\limits_{\begin{subarray}{l} {\text{(XT ,YT ),(XV ,YV )}} \\ \in {\text{CV}}_{{\text{k}}} {\text{(X)}} \end{subarray} } \varepsilon (\hat{r},\;r)$$
(2)

with

$$\begin{aligned} {\hat{r}} = \lceil Y_V \rceil ^{\uparrow } \quad \textrm{and} \quad r = \lceil {\hat{f}}_{_{X_T, Y_T}}(X_V) \rceil ^{\uparrow } \end{aligned}$$
(3)

where \(\lceil \cdot \rceil ^\uparrow\) assigns the non-dominating rank to each vector, since ParDen-Sur uses the k-fold cross-validation function \({\text {CV}}_k(\cdot )\) to estimate this value, the mean error across the k splits is a suitable aggregation.

Algorithm 1
figure a

ParDen-Sur Algorithm

Full size image
Fig. 2
figure 2

Flowchart for the ParDen-Sur Algorithm

Full size image

4 Methodology

In this study, the experimentation is split into two stages, referred to as the motivating and primary examples, respectively, for both the SPO and MPO cases. The motivating example is a scaled-down version of the problem presented in the primary example. In the motivating example, several well-known MOP EAs are initially applied to the aforementioned problem (see Sect. 2) to determine which performs best and to provide a relevant baseline, after which, the study then applies ParDen-Sur with the two best performing EAs in the primary example.

All experiments are repeated ten times, and average results are compared to the baseline EAs. The outperformance of the Parden-Sur algorithm is assessed for statistical significance using one-sided Mann-Whitney U tests and adjusted for multiple testing using the Simes-Hochberg procedure. Hyper-parameters for the EAs are manually adapted from van Zyl et al. [19].

4.1 Method metrics

This study considers three metrics as performance indicators for the solution set generated by each algorithm. These include the two modified distance calculations, generational distance plus (GD+) and inverted generational distance plus (IGD+) [49], as well as the Hypervolume (HV) [50]. For GD+ and IGD+, an optimal target set needs to be specified, which is specified in the results below as the Pareto frontier from a random grid search with 6510 hyper-parameters. For HV, only a reference point needs to be provided, which is (40, 0) in the risk-return space.

This study considers three metrics as performance indicators for the solution set generated by each algorithm. These include the two modified distance calculations, generational distance plus (GD+) and inverted generational distance plus (IGD+) [49], as well as the Hypervolume (HV) [50].

Consider the objective vector set \(A = \lbrace a_1, a_2, \dots , a_{|A|}\rbrace\) representing the points found by the algorithm, and the reference points set \(Z = \lbrace z_1, z_2, \dots , z_{|Z|}\rbrace\), which corresponds to the Pareto frontier.

For GD+ and IGD+, an optimal target set needs to be specified, which is specified in the results below as the Pareto frontier from a random grid search with 6510 hyper-parameters. For HV, only a reference point must be provided, chosen to be (40, 0) in the risk-return space.

  • Generational distance plus (GD+): This metric measures the average distance between the non-dominated solutions generated by the algorithm and the closest points in the optimal target set (Pareto frontier). A smaller GD+ value indicates better algorithm convergence towards the Pareto frontier. The formula for GD+ is:

    $$\begin{aligned} \begin{aligned} \text {GD}^+(A)&= \; \frac{1}{|A|} \; \bigg ( \sum _{i=1}^{|A|} {d_i^{+}}^2 \bigg )^{1/2}\\ \end{aligned} \end{aligned}$$
    (4)

    where \(d_i^{+} = \max {(a_i - z_i, 0)}\) represents the modified distance from \(a_i\) to its nearest reference point in Z with the corresponding value \(z_i\).

  • Inverted generational distance plus (IGD+): This metric calculates the average distance between the points on the Pareto frontier and the closest non-dominated solutions generated by the algorithm. A smaller IGD+ value implies better convergence and diversity of the solutions, as they cover the optimal target set more effectively. The formula for IGD+ is:

    $$\begin{aligned} \begin{aligned} \text {IGD}^{+}(A)&= \; \frac{1}{|Z|} \; \bigg ( \sum _{i=1}^{|Z|} {d_i^{+}}^2 \bigg )^{1/2}\\ \end{aligned} \end{aligned}$$
    (5)

    where \(d_i^{+} = \max {(a_i - z_i, 0)}\) represents the modified distance from \(z_i\) to the closest solution in A with the corresponding value \(a_i\).

  • Hypervolume (HV): This metric quantifies the volume of the objective space dominated by the current set of solutions generated by the algorithm. Higher Hypervolume values indicate better convergence and diversity of the solutions, as they cover a larger portion of the Pareto-optimal region. As the algorithm progresses through generations, an increase in Hypervolume signifies that the algorithm is approaching the Pareto frontier more closely, achieving better trade-offs between the multiple objectives.

Evaluating the solution quality of evolutionary approaches can be challenging, as no single metric can provide a complete picture of the performance across all scenarios. Therefore, it is essential to consider multiple metrics to assess the algorithms’ effectiveness comprehensively. In this study, we employ solution quality metrics as defined by [51]:

  • Success rate (SR): Success is defined as meeting a required quality criterion, such as a solution within 99% or 95% of the known optimal value. For this analysis, the Hypervolume of the random 6510 grid search is considered the optimal solution. The success rate is the percentage of algorithm executions that meet the success criterion.

  • Average evaluations to success rate (AESR): This metric measures the average number of evaluations required by the EA to reach a solution at a selected success rate. For example, the AESR at a 99% SR would be the average number of evaluations needed to achieve that SR. The runs of the EA that do not meet the SR criterion are disregarded.

  • Average generations to success rate (AGSR): Similar to AGSR, AGSR calculates the average number of generations required by the EA to reach a solution at a given success rate. For instance, the AGSR at a 99% SR would be the average number of generations needed to reach that level. Runs of the EA that do not meet the SR criterion are not considered.

We can better understand their performance and robustness in different circumstances by evaluating the algorithms using multiple solution quality metrics. This approach helps identify the strengths and weaknesses of each algorithm and supports informed decision-making when selecting an optimisation method.

4.2 Hyper-parameters

The experiments use Latin Hyper-cube Sampling for random selection for all the EAs, real Uniform Crossover (UX) for crossover, and real Polynomial Mutation (PM) for mutation. For all comparisons, the results use a population size of 60 and an offspring size of 30. The EAs techniques all had a total evaluation budget of 510. The study uses Riesz s-Energy to generate reference directions or reference points. Table 1 shows the selected hyper-parameter values unique to the individual EAs. In the study, the hyper-parameters are selected once, and these values are re-used for both the SPO and MPO problems [32].

Table 1 Hyper-parameters used for the various EAs
Full size table

For ParDen-Sur, the free parameter is the termination criteria for the look-ahead reservoir sampling. Multi-objective space tolerance termination was selected with a value of 0.0001 [32] set according to the scale of the solutions, which are values in the range 0 to 60 with up to three decimal places being significant.

4.3 Research instruments and data

The motivating and primary examples for the SPO and MPO cases are prepared using two different datasets. The dataset used in the primary examples is prepared exactly as in Boyd et al. [2]. In contrast, a scaled-down version of this dataset is used in the motivating example. The scaled-down version is explored to determine the most appropriate application of ParDen-Sur within the primary example. The need arises from the time-consuming nature of the experiments - on the order of days.

In the primary example, consideration is limited to \(\pm\, 410\) assets from the S&P 500 Index with a full set of \(\pm\, 1800\) daily price data points over the five years from January 2012 to December 2016. Daily volatilities for determining transaction costs are calculated using the absolute difference between log open and close prices, while the bid-ask spread is fixed at \(0.05\%\). Holding costs are fixed at \(0.01\%\). These quantities are used to calculate the backtest performance of a policy.

Furthermore, risk, return, and trading cost forecasts are required at each backtest period to construct the portfolio. Investigating different forecasting techniques is out of the scope of this study. Instead, return forecasts are imitated by adding zero-mean Gaussian noise to realised returns, whilst volatility and volume forecasts are specified using ten-day moving averages. For the MPO case, we consider a two-period optimisation (i.e. \(H=2\) in Eq. 1). The two-period case increases the computational time by a factor of three over the single period-case.

The datasets for the motivating example are prepared similarly, except that consideration is limited to \(\pm 30\) assets from the Dow Jones Industrial Index over the eighteen months (\(\pm 547\) data points) from July 2015 to December 2016. For further details, consult the supplementary materials.

All experiments use Ubuntu 20.04.1 LTS and are run on Intel(R) Xeon(R) CPU E5-2683 and E5-2695 v4 @ 2.10GHz. The study uses pymoo v0.5, pysamoo v0.1, and cvxportfolio [2]. The source code and data for reproducing the results are available on GitHub, here.

5 Results

The following section discusses the results for the SPO and then for the MPO.

5.1 Single-period portfolio optimisation

5.1.1 Motivating example

One of the objectives of the motivating example is to ascertain which two of the various seminal MO EA optimisation techniques are most appropriate for applying the ParDen-Sur algorithm within the Single-period Portfolio Optimisation (SPO) problem. Considering Table 2 we note that the results for NSGA-II and R-NSGA-II are mixed, with neither method outperforming the other across all indicators. It is worth noting that none of the implemented methods outperforms the 6510 random points.

Having identified the top-performing MO EA optimisation, the second objective of the motivating example is to determine which of the two selected methods is best suited for the application of ParDen-Sur. The results in Table 2 highlight the superiority of ParDen-Sur applied to NSGA-II over R-NSGA-II. Further, the statistical tests indicate that ParDen-Sur results are indeed significant and support an argument for ParDen-Sur’s superiority over the baseline EA as well as the superiority of using look-ahead with reservoir sampling over the original ParDen-Sur algorithm. Further, the results show that no matter which underpinning EA is used, the ParDen-Sur results are always statistically significantly superior.

We consider the quality indicators next, where the objective is to ascertain the degree to which ParDen-Sur is assisting the underpinning EA. Table 3 reinforces the selection of NSGA-II over R-NSGA-II given the superior SR and similar total evaluations as measured by AESR and AGSR. Further, the results show that no matter which underpinning EA is used, the superiority of ParDen-Sur results is always statistically significant.

Table 2 SPO (Motivating Example): Performance indicators for the best-observed value. Bold: best, italics: top two
Full size table
Table 3 SPO (Motivating Example): Quality Indicators. Bold: best, italics: top two, underline: warning indicator
Full size table

5.1.2 Primary example

The main objective of the SPO primary example is to replicate the existing research and provide context for the current ParDen-Sur results. To this end, Table 4 replicates the previous studies by [18] and [19]. The results reinforce the superior performance of ParDen-Sur over both NSGA-II and MO-CMA-ES as underpinning EAs. Further, the results highlight the superiority of look-ahead with reservoir sampling as found in ParDen-Sur over using just acceptance sampling. One interesting result requiring further investigation is the superior performance of R-NSGA-II when considering GD+.

Looking toward the quality indicators, the results in Table 5 reinforce the superior performance of ParDen-Sur with look-ahead over ParDen-Sur without for both NSGA-II and MO-CMA-ES. Having established the superiority of ParDen-Sur with a look-ahead in the SPO problem space, the study now turns to the more challenging MPO problem.

Table 4 SPO (Primary Example): Performance indicators for the best-observed value. Bold: best, italics: top two
Full size table
Table 5 SPO (Primary example): Quality indicators. Bold: best, italics: top two, underline: warning indicator
Full size table

5.2 Multi-period portfolio optimisation

5.2.1 Motivating example

The main objective of the motivating example was to establish which MO EA algorithms to use in conjunction with ParDen-Sur. Table 6, like in the SPO motivating example, indicates that NSGA-II and R-NSGA-II are superior choices for underpinning EAs. These techniques significantly outperform MO-CMA-ES previously proposed by Nystrup et al. [18].

When considering the second objective of the motivating example as to which of the top two underpinnings EAs are best suited to further exploration with ParDen-Sur, Table 6 shows a slight benefit in favour of NSGA-II. However, when we consider the quality indicators in Table 7, the results show that any gains by R-NSGA-II are also linked to substandard Success Rates at the 99% threshold. Interestingly, the quality indicators indicate that ParDen-Sur has lower AESR@99 and AGSR@99 than the underpinning EAs. However, the jump in SR@99 to 100% warrants further exploration and points to the superiority of ParDen-Sur not just for reducing the convergence rate but also for improving the probability of convergence. This argument is further supported when considering the superiority of ParDen-Sur at the 95% threshold.

Having established the superiority of ParDen-Sur coupled with NSGA-II on the multi-period portfolio optimisation (MPO) motivating example, the study now focuses on the MPO primary results.

Table 6 MPO (Motivating Example): Performance indicators for the best-observed value. Bold: best, italics: top two
Full size table
Table 7 MPO (Motivating Example): Quality Indicators. Bold: best, italics: top two, underline: warning indicator
Full size table

5.2.2 Primary example

The main aim of this study is to evaluate the use of ParDen-Sur in the context of MPO in the primary example. Table 9 shows the out-performance of all variants of ParDen-Sur. HV improvement is marginal (0.8%) over the state-of-the-art (SOTA) - NSGA-II. However, for GD+ and IGD+, these improvements over the SOTA (R-NSGA-II and NSGA-II) are 19.4% and 66.5%, respectively. Most interesting is the superior performance obtained using look-ahead. The p-values of the Mann–Whitney U tests (with multiple testing adjustments) in Table 8 add further weight by demonstrating the out-performance is statistically significant at the \(5\%\) level for all tests (with nearly all tests being significant at the \(1\%\) level).

Table 8 MPO (Primary Example): p-values from testing differences in performance indicators between Parden-Sur and baseline methods
Full size table

When considering the quality indicators in Table 10 the results show marked improvements in both AESR@99 and AGSR@99, with ParDen-Sur having a \(1.84\times\) and \(2.02\times\) speedup over the underpinning EA in both these metrics. We also note that ParDen-Sur without acceptance sampling outperforms when considering the AESR@99. This interesting result suggests the benefit of one less free parameter and a possible algorithm simplification. It is worth contrasting this with the results in Tables 3 and 7, which have both supporting and conflicting support of this observation.

Table 9 MPO (Primary Example): Performance indicators for the best-observed value. Bold: best, italics: top two
Full size table
Table 10 MPO (Primary Example): Quality Indicators. Bold: best, italics: top two, underline: warning indicator
Full size table

6 Discussion

The presented results demonstrate that the challenges of optimal hyper-parameter search related to multi-period optimisation are tractable within the context of surrogate-assisted MO optimisation. Further, the results support the use of the ParDen-Sur algorithm with NSGA-II to significantly improve the rate at which one can arrive at a solution and the quality of the solutions found. These solutions could be acquired using commodity hardware without significantly impacting computational resources other than the need for additional CPUs.

Previously, surrogate-assisted portfolio optimisation has been shown to speed up single-period hyper-parameter searches [19]. This study confirms and extends those results to the multi-period optimisation use case. The outcome suggests that all versions of ParDen-Sur, the proposed method, lead to a speed-up in acquiring optimal frontiers in the portfolio optimisation task, as seen in Fig. 3.

Previous work [19] showed that the ParDen framework could speed up both MO-CMA-ES and NSGA-II, and the results in this study show that this extends to R-NSGA-II. Furthermore, the results are demonstrated on more than one dataset and for multiple periods. However, without testing this statement across the full battery of EAs, it is impossible to ascertain if the extensions to ParDen as contained in ParDen-Sur are a general-purpose surrogate-assisted optimisation framework.

In the previous study, ParDen used only acceptance sampling to improve speed-up [19]. The results demonstrate that including look-ahead with acceptance, sampling is a superior approach, as confirmed in Fig. 4. Further, when AESR is not a concern, forgoing acceptance sampling in favour of looking ahead provides the best speed-up.

It is worth noting that the combination of acceptance sampling and look-ahead has a net positive impact on AESR. The case for minimal AESR would occur when one is, for instance, being charged for resources. Here using the smallest amount of simulation evaluations is desirable over the smallest number of generations as measured by AGSR.

Fig. 3
figure 3

Hypervolume comparison of ParDen-Sur variants and NSGA-II (higher is better). All ParDen-Sur variants with Look-ahead achieve, on average, an optimal solution in fewer generations, as indicated by their positions in the upper left-hand corners. Trial lines are shown in grey

Full size image
Fig. 4
figure 4

Hypervolume comparison of the best ParDen-Sur variants and NSGA-II (higher is better). The max-fill variant with Look-ahead achieves an optimal solution in the fewest generations, as indicated by its dominant position in the upper left-hand corner

Full size image

7 Conclusion

This study presents the ParDen-Sur surrogate-assisted optimisation algorithm, an extension to the original ParDen algorithm by van Zyl et al. [19], to address the computational difficulty of finding the efficient frontier for multi-period portfolio optimisation. The extension is a reservoir sampling-enabled look-ahead mechanism for generating new offspring. Both the look-ahead and the acceptance sampling rely on the NDScore. Here the NDScore is extended to include Kendall-\(\tau\). The extension and the original acceptance sampling mechanism are tested on the problems of SPO and MPO. The three variants of ParDen-Sur are evaluated across several EAs. Both performance and quality metrics are taken into account.

The experiments involve an empirical performance comparison of several seminal MOP EA for both SPO and MPO. The effects demonstrate the superior efficacy of surrogate-assisted optimisation in alleviating the computational burden of constructing a Pareto frontier and support the presentation of a new algorithm, ParDen-Sur, which improves upon the state-of-the-art surrogate-assisted portfolio optimisation by introducing a reservoir sampling-based look-ahead mechanism. The results demonstrate a statistically significant improvement in both performance and quality of solutions when ParDen-Sur is applied to the aforementioned problems with the underpinning EAs considered. However, reservoir sampling-enabled look-ahead has the most impact on the results.

The HV improvement with ParDen-Sur is marginal over the state-of-the-art (SOTA). However, for GD+ and IGD+, these improvements are statistically significant. In practice, these improvements are both realisable on commodity hardware and would result in substantive improvements in arriving at optimal solutions to the multi-period portfolio optimisation problem.

The study has demonstrated the benefit of ParDen-Sur for the portfolio optimisation hyper-parameter search problem. Although the study evaluates the use of surrogates in general, the study does not say anything about which of the current multitude of approaches to the surrogate-assisted optimisation is best overall. Extensive coverage of further approaches to surrogate-assisted optimisation would go a long way towards answering these questions. Secondly, the study is constrained to a particular market with particular characteristics. Future work will look to explore additional markets as well as additional problem domains in which ParDen-Sur might be of value.