Multi-objective reinforcement learning for designing ethical multi-agent environments

Abstract

This paper tackles the open problem of value alignment in multi-agent systems. In particular, we propose an approach to build an ethical environment that guarantees that agents in the system learn a joint ethically-aligned behaviour while pursuing their respective individual objectives. Our contributions are founded in the framework of Multi-Objective Multi-Agent Reinforcement Learning. Firstly, we characterise a family of Multi-Objective Markov Games (MOMGs), the so-called ethical MOMGs, for which we can formally guarantee the learning of ethical behaviours. Secondly, based on our characterisation we specify the process for building single-objective ethical environments that simplify the learning in the multi-agent system. We illustrate our process with an ethical variation of the Gathering Game, where agents manage to compensate social inequalities by learning to behave in alignment with the moral value of beneficence.

1 Introduction

The challenge of guaranteeing that autonomous agents act value-aligned (in alignment with human values) [59, 66] is becoming critical as agents increasingly populate our society. Hence, it is of great concern to design ethically-aligned trustworthy AI [15] capable of respecting human values [18, 35] in a wide range of emerging application domains (e.g. social assistive robotics [12], self-driving cars [29], conversational agents [13]). Indeed, there has recently been a rising interest in both the Machine Ethics [58, 79] and AI Safety [5, 41] communities in applying Reinforcement Learning (RL) [70] to tackle the critical problem of value alignment. A common approach in these two communities to deal with the value alignment problem is to design an environment with incentives to behave ethically. Thus, we often find in the literature that a single agent receives incentives through an exogenous reward function (e.g. [2, 9, 51, 54, 55, 78]). Firstly, this reward function is specified from some ethical knowledge. Afterwards, rewards are incorporated into an agent’s learning environment through an ethical embedding process. Besides focusing on a single agent, with the exception of [55], providing guarantees that an agent learns to behave ethically in an environment is typically disregarded. Therefore, to the best of our knowledge, guaranteeing that all agents in a multi-agent system learn to behave ethically remains an open problem.

Against this background, the objective of this work is to automate the design of ethical environments for multi-agent systems wherein agents learn to behave ethically. For that, we propose a novel ethical embedding process for multi-agent systems that guarantees the learning of ethical behaviours. In more detail, our embedding process guarantees that agents learn to prioritise the ethical social objective over their individual objectives, and thus agents learn to exhibit joint ethically-aligned behaviours. Particularly, here we focus on guaranteeing ethically-aligned behaviours on environments where it is enough that some of the agents (not necessarily all of them) intervene to completely fulfil a shared ethical social objective. Such environments are founded in the Ethics literature. For instance, not all people walking near a pond must act to rescue someone drowning in it [65]. Another well-known example, from the AI literature, is a sequential social dilemma called the Cleanup Game [34], in which a handful of agents stop collecting apples from time to time to repair the aquifer supplying water.

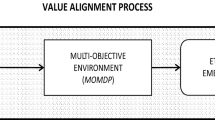
Figure 1 outlines the Multi-Agent Ethical Embedding (MAEE) process that we propose in this paper, which is founded on two main contributions.

First, we formalise the MAEE Problem within the framework of Multi-Objective Markov Games (MOMG) [60, 61] to handle both the social ethical objective and individual objectives. This formalisation allows us to characterise the so-called Ethical MOMGs, the family of MOMGs for which we can solve the problem. As Fig. 1 shows, solving the problem amounts to transforming an ethical MOMG into an ethical Markov Game (MG), where agents can learn with Single-Objective RL [39, 44] instead of Multi-Objective RL [56, 57]. Hence, we propose to create a (simpler) single-objective ethical environment that embeds both ethical and individual objectives to relieve agents from handling several objectives. For that purpose, we follow the prevailing approach (e.g. [9, 78]), of applying a linear scalarisation function that weighs individual and ethical rewards.

Importantly, our formalisation involves the characterisation of ethical joint behaviour through the definitions of ethical policies and ethical equilibria. An ethical policy defines the behaviour of an agent prioritising the shared ethical objective over its individual objective. An ethical equilibrium is a joint policy composed of ethical policies that characterises the target equilibrium in the ethical environment, namely the joint ethically-aligned behaviours.

Secondly, we propose a novel process to solve the MAEE problem that generalises the single-agent ethical embedding process in [55]. Our process involves two consecutive decompositions of the multi-agent problem into n single-agent problems: the first one (Fig. 1 left) allows the computation of the ethical equilibrium (i.e. the target joint policy); whereas the second one (right) computes the weight vector that solves our multi-agent embedding problem. As a result of these two steps, our MAEE process transforms an input multi-objective environment into a single-objective ethical environment, as shown by Fig. 1. Interestingly, each agent within an ethical environment can independently learn its policy in the ethical equilibrium.

Finally, as a further contribution, we showcase our MAEE process by applying it to a variation of the widely known apple gathering game [34, 36, 40], a Markov game where several agents collect apples to survive. In our ethical gathering game, agents have unequal capabilities, similarly to [67, 68]. As a mechanism for reducing inequality, we include in the game a donation box to which agents can either donate or take apples from. After applying our embedding process, we empirically show that agents can compensate for social inequalities and ensure their survival by learning how to employ the donation box (when to donate or take) in alignment with the moral value of beneficence. Each agent learns its ethical policy with an independent Q-learner.

Fig. 1

Multi-Agent Ethical Embedding process for environment design. Rectangles stand for objects whereas rounded rectangles correspond to processes. Process steps: Computation of the ethical equilibrium from the input multi-objective environment; and computation of the solution ethical weight that creates an output ethical (single-objective) environment

In what follows, Sect. 2 presents the necessary background on Multi-Objective Reinforcement Learning. Next, Sect. 3 presents our formalisation of the MAEE problem and Sect. 4 characterises the multi-agent environments to which we can apply a MAEE process. Then, Sect. 5 details our process to build ethical environments. Subsequently, Sect. 6 illustrates our approach to an apple gathering game. Finally, Sect. 7 analyses related work and Sect. 8 concludes the paper and sets paths to future work.

2 Background

This section is devoted to present the necessary background for our approach of designing ethical environments in a multi-agent system with reinforcement learning. Thus, Sect. 2.1 introduces single-objective reinforcement learning, and Sect. 2.2 presents the basics of multi-objective reinforcement learning, in both cases from a multi-agent perspective. Thereafter, in Sect. 2.3 we briefly describe the algorithm for designing ethical environments for a single agent introduced in [55]. We do so because such algorithm is an important building block for the approach to build multi-agent ethical environments that we present in this paper.

2.1 Single-objective multi-agent reinforcement learning

In single-objective multi-agent reinforcement learning (MARL), the learning environment is characterised as a Markov game (MG) [39, 44, 50]. A Markov game characterises an environment in which several agents are capable of repeatedly acting upon it to modify it, and as a consequence, each agent receives a reward signal after each action. Formally:

Definition 1

(Markov game) A (finite single-objective)¹ Markov game (MG) of n agents is defined as a tuple $\langle {\mathcal {S}}, {\mathcal {A}}^{i=1,\dots ,n}, {R}^{i=1,\dots ,n}, T \rangle$ where ${\mathcal {S}}$ is a (finite) set of states, ${\mathcal {A}}^i(s)$ is the set of actions available at state s for agent i. Actions upon the environment change the state according to the transition function $T: {\mathcal {S}} \times {\mathcal {A}}^1 \times \cdots \times {\mathcal {A}}^n \times {\mathcal {S}} \rightarrow [0, 1]$. After every transition, each agent i receives a reward based on function $R^i: {\mathcal {S}} \times {\mathcal {A}}^1 \times \cdots \times {\mathcal {A}}^n \times {\mathcal {S}} \rightarrow {\mathbb {R}}$.

In a Markov game, each agent i decides which action to perform according to its policy $\pi ^i: {\mathcal {S}} \times {\mathcal {A}}^i \rightarrow [0, 1]$ and we call joint policy $\pi = (\pi ^1, \dots , \pi ^n)$ to the union of all agents’ policies. We also use the notation $\pi ^{-i}$ to refer to the joint policy of all agents except agent i.

A Markov game with a single agent (i.e. $n=1$) is called a Markov decision process (MDP) [11, 37, 70]. Moreover, if we enforce that all the agents but i follow a fixed joint policy $\pi ^{-i}$, then the learning problem for agent i becomes equivalent to learning its policy in an MDP.

During learning, agents are expected to learn policies that accumulate as many rewards as possible. The classical method to evaluate an agent’s policy is to compute the (expected) discounted sum of rewards that an agent obtains by following it. This operation is formalised by means of the so-called value function $V^i$, defined as:

$$\begin{aligned} V^i_{\langle \pi ^i, \pi ^{-i} \rangle }(s)&\doteq {\mathbb {E}}\left[ \sum _{k=0}^{\infty } \gamma ^k r^i_{t+k+1} \mid S_t = s, \langle \pi ^i, \pi ^{-i} \rangle \right] \nonumber \\&\quad \text { for every state }s \in {\mathcal {S}}, \end{aligned}$$

(1)

where $\gamma \in [0,1)$ is referred to as the discount factor, t is any time step of the Markov game, $\pi ^i$ is the policy of agent i and $\pi ^{-i}$ is the joint policy of the rest of the agents. Notice that we cannot evaluate the policy of an agent without taking into consideration how the rest of the agents behave.

The individual objective of each agent is to learn a policy that maximises its corresponding value function $\pi _* \doteq {{\,\mathrm{\mathop {{\mathrm{arg\,max}}}\limits }\,}}_{\pi ^i} V^i$. Typically, there does not exist a joint policy $\pi$ for a Markov game for which every agent maximises its policy. Instead, the literature considers solution concepts imported from game theory [50].

Firstly, consider the simple case in which an agent i tries to maximise its $V^i$ with respect to all the policies $\pi ^{-i}$ of the other agents (assuming that the rest of agents have fixed policies). Then, such policy $\pi ^i_*$ receives the name of a best-response² against $\pi ^{-i}$ [50]. When all agents reach a situation such that all have a best-response policy, we say that we have a Nash equilibrium (NE). NEs are stable points where no agent would benefit from deviating from its current policy. Formally:

Definition 2

(Nash equilibrium) Given a Markov game, we define a Nash equilibrium (NE) [33] as a joint policy $\pi _{*}$ such that for every agent i,

$$\begin{aligned} {V^i}_{\langle \pi ^{i}_*, \pi ^{-i}_{*} \rangle }(s) = \max _{\pi ^i} {V^i}_{\langle {\pi ^{i}}, \pi ^{-i}_{*} \rangle }(s) \end{aligned}$$

for every state s.

One of the main difficulties of Nash equilibria is the fact that each agent needs to take into account the policies of the others in order to converge to an equilibrium. However, there is a subset of Nash equilibria for which each agent can reach an equilibrium independently: dominant equilibria [45]. For that reason, we propose a concept of dominant equilibrium for Markov games based on the game theory literature. First, we generalise the concept of dominant strategies [45] to define dominant policies in a Markov game as follows: we say that a policy $\pi ^i$ of agent i is dominant if it yields the best outcome for agent i no matter the policies that the other agents follow. Then, we say that the dominant policy $\pi ^i$ dominates over all possible policies:

Definition 3

(Dominant policy) Given a Markov game ${\mathcal {M}}$, a policy $\pi ^i$ of agent i is a dominant policy if and only if for every joint policy $\langle \rho ^i, \rho ^{-i} \rangle$ and every state s in which $\rho ^i(s) \ne \pi ^i(s)$ it holds that:

$$\begin{aligned} V^i_{\langle \pi ^i, \rho ^{-i} \rangle }(s) \ge V^i_{\langle \rho ^i, \rho ^{-i} \rangle }(s). \end{aligned}$$

(2)

A policy is strictly dominant if we change $\ge$ to >. Finally, if the policy $\pi ^i$ of each agent of an MG is a dominant policy, we say that the joint policy $\pi = (\pi ^1, \dots , \pi ^n)$ is a dominant equilibrium.

As a practical note about the equilibrium concepts of Multi-Agent RL defined, we briefly refer to how to compute them. There exist several kinds of algorithms to find an equilibrium in a Markov game depending on whether agents cooperate (i.e. they share the same reward function) or not [39]. For the most general case (if no prior information is assumed) a simple option is to apply a single-agent reinforcement learning algorithm to each agent independently, such as Q-learning [77].

2.2 Multi-objective multi-agent reinforcement learning

Multi-objective multi-agent reinforcement learning (MOMARL) formalises problems in which agents have to ponder between several objectives, each represented as an independent reward function [57]. Hence, in MOMARL, the environment is characterised as a Multi-Objective Markov game (MOMG), an MG composed of vectorial reward functions. Formally:

Definition 4

A (finite) m-objective Markov game (MOMG) of n agents is defined as a tuple $\langle {\mathcal {S}}, {\mathcal {A}}^{i=1,\dots ,n}, \vec {R}^{i=1,\dots ,n}, T \rangle$ where: ${\mathcal {S}}$ is a (finite) set of states; ${\mathcal {A}}^{i}(s)$ is the set of actions available at state s for agent i; $\vec {R}^i = ( R^i_1, \dots , R^i_m )$ is a vectorial reward function with each $R^i_j$ being the associated scalar reward function of agent i for objective $j \in \{1, \dots , m\}$; and T is a transition function that, taking into account the current state s and the joint action of all the agents, returns a new state.

Each agent i of an MOMG has its associated multi-dimensional state value function $\vec {V}^i = ( V^i_1, \dots , V^i_m )$, where each $V^i_j$ is the expected sum of rewards for objective j of agent i.

A multi-objective Markov game with a single agent (i.e. $m=1$) is called a multi-objective Markov decision process (MOMDP) [56, 57]. Moreover, given an MOMG ${\mathcal {M}}$, if we enforce that all the agents but i follow a fixed joint policy $\pi ^{-i}$, we obtain an MOMDP ${\mathcal {M}}^i$ for agent i.

In multi-objective reinforcement learning, in order to evaluate the different policies of the agents, a classical option is to assume the existence of a scalarisation function f capable of reducing the number of objectives of the environment into a single one (e.g. [14, 49, 51]). Such scalarisation function transforms the vectorial value function $\vec {V}^i$ of each agent i into a scalar value function $f^i(\vec {V}^i)$. With $f^i$, each agent’s goal becomes to learn a policy that maximises $f^i(\vec {V}^i)$, a single-objective problem encapsulating the previous multiple objectives.

It is specially notable the particular case in which $f^i$ is linear, because in such case the scalarised problem can be solved with single-objective reinforcement learning algorithms³. Any linear scalarisation function $f^i$ is a weighted combination of rewards, and henceforth we will refer to such function by the weight vector $\vec {w} \in {\mathbb {R}}^n$ that it employs. Moreover, any policy $\pi$ such that its value $\vec {V}^{\pi }$ maximises a linear scalarisation function is said to belong to the convex hull of the MOMDP [56]⁴.

Several reasons explain the appeal of linear scalarisation functions. Firstly, from a theoretical perspective, a linear scalarisation function transforms a Multi-Objective MDP into an MDP in which all existing proofs of convergence for single-objective RL apply [31]. Secondly, from a practical perspective, if the desired solution of an MOMDP belongs to its convex hull, transforming it first into an MDP simplifies the learning of the agent. In addition, it gives the access to all the single-objective reinforcement learning algorithms.

Nevertheless, it is necessary to remark on the limitations of linear scalarisation functions. By definition, they restrict the possible solutions to only those in the convex hull. Such a restriction is enough when the learning objective of the agent is to maximise a weighted sum of the objectives. However, in many cases, the desired behaviour cannot be expressed as the one that maximises a linear scalarisation function. For example, consider the problem of finding all the Pareto-optimal policies of an MOMDP, then select the one that better satisfies our needs. The convex hull is only a subset of the Pareto front (in many cases, a closed subset), so a linear function will not be able to find some potential solutions. We refer to [73, 75] for more detailed examples of simple MOMDPs wherein the convex hull cannot capture the whole Pareto front.

The following Sect. 2.3 provides the intuition on why these limitations of linear scalarisation functions do not apply in the particular case of our ethical embedding process.

2.3 Designing ethical environments for the single-agent case

As previously stated in the introduction, we aim to design a process that guarantees that all agents in a multi-agent system learn to behave in alignment with a given moral value. To do so, we build upon a formal process for designing an ethical environment for a single-agent: the Single-Agent Ethical Embedding Process (SAEEP)⁵ [55]. Being single agent, the SAEEP transforms an initial environment encoded as a multi-objective Markov decision process (MOMDP) into an ethical (single objective) environment in which it is easier for the agent to learn to behave ethically-aligned.

Briefly, the SAEEP takes as input a so-called ethical MOMDP, a two-objective MOMDP characterised by an individual objective and an ethical objective. In turn, this ethical objective is defined in terms of: (1) a normative component, that punishes the violation of normative requirements; and (2) an evaluative component rewarding morally praiseworthy actions. Although further details are provided in Sect. 3, here we just highlight that we consider these two components to be equally important so that we can define an ethical policy for the MOMDP as that being optimal for both ethical components. Furthermore, since we expect the agent to fulfil its individual objective as much as possible, we define ethical-optimal policies as the ethical policies with the maximum accumulation of individual rewards. Then, we guarantee in [55] that if at least one ethical policy exists for the input MOMDP M, then the SAEEP will always find a weight vector $\vec {w}$ to scalarise M in such a way that all optimal policies in the resulting scalarised ethical MDP turn out to also be ethical-optimal policies. This ensures the aforementioned transformation of the input ethical MOMDP into a simpler-to-learn ethical MDP.

Without entering into details, we can always compute such a weight vector because of our definition of ethical policy. Any ethical policy maximises completely the ethical objective by definition. Hence, they maximise the linear scalarisation function with the individual weight set to $w_0 = 0$ and the ethical weight set to $w_e = 1$.⁶ Thus, all ethical policies belong to the convex hull. Since ethical-optimal policies are a subset of ethical policies, they also belong to the convex hull. Thus, we can find within the convex hull a specific weight vector for which ethical-optimal policies are optimal. For that reason, a linear scalarisation function for which ethical-optimal policies are optimal is guaranteed to exist in finite MOMDPs.

3 Formalisation of the multi-agent ethical embedding problem

In Ethics, a moral value (or ethical principle) expresses a moral objective worth striving for [53]. Following [55], current approaches to align agents with a moral value propose: (1) the specification of rewards to actions aligned with a moral value, and (2) an embedding that ensures that an agent learns to behave ethically (in alignment with the moral value). In this work we generalise the single-agent embedding process presented in [55] for the multi-agent case.

In more detail, in this work we assume that the specification of an ethical reward function is already provided to us. Furthermore, we assume that such an ethical reward function already encodes all the necessary ethical knowledge of the environment. Hence, it is not the work of the environment designer to select the specific ethical rewards for each action. For that reason, here we focus on the second step of value alignment, the ethical embedding. Furthermore, we remark that the reward specification only deals with adding rewards to the Markov Game. Hence, the reward specification process does not modify the state set or the action set of the environment at any point. Likewise, the ethical embedding process only modifies the reward functions of the environment.⁷

Thus, in this work, we assume that individual and ethical rewards are specified as a Multi-Objective Markov Game (MOMG) [61]. More precisely, we propose the concept of ethical MOMG as a type of MOMG that incorporates rewards considering a given moral value. We define an ethical MOMG as a two-objective learning environment where rewards represent both the individual objective of each agent and the social⁸ ethical objective (i.e. the moral value). Then, the purpose of the multi-agent ethical embedding (MAEE) problem, which we formalise below, is that of transforming an ethical MOMG ${\mathcal {M}}$ (the input environment) into a single-objective MG ${\mathcal {M}}_*$ (the target environment) wherein it is ensured that all agents learn to fulfil a social ethical objective while pursuing their individual objectives.

In this work we aim at solving an MAEE problem via designing single-objective environments in which each agent learns that its best strategy is to behave ethically, independently of what the other agents may do. In game theory, such strategy is called dominant, and when all agents have one, then we say that a dominant equilibrium exists. Dominant equilibria have several attractive properties. First of all, every dominant equilibrium is a Nash equilibrium [45]. Secondly, if an agent has a dominant policy, it can learn such policy without considering the other agents’ policies [76]. For those reasons, here we characterise an ethical embedding process that leads to a dominant equilibrium wherein agents behave ethically.

To begin with, we define an ethical MOMG as a two-objective Markov game encoding the reward specification of both the agents’ individual objectives and the social ethical objective (i.e. the moral value).

Following the Ethics literature [16, 23] and recent work in single-agent ethical embeddings [55], we define an ethical objective through two dimensions: (1) a normative dimension, which punishes the violation of moral requirements (e.g. taking donations when being wealthy); and (2) an evaluative dimension, which rewards morally praiseworthy actions (e.g. rescuing someone that is drowning). Formally:

Definition 5

(Ethical MOMG) We define an Ethical MOMG as any n-agent MOMG

$$\begin{aligned} {{\mathcal {M}}} = \langle {\mathcal {S}}, {\mathcal {A}}^{i=1,\ldots ,n}, (R_0, R_{{\mathcal {N}}}+ R_{E})^{i=1,\dots ,n}, T \rangle , \end{aligned}$$

(3)

such that for each agent i:

• $R^i_{{\mathcal {N}}}: {\mathcal {S}} \times {\mathcal {A}}^i \rightarrow {\mathbb {R}}^-$ penalises violating moral requirements.

• $R^i_{E}:{\mathcal {S}} \times {\mathcal {A}}^i \rightarrow {\mathbb {R}}^+$ positively rewards performing praiseworthy actions.

We define $R^i_0$, $R^i_{{\mathcal {N}}}$, and $R^i_E$ as the individual, normative, and evaluative reward functions of agent i, respectively. We refer to $R^i_e = R^i_{{\mathcal {N}}}+R^i_E$ as the ethical reward function. Furthermore, we define the ethical reward function as social if and only if it satisfies the following equal treatment condition, in which we impose agents to be equally treated when assigning the (social) ethical rewards:

• The same normative and evaluative rewards are given to each agent for performing the same actions.

Finally, we also assume coherence in the ethical rewards and impose a no-contradiction condition:

• For each agent, an action cannot be ethically rewarded and punished simultaneously: $R^i_E(s,a^i) \cdot R^i_{{\mathcal {N}}}(s, a^i) = 0$ for every $i, s, a^i$.

Although actions cannot be rewarded and punished simultaneously, having a twofold ethical reward prevents agents from learning to disregard some of its normative requirements while learning to perform as many praiseworthy actions as possible. Moreover, the equal treatment condition makes uniform what is considered as praiseworthy or blameworthy along all agents. Thus, it ensures that the ethical objective is indeed social. Finally, also notice that a single-agent Ethical MOMG corresponds to an Ethical MOMDP as previously defined in the Background Section.

Within ethical MOMGs, we define the ethical policy $\pi ^i$ for an agent i as that maximising the ethical objective subject to the behaviour of the other agents (i.e. their joint policy $\pi ^{-i}$). This maximisation is performed over the normative and evaluative components of agent i’s value function:

Definition 6

(Ethical policy) Let ${{\mathcal {M}}}$ be an ethical MOMG. A policy $\pi ^i$ of agent i is said to be ethical in ${\mathcal {M}}$ with respect to $\pi ^{-i}$ if and only if the value vector of agent i for the joint policy $\langle \pi ^i, \pi ^{-i} \rangle$ is optimal for its social ethical objective (i.e. its normative $V^i_{{\mathcal {N}}}$ and evaluative $V^i_{E}$ components):

$$\begin{aligned} V^i_{{\mathcal {N}}_{\langle \pi ^{i}, \pi ^{-i} \rangle }}&= \max _{\rho ^i} V^i_{{\mathcal {N}}_{\langle {\rho ^{i}}, \pi ^{-i} \rangle }}, \\ V^i_{E_{\langle \pi ^{i}, \pi ^{-i} \rangle }}&= \max _{\rho ^i} V^i_{E_{\langle {\rho ^{i}}, \pi ^{-i} \rangle }}. \end{aligned}$$

Ethical policies pave the way to characterise our target policies, the ones that we aim agents to learn in the ethical environment: best-ethical policies. These maximise pursuing the individual objective while ensuring (prioritising) the fulfilment of the ethical objective. Thus, from the set of ethical policies, we define as best those maximising the individual value function $V^i_0$ (i.e. the accumulation of rewards $R^i_0$):

Definition 7

(Best-ethical policy) Let ${\mathcal {M}}$ be an Ethical MOMG. We say that a policy $\pi ^i$ of agent i is best-ethical with respect to $\pi ^{-i}$ if and only if it is both an ethical policy and also a best-response in the individual objective among the set $\Pi _e(\pi ^{-i})$ of ethical policies with respect to $\pi ^{-i}$:

$$\begin{aligned} V^i_{0_{\langle \pi ^i, \pi ^{-i}\rangle }} = \max _{\rho ^i \in \Pi _e(\pi ^{-i})} V^i_{0_{\langle \rho ^i, \pi ^{-i} \rangle }}. \end{aligned}$$

Notice that best-ethical policies impose a lexicographic ordering between the two objectives: the ethical objective is preferred to the individual objective.

In the MARL literature, if the policy $\pi ^i$ of each agent i is a best-response (i.e. optimal with respect to $\pi ^{-i})$, then the joint policy $\pi = (\pi ^1, \dots , \pi ^n)$ that they form is called a Nash equilibrium [44].

The definitions above focus on the ethical policy of a single agent. In order to define ethical joint policies, here we propose two equilibrium concepts for ethical MOMGs. First, an ethical equilibrium $\pi = (\pi ^1, \dots , \pi ^n)$ occurs when all agents follow an ethical policy, and hence behave ethically. Second, a best-ethical equilibrium is more demanding than an ethical equilibrium, because it occurs when each agent follows the ethical policy that is best for achieving its individual objective.

Our approach consists in transforming an Ethical Multi-Objective MG into an Ethical (single-objective) MG. This way, the agents can learn within the single-objective MG by applying single-objective reinforcement learning algorithms [61]. We perform this transformation by means of what we call a multi-agent embedding function. In the multi-objective literature, an embedding function receives the name of scalarisation function [61]. Therefore, our goal is to find an embedding function $f_e$ that guarantees that agents are incentivised to learn ethical policies in the ethical environment (the single-objective Markov Game created after applying $f_e$).

Formally, we want to ensure that such $f_e$ guarantees that best-ethical equilibria in the Ethical MOMG correspond with Nash equilibria in the single-objective MG created from $f_e$ (see second row in Table 1, which summarises the correspondences between equilibria in an Ethical (Single-Objective) MG and an Ethical MOMG). For that reason, we refer to the MOMG scalarised by $f_e$ as the Ethical MG. In its simplest form, this embedding function $f_e$ will be a linear combination of individual and ethical objectives for each agent i:

$$\begin{aligned} f^i_e(\vec {V}^i ) = \vec {w}^i \cdot \vec {V}^{i}= w^i_0 V^i_0 + w^i_{e} ( V^{i}_{{\mathcal {N}}} + V^{i}_E), \end{aligned}$$

(4)

where $\vec {w}^i \doteq ( w^i_0, w^i_e)$ is a weight vector with all weights $w^i_0, w^i_e > 0$ to guarantee that each agent i takes into account all rewards (i.e. both objectives). Without loss of generality, hereafter we fix the individual weight of all agents to $w^i_0 = 1$ and set the same ethical weight for each agent⁹: $w_e \doteq w^1_e = \dots = w^n_e$. Furthermore, we shall refer to any linear $f_e$ by its ethical weight $w_e$.

Moreover, as previously mentioned, here we also consider an ethical embedding function that not only guarantees that there are ethical Nash equilibria, but also that there are ethical dominant equilibria. As previously mentioned in the Background Section, we say that a policy $\pi ^i$ of agent i is dominant in a Markov game context if it yields the best outcome for agent i no matter the policies that the other agents follow. We will also say that the policy $\pi ^i$ dominates over all possible policies [45].

Finally, we can formalise our multi-agent ethical embedding problem as that of computing a weight vector $\vec {w} \doteq (1, w_e)$ that incentivises all agents to behave ethically while still pursuing their respective individual objectives. Formally:

Problem 1

(MAEE: Multi-Agent Ethical Embedding) Let ${{\mathcal {M}}} = \langle {\mathcal {S}}, {\mathcal {A}}^i,(R^i_0, R^i_{{\mathcal {N}}} + R^i_{E}), T \rangle$ be an ethical MOMG. The multi-agent ethical embedding problem is that of computing the vector $\vec {w} = (1, w_e)$ of positive weights such that there is at least one dominant equilibrium in the Markov Game ${\mathcal {M}}_* = \langle {\mathcal {S}}, {\mathcal {A}}, R_0 + w_e ( R_{{\mathcal {N}}} + R_{E}), T \rangle$ that is a best-ethical equilibrium in ${\mathcal {M}}$.

Any weight vector $\vec {w}$ with positive weights that guarantees that at least one dominant equilibrium (with respect to $\vec {w}$) in the original environment ${\mathcal {M}}$ is also a best-ethical equilibrium in the scalarised environment ${\mathcal {M}}_*$ is then a solution to Problem 1.

3.1 The benefits of an environment-designer approach

Before addressing the solvability of Problem 1 and determining the theoretical conditions for designing an ethical environment where best-ethical equilibria are dominant, it is important to consider why we should design such an environment in the first place. Why not let the agents learn using a multi-objective reinforcement learning algorithm directly? We will refer to the former approach as the environment-designer approach and the latter as the agent-centric approach.

There are two primary reasons why we advocate for the environment-designer approach. Firstly, transforming the multi-objective environment into a single-objective one simplifies the learning problem for the agents. Secondly, we focus on ensuring that agents are incentivised to act ethically. The agent-centric approach introduces complexity to the agents’ learning process, assuming they will inherently consider ethical rewards, which may not always be the case. Moreover, we assume that each agent autonomously selects its reinforcement learning algorithm. In this paper, we follow the mechanism design literature [20], where it is assumed that we cannot alter agents’ preferences. Although agents could directly learn a best-ethical equilibrium using a lexicographic reinforcement learning algorithm (such as TLO [74]), there is no guarantee that they will choose such an algorithm during training.

These reasons justify the need for an environment-designer approach, which involves designing an ethical single-objective environment that incentivises agents’ ethical behaviour. This approach allows us to be resilient against agents equipped with their own learning algorithms and preferences beyond our control.

4 Solvability of the MAEE problem

We devote this section to describing the minimal conditions under which there always exists a solution to Problem 1 for a given ethical MOMG, and also to proving that such solution actually exists. This solution (a weight vector) will allow us to apply the ethical embedding process to the ethical MOMG ${\mathcal {M}}$ at hand to produce an ethical environment (a single-objective MG ${\mathcal {M}}_*$) wherein agents learn to behave ethically while pursuing their individual objectives (i.e. to reach a best-ethical equilibrium). In what follows, Sect. 4.1 characterises a family of ethical MOMGs for which Problem 1 can be solved, and Sect. 4.2 proves that the solution indeed exists for such family.

4.1 Characterising solvable ethical MOMGs

We introduce below a new equilibrium concept for ethical MOMGs that is founded on the notion of dominance in game theory, the so-called best-ethically-dominant equilibrium. We find such equilibrium in environments where the best behaviour for each agent is to follow an ethical policy, provided that the ethical weight is properly set. The existence of such equilibria is important to characterise the ethical MOMGs for which we can solve the MAEE problem (Problem 1). Thus, as shown below in Sect. 4.2, we can solve Problem 1 for Ethical MOMGs with a best-ethically-dominant equilibrium.

Now we adapt the concept of dominance in game theory for Ethical MOMGs. We start by defining policies that are dominant with respect to the ethical objective. We call these policies ethically-dominant policies. Formally:

Definition 8

(Ethically-dominant policy) Let ${{\mathcal {M}}}$ be an ethical MOMG. We say that a policy $\pi ^i$ of agent i is an ethically-dominant policy in ${\mathcal {M}}$ if and only if the policy is dominant for its ethical objective (i.e. both its normative $V^i_{{\mathcal {N}}}$ and evaluative $V^i_{E}$ components) for every joint policy $\langle \rho ^{i}, \rho ^{-i} \rangle$ and every state s in which $\rho ^i(s) \ne \pi ^i(s)$:

$$\begin{aligned} V^i_{{\mathcal {N}}_{\langle \pi ^{i}, \rho ^{-i} \rangle }}(s)&\ge V^i_{{\mathcal {N}}_{\langle {\rho ^{i}}, \rho ^{-i} \rangle }}(s), \\ V^i_{E_{\langle \pi ^{i}, \rho ^{-i} \rangle }}(s)&\ge V^i_{E_{\langle {\rho ^{i}}, \rho ^{-i} \rangle }}(s). \end{aligned}$$

Following Definition 6, every ethically-dominant policy $\pi ^i$ is an ethical policy with respect to any $\pi ^{-i}$.

We also adapt the concept of dominance from game theory for defining best-ethically-dominant policies. Given an ethical MOMG, we say that a best-ethically-dominant policy is: (1) dominant with respect to the ethical objective among all policies; and (2) dominant with respect to the individual objective ($V^i_0$) among ethical policies. Formally:

Definition 9

(Best-ethically-dominant policy) Let ${\mathcal {M}}$ be an Ethical MOMG. A policy $\pi ^i$ of agent i is a best-ethically-dominant policy if and only if it is ethically-dominant and

$$\begin{aligned} V^i_{0_{\langle \pi ^i, \rho ^{-i}\rangle }}(s) \ge V^i_{0_{\langle \rho ^i, \rho ^{-i} \rangle }}(s), \end{aligned}$$

for every joint policy $\langle \rho ^{i}, \rho ^{-i} \rangle$ in which $\rho ^i$ is an ethical policy with respect to $\rho ^{-i}$, and every state s in which $\rho ^i(s) \ne \pi ^i(s)$.

Next, we define the generalisation of previous dominance definitions considering the policies of all agents. This will lead to a new equilibrium concept. If the policy $\pi _i$ of each agent of an Ethical MOMG is best-ethically-dominant, then the joint policy $\pi$ is a best-ethically-dominant (BED) equilibrium. Observe that every best-ethically-dominant equilibrium is a best-ethical equilibrium. Finally, we say that a joint policy $\pi = (\pi ^1, \dots , \pi ^n)$ is a strictly best-ethically-dominant equilibrium if and only if every $\pi ^i$ is strictly dominant with respect to the individual objective among ethical policies (i.e. by changing $\ge$ with > in Def. 9).

In the following subsection, we prove that we can solve the multi-agent ethical embedding problem (Problem 1) for Ethical MOMGs with a best-ethically-dominant equilibrium.

4.2 On the existence of solutions

Next we prove that we can find a multi-agent ethical embedding function for ethical MOMGs with best-ethically-dominant (BED) equilibria. Henceforth, we shall refer to such ethical MOMGs as solvable ethical MOMGs, and if the BED equilibrium is strict, we will refer to such Ethical MOMGs as strictly-solvable.

Below, we present Theorem 1 as our main result. The theorem states that given a solvable ethical MOMG (Multi Objective Markov Game), it is always possible to find an embedding function that transforms it into a (single-objective) MG where agents are guaranteed to learn to behave ethically. More in detail, the following Theorem 1 guarantees that —given the appropriate ethical weight in our embedding function— there exists a dominant equilibrium in the resulting MG (i.e. the agents’ learning environment) that is also a best-ethical equilibrium in the input ethical MOMG. In other words, such embedding function is the solution to Problem 1 we aim at finding.

The proof of Theorem 1 requires the introduction of some propositions as intermediary results. The first proposition establishes the relationship between dominant and ethically-dominant policies.

Proposition 1

Given an ethical MOMG ${\mathcal {M}} = \langle {\mathcal {S}}, {\mathcal {A}}^i, (R_0, R_{{\mathcal {N}}} + R_{E})^i, T \rangle$ for which there exists ethically-dominant equilibria, there exists a weight vector $\vec {w} = (1, w_e)$ with $w_e > 0$ for which every dominant policy for an agent i in the MG ${\mathcal {M}}_* = \langle {\mathcal {S}}, {\mathcal {A}}^i, R^i_0 + w_e ( R^i_{{\mathcal {N}}} + R^i_{E}), T \rangle$ is also an ethically-dominant policy for agent i in ${\mathcal {M}}$.

Proof

Without loss of generality, we only consider deterministic policies, by the Indifference Principle [45].

Consider a weight vector $\vec {w} = (1, w_e)$ with $w_e \ge 0$. Suppose that for that weight vector, the only deterministic $\vec {w}$-dominant policies (i.e. policies that are dominant in the MOMG scalarised by $\vec {w}$) are ethically-dominant. Then we have finished.

Suppose now that it is not the case, and there is some $\vec {w}$-dominant policy $\rho ^i$ for some agent i that is not dominant ethically. This implies that for some state $s'$ and for some joint policy $\rho ^{-i}$ we have that:

$$\begin{aligned} V^i_{{\mathcal {N}}_{\langle \rho ^i, \rho ^{-i} \rangle }}(s') + V^i_{E_{\langle \rho ^i, \rho ^{-i} \rangle } }(s') < V^i_{{\mathcal {N}}_{\langle \pi ^i, \rho ^{-i} \rangle }}(s') + V^i_{E_{\langle \pi ^i, \rho ^{-i}\rangle }}(s'), \end{aligned}$$

for any ethically-dominant policy $\pi ^i$ for agent i.

For an $\epsilon > 0$ large enough and for the weight vector $\vec {w}' = (1, w_e + \epsilon )$, any ethically-dominant policy $\pi ^i$ will have a better value vector at that state $s'$ than $\rho ^i$ against $\rho ^{-i}$:

$$\begin{aligned} \vec {w}' \cdot \vec {V}^i_{\langle \rho ^i, \rho ^{-i} \rangle }(s') < \vec {w}' \cdot \vec {V}^i_{\langle \pi ^i, \rho ^{-i} \rangle }(s'). \end{aligned}$$

Therefore, $\rho ^i$ will not be a $\vec {w}'$-dominant policy. Notice that $\rho$ will remain without being dominant even if we increase again the value of $w_e$ by defining $\vec {w}'' = (1, w_e + \epsilon + \delta )$ with $\delta > 0$ as large as we wish.

Now consider the policy $\rho ^i$ not ethically-dominant that requires the maximum $\epsilon _* > 0$ in order to stop being $\vec {w}$-dominant. We can guarantee that this policy exists because there is a finite number of deterministic policies in a finite MOMG. Therefore, by selecting the weight vector $\vec {w}_* = (1, w_e + \epsilon _*)$, then only ethically-dominant policies can be $\vec {w}_*$-dominant for this ethical weight $w_e + \epsilon _*$. In other words, every $\vec {w}_*$-dominant policy is also ethically-dominant for this new weight vector. $\square$

The former proposition helps us establish a formal relationship between dominant equilibria and ethically-dominant equilibria through the following proposition.

Proposition 2

Given an ethical MOMG ${\mathcal {M}} = \langle {\mathcal {S}}, {\mathcal {A}}^i,$ $(R_0, R_{{\mathcal {N}}} + R_{E})^i, T \rangle$ for which there exists a best-ethically-dominant equilibria, there exists a weight vector $\vec {w} = (1, w_e)$ with $w_e > 0$ for which every dominant policy for an agent i in the Markov Game ${\mathcal {M}}_* = \langle {\mathcal {S}}, {\mathcal {A}}^i, R^i_0 + w_e ( R^i_{{\mathcal {N}}} + R^i_{E}), T \rangle$ is also a best-ethically-dominant policy for agent i in ${\mathcal {M}}$.

Proof

By Proposition 1, there is an ethical weight for which every dominant policy in ${\mathcal {M}}_*$ is ethically-dominant in ${\mathcal {M}}$.

Best-ethically-dominant policies dominate all ethically-dominant policies, and thus every dominant policy in ${\mathcal {M}}_*$ is in fact a best-ethically-dominant policy in ${\mathcal {M}}$.

Combining these two facts, we conclude that at least one best-ethically-dominant policy is dominant for this ethical weight.

$\square$

Thanks to Proposition 2 we are ready to formulate and prove Theorem 1 as follows.

Theorem 1

(Multi-agent solution existence (dominance)) Given an ethical MOMG ${\mathcal {M}} = \langle {\mathcal {S}}, {\mathcal {A}}^i, (R_0, R_{{\mathcal {N}}} + R_{E})^i, T \rangle$ for which there exists at least one best-ethically-dominant equilibrium $\pi _*$ , then there exists a weight vector $\vec {w} = (1, w_e)$ with $w_e > 0$ for which $\pi _*$ is a dominant equilibrium in the scalarised MOMG ${\mathcal {M}}_*$ by $\vec {w}$.

Proof

By Proposition 2, there exists a weight vector $\vec {w} = (1, w_e)$ for which all best-ethically-dominant policies of agent i are dominant policies in the scalarised MOMG ${\mathcal {M}}_*$.

Thus, for every ethically-dominant equilibrium $\pi _*$ in ${\mathcal {M}}$, there is an ethical weight $w_e$ for which every policy $\pi ^i_*$ of $\pi _*$ is also a dominant policy in ${\mathcal {M}}_*$ and, hence, by definition, $\pi _*$ is also a dominant equilibrium in ${\mathcal {M}}_*$. $\square$

Theorem 1 guarantees that we can solve Problem 1 for any Ethical MOMG with at least one best-ethically-dominant equilibrium. Indeed, for that reason we refer to such family of Ethical MOMGs as solvable. In particular, we aim at finding solutions $\vec {w}$ that guarantee the learning of an ethical policy with the minimal ethical weight $w_e$. The reason for it is to avoid that an excessive ethical weight makes the agents completely disregard their individual objective, jeopardising their learning.

To finish this Section, Table 1 summarises the connection that Theorem 1 establishes between the solution concepts (equilibria) and ethical policies of an Ethical MOMG ${\mathcal {M}}$ and the equilibria and policies of the scalarised MOMG ${\mathcal {M}}^*$. Given a solvable Ethical MOMG, there exists a weight vector for which the policy concepts in the left will become equivalent to their counterparts at the right, for at least one dominant equilibrium.

Table 1 Different kinds of policies that exist within either a Single-Objective Markov game (SOMG, obtained by employing a scalarisation function $f_e = (1, w_e)$) or an Ethical Multi-Objective Markov Game (MOMG)

5 Solving the multi-agent ethical embedding problem

Solving the Multi-Agent Ethical Embedding (MAEE) problem amounts to computing a solution weight vector $\vec {w}$ so that we can combine individual and ethical rewards into a single reward to yield a new, ethical environment, as defined by Problem 1. Next, Sect. 5.1 details our approach to solving the MAEE problem, the so-called MAEE Process, which is graphically outlined in Fig. 1. Thereafter, in Sect. 5.2, we formally analyse the soundness of our MAEE Process.

5.1 The multi-agent ethical embedding process

Figure 1 illustrates our approach to solving a MAEE problem, which follows two main steps: (1) computation of a best-ethical equilibrium (the target joint policy), namely the joint policy that we expect the agents to converge to when learning in our target ethical environment; and (2) computation of a solution weight vector $\vec {w}$ based on the target joint policy. Interestingly, we base both computations on decomposing the ethical MOMG (the input to the problem) into n ethical MOMDPs¹⁰ (one per agent), solving one local problem (MOMDP) per agent, and aggregating the resulting solutions.

In what follows we provide the theoretical grounds for computing a target joint policy and a solution weight vector. For the remainder of this Section we assume that there exists a strictly best-ethically-dominant equilibrium in the Ethical MOMG, that is, that the Ethical MOMG is strictly-solvable.

5.1.1 Computing the ethical equilibrium

As previously mentioned, we start by computing the best-ethical equilibrium $\pi _*$ to which we want agents to converge to (the one they will learn in our ethical target environment). Figure 1 (bottom-left) illustrates the three steps required to compute such joint policy. In short, to obtain the joint policy $\pi _*$, we can resort to decomposing the ethical MOMG ${\mathcal {M}}$, encoding the input multi-objective environment, into n ethical MOMDPs ${\mathcal {M}}^{i=1,\dots ,n}$, one per agent. For each ethical MOMDP ${\mathcal {M}}^i$, we compute the individual policy of agent i in the ethical equilibrium $\pi ^i_*$ by applying a single-agent multi-objective reinforcement learning method.

More in detail, we must first notice that building the ethical equilibrium $\pi _*$ via decomposition is possible whenever the ethical MOMG ${\mathcal {M}}$ is strictly-solvable, hence satisfying the conditions of Theorem 1. This means that the best-ethical equilibrium $\pi _*$ is also strictly dominant. Thus, each agent has one (and only one) strictly best-ethically-dominant policy ($\pi ^i_*$), which by Def. 9 is the unique best-ethical policy against any other joint policy.

Second, we know that each policy $\pi ^i_*$ of the ethical equilibrium is the only best-ethical policy against any other joint policy $\rho ^{-i}$. From this observation, we can select a random joint policy $\rho$, and for each agent i fix $\rho ^{-i}$ (i.e. the policies of all agents except i) to create an Ethical MOMDP ${\mathcal {M}}^i$. This gives us the decomposition of the ethical MOMG ${\mathcal {M}}$.

After creating all Ethical MOMDPs ${\mathcal {M}}^{i=1,\dots ,n}$, we compute the policy $\pi ^i_*$ of each agent i as its best-ethical policy in the ethical MOMDP ${\mathcal {M}}^i$. We can do this by using multi-objective single-agent RL. In particular, we apply the Value Iteration (VI) algorithm with a lexicographic ordering [74] (prioritising ethical rewards), since it has the same computational cost as VI.

Finally, we join all best-ethical policies $\pi ^i_*$ to yield the joint policy $\pi _*$.

5.1.2 Computing the solution weight vector

Once computed the target ethical equilibrium $\pi _*$, we can proceed to compute the corresponding ethical weight $w_e$ that guarantees that $\pi _*$ is the only Nash equilibrium in the ethical environment (the scalarised MOMG) produced by our embedding. Figure 1 (bottom-right) illustrates the steps required to compute it.

Similarly to Sect. 5.1.1, we compute $w_e$ by decomposing the input environment (the ethical MOMG ${\mathcal {M}}$) into several MOMDPs, one per agent: ${\mathcal {M}}^{i=1,\dots ,n}_*$. Thereafter, we compute a single-agent ethical embedding process for each ethical MOMDP. Finally, we aggregate the individual ethical weights to obtain the ethical weight $w_e$.

More in detail, we first exploit the target ethical equilibrium $\pi _*$ to decompose the input environment. Thus, we create an Ethical MOMDP ${\mathcal {M}}^i_*$ per agent i by fixing the best-ethical equilibrium $\pi ^{-i}_*$ for all agents but i. Then, computing the ethical weight for each ethical MOMDP amounts to solving a Single-Agent Ethical Embedding (SAEE) problem as introduced in [55]. For that, we benefit from the algorithm already introduced in that work (see 2.3). Afterwards, we obtain an individual ethical weight $w^i_e$ for each MOMDP that ensures that each agent i would learn to behave ethically (following $\pi ^i_*$) in the ethical MOMDP ${\mathcal {M}}^i_*$.

Finally, we select the value of the ethical weight for which all agents are incentivised to behave ethically. This value is necessarily the greatest ethical weight $w_e = \max _i w^i_e$ among all agents, and thus such $w_e$ compounds the weight vector $(1, w_e$) that solves our Multi-Agent Ethical Embedding problem.

The above-described procedure to produce an ethical environment (based on decomposing, individually solving single-agent embedding problems, and aggregating their results) does guarantee that behaving ethically will be a dominant strategy for agents.

Notice that the cost of computing the solution weight vector mainly resides in applying n times the SAEE algorithm in [55], once per agent. Following [55], the cost of such algorithm is largely dominated by the computational cost of the Convex Hull Value Iteration algorithm [10].

5.2 Analysing the multi-agent ethical embedding process

Our approach in Sect. 5.1 above requires that the Ethical MOMG fulfils the following condition: although the ethical objective is social, it is enough that a fraction of the agents (not all of them) intervene to completely fulfil it. To give an example inspired on the Ethics literature, consider a situation where several agents are moving towards their respective destination through a shallow pond and at some point a child that cannot swim falls into the water (similarly to the Drowning Child Scenario from [65]). To save the child, it is enough that one agent takes a dive to rescue them.

In terms of the ethical weights, this assumption implies that we will require the greatest ethical weight $w_e$ to incentivise an agent i to behave ethically (formally, to follow an ethically-dominant policy) when the rest of agents are already behaving ethically by following an ethical equilibrium $\langle pi^i_*, \pi ^{-i}_* \rangle$.

Such ethical weight $w_e$ is the maximum weight needed for agent i against any possible joint policy $\pi ^{-i}$. In other words, for the weight $w_e$ it will be a dominant policy for agent i to follow an ethically-dominant policy.

In summary, the ethical weight required to guarantee that $\pi ^i_*$ is dominant is the same as the ethical weight required to guarantee that $\pi ^i_*$ is a best-response against $\pi ^{-i}_*$. This is formally captured by the next condition:

Condition 1

Let ${\mathcal {M}}$ be an ethical MOMG ${\mathcal {M}} = \langle {\mathcal {S}}, {\mathcal {A}}^i, (R_0, R_{{\mathcal {N}}} + R_{E})^i, T \rangle$ for which there exists at least one best-ethically-dominant equilibrium $\pi _*$. Consider the weight vector $\vec {w} = (1, w_e)$ and the scalarised MOMG ${\mathcal {M}}_* = \langle {\mathcal {S}}, {\mathcal {A}}^i, R_0 + w_e \cdot ( R_{{\mathcal {N}}} + R_{E})^i), T \rangle$. We require that the best-ethically-dominant equilibrium $\pi _*$ is a Nash equilibrium in ${\mathcal {M}}_*$ if and only if $\pi _*$ is also a dominant equilibrium in ${\mathcal {M}}_*$.

We would like to remark that Condition 1 is only required so that our Multi-Agent Ethical Embedding Process finds the solution weight vector to create an ethical environment. However, Theorem 1 guarantees that such weight exists irregardless of whether Condition 1 holds or not. Thus, it is always guaranteed that for any ethical weight large enough a best-ethically-dominant equilibrium is dominant.

Now we can proceed with proving the soundness of our method for computing a solution weight vector. First, we recall that our objective is to find the solution weight vector $(1, w_e)$ with the minimal ethical weight $w_e$ necessary for $\pi _*$ to be a dominant equilibrium. In other words, our solution ethical weight is the minimum necessary for each $\pi ^i_*$ to be a dominant policy. Condition 1 tells us that such ethical weight has to be the minimum one that guarantees that each $\pi ^i_*$ is a best-response policy. Formally:

Observation 1

Given any joint policy $\pi$, the minimum ethical weight $w_e$ for which every policy $\pi ^i$ is a best-response against $\pi ^{-i}$ is also the minimum ethical weight $w_e$ for which $\pi$ is a Nash equilibrium.

Second, the following Theorem tells us the minimal $w_e$ necessary for $\pi _*$ is also a dominant equilibrium. Such $w_e$ is any ethical weight that guarantees that $\pi$ is a Nash equilibrium:

Theorem 2

Given an ethical MOMG ${\mathcal {M}} = \langle {\mathcal {S}}, {\mathcal {A}}^i, (R_0, R_{{\mathcal {N}}} + R_{E})^i, T \rangle$ for which there exists at least one best-ethically-dominant equilibrium $\pi _*$ and for which Condition 1holds, if for a weight vector $\vec {w} = (1, w_e)$ with $w_e > 0$ we have that $\pi _*$ is a Nash equilibrium, then it is also a dominant equilibrium for the same weight vector $\vec {w}$.

Proof

Direct from Condition 1. Given a best-ethically-dominant equilibrium $\pi _*$, if for a weight vector $\vec {w} = (1, w_e)$ we have that $\pi _*$ is a Nash equilibrium, then by Condition 1, the joint policy $\pi _*$ is also dominant for $\vec {w}$. $\square$

Thus, when Condition 1 holds, our approach to compute the ethical weight is guaranteed to help build an ethical environment by Theorem 2. In other words, the weight vector $(1, w_e)$ will solve the MAEE problem.

5.3 Linear properties of the multi-agent ethical embedding process

With the Multi-Agent Ethical Embedding Process already explained, we now explain an important property of it. This process receives as input an MOMG where the ethical reward functions are already defined. We know by Theorem 2 that our MAEE process guarantees that, in the designed environment, ethical equilibria are incentivised. In this section, we study the implications of this Theorem: that regardless of the differences in the scales of the reward functions (either between agents or between objectives), in the designed environment ethical policies are incentivised. Formally, we prove that modifying the scale of each component of the ethical reward function of each agent does not modify the best-ethically-dominant equilibrium that the agents will be incentivised to learn. Our MAEE process conveniently adjusts the ethical weight to guarantee that ethical equilibria are incentivised.

In order to prove that our Multi-Agent Ethical Embedding Process is unaffected by the scales of the different reward components, we first prove an intermediate result. We prove that if a joint policy is an ethical equilibrium, it is also an ethical equilibrium even if we modify the scales of the ethical reward components. Formally:

Proposition 3

Consider an Ethical MOMG ${\mathcal {M}}$ with an ethical reward function $R^i_{{\mathcal {N}}} + R^i_E$ for each agent i , and another Ethical MOMG ${\mathcal {M}}'$ with an ethical reward function $(\alpha ^i R^i_{{\mathcal {N}}} +\gamma ^i) + (\beta ^i R^i_E + \delta ^i$) per agent i with $\alpha ^i, \beta ^i > 0$ and $\gamma ^i, \delta ^i \in {\mathbb {R}}$ . Then:

• A policy is ethical in ${\mathcal {M}}$ if and only if it is ethical in ${\mathcal {M}}'$.

• A policy is ethically-dominant in ${\mathcal {M}}$ if and only if it is ethically-dominant in ${\mathcal {M}}'$.

• A policy is best-ethical in ${\mathcal {M}}$ if and only if it is best-ethical in ${\mathcal {M}}'$.

• A policy is best-ethically-dominant in ${\mathcal {M}}$ if and only if it is best-ethically-dominant in ${\mathcal {M}}'$.

Proof

Given any ethical policy $\pi _*$ of ${\mathcal {M}}$ and any ethical policy $\pi '_*$ of ${\mathcal {M}}'$:

$$\begin{aligned} V^i_{{\mathcal {N}}_{\langle \pi '^{i}_*, \pi ^{-i} \rangle }}&= \max _{\rho ^i} [\alpha ^i V^i_{{\mathcal {N}}_{\langle {\rho ^{i}}, \pi ^{-i} \rangle }} + K_{\gamma ^i}]\\&= \alpha ^i \max _{\rho ^i} V^i_{{\mathcal {N}}_{\langle {\rho ^{i}}, \pi ^{-i} \rangle }} + K_{\gamma ^i} = \alpha ^i V^i_{{\mathcal {N}}_{\langle \pi ^{i}_*, \pi ^{-i} \rangle }} + K_{\gamma ^i}, \\ V^i_{E_{\langle \pi '^{i}_*, \pi ^{-i} \rangle }}&= \max _{\rho ^i} [\alpha ^i V^i_{E_{\langle {\rho ^{i}}, \pi ^{-i} \rangle }} + K_{\delta ^i}] \\&= \beta ^i \max _{\rho ^i} V^i_{E_{\langle {\rho ^{i}}, \pi ^{-i} \rangle }} + K_{\delta ^i} = \beta ^i V^i_{E_{\langle \pi ^{i}_*, \pi ^{-i} \rangle }} + K_{\delta ^i} , \end{aligned}$$

with $K_{\gamma ^i}$ and $K_{\delta ^i}$ being constants depending on $\gamma ^i$ and $\delta ^i,$ respectively. Thus, any ethical policy of ${\mathcal {M}}$ is ethical in ${\mathcal {M}}'$, because it also maximises the accumulation of evaluative and normative rewards in ${\mathcal {M}}'$. Hence, ethical policies of ${\mathcal {M}}'$ are also ethical in ${\mathcal {M}}$. The proof for ethically-dominant policies is analogous.

Consequently, the same applies for best-ethical policies and best-ethically-dominant policies, since the individual reward function is the same in ${\mathcal {M}}$ and ${\mathcal {M}}'$. $\square$

Now we are ready to state the main result: modifying the scale of each component of the ethical reward function of each agent does not modify the best-ethically-dominant equilibrium that the agents will be incentivised to learn. Formally:

Theorem 3

Consider an Ethical MOMG ${\mathcal {M}}$ with an ethical reward function per agent $R^i_{{\mathcal {N}}} + R^i_E$ , and another Ethical MOMG ${\mathcal {M}}'$ with an ethical reward function per agent $(\alpha ^i R^i_{{\mathcal {N}}} + \gamma ^i) + (\beta ^i R^i_E + \delta ^i)$ with $\alpha ^i, \beta ^i > 0$. Assume that Condition 1holds in both Ethical MOMGs. We define the resulting single-objective Markov Game of applying the MAEEP to ${\mathcal {M}}$ as ${\mathcal {M}}_*$. Similarly, we define the resulting single-objective Markov Game of applying the MAEEP to ${\mathcal {M}}'$ as ${\mathcal {M}}'_*$. Then:

• A best-ethically-dominant equilibrium $\pi _*$ in ${\mathcal {M}}$ is dominant in ${\mathcal {M}}_*$ if and only if $\pi _*$ is best-ethically-dominant in ${\mathcal {M}}'$ and dominant in ${\mathcal {M}}'_*$.

Proof

Notice first that these two Markov Games (${\mathcal {M}}_*$ and ${\mathcal {M}}'_*$) may have different reward functions, so a priori we do not know if they share the same Nash equilibria.

In more detail, by Theorem 2 we know that applying the MAEEP guarantees that any best-ethically-dominant equilibrium $\pi _*$ in ${\mathcal {M}}$ is dominant in ${\mathcal {M}}_*$. By the previous proposition, both Ethical MOMGs ${\mathcal {M}}$ and ${\mathcal {M}}'$ share the same best-ethically-dominant equilibria. Therefore, the joint policy $\pi _*$ is also best-ethically-dominant in ${\mathcal {M}}'$.

Again by Theorem 2, the joint policy $\pi _*$ is also dominant in ${\mathcal {M}}'_*$. Thus, the Ethical Markov Games ${\mathcal {M}}_*$ and ${\mathcal {M}}'_*$ also share all the dominant policies that are best-ethically-dominant (their value vectors will probably be different between the two Markov Games though). $\square$

6 Experimental analysis: the ethical gathering game

The Gathering Game [40] is a renewable resource allocation setting where, if agents pursue their individual objectives and gather too many apples, these resources become depleted. Here, we follow [67] in considering that agents have uneven gathering capabilities and propose the Ethical Gathering Game as an alternative scenario to focus on agent survival rather than on resource depletion as they do in [67]. This way, we transform the Gathering Game into an environment where we expect agents to behave in alignment the moral value of beneficence¹¹ by including a donation box to the environment. Thus, our ethical embedding process takes the modified Ethical Gathering Game as an input. We expect that agents trained in the resulting environment of our ethical embedding process learn to behave in alignment with this value. This means that they are expected to learn to use the donation box in an ethical manner, that is, by donating and taking apples when appropriate. We do so with the aim of ensuring the survival of the whole population (i.e. having enough apples despite their gathering deficiencies). Finally, we would like to remark that our Ethical Gathering game constitutes an example of a multi-agent moral gridworld [26].¹²

Although our paper is eminently theoretical, this section is devoted to illustrate the application of our Multi-Agent Ethical Embedding (MAEE) process to this Ethical Gathering Game. Additionally, we analyse the resulting best-ethical policies (and best-ethical equilibria) that agents learn. In particular, we observe that the agents’ learnt policies employ the donation box to behave in alignment with the moral value of beneficence and, as a result, achieve survival (i.e. they learn a best-ethical equilibrium).

Fig. 2

a Example of a possible initial state of the Ethical Commons Game, as shown in our graphical interface. The environment is a gridworld wherein agents learn by means of tabular reinforcement learning. In this initial state, $p_1 = (1, 1)$ and $p_2 = (3, 3)$. Since it is an initial state, the three apple cells are green, showing they currently contain an apple. b) Example of another state several steps ahead. In this state, $p_1 = (1, 2)$ and $p_2 = (3, 1)$. Agent 1 has $ap_1 = 10$ apples, which are enough to survive (represented with a green rectangle in the left of the grey area), whereas agent 2 only has $ap_2 = 4$ apples, which are not enough to survive (visualised as a green square in the right hand side of the grey area)

Figure 2 depicts two possible states of our environment, where two agents (represented as red cells) gather apples in a 4 $\times$ 3 grid (black area). Apples grow and regenerate in the three fixed cells depicted in green in Fig. 2 a). Each agent gathers apples by moving into these green cells. Both agents need k apples to survive, but they have different gathering capabilities, so that when two agents step into the same green cell, the most efficient one will actually get it. Moreover, the donation box can store up to c apples. Numbers on top show the data of the current state: the number of apples for each agent and the donation box. The green rectangle on the left of the grey area signals Agent 1 has enough apples to survive, whereas the green square on the right indicates Agent 2 has less than k apples.

In what follows, Sect. 6.1 characterises the agents in the Ethical Gathering Game. Then, Sect. 6.2 provides the full description of the Multi-Objective Markov Game of the Ethical Gathering Game, which defines the input environment to which we apply our ethical embedding. Subsequently, Sect. 6.3 shows how we applied our MAEE process to the Ethical Gathering Game. Finally, Sect. 6.4 provides an in-detail evaluation of the ethical equilibria obtained after applying our MAEE process to the Ethical Gathering game.

6.1 The agents of the ethical gathering game

As previously mentioned, both agents need the same amount of k apples to survive. However, they have different gathering capabilities, which causes some agents to have more difficulties to survive. The different gathering capabilities of agents are formalised as the efficiency $e\!f_i$ of each agent i. We represent efficiency with a positive number, and each agent has a different efficiency (i.e. $e\!f_i \ne e\!f_j)$. Despite differences in efficiencies, both agents have the possibility of surviving if the donation box is properly used. Notice that the donation box stores apples from donations that are made available to all agents. A proper usage of the box would mean that once an agent has an apple surplus, it should transfer exceeding apples to the donation box, and in turn an agent in need should take apples from the box to guarantee its survival. Neither the concept of the donation box nor efficiency are present in the original Gathering Game.

6.2 The input MOMG of the ethical gathering game

The Ethical Gathering Game, as an ethical MOMG, is defined as a tuple ${{\mathcal {M}}} = \langle {\mathcal {S}}, {\mathcal {A}}^{i=1,\ldots ,n}, (R_0, R_{{\mathcal {N}}}+ R_{E})^{i=1,\dots ,n}, T \rangle$, where ${\mathcal {S}}$ is the set of states, ${\mathcal {A}}^i$ is the action sets of agent i (actions are further explained in Sect. 6.2.2), T is the transition function of the game (see Sect. 6.2.3), and $R^i = (R_0, R_{{\mathcal {N}}}+ R_{E})^{i}$ is the reward function of agent i (see Sect. 6.2.4).

Section 6.2.1 details the states S in our input MOMG representing the Ethical Gathering Game. They include the number of apples that both agents and the donation box have. However, this may lead to an arbitrarily large number of states. Therefore, we apply some abstractions in order to drastically reduce the number of states of the input MOMG. Section 6.2.5 presents our approximate version of our Ethical Gathering Game (which we use for both the input of the MAEE process and the ethical environment where the agents learn).

6.2.1 States

We define the states of the environment as tuples $s = \langle p_1, p_2, ap_1, ap_2, cp, g \rangle$ where:

• $p_i=(x_i, y_i)$ is the position of agent $i\in \{1,2\}$ in the environment (see red squares in Fig. 2), with $x_i \in \{1, 2, 3 \}, y_i \in \{1, 2, 3, 4 \}$. Agents can share positions like in the original code of the Gathering Game from Leibo et al. [40] (i.e. $p_1$ can be equal to $p_2$).

• $ap_i$ is the number of apples owned by agent i.

• cp represents the current number of apples in the donation box, being c its maximum capacity (i.e. $0 \le cp\le c$).

• Finally, there are three apple gathering cells at positions $p_{g_1} = (1, 2)$, $p_{g_2} = (1, 3)$ and $p_{g_3} = (2, 2)$ (see the three green cells in Fig. 2 a). The state of the apple gathering cells is represented by $g = (g_1, g_2, g_3)$, where each $g_j \in [True, False]$ represents if the apple cell at position $p_{g_j}$ currently contains an apple or not.

Henceforth we will use the “.” notation to refer to the elements in a state s. Thus, for instance, $s.p_1$ denotes the position of agent 1 in state s. Moreover, we define initial states as those where both agents and the donation box have 0 apples each, and there are apples in the three apple cells.

Observe that in the gathering game from [40] there was no donation box nor a count of the number of apples that each agent gathers. Thus, each state was only defined by the agents’ positions together with the number of available apples on the ground.

6.2.2 Actions

Each agent has seven possible actions. Five are related to their movement (move_up, move_down, move_left, move_right and stay) to move on each of the four possible directions or stand still, respectively. Besides that, they have two additional actions related to the donation box: donate and take_donation.

6.2.3 Transitions

The Ethical Gathering Game is almost a deterministic Markov game. Stochasticity exclusively appears from two factors in states. The first one is independent of the agents’ actions and occurs in the transitions involving gathering cells. If for some state s there is an empty apple cell (that is, $s.g_j = False$ for some $j \in \{1, 2, 3\}$), there is a probability $p = 0.05$ that in the following state $s'.g_j = True$, independently of the agents’ actions if there is no agent on top at that state. Formally, $P( s'.g_j = True \mid s.g_j = False, p_i \ne p_{g_j} \text { for all i}) = 0.05$. The original Gathering Game [40] also shares this stochasticity with the apple cells except for an important difference: apples only continue spawning in apple gathering cells as long as there is at least one apple cell remaining (i.e. $s.g_j = True$ for some j). Otherwise, in the original Gathering game, when $s.g_j = False$ for every j, the game ends. This difference is the main reason why there is a depletion problem in the original game, as previously mentioned.

The second factor for stochasticity depends on the actions of both agents and occurs only when the two of them apply the action take_donation when the donation box has exactly one apple $c = 1$. In such case, only one of the two agents receives the apple (and the corresponding reward for receiving it). The agent getting it is decided randomly, with each agent having the same probability. Formally, $P(s'.ap_1 = s.ap_1 + 1, s'.ap_2 = s.ap_2, s'.cp=0 \mid s.cp = 1, a=\langle \texttt {take\_donation}, \texttt {take\_donation} \rangle ) = P(s'.ap_1 = s.ap_1, s'.ap_2 = s.ap_2 + 1, s'.cp=0 \mid s.cp = 1, a=\langle \texttt {take\_donation}, \texttt {take\_donation} \rangle ) = 0.5$. This second factor of stochasticity is novel to our ethical Gathering Game since in the original Gathering Game [40] there was no donation box.

All other transitions are deterministic, that is, $P(s' \mid s, \langle a_1, a_2 \rangle )$ are direct consequences of the agents’ actions $\langle a_1, a_2 \rangle$ in a given state s. In this manner, each agent’s position $p_i$ is altered by any action $a_i$ related to movement. Moreover, if the agent moves to an apple cell that currently has an apple ($g_j = True$, where $p_{g_j}=p_{i\in \{1,2\}})$, then the apple cell loses temporarily its apple ($g_j \leftarrow False$) and the agent receives it ($ap_i \leftarrow ap_i + 1$). Notice that there is no action for explicitly gathering apples from the ground. We inherit this simplification from the Gathering Game in [40].

In the same vein, if agent i has apples ($ap_i > 0$) and performs the action donate, then the agent loses one apple ($ap_i \leftarrow ap_i - 1$) and the donation box receives it ($cp \leftarrow cp + 1$) until the donation box reaches its maximum capacity. However, if the donation box is full, then the agent is not allowed to donate its apple and its number of apples remains unchanged. Analogously, if the agent performs the action take_donation and the donation box has apples ($cp > 0$), then the agent receives the apple ($ap_i \leftarrow ap_i + 1$) and the donation box loses it ($c \leftarrow cp - 1$).

There is only one exception to the previous game mechanics, which occurs when the two agents move simultaneously to the same apple cell (i.e. $s'.p_1=s'.p_2=p_{g_j}$) with an apple (i.e. $g_j = T$). In such case, only one of the two agents receives the apple (and the corresponding reward for receiving it): the one with the greatest efficiency $e\!f_i$.

6.2.4 Rewards

Rewards in our ethical gathering game are always determined by the current state s and the current agents’ actions $\langle a_1, a_2 \rangle$. They encode both the individual and ethical objectives, which correspond to self-survival and beneficence, respectively.

We assume that the reward specification of ethical rewards has been already provided to us. Thus, we assume that maximising the following normative and evaluative reward functions fulfils the moral value of beneficence. Indeed, defining the appropriate ethical reward structure is a difficult problem, but in this work we have focusing on the second step of value alignment, the ethical embedding of ethical rewards. Thus, the following ethical reward function should be seen as an illustrative example.

• Individual reward: agent i receives a negative reward of −1 in the current state if it does not have enough apples to survive (i.e. $s.ap_i < k$).

  Conversely, agent i receives a positive reward of +1 for gathering apples (moving to a position with an apple). The reward is only given if the agent actually obtains an apple (i.e. $s.ap_i < s'.ap_i$).

  Furthermore, agent i receives an extra negative reward of −1 for donating an apple. The reward is only given if the agent actually gives away an apple (i.e. $s.ap_i > s'.ap_i$).

• Normative reward: agent i receives a negative reward of −1 for performing the ethically unacceptable action take_donation when it already has enough apples to survive (i.e. $s.ap_i \ge k$). Since the action itself is morally blameworthy in such context, the negative reward is received even if the agent does not obtain an extra apple.

• Evaluative reward: agent i receives a positive reward of +0.7 for performing the praiseworthy action donate when it has more than enough apples to survive (i.e. $s.ap_i > k$) and the donation box is not full (i.e. $s.cp < c$, where we recall that c is a constant representing the maximum apple capacity of the donation box).

Notice that, thanks to Theorem 3, we do not need to worry about the specific scale of the evaluative and normative rewards. If the evaluative reward for donating an apple were any other positive value (2.34, for example) instead of 0.7, our MAEEP would produce an ethical environment that incentivises exactly the same ethical equilibria.

6.2.5 The abstract model

In order to reduce the number of states agents have to deal with while learning, each agent uses an abstraction (a common technique in Reinforcement Learning, see for instance [8, 32, 42]) to represent each state of the environment in a simplified manner $z^i = \langle p_1, p_2, abs_{ap}(ap_i), abs_{cp}(cp), g \rangle$, where:

• the abstract number of apples of each agent $abs_{ap}(ap_i)$ can take 4 possible values: 0 if the agent has no apples, 1 if the agent has not enough apples to survive, 2 if it has exactly enough apples to survive, and 3 if it has surplus of apples. Formally:

  $$\begin{aligned} abs_{ap}(ap_i)= {\left\{ \begin{array}{ll} \text {0,} &{}\quad \text {if } ap_i=0\\ \text {1,} &{}\quad \text {if } ap_i< k \\ \text {2,} &{}\quad \text {if } ap_i= k \\ \text {3,} &{}\quad \text {if } ap_i> k \\ \end{array}\right. } \end{aligned}$$

• the abstract number of apples in the donation box $abs_{cp}(cp)$ can take 4 possible values: 0 if the donation box is empty, 1 if it has 1 apple, 2 if it has more than 1 apple but is not full, and, finally, 3 if the box is full.

  $$\begin{aligned} abs_{cp}(cp)= {\left\{ \begin{array}{ll} \text {0,} &{}\quad \text {if } cp=0\\ \text {1,} &{}\quad \text {if } cp=1 \\ \text {2,} &{}\quad \text {if } 1<cp<c \\ \text {3,} &{}\quad \text {if } cp=c \\ \end{array}\right. } \end{aligned}$$

With this abstraction, there is a total of $| S | = 12^2 \cdot 4 \cdot 4 \cdot 2^3 = 18,432$ possible states, where 12 is the number of possible positions for each agent, 4 is the number of possible values for the donation box, 4 is the number of possible values for the agent’s inner count of apples and there are also 3 cells where apples can appear. Moreover, the total number of state-action pairs is $|S| \cdot |A| = 18,432 \cdot 7 = 129,024$. Notice that, if for example, we assume that our simulation will last for enough time to spawn m apples, and the donation box can store up to c apples, the number of states with no abstraction would grow to¹³:

$$\begin{aligned} | S |&= 12^2 \cdot \sum _{j=0}^c \sum _{l=0}^{m-j} \left( {\begin{array}{c}l+1\\ 1\end{array}}\right) \cdot 2^3 \\&= 96 \cdot (c+1)\cdot [6 \cdot (m^2+3m+2) + c \cdot (2c - 6m - 8)]\\&= O(c\cdot m^2) \end{aligned}$$

So if we set $m=40$ and $c=5$ (which are the kind of scenarios that we consider in the experiments below), then |S| grows to more than 5 million states, whereas with our abstraction it always states at 18,432. Thus, although abstraction necessarily involves information loss, it becomes very handy on limiting the total number of states of the learning environment.

6.3 Applying the multi-agent ethical embedding process

For all our experiments, we set the input ethical MOMG with the following setting:

• Efficiency: we set Agent 2 with a higher efficiency than Agent 1 (i.e. $e\!f_2 > e\!f_1$).

• Discount factor: for all agents we select as the discount factor of their respective value functions $\vec {V}^i$ a value of $\gamma = 0.8$. The value of the discount factor is large enough so that the agents can be farsighted. We select this value for $\gamma$ because the process of obtaining enough apples to survive is long, potentially taking hundreds of time-steps for agents.

• Survival threshold: We fixed the amount of necessary apples to survive for each agent as $k=10$.

Furthermore, we consider different capacities for the donation box. In particular, we apply our MAEE process to three input environments. These three MOMGs ${\mathcal {M}}^c$ (all three with the structure defined in Sect. 6.2) have, respectively, a donation box capacity $c \in \{1, 5, 15 \}$. We refer to these environments as low, medium and high beneficence, respectively, since the larger the capacity of the donation box, the more room for donations the environment provides.

We recall that the MAEE process consists in two steps: the ethical equilibrium computation and the solution weight vector computation, as illustrated in Fig. 1.

We applied the Multi-Agent Ethical Embedding Process for each environment with different capacities of the donation box. For simplicity, here we explain the process for the environment with medium beneficence (i.e. ${\mathcal {M}}^5$). Moreover, when referring to the MOMDP of each agent i decomposed from ${\mathcal {M}}^5$, we use the notation ${\mathcal {M}}^{\langle 5, i \rangle }$.

6.3.1 Solvability of the ethical gathering game

Prior to applying our Multi-Agent Ethical Embedding Process, it is worth mentioning why our theoretical results guarantee its success. For the sake of understanding, we avoid to go through a normal proof, and instead we informally discuss the existence of a best-ethically-dominant policy for each agent. If each agent has such best-ethically-dominant policy, Theorem 1 holds true, and thus, the Ethical Gathering Game is a solvable Ethical MOMG.

The reason why each agent has a best-ethically-dominant policy is the same for the two: no matter what the other agent is doing, the best-ethical policy is to always:

• 1. Gather as many apples as possible either from the ground or from the donation box if the agent does not have enough for survival. This is mandatory to maximise the accumulation of individual rewards of the agents $R_0$.

• 2. Gather as many apples as possible only from the ground if the agent has enough for survival and the donation box is full. Not taking them from the donation box ensures that the accumulation of negative normative rewards $R_N$ is null. This strategy maximises the accumulation of individual rewards by the agent.

• 3. Donate immediately any apple surplus while the donation box is not full. This strategy maximises the accumulation of positive ethical rewards $R_E$.

Thus, since both agents have a best-ethically-dominant policy, a best-ethically dominant equilibrium exists. Therefore, by definition the Gathering Game is solvable. We refer to such best-ethically-dominant equilibrium as $\pi _*$.

Secondly, we must also prove that Condition 1 holds in the Ethical Gathering Game. That is, we need to prove that if the equilibrium $\pi _*$ is a Nash equilibrium in the scalarised MOMG by some ethical weight $w_e$, then $\pi _*$ is a dominant equilibrium as well. That is, we assume that we already have an ethical weight $w_e$ large enough to guarantee that $\pi _*$ is a Nash equilibrium. To better illustrate that the $\pi _*$ equilibrium is indeed dominant, Table 2 shows the payoff matrix of a particular state of a scalarised Ethical Gathering Game. Notice how, for instance, if Agent 1 decides to choose the action take_donation (second row), then its reward is always $-w_e$ in the whole row, irregardless of the other agent’s action. The same occurs for Agent 2: if, for instance, we fix its action to be Donate (first column), then its reward is always $0.7 w_e - 1$ in the whole column. We can conclude that the rewards that each agent receives are unaffected by the other agent’s actions in this state.

Now we have the intuition to show that Condition 1 is fulfilled in the Gathering Game. Notice that agent 1’s best-response in the above-identified equilibrium $\pi _* = (\pi ^1_*, \pi ^2_*)$ is to donate its apple surplus and to refuse to take apples from the donation box when having enough. This is because in this way agent 1 maximises its (ethical and individual) rewards independently of what agent 2 does. Therefore, the policy $\pi ^1_*$ is indeed dominant for agent 1. Following the same reasoning, we conclude that policy $\pi ^2_*$ is dominant for agent 2 as well. Therefore, $\pi _*$ is indeed a dominant equilibrium in the scalarised MOMG, and hence Condition 1 holds.

Table 2 Payoff matrix for the Gathering Game of the immediate scalarised rewards that both agents obtain in a single state in which both agents have surplus apples, the donation box is neither full nor empty, and there are currently no apples near any agent

Thus, both Theorem 1 and Condition 1 hold, and in conclusion so does Theorem 1. Theorem 1 guarantees that our Multi-Agent Ethical Embedding process succeeds. Therefore, following a best-ethical policy is a dominant strategy for both agents in the ethical environment resulting from the ethical embedding. Finally, we deem important to remark that these conclusions hold true irregardless of the map size of the Ethical Gathering Game or how many apple gathering spots there are.

6.3.2 Ethical equilibrium computation

Following the steps in Fig. 1, first we selected a random joint policy. For simplicity, we chose the joint policy $\pi = (\pi ^1, \pi ^2)$ where both agents always select the action stay. Then, we proceeded with the following sequence of steps:

• 1. Decompose: To create the Ethical MOMDP ${\mathcal {M}}^{\langle 5,1 \rangle }$ for Agent 1 from $\pi$, we fixed policy $\pi ^2$ in the input environment (the ethical MOMG ${\mathcal {M}}^5$). Analogously, we fixed $\pi ^1$ to create the MOMDP ${\mathcal {M}}^{\langle 5, 2 \rangle }$ for Agent 2.

• 2. Solve: To find the best-ethical policy $\pi ^1_*$ of Agent 1 in its ethical MOMDP ${\mathcal {M}}^{\langle 5,1 \rangle }$, we applied value iteration with lexicographic ordering [74] (the applied lexicographic ordering prioritises the ethical rewards $R^i_e$ to the individual ones $R^i_0$). We analogously proceeded for Agent 2 to obtain its best-ethical policy $\pi ^2_*$ from ${\mathcal {M}}^{\langle 5,2 \rangle }$.

• 3. Join: We joined the two best-ethical policy $\pi ^1_*$ and $\pi ^2_*$ to create the ethical equilibrium $\pi _*$.

We analysed the obtained ethical equilibrium to characterise the behaviour of each agent (details are further discussed in Sect. 6.4.2). In the ethical equilibrium, both agents survive because the efficient agent 2 donates all its surplus to the donation box until it is full. The less efficient agent 1 takes the donated apples from the box as soon as possible until it gets enough apples to survive itself. Thus, when agents follow an ethical equilibrium, the donation box properly channels donations. After the box is full, Agent 2 keeps gathering most of the apples until the simulation ends.

6.3.3 Solution weight vector computation

With the target ethical equilibrium $\pi _*$ computed, the following step was to apply it as a target policy to obtain the desired solution weight vector, as shown by Fig. 1. In more detail, we proceeded with the following sequence of steps:

• 1. Decompose: To create the second Ethical MOMDP ${\mathcal {M}}^{\langle 5,1 \rangle }_*$ for Agent 1 from $\pi _*$, we fixed policy $\pi ^2_*$ in the input environment (the ethical MOMG ${\mathcal {M}}^5$). Analogously, we fixed $\pi ^1_*$ to create the MOMDP ${\mathcal {M}}^{\langle 5, 2 \rangle }_*$ for Agent 2.

• 2. Solve: We applied the publicly-available algorithm to compute the Single-Agent Ethical Embedding introduced in [55] to each Ethical MOMDP ( ${\mathcal {M}}^{\langle 5, 1 \rangle }_*$ and ${\mathcal {M}}^{\langle 5, 2 \rangle }_*$). This computation amounts to finding the ethical weight that incentivises each agent to behave ethically. To obtain each ethical weight, we needed to compute the partial convex hull of each MOMDP. We applied Optimistic Linear Support [56] to compute them, since it is an outer-loop algorithm, meaning that it can be used on top of any single-objective RL algorithm (Value Iteration in our case) without modifying it.

  We found that an ethical weight $w^{\langle 5, 1 \rangle }_e = 2.6$ incentivises Agent 1 to follow its best-ethical policy in the ethical MOMDP ${\mathcal {M}}^{\langle 5, 1 \rangle }_*$ and an ethical weight $w^{\langle 5, 2 \rangle }_e = 1.6$ incentivises Agent 2 in the ethical MOMDP ${\mathcal {M}}^{\langle 5, 2 \rangle }_*$. As expected, the found ethical weight is greater for Agent 1 since it is the less efficient agent.

• 3. Join: In order for both agents to behave ethically in the ethical environment we selected an ethical weight of $w^5_e = \max (w^{\langle 5, 1 \rangle }_e, w^{\langle 5, 2 \rangle }_e) = 2.6$.

We performed the Multi-Agent Ethical Embedding Process for the other two input environments (${\mathcal {M}}^1$ and ${\mathcal {M}}^{15}$). We obtained the following ethical weights for each case: $w^1_e = 2.2$ for ${\mathcal {M}}^1$ and $w^{15}_e = 1.9$ for ${\mathcal {M}}^{15}$. Finally, from the three computed ethical weights, we obtained the three corresponding ethical (single-objective) environments: ${\mathcal {M}}^1_*$, ${\mathcal {M}}^5_*$ and ${\mathcal {M}}^{15}_*$.

6.4 Evaluating the multi-agent ethical embedding process

6.4.1 Training

After applying our Multi-Agent Ethical Embedding Process for the three MOMGs (with low beneficence ${\mathcal {M}}^1_*$, medium beneficence ${\mathcal {M}}^5_*$, and large beneficence ${\mathcal {M}}^{15}_*$, respectively) we obtain three ethical environments. For each of them, agents simultaneously learnt the ethical Nash equilibrium by applying independent Q-learners [39]. The necessary amount of apples to survive per agent is always $k=10$. We recall that the only difference among environments consists of the capacity $c \in \{1, 5, 15 \}$ of the donation box. Moreover, for comparison, agents also learnt in an unethical environment, an MG ${\mathcal {M}}_0$ where agents only receive rewards from their individual reward functions $R^i_0$.

During training, agents applied an $\epsilon$-greedy policy and a decaying learning rate $\alpha \in [0.9, 0.05]$ per state. Agents trained during 60,000 episodes with 1500 time-steps per episode. After training, we made them use their learnt policies in 50 simulations per environment. Each simulation lasted 400 time-steps. The reason why we chose 400 time-steps is because in such time-length, the amount of apples that are generated in the Ethical Gathering Game is at least enough for both agents to survive (20 apples). Specifically, this computation comes from the fact that for each apple cell there is a $5\%$ probability of spawning an apple when it does not have one and no agent is currently on top of it. There are three apple cells, which means that at best in 400 time-steps there will grow $3 \cdot 0.05 \cdot 400 = 60$ apples in the environment. However, at worst, if both agents stay each in an apple cell thorough the simulation, only $(3-2) \cdot 0.05 \cdot 400 = 20$ apples will grow. Thus, on average the expected amount of apples that will grow is 40.

6.4.2 Results analysis

Once the agents have learnt their policies in these ethical environments, we observe that learning in the unethical environment (${\mathcal {M}}_0$) leads to a situation where Agent 1 does not survive as it fails to accumulate enough apples (Fig. 3a shows its blue line below the $k=10$ threshold) whilst the efficient Agent 2 accumulates most apples. Thus, it becomes apparent the need to craft ethical environments that compensate such clear social inequalities. Indeed, as expected, when agents learn in the ethical environments, they manage to learn ethical-optimal policies that lead to an ethical equilibrium where all agents in the population survive. Figure 3b–d illustrates this for the low, medium, and high beneficence (${\mathcal {M}}^1_*$, ${\mathcal {M}}^5_*$, ${\mathcal {M}}^{15}_*$) environments, where both agents end up having more than enough apples to survive. This is so because the learnt policies are aligned with the moral value of beneficence, that generally refers to actions aimed at benefiting others and in our specific scenario prescribes a proper usage of the donation box to accumulate and distribute resources when needed. Thus, agents learn to donate and take apples from the donation box so that they reach an ethical equilibrium that ensures the population survival. Briefly, these policies follow the general trend of donating most surplus until the donation box reaches full capacity. That is, first of all, the efficient Agent 2 accumulates enough apples to guarantee its own survival, and only afterwards it starts donating apples. Later, once Agent 1 also accumulates enough apples to survive, it also starts sharing its surplus to the donation box. This means that, as expected by our definition of the evaluative reward function, each agent prioritises surviving to donating apples, and prioritises donating apples to maximising its amount of apples. However, this prioritisation does not prevent them from pursuing their individual objective of gathering apples once survival is guaranteed.

Fig. 3

Number of apples (y-axis) shown as mean ± std, that both agents and the box accumulate along time (x-axis) in environments a ${\mathcal {M}}_0$, b ${\mathcal {M}}^1_*$, c ${\mathcal {M}}^5_*$, and d ${\mathcal {M}}^{15}_*$. Horizontal lines signal the survival threshold ($k=10$) and donation box capacity ($c \in \{1, 5, 15 \}$)

Each row in Table 3 provides the end results of every graph in Fig. 3. Columns 2, 3, and 4 show the average amount of apples with which Agent 1, Agent 2, and the donation box end up, respectively.

In the fifth column of Table 3 we also registered the survival rate in each environment. We measured the survival rate as the percentage of times that both agents survived in the 50 simulations per environment. In the unethical environment, Agent 1 fails to survive $60\%$ of the simulations, whilst in all three ethical environments all agents always survive. This difference in the survival rate is caused by the fact that in the ethical environments agents perform an ethical use of the donation box and, as a consequence, apples are distributed among agents guaranteeing that both survive. This is the main empirical proof that indeed our MAEE process promotes the value of beneficence in the Ethical Gathering Game. Since agents survive in all three ethical environments, another interesting conclusion is that the size of the donation box does not affect the survival of either agent.

Finally, in order to study the degree of inequality of each environment, in the sixth column of Table 3 we registered its unbiased¹⁴ Gini ratio [19]. The lowest possible value for the Gini ratio is 0.0 (indicating that both agents obtained the same amount of apples) and the maximum one is 1.0 (indicating that one agent obtained all the apples and the other one none). As Table 3 shows, inequality decreases as we increase the size of the donation box (mostly because the larger it is, the longer it takes for the agents to fill it). Thus, the donation box reduces inequality within the system, with the most extreme case being in the high beneficence environment. In summary, we observe that even though both agents manage to survive in all three beneficence scenarios, there are still significant differences in inequality in the three ethical scenarios.

Table 3 All measures are taken at the end of the simulations

To conclude this section, we illustrate in Fig. 4 the evolution of apples obtained in a single run in all four environments. This way we can get a better understanding of the policies reached in the equilibria, and stress the fact that agents actually learn to behave differently within such equilibria. As in Fig. 3, only the efficient Agent 2 survives in the unethical environment (see Fig. 4a) because agents only pursue their individual objectives. Conversely, when learning in any of our ethical environments, this efficient Agent 2 learns to donate to the donation box as soon as it has guaranteed its own survival (see triangles pointing up between time steps 121 and 190 in Fig. 4b, between 96 and 209 in Fig. 4c, and between 140 and 292 in Fig. 4d).

Thus, Agent 2 learns to display beneficence and helps Agent 1 to survive, as the latter in turn learns to take apples form the donation box (see triangles pointing down between time steps 122 and 183 in Fig. 4b, between time steps 97 and 181 in Fig. 4c, and between 118 and 197 in Fig. 4d). However, these “giver-taker” roles are not fixed, as Agent 1 also learns to donate whenever the donation box is not at its full capacity, and its survival is guaranteed (see Agent 1 donations at time steps 220 and 267 in Fig. 4d).

Fig. 4

Evolution of the number of apples held by each agent and the number of apples in the donation box in 400-timestep simulations for the four different environments. A triangle with a black edge pointing upwards represents a donation to the box whereas pointing downwards represents a taking from the box. Triangles’ colours match agents’ colours

6.4.3 An alternative to our ethical embedding

As previously mentioned, our ethical embedding process consists of aggregating the two reward functions to create an ethical single-objective environment wherein the agents learn the best-ethical equilibrium (i.e. to behave ethically whilst maximising their respective individual objectives).

Alternatively, we could place the learning agents directly within the Ethical MOMG and expect them to handle the two objectives themselves. This approach would require the agents to use a multi-objective reinforcement learning (MORL) algorithm such as independent lex [74], a non-linear MORL that introduces a lexicographic ordering between objectives. Thus, it can be applied to prioritise fulfilling the ethical objective over the individual one. Specifically, this algorithm extends Q-learning for multi-objective environments to respect the ordering between the different objectives.

In order to test this alternative, we have developed two agents that learn within the Ethical MOMG ${\mathcal {M}}$ of the Ethical Gathering game. Then, we performed two tests by running lex for two cases: one where both agents prioritise the ethical objective, and another one where agents prioritise to the individual objective. As Fig. 5a shows, when the ethical objective is prioritised, the algorithm converges to an Ethical equilibrium. Similarly to the equilibrium learned in the ethical environment (Fig. 3c), results show how both agents always survive, and the donation box is filled to its maximum capacity. However, the equilibrium learnt with lex prioritising the ethical objective underperforms with respect to the individual objective (on average, the efficient Agent 2 obtains 5 apples less than when applying scalarised Q-learning (Fig. 3c)). Such a result was expected because, in both cases, we are applying a single-agent algorithm (lex) to a multi-agent environment, wherein there are no theoretical guarantees that agents will learn a Nash equilibrium, which could lead agents to a suboptimal solution. In any case, agents indeed learn to behave ethically (but not best-ethically).

Fig. 5

Number of apples (y-axis) shown as mean ± std, that both agents and the box accumulate along time (x-axis) in the Ethical MOMG after training with multi-objective lex algorithm. Horizontal lines signal the survival threshold ($k=10$) and donation box capacity ($c=5$)

Meanwhile, when the learning agents prioritise their respective individual objectives, Fig. 5b shows that the algorithm converges to a joint policy where only the efficient Agent 2 survives (like in the unethical environment), also as expected. This result implies that with this joint policy, agents do not use the donation box, making it impossible for the inefficient Agent 1 to survive, as shown by Fig. 5b.

Recall that there is no guarantee that learning agents in a multi-objective environment learn to behave ethically when employing a MORL algorithm such as lex, as explained in Sect. 3.1. Indeed, when using lex, the learning agents can either behave ethically (Fig. 5a) or not (Fig. 5b), depending on whether they prioritise the ethical objective or not. However, the environment designer has no guarantees that the latter will occur. This is not the case with our algorithm. In the resulting single-objective ethical environment, the environment designer knows that learning an ethical behaviour is guaranteed because it is a dominant equilibrium. For those reasons, we advocate for our more generic approach of designing an ethical environment that incentivises the agents to behave ethically, independently of their learning algorithms.

6.4.4 Source code

The source code for our work is available at https://github.com/Lenmaz/Ethical-Gathering. Our algorithms and our Ethical Gathering Game have been implemented from scratch on top of the Gathering Game Python implementation by Santiago Cuervo in https://github.com/tiagoCuervo/CommonsGame, which has an MIT License providing permission for modification, distribution, and private use.

All our experiments were performed on a machine with a 12-core 3.70GHz CPU and 64GB RAM. Computing the solution weight vector on each environment required one hour of computation time, whilst training with Q-learning the agents required 24 h per ethical environment.

7 Related work

As mentioned in the introduction, the AI literature on value alignment is divided between two different communities: the AI Safety community [5, 41] and the Machine Ethics community [58, 79].

In AI Safety, the focus is on ensuring that the agent is not harmful to humans or to itself [5]. The general approach is to constrain [17, 25] the agent to guarantee that it performs its intended objective without negative consequences. More in detail, they tackle topics such as reducing the side effects of the agent [38, 62], minimising its impact on the environment [41, 74], or directly creating a shield to protect the agent or others from unsafe behaviours [4, 22].

Alternatively, the objective of Machine Ethics is to develop agents that are beneficial to humans [59]. This of course arises the extra question about what is beneficial from a computational point of view [24, 69]. There is an effort on deciding and studying the moral values that an agent should align with [43, 64], or how to incorporate the moral theories studied by ethicists into the agent decision making process [48, 71]. Since there is still a lack of consensus on such topics, an alternative agnostic approach has emerged that can work under moral uncertainty [21]. Similarly, in our work we do not focus on which are the moral values that an agent ought to align with. Instead, we provide a formal definition of the structure of a moral value, so that we can computationally handle it.

Related with the divide between explicitly defining what is ethical or not, the different approaches for implementing ethical behaviour are divided between top-down, bottom-up and hybrid, as surveyed in [3, 72]. In brief, top-down approaches focus on formalising ethical knowledge to encode it directly into the agent’s behaviour, whereas bottom-up approaches resort to the agent learning the ethical knowledge by itself. Hybrid approaches combine bottom-up and top-down approaches.

Some top-down proposals on formalising moral values include the work of Sierra et al. [64], in which values are formalised as preferences, and also the work of Mercuur et al. [47], in which values and norms are formalised as two distinct concepts, where values serve as a static component in agent behaviour, whereas norms serve as a dynamic component. There has also been studies about the formal relationship between norms and values by Hansson et al. in [30]. In other approaches, such as the work of Liscio et al. [43], they consider that values are context-specific, similarly to how in our approach an action is either good or bad depending on the current environment state. Other top-down proposals aim at formalising moral theories in terms of Markov Decision Processes. This is the case of Nashed et al. [48, 71], in which they modify the decision processes of the agents with an additional constraint that enforces compliance with an ethical theory. Solving the problem produces behaviour that is guaranteed to comply with the constraints of the chosen ethical theory (act utilitarianism, Kantianism, etc, for a brief explanation of each ethical theory see [7]). In general, the contributions to formalising moral values and moral theories is a clear contribution to the value alignment area, since the top-down approaches typically guarantee that an agent following them will behave ethically. However, they are computationally costly or even intractable in the worst cases. For that reason it is widely accepted that pure top-down approaches cannot deal with the whole value alignment problem, as explained by Arnold et al. in [6].

Regarding bottom-up approaches, they almost exclusively focus on reinforcement learning for teaching moral values to agents, following the proposed approaches of Russell, Soares and Fallenstein, among others [59, 66]. In particular, inverse reinforcement learning (IRL) [1] has been proposed as a viable approach for solving the value alignment problem. Inverse reinforcement learning deals with the opposite problem of reinforcement learning: to learn a reward function from a policy. Hence, applying IRL, the agent would be able to infer the values of humans by observing their behaviour. Examples of the use of IRL for the value alignment problem include [27, 51, 54].

One of the first criticisms that IRL received about tackling the value alignment problem was expressed by Arnold et al. in [6]. The authors claim that IRL cannot infer that there are certain norms that the agent needs to follow. Arnold et al. propose instead to combine the strength of RL and logical representations of norms as a hybrid approach. Following the proposal of Arnold et al., an agent would learn to maximise a reward function while satisfying some norms at the same time. While we consider this approach related to ours, we differ in that we are capable of also integrating norms directly into the agent’s ethical reward function as the normative reward component, thus using an approach completely integrated in RL.

Another major criticism of the majority of bottom-up approaches consider the problem of reward specification as equivalent to the whole value alignment problem. This has only recently started to be considered as a two-step process (reward specification and ethical embedding) that must take into account that the agent will have its own objectives (for instance, in [9, 51, 78]). This way, the learning environment of the agent is modelled as a multi-objective one. All of these approaches consider a linear combination of rewards for the ethical embedding similarly to our approach. However, none of them consider the problem of how to guarantee that such linear combination actually incentivises the agent to behave ethically. It is left to the environment designer to hand-tune rewards.

The literature in AI Safety has recently started to answer these questions by providing non-linear approaches for tackling the multi-objective learning environment of the agent [63, 74]. In both the works of Saisubraminan et al. and Vamplew et al., they incorporate a lexicographic ordering between the objectives of the agents with slack.¹⁵ A lexicographic ordering guarantees that the agent will learn to behave ethically (if so demands the ordering), but the problem of this approach is that it complicates the learning process of the agent compared with a linear approach since it is not possible to reduce it to a single-objective process.

An alternative approach presented by Saisubramanian et al. in [63] trying to tackle the drawbacks of these non-linear approaches consist in reconfiguring the agent’s states so the agent is more capable of avoiding causing negative side effects. Similarly to our approach, they consider that the work of the environment designer has a cost, and thus they aim at finding the minimal required changes to the environment to guarantee a safe behaviour. Their approach is promising, but modifying the states of an environment becomes progressively harder for more complex environments. Furthermore, as an AI Safety approach, they are only concerned on guaranteeing that the agent does not perform harmful (blameworthy) actions. In our approach we consider such problem and also the problem of guaranteeing that it performs beneficial (praiseworthy) actions.

Finally, we should also consider multi-agent approaches in which the objective is to guarantee cooperation (as a very broad term) in the multi-agent system, such as [34, 46, 52]. In all three cases the approach is to give incentives to the agents to solve a social dilemma (such as the gathering game) by means of altering the agent’s utility functions so that they also care about the rest of the agents. This is in contrast to our approach, in which each agent can learn an ethical behaviour independently of the others.

8 Conclusions and future work

The literature in value alignment has largely focused on aligning a single agent with a moral value, and with the exception of [55], disregarding guarantees on an agent’s ethical learning. Here we have tackled the open problem of building an ethical environment for multiple agents that guarantees that all agents in the system learn to behave ethically while pursuing their individual objectives. Our novel contributions are founded in the framework of Multi-Objective Markov Games (MOMGs). First, we characterise a family of MOMGs, the so-called ethical MOMGs, for which we formally guarantee the joint learning of ethical equilibria. For such family of MOMGs, we specify the process for building an ethical environment with a so-called multi-agent ethical embedding (MAEE) process. Such embedding process transforms a multi-objective learning environment into a scalarised ethical environment. In the resulting ethical environment, agents are guaranteed to learn an ethical equilibrium.

Interestingly, our MAEE approach for multiple agents generalises that for a single agent in [55]. We illustrate our proposal with the Ethical Gathering Game and solve it with our MAEE process. We empirically show that in the designed ethical environment, agents compensate their social inequalities by learning when to donate to or take from the donation box, in alignment with the value of beneficence. Nevertheless, we would like to remark that the main contributions of our paper are theoretical and not empirical. We perform an empirical evaluation to illustrate and corroborate the theoretical guarantees provided.

It is important to remark that the designed ethical environment by our MAEE process will be ethical only if the appropriate ethical knowledge has been provided. If a malicious environment designer provides an incorrect ethical reward specification, agents will aim at maximising it as if it actually was morally good knowledge. Thus, if this process was to be deployed in a real-world application, an Ethics expert should oversee the design of the ethical environment. Our theoretical results tell the ethical weight necessary for behaving ethically as specified by the ethical reward function. However, the MAEE process has no saying in if it was a correct specification or not.

As future work, we plan to develop methods for testing if an MOMG has ethically-dominant equilibria or not to help assess whether and Ethical MOMG is solvable. This is a challenging problem since testing the existence of dominant equilibria in Markov Games is still an open problem [80]. Also, we aim at extending our empirical study of the MAEE process for environments with more than two agents.