Data-driven and uncertainty-aware robust airstrip surface estimation

Abstract

The performances of aircraft braking control systems are strongly influenced by the tire friction force experienced during the braking phase. The availability of an accurate estimate of the current airstrip characteristics is a recognized issue for developing optimized braking control schemes. The study presented in this paper is focused on the robust online estimation of the airstrip characteristics from sensory data usually available on an aircraft. In order to capture the nonlinear dependency of the current best slip on sequential slip-friction measurements acquired during the braking maneuver, multilayer perceptron (MLP) approximators have been proposed. The MLP training is based on a synthetic data set derived from a widely used tire–road friction model. In order to achieve robust predictions, MLP architectures based on the drop-out mechanism have been applied not only in the offline training phase but also during the braking. This allowed to online compute a confidence interval measure for best friction estimate that has been exploited to refine the estimation via Kalman Filtering. Open loop and closed loop simulation studies in 15 representative airstrip scenarios (with multiple surface transitions) have been performed to evaluate the performance of the proposed robust estimation method in terms of estimation error, aircraft braking distance, and time, together with a quantitative comparison with a state-of-the-art benchmark approach.

1 Introduction

Brake controllers are designed to guarantee the minimum braking time while simultaneously preventing wheel slippage. This is possible by designing Electro-Mechanically Actuated (EMA) anti-skid systems that maximize the tire–road friction coefficient [4]. For this purpose, however, the knowledge of the actual surface characteristics is required to allow the braking controller to track the maximum friction point in the current slip-friction curve. Under the circumstances of sudden changes in surface conditions, a reliable estimation of the tire–road friction coefficient would lead to relevant benefits in braking efficiency and passenger safety [30]. In this context, the accuracy, reliability, and velocity of the estimation play a crucial role. In case the road surface characteristics are unknown, these have to be inferred from sensory data. Due to the strongly nonlinear and uncertain physical phenomena involved, the underlined estimation process is challenging and still an open problem. This is particularly relevant in the aeronautical context, where the aircraft’s high speed and the potential fast-changing conditions on the runway make the inference process even more tricky.

1.1 Related work and main contribution

The problem of estimating the tire–road friction coefficient has been extensively investigated in the literature over the last years. In this paper, we focus on “slip-oriented” methods, which exploit the functional dependence of friction $\mu$ on slip $\lambda$ (i.e., the normalized difference between longitudinal and tangent velocities) to estimate the actual tire–road conditions. In such a framework, it is common practice to model the longitudinal tire-force $F_{x}$ as $F_{x}:= \mu F_{z}$, where $\mu$ is the normalized friction coefficient. It can be described, among others, by the Pacejka [2] and the Burckhardt models [5, 19], which assume a nonlinear dependence of $\mu$ on the slip signal $\lambda$.

An extended Kalman filter (EKF) has been used in [26] to estimate a piece-wise constant friction coefficient $\mu$, without any specific relation to the slip. Later [1, 15, 21] proposed other simplified $(\lambda , \mu )$ models to estimate the actual road friction coefficient. In [34, 35], a least square and maximum likelihood approach has been proposed, to estimate the parameters of a linearly parametrized approximation of the Burckhardt model, based on a sequence of $(\lambda , \mu )$ pairs as input, and using a Quarter Car Model (QCM) for the system dynamics. In [10], Recursive Least Square is used to online estimate the parameters of a linearized approximation of the Burckhardt model, and in [11], an enhanced constrained version of the same algorithm is proposed. A detailed and accurate discussion on model-based and black-box approaches to slip estimation is given in [24].

Optimal slip estimation has also been addressed by using data-driven approaches; [27, 36], respectively, employ a Support Vector Machine (SVM) and a General Regression Neural Network (GRNN) to solve the estimation problem. In [17], neural network and fuzzy approaches are discussed jointly with a sliding mode controller. The deep learning paradigm has, instead, been explored in [31], although with the assumption of having access to a considerable amount of different input measurements, which does not apply to most braking systems. More recently, the authors of [8] proposed a multilayer perceptron (MLP) to predict the best slip value by processing sequences of slip-friction pairs computed online from the onboard sensor readings.

Although all the abovementioned data-driven methods, including Neural Networks, SVM and Fuzzy models, are undoubtedly effective in mapping the uncertain and nonlinear relation between slip and friction, they do not provide confidence measures about their estimates. To overcome this limitation, in this study, we propose an approach derived from [7], which provides, in addition to the MLP-based estimation, a confidence interval for the estimate. Specifically, in order to provide a robust prediction, the Neural Network (NN) has been trained using the stochastic weights dropout method [32]. This mechanism was employed not only in the offline training phase but also at inference time, during the braking. This modification makes available online a confidence interval measure for the MLP estimate of the best friction coefficient. This information has been exploited to further refine the MLP best slip estimate by filtering it via a Kalman Filter whose measurement covariance is made proportional to the estimated confidence interval provided by the dropout MLP. We believe that such online confidence information may be useful also for other purposes within an advanced braking control scheme. For example, it may be possible to schedule different authority closed loop controllers as a function of the estimated friction coefficient and its confidence interval. In order to evaluate the performance of the proposed robust optimal friction estimation algorithm, open-loop and closed-loop simulation studies in 15 representative airstrip scenarios (with multiple surface transitions) have been performed. Different MLP architectures (with and without the dropout mechanisms, with and without Kalman filtering) have been compared with a state-of-the-art surface estimation method based on Recursive Least Squares (RLS).

1.2 Paper organization

The paper is organized as follows. Section 2 formulates the optimal friction estimation problem and discusses the underlying dynamic model. Section 3 presents the proposed estimation MLP networks, the uncertainty computation mechanism, the Kalman filtering with the associated offline and online learning approach. Section 4 presents an RLS-based existing algorithm used as a baseline for comparison. Section 5 illustrates the experimental setup, and the closed-loop control scheme. Section 6 discusses the MLP performance on a number of simulated open and closed loop tests. Finally, Sect. 7 draw some conclusions.

2 Aircraft friction estimation problem

2.1 Friction modeling

The dynamics of a vehicle, for the purpose of braking control, can be described by the well-known Quarter-Car Model (QCM) [10, 35]:

$$\begin{aligned} \begin{aligned} J {\dot{\omega }}&= r F_{x} - T_{\rm{b}}, \\ M {\dot{v}}&= - F_{x}, \end{aligned} \end{aligned}$$

(1)

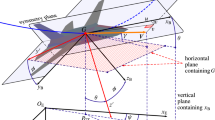
where $\omega$ and v are the wheel angular velocity and vehicle longitudinal speeds, J and M are the corresponding momentum of inertia and mass, r is the wheel radius, and $T_{\rm{b}}$ is the braking torque, i.e., the control signal (see Fig. 1).

Fig. 1

The friction model. A more detailed wheel and landing gear model can be found in [4]

The braking performance depends heavily on the longitudinal slip $\lambda \in [0,1]$, which is defined as:

$$\begin{aligned} \lambda := \dfrac{v - r \omega }{v} = 1 - r \dfrac{\omega }{v}. \end{aligned}$$

(2)

From the braking control point of view, the key term in model (1) is the friction longitudinal force $F_{x}$, which characterizes the tire–road contact force. A widely adopted model for $F_{x}$ [10, 35] assumes the dependence on the current vertical force $F_{z}$ at the tire–road contact point, on the longitudinal slip $\lambda$ and on the wheel side-slip angle $\gamma$ according to the general formula:

$$\begin{aligned} F_{x} = \mu (\lambda ,\gamma , \beta ) \, F _{z}, \end{aligned}$$

(3)

where the additional vector of parameters $\beta$ characterizes the normalized friction function $\mu$ with respect to the specific road surface. In the following, it will be assumed that the aircraft braking occurs during a straight line motion, a reasonable assumption during the landing or reject-take-off. In this case, the dependence of function $\mu$ on the wheel side-slip angle $\gamma$ can be neglected.

It is important to highlight that the nonlinear relation between $F_x$ and $F_z$ is ”embedded” into the normalized friction function $\mu (\lambda , \beta )$, which has a strong nonlinear dependence on its arguments. The function $\mu (\cdot )$ is typically represented by a lumped nonlinear model such as the Burckhardt one [5, 19]:

$$\begin{aligned} \mu (\lambda , \varvec{\beta }) = \beta _{1}(1 - \text{e}^{-\beta _{2}\lambda }) - \beta _{3}\lambda \end{aligned}$$

(4)

or the Pacejka one (also known as the Magic Formula) [2]:

$$\begin{aligned} \mu (\lambda , \varvec{\beta }) = \beta _{1}\text {sin}(\beta _{2}\text {atan}((1-\beta _{4})\beta _{3}\lambda + \beta _{4}\text {atan}(\beta _{3}\lambda ))) \end{aligned}$$

(5)

These models have been shown to match very well experimental data and to exhibit a similar behavior [22]: in all road conditions, the friction curve has a single maximum as a function of slip $\lambda$ (see Fig. 2).

Let denote with $\mu ^{*}$ the optimal friction, i.e., the maximum of the friction curve, and with $\lambda ^{*}$ the corresponding optimal slip value. The presence of such a single maximum entails that, for each surface, there is only a specific slip value yielding the best braking performance.

Fig. 2

Burckhardt and Pacejka friction models: each road condition has a single maximum $\mu ^*$, corresponding to the “optimal slip” $\lambda ^*$, which maximizes the friction function (hence, the Friction Force $F_x$)

Under real-time braking operation, the road surface is not known a-priori, so that the identification of the specific curve and of the associated optimal slip $\lambda ^{*}$ is requested in order to maximize the braking performance.

In the following, the Burckhardt model will be used. The “challenging scenarios” that have been considered for validation tests are the Burckhardt reference surfaces: Asphalt-Dry, Asphalt-Wet and Asphalt-Snow (briefly, Dry, Wet and Snow, respectively), depicted in red in Fig. 2 and characterized by the parameters $(\beta _1, \beta _2, \beta _3)$ in Table 1.

Table 1 Burckhardt reference surfaces

2.2 Problem formulation

To study the braking control problem, it is convenient to carry out coordinate transformation in the state space, and to use the slip function $\lambda$ as a state variable in place of the wheel speed $\omega$. In addition, since the time scale of the aircraft velocity v is typically slower compared to the slip one, it can be considered as a slowly varying parameter. Assuming that $F_{z} = M g$, and using $\lambda$ as the state variable, the QCM dynamics in (1) can be rewritten as follows:

$$\begin{aligned} \begin{aligned} {\dot{\lambda }}&= - \alpha (\lambda ) + \gamma T_{\text{b}}, \end{aligned} \end{aligned}$$

(6)

where

$$\begin{aligned} \begin{aligned} \alpha (\lambda )&:= \dfrac{1}{v} \left[ (1-\lambda ) + \dfrac{M\,r^{2}}{J} \right] g \mu (\lambda , \beta ), \\ \gamma&:= \dfrac{r}{J \,v}. \end{aligned} \end{aligned}$$

(7)

Based on the above model (6), (7), the problem of interest in this paper is the development of data-oriented online estimators of the optimal slip $\lambda ^*$ for the current, unknown runway surface and of the associated estimation uncertainty. The estimation of $\lambda ^{*}$ is crucial since its availability allows to use a closed-loop slip controller to track it in order to produce the maximum friction effect for the current runway conditions.

This paper proposed a multilayer perceptron to infer online the values of $\lambda ^{*}$ using as input vector sequences of $(\lambda ,\mu )$ pairs.

In addition, a measure of estimation uncertainty for the estimated best slip is also provided. This information can be exploited in different ways during braking. In this study, the estimation uncertainty has been used as an online confidence estimation combined with a Kalman Filter (KF) to smooth the best slip signal provided by the neural estimators.

The proposed MLP estimation scheme has been simulated for the case of a landing aircraft under a number of conditions, as detailed in Sects. 5 and 6.

The proposed estimation scheme requires the current slip and friction values as input (both in test phase and during online operation). The values of $\lambda$ are computed using the longitudinal aircraft velocity v and the wheel angular velocity $\omega$. In real applications, the first can be measured for example through GPS readings, while the latter can be obtained from encoder measurements. A more advanced techniques to estimate the wheel slip is discussed in [23]. Since is not possible to measure $\mu$ directly, a common approach [11, 12] is referring to the dynamical model (1). In particular, first $F_x$ is obtained from (1) by using a derivative filter to compute ${\dot{v}}$ and ${\dot{\omega }}$ (in this work, the filter is band-limited at 100 Hz to dampen the effect of noise). Afterward, $F_x$ and $F_z$ (the latter can be directly obtained from the mass M) are plugged into (3) to get $\mu$. Other approaches, e.g., [24, 33], could also be considered and easily integrated with the proposed methodology.

Remark 1

It is observed that although the QCM might be an over-simplification with respect to the actual dynamics, it is widely employed in the literature studies dealing with tire–road interaction from the control design point of view. For instance, the authors in [10, 11, 29] found this model adequate; the same model has also been used in application studies such as in [34, 35] achieving convincing results. Motivated by this well-consolidated literature we have used the same model in our study. Specifically, in our scheme, the QCM is employed within the dynamic inversion block that provides an online estimate of the friction $\mu$ for a given $\lambda$ computed using velocity measurements and inertial parameters (according to the procedure described above).

Remark 2

In case the employed model is not accurate enough, the estimation of the friction provided by the inverse model may not be accurate entailing that the output provided by the MLP would be inaccurate as well. In order to achieve more accurate results, it is not necessary to redesign the entire feedback estimation and control scheme but, “simply,” to exchange (within the model inversion block) the QCM with a more accurate model of the braking dynamics for the specific aircraft under study. Such a model could be derived from first-principles or directly from data. As an example, the ideas discussed in [23, 24] could be pursued, without the need for interventions on the trained MLP.

In our simulation study, we used the QCM model both to emulate the dynamics of the “physical system” and to implement the dynamic inversion, so the estimated $(\lambda , \mu )$ pairs are consistent with the “physical system.” It is finally underlined that, as explained above, the MLP has been trained using segments of the $(\lambda , \mu )$ curves sampled from the Burckhardt model, therefore the performance of this block is independent from the particular “physical model” used in the closed loop simulations.

Fig. 3

The proposed estimation and control scheme. The input to the multilayer perceptrons (MLPs) is given by a sequence of $({\hat{\lambda }}, {\hat{\mu }})$ pairs, computed through the inverse dynamical model, using measured ground speed v and angular velocity $\omega$ as inputs. The uncertainty estimation block, in the Dropout MLP (MLP-D) case, returns both the MLP best slip estimate ${\hat{\lambda }}^{*}$ and the corresponding uncertainty $\sigma$. The output of the MLP-D is then further refined by a Kalman Filter (MLP-D KAL). The predicted best slip values are used as a set point for the slip controller, aimed at regulating the braking torque $T_b$

3 Data-driven optimal slip estimation

A key aspect in the estimation of the normalized friction $\mu (\lambda )$ is closely related to the nonlinear nature of the lumped model (3).

Over the last years, this has led to a number of approaches based on approximate models, such as those proposed in [10, 25, 34, 35], aimed at estimating the whole friction curve.

To overcome these limitations, we start from a different hypothesis, extending initial ideas in [8, 9]: the key properties of the road–tire function $\mu (\lambda )$ can be inferred from sequence of samples of $(\lambda , \, \mu )$ pairs collected during the normal operation of the braking system. More specifically, the idea is to avoid reconstructing the overall slip friction curve; instead, given a sequence of $(\lambda , \, \mu )$ pairs, we only focus on the computation of an estimate ${\hat{\lambda }}^{*}$ of the optimal slip value $\lambda ^{*}$ associated with the current surface. The proposed approach is therefore model free and can be classified as a data-driven method.

The mapping between a sequence of $(\lambda , \, \mu )$ samples and the corresponding optimal slip $\lambda ^{*}$ has been approximated through an MLP network, whose input features are $(\lambda , \, \mu )$ samples, that is:

$$\begin{aligned} \begin{aligned} \lambda ^{*}(k)&= \text{ MLP } \left[ (\lambda (k), \mu (k)), \, (\lambda (k-1), \mu (k-1)), \cdots , \right. \\&\quad \left. (\lambda (k-N), \mu (k-N) ) \right] + \epsilon \\&= \text{ MLP } \left( \mathbf {\mathcal {X}}_{k} \right) + \epsilon = {\hat{\lambda }}^{*}(k) + \epsilon \\ \mathbf {\mathcal {X}}_{k}&= \left[ (\lambda (k), \mu (k)), \cdots (\lambda (k-N), \mu (k-N)) \right] \end{aligned} \end{aligned}$$

(8)

with $\mathbf {\mathcal {X}}_{k}$ denoting the sequence of N pairs $(\lambda , \, \mu )$, from sample k backward to sample $k-N$, where N is the window length, and $\epsilon$ is the MLP approximation error.

The block diagram of the proposed estimation algorithm is reported in Fig. 3, together with the slip control scheme.

3.1 Dataset construction

In order to train the MLP networks, a large set $\mathcal{T}\mathcal{S}$ of P training samples is required:

$$\begin{aligned} \mathcal{T}\mathcal{S}=\{(\mathbf {\mathcal {X}}_{1}, \lambda ^*_{1}), (\mathbf {\mathcal {X}}_{2}, \lambda ^*_{2}), \dots , (\mathbf {\mathcal {X}}_{P}, \lambda ^*_{P})\}, \end{aligned}$$

(9)

where $\mathbf {\mathcal {X}_{i}}$ are the sequences of slip-friction pairs in (8) and $\lambda ^*_{i}$ are the associated optimal slip values. Sampling the Burckhardt surfaces (i.e., the red curves in Fig. 4), would not provide a sufficiently rich amount of data for the training process.

This aspect is crucial since, to achieve generalization capabilities and avoid overfitting, the model needs to experience a reasonable variety of input–output configurations during the training phase. This, in practice, implies that the $(\mathbf {\mathcal {X}}_{i}, \lambda ^*_{i})$ samples should represent most of the different possible road conditions that characterize real scenarios. To this purpose, the following approach has been pursued. For each parameter $\beta _j$, an interval $B_j$ of possible values has been defined, in order to cover a large set of reference surfaces.

Then, the friction cube has been generated, i.e., the space $(B_{1} \times B_{2} \times B_{3}) \in \mathrm{IR}^3$. To sample such a cube, two different strategies have been explored. The first one generates the set of surfaces by sampling $N_{\text{diag}}$ points along the cube diagonal. This choice stems from the observation that the reference surfaces lie close to the diagonal. To add more variety to the training set, a second strategy has also been considered, by selecting $N_{\text{lat}}$ additional points within the cube using the Latin Hypercube Algorithm [16]. However, it has been experimentally verified that the NN models trained with samples from curves sampled from both strategies achieved worse performance. This can be explained by considering that curves associated with off-diagonal points do not represent Burckhardt road conditions. Therefore, adding them to the training set increases the complexity of NN model optimization without adding substantial benefits. Therefore, in this work, $N_{\text{lat}}$ has been set to 0, while $N_{\text{diag}}=35$.

To generate the complete data set, each one of the slip-friction curves is discretized with 1000 points in the range $\lambda \in [0,1]$. Afterward, a sliding window of fixed size is used to select the N pairs $\mathbf {\mathcal {X}_{i}}$ in (8). Here, $N=50$ has been selected following extensive experimental tests. Each set of N windowed samples is then associated with the optimal slip value $\lambda ^{*}_{\text{GT}}$, which is computed based on the closed form model (4) for friction $\mu$.

To model the ground and wheel speed (v and $\omega$, respectively) measurement process, the $\mu$ signal is corrupted with zero-mean Additive White Gaussian Noise (AWGN) $\mathcal {N}(0,\,\sigma ^{2})$. The value of $\sigma =0.005$, has been chosen taking into account the range of $\mu$ values in typical scenarios, also in case of small slip values ($\lambda < 0.05$).

Note that, to generate the $(\lambda , \mu )$ pairs for training, the Burckhardt model (4) is directly used and there is no need to use the QCM. This differs from the inference phase where instead, as detailed in Sect. 2.2, $\lambda$ and $\mu$ are computed by using Eqs. 1 and 3.

Fig. 4

The training dataset based on the Burckhardt model. The reference cases (i.e., the Burckhardt reference surfaces) are shown in red color. Training (blue) and validation (yellow) curves have been generated by suitably exploring the friction cube (Color figure online)

3.2 Optimal slip estimation through MLP approximators

This work considers two neural network architectures: a Standard Multilayer Perceptron (MLP-S) and a Dropout-based variant (MLP-D) that features dropout layers to achieve regularization and to perform uncertainty estimation. Hyper-parameters (i.e., number of hidden layers, number of neurons per hidden layers, activation functions, learning rate and weight decay) are selected through model selection, cross-validating their values on the training and validation datasets. For both the architectures, the best validation performance is obtained with a configuration characterized by Rectified Linear Units (ReLU) as nonlinear activations, two hidden layers with 250 neurons each and the Adam optimizer, which updates the network weights for 100 epochs [3] with a learning rate of 0.001 and a weight decay of 0.0001.

MLP-S is optimized by minimizing the standard Mean Squared Error (MSE) regression loss function, which measures the difference between the estimated and the actual optimal slip value:

$$\begin{aligned} L_{\text {MLP-S}} = \frac{1}{P_{\text{tr}}} \sum _{p=0}^{P_{\text{tr}}-1} (\lambda _{GT, p}^* - {\hat{\lambda }}_{p}^*)^2, \end{aligned}$$

(10)

where $P_{\text{tr}}$ refers to the number of samples in the training set, while $\lambda _{GT, p}^*$ and ${\hat{\lambda }}_{p}^*$ indicates the actual and the estimated slip value, respectively. By optimizing this objective function, the model aims to minimize the MLP approximation error in Eq. (8) between the true and the estimated optimal slip values on the training samples.

On the other hand, the MLP-D architecture’s purpose is also to provide uncertainty measures associated with the optimal slip prediction. Therefore, it cannot be trained by minimizing the MSE loss in (10); instead, a different paradigm is employed. More specifically, dropout layers are placed after the activation of each hidden layer. Their role is to randomly "disconnect" the neurons between two consecutive layers of the network according to a Bernoulli distribution parameterized by a hyper-parameter p (which we set to 0.075 after performing model selection). During the training phase, dropout is used to regularize the network and avoid overfitting. Intuitively, by switching off connections between layers, the network is forced to focus on the true pattern describing the underlying process and avoid modeling noise.

Dropout layers are also fundamental in order to perform uncertainty estimation at test time (during online operation). To describe how they are used in this work, it is necessary to introduce the concept of uncertainty computation for MLPs. In most cases, neural networks are indeed regarded as “black boxes” whose outputs cannot be associated with confidence measures. It is only in recent years that this topic has attracted the interest of the research community [13, 18]. More specifically, estimation uncertainties can be obtained by modeling the Epistemic Uncertainty (EU), which accounts for the uncertainty that the model has about its own parameters. The key intuition behind EU is that the model generally has lower confidence with respect to samples that belong to parts of the input space different from those experienced during training.

To formalize this concept in our scenario, consider the estimated optimal slip value ${\hat{\lambda }}_{p}^*$ computed by processing an input sequence $\mathbf {\mathcal {X}}_{p}$ of N ($\lambda$, $\mu$) pairs. To estimate the prediction uncertainty associated with ${\hat{\lambda }}_{p}^*$, it is necessary to model its predictive posterior distribution $p({\hat{\lambda }}^{*}_{p} \vert \mathbf {\mathcal {X}}_{p})$. This can be achieved by introducing a prior over the network weights and a likelihood as follows:

$$\begin{aligned} & p({\textbf{W}}) \thicksim \mathcal {N}(0, l^{-2}{\textbf{I}}), \end{aligned}$$

(11)

$$\begin{aligned} & p({\hat{\lambda }}^{*}_{p} \vert f(\mathbf {\mathcal {X}}_{p}, {\textbf{W}})) \thicksim \mathcal {N}(f(\mathbf {\mathcal {X}}_{p}, {\textbf{W}}),\varvec{\Sigma }), \end{aligned}$$

(12)

where, in this work, both the distributions are Gaussian. In the above formulas, $f(\mathbf {\mathcal {X}}_{p}, {\textbf{W}})$ is the output of the neural network that depends on the set of weights ${\textbf{W}}$, $\Sigma$ is the variance of the Gaussian and l controls the belief over ${\textbf{W}}$. To obtain $p({\hat{\lambda }}^{*}_{p} \vert \mathbf {\mathcal {X}}_{p})$, the aforementioned distributions and dataset $\mathcal {X}$ are used to compute the posterior distribution and marginalize over the parameters ${\textbf{W}}$:

$$\begin{aligned} p({\hat{\lambda }}^{*}_{p} \vert \mathbf {\mathcal {X}}_{p}, \mathcal {X}) = \int p({\hat{\lambda }}^{*}_{p} \vert \mathbf {\mathcal {X}}_{p}, {\textbf{W}})p({\textbf{W}} \vert \mathcal {X})\text{d}{\textbf{W}}. \end{aligned}$$

(13)

Unfortunately, the computation of the posterior $p({\textbf{W}} \vert \mathcal {X})$ is analytically intractable for neural networks. This is where dropout layers become crucial. In particular, the dropout variational inference framework [14] is used to approximate the posterior distribution with a tractable one.

This, in practice, means minimizing the following objective:

$$\begin{aligned} \begin{aligned} L_{\text {MLP-D}}&\propto \frac{1}{P_{\text{tr}}} \sum _{p=0}^{P_{\text{tr}}-1} \left( \frac{1}{2} {\tilde{\lambda }}_{p}^T \, \varvec{\Sigma }^{-1} \, {\tilde{\lambda }}_{p} +\frac{1}{2} \log \left\| {\varvec{\Sigma }}\right\| \right) \\&\quad + \sum _{j=0}^{L-1} \left( \frac{p_j l^2 {{\,\text{Tr}\,}}(\varvec{\Sigma })}{2N} \Vert \varvec{M}_j\Vert ^{2}_{2} \right. \\&\quad + \left. \frac{l^2 {{\,\text{Tr}\,}}(\varvec{\Sigma })}{2N} \Vert \varvec{m}_j\Vert ^{2}_{2} \right) , \end{aligned} \end{aligned}$$

(14)

where ${\tilde{\lambda }}_{p}:= \lambda ^{*}_{p} - f(\mathbf {\mathcal {X}}_{p}, \tilde{{\textbf{W}}}_{p})$, and with L referring to the number of hidden layers, $p_j$ to the dropout probability at the j-th layer, $\tilde{{\textbf{W}}}_{p}$ are the weights sampled with the dropout layer for the p-th forward, and $\varvec{M}_j$ and $\varvec{m}_j$ to the variational parameter of the j-th layer. At test time, the mean and the variance of the predictive distribution are obtained by using Monte Carlo sampling keeping active the dropout layers and performing S stochastic forwards. Therefore, for a generic test sample $\mathbf {\mathcal {X}}_{T}$:

$$\begin{aligned} & \mathbb {E}_{EU}({\hat{\lambda }}^{*}_{T}) \approx \frac{1}{S}\sum _{s=1}^{S}f(\mathbf {\mathcal {X}}_{T}, \tilde{{\textbf{W}}}_{s}), \end{aligned}$$

(15)

$$\begin{aligned} \text{Var}_{EU}\left( {\hat{\lambda }}^{*}_{T} \right) & \approx \varvec{\Sigma } + \frac{1}{S}\sum _{s=1}^{M} f(\mathbf {\mathcal {X}}_{T}, \tilde{{\textbf{W}}}_{s}) f(\mathbf {\mathcal {X}}_{T}, \tilde{{\textbf{W}}}_{s})^T \nonumber \\ & \quad - \mathbb {E}_{EU}({\hat{\lambda }}^{*}_{T}) \mathbb {E}_{EU}({\hat{\lambda }}^{*}_{T})^T. \end{aligned}$$

(16)

In the experiments, at test time, S is set to 100.

3.3 Kalman filtering based on uncertainty measure

The availability of the uncertainty measure (16) makes it possible to implement an optimal filtering strategy of the best slip estimate.

To this purpose, a model of the best slip behavior has to be considered. The following two discrete-time models can be considered:

$$\begin{aligned} \begin{aligned} x_{1}(k)&= x_{1}(k-1) + \eta (k), \\ \lambda ^{*}(k)&= x_{1}(k) + \nu (k), \end{aligned} \end{aligned}$$

(17)

and

$$\begin{aligned} \begin{aligned} x_{1}(k)&= x_{1}(k-1) + x_{2}(k-1) + \eta _{1}(k), \\ x_{2}(k)&= x_{2}(k-1) + \eta _{2}(k), \\ \lambda ^{*}(k)&= x_{1}(k) + \nu (k), \end{aligned} \end{aligned}$$

(18)

where the $\eta$ and $\nu$ terms are state and output noise signals, respectively.

The first model assumes the best slip is (piece-wise) constant, while the latter assume the best slip changes over time according to a (piece-wise) constant rate of variation. Both models can be described in matrix form as follows, for suitable A and C matrices and state vector x:

$$\begin{aligned} \begin{aligned} x(k)&= A \, x(k-1) + \eta (k), \\ \lambda ^{*}(k)&= C \, x(k) + \nu (k). \end{aligned} \end{aligned}$$

(19)

It should be noticed that the KF model in Eq. (19) does not depend on physical (possibly drifting) parameters, i.e., the QCM dynamical model. Instead, the structure of the matrices A and C only models the optimal slip temporal behavior.

Based on the model (19), the following Kalman filter can be devised:

$$\begin{aligned} \begin{aligned}&{\hat{x}}^{-}(k) = A \, {\hat{x}}(k-1) , \\&{P}^{-}_{k} = A \, {P}_{k-1} \, A^{T} + Q , \\&K_{k} = {P}^{-}_{k} \, C^{T} \left( C\, {P}^{-}_{k} C^{T} + R_{k}\right) ^{-1} ,\\&z(k) = \mathbb {E}_{EU}({\hat{\lambda }}^{*}_{k}) ,\\&{\hat{x}}(k) = {\hat{x}}^{-}(k) + K_{k} \left( z(k) - C {\hat{x}}^{-}(k) \right) ,\\&{P}_{k} = \left( I - C K_{k} \right) {P}^{-}_{k} ,\\&{\hat{\lambda }}^{*}_{\text{Kal}}(k) = {\hat{x}}(k), \end{aligned} \end{aligned}$$

(20)

where $\mathbb {E}_{EU}({\hat{\lambda }}^{*}_{k})$ is the k-th best slip estimate (15), Q is the variance of the state noise $\eta$, $R_{k}$ is the variance of the output noise $\nu$ and $P_{k}$ is the error variance. In order to increase sensibility to the actual uncertainty, the variance $R_{k}$ has been chosen as a polynomial modification of the estimated one. Good performance have been obtained by choosing $R_{k}=\left[ \text{Var}_{EU}\left( {\hat{\lambda }}^{*}_{k} \right) \right] ^3$. In addition, the state variance Q has been chosen as $Q=(1.0e^{-5})^3$, the variance P has been initialized to zero, and the Kalman filter state, i.e., the best slip estimate, has been initialized to ${\hat{x}}(0) = 0.15$.

4 Data-driven baselines

Using the Burckhardt or Pacejka models to estimate the actual value of friction requires, implicitly, the on-line estimation of an unknown nonlinear function. A state-of-the-art approach is to use an approximate nonlinear model for the friction, Linearly Parameterized (LP), as in [10, 11, 29, 34, 35]. Based on such a LP approximation, a Recursive Least Squares (RLS) filter [6, 20] can be used, to online estimate the model parameters.

In [10, 11] the authors approximate the Burckhardt model (4) using the following LP approximation:

$$\begin{aligned} \mu (\lambda , \varvec{\beta }) \approx {\hat{\mu }}_{LP}(\lambda , \varvec{\theta })= {\textbf{H}}(\lambda )\varvec{\,} \theta , \end{aligned}$$

(21)

where ${\textbf{H}}(\lambda ) = [1, \; \lambda , \; e^{-4.99\lambda }, \, e^{-18.43\lambda }, e^{-65.62\lambda }]$ is the vector of basis functions and $\varvec{\theta ^T}=[\theta _1, \theta _2, \dots , \theta _5]$ is the vector of the unknown parameters characterizing the surface.

Based on the LP model (21), following [10, 11] a RLS algorithm is used to online estimate the parameter vector $\varvec{\theta }$. A similar approach, with a different set of basis function, is discussed in [34, 35].

Finally, based on the estimated vector $\varvec{\theta }$, the associated friction curve ${\hat{\mu }}_{LP}(\lambda , \varvec{\theta }) = {\textbf{H}}(\lambda ){\varvec{\theta }}$ can be obtained, which is then used to analytically derive the peak friction point $P_{\text {Max}}=(\hat{\mu ^*}, \hat{\lambda ^*})$.

Such a method, based on (21) and RLS estimation (which in the following will be referred to as RLS), will be used as the baseline scheme to assess the performance of the approaches proposed in this paper.

5 Experimental set-up

Three sets of experimental tests have been carried out to illustrate the performance of the proposed approaches and the benefit of best slip estimation on braking performances: (1) the learning performance tests, (2) open-loop braking maneuvers, and (3) closed-loop braking maneuvers. The first one aims to evaluate the learning and generalization capabilities of the MLP on different sets of friction curves, while the latter focus on the estimation accuracy in real-time scenarios. In particular, the closed-loop tests show the benefit of best slip estimation on braking performances.

The open loop and closed loop results are also compared with those of the baseline RLS approach discussed in Sect. 4.

5.1 The learning performance

The first set of experiments is focused on evaluating the learning and generalization capabilities of the MLP-based estimators. For this purpose, the analysis is carried out by computing the Root Mean Square Error (RMSE) [3] achieved by the MLP(s) using the data set $\mathcal{T}\mathcal{S}$ introduced in Sect. 3.1 and depicted in Fig. 4. It consists of $P=33285$ windowed sets $\mathbf {\mathcal {X}_{i}}$, randomly split into training (23775), validation (4755) and test (4755) sets. This choice allows testing whether the learned model can generalize with respect to unseen road surfaces. Furthermore, the three Burckhardt surfaces i.e., Asphalt Dry (D), Asphalt Wet (W), and Snow (S), are used as additional test scenarios (since these have been excluded from the training set).

5.2 Braking maneuvers

To test the proposed estimation schemes in realistic scenarios, an aircraft landing maneuver is simulated over an unknown, possibly time-varying, surface.

In all the simulations, the QCM model parameters are set as $M = 1600\, [\text{kg}]$, $J = 4500 \, [\text{kg}/\text{m}^{2}]$, and $r = 0.3 \, [\text{m}]$. The initial aircraft speed is set to $80 \, [\text{m}/\text{s}]$ and the initial wheel velocity is set accordingly to produce zero slip at time $t_{0}=0$, i.e., the braking action starts immediately after ground contact.

The proposed MLP estimators have been evaluated by simulating the landing in different operative scenarios: the case of braking on a uniform, unknown airstrip and the case of braking on an unknown airstrip, whose surface changes abruptly. Specifically, we considered transitions between the three Burckhardt surfaces: the complete set of tested scenarios are summarized in Table 2.

Table 2 Airstrip scenarios used to evaluate the uncertainties estimates provided by both the reference RLS estimator and the original ones proposed in the paper

It is important to underline that surface transitions are not considered in the generation of the training data set; hence, those scenarios are handled by the MLPs in view of their generalization capabilities.

For each simulation, as outlined in Sect. 2.2, sequences of $(\lambda ,\mu )$ pairs are computed using the longitudinal aircraft velocity v and the wheel angular velocity $\omega$ within the QCM model. Each sequence $\mathbf {\mathcal {X}_{i}}$ is then provided to the estimation algorithms, e.g., RLS, MLP-S, MLP-D and KAL (MLP-D with Kalman Filtering), to obtain the actual best slip prediction. The estimates provided by the MLP-S, the MLP-D and the RLS schemes have been low pass filtered both to mitigate the measurement noise and to recover the intrinsic dynamic nature of the friction phenomena, which is neglected in the multi-transition tests. Such a filtering step is omitted in the Kalman-based estimation case.

The optimal slip estimates ${\hat{\lambda }}^*_{i}$ obtained by all the studied schemes are compared with the ground truth values (${\hat{\lambda }}^*_{\text{GT}}$) to provide qualitative and quantitative results. The metric used to evaluate the estimation error for both open-loop and closed-loop simulations is the RMSE, which has some interesting implications: it gives a relatively high weight to large errors, so small amount but significant deviations from the Ground Truth (GT) will be penalized. This is particularly useful in identifying regressors that could produce estimates that are considerably distant from the actual ground condition and could create erroneous set-points for the braking control system.

5.2.1 Open loop tests

In this set of tests, the system operates in open loop configuration, i.e., a constant braking signal $T_{\text{b}}$ is directly applied to the aircraft and kept constant for the whole maneuver. In case of changing surface conditions, the value is set equal to the best torque value (the maximum value that does not cause the wheels to lock) for the initial surface.

5.2.2 Closed loop tests

In the third set of experiments, the online estimate of the optimal slip provided by the two MLPs and the one provided by the Kalman filter are used as reference signals for the feedback slip controller (see Fig. 3). A Proportional-Integral (PI) regulator has been employed, to track the optimal slip computed by the proposed estimators. The braking torque produced by the PI controller is given by:

$$\begin{aligned} \begin{aligned} T_{\text{b}}&= - K_{P} (\lambda - {\hat{\lambda }}^{*}) - K_{I} \zeta , \\ {\dot{\zeta }}&= \lambda - {\hat{\lambda }}^{*}, \end{aligned} \end{aligned}$$

(22)

where ${\hat{\lambda }}^{*}$ is the output of one of the MLP and Kalman friction estimators. The closed loop system, in the $\lambda$ coordinate, is given by:

$$\begin{aligned} \begin{aligned} {\dot{\lambda }}&= - \alpha (\lambda ) - \gamma \left[ K_{P} (\lambda - {\hat{\lambda }}^{*}) + K_{I}\, \zeta \right] ,\\ {\dot{\zeta }}&= \lambda - {\hat{\lambda }}^{*}. \end{aligned} \end{aligned}$$

(23)

The proposed control scheme is in the class of the slip controllers, according to the terminology in [28]. It takes important advantage from the availability of an estimate of the optimal slip. On the other side, the closed loop controllers discussed in [9] aimed to reduce pilot braking signal to avoid wheel blocking.

Considerations about the closed loop stability can be drawn by a linear approximation of the system in Eq. (23), e.g., by using the Routh criterion. In particular, it has been found that the stability is guaranteed for positive $K_{P}$ and $K_{I}$ values, which, in this work, have been set experimentally to guarantee the best performance.

The proposed closed loop scheme has been evaluated over the same set of scenarios considered in the open loop studies (see Table 2). In addition to the metrics used in the open-loop scheme, the braking time required to stop the aircraft and the traveled distance have been also evaluated. This additional information makes it possible to identify approaches that can provide a real advantage in terms of braking efficiency, especially in those scenarios where the RMSE scores are comparable.

6 Experimental results

6.1 The learning performance

The first set of experiments dealt with the evaluation of the approximation and generalization capabilities of the neural networks. Table 3 reports the RMSE scores achieved by the MLP-S and MLP-D, respectively.

Table 3 RMSE scores (dimensionless) on the synthetic dataset $\mathcal{T}\mathcal{S}$ for the Standard MLP (MLP-S) and the Dropout one (MLP-D)

For both structures, it is observed that the performance on the Test data and the Burckhardt surfaces is comparable to the performance achieved in the training phase. Because the test and the Burckhardt surfaces have been excluded in the training phase, it is reasonable to assert that both MLP structures can generalize with respect to previously “unseen” surfaces. Moreover, taking into account that a typical value for the optimal slip is $\lambda ^{*} = 0.15$, the percentage error of both NNs (with respect to the RMSE) is $19\%$ on average. As it will be clarified in the following paragraphs, this level of accuracy in the estimation is deemed satisfactory when compared with most of standard slip control schemes where the reference slip is typically kept constant to a set-point value that is selected relying on a-priori assumptions on the current airstrip characteristics.

6.2 Open loop analysis

The open loop performance of the proposed MLP-S and MLP-D estimators is discussed and compared to the Recursive Least Squares (RLS) method introduced in Sect. 4.

The RMSE between the actual and the estimated optimal slip during the entire braking operation is computed, to provide a quantitative evaluation. The comparison has been performed using the 15 validation scenarios reported in Table 2. The overall results are reported in Table 4.

In general, the MLPs achieve lower estimation errors in most of the scenarios, with only a few exceptions where the RLS score is slightly better than the neural networks. In the latter case, it is observed that several scenarios include snow surface transitions (see Fig. 5a). The reason behind such a slight MLP performance drop compared to RLS can be explained by observing that the optimal slip for the snow surface is close to zero, and that, as shown in Fig. 4, for small values of $\lambda$, all the slip curves have a very similar shape. Consequently, it is more challenging for the neural networks to handle ambiguities in these contexts. This effect is further emphasized by the measurement noise, which makes the curves nearly indistinguishable for small slip values. Nevertheless, even in those situations, the MLP performance is very close to the RLS ones.

Table 4 RMSE (dimensionless) performance of the Standard MLP (MLP-S), the Dropout one (MLP-D) and the reference RLS: open loop data

Fig. 5

Open loop braking maneuvers: time behavior of true optimal slip ${\hat{\lambda }}^*_{\text{GT}}$, Standard MLP (${\hat{\lambda }}^*_{\text {MLP-S}}$), Dropout MLP (${\hat{\lambda }}^*_{\text {MLP-D}}$) and reference ${\hat{\lambda }}^*_{\text {RLS}}$

6.2.1 Time domain analysis

The time responses of the proposed estimators are illustrated in Fig. 5. It shows the temporal evolution of the estimated best slip for the different techniques for three challenging airstrip transitions experienced by the aircraft during the braking phase. In the figures, $\lambda ^*_{\text{GT}}$ denote the true optimal slip values, while ${\hat{\lambda }}^*_{\text {MLP-S}}$, ${\hat{\lambda }}^*_{\text {MLP-D}}$ and ${\hat{\lambda }}^*_{\text {RLS}}$ are the estimated ones. Although all the estimators cannot accurately track the actual best slip during the transitions, a clear difference is observed in the performance provided by the different estimators. In fact, the MLP-based estimators show better performance compared to the RLS method, especially when airstrip surface transitions occur. The spikes affecting the MLPs estimation following a surface transition are induced by the temporary presence of spurious $(\lambda , \mu )$ pairs in the input buffer of the neural network. In fact, due to the instantaneous surface transitions, the input buffer contains samples from the two surfaces across the transitions. Therefore, the MLPs are exposed to an unforeseen situation, and they are not able to accurately discriminate between the two surfaces. Nonetheless, the estimated slip rapidly converges toward a steady value once a sufficient number of samples of the new scenario enter in the buffer. It is expected that such an effect will decrease in the case of, more realistic, smooth surface transitions.

6.2.2 Online uncertainty estimation

The previous analysis shows that, mostly during surface transitions, the estimates provided by neural networks may lose in accuracy. It would therefore be useful to online infer information about the current accuracy (reliability) of the estimate during the braking. Such an information was derived exploiting the approach described in Sect. 3.2. The following study highlights the role and usefulness of the online uncertainty estimation mechanism provided by the dropout network. Results of a representative open-loop uncertainty estimation study are shown in Fig. 6, where a fixed amplitude sinusoidal braking torque is applied under the wet airstrip scenario (for which $\lambda ^* = 0.13$). This torque shape has been selected so that the whole range of slip values $[0, \, 1]$ is explored during the braking (see Fig. 6 (lower, left)), and therefore the whole range of friction values are experienced during the simulation.

Figure 6 (upper, left) shows the collected $(\lambda , \mu )$ signals, and the normalized uncertainty provided by MLP-D. It is observed that the uncertainty is larger in the low-slip region ($\lambda \in [0, 0.08]$). This enforces the idea that since most of the airstrip surfaces in the low-slip region have similar $\mu (\lambda )$ shapes (see Fig. 4), the MLP has inherent difficulties in discriminating the correct airstrip condition. Vice-versa, for slip values around the optimal one (the maximum), the differences among the slip curves increase and, consequently, the MLP-D provides more accurate and reliable estimates and the corresponding uncertainty estimation decreases. Figure 6 (upper, right) illustrates the corresponding time-response estimate ${\hat{\lambda }}^*$ provided by the MPL-D, while Fig. 6 (lower, right) shows the corresponding uncertainty normalized with respect to ${\hat{\lambda }}^*$. When the MLP-D estimate moves away from the true optimal slip $\lambda ^*$, the normalized uncertainty increases significantly (see Fig. 6 (lower, right)) signaling that the actual friction prediction is less reliable. Notice also that in the time intervals when the predicted uncertainty is low the corresponding slip estimate is satisfactory. These latter considerations are notably interesting because they suggest that the measures of the estimation accuracy can be exploited online in a Kalman filtering framework to optimally filter the best slip estimates provided by the MLP-D network. The usefulness of such strategy will be clear in the next section on closed loop studies.

Fig. 6

Open loop experiment: a sinusoidal braking signal is applied in a wet airstrip condition. The $\lambda$, $\mu$ values are used by the Dropout Multilayer Perceptron to compute the estimated best slip ${\hat{\lambda }}^*$ and to compute the corresponding uncertainty $\sigma$

6.3 Closed loop analysis

The last set of experiments have been performed using the online best slip estimate ${\hat{\lambda }}^{*}$ as the set point for the closed loop PI controller. All the four estimation schemes have been studied, i.e., RLS, MLP-S, MLP-D and KAL (MLP-D with Kalman Filtering).

All the 15 validation scenarios have been tested. The overall results are reported in Table 5 where, in addition to the RSME, also the distance covered during braking is reported, and the corresponding temporal duration.

Table 5 Performance of proposed estimators under closed loop control schemes (GT: Real optimal set point ${\lambda }^*$; MLP-S: Standard MLP estimated setpoint; MLP-D: Dropout MLP estimated setpoint; KAL: Kalman filter estimated setpoint; RLS: reference RLS estimated setpoint)

Fig. 7

Time behavior of braking maneuvers under the PI regulator for the four slip estimators and three runway conditions (True optimal slip ${\hat{\lambda }}^*_{\text{GT}}$; Standard MLP (${\hat{\lambda }}^*_{\text {MLP-S}}$); Dropout MLP (${\hat{\lambda }}^*_{\text {MLP-D}}$); Kalman filter (${\hat{\lambda }}^*_{\text {Kalman}}$) and reference RLS ${\hat{\lambda }}^*_{\text {RLS}}$)

Concerning the RMSE performance, all the techniques show a trend similar to the open loop tests, i.e., the MLP-S and the MLP-D networks outperform the RLS in most scenarios. It is evident that the uncertainty-based Kalman Filter has a remarkably effects on the RMSE, in fact the KAL estimate outperforms the unfiltered estimates in 11 over the 15 scenarios. Generally, the use of the neural network estimators allows to improve (compared to the RLS) the efficiency of the braking in terms of the distance traveled by the aircraft before reaching a target (near zero) velocity and the corresponding braking time. This is evident in a number of scenarios. For example, in the $S\rightarrow W \rightarrow S$ case, the braking maneuver based on the RLS estimator requires up to 1318 m and 30 s to stop the aircraft while all the MLP architectures perform much better, with a contraction of the braking distance on the order of 30%. It is noteworthy that the good best slip estimates provided by the KAL scheme in all the scenarios have a direct impact on the braking distance resulting the best one in 7 over the 15 scenarios. Table 5 also reports the performance in the case the controller reference is given by the ground truth (GT) best slip $\lambda ^{*}$. In other words, it is assumed that the PI controller reference input is exactly equal to the best slip in each instant. This ideal condition is obviously not realistic, and it is only included to evaluate the loss of performance employing the proposed best slip estimators.

Figure 7 shows the temporal evolution of the best slip estimates in three braking scenarios, for the proposed approaches and for the RLS estimators, under the PI regulator. It is observed that the MLP-S, MLP-D, and KAL estimators provide lower errors than the RLS, except during the surface transitions, for the reasons explained in the previous sections. After the surface switch, the neural network estimates always converge to a new steady state value in about 1 s. It is not observed a relevant performance difference between the MLP-S and the MLP-D estimators, highlighting the fact that the dropout layers used for regularization (during the training phase) and kept active during the inference (to estimate the uncertainty) don’t affect the overall predictive performances of the MLPs (-S and -D) making them comparable. Conversely, the RLS is heavily affected by surface transitions, and, in most cases, the estimate diverges and becomes unreliable.

Fig. 8

Closed loop Experiments for the DSD (i.e., $\text {Dry}\rightarrow \text {Snow}\rightarrow \text {Dry}$) transition case. On the left side the online estimation of the Dropout MLP (MLP-D) best slip and the normalized uncertainty estimates. On the right side, the time response of the slip $\lambda$ and the friction $\mu$

Fig. 9

Closed loop Experiments for the DSW (i.e., $\text {Dry}\rightarrow \text {Snow}\rightarrow \text {Wet}$). On the left side the online estimation of the Dropout MLP (MLP-D) best slip and the normalized uncertainty estimates. On the right side, the time response of the slip $\lambda$ and the friction $\mu$

To better illustrate the role of the uncertainty estimation, a study has been performed by analyzing the temporal evolution of the uncertainty signal provided by the MLP-D estimator. For this purpose in Figs. 8 and 9 closed loop simulation results for two Multi-transition scenarios: Dry $\rightarrow$ Snow $\rightarrow$ Wet (DSW) and Dry $\rightarrow$ Snow $\rightarrow$ Dry (DSD) have been reported. In particular, Figs. 8 and  9 (left, upper) show the temporal evolution of the best slip prediction provided by the MLP-D estimator against the true values. It can be observed that the MLP-D estimator correctly tracks the actual best slip changes. At the same time, the estimated uncertainty is significantly influenced by the airstrip characteristics and by the surface switching sequence (observe that uncertainty increases significantly in case of transitions from high to low friction surfaces). This aspect is further confirmed by the $\lambda$ and $\mu$ time evolution shown in the same figure: when a transition toward a lower friction surface occurs, the applied braking force induces a sudden increase of the slip (thus causing a shift toward the right region of the Burckhardt surfaces). The sequence of $(\lambda , \, \mu )$ pairs experienced during the transition phase produces input vectors that differ significantly from those used for training; nevertheless, such a pattern contains enough information to quickly infer the new airstrip surface. Conversely, the transition to higher friction surfaces seems to be less critical due to the absence of uncertainty spikes following the transition.

A significant difference is observed in the KAL case compared to the MLP-S and MLP-D estimators, as (thanks to the uncertainty-based filtering) the KAL estimate effectively smoothes the peaks observed in the unfiltered cases. In fact, during the transients, the MLP-D best estimation accuracy decrease: this directly affects the current value of the measurement variance R employed within the Kalman Filter. As a result, during transients, the contribution of the innovation signal to the output of the KF is significantly reduced as long as the variance R remains large. This results in a slower but more reliable estimation of the best slip.

Figure 10 shows two different scenarios in which the transitions occur to lower (high to low) and combined (medium–high–medium) friction surfaces: $\text {Dry}\rightarrow \text {Wet}\rightarrow \text {Snow}$, and $\text {Wet}\rightarrow \text {Dry}\rightarrow \text {Wet}$. It is possible to notice how the KAL scheme generate estimates avoiding transition spikes that affect the MLPs schemes instead.

Fig. 10

Closed loop experiments for the DWS (i.e., $\text {Dry}\rightarrow \text {Wet}\rightarrow \text {Snow}$) (left) and WDW (i.e., $\text {Wet}\rightarrow \text {Dry}\rightarrow \text {Wet}$) (right) cases, using as setpoint the real best slip (${\hat{\lambda }}^*_{\text{GT}}$), the Dropout MLP (${\hat{\lambda }}^*_{\text {MLP-D}}$) estimate and the Kalman filtered estimate (${\hat{\lambda }}^*_{\text {Kalman}}$). On the upper panel the slip values and the uncertainty estimates on the lower ones

7 Conclusions

This work proposes a novel robust data-driven strategy to infer online the airstrip characteristics for a landing aircraft on an unknown surface in order to perform an efficient braking control. The approach exploits MLP neural network architectures to reconstruct the airstrip characteristics by processing a sequence of measured slip-friction pairs compoundable from available sensor measurements. In order to produce a robust prediction, a MLP neural network based on the stochastic weights drop-out mechanism has been proposed not only in the offline training phase but also during the online braking. This last modification makes available online a confidence interval for the best friction coefficient estimate. This information has been exploited to further refine the best slip estimate by filtering it via a Kalman filter whose measurement covariance is made proportional to the estimated confidence interval provided by the drop-out MLP. Open loop experiments have shown that the KAL architecture is effective in estimating the region of the $(\lambda , \, \mu )$ plane where the epistemic uncertainty produced by MLP approximators is large and the online prediction is not fully reliable requiring additional filtering to improve the accuracy, especially during transients. Closed loop simulations have confirmed that the KAL architecture performs significantly better than the MLP-D and MLP-S architectures in terms of RMSE, aircraft braking distance, and braking time for 15 test scenarios. The study has also shown that the proposed MLP-based schemes outperform a RLS state-of-the-art approach to estimate the airstrip characteristics. In conclusion, although the optimal slip estimates may not be very accurate in some cases, this is undoubtedly better than control schemes based on the RLS estimator or widespread schemes where the optimal slip coefficient is fixed to a constant value for all the airstrip surfaces. Future work will analyze other structures of neural networks. In particular, Recurrent Neural Network will be considered to better model temporal dependencies. In addition, NN models with reduced complexity will also be considered to meet the constraints of real systems with limited computational resources.