1 Introduction

Nowadays, the development of new technologies and computing systems gives humans the ability to collect large amounts of data. The more data we have on a system, the better representation we obtain of it, and this will give us greater capacity to extract information and describe it [1]. The problem arises when, in real-world applications, the amount of data needed is too large. For instance, in banking applications, where there are millions of clients, with many different behaviors and operations, the computational resources needed are unaffordable [2]. In this paper, the results for a bank with more than 2 million customers will be presented.

One of the most thrilling problems in the banking sector is the classification of customers to detect unusual behaviors. The k-nearest neighbors (k-NN) technique is widely used for recognition tasks. It consists of obtaining a representative dataset formed by prototypes for which the classes are known. When new data are fed to the algorithm, the class corresponding to its k nearest neighbors is assigned within the prototype space. It is one of the most useful algorithms in data mining, but it has the drawbacks of high storage requirements, low efficiency, and low noise tolerance, especially in the case of 1-NN, since it gives importance to all data [3]. One way to improve the performance of the k-NN classifier is to use data reduction techniques, more specifically, prototype reduction, which can be achieved by either prototype selection or generation.

Prototype selection consists of choosing some representative instances from the dataset to use them as prototypes. The objective is to obtain a training set of smaller size than the original one, but with the same characteristics, achieving similar or higher classification accuracy for new data [3]. On the other hand, prototype generation consists of creating new training data that represent the previous one with the same objective as prototype selection.

The self-organizing map, also called Kohonen map after the first person who described it as a neural network, is an unsupervised method that organizes data and also provides a low-dimensional representation employing competitive learning [4,5,6,7]. This algorithm consists of a non-linear, ordered, and smooth assignation of high-dimensional input data to a low-dimensional matrix–typically 2D—by assigning weights to each node of its topology. Since a SOM organizes the data in groups, it allows for a better understanding of the input space and is very useful in applications like data mining or pattern recognition. A SOM can be understood in two different ways: considering the output as the low-dimensional map gives a dimensional reduction and can be used as a clustering technique; considering the output as the weights gives a data reduction in which each weight conforms a new prototype. A drawback of the SOMs is that the number of neurons must be pre-specified before the training phase. A low number of nodes leads to general information and a relatively straightforward explanation of the data, whereas more nodes allow for more detailed information. The growing self-organizing map (GSOM) addresses this issue by creating new neurons during the training process so that it can adapt its structure [8]. This, along with a high reduction in training times [9], is a great advantage over the SOM. This work addresses the problem of data reduction for k-NN using a GSOM.

The main contribution of this work is the implementation of a GSOM for prototype generation in large datasets. To the best of the authors’ knowledge, this is a novel approach for prototype generation that has not been previously published. The main objective of the work is to reduce the number of instances in large datasets without compromising the accuracy. Moreover, a real dataset with 350000 clients was used. The GSOM is applied over the Census Income dataset and a bank dataset to obtain a representative space of the data used afterward in a 1-NN classification problem. This way, it is easier to distinguish patterns of behavior in clients and make predictions. The advantages of this method are the decrease in time needed to apply the 1-NN algorithm and the use of a machine learning technique that allows a visual understanding of the problem. To enhance the adaptation of the network, we have added the use of several iterations of the algorithm in each of its phases. This aspect is pre-selected.

This document organizes as follows. Section two provides a literature review and discusses some related work. In section three, the proposed methodology is defined and the techniques are described, as well as the evaluation and visualization metrics. The experimental setup is outlined in section four, showing the results obtained for two different datasets. Next, a discussion is provided in section five and, finally, section six extracts some conclusions from the work.

2 Literature overview

2.1 k-nearest neighbors

The k-NN classifier is an algorithm that assigns a class to an input vector based on the classes of the k nearest prototypes in the input space. It is a well-known technique used in many different applications. For example, Konieczny and Stojek [10] use a k-NN classifier to classify the wear condition of a pump, Santos Ruiz et al. [11] apply the k-NN algorithm to locate leaks in water distribution networks and Tharwat et al. [12] classify human activities with information from smart devices.

Despite their wide use and ease of application, k-NN classifiers have low efficiency, low noise tolerance, and high data storage requirements. To overcome these problems, there are different approaches [13]. Some of them are based on modifying the parameters and equations of the k-NN, for example, by selecting the optimal value of k [14] or doing it adaptively [15], combining with genetic algorithms in the selection of neighbors [16], designing distance functions [17] or using frameworks prepared for big data applications [18]. Other techniques include reducing the number of prototypes, either by prototype selection or by prototype generation.

2.2 Prototype reduction

There are many approaches to prototype selection. Rosero-Montalvo et al. [19] present an analysis of neighborhood criterion using the condensed neighbor algorithm to eliminate redundant data. The work by Suyal and Singh [20] approaches the problem of prototype selection by using multi-label k-NN. Gurumoorthy et al. [21] propose a framework for prototype selection based on optimal transport and compare it with other methods evaluating it with a 1-NN classifier on several datasets. The study by Kasemtaweechok and Suwannik [22] proposes a technique based on geometric median and compares it with different methods that show high accuracy with low times.

Prototype generation, on the other hand, also has various applications in literature. Triguero et al. [23] classify and compare different types of prototype generation algorithms applied to k-NN classifiers. Ougiaroglou et al. [24] use an algorithm based on reduction through homogeneous clustering for multilabel k-NN classification. Elkano et al. [25] propose the use of a new distributed MapReduce method called CHI-PG for big data classification problems. Few works in the literature address the problem of prototype reduction by using a SOM. For instance, Lechevallier and Ciampi [26] integrate a SOM with other clustering methods and apply it to nutritional data and, with regard to financial applications, Sarlin and Peltonen [27] use a SOM for data and dimensionality reduction to monitor vulnerabilities and map the state of financial stability.

2.3 Self-organizing maps

The SOM and all its variations have great potential in applications where it is necessary to analyze great amounts of data, and it becomes extremely expensive computationally. For that reason, it can be used in many preprocessing tasks in areas such as data mining: data and dimensionality reduction, master and multiple curves approximation, clustering, and classification. Self-organizing maps have also been widely used in cybersecurity since ten years after the appearance of the algorithm [28]. Ichimura et al. [29] use a SOM and automatically defined groups to obtain the distribution of spam email and classification that would serve to adjust email filtering. Sarkar et al. [30] use a k-means algorithm combined with SOM to extract patterns in accidents at work. Christyawan et al. [31] propose the use of a type of GSOM with a clustering reference vector for an intrusion detection system. Since the 1990 s, SOMs have been used in financial applications [32]. Regarding performance analysis, Shanmuganathan [33] states that the SOM is a useful tool to examine the returns and measures implemented in financial sectors. Concerning financial crisis monitoring, López Iturriaga and Pastor Sanz [34] use neural networks based on SOMs to compare macroeconomic imbalances in European countries. In these fields, SOMs allow a visual representation of the data and their relationship, which leads to a better understanding of its triggering factors. Barman and Chowdhury [35] use a SOM and a minimum spanning tree for customer segmentation. In the field of fraud detection, Quah and Sriganesh [36] analyze the behavior of credit card customers in real time to find hidden patterns without the need for previous information, and Balasupramanian et al. [37] propose a fraud detection and prevention method that uses a SOM to detect patterns. Ganegedara and Alahakoon [38] address the use of parallel GSOM and propose a method to reduce redundant neurons. Studies like the work by Kuo et al. [39] prove that GSOMs perform computationally better than SOMs, in this case, combined with bee colony optimization.

3 Techniques applied

The outline of this work is presented in figure 1. The first step is to train the neural network with a three-phase process [9] over a training set of data. After that, different error measures are calculated, as well as the U-matrix, which allows a visual explanation of the relationships between neurons. Finally, we use the GSOM as prototypes for a one-neighbor k-NN in order to classify the clients and assess the neural network’s capacity to represent the input space.

Fig. 1
figure 1

General schema of the work, with the data reduction stage marked in green and the classification stage marked in yellow

Full size image

3.1 GSOM

This subsection aims to describe the GSOM and the metrics used in this paper to evaluate it. The general idea of a self-organizing map consists of a network with a given topology that adapts the weights of its nodes as it receives input data without losing topological properties. A neighborhood accomplishes the adaptation of the weights to the net so that the arrival of new data during the training process will lead to a major adaptation in those neurons whose weights are closer to these data. A two-classes dataset with 700 vectors is used for exemplification purposes, obtaining a GSOM with 88 nodes.

The growing self-organizing map includes the possibility of automatically modifying the size of the network, which allows the use of the number of neurons necessary for each application without the need for it to be fixed beforehand.

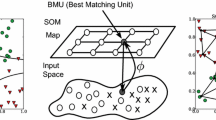
The GSOM training process is as follows [9]. Initially, there is a small net, generally composed of four nodes or neurons, each with a weight vector of the same size as the input data that will fit in the input space. In SOMs and GSOMs, as new data arrive, the neuron with the greatest activation–this is generally calculated as the lowest Euclidean distance between the weights and the input data–will be elected as the winner (best matching unit or BMU), as shown in Fig. 2. With a decreasing learning rate, this weight vector will be modified to resemble the input data. This learning rate can be linear, potential, or inverse time. Similarly, the nearest nodes to the BMU weights will adapt too by a space-time neighborhood function–the most common is the Gaussian function. The adaptation is usually expressed as:

$$\begin{aligned} w_j(k+1) = w_j(k) + {LR(k)} \epsilon (k)\left( v(k) - w_j(k) \right) \end{aligned}$$
(1)

where k denotes the current learning epoch, j is the node, LR(k) is the learning rate, \(\epsilon (k)\) is the neighborhood, and v(k) represents each element of the input data. This learning procedure leads to an ordered topological mapping of the represented input data.

Fig. 2
figure 2

Scheme of the training process of a SOM. For each input vector, the BMU is selected and the SOM weights are adapted

Full size image

The learning rate LR is calculated from the following equation, where \(\alpha\) and R are parameters that must be pre-selected and n(k) is the number of nodes.

$$\begin{aligned} LR(k) = LR (k-1) \cdot \alpha \cdot \left( 1 - \frac{R}{n(k)}\right) \end{aligned}$$
(2)

In a GSOM [40], it is required to keep track of the accumulated error so that when a given threshold is reached, it will be necessary to expand the number of nodes. The growth of the map GT is controlled by the spread factor SF as given by the following equation, where D is the dimension of the data.

$$\begin{aligned} GT = - D \cdot ln({SF}) \end{aligned}$$
(3)

As the network receives new data, the maximum error of the nodes is calculated. If it reaches GT, new nodes will be added around the winner. When a node not belonging to the frontier is selected for growing, the error of its neighbors increases by the distribution factor FD, as in Eq. 5, with the computation of the BMU given by Eq. 4.

$$\begin{aligned} BMU(k)= & {} \arg \min _j{||v(k)-w_j(k) ||,\;\;\;\; j = 1,...,n(k)} \end{aligned}$$
(4)
$$\begin{aligned} E= & {} \left\{ \begin{matrix} GT /2 &{} \text{ if } &{} \text{ node } \text{ is } \text{ BMU } \\ E(1+FD) &{} \text{ if } &{} \text{ node } \text{ is } \text{ neighbor } \text{ of } \text{ BMU } \end{matrix}\right. \end{aligned}$$
(5)

The neighborhood function is given by Eq. 6, where \(d_t\) is the topological distance between each neuron j and the winner BMU, and \(\sigma\) represents the selection of neighbors and decreases each epoch a given value \(\Delta \sigma\).

$$\begin{aligned} \epsilon = e(k)^{-\frac{d_t(j,BMU(k))}{2\sigma ^2}} \end{aligned}$$
(6)

For a major control over the neighborhood, we added the possibility of selecting the value of \(\sigma\) with a certain number of iterations. The decrease \(\Delta \sigma\) is generally selected directly, but this is not as intuitive when it comes to parameter tuning. This work will fix it through the number of iterations in each phase of the algorithm so that the increment will be equal to an initial value of \(\sigma\) minus a minimum value divided by the number of total iterations N.

$$\begin{aligned} \Delta \sigma = \frac{\sigma _{ini}-\sigma _{min}}{N} \end{aligned}$$
(7)

This process is accomplished in three phases: initialization, growing and smooth. The last one consists of refining the weights of the nodes once the net has reached its definite size. This is detailed in algorithm 1 [9].

Several tests with different network topologies (squared and hexagonal) have been conducted. In squared networks, a neuron can have up to four neighbors, while the number of neighbors may reach six in the hexagonal topologies. Thus, when new nodes are added to the net, the growth will be more intense in the case of hexagonal topologies.

figure a

3.1.1 U-matrix

The U-matrix (Unified Distance Matrix) is a bidimensional representation of the neurons in the input space to visualize the distances between them. The mean distance between the weight vector and its neighbors is calculated for each neuron, and a color is associated. The nodes whose colors correspond to lower values will have more similar weights [41].

The self-organizing maps allow a bidimensional representation of the data space that will be able to be visualized through the U-matrix. This work employs a GSOM representation with a U-matrix intending to facilitate its comprehension and favor the following analysis process.

3.1.2 Evaluation

Three tools have been employed to compare the performance of the various networks obtained: standard deviation, quantification error, and simplicity. The first one (stdNodes, in Eq. 8) collects the mean standard deviation of the distances between the input data and the associated BMUs. The quantification error or heterogeneity (quantE, in Eq. 9) provides a measure of the adjustment of neurons to training vectors using the mean of the distances to the corresponding winning node [42]. Simplicity [43], in Eq. 10, is the accumulated neighborhood distance. It measures the network expansion and collects the sum of the distance between the BMUs and their neighbors. Also, the percentage of prototype reduction will be computed.

$$\begin{aligned} stdNodes = \frac{1}{n(N)} \sum _{j=1}^{n(N)} { s_{X(j)}(||w_j(N) - v(N) ||)} \end{aligned}$$
(8)

with s the standard deviation and \(X(j) = \lbrace x: j = BMU(x) \rbrace\)

$$\begin{aligned} quantE= & {} \frac{1}{N_p} \sum _{i=1}^{N_p}{||v(i) - w_{BMU(v(i))}||} \end{aligned}$$
(9)
$$\begin{aligned} simplicity= & {} \sum _{i: X(i)\ne \emptyset }{\sum _{j: j\; neighbor\; of\; i}{||w_i-w_j||} } \end{aligned}$$
(10)

3.1.3 Illustrative examples

GSOM alone can be used for classification and generation of new neurons presenting the initial topology. To validate the proposed methodology and visually check the adaptation of the net, two preliminary experiments are presented. The GSOM features shown in the examples (ring and letter G) will be exploited as a prototype generation method for a k-NN classifier in the results section.

The use of the U-matrix for classification is exemplified in Figs. 3 and 4. They show, respectively, the weight vectors and U-matrix of a GSOM applied to a 700 vectors dataset with two features (x,y) in which two classes (z-axis) are distinguished. Neurons with blue tones are associated with minor distances to neighboring nodes, and reddish tones associate with major distances. The U-matrix allows one to visually distinguish both classes, since orange neurons constitute a frontier between them.

Fig. 3
figure 3

Ring with two classes, where the red and green dots differentiate both of them

Full size image
Fig. 4
figure 4

U-matrix of a GSOM applied to the dataset with ring shape

Full size image

The second example was conducted on a set of tridimensional data distributed in the space and forming a figure. The dataset is conformed by points randomly scattered building a letter G. It has been divided into three subsets (s1, s2 and s3) that contain 1000, 10000 and 20000 data, respectively. The variables are x, y and z. This example shows the advantages of GSOMs since they can generate the number of nodes necessary to adapt to datasets of different sizes without the need to know it beforehand. Not necessarily a set with more data must be represented with a larger map.

Table 1 shows the parameters used for training the different GSOMs. Id is the GSOM identifier (which starts with the subset identifier x, meaning 1, 2 or 3), type is the shape of the net (GRID means squared network and HEX means hexagonal network), \(LR_{ini}^g\) is the initial learning rate in the growth phase and \(LR_{ini}^s\) is the initial learning rate in the smooth phase. In all cases, it has been used an initial network of four nodes, a spread factor \(SF=0.5\), a distribution factor \(FD=0.1\), a value of \(R=3.8\), [9], and initial and final \(\sigma\) values of 1 y 0.1, respectively. Some of the GSOMs have been trained setting \(\Delta \sigma\) and others fixing the number of iterations in each phase.

Table 1 Training parameters for each letter G GSOM, where sx indicates subsets 1, 2 or 3
Full size table

The final numbers of neurons and error measures are collected in Table 2, where Neurons indicate the final size of the GSOM (which is the result of the data reduction) and Reduction is the reduction rate = (1 - number of samples in the reduced set /number of samples in the original set)\(\cdot\) 100. Figure 5 shows the weight vectors of the GSOMs \(s1\_2\), \(s2\_2\) and \(s3\_2\) in the input space. The results show similar adaptations of the GSOMs independently of the number of inputs, and the reduction increases with the size of the input dataset. The values of quantE, stdNodes and simplicity differ, as they depend on the amount of input data, but the variation between subsets is low. More detailed visualizations of the adaptability of growing self-organizing networks are made by [44].

Table 2 Results obtained for each GSOM of the letter G
Full size table
Fig. 5
figure 5

Weight vectors of the GSOMs applied to the three different subsets of the letter G

Full size image

3.2 k-NN

Finally, the k-nearest neighbor algorithm for classification [45] is used, which assigns a class for each input vector based on the class of the k closest prototypes in the space. Initially, a set of labeled prototypes is required. These are vectors that represent the data the best as possible to obtain good classifications. A set of prototypes could be a real dataset, but this will carry a great computational cost. It is essential to use a helpful dataset, given that poorly balanced sets will falsify predictions. If the real data and the prototypes contain a very different proportion of positives, the assignments will not be correct. The weight vectors of the GSOM will be used as prototypes for the classifier.

3.2.1 Evaluation

To measure the performance of the binary classifier [45], three different ratios that take into account the number of true positives (TP), true negatives (TN), false positives (FP) and false negatives (FN) are used:

  • Average accuracy (ACC): the hit rate.

    $$\begin{aligned} ACC = \frac{TP + TN}{TP + TN + FP + FN} \end{aligned}$$
    (11)

  • Sensitivity (SEN) or recall: the rate of properly detected defaults.

    $$\begin{aligned} SEN = \frac{TP}{TP + FN} \end{aligned}$$
    (12)

  • False Positive rate (FPR): the rate or improperly detected defaults.

    $$\begin{aligned} FPR = \frac{FP}{FP + TN} \end{aligned}$$
    (13)

  • Balanced accuracy (BA): the mean between the sensitivity and the true negative rate, which is 1 - FPR.

    $$\begin{aligned} BA = 1 - \frac{1}{2} \left( \frac{TP}{TP+FN} + \frac{TN}{TN+FP} \right) \end{aligned}$$
    (14)

  • Precision (PRE): the rate of true positives over all predicted as positive classes.

    $$\begin{aligned} PRE = \frac{TP}{TP+FP} \end{aligned}$$
    (15)

  • F1-score (F1): the harmonic mean of precision and sensitivity.

    $$\begin{aligned} F1 = 2\frac{PRE\cdot SEN}{PRE + SEN} \end{aligned}$$
    (16)

  • Cohen’s Kappa: a measure of the agreement between the actual and predicted classes that compensates for the effect of randomness.

    $$\begin{aligned} \kappa= & {} \frac{P_o - P_e}{1 - P_e}, where \nonumber \\{} & {} \left\{ \begin{array}{c} P_o =\frac{TP+TN}{TP+TN+FP+FN} \\ P_e = \frac{(TP+FP)\cdot (TP+FN)}{(TP+TN+FP+FN)^2} + \frac{(TN+FN)\cdot (TN+FP)}{(TP+TN+FP+FN)^2} \end{array}\right. \end{aligned}$$
    (17)

4 Application results

This section shows the different tests carried out in two datasets to observe the adaptation of the GSOMs to the input space. These datasets correspond to an annual income register and bank records. A 1-NN classifier has been applied to obtain predictions using the GSOMs as prototypes. All neural networks have been trained using Intel®  Xeon®  CPU E3-1220 v6 at 3.00GHz and 48 GB DDR3.

4.1 Census income results

In this work, different experiments were carried out using the Census Income dataset, also known as the Adult dataset, from the UCI Machine Learning Repository [46]. Its use is intended for the classification between two types of incomes to predict whether a given person makes more than $50000 a year based on attributes such as age, sex, education, marital status, etc. It contains 48842 instances of multivariable data with 14 attributes with categorical and integer variables. The last variable corresponds to the output of the dataset, which represents the classification, meaning 1 a positive value and 0 otherwise. These data are divided into two sets. After a preprocessing step by joining the data and eliminating incomplete instances, a dataset of 45222 instances is obtained. As the original data are unbalanced, a balanced subset of 22416 instances with 50% of each class is created. Both were divided into training sets of 80% (36177 instances for the unbalanced data and 17933 for the balanced data) and a test set of 20% (9045 unbalanced instances and 4483 balanced). As a baseline, the case without data reduction in the unbalanced dataset is used. The results on the test set are as follows: accuracy of 79.67%, sensitivity of 58.95%, false positive ratio of 13.56%, F1-score of 58.83% and Cohen’s Kappa of 45.33%.

4.1.1 GSOM and k-NN performance

Many experiments have been conducted on this dataset modifying the training parameters and the network topology, defined by the size–It is automatically obtained from the GSOM. Table 3 contains the parameters of the different GSOMs applied to the Census Income dataset, either the unbalanced data (GSOMs 1 to 10) and the balanced data (GSOMs 11 to 20). The same parameters have been used for each type of dataset to compare the results. Id is the GSOM identifier and \(LR_{ini}^g\) and \(LR_{ini}^s\) are the initial learning rates in growth and smooth phases. In every GSOM, it has been employed a spread factor \(SF=0.5\), a factor of distribution \(FD=0.1\), a value of \(R=3.8\), [9], and initial and final \(\sigma\) values of 1 and 0.1, respectively.

Table 3 Training parameters for each GSOM applied to Census Income dataset
Full size table

Before training the GSOMs, several SOMs have been trained to compare them with the GSOMs and validate the method. Each SOM was trained with 75 iteration steps, and a hexagonal topology. Four grid sizes were tested: 10 nodes \(\times\) 10 nodes, 15 nodes \(\times\) 15 nodes, 20 nodes \(\times\) 20 nodes and 25 nodes \(\times\) 25 nodes. The error measures are gathered in Tables 4 and 5. The time to train each model was recorded in the "Tr. time" column. As the SOM maps the space obtaining non-binary variables, the output was binarized, assigning to each neuron the mode output of the training vectors for which it is the BMU. Both datasets produce similar measures, although the training times are significantly lower using the balanced dataset.

Table 4 Training results for each SOM with the unbalanced CI dataset
Full size table
Table 5 Training results for each SOM with the balanced CI dataset
Full size table

The error measures and training times for each GSOM are listed in Table 6 for the unbalanced data and 7 for the balanced data. As well as with the SOMs, the training times are lower with the balanced dataset, and the rest of the measures are of the same order. However, the values of simplicity vary significantly from one experiment to other. In general, for models of the same size, GSOMs require much less training time than SOMs.

Table 6 Training results for each GSOM applied to the Census Income Dataset with unbalanced training set
Full size table
Table 7 Training results for each GSOM applied to the Census Income dataset with balanced straining set
Full size table

The accuracy, sensitivity, and false positives rates calculated after applying the 1-NN classifier are listed in Tables 8 and 9 for the SOMs, and 10 and 11 for the GSOMs. The models with the unbalanced dataset have slightly higher accuracy, but lower sensitivity compared to the ones with the balanced dataset. Moreover, the increase in sensitivity is more significant with GSOMs.

Table 8 Results obtained for each SOM+1-NN applied to Census Income dataset with unbalanced data, expressed in %
Full size table
Table 9 Results obtained for each SOM+1-NN applied to Census Income dataset with balanced data, expressed in %
Full size table
Table 10 Results obtained for each GSOM+1-NN applied to Census Income dataset with unbalanced data, expressed in %
Full size table
Table 11 Results obtained for each GSOM+1-NN applied to the Census Income dataset with balanced data, expressed in %
Full size table
Fig. 6
figure 6

Accuracy against data reduction percentage for the GSOMs of the Census Income dataset

Full size image

The results from both the unbalanced and balanced data have values of quantE, stdNodes, and reduction that are similar, indicating that the networks are equally adapted to the input data and near the BMUs. Nevertheless, the similarity values are lower for the balanced data, indicating that the models are less spread out. Although the reduction is similar in most cases, as shown in Fig. 6, the balanced dataset was smaller, so it provides GSOMs with fewer nodes, obtaining better training times. With unbalanced data, the accuracy is higher than with the balanced data, but the false positive rate is higher too, and the sensitivity is lower. Compared to the baseline accuracies, better results are obtained: with accuracies in the test subset over 80% for GSOMs 6, 7, 10 and 14. Figure 7 gathers the mean reductions, accuracies, balanced accuracies, F1-scores, Cohen’s Kappa values and inverse of training times for the five best experiments in the test set. This graph allows associating the best models with larger areas covered by their corresponding polygon, which highlights the superior performance of the GSOMs on the balanced dataset compared to the other models.

Fig. 7
figure 7

Mean reductions, accuracies, balanced accuracies, F1-scores, Cohen’s Kappa values and inverse of training times for the Census Income dataset

Full size image

To obtain a better understanding of the results, the U-matrix and an output map of GSOM 16 have been plotted in Fig. 8. The U-matrix helps to distinguish the zones where the neurons are more similar, displaying clustering capabilities, while the output map prints a color associated to the classification value (or output) of each neuron. Given that the GSOM is adapted, its values need to be binarized, considering that values closer to 1 correspond to positive classifications. Bluer neurons in the U-matrix relate to homogeneous zones in the output map and red colors in the U-matrix correspond to zones with more color variety in the output map. With GSOM 16, a reasonably expanded network is obtained, and it is possible to distinguish clearly two great areas in the U-matrix, implying that there are two types of people in the dataset. By further analysis, even three or four groups could be identified.

Fig. 8
figure 8

U-matrix and Output visualizations of the GSOM_CI 16

Full size image

4.2 Bank data results

Different GSOMs have been implemented in GAMCO’s ARM (Advanced Risk Management) solutions using bank clients datasets. Starting from an initial network of four nodes, the GSOMs have been trained to sample the data. The aim is to obtain a small set of prototypes for a 1-NN classifier. It also provides a low-dimensional representation of them that allows faster analysis and easier comprehension at a human level. The weight vectors of the GSOM are clusters that constitute a new dataset themselves. They can be subsequently combined with further analysis and classification algorithms such as k-NN. The dataset used is too large, so it is not feasible to apply a k-NN classifier without first applying a prototype reduction method. Therefore, a comparison between SOM+k-NN and GSOM+k-NN has been performed.

The dataset corresponds to different anonymous clients of a bank, and the objective is to determine well in advance when a customer is going to default. The total client portfolio is made up of around 2 million clients, and their data is obtained from four different sources: customers, bank transactions, contracts, and defaults. There are approximately 2.5 billion transactions and 500 million hires. Three-year historical data were used to build the training data, looking for examples of customer defaults and payment cases with different previous histories. Table 12 shows a summary of the type of data used.

Table 12 Brief description of the data used in ARM
Full size table

To obtain the dataset, every month, more than 7 million bank customers were processed and more than 1.6 million customers were evaluated by the models. The steps to verify to obtain the customers to be evaluated by the model are as follows:

  1. 1.

    Customers associated with any loan contract (asset).

  2. 2.

    The customer must be the holder of at least one contract of both assets and deposits.

  3. 3.

    Any loan contract was still in vigor.

  4. 4.

    With a contract that did not have a grace period on the date of evaluation of the client’s risk by the model.

  5. 5.

    With no incidences in the credit payments (they are healthy clients).

  6. 6.

    They have some movement in their bank accounts.

On the other hand, for the training of the models, sets of input/output vectors had to be created, each vector corresponding to the features of a customer. These feature vectors are divided into three sets of input/output vectors: training, validation, and test. For this purpose, we worked primarily with the following information sources or datasets:

  • Customers: 7 million records.

  • Transactions: more than 2.9 billion transactions.

  • Contracts: more than 6.5 million loan contracts and 494 million contracts for other products.

  • Incidents: more than 14.3 million defaults.

A very important and costly step is the labeling of the vectors corresponding to a client and a date, that is to say, to mark if that client will default or not at a given time from a date. For example, customers on day d will be labeled as unpaid, if on \(d+180\) they will have a default of more than 30 days on any of their receivables. These vectors will be used to create models that detect defaults of more than 30 days and 180 days before a given date. In the sets of input and output vectors, great care was taken to include customers with the following characteristics, thus achieving to have feature vectors of the different typologies of customers in terms of defaults on a specific historical date, in which the feature vector is labeled:

  • Customers with no defaults

  • Customers who have defaults prior to the date on which it is labeled, but no subsequent defaults.

  • Customers who have defaults after the date on which it is labeled.

  • Customers who have defaults on the date being labeled (in the example above: 180 days after the date being labeled are at least 30 days late on any of their loans).

  • Customers who have not defaulted, but who have had and will have defaults (beyond the 180 days that serves as an example).

Finally, a balanced dataset was built (same number of payments as of defaults) with more than 350,000 clients and is divided into a training set of 284259 clients (\(75\%\)), a validation set of 56852 (\(15\%\)) clients and a test set of 37900 clients (\(10\%\)). The vectors contain 125 features of the individuals and their bank records. One of the variables corresponds to the output, which indicates if the client has committed default.

4.2.1 GSOM and k-NN performance

Table 13 contains the parameters used for training the different GSOMs implemented. The GSOM is expected to obtain similar results to those achieved with a SOM in a much shorter time. To verify it, several SOMs have been trained with different topologies. Tables 14 and 16 collect the results of best SOMs obtained for four different topologies (squared of 20 nodes \(\times\) 20 nodes for SOM 1, hexagonal of 23 nodes \(\times\) 23 nodes for SOM 2, hexagonal of 25 nodes \(\times\) 25 nodes for SOM 3 and hexagonal of 27 nodes \(\times\) 27 nodes for SOM 4). Each of the selected SOMs was trained using 75 iteration steps, which were necessary to obtain good results. The training times are around 3 and 4 h, and the accuracies in the test set are all over 70%. Only one of the false positive rates is lower than 20%.

Table 13 Training parameters for each GSOM with the bank dataset
Full size table

The error measures described in Sect. 3 have been calculated, as well as the definite number of neurons and the training duration in hours for each one of the GSOMs implemented. The results are gathered in Table 15. The most significant reductions are in GSOMs 1, 3 and 4, which had only 10 growth iterations, a squared topology and an initial growth learning rate of 0.5. The GSOM with a lower initial growth learning rate obtains the lowest stdNodes and QuantE values, and also one of the lowest simplicities. It should be mentioned that GSOM 1 is comparable to SOM 1, GSOM 7 to SOM 2, SGOM 9 to SOM 3 and GSOM 10 to SOM 4, with higher simplicities and much shorter training times.

Table 14 Training results for each SOM with the bank dataset
Full size table
Table 15 Training results for each GSOM with the bank dataset
Full size table

After applying 1-NN to the GSOMs to classify the clients in default (positive output) versus payment (negative output), the number of true and false positives and negatives have been obtained. Those numbers serve to obtain the previously mentioned performance ratios: Accuracy (hit rate), Sensitivity (correctly detected defaults) and False Positive rate (improperly detected defaults). These have been calculated and presented in Table 17. The accuracies in the test set are above 70% in most GSOMs, with 74.7% in the case of GSOM 5. The false positives only exceed 20% in GSOMs 1 and 6.

Table 16 Performance of each SOM+1-NN, expressed in % with the bank dataset
Full size table
Table 17 Performance of each GSOM+1-NN, expressed in % with the bank dataset
Full size table

The obtained accuracies are represented over the reduction percentages of all GSOMs in Fig. 9. The highest accuracy is associated with a low reduction percentage, although the highest reduction also obtains a high accuracy in the test subset.

Fig. 9
figure 9

Accuracy against data reduction percentage for the GSOMs of the bank dataset

Full size image

The average results of the best five experiments of each type are collected in Fig. 10, including mean reductions, accuracies, balanced accuracies, F1-scores, Cohen’s Kappa values, and inverse of training times. The mean Kappa values, F1-scores, balanced accuracies, and reductions are similar between the SOMs and the GSOMs, however, the GSOMs tend to provide slightly higher accuracies and take much less training time.

Fig. 10
figure 10

Mean reductions, accuracies, balanced accuracies, F1-scores, Cohen’s Kappa values and inverse of training times of each experiment for the bank dataset

Full size image

Figure 11-left shows the adaptation of the GSOM 3 (with squared topology) to the input space in different features chosen randomly–feature 4 is related to the customer client, feature 8 refers to monthly charges, feature 21 relates to payments and feature 30 takes account of daily balances. The data output is the class, which indicates if the client has committed payment (0) or default (1). After a discretization process, the arrangement of the GSOM is shown in Fig. 12-left. For a better visualization of the performance using a GSOM of different topology, the weight vectors of the GSOM 9 and their adaptation to the input space are represented in Figs. 11-right and 12-right. This map has a hexagonal topology and has been trained using the same parameters as for the GSOM 3. As previously mentioned, hexagonal topologies have faster growth. The expansion of the GSOM can be perceived, as well as its adaptation to the training data, providing more prototypes in the zones with higher data density. At first sight, there is not a huge difference in the adaptability of the two topologies used.

Fig. 11
figure 11

Representation of features 21 and 30 with the bank dataset

Full size image
Fig. 12
figure 12

Representation of features 4, 8 and the class with the bank dataset

Full size image

As well as for the Census Income case, the U-matrices and output maps have been represented in Figs. 13 and 14 to obtain a visual explanation of the mapping made by the GSOMs and the subsequent classifications carried out by the 1-NN classifiers. Higher values in the U-matrix relate to more variability in the output map. Two main groups can be distinguished for GSOM 3, whereas in GSOM 9 the visual explanation is not straightforward.

Fig. 13
figure 13

U-matrix and Output visualizations of the GSOM 3 with the bank dataset

Full size image
Fig. 14
figure 14

U-matrix and Output visualizations of the GSOM 9 with the bank dataset

Full size image

The GSOMs have lower training times than the SOMs and, although the accuracies are lower in most cases, the false positive rates are lower too, giving similar balanced accuracies. Better evaluations are related to a combination of high sensitivity and low false positive rate, instead of only taking into account the accuracy. For comparing better the results, the sensitivity (SEN) and false positive rate (FPR) of the GSOMs and SOMs in the test subset are represented in Fig. 15. The points with the highest SEN are given by SOMs, while the points with the lowest FPR are given by GSOMs. However, in the central area of the graph, there are points with high SEN and FPR below 20% that correspond to GSOMs.

Fig. 15
figure 15

Sensitivity versus False positive rate for all SOMs and GSOMs with the training subset of the bank dataset. The numbers in the graphic represent the accuracy

Full size image

5 Discussion

This section aims to provide a brief discussion of the results obtained. Some observations are extracted:

  • The Census Income dataset was used to create balanced and unbalanced sets. The unbalanced set showed better accuracy and false positive rate, but lower sensitivity. Balancing the data prevented a significant decrease in detecting true positives, improving training times, Kappa values, F1-scores, and balanced accuracies.

  • The results reveal that the GSOMs reduce the training data size in more than a 99% with a low loss of information by mapping the input space.

  • A spatial adaptation of the data is observable. In the illustrative example, it is possible to recognize perfectly a 3-dimensional letter G, and in the bank dataset, the weight vectors are capable of adapting to the input space with more neurons in the zones with a major density.

  • The use GSOMs allows the creation of a group of prototypes that can be used with algorithms like 1-NN, obtaining accuracies of more than 70% with false positives lower than 20% in a banking application and saving a great computational time.

The resulting number of nodes in each one of the GSOMs indicates that it is possible to represent the different datasets with no need for the complete growth of the maps. With more neurons, it is expected that the standard deviation will be lower, as there will be more neurons, but this will not necessarily lead to much better results. For example, GSOM 8 of the bank dataset contains 936 neurons, almost twice GSOM 7, but the quantification error remains stable and training time is quintupled. The results also highlight the need for a suitable parametrization, as too low initial learning rates in the growing phase lead to an overgrow of the map, a great difference between growing and smoothing iterations reduce the sensitivity and a lower \(\alpha\) increases the false positive rate.

The U-matrix representation offers the possibility of separating clients into different groups, which serves as a preliminary step to customer classification and analysis, and its potential is strengthened when combined with tools as the output map. This feature is noticeable in the Census Income dataset. However, due to the great number of features in the bank dataset and the unknown correlation between them, the clusters obtained with the U-matrix are not easy to extrapolate, which highlights the difficulty of finding patterns between data when it diverges from a theoretical distribution.

6 Conclusions

This work addresses the application of a GSOM with 1-NN to different datasets to address the problem of prototype generation for a binary classifier. First, the Census Income dataset is used for an academic application of the method and then, a real application is carried out on an actual dataset from a bank. Specifically, in the case of banking data, the number of clients and the challenge of selecting a low number of features for tasks as classification lead to the need for reducing its size. This work addresses the problem of classifying the clients into two categories using a 1-NN classifier and, for training the classifiers, the use of prototypes obtained from a GSOM is proposed.

The proposed methodology divides the data into training, validation and test subsets and trains different GSOMs to represent the training set. Then, the weight vectors of the GSOMs are used as prototypes for a 1-NN classifier that makes predictions on new data. In the case of the Census Income dataset, two types of experiments were conducted, using either balanced and unbalanced data. Different SOMs and GSOMs were used for comparison purposes for the bank dataset.

The application to Census Income (a smaller dataset where it is possible to apply the 1-NN classifier without any data reduction method) has been carried out to demonstrate that the proposed method is effective since the classification performances are maintained or even improved from 1-NN to GSOM+1-NN, with very high reduction rates. This application gives us guarantees of the good performance of the proposed method. In the application to the banking sector, where very large datasets are used, it is not possible to apply k-NN without data reduction, so a comparison is made between SOM+k-NN and GSOM+k-NN.

The results obtained demonstrate that the use of a GSOM in data with a great number of vectors and variables achieves a small size representation that facilitates further classification tasks, with reductions of more than 99% in the training data. The GSOMs obtain similar results to the SOMs with even higher accuracy in some experiments (accuracies over 70% and false positive rates under 20%) and much lower training times (from more than 3 or 4 h to even less than 1 h in some cases).

When dealing with large datasets, not only the reduction of the size is of great interest. A dimensionality reduction with correct feature selection can also be crucial in the performance and cost of the classification process. A complete improvement in computational cost will come from a combination of data and dimensionality reduction techniques. This issue is part of future lines of development. Another aspect to analyze as future work is the normality of the data and its deviations, e.g., the work by Mantalos et al. [47].