Multi-objective optimal allocation of multiple capacitors and distributed generators considering different load models using Lichtenberg and thermal exchange optimization techniques

Abstract

Integrating distributed generations (DGs) into the radial distribution system (RDS) are becoming more crucial to capture the benefits of these DGs. However, the non-optimal integration of renewable DGs and shunt capacitors may lead to several operational challenges in distribution systems, including high energy losses, poor voltage quality, reverse power flow, and lower voltage stability. Therefore, in this paper, the multi-objective optimization problem is expressed with precisely selected three conflicting goals, incorporating the reduction in both power loss and voltage deviation and improvement of voltage stability. A new index for voltage deviation called root mean square voltage is suggested. The proposed multi-objective problems are addressed using two freshly metaheuristic techniques for optimal sitting and sizing multiple SCs and renewable DGs with unity and optimally power factors into RDS, presuming several voltage-dependent load models. These optimization techniques are the multi-objective thermal exchange optimization (MOTEO) and the multi-objective Lichtenberg algorithm (MOLA), which are regarded as being physics-inspired techniques. The MOLA is inspired by the physical phenomena of lightning storms and Lichtenberg figures (LF), while the MOTEO is developed based on the concept of Newtonian cooling law. The MOLA as a hybrid algorithm differs from many in the literature since it combines the population and trajectory-based search approaches. Further, the developed methodology is implemented on the IEEE 69-bus distribution network during several optimization scenarios, such as bi- and tri-objective problems. The fetched simulation outcomes confirmed the superiority of the MOTEO algorithm in achieving accurate non-dominated solutions with fewer outliers and standard deviation among all studied metrics.

1 Introduction

1.1 Background

Due to the increasing demand for electric energy, which is mostly supplied by burning fossil fuels, environmental and economic concerns arise [1]. Distributed generations (DGs) will take the initiative for a few decades to address these challenges by utilizing different sustainable energies, such as wind turbines, photovoltaic systems, etc. On the other hand, the distribution networks account for around 70% of the total power losses due to their low operating voltage level and high current carrying design [2]. Low voltages, which cause appliances to malfunction and shorten their lifetimes, have a higher impact on customers positioned distant from the power source. Also, higher reactive power demands at the load lead to an increased current that flows in distribution lines, poor power factor, higher energy losses, and low node voltages. These issues are the real challenges in distribution systems, owing to the increased R/X ratio, load growth, and the inductive nature of loads [3, 4]. Thus, reducing power loss is among the most meaningful and essential topics in power system research. In this context, the distribution of renewable DG sources may be considered an economically feasible and cheap solution for this issue. If these DGs are appropriately allocated [5,6,7], they will improve the voltage level, reduce system losses, enhance the stability of the network, and boost the reliability of the distribution networks. Consequentially, the use of DGs is also rising and being adopted in many networks to prevent the installation of additional transmission and distribution lines to supply the growing demand. In general, DGs can be categorized into four classes based on their principal operations, as explained in [7].

On the other hand, shunt capacitors (SCs) are commonly employed in radial distribution systems. The optimal installation of SCs for compensating reactive power not only fixes power quality concerns but also offers several monetary and technical benefits [8]. So, to deal with the ever-increasing energy consumption and technical and financial problems of distribution systems, an efficient and appropriate reactive power compensation design is required. Finally, to get the advantages of DGs and SCs mentioned above, they should be optimally determined to specify their suitable size and location. When just one goal is included, the problem acts as a single objective optimization (SO). The problem is transformed into a multi-objective (MO) optimization when many objectives are included. The MO optimization problem will be studied in this paper under several scenarios to gain the best DG benefits mentioned above.

1.2 Related work

During the last decade, researchers have been concerned with the problem of DG allocation because of its considerable benefits. Numerous techniques are proposed for solving the optimum allocation issues, such as heuristic and metaheuristic applications [9], as well as traditional and analytical methods [10, 11]. Heuristic approaches, which depend on the experience of engineering, are the most often utilized in this situation. Due to their more advanced computing methodologies, ease of implementation, and derivatives-free, the metaheuristic and heuristic techniques outweigh the analytical and classical methods. So, metaheuristic algorithms can handle the optimal allocation problem of DGs on distribution systems, whether the problem is single or multi-objectives. A recent single objective metaheuristic technique, honey badger Algorithm [7], has previously been suggested to solve the DG optimal allocation problem by taking the total active power loss into account as a single objective function. On the contrary, weighted sum and Pareto optimal frontier (POF) are two strategies that may be utilized to tackle the multi-objective challenges. At first, it may be reduced to a single objective with a single-dependent solution by employing a weighting variable for each SO function. However, the size and location of the DG may be drastically varied by even a slight adjustment in the parameter’s weight. So, single objective optimization techniques should be developed to discover the non-dominant Pareto optimal frontier in the second strategy.

Several developed techniques have been suggested considering the weighting factors to convert the SO into MO optimization to deal with the DG optimal allocation problem. The authors in [12] presented an advanced solution for optimal integration of DGs and SCs on practical Brazil 136-bus and IEEE 33-bus distribution networks to mitigate the real and reactive line losses, minimize voltage deviation, and increase voltage stability. These multiple goals were combined by weighting coefficient and solved using the constriction factor-based PSO algorithm (CF-PSO). The results acquired were compared with the original PSO and MPSO to prove the robustness of the CF-PSO technique, which demonstrated its capability to solve the DG optimal allocation issue. The binary particle PSO and shuffled frog leap (BPSO-SLF) techniques were developed [13] to solve the single and multi-objective optimal allocation of DG to minimize the apparent power and enhance the voltage stability of 33-bus and 69-bus RDSs. Three different objectives involving environmental, technical, and monetary functions were considered for the optimal allocation of DGs and SCs into RDS to elevate the system’s performance. These objectives were converted to a weighted multi-objective problem and solved using the spring search algorithm (SSA) [14] and hybrid PSO-GWO algorithm [15]. The Archimedes optimization algorithm (AOA) was applied in [16] to detect the optimal placement of photovoltaic systems in RDS, considering different categories of load models, aiming to decrease the dependence of the network and emissions of greenhouse gas to the maximum degree attainable. The authors in [17] presented the application of a newly developed transient search optimization (TSO) to optimally specify the location and capacity of DG at different operating modes in the IEEE 33-bus and 69-bus RDSs. In this algorithm, the aggregated sum method was assumed to solve the technical objective, which includes system loss reduction, voltage deviation mitigation, and voltage-stability improvement. The application of the stud krill herd (SKH) method was further suggested in [18] to specify the best position and size of only one type of DG on the IEEE 33-bus, IEEE 69-bus, and IEEE 94-bus RDSs considering different static load models. The aggregated MO seeks to reduce line losses, decrease operation costs, and increase the voltage stability of the distribution systems.

From the literature mentioned above, the weighted sum-based MO method mainly depends on the predefined weighting factors that might have drastic effects on design variables by even a slight change in their weights. On the other hand, the principal purpose of the MO optimization techniques is to provide the non-dominated solutions (Pareto optimal frontiers) to help the decision-making algorithm choose the appropriate solution involving several helpful and optimum preferences. In other words, the MO optimization algorithms aim to optimize two or higher goals together and simultaneously provide several important design considerations. So, the MO algorithms are studied under different objectives regarding the DG optimal allocation problem. The technical objectives such as line loss reduction, enhancement of voltage stability, and minimization of voltage deviation summation are commonly employed in most research to enhance the overall system performance. To accomplish two or more of those objectives jointly, the MO techniques with a decision-making-based method optimally select the location and capacity of DGs and SCs integrated into distribution networks as depicted in [19, 20].

Freshly, the MO artificial hummingbird algorithm (MOAHA) [21] and improved decomposition-based evolutionary algorithm (I-DBEA) [22] were developed to identify the optimal placement of DGs into RDS to maximize the technical benefits of the distributed generators under constant full load model. The MOHTLBOGWO is also a multi-objective evolutionary algorithm developed in [23] to decrease the loss and improve the system’s reliability depending on the energy not supplied. This algorithm was adopted for SO and MO optimization problems and implemented on the 33-bus and 69-bus RDSs. The results proved its ability to escape from local minima and have good convergence characteristics. An enhanced artificial ecosystem optimization (EAEO) was suggested [24] to discover the best size and position of numerous DGs Type-I and III in various RDS by applying the POF together with the fuzzy decision algorithm. The goals were to reduce system loss, mitigate total voltage drop, and improve system stability and reliability. The DG optimal allocation problem has been optimized using the MO differential evolution (MODE) to accomplish such environmental, technical, and economic benefits of DGs [25]. The MODE algorithm was implemented on different distribution systems considering the reduction in energy cost, power loss, power generating emissions, voltage deviation, and stability enhancement. The POF acquired using MODE was also compared with the MOPSO algorithm, demonstrating the MODE algorithm’s superior capacity to specify optimum solutions with minimal computational effort.

Moreover, the authors of [26] used a method known as enhanced raven roosting optimization (IRRO) to reap the financial and technical advantages of distributed generators when incorporated into distribution networks. The best compromise solution (BCS) was chosen using the minimax-based game theory algorithm. The Pareto optimal front-based artificial bee colony (ABC) optimization algorithm has been used for identifying the optimal size and distribution of DG in RDS [27]. Total energy, power loss, and voltage drop were formulated as a MO optimization problem to increase the performance of distribution systems. To optimally locate DG units in distribution networks, authors in [28] developed an improved Harris Hawks Optimizer (IHHO) in a multi-objective space. Different types of DG units were optimized to improve the system’s stability. The gray relational projection (GRP) algorithm was utilized to find the BCS from the acquired POF. It should be noted that the GRP is efficient only for closely related goals. The multi-objective Archimedes optimization (MOAOA) algorithm has been adopted [29] for the reduction in energy losses during a day operation of RDS incorporated with DGs. Compared to PSO and ASO techniques, the MOAOA is the best technique for the current optimization problem. The authors in [30] introduced the application of the three new versions of the MO Bonobo Optimizer (MOBO) for solving the optimal installation of DG Type-I on the 33-bus and 85-bus distribution systems to minimize only the voltage deviation summation and power loss. The POF obtained using the MOBO versions was compared with other well-known multi-objective optimization techniques such as MOPSO, MOAEO, MOGSA, and MOJAYA using MO indicators. The fuzzy best compromise solutions for all suggested approaches were also assessed using different statistical analyses under demand load. The different versions of the MOBO algorithm were successful for different situations.

According to previous studies, numerous metaheuristic techniques are adopted for the DG and SC placement problem using weighted MO optimization. In other words, a few strategies based on Pareto optimal sets were employed to optimally allocate shunt capacitors, DG Type-I, and DG Type-III presuming different load models. Therefore, this paper aims to present a general framework for integrating SCs and multi-type DGs into RDS under several load models to enhance voltage stability, mitigate voltage deviation, and minimize active power loss. This is accomplished using the recent and efficient Multi-objective Lichtenberg Algorithm (MOLA) [31] and Multi-Objective Thermal Exchange Optimization (MOTEO) [32] algorithm, which are physics-inspired algorithms that are freshly developed. The MOLA and MOTEO addressed common optimization problems effectively and quickly compared with other well-known techniques. Hence, they will be adopted here to maximize the technical benefits of DGs and SCs when integrated into the IEEE 69-bus distribution system. From the literature discussed above, this is the first article that systematically provides the best allocation of DGs and SCs utilizing the MOLA and MOTEO algorithms under several types of static loads. Moreover, the outcomes achieved using the present techniques are compared with efficient and recent Pareto optimal front-based methods, such as MOAHA [21], MOIHHO [28], and I-DBEA [22], under different optimization scenarios.

1.3 Paper contributions and structures

This paper aims to present a multi-objective strategy for the optimal incorporation of different types of DGs and SCs in distribution systems under different voltage-dependent load models. This is conducted using the MOLA and MOTEO techniques with the help of minimizing active power loss, mitigating voltage drop, and enhancing the voltage stability of the IEEE 69-bus RDS. This study includes several statistical analyses, as well as multi-objective performance metrics, such as hypervolume (HV), spacing, diversity, and hole relative size (HRS), to evaluate the performance of the MOLA and MOTEO techniques. The main goals of the paper can be outlined as follows:

• 1. Applying two novel and effective physics-based metaheuristic techniques named multi-objective Lichtenberg algorithm (MOLA) and multi-objective thermal exchange optimization (MOTEO) for optimally sitting and sizing of multiple SCs and DGs in RDS.

• 2. Integrating multiple DGs with different operating modes and SCs to maximize the technical benefits of these DGs and SCs under several different load levels considering bi- and tri-objective optimization scenarios.

• 3. Employing the active power loss sensitivity factor, which predefines the possible locations for installing DGs and SCs, to improve the execution time and decrease the search space of the proposed strategy.

• 4. Applying the fuzzy decision-making algorithm to obtain the BCS from the Pareto optimal set achieved using MOLA and MOTEO algorithms.

• 5. Measuring the performance of the acquired non-dominated solutions through different multi-objective performance metrics. Furthermore, the numerical results are compared with efficient and recent Pareto optimal front-based methods to validate the accuracy of the MOLA and MOTEO algorithms.

The remaining of the present article will be structured as follows: the following section expresses the mathematical problem of RDS, which comprises proposed multi-objective functions, fuzzy decision-making technique, objective constraints, voltage-dependent load models, and active power loss sensitivity index. Section three introduces the basic concept of the MOLA and MOTEO techniques and their implementation strategy for specifying the best location and size of DGs and CBs in RDS, presuming different load levels. Section four extensively shows the different scenarios implemented on the present RDS using the suggested techniques. The statistical analysis of the MOTEO and MOLA techniques under constant power full load is depicted in section five. The last section provides the conclusion of the work depending on the results achieved and the recommended future study.

2 Mathematical problem formulation

The problem formulation entails determining the optimal size and placement of DGs and SCs using multi-objective functions while ensuring operational constraints under different load models. These will be explained in the following subsections.

2.1 Single objective functions

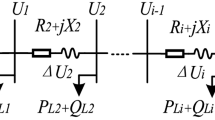
In this paper, the three optimized objective functions are the total line loss, root mean square voltage index, and the voltage stability index. In this context, Fig. 1 shows a portion of two buses in radial distribution networks that have an impedance of ${Z}_{ij}={R}_{ij}+j{X}_{ij}$ and ${S}_{j}={P}_{j}+{jQ}_{j}$ is the apparent power at the receiving end bus. The ${V}_{i}$ and ${V}_{j}$ denote the voltage at the sending and receiving end buses, respectively. Now, the current $({I}_{ij})$ through the line between two nodes $i$ and j is a function of the demand $({S}_{j})$ at bus j and is given by the following expression, as follows [30]:

Fig. 1

Portion of two nodes in radial distribution system

$${I}_{ij}={\left(\frac{{S}_{j}}{{V}_{j}}\right)}^{*},$$

(1)

Here, $\left(*\right)$ represents the complex conjugate. The total line loss is determined after performing the forward–backward algorithm [33] for solving the load flow problem with a tolerance of 10^–6. The k-th line loss $({P}_{loss,k})$ can be calculated from the current $({I}_{ij})$ and the real impedance $({R}_{ij})$ without installing any DGs/SCs using Eq. (2):

$${P}_{\mathrm{loss},k}={\left|{I}_{ij}\right|}^{2}\times {R}_{ij},$$

(2)

With distribution system contains number of branches ${n}_{br}$, the total line loss $({P}_{loss})$ can be evaluated by:

$${P}_{\mathrm{loss}}=\sum_{k=1}^{{n}_{br}}{P}_{\mathrm{loss},k},$$

(3)

So, the first objective function $({\mathrm{f}}_{\mathrm{obj},1})$ aims to minimize the total line loss as follows:

$${\mathrm{f}}_{\mathrm{obj},1}=\mathrm{min}\left({\mathrm{P}}_{\mathrm{loss}}\right),$$

(4)

The radial design of the distribution networks assists in voltage reduction when large loads are located far from the swing bus. Therefore, the second objective function considered in this work is to enhance the voltage quality of the distribution systems by minimizing the root mean square voltage index $(\mathrm{RMSVI})$ as per Eq. (5):

$${\mathrm{f}}_{\mathrm{obj},2}=\mathrm{min}\left(\mathrm{RMSVI}\right),$$

(5)

$$\mathrm{RMSVI}={\left(\frac{\mathrm{TVD}}{{n}_{\mathrm{bus}}}\right)}^{0.5},$$

(6)

$$\mathrm{TVD}=\sum_{o}^{{n}_{\mathrm{bus}}}\left|{V}_{\mathrm{swing}}-{V}_{o}\right|,$$

(7)

where ${V}_{\mathrm{swing}}$ depicts the swing bus voltage magnitude, i.e., reference bus, while ${V}_{o}$ is the o-th bus voltage. The total number of bus is represented by ${n}_{\mathrm{bus}}$, while the TVD denotes the summation of voltage deviation index.

Further, maintaining an appropriate voltage-stability range at the distribution system level is critical to avert the whole power system from collapsing, as has previously occurred [34]. In other words, the voltage stability index (VSI) is utilized to provide the sensitivity level of the distribution systems. The VSI at bus j is denoted by the following relation [35]:

$${\mathrm{VSI}}_{\mathrm{j}}={\left|{\mathrm{V}}_{\mathrm{ i}}\right|}^{4}-4{\left({{\mathrm{P}}_{\mathrm{j}}}_{ }{\mathrm{X}}_{\mathrm{i},\mathrm{j}}-{{\mathrm{Q}}_{\mathrm{j}}}_{ }{\mathrm{R}}_{\mathrm{i},\mathrm{j}}\right)}^{2}-4\left({{\mathrm{P}}_{\mathrm{j}}}_{ }{\mathrm{X}}_{\mathrm{i},\mathrm{j}}+{{\mathrm{P}}_{\mathrm{j}}}_{ }{\mathrm{R}}_{\mathrm{i},\mathrm{j}}\right){\left|{\mathrm{V}}_{\mathrm{ i}}\right|}^{2},$$

(8)

If the bus has a good VSI value, it will be more stable, and the possibilities of voltage collapse are reduced. So, the third objective function aims to maximize the total voltage stability index $(TVSI)$ as per Eq. (9) given below:

$${\mathrm{f}}_{\mathrm{obj},3}=\mathrm{max }\left(\mathrm{TVSI}\right)=\mathrm{min}\left(\frac{1}{\mathrm{TVSI}}\right),$$

(9)

$$\mathrm{TVSI}=\sum_{\mathrm{j}}^{{\mathrm{n}}_{\mathrm{bus}}}{\mathrm{VSI}}_{\mathrm{j}},$$

(10)

Note that each objective function will be normalized by its base value (before compensation) to be used in different optimization scenarios, as per Eqs. (11), (12), and (13), respectively:

$${\mathrm{f}}_{1}=\mathrm{min}\left(\frac{{\left|{\mathrm{P}}_{\mathrm{loss }}\right|}_{\mathrm{DG}}}{{\left|{\mathrm{P}}_{\mathrm{loss }}\right|}_{\mathrm{no DG}}}\right),$$

(11)

$${\mathrm{f}}_{2}=\mathrm{min}\left(\frac{{\left|\mathrm{RMSVI}\right|}_{\mathrm{DG}}}{{\left|\mathrm{RMSVI}\right|}_{\mathrm{no DG}}}\right),$$

(12)

$${\mathrm{f}}_{3}=\mathrm{min}\left(\frac{{\left|\mathrm{TVSI}\right|}_{\mathrm{no DG}}}{{\left|\mathrm{TVSI}\right|}_{\mathrm{DG}}}\right),$$

(13)

2.2 Multi-objectives and fuzzy decision-making algorithm

This research aims to solve the three single objective functions discussed before under different optimization scenarios, such as bi- and tri-objective problems, i.e., ${\mathrm{F}}_{1}=\mathrm{min}({\mathrm{f}}_{1},{\mathrm{f}}_{2}$) or ${\mathrm{F}}_{2}=\mathrm{min}({\mathrm{f}}_{1},{\mathrm{f}}_{3}$), and ${\mathrm{F}}_{3}=\mathrm{min}({\mathrm{f}}_{1}, {\mathrm{f}}_{2}, {\mathrm{f}}_{3}$) to achieve their benefits simultaneously using the MOLA and MOTEO techniques. In contrast to SO optimization, there are several solutions to build a POF in the MO optimization problem, all of which are non-dominated. It is tough to choose a single optimal solution while modeling multiple goals. Different methods, such as technique for order of preference by similarity to ideal solution (TOPSIS), gray relational analysis (GRA), and simple additive weighting (SAW), are utilized for choosing the best compromise solution (BCS) from a set of non-dominant points that do not conflict with each other. In this study, the fuzzy decision-making-based algorithm is adopted for this purpose, which is robust and has a wide area of applications. The i-th objective function of a non-dominated solution in Pareto set f_i is expressed by a membership function ${\upmu }_{{\mathrm{f}}_{\mathrm{i}}}$, as follows [36]:

$${{\upmu }_{{\mathrm{f}}_{\mathrm{i}}}}^{\mathrm{k}}=\left\{\begin{array}{c}0 \\ \frac{{\mathrm{f}}_{\mathrm{i}}^{\mathrm{max}}-{\mathrm{f}}_{\mathrm{i}}^{\mathrm{k}}}{{\mathrm{f}}_{\mathrm{i}}^{\mathrm{max}}-{\mathrm{f}}_{\mathrm{i}}^{\mathrm{min}}}\\ 1 \end{array}\right.\begin{array}{c}{\mathrm{f}}_{\mathrm{i}}(\mathrm{x})\ge {\mathrm{f}}_{\mathrm{i}}^{\mathrm{max}}\\ {\mathrm{f}}_{\mathrm{i}}^{\mathrm{min}}{<\mathrm{f}}_{\mathrm{i}}(\mathrm{x})>{\mathrm{f}}_{\mathrm{i}}^{\mathrm{max}}\\ {\mathrm{f}}_{\mathrm{i}}(\mathrm{x})\le {\mathrm{f}}_{\mathrm{i}}^{\mathrm{min}}\end{array},$$

(14)

Here, ${\mathrm{f}}_{\mathrm{i}}^{\mathrm{k}}$ denotes the objective function with non-dominated solution k; ${\mathrm{f}}_{\mathrm{i}}^{\mathrm{max}}$ and ${\mathrm{f}}_{\mathrm{i}}^{\mathrm{max}}$ are, respectively, the maximum and minimum values of the current objective function ${\mathrm{f}}_{\mathrm{i}}$. Afterward, for each individual k, the normalized membership function $({\upmu }^{\mathrm{k}})$ is calculated using the following expression [36]:

$${\upmu }^{\mathrm{k}}=\frac{\sum_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{f}}}{{\upmu }_{{\mathrm{f}}_{\mathrm{i}}}}^{\mathrm{k}}}{\sum_{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{s}}}\sum_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{f}}}{{\upmu }_{{\mathrm{f}}_{\mathrm{i}}}}^{\mathrm{k}}},$$

(15)

Here, ${N}_{f}$ and ${N}_{s}$ represent the number of objectives and the number of non-dominated solutions. This normalized membership function is arranged in descending order, and the first value is considered as the BCS among these non-dominated solutions. In other words, the solution having the largest value of ${\upmu }^{\mathrm{k}}$ is chosen as the best compromise solution.

2.3 Operation constraints

The suggested approach for the optimum allocation of DGs and SCs in multi-objective form does not break either system or problem limitations. These restrictions involve voltage limits and DGs and SCs sizes and locations. The voltage limitation maintains the voltage within the accepted range as per Eq. (16):

$${V}_{\mathrm{min},k}\le \left|{V}_{k}\right|\le {V}_{\mathrm{max},k},$$

(16)

In the above expression, ${V}_{\mathrm{max},k}$ and ${V}_{\mathrm{min},k}$ denote the maximum and minimum of the voltage absolute value at bus k. They are often assumed to be 1.05 and 0.95 p.u, respectively.

It is recommended that the installed DGs and SCs capacity in the network should not surpass the power provided by the grid as given in Eqs. (17), (18), and (19) to avoid reverse power flow [16]:

$$\sum_{i=1}^{{N}_{DG}}{P}_{DG,i}\le 0.75\times \left(\sum_{k=1}^{{n}_{br}}{P}_{\mathrm{loss},k}+\sum_{g=1}^{{n}_{\mathrm{bus}}}{P}_{l,g}\right),$$

(17)

$$\sum_{i=1}^{{N}_{DG}}{Q}_{DG,i}\le 0.75\times \left(\sum_{k=1}^{{n}_{br}}{Q}_{\mathrm{loss},k}+\sum_{g=1}^{{n}_{\mathrm{bus}}}{Q}_{l,g}\right),$$

(18)

$$\sum_{i=1}^{{N}_{SC}}{Q}_{SC,i}\le 0.75\times \left(\sum_{k=1}^{{n}_{br}}{Q}_{\mathrm{loss},k}+\sum_{g=1}^{{n}_{\mathrm{bus}}}{Q}_{l,g}\right),$$

(19)

where ${\mathrm{P}}_{\mathrm{DG},\mathrm{i}}$ and ${\mathrm{Q}}_{\mathrm{DG},\mathrm{i}}$ are the active and reactive power generated by the i-th DGs; the active and reactive power loss of the k-th branch are represented by ${\mathrm{P}}_{\mathrm{loss},\mathrm{k}}$ and ${\mathrm{Q}}_{\mathrm{loss},\mathrm{k}},$ respectively; the active and reactive load connected at bus $\mathrm{g}$ are denoted by ${\mathrm{P}}_{\mathrm{l},\mathrm{g}}$ and ${\mathrm{Q}}_{\mathrm{l},\mathrm{g},}$ respectively; ${\mathrm{Q}}_{\mathrm{SC},\mathrm{i}}$ depicts the reactive power supplied by the i-th SCs; ${\mathrm{N}}_{\mathrm{SC}}$ and ${\mathrm{N}}_{\mathrm{DG},}$ respectively, illustrate the number of the installed SCs and DGs units in the distribution system.

However, the minimum and maximum capacities for DGs and SCs themselves are given by the following expressions:

$${{\mathrm{P}}_{\mathrm{DG},\mathrm{i}}}^{\mathrm{min}}\le {\mathrm{P}}_{\mathrm{DG},\mathrm{i}}\le {{\mathrm{P}}_{\mathrm{DG},\mathrm{i}}}^{\mathrm{max}} \quad \forall \mathrm{i}=1:{\mathrm{N}}_{\mathrm{DG}},$$

(20)

$${{\mathrm{PF}}_{\mathrm{DG},\mathrm{i}}}^{\mathrm{min}}\le {\mathrm{PF}}_{\mathrm{DG},\mathrm{i}}\le {{\mathrm{PF}}_{\mathrm{DG},\mathrm{i}}}^{\mathrm{max}} \quad \forall \mathrm{i}=1:{\mathrm{N}}_{\mathrm{DG}},$$

(21)

$${{\mathrm{Q}}_{\mathrm{SC},\mathrm{j}}}^{\mathrm{min}}\le {\mathrm{Q}}_{\mathrm{SC},\mathrm{j}}\le {{\mathrm{Q}}_{\mathrm{SC},\mathrm{j}}}^{\mathrm{max}} \quad \forall \mathrm{i}=1:{\mathrm{N}}_{\mathrm{SC}},$$

(22)

Typically, the limits for the active power generated by renewable DGs are 0.3 and 3 p.u with operating power factor (PF) limits [0.7, 1], while the shunt capacitor is constrained within the interval [ 0.15, 1.5] p.u.

Except for the swing bus, the DG and SC units may be installed anywhere on the system bus as expressed in Eq. (23). In other words, the active power loss sensitivity (APLS) factor will specify the candidate buses for installing the distributed generators and shunt capacitors, which will be discussed in the subsequent section:

$${\mathrm{Loc}}_{DG/\mathrm{SC},i}={L}_{i}, i=1:{n}_{\mathrm{CB}},$$

(23)

where ${n}_{CB}$ is the number of candidate buses provided by the APLS factor; ${\mathrm{Loc}}_{\mathrm{DG}/\mathrm{SC},i}$ represents the location of the i-th DGs or SCs units; ${L}_{i}$ is the i-th candidate bus.

2.4 Load models

In a traditional load flow study, it was assumed that the apparent power demands are consistent and independent of the level of voltages present in the same bus. Various voltage-dependent load models will be used in this study since distribution loads are voltage dependent. These models are residential, commercial, industrial, constant power (light, standard, and heavy), constant current, and constant impedance. Voltage-dependent load models are static models that illustrate the relationship between power and voltage as an exponential formula as expressed below [37]:

$${P}_{l,k}=\gamma {P}_{\mathrm{actual},k}{{V}_{k}}^{\sigma },$$

(24)

$${Q}_{l,k}=\gamma {Q}_{\mathrm{actual},k}{{V}_{k}}^{\rho },$$

(25)

where ${\mathrm{Q}}_{\mathrm{actual},\mathrm{k}}$ and ${\mathrm{P}}_{\mathrm{actual},\mathrm{k}}$ are, respectively, the reactive and active load at normal operating conditions; $\sigma$ and $\rho$ are the coefficients of the load models whose values are depicted in Table 1. Load factor $\gamma$ is a multiplier used to raise or reduce the load power demand for all nodes in the network; ${V}_{k}$ is the voltage at the k-th load bus.

Table 1 Different load models and their exponent values

These various load models at specific load levels are utilized to prove the reliability and capabilities of the suggested techniques for practical implementation.

2.5 Active Power Loss Sensitivity

In this research, the active power loss sensitivity (APLS) index is utilized to identify the buses that are more critical for installing the DGs and SCs [16]. Using this factor may also lower the search area and the time required for the optimization process. In other words, this factor identifies the buses suffering from losses, allowing the optimization algorithm to focus solely on these buses rather than exploring the whole network for installing the distributed generators and shunt capacitors. As a result, it will shorten the computational time. From Fig. 1, the active losses of each branch can be rewritten as per Eq. (26):

$${P}_{\mathrm{loss},ij}=\frac{{R}_{ij}\left({{P}_{j}}^{2}+{{Q}_{j}}^{2}\right)}{{\left|{V}_{j}\right|}^{2}},$$

(26)

and the APLS index can be expressed by Eq. (27) as follows:

$$\frac{\partial {P}_{loss,ij}}{\partial {P}_{j}}=\frac{2{R}_{ij}{P}_{j}}{{\left|{V}_{j}\right|}^{2}},$$

(27)

Figure 2 shows the APLS index for each bus of the IEEE 69-bus distribution system, which is also arranged descendingly. It is clear from this figure the buses with a high APLS value qualify as candidate buses for DGs/SCs installation. These possible buses are 57, 58, 7, 6, 61, 60, 10, 59, 55, 56, 12, 13, 14, 54, 15, 53, 8, 64, 49, 11, 9, 17, 65, 16, and 5. They will make up to 36% of the system’s buses.

Fig. 2

APLS index for the IEEE 69-bus RDS

3 Optimization techniques

As discussed earlier, the MOLA and MOTEO algorithms will be adopted for solving the optimal allocation problem of DGs and SCs under different load models and will be discussed in the following subsections as follows:

3.1 Multi-objective Lichtenberg algorithm (MOLA)

The multi-objective Lichtenberg algorithm (MOLA) was inspired by the physical phenomena of lightning storms and Lichtenberg figures (LF). It was recently developed by Pereira et al. in 2022 [31], who also introduced the SO version of this algorithm. MOLA as a hybrid algorithm differs from many in the literature since it combines the population and trajectory-based search approaches. The Lichtenberg algorithm (LA) was applied in several optimization problems, such as damage detection [38], designing of the isogrid lower limb prosthesis from the carbon fiber reinforced polymer [39], among others. MOLA is based on Lichtenberg’s Figures, which are created utilizing the theory of diffusion-limited aggregation [40], and the different points covered by the figure are assessed. Note that the size and orientation of LF are changed with every iteration to improve its reliability and coverage of an ampler search area. The optimal solution for every iteration is utilized as a motivation point for the next iteration. The FL is formed by randomly distributing the population in which the MOLA user has selected. Moreover, this LF is built in every iteration with a new set of random sizes and rotations, increasing the refinement of the search and allowing MOLA to become even more capable of exploration and exploitation.

Pareto dominance is employed to compare the objective space solutions generated by all points determined in the search space. The non-dominated sets are preserved in the solution space, while the dominated ones are eliminated. During each iteration, the collection of non-dominated solutions provides the Pareto optimal frontier of the problem. This front tends to get closer to the actual one as the iterations go on. At every iteration, one of these points is randomly chosen to build the LF, resulting in a forced search in the variable space for areas with superior values of objective functions. Tables 2 and 3 give the pseudo-code for the suggested MOLA algorithm and creation of LF, respectively.

Table 2 Multi-objective Lichtenberg Algorithm Pseudo-code

Table 3 Design of Lichtenberg Figure

Table 4 Recommended parameters for the MOLA algorithm

Table 4 depicts the sex recommended parameter ranges that may be utilized to customize the Lichtenberg algorithm: creation radius (${\mathrm{R}}_{\mathrm{c}}$), which represents the space for the construction of the figure, the number of particles employed in its construction (${\mathrm{N}}_{\mathrm{p}}$), stickiness coefficient ($\mathrm{S}$) that affects considerably the cluster’s density, the local search refinement ($\mathrm{ref}$), switching factor ($\mathrm{M}$) which responsible for the construction or not of a new LF at each iteration, population ($\mathrm{pop}$) which is usually ten times the number of decision variables, and finally, the number of iterations (${\mathrm{N}}_{\mathrm{iter}}$) being equal to 100, which is a common iteration number for different optimization algorithms reported in the literature. All the parameter values should be adopted considering the complexity of the problem.

3.2 Multi-objective thermal exchange optimization (MOTEO) algorithm

Recently, a metaheuristic optimization technique named thermal exchange optimization (TEO) based on the Newtonian cooling rule was introduced by Kaveh and Dadras in 2017 [41]. Comparable to the LA algorithm, the TEO is also a physics-inspired algorithm that employs the physical phenomena to update the search agents inside a given search space. In the TEO algorithm, the search agents are partitioned into two sets, one for the environment and the other for the cooling objects whose temperature defines the optimization parameters. For more detailed information concerning a single objective version of the TEO algorithm, see Ref. [41]. For briefness, the following sections will only describe the modifications required to create the multi-objective thermal exchange optimization (MOTEO) algorithm [32], where the changes lie in how the objects inside the search space are sorted and how the $\beta$ variable is calculated.

3.2.1 Selection mechanism

Objects in multi-objective problems have many cost values depending on the number of objective functions. Thus, a possible way to rank them is to arrange them according to their Pareto fronts. Accordingly, a non-dominated sorting method is implemented to classify the solutions into many Pareto sets. Regarding the objects that have the same ranking inside each Pareto solution, the crowding distance is executed to rank these objects, which is commonly utilized to measure the density of solutions that surround a specific one in the population in multi-objectives optimization. Crowding distance is determined using the following expression [42]:

$${\mathrm{D}}^{\mathrm{i}}=\sum_{\mathrm{k}=1}^{\mathrm{n}}\frac{{\mathrm{d}}_{\mathrm{k}}^{\mathrm{i}}}{\left|{\mathrm{f}}_{\mathrm{k}}^{\mathrm{max}}-{\mathrm{f}}_{\mathrm{k}}^{\mathrm{min}}\right|},$$

(28)

Where  ${\mathrm{D}}^{\mathrm{i}}$ represents the crowding distance of the ${\mathrm{j}}^{\mathrm{th}}$ object, and the distance between surrounding solutions is denoted by ${\mathrm{d}}_{\mathrm{k}}^{\mathrm{i}}$ taking the i-th cost function into account. Figure 3 illustrates the crowding distance calculation for a bi-dimensional problem. $\mathrm{n}$, ${\mathrm{f}}_{\mathrm{k}}^{\mathrm{max}}$, and ${\mathrm{f}}_{\mathrm{k}}^{\mathrm{min}}$ depict, respectively, the number of objective functions, the cost of the maximum and minimum values for the objects considering the i-th cost function. It is worth noting that the crowding distance of the maximum and minimum objects is supposed to be infinite.

Fig. 3

An illustration for crowding distance calculation

The crowding distance of the objects found within each group is compared, and those with greater distances are given better rankings to maintain diversity. In other words, a solution of iteration ${iter}_{i}$ receives a higher rating than the solution of iteration ${iter}_{j}$ if it belongs to a superior front. When the front ranks are equal for both iterations but ${D}^{i}>{D}^{j}$, the solution of ${iter}_{i}$ acquires a better rank because it has a higher crowding distance.

The selection process employed in the MOTEO algorithm is pictorially depicted in Fig. 4. Firstly, the current and previous search agents are merged to create a new one that is separated into numerous fronts using the non-dominant sorting method. So, several different fronts are generated, where agents within ${f}_{i}$ dominate those on the frontier of ${f}_{j}$ $({f}_{i}\prec {f}_{j})$, if and only if the index $i$ is less than $j$ $(i\, < \,j)$. After that, each agent’s crowding distance is determined using Eq. (1), and the objects are arranged in descending order inside the fronts. Eventually, the worst half of the sorted solutions are discarded. Because of this, there will always be the same amount of population every iteration.

Fig. 4

MOTEO’s selection process

3.2.2 $\beta$ parameter

In the single objective version of the presented MOTEO algorithm, the β parameter is directly proportional to the cost value of the solution. In other words, the larger the cost value of a solution, the larger its β parameter. However, each solution in MOTEO incorporates many cost values. The β parameter will be modified as given in Eq. (29), whereas a higher β parameter will be assigned to the solution that corresponds to a higher rank of the Pareto solution:

$$\upbeta =\frac{{r}_{i}}{{n}_{\mathrm{pop}}},$$

(29)

where ${r}_{i}$ denotes the conclusive rank of the outcome of ${iter}_{i}$ depending on its Pareto front and crowding distance, while ${n}_{pop}$ illustrates the population numbers.

Eventually, the presented MOTEO algorithm can be implemented, by modifying only the selection mechanism and calculation of the β parameter in the single version of MOTEO, as discussed earlier. Further, Fig. 5 provides the complete flowchart of the MOTEO algorithm for ease of implementation process. The non-dominated sorting and the assessment of cost functions are the two main processing tasks in the MOTEO technique. The computational complexity of the MOTEO method is $(n{N}_{iter}pop)$ for the cost function assessment task and $({n{N}_{iter}pop }^{3})$ for the non-dominated sorting task [43], where $pop$ represents the size of populations, $n$ illustrates the number of the objectives, and ${N}_{iter}$ denotes the iterations number.

Fig. 5

Complete flowchart of the MOTEO algorithm

3.3 Proposed methodology based on MOLA and MOTEO techniques

It is the first time to utilize hybrid physics-based metaheuristic techniques named MOLA and MOTEO for optimal sitting and sizing of multiple SCs and renewable DGs into the distribution system presuming several voltage-dependent load models. The proposed multi-objective goals seek to minimize the loss and improve the voltage levels and stability. Further, the renewable DGs will be studied under different operating power factors, i.e., unity power factor (DG Type-I) and optimal power factor (DG Type-III). It will be also accomplished under different cases such as minimizing loss and RMSVI, minimizing loss and maximizing VSI, and finally, combining all simultaneously by reducing the system loss and RMSVI while maximizing VSI. The detailed process of the proposed strategy based on MOLA and MOTEO physics hybrid algorithms is depicted in Fig. 6. The following steps outline the proposed strategy for the optimal allocation of DGs and SCs under different static load models (Fig. 7).

Fig. 6

Flowchart of the proposed strategy based on MOLA and MOTEO techniques

Fig. 7

Layout of the IEEE 69-bus RDS

Step 1: Read the line and bus data of the network.

Step 2: Run the load flow program using forward-backward algorithm and compute the bus voltages.

Step 3: Load the exponential factors and simulate the voltage-dependent load models using Eqs. (24) and (25).

Step 4: Identify the buses that are more critical for installing the DGs and SCs using the APLS index from expression (27).

Step 5: Run the load flow method to determine the values of chosen objective functions before compensation for all load models.

Step 6: Choose the number of DG/SC units for the network to be optimized.

Step 7: Specify the limits for the inequality constraints, i.e., location, and DGs/SCs size using Eqs. (23), (20), (21), and (22), respectively.

Step 8: Choose the multi-objective optimization technique, whether MOLA or MOTEO and set its parameters as discussed above.

Step 9: Iteration is accomplished utilizing efficient MOLA or MOTEO multi-objective optimization techniques with the studied objective function given in Eqs. (11) or (12) or (13).

Step 10: The position and size of DG/SC are randomly selected every iteration and then, check for the DGs/SCs constraints using expressions (16-23) and evaluate the objective functions as expressed in step 9.

Step 11: In every iteration, apply the non-dominated sorting algorithm and crowding distance function for the MOTEO algorithm or create the LF and employ the Pareto dominance for MOLA technique to choose the non-dominated solutions and build the global POF.

Step 12: Check the system equality and non-equality constraints for the achieved outcomes.

Step 13: Repeat steps 9, 10, 11, and 12 until the number of iterations is achieved.

Step 14: Apply the fuzzy decision-making-based algorithm to the select the BCS as expressed in Eqs. (14) and (15).

Step 15: Finally, display the objective functions with the optimized size and location of DGs/SCs and determine the reduction in system loss, RMSVI, and voltage stability index.

Step 16: Conduct the different statistical tests and display the achieved outcomes.

4 Simulation results and discussion

The proposed multi-objective functions solved by MOLA and MOTEO techniques are applied to the IEEE 69-bus RDS (illustrated in Fig. 9) to find the optimal location and size of SCs and renewable DGs while considering different static load models. The proposed strategy is simulated under three different scenarios: integration of three units of SCs, integration of three units of DGs Type-I, and integration of three units of DGs Type-III. Each scenario is performed under two- and three-dimensional optimization problem, i.e., (${\mathrm{F}}_{1}=\mathrm{min}\left({f}_{1},{f}_{2}\right)$: minimize the active power loss and mitigate voltage deviation), (${\mathrm{F}}_{2}=\mathrm{min}\left({f}_{1},{f}_{3}\right)$: minimize the active power loss and maximize voltage stability), (${\mathrm{F}}_{3}=\mathrm{min}\left({\mathrm{f}}_{1}, {\mathrm{f}}_{2}, {\mathrm{f}}_{3}\right)$: minimize the active power loss, maximize voltage stability, and mitigate voltage deviation). The software for the proposed strategy based on MOLA and MOTEO techniques is coded using MATLAB 2020b M files and performed on an Intel Core i7-G15 5511 CPU operating at 2.3 GHz with 16 GB Ram. The initialization parameters of the present techniques are given in Table 5.

Table 5 Parameter initialization for the MOLA and MOTEO algorithms

Table 6 gives the basic information about the present test system before installing DGs or SCs, which involves 69 buses and 68 lines, with load demands of 2694.6 KVAR and 3801.49 KW [44]. The testing system also employs a standard base voltage of 12.66 kV and a base power of 10 MVA.

Table 6 Summary of the IEEE 69-bus RDS base value under different load models

4.1 Scenario I: Integration of shunt capacitors into IEEE 69-bus RDS

In this study case, the MOLA and MOTEO techniques are employed to detect the optimal site and size of three units of SCs under different load models during the minimization of F₁, F₂, and F₃, as structured in Tables 7, 8, and 9, respectively. For instance, Table 7 illustrates the BCS obtained using the MOLA and MOTEO algorithms to mitigate the losses and voltage deviation of the IEEE 69-bus RDS at different voltage-dependent load models. In the CPFL model, the total active power loss was decreased to 146.33 KW and 150.39 KW, representing a reduction in 34.9580 and 33.1603 percent, respectively, for the MOLA and MOTEO approaches. While, the corresponding RMSVI is mitigated from the base case, i.e., 0.03795 p.u to 0.027563 p.u and 0.026712 p.u, respectively. The voltage profiles for the present test system after installation of three units of SCs are depicted in Fig. 8 at different load models. The lowest voltage level is found for the CPHL model at bus 65, while the MOLA and MOTEO techniques improve it from the base case, i.e., 0.8445 p.u to 0.9009 p.u and 0.9000 p.u, respectively. Note that the integration of three units of SCs does not satisfy the voltage constraints in all test cases, as illustrated in the following figures. Moreover, Fig. 9 shows the POFs with BSC for the presented MO optimization techniques. It can be seen from this figure that the MOTEO algorithm provides an accurate POF for all different load models regardless of the BCS.

Table 7 BCS for the optimal allocation of SC using MOLA and MOTEO techniques through minimizing power loss and reducing voltage deviation under different load models

Table 8 BCS for the optimal allocation of SC using MOLA and MOTEO techniques through minimizing power loss and maximizing voltage stability under different load models

Table 9 BCS for the optimal allocation of SC using MOLA and MOTEO techniques through minimizing power loss, maximizing voltage stability, and reducing voltage deviation under different load models

Fig. 8

Voltage profiles for the IEEE 69-bus under different load models with the optimal allocation of SC using MOLA and MOTEO Techniques through minimizing active power loss and reducing voltage deviation

Fig. 9

POF with fuzzy-based BCS for the optimal allocation of SC using MOLA and MOTEO techniques through minimizing power loss and mitigating voltage deviation under different load models

During the minimization of F₂, which aims to reduce the total line loss and improve the voltage stability index, Table 8 depicts the non-dominated BCS obtained using the two present techniques for the optimal allocation of three units of SCs on IEEE 69-bus RDS. The MOLA and MOTEO approach successfully optimize the current objective function (F₂) to decrease the total active loss to 150.94 KW and 152.5 KW, respectively, for the CPFL model. The enhancement of the corresponding TVSI is 63.128 p.u and 63.135 p.u. Figures 10 and 11 clarify that MOLA and MOTEO provide approximately similar solutions. The total voltage deviation is decreased from the base case of 1.83734 p.u to 1.2875p.u and 1.2866 p.u for MOLA and MOTEO algorithms, respectively, at the constant power load model. Note that if the algorithm provides a better value for one objective, it will give an acceptable solution for the other and vice versa. It mainly depends on the non-dominated solutions obtained using the multi-objective optimization technique and the method for selecting the best compromise solution.

Fig. 10

Voltage profiles for the IEEE 69-bus under different load models with the optimal allocation of SC using MOLA and MOTEO Techniques through minimizing active power loss and maximizing voltage stability

Fig. 11

POF with fuzzy-based BCS for the optimal allocation of SC using MOLA and MOTEO techniques through minimizing power loss and maximizing voltage stability under different load models

Table 9 furnishes the optimal location and size of three SCs units blended into the test network by minimizing F₃, which seeks to mitigate the total active loss, decrease voltage deviation, while enhancing voltage stability. The MOLA algorithm provides the lowest value for the total active loss of about 150.91 KW for the CPFL model, as opposed to the MOTEO method, which provides a value of 151.55 KW. The MOTEO algorithm decreases the corresponding RMSVI to 0.026541 p.u and improves the TVSI to 63.127 p.u, while the MOLA algorithm lowers the RMSVI to 0.026777 p.u and enhances the TVSI to 63.044 p.u. Figure 12 displays the system’s voltage profiles under various load levels. Also, the POFs are illustrated in Fig. 13 under different load conditions while minimizing F₃. The results demonstrate the superiority of the MOLA and MOTEO algorithms for the multi-objective optimal allocation problems of SCs under different static load models.

Fig. 12

Voltage profiles for the IEEE 69-bus under different load models with the optimal allocation of SC using MOLA and MOTEO Techniques through minimizing active power loss, reducing voltage deviation and maximizing voltage stability

Fig. 13

POF with fuzzy-based BCS for the optimal allocation of SC using MOLA and MOTEO techniques through minimizing power loss, mitigating voltage deviation, and maximizing voltage stability under different load models

4.2 Scenario II: Integration of DG Type-I with unity power factors into IEEE 69-bus RDS

In this scenario, the integration of three units of DGs at unity power factor to the IEEE 69-bus RDS is optimized using the MOLA and MOTEO approaches at different load models during minimizing F₁, F₂, and F3, as represented in Tables 10, 11, and 12, respectively. For instance, Table 10 shows the BCS achieved using the MOLA and MOTEO algorithms to reduce the RMSVI and losses of the IEEE 69-bus RDS at various voltage-dependent load models. The summation of the active power loss at the CPFL model was reduced to 71.947 KW and 71.844 KW, with a reduction in 68.0237 and 68.0694 percent for the MOLA and MOTEO methods, respectively. Furthermore, the corresponding RMSVI has been reduced from the base case of 0.03795 to 0.0052885 p.u and 0.0052432 p.u using MOLA and MOTEO techniques, respectively. The total installed capacity of three PV units for the CPFL model is 2895.74 KW for the MOLA algorithm and 2904.87 KW for the MOTEO algorithm. Figure 14 shows the voltage profiles for the current test system at various static load models with the installation of three DG Type-I units. This figure demonstrates that the minimum level is 0.9703 p.u and 0.9751 p.u at bus 65 for the CPHL model using MOLA and MOTEO, respectively. In other words, the restriction for the operating voltage is satisfied by installing three units of DGs Type-I at a unity power factor. Furthermore, the POFs are represented in Fig. 15, which demonstrates the superiority of the MOTEO algorithm for IL and RL load models, independent of BCS.

Table 10 BCS for the optimal allocation of DG Type-I using MOLA and MOTEO techniques through minimizing power loss and reducing voltage deviation under different load models

Table 11 BCS for the optimal allocation of DG Type-I using MOLA and MOTEO techniques through minimizing power loss and maximizing voltage stability under different load models

Table 12 BCS for the optimal allocation of DG Type-I using MOLA and MOTEO techniques through minimizing power loss, maximizing voltage stability, and reducing voltage deviation under different load models

Fig. 14

Voltage profiles for the IEEE 69-bus under different load models with the optimal allocation of DG Type-I using MOLA and MOTEO Techniques through minimizing active power loss and reducing voltage deviation

Fig. 15

POF with fuzzy-based BCS for optimal allocation of DG Type-I using MOLA and MOTEO techniques through minimizing power loss and mitigating voltage deviation under different load models

Seeking to minimize the overall line loss while also improving the voltage stability index, i.e., minimize F₂, Table 11 shows the non-dominated solutions with the BCS derived using the two current approaches for the optimum distributions of three DGs Type-I units on IEEE 69-bus RDS. The total active losses for the CPFL model were reduced by 80.484 KW and 82.079 KW, using the MOLA and MOTEO algorithms, respectively, while the corresponding TVSI is increased from the base value of 61.2184 p.u to 67.414 p.u and 67.686 p.u, respectively. Moreover, the graphical illustration for the voltage profile of all voltage-dependent load models is described in Fig. 16, which proves that the MOTEO algorithm provides better voltage levels for all models than the MOLA algorithm. On the other hand, as shown in Fig. 17, the MOTEO algorithm provides more accurate POF than MOLA for IL and CI models. The MOTEO technique provides more range for the objective functions during all studied load models, allowing the system operator to select a suitable value among these non-dominated solutions.

Fig. 16

Voltage profiles for the IEEE 69-bus under different load models with the optimal allocation of DG Type-I using MOLA and MOTEO Techniques through minimizing active power loss and maximizing voltage stability

Fig. 17

POF with fuzzy-based BCS for the optimal allocation of DG Type-I using MOLA and MOTEO techniques through minimizing power loss and maximizing voltage stability under different load models

Ultimately, regarding F₃, which seeks to decline the line loss and voltage deviation and increase voltage stability, Table 12 offers the best placement and capacity for three DGs Type-I units incorporated into the 69-bus test system. The MOLA algorithm gives the lowest value for the total active loss, i.e., 76.616 KW for the CPLFL model, as opposed to the MOTEO method, which provides 77.517 KW. In contrast to the MOLA algorithm, which drops the RMSVI to 0.0057076 p.u and raises the corresponding TVSI to 67.395 p.u, the MOTEO algorithm reduces the RMSVI to 0.0037401 p.u and increases the corresponding TVSI to 67.278 p.u. The system’s voltage profiles under the studied load levels are shown in Fig. 18. It demonstrates that the MOTEO also provides better voltage levels than MOLA under all static load models. Additionally, the POFs with BCS is presented in Fig. 19 through minimizing F₃ using MOLA and MOTEO techniques. The results revealed that the MOLA and MOTEO algorithms are better for multi-objective optimal allocation problems of DG Type-I.

Fig. 18

Voltage profiles for the IEEE 69-bus under different load models with the optimal allocation of DG Type-I using MOLA and MOTEO Techniques through minimizing active power loss, reducing voltage deviation and maximizing voltage stability

Fig. 19

POF with fuzzy-based BCS for the optimal allocation of DG Type-I using MOLA and MOTEO techniques through minimizing power loss, mitigating voltage deviation, and maximizing voltage stability under different load models

4.3 Scenario III: Integration of DG Type-III with Optimal Power Factor into IEEE 69-bus RDS

Similarly, in the last scenario, the incorporation of three units of DG Type-III with optimal power factor to the IEEE 69-bus RDS is optimized using the MOLA and MOTEO techniques at different load models with the minimization of F₁, F₂, and F₃, as represented in Tables 13, 14, and 15, respectively. Table 13 illustrates, for instance, the BCS obtained using the fuzzy decision-based algorithm during minimizing F₁ using the MOLA and MOTEO algorithms at different load levels. This Table indicates that the DG Type-III performs better results than the DG Type-I because it provides the RDS with apparent power at the lagging power factor. Regarding the CPFL model, the MOTEO technique successfully identifies the best size and location of three DG Type-III units that decrease the line losses to 4.685 KW and mitigate the corresponding RMSVI to 0.0011604 p.u, while the MOLA algorithm reduces the system loss to 5.3653 KW and lowers the RMSVI to 0.0013749 p.u. With the presence of three DG Type-III units, the voltage profiles for the present test system under different load levels have been improved compared to the previous scenarios, as shown in Fig. 20. The minimum voltage level is recorded at bus 50 with 0.99080 p.u and 0.99081 p.u for MOLA and MOTEO, respectively. Moreover, Fig. 21 displays the POF with BSC for the presented optimization techniques, which depicts that the MOTEO algorithm offers an accurate POF for CPFL, CPHL, CI, CC, and RL load models. On the other hand, the MOLA algorithm provides the best POF for the IL and CL models.

Table 13 BCS for the optimal allocation of DG Type-III using MOLA and MOTEO techniques through minimizing power loss and reducing voltage deviation under different load models

Table 14 BCS for the optimal allocation of DG Type-III using MOLA and MOTEO techniques through minimizing power loss and maximizing voltage stability under different load models

Table 15 BCS for optimal allocation of DG Type-III using MOLA and MOTEO techniques through minimizing power loss, maximizing voltage stability, and reducing voltage deviation under different load models

Fig. 20

Voltage profiles for the IEEE 69-bus under different load models with the optimal allocation of DG Type-III using MOLA and MOTEO Techniques through minimizing active power loss and reducing voltage deviation

Fig. 21

POF with fuzzy-based BCS for optimal allocation of DG Type-III using MOLA and MOTEO techniques through minimizing power loss and mitigating voltage deviation under different load models

Table 14 shows the non-dominated solutions with the BCS acquired using the two optimization approaches for the integrations of three DGs Type-III units on the 69-bus system through the minimization of F₂. In the CPFL model, the total active power loss was decreased by 11.443 KW and 19.388 KW, respectively, for MOLA and MOTEO techniques, while the corresponding TVSI was raised to 68.967p.u and 69.578 p.u. It is important to note that the reduction in active power loss that results from decreasing F1 is significantly more than its value from minimizing F₂ and vice versa for the voltage stability index. Also, the graphical representation of the voltage profiles for all static load models is illustrated in Fig. 22, which establishes that the two optimization algorithms provide good voltage levels under various load models. In this situation, both optimization techniques provide approximately analogous non-dominated solutions, as depicted in Fig. 23.

Fig. 22

Voltage profiles for the IEEE 69-bus under different load models with the optimal allocation of DG Type-III using MOLA and MOTEO Techniques through minimizing active power loss and maximizing voltage stability

Fig. 23

POF with fuzzy-based BCS for the optimal allocation of DG Type-III using MOLA and MOTEO techniques through minimizing power loss and maximizing voltage stability under different load models

In the last studied case, the MOLA and MOTEO are utilized to optimize the proposed multi-objective function (F₃) to identify the optimum size and location of three units of DGs Type-III integrated into the 69-bus test system. The performance of the optimization techniques has been tabulated in Table 15 at different load levels. The MOLA algorithm reduces total active loss and related RMSVI in the CPFL model to 7.5257 KW and 0.028366 p.u, respectively, while raising the corresponding TVSI to 68.316 p.u. On the other hand, the MOTEO method decreases the total active power loss and RMSVI to 7.0665 KW and 0.0033846 p.u, respectively, and enhances the corresponding TVSI to 68.499 p.u. The MOLA algorithm provides the lowest active power loss and rout mean square voltage error, approximately 4.4841KW and 0.0015184 p.u under the CPLL and CC model, respectively. However, the MOTEO algorithm specifies the maximum voltage stability of around 68.889 p.u at the IL model. The system’s bus voltages at different load levels are depicted in Fig. 24. The POF with BCS is clarified in Fig. 25 while minimizing F₃ using MOLA and MOTEO techniques. The results proved that the MOLA and MOTEO algorithms are efficient techniques for multi-optimal allocation of DG Type-III at optimal power factor.

Fig. 24

Voltage profiles for the IEEE 69-bus under different load models with the optimal allocation of DG Type-III using MOLA and MOTEO Techniques through minimizing active power loss, reducing voltage deviation and maximizing voltage stability

Fig. 25

POF with fuzzy-based BCS for the optimal allocation of DG Type-III using MOLA and MOTEO techniques through minimizing power loss, mitigating voltage deviation, and maximizing voltage stability under different load models

5 MOLA and MOTEO comparison to other algorithms

The MOLA as a hybrid algorithm differs from many in the literature since it utilizes population and trajectory-based search strategies. It might provide some promising solutions for resolving MO issues. However, it may furnish local solutions for another set of MO problems. So, the outcomes obtained using MOLA and MOTEO techniques are compared with recent multi-objective optimization approaches, such as multi-objective artificial hummingbird algorithm (MOAHA) [21], multi-objective improved Harris Hawks optimizer (MOIHHO) [28], multi-objective Harris Hawks optimizer (MOIHHO) [28], mutated slap swarm algorithm (MSSA) [21], multi-objective gray wolf optimizer (MOGWO) [21], multi-objective water cycle algorithm (MOWCA) [21], and improved decomposition-based evolutionary algorithm (I-DBEA) [22]. Optimization algorithms based on Pareto optimum sets are considered for fair comparative analysis. Table 16 compares the outcomes of the presented algorithms with various multi-objective techniques during minimizing F₁ and F₃ through the optimal allocation of DG Type-I and III for the constant power load model. Here, the VSI_min and VD symbolize the lowest voltage stability index and square voltage deviation, respectively. It demonstrates that the MOLA and MOTEO algorithms provide efficient BCS during installing DG Type-I and III. The MOTEO algorithm specifies the lowest power loss of around 7.07KW for integrating DG Type-III at optimal power factor through minimizing active power loss, mitigating voltage deviation, and maximizing voltage stability.

Table 16 Results obtained using MOLA and MOTEO algorithms compared with different multi-objective techniques under different optimization scenarios during the incorporation of DG Type-I and III

6 Statistical analysis and over all evaluation

The proposed multi-objective functions solved by the present optimization techniques are evaluated statistically by implementing several times, and then, some statistical tests are conducted. This section outlines different statistical analysis that includes multi-objective metrics, t test, and other statistical analysis such as mean, DS, etc., as explained below.

6.1 Classical statistical analysis

With the optimal allocation of three units of SCs, DGs Type-I, and DGs Type-III, Table 17 depicts the statistical analysis for the indices of system loss, RMSVI, and TVSI during different optimization scenarios for the CPFL of the 69-bus RDS. The performance metrics compromise best, wrest, mean, median, standard deviation (SD), and standard error (SE). The MOTEO algorithm achieves the lowest SD and SE among all different scenarios during the optimization of F₁, F₂, and F₃. Nonetheless, the MOLA provides the best value for the BCS of f₁ through all studied cases. The boxplot for the statistical indices reported in Table 17 is also illustrated in Fig. 26. This figure show that the MOTEO technique has fewer outliers compared with the MOLA algorithm, which has the largest whisker for most studied cases.

Table 17 Statistical analysis for BCS of ${f}_{1}$, ${f}_{2}$, and ${f}_{3}$ under different optimization problems at the CPFL model of the IEEE 69-bus system

Fig. 26

Boxplot for fitness values via a set of separate trials during the integration of SC into IEEE 69-bus system at CPFL model

6.2 Statistical t test method

Another statistical-based t test approach conducted for the CPFL model of the 69-bus network during the optimization of F₁ is adopted under the integration of three units of SCs. The t test is commonly used on two or more samples that are almost normally distributed to determine whether their means are substantially different or not. In this context, the two-tail paired t test is considered here since both techniques solve the same objectives. The paired t test is conducted for the POF of total active power loss (f₁) and the corresponding RMSVI (f₂), which fit a normal distribution. The t test also offers an investigation of the hypothesis (null and alternative) of the difference between population means $\left({\mu }_{diff}\right)$ for a set of random samples. The null hypothesis $\left({H}_{o}\right)$ assumes that the ${\mu }_{diff}$ is zero, i.e., ${H}_{o}: {\mu }_{diff}=0$, while the alternative $\left({H}_{A}\right)$ assumes that $\left({\mu }_{diff}\right)$ is not equal to zero, i.e., ${H}_{A}: {\mu }_{diff}\ne 0$. Table 18 illustrates the p values and t-values for two degrees of freedom (DF), respectively, 29, and 73 with a significance level of 0.05%. These p values are much less than 5% except for f₁ at degree of freedom 30, and it supports the alternative hypothesis. In other words, the results of MOLA and MOTEO algorithms are statistically significant with a 95% confidence interval.

Table 18 Statistical t test analysis for the total active power loss (f₁) vs. RMSVI (f₂) at allocating three SCs units

6.3 Multi-objective performance metrics

Additionally, different multi-objective performance indicators such as spacing, diversity, hypervolume (HV), and hole relative size (HRS) have been employed to measure the quality of the POF acquired by MOLA and MOTEO techniques, see Table 18. These metrics can be defined as follows [45]: the HRS identifies the most extensive hole in the POF. This metric depends on Manhattan distance; the spacing metric specifies the spread of the non-dominated solutions along with POF. It precisely evaluates the distance between each solution and its nearest one in the same set. The diversity index attempts to quantify the extent of the spread accomplished in a computed POF. This metric needs the resolution of each single objective optimization problem, which is called extreme solutions, see Table 19. The hypervolume, also named S-metric, is defined as the volume of the objective space dominated by the computed POF bounded by a reference point. Note that these metrics are computed after separate trials of optimization techniques and tabulated in Table 20 in terms of average and SD. Across all studied scenarios, the MOTEO algorithm performs the best HV, while the MOLA achieves the lowest spacing index. Additionally, the smallest SD is precisely accomplished by the MOTEO algorithm. The MOLA records the lowest average value for the HRS and diversity during minimizing F₂ under all scenarios, while the MOTEO algorithm reports only the minimum average of HRS under scenario II, approximately 45.8447 against 56.0769 for MOLA. Regarding F₁, the MOTEO provides the minim average of HRS and diversity under scenarios I, and III, while the MOLA is better in the case of scenario II.

Table 19 Extreme solutions for the IEEE 69-bus RDS at CPFL model considering different objective functions

Table 20 Diversity, HV, Spacing, and HRS metrics for different MO functions for the IEEE 69-bus system at CPFL model

6.4 Overall evaluation of MOLA and MOTEO algorithms

Ultimately, the MOTEO technique is the most efficient algorithm based on SD and SE, as previously mentioned in Tables 16 and 18. So, the comparison is conducted regardless of SD to be independent of the best parameters. Table 21 shows a comparison study between MOLA and MOTEO algorithms through different performance indicators at the CPFL model of the 69-bus distribution network. Note that this table can be constructed as follows: the algorithm will record a point if it achieves the best value. Otherwise, it will have no scores. As can be observed that the MOLA superiority appears in achieving the highest rates for the HV indicator, i.e., 6 points, and the lowest values for the diversity, i.e., 5 points, while the MOTEO specifies the minimum values for the spacing metric, i.e., 6 points. However, both techniques provide equally HRS indicators. Regarding the statistical analysis listed in Table 4, the MOTEO is better than MOLA, with a total score of 24 against 18 for MOLA. Consequentially, the MOTEO is the best with a total score of 34, representing 51.5 percent, against 32, representing 48.5 percent for MOLA.

Table 21 Overall evaluation of MOLA and MOTEO techniques under CPFL model of 69-bus RDS

7 Conclusion and future work

This paper has presented recently developed multi-objective optimization techniques for optimal allocation of SCs and different DG types considering several voltage-dependent load models. The proposed multi-objective functions seek to minimize the active power loss and voltage deviation level while improving voltage stability. A new index for the voltage deviation called root mean square voltage has been proposed. The fuzzy decision-making-based algorithm has been adopted to select the best compromise solution from a non-dominated Pareto set computed by the hybrid of APLS factor and MOLA/MOTEO techniques. The developed methodology has been tested under three test scenarios implemented on the IEEE 69-bus distribution network. Three units of SCs and DGs with unity and optimal power factors are optimally allocated during several optimization scenarios, such as bi- and tri-objective problems. This study concluded numerous statistical analyses to assess the performance of the MOLA and MOTEO techniques. The traditional statistical analysis is conducted in terms of BCS, while the t test is applied to determine whether the averages of the suggested algorithms are significantly different or not. Additionally, multi-objective performance indicators such as spacing, hypervolume, diversity, and hole relative size are included. The total active power loss with their corresponding RMSVI and TVSI is tabulated, while the voltage profile and POF for each case are graphically illustrated. The fetched simulation results verified the superiority of the MOTEO algorithm in achieving accurate POF and fewer outliers and SD among all studied metrics. For instance, for optimal allocation of DG Type-III with optimal power factor during minimizing a three-dimensional problem, the MOLA reduces power loss and TVD by a percent of 96.86 and 90.47, respectively, while increasing the corresponding TVSI by 11.89%. On the other hand, the MOLA algorithm lowers the system active loss and TVD by a percent of 96.66 and 92.75, respectively, while improving the corresponding TVSI by 11.59%. The comprehensive evaluation based on different metrics also demonstrated the MOTEO performance, approximately 51.5% percent, against 48.5 percent for the MOLA technique. The authors suggest the application of MOTEO to solve other different objectives such as annual cost, energy not supplied, and reliability indices in future studies, as it has a good exploitation and exploration phase.