1 Introduction

Nowadays, Artificial Intelligence approaches in Finance are becoming dominant. This is due to the broad discussion about the analysis of financial data developed over the years. In fact, since the earliest works related to time series, the subject has pulled in many academics and practitioners. Among the others, one of the most exciting application fields is the development of investment strategies and risk management. In particular, statistical arbitrage is concerned with creating trading strategies that exploit hidden patterns in the behavior of related assets. Currently, most of the works in this field are based on future price predictions. However, the reliability of such forecasting approaches is hugely discussed. Furthermore, one can also argue that risk hedging is sometimes inefficient because it does not consider that some risk factors are specific to only an asset subset.

In this work, we propose a methodology to overcome these limitations. The main task we are involved in is building a portfolio that is able to reduce investment risk. In more detail, we consider a set of time \(\mathcal {T}=\{1,..., T\}\) and a universe of stocks \(\mathcal {J}=\{1,..., J\}\). As a common practice in the financial literature, we work with the stocks returns, i.e., \(\textbf{R} = \{r^j\}_{j\in \mathcal {J}}\). Each return is a time series indexed in \(\mathcal {T}\), that is \(r^j = \{r^j_t\}_{t\in \mathcal {T}}\). A portfolio is a linear combination of stock returns obtained with a weight vector \(\varvec{\phi }=(\phi ^1,..., \phi ^J)\in [-1,1]^J\) such that the norm \(l_1\) of \(\varvec{\phi }\) is equal to 1. In other words, taking into account that each \(\phi ^j\) can be considered as the portfolio exposition on stock jth, we require that the full exposition, on both long and short positions, is unitary. It should be noted that by exploiting the above formulation, two assumptions are made: i) the assets are infinitely divisible, and ii) short positions are allowed. Furthermore, for convenience, we also assume iii) there are not transaction costs and iv) our trades have no impact on prices.

Among all the possible portfolios, we are interested in finding the one which cuts back on the risk related to the investment. Actually, this is not a straightforward task, starting from the definition and the type of risk we aim to minimize. In the following, we evaluate portfolio strategies with several performance measures through Cross-Validation (CV), measuring the mean and standard deviation (std) of each investment. Then, we consider a portfolio as robust if its mean is optimal and its deviation is low. This is the main task of this work: we want to find an investment strategy that exhibits good performance and is reliable, i.e., whose results do not change a lot according to the time in which it works.

To achieve our goal, we exploit a multi-step procedure. Firstly, we represent each stock return with a convenient linear factor model by using the Principal Component Analysis (PCA). We aim to extract risk factors at different time granularities to have a complete overview of both short-term and long-term risk factors. In this stage, a multicollinearity filter is applied to avoid the presence of multicollinearity, which is a linear dependence between two or more regressors that introduces a bias in the parameters estimate. Then, we exploit this representation and the Adaptive-Lasso to perform feature selection and to partition stocks universe \(\mathcal {J}\) by grouping those stocks whose behavior is affected by similar factors. Finally, we work inside each cluster to obtain a local portfolio that deletes the exposition on such factors, and we aggregate the portfolios resulting from each cluster to get the final one.

Consequently, the main contributions of this paper can be summarized as follows:

  • we propose a novel multi-horizons methodology for stocks clustering;

  • we propose a statistical arbitrage strategy based on the previous clustering procedure;

  • we prove the stability of our strategy by carefully comparing it with three well-known benchmarks, i.e., the minimum variance portfolio, the mean-var portfolio, and the Exponential Gradient, on both the Italian, German, American, Japanese, Brazilian, and Indian stock markets.

The following of this paper can be summarized as follows. In Sect. 2 a brief literature review of the building blocks of our proposal is offered. Section 3 introduces our methodology. Section 4 describes the experimental stage by providing detailed information about the exploited datasets, the experimental setup, and the obtained results. Finally, Sect. 5 concludes this work by summarizing limitations and findings and providing further analysis directions.

2 Contextualization and related work

This section provides a short overview of related work and state-of-the-art approaches linked to our proposal. In this way, it is provided a contextualization of the problem and, in particular, of our framework.

2.1 Model determination

Linear factor models play a crucial role in finance ranging from asset pricing theory to portfolio optimization. In the literature, there are different types of linear factor models (e.g., dominant residuals, systematic-idiosyncratic, and pure exogenous). In this manuscript, we focus on the systematic-idiosyncratic class of the linear factor model. It relates the rate of return on an asset \(j-th\) to the values of a limited number of factors by a linear equation, as in Eq. 1:

$$\begin{aligned} r^j_t = \alpha ^j + \beta ^j_1F_{1,t} +... + \beta ^j_nF_{N,t} + \varepsilon ^j_t \quad \forall j\in \mathcal {J}, \ \forall t\in \mathcal {T} \end{aligned}$$
(1)

we can also rewrite Eq. 1 in matrix form, as:

$$\begin{aligned} \textbf{R}= \varvec{I\alpha }^T+ \varvec{F\beta }+\varvec{\varepsilon } \end{aligned}$$

where \(\textbf{R}= (r^1, \ldots , r^J)\in \mathbb {R}^{T\times J}\) is the matrix whose columns are the stock returns time series, \(\textbf{I}= (1, \ldots , 1)\in \mathbb {R}^T\) is the unitary vector, \(\varvec{\alpha }=(\alpha _1, \ldots , \alpha _J)\in \mathbb {R}^J\) are J constants and \(\varvec{\alpha }^T\) is the transpose of \(\varvec{\alpha }\), \(\textbf{F}=(F_1, \ldots , F_N)\in \mathbb {R}^{T\times N}\) is the matrix whose columns are the N risk factors \(F_{i}=\{F_{i,t}\}_{t\in \mathcal {T}}\), \(\varvec{\beta }=\{ \beta ^j_n\}\in \mathbb {R}^{N\times J}\) is a matrix of factor loadings and \(\varvec{\varepsilon }=(\varepsilon ^1, \ldots , \varepsilon ^J)\in \mathbb {R}^{T\times J}\) is the matrix whose columns are the residuals time series \(\varepsilon ^j=\{\varepsilon ^j_t\}_{t\in \mathcal {T}}\). In this model, the factors and the residuals satisfy two types of constraints. More specifically, the residual is assumed to be uncorrelated with each factor, \(E(\varepsilon ^j, F_n)=0, j=1, \ldots , J, n=1, \ldots N\). In addition, the residual for one asset’s return is assumed to be uncorrelated with that of any other, \(E(\varepsilon ^j, \varepsilon ^q)=0, j \ne q=1, \ldots , J\). Since the risk factors are systematic, the only sources of correlations among asset returns are given by their exposures to the factors and the covariances among the factors. So, in this model, we assume asset return residual components are unrelated. Hence, residual components are particular to each asset. Thus, the risk associated with the residual return is idiosyncratic for that asset.

Several works employ and discuss such a type of model. For example, [1] studies the asymptotic properties of the covariance structure, as both the size of the time-series universe and the number of available observations tend to infinity. Instead, [2] is related to determining the risk factors in a context that allows risk factors to be correlated with each other.

By contrast, in constructing our framework, we need independence between the regressors in the factor model. In particular, as common in the standard financial literature, we assume the risk factors are the observations of independent, identically distributed random variables with 0 mean and unitary variance. In particular, we are assuming the absence of multicollinearity among them. This hypothesis is central to our work, as both the clustering and the statistical arbitrage strongly depend on the model parameters. So, we verify it by applying condition number measures that is usually applied to detect the presence of collinearity (see, for example, [3]). It is a widely used approach in the recent literature, see for example [4, 5].

Another critical point related to applying a linear factor model as that in Eq. 1 is the determination of the risk factors. As pointed out by [6], three different approaches exist to solve this task. The fundamental approach uses the fundamentals of the stocks considered as risk factors, e.g., P/E Ratio. It is exploited by several researchers, including the Nobel Prize Fama. In particular, there are a series of articles, such as [7, 8], which develop a five-factor model for stock pricing. Similarly, the macroeconomic approach exploits as risk factors some macroeconomic variables like the return of market indexes or the inflation rate. An example of this approach is [9], where the yield curve is approximated with a dynamic factor model obtained with dimensionality reduction techniques applied to many macroeconomic features. Instead, in [10] South Africa stocks returns are analyzed with the help of both national and international variables. The main aim is to understand how different features impact the national industrial process.

In the two approaches above, the risk factors are searched outside the data. In contrast, the statistical approach employs feature extraction techniques to extract risk factors from the stocks universe itself. Usually, these techniques belong to both the fields of statistical and machine learning. The aim is to rely on data analysis instruments to obtain factors highly representative of the data we are working with, particularly their variance. [11] work with time series from the Japanese Stock Market by applying the Independent Component Analysis to extract risk factors fed into a linear factor model, on the background of Arbitrage Pricing Theory. Instead, several other works focused on applying PCA, thanks to its simplicity, speed, and reliability. In [12], the asymptotic properties of the factors obtained via PCA are analyzed, under the stationary condition, as the dimension of the sample and of the time series go to infinity. Furthermore, the results are tested on stocks belonging to the \(S \& P\) index. Instead, in [13], risk factors are obtained by applying the PCA on the projection of the input matrix on an appropriate space. The proposal is then evaluated on the \(S \& P\) constituent stocks. Finally, [14] exploits the PCA to extract risk factors for a linear model, which is then used as a starting point for constructing a minimum variance portfolio. Also, the experimental stage of this study is carried out on the stocks in the \(S \& P\) index.

2.2 Clustering

The linear factor models built with the PCA performed on multiple granularities are then exploited to cluster the stocks. Time-series clustering is an open debate widely discussed in the literature, which is far more complex than static data. Due to the enormous complexity of the task, several works for specific-purpose goals have been proposed, such as [15,16,17,18]. Furthermore, several papers have also been concerned with reviewing and classifying the existing methodologies. For example, [19] divides clustering methodologies according to the way they operate. In particular, raw-data-based approaches directly work with time series. This goal is often achieved by exploiting some particular distance metrics that considers the input’s temporal evolution. Instead, model-based approaches work with a specific time-series model for each series by clustering the fitted coefficients. Finally, features-based approaches extract from each time series a feature vector, and the clustering is performed on those vectors.

Actually, our proposal can be placed in the framework of features-based clustering. In fact, from each stock j, it is extracted the binary vector of features \(\theta ^j\) that represents if the stock is significantly affected by the corresponding risk factor. So, indicating with \(\beta ^j=(\beta ^j_1,...,\beta ^j_N)\) the estimated coefficients of the linear factor model representing the stock j, the feature vector \(\theta ^j\in \mathbb {R}^N\) can be written as:

$$\begin{aligned} \theta ^j = (\theta ^j_1,...,\theta ^j_N)\in \mathbb {R}^N, \quad s.t. \quad \theta ^j_i = \bigg \{ \begin{array}{l} 1 \quad if \; \beta ^j_i\ne 0 \\ 0 \quad if \; \beta ^j_i=0 \end{array} \end{aligned}$$
(2)

In the recent literature, several works try to exploit clustering methodologies for portfolio optimization or trading/investment strategies. For example, [20] uses different clustering techniques such as K-means to partition the assets universe. Then, standard portfolio optimization techniques are applied to each cluster. The strategy is tested on the high-frequency data of the Russell 1000 stocks. Instead, [21] exploits the correlation between stocks as a critical feature to cluster assets and create optimal portfolios. Furthermore, the authors develop a framework that unifies the typical two stages of this strategy, i.e., clustering and portfolio construction. However, several other methods for portfolio construction based on a clustering and unsupervised learning approach have been proposed in the financial literature. See, for example, [22] which shows in detail different state-of-the-art methodologies and how they can impact academic financial research.

2.3 Statistical arbitrage and portfolio construction

Once the clustering is obtained, our methodology constructs a market-neutral portfolio within each cluster, which is a portfolio such that the exposition on each risk factor is 0. In other words, the return of such a portfolio type is not related to the overall market conditions, and it is affected only by the weighted sum of \(\alpha ^j\) and \(\varepsilon ^j\). According to the classical financial literature, in a well-diversified portfolio, the idiosyncratic risks should delete themselves for the diversification effect. However, it has been shown in recent works that they could contain valuable information and undiscovered patterns. Such information should be taken into account to improve investment strategies significantly. For example, [23] constructs a portfolio by exploiting the residual of a linear factor model with a fundamental approach. Their proposal is compared with the portfolio obtained without considering the idiosyncratic risks. The experiments on the American market show the effectiveness of their proposal, with a Sharpe Ratio significantly higher than the benchmark one, thanks to the reduced portfolio variance. In [24], the authors develop a strategy to exploit hidden patterns in the residuals to construct a zero investment portfolio in a deep learning framework. Their proposal has been accurately tested on stocks markets over the years, showing good robustness also during the financial crisis.

As for statistical arbitrage, several experiments have been carried out through the years. Among them, [25] compares the statistical and macroeconomic approaches to constructing a market-neutral portfolio. In more detail, the authors test the strategy obtained with PCA and that obtained by using the Exchange Traded Funds as a proxy of risk factors. The experiments are carried out on the American stock market data between 1997 and 2007. In particular, the reliability of the strategies is tested during both bull and bear periods (the so-called Dot-com Bubble). The final results show the profitability of both approaches in the considered period. [26] contains a comparison among the applications of different machine learning techniques for constructing statistical arbitrage and portfolio optimization strategies. In particular, to provide a reliable analysis of these state-of-the-art methods, the author exploits a dataset made up of hundreds of American stocks over about two decades. Also, [27] discusses the properties behind the statistical arbitrage to provide a theoretical background and a strong characterization of this strategy. Finally, Table 1 contains a comparison among different statistical arbitrage approaches presented in the last years. In particular, we highlight the peculiarities of each work and its weaknesses when compared to our proposal.

Table 1 Comparison among statistical arbitrage approaches. For each work, a short description and the main differences with our proposal are provided
Full size table

3 The methodology

In this section, we briefly show the primary data analysis tools we exploit. Then, we describe the proposed methodology by providing both pseudo-codes and illustrative images. Finally, we discuss some issues related to our proposal.

3.1 Feature selection: adaptive lasso

In our framework, a key role is played by the feature selection, which should identify the risk factors which actually drive stock returns. Several approaches for feature selection are discussed in the literature. For example, see [34, 35] for a comprehensive review of the several methodologies, their application field, and their statistical properties. Among them, we exploit the Adaptive Lasso (A-Lasso) [30]. It is a linear regression technique with weighted \(l_1\) regularization terms, so the loss function can be written as:

$$\begin{gathered} {\mathcal{L}} = \frac{1}{T}\sum\limits_{{t = 1}}^{T} {\left[ {r_{t}^{j} - \sum\limits_{{i = 1}}^{N} {F_{{i,t}} } \beta _{i}^{j} } \right]^{2} } \hfill \\ \quad \quad + k\sum\limits_{{i = 1}}^{N} {\mid } w_{i}^{j} \beta _{i}^{j} {\mid }\quad \quad w_{i}^{j} = \left( {\frac{1}{{\hat{\beta }_{i}^{j} }}} \right)^{\tau } \hfill \\ \end{gathered}$$
(3)

where the weights \(w_i\) are obtained from the inverse of the Ordinary Least Square coefficients \(\hat{\beta }^j_i\) and \(k, \tau\) are two nonnegative hyperparameters.

It can be shown that thanks to the \(l_1\) regularization terms, the parameters related to the negligible regressors are set to zero. In this way, we can effectively know which risk factors play a role in the return of each stock. Furthermore, the reason behind our choice of using A-Lasso is twofold. From one side, it is designed to handle a linear relationship between the target and the predictors, such as that in Eq. 1, with little computational requirements. On the other side, it has been shown that A-Lasso satisfies the oracle properties specified in [36]. These properties ensure the asymptotic consistency of the estimator in terms of both relevant features detected and parameters estimate.

So, thanks to its reliability and accuracy in determining relevant features, A-Lasso has been widely used in the modern financial literature; see, for example, the works [37, 38]. The former is related to bankruptcy prediction. Several markets from Europe and Japan are analyzed, and the A-Lasso is applied to determine which features are relevant for this task. The experimental stage proves that, in almost all the considered study cases, the feature selection can improve the performance of the prediction. The latter is concerned with explaining excess returns in the stock market. To face this task, the authors propose the Specification-Lasso, a modified version of Lasso and A-Lasso. The strategy’s validity is shown by both simulated and real experiments, where the regressors are several fundamentals related to the stocks under observation.

3.2 Risk factors extraction

In this work, the dataset of each experiment we carry out is made up of daily observations of stocks in six different markets: Italian, German, American, Japanese, Brazilian, Indian (see Sect. 4 for further information on the datasets). So, for each experiment, we use a set of risk factors obtained starting from the daily returns dataset. Furthermore, as our investment strategies have monthly horizons, we also exploit risk factors obtained from the monthly returns dataset, which is the dataset obtained by aggregating daily returns each month.

We extract the risk factors in Eq. 1 via PCA. Actually, there exist several feature extraction techniques. PCA is a linear approach, while more sophisticated nonlinear approaches are the Neural Network PCA (NNPCA) or the Variational AutoEncoder (VAE). However, previous study [39] shows that in the stock markets, PCA performs as well as the nonlinear methods, with the strong advantage of being computationally cheaper. The great advantage in computational time, while the output results are almost similar, is the reason for our choice.

Once extracted, the risk factors are standardized to obtain values distributed as a zero-mean random variable with unitary variance. As already pointed out, we focus on extracting two different sets of factors: daily and monthly. The formers are obtained by applying the PCA to the daily returns dataset. For the latter, we first apply the PCA on the monthly returns dataset to obtain the weights of the Principal Components (PCs). Then, the weights matrix is applied to the daily returns dataset in order to extract the monthly risk factors on a daily basis. Figure 1 describes the process of feature extraction.

Fig. 1
figure 1

The extraction of the risk factors. Two different granularities are considered: daily and monthly. The raw data are fed into the PCA, which extracts the weights of the Principal Components (PCs). In particular, two sets of weights are obtained: one from the PCA applied to daily data and the other from the PCA applied to monthly data. Then, the daily and monthly PCs are obtained by multiplying these weights with the daily dataset. Finally, the Risk Factors set is constructed by considering all the daily PCs and the monthly PCs that pass the Multicollinearity Filter

Full size image

In other words, consider the overall set of risk factors in Eq. 1, i.e., \(F=\{F_i\}_{i\in \{1,...,N\}}\). We aim to split it into two subsets. The first one is \(F_d=\{F_i\}_{i\in \{1,...,N_d\}}\) and it is referred to the risk factors extracted on daily basis. The second one is \(F_m=\{F_i\}_{i\in \{N_d+1,...,N\}}\) and it contains the PCs obtained on monthly basis.

One of the significant issues for this type of approach is determining how many PCs have to be considered. The choice of the number of PCs to consider is empirically made by considering the results of previous experiments carried out in similar contexts. Another issue is related to the multicollinearity that could affect parameters estimate. If we extracted risk factors on a singular basis, this would not be a problem as the PCs, for construction, are independent of each other. Instead, in our framework, multicollinearity could seriously harm strategy performances. For example, let us consider the first PC in the daily and monthly settings. As shown in the example in Fig. 2, they are almost the same.

Fig. 2
figure 2

The comparison between the first Principal Component obtained from daily returns and that extracted from monthly ones. The two components are almost one the translation of the other, with a very high correlation coefficient, about 0.99. This justifies the needing for a strategy to handle the multicollinearity which can arise when working with different granularities

Full size image

We handle this problem by applying a multicollinearity filter, i.e., we add the risk factors to the set F in three stages with a threshold rule. In the first stage, the daily PCs, which are referred to as \(PCs_d=\{D_1,...,D_{N_d}\}=F_d\), are added without any restriction. In the second stage, the monthly PCs are computed \(PCs_m=\{M_1,...,M_{N_m}\}\). For each one, a score is obtained as the maximum absolute correlation of the monthly component with the daily ones, that is \(score_M = \max _{D\in PCs_d} \mid corr(M, D)\mid , \quad \forall M\in PCs_m\). In the third stage, the monthly PCs whose score is lower than a fixed threshold \(\textbf{th}\) are added to F, so \(F_m=\{M\in PCs_m \ s.t. \ score_M < \textbf{th}\}\). Finally, F is defined as the union \(F_d \cup F_m\). In this way, we can avoid multicollinearity. The generation and selection of the risk factors are definitely described by Algorithm 1. Finally, observe that the number of PCs which survive the multicollinearity filter could vary according to time. This should ensure our strategy has the necessary flexibility to catch temporal evolution in the covariance of the assets. Anyway, we do not notice a significant variation in the risk factors set through our experiments.

figure a

3.3 Clustering approach

Once extracted the risk factors in F as described in the previous Subsection, A-Lasso is applied in order to obtain, for each stock \(j\in \mathcal {J}\), a subset \(\mathcal {A}_j\subset F\) made up of the more relevant risk factors, i.e., those which have the most significant impact on j. As already pointed out, by applying the A-Lasso, we obtain an estimate for each coefficient in Eq. 1. Furthermore, thanks to the \(l_1\) regularization, there are some coefficients set to zero. In this way, we can work with only the most important risk factors, which are contained in the subset \(\mathcal {A}_j\) defined as \(\mathcal {A}_j=\{i\in \{1,...,N\} s.t. \beta _i^j\ne 0\}\) where \(\beta _i^j\) is the coefficient estimate provided by A-Lasso.

figure b

To achieve our goal, the two hyperparameters of A-Lasso, \(k, \tau\), have to be set. This task is done by exploiting Grid Search and 5 folds CV. In particular, we set five folds whose length is equal to that of the investment, and we search the hyperparameters couple that minimizes the average mean square error (mse) among the folds. Furthermore, we consider only hyperparameter combinations that save between 2 and 4 PCs. In this way, we avoid too strong regularization (number of PCs \(\ge 2\)) and too complex models (so we set the number of PCs \(\le 4\)). This stage is the most computationally expensive of the whole procedure. In fact, as a Grid Search is executed for each asset, more than 10000 CVs are performed. This highlight the needing for a fast feature selection technique. However, some tricks can be used to reduce the time, as discussed in the Conclusion.

Finally, the clusters are constructed by grouping stocks with similar expositions to the same risk factors. More formally, once the sets \(\mathcal {A}_j\) have been determined, we define the equivalence relationship \(\sim\) in the stocks universe \(\mathcal {J}\) in this way:

$$\begin{aligned} j\sim i \iff \mathcal {A}_j = \mathcal {A}_i \quad \forall i,j \in \mathcal {J} \end{aligned}$$
(4)

Then, the clusters are defined as the equivalence classes associated with \(\sim\), that is, the clusters set \(\mathcal {C}\) is the quotient set \(\mathcal {J} / \sim\). Algorithm 2 describes the clustering methodology. The computational time of this algorithm is negligible compared to that of the total procedure.

3.4 Statistical arbitrage strategy

Once the clusters are obtained, a statistical arbitrage strategy, specifically a market-neutral portfolio, is constructed within each cluster. The starting point is the equation representing the stocks in a fixed cluster. Let us consider \(C\in \mathcal {C}\), let c be the cardinality of C, and let \(\mathcal {A}_C\) and a, respectively, be the set of risk factors relevant for the stocks in C and its cardinality. We can represent each stock in C by using Eq. 5:

$$\begin{aligned} r^j_t = \alpha ^j + \sum _{i\in \mathcal {A}_C} \beta ^j_iF_{i, t} + \varepsilon ^j_t \quad \forall j\in C, \ \forall t\in \mathcal {T} \end{aligned}$$
(5)

The first issue related to Eq. 5 is the estimate of the coefficients. We accomplish this task by applying the Pooled Ordinary Least Squares (OLS) Regression. That is, we separately estimate \(\alpha ^j\) and the vector \(\beta ^j\) in each time window, and then we average the single estimates. In more detail, we split the data into Time Windows (TW) whose length is coherent with the investment temporal horizon. Then, for each time window \(tw\in TW\), we obtain an estimate of the parameters \(\alpha ^j_{tw}\) and \(\beta ^j_{tw}\) by applying the OLS. Finally, we average the estimates in each window to obtain the final parameters, as in 6.

$$\begin{aligned} \alpha ^j = \frac{1}{\mid TW \mid }\sum _{tw\in TW}\alpha ^j_{tw} \quad \quad \beta ^j = \frac{1}{\mid TW \mid }\sum _{tw\in TW}\beta ^j_{tw} \end{aligned}$$
(6)

After determining the model coefficients, we aim to delete the exposition on each risk factor. In other words, we want to create a portfolio such that the weighted sum of the coefficients associated with the risk factor \(F_i\) is zero for each \(i\in \mathcal {A}_C\). As mentioned in the Introduction, we define a portfolio as a linear combination of stock returns where each component of the weights vector \(\phi =(\phi ^1,...,\phi ^c)\) represents the exposition on the related stock. Furthermore, as we allow for both long and short positions and we require the invested amount to not exceed the total capital, we impose the \(l_1\) norm of the weights to be 1. Accordingly, we can represent a portfolio made up of the stocks in C as:

$$\begin{aligned}{} & {} Port_t = \sum _{j\in C}\phi ^jr^j_t = \sum _{j\in C}\phi ^j\alpha ^j + \sum _{i\in \mathcal {A}_C} \bigg ( \sum _{j\in C}\phi ^j\beta ^j_i \bigg ) F_{i, t} \nonumber \\{} & {} \quad + \sum _{j\in C}\phi ^j\varepsilon ^j_t \quad \forall t\in \mathcal {T} \end{aligned}$$
(7)

Observe that as there is a one-to-one correspondence between admissible weights vectors and portfolios, we sometimes overlap the two concepts in the following.

If we impose the market neutral condition, then we require the terms into the curved brackets to be zero, so we have a homogeneous linear system of a equations in the c variables \(\phi ^1,...,\phi ^c\). Furthermore, with the \(l_1\) condition, we obtain an optimization problem with both linear (8) and nonlinear (9) constraints:

$$\begin{aligned} \sum _{j\in C}\phi ^j\beta ^j_i= & {} 0 \quad \forall i \in \mathcal {A}_C \end{aligned}$$
(8)
$$\begin{aligned} \sum _{j\in C} \mid \phi ^j\mid= & {} 1 \end{aligned}$$
(9)

Assuming that there are at least \(a+1\) stocks in C, we can construct a market-neutral portfolio. We indicate with \(\mathcal {P}_C\) the set of all the weights vectors such that both 8 and 9 are satisfied. For a generic portfolio in \(\mathcal {P}_C\), the return at time t can be reduced as the sum of \(\alpha ^{Port}\) and \(\varepsilon _t^{Port}\):

$$\begin{aligned} Port_t = \sum _{j\in C}\phi ^jr^j_t = \sum _{j\in C}\phi ^j\alpha ^j + \sum _{j\in C}\phi ^j\varepsilon ^j_t = \alpha ^{Port} + \varepsilon _t^{Port} \quad \forall t\in \mathcal {T} \end{aligned}$$
(10)

where \(\alpha ^{Port}\) is a constant and \(\varepsilon _t^{Port}\) is the sum of c Gaussian random variables. As already discussed above, several works in the recent literature have assessed the utility of the idiosyncratic risks in constructing an investment strategy. In other words, it has been shown that there are hidden patterns in the residual sum that can improve the quality and the performance of a strategy for portfolio construction. So, we consider them by searching in \(\mathcal {P}_C\) the portfolio \(P_C\) that optimizes a specific criterion.

As there are infinite portfolios that satisfy the constraints, which are both linear and nonlinear, we apply a nonlinear optimization algorithm to find the optimal one. In particular, the Sequential Least SQuares Programming (SLSQP) is used (see [40] and [41] for further references). The choice for this algorithm is due to its global convergence property [42] and super-linear speed. It works by repeatedly splitting the main problem into subproblems solved by linearizing the constraints. Regarding the objective function, which is the criterion used to choose the portfolios to invest in, we carry out experiments by trying to minimize the variance, that is, \(P_C = {{\,\textrm{argmin}\,}}_{P\in \mathcal {P}_C}Var(P)\). Once a portfolio for each cluster is obtained, we apply the same criterion to select the three optimal ones. Finally, we invest in them. We choose three portfolios and not just one to increase the diversification effect and to reduce the investment risk by making the strategy more robust. The entire investment strategy is reported in Algorithm 3.

The computational time is contained, in the order of a few seconds for the whole Algorithm 3.

4 Experimental results

This Section is concerned with the experimental stage. Firstly, we describe the datasets used and the preprocessing stage. Then, we describe the evaluation strategy used for the comparison and show and discuss the experimental results obtained in the various markets.

4.1 The dataset

We assess our proposal in six different stock markets in the experimental stage. In particular, the datasets cover both developed and emerging markets. In this way, we are able to analyze our proposal performances in different situations. The experiments are carried out individually, without any interactions between each other. The period considered is the same for all the experiments: from 2011-12-21 to 2021-12-20. The employed datasets are:

figure g

  • Italian Stock Market: the dataset contains stocks from the FTSE Italia All Share. The data are publicly available on the website of Il Sole 24 Ore, an Italian newspaper. The exact link is provided at the end of this article.

  • German Stock Market: the dataset is referred to the stocks belonging to the index Classic All Share - German and whose time series are available on Investing.com, one of the most significant sources for public financial data. The exact link can be found at the end of this article.

  • American Stock Market: the dataset is created starting from the stocks belonging to the index \(S \& P 100\). The data are provided by Investing.com, see the Data & Code Availability Statement.

  • Japanese Stock Market: the stocks belonging to the Topix 100 index are grouped in this dataset. The data provider is Investing.com and further information can be found at the end of this work.

  • Brazilian Stock Market: the dataset collects stocks from the Bovespa index. For the data link, see the Data & Code Availability Statement.

  • Indian Stock Market: the dataset is related to the Nifty 100 index. The data are provided by Investing.com, as stated at the end of the paper.

All the datasets considered can be viewed as matrices whose rows represent the time axis (i.e., the observations) and whose columns are the stocks considered. The preprocessing stage is done through multiple steps. Firstly, from the prices dataset, we calculate the returns one. After that the rows representing the weekends and holidays are removed from the dataset, as for the columns corresponding to stocks with poor data, i.e., full of missing values. Moreover, in the case of the Italian dataset, some initial rows are deleted as many missing values for several stocks occurred in the first observations. Then, the remaining missing values are imputed with 0 (that is, no price change has occurred these days). Finally, in the train set and for the computation of the investment strategy, the values are standardized columns by columns. That is, if \(\hat{r}^j\) is the row return corresponding to stock j, we consider \(r^j = \frac{1}{\sqrt{Var(\hat{r}^j)}}(\hat{r}^j - Mean(\hat{r}^j))\) in place of \(\hat{r}^j\). The data used for the comparison are not handled in any way.

As for the number of PCs we consider, it is empirically determined by looking at the results obtained in similar previous experiments. The same is true also for the threshold \(\textbf{th}\), which is chosen in such a way to preserve many monthly components and avoid multicollinearity. In this direction, we set \(\textbf{th}=0.5\) for all the experiments. The condition number gives output values lower than 10 (specifically, values lower than 5 in all the experiments), which means negligible multicollinearity among variables. Table 2 summarizes the final datasets we work with after the preprocessing stage and the number of PCs considered, which is determined as a function of the overall number of stocks. Furthermore, the condition number results are also shown (in particular, for each dataset, the highest value obtained among all the folds is reported). Finally, also the number of resulting PCs is displayed. As already stated in Sect. 3.2, within the same dataset, the considered risk factors could vary as time progress, so our proposal can follow covariance shifts. However, the risk factors set exhibits certain robustness among the 12 folds we consider for CV in that it does not show huge variations. We can interpret this result as no considerable changes have occurred in such a short time. In other words, significant variations in the patterns among assets are noticeable at bigger time intervals.

Table 2 Summary statistics of the datasets after the preprocessing stage. For each of the considered markets, we report: the number of stocks in the universe \(\mathcal {J}\) (Num Stocks); the number of observations in the whole dataset (Num Obs.); the number of observations in the first train set and the first test set (\(Tr_1 / Te_0\)); the number of PCs extracted on both daily and monthly basis (Num PCs); the number of total risk factors \(F_i\), obtained by merging the daily and monthly PCs as described above (Num \(F_{i}\)); the highest result (with respect to the 12 folds) obtained in the condition number (Cond. Num.)
Full size table

4.2 Results and discussion

Before describing the results obtained, we briefly show some details about the evaluation of the proposal and the comparison with other benchmarks. Firstly, we describe the performance measures used for the comparison. In the following, we indicate the value of the portfolio to analyze with \(P=\{P_t\}_{t\in Te_0}\) and its returns with \(Pr=\{Pr_t\}_{t\in Te_0}\), where \(Te_0=\{1,...,N\}\) is the test set. The performance measures are:

  • Percentage Profit P\(\%\) It is the percentage profit obtained by the strategy. It can be defined as the ratio \(P\% = \frac{P_N}{P_1} - 1\). In comparing different strategies, we prefer high values.

  • Max Percentage Drawdown (MD\(\%\)) It is the maximum percentage loss the portfolio suffered. Formally, it can be viewed as \(MD\% = 1 - \min _{t<s\in Te}(\frac{P_s}{P_t})\). In comparing different strategies, we prefer low values.

  • Recovery Factor (RF) It is a proxy of the capability of the portfolio to recover losses. It can be defined as the ratio between the final profit and the max suffered loss. Formally, \(RF = \frac{Profit}{Loss}\) with \(Profit = P_N - P_1\) and \(Loss = \max _{t<s\in Te}(P_t - P_s)\). In comparing different strategies, we prefer high values.

  • Profit Factor (PF) It is the ratio between the sum of the profits and the losses computed daily. That is, \(PF = \frac{Profits Sum}{Losses Sum}\) with \(Profits Sum = \sum _{t=2}^N \max \{P_t - P_{t-1}, 0\}\) and \(Losses Sum = \sum _{t=2}^N \max \{P_{t-1} - P_t, 0\}\). In comparing different strategies, we prefer a high value.

  • Sharpe Ratio (ShR) It is a measure of how the risk is rewarded in terms of extra gain. It is formally defined as the ratio between the difference of the expected return and the risk-free rate, and the standard deviation of the portfolio returns, which is used as a proxy for the riskiness, i.e., \(ShR = \frac{Mean(Pr) - i_r}{\sqrt{Var(Pr)}}\) where \(i_r\) is the risk-free rate. Observe that, in the computation of ShR, we approximate \(i_r\) with zero. This assumption is not relevant to the comparison as ShR is a monotonic function with respect to \(i_r\). In comparing different strategies, we prefer a high value.

  • Sortino Ratio (SoR) It is a measure of the reward for the risk, as ShR. The only difference is that, as a riskiness proxy, the downside deviation, i.e., the standard deviation referred only to negative returns, is considered. So, we can write \(SoR = \frac{Mean(Pr) - i_r}{\sqrt{Down\_Var(Pr)}}\). The assumption regarding \(i_r\) is the same as in ShR. In comparing different strategies, we prefer high values.

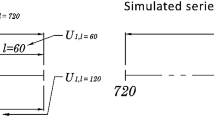
As already stated in the Introduction, we remind that our aim is the construction of a strategy that is robust through time. To achieve this task, we perform the CV to evaluate some of the most commonly used metrics for investment strategies. In more detail, we apply a block W-fold CV, so each fold preserves the temporal dimension. So, the dataset is split into train and test sets, which are indicated with \(Tr_1\) and \(Te_0\), respectively. The test set is further split into W consecutive folds according to the temporal dimension. So, where is the disjoint union of sets. Then, for the first iteration, we consider \(Tr_1\) as the train set and \(Te_1\) as the test set. For the \((w+1)\)-th iteration, we exploit as the train set and \(Te_{w+1}\) as the test set. Figure 3 graphically explains the procedure.

Fig. 3
figure 3

The block Cross-Validation we adopted for the comparison. The time set \(\mathcal {T}\) is split into two subsets, namely \(Tr_1\) for the training and \(Te_0\) for the test. Then, \(Te_0\) is split into W disjoints consecutive subsets \(Te_1,...,Te_W\). The first iteration of the strategy is trained on \(Tr_1\) and tested on \(Te_1\). Then, the \(w+1\)-th iteration is trained on and tested on \(Te_{w+1}\)

Full size image

After applying the CV, we have a vector of results for each metric, one for each fold. Then, the mean and the standard deviation of these vectors are computed. Finally, the mean minus the std is considered the proxy of the lower bound confidence interval, which is a proxy of the worst-case scenario (wcs). By evaluating this quantity, we expect to assess the robustness of the strategy. That is, it not only has to be profitable, i.e., with a high mean, but it also has to be stable with respect to the time, i.e., its std among the fold should be as low as possible. Finally, note that, only in the case of \(MD\%\), as for this metric a lower value is better, we consider as target measure for the wcs, the upper bound, i.e., the sum between mean and std.

Regarding the number and the length of the folds used for the comparison, as we extract monthly risk factors as long-term ones, the investment strategy has a monthly time horizon. So, the length of each fold is one month. Furthermore, we use one year of data as the test set. So, there are \(W=12\) folds, and each one is made up of one month of data.

The last detail to be clarified is the benchmarks used for the comparison. As we work in a context where both long and short positions are allowed, we use as benchmarks the minimum variance and the mean-var portfolios. These portfolios are constructed by looking at the historical data. A vector of weights is optimized through the SLSQP by means of minimum variance or maximal ratio between mean and variance, respectively. These weights form the portfolios in which we invest. Moreover, also the Exponential Gradient is used, as done in [32, 43].

Now, we show the results obtained in the experimental stage. For each fold in the CV, we simulate the performance obtained by a portfolio with an initial amount of wealth equal to 1000. Table 3 shows the results obtained in the Italian, German and American markets. Instead, the results for the Japanese, Brazilian and Indian stock markets are reported in Table 4.

Table 3 The results we obtained during the experimental stage in the Italian, German, and American markets. Our proposal is reported under the columns Port. The benchmarks are MinVar, M-V, and ExpGrad for the portfolio with minimum variance, the portfolio which maximizes the ratio \(\frac{mean}{var}\), and the Exponential Gradient, respectively. Furthermore, also the Exponential Gradient strategy ExpGrad is considered. We report both the mean (mean) and the standard deviation (std) of the performance indicators among the folds. Furthermore, we also report the worst-case scenario (wcs) in the confidence interval. Such interval is defined as the mean minus the standard deviation for all the performance measures considered except for MD%, where it is the sum of them. The better result for each metric is reported in bold, and the second best is underlined
Full size table
Table 4 The results we obtained in the Japanese, Brazilian, and Indian stock markets. There are four columns representing our methodology (Port), the minimum variance (MinVar) portfolio, the mean-var (M-V) portfolio, and the Exponential Gradient strategy (ExpGrad). Each column is split into three sub-columns representing the mean (mean), the standard deviation (std) and the worst-case scenario (wcs) in the confidence interval. We highlight the best results and the second one by reporting them in bold and underlined, respectively
Full size table

For each table, we report the mean, the variance, and the wcs. Furthermore, the results obtained by both our strategy (Port), the minimum variance portfolio (MinVar) and the mean-variance portfolio (M-V) are reported for comparison. Finally, the best result in each field is reported in bold, and the second one is underlined.

For a visual inspection, we also report the plots of the strategies in the evaluation stage. In particular, Figures from 4 to 9 show the results in each market.

Fig. 4
figure 4

The results we obtained in the Italian Stock Market by the portfolios constructed through the 12-Folds CV. All the portfolios are considered to have an initial value of 1000. Our strategy is reported in blue, the minimum variance portfolio in green and the mean-variance one in red. The horizontal dotted line represents the value 1000, i.e., the initial value of the portfolios. (Color figure online)

Full size image
Fig. 5
figure 5

The plots of the experimental results obtained in the German Stock Market. The 12 plots represent the 12-Folds in the CV, each one with a starting amount equal to 1000. The blue line represents the proposed strategy, the green line represents the minimum variance portfolio and the red line represents the mean-variance portfolio. Finally, the dotted black line represents the 0 returns portfolio. (Color figure online)

Full size image
Fig. 6
figure 6

The results obtained during the experimental stage in the American stock market. The 12 plots correspond to the folds in the CV. The portfolios have an initial value of 1000, which is represented by the black horizontal line. The three lines, blue, green and red, correspond to the portfolios obtained by our strategy, minimum variance and mean-var criteria, respectively. (Color figure online)

Full size image
Fig. 7
figure 7

The plot of the experimental results in the Japanese stock market. Our proposal, in blue, is compared with minimum variance (green) and mean-var portfolio (red). (Color figure online)

Full size image
Fig. 8
figure 8

Results in the Brazilian stock market. Our proposal, the minimum variance, and mean-variance portfolios are plotted in blue, green, and red, respectively. (Color figure online)

Full size image
Fig. 9
figure 9

Comparison of strategies behavior in the Indian stock market. Our proposal is drawn in blue, while the minimum variance and the mean-variance portfolios are in green and red, respectively. (Color figure online)

Full size image

As already mentioned above, all the strategies in each fold are considered to start with an initial capital of 1000. The proposed strategy is reported in blue, the minimum variance benchmark is represented by the green line, and the mean-variance portfolio is shown by the red line. Furthermore, the black dotted line represents the value 1000, which corresponds to an overall return of 0.

As the results show, our portfolio optimization strategy seems promising. In fact, despite the mean value often is not the best, the wcs, which is our target, is very often the optimal one, with the only exception of the American dataset. This happens because the std is almost ever the lowest or the second-lowest, in all the considered datasets.

In particular, it can be interesting to compare the American and Brazilian Stock Markets from one side, and the others on the other side. In fact, in the second case, the mean across the folds is not very exciting. Indeed, the benchmark strategies obtain better results. However, the strategy shows its robustness by obtaining a low variance. In the Italian and Japanese cases, this allows it to overcome the benchmarks when evaluating the worst-case scenario in all performance measures except for the Profit and the Max Drawdown, where the results obtained are still far from the best. In the Indian dataset, the wcs performances are significantly better than benchmark approaches. The only exception is Max Drawdown, where the difference between our proposal and the mean-variance portfolio is very low, less than 0.007%. Instead, in the American example, the proposal fails to overcome the competitors. However, it obtains discrete results, especially in the Max Drawdown and the Recovery Factors, where it is the best, and in the Profit and Profit Factor, where it is very close to the best result. Finally, in the German and Brazilian datasets, the strategy achieves the best mean in almost all the considered metrics, and also, the std is relatively low. This means the worst-case scenario overcomes that obtained by competitors in all the cases except that Max Drawdown.

5 Conclusion

In this work, a framework for statistical arbitrage is discussed. We proposed a cluster-based multi-step data-driven strategy that considers risk factors related to different temporal horizons. Our proposal is contextualized in the literature, and its performance is repeatedly assessed through several experiments on several stock markets. We find that this kind of strategy seems to be quite robust and profitable in various stock markets belonging to both emerging and developed countries. Furthermore, this finding holds also when comparing our proposal with other benchmark strategies. In fact, the comparison shows that our methodology obtains almost every good performance, superior to those obtained by the benchmarks.

To summarize, we can analyze more in detail the proposed framework by highlighting its strengths and weakness, thus providing possible directions for further studies. Firstly, the assumptions we made, although classical in the financial literature, can represent an obstacle in applying the proposal in a real-world scenario. In fact, there is an open debate on their reliability ([44, 45]). So, it can be worth investigating what happens when some of the assumptions are relaxed.

Then, regarding the feature extraction, the proposed factor model, and the feature selection, we have chosen to stay in the linear case. In fact, a previous empirical study has shown the reliability of such a model and the complexity and the computational times are lower than in nonlinear environments. However, a careful study of the problem through nonlinear methods could show hidden patterns that can improve the performance of our methodology. Moreover, the patterns among asset time series could change accordingly to the considered time granularity. In other words, it is also noteworthy to investigate hybrid approaches where different extraction methods are used in different granularities.

Regarding hyperparameter optimization, it has been observed it is the most expensive part of the whole framework. A trick to reduce the number of iterations and alleviate its computational cost can be the introduction of the Randomized Grid Search. Another idea is the shrinkage of the searching space to a narrow boundary surrounding the solution in the previous period. However, they should be further investigated in the future. As for the clustering strategy, it shows both pros and cons. For example, it does not need to explicitly define a distance between time series, which can be a difficult task. In contrast, some of the clusters show little significance in that they are made up of a small number of stocks, so they are unusable for the investment strategy. Furthermore, the number of PCs to consider is currently empirically determined, which could lead to a bias. Future works could try to fix these disadvantages. For example, it can be worth investigating the optimal number of PCs to consider by analyzing the trade-off between representation accuracy and sensitivity to noise.

Regarding the investment strategy and the idiosyncratic risks, other experiments have been carried out to find the optimal portfolio by means of the Sharpe ratio instead of minimum variance. However, these experiments have shown no profitability. In more detail, it seems that a mean-reverting process in such a case is more convenient for describing the price dynamic. In the future, it could be helpful to accurately investigate what type of dynamic (mean-reverting rather than momentum) better fits the particular context under evaluation.