Graph learning-based generation of abstractions for reinforcement learning

Abstract

The application of reinforcement learning (RL) algorithms is often hindered by the combinatorial explosion of the state space. Previous works have leveraged abstractions which condense large state spaces to find tractable solutions. However, they assumed that the abstractions are provided by a domain expert. In this work, we propose a new approach to automatically construct abstract Markov decision processes (AMDPs) for potential-based reward shaping to improve the sample efficiency of RL algorithms. Our approach to constructing abstract states is inspired by graph representation learning methods, it effectively encodes the topological and reward structure of the ground-level MDP. We perform large-scale quantitative experiments on a range of navigation and gathering tasks under both stationary and stochastic settings. Our approach shows improvements of up to 8.5 times in sample efficiency and up to 3 times in run time over the baseline approach. Besides, with our qualitative analyses of the generated AMDPs, we are able to visually demonstrate the capability of our approach to preserve the topological and reward structure of the ground-level MDP.

1 Introduction

Reinforcement learning algorithms often suffer from a high sample complexity that is frequently due to a very large state space. As the number of feature variables describing the state grows, the size of state space increases exponentially (the so-called curse of dimensionality [4]). A lot of research effort has been spent to tackle this problem, e.g. via reward shaping [20, 27, 37, 43], option framework [42, 48], hierarchical RL [29, 50], hindsight experience replay [3], etc. This paper focuses on leveraging abstraction [1, 33] to condense large state spaces such that essential information is preserved. Consequently, solutions can be computed in a tractable manner. Abstraction methods reduce ground-level MDPs with large state spaces to abstract MDPs (AMDPs) with smaller state spaces by aggregating states according to some notion of similarity. Abstractions can be realized by aggregating states with equal values of particular quantities, for example, optimal Q-values. Our approach exploits state abstractions to build informative AMDPs that can be solved a lot faster and provide a “rough” solution to the RL task. This solution is then used to shape the reward function of the ground-level learning on the original MDP and thus improves the convergence speed of RL algorithms, as suggested in [19, 33].

Fig. 1

Manually created abstraction, states in the maze are aggregated into abstract states according to “rooms”, which are in different colours and labelled by numbers

Fig. 2

Two states in label “X” are spatially close, but topologically quite far from each other. They are likely to be aggregated into same abstract state using uniform partitioning

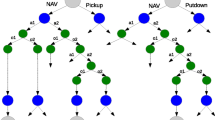
Most of the existing works assume abstractions to be provided by experts [11, 12, 19, 33]. An example is shown in Fig. 1 where a domain expert creates abstractions based on the intuitive concept of “Rooms”. However, such manual approaches become infeasible as environments scale up. In an attempt to automatically generate abstractions, [6] proposed to uniformly partition the state space to build abstract states. While this has been shown to improve the convergence rate of RL, it first needs to know the boundaries of the state features of the environment to perform uniform partitioning. Moreover, the resulting abstract states ignore the connectivity and reward structure of the underlying MDP. Consider for example (see Fig. 2) two states are spatially close but are separated by an obstacle and it takes a large number of steps to move between the states, but these two states can likely be aggregated into the same abstract state using [6].

We argue that the state aggregation for reward shaping should be based on properties of topological and value function similarity. Intuitively, the ground-level states belonging to the same abstract state should be topologically close and should appear more frequently together within high reward paths from the start state to the goal state. Moreover, if two states are in the same abstract state, their long-term expected discounted rewards (value functions) should also be similar.

To satisfy the above two properties, we propose a new approach to generate state abstractions that exploits the underlying topology and reward structure of the ground-level MDP. Borrowing ideas from graph representation learning, we first extract latent state representations which encode the similarity among states in terms of topological and reward structure. The state representations are then clustered to generate abstract states of the AMDP. In both stationary and stochastic environments, our experimental results show vast improvements in convergence speed compared to the previous state-of-the-art [6] which constructs AMDPs by uniformly partitioning each state dimension into a predefined number of abstract cells. We attribute the performance gains to an improved cluster structure which qualitatively and intuitively agrees well with the cluster structure induced by the state-value functions of the ground-level MDP.

Regarding state representation learning for RL, [9, 17, 52] also attempt to encode behavioural similarity of states in the underlying MDP. The main goal of these works is to incorporate representation learning into RL learning frameworks so that informative state representations can help converge to better policies. In contrast, we learn representations in order to explicitly build transparent and interpretable abstractions for hierarchical RL, so that sample complexity of learning on the ground-level can be reduced.

To sum up, our main contributions are as follows.

• 1. We introduce a new approach to construct abstract states to preserve properties of topological and value function proximity among the ground-level states.

• 2. We show that reward shaping with our constructed AMDP results in improvements for the Qλ algorithm of up to (i) 8.5 times in convergence speed and sample efficiency for stochastic environments and 6.5 times for stationary environments and (ii) 3 times in run time for stationary environments.

• 3. With our qualitative analysis of the generated AMDP, we demonstrate that our approach is able to preserve the topological and reward structure of the ground-level MDP.

For reproducibility, we release our code at https://github.com/xy9485/GraphLearningBasedAMDP.

2 Background

2.1 Reinforcement learning

Reinforcement learning consists of an environment and an agent which is driven by a policy to interact with the environment. For each interaction, the agent observes the response of the environment to its actions and updates its behaviours. The goal for the agent is to maximize the long-term accumulated reward given by the environment. The environment is typically represented by a Markov decision process (MDP). The standard notation for MDPs:

$$\begin{aligned} \mathcal {M}=(S_{\mathcal {M}}, A_{\mathcal {M}}, R_{\mathcal {M}}, P_{\mathcal {M}}) \end{aligned}$$

(1)

where $S_{\mathcal {M}}$ is a set of available states the agent may find itself in the environment, $A_{\mathcal {M}}$ denotes available actions for each state, $R_{\mathcal {M}}(s,a,s')$ defines the immediate reward after the agent transitions from s to $s'$ via a, $P_{\mathcal {M}(s,a,s')}$ denotes the probability of reaching $s'$ when performing action a at state s.

When the complete knowledge of the environment’s MDP is unknown, algorithms based on utilizing temporal difference are often used. Q-Learning is one of the fundamental TD learning algorithms, and it updates the value of a state-action pair after each transition:

$$\begin{aligned} Q(s, a)=Q(s, a)+\alpha (R(s, a, s^{\prime })+\gamma \max _{a^{\prime }} Q(s^{\prime }, a^{\prime })-Q(s, a)) \end{aligned}$$

(2)

where $\alpha$ denotes the learning rate and $\gamma$ is the discount factor.

To improve the learning rate of Q-Learning, updates of the Q function can be made for multiple state-action pairs after each transition. Since an action made by the agent will likely influence not only immediate, but also future rewards, it is reasonable to give more credit to more recently experienced state-action pairs. The extent of updates to those state-action pairs is quantified by their eligibility. After each transition, the current state-action pair has its eligibility to 1, and the eligibility of other state-action pairs in the same trajectory decays in contrast. Q-Learning utilizing eligibility is referred to as Q($\lambda$) algorithm. A more detailed introduction regarding reinforcement learning is referred to [47].

2.2 Potential-based reward shaping

Reward sparsity is one of the main challenges of reinforcement learning; one intuitive solution is reward shaping in which the agent receives an additional pseudo-reward $F(s,a,s')$, which imparts the external domain knowledge to the agent and stimulates the agent towards desired behaviours.

It has been proven in [37] that if $F(s,a,s')$ is defined as the difference of potential $\phi (s)$ between two states, the optimal policy will remain unchanged.

$$\begin{aligned} F\left( s, a, s^{\prime }\right) =\gamma \phi \left( s^{\prime }\right) -\phi (s) \end{aligned}$$

(3)

Reward shaping methods employing Eq.(3) to compute pseudo-rewards are referred to as potential-based reward shaping (PBRS) techniques. To obtain reasonable potential functions, domain experts are often required to provide domain knowledge [10, 19] or demonstration [5, 21]. However, it might be infeasible to manually define such a potential function for complex tasks, instead, it is preferable to construct such a function automatically.

A potential function can be generated by solving an abstract version of the task, represented by an abstract Markov decision process (AMDP):

$$\begin{aligned} \mathcal {A}=\left( S_{\mathcal {A}}, A_{\mathcal {A}}, R_{\mathcal {A}}, P_{\mathcal {A}}\right) \end{aligned}$$

(4)

where each element is an abstraction corresponding to its counterpart in an MDP. A mapping function Z is also constructed between ground states and abstract states. AMDPs can induce potential-based reward shaping. Once an AMDP is built, dynamic programming is used to compute the optimal value function V over the AMDP. Then, V is treated as the potential function $\phi (s) \leftarrow V(Z(s))$.

Since we have multiple agents operating on different levels of abstraction, we refer to the agent interacting with the AMDP as the abstract agent and the agent interacting with ground-level MDP as the ground agent. We denote this similarly for the abstract and ground learning processes.

2.3 Graph representation learning

The key idea of graph (or node) representation learning (GRL) is to learn low-dimensional latent node representations while preserving the structural properties of the underlying graph together with node attributes. These techniques can be broadly classified into (i) random walk-based methods, (ii) matrix factorization based methods and (iii) deep learning-based methods like graph neural networks (GNNs).

Random walk-based methods [23, 24, 41, 54] find node embeddings such that nodes co-occur on random walks over the graph are embedded closer. Matrix factorization-based methods [39] rely on the low-rank decomposition of a target matrix such as the k-step transition probability matrix and modularity matrix to obtain node embeddings. Both the above classes of methods operate mainly in an unsupervised manner on unattributed (when nodes do not have features) graphs. GNNs are deep learning models designed to extract features from the graph structure as well as the input node attributes and can be further categorized into recurrent graph neural networks [45], convolutional graph neural networks [26, 38] and graph autoencoders [25, 44].

We observe that while matrix factorization and GNNs would need the knowledge of the complete graph, random walk-based methods are more flexible and can be applied even if the complete graph is unknown beforehand. In particular, for our current setting, when the exact MDP is unknown and can only be explored, we develop a random walk-based graph representation learning strategy (more details in Sect. 4.1) to learn abstract states while encoding the topology and reward structure of the ground-level MDP.

Our approach employs random walk-based graph representation learning or node embedding approaches [18, 23, 24, 41]. The goal is to learn low-dimensional representations of the nodes such that the topological and reward structure of the ground-level MDP is preserved. Other work [51] showed that graph representation learning techniques can be leveraged to learn informative state representations for DeepRL models. Madjiheurem and Toni [31] employ graph-based feature learning techniques for value function approximation. In particular, they empirically show that low-dimensional-state embeddings learned using graph representation learning techniques are better suited for linear approximation of value functions than the proto-value functions. Our work can be considered to be complementary to the above works; in that we further demonstrate the usefulness of GRL techniques in hierarchical RL.

3 Related work

3.1 Hierarchical reinforcement learning

To improve the reward performance and sample efficiency of RL algorithms, hierarchical reinforcement learning (HRL) is a popular paradigm that enables the decomposition of a challenging long-horizon decision-making task into simpler subtasks [40].

One pattern of HRL which our approach complies with is to construct a hierarchical structure of MDPs so that high-level MDPs are less complex to solve and aid in the learning over low-level MDPs. Marthi [33] first introduced the idea to automatically modify the reward function of a Markov decision process by defining an abstract MDP to speed up standard reinforcement learning algorithms. In past works (e.g. [13, 19]), AMDPs were manually built by a domain expert. However, generating AMDPs in this way often requires utilizing external domain knowledge which can be hard to acquire or encode. When facing complex domains, human experts could be inefficient and even fail to build AMDPs. In [6, 7], a conceptually simple method for constructing state abstractions was proposed. In this approach, the state space is partitioned uniformly along each dimension, and each partition forms an abstract state. While the results showed a speed-up of RL, the resulting state abstractions do not always match the topological and reward structure of the underlying MDP. Consequently, the reward shaping derived from corresponding AMDPs could be inaccurate and mislead the ground learning process. Our approach can handle this limitation.

In [22, 28, 32, 49], clustering algorithms are applied to an MDP model or a graph estimated from states trajectories to identify abstract states or bottlenecks and subsequently generate options. This method struggles to generate effective and robust abstractions that are aligned with the underlying topological and reward structure. Note that given the state transition history, there is no unique way to construct the corresponding graph. It is therefore inevitable to lose some information at this approximation step. These approaches could require huge storage for the estimated graph when facing large and complex environments. Our approach, on the other hand, directly learns low-dimensional latent-state representations from the state transitions. The latent-state representations are then clustered to generate abstract states.

Another line of work to achieve HRL employs option framework [42, 48]. Compared to constructing state abstractions, option framework achieves temporal abstraction by modelling courses of actions as options. Policies over options and intra-option policies make up the hierarchical RL structures. While useful options are proven to speed up RL learning, approaches using option framework often require prior knowledge to define options. To mitigate the reliance on prior knowledge, automated discovery of options [8, 34, 46, 53] has become an active research area.

Feudal reinforcement learning [50] performs HRL by employing a layered learning strategy with two modules: Manager and Worker. States are first embedded into a latent space. The Manager in the higher layer is trained to predict advantageous directions of transitions in the latent space. The Worker in the lower layer is intrinsically rewarded by following these advantageous directions. For those RL tasks where long-term credit assignment does not play an important role, the feudal network can be inferior to a CNN connected by an LSTM network. In addition, advantageous directions predicted by the Manager in the latent-state space are learned in an implicit manner, which makes the policy learned by the Manager lack interpretability. In our approach, the abstract state space is explicitly built according to topological and reward structure similarity; therefore, the learned abstract-level policy is more transparent.

In [29], a hierarchical deep RL framework is proposed. The high-level agent takes actions from a set of sub-goals defined by domain experts, the low-level agent operates on the initial action space to achieve the sub-goal from the high-level controller. The high-level policy is learned based on the accumulative extrinsic reward gathered by the low-level agent given a sub-goal. The low-level policy is then updated based on the intrinsic reward, describing whether the assigned sub-goal is reached or not. This framework can be practical in application when useful prior knowledge can be imparted to the high-level agent. However, it becomes hard to impart prior knowledge when scaling up the RL task.

3.2 State representation learning in RL

Research has been focusing on learning informative state representations for RL algorithms. In [52], Zhang et al. learn state representations based on bisimulation metric [14,15,16] to measure behavioural similarity between two states. The learning of representations is integrated into the RL learning framework. Note that their objective is quite different from ours, in which they learn representations to improve the robustness of the learned policy against background distraction of pixel observations. Our objective is to learn representations to explicitly construct abstractions and reduce sample complexity of ground-level RL algorithms subsequently.

Another related representation learning strategy is successor representation (SR) [9] which encodes the expected discounted future visitations of each state j along trajectories originating in a given state i. Consequently, each state is represented as a sparse vector of n dimensions where n is the total number of states. Though in principle one can use these representations in our framework, low-dimensional dense representations like ours are better suited to obtain clusters as abstract states. Though there are recent works [30] on approximating low-dimensional SR representation within deep RL frameworks, those methods have a different objective as ours. Specifically, we are interested in finding state abstractions which facilitate reward shaping for faster convergence of ground-level policy learning, whereas deep successor representations are approximated as a component of the whole network for learning the optimal policy.

Agarwal et al. [2] proposed to learn policy similarity embeddings in which states from different MDPs (sharing the same action space) are close in the embedding space if their optimal policies and future states are similar. The main goal of learning such embeddings is to train a generalizable policy over multiple unseen environments. That is quite different from our focus, which is to speed up the RL process.

4 Our approach

Solving dynamic programming over AMDP to achieve reward shaping is a well-known paradigm to boost the convergence rate of model-free RL algorithms. It is crucial to build appropriate AMDPs which can preserve the topological and reward structure of the environment. Inappropriate abstraction can result in inaccurate reward shaping, which could slow down the convergence rate or even make the ground learning process infeasible.

To get useful reward shaping, we formulate two important properties for state abstraction, namely (i) topological proximity and (ii) value-function proximity. First, the generated abstract states should preserve topological proximity among the ground-level states. We say that two states are topologically proximal if the states are reachable from each other in a small number of steps. In other words, the construction of abstract states should obey the underlying topology of the ground-level MDP. Second, any two states in an abstract state should have similar value functions. To understand the intuition behind the second property, note that the member states of the same cluster receive the same shaped reward. Now, if the actual value functions of the states differ too much, then providing the same shaped rewards would have a negative impact on the learning of the ground-level policy.

Towards incorporating the desired properties, we first generate latent representations of the states preserving the topology as well as the reward structure of the ground-level MDP. In particular, we design a exploration strategy, which collects experiences (trajectories of states) with a bias towards making states sharing similar reachability and ground value functions co-occur more frequently. The experiences are then used to learn state representations. The more co-occurring the states are, the closer the states will be embedded in the low-dimensional representation space. These representations are then clustered into abstract states for constructing an AMDP. Finally, the AMDP is exactly solved to induce reward shaping for the ground agent. In the following subsections, we further elaborate on our approach which we refer to as the Topology approach.

4.1 Graph-based learning of abstract states

Let a graph $G=(V,E)$ represent the MDP where each node $s\in V$ corresponds to a state and two nodes $(s,s')$ have an edge between them if $s^\prime$ can be reached from s in a single-step transition. We adopt the ideas from graph representation learning [23, 41] to learn continuous representations of the nodes in V such that the topology of G is preserved. As G is not known in advance, we devise a novelty-based SARSA strategy to collect sequences of states. The co-occurrence frequency of nodes in one episode within a predefined window range then quantifies the similarity between the nodes.

Given the state sequences, we use the Skip-gram model [35, 36] with negative sampling to learn state representations. States will be closer embedded if they co-occur more frequently. Let $\mathcal {N}(s)$ denote the higher-order neighbourhood or the co-occurring states of state s. We are interested in learning the state and context representations $\Phi (\cdot )$ and $\Theta (\cdot )$ such that the following objective is maximized:

$$\begin{aligned} \sum _{s\in V}\sum _{s'\in \mathcal {N}(s)}\left( \log (\sigma (\Phi (s)\cdot \Theta (s')) + \sum _{k=1}^K \mathbb {E}_{s''\sim P}\log (\sigma (-\Phi (s)\cdot \Theta (s''))\right) \end{aligned}$$

(5)

where $\sigma (x)={1/(1+\exp (-x))}$ is the sigmoid function, K is some constant denoting the number of negative samples and P denotes a random distribution over the observed node set. The state representations are then used to construct the abstract states.

4.1.1 Exploring the environment

In this section, we describe in detail our novelty-based SARSA strategy employed to explore the ground-level MDP and generate state sequences used in state representation learning. Our exploration strategy is motivated by two main objectives: (i) explore the environment as much and as uniformly as possible with limited cost, and (ii) more similar states (in terms of their reachability and ground value functions) should co-occur more frequently during exploration.

The pseudocode of our ground-level exploration policy is provided in Algorithm 1. To enforce our above two objectives, we develop a dynamic reward function to favour certain transitions over others. In particular, for a transition $(s,a,s')$, a dynamic reward r (line 12 in the pseudocode) is computed by taking into account both the novelty (visit count) of $s'$ and the change in the ground reward function (compared to the recent mean reward) for this transition. If only the novelty of states matters the reward function during exploration phase, the resulting representations learned from collected experiences will not encode the value function, but just the topology of the state space. We learn Q-values for state-action pairs using a SARSA-based feedback mechanism (see lines 17–20). Note that we do not require Algorithm 1 to converge and are only interested in using the learned Q-values to weakly guide our exploration.

Moreover, if there are some states which cause rewards lower than a predefined threshold value $\phi$ (could be a large negative value), they are treated as undesirable states to visit and stored in a set called traps. The traps can be useful when building the dynamics of the AMDP (see Sect. 4.2 for a more detailed explanation of this).

The length M and number N of episodes are fixed to a small number so that the size of the experiences will be $(M+1)\cdot N$. The time complexity of the exploration phase is therefore O(MN). In our experiment, we are able to keep the time consumption for exploration acceptable so that the total time of solving tasks is still substantially reduced, as compared to the uniform partitioning approach. Detailed comparison of run time is discussed in Sect. 5.2.2.

4.1.2 Constructing the abstract states

We employ K-Means clustering to cluster the learned state representations into k clusters, as k abstract states, where k determines the granularity of state abstraction. States in each abstract state should be similar in terms of reachability and ground value function. A mapping function $Z: S\rightarrow S_{\mathcal {A}}$ is built which maps ground states in S to their corresponding abstract states (clusters).

4.2 Dynamics of AMDP

Once the set of abstract states $S_{\mathcal {A}}$ are determined, we construct an AMDP which describes the dynamics of the explored environment on the abstract-level as described in Algorithm 2.

The transitions of the AMDP are determined by the experiences from the exploration phase. The experiences consist of sequences of states for each exploration episode, if step $(s \rightarrow s')$ is observed in an episode while $Z(s) \ne Z(s')$, this indicates an abstract transition $(Z(s) \rightarrow Z(s'))$. For each episode during the exploration phase, if $(Z(s) \rightarrow Z(s'))$ is observed at least once, the probability $P_\mathcal {A}(Z(s), Z(s)\rightarrow Z(s'), Z(s'))$ will be correspondingly increased (line 17 in Algorithm 2). The probability of abstract transitions that are not observed in any of the exploration episodes will remain zero as initialized. During the exploration phase, the ground-level goal state $s_g$ should also be observed. In the AMDP, the agent in an abstract state containing the goal state always stays in that same abstract state, i.e.

$$P_\mathcal {A}(Z(s_g),Z(s_g)\rightarrow Z(s_g), Z(s_g))=1.$$

The corresponding abstract reward function is defined as follows. We set

$$R(Z(s_g),Z(s_g)\rightarrow Z(s_g), Z(s_g))=0,$$

so that the abstract state corresponding to the goal state, $Z(s_g)$ will receive the highest value once the AMDP is solved by value iteration [47].

As mentioned in Sect. 4.1.1, in case there are some states in the environment that are undesirable (i.e. having very low ground value functions) for the ground agent to visit, those states are stored in a set traps during the exploration phase. Algorithm 2 ensures that the value function of the generated AMDP agrees with the ground value function. More specifically, for transitions starting from abstract states that contain ground states which belong to traps, huge negative rewards are given (line 13 Algorithm 2). Thus, the abstract states corresponding to traps will eventually obtain lower-state values than their neighbours once the AMDP is solved. This helps the ground-level agent avoid states in traps when using reward shaping induced by the AMDP.

4.3 Exploiting AMDP

Once a complete AMDP is constructed, value iteration [47] is employed to solve the AMDP exactly, so that we can acquire value function V(t), which is used to compute the potential-based reward shaping to inform the ground-level RL. V(t) is also called potential value in such context. More specifically, for a ground-level transition $(s \rightarrow s^\prime )$ such that $Z(s) \ne Z(s')$ (which means an abstract transition happens) the agent gets a combined reward, r, as follows

$$\begin{aligned} r = r_{{\text{env}}} + \omega F(t, t^\prime ), \end{aligned}$$

(6)

where $t = Z(s), t'= Z(s^\prime )$, $F(t,t^\prime ) = \gamma V(t') - V(t)$, $\gamma$ is the discount factor (close to 1 normally), and $\omega$ is a scaling parameter. The reward $r_{{\text{env}}}$ given by the environment plus the scaled difference between two potential values $\omega F(t,t^\prime )$ can be treated as an augmented reward to update the agent’s policy. This helps reduce the sparsity of the reward distribution of the ground-level MDP and improve the convergence rate of RL algorithms.

In the solved AMDP, except for the abstract states corresponding to traps, the closer an abstract state, t, to the abstract state containing the ground goal state is, the higher would be the corresponding value V(t). This property of the AMDP intuitively ensures that the shaped reward r can always steer the agent towards abstract states with higher potential values. Now if the constructed AMDP reflects the topology and value function of the ground-level MDP well, the agent employing the shaped reward is able to approach the goal state more efficiently.

5 Experimental evaluation

Our evaluation is conducted both in stationary as well as stochastic environments and is divided into two parts. First, we perform quantitative evaluations in which we show the superiority of our approach in terms of sample efficiency, convergence speed and run times. Besides, we conduct sensitivity experiments in which we show that our approach is robust (as compared to the baseline) towards the number of clusters (or the granularities of state abstraction) and the stochasticity within the environment. We used the Flag Collection Domain to evaluate the performance of our approach as compared to the uniform partitioning approach[6] which we refer to as Uniform approach in our experiments. Second, we perform a qualitative analysis of the constructed AMDPs on the Grid World and Flag Collection domains. In particular, through visualizations of value function heatmaps of ground-level MDPs and generated AMDPs, we demonstrate that our approach achieves the two desired properties of topological and value function proximity.

5.1 Setup

In the following, we describe the two navigational domains employed for our experiments.

Flag collection domain We quantitatively evaluated our approach on four different variants (shown in Fig. 3) of the Flag Collection domain [19]. The actual sizes of the maze variants are provided in the captions.

As an augmentation of the normal Grid World Navigation domain, the Flag Collection domain tasks the agent with traversing a Grid World environment, collecting flags marked as F and bringing them to the goal marked as G. The agent cannot move out of the environments’ boundary and reappear on the opposite side. There are impassable walls spread throughout the environments, which determine the connectivity of the environments. The cells in blue are doors on the walls, which could be open with a certain probability at each time step. Each state has up to four actions to choose from, corresponding to the four orthogonal directions. Each episode begins from the starting point marked as S and terminates when the agent reaches the goal coordinate, no matter how many flags are collected. In all the experiments, the number of flags is fixed to 3. For steps picking up a flag, a reward of 10,000 is given. For reaching the goal state $(x_{{\text{goal}}},y_{{\text{goal}}},1,1,1)$, the agent receives a reward of 0. Here, $(x_{{\text{goal}}},y_{{\text{goal}}})$ corresponds to the coordinates of the goal state in the maze, the last three binary dimensions (1, 1, 1) indicate that all three flags are collected. For each ordinary step, where no flag is collected and the goal state is not reached, the agent gets a step penalty of − 1.

Fig. 3

Flag Collection variations, with the starting point marked as S, the goal marked as G and flags marked as F. Black blocks are walls which are untraversable. Blocks in blue are doors which are stochastic to be close (Color figure online)

Grid world with traps For the qualitative analysis, we also used a Grid World maze as shown in Fig. 4, which is $33\times 48$ in actual size. The task is to reach the green cell marked as G starting from the red cell marked as S. The agent should avoid getting into purple cells (traps) marked as T, which cause substantial negative rewards. For each ordinary step, a reward of − 1 is given; for a step reaching the goal state $s_{{\text{goal}}}=(x_{{\text{goal}}}, y_{{\text{goal}}})$, a reward of 0 is given, and for steps getting into the traps, a reward of $-2000$ is given.

Fig. 4

Grid World with traps ($33\times 48$), with the starting point marked as S, the goal marked as G, traps marked as T. Black blocks are untraversable walls

5.1.1 Hyperparameter settings

For the Flag Collection domain, the hyperparameter settings of our Topology approach for the exploration agent and the ground agent are listed in Table 1. The learning rate is denoted by $\alpha$; $\gamma$ is the discount rate; $\epsilon$ controls the probability of choosing actions at random when using $\epsilon$-greedy policy; $\omega$ stands for the scale factor of the difference between potential values; $\lambda$ indicates the decay rate of the eligibility of state-action pairs; $steps\ per \ episode$ for the ground agent is unlimited until it visits the goal coordinate. The Uniform approach also shares the same hyperparameters for the ground agent.

For the domain of Grid World with traps, the number of exploration episodes is reduced to 5,000, since the actual state space of Grid World with traps is much smaller than that of Flag Collection domain. More specifically, a state of Flag Collection domain has three more binary dimensions (indicating how many flags are carried) than a state of Grid World with traps; regarding this point, a visualization can be found in Sect. 5.3.

Moreover, parameter $\gamma$ for solving AMDP by value iteration algorithm is set to 0.99 for both experimental domains. In each Flag Collection domain, we quantitatively evaluate the performance based on mean results of 25 repetitions for both Topology approach and Uniform approach.

Table 1 Hyperparameters of experiments for exploration and ground learning process

To prepare the data for training state representation, each collected state sequence is 50% downsampled at random, while still maintaining the original sequence order. We observed that such downsampling allowed the reduction in training time without any adverse affects on the quality of the learned abstractions. Then, we use a window size of 75 to collect the context states.

5.2 Quantitative results

For evaluation, we commence by analysing quantitative results on the Flag Collection domain.

5.2.1 Convergence speed and sample efficiency

We compare Topology and Uniform approaches over four variants of the Flag Collection domain, in stationary and stochastic environments, respectively. In stochastic environments, a part of states are stochastic to be accessible. The two approaches are compared based on: (i) the number of flags collected with respect to the number of episodes (ii) the cumulative reward with respect to the number of episodes and (iii) the cumulative reward with respect to the number of total steps. The results are shown in Figs. 5 and 6.

Fig. 5

Comparison of performance in stationary environments between Topology approach (T) and Uniform approach (U), using same number of abstract states (abstract granularity). On average, there are 16 abstract states in each subspace, and more intuitive explanation locates in Sect. 5.3.2

Fig. 6

Comparison of performance in stochastic environments between Topology approach (T) and Uniform approach (U), where 50% of doors have probability of 25% to be closed for each time step. Using same number of abstract states (abstract granularity), on average there are 16 abstract states in each subspace

Fig. 7

Sample efficiency for different stochastic settings with abstract granularity of 16 abstract states per subspace in average. T-90% indicates 90% of doors in the maze has probability of 25% to be closed. The left right columns present the performance of Topology and Uniform approaches, respectively

In both stationary and stochastic environments, our Topology approach (denoted as T) is more stable and faster than Uniform approach (denoted as U). The Topology approach successfully converges (collecting all 3 flags) in 500 episodes, while the Uniform approach fails to collect all flags in some mazes. Meanwhile, to achieve the same or even higher reward, the Topology approach requires fewer total steps than the Uniform approach in 500 episodes. In particular, our approach uses up to 6.5 times and 8.5 times fewer steps to reach the same reward in stationary environments and stochastic environments, respectively. This showcases the better sample efficiency of the Topology approach than the Uniform approach. In stochastic environments, the sample efficiency gap between the two approaches increases further.

In addition, we investigate the performance of both approaches under various levels of stochasticity in the environment. In Fig. 7, we plot sample efficiency under different stochastic settings for doors in environments while using the same abstract granularity of 16 abstract states per subspace on average. For example, T-90% indicates that 90% of doors in the maze have a probability of 25% to be closed. For all levels of stochasticity, the Topology approach converges to the optimal reward in at most 500 episodes. On the other hand, in different stochastic settings, the Uniform approach sometimes even fails to obtain the optimal reward in three mazes and is much slower to converge when the optimal reward is eventually found.

We attribute the inferior performance of the Uniform approach to its naive state partitioning. The way in which the Uniform approach partitions mazes might cause conflicts between the layout of abstract states and the topology of the environment. For example, two states separated by an obstacle might belong to the same abstract state when using the Uniform approach, but actually, they are topologically pretty far from each other. Consequently, the guidance of reward shaping provided by Uniform approach could likely convey noise and be partially misleading.

5.2.2 Run time comparison

In Fig. 8, we present a detailed run time comparison for the Flag Collection task over stationary maze Basic while considering different abstraction granularities. In maze Basic, both approaches can converge to the same reward. It is not meaningful enough to do run time comparison for the rest of three maze variants in which Uniform approach is not able to reach the highest reward in 500 episodes. Our Topology approach, on the other hand, always converges in less than 500 episodes even under varying abstraction granularities. Topology approach has three phases before solving the AMDP: exploration, state representation learning and state clustering, which Uniform approach does not have. Nevertheless, Topology approach is in total up to 3 times faster than Uniform approach while achieving the same reward.

We remark that the time taken to solve the AMDP by dynamic programming (using the chosen numbers of abstract states in Fig. 8) is negligible for both approaches. The reason is that abstract state transitions in the AMDP are deterministic given abstract state-action pairs, consequently, the time complexity of the Value Iteration algorithm is reduced. Nevertheless, the time to solve the AMDP should not be neglected when drastically increasing the number of abstract states.

Fig. 8

Run time comparisons of both approaches in Flag Collection domain over Maze Basic for four abstraction granularities from coarser (9 abstract states per subspace on average) to finer (36 abstract states per subspace on average)

5.2.3 Effect of abstraction granularity

Figure 9 compares the performance in terms of sample efficiency under varying abstraction granularities. As shown in Fig. 9 (left column), Topology approach shows robustness towards different abstraction granularities in different mazes. In contrast, as shown on the right side of Fig. 9, the performance of Uniform approach under fixed abstraction granularity is quite unstable among different mazes. In addition, for Uniform approach, the abstraction granularity achieving the best performance in one maze is not necessarily the best one in another or could even result in task failure.

Another advantage of Topology approach is that the efficacy of reward shaping from AMDP is predictable as the abstraction granularity varies. As shown on the left side of Fig. 9, for each flag collection task, when the abstraction granularity becomes finer, the extent of acceleration increases correspondingly, and vice versa. This can be observed among all maze variants.

However, for Uniform approach, finer abstraction granularity does not necessarily increase the convergence time and may result in failure. For some mazes, the best uniform abstraction granularity turns out to be a coarser one. Therefore, a proper abstraction granularity would need to be determined experimentally, which costs extra time and computational resources.

Fig. 9

Performance comparison with respect to sample efficiency under different abstraction granularities. The left and the right columns present correspond to Topology and Uniform approaches, respectively

5.3 Qualitative analysis

5.3.1 Preserving topological and value function proximity

We use the domain of Grid World with traps (see Fig. 4) to demonstrate through visualizations that our Topology approach can preserve both the topological and reward structure of the ground-level MDP into the AMDP. Towards that we first solve the ground-level MDP by dynamic programming to obtain the optimal policy, which certainly avoids the traps to reach the goal state. The corresponding value function as a heatmap for the ground-level MDP is shown in Fig. 10b. According to Algorithm 1, the exploration agent always prefers to visit states with higher novelty (lower visit counts). Meanwhile, the exploration agent tries to avoid traps, once it gets into them, then it is relatively hard to come out. Consequently, the whole state space can be explored relatively uniformly and the states sharing similar topological structure and ground value functions will co-occur more frequently, as shown in Fig. 10a.

Fig. 10

Comparison of solved AMDPs for both approaches in Grid World with traps. Green cell on the left side denotes starting state, goal state is the blue cell on the right side (Color figure online)

Generated abstract states by clustering (K-Means) together with the heatmaps corresponding to solved AMDPs are shown in Figs. 10c and 10d for the Topology and Uniform approaches, respectively. Clearly, the layout of abstract states for the Topology approach agrees with both the topology and value function of the ground-level MDP (Fig. 10b). More prominently, our approach was able to cluster the adjoining trap states together into a single abstract state. By comparison, in Fig. 10d, Uniform approach constructs abstract states ignoring the topological structure and traps in the environment.

In particular, in Fig. 10c, we also note that the abstract state containing traps gets a much lower value than its neighbours. The closer an abstract state is to the goal state, the higher its value. The difference (scaled by $\omega$) between the values of two abstract states can be taken as an additional reward for the ground agent. Therefore, the guidance from reward shaping will roughly agree with the optimal policy derived from the solved ground-level MDP (Fig. 10b). One can always simulate a successful path to the goal state by following the colour of the heatmap from darker to lighter regions.

In contrast, the reward shaping from Uniform approach guides the agent straight towards the goal state, directly traversing the region of traps, as indicated in Fig. 10d. This looks correct in the abstract MDP, but actually causes huge negative rewards in the environment. Moreover, reward shaping in Fig. 10d is actually hindering the ground agent from learning the optimal policy in a certain area (from the bottom right to the top left) of the maze.

5.3.2 Visualization in flag collection domain

Fig. 11

Solved AMDP for Topology approach in Flag Collection domain over maze: low connectivity. The agent starts from the white cell (left bottom corner) in subspace (0-0-0) and tries to reach the goal state (blue cell on left bottom side) in subspace (1-1-1). Green cells located in the upper half of the maze are flags (Color figure online)

Figure 11 visualizes how our Topology approach works over the actual state space of the Flag Collection domain (stationary setting). In our Flag Collection domain, a state is in form of $s=(x,y,a,b,c)$, where x, y indicate coordinates and a, b, c are binary variables indicating whether the corresponding flag is collected or not. Since the last three dimensions are binary, we are able to visualize the five-dimensional state space by converting it into eight two-dimensional subspaces, corresponding to each status of flag collection. Certain transitions are only uni-directional, for instance, from state (x, y, 0, 0, 0) one can transit to state (x, y, 0, 1, 0), but the transition in the reverse direction is impossible.

As shown in Fig. 11, the regions with irregular boundaries correspond to the abstract states generated by Topology approach and they all abide by the topology of the environment. It is possible that one abstract state containing a flag could span across two subspaces because the Topology approach generates abstract states following the topology of the complete five-dimensional state space. This characteristic enables our approach to build the transition and reward function of AMDPs automatically, based on stored experiences without external domain knowledge (according to Algorithm 1 and 2). That is to say, our Topology approach is able to generalize to various state spaces, in which each dimension could have very different properties.

In Fig. 11, value function of the AMDP is presented as a heatmap, where lighter colours indicate higher values and vice versa. Starting from the white cell (left bottom corner) in subspace (0-0-0), reward shaping can always steer the agent towards abstract states with higher values so that the agent can approach the goal state (blue cell on the left bottom side) in subspace (1-1-1) efficiently.

6 Conclusion

We proposed a novel approach for generating high-quality AMDPs that helps accelerate existing model-free RL algorithms. Our approach to construct abstract states is inspired by graph representation learning methods and effectively encodes the topological and reward structure of the ground-level MDP. Meanwhile, it requires little external domain knowledge and generalizes well to various state spaces. We showed strong performance improvements over the baseline approach in Flag Collection domain in terms of convergence speed, sample efficiency and run time consumption. In our qualitative analysis, we visually showcased that our approach can generate AMDPs that preserve the topological and reward structure of underlying MDPs. In future work, we intend to incorporate our approach with Deep RL algorithms.