EmulART: Emulating radiative transfer—a pilot study on autoencoder-based dimensionality reduction for radiative transfer models

Abstract

Dust is a major component of the interstellar medium. Through scattering, absorption and thermal re-emission, it can profoundly alter astrophysical observations. Models for dust composition and distribution are necessary to better understand and curb their impact on observations. A new approach for serial and computationally inexpensive production of such models is here presented. Traditionally these models are studied with the help of radiative transfer modelling, a critical tool to understand the impact of dust attenuation and reddening on the observed properties of galaxies and active galactic nuclei. Such simulations present, however, an approximately linear computational cost increase with the desired information resolution. Our new efficient model generator proposes a denoising variational autoencoder (or alternatively PCA), for spectral compression, combined with an approximate Bayesian method for spatial inference, to emulate high information radiative transfer models from low information models. For a simple spherical dust shell model with anisotropic illumination, our proposed approach successfully emulates the reference simulation starting from less than 1% of the information. Our emulations of the model at different viewing angles present median residuals below 15% across the spectral dimension and below 48% across spatial and spectral dimensions. EmulART infers estimates for $\sim$85% of information missing from the input, all within a total running time of around 20 minutes, estimated to be 6$\times$ faster than the present target high information resolution simulations, and up to 50$\times$ faster when applied to more complicated simulations.

1 Introduction

Cosmic dust is ubiquitous in the Universe, particularly present in the interstellar medium (ISM) [56] and in the line of sight towards astrophysical objects such as supernovae remnants [42], galaxies [15] and active galactic nuclei (AGN) (AGN, Haas et al. [21]). Dust grains absorb and scatter UV/optical radiation and re-emit that energy at infrared wavelengths and are thus responsible for both attenuation and reddening of light in the line of sight, which also impact distance measurements for cosmology when using “standard candles” such as supernovae [7]. Moreover, scattering on the dust grains and dichroic absorption in the dusty medium may lead to polarization of the light as it traverses the interstellar medium.

The effect these processes—of dust absorption, scattering and emission—have on the light detected from astronomical objects must be accounted when studying their intrinsic properties. Moreover, the nature of the dust can also inform us on physical and chemical processes related to its own history, from formation, variation in composition, growth and destruction in different astrophysical structures such as accretion disks, clouds and galaxies, as well as its interaction with magnetic fields through dust grain alignment. The analysis of the aforementioned interactions requires performing radiative transfer (RT) calculations [49], allowing us to simulate the light path, from the source to the observer, depending on the physical properties of the emitting source embedded in dust structures of different geometries, sizes and composition. Comparing various RT models, based on different simulated properties, to global and pixel-by-pixel spectral energy distributions (SEDs) obtained in astronomical observations we can infer valuable information on the properties of the light sources, as well as the distribution and properties of the dust [2, 12, 17].

Observations of molecular clouds [6, 16] have shown that dust distributions are often inhomogeneous and complex; consequently, the understanding of their intrinsic properties requires 3D radiative transfer calculations. This type of non-local and nonlinear problem requires calculations which are computationally very costly [49]; this has prompted the search for alternative non-analytic approximate ways to address them. One of the most successful ways is Monte Carlo Radiative Transfer (MCRT, Mattila [34]; Roark et al. [43]).

Monte Carlo Radiative Transfer methods simulate a large number of test photons, which propagate from their emission by a source through their journeys through the dusty medium. At every stage, the characteristics that define their paths are determined by generating numbers from the probability density function most suited for each process they may undergo (absorption, scattering, re-emission, etc.). At the end of the simulation, the radiation field is recovered from a statistical analysis of the photon paths. As an ensemble, the distribution of particles provides a good representation of the radiative transfer, as long as a sufficient number of photons is chosen.

Stellar Kinematics Including Radiative Transfer (SKIRT, Baes et al. [5]; Camps and Baes [9]) is an MCRT suite that offers some built-in source templates, geometries, dust characterizations, spatial grids, and instruments, as well as an interface so that a user can easily describe a physical model. The user can in this way avoid coding the physics that describes both the source (e.g., AGN or galaxy type, observation perspective, emission spectrum) and environment (between the simulated source and observer, such as dust grain type and orientation, dust density distribution, etc.) but instead design a model of modular complexity by following a Q &A prompt (itself adaptable to the user expertise).

MCRT simulations suffer from computational limitations, namely the memory requirement scaling with the volume grid density, and the processing time scaling quasi-linearly with the amount of photons simulated [10]. Autoencoders [55] together with collocation strategies [20] have been applied to solve complex interactions such as the ones described above; our approach differs by attempting to upscale the information density within a simulated data product instead. Considering that the objects and phenomena modeled by MCRT simulations present non-random spatial structures with heavily correlated spectral features, we tackle the computational cost issue through the development of an emulator that can achieve HPN-like MCRT models by exploring and implementing an autoencoder neural network in combination with integrated nested Laplace approximation (INLA, Rue et al. [44]), an approximate method for Bayesian inference of spatial maps modeled with Gaussian Markov random fields, on LPN-like MCRT simulations. The results are then compared against an analogous implementation employing principal component analysis (PCA).

Section 2 provides a brief highlight of the employed methods. Section 3 describes our pipeline architecture and some of steps that lead to its development. Results and performance evaluation follow in Sect. 4. Section 5 presents our perspective on the significance of the obtained results and provides the steps to follow in order to both improve and generalize them in future developments.

All files concerning this work (SKIRT simulations, R scripts, neural network models, emulation products and performance statistics) can be obtained from our repository.¹

2 Methods

To reduce the computational cost of SKIRT simulations, without compromising, as much as possible, the quality of the resulting models, an autoencoder, i.e., a dimensionality reduction neural network, is implemented to compress the spectral information within LPN spectroscopic data cubes. Then, approximate Bayesian inference is performed with INLA on the spatial information of the compressed feature maps. Lastly, the reconstructed feature maps are decompressed to an HPN emulation.

2.1 SKIRT

As previously state, SKIRT allows the creation of models by prompting a Q &A. Through it the user can configure any one- to three-dimensional geometry and combine multiple sources and media components, each with their own spatial distribution and physical properties, by either employing the built-in library or importing components from hydrodynamic simulations. Media types include dust, electrons and neutral hydrogen; the user can configure their own mixture, including optical properties and size distributions or simply choose from the available built-in mixtures. The included instruments allow the “observation” and recording of spectra, broad-band images or spectroscopic data cubes.

SKIRT uses Monte Carlo method for tracing photon packets through the spatial domain (both regular and adaptive spatial grids area available, as well as some optimized for 1D or 2D models); these packets are wavelength sampled from the source/medium spectrum (the wavelength grids can be separately configured for both storing the radiation field and for discretizing medium emission spectra). As they progress through the spatial grid cells, these photon packets can experience different physical interactions, such as multiple anisotropic scattering, absorption and (re-)emission by the transfer medium, Doppler shifts due to kinematics of sources and/or media, polarization caused by scattering off dust grains as well as polarized emission, among others.

The present application is intended for the combination of both spatial and spectral information. The outputs used here will be spectroscopic data cubes; these are in the flexible image transport system (FITS) format [54] and are composed of 2D spatial distributions at the desired wavelength bins.

The simulated spatial flux densities vary according to the amount of photons/photon packets simulated. The simulation starts by assigning some energy to those photons following the spectral energy distribution (SED) of a given astrophysical source, ensuring that no matter how many photons are simulated the spectral information is preserved. Simulations with a lower photon number (LPN) will consequently display fewer spatial positions with information (nonzero flux) and some of these pixels will have higher flux, some lower, i.e., the SED will have lower signal-to-noise ratio than in simulations with higher photon number (HPN). SKIRT has already been employed in the study of various galaxies [13, 51, 52], AGN [47, 48] and other objects.²

2.2 Dimensionality reduction

Dimensionality reduction methods can more familiarly be called as compressors. These are methods that analyze and transform data from a high-dimensional space into a low-dimensional space while attempting to retain as much meaningful properties of the original data as possible. Working in high-dimensional spaces can be undesirable for many reasons; raw data are often sparse as a consequence of the curse of dimensionality,³ and analyzing the data usually becomes computationally intractable. Popular dimensionality reduction techniques in astronomy include PCA [32, 33] and non-negative matrix factorization (NMF, Ren et al. [41]; Boulais et al. [8]).

Autoencoder networks are an alternative method which has been gaining attention within the astronomy, astrophysics and cosmology community [24, 28, 37, 38, 40, 53].

2.2.1 Denoising variational autoencoders

Autoencoders (AEs) are a type of neural network architecture employed to learn compressed representations of data. In such architectures, the input and output layers are equal, and the hidden layers display a funneling in and out scheme in regard to the number of neurons per layer, with the middle layer having the least amount of neurons and the input and output layers having the most. The models built this way can be seen as the coupling of a compressor/encoder and a decompressor/decoder, the first generating a more (ideally) fundamental representation of the data, and the second bringing it back to its initial feature space. After training, the encoder can be coupled at the beginning of other architectures, providing them with more efficient features from which to learn from. Interesting to note that AEs have shown promise as auxiliary tools in citizen science projects,⁴ such as the Radio Galaxy Zoo [40].

Alternative ways of training this kind of network exist, such as:

• Having multiple instances of each data point, resulting from the injection of noise or from a set of transformations. Each instance of the same data point is then matched to the same output with the aim of making the model robust to noise and/or invariant to those transformations.

• Having the mid-layer composed by two complementary layers of neurons (a mean layer and a standard deviation layer) instead of a single layer. Complemented with an appropriate loss function, the model will learn approximate distributions of values instead of single values, making it more robust and allowing for the decoder to also become a generator of different, yet statistically identical, examples.

Such strategies fall under different categories such as denoising autoencoders (DAEs) [31] and variational autoencoders (VAEs) [22], respectively. In this work, we implement both, a denoising variational autoencoder (DVAE).

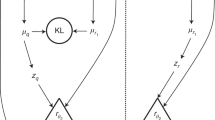
Im et al. [25] showed that the DVAE, by introducing a corruption model, can lead to an encoder that covers a broader class of distributions when compared to a regular VAE (the corruption model may, however, remove the information necessary for reconstruction). In this context, the loss function, $\mathcal {L}_{\mathrm{DVAE}}$, to be minimized is given by the weighted sum of the Kullback–Leibler divergence (which influences the encoder) and the reconstruction error (see Eq. 1), similarly to a VAE, with the difference that the encoder now learns to approximate a prior p(z) given corrupted examples and that in this case the reconstruction error can be interpreted as a denoising criterion:

$$\begin{aligned} \mathcal {L}_{\mathrm{DVAE}} \propto a_1\mathbb{KL}\mathbb{}(q(z\mid y')\mid p(z)) + a_2\ln {p(y \mid z)}, \end{aligned}$$

(1)

where $\mathbb{KL}\mathbb{}$ refers to the Kullback–Leibler divergence, $y'\sim q(y'\mid y)$ is a sample of the corruption model, p(z) is the prior for the latent feature, $q(z\mid y')$ models the encoder, $p(y \mid z)$ models the decoder/generator and ($a_1$, $a_2$) are weights. For more details, the reader is referred to [14, 25].

2.2.2 Principal component analysis

Principal component analysis (PCA) is a method that analyzes the feature space of the training data and creates orthogonal vectors (linear combinations of the initial variables) whose direction indicates the most variability. These new vectors in the transformed data set are called eigenvectors, or principal components, while the eigenvalues represent the coefficients attached to eigenvectors and give the relative amount of variance carried by each principal component.

PCA transforms the original space through rotation of its axes and re-scaling of the axes range. The first new PC is aligned with the direction of largest variance in the data. The second PC should also maximize the variance, while being orthogonal to the first, and, respectively, for the remaining PCs. Mathematically, these directions can be determined through the covariance matrix, as expressed in Eq. (2):

$$\begin{aligned} \Sigma _{ff'} = \sum _{j=1}^{j=N} \frac{(X_f^j - \bar{X}_f)(X_{f'}^j - \bar{X}_{f'})}{N} , \end{aligned}$$

(2)

where $X_f$ is the mean of all values at feature f and N is the total number of data points (for more details and a modern review on PCA, we suggest [29]). Once $\Sigma _{ff'}$ is diagonalized, the PCs are its eigenvectors, the first PC being the one with the largest associated eigenvalue and so on.

PCs are uncorrelated and frequently the information is compressed into the first K components, with $K \ll M$ (where M is the total number of features of the original space).

A data point from the original data set can then be reasonably recovered using those K PCs,

$$\begin{aligned} \hat{{\mathbf {X}}} \approx \bar{{\mathbf {X}}} + \sum _{m=1}^{m=K} c_m {\mathbf {P}}_m, \end{aligned}$$

(3)

where $\bar{{\mathbf {X}}}$ represents the mean of all data points, ${\mathbf {P}}_m$ is the m-th PC and $c_m$ is the projection of the data point on ${\mathbf {P}}_m$.

Using all the M PCs, the reconstruction becomes identical to the original data, but with a new basis that captures a large fraction of the variance in a small number of components K, dimensionality reduction is achieved. In this work, we used two approaches to determine K (see Sect. 3.4).

Further discussion on the importance of PCA and its applications in astronomy can be found in, e.g., [26, 27, 45].

2.3 Spatial approximate Bayesian inference

Bayesian inference (BI) refers to a family of methods of statistical inference where a hypothetical probabilistic model is updated, following Bayes theorem (Eq. 4), whenever new data are obtained. Bayes theorem allows to calculate a posterior distribution $p(\theta \mid y)$ (the conditional probability of $\theta$ occurring given y) by weighting in $p(y\mid \theta )$ (the likelihood of y occurring given $\theta$), $p(\theta )$ (estimation of the probability distribution of $\theta$ before observing y, also designated as a prior), and p(y) (the marginal probability of y, obtained from integrating $\theta$ out of $p(y\mid \theta )$):

$$\begin{aligned} p(\theta \mid y) = \frac{p(y\mid \theta )}{p(y)} p(\theta ) , \end{aligned}$$

(4)

$$\begin{aligned} p(y) = \int {p(y \mid \theta )p(\theta )\text {d}\theta }. \end{aligned}$$

(5)

This kind of update is of utmost relevance in the dynamical analysis of data streams or in the analysis of correlated data and has been proposed in astronomy, from the study of variable stars [57] to 3-D mapping of the Milky way [3].

Approximation techniques [23, 35, 50] have been developed over the years in order to help curb the very time-consuming process of sampling the whole likelihood $p(y\mid \theta )$. To this end, we here implement the integrated nested Laplace approximation (INLA, Rue et al. [44]).

2.3.1 Integrated nested Laplace approximation

INLA is an approximate BI method that accounts for spatial correlations between observed data points to recover an assumed Gaussian latent field and, in doing so, it is not only capable of predicting unobserved points of that field but also of correcting noisy observed ones, as well as associating a variance to those inferences.

Most techniques for calculating posterior distribution rely on Markov chain Monte Carlo (MCMC, Collins et al. [11]) methods. In this class of sampling-based numerical methods, the posterior distribution is obtained after many iterations, which is often computationally expensive. INLA provides a novel approach for faster BI. While MCMC methods draw a sample from the joint posterior distribution, the Laplace approximation is a method that approximates posterior distributions of the model parameters to Gaussians, which is computationally more effective. Within the INLA framework, the posterior distribution of the latent Gaussian variables $\pmb {x}$ and hyper-parameters of the model $\boldsymbol{\theta}$ is:

$$\begin{aligned} p(\pmb {x},\boldsymbol{\theta} \mid \pmb {y}) = \frac{p(\pmb {y} \mid \pmb {x}, \boldsymbol{\theta})\; p(\pmb {x}, \boldsymbol{\theta})}{p(\pmb {y})} \propto p(\pmb {y} \mid \pmb {x}, \boldsymbol{\theta})\; p(\pmb {x}, \boldsymbol{\theta}), \end{aligned}$$

(6)

where $\pmb {y}=(y_{1},\ldots ,y_{n})$ represents a set of observations. Each observation is treated with a latent Gaussian effect, with each $x_{i}$ (a Gaussian distribution of mean value $\mu _{i}$ and standard deviation $\sigma _{i}$) corresponding to an observation $y_{i}$, where $i\in [1,\ldots ,n]$. The observations are conditionally independent given the latent effect $\pmb {x}$ and the hyper-parameters $\boldsymbol{\theta}$, and the model likelihood is then:

$$\begin{aligned} p(\pmb {y} \mid \pmb {x}, \boldsymbol{\theta}) = \prod _{i} p(y_{i} \mid x_{i}, \boldsymbol{\theta}). \end{aligned}$$

(7)

The joint distribution of the latent effects and the hyper-parameters, $p(\pmb {x}, \boldsymbol{\theta})$ can be written as $p(\pmb {x}\mid \boldsymbol{\theta}) p(\boldsymbol{\theta})$, where $p(\boldsymbol{\theta})$ represents the prior distribution of hyper-parameters $\boldsymbol{\theta}$. It is assumed that the spatial information can be treated as a discrete sampling of an underlying continuous spatial field, a latent Gaussian Markov random field (GMRF), that takes into account the spatial correlations, and whose hyper-parameters are inferred in the process. For a GMRF, the posterior distribution of the latent effects is:

$$\begin{aligned} p(\pmb {x} \mid \boldsymbol{\theta}) \propto \mid \pmb {Q}(\boldsymbol{\theta})\mid ^{1/2} \exp {-\frac{1}{2} \pmb {x}^{T}\pmb {Q}(\boldsymbol{\theta})\pmb {x}} , \end{aligned}$$

(8)

where $\pmb {Q}(\boldsymbol{\theta})$ represents a precision matrix, or inverse of a covariance matrix, which depends on a vector of hyper-parameters $\boldsymbol{\theta}$. This kernel matrix is what actually treats the spatial correlation between neighboring observations. Using Eq. (6), the joint posterior distribution of the latent effects and hyper-parameters can be written as:

$$\begin{aligned} \begin{aligned}&p(\pmb {x}, \boldsymbol{\theta} \mid \pmb {y})\propto p(\boldsymbol{\theta}) \mid \pmb {Q}(\boldsymbol{\theta})\mid ^{1/2} \exp \\&\qquad {-\frac{1}{2} \pmb {x}^{T}\pmb {Q}(\boldsymbol{\theta})\pmb {x}} \prod _{i} p(y_{i} \mid x_{i}, \boldsymbol{\theta}) \\&\quad =p(\boldsymbol{\theta}) \mid \pmb {Q}(\boldsymbol{\theta})\mid ^{1/2} \exp \\&\qquad {-\frac{1}{2} \pmb {x}^{T}\pmb {Q}(\boldsymbol{\theta})\pmb {x} + \sum _{i} \log (p(y_{i} \mid x_{i}, \boldsymbol{\theta}))}. \end{aligned} \end{aligned}$$

(9)

Instead of obtaining the exact posterior distribution from Eq. (9), INLA approximates the posterior marginals of the latent effects and hyper-parameters, and its key methodological feature is to use appropriate approximations for the following integrals:

$$\begin{aligned} p( x_{i} \mid \pmb {y})=\int p( x_{i} \mid \boldsymbol{\theta}, \pmb {y})p( \boldsymbol{\theta}\mid \pmb {y})\,\mathrm{d}\boldsymbol{\theta} \end{aligned}$$

(10)

$$\begin{aligned} p( \theta _{j} \mid \pmb {y})=\int p( \boldsymbol{\theta}\mid \pmb {y})\, \mathrm{d}\boldsymbol{\theta}_{-j}, \end{aligned}$$

(11)

where $\boldsymbol{\theta}_{-j}$ is a vector of hyper-parameters $\boldsymbol{\theta}$ without element $\theta _{j}$.

INLA constructs nested approximations:

$$\begin{aligned} \tilde{p}( x_{i} \mid \pmb {y})=\int \tilde{p}( x_{i} \mid \boldsymbol{\theta}, \pmb {y})\tilde{p}( \boldsymbol{\theta}\mid \pmb {y})\, \mathrm{d}\boldsymbol{\theta}, \end{aligned}$$

(12)

$$\begin{aligned} \tilde{p}( \theta _{j} \mid \pmb {y})=\int \tilde{p}( \boldsymbol{\theta}\mid \pmb {y})\,\mathrm{d}\boldsymbol{\theta}_{-j}, \end{aligned}$$

(13)

where $\tilde{p}(\cdot \mid \cdot )$ is an approximated posterior density. Using the Laplace approximation, the posterior marginals of hyper-parameters $p( \boldsymbol{\theta}\mid \pmb {y})$ at a specific value $\boldsymbol{\theta}=\boldsymbol{\theta}_{j}$ can be written as:

$$\begin{aligned} \tilde{p}( \boldsymbol{\theta}_{j}\mid \pmb {y})\propto \frac{p(\pmb {x},\boldsymbol{\theta}_{j},\pmb {y})}{\tilde{p}_{G}(\pmb {x}\mid \boldsymbol{\theta}_{j},\pmb {y})} \propto \frac{p(\pmb {y}\mid \pmb {x},\boldsymbol{\theta}_{j}) p(\pmb {x}\mid \boldsymbol{\theta}_{j}) p(\boldsymbol{\theta}_{j})}{\tilde{p}_{G}(\pmb {x}\mid \boldsymbol{\theta}_{j},\pmb {y})} \mid _{\pmb {x}=\pmb {x}^{*}(\boldsymbol{\theta}_{j})}, \end{aligned}$$

(14)

$$\begin{aligned} \tilde{p}_{G}(\pmb {x}\mid \boldsymbol{\theta},\pmb {y}) \propto \exp {-\frac{1}{2}\pmb {x}^{T}\pmb {Q}(\boldsymbol{\theta})\pmb {x} + \sum _{i} g_{i}(x_{i})}, \end{aligned}$$

(15)

where $\tilde{p}_{G}(\pmb {x}\mid \boldsymbol{\theta},\pmb {y})$ is the Gaussian approximation to the full conditional of $\pmb {x}$, and $\pmb {x^{*}}(\boldsymbol{\theta}_{j})$ is the mode of the full conditional $\pmb {x}$ for given $\boldsymbol{\theta}_{j}$. The posterior marginals of the latent effects are then numerically integrated as follows:

$$\begin{aligned} \tilde{p}(x_{i} \mid \pmb {y}) \backsimeq \sum _{j} \tilde{p}( x_{i} \mid \boldsymbol{\theta}_{j}, \pmb {y})\tilde{p}( \boldsymbol{\theta}_{j}\mid \pmb {y}) \Delta _{j}, \end{aligned}$$

(16)

where $\Delta _{j}$ represents the integration step.

A good approximation for $\tilde{p}( x_{i} \mid \boldsymbol{\theta}, \pmb {y})$ is required and INLA offers three different options: Gaussian approximation, Laplace approximation and simplified Laplace approximation [44]. In this work, we used the simplified Laplace approximation, which represents a compromise between the accuracy of the Laplace approximation and the reduced computational cost achieved with the Gaussian approximation.

INLA has been shown [44] to greatly outperform MCMC sampling under limited computational power/time conditions, with the estimation error of INLAs results being invariably smaller than those of MCMC. Other approximated inference methods exist, such as variational Bayes [23] and expectation-propagation [35], however these methods are not only slower, but they struggle with estimating the variance of the posterior since they execute iterative calculations instead of analytic approximations, unlike INLA [44].

INLA suffers nonetheless from some limitations. The first, already mentioned above, is that to get meaningful results the latent field to be inferred must be Gaussian—which is not always the case—and it must display conditional independence properties; the second is that for fast inference it is required that the number of hyper-parameters (characterizers of the parameter models) should be inferior to 6 and that the number of available observations of the field to infer be much smaller than the size of that field.

INLA is freely available as an R package [4], and it has already been shown to: (1) be capable of recovering structures in scalar and vector fields, with great fidelity, out of sparse sets of observations, and even of inferring structures never seen before; (2) be robust to noise injections [19]. We refer to [18, 44] for more details on the mathematical background of INLA and the methods it employs.

3 Implementation

This section describes both the dataset, the combination of a DVAE/PCA with INLA to enhance low information density SKIRT simulation data cubes and the tools to do so.

Our pilot pipeline aims to emulate radiative transfer models, as such we named it EmulART. All scripts were written and executed under R [39] (version 3.6.3) and make use of the Keras API [1].

The DVAE architecture was adapted from the one described in the Keras documentation (https://tensorflow.rstudio.com/guides/keras/making_new_layers_and_models_via_subclassing.htmlputting-it-all-together-an-end-to-end-example). The encoder block starts with an input layer of 64 features/neurons (the wavelengths of the SEDs), and each consecutive layer halves the amount of features until the latent space layer is reached. That layer, unlike the ones that precede it, is comprised of a vector doublet, each with 8 neurons. One vector corresponds to the mean value of the latent features and the other to their variance, together these vectors, describe a value distribution for each of the latent features. The input of the decoder will be drawn from those distributions, and each subsequent layer will double the amount of features, decompressing the data, until the output, with the same number of features as the input layer of the encoder, 64, is reached.

Two pipelines using principal component models were used to compare against the DVAE pipeline. One pipeline makes use of the 8 PCs which explained the most variance (the same number of latent variables as available for the DVAE), while the other uses the number of PCs determined by the elbow method.

3.1 Dataset

In this work, 30 SKIRT simulations were used for separate purposes. All simulations model a spherical dust shell composed by silicates and graphites surrounding a bright point source with anisotropic emission [47], as defined by Eq. (17) following Netzer [36]:

$$\begin{aligned} L(\theta ) \propto \cos {\theta }(2\cos {\theta } + 1) , \end{aligned}$$

(17)

where $\theta$ is the polar angle of the coordinate system. Each realization is a cube of 300-by-300 pixel maps at 103 distinct wavelength bins. The first 39 wavelength bins were discarded (leaving us with 64) for displaying very low signal of randomly scattered emission (less than 0.0001% of the pixels at these wavelengths display flux density different than 0). The final dataset thus includes 90,000 spaxels⁵ per cube, each spaxel with 64 fluxes, or “features”, at wavelength bins ranging from $\sim$1 $\upmu$m to 1 mm.⁶

The 30 realizations differ from each other by up to three parameters: the tilt angle, $\phi$, of the object as seen by the observer ($0^\circ$, face-on, and $90^\circ$, edge-on;⁷) the optical depth,⁸$\tau _{9.7}$,⁹ of the dust shell (0.05, 0.1 and 1.0); the amount¹⁰ of photon packets simulated, $N_p \in \{10^4, 10^5, 10^6, 10^7, 10^8\}$. For each particular $\tau _{9.7}$ and $\phi$ combination, the corresponding $N_p = 10^8$ realization was regarded as the HPN reference, or “ground truth”, for the purpose of evaluating the performance of our routines, since those yield the highest information density, while all other simulations, with $N_p \in \{10^4, 10^5, 10^6, 10^7\}$, were considered LPN simulations. Figure 1 illustrates the difference between HPN references through different $\tau _{9.7}$ and $\phi$ combinations, while Fig. 2 shows LPN models with differing $N_p$, keeping $\tau _{9.7} = 0.05$ and $\phi = 0^\circ$. Table 1 displays the difference between the quality of the individual spaxels¹¹ that compose each LPN realization and HPN reference; the median, M, and mean absolute deviation (MAD) of the normalized residuals (see Eq. 18) of every pixel within each LPN realization; as well as the total information ratio (TIR) for all realizations, here defined as the ratio of the number of pixels with flux different than 0 of an LPN input or emulation, $N_{X' \ne 0}$, and that same number for the HPN reference, $N_{X \ne 0}$ (see Eq. 19), as an information metric to balance against the normalized residuals¹²:

$$\begin{aligned} \mathrm{Residuals} (\%) = \left| \frac{X' - X }{X}\right| \times 100\%, \end{aligned}$$

(18)

$$\begin{aligned} \mathrm{TIR} (\%) = \frac{N_{X' \ne 0}}{N_{X \ne 0}} \times 100\%. \end{aligned}$$

(19)

Fig. 1

High photon number references of a spherical dust shell composed of silicates and graphites surrounding a bright anisotropic point source. The present flux density maps represent the simulated observations at wavelength 1,85 $\upmu$m, with $\phi = 0^\circ$ (a) and $\phi = 90^\circ$ (b) for $\tau _{9.7} \in \{0.05, 1.0\}$. Color indicates flux density in W/m$^2$ (Color figure online)

Fig. 2

Models of a spherical dust shell composed of silicates and graphites surrounding a bright anisotropic point source, with $\tau _{9.7} = 0.05$ and $\phi = 0^\circ$, realized by simulating different photon amounts. The present flux density maps represent the simulated observations at wavelength 9.28 $\upmu$m. a Presents the realization obtained by simulating $N_p \in \{10^4, 10^5, 10^6\}$, while b presents the realizations obtained by simulating $N_p \in \{10^7, 10^8\}$. Color indicates flux density in W/m$^2$ (Color figure online)

Table 1 Statistics regarding how the LPN realizations compare to the HPN reference

The realizations were split into two subsets: one to train the autoencoder and perform the first batch of tests to the emulation pipeline, labeled AESet and described in Sect. 3.1.1; and another, comprised exclusively by data, the autoencoder did not see during training, to better assess EmulARTs performance, labeled EVASet and described in Sect. 3.1.2.

3.1.1 AESet

This subset is comprised of 5 SKIRT simulation outputs of the same model, a spherical shell of dust composed by silicates and graphites, with optical depth $\tau _{9.7} = 0.05$, surrounding a bright point source with anisotropic emission seen face-on, $\phi = 0^\circ$, making the emission appear isotropic. The only different parameter across the realizations in AESet was $N_p \in \{10^4, 10^5, 10^6, 10^7, 10^8\}$ (see Fig. 2). The $N_p = 10^8$ realization is the HPN and was used as the reference, or “ground truth”, for the purpose of both training the autoencoder model as well as evaluating the performance of EmulART.

Since the goal of our methodology is to reconstruct the reference simulation using LPN realizations as input, the values of each cube were multiplied by the ratio between the amount of photons simulated for the LPN input, $N_p^{\mathrm{LPN}}$ and the amount of photons simulated for the HPN reference ($N_p^{\mathrm{HPN}} = 10^8$). In Fig. 3, we can see the impact of this de-normalization on the integrated SEDs¹³ of the LPN realizations: LPN realizations have less flux when not including SKIRTs normalization.

Fig. 3

Integrated SEDs (upper panel) and normalized residuals (lower panel) for each of the five SKIRT simulations in our dataset: a due to normalization, realizations with different amounts of photons simulated display very similar integrated SEDs; b integrated SEDs of realizations in AESet after de-normalization (total flux is here proportional to $N_p$). The labels indicate the value of $N_p$ for each realization

The spaxels of all cubes within AESet were used to train the DVAE model. For this, we split AESet into training set (5/6) and test set (1/6). Spaxels of different cubes but which share the same spatial coordinates were assigned to the same ensemble. This strategy aimed for the DVAE model to achieve a denoising capability and consists on having input spaxels that result from realizations with different $N_p$ always matches the HPN references version on the output layer.

In SKIRT, choosing to simulate fewer photons results in an output with more zero flux density pixels which in turn means that more spaxels will be null at more wavelength bins. Even though this is different than noise, it is akin to missing data whose impact we aim to curb by implementing a DVAE architecture.

Before training the DVAE model, we perform some spaxel selection and preprocessing tasks on AESet which is thoroughly described in Appendix A.

Later, when performing preliminary tests on EmulART, we used the 4 LPN realizations within AESet ($N_p \in \{10^4, 10^5, 10^6, 10^7\}$) as input.

3.1.2 EVASet

This subset is comprised of the 25 SKIRT simulation cubes that also model a spherical shell of silicates and graphites surrounding a bright anisotropic point source but have different combinations of $\phi$, $\tau _{9.7}$ and $N_p$ from those in AESet. To all realizations in EVASet, we performed the same feature selection and flux de-normalization tasks described both in Sect. 3.1.1 and Appendix A.

The 20 LPN realizations within EVASet($N_p \in \{10^4, 10^5, 10^6, 10^7\}$) were used as input for EmulART for a deeper assessment of the capabilities of our emulation pipeline. The remaining 5 HPN cubes (those with $N_p = 10^8$) were used as references to compute performance metrics.

A list detailing the parameters of the SKIRT simulations used in this work, as well as their split into AESet and EVASet, can be consulted in Appendix B.

3.2 Training the DVAE

To determine which set of hyper-parameters for the DVAE suited our needs best, we performed some tests, grid-searches and explored: amounts of features in the latent space; activation, loss and optimization functions; batch size;¹⁴ bias constraint;¹⁵ learning rate¹⁶; and, patience¹⁷ values. These exploratory tests were performed by training the models during 100, 500 and 2000 epochs, according to the need to differentiate performance between hyper-parameter sets.

We measured performance by the percentage residuals of both the individually reconstructed spaxels, of the test subset of AESet, and of each of AESets cubes integrated SEDs. We selected the set of hyper-parameters listed below for being the most consistent across different tests. Figure 4 shows the validation loss closely following the training loss, indicating successful convergence of the model to our data.

• Latent feature amount: 8

• Activation function: SELU [30] and sigmoid (for the output layer only)

• Loss function: weighted sum of the Kullback–Leibler divergence and mean percentual error¹⁸

• Optimization function: Adam¹⁹

• Batch size: 32

• Bias constraint: 0.95

• Train - Validation split: 4/5, 1/5

• Maximum $N_{\mathrm{Epoch}}$: 4500

• Patience 1²⁰: 500 epochs

• Patience 2²¹: 3000 epochs

• Initial learning Rate (LR): 0.001

• Learning rate decrease²²: 0.25

Fig. 4

Loss, in log scale, as function of the number of epochs. The training loss is represented by $\blacksquare$ and the validation loss by red $\blacklozenge$. The plot shows that both metrics converge to comparable values (Color figure online)

After training, the weights were saved to files which are loaded into the pipeline (see Sect. 3.3).

Appendix C shows the relationship between the compressed (or latent) features of the test set, as well as the Pearson’s correlation coefficients (PCCs) between those features. Based on the analysis of the correlations of the latent features, we decided to stop further compression of the spectral dimensions of the data.

3.3 DVAE Emulation pipeline

Within EmulART, the feature space is first compressed with the variational encoder; the latent space is then sampled and the resulting latent features spatial maps are reconstructed with INLA; finally the reconstructed wavelength (original feature space) maps are recovered with the decoder. Additionally, to conform the data to each of the different stages of the pipeline, we perform some operations described below. Figure 5 presents a scheme²³ of the emulation pipeline, while a flowchart including all relevant data pre- and post-processing operations, integrated within the emulation pipeline, can be found in Appendix D.

Fig. 5

Scheme with the most relevant operations of the pipeline. Data shaping is represented in cyan; feature combination is in dark blue; and statistical operations are in red. Feature dimensionality is given along the axis of the arrows, at the top of each layer. ${\varvec{\mu }}$ is the vector holding the mean value of the latent features distribution, while ${\varvec{\sigma }}$ is the vector holding their variance; ${\mathbf {z}}$ is the vector built by randomly drawing values from the latent features distributions $G({\varvec{\mu }},{\varvec{\sigma }})$ (Color figure online)

Prior to being parsed by the encoder network module, the data are initially preprocessed as described in Appendix A. After the data go through the encoding and variational sampling stages (see Fig. 5), the resulting latent features maps, $Z_f(x,y)$,²⁴ are then transformed according to the following steps²⁵ for each feature map, $Z_f(x,y)$:

• 1. Determine the minimum, $m^0_f$, and maximum, $M^0_f$, values of the map,

  $$\begin{aligned} m^0_f = \min (Z_f(x,y)),\quad M^0_f = \max (Z_f(x,y)); \end{aligned}$$

• 2. Determine the value range, $R_f$, of the map,

  $$\begin{aligned} R_f = M^0_f - m^0_f; \end{aligned}$$

• 3. Offset the value range of the map so that the new minimum is 0,

  $$\begin{aligned} Z'_f(x,y) = Z_f(x,y) - m^0_f; \end{aligned}$$

• 4. For the offset map, $Z'_f(x,y)$, determine the minimum positive value, $m^1_f$, and divide it by $R^2_f$ to obtain the new minimum, $m^2_f$,

  $$\begin{aligned} m^1_f&= \min (Z'_f(x,y)): Z'_f(x,y)>0,\\ m^2_f&= m^1_f / R^2_f; \end{aligned}$$

• 5. Obtain the final map, $Z''_f(x,y)$, by offsetting the value range by $m^2_f$,

  $$\begin{aligned} Z''_f(x,y) = Z'_f(x,y) + m^2_f. \end{aligned}$$

These transformations, found by trial and error, are useful in conveying the data to INLA in a value range where its performance is both consistent (across different inference task in this scientific domain), less prone to run-time errors and more accurate. It should be noted that the validity and the improvement on performance granted by this interval transformation have only been empirically verified for our particular case, and it may well be improved upon.

After these transformations, the latent feature maps are reconstructed by INLA. Then, they are transformed back to the original value range and are parsed by the decoder network module.

3.4 PCA Emulation pipelines

For the PCA emulation pipeline, a new PCA model of the input feature space is constructed every time (unlike with the EmulART which DVAE model was trained on a subset of AESet, as described in Sect. 3.2). Once that model is constructed, two approaches are followed: the first being the usage of the elbow method (see Fig. 6) to find the threshold number of components, K, that would explain the data without over-fitting it, using INLA to spatially reconstruct those components maps, and then return to them to the original feature space. In the second approach, 8 principal components are used (the same number as the latent features in the DVAE emulation pipeline).

Fig. 6

Plot of cumulative percentage of variance explained as a function of the number of principal components, K used to encode the data. Increasing the amount of PCs used naturally increases the percentage of variance explained, but it also risks over-fitting the model. In this case, the elbow can be found at around $K = 30$

After some preliminary tests, the data range transformations described in the previous section, before and after spatial reconstruction, were also removed as they failed to lead to execution time or reconstruction accuracy improvement. Moreover, spaxel de-normalization (see Sect. 3.1.1) was removed as it leads to the underestimation of the integrated SEDs of the reference model (possible reasons for this are presented in Sect. 4.1.1).

A scheme presenting the most relevant operations for both implementations of the PCA emulation pipeline can be found in Appendix D.

4 Results and discussion

In this section, we present and discuss some of the results from testing EmulART on AESet; these are compared against the results obtained with the PCA emulation implementations, and EVASet. Our goal in first using AESet was to evaluate the performance of the pipeline as a whole, mostly because the decoder network was not trained on latent and INLA reconstructed spaxels. The realizations from EVASet were then used to better gauge its performance.

We created the emulations using different LPN inputs ($N_p \in \{10^4, 10^5, 10^6, 10^7\}$). Because INLA performs faster on sparse maps, for each of those LPN realizations an emulation was performed by sampling different percentages of each latent feature map. These sampling percentages resulted from sampling 1 pixel in each bin of $2\times 2$, $3\times 3$ and $5\times 5$ pixels, corresponding, respectively, to 25, 11 and 4% of the spatial data. With the intent of reducing the influence of null spaxels in the spatial inference, 90% of the null spaxels were rejected from each map sampling pool.

Our analysis of the results consisted on inspecting how well EmulART reproduces the spectral and spatial features of the reference simulations, as well as the total computational time it took for the emulation to be completed.

To evaluate the spectral reconstruction, we looked at the normalized residuals (see Eq. 18) between the integrated SEDs$^{13}$ of our emulations and of the HPN reference. We also inspected the spatial maps of the compressed features looking for spatial distributions compatible with physical properties of the simulated model. The spatial reconstruction was also evaluated by the median and MAD of the normalized residuals of our emulations as well as of their LPN inputs²⁶ at each wavelength. For the statistical analysis of the residuals, reference pixels with value 0 were not considered since this metric diverges, so the TIR for all emulations and simulations was calculated as well.

4.1 AESet predictions

In this section, we present and discuss the results obtained emulating the HPN reference of AESet using the different LPN realizations within it.

The upper panels of Fig. 7 show that the emulation-integrated SEDs reproduce the shape of the references: a slow rise in the 1–8 $\upmu$m range, the two emission bumps in the 8–20 $\upmu$m range and the steep decline towards longer wavelengths. Moreover, Table 2 displays the median and MAD of the residuals of the integrated SEDs for the LPN input realizations before and after being de-normalized (as we describe in Sect. 3.1.1), as well as those of the different emulations obtained from them. It is clear that using $N_p \ge 10^6$ realizations as input yields emulations integrated SEDs that closely (median residuals smaller than 15%) follow the references throughout the whole wavelength range, independently (within this subset) of the sampling percentage chosen for the spatial inference task.

Fig. 7

Emulation-integrated SEDs resulting from spatial inference using 4% (a), 11% (b) and 25% (c) samples of the spatial information, and the respective normalized residuals, for the case of a dust shell with $\tau _{9.7} = 0.05$ and $\phi = 0^\circ$. The HPN reference is represented in black ($\circ$), the emulation based on the $N_p = 10^4$ realization is in red ($\triangle$), on the $N_p = 10^5$ in green ($+$), on the $N_p = 10^6$ in blue ($\times$) and on the $N_p = 10^7$ in cyan ($\diamond$) (Color figure online)

Table 2 Comparison of statistics for the residuals of the integrated SEDs, for the case of a dust shell with $\tau _{9.7} = 0.05$ and $\phi = 0^\circ$, for the different LPN realizations (columns 2 and 3), for those same realizations but after they have been de-normalized (columns 4 and 5), as described in Sect. 3.1.1, and for the resulting emulations (columns 7 and 8), while using different sampling amounts (column 6) for the spatial reconstruction

From the residuals of the emulations integrated SEDs, shown in the lower panels of Fig. 7, we conclude that: shorter wavelengths yield higher residuals; more input data for the spatial reconstruction does yield a better emulation but at the cost of an increased run time,²⁷ as can be confirmed in Table 3 and that the usage of the $N_p = 10^6$ realization as input greatly improves the quality of the emulation in relation to the two lowest photon number alternatives.

Looking at Tables 1 and 3, we can also compare the overall performance of the pipeline at estimating information that was not available in the LPN input realizations. The amounts of differently classified spaxels in both LPN inputs and respective emulations show, together with median of the normalized residuals, that EmulART successfully estimates information missing from the input.

Table 3 Statistics regarding how the different emulations of the case of a dust shell with $\tau _{9.7} = 0.05$ and $\phi = 0^\circ$, compared to the HPN reference

Figure 8 shows the comparison, at wavelength 9.28 $\upmu$m, between the emulations resulting from the LPN inputs (see Fig. 2) and the HPN reference. Once again we can see that with the $N_p = 10^6$ realization the emulations start to display resemblances to the HPN reference not only in the range of flux density values but also in the morphology that emerges from their distribution.

Fig. 8

Spatial maps of emulations, of the case of a dust shell with $\tau _{9.7} = 0.05$ and $\phi = 0^\circ$, at wavelength 9.28 $\upmu$m, based on the input of 4% of $N_p = 10^6$ LPN realization spatial information (a), 4% of $N_p = 10^7$ LPN realization spatial information (b) and the HPN reference (c). Color indicates flux density in W/m$^2$ (Color figure online)

From Tables 2 and 3, as well as from Figs. 7 and 8, it would be natural to conclude that using the $N_p = 10^7$ realization as input would bring the most benefit in terms of the amount of information inferred by the emulation as well as its accuracy. Moreover, as can be seen in the second column of Table 3, the run time of the emulations is more dependent on the amount of information sampled for the spatial reconstruction than on the $N_p$ of the LPN input. Nevertheless, considering how SKIRTs run time for a model scales with the simulated $N_p$, the choice of LPN input to use with EmulART should weight the time it takes to produce that LPN input as well as the quality of the emulation we expect from it.

4.1.1 PCA Pipeline predictions

The results of testing the PCA pipelines on AESet were processed in the same way as EmulARTs (statistical indicators regarding residuals of the emulation and of its spatial integration were calculated as well as the TIR; the number of different types of spaxels and execution time were measured).

The execution times²⁸ for the pipeline implementing an 8 PC model were indiscernible from the execution times of EmulART on the same input, while the execution time for the pipeline implementing a PCA model with number of components, K, determined by the elbow method was in general much higher since for all except one of the LPN inputs K was larger than 30 (the time per component map was very similar depending mostly on the amount of spatial information sampled).

Tables 4 and 5 present the most significant indicators to be compared to EmulARTs. At first sight, the performance of both PCA models on the emulation pipeline seems to be similar to, and in some cases even better than that of EmulARTs, showing statistically similar residuals, and presenting residuals regarding the spatially integrated SEDs 2 to 3 times lower. They are, however, unable to consistently recover complete spaxel information, which then leads to poor spatial reconstructions at longer wavelengths, even when using $K > 8$ (see Fig. 9), as can be inferred from the TIR values (as well as the number of full and partial spaxels).

Fig. 9

Spatial maps of emulations (Top), performed with a pipeline including a PCA model with $K = 30$ components based on the input of 11% of the spatial information of the $N_p = 10^7$ LPN realization; and, reference simulation (Bottom) of the case of a dust shell with $\tau _{9.7} = 0.05$ and $\phi = 0^\circ$, at wavelengths 1.85 $\upmu$m (a, d), 9.28 $\upmu$m (b, e) and 211.35 $\upmu$m (c, f). Color indicates flux density in W/m$^2$ (Color figure online)

Table 4 Statistics regarding PCA pipeline emulations, using K PCs (where K was determined by the elbow method) of the case of a dust shell with $\tau _{9.7} = 0.05$, $\phi \in \{0^\circ , 90^\circ \}$ and spatial sampling of 11%

Table 5 Statistics regarding PCA pipeline emulations, using 8 PCs, of the case of a dust shell with $\tau _{9.7} = 0.05$, $\phi \in \{0^\circ , 90^\circ \}$ and spatial sampling of 11%

In the present application, we thus find the implementation of a DVAE model for spectral compression to be justified. Unlike the PCA models, it not only captures nonlinear relationships between the spectral features but also achieves comparable results. Despite some loss regarding the reconstruction of integrated SED profile, when compared to PCA models, it achieves equal/higher compression rate and lower/equal execution time and most importantly the spatial structure can successfully be reconstructed by the remaining parts of the pipeline.

As such, the test results of EmulART on EVASet are compared against its results on AESet. Testing results obtained with PCA emulation pipelines on EVASet did not offer a perspective different from the one above and as such will not be discussed further here (a successful implementation of PCA in an emulation pipeline is described in Smole et al. [46]).

4.2 EVASet Predictions

In this section, we present and discuss the results obtained by emulating the HPN references of EVASet using the respective LPN realizations within it. The DVAE model was not trained on any data within this set, which allows us to evaluate whether it manages to accurately predict HPN-like spaxels from LPN spaxels that originate from simulations with different $\tau _{9.7}$ and $\phi$ values.

First, we tested EmulART on realizations with $\tau _{9.7} = 0.05$ and $\phi = 90^\circ$; we then applied the pipeline to different LPN realizations with $\tau _{9.7} \in \{0.1, 1.0\}$ and $\phi \in \{0^\circ , 90^\circ \}$.

Similarly to the $\tau _{9.7} = 0.05$ and $\phi = 0^\circ$ emulations, the edge-on, $\phi = 90^\circ$, emulations appear to preserve well the spectral information, reproducing the slow rise in the 1–8 $\upmu$m range, the two emission bumps in the 8–20 $\upmu$m range, and the steep decline towards longer wavelengths, as can be seen in Fig. 10. Table 6 shows that 4% sampling of the spatial information of the $N_p = 10^6$ realization is enough to get median-integrated residuals below 15%. We note, however, the abnormal performance of the emulations that took as input the $N_p = 10^7$ realizations, displaying higher median integrated residuals than the ones that used different samplings of the $N_p = 10^6$ LPN. This may indicate that one or more of the spatial data manipulation modules, or their interface, should be improved upon.

Fig. 10

Emulation-integrated SEDs, resulting from spatial inference using 4% (a), 11% (b) and 25% (c) samples of the spatial information, and the respective normalized residuals, for the case of a dust shell with $\tau _{9.7} = 0.05$ and $\phi = 90^\circ$. The HPN reference is represented in black ($\circ$), the emulation based on the $N_p = 10^4$ realization is in red ($\triangle$), on the $N_p = 10^5$ in green ($+$), on the $N_p = 10^6$ in blue ($\times$) and on the $N_p = 10^7$ in cyan ($\diamond$) (Color figure online)

Table 6 Comparison of statistics for the residuals of the spatial integration SEDs, for the case of a dust shell with $\tau _{9.7} = 0.05$ and $\phi = 90^\circ$, for the different LPN realizations (columns 2 and 3), for those same realizations but after they have been de-normalized (columns 4 and 5), as described in Sect. 3.1.1, and for the resulting emulations (columns 7 and 8)

As for the emulations using as input LPN realizations of simulations with $\tau _{9.7} \in \{0.1, 1.0\}$, at both tilt angles, we observe that both the shape and flux density value range of the integrated SED degrade as $\tau _{9.7}$ increases. As shown in Fig. 11, the emulation-integrated SEDs fail to reproduce the shape of the HPN references, reproducing instead the shape that characterized the realizations present in AESet, a clear sign of over-fitting of the DVAE model. This can be solved by expanding the training set of our DVAE architecture to include spaxels originating from simulations with different optical depths.

Fig. 11

Emulation-integrated SEDs, resulting from spatial inference using 25% of spatial information, and the respective normalized residuals, for the case of a dust shell with $\tau _{9.7} = 1.0$, $\phi = 90^\circ$ (a) and $\phi = 0^\circ$ (b). The HPN reference is represented in black ($\circ$), the emulation based on the $N_p = 10^4$ realization is in red ($\triangle$), on the $N_p = 10^5$ in green ($+$), on the $N_p = 10^6$ in blue ($\times$) and on the $N_p = 10^7$ in cyan ($\diamond$) (Color figure online)

For $\tau _{9.7} = 1.0$, with both $\phi$ cases, we observe the influence of the first wavelengths (see Fig. 12) in the overall residuals.²⁹ Figure 13 shows that though the overall morphology of the spatial distribution is well recovered the value range for the emulations flux density value range is drastically underestimated, while the contrast between the central and peripheral regions is considerably higher than what the HPN references display.

Fig. 12

Median of the normalized residuals, at each wavelengths spatial map, for every emulation obtained with $N_p = 10^4$ (red), $N_p = 10^5$ (green), $N_p = 10^6$ (blue) and $N_p = 10^7$ (cyan) realizations, for the case of a dust shell with $\tau _{9.7}=1.0$, with $\phi = 0^\circ$ (a) and $\phi = 90^\circ$ (b). Emulations whose spatial inference was performed using 25% of data are represented by ($\triangle$), 11% by ($+$) and 4% by ($\times$). The interrupted black line marks the same metric for the LPN inputs (Color figure online)

Fig. 13

Emulation produced using as input a 25% sample of the $N_p = 10^6$ realization (left panel) and HPN reference (right panel) at wavelength 9.28 $\upmu$m, for the case of a dust shell with $\tau _{9.7} = 1.0$, $\phi = 0^\circ$ (a) and $\phi = 90^\circ$ (b)

These results appear to show that our pipeline is capable of recovering 40–60% of the emergent spatial information of HPN MCRT models from LPN realizations, taking as input as little as 0.04% of the information that would be present in the HPN model, all while preserving 85–95% of the spectral information.

Furthermore, the results also show a clear bias in the performance of the DVAE model as a compressor and decompressor of spectral information, with the performance degrading substantially as the LPN inputs models depart from the optical depth, $\tau _{9.7}$, value present within the training set.

Further details of the results we obtained with AESet and EVASet are discussed in Appendix E.

5 Summary

We report the development of a pipeline that implements in conjunction a denoising variational autoencoder (or alternatively PCA), and a reconstruction method based on approximate Bayesian inference, INLA, with the purpose of emulating high information-like MCRT simulations using LPN MCRT models, created with SKIRT, as input. With this approach, we aim for the hastily expansion of libraries of synthetic models against which to compare future observations. By producing positive preliminary indicators, we show that such a framework is worth pursuing further, with multiple alleys to explore.

Conditions for systematically measuring the computational cost are necessary to properly evaluate the merit of this approach. However, in this work our aim was to qualitatively assess the potential of this method to be applied to MCRT simulations images. In this pilot study, we chose a very simple model of a centrally illuminated spherical dust shell, which is computationally inexpensive, whose reference simulations took around two hours to be computed. Thus, in our particular examples we reduced the computational time by approximately 6$\times$. Nevertheless, the computational cost of SKIRT simulations scales with the amount of photon packets simulated, the spatial resolution of the grid and the actual geometrical complexity of the model. As for our emulation pipeline, its computational cost is only impacted noticeably when increasing the size and density of the spatial grid to be processed by INLA. This leads us to believe that a generalized version of this pipeline may expedite, by up to 50$\times$, the study of dust environments through this kind of radiative transfer models.

Further exploration of the proposed DVAE architecture is being undertaken, via expansion and diversification of the training set to improve the prediction of the spectral features.

Other approaches to be tested include the use of dropout (cutting the connections, mid training, whose weights are below a given threshold) and incremental learning (training a model with new data with the starting point of the network being the weights obtained in a previous training session). The first serves as feature selection tool, removing those of little importance, which also prevents the model from over-fitting the training data; the second would be of great use to quickly adapt an already trained model to new data, which is important in the context of emulating simulations.

To improve the reconstruction of the spatial features, using non-uniform sampling methods based on the information spatial density may help improve the reconstruction of the latent features that result from the compression of models simulated with insufficient number of photon ($N_p < 10^6$, in the particular case of our study). Alternative pre-INLA data preprocessing, such as data value range manipulations and sampling grids, may also be worth exploring.

Appendices

Appendix A: Data preprocessing

1.1 Appendix A.1: Identifying and sampling null-spaxels

The SKIRT simulations of the spherical simulated models result in a peripheral region filled with spaxels with value 0 at all wavelength bins; these will be henceforth be referred to as null-spaxels. We perform two routines to identify and filter out null-spaxels, to curb their potential impact in both training the DVAE model and when (within the emulation procedure) reconstructing the spatial information of the latent feature maps:

• 1. Each feature (wavelength) of each spaxel is checked, if all features of a spaxel have value 0, then that spaxel is temporarily tagged as null-spaxel;

• 2. An iterative process then checks the immediate neighborhood of each previously tagged spaxel (a $5\,\mathrm{pix}\times 5\,\mathrm{pix}$ grid centered at the spaxel being tested) for other tagged spaxels, if a minimum of 4 neighbors share the null-spaxel tag, then that spaxel is tagged as a true null-spaxel, otherwise its temporary tag is removed.

The second routine serves as a way to discriminate spaxels that have zero information at given wavelengths, possibly from the spaxel being the result of a low photon count simulation, from actual null-spaxels—spaxels resulting from the lack of photons traveling from the source to the observer through that direction, neither by direct emission nor by scattering nor by absorption and re-emission by dust. Figure 14 illustrates the results of routine 1 and 2.

Fig. 14

On the left, in black, the spaxels temporarily tagged as null-spaxels by routine 1; on the right, also in black, the final selection of null-spaxels that resulted from applying routine 2 with a search grid of $5\,\mathrm{pix}\times 5\,\mathrm{pix}$ around each temporary null-spaxel. The result on the right shows that for this particular case of a spherical shell of dust surrounding an isotropic emitter we only find null-spaxels on the outskirts of the shell, as expected

After identifying the null-spaxels, we sample them to incorporate the filtered dataset.

For the DVAE training, complete removal of these null-spaxels could be done, but we decided to reduce their incidence rate instead. Since there is no guarantee that their latent representation (where the spatial reconstruction will take place) will also be a null-vector we want the DVAE model to learn null-spaxels, too many of these will nevertheless be uninformative and may lead to unintended biases. For this reason, we sample 10% of them, reducing the null-spaxel prevalence in the training dataset from $\sim$25% to $\sim$2.5%. Empty spaxels (spaxels tagged as null for LPN realizations but non-null for the respective HPN reference) were completely removed from training.

For the emulation process, and more specifically for the spatial reconstruction of the latent feature maps, we sample 10% of the null-spaxels selected by the spatial sampling grid, for INLA is faster with little data and that amount is sufficient for the null-region to be properly recovered.³⁰ After the emulation process, spaxels that were at this stage identified as being null-spaxels have their values changed to 0.

1.2 Appendix A.2: Reshaping data structures

Once all spaxels are selected the data cubes are reshaped into a 2D structure, with a given pixel corresponding to a row with its spectral information on the columns (see Fig. 5), to match the input format of the DVAE. The inverse reshaping, from a 2D to a 3D structure, is performed after the DVAE output layer.

Within the emulation pipeline, the data are reshaped two more times. First, after sampling the latent feature distributions (to obtain the Z arrays, as seen in Fig. 5) the resulting sample is reshaped from a 2D to a 3D structure to obtain latent feature spatial maps (the 8 1D arrays become 8 2D maps) whose spatial information can then be reconstructed with INLA. The second reshape is performed on INLAs reconstructed results to conform that data to the decoder accepted input format, once again going from a 3D to a 2D structure.

Appendix B: Dataset

Table 7 presents the list of SKIRT simulations used in this work. Every realization models a spherical dust, composed by silicates and graphites, surrounding a bright point source with anisotropic emission, differing in parameters such as the tilt angle, $\phi$, the optical depth, $\tau _{9.7}$, and the amount of photon packets simulated, $N_p$.

Table 7 Parametrical description of the SKIRT realizations used in this work, along with the distribution of these realizations by subset

Appendix C: Latent Features

In this section, we briefly discuss the relationship between each of the compressed features, as well as how they may relate to some physical attributes of the simulated models.

The PCC measures how strongly linearly correlated different parameters are and is defined as the ratio between the covariance of the parameters and the product of their standard deviations (see Eq. C1):

$$\begin{aligned} \rho _{X,Y} = \frac{\mathrm{cov}(X,Y)}{\sigma _X\sigma _Y}. \end{aligned}$$

(C1)

Figure 15 illustrates the relationships between our datasets latent features along with their respective PCC. The PCC indicates that only the first feature shows little correlation with the others, ranging from $-0.42$ to 0.39, while the remaining features display high correlations (and anti-correlations) between themselves, most either above 0.9 or below $-0.8$. This would indicate that the information in those features presents a high level of redundancy.

The point spread in the panels of Fig. 15 shows, however, something unexpected given the PCC values. There are clearly distinct populations, some presenting linear behavior, while others show highly nonlinear relationships (see, for example, Z3 vs Z5) and even dual linear populations (see Z6 vs Z7).

The overall large Pearson correlation values thus indicate that the population density within the linear spreads is higher. But even if the compressed features show at best linear correlations (and anti-correlations) for a greater fraction of our data, we decided not to ignore the nonlinear behavior being expressed for the remaining data. In future implementations, we will tackle this by both expanding the dataset, including models with different dust distributions and compositions and employing different training strategies (this can be achieved by changing loss function terms and adding different training stages).

Fig. 15

Corner plot of the latent features, $Z_f$ of the test set. Pearson’s correlation coefficients are indicated in navy blue (Color figure online)

Figure 16 shows the spatial reconstruction of 3 latent feature maps³¹ obtained from the $N_p = 10^6$ LPN realization of the case of a dust shell with $\tau _{9.7}=0.05$ and $\phi = 90^\circ$.

In the map of latent feature Z1 (Fig. 16a), we can relate the spatial distribution to the hot dust emission, at wavelengths 1–3 $\upmu$m, of the region close to the sublimation zone around the central source. Conversely, in the map of latent feature Z2 (Fig. 16b), the larger structure further away form the center, which corresponds to the colder dust emission at longer wavelengths is outlined.

Fig. 16

Spatial reconstruction of 3 latent feature maps of the LPN case $N_p = 10^6$, $\tau _{9.7}=0.05$ and $\phi = 90^\circ$, using 25% of the available data

As mentioned in Sect. 3.1, the model used along this work is that of a bright point like source with anisotropic emission [47], where the emission is defined by Eq. (17), following Netzer [36]. Looking at the map of latent feature Z8 (Fig. 16c), the geometric signature of the model is clearly identifiable.

Appendix D: Emulation flowcharts

This section presents flowcharts for different emulation pipelines used in this work. In these, circles and ellipses represent data cubes at different stages of the pipeline and round cornered squares present lists of indexes. Grey rectangle boxes are operations using the data, purple diamond boxes indicate set operations ($\cap$ for intersection and $\cup$ for union) on indexes, green boxes indicate operations related to dimensionality transformation models. $\blacklozenge$ refers to the de-normalization procedure mentioned in Sect. 3.1.1 and $\dagger$ refers to operations described in Sect. 3.3 (Figs. 17 and 18).

Fig. 17

Flowchart for EmulART

Fig. 18

Flowchart for the emulation pipeline that employs the PCA model with the number of components, K, determined by the elbow method. For the emulation pipeline that employs the PCA model with a number of components equal to the number of latent features of the DVAE model in EmulART ($K = 8$), the Elbow method block is skipped

Appendix E: Result analysis

This section presents a detailed view of the results obtained with both AESet and EVASet. As mentioned in Sect. 4, for every $\tau _{9.7}$ and $\phi$ case, the realization with $N_p = 10^8$ was considered as the HPN reference, or “ground truth”. The remaining LPN realizations and the emulations obtained from those were compared to the HPN reference in regard to their spectral and spatial features.

For the spectral analysis, we computed the normalized residuals (Eq. 18) of the spatially integrated SEDs, compared the shape of those SEDs and inspected the spatial maps of the DVAE-compressed features looking for distributions compatible with the physical properties of the HPN reference.

For the spatial analysis, we computed the normalized residuals and measured statistical descriptors—median and mean absolute deviation (MAD)—for each wavelength bin spatial map, for both LPN inputs and resulting emulations. To measure the impact of INLA on the reconstruction of input spaxels, we count how many full, partial and null spaxels are present in the HPN reference, LPN input and the resulting emulations, and compute the TIR of each.

1.1 Appendix E.1: AESet predictions

1.1.1 Appendix E.1.1: Spectral predictions

In this section, we discuss how well the spectral information is preserved, after the LPN inputs of AESet are processed by EmulART, by looking into the emulations spatially integrated SEDs.

From both Fig. 7 and Table 2, we determine the $N_p = 10^6$ realization, with spaxel sampling of 4%, to be the most favorable input for our pipeline. This simulation is the result of 100$\times$ less photons simulated than the reference, and with the corresponding emulation using as input 4% of its spaxels which results in 2500$\times$ less input information than the present in the HPN reference. This emulation presents median residuals of $\sim$85% between 1 and 4 $\upmu$m, $\sim$33% between 4 $\upmu$m and 1 mm and $\sim$42% over the whole spectral range, and 2.8% when considering the SED that results from the spatial integration of each wavelength map (less than 2% worse than the realization which was used as input). It also reconstructs over 71,000 spaxels presenting almost two times the amount of full spaxels of the reference. Appendix F shows how the pipeline goes even further with the emulated individual spaxels presenting smoother profiles than the references.

1.1.2 Appendix E.1.2: Spatial predictions

This section looks at the reconstructions of sparse samples of pixels from latent feature maps and the spatial distributions that result after returning those to the original spectral space.

The impact of INLAs spatial reconstruction is evidenced by the emulations residuals having lower median values than all realizations but the reference, and mean deviations of the same order of magnitude. In the case of the emulations performed using the $N_p = 10^7$ realizations as input that is even clearer, with median of the spatial residuals at wavelengths greater than 5 $\upmu$m going below 30%. Furthermore, as Fig. 19 shows, there are two transitions in quality evidenced by the gaps between the median residuals. It is also shown that all lower photon count simulations have their residuals dominated by lack of information (the reader is reminded that a 100% normalized residual means that pixel holds no information), and that the spatial inference at lower wavelengths results in large over-estimations. The absence of information which heavily influences the statistical descriptors of the simulations residuals is thus curbed. This is confirmed when comparing the TIR values, where we can see that the emulation based on the lowest $N_p$ realizations has a TIR of 98.3% compared to the reference realization (see Table 2), while the $N_p = 10^7$ realization’s is 65.2% (see Table 1).

Fig. 19

Median of the normalized residuals, at each wavelengths spatial map, for every emulation obtained with $N_p = 10^4$ (red), $N_p = 10^5$ (green), $N_p = 10^6$ (blue) and $N_p = 10^7$ (cyan) realizations, for the case of a dust shell with $\tau _{9.7}=0.05$ and $\phi = 0^\circ$. Emulations whose spatial inference was performed using as input 25% of data are represented by ($\triangle$), 11% by ($+$) and 4% by ($\times$). The interrupted black line marks the same metric for the LPN realizations (Color figure online)

Figure 20 shows the spatial distribution of the emulation residuals at some wavelengths; it is clear that:

• The residuals are correlated with the distance towards the center of the object, with the highest residuals populating the outer edge and the lowest in the center.

• Shorter wavelengths display higher residuals.

Fig. 20

Spatial distribution of residuals, as defined in Eq. (18), for the emulation produced using as input a 4% sample of the $N_p = 10^6$ realization, for the case of a dust shell with $\tau _{9.7} = 0.05$ and $\phi = 0^\circ$, at wavelengths 0.84 $\upmu$m (a), 1.85 $\upmu$m (b), 9.28 $\upmu$m (c) and 211.35 $\upmu$m (d)

The above results were expected, given that: we performed a uniform spatial sampling of an object central to a spherically symmetric dust distribution; more spatial information is available at the center of the simulated object than in the outskirts; and, at shorter wavelengths there is overall less information, as seen in the previous section, from which to build the spatial reconstruction.

It is harder to assess how accurate INLAs inference of the outskirt regions is. Those regions, given the spatial distribution of the simulated model, tend to be less dense. Nevertheless, at most wavelengths and most of the spatial distribution of the object, the residuals place the emulated value at the same order of magnitude as the reference values. Moreover, it is in these regions that INLA recovers more information, filling in the gaps.

1.2 Appendix E.2: EVASet predictions

1.2.1 Appendix E.2.1: Spectral predictions

In this section, we discuss how well the spectral information is preserved, after the LPN inputs of EVASet, with $\tau _{9.7} \ne 0.05$, are processed by EmulART, by once again looking into the emulations spatially integrated SEDs.

Regarding the case with $\tau _{9.7} = 0.1$, Fig. 21 and Table 8 show that, for both tilt angles, while the shape of the emulations integrated spectra still follows closely that of the references, the residuals are now over 2$\times$ higher than with $\tau _{9.7} = 0.05$. The results for the cases with $\tau _{9.7} = 1.0$ confirm this trend in degrading quality of the pipeline’s spectral predictions. As seen in Fig. 11, the emulation-integrated spectrum completely misses the shape of the reference spectrum, keeping the shape displayed for the cases with $\tau _{9.7} = 0.05$ and $\tau _{9.7}=0.1$, a sign of over-fitting which is confirmed when inspecting individual spaxels (see Appendix F). It also underestimates the flux density and overestimates the relative magnitude of the two emission bumps in the 8–20 $\upmu$m range. The median residual of the total flux density per wavelength, displayed in Table 8, further confirms the poor quality of the spectral predictions.

Fig. 21

Emulation-integrated SEDs, resulting from spatial inference using 25% of spatial information, and the respective normalized residuals, for the cases of dust shells with $\tau _{9.7} = 0.1$, $\phi = 90^\circ$ (a) and $\phi = 0^\circ$ (b). The HPN reference is represented in black ($\circ$), the emulation based on the $N_p = 10^4$ realization is in red ($\triangle$), on the $N_p = 10^5$ in green ($+$), on the $N_p = 10^6$ in blue ($\times$) and on the $N_p = 10^7$ in cyan ($\diamond$) (Color figure online)

Table 8 Comparison of statistics for the residuals of the spatial integration SEDs (columns 4 and 5) and of the residuals overall wavelengths (columns 6 and 7), for the emulations that took as input LPN realizations of dust shells with $\tau _{9.7} \in \{0.1, 1.0\}$, $\phi \in \{0^\circ , 90^\circ \}$, and $N_p \in \{10^6, 10^7\}$

1.2.2 Appendix E.2.2: Spatial predictions

Regarding spatial information, for emulations with LPN inputs of $\tau _{9.7}=0.05$ and $\phi = 90^\circ$ we observe the same behavior in the performance metrics as with the $\phi = 0^\circ$ case. Table 9 shows that the overall median residuals decrease with the increase of $N_p$. The median residuals per wavelength, displayed in Fig. 22, present a similar behavior to those of the $\phi = 0^\circ$ case.

Table 9 Statistics regarding how the different emulations, of the case of a dust shell with $\tau _{9.7} = 0.05$ and $\phi = 90^\circ$, compared to the HPN reference

Fig. 22

Median of the normalized residuals, at each wavelengths spatial map, for every emulation obtained with $N_p = 10^4$ (red), $N_p = 10^5$ (green), $N_p = 10^6$ (blue) and $N_p = 10^7$ (cyan) realizations, for the case of a dust shell with $\tau _{9.7}=0.05$ and $\phi = 90^\circ$. Emulations whose spatial inference was performed taking as input 25% of the data are represented by ($\triangle$), 11% by ($+$) and 4% by ($\times$). The interrupted black line marks the same metric for the realizations used as input (Color figure online)

Figure 23 shows that the emulation of models with excessive emission within the central regions in comparison with the reference, while in Fig. 24 the prediction for the peripheral region is more isotropic than the reference; this is even clearer when consulting the spatial distribution of residuals for these emulations in Fig. 25 (Fig. 26).

Fig. 23

Emulation produced using as input a 4% sample of the $N_p = 10^6$ realization, left, and HPN reference, right, for the case of a dust shell with $\tau _{9.7} = 0.05$ and $\phi = 90^\circ$, at wavelengths 0.84 $\upmu$m (a) and 1.85 $\upmu$m (b)

Fig. 24

Emulation produced using as input a 4% sample of the $N_p = 10^6$ realization, left, and HPN reference, right, for the case of a dust shell with $\tau _{9.7} = 0.05$ and $\phi = 90^\circ$, at wavelengths 9.28 $\upmu$m (a) and 211.35 $\upmu$m (b)

Fig. 25

Spatial distribution of residuals, as defined in Eq. (18), for the emulation produced using as input a 4% sample of the $N_p = 10^6$ realization, for the case of a dust shell with $\tau _{9.7} = 0.05$ and $\phi = 90^\circ$, at wavelengths 0.84 $\upmu$m (a), 1.85 $\upmu$m (b), 9.28 $\upmu$m (c) and 211.35 $\upmu$m (d)

As with the $\tau _{9.7} = 1.0$ cases, for both tilt angle cases of $\tau _{9.7} = 0.1$ we observe a similar trend in the overall residuals. Figure 27 shows that while the overall morphology of the spatial distribution is well recovered, the flux density value range for the emulations is underestimated, though not as considerably as with the $\tau _{9.7} = 1.0$ cases, and the contrast between the central and peripheral regions is higher than in the HPN references. This indicates a bias within the pipeline. Appendix F further details into the likely source of such bias by comparing individual spaxels of emulations and HPN simulations.

Fig. 26

Median of the normalized residuals, at each wavelengths spatial map, for every emulation obtained with $N_p = 10^4$ (red), $N_p = 10^5$ (green), $N_p = 10^6$ (blue) and $N_p = 10^7$ (cyan) realizations, for the case of a dust shell with $\tau _{9.7}=0.1$, with $\phi = 0^\circ$ (a) and $\phi = 90^\circ$ (b). Emulations whose spatial inference was performed using 25% of data are represented by ($\triangle$), 11% by ($+$) and 4% by ($\times$). The interrupted black line marks the same metric for the LPN inputs (Color figure online)

Fig. 27

Emulation produced using as input a 25% sample of the $N_p = 10^6$ realization, left, and HPN reference, right, for the case of dust shells with $\tau _{9.7} = 0.1$, at wavelengths 9.28 $\upmu$m, with $\phi = 0^\circ$, (a) and $\phi = 90^\circ$ (b)

Appendix F: Single spaxels

Figures 28, 29 and 30 compare 3 different spaxels between their versions in the LPN input, HPN reference and emulation based on the LPN input. These spaxels are radially aligned: one at the center of the object, another on the outskirts and another in-between those two. The emulations were achieved using 25% of the corresponding source cube spaxels.

Some things easily noticeable are the underestimation of the shorter wavelengths for the versions of these spaxels taken from emulations based on $N_p = 10^4$ and $N_p = 10^5$ realizations. Nevertheless, in those cases the LPN input spaxel is not complete, i.e., there are zero values at some wavelengths, if not all, meaning the pipeline is reaching what it was designed to do: take a sparse compressed model, infer the missing information and then decompress it.

Fig. 28

Comparison of some emulations spaxels located in row = 150, col = 150, against the HPN references and the LPN input (indicated in each plot), for the case of a dust shell with $\tau _{9.7} = 0.05$ and $\phi = 0^\circ$. The emulations were performed using 25% of the LPN input spatial information. HPN references spaxel in black ($\circ$), emulations in gold ($\triangle$) and LPN inputs, upon which the emulation was performed, in pink ($+$) (Color figure online)

Fig. 29

Comparison of some emulations spaxels located in row = 150, col = 210, against the HPN references and the LPN input (indicated in each plot), for the case of a dust shell with $\tau _{9.7} = 0.05$ and $\phi = 0^\circ$. The emulations were performed using 25% of the LPN input spatial information. HPN references spaxel in black ($\circ$), emulations in gold ($\triangle$) and LPN inputs, upon which the emulation was performed, in pink ($+$) (Color figure online)

Fig. 30

Comparison of some emulation spaxels located in row = 150, col = 270, against the HPN references and the LPN input (indicated in each plot), for the case of a dust shell with $\tau _{9.7} = 0.05$ and $\phi = 0^\circ$. The emulations were performed using 25% of the LPN input spatial information. HPN references spaxel in black ($\circ$), emulations in gold ($\triangle$) and LPN inputs, upon which the emulation was performed, in pink ($+$) (Color figure online)

Figures 31, 32 and 33 compare 3 different spaxels from the same spatial locations as before. The emulations were achieved using 11% of the corresponding LPN input cube spaxels, which are the $\tau _{9.7} = 1.0$ and $\phi \in \{0^\circ , 90^\circ \}$ cases. Since the simulated bright central source has anisotropic emission at greater optical depths, $\tau _{9.7}$, we can expect that for different viewing angles, $\phi$, the shapes of spaxels near the central region of the spatial distribution³² will present differences as can be seen in the reference curves of Fig. 31.

For both the face-on and edge-on cases, at all displayed positions, we can make the same assessment that the shape of the emulated spaxels does not follow the shape of the HPN references. As the simulated models dust density increases so does the likelihood of scattering and absorption of light by the medium, consequently the peak emission features are flattened into the continuum. Figures 31 and 32 show that the emulation of the spaxels in those regions is one to two orders of magnitude too low while the relative flux between the emission peak, at 9.7 $\upmu$m, and the continuum is over-estimated, the allocation of flux along the spaxels does not match that of the reference. For the outer spaxels, Fig. 33, the flux mismatch is greater for longer wavelengths, but still the emulation spaxels present a peak emission feature while the references no longer show it. This is a clear sign that the DVAE model is biased.

Fig. 31

Comparison of emulations spaxels, located in row = 150, col = 150, against the HPN references and the $N_p = 10^6$ realization, for the case of a dust shell with $\tau _{9.7} = 1.0$, with $\phi = 0^\circ$ (a) and $\phi = 90^\circ$ (b). HPN references spaxel in black ($\circ$), emulations in gold ($\triangle$) and LPN inputs, upon which the emulation was performed, in pink ($+$) (Color figure online)

Fig. 32

Comparison of emulations spaxels, located in row = 150, col = 210, against the HPN references and the $N_p = 10^6$ realization, for the cases of dust shells with $\tau _{9.7} = 1.0$, with $\phi = 0^\circ$ (Fig. 31a) and $\phi = 90^\circ$ (Fig. 31b). HPN references spaxel in black ($\circ$), emulations in gold ($\triangle$) and LPN inputs, upon which the emulation was performed, in pink ($+$) (Color figure online)

Fig. 33

Comparison of emulations spaxels, located in row = 150, col = 270, against the HPN references and the $N_p = 10^6$ realization, for the cases of dust shells with $\tau _{9.7} = 1.0$, with $\phi = 0^\circ$ (Fig. 31a) and $\phi = 90^\circ$ (Fig. 31b). HPN references spaxel in black ($\circ$), emulations in gold ($\triangle$) and LPN inputs, upon which the emulation was performed, in pink ($+$) (Color figure online)