1 Introduction

The paper presents a design strategy for the digital implementation of randomization-based networks (RBNs) on energy-constrained edge devices. The applications include implantable devices [1, 2], smart sensors operating in hostile or remote areas [3], and devices relying on energy-harvesting techniques [4]. The latter case represents a critical scenario, as it often requires careful budgeting of the collected energy in real time. In general, the method is suitable for all the applications where a small and non-constant power source is available. This setup is becoming always more popular with the development of harvesting methods and battery-less paradigms.

Energy constraints may limit severely the integration of machine learning (ML) models into edge devices; the basic implementation of the (forward) inference function might by itself exhaust the available energy budget [5, 6]. RBNs with threshold activation functions are hardware-friendly solutions for the digital implementations of single layer feedforward neural networks (SLFNs) [7, 8]. The associate digital architectures can support the inference step without any multiplier and with negligible memory requirements; at the same time, those approaches may suffer from reduced classification accuracy.

As compared with those approaches, this paper describes a novel end-to-end design strategy for a digital architecture that includes adjustable neurons to regulate energy consumption dynamically.

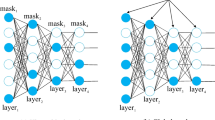
In the seven-dimensional example shown in Fig. 1, the n-th neuron can work out its own activation function in either the complete version, \(\phi _n({\textbf {x}})\), which includes all input terms, or an approximate formulation, \({\tilde{\phi }}_n({\textbf {x}})\), that only involves a subset to reduce the computation cost. The choice depends on the available energy budget.

A specific scheme supports the overall strategy. At run time, the inference function of the eventual RBN embeds both the complete and approximate version of the activation function. The pair of configurations share the same network parameters; hence, the supporting hardware device needs not store separate models. The overall operation relies on a criterion to turn off—within each neuron—the input connections that have a marginal impact on the network behavior. That mechanism sets the approximate activation within each neuron. The associate learning strategy includes a specific cost function that takes into account the perturbations brought about by approximate neurons. That formulation leads to a) a shared set of network parameters that maintain competitive accuracy in both configurations, and b) an inference function that embeds a performance trade-off between the two alternative operating modes. The switch between either modality takes place without any reprogramming of the hardware.

Fig. 1
figure 1

Example of the proposed computing modes: the complete activation involves all the seven input terms, while the approximate activation involves only a subset of the input terms to reduce the computation cost

Full size image

From an application viewpoint, the paper describes the digital architecture that can support the RBNs trained according to the proposed strategy. The experimental verificationFootnote 1 involved a CMOD S7-25 board.Footnote 2 The evaluation session pointed out some relevant features. A comparison with state-of-the-art training procedures on ten datasets proved that the loss function empowering the above strategy could preserve generalization ability even in the presence of approximate activation functions. Furthermore, when considering energy consumption, the digital implementations of the trained RBNs compared favorably with state-of-the-art design approaches for ultra-low-power devices. The tests showed that the hardware RBN set-ups hosting approximate neurons could almost halve the energy consumption per prediction. Those networks yet featured the same energy consumption as conventional RBNs, not including approximate neurons. Finally, the static power introduced by the additional circuitry turned out to be negligible.

1.1 Contribution

The main contributions of the paper are:

  • an end-to-end design strategy for the digital implementation of RBNs on edge devices that can regulate energy consumption in real-time.

  • A cost function supporting the training of RBNs with online-reconfigurable units, i.e., neurons that may switch to an approximate activation function to reduce the computation cost dynamically, without reloading the network weights. The cost function makes the network robust against approximate computations within the neurons and ensures a satisfactory trade-off between energy consumption and generalization performance.

  • A digital architecture for the implementation of the trained RBNs with reconfigurable neurons, tested on a commercial FPGA.

In the following, Sect. 2 summarizes the theoretical background of RBNs and reviews state-of-the-art works dealing with the digital implementations of those networks on embedded devices. Section 3 introduces the end-to-end design approach for the digital implementation of RBNs under energy budget constraints. Section 4 presents the digital architecture to support the trained RBNs. Section 5 reports on the experimental sessions, and some concluding remarks are made in Sect. 6.

2 Digital implementation of randomization-based neural networks: background

2.1 Randomization-based neural networks

The literature shows that RBNs provide a valuable tool for machine learning because they feature a simple training phase and prove effective. Random radial basis functions [9], random vector functional-link (RVFLs) [10], extreme learning machines (ELMs) [11, 12], and weighted sum of random kitchen sinks [13] are nowadays largely employed in practical applications [14,15,16,17,18,19], mostly thanks to their ability to trade-off computational cost and generalization performance.

The hypothesis space spanned by RBNs can be formalized as a weighted sum of nonlinear functions:

$$\begin{aligned} y({\varvec{x}}) = \sum _{n=1}^N \beta _n \phi _{n}({\varvec{x}}) = \sum _{n=1}^N \beta _n \phi ({\varvec{w}}_{n}{\varvec{x}}+b_n) \end{aligned}$$
(1)

where \({\varvec{x}} \in R^D\) is the input pattern, \({\varvec{w}}_n \in [-1;1]^D\) and \(b_n \in R\) are the parameters that characterize a neuron, \(\phi\) is a general nonlinear activation function \(R^D \rightarrow R\), and \(\varvec{\beta }\in R^N\) is the vector of adjustable weights that combine the neurons’ activation functions.

RBNs use a simplified training procedure that sets a-priori random values for the parameters of the hidden neurons, \({\varvec{w}}_n\) and \(b_n\). Given a set of labeled data \({\mathcal {T}} = \{({\varvec{x}}_i, y_i),i=1,\ldots ,Z, {\varvec{x}}_i \in [0,1]^D, y_i \in [-1;1]\}\), the training of an RBN consists in tuning the free parameters, \(\beta _n\), to minimize some loss function. The regularized mean square error is usually adopted for that purpose:

$$\begin{aligned} \min _{\varvec{\beta }}\{\Vert {\varvec{y}}-\varvec{H\beta }\Vert ^2+\lambda \Vert \varvec{\beta }\Vert ^2\} \end{aligned}$$
(2)

When \(Z\le N\), one has:

$$\begin{aligned} \varvec{\beta }= {\varvec{H}}^T(\lambda {\varvec{I}} + {\varvec{H}}{\varvec{H}}^T)^{-1}{\varvec{y}} \end{aligned}$$
(3)

conversely, when \(Z>N\) one has:

$$\begin{aligned} \varvec{\beta }= (\lambda {\varvec{I}} + {\varvec{H}}^T{\varvec{H}})^{-1}{\varvec{H}}^T{\varvec{y}} \end{aligned}$$
(4)

where \({\varvec{H}}\) denote a \(Z \times N\) matrix with \(h_{in} = \phi _n({\varvec{x}}_i,{\varvec{w}}_n, b_n)\). The quantity \(\lambda\) is a regularization term that rules the trade-off between the quality of data fitting and the smoothness of the solution. It is worth noting that efficient algorithms for the solution of linear systems can solve (3) and (4), thus avoiding explicit matrix inversions.

The size, N, of the mapping layer plays a crucial role, as it affects a) the generalization performance of the overall inference function, and b) the computational cost of both training and run-time inference. The latter aspect proves critical when targeting hardware implementations on embedded systems. Several approaches in the literature aimed to set up the mapping layer to trade off those issues. Regularization techniques favored sparse solutions and removed ineffective neurons [20, 21]. Biologically inspired optimization stimulated several strategies [22, 23] to enhance the generalization ability of the trained models. The method described in [24, 25] used the theory of learning with similarity functions to set the hidden layer, and connected randomization-based solutions with kernel-based learning theory [26]. Otherwise, constructive approaches aimed to induce well distributed hidden parameters [27,28,29], or combined with other algorithms to speed-up learning procedures [30].

2.2 Implementation of randomization-based networks on resource-constrained devices

RBNs provide a valuable option for on-device training [31,32,33,34,35,36,37,38], as the training procedure can be easily implemented. Several works in the literature focused on the efficient support of the inference function on resource-constrained devices. In the case of RBNs, that function complies with the constraints of low-power devices, as it can attain satisfactory generalization performances even the size, N, of the mapping layer is limited.

Neuromorphic realizations of the hidden layer were implemented using massively parallel and energy-efficient circuits [39, 40]. Those approaches stemmed from the analogy between biological neurons and the behavior of transistors operating under the threshold and yielded extremely efficient implementations. Each circuit was characterized by a specific set of parameter settings \({\varvec{w}}_n\) and \(b_n\). As a result, the training procedure had to be executed for every single chip. This also held for mixed-signal realizations, which featured a dispersion of parameters, thus providing high performances [41] and supporting ultra-low-power implementations of the RBN inference step [31, 42, 43]

Purely digital implementations for resource-constrained devices were presented in [7, 8, 21, 44]. Those works explored design strategies that removed the need for multipliers in digital architectures. In [8], the memory storage of random parameters, \({\varvec{w}}_n\) and \(b_n\), was bypassed altogether thanks to the adoption of a pseudo-random generator; by forcing a fixed seed in the generator, the device could replicate at run time the exact sequence of parameters that had been used in the (offline) training phase.

The above hardware implementations mostly relied on the ability to generate the sequence of random parameters at run time, especially to fit resource-constrained devices. Those approaches, however, seem incompatible with the training strategies discussed in Sect. 2.1. In the latter case, the distribution from which parameters \({\varvec{w}}_n\) and \(b_n\) are drawn is not fixed a priori but is adapted to trade off generalization ability and the network size. This in turn means that a hardware implementation of the eventual inference function should store the set of parameters, \({\varvec{w}}_n\) and \(b_n\), adjusted during training.

This paper introduces a design strategy that bridges the gap between those approaches. The digital architecture actually stores the parameters in memory, thus supporting a flexible sampling distribution; at the same time, the digital architecture can limit the computation cost and adapt run-time operation to the available energy budget.

Noise and fault events affect the behavior of low-power digital and analog implementations of RBNs. Solutions based on an explicit model of noise distribution and error probability offer a viable solution to reduce the impact of these phenomena on the generalization performances of the networks [45, 46]. The effectiveness of those approaches, however, depends on the quality of the noise/fault probability model, which in fact can be unknown a-priori. Regularization techniques can limit the degradation of generalization [47] without prior knowledge of noise/error probability distribution. The well-known \(L_2\) regularization, for example, usually yields robust networks because it inherently penalizes inference functions that depend on a small subset of neurons. Dropout regularization achieves the same goal by removing a random subset of neurons during the training procedure [48, 49].

Approximate computing techniques have been largely explored for deep neural networks (DNNs) [50]. However, DNNs techniques tackle a different scenario that makes unfeasible the straightforward application of the same principles to RBNs. Conventional pruning approaches [51, 52] to reduce the number of active neurons might affect the generalization ability of RBNs, especially when the goal is to shrink the hidden layer considerably. Binary neural networks [53,54,55] represent a viable approach for the deployment of Deep Neural Networks (DNNs) on resource-constrained devices. When addressing shallow networks, however, the coarse quantization of the weights brought about by binarization might severely compromise generalization ability.

3 Randomization-based neural networks with adjustable power consumption

The implementation of (1) on low-power resource-constrained digital devices brings about some design issues. The inference function includes N multiplications \(\beta _n \phi _n\), and each term \(\phi _n\) requires in turn D products. Threshold activation functions facilitate the development of hardware-aware architectures. State-of-the-art approaches [7], moreover, constrain the distributions of hidden weights to replace products with binary-shift operations or to avoid parameter storing [8, 31, 43].

Apparently, the threshold function limits the general applicability of the presented solution. However, a detailed discussion of the relationship between threshold and other activation functions [8, 25] highlights that in the context of RBNs a threshold activation can be considered as a sufficient approximation of the most common activation functions, like radial basis function and sigmoid. Instead, weight constraints significantly limit the pool of learning paradigms supported.

The novel design strategy proposed in this paper avoids weights constraint and can reduce adaptively the number of products (and therefore power consumption) required to compute \(\phi _n\). To comply with the available energy budget, the digital architecture switches between two operating modes (as per Fig. 1). In Complete-mode, the inference function \(\phi _n\) is computed by accumulating all the D contributions. Conversely, the Approximate-mode relies on an approximate activation, \({\tilde{\phi }}_n\), which accumulates a limited number of products, \(D'_n\) (\(D'_n < D\)). In the latter case, the main challenge is to manage the trade-off between power consumption and the loss in accuracy brought about by the use of \({\tilde{\phi }}_n\). In addition, the additional circuitry that implements the run-time switching capability should not affect power consumption significantly.

Figure 2 schematizes the structure of the envisioned digital implementation, which inherits a state-of-the-art design strategy for low-power implementation of RBNs [8]. In such a design, the Input block stored the input datum, the Neuron block computed the activation sequentially, and finally, the Output block supported the weighted sum of neurons activation. In the proposed scheme, the Controller sets the mode to be adopted by the Neuron block based on the available energy budget. Accordingly, the Neuron block should be able to both implement the complete activation and the approximate activation.

The overall challenge faced by this research is to find a proper trade-off between the gain in power consumption achieved with the Approximate-mode, the loss in accuracy caused by the use of \({\tilde{\phi }}_n\), and the impact on the digital implementation in terms of area consumption without compromising the benefits of RBNs, i.e., fast training procedure and light-weight forward phase.

Fig. 2
figure 2

Structure of the proposed digital implementation

Full size image

3.1 Approximate activation function

Let assume, without loss in generality, that \({\varvec{x}} \in [0,1]^D\). Accordingly, the sign of \(w_{nj}\) determines the sign of each addend \(w_{nj}x_j\) in (1). Thus, one can split that summation into two sets, i.e., \(W^+=\{w_{nj}x_j | w_{nj}>0\}\) and \(W^-=\{w_{nj}x_j | w_{nj}<0\}\). In practice, \(W^+\) and \(W^-\) aggregate, respectively, the positive and the negative addends separately. As a result, one rewrites \(\phi ({\varvec{x}})\) as

$$\begin{aligned} \phi _n({\varvec{x}}) = {\mathrm{sign}}\left( \sum _{W^-} w_{n,j}x_j+\sum _{W^+}w_{n,j}x_j+b_n\right) \end{aligned}$$
(5)

For the sake of clarity, it is assumed now that \(b_n=0\); the extension to the general case will be discussed later. Figure 3 illustrates an example for a neuron with \(D=81\); the x axis marks the index of each j-th addend, whereas the y axis gives the cumulative value of \(\sum _{W^-} w_{n,j}x_j+\sum _{W^+}w_{n,j}x_j\), when the j-th addend has been included. The terms in \(W^-\) and \(W^+\) have been sorted in descending order according to their magnitudes. At first, the cumulative value decreases and reaches its minimum as soon as the least significant term in \(W^-\) is added (in the example, j=36). Then, the cumulative function increases progressively as long as the terms in \(W^+\) are added. Although the sorting operation does not affect the eventual result (5), it yet highlights the relative contribution of each term to the overall aggregate. The contribution of the last six addends in \(W^-\) (marked in red on the x-axis) is marginal as compared with the preceding elements; the same holds true for the last seven positive terms in \(W^+\). The extension to the general case \(b_n\ne 0\) is straightforward, as \(b_n\) actually represents an offset.

Overall, one expects that the eventual sign of the activation might not change even if selected terms are removed from the summation (5). The idea is to look for those terms that carry the smallest relative contributions to the overall aggregate. For the n-th neuron, denote with \(a_{n,j}\) the expected value of the j-th term:

$$\begin{aligned} a_{n,j} =E_{{\mathcal {T}}}(x_jw_{n,j})=E_{{\mathcal {T}}}(x_j)w_{n,j} \end{aligned}$$
(6)

The expectation can be replaced by the optimal estimator, i.e., the sample mean

$$\begin{aligned} a_{n,j} = E_{{\mathcal {T}}}(x_jw_{n,j})\simeq \frac{1}{Z}\sum _{z=1}^{Z}(x_{z,j})w_{n,j}= {\bar{x}}_jw_{n,j} \end{aligned}$$
(7)

where \({\bar{x}}_j\) is the average of the j-th feature on the training set \({\mathcal {T}}\). Then, a set \(A_n^+\) grouping all the \(a_{n,j}>0\) can be derived from \(W_n^+\): \(A^+=\{a_{n,j} | w_{n,j}>0\}\). Likewise, the set \(A_n^-\) corresponds to \(W_n^-\). The relevance \(c_{n,j}\) of the j-th term in the n-th neuron can be formalized as follows:

$$\begin{aligned} c_{n,j} = a_{n,j}/{\mathrm{max}}(A_n^+) \quad a_{n,j} \in A_n^+\nonumber \\ c_{n,j} = a_{n,j}/{\mathrm{min}}(A_n^-) \quad a_{n,j} \in A_n^- \end{aligned}$$
(8)

In the example, the irrelevant addends according to (8) are marked in red. The definition of the relevance \(c_{n,j}\) allows to rewrite the approximate activation \({\tilde{\phi }}_n\):

$$\begin{aligned} {\tilde{\phi }}_n({\varvec{x}}) = {\mathrm{sign}}\left( \sum _{j=1}^D w_{n,j}x_jU(c_{n,j}-\alpha )+b_n\right) \end{aligned}$$
(9)

where U is the step function and \(\alpha\) is a threshold.

The expression (9) highlights the approximation that one introduces when using \({\tilde{\phi }}_n\) instead of \(\phi _n\). The size, \(D'_n\), of the subset depends on both the value \(\alpha\) and the distribution of the values {\(c_{n,j}\)}. The relevance \(c_{n,j}\) is worked out by averaging the j-th feature over the training set. This allows one to select, for the n-th neuron, a subset \(D'_n\) that does not affect the neuron’s activation on the training data. At the same time, one cannot guarantee that \({\tilde{\phi }}_n({\varvec{x}})=\phi _n({\varvec{x}})\) for any input sample. This issue calls for a trade-off between computational cost and accuracy and should be addressed in the training process.

Fig. 3
figure 3

Example of the cumulative trend with terms sorted in descending order

Full size image

3.2 Loss function: balancing power consumption and accuracy

In the digital implementation of the SLFN, the inference step can be carried out in either Complete- (1) or Approximate-mode as per (9). In the Complete-mode, the inference function is computed by involving the activation function \(\phi _n\). Hence, such configuration represents the baseline for evaluating the trade-off between loss in accuracy and saved power consumption that characterizes the Approximate-mode, which—for every neuron—adopts the approximate activation \({\tilde{\phi }}_n\) in place of \(\phi _n\).

In principle, one should train independently the two networks derived from the two configurations, thus obtaining the vector of weights \(\varvec{\beta }^{(S)}\) for the Complete-mode and the vector of weights \(\varvec{\beta }^{(A)}\) for the Approximate-mode, given a threshold \(\alpha\). However, memory requirements in the corresponding digital implementation would in turn double. A second option is to train a single network that is robust against perturbations at the neuron level. Thus, a sign inversion in the activation function \(\phi _n\) caused by its replacement with \({\tilde{\phi }}_n\) is treated as a fault. Recently, Ragusa et. al. [46] addressed this problem by introducing a suitable regularization term in the cost function of a SLFN.

This paper follows an alternative approach, which has been adopted in similar problems [48, 56]. Let \({\varvec{H}}_0\) be the training matrix computed by using \({\tilde{\phi }}_n\) with a given value of the threshold \(\alpha\); likewise, \({\varvec{H}}\) is the (complete) training matrix computed by using \(\phi _n\). The learning strategy sets the optimization problem by searching a single solution for both configurations and introduces a regularization term that forces the approximate solution \({\varvec{H}}_0\) to stick to \({\varvec{H}}\). The resulting learning problem \({\mathcal {L}}\) is:

$$\begin{aligned}&\min _{\varvec{\beta }} \mathcal {L(\varvec{\beta })} = \min _{\varvec{\beta }}\left\{ \frac{1}{2}\Vert{\varvec{y}}-\varvec{H\beta }\Vert ^2+\frac{1}{2}\Vert {\varvec{y}} -\varvec{H_0\beta }\Vert ^2+\frac{\lambda }{2}\Vert \varvec{\beta }\Vert ^2\right\} \end{aligned}$$
(10)

The solution \(\varvec{\beta }\) is obtained by imposing the gradient of Eq. 10 equal to 0; hence:

$$\begin{aligned}&\nabla _{\varvec{\beta }}\mathcal {L(\varvec{\beta })} = -{\varvec{H}}^T{\varvec{y}}+{\varvec{H}}^T{\varvec{H}}\varvec{\beta }\nonumber \\&\quad -\varvec{H_0}^T{\varvec{y}}+\varvec{H_0}^T\varvec{H_0}\varvec{\beta }+\lambda \varvec{\beta }=0 \end{aligned}$$
(11)

One can group the terms containing \(\varvec{\beta }\)

$$\begin{aligned}&({\varvec{H}}+ \varvec{H_0})^T{\varvec{y}}= +{\varvec{H}}^T{\varvec{H}}\varvec{\beta }\nonumber \\&\quad +\varvec{H_0}^T\varvec{H_0}\varvec{\beta }+\lambda \varvec{\beta } \end{aligned}$$
(12)

The closed-form solution of (10) is:

$$\begin{aligned}&\varvec{\beta }= (\lambda {\varvec{I}} + {\varvec{H}}^T{\varvec{H}}+{\varvec{H}}_0^T{\varvec{H}}_0)^{-1}({\varvec{H}}_0\nonumber \\&\quad +{\varvec{H}})^T{\varvec{y}} \end{aligned}$$
(13)

The quantity \(\lambda\) rules the trade-off between the performances of each configuration {\({\varvec{H}}_0\), \({\varvec{H}}\)}. In principle, the loss function (10) might also include a regularization parameter, \(\lambda _2\), for tuning the relative relevance of either configuration. For the sake of simplicity, in the following, the two configurations will be treated as equally relevant.

4 Digital implementation: RBN with adaptable energy consumption

The digital implementation of (1) targets low-power resource-constrained digital devices, and inherits the digital architecture described in [7, 8]. Such architecture exploited three single-cycle modules that operate in the pipeline. Figure 4 schematizes the processing flow with \(D=4\) and \(N=3\). In phase \(I_j\), the Input module acquires and stores the j-th feature of an input sample. In phase \(N_j^{(n)}\), the Neuron module processes the j-th feature, and incrementally computes the activation \(\phi _n({\varvec{x}})\) of the n-th neuron by adding the term \(w_{nj}x_j\). In phase \(O^{(n)}\), the Output module incrementally updates the activation (1) by adding the term \(\beta _n\phi _n\). Accordingly, the Neuron stage needs D clock cycles to yield the activation of the n-th neuron; the Output stage updates y as soon as a new activation is available.

Fig. 4
figure 4

Processing flow of SLFN inference as designed in [7]

Full size image

In the present work, the internal structure of the Neuron module (Fig. 5) fits the design strategy outlined in Sect. 3, and embeds a single multiply-and-accumulate (MAC) circuit to privilege power consumption over latency. The Neuron module receives—at the rising edge of a clock cycle—the j-feature of the input sample and the signal \(e_{nj}=U(c_{n,j}-\alpha )\), which acts as an enable signal to the three registers involved. When enabled, a pair of registers store the j-feature and the associate weight \(w_{nj}\), respectively. At the subsequent rising edge, the accumulator is loaded with the updated value of the function; a flip-flop ensures the correct synchronization with \(e_{nj}\). The accumulator is initialized with the value \(b_n\) whenever the computation of a new \(\phi _n\) starts. The parameters \(w_{nj}\), \(b_n\) are all stored in dedicated memories.

This energy-efficient architecture allows the Neuron module to compute either \(\phi _n\) or \({\tilde{\phi }}_n\) [57]. Each term \(w_{nj}x_j\) is only added if \(e_{nj}=1\); otherwise, when the inputs remain unchanged, the multiplier circuitry remains inactive and power consumption only stems from leakage. The Enable module relies on memory U to control the signal \(e_{nj}\); for each neuron, one has \(e_{nj}=1\) if \(c_{n,j}>\alpha\), and \(e_{nj}=0\) otherwise. The Control Unit drives the associated MUX: in Complete-mode, one always has \(e_{nj}=1\); in Approximate-mode, the MUX status depends on the associated value stored in U.

Fig. 5
figure 5

The digital architecture

Full size image

As in [7, 8], the Input module just includes a memory for the serial acquisition of each input sample. In the Output module, the memory stores the weights \(\beta _n\phi _n\), and an add-and-accumulate block carries out the sequential computation of (1). A finite-state machine controls the whole process.

Data representation affects both rounding errors and the computation cost [58]. The literature proved that a signed integer representation is adequate for shallow networks with threshold activation [8]. In this paper, the input features \(x_j\) and the parameters {\(w_{nj}\), \(b_n\), \(\beta _n\)} are encoded by 8-bit signed integers, while the MAC unit handles 16-bit signed integers. Such configuration should preserve classification accuracy and, at the same time, limit the energy consumption of the MAC stage.

Overall, the proposed digital architecture minimizes hardware requirements by involving a single multiplier. The latency of the inference for the input datum \({\varvec{x}}\) does not depend on the configuration adopted (Complete/Approximate). Conversely, when operating in Approximate-mode the number of products does decrease; this in turn means that the circuit saves both energy and power. Obviously, such an approach penalizes latency for the purpose of constraining the energy budget.

5 Results

The experimental setup was divided into two parts. First, the generalization performance is tested using ten real-world datasets. Later, the implementation results using a commercial FPGA were tested.

The experiments involved ten bi-class datasets for assessing the generalization ability of the RBNs with online adjustable neurons described in Sect. 3. Seven datasets belonged to the UCI repository [59]; in addition, MNIST81, ds2os, and fog provided benchmarks for significant IoT applications [49]. Table 1 summarizes the characteristics of the datasets. The first column marks the dataset. The second column gives the dataset dimensionality, D. The third and fourth columns show the number of patterns available for classes 0 (\(Z_0\)) and 1 (\(Z_1\)), respectively. The fifth column gives the number of training samples Z. The last column shows the number of test patterns \(Z_{\mathrm{test}}\). The data were normalized in the range [0,1]; the most frequent categories were possibly sub-sampled to avoid issues deriving from imbalanced distributions. In each dataset, 70% of the patterns formed a training set, whereas the remaining patterns composed the test set. The experiments concerning generalization capability were executed using Matlab software on a standard desktop computer.

Table 1 Dataset summary
Full size table

5.1 Generalization performance

The comparisons involved five different classifiers, i.e., five RBNs with as many different loss functions. In addition, two versions of each classifier were instantiated: the Complete and the Approximate versions. The first pair of classifiers adopted the standard L2 loss function (2). The \(L_2\) loss is well known for inducing good generalization performance; in addition, it enables a satisfactory robustness against perturbations of the hidden neurons’ activation [47]. In the following, \(L2_S\) will mark the Complete-mode classifiers using (5); conversely, \(L2_A\) will refer to the Approximate-mode classifiers as per (9). The second pair of classifiers involved a perturbation-sensitive loss function [45]. In particular, we refer to [46] where the technique proposed in [45] was tailored to threshold units measuring the probability of a neuron ’flip’ on the training set. In practice, one counted how many times the activation computed with \({\tilde{\phi }}_n\) did not match the same function computed with \({\phi }_n\). In the following, \(F_S\) and \(F_A\) will refer to the classifiers tested in Complete- and Approximate-mode, respectively. The third and fourth classifiers refer to two different implementations of the dropout mechanism in RBNs. The third classifier [49], indicated as DE, implements the technique using an ensemble-based algorithm. The fourth classifier, indicated as DR, uses a penalization term inside the loss function [48]. Dropout is expected to reduce the impact of distortions introduced by the Approximate-mode. The last pair of classifiers covered RBNs trained with the novel design-oriented loss function described in this paper (10): \(M_S\) and \(M_A\) will refer to the Complete- and Approximate-mode classifiers, respectively.

In each experiment, the hyper-parameters {\(\lambda ,N\)} were set by applying model selection on the RBN trained with the \(L2_S\) loss function. This approach allowed fair comparisons among the classifiers, which shared the size of the hidden layer. It is worth noting that, as a result, the accuracy values \(F_S\), \(F_A\), \(DR_S\), \(DR_A\), \(DE_S\), \(DE_A\), \(M_S\), and \(M_A\) actually reflected sub-optimal configurations. Model selection covered the settings \(\lambda =\{10^i,i=-4,-3,\ldots ,4\}\), \(N=\{50, 100, 200, 500\}\). Additional hyper-parameter of single loss functions, like dropout probability, were set through a grid search procedure as for the case of \(\lambda\) and N. In each experiment, the estimated accuracy stemmed from an average over twenty runs; in each run, the set of hidden parameters was drawn at random [60] and the compared RBNs all shared the same set.

Figure 6 shows the effect of the proposed approximation technique on the neurons’ activations. Figure 6a reports on the y-axis the flip probability measured on the hidden layer of trained networks when fed with testing data. The x-axis groups the result based on the value of \(\alpha\). The groups collect the results for all ten datasets. Figure 6b reports on the y-axis the average percentage of ’active’ terms, i.e., terms that were not pruned in the Approximate-mode. The x-axis follows the same format of Fig. 6a. When adopting a mild setting of \(\alpha\) (i.e., \(\alpha =0.2\)), the network skips a considerable number of multiplications for each activation (i.e., from 20% to 40%), as shown in Fig. 6b. The percentage of flipped neurons is smaller than 10% except for two datasets. With \(\alpha =0.5\) one obtains different outcomes. The percentage of active terms approaches 40% for most of the datasets, but the number of flipped neurons remains smaller than 20% for all datasets except one. The intermediate value \(\alpha =0.3\) yields flip probability values and percentages of active terms halfway between the other configurations. The overall trend highlights the effect of parameter \(\alpha\) on the behavior of the neurons. These outcomes confirm that the proposed strategy selects connections with a limited effect on neurons’ behavior.

Fig. 6
figure 6

Average effect of the proposed approximation technique on the activation of the hidden layer for testing data

Full size image

The impact of the proposed approximation technique on the generalization performance of the classifiers is shown in Table 2. The first column marks the dataset. The second column reports the average size of the hidden layer over the twenty runs. The third column shows the average percentage classification error on the test set when using \(L2_S\). That quantity, highlighted for readability, was independent of the value of \(\alpha\) and provided a reference for each dataset. Columns from 3 to 10 give, respectively, the average classification errors scored by \(L2_A\), \(F_S\), \(F_A\), \(DE_S\), \(DE_A\), \(DR_S\), \(DR_A\), \(M_S\), and \(M_A\).

Table 2 Results: generalization performances \(\alpha =0.2\)
Full size table

The results refer to the setting \(\alpha =0.2\). Both classifiers \(M_S\) and \(M_A\) attained performances close to that scored by \(L2_S\); in fact, \(M_A\) could skip a considerable fraction (20–40%) of multiplications for each activation (as shown in Fig. 6). Both the dropout-based methods present a trend similar to the \(L_2\)-based classifier. In Complete-mode, the classification error is similar between the three solutions. When the networks are fed with approximate activation, the error increases significantly. The narrow gap between \(M_S\) and \(M_A\) mostly confirmed the effectiveness of the proposed cost function. It is also worth noting that \(L2_A\), \(M_S\), and \(M_A\) proved less effective than \(M_A\). Again, such an outcome empirically proved that the Approximate-mode should be supported by a customized cost function.

Table 3 mimics Table 2 showing the results for \(\alpha =0.5\). The performance of \(M_S\) and \(M_A\) slightly deteriorated when setting \(\alpha =0.5\); at the same time, using \(M_A\) resulted in a remarkable reduction in multiplications (Fig. 6) for each activation (more than 50%). As expected, that gap sometimes widened when adopting such a more stringent setting. In practice, the presence of two terms in that loss function acted as a regularizer [48, 56]. Conversely, the performance of other networks with Approximate-mode active deteriorate significantly: in most cases, the error increment was higher than \(30\%\) for \(L2_A\) and \(F_A\). In this case too, the trend for dropout-based and \(L_2\) classifiers was similar. The large difference with \(F_A\) proves that the proposed objective function outperforms fault-tolerant regularization techniques [45, 46].

Table 3 Results: generalization performances \(\alpha =0.5\)
Full size table

A last experiment involved the implementation of the classifiers \(M_S\) and \(M_A\) by adopting 8-bit signed integers; such data representation is compliant with the digital implementation on constrained edge devices. Table 4 reports the outcomes of such an experiment. The first column marks the dataset. Columns from 2 to 5 refer to the experiments with \(\alpha =0.2\). The second and the third column give, respectively, the classification error scored by \(M_S\) and \(M_S-8\), which is the quantized implementation of \(M_S\). Similarly, the fourth and the fifth column give, respectively, the classification error scored by \(M_A\) and \(M_A-8\). Columns 6 to 9 refer to the experiments with \(\alpha =0.5\) and adopt the same format. Overall, the results of Table 4 proves that the impact of quantization is very limited.

Table 4 Analysis of the impact of 8-bit integer representation
Full size table

5.2 Digital implementation

This section provides first an example of functional simulation of the proposed digital architecture; then, the circuit is characterized and compared in detail with the low-power digital implementation of SLFNs discussed in [8], which represents a baseline. A general comparison with state-of-the-art works is given in the following section.

The proposed digital architecture was tested using Vivado2020.1 design suite. A low-power FPGA, namely CMOD-S725, was set as the target for the simulation. The overall goal was to complete both functional simulation and timing simulation of the architecture. In fact, the eventual target should be the ASIC implementation of the edge device. FPGA implementations would inevitably have an impact on the overall power consumption, as the architecture of Fig. 5 would use only a small amount of resources even on a low-end FPGA.

Fig. 7
figure 7

Functional simulation in approximate-mode (\(D = 3, N = 2\))

Full size image

Figure 7 gives an example of the functional simulation of the architecture.Footnote 3 For the sake of clarity, the simulation involved a basic classifier with \({\varvec{x}} \in R^3\) and two hidden neurons; in this example, \({\varvec{x}}=[01h,02h,03h]\), \({\varvec{w}}_1=[06h,05h,04h]\), \({\varvec{w}}_2=[03h,02h,01h]\), \(b_1=b_2=0\). The waveform pane shows: the clock signal, the enable signal \(e_{nj}\), and the values stored in the three registers within the Neuron module, namely, \(x_j\), \(w_{nj}\), and the accumulator acc. The simulation illustrates the main operation steps of the Neuron module; the term to be skipped is \(w_{23}x_3\), i.e., the third term in \({\varvec{w}}_2{\varvec{x}}\).

Table 5 reports on the results of the tests for evaluating the circuit efficiency values; the experiments were performed in Vivado using Vector (SAIF) Based Power Estimation based on post-implementation simulation. In general, the tests confirmed that the architecture can support clock frequencies up to 120 MHz. In low-power applications, though, the clock frequency is typically set to small values to cope with the low energy budget. Accordingly, all the tests reported in this paper refer to an implementation where \(f=12\) MHz.

The simulation fed the network with thirty random inputs to estimate the switching activity of the circuit. The analysis compared the implementation of a SLFN proposed in [8] with unconstrained weights and the digital implementation schematized in Fig. 5. The former case represented the baseline for each test as it compared favorably in terms of hardware occupation with recent solutions for low-power SLFNs.

Table 5 compares the baseline implementation and the proposed implementation according to energy consumption per single inference (i.e., inference on a single datum). The second column gives the circuit implementation, while the remaining five columns refer to as many configurations of the pair {D, N}. In the tests with Approximate-mode classifiers, the experiments involved \(D'_n=D/2\) for every neuron.

Table 5 Energy performance: baseline [8] and proposal
Full size table

The energy per single inference of the architecture operating in Complete-mode matched the consumption of the baseline implementation, which lacked the ability to switch to Approximate-mode. When operating in Approximate-mode {\(TP\approx 50\%\)}, the proposed architecture yielded a significant reduction of energy consumption. Further tests confirmed that this gap scaled linearly with TP.

Table 6 compares the baseline implementation and the proposed implementation in terms of resource usage. The same five configurations of Table 5 are characterized according to: the percentage of used LUTs over the total number of available LUTs, the percentage of used FFs over the total number of available FFs, and the percentage of used BRAMs over the total number of available BRAMs. In terms of resource occupation, flip-flop usage was equal for the two solutions and kept lower than \(1\%\). The circuitry always included 1 block of BRAM. The block RAM usage remains constant in all the settings because the amount of the required memory is small independently of D and N. In fact, in this case, memories are typically synthesized using registers and flip-flops. The configuration of the pair (D, N) only affected the amount of LUTs, which indeed grew slower than \(D \times N\).

Table 6 Hardware performance: baseline [8] and Proposal
Full size table

5.3 Comparison with literature

The literature proposes other approaches suitable for the efficient implementation of neural networks with threshold activation or RBNs. However, a direct comparison with the present paper would be unfair due to the fact that the adopted design targets a scenario where the constraints on the available resources are very severe. In the following, a detailed qualitative comparison analyzes the discrepancies and similarities with state-of-the-art implementations.

In [7], a redesigned ELM based on a constrained distribution of the hidden weights has been implemented in a digital architecture without multipliers. The digital architecture was tested on different devices; the most constrained was a CPLD 5M1270Z, where a network with D=81 and N=18 was implemented with a clock frequency of 33 MHz. The power consumption reached 48 mW with an occupation of 73% of the area available in the CPLD. In our experiments, we implemented a classifier with D=100 and N= 100. In this setup, with a clock frequency of 12 MHz, the power consumption was 67mW on the MOD-S725, where 61mW was ascribed to static power. In practice, one should consider that a CPLD has a much smaller static power consumption. On the other hand, CPLD cannot support multipliers; this aspect imposes a constraint on the set of implementable RBNs.

Gao et al. [44] presented an implementation of RBNs based on a three-stage architecture. The network was deployed on a Xilinx XC7 with a 50MHz clock frequency. Power consumption was toward 1.0 W, which is two orders of magnitude larger than the largest power consumption measured with our architecture.

Recent implementations of non-random binary networks on FPGA featured a power consumption above 2.5 W [53]. The implementations presented in [54] and [55] reached a power consumption close to 2.5W. In the former case, the network was deployed on a Zynq-8020 with a clock frequency of 100 MHz; in the latter case, the deployment involved a Zynq-7020 with a clock frequency of 120 MHz. The proposed architecture when implemented with clock frequency \(f = 120\) MHz, \(D = 100\), and \(N = 500\) showed a dynamic power consumption of about 20 mW. This gap can be ascribed to the difference in terms of the number of parameters between a DNN and a RBN. This in turn lessens hardware requirements for the implementation of a RBN and makes binary-quantization strategies for deep learning ineffective.

An important feature of RBNs is the capability of supporting online learning on resource-constrained devices. Recently, different works proposed efficient digital architectures implementing both online learning and the inference phase on FPGA. The recursive least mean p-power algorithm for training an ELM was proposed in [36]. The paper reported a power consumption of around 1.5 Watts, where only 160 mW were ascribed to dynamic power. In [37] online sequential ELM was deployed on FPGA with very similar power consumption. Huang et al. [38] achieved on-chip training of ELM with 1.45 Watts power consumption. Obviously, the inclusion of online training contributes to increasing the power consumption of the final device.

6 Conclusions

The paper presented a design strategy for the efficient, digital implementation of RBNs with hard-limit activation functions, under variable and tight energy constraints.

A suitable strategy based on approximated computing exploits the peculiarities of hard-limit activation to control the number of operations during the inference phase based on the available energy budget. Eventually, the complete and approximated working modes use the same set of weights trained using a custom loss function proposed in this paper. A dedicated digital architecture supports the two operation modes and allows a satisfactory trade-off between accuracy and energy budget.

Experimental results assessed generalization performance and hardware performance. Generalization capabilities were assessed employing ten real-world datasets. The digital architecture was characterized using Vivado and a low-cost development board, namely CMOD-S7. Experiments confirmed that the proposed solution can trade off generalization performance and hardware requirements better than the alternative solution. In addition, the experiments confirmed that the design strategy, in Approximate-mode, attained considerable reductions in energy consumption, while ensuring satisfactory generalization performances.

Future development concerns the deployment of the proposed digital architecture on ASIC to fully exploit the low power features of the present design. In addition, a possible research direction concerns adapting the method to more general architecture, also multi-layer, not based on randomization of the input layer by suitably reformulating the learning procedure.