1 Introduction

Lung cancer is known as a disease that consists of uncontrollable growth of lung cells which may lead to metastasis. Metastasis is the infestation of adjacent and nearby tissue and infiltration beyond the lungs. From epithelial cells Carcinomas are derived which are the vast majority of primary lung cancers. Lung cancer is the most usual cause of cancer-imputed death in men and women. An estimated number of new lung cancer cases, by sex type, are 119,100 for males and 116,660 for females in the US [1].

The early detection of lung cancer can increase overall 5-year survival rates by extracting the lung nodules and distinguishing their location for surgery. Hence, this diagnosis according to nodule location (solitary and juxtapleural) can improve the treatment. In this paper, we aim to classify small lung masses as nodule or non-nodule by using a Computer Aided Diagnosis (CADx) system. Also, classify this nodule as a solitary nodule or juxtapleural nodule.

Traditional X-ray and computed tomography (CT scan) is attempted to diagnose lung nodules [2]. The most accurate modality for imaging lung nodules is CT. It allows the detection of a small lung nodule, but a large amount of data leads to a high false negative rate to detect the small nodules. Computer Aided Diagnosis (CADx) system is one of the robust systems which is used in the detection and diagnosis of lung cancer. Because of the nodule’s small size in the lung, it is difficult to distinguish between it and another mass in a 2D slice. Actually, micro-nodules cannot be recognized on single slices: the nodule shape, size, and gray tone are very similar to vessel sections. Therefore, segmentation is a very important step to distinguish between the small nodules and blood vessels. Hence, the type of nodules according to their location (solitary or juxtapleural) will be easily classified.

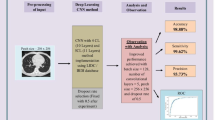
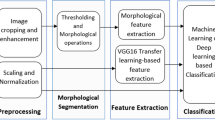
In this study, two main schemes of supervised learning for classification are proposed in which; two segmentation approaches are achieved (Thresholding + K-means clustering and Bounding box + Maximum intensity projection) for both two schemes. For the first scheme, a combination of the first-order and second-order features is extracted. Fisher score ranking is used as a feature selection method. The higher five, ten, and fifteen ranks of features are selected, respectively, from the two sets of features. The first scheme is implemented by using Support Vector Machine (SVM) classifier. The second scheme used Deep Convolutional neural network (DCNN) for deep learning classification. Tenfold cross-validation and random oversampling are used to manage limited and imbalanced data. ROC curve is used to evaluate the DCNN classifier. The general block diagram which represents the methodology and system overview is shown in Fig. 1. Our algorithm outperforms MIP as a 2D segmentation technique achieving good results although it is generally used in a 3D volume rendering. Also, achievement of promising results when using a quite small dataset with DCNN.

Fig. 1
figure 1

Methodology and system overview

Full size image

2 Related work

To date, many types of research about the detection of the nodule by using CAD systems have been developed. It begins with preprocessing and segmentation followed by the classification step. For instance, Diego et al. [3] used a method composed of four steps for lung nodule detection. The first employed acquisition of an image and pre-processing. The second phase involved a 2D algorithm to inspire every layer of a scan which eliminates the non-informative structures in the. The final step utilized a support vector machine for separating the candidate masses into nodules and non-nodules according to their features.

QingZeng et al. [4] proposed a stacked autoencoder (SAE), convolution neural network (CNN), and deep neural network (DNN), respectively, to detect pulmonary nodules. The results showed that the CNN network achieved the best performance with an accuracy of 84.15%, sensitivity of 83.96%, and specificity of 84.32%, which induces the best result among the three networks. Yang et al. [5] described a 3D detection of pulmonary nodule scheme using MSCT images. This method segmented the candidate nodules first and extracted voxels feature based on eigenvalues analysis. Then support vector machine (SVM) and decision rule are applied to reduce the false positives.

Sarah et al. [6] used a Gaussian smoothing kernel for filtration which helps to reduce noise effects. Next, features such as sphericity, mean and variance of the gray level, elongation, and border variation of potential nodules are extracted to classify detected nodules as malignant and benign tumors. Fuzzy KNN is employed to classify potential nodules as non-nodule or nodules with different levels of malignancy. She achieved a sensitivity of 88% for nodule detection with approximately 10.3 False-Positive (FP)/subject.

Serhat et al. [7] used Genetic Cellular Neural Networks (G-CNN) for segmentation. A 3D template was made to find the structures which are like a nodule in the 3D image. The computer-aided diagnosis (CAD) system achieved 100% sensitivity with 13.375 FPs per case when the nodule thickness was greater than or equal to 5.625 mm. To test the system's efficiency, they used 16 cases with a total of 425 slices, which were taken from the Lung Image Database Consortium (LIDC) dataset.

Jin et al. [8] put forward a kind of lung segmentation method based on morphology and statistic of the size of the image area, while effectively eliminating the influence of the trachea on pulmonary parenchyma image segmentation. He also proposed a method of the region of interest(ROI) extraction based on morphology and circular filter, reducing the number of false positives and trying to retain the integrity of the ROI form. Finally, he has realized reliable lung nodules compute aided diagnosis application on CT image, using convolution neural network. The system achieved 84.6% of accuracy, 86.7% of specificity, and 82.5% of sensitivity.

Thomas et al. [9] developed a CAD system that can localize as many nodules as possible while keeping the number of false positives low. To localize the nodules in the three-dimensional space of a scan, a quantile approach over the cross-sectional slices is applied to retrieve a two-dimensional slice. Next, a sliding window method on the slice is used to obtain the (x, y) coordinates of the nodule. A two-dimensional convolutional neural network is used as a classifier of these windows. The developed CAD system can detect and localize 60.1% of all the nodules with an average number of 2.1 (1.5%) false positives per slice. With 95% confidence, he concluded that deeper neural networks decrease the false positives significantly. In this research, the publicly available LIDC-IDRI database has been used.

Wu et al. [10] combined several common image processing techniques with segmentation steps, such as hole-filling, binarization, and mathematical operation. Ming et al. [11] proposed a learning-based method to reduce the number of false positives given by CG based on a new general 3D volume shape descriptor. The 3D volume shape descriptor is constructed by concatenating spatial histograms of gradient orientations, which are robust to large variabilities in intensity levels, shapes, and appearances. The proposed method achieved promising performance on a difficult mixture lung nodule dataset with an average 81% detection rate and 4.3 false positives per volume. He used the watershed algorithm and then utilized a region-growing method.

Xujiong et al. [12] proposed a segmentation method for lung extraction by applying a 3-D adaptive fuzzy thresholding technique and a 2-D-based post-refinement process. The proposed method has been trained and validated on a clinical dataset of 108 thoracic CT scans using a wide range of tube dose levels that contain 220 nodules (185 solid nodules and 35 GGO nodules) determined by a ground truth reading process. The data were randomly split into training and testing datasets. The experimental results using the independent dataset indicated an average detection rate of 90.2%, with approximately 8.2 FP/scan.

Michela et al. [13] used a dynamic threshold for the identification of three groups corresponding to the upper, middle, and lower parts of the 3D volume of the lung. They proposed a combination of image processing techniques applied to each slice. More precisely, the following steps are performed: (1) the background (i.e., the pixels outside the chest) is removed from the image; (2) a thresholding technique is used to produce a binary image; (3) the morphological opening and closing operators are applied; in particular, the opening operator is adopted to eliminate the small objects inside the lung and to separate some regions that should be separate but are joined by a thin area of foreground pixels, whereas the closing operator aimed to get rid of small holes that represent border interruptions; (4) the image borders are detected by means of a tracking algorithm; (5) thinning is used to reduce the border size to one pixel; (6) the border chains that delimit the two pulmonary lobes are identified; (6) reconstruction of pulmonary lobes borders is performed by an operator which, based on the border shape, reinserts erroneously erased zones; in particular, the nodules adjacent to the pleura that have been eliminated by thresholding are recovered; (7) a filling operator is applied to the pulmonary lobes chains, thus reintroducing the correct values of gray levels inside the lungs.

Sasidhar et al. [14] involved: a. Automated Segmentation of lung regions b.Automated Detection of lung cancer. To speed up the process of detecting lung cancer, segmentation of the lung region plays an important role. He applied two steps of segmentation: firstly, extracted lung parenchyma by using a Hounsfield Unit (HU) with a threshold of − 420 as Gray Level Value = 1024 + HU. Secondly, extract lung nodules using the threshold of − 150 HU.

Qingxiang et al. [15] studied pulmonary nodule and blood vessel detection and segmentation. His proposed algorithm is composed of four steps: pre-segmentation, structure enhancement, active evolution, and refinement. Through the initial extraction of the 3D region growing, the line structure of the vessel and blob-like structure of the nodule would be enhanced by multi-scale filtering. In particular, the active evolution is devoted to the maximum likelihood estimation with a vessel energy function (VEF) of intensity, gradient, and structure. The VEF aims to shape a precise extraction by adapting all the cue distribution along the vessel region from nodules. Furthermore, a radius-variable sphere model is adopted to refine the contour with the smoothness of the radius along the centerline of the blood vessel. Finally, the proposed scheme is sufficiently evaluated to exceed the existing techniques for lung image database consortium (LIDC) database and DICOM images.

Qing et al. [16] transformed correlated variables into uncorrelated variables, which are called principal components based on their cumulative variance proportion which is called principal component analysis (PCA). El-Regaily et al. [17] proposed an algorithm for a Convolutional Neural Network which achieved a high detection sensitivity of 85.256%, a specificity of 90.658%, and accuracy of 89.895%. Experimental results indicate that the proposed algorithm outperforms most of the other algorithms in terms of accuracy and sensitivity. LIDC datasets are used to train and test the network.

Blanc et al. [18] create an algorithm to detect and classify pulmonary nodules into two categories using machine learning and deep learning techniques. Lung segmentation was achieved using a 3D U-NET algorithm; nodule detection was done using 3D Retina-UNET and classifier stage with a support vector machine algorithm on selected features. Performances were assessed using the area underreceiver operating characteristics curve. The pipeline showed good performance for pathological nodule detection and patient diagnosis of 87% yielding accuracy for the “nodule detection” stage, corresponding to 86% specificity and 89% sensitivity.

Zaimah et al. [19] focused on the detection of lung cancer using classification with the Support Vector Machine (SVM) method based on the features of Gray Level Co-occurrence Matrices (GLCM) and Run Length Matrix (RLM). The lung data used were obtained from the Cancer imaging archive Database, consisting of 500 CT images. CT images were grouped into 2 clusters, including normal and lung cancer. The research steps include image processing, region of interest segmentation, and feature extraction. The best learning result based on the classification process using SVM is at an accuracy of 85.63% with a specificity of 66.35%, and a sensitivity of 100.00%. In their study, optimization of SVM parameters was carried out to get the best hyperplane.

Regarding the literature review in this area of research, we focused on achieving the highest accuracy results with a small number of images compared to the number of images in the literature review.

3 Materials and methods

3.1 Dataset

A 14 digital CT consisting of 2991 2D slices which contain 172 nodules (100 solitary nodules and 72 juxtapleural nodules) were downloaded from Cornell University [20] LIDC dataset. Each abnormal image contained a tumor with equivalent diameters of lung nodules ranging from 3 to 30 mm and the total number of normal images is 232 images. For the training phase, (86 abnormal (50 solitary + 36 juxtapleural), and 116 normal) images are used and for the testing phase, the same number is used. This number of images is quite small to train and test the classifiers, especially the DCNN classifier. We want to compare SVM and DCNN results by using the same dataset so we tackled this point. The in-slice (x, y) resolution is 0.703 × 0.703 mm and the CT slice thickness is 1.25 mm in DICOM format and has 512 × 512 pixels.

3.2 Segmentation and enhancement for nodule emphasis

Inhomogeneity in the lung region is a very challenging problem as there are similar densities such as veins, arteries, and bronchioles. It is necessary to enhance the quality of the displayed image by rectifying distortions due to media decay or motion artifacts.

In this paper, two approaches to segmentation are presented to reach the best segmentation results as follows:

3.2.1 Approach I (bounding box + maximum intensity projection)

It consists of Bilateral filter [21, 22], Thresholding gray-level transformation function [23], Bounding box [24] 25, erosion and dilation [26] and Maximum intensity projection (MIP) [27] as shown in Fig. 2. The resulted images of approach I are shown in Fig. 3.

Fig. 2
figure 2

(Bounding box + maximum intensity projection) segmentation approach

Full size image
Fig. 3
figure 3

Segmentation results of approach I (MIP + bounding box): a Original CT image, b bilateral filtering, c bit plane slicing, d bounding box, e thresholding, f clearing lung border, g filling holes, h superimposing and i candidate nodule with MIP

Full size image

3.2.2 Approach II (thresholding + K-means clustering)

It achieved by using Median filter [28], Histogram equalization [29], Adaptive histogram equalization [30], Otsu’s method [31], Edge detection [32, 33] and K-means clustering [34, 35] as shown in Fig. 4. The resulted images of approach II are shown in Fig. 5.

Fig. 4
figure 4

(Thresholding + Kmeans clustering) segmentation approach

Full size image
Fig. 5
figure 5

Segmentation results of approach II (thresholding + K-means clustering): a original CT image, b median filter, c histogram equalization, d adaptive histogram equalization, e Otsu’s method, f–h Canny filter, erosion and dilation, i Superimposing, j Cluster 1, k Cluster2, l Cluster 3(Candidate nodules)

Full size image

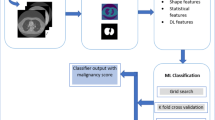
3.3 Features extraction and selection

It is the main step of the Scheme i supervised learning model as the algorithm learns on labeled images; feature extraction; by fitting an answer key that the model can use to evaluate its accuracy on training images. Feature extraction presents all the obtained information in lung CT images to differentiate between the different tissues inside the image. A combination between first-order features (33 shape and texture features (1st set)) and second-order features (80 texture features (2nd set)) are extracted, so the total number of features is 113 (3rd set). Some examples of first-order features are mean [26], standard deviation [26], variance [36], kurtosis [36, 37], entropy [38], nine percentile features [36], 7 invariant moments [36] and Perimeter [39]. Second-order features are the features of gray level co-occurrence matrix (GLCM) [34] such as autocorrelation, contrast, cluster prominence, cluster shade, dissimilarity, and entropy.

Because of a large number of features, a filter approach technique is used to rank the strength of these features to achieve high standard accuracy, this technique is called Fisher score ranking [40]. It can differentiate between nodules and non-nodules when calculating the difference [41] between the mean and the standard deviation of the positive (nodule) and negative (non-nodule) relative to a definite feature. Equation (1) clarifies the Fisher score, in which Ri is the feature rank i, representing the proportion of the substitution of the feature mean i values in the nodule examples (p) and the non-nodule examples (n), and the sum of the standard deviations. The bigger the Ri, the bigger the difference between the values of (p) and (n) examples relative to feature i The highest 5, 10, and 15 ranks of each feature set are obtained to minimize the classification error and decrease the computation time.

$$ R_{i} = \frac{{\left| {\mu_{i,p} - \mu_{i,n} } \right|}}{{\sigma_{{i,p + \sigma_{i,n} }} }} $$
(1)

where \(\mu_{i,p}\) and \(\mu_{i,n}\) are the means of the positive (abnormal) and negative (normal), \(\sigma_{i,p}\) and \(\sigma_{i,n}\) are the standard deviations of the positive (abnormal) and negative (normal).

3.4 Fold cross-validation

Cross-validation (CV) is a resampling procedure used to evaluate machine learning models on a limited data sample. The procedure has a single parameter called k which refers to the number of groups that a given data sample is to be split into. As such, the procedure is often called k-fold cross-validation. When a specific value for k is chosen, it may be used in place of k in the reference to the model [35, 42]. In this research, k = 10 is used becoming tenfold cross-validation.

3.5 Random over sampling

As the abnormal images and normal images are not equal (imbalanced), therefore the classifiers tend to provide a severely imbalanced degree of accuracy. Random oversampling (ROS) is proposed to balance the data by increasing the size of the minority class (abnormal) when replicating randomly a set of samples of it as shown in Eq. (2) [43, 44].

$$ \left| S \right| = \left| {S_{\min } } \right| + \left| {S_{{{\text{maj}}}} } \right| + \left| {E_{\min } } \right| $$
(2)

where \(E_{\min }\) represents the set of replicated sample, \(S_{\min }\) represents the minority class (abnormal), \(S_{{{\text{maj}}}}\) represents the majority class (normal).

4 Classification

In the proposed scheme I, the classifier used the trained dataset to classify the abnormality, and the features of the bigger R are fed into the classifier. On the other hand, in scheme II a deep learning classification is done. The total number of abnormal images is 172 images containing (100 solitary nodules and 72 juxtapleural nodules) and the total number of normal images is 232 images. The training phase has 202 images (116 normal and 86 abnormal (50 solitary and 36 juxtapleural)) and the same number for testing, therefore the total number of images was 404. The dataset was split 50–50 to minimize the computation time.

4.1 Scheme I (supervised learning model)

In scheme I, Support Vector Machine (SVM) classifier is used. SVM is considered as a linear classifier related to supervised learning algorithms which are applied for classification problems. In a high-dimensional feature space, SVM constructed a hyperplane that separates the data points (samples) of the two classes. But many hyperplanes can be found for this separation (Fig. 6), so it’s the SVM’s second function to find the optimum hyperplane (maximum margin hyperplane). SVM uses a linear functions hypothesis space to achieve the classification easier These kernel functions produce nonlinear separators to map the input space attributes to the feature space [45, 46]. Three basic kernels are used Linear, Quadratic, and Radial Basis Functions as shown in Eqs. (3), (4), and (5).

$$ {\text{Linear:}}\,K\left( {x_{i} x_{j} } \right) = x_{i} ,x_{j} \quad {\text{where}}\,x\,{\text{is}}\,{\text{a}}\,{\text{sample}}\,{\text{data}} $$
(3)
$$ {\text{Quadratic}}: K(x_{i} ,x_{j} ) = \left( {\left\langle {\gamma x_{i} ,\left. {x_{j} } \right\rangle + r} \right.} \right)^{d} \quad {\text{where }}\gamma \, > \,0 $$
(4)
$$ {\text{Radial}}\,{\text{Basis}}: K(x_{i} ,x_{j} ) = e^{{ - \gamma \left| {x_{i} - \left. {x_{j} } \right|^{2} } \right.}} \quad {\text{where}}\,\gamma \, > \,0 $$
(5)

where γ, r, and d are kernel parameters. There is no theory about deciding which kernel is the best, so in our system, we tried using the three mentioned kernel functions.

Fig. 6
figure 6

Different hyperplanes with H2 is seen to be the best

Full size image

4.2 Scheme II (supervised learning model)

Convolutional neural network (CNN) for deep learning classification is used. It is a successful tool for deep learning classification [47, 48] and developed to suit image recognition as it is a multilayer neural network, which consists of single or more convolution layers followed by one or more fully connected layers. Our convolutional neural network architecture is consisting of a convolution layer, max pooling layer, fully connected layer, and softmax layer as shown in Fig. 7.

Fig. 7
figure 7

The convolutional neural network DCNN architecture

Full size image

In the input image layer, we specify the input image size as 512 × 512 and the channel size is 1. The filter size in the convolution layer is (5,5) and number of filters are 20. The max pooling layer returns the maximum values of rectangular regions of inputs, in our study the size of the rectangular region is (2,2). The fully connected layer combines all of the features (local information) that were learned by all previous layers across the image to classify these images. As the output parameter in this layer is equal to the number of classes in the target data, the output size will be 2 classes (solitary and juxtapleural nodules).

4.3 Performance measures

The classification binary test may have an error if the classifier misses to distinguish the abnormality or distinguish an abnormality that is not present. This error can be characterized by True Positive (TP), False Positive (FP), True Negative (TN), and False Negative (FN) [49]. Where A true positive is an outcome where the model correctly predicts the positive class. Similarly, a true negative is an outcome where the model correctly predicts the negative class. A false positive is an outcome where the model incorrectly predicts the positive class. And a false negative is an outcome where the model incorrectly predicts the negative class.

According to these four terms sensitivity (recall), specificity, accuracy, and precision or positive predictive value (PPV) the classifier performance is evaluated as shown in Eqs. (6), (7), (8), and (9), respectively.

$$ {\text{Sensitivity}}\left( {{\text{recall}}} \right) = {\text{TP}}/\left( {{\text{TP}} + {\text{FN}}} \right) \, *100 \, \% $$
(6)
$$ {\text{Specificity}} = {\text{TN}}/\left( {{\text{TN}} + {\text{FP}}} \right)*100 \, \% $$
(7)
$$ {\text{Accuracy}} = \left( {{\text{TP}} + {\text{TN}}} \right)/\left( {{\text{TP}} + {\text{TN}} + {\text{FP}} + {\text{FN}}} \right)*100 \, \% $$
(8)
$$ {\text{PPV}} = {\text{TP / }}\left( {{\text{TP}} + {\text{FP}}} \right) $$
(9)

Receiver operating characteristics (ROC) curve is used to evaluate the ANN classifier [50] as it is a two-dimensional graph in which the y-axis represents the TPR and the x-axis represents the FPR. The Area under the ROC curve (AUC) metric is used to estimate the area under this curve. The score of AUC is always confined between zero and one, and there is no factual classifier that has an AUC lower than 0.5.

5 Results and discussions

In this section, the best sensitivity, specificity, and accuracy of our learning schemes are presented in Table 2 after applying CV and ROS. Table 2 shows the results of the SVM classifier of the scheme I with feature set (combination between 1st and 2nd order features) and the result of DCNN classifier of the scheme II which are combined in the two approaches of segmentation (MIP + Bounding box and Thresholding + K-means clustering).

Regarding approach, I of segmentation (Bounding box + Maximum Intensity Projection) our proposed CAD system before applying the CV and ROS achieved classification for:

  1. a.

    The solitary nodules:

SVM classifier achieved 80%, 89%, and 71% as an acc., sen., and spec., respectively, when using the radial basis function and extracting the best 5 features of the 1st set, Table 1.

  1. b.

    The juxtapleural nodules:

Table 1 The results of the supervised schemes for detection of solitary and juxtapleural nodules
Full size table

SVM classifier achieved 82.7%, 88%, and 79% as an acc., sen., and spec., respectively, when using quadratic function and extracting the best 15 features of the 1st set, Table 1.

DCNN results are overfitted before applying CV and ROS.

Regarding approach, II of segmentation (Thresholding + Kmeans clustering) the proposed CAD system before applying the CV and ROS achieved classification for:

  1. c.

    The solitary nodules:

SVM classifier achieved 81.2%, 83%, and 79.8% as an acc., sen., and spec., respectively, when using a quadratic function with the best 10 features of the 3rd set, Table 1.

  1. d.

    The juxtapleural nodules:

SVM classifier achieved 73.9%, 80%, and 67.8% as an acc., sen., and spec., respectively, when using the RBF function with the best 5 features of the 3rd set, Table 1.

Regarding approach, I of segmentation (Bounding box + Maximum Intensity Projection) our proposed CAD system after applying the CV and ROS achieved classification for:

  1. e.

    The solitary nodules:

SVM classifier achieved 87.7%, 95.4%, and 94.4% as an acc., sen., and spec., respectively, when using radial basis function and extracting the best 15 features of the 3rd set, Table 2.

Table 2 The final results of the supervised schemes for detection of solitary and juxtapleural nodules after applying the CV and ROS
Full size table

DCNN achieved the highest accuracy, sensitivity, and specificity 96 %, 95 %, and 97 %, respectively, to detect the solitary nodule, Table 2.

  1. f.

    The juxtapleural nodules:

SVM classifier achieved 83.9%, 85.2%, and 82.6% as an acc., Sen., and spec., respectively, when using the radial basis function with the best 10 features of the 2nd set, Table 2.

DCNN achieved accuracy, sensitivity, and specificity of 84%, 78%, and 90%, respectively, Table 2.

Regarding approach, II of segmentation (Thresholding+ Kmeans clustering) the proposed CAD system after applying the CV and ROS achieved classification for:

  1. g.

    The solitary nodules:

SVM classifier achieved 91.4%, 89.3%, and 94.6% as accuracy, sensitivity, and specificity, respectively, when using RBF function with the best 15 features of the 3rd set, Table 2.

DCNN achieved the highest accuracy, sensitivity, and specificity 85 %, 90 %, and 80 %, respectively, to detect the solitary nodule, Table 2.

  1. h.

    The juxtapleural nodules:

SVM classifier achieved 90.6%, 83.3%, and 98.4% as an acc., Sen., and spec., respectively, when using the RBF function with the best 15 features of the 1st set, Table 2.

DCNN achieves accuracy, sensitivity, and specificity of 60%, 70%, and 80%, respectively, Table 2.

The highest Area Under the Curve (AUC) of the receiver operating characteristic (ROC) curve for the CNN classifier is 90.3%, which is shown in Fig. 7b.

The results of sensitivity, specificity, and accuracy of the Scheme I (SVM) and scheme II (DCNN) are shown in the results section; Tables 1 and 2 for distinguishing between solitary and juxtapleural nodules. At first, the performance measures of the classifiers are estimated as follows (Table 1).

For the SVM, it achieved 82.6%, 87.9%, and 78.9% as accuracy, sensitivity, and specificity, respectively, to classify the juxtapleural nodules when applying approach I of segmentation (Bounding Box + Maximum intensity projection) before applying the CV and ROS.

There were some challenges, but we tackled with it to improve the overall classification performance by upgrading the overall performance measures as shown in Table 2 and also increasing the area under the curve of ROC curves.

At first, the proposed system is applied to a total number of abnormal images which is 172 images containing (100 solitary nodules and 72 juxtapleural nodules) and a total number of normal images which is 232 images. For the training phase (86 abnormal (50 solitary + 36 juxtapleural) images, 116 normal images) and for the testing phase, the same number is used (50–50). This number of images achieved results which are shown in Table 1. To enhance these results by increasing the images number, tenfold cross-validation is used. The total number is divided by 10. For example, the abnormal images are 172/10 ≈ 17 (for testing) and 172–17 ≈ 155 (for training), and then this step is repeated 10 times. Therefore, the abnormal images increases to 1550 images for the training phase and 170 for testing (the total number of abnormal images became (1550 + 170 = 1720)).

Also, tenfold cross-validation was applied to the normal images in the same manner. It increases to 2320 images for the training phase and testing phase, so the limited data sample becomes 1720 abnormal images and 2320 normal images.

At first, for the DCNN only 20, 30, and 40 images for training and the same for testing to decrease the time of computation as it consumes averaging time of 5 min only, but the results are overfitted, so tenfold CV was applied to increase the number of images to 2320 normal images and 1720 abnormal images as mentioned previously. Hence, the computation time increases to around 20 min based on our hardware and software specifications. DCNN achieves good results of accuracy, sensitivity, and specificity 96%, 95%, and 97%, respectively, when classifying solitary nodules, so it does not need an additional samples of training data as the results of CNN model fulfilled the requirements. Most models that use imageNet trained for five to six days such as network which is called AlexNet which has 15 million training images [39].

There is another challenge we tackled with, the imbalanced data, it reduced the overall classification performance as the normal and abnormal images are not equal and hence the images of training and testing phases are not equal. After applying CV, the normal images became 2320 and the abnormal images became 1720 which are not equal. After applying ROS the abnormal images (minority class) increased to 2320 (the same number as the majority class). Therefore, the total number of images increased from 404 (172 + 232) images to 4640 (2320 + 2320) images, so the classifiers provide optimum results as shown in Table 2 and the ROC curve result will be near the best.

  • Before applying CV and ROS: Table 1

SVM classifier achieved 82.7%, 88%, 79%, and 74.5% as the highest accuracy, sensitivity (recall), specificity, and PPV, respectively, in the diagnosis of juxtapleural nodule when using BB + MIP segmentation. This result is achieved with FP = 50, TN = 188, TP = 146, and FN = 20.

Also, the SVM classifier achieved 81.2%, 83%, 79.8%, and 76% as the highest accuracy, sensitivity (recall), specificity, and PPV, respectively, in the diagnosis of solitary nodule when using k-means clustering segmentation. This result is achieved with FP = 46, TN = 182, TP = 146, and FN = 30.

DCNN results are overfitted before applying CV and ROS. The AUC of the ROC curve was 88.9% as shown in Fig. 8a.

  • After applying CV and ROS: Table 2

Fig. 8
figure 8

The receiver operating characteristic (ROC) curves of DCNN a before applying CV and ROS (AUC = 88.9%), b after applying CV and ROS (AUC = 90.3%)

Full size image

SVM classifier achieved 90.6%, 83.3%, 98.4%, and 98.3% as the highest accuracy, sensitivity, specificity, and PPV, respectively, in the diagnosis of juxtapleural nodule when using k-means clustering segmentation. This result is achieved with FP = 35, TN = 2200, TP = 2005, and FN = 400.

Also, the SVM classifier achieved 91.4%, 89.3%, 94.6%, and 96.2% as the highest accuracy, sensitivity, specificity, and PPV, respectively, in the diagnosis of solitary nodule when using k-means clustering segmentation. This result is achieved with FP = 100, TN = 1740, TP = 2500, and FN = 300.

The DCNN achieved 96%, 95%, and 97% as accuracy, sensitivity, and specificity, respectively, in the diagnosis of the solitary nodule. The AUC of the ROC curve was increased to 90.3% as shown in Fig. 8b.

Based on literature research shown in Table 3, sensitivity, accuracy, nodule type, classifier and database are observed. The systems compared to our system are Supriya et al. [51], Noor et al. [52], Patrice et al. [53], and Mizuho et al. [54]. The first used a CNN classifier with 5188 images which achieved accuracy and sensitivity of 93.9% and 93.4%, respectively. The second used an SVM classifier using 350 images from the LIDC dataset. She achieved an accuracy of 87.67% and a sensitivity of 86.21%. However, validation of the systems was not tested with all nodule types; it showed promising results. The third tested his method with 2635 nodules and achieved 88.28% accuracy and a sensitivity of 83.82% when using Deep Convolutional Neural Network (DCNN) for nodule detection knowing that the nodule type was not informed. The fourth used CNN classifier with 665 nodules and obtained an accuracy of 68%. The presented system showed the best result when using DCNN achieving 96% accuracy for detection of solitary nodules when using CNN for deep learning classification with a sensitivity of 95% when compared to Supriya et al. [51]. We registered the highest results with SVM compared to Noor et al. [52] with accuracy and sensitivity of 91.4% and 89.3%, respectively.

Table 3 Comparing the proposed system with published studies
Full size table

6 Conclusions

In this research, a Computer Aided Diagnosis (CADx) system of candidate lung nodules either solitary or juxtapleural nodules is proposed regarding its location. This CAD system acts as a second opinion for the radiologist to help in the early diagnosis of lung cancer. A database consisting of 14 digital CT consisting of 2991 2D slices containing 172 nodules with equivalent diameters of lung nodules (solitary and juxtapleural) ranging from 3 to 30 mm is used. For classification, SVM is used in scheme I, and Convolutional Neural Network is used in scheme II. A Segmentation and enhancement approaches (bounding box + MIP) and (Thresholding + K-means clustering) are proposed. A combination of two sets of features is extracted. Fisher score ranking is used as a feature selection method. Selected features are input to SVM classifiers in the scheme I. K-fold cross-validation is used as a resampling procedure by which our supervised learning algorithm has higher average accuracy, we used k = 10. Random oversampling provides a balanced distribution by increasing the number of examples of the two classes through the random replication of examples of this class therefore the overall classification performance is improved.

As it is known to all, deep learning architectures require a large amount of training data. Besides, most deep learning techniques, for example, CNN-based methods, require labeled data for supervised learning, which is difficult and time-consuming clinically. How to take the best advantage of limited data for training and how to train deeper networks effectively remains to be addressed. As the dataset was quite small, the DCNN classifier is overfitted. To tackle the overfitting problem we increased the number of images from 404 to 4640 images. Therefore, the processing time of the DCNN model is considered a limitation as it increased from 5 to around 20 min based on our hardware and software specifications. In the second phase of our CAD system, we intend to use a bigger dataset to generalize the proposed techniques. We demonstrated that our algorithm outperforms the previous state-of-the-art techniques in terms of segmentation (bounding box + MIP) and (thresholding + K-means clustering). The segmentation techniques are significantly robust for the two nodule types (solitary and juxtapleural), respectively. The results suggest that MIP can be used as a 2D segmentation technique achieving good results although it is generally in many researches used in a 3D volume rendering. Suggesting the suitability of our CAD system to minimize the radiologist’s effort through the early diagnosis of the lung nodules. Also, it can achieve diagnostic and therapeutic quality assurance. Although the model showed some promising results in the early diagnosis of lung cancer, the Juxtavascular nodule can be considered in the future, which would require a modification of the current segmentation algorithm. Also, the processor family of the hardware can be upgraded so that the computation time of the DCNN classifier will decrease and we can use a large database. Lung cancer diagnosis either benign or malignant according to its equivalent diameter can be done which requires a database with malignant and benign nodules.