1 Introduction

Since many real-time implementations of nonlinear systems involve nonlinearity, nonlinear systems play an important role in engineering research that are defined as systems whose manner is not proportional to their inputs [1]. These systems suffer inherent uncertainty, time-varying parameters and nonlinear dynamic behavioral. In this concern, non-optimal control suffers from some limitations due to the assumptions made for the control system such as linearity and time-invariance. Therefore, the non-optimal control methods are not suitable for controlling nonlinear systems in practical applications [2, 3]. These problems can be overcome by optimal control techniques. Artificial intelligence (AI)-based controllers are one of these techniques, which have many advantages, such as [4, 5]: (1) it can lead to better performance when properly tuned. (2) It requires less tuning effort than non-optimal controllers. (3) It can be designed based on data from the real system or plant if an expert knowledge is not available. (4) It can be designed using a combination of linguistic and response-based information. [6,7,8,9]. The neural networks (NNs) are considered as one of AI, which are a series of algorithms to recognize underlying relationships in a set of data through a process, which like the operation of human brain [10].

In this concern, there are various structures of NNs such as recurrent neural networks (RNNs) [11,12,13,14] and multilayer feed-forward neural networks (MLFFNNs) [15, 16]. MLFFNN is called static network, where there are not tapped delay lines. Several MLFFNN models from observational data were created for predicting the groundwater levels [17]. The NN controller was designed as a direct adaptive inverse control based on MLFFNN to control and estimate the model of nonlinear plants [18]. In [19], the researchers designed MLFFNN for classification of nonlinear mappings based on input and output samples.

However, there are tapped delay lines in RNN, and this is called a dynamic network. The RNN is more robust than MLFFNN because it contains the MLFNN framework with tapped delay lines [20]. Various RNN structures exist in this regard, including Elman NNs; the feedback connections from the output to the input of the hidden layer are performed via a context layer. Another RNN is Jordan NNs; the feedback connections from the output to the input layer are performed via a state layer. [21,22,23]. Recently, the fully connected RNN (FCRNN) was modified to provide a diagonal RNN (DRNN). In the hidden layer, the DRNN contains self-recurrent neurons that feed only their output back into themselves, not to other neurons in the same layer. [24,25,26]. In [27], in order to achieve high performance of the shunt active power filter, researchers designed a controller based on RNN. A self-organizing RNN for the nonlinear model predictive controller was designed to foresee the nonlinear systems behavior [28]. In [29], a flexible manipulator was designed with a DRNN controller to limit backward vibration, which is performed based on a shaking control signal generator and an online identification system. The DRNN was introduced as a controller and an observer for estimating the anonymous dynamics of the nonlinear system [30]. DRNN was developed to determine the optimal parameters of the PID controller for controlling induction motors [31]. In [32], based on the control inputs and current quadrotor states, researchers developed the PID controller using virtual sensing based on DRNNs and Kalman filters to predict the immeasurable cases of the quadrotor system.

Machine learning (ML) is one of the applications of AI that can automatically learn from experience without explicit programming. ML focuses on the development of programs that can access data and use it to learn them [33]. In this significance, the deep learning (DL) is a part of a wider family of ML based on ANN's that learn representations either supervised, unsupervised, or semi-supervised [34]. In this concern, there are various applications of DL exist as follows: (1) In automation systems, an approach for detecting and assessing food waste trays based on hierarchical DL algorithm was presented [35], (2) in medicine field, a DL algorithm was used to classify and predict mutations from non-small cell lung cancer histopathology images [36], (3) in agriculture field, a DL algorithm was introduced to locate paddy fields at the pixel level for a whole year long and for each temporal instance based on real imagery datasets of different landscapes from 2016 to 2018 [37], and (4) in recognition, a DL algorithm was used for real-time modeling of the human activity recognition with smartphones [38]. According to definitions [39, 40], the DL of NN's includes two steps: firstly is the unsupervised training and secondly is using the weights from the unsupervised training for initializing the multilayer NNs. This is considered as the main advantage of DL because the initializing weights process is very critical issue.

1.1 Literature review

In [41], the parameters of the classical PID controller were tuned based on DL for controlling maglev train, which is a new type of the ground transports. The deep NNs (DNN) were introduced for dynamical systems modeling based on complex manner [42]. Three DNN structures are trained on successive data for studying validation of these networks in modeling of dynamical systems. In [43], DL was designed for analyzing the performance of a nonlinear continuous stirred tank reactor, which trained its weights tuned by hybrid algorithm. The DL was introduced as a hybrid algorithm with the fuzzy system for tuning the parameters of the PID controller [44], which was used for controlling the speed of brushless DC motor. In [45], DL controller was introduced, which is performed based on the MLFFNN and the RBM. It is used for initializing the weights values of a network for the nonlinear systems. In [46], DL was introduced for modeling the nonlinear systems based on Elman RNN and restricted Boltzmann machine (ERNN-RBM), which is considered as an unsupervised method for initializing only the first layer.

1.2 Motivation

It is evident from the literature review that DL applications are widely used for modeling systems and it does not cover the control research. Since nonlinear systems suffer from external disturbances and uncertainties, the main purpose of the present paper is to shed further light on the design of stable controllers for overcoming nonlinear system problems. In this concern, self-organizing map (SOM) is an unsupervised learning algorithm trained using dimensionality reduction (typically two-dimensional), discretized representation of input space of the training samples, and called a map. It differs from other ANN as it depends on the competitive learning and not the error-correction learning (like backpropagation with gradient descent). It uses a neighborhood function to preserve the topological properties of the input space to reduce data by creating a spatially organized representation, and also, it helps to discover the correlation between data [47,48,49,50]. On the other hand, the RBM is an unsupervised learning algorithm that makes inferences from input data without labeled responses. The controllers and models based on NNs are always stuck with the initialized weights. If the initialized weights are not appropriate, the network gets stuck in local minima and leads the training process to a wrong ending and the network becomes infeasible to train therefore. Therefore, RBM is used to overcome this problem [46, 51]. Hence, a merge utilizing the features of SOM and RBM is proposed to improve the learning performance of the proposed network. To control the nonlinear systems, the hybrid deep learning DRNN controller (HDL-DRNNC) based on SOM and RBM is proposed. Initial weights for the DRNN are obtained using a hybrid deep learning (HDL) procedure, which is regarded as an unsupervised learning procedure. The HDL is performed based on RBM and self-organizing map (SOM) of the Kohonen procedure.

To ensure the stability of the adaptation parameters laws, the Lyapunov procedure is applied. The proposed HDL-DRNNC is trained quickly for keeping the trajectory and overcoming the system parameters variations and external disturbances. As shown in the simulation results, these features of the proposed HDL-DRNNC make it more robust than those of other controllers under the same conditions.

1.3 Novelties and contributions

The main contributions of the paper are summarized as:

  • A new HDL for DRNN controller is proposed for nonlinear systems.

  • Developing the updating weights law for the DRNN of the proposed algorithm using Lyapunov theory to achieve stability.

  • Compared to other existing controllers, the HDL-DRNNC can handle problems of system uncertainties in both a mathematical system and a physical system.

The organization of the paper is as follows: the DRNN structure is exhibited in Sect. 2. The proposed HDL-DRNNC is introduced in Sect. 3. The weights updating based on Lyapunov stability criterion is introduced in Sect. 4. The HDL-DRNNC pseudocode is explained in Sect. 5. The simulation results for the mathematical and physical nonlinear systems are introduced in Sect. 6. At final, Sect. 7 exhibits the conclusion, which followed by the references.

2 Diagonal recurrent neural network structure

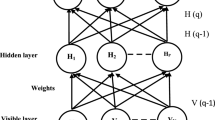
As shown in Fig. 1, the structure of DRNN consists of four layers, namely two hidden layers, an input layer, and an output layer.

Fig. 1
figure 1

Structure of DRNN

Full size image

Input layer: the external input vector is represented by \({\varvec{E}}\left( \kappa \right) = \left[ {\begin{array}{*{20}c} {e_{x1} \left( \kappa \right)} & \cdots & {e_{xn} \left( \kappa \right)} \\ \end{array} } \right]^{T}\) and \(\Re^{\left( 1 \right)} \left( \kappa \right)\) is the input weight matrix, which links the input vector to the hidden layer (1) neurons and it is represented as:

$$ \Re^{{( 1)}} \left( \kappa \right) = \left[ {\begin{array}{*{20}c} {\Re_{11}^{{^{{( 1)}} }} \left( \kappa \right)} & \cdots & {\Re_{1n}^{{^{{( 1)}} }} \left( \kappa \right)} \\ \vdots & \ddots & \vdots \\ {\Re_{J1}^{{^{{( 1)}} }} \left( \kappa \right)} & \cdots & {\Re_{Jn}^{{^{{( 1)}} }} \left( \kappa \right)} \\ \end{array} } \right] $$
(1)

Generally, \(\Re_{Jn}^{\left( 1 \right)} \left( \kappa \right)\) denote the input weight between input neuron \(n\) and the hidden layer (1) neuron \(J\).

Hidden layer (1): the output of each node is denoted by \(\chi_{j}^{(1)} \left( \kappa \right)\), which is specified as:

$$ \begin{aligned} \Lambda _{j}^{{(1)}} \left( \kappa \right) = & \chi _{j}^{{(1)}} \left( {\kappa - 1} \right)\Re _{j}^{{D1}} \left( \kappa \right) + \sum\limits_{{i = 1}}^{n} {\Re _{{ji}}^{{(1)}} \left( \kappa \right)e_{{xi}} \left( \kappa \right)} \\ & + T_{j} \left( \kappa \right),\;\;j = 1, \ldots ,J \\ \end{aligned} $$
(2)
$$ \chi_{j}^{(1)} \left( \kappa \right) = f\left( {\Lambda_{j}^{(1)} \left( \kappa \right)} \right),\,\,\,\,\,\,\,j = 1,\, \ldots ,\,J $$
(3)

where \(\Re^{D1} \left( \kappa \right) = \left[ {\begin{array}{*{20}c} {\Re_{1}^{D1} \left( \kappa \right)} & \cdots & {\Re_{J}^{D1} \left( \kappa \right)} \\ \end{array} } \right]^{T}\) denotes the diagonal weight vector at the hidden layer (1), \(J\) is the nodes number, \(T_{j} \left( \kappa \right)\) denotes the threshold value for every node, and \(f\left( {} \right)\) denotes hyperbolic tangent function, which is defined as:

$$ f\left( \upsilon \right) = \tanh \left( \upsilon \right) $$
(4)

and its derivative can be defined by \(f^{\prime}\left( \upsilon \right) = 1 - f^{2} \left( \upsilon \right)\).

Hidden layer (2): the output of each node is denoted by \(\chi_{m}^{(2)} \left( \kappa \right)\), which is specified as:

$$ \Lambda_{m}^{(2)} \left( \kappa \right) = \,\chi_{m}^{(2)} \left( {\kappa - 1} \right)\,\Re_{m}^{D2} \left( \kappa \right)\, + \sum\limits_{j = 1}^{J} {\Re_{mj}^{{^{{( 2)}} }} \left( \kappa \right)\,\chi_{j}^{(1)} \left( \kappa \right)} + T_{m} \left( \kappa \right)\,,\,\,\,\,\,\,m = 1,\,..,\,M $$
(5)
$$ \chi_{m}^{(2)} \left( \kappa \right) = f\left( {\Lambda_{m}^{(2)} \left( \kappa \right)} \right),\,\,\,\,\,\,\,m = 1,\,..,\,M $$
(6)

where \(\Re_{{}}^{D2} \left( \kappa \right) = \left[ {\begin{array}{*{20}c} {\Re_{1}^{D2} \left( \kappa \right)} & \cdots & {\Re_{M}^{D2} \left( \kappa \right)} \\ \end{array} } \right]^{T}\) denotes the diagonal weight vector at the hidden layer (2), \(M\) denotes the nodes number, \(T_{m} \left( \kappa \right)\) denotes the threshold value for each node and \(\Re^{{^{{( 2)}} }} \left( \kappa \right)\) denotes the weights matrix between the hidden layer (1) and the hidden layer (2), which is defined as:

$$ \Re^{{^{{( 2)}} }} \left( \kappa \right) = \left[ {\begin{array}{*{20}c} {\Re_{11}^{{^{{( 2)}} }} \left( \kappa \right)} & \cdots & {\Re_{1J}^{{^{{( 2)}} }} \left( \kappa \right)} \\ \vdots & \ddots & \vdots \\ {\Re_{M1}^{{^{{( 2)}} }} \left( \kappa \right)} & \cdots & {\Re_{MJ}^{{^{{( 2)}} }} \left( \kappa \right)} \\ \end{array} } \right] $$
(7)

Generally, \(\Re_{MJ}^{\left( 2 \right)} \left( \kappa \right)\) denote the weight between the hidden layer (1) neuron \(J\) and the hidden layer (2) neuron \(M\).

Output layer: its output is denoted by \(u\left( \kappa \right)\), which is calculated as:

$$ u\left( \kappa \right) = \sum\limits_{m = 1}^{M} {\Re_{m}^{{^{{( 3)}} }} \left( \kappa \right)\,\chi_{m}^{(2)} \left( \kappa \right) + T} \left( \kappa \right) $$
(8)

where \(T\left( \kappa \right)\) denotes the threshold value and \(\Re^{{^{{( 3)}} }} \left( \kappa \right) = \left[ {\begin{array}{*{20}c} {\Re_{1}^{{^{{( 3)}} }} \left( \kappa \right)} & \cdots & {\Re_{M}^{{^{{( 3)}} }} \left( \kappa \right)} \\ \end{array} } \right]^{T}\) denotes the weight vector between the hidden layer (2) and the output layer.

3 Hybrid deep learning diagonal recurrent neural network controller

The initializing weights process for DRNN controllers is very critical issue. Where, if this process is zero or not suitable, then the DRNN will stumble in local minimum and it will lead to wrong network termination as learning due to the initial layers learning of a network will become impossible [46]. This issue may be leading the controller to become unstable. For this reason, DL is proposed. In this regard, any NN with more than one hidden layer is referred to as a deep network, which can be learned by DL. The proposed HDL-DRNNC consists of DRNN that can be trained by DL. The DL algorithm based on SOM and RBM is considered as an unsupervised learning for initializing the weights values of the DRNN. DRNN's two hidden layers, which are described in the previous section, are trained using SOM algorithm. On the other hand, the RBM algorithm is used for training the DRNN output layer. The proposed HDL-DRNNC structure is shown in Fig. 2.

Fig. 2
figure 2

Structure of HDL-DRNNC

Full size image

3.1 SOM of the Kohonen learning procedure

The initializing weights values for the hidden layers of the DRNN, which is introduced in Sect. 2, are the main purpose of this section. The NN, which is used to initialize the weights of the hidden layers of the DRNN, is shown in Fig. 3. The weights of the NN are trained based on SOM of the Kohonen process [52]. The training is performed based on the hypothesis that one of the layer neurons responds most to the input, which is called the winner neuron.

Fig. 3
figure 3

NN based on SOMK unsupervised learning

Full size image

For training the hidden layer (1) of the DRNN, the number of neurons in the input layer of the NN (Fig. 3), which is used to initialize the weights of the hidden layers, is equal to the number of input neurons of the hidden layer (1) of the DRNN where their values are \(I_{f} \left( \kappa \right) = e_{xi} \left( \kappa \right)\); \(\left( {f = i = 1,..,n} \right)\). \(\,f\,\) denotes the number of neurons in the input layer of the NN (Fig. 3) and \(\,i\) denotes the number of the input neurons of the hidden layer (1) of the DRNN. The number of neurons in the output layer of the NN (Fig. 3) is equal to the number of output neurons of the hidden layer (1) of the DRNN and the weights number for the hidden layer (1) of the DRNN are equal to the weights number for the NN. After the training of NN is completed, the values of the hidden layer (1) weights of the DRNN \(\Re_{ji}^{{^{{( 1)}} }} \left( \kappa \right)\) will be equal to the values of NN weights, \(\varpi_{lf}^{(1)} \left( \kappa \right)\); \(\left( {\,l = j = 1,...,J} \right)\).

For training the hidden layer (2) of the DRNN, the number of neurons in the input layer of NN (Fig. 3) are equal to the number of input neurons of the hidden layer (2) of the DRNN where their values are \(I_{f} \left( \kappa \right) = \chi_{j}^{(1)} \left( \kappa \right)\); \(\left( {f = j = 1,...,J} \right)\). The number of the input neurons of the hidden layer (2) are denoted by \(\,j\), where \(\,f\,\) is defined previously. The number of neurons in the output layer of the NN (Fig. 3) is equal to the number of output neurons of the hidden layer (2) of the DRNN and the number of weights for the hidden layer (2) of the DRNN are equal to the number of weights for the NN. After the training of NN is completed, the values of the hidden layer (2) weights of the DRNN \(\Re_{mj}^{{^{{( 2)}} }} \left( \kappa \right)\) will be equal to the values of NN weights, \(\varpi_{lf}^{(2)} \left( \kappa \right)\); \(\left( {\,l = m = 1,...,M} \right)\).

The SOM of the Kohonen (SOMK) procedure is summarized as:

  • Step 1: All the weights \(\varpi_{{_{lf} }}^{(Q)}\); \(Q = 1\,,\,\,2\) of the NN, which is shown in Fig. 3, are initialized at zero values.

  • Step 2: Enter the values of \({\varvec{E}}\left( \kappa \right)\) to the NN.

  • Step 3: The winner neuron \(\omega\) is selected using the Euclidean distance between the input and the neuron weights \(\varpi_{{_{\omega } }}^{(Q)}\) as:

    $$ \left\| {e_{x} - \varpi_{\omega }^{(Q)} } \right\| = \mathop {\min }\limits_{l} \left\| {e_{x} - \varpi_{\omega }^{(Q)} } \right\| $$
    (9)

    where \(Q\), \(l\) and \(\omega\) are the number of the NN layer, the index of any neuron and the index of the winner neuron, respectively.

  • Step 4: Calculate the Gaussian neighborhood function as:

    $$ \rho_{\omega l}^{\left( Q \right)} \left( \kappa \right) = \ell \exp \left( { - \frac{{(\omega - l)^{2} }}{2\zeta }} \right),\,\,0\, < \rho_{\omega l}^{\left( Q \right)} \left( \kappa \right) \le 1 $$
    (10)

    where \(\ell\) and \(\zeta\) are constants.

  • Step 5: The updating law of the weights of the NN \(\varpi_{lf}^{(Q)} (\kappa )\), where \(Q = 1\), is obtained as:

    $$ \Delta \varpi_{lf}^{(1)} (\kappa ) = \,\rho_{\omega l}^{{^{(1)} }} \left( \kappa \right)(e_{x} (\kappa ) - \varpi_{lf}^{(1)} (\kappa )) $$
    (11)
    $$ \varpi_{lf}^{(1)} (\kappa + 1) = \varpi_{lf}^{(1)} (\kappa )\, + \,\Delta \varpi_{lf}^{(1)} (\kappa ),\,\,\,\,\left( {\,l = j = 1,...,J} \right)\;{\text{and}}\;\left( {f = i = 1,...,n} \right) $$
    (12)

    The updating law of the weights of the NN \(\varpi_{\lg }^{(Q)} (\kappa )\), where \(Q = 2\), is obtained as:

    $$ \begin{aligned} \varpi_{lf}^{(2)} (\kappa + 1) = & \varpi_{lf}^{(2)} (\kappa )\, + \,\rho_{\omega l}^{{^{(2)} }} \left( \kappa \right)(e_{x} (\kappa ) - \varpi_{lf}^{(2)} (\kappa )), \\ \left( {l = m = 1,...,M} \right)\;{\text{and}}\;\left( {f = j = 1,...,J} \right) \\ \end{aligned} $$
    (13)

3.2 Restricted Boltzmann machine

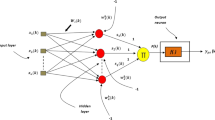
Initializing the weights values for the output layer of the DRNN is performed based on RBM [45, 53]. The RBM that is used in this section is illustrated in Fig. 4. Where all the weights of the output layer are equal to zero, RBM contains two main layers: firstly, the visible layer, which contains a visible nodes group \(S\) and secondly, the hidden layers, which contains a hidden nodes group \(D\) [46, 54].

Fig. 4
figure 4

Structure of RBM

Full size image

For training the DRNN output layer, the number of neurons in the input layer of the RBM is equal to the number of input neurons of the output layer of the DRNN where their values are \(S_{i} \left( \kappa \right) = \chi_{m}^{(2)} \left( \kappa \right)\); \(\left( {i = m = 1,..,M} \right)\). The number of neurons in the output layer of the RBM is equal to the number of neurons in the output layer of the DRNN and the weights number of the output layer of the DRNN equals to the weights number of the RBM. After the training of RBM is completed, the values of the output layer weights of the DRNN \(\Re_{m}^{\left( 3 \right)} \left( \kappa \right)\) will be equal to the RBM weights values, \(X_{ji} \left( \kappa \right)\); \(\left( {\,j = 1,...,P} \right)\) and \(\left( {\,i = m = 1,..,M} \right)\). In this paper, \(P = 1\).

Based on the approach in [53, 55], Hinton introduced contrastive divergence (CD) for training RBM. The RBM input is \(S(r - 1)\), which shifts to the visible layer at time \((r - 1)\). Then, the hidden layer output is obtained as:

$$ D_{j} \left( {r - 1} \right) = F\left( {\sum\limits_{i}^{N} {X_{ji} } S_{i} \left( {r - 1} \right) + B_{j} \,} \right)\,,\,\,\,\,r = 1,.....,\Re ,\,\,j = 1,\,..,\,P\,\,{\text{and}}\,\,i = 1,\,\,..,\,N $$
(14)

where \(X_{ji}\) represents the weight between a visible node \(i\) and a hidden node \(j\) and \(S_{i}\) represents the binary state of the visible node. \(P\) and \(N\) are the hidden nodes number and the visible nodes number, respectively. \({\varvec{B}} = \left[ {\begin{array}{*{20}c} {B_{1} } & \cdots & {B_{P} } \\ \end{array} } \right]^{T}\) represents the hidden nodes biases and \(F\) denotes sigmoid activation function \(F\left( z \right) = {1 \mathord{\left/ {\vphantom {1 {\left( {1 + \exp \left( { - z} \right)} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1 + \exp \left( { - z} \right)} \right)}}\).

The inverse layer reconstructs the data from the hidden layer. As a result, \(S\left( r \right)\) is obtained at \(r\) as follows:

$$ S_{i} \left( r \right) = F\left( {Q_{i} \left( r \right)} \right) = F\left( {\sum\limits_{j = 1}^{P} {X_{ij} D_{j} \left( {r - 1} \right) + A_{i} } } \right) $$
(15)

where \(X_{ij}\) represents the weight between a hidden node \(j\) and a visible node \(i\), \(D_{j}\) represents the binary state of a hidden node and \({\varvec{A}} = \left[ {\begin{array}{*{20}c} {A_{1} } & \cdots & {A_{N} } \\ \end{array} } \right]^{T}\) represents the visible nodes biases. Subsequently, \(S\left( r \right)\) transfers to the visible layer and the hidden layer output is obtained as:

$$ D_{j} \left( r \right) = F\left( {Q_{j} \left( r \right)} \right) = F\left( {\sum\limits_{i = 1}^{N} {X_{ji} S_{i} \left( r \right) + B_{j} } } \right) $$
(16)

\(CD - \Re\) case: The parameters learning rules for the weights and biases of nonlinear RBM are clarified as [55]:

$$ \begin{gathered} X_{{ji}} \left( {\kappa + 1} \right) = X_{{ji}} \left( \kappa \right) + \varepsilon \hfill \\ \quad \left( \begin{gathered} \sum\limits_{{r = 1}}^{\Re } {\left( {D_{j} \left( r \right) - D_{j} \left( {r - 1} \right)} \right){\mkern 1mu} S_{i} \left( r \right){\mkern 1mu} F^{\prime } \left( {Q_{j} \left( r \right)} \right)} \hfill \\ \quad + \left( {S_{i} \left( r \right) - S_{i} \left( {r - 1} \right)} \right){\mkern 1mu} D_{j} (r - 1){\mkern 1mu} F^{\prime } \left( {Q_{i} \left( r \right)} \right) \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} $$
(17)
$$ B_{j} \left( {\kappa + 1} \right) = B_{j} \left( \kappa \right) + \varepsilon \left( {\sum\limits_{r = 1}^{\Re } {\left( {D_{j} \left( r \right) - D_{j} \left( {r - 1} \right)} \right)\,F^{\prime}\,\left( {Q_{j} \left( r \right)} \right)} } \right) $$
(18)
$$ A_{i} \left( {\kappa + 1} \right) = A_{i} \left( \kappa \right) + \varepsilon \left( {\sum\limits_{r = 1}^{\Re } {\left( {S_{i} \left( r \right) - S_{i} \left( {r - 1} \right)} \right)\,F^{\prime}\,\left( {Q_{i} \left( r \right)} \right)} } \right) $$
(19)

where \(\varepsilon\) is the RBM learning rate and \(\kappa\) is the iteration number. When the parameters of RBM are learned, hence the output layer of the DRNN can be initialized based on the weights of RBM \(X_{ji} \left( {\kappa + 1} \right)\).

4 Weights updating based on Lyapunov stability

The performance function is denoted by \(E_{l} \left( \kappa \right)\), which is defined as:

$$ E_{l} \left( \kappa \right) = \frac{1}{2}\left( {\Upsilon_{d} \left( \kappa \right) - \Upsilon_{a} \left( \kappa \right)} \right)^{2} = \frac{1}{2}e_{x}^{2} \left( \kappa \right) $$
(20)

where \(\Upsilon_{d} (\kappa )\) and \(\Upsilon_{a} (\kappa )\) denote the reference input and the actual output, respectively. The DRNN is trained to minimize the error signal [56].

To achieve stability, the updating weights of DRNN of the proposed HDL-DRNNC are developed using Lyapunov stability criteria. Two conditions must be met in order to the system to be asymptotically stable, as outlined in Eqs. (21 and 22)

$$ R_{x} \left( \kappa \right) > 0\;{\text{for}}\;{\text{all}}\;\kappa \;{\text{except}}\;\kappa = 0 $$
(21)
$$ \Delta R_{x} \left( \kappa \right) = R_{x} \left( {\kappa + 1} \right) - R_{x} (\kappa ) \le 0 $$
(22)

where \(R_{x} \left( \kappa \right)\) is a positive definite function. The updating weight equation can be expressed as a common form:

$$ \Phi_{l} \left( {\kappa + 1} \right) = \Phi_{l} (\kappa ) - \eta \Delta \Phi_{l} (\kappa ) $$
(23)

where \(\Phi_{l} \left( \kappa \right)\) and \(\Delta \Phi_{l} \left( \kappa \right)\) denote a generalized weight vector and its desired modification and the learning rate is denoted by \(\eta\).

Theorem 1

To achieve the stability of the controlled process, the updating equation for the DRNN weights of the proposed scheme is obtained as the following:

$$ \Phi_{l} \left( {\kappa + 1} \right) = \Phi_{l} \left( \kappa \right) + \eta \frac{{\beta \,\left( {\Phi_{l} \left( \kappa \right)\,\left( {1 + \frac{\sigma }{\beta }\,e_{x}^{2} \left( \kappa \right)} \right) + \frac{\sigma }{\beta }\,e_{x} \left( \kappa \right)\,\Phi_{l}^{2} \left( \kappa \right)\,\frac{{\partial e_{x} \left( \kappa \right)}}{{\partial \Phi_{l} \left( \kappa \right)}}} \right)}}{2\lambda } $$
(24)

where \(\beta \,,\,\sigma\) and \(\lambda\) are positive constants.

Proof

Suppose the next Lyapunov function:

$$ R_{x} \left( \kappa \right) = R_{a} \left( \kappa \right) + R_{b} (\kappa ) + R_{c} \left( \kappa \right) $$
(25)

where \(R_{a} \left( \kappa \right) = \frac{\sigma }{2}\left( {e_{x} \left( \kappa \right)\Phi_{l} \left( \kappa \right)} \right)^{2}\), \(R_{b} \left( \kappa \right) = \frac{\beta }{2}\left( {\Phi_{l} \left( \kappa \right)} \right)^{2}\), \(R_{c} \left( \kappa \right) = \frac{\lambda }{2}\left( {\Delta \Phi_{l} \left( \kappa \right)} \right)^{2}\), \(\Delta R_{a} \left( \kappa \right)\), \(\Delta R_{b} \left( \kappa \right)\) and \(\Delta R_{c} \left( \kappa \right)\) are defined as:

$$ \begin{aligned} \Delta R_{a} \left( \kappa \right) = & \, R_{a} \left( {\kappa + 1} \right) - R_{a} (\kappa ) \\ = & \, \frac{\sigma }{2}\left( {e_{x} \left( {\kappa + 1} \right)\Phi_{l} \left( {\kappa + 1} \right)} \right)^{2} - \frac{\sigma }{2}\left( {e_{x} \left( \kappa \right)\Phi_{l} \left( \kappa \right)} \right)^{2} \\ \end{aligned} $$
(26)
$$ \begin{aligned} \Delta R_{b} \left( \kappa \right) = & R_{b} \left( {\kappa + 1} \right) - R_{b} (\kappa ) \\ = & \frac{\beta }{2}\left( {\Phi_{l} \left( {\kappa + 1} \right)} \right)^{2} - \frac{\beta }{2}\left( {\Phi_{l} \left( \kappa \right)} \right)^{2} \\ \end{aligned} $$
(27)
$$ \begin{aligned} \Delta R_{c} \left( \kappa \right) = & \, R_{c} \left( {\kappa + 1} \right) - R_{c} (\kappa ) \\ = & \, \frac{\lambda }{2}\left( {\Delta \Phi_{l} \left( {\kappa + 1} \right)} \right)^{2} - \frac{\lambda }{2}\left( {\Delta \Phi_{l} \left( \kappa \right)} \right)^{2} \\ \end{aligned} $$
(28)

The term \(\frac{\sigma }{2}\left( {e_{x} \left( {\kappa + 1} \right)\Phi_{l} \left( {\kappa + 1} \right)} \right)^{2}\) can be defined based on Taylor series in the linear form as [24]:

$$ \begin{aligned} \frac{\sigma }{2}\left( {e_{x} \left( {\kappa + 1} \right)\Phi _{l} \left( {\kappa + 1} \right)} \right)^{2} = & \frac{\sigma }{2}\left( {e_{x} \left( \kappa \right)\Phi _{l} \left( \kappa \right)} \right)^{2} \\ & + \frac{{\partial \left( {\frac{\sigma }{2}\left( {e_{x} \left( \kappa \right)\Phi _{l} \left( \kappa \right)} \right)^{2} } \right)}}{{\partial \Phi _{l} \left( \kappa \right)}}\Delta \Phi _{l} \left( \kappa \right) \\ & + {\text{HOT}} \\ \end{aligned} $$
(29)

where HOT denotes to the higher order term, which can be ignored. Therefore, Eq. (29) can be rewritten as:

$$ \frac{\sigma }{2}\left( {e_{x} \left( {\kappa + 1} \right)\,\Phi_{l} \left( {\kappa + 1} \right)} \right)^{2} - \frac{\sigma }{2}\,\left( {e_{x} \left( \kappa \right)\,\Phi_{l} \left( \kappa \right)} \right)^{2} = \frac{\sigma }{2}\,\frac{{\partial \left( {\left( {e_{x} \left( \kappa \right)\,\Phi_{l} \left( \kappa \right)} \right)^{2} } \right)}}{{\partial \Phi_{l} \left( \kappa \right)}}\,\Delta \Phi_{l} \left( \kappa \right) $$
(30)

The right side of the previous equation is rewritten as follows:

$$ \begin{aligned} \frac{\sigma }{2}\frac{{\partial \left( {\left( {e_{x} \left( \kappa \right)\,\Phi_{l} \left( \kappa \right)} \right)^{2} } \right)}}{{\partial \Phi_{l} \left( \kappa \right)}}\Delta \Phi_{l} \left( \kappa \right) = & \sigma \,e_{x} \left( \kappa \right)\Phi_{l}^{2} \left( \kappa \right)\frac{{\partial e_{x} \left( \kappa \right)}}{{\partial \Phi_{l} \left( \kappa \right)}}\Delta \Phi_{l} \left( \kappa \right) \\ & + \sigma \,e_{x}^{2} \left( \kappa \right)\Phi_{l} \left( \kappa \right)\Delta \Phi_{l} \left( \kappa \right) \\ \end{aligned} $$
(31)

Similarity,

$$ e_{x} \left( {\kappa + 1} \right) = e_{x} \left( \kappa \right) + \frac{{\partial e_{x} \left( \kappa \right)}}{{\partial \Phi_{l} \left( \kappa \right)}}\Delta \Phi_{l} \left( \kappa \right) $$
(32)

Equation (32) can be rewritten as:

$$ e_{x} \left( {\kappa + 1} \right) - e_{x} \left( \kappa \right) = \Delta e_{x} \left( \kappa \right) = \frac{{\partial e_{x} \left( \kappa \right)}}{{\partial \Phi_{l} \left( \kappa \right)}}\Delta \Phi_{l} \left( \kappa \right) $$
(33)

Then, by replacing the term \(\frac{{\partial e_{x} \left( \kappa \right)}}{{\partial \Phi_{l} \left( \kappa \right)}}\Delta \Phi_{{}} \left( \kappa \right)\) in Eq. (31), we obtain the following:

$$ \begin{aligned} \Delta R_{a} \left( \kappa \right) = & \frac{\sigma }{2}\left( {e_{x} \left( {\kappa + 1} \right)\Phi_{l} \left( {\kappa + 1} \right)} \right)^{2} - \frac{\sigma }{2}\left( {e_{x} \left( \kappa \right)\Phi_{l} \left( \kappa \right)} \right)^{2} \\ = & \sigma \,e_{x} \left( \kappa \right)\Phi_{l}^{2} \left( \kappa \right)\Delta e_{x} \left( \kappa \right) + \sigma \,e_{x}^{2} \left( \kappa \right)\Phi_{l} \left( \kappa \right)\Delta \Phi_{l} \left( \kappa \right) \\ \end{aligned} $$
(34)

Similarity, \(\Delta R_{b} \left( \kappa \right) = \beta \,\Phi_{l} \left( \kappa \right)\Delta \Phi_{l} \left( \kappa \right)\,\,\,{\text{and}}\,\,\,\Delta R_{c} = \lambda \left( {\Delta \Phi_{l} \left( \kappa \right)} \right)^{2}.\)

The second condition for stability is determined as:

$$ \begin{aligned} \Delta R_{x} \left( \kappa \right) = & \, \sigma \,e_{x} \left( \kappa \right)\Phi_{l}^{2} \left( \kappa \right)\Delta e_{x} \left( \kappa \right) + \sigma \,e_{x}^{2} \left( \kappa \right)\Phi_{l} \left( \kappa \right)\Delta \Phi_{l} \left( \kappa \right) + \beta \,\Phi_{l} \left( \kappa \right)\Delta \Phi_{l} \left( \kappa \right) \\ & + \lambda \left( {\Delta \Phi_{l} \left( \kappa \right)} \right)^{2} \le 0 \\ \end{aligned} $$
(35)

Equation (35) can be rewritten as:

$$ \begin{aligned} \Delta R_{x} \left( \kappa \right) = & \, \sigma \,e_{x} \left( \kappa \right)\Phi_{l}^{2} \left( \kappa \right)\Delta e_{x} \left( \kappa \right) + \sigma \,e_{x}^{2} \left( \kappa \right)\Phi_{l} \left( \kappa \right)\Delta \Phi_{l} \left( \kappa \right) + \beta \,\Phi_{l} \left( \kappa \right)\Delta \Phi_{l} \left( \kappa \right) \\ & + \lambda \left( {\Delta \Phi_{l} \left( \kappa \right)} \right)^{2} = - \xi \\ \end{aligned} $$
(36)

where \(\xi \ge 0\), so as to guarantee the condition, \(\Delta R_{x} \left( \kappa \right) \le \,0\), the following equation is obtained:

$$ \lambda {\mkern 1mu} \left( {\Delta \Phi _{l} \left( \kappa \right)} \right)^{2} + \Delta \Phi _{l} \left( \kappa \right){\mkern 1mu} \left( \begin{gathered} \sigma {\mkern 1mu} e_{x} \left( \kappa \right){\mkern 1mu} \Phi _{l}^{2} \left( \kappa \right)\frac{{\Delta e_{x} \left( \kappa \right)}}{{\Delta \Phi _{l} \left( \kappa \right)}} \hfill \\ + \sigma {\mkern 1mu} e_{x}^{2} \left( \kappa \right){\mkern 1mu} \Phi _{l} \left( \kappa \right) + \beta {\mkern 1mu} \Phi _{l} \left( \kappa \right){\mkern 1mu} {\mkern 1mu} \hfill \\ \end{gathered} \right){\mkern 1mu} {\mkern 1mu} + \xi = 0 $$
(37)

The general quadratic equation is determined as:

$$ c\,\chi^{2} + b\,\chi + a = 0 $$
(38)

The roots of Eq. (38) are calculated as:

$$ \chi_{1,2} = \frac{{ - b \pm \sqrt {b^{2} - 4ca} }}{2c} $$
(39)

From Eqs. (37) and (38), obviously, \(\Delta \Phi_{l} \left( k \right)\) acts as \(\chi\) in Eq. (38) and the values of \(c,\,b\,\) and \(a\) in Eq. (37) are obtained as:

$$ c = \lambda ,\,\,b = \beta \,\left( {\frac{\sigma }{\beta }e_{x} \left( \kappa \right)\,\Phi_{l}^{2} \left( \kappa \right)\,\frac{{\Delta e_{x} \left( \kappa \right)}}{{\Delta \Phi_{l} \left( \kappa \right)}} + \left( {1 + \frac{\sigma }{\beta }\,e_{x}^{2} \left( \kappa \right)\,} \right)\,\Phi_{l} \left( \kappa \right)} \right)\,\,{\text{and}}\,\,a = \xi $$
(40)

There is a single unique solution for Eq. (38), if \(\sqrt {b^{2} - 4ca} = 0\). Therefore,

$$ \left( {\beta \,\left( {\frac{\sigma }{\beta }\,e_{x} \left( \kappa \right)\,\Phi_{l}^{2} \left( \kappa \right)\frac{{\Delta e_{x} \left( \kappa \right)}}{{\Delta \Phi_{l} \left( \kappa \right)}} + \left( {1 + \frac{\sigma }{\beta }e_{x}^{2} \left( \kappa \right)\,} \right)\,\Phi_{l} \left( \kappa \right)} \right)} \right)^{2} - 4\lambda \,\xi \, = \,0 $$
(41)

and, \(\xi\) can be calculated as:

$$ \xi = \frac{{\left( {\beta \,\left( {\frac{\sigma }{\beta }e_{x} \left( \kappa \right)\,\Phi_{l}^{2} \left( \kappa \right)\,\frac{{\Delta e_{x} \left( \kappa \right)}}{{\Delta \Phi_{l} \left( \kappa \right)}} + \left( {1 + \frac{\sigma }{\beta }\,e_{x}^{2} \left( \kappa \right)\,} \right)\,\Phi_{l} \left( \kappa \right)} \right)} \right)^{2} }}{4\lambda } $$
(42)

Since \(\xi \ge 0\), which means

$$ \frac{{\left( {\beta \,\left( {\frac{\sigma }{\beta }e_{x} \left( \kappa \right)\,\Phi_{l}^{2} \left( \kappa \right)\,\frac{{\Delta e_{x} \left( \kappa \right)}}{{\Delta \Phi_{l} \left( \kappa \right)}} + \left( {1 + \frac{\sigma }{\beta }\,e_{x}^{2} \left( \kappa \right)\,} \right)\,\Phi_{l} \left( \kappa \right)} \right)} \right)^{2} }}{4\lambda } \ge 0 $$
(43)

So, the unique root of Eq. (37) is \(\chi_{1,2} = \frac{ - b}{{2c}}\), similarly,

$$ \Delta \Phi_{l} \left( \kappa \right) = - \frac{{\beta \left( {\Phi_{l} \left( \kappa \right)\,\left( {1 + \frac{\sigma }{\beta }\,\,e_{x}^{2} \left( \kappa \right)} \right) + \frac{\sigma }{\beta }\,e_{x} \left( \kappa \right)\,\Phi_{l}^{2} \left( \kappa \right)\,\frac{{\partial e_{x} \left( \kappa \right)}}{{\partial \Phi_{l} \left( \kappa \right)}}} \right)}}{2\lambda } $$
(44)

Equation (44) can be reformulated as:

$$ \Delta \Phi_{l} \left( \kappa \right) = - \frac{{\beta \,\left( {\frac{\sigma }{\beta }\,e_{x} \left( \kappa \right)\Phi_{l}^{2} \left( \kappa \right)\,\frac{{\partial e_{x} \left( \kappa \right)}}{{\partial \Phi_{l} \left( \kappa \right)}} + \left( {1 + \frac{\sigma }{\beta }e_{x}^{2} \left( \kappa \right)\,} \right)\,\Phi_{l} \left( \kappa \right)} \right)}}{2\lambda } $$
(45)

So, by replacing \(\Delta \Phi_{l} \left( \kappa \right)\) in Eq. (23), the updating equation for the parameters of the DRNN of the HDL-DRNNC can be given as in Eq. (24).

5 Steps of the proposed HDL-DRNNC

The system block diagram with the proposed HDL-DRNNC is shown in Fig. 5. The error signal \(e_{x} \left( \kappa \right)\) is the difference between the reference input \(\Upsilon_{d} (\kappa )\) and the actual output of the nonlinear system \(\Upsilon_{a} (\kappa )\). The proposed controller input is \(e_{x} \left( \kappa \right)\) and its output is the control signal \(u\left( \kappa \right)\), which forward to the nonlinear system.

Fig. 5
figure 5

HDL-DRNNC block diagram with nonlinear system

Full size image

As shown in Figs. 1 and 2, the first layer of the HDL-DRNNC contains three inputs, which are the error signal \(e_{x1} \left( \kappa \right) = e_{x} \left( \kappa \right)\), the change of error signal \(e_{x2} \left( \kappa \right) = e_{x} \left( \kappa \right) - e_{x} \left( {\kappa - 1} \right)\) and the change of the change of error signal \(e_{x3} \left( \kappa \right) = e_{x} \left( \kappa \right) - 2e_{x} \left( {\kappa - 1} \right) + e_{x} \left( {\kappa - 2} \right)\). The output layer contains one output \(u\left( \kappa \right)\). Algorithm 1 summarizes the proposed HDL-DRNNC pseudocode for reader’s convenience.

6 Simulation results

A comparison of the proposed HDL-DRNNC and DRNNC is performed under the same conditions with zero initial weights to show the performance of the hybrid learning algorithm. In the present paper, assign \(J = M = l = 10{,}\,\,n = 3\), \(R = 10\), \(N = 10\), \(\Re = 1\) and \(P = 1\). In order to evaluate the performance and demonstrate the robustness of the proposed controller, the mean absolute error (MAE) and the root-mean-square error (RMSE) are used. MAE and RMSE are clarified as [57, 58]:

$$ {\text{MAE}} = \frac{1}{{K_{L} }}\sum\limits_{\kappa = 1}^{{K_{L} }} {\left| {e_{x} \left( \kappa \right)} \right|} $$
(46)
$$ {\text{RMSE}} = \sqrt {\left( {\frac{1}{{K_{L} }}\sum\nolimits_{\kappa = 1}^{{K_{L} }} {\left( {e_{x} \left( \kappa \right)} \right)^{2} } } \right)} $$
(47)

where \(K_{L}\) denotes iterations number.

figure a

6.1 Case1: mathematical system

A non-affine nonlinear system is used to test the performance of the proposed controller, which is given as [59, 60]:

$$ G_{1} \left( {\kappa + 1} \right) = \alpha_{1} \left( \kappa \right)\,G_{2} \left( \kappa \right) + \alpha_{2} \left( \kappa \right)\,\sin \left( {G_{1} \left( \kappa \right)} \right) $$
(48)
$$ G_{2} \left( {\kappa + 1} \right) = \alpha_{3} \left( \kappa \right)\,\cos \left( {G_{2} \left( \kappa \right)} \right)\sin \left( {G_{1} \left( \kappa \right)} \right) + \alpha_{4} \left( \kappa \right)\,u\left( \kappa \right) + \alpha_{5} \left( \kappa \right)\tanh \left( {u\left( \kappa \right)} \right) $$
(49)
$$ \Upsilon_{a} \left( {\kappa + 1} \right) = G_{1} \left( {\kappa + 1} \right) $$
(50)

where \(\alpha_{1} \left( \kappa \right) = 0.5,\,\alpha_{2} \left( \kappa \right) = - 0.3,\,\alpha_{3} \left( \kappa \right) = - 1,\,\alpha_{4} \left( \kappa \right) = 2\,\) and \(\,\alpha_{5} \left( \kappa \right) = - 2\).

6.1.1 Task 1: tracking the reference signal trajectory

The reference signal in this task is defined as:

$$ \Upsilon_{d} \left( \kappa \right) = 1 + 0.5\sin \left( {0.05\kappa T} \right) $$
(51)

where \(T\) denotes the sampling period.

Figures 6 and 7 exhibit the system response and the control signal for the proposed HDL-DRNNC and DRNNC. It is clear that there is an error between the set-point and the system output under using the DRNNC at the beginning of simulation task. However, the proposed controller using hybrid learning algorithm based on SOM and RBM is able to track the set-point without a steady-state error.

Fig. 6
figure 6

Output response for the mathematical system (Task 1)

Full size image
Fig. 7
figure 7

Control signal (Task 1)

Full size image

6.1.2 Task 2: uncertainty due to disturbance

To evaluate the robustness of the proposed HDL-DRNNC, a disturbance value of 50% of its desired output is added to the system output at \(\kappa = 2950\). Figure 8 illustrates that the system output tracks the set-point without a steady-state error after adding a disturbance value to the measured output for the proposed HDL-DRNNC. After adding a disturbance value for the DRNNC, there is still a steady-state error. Figure 9 exhibits the control signal of the system for both controllers. In contrast with the DRNNC, the proposed HDL-DRNNC clearly responds to disturbance effects.

Fig. 8
figure 8

Output response for the mathematical system (Task 2)

Full size image
Fig. 9
figure 9

Control signal (Task 2)

Full size image

6.1.3 Task 3: Uncertainty due to disturbance with parameters variation

At \(\kappa = 2950\) instant and after the system output reaches the reference input, the system parameters are varied as follows: \(\alpha_{1} \left( \kappa \right) = 0.35,\,\)\(\alpha_{2} \left( \kappa \right) = - 0.35,\,\)\(\,\alpha_{3} \left( \kappa \right) = - 1.5,\,\)\(\,\alpha_{4} \left( \kappa \right) = 2\,.5\) and \(\alpha_{5} \left( \kappa \right) = 1\) with an effect 40% disturbance. The output response and the control signal of the system are shown in Figs. 10 and 11, respectively, for both controllers. It is evident that the proposed HDL-DRNNC is capable of responding to the uncertainty effects (the parameters variation and disturbance) as compared to the DRNNC.

Fig. 10
figure 10

Output response for the mathematical system (Task 3)

Full size image
Fig. 11
figure 11

Control signal (Task 3)

Full size image

6.1.4 Task 4: uncertainty due to noise

A random noise signal is added at \(\kappa = 2950\) instant. The output response and the control signal of the system are shown in Figs. 12 and 13, respectively. In contrast to the output response based on DRNNC, the proposed HDL-DRNNC has the ability to recover from the impact of random noise more quickly. The proposed HDL-DRNNC is more robust than the DRNNC.

Fig. 12
figure 12

Output response for the mathematical system (Task 4)

Full size image
Fig. 13
figure 13

Control signal (Task 4)

Full size image

Tables 1 and 2 illustrate the values of MAE and RMSE for the proposed HDL-DRNNC, the DRNNC and other schemes, that are published previously such as feed-forward neural network based on RBM (FFNN-RBM) [45], ERNN-RBM [46], feed-forward neural network with hybrid learning controller (FFNNHLC) [61], FCRNNC [62] and adaptive interval type-2 Takagi–Sugeno–Kang fuzzy logic controller based on reinforcement learning (AIT2-TSK-FLC-RL) [63]. On the other hand, the proposed HDL-DRNNC is compared with DRNNC based on SOM (DRNNC-SOM) to show the benefits of hybrid learning.

Table 1 The mathematical system MAE values
Full size table
Table 2 The mathematical system RMSE values
Full size table

The MAE and RMSE values for the proposed HDL-DRNNC scheme are clearly smaller than those obtained for other schemes. Due to use of DL to initialize the weight values of the proposed HDL-DRNNC, it can reduce the impact of the system uncertainties caused by external disturbance, parameter variations, and random noise compared with other schemes. The hybrid algorithm is used because it gave better results than the DRNNC-based SOM algorithm as shown in Tables 1 and 2.

6.2 Case 2: physical system

In this section, the proposed controller is used for controlling a physical system, which is the electrical vehicle system (EVS). Nowadays, EVSs are increasingly advancing because of the importance of environmental protection and lack of energy sources [64]. The control of EVSs is important role in order to determine a high-performance EVS with an optimal balance of travelling range per charge, maximum speed and acceleration performance [64]. EVSs are basically time-variant (e.g. the EVS parameters and the road condition are consistently varying) nonlinear system, which making the control of an EVS quite cumbersome [64]. Therefore, the control of EVS should be designed robustly and adaptively to improve the system in both dynamic and steady performance states.

Figure 14 shows the schematic diagram of an EVS and the mathematical model is given as [63,64,65,66]:

$$ \begin{aligned} \dot{\hbar } = & V\left( \hbar \right) + q\left( \hbar \right)u, \\ \Upsilon_{a} = & Z\left( \hbar \right) \\ \end{aligned} $$
(52)

where \(\hbar = \left[ {\begin{array}{*{20}c} i \\ \omega \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\hbar_{1} } \\ {\hbar_{2} } \\ \end{array} } \right]\), \(\,V\left( \hbar \right),\,q\left( \hbar \right)\) and \(Z\left( \hbar \right)\) are defined as:

$$ V\left( \hbar \right) = \left[ {\begin{array}{*{20}c} {\left( {\frac{ - 1}{{\Gamma_{a} + \Gamma_{f} }}} \right)C_{1} } \\ {\left( {\frac{1}{{J + m\,\left( {\frac{{r_{e} }}{G}} \right)^{2} }}} \right)\,\left( {\Gamma_{af} \,\hbar_{1}^{2} - B\,\hbar_{2} - \left( {\frac{{r_{e} }}{G}} \right)\,C_{2} } \right)} \\ \end{array} } \right] $$
(53)
$$ q\left( \hbar \right) = \left[ {\begin{array}{*{20}c} {\left( {\frac{1}{{\Gamma_{a} + \Gamma_{f} }}} \right)} \\ 0 \\ \end{array} } \right]\;{\text{and}}\;Z\left( \hbar \right) = \hbar_{2} $$
(54)
$$ C_{1} = \left( {\Re_{a} + \Re_{f} } \right)\,\hbar_{1} + \Gamma_{af} \,\hbar_{1} \,\hbar_{2} $$
(55)
$$ C_{2} = 0.5\,\rho \,A\,C_{d} \,\left( {\frac{{r_{e} }}{G}} \right)^{2} \hbar_{2}^{2} + \mu_{rr} \,m\,g\tanh \,\left( {\hbar_{2} } \right) $$
(56)

where \(\omega \,\) and \(i\) denote to angular speed and angular speed of the motor. \(\Gamma_{f} ,\,\Gamma_{a} ,\Re_{f}\) and \(\Re_{a}\) denote the field inductance, armature inductance, the field resistance and armature resistance, respectively.\(J\) denotes the inertia of the motor, \(r_{e}\) denotes the tire radius of the EVS, which includes the tires with gearing system, \(\Gamma_{af}\) is the mutual inductance between the armature and the field windings, and \(\rho\), \(A\) and \(m\) denote the air density, the frontal area of the vehicle and the mass of the EVS, respectively. \(\mu_{rr}\),\(B\),\(G\) and \(C_{d}\) denote the rolling resistance coefficient, the viscous coefficient, the gearing ratio and the drag coefficient, respectively. The values of EVS parameters are listed in Table 3.

Fig. 14
figure 14

EVS schematic diagram

Full size image
Table 3 EVS parameters
Full size table

6.2.1 Task 1: tracking the reference signal trajectory

Figures 15 and 16 exhibit the EVS response and its control signal when the desired input is given as:

$$ \Upsilon_{d} = \left\{ {\begin{array}{*{20}c} {0.02t} & {0 < t \le 210} \\ {10} & {210 < t \le 420} \\ {15} & {420 < t \le 630} \\ { - 0.0237t + 30} & {630 < t \le 840} \\ 2 & {840 < t \le 1050} \\ \end{array} } \right. $$
(57)
Fig. 15
figure 15

Output response for the EVS (Task 1)

Full size image
Fig. 16
figure 16

The EVS control signal (Task 1)

Full size image

In this task, the set-point changing is carried for testing the proposed HDL-DRNNC, which is compared with the DRNNC. It is clear that the EVS response using the proposed HDL-DRNNC reaches the set-point faster than the DRNNC.

6.2.2 Task 2: uncertainty due to parameters variation with disturbance

In this task, the EVS parameters are varied as in Table 4 with an effect 40% disturbance after the system output reaches the reference input at \(t = 240\,\,\sec\). The system response and its control signal for both controllers are exhibited as in Figs. 17 and 18. It is clear that the robustness of the proposed HDL-DRNNC is better than the DRNNC due to its ability of reducing the effect of system uncertainties.

Table 4 EVS parameters variation values
Full size table
Fig. 17
figure 17

Output response for the EVS (Task 2)

Full size image
Fig. 18
figure 18

The EVS control signal (Task 2)

Full size image

6.2.3 Task 3: uncertainty due to random noise

A random noise signal is added at \(t = 240\,\,\sec\). The EVS response and its control signal are shown in Figs. 19 and 20. It is clear that the EVS response for the proposed HDL-DRNNC is quickly recovering from the impact of random noise as compared to the output response based on DRNNC. The robustness of the proposed HDL-DRNNC is better than that compared with DRNNC.

Fig. 19
figure 19

Output response for the EVS (Task 3)

Full size image
Fig. 20
figure 20

The EVS control signal (Task 3)

Full size image

The analyses of the MAE and RMSE values for the proposed HDL-DRNNC, the DRNNC and other schemes are presented in Tables 5 and 6. It is clear that the MAE and RMSE values for the proposed HDL-DRNNC are smaller than those obtained for other schemes. Compared with other schemes, HDL-DRNNC has the ability to reduce the impact of system uncertainties.

Table 5 MAE values for the EVS
Full size table
Table 6 RMSE values for the EVS
Full size table

The main features of the proposed HDL-DRNNC are gathered as follows: (1) It has a swift learning control due to its use of hybrid DL, which uses SOM and RBM to initialize the weights values, (2) the controller is stable as it uses the Lyapunov stability method to update the weight values and it guarantees the stability, and (3) it is successful for reducing the system uncertainties and tracking the performance output for both mathematical system and physical system.

7 Conclusion

In the present paper, the HDL-DRNNC is proposed for nonlinear systems. The HDL-DRNNC uses the DRNN, which can be learned from HDL. In order to guarantee the stability of the proposed controller, the updating weights of the DRNN are derived using the Lyapunov stability criterion. Two nonlinear systems, namely mathematical and physical, are used to estimate the performance of the proposed controller. According to the obtained results, the proposed HDL-DRNNC can overcome uncertainty and track the performance of the controlled systems. By comparing MAE and RMSE indicators, it is evident that the response of mathematical and physical systems based on HDL-DRNNC is able to recover fast from the effects of uncertainties as compared with the response of mathematical and physical systems based on DRNNC and other existing controllers. As conclusion, HDL-DRNNC robustness has superior performance and a faster ability to recover from uncertainty as compared to DRNNC and other controllers. In the future work, the authors will try to implement practically the proposed algorithm using microcontrollers for controlling a real system.