1 Introduction

During a human interaction, people should feel comfortable when they perceive that other are approaching. Therefore, the approaching person should respect the intimate area. Proxemics is the study of spatial behavior, concerned with territoriality, interpersonal distance, spatial arrangements, crowding, and other aspects of the physical environment that affect behavior. The term was coined by Hall et al. [1]. He proposed a fixed measure of personal space, a set of regions around a person to delimit the acceptable distance to interact with other people.

In recent years, human-agent interaction has gathered popularity in the scientific community [2]. Furthermore, the humanization of agents is an expected event, given technological advances and human nature. Thus, optimal interaction is necessary for both the agent and the person [3].

Reinforcement Learning (RL) is a learning paradigm that tries to solve the problem of an agent interacting with the environment to learn a desired task autonomously [4]. The agent must sense a state from the environment and take actions that affect it to reach a new state. The agent receives a reward signal from the environment that they try to maximize throughout the learning for each action taken. The agent takes actions from their own experience, or can be guided by an external trainer that provides feedback [5, 6] .

Proxemic behavior has been used in different areas with cognitive agents. For example, human-robot interaction studies how people behave in the presence of an artificial agent or robot and how the agent perceives the personal space [7, 8]. Moreover, machine learning has been used to study how artificial agents sense the personal space of other cognitive agents, and it has been used to identify and learn personal space [9, 10]. These implementations consider that the personal space is fixed and that the agent previously knows such space. However, these assumptions are not necessarily accurate in real-world scenarios; personal space is different for each person and unknown. Different characteristics dynamically modify the personal space, such as culture, family environment, the territory where they live, and previous experiences, making proxemics’ identification more complex and requiring external information to estimate it. In navigation tasks, RL agents learn a policy to control their movement in space and move. In the sense of approximation, they perceive the cognitive agent as one more obstacle or a goal, so the distance relationship is limited to that allowed by the agent to avoid colliding. In this work, we study how a RL agent learns to approach another cognitive agent in two proxemics-based environments. To address this problem, we implement Q-Learning and advantage actor-critic (A2C) algorithms in a modified grid-world and a simulated robot approaching problem, respectively, where a cognitive agent, the issuer, gives information to the learning agent. Our study is limited to experiments with fixed initial values, i.e., the RL agent remains in the same position at the beginning of each episode. Also, cognitive agents and their personal space remain fixed during training. However, we find that the trajectories of an RL agent may be able to identify the proxemic region of cognitive agents. Thus, the agent learns a policy to move in an environment and finds a limit to which to move.

This paper is organized as follows: In Sect. 2, we present related works. Section 3 introduces the basics of RL, Q-learning and advantage actor-critic. In Sect. 4, we describe the environments with proxemic behavior in cognitive agents, a modified grid-world and the robot approaching based on ship steering. Experiments, results and discussion are described in Sect. 5. Finally, Sect. 6 presents the main conclusions and describes future research.

2 Related works

The interaction process is an animal and human characteristic that allows the creation of social bonds for survival or with a specific objective. This process generally has an approach, action execution, and mutual response. However, the mere approach is already an interaction in itself. The execution is the act of approaching, and the response is how the other reacts to the action of approaching. In nature, the animals have a behavior based on the species and the crowd, when each group of animals remain in a territory because of the feed source or security [11, 12]. In the interaction process, each human uses their personal space and perceives the space of another being. The way how each human uses and perceive depends on the experience of previous interactions or contact [1]. It is clear that the experience is unique in the sense that each human creates relations with other beings, based on nature, beliefs, culture and society. These aspects constitute a set of rules that allow an effective interaction avoiding disagreement between the parties.

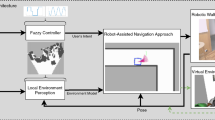
Including artificial agents in a human environment humanizes these entities, in the sense that they have to behave according to the rules that people build from their experience. Figure 1 shows how the human-robot interaction process is in the presence of proxemic behavior. The interaction process includes the robot perception, where the artificial agent perceives the reactions of the person, the robot learning and robot performance, where the robot uses human information to learn the task and perform it and, finally, the human perception and reaction, where the human reacts to the performed action by the agent.

Fig. 1
figure 1

General process of interaction with proxemic behavior: Human perception, Human reaction, Human response, Robot perception, Learning, and approach (task)

Full size image

2.1 How the human perceives an artificial proxemic behavior?

It is essential to know how a person perceives the artificial agent. Previous works have found that people tend to maintain social aspects in environments that involve robots or virtual agents [13]. For instance, Li et al. [14] has shown that humans maintained social distance in virtual environments. In addition, people responded to the actions of virtual agents and tried to remain at a comfortable distance. Humans not only responded to the movement of other cognitive agents, but they also needed another signal to react according to their personal space. Another type of interaction could change the personal space; for instance, when the virtual agent made a wave, the human reacted and modified their social space [15].

In social environments, humans maintain appropriate distances between themselves. Furthermore, this behavior is extended to virtual environments, where a human maintains a relative distance according to the perception in this environment [16]. Kastanis and Slater [17] investigated how a learning agent could drive human participants to a certain previously established position in a virtual space, exploiting human proxemic behavior. In their work, a reinforcement learning approach was used for a robot to learn how to influence people to move to another position. The authors concluded that the goal was affected by human behavior. The agent learned to approach the participant when they were too far and exploited the proxemics to carry the person back to the goal position. Another case is to use an action that maintains the attention of the human/agent. For instance, Kastanis and Slater [17] used wave action to get the participants’ attention when it was too far from them. Millan et al. [18] used PING action to communicate with a learning agent and an informative issuer.

2.2 How do artificial agents identify non-verbal aspects?

In non-verbal communication, there are different ways of identifying social cues to predict discomfort, agreement, attitude, or another behavioral trait of interest. Individually, each non-verbal aspect gives some information about the behavior of the human being. Ponce-Lopez et al. [19] applied a non-invasive ambient intelligence framework for analysis of non-verbal communication in conversation settings. The learning was a binarized classification problem, where the authors used Adaboost, Support Vector Machines (SVM), and two kinds of Artificial Neural Networks (ANN), in particular Cascade-Forward (CF) and FeedForward neural networks (FF) [20, 21]. Another approach to identifying nonverbal communication was presented in [22]. The authors propose a computational framework for nonverbal communication for human-robot interaction, where a storyteller had to recognize attention from a listener. The main objective was to recognize that attention encodes social-emotional states through nonverbal behaviors.

Concerning proxemics, several works try to predict or estimate the social space from humans. Different strategies in the human-robot interaction area suggest extracting information to construct this space out of the robot control. For instance, personal space can be related to an uncomfortable level that indicates how much the agent discomforts the human. Generally, this discomfort level is estimated based on information about the demography, sociology, or psychology aspects from participants in a study. For instance, Kosinski et al. [23] performed a study with participants to obtain information about demographic aspects. The study was performed in a robotic environment, where the participants stopped the robot when they felt discomfort. The robot’s position from different angles was captured and used to construct the comfort level.

On the other hand, machine learning is used to find relationships between a person’s level of discomfort during the interaction and personal information. Gao et al. [24] used different deep learning neural networks architectures to predict comfortable human-robot proxemics based on the personal information obtained from each participant. The authors drove the problem as a regression problem, where the response was the numerical discomfort and the regressors variables were the values of distance, angles, and demographic aspects. Kosinski et al. [23] used a fuzzy dataset-based model, to encode the study information parametrizing rules to reflect user preferences in the sense of personal space. Other approaches intend to exploit the image information to estimate distance. This methodology can carry several issues due to the camera, quality, and configuration of images. Seker et al. [25] proposed a benchmark to evaluate the social distance. For this, the authors created a dataset with measured pair-wise social distance under different camera positions. The authors used YOLOv4 [26] and OpenPose [27] to detect and identify skeletal points from the people.

2.3 How do artificial agents learn proxemic behavior?

In environments that involve humans’ proxemic behavior, an agent has to find the best path to reach a specific place navigating among humans. The learning agent must be socially aware that its movement cannot perturb human activity [28, 29]. In general, the agent moves in the social or public space, avoiding getting closer to the people. However, several works show that the estimated paths invade the personal space from proxemic theory [30]. These findings suggest that motion-based in proxemic behavior has poorer performance than methods that imitate human behavior. Nevertheless, the works do not consider that humans’ proxemic behaviors can change based on external factors or the situation, as in the navigation process. Charalampous et al. [31] proposed a robot framework to navigate in a human-populated environment. This approach considered that the robot exhibits socially accepted behavior by considering the actions being performed by individuals. The methodology was applied in indoor areas and working environments, where people gathered in groups of two or three, but not in a congested environment. The robot navigated based on a known precomputed 3D metric map (constructed offline) during the learning. The authors used a deep learning action recognition with HTM, consequently, an SVM to classify each action. Luber et al. [30] suggested a learning model from observations of humans, i. e., the learning agent learned through human relative motion behavior. The authors used an unsupervised way to classify the relative motion prototypes in the methodology. Also, they used a distance function with an asymmetric Dynamic Time Warping algorithm (DTW) to ensure that the motion sequences did not differ in duration and relative speed. They showed that their methodology can imitate human motion behavior, and its performance was better than learning using the proxemic theory (Hall’s theory).

During navigation, it is expected that cognitive agents tend to intrude the personal space, differently to the interaction where this nearness is acceptable only for people of great social acceptability as good friends or family members. Luber et al. [30] used relative motion prototypes (RMP) and showed that social acceptability or comfort in humans is higher when the learning agent exhibits the same behavior as a human. They used the person orientation as a criterion to quantify and distinguish what they defined here to be social context. Besides, they compared Hall’s theory of proxemics and highlighted that invading personal space appears frequent during navigation. However, the personal space was considered fixed, and it reduced its size during the trajectory due to the social situation. Feldmaier et al. [32] combined an emotion model with the SLAM algorithm to allow the robot to give non-verbal feedback to a user about the internal processes. The learning agent explored the environment using the SLAM algorithm while simultaneously appraising its current progress with emotions. The estimations of the SLAM were used as input in an appraisal model to perform the Stimulus Evaluation Checks (SECs) that were independent modules in which the agent did its subjective assessment of the situation based on personal needs, goals, and values. Then, a categorization module was used to map the pleasure and arousal space defined by Russell [33].

Other works consider the robot as part of a human group, in the sense that the robot behaves similarly to the individuals or behaves according to social rules. Fuse et al. [34] proposes a robotic model that enables identifying the robot’s position in a social people group. Furthermore, the robot considered the change of personal space during the navigation process. Also, they examined if a robot could imitate the trajectory of humans. They used an RL framework in their implementation, considering a value function to the states and actions and a value function to the distance. The latter function was used to learn the agent’s physical distances and determine its physical position. They concluded that the learning agent maintained a behavior like humans while it was approaching them. In addition, a group of participants assessed the agent trajectories and determined that they were similar to human trajectories. The main goal of their work was that the learning agent does not use trajectory demonstrations from humans to imitate their behavior. Our work studies the behavior of an agent in an environment with proxemic behavior, where it learns trajectories that do not invade the personal space of an issuer. Table 1 shows a comparison of some works mentioned above and the objective of each one.

Table 1 Comparison of different works and its methods to estimate trajectories. Our study shows that it is possible to identify the issuer’s proxemic region based on the agent’s trajectories
Full size table

In Silva and Romero [35], the authors proposed a framework of sharing attention, where a learning agent was provided the capacity of joint attention with a human. Their framework used a combination of relational reinforcement learning (RRL) and recurrent neural network (RNN) with state classification, the so-called RLSSACTG. The main idea was to maintain the attention in a human based on gaze behavior, changing the attention to an object when this appeared, and backing to pay attention to the human. They studied the framework’s performance in a simulated environment, where a learning agent faced a human agent. They compared the RL (Q-learning) approach, ETG algorithm [36], and RLSSACTG. The obtained results showed that architecture is a potential tool to control sociable robots.

Inverse reinforcement learning (InvRL) is commonly used in navigation problems. The main idea is learning from demonstration, where the agent tries to find the patterns of experts based on their demonstration behavior. This approach facilitates the agent to learn how to navigate among people because it recognizes human behavior in demonstrating paths [28]. InvRL is generally used to learn the cost function associated with the path planning algorithm or the navigation controller. InvRL shows better results than the policy based on proxemic theory because cost functions can be used in different human environments [29].

3 Reinforcement learning framework

Reinforcement learning is a learning approach that involves an autonomous agent learning from interactions with its environment to achieve a goal [4]. The agent must be able to learn from its own experience by selecting actions that affect the environment, reaching situations that allow it to complete the task. In this approach, the learning agent receives a numerical reward signal from the environment it that attempts to maximize [37].

The agent and the environment interact at each time step \(t = 0, 1, 2,\ldots\). At each step, the learning agent receives a representation of the state of the environment \(x_t \in X\), and of the action selected by the agent \(u_t \in U(x_t)\), where X is a set of the all possibles states, and \(U(x_t)\) is a set of the actions available in the state \(x_t\). Eventually, as a result of performing an action, the agent receives a scalar reward \(r_{t+1} \in {\mathbb {R}}\) and reaches a new state \(x_{t+1}\) [4]. Figure 2 shows the diagram of the interaction between the agent and the environment, in the context of RL.

Fig. 2
figure 2

Interaction between the agent and the environment in the Reinforcement Learning context. Figure adapted from Sutton and Barto’s book [4]

Full size image

At each time step, the agent relates states to probabilities to select each possible action. These relations are called the agent policy and denoted by \(\pi _t\), where \(\pi _t(u_t \mid x_t)\) is the probability to select \(u_t\) given the current state \(x_t\) at time t. The RL method specifies how the agent changes the policy as a consequence of its experience. Thereby, the goal of the reinforcement learning agent is to approximate a function \(\pi : X \times U \longrightarrow (0,1)\) that maximizes the total amount of reward it receives over the long run.

A value function represents an estimation of how good a particular action from that state is in terms of future expected reward [38]. The state-value function of x, under all the actions, is the expected return of the discounted sum starting in the state x and following a policy \(\pi\). Formally, we can define it by [4, 38]

$$\begin{aligned} V^\pi (x) = E_\pi \left[ \sum _{k=0}^{\infty } \gamma ^k r_{t+k+1} \mid x_t = x \right] , \end{aligned}$$
(1)

where \(E_\pi [\cdot ]\) denotes the expected value given that the agent follows the policyFootnote 1\(\pi\).

Similarly, it is defined as an action-value function as the value of taking action u in the state x under the policy \(\pi\). Roughly speaking, it is the expected return starting from state x, taking action u and following the policy \(\pi\) [4]

$$\begin{aligned} Q^\pi (x,u) = E_\pi \left[ \sum _{k=0}^{\infty } \gamma ^k r_{t+k+1} \mid x_t = x, u_t = u \right] . \end{aligned}$$
(2)

In addition, the value functions satisfy a recursive property. The expression in (1) can be defined recursively in terms of the so-called Bellman equation [39]. It is denoted as the expected return in terms of the immediate reward and the value of the next state, defined formally by

$$\begin{aligned}V^\pi (x) & = \sum _{{\mathbb {U}}} \pi (u\mid x) \sum _{X} P(x^\prime \mid x,u) \Big [\rho (x,u,x^\prime )\nonumber \\&\quad + \gamma V^\pi (x^\prime ) \Big ] \mathrm{d}x^\prime \mathrm{d}u, \end{aligned}$$
(3)

where x is the current state, u is the selected action and \(x^\prime\) is the new state reached by performing the action u in the state x. The function Q(x, u) in (2) can also be defined recursively in terms of the Bellman equation.

3.1 Q-learning

The Q-learning algorithm [40] is an off-policy method based on TD learning. The one-step Q-learning is a simple algorithm, in which the update of the value \(Q(x_t, u_t)\) is carried out using the value \(\max _{u\in U(x_{t+1})}Q(x_{t+1}, u_t)\). The core of the algorithm is based on Bellman equation as a simple value iteration update, using the weighted average of the old value and the new information of state:

$$\begin{aligned}&Q(x_t, u_t) \leftarrow Q(x_t, u_t) + \alpha \left[ \rho _{t+1}\right. \nonumber \\&\quad \left. + \gamma \max _{u\in U(x_{t+1})}Q(x_{t+1}, u_t) - Q(x_t, u_t) \right] , \end{aligned}$$
(4)

where \(\alpha\) is the learning rate, and \(\gamma\) is the discount factor. The value of \(Q(x_t,u_t)\) estimates the action-value after applying action \(u_t\) in state \(x_t\). The learned action-value function, Q, directly approximates the optimal action-value function \(Q^*\), independent of the policy being followed [4].

3.2 Advantage actor-critic

The advantage actor-critic (A2C) algorithm is an on-policy method based on TD actor-critic that keeps a separate memory structure to represent the policy, independent of the value function [41]. The agent is separated into two entities: the actor and the critic. The policy takes the role of the actor, selecting actions in each iteration. The critic, commonly a state-value function, evaluates or criticizes the actions performed by the actor [42]. Figure 3 shows the schematic structure of the general actor-critic algorithm.

In each iteration, the critic values each action through TD error:

$$\begin{aligned} \delta _t = r_{t+1} + \gamma V(x_{t+1}) - V(x_t). \end{aligned}$$
(5)
Fig. 3
figure 3

Schematic overview of an actor-critic algorithm. Taken from Sutton and Barto’s book [4]

Full size image

Policy-gradient methods [43] are a methodology to approximate functions in RL. These methods are the most popular class of continuous action RL algorithms [44]. With this approach, a stochastic policy is approached through an approximation function, independent of the value function, with its parameters. A measure is used to improve the performance of the policy and adjusts the parameters.

In this context, the policy-gradient framework uses a stochastic policy \(\pi\), parametrized by a column vector of weights \(\upsilon \in {\mathbb {R}}^{N_a}\), for \(N_a \in {\mathbb {Z}}\). \(\pi (u \mid x)\) denotes the probability density for taking action u in the state x. The objective function \(\Gamma (\pi )\) maps policies to scalar measure of performance, defined by

$$\begin{aligned} \Gamma (\pi ) = \int _X d^\pi (x) \int _U \pi _\upsilon (u\mid x)Q^\pi (x,u) du dx, \end{aligned}$$
(6)

where \(d^\pi (x) := \int _X \sum _{t=0}^\infty \gamma ^{t-1}P(x\mid x_0,u)\) is the stationary distribution of the discounted states occupancy under \(\pi\) and \(Q^\pi (x,u)\) is the action value function. The basic idea of policy-gradient methods is to adjust the parameter \(\upsilon\) of the policy in the direction of the gradient \(\nabla _\upsilon \Gamma (\pi )\):

$$\begin{aligned} \upsilon _{t+1} - \upsilon _{t} \approx \alpha _\upsilon \nabla _\upsilon \Gamma (\pi ). \end{aligned}$$
(7)

The fundamental result of these methods is the policy-gradient theorem [43], which defines the gradient as

$$\begin{aligned} \nabla _\upsilon \Gamma (\pi ) = \int _X d^\pi (x) \int _U \nabla _\upsilon \pi _{\upsilon }(u\mid x) Q^{\pi }(x,u) \mathrm{d}u \mathrm{d}x. \end{aligned}$$
(8)

Let \(h_\theta : X\times U \longrightarrow {\mathbb {R}}\) be an approximation of the value function \(Q^\pi (x,u)\) with the parameter \(\theta \in {\mathbb {R}}^{N_c}\), for \(N_c \in {\mathbb {Z}}\), so that it does not affect the unbiasedness of the policy-gradient estimate. To find a close approximation of \(Q^\pi (x,u)\) by \(h_\theta (x,u)\), the parameter \(\theta\) must be found to minimize the quadratic error of the approximation as follows:

$$\begin{aligned} \epsilon _t^\pi (x,u) = \dfrac{1}{2}\left[ Q^\pi (x,u) - h_\theta (x,u) \right] ^2. \end{aligned}$$
(9)

The gradient of the quadratic error can be used to find an optimal value of \(\theta\). Considering the approximation of \(Q^\pi\) by \(h_\theta\), Eq. (8) is expressed as:

$$\begin{aligned} \nabla _\upsilon \Gamma (\pi )&= \int _X d^\pi (x) \int _U \nabla _\upsilon \pi _\upsilon (u\mid x)h_\theta (x,u) \mathrm{d}u \mathrm{d}x. \end{aligned}$$
(10)

This approximation is acceptable if \(\nabla _\theta h_\theta (x,u) = \nabla _\upsilon \log \left( \pi _\upsilon (u \mid x)\right)\) is satisfied.

Under this approach, the expected value of \(h_\theta\) given policy \(\pi\) is zero, indicating the value function has zero mean in each state. The most convenient is to approximate an advantage function \(A^\pi (x,u) = Q^\pi (x,u) - V^\pi (x)\) instead of \(Q^\pi (x,u)\) [45]. This implies that the approximation function only represents the relative value of an action u in some state x and not the absolute value of \(Q^\pi\) [46]. The value function \(V^\pi (x)\) is a baseline in the advantage function, such that the variance of the policy-gradient is minimized [47]. In other view, as

$$\begin{aligned} Q^{\pi }(x,u) = E_\pi \left[ r_{t+1} + V^\pi (x_{t+1}) \mid x_t = x, u_t = u, \right] , \end{aligned}$$
(11)

then, according to Sutton and Barto [4]:

$$\begin{aligned} A^\pi (x,u) = E_\pi \Big [ r_{t+1} + \left( V^\pi (x_{t+1}) - V^\pi (x_{t}) \right) \mid x_t = x, u_t = u, \Big ], \end{aligned}$$
(12)

that is the expected value of the TD error (5). Thus, \(h_\theta\) would approximate a value function \(V^\pi (x)\), and the gradient in (10) takes the form of

$$\begin{aligned} \nabla _\upsilon \Gamma (\pi )&= \int _X d^\pi (x) \int _U \nabla _\upsilon \pi _\upsilon (u\mid x)\hat{\delta _t} \mathrm{d}u \mathrm{d}x \nonumber \\&= E_{\pi }\left[ \hat{\delta _t} \nabla _\upsilon \log \left( \pi _\upsilon (u\mid x)\right) \right] , \end{aligned}$$
(13)

where \(\hat{\delta _t} = r_{t+1} + \gamma h_\theta (x_{t+1}) - h_\theta (t)\), and \(h_\theta (x): X \longrightarrow {\mathbb {R}}\) the function approximation of value function \(V^\pi (x)\).

In the context of A2C, let \(h_\theta (x) = V_\theta (x)\) be the approximate state value function from the critic. The update from the value function is through \(\theta\). The parameter \(\theta\) is adjusted by the gradient of the quadratic error (9) as follows:

$$\begin{aligned} \theta _{t+1}&= \theta _t + \alpha _\theta \hat{\delta _t} \nabla _\theta V_{\theta _{t}}(x_t), \end{aligned}$$

where \(\alpha _\theta > 0\) is a step-size parameter of the critic. It is clear that the gradient of the quadratic error is the gradient of the approximation scaled by the TD error. On the other hand, the policy, that represents the actor, is updated based on the gradient in (12) as follow:

$$\begin{aligned} \upsilon _{t+1} = \upsilon _t + \alpha _{\upsilon } \hat{\delta _t} \nabla _\upsilon \log \left( \pi _\upsilon (u\mid x)\right) , \end{aligned}$$

where \(\alpha _\upsilon > 0\) is a step-size parameter of the actor.

4 Proxemics behavior in cognitive agents

In this section, we present different scenarios where agents confront another artificial agent with a proxemic characteristic. These scenarios are modifications of state-of-the-art environments, mimicking a proxemics human scenario, where cognitive agents give signals or react to the agent behavior.

4.1 Proxemics grid-world problem

We propose a modified version of the discrete grid-world problem [18]. In this environment, an issuer is placed on one fixed state and is responsible for giving a signal of disagreement when the learning agent is too close. Two regions are defined around the issuer, the uncomfortable region and the target region. The uncomfortable region comprises the states that make up a square around the issuer. In this environment, the uncomfortable region is only an area of negative reward. Similarly, the target region comprises the states that make up a square around the uncomfortable region. Figure 4 shows the proxemics grid-world domain with uncomfortable and target regions. A new action, PING, is added to the four traditional ones (UP, DOWN, LEFT, RIGHT). This action represents a communication signal with the issuer, i.e., the approaching agent sends a ping to ask the issuer if it is in the target region.

Fig. 4
figure 4

Proxemics grid-world domain. A robot starts in an initial position. The issuer is placed in a fixed position and has two regions, the uncomfortable region (red) and the target region (blue) (color figure online)

Full size image

The task finishes in three conditions:

  • Condition C1: When the agent reaches the issuer.

  • Condition C2: When the agent sends ping five times out of the target region.

  • Condition C3: When the agent sends ping in the target region.

The reward function is defined as

$$\begin{aligned} \rho = \rho _\mathrm{issuer} + \rho _\mathrm{grid}, \end{aligned}$$
(14)

where \(\rho _\mathrm{issuer}\) is a numerical reward given by the issuer when the agent performs the PING action, and \(\rho _\mathrm{grid}\) is the environment reward defined as

$$\begin{aligned} \rho _{grid} =\left\{ \begin{array}{lll} -1.0 &{}\text{ if } &{} \text{ conditions } \text{ C1 } \text{ or } \text{ C2 } \\ -0.8 &{} \text{ if }&{} \text{ the } \text{ agent } \text{ reaches } \text{ the } \text{ uncomfortable } \text{ region } \\ -0.4 &{} \text{ if } &{} \text{ the } \text{ agent } \text{ sends } \text{ PING } \text{ out } \text{ of } \text{ the } \text{ target } \text{ region } \\ +1.0 &{} \text{ if }&{} \text{ condition } \text{ C3 } \\ -0.1 &{} \text{ if } &{} \text{ the } \text{ agent } \text{ reaches } \text{ another } \text{ state } \\ \end{array} \right. . \end{aligned}$$
(15)

In our experiments, we use a \(10\times 12\) grid-world, the issuer is placed in (6, 8) and is fixed during the training. Each agent starts the training in the superior left corner of the grid (0, 0).

4.2 Robot approaching problem

We present a robot approaching problem based on the ship steering problem. This is an episodic problem [48, 49] where a ship has to maneuver at a constant speed through a gate placed in a fixed position. At each time t, the state of the ship is given by its coordinate position x and y, orientation \(\theta\), and actual turning rate \({\dot{\theta }}\). The action is the desired turning rate of the ship r. In each episode, the goal is to learn a sequence of actions to get the ship through the gate in the minimum amount of time.

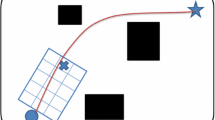
Based on the mechanic of the ship steering, we propose the robot approaching problem to include proxemic behavior (see Fig. 5). In our environment, a robot replaces the ship, that is the learning agent. The issuer replaces the gate, giving the signal or information when the agent is too close. Concerning the proxemic problem, the issuer, placed in a fixed position, has an individual space that avoids the robot hitting it.

To explore the behavior of the learning agent when the issuer gives any information during the learning, we propose two modifications on our environment. These modifications involve the personal space area and the direct information given by the issuer.

4.2.1 Robot approaching in uncomfortable region

In this environment, two regions are defined around the issuer, the uncomfortable and the target regions (similar to the grid-world problem). The uncomfortable region is a circle area of radius \(r_{u}\) around the issuer that mimics the intimate space of a person. The agent receives a negative reward if it invades this region. The target region (or social region) is a circle area of radius \(r_{T}\) \((r_{T} \gg r_{u})\) that contains the uncomfortable region (two concentric regions). In our implementation, the values of \(r_u\) and \(r_T\) are 10 and 20 meters, respectively. Figure 5 shows the robot approaching domain with the uncomfortable and target regions.

Fig. 5
figure 5

The robot approaching domain. A robot starts in an initial position, direction and turning rate. The issuer is placed in a fixed position and has two regions, the uncomfortable region (red) and the target region (blue) (color figure online)

Full size image

Similarly to the grid-world problem, we add the probability of sending PING, due to the PING being a binary action. Then, in each time step, the agent selects a two dimensional action, the turning rate and the probability of sending PING in this position.

In our experiments, we use the logit of the probability as action:

$$\begin{aligned} logit(p) = \log \left( \dfrac{p}{1-p}\right) . \end{aligned}$$
(16)

The logit modifies the domain of the action, allowing that the action concerning the PING has the same domain that the turning rate. The task finishes under the next conditions:

  • Condition C1: When the agent is out of bounds.

  • Condition C2: When the agent reaches the uncomfortable region.

  • Condition C3: When the agent sends PING in the target region.

The reward function is defined as

$$\begin{aligned} \rho =\left\{ \begin{array}{rl}-100 &\text{if conditions C1 or C2} \\ -4K & \text{if the agent sends PING out of target region} \\ -1 & \text{if another state} \\ 0 & \text{if condition C3} \\ \end{array} \right. . \end{aligned}$$
(17)

where \(K = d(A_{(x,y)}, I_{(x,y)})(x_I^2 + y_I^2)^{-\frac{1}{2}}\), and \(d(A_{(x,y)}, I_{(x,y)})\) is the euclidean distance between the agent, in the position \((x_A,y_A)\), and the issuer, in the position \((x_I,y_I)\).

4.2.2 Robot approaching with disagreement area

In this environment, the field is divided in two areas, the disagreement area and the agreement area. The disagreement area is a circle area of radius \(r_{d}\) with the center in the issuer. This area is composed of two subregions, the disagreement no stop region and the disagreement stop region. In the former, the agent is free to move in everywhere, but receives a negative reward in each step. In the latter, the agents stop immediately when they reach there. The disagreement area mimics the private area from a person when a no intimate interaction occurs, i.e., when the two agents (learning agent and issuer) should be too close to occur the interaction. The disagreement stop region allows that the agent does not reach too close to the issuer. In our implementation, the value of \(r_d\) is 20 meters, and the disagreement stop region has a radius of 10 meters. Finally, the agreement area includes the points outside of the disagreement area. In this area, the issuer is indifferent to the behavior of the learning agent, except when the agent stops. Figure 6 shows the robot approaching domain with disagreement areas, where blue is the agreement area, light red is the disagreement no stop region and dark red is the disagreement stop region.

Fig. 6
figure 6

The robot approach domain with disagreement area. A robot starts in the agreement area (blue) with an initial position, direction and turning rate. The issuer is placed in a fixed position and has two regions, the disagreement no stop region (light red) and the disagreement stop region (dark red) (color figure online)

Full size image

With the aim at using the area as information to the learning agent, we consider the area as a part of the state. Then, at each time t, the state of robot is given by its coordinate position x and y, orientation \(\theta\), actual turning rate \({\dot{\theta }}\), and the disagreement region \(\delta\). Here, \(\delta = 1\) if the robot is in the disagreement area, and \(\delta =0\) if the robot is in the agreement area. A new action, STOP, is added to the turning rate one. This action decides whether to stop or not the robot’s trajectory. Basically, the STOP action is the decision of the agent if it stops or continues moving in the environment. Similarly to the previous environment, we use the logit of the probability of STOP (see expression (15)) as action to maintain the same domain that the turning rate.

It is clear that the task ends when the learning agent selects STOP as action. However, there are other conditions to finish the task:

  • Condition C1: When the agent is out of bounds.

  • Condition C2: When the agent reaches the disagreement stop region.

  • Condition C3: When the agent stops.

The reward function is defined as

$$\begin{aligned} \rho =\left\{ \begin{array}{rl} -100 & \text{if conditions C1 or C2} \\ -\rho_d & \text{if condition C3} \\ -50 & \text{if the agent is on disagreement no stop region} \\ -1 & \text{if another state} \\ \end{array} \right. ,\end{aligned}$$
(18)

where \(\rho _d = 100 K (d(A_{(x,y)}, I_{(x,y)}) - r_d)\), \(d(A_{(x,y)}, I_{(x,y)})\) is the euclidean distance between the agent (in the position \((x_A,y_A)\) and the issuer (in the position \((x_I,y_I)\), and

$$\begin{aligned} K =\left\{ \begin{array}{rcl} (x_I^2 + y_I^2)^{-\frac{1}{2}} &{} \text{ if } &{} \delta = 0 \\ r_d &{} \text{ if } &{} \delta = 1 \\ \end{array} \right. . \end{aligned}$$
(19)

The \(-\rho _d\) value punishes the agent when it stops far away from the issuer, and benefits the agent when it is too close to the disagreement area. The K factor weighs the reward based on which region the agent is in.

5 Experimental results

This section presents the results obtained and the discussion of the research. To study the performance of the agents, we observe the behavior of the maximum action-value Q for the grid-world problem and the action-value Q for each action. Furthermore, for the continuous scenarios of the robot approaching problem, we study the behavior of the obtained discounted reward and the trajectories of the agents. We present a discussion about the behavior of the agents and what is the influence of each feature from the environment.

5.1 Grid-world problem

We perform the training of 100 agents with the Q-learning algorithm [40] in the modified grid-world problem. Each agent is trained during 10, 000 time-steps using the reward function presented in (13). We use \(\epsilon\)-greedy as action selection policy. We set the values of both \(\epsilon\) and the learning rate \(\alpha\) at 0.6 and the discount factor \(\gamma\) at 0.9.

To study how the issuer influences the performance of the learning agent, we consider three scenarios where the issuer gives numerical information through the reward:

  • Scenario S1: \(\rho _\mathrm{issuer}=0\) in each PING action selection.

  • Scenario S2: \(\rho _\mathrm{issuer}\) is a random value in \((-1,1)\).

  • Scenario S3: \(\rho _\mathrm{issuer}=-\dfrac{d_1(P_\mathrm{agent}, P_\mathrm{issuer})}{d_1(P_\mathrm{start}, P_\mathrm{issuer})},\) where \(d_1(\cdot , \cdot )\)is the \(L_1\) distance, \(P_\mathrm{agent}\), and \(P_\mathrm{issuer}\), and \(P_\mathrm{start}\) are the position on the grid from the agent, the issuer and the start point. The factor \(\rho _{issuer}\) indicates that states further from the issuer have a low reward, and the denominator standardizes it on (\(-1\), 0).

Fig. 7
figure 7

Results of our experiments in three scenarios. The first row (a–c) shows the average of maximum Q-values per time step, the shaded area is between the maximum and minimum Q values from 100 agents. The second row (d–f) shows the average of the final Q-value for the actions UP, DOWN, LEFT, and RIGHT. The last row (g–i) shows the average final Q-values for the PING action

Full size image

Figure 7 shows the results of our experiments in the three scenarios. In terms of maximum Q-value per time step (Fig. 7a–c), there exists more variability when the issuer gives random rewards. However, according to the other scenarios, the maximum Q-value reaches values around 1 in several time steps. On the other hand, when the issuer gives rewards based on distance, the variability of Q-values is minor.

The Q-values for each action are more focused on the target region than on the other scenarios when the issuer gives rewards based on distance (Fig. 7d–f). This is expected due to the agent receiving additional information on how to move through the grid.

Concerning the PING, the issuer reward highlights the importance of giving PING in the target region, as shown in Fig. 7g–i. The graph shows how the states of the target region have only Q-values greater than zero. While with the lack of information (Scenario S1), states outside the target region have Q-values greater than zero.

5.2 Robot approaching problem

We study the performance of 20 learning agents in a continuous domain with proxemic behavior. We analyze the average collected discounted reward from a training and validation phase. The training phase consists of 1000 steps per episode, where weights are updated every 10 steps. The validation phase consists of 1000 steps after each episode, during these steps, the weights are not updated. In our experiments, the field size is \(150 \times 150\), the issuer is placed in (110, 110) and is fixed during the training. The agents are trained using advantage actor-critic (A2C) algorithm [41] for 10000 episodes, each one with 1000 time-steps. Each agent starts the training in the coordinate (1, 1). We use a Gaussian distribution to select random actions, with mean \(\mu (x_t)\) depending on states. We used a multilayer perceptron (MLP) as function approximation with a hidden layer for the actor and the critic, the mean of distribution \(\mu (x_t)\) and the value function \(Q(x_t)\), respectively. The approximation is carried out as follows:

  • For the value function \(Q(x_t)\), an MLP with a hidden layer of 256 units, and an output layer with one unit is used.

  • For the mean \(\mu (x_t)\) of the policy, an MLP with a hidden layer of 256 units, and an output layer with two units (the turning rate and the logit) is used.

The input layer depends on the environment, four units are used for the robot approaching in uncomfortable region problem, and five units for the robot approaching with disagreement area problem. In both architectures, we apply as activation function the hyperbolic tangent (tanh) in the hidden layer, and in the output layer a linear activation. The learning rate is empirically set at \(\alpha = 0.0007\), the discount factor \(\gamma\) is set at 0.9, and the standard deviation from policy at (1.5, 0.5), for turning rate and logit, respectively. The values of the weights in the neural network are randomly initialized from a uniform distribution based on Xavier weight initialization [50].

5.2.1 Uncomfortable region

First, we study the behavior of the learning agent in the robot approaching in uncomfortable region problem. Figure 8 shows the average discounted reward for 20 agents, where the red line is the average during the training and the blue line is the average during validation steps. We can observe that after 4000 episodes, the average reward is steady, however, after 6000 episodes, the average increases and finds a higher steady point. This behavior suggested that the weights of the value function \(Q(x_t)\) reach a local minimum in these episodes.

Fig. 8
figure 8

Average collected discounted reward over 20 agents using A2C in the robot approaching in uncomfortable region environment. The red line is the collected reward during the training, and the blue line is the collected reward during the validation phase

Full size image

To explore how the behavior of the trajectories is, we empirically select the agent with the highest reward in the validation phase. Figure 9 shows the trajectories of the agent during the task. We compute these trajectories with different start positions and orientations, and these only are shown when the agent reaches the target region and sends PING. Due to the fixed start position, the agent only learns to reach the target region in some part of the coordinate plane. However, the agent always finds the better way to finish the task independently of the start orientation. On the other hand, we observe that the agent always stops in the frontier of the target position. This behavior is due to the environment configuration, given that the agent stops immediately when it sends PING in the target region.

Fig. 9
figure 9

Trajectories in the robot approach in uncomfortable region environment. The trajectories are computed from agent with the highest reward in the validation phase in different start positions. Only success trajectories are shown

Full size image

Figure 10 shows the trajectories with the probability of sending PING, where the blue region indicates a value of probability closer to zero, and the red region shows a value closer to one. We observe that the agent commences to send PING when it is close to target region. This behavior makes the space into two parts. In the first one, the agent does not communicate with the issuer, and in the second one, the agent maintains a constant communication with the issuer until the task has finished.

Fig. 10
figure 10

Probability of sending PING in the robot approach in uncomfortable region environment. Red points show probability closer to one, and blue points show values closer to zero. The trajectories are computed from agent with the highest reward in the validation phase from different start positions. Only success trajectories are shown

Full size image
Fig. 11
figure 11

Average collected discounted reward over 20 agents using A2C in the robot approaching in disagreement area environment. The red line is the collected reward during the training, and the blue line is the collected reward during the validation phase

Full size image

5.2.2 Disagreement area

Finally, we study the behavior of the learning agent in the robot approaching in disagreement area problem. Figure 11 shows the average discounted reward for 20 agents. We can observe that until 4000 episodes the average reward is increasing. However, in episode 4000, there is a breakpoint, where the average reward decreases but has a growing tendency afterward. This behavior suggests that the weights of the value function \(Q(x_t)\) could reach a different local minimum in these episodes.

Fig. 12
figure 12

Trajectories in the robot approach in disagreement area environment. The trajectories are computed from the agent with the highest reward in the validation phase from different start positions. Only success trajectories are shown

Full size image

Figure 12 shows the trajectories of the agent with highest reward in the validation phase. These are shown only when the agent selects the STOP action. Due to the start position, the agent does not complete the task successfully in some parts of the coordinate plane. We also observe that with angles \(-\pi\) and \(-\frac{3}{4}\pi\), the agent completes fewer successfully trajectories in comparison with other angles. Another important aspect is that several trajectories do not even reach the frontier of the disagreement area. This performance can be explained by the STOP action. Figure 13 shows the trajectories with the probability of STOP. Similarly to the PING action, the STOP action divides the coordinate plane into two big areas. In the first one, the agent is free to move, and in the second one, the agent is obligated to stop. The light red region is an overestimate of disagreement areas. We empirically mark this part of the field. In that section of the coordinate plane, the agent decides to stop because of the high negative reward, manifesting a conservative behavior by the agent.

Fig. 13
figure 13

Probability of STOP in the robot approach in disagreement area environment. Red points show probability closer to one, and blue points show values closer to zero. The light red region shows an overestimate of the disagreement area. The trajectories are computed from the agent with the highest reward in the validation phase from different start positions. Only success trajectories are shown

Full size image

5.3 Discussion

In the environments presented above, the agent can complete the task successfully. However, there is a dependency on the agent’s initial position that affects its performance in areas far from that point. Also, the fixed position of the issuer is an essential factor for agent learning, because the agent could not perform well if the issuer moves through space. On the other hand, the agent can identify the best path to reach the region of interest, obtaining the highest reward. Furthermore, the agent can identify those regions where it can freely move without suffering punishment (based on reward). In the grid-world problem, the Q-value of the PING highlights those points with the highest reward, which are also the points in the target region. In continuous environments, with the help of PING and STOP, we can see a division of the space that separates areas where it is more likely to select these actions. These regions are conservative because they move away from the target region, implying that the agent prefers to stop rather than invade that region. This situation is more evident in the disagreement area, where the STOP high probability area contains the disagree area (see Fig. 13, light red covers up the circle), the latter being smaller than the former. Unlike the uncomfortable area, where the area of the high probability of sending PING is larger than the disagreement area. However, this is not surprising since the agent sends PING with information communicated by the issuer and not with the information perceived by the agent (in the disagreement area, the agent has information on the level of disagreement in its state).

6 Conclusions and future works

In this paper, we studied the agent performance in an environment based on proxemic behavior. We implemented a modified grid-world problem and the robot approaching problem in two versions, uncomfortable region, and disagreement area. These environments consider that an issuer agent gives information about its disagreement level to an RL agent that performs a trajectory, reaching the goal. Different regions around the issuer mimic their personal space, which replaces the traditional target of the agent. We implemented a Q-learning algorithm for the grid-world problem and A2C for the robot approaching problems. Our results show that the agent can reach the target region or get close to the issuer, even without giving information. Regarding the PING and STOP action, the agent manages to select these actions in a right place of the space, allowing the task to be performed satisfactorily. However, the agent is conservative because it performs these actions where the reward is not so high. On the other hand, the agent can identify nonconformity regions, even when it does not have information about them. This aspect gives the possibility to overestimate the personal space of the issuer (due to its conservative characteristic). The environments represent simply the interaction of the agent and the issuer, which helps to explore the behavior of the agent in an environment with proxemic behavior. However, it is necessary to include other features to approximate an environment with proxemic behavior accurately. For example, it is necessary for the personal space to be variable and to depend on characteristics expressed by the issuer, in addition to the agent positively or negatively influencing the issuer to modify their proxemics.

In future alignments, we explore identifying the proxemics region based on issuer information, such as gaze, orientation, emotion, or other aspects. Also, we intend to implement asymmetric proxemic regions to mimic human proxemic behavior. In our experiments, the fixed start position influences the trajectory performance and the agent’s capability to reach the target. Then, we intend to implement no fixed proxemic region, considering that the proxemic space changes by external factors. Finally, we intend to study the agent performance in more complex environments, involving other algorithms and techniques of reinforcement learning and deep learning.