Optimal design of fuzzy-PID controller for automatic generation control of multi-source interconnected power system

Abstract

This paper suggests a fuzzy logic controller (FLC) structure from seven membership functions (MFs) and its input–output relationship rules to design a secondary controller to reduce load frequency control (LFC) issues. The FLC is coupled to a proportional–integral–derivative (PID) controller as the proposed FPID controller, which is tuned by an optimized water cycle algorithm (WCA). The proposed WCA: FPID scheme was implemented with two models from the literature under the integral time absolute error cost function. Initially, a two-area non-reheat unit was implemented, and the gains of PID and FPID controllers were adjusted to verify the suitability of WCA in solving LFC issues. Then, in order to identify the robustness of the closed-loop system, sensitivity analysis is carried out. Additionally, a two-area non-reheat unit was tested under the governor dead band nonlinearity. To guarantee the suitability of the proposed FPID controller, a model with a mixture of power plants, such as reheat, hydro, and gas unit in each area was carried out with and without the HVDC link, which can increase practical issues with LFC. The proposed controller's robustness was studied for all models under numerous scenarios, step load perturbations (SLP), and different objective functions. Simulation results proved that the proposed FPID controller provided superior performance compared to recently reported techniques in terms of peaks and settling time.

1 Introduction

Advanced power generation systems face significant challenges in order to match power generation with consumer demand. The power systems frequency is sensitive to fluctuations caused by consumer requests, making the frequency and tie-line power deviate from nominal performance. A significant deviation increases the possibility of overloading susceptible equipment, which poses a substantial threat to the stability of power systems. The primary controller is typically not adequate to return the power system to a steady state. Consequently, a secondary controller, LFC, or automatic generation control (AGC), is necessary to maintain system frequency and tie-line power within their nominal bounds during any step load perturbations (SLP) and ensure the connected generators maintain synchronization. The AGC output is the area control error (ACE), which is driven to zero to minimize the deviations in frequency and tie-line power [1, 2].

Many approaches to address the concerns of LFC have been suggested, such as adaptive control, intelligent control, and optimal control [3,4,5]. Standard proportional–integral/proportional–integral–derivative (PI/PID) controllers are often used to address LFC issues because of their reliability, structural simplicity, and the satisfactory ratio between performance and reasonable cost [6]. Therefore, tuning PI/PID controllers are used in many optimization approaches, such as bacterial foraging optimization [7], differential evolution [8], firefly algorithm [9], quasi-oppositional harmony search [10], and teaching–learning-based optimization [11]. So far, due to the outcome of nonlinearity, realistic aspects of power system such as load disturbances and uncertainties such as governor dead band, generation rate control (GRC), and time delay, increase the chance of causing instability in power systems [12].

Conventional PID controllers are used at the explicit operating states. Due to the nonlinear behavior in real systems, PID controllers are not appropriate for fluctuating conditions; hence, the performance of the PID controller must be improved [13]. To overcome this weakness, the application of a fuzzy logic design is recognized as one of the most effective PI/PID controller design methods in the presence of nonlinearity [14,15,16] and including PV and wind turbine plants [17], making the FPID an expandable controller. The FLC was used to address LFC issues, to confirm that the FLC has a good dynamic response over control structures, such as optimal control, and traditional PI and PID controller [18, 19]. The fuzzy plus PID (FPID) controller was designed for automatic LFC of a two-area non-reheat system to improve stability [20, 21]. Previously, a FPID controller that was adjusted using the firefly algorithm (FA) for a multi-area multi-unit power system showed superior dynamic response, which was verified using traditional methods [22]. Also, for sophisticated interconnected power systems in a deregulated circumstance, including nonlinearity, a FPID controller with a derivative filter (FPIDF) was established in [23]. The design of an optimal fuzzy fractional-order PID controller for of a photovoltaic–reheat thermal is presented in [24]. More recently, for a better result, hybrid particle swarm optimization-pattern search (hPSO-PS) based on a fuzzy PI controller was implemented [25]. Additionally, an effective hybrid of the local unimodal sampling (LUS) algorithm combined with the teaching–learning-based optimization (TLBO) called LUS-TLBO [26] and a hybrid of the cuckoo optimization algorithm (COA) with a harmony search (HS) algorithm (HSCOA) [15] have been magnificently employed to adjust the gains of FPID controllers for LFC problems.

From the above discussion, the enhancement of the fuzzy plus fundamental controller performance comes from:

• 1. The structure of the fundamental controller such as PI, PID, PIDF, and fractional-order PID (FOPID).

• 2. The optimization algorithm (which plays a key role in the system enhancement),

• 3. The structure of fuzzy; including the membership functions (MFs) and the input–output relationship rules.

Many structures of the basic controller, optimization algorithms, and the hybrids are clearly explained in the literature. However, considering the key role in system enhancement of the MFs of input–output, its rules, and relative weights, there is little information present in the literature. There are many fuzzy structures with different numbers of MFs, that are designed to address LFC issues [2, 21]. The most extensively used fuzzy structure is the five MFs, based on the prevalence in the literature [2, 27]. Therefore, in this paper, design of an effective fuzzy structure in terms of MFs with enhanced rules is the hypothesized strategy in reducing LFC issues. Fuzzy structures with seven MFs and the adjusted rules plus a conventional PID (proposed FPID) controller to obtain the best dynamic performance of LFC problems are presented. As mentioned before, the optimization algorithm plays an essential role in the enhanced performance of power systems. According to the “no free lunch” principle, any meta-heuristic optimization algorithm might be more efficient than other algorithms in tackling a specific problem while not doing well in other problems [28]. To obtain a more desirable degree of smooth and damp fluctuations and owing to the continual development of integrated power generation, computational algorithm-based controllers give a significant motivation for research to design novel mixtures to discover the best suitable ones in LFC difficulties. One of the best optimization algorithms is the water cycle algorithm (WCA) [29], which is commonly used in different engineering challenges [30,31,32]. WCA is extensively used to combat LFC issues [1, 33,34,35]. Therefore, the optimization of the WCA was chosen to achieve the best improvements and scaling factors of the proposed FPID. Furthermore, the WCA-based FPID with five MFs (WCA: FPID) was also implemented to fairly compare its performance with the proposed FPID controller with seven MFs under the same environment. A common two-area multi-unit thermal-hydro-gas power source was also considered with and without the HVDC tie-line in test system 2 to demonstrate the effectiveness and robustness of the proposed FPID controller.

In summary, the main contributions of this study are:

• i. To propose a powerful scheme such as a WCA-based PID and FPID with five and seven MFs to resolve LFC issues in interconnected power systems.

• ii. To complete the sensitivity analysis by changing the system parameters and loading conditions.

• iii. To employ a two-area multi-unit system with/without an HVDC link, which is raised for the practical issues of LFC.

• iv. To carry out the dynamic transient responses of the interconnected power system.

• v. To compare the dynamic performance of the proposed FPID controller with recently reported strategies.

2 Materials and methods

2.1 Power system under study

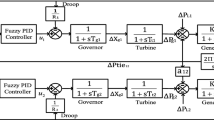
The system described herein is widely used in the literature to design and analyze the AGC of the interconnected power system. This is the first example of a system model approach that discusses and analyzes, in a straightforward manner, the limitations and issues arising from LFC. The transfer functions of test system 1 (two-area non-reheat thermal power plant) are presented in Fig. 1a [2, 15]. Each non-reheat power plant consists of a speed governing system, turbine, and generator with capacity of 2000 MW , and a nominal preliminary loading of 1000 MW. The transfer functions (TF) of various blocks used in each non-reheat thermal power plant are carried out in [2, 15].

Fig. 1

a Transfer function model of test system 1 of non-reheat thermal power system. b Simulink file of test system 1 of non-reheat thermal power system

The steam turbine is characterized by:

$$G_{T} \left( s \right) = \frac{1}{{1 + T_{t} S}} .$$

(1)

Whenever the perturbation occurs, the frequency fluctuates, resulting in system instability. As a result, the controlling system detects these fluctuations and adjusts the turbine speed to achieve an optimum speed that suppresses the frequency fluctuations. The speed governor valve TF is:

$$G_{G} \left( s \right) = \frac{1}{{1 + T_{g} S}} .$$

(2)

The general TF of the generator-load is presented by:

$$G_{P} \left( s \right) = \frac{{K_{{{\text{PS}}}} }}{{1 + T_{{{\text{PS}}}} S }}$$

(3)

where $K_{{{\text{PS}}}} {\text{ and }}T_{{{\text{PS}}}}$ are the power system gain and the power system time constant, respectively [11, 15].

Each area has three inputs and two outputs. The inputs are the input of the controller $\Delta P_{{{\text{ref}}}}$, tie-line power deviation $\Delta P_{{{\text{tie}}}}$, and the load perturbation $\Delta P_{L}$ and the outputs are the generator frequency deviation $\Delta f.$ The combination of frequency deviation and tie-line power error is known as the area control error (ACE). The ACEs are taken as input to the FPID controllers corresponding to each area. ACEs for the test system 1 as shown in Fig. 1a are:

$${\text{ACE}}_{1} = \Delta P_{{{\text{tie}}}} + B_{1} \Delta f_{1}$$

(4)

$${\text{ACE}}_{2} = \Delta P_{{{\text{tie}}}} - { }B_{2} \Delta f_{2}$$

(5)

where $\Delta P_{{{\text{tie}}}}$ is the change in tie-line power, $\Delta f_{1}$ and $\Delta f_{2}$ are the frequency deviations in area 1 and area 2, respectively, and B is the frequency bias factor, [36]. When the power system is subjected to a load perturbation, ACEs are used as a regulating signal to diminish $\Delta P_{{{\text{tie}}}}$ and $\Delta f_{{\text{i}}}$ to zero at the steady state. Thus, the inputs and outputs scaling factors of the FPID controller must be selected suitably to enhance the transient performance of the system.

Additionally, the governor dead band (GDB) is designed in the considered system to add more challenge and to prove the robustness of the HHO/PD-PI in the presence of nonlinearity properties [15].

2.2 Controller structure

The PID is extensively used in industry because of its reliability, structural simplicity, and effective performance [37]. Therefore, employing FLC cascaded by the PID controller, referred to as a fuzzy-PID (FPID) controller, has confirmed superior reliability compared to a PID controller in overcoming the challenges in the growth of power systems [15, 38]. Test system 1 being studied with the FPID was built in MATLAB/SIMULINK and incorporated the parameter values shown in Fig. 1b. The typical structure of the FPID controller is demonstrated in Fig. 2, where ${K}_{1},{ K}_{2}$ are the input scaling factors and ${K}_{P}, {K}_{I,} \mathrm{and }\,\,{K}_{D}$ are the output scaling factors. The FLC has four components. (i) The fuzzifier which alters the value into fuzzy sets. (ii) The fuzzy inference system which performs all the logical manipulations. (iii) The rule base which contains the control rules and MFs. (iv) The fuzzy inference system's output (which is the fuzzy value that is transformed into real value by the defuzzification method) [16]. However, there are many MFs in the FLC; the triangular MFs are commonly accepted in FLC strategies because of their real-time applications, economical nature, and improved performance [39]. The fuzzy controller with scaling factors, where five linguistic variables of MFs for inputs and output of fuzzy are used, was planned in [40] and was used effectively used many times in the literature [2, 15, 16].

Fig. 2

Structure of fuzzy-PID controller

In this study, the proposed fuzzy controller structure consists of seven triangular MFs, as shown in Fig. 3. The fuzzy inputs are the ACE and the rate of change of ACE (ACE derivative). The outputs were converted into seven linguistic variables NL (Negative Large), NM (Negative Medium), NS (Negative Small), Z (Zero), PS (Positive Small), PM (Positive Medium), and PL (Positive Large). Identical MFs with a similar range are used for both the inputs and the FLC design's output to get simplicity, enhanced computational efficiency, a smaller amount of memory usage, and enhanced performance analysis [41, 42]. The Mamdani fuzzy interface system with the centroid defuzzification technique was chosen in the proposed design. The proposed rules that relate the inputs and outputs of the FLC are given in Table 1. The fuzzy rules represent a significant function in the FLC performance [36]. Therefore, in this study, the input–output rules are studied extensively by examining the systems dynamic behavior and checking the rules suitability with four test systems. The surface of the fuzzy-PID controller is given in Fig. 4. A similar controller with the same gains is employed in area 1 and 2.

Fig. 3

Membership functions of the proposed FPID controller for error, error derivative, and the output of FLC

Table 1 Rule base for error, derivative of error, and FLC output

Fig. 4

Surface of fuzzy controller

Designing an optimum FPID controller, the gains/factors must be appropriately tuned. The preferred dynamic response has minimum settling time, in seconds, with a trivial overshoot and undershoot, in hertz, when the system is subjected to adequate perturbation. In this study, a robust algorithm such as WCA is used to adjust the FPID controller to extract greater dynamic performance from the AGC-controlled FPID. The WCA will be discussed in the following section.

2.3 Design of objective function

The power systems frequency is sensitive to fluctuations caused by consumer requests, making the frequency and tie-line power $(\Delta F,\,\, \mathrm{and}\,\, \Delta {P}_{\text{tie}-\text{line}})$ deviate from nominal performance. AGC's desired control designations should include ability to return the frequency deviations and tie-line error to predefined states, ensuring a satisfactory degree of stability for the closed-loop system, and providing a fast response with a rapidly dampened oscillation. A suitable objective function should be applied appropriately before using modern heuristic optimization-based controller schemes to achieve the best LFC performance. [27]. Many objective functions have been applied to the AGC problems in the literature, such as the integral square error (ISE), integral of time multiplied absolute error (ITAE), integral absolute error (IAE), and integral time square error (ITSE) to restore nominal performance. Although, the ITSE-based controller decreased the contribution of large initial errors and emphasized errors later in the response [6]. This provides more time to settle compared to the ITAE. The ITAE criterion better decreased the settling time than IAE or ISE, and also decreased the peak overshoot but less-so than the ITSE criterion [6, 43].

From the literature, the ITAE criterion is preferred in AGC studies. Thus, in this study, the ITAE criterion was used to adjust the scaling factors of the FPID controller. Furthermore, it was valuable to confirm the performance of the proposed controller under various performance criteria. Therefore, the corresponding value of the ITSE will be also calculated.

The ITAE and the ITSE objective functions are represented as:

$$J_{1} = {\text{ITAE}} = \mathop \int \limits_{0}^{{t_{{{{\rm sim}}}} }} \left( {\left| {\Delta F_{1} } \right| + \left| {\Delta F_{2} } \right| + \left| {\Delta P_{{{\text{tie}} - {\text{line}}}} } \right|} \right).t.dt$$

(6)

$$J_{2} = {\text{ITSE}} = \mathop \int \limits_{0}^{{t_{{{\text{sim}}}} }} [(\Delta F_{1} )^{2} + (\Delta F_{2} )^{2} + (\Delta P_{{{\text{tie}} - {\text{line}}}} )^{2} ].t.d$$

(7)

where $\Delta F_{1} ,\Delta F_{2}$ are the power system frequency deviations; $\Delta P_{{{\text{tie}} - {\text{line}}}}$ is the incremental variation in tie-line power; $t_{{{\text{sim}}}}$ is the simulation time which is 10 s for test system 1 and 20 s for test system 2. The optimum performance has the lowest value of $J$.

Minimize $J$ for FPID controller is subject to:

$$\begin{aligned} & K_{1}^{\min } \le K_{1} \le K_{1}^{\max } , \\ & K_{2}^{\min } \le K_{2} \le K_{2}^{\max } , \\ & K_{P}^{\min } \le K_{P} \le K_{P}^{\max } , \\ & K_{I}^{\min } \le K_{I} \le K_{I}^{\max } , \\ & K_{D}^{\min } \le K_{D} \le K_{D}^{\max } \\ \end{aligned}$$

(8)

where the min and max superscripts stand for the lower and the upper values of the corresponding parameter. The minimum and maximum values of the parameters are $0.0$ and $2.0$, respectively [2, 15, 36]. To examine the comparative evaluation between the proposed strategy and the published methods in the literature, the settling times and peak undershoots of the frequency deviation and tie-line power error results under different load demands have been considered. The parameters values point out the speed of the dynamic response profiles of the test systems in consideration.

3 Water cycle algorithm

The WCA is an advanced, nature-inspired heuristic scheme based on the water cycle procedure. The main idea of the WCA arises from the flow of rivers/streams to the sea. The procedures of the WCA are realizable, simple, and require a few parameters that are defined by the user [29]. To solve the optimization problem, the problem variables must be planned as a matrix of raindrops with dimensions $N_{{{\text{pop}}}} \times N_{{{\text{var}}}}$.

$${\text{Var}} = \left[ {\begin{array}{*{20}c} {X_{1}^{1} } & {X_{2}^{1} } & . & { .} & . & {X_{{N_{{{\text{var}}}} }}^{1} } \\ {x_{1}^{2} } & {X_{2}^{2} } & . & { .} & { .} & {X_{{N_{{{\text{var}}}} }}^{2} } \\ . & . & . & { .} & { .} & . \\ . & . & . & { .} & { .} & . \\ . & . & . & . & { .} & . \\ {X_{1}^{{N_{{{\text{pop}}}} }} } & {X_{2}^{{N_{{{\text{pop}}}} }} } & . & . & . & {X_{{N_{{{\text{var}}}} }}^{{N_{{{\text{pop}}}} }} } \\ \end{array} } \right]$$

(9)

where and are the population size and number of design variables, respectively. The cost of the streams, i.e., objective function (ITAE), is calculated by

$$C_{i} = {\text{Cost}}_{i} = f\left( {{\text{Var}}_{1}^{i} ,{\text{Var}}_{2}^{i} ,..,{\text{Var}}_{D}^{i} } \right), i = 1, 2, \ldots , N_{{{\text{Pop}}}} .{ }$$

(10)

The streams ($N_{{{\text{SR}}}}$) that provide the best cost are chosen as one sea and several rivers $(N_{R}$)

$$N_{{{\text{SR}}}} = N_{R} + 1.$$

(11)

The streams flow toward the rivers or toward the sea as

$$N_{{\text{Raindrops }}} = N_{{{\text{Pop}}}} - N_{{{\text{SR}}}} { }.$$

(12)

Allocating the streams to the rivers and/or to the sea depends on the flow intensity, as in the following equation [44]:

$$N_{{{\text{sn}}}} = {\text{round}}\left\{ {\left| {\frac{{{\text{Cost}}_{n} }}{{\mathop \sum \nolimits_{i = 1}^{{N_{{{\text{SR}}}} }} {\text{Cost}}_{i} }}} \right| \times N_{{{\text{Stream}}}} } \right\},\,\,{\text{n}} = 1,2, \ldots ,N_{{{\text{SR}}}} { }$$

(13)

where $N_{sn}$ is the number of streams. Figure 5 shows the WCA flowchart. Let us assume that $d$ is the remoteness of the river and sea [44]. Let $X (X \in \left( {0,C \times d} \right) C > 1)$ is the river path flowing to the sea which is randomly connecting [45], $C$ lies between $1\,\,\mathrm{and}\,\,2,\,\,\mathrm{and} \,\,d$ is the present distance among the river and the sea. Hence, the location will be updated according to the $\mathrm{jth}$ stream $X_{{{\text{Stream}}}}^{j + 1}$ and river $X_{{\text{River }}}^{j + 1}$ in the exploitation phase, which are characterized by [45]

$$\begin{aligned} X_{{{\text{Stream}}}}^{j + 1} = & X_{{{\text{Stream}}}}^{j} + {\text{rand}} \times C \times \left( {X_{{\text{River }}}^{j} - X_{{{\text{Stream}}}}^{j} } \right) \hfill \\ X_{{{\text{Stream}}}}^{j + 1} = & X_{{{\text{Stream}}}}^{j} + {\text{rand}} \times C \times \left( {X_{{\text{Sea }}}^{j} - X_{{{\text{Stream}}}}^{j} } \right) \hfill \\ X_{{\text{River }}}^{j + 1} = & X_{{\text{River }}}^{j} + {\text{rand}} \times C \times \left( {X_{{\text{Sea }}}^{j} - X_{{\text{River }}}^{j} } \right) \hfill \\ \end{aligned}$$

(14)

Fig. 5

Flowchart of WCA

where a rand is a random number within 0 and 1, if the finest results achieved by the stream are better than the river to be connected, then it changes their position. Furthermore, a similar condition can be appropriate when the river's finest value is greater than the sea. Once the streams are greater than the river, the optimal solution is obtained, and they swap their positions. Evaporation is a very important factor, as it prevents fast convergence of the algorithm to local optima. From rivers and lakes, water evaporates; this process completes the cycle.

The next pseudocode expresses whether a river flows to the sea.

$$\begin{aligned} & {\text{for}}\, j = 1:\left( {N_{sr} - 1} \right) \\ & {\text{if}} \left[ {\left| {X_{{\text{Sea}}}^{i} - X_{{{\text{River}}}}^{i} } \right| < d_{{{\text{max}}}} , i = 1,2, \ldots ,N_{{{\text{SR}}}} - 1} \right] \\ & {\text{Perform}}\; {\text{Evaporation}}\; {\text{and}} \;{\text{raining}} \;\text{process} \text{using} \left( {16} \right) \\ & {\text{end}} \\ & {\text{end}} \\ \end{aligned}$$

The ${d}_{\mathrm{Max}}$ value is set constant and near zero. ${d}_{\mathrm{Max}}$ is adaptively reduced, and its value at the ith iteration is evaluated by the following equation:

$$d_{{\text{Max}}}^{i + 1} = d_{{\text{Max}}}^{i} - \frac{{d_{{\text{Max}}}^{i} }}{{\text{max}\;{\text{ iteration}}}}$$

(15)

Afterward evaporation, rain occurs. The new raindrops are found in different areas and create a new stream equivalent to the previous one. To specify the new streams of new areas, the following equation is applied:

$$X_{{{\text{Stream}}}}^{{{\text{new}}}} = {\text{LB}} + {\text{rand}} \times \left( {{\text{UB}} - {\text{LB}}} \right)$$

(16)

where ${\text{LB}}$ and ${\text{UB}}$ are the lower and the upper values of design variables. According to the finest/least value of the objective function (ITAE), the best stream is considered a new river, and the excess of the streams flow to the new river or flow to the sea directly. Finally, to get the best value of the FPID design parameters, WCA needs to set the values of three parameters, such as $d_{{{\text{Max}}}}$, $N_{{{\text{pop}}}}$, ${\text{and}} \;\;N_{{{\text{Sr}}}}$.

The WCA has several benefits over other swarm systems, such as (i) avoiding entrapment at minima due to the balance of exploitation and exploration phases. (ii) Fast convergence properties, and (ii) Its adaptability, recently, the WCA is implemented many times in the interconnected power system, [45,46,47]. WCA's suitability in the presence of the nonlinearity was demonstrated in [48, 49]. Also, the multi-objective WCA was applied [50, 51]. Recently, WCA has shown improved performance compared to other algorithms such as the genetic algorithm, TLBO, particle swarm optimization, and differential evolution techniques when dealing with LFC [52, 53].

The WCA scheme adjusts PID and the proposed FPID controllers' gains according to the ITAE criterion. The block diagram of the gain organizing controller-based ITAE is revealed in Fig. 6, where the power system's output is a combination of tie-line power error and the frequency deviation relating to the concerned area. This output is estimated using ITAE criterion. The optimizer WCA compares the obtained value of ITAE with the previous one to get the lowest ITAE value and generates a new gain for the controller parameters. It repeats this operation based on the number of iterations. The lowest obtained ITAE value corresponds to the best controller gains, which provide a trivial deviation. For WCA-based PID or FPID real-time implementation, the dominant parameter of meta-heuristic algorithms is population size [1]. According to [54], “large initial population sizes do not outperform small populations in terms of identifying the optimum solution,” making the output results satisfied, which is suitable for real-time situations of LFC problems. Furthermore, because the number of PID or FPID controller gains is quite low, they do not require a significant number of iterations to get the best solution, allowing them to be tuned online very fast in response to the power system variations.

Fig. 6

WCA-based proposed FPID controller

4 Simulation results and discussion

4.1 Test system 1

4.1.1 Implementation of WCA

The test systems were studied in the MATLAB/SIMULINK (2017b) environment at $0.01$ fixed step size with a simulation time of 20 s. They are operating on an Intel Core $\mathrm{i}$-$3$, $2.4\,\mathrm{ GHz},\,\,\mathrm{ and }\,\,4\,\mathrm{GB} \mathrm{RAM}$. For competent system performance, the three input parameters of WCA were carefully selected. Thus, the optimization process was performed 20 times; each with 50 iterations, changing the values of ${d}_{\mathrm{Max}}$, ${N}_{\mathrm{pop}}$, ${\mathrm{and}}\,\, N_{\mathrm{Sr}}$ parameters (try and error method) to select the best gains for the PID controller.

Primarily, the WCA based on the PID controller utilizing the ITAE criterion was employed at the two identical non-reheat thermal power plants in test system 1, under a 10% SLP in area 1 to guarantee the suitability of WCA for the AGC issues. The values of the parameters of the WCA-based PID controller of the best run are $N_{{{\text{pop}}}} = 50,\,\, d_{{{\text{Max}}}} = 10^{ - 9} , \;\;{\text{and}}\;\; N_{{{\text{Sr}}}} = 5$ corresponding to the best value for $\mathrm{ITAE }= 0.13065,$ and the gains of PID are $\mathrm{P}= 1.0935,\,\,\mathrm{ I }= 2.0000,\,\,\mathrm{ D}=0.3978$. To demonstrate the superiority of the WCA-based PID controller, the obtained results were compared to the other existing schemes like TLBO [11], DE [8], and FA [55], as shown in Table 2. From Table 2, it is revealed that the minimum ITAE value was obtained with the WCA ($\mathrm{ITAE }= 0.13065$) compared to the TLBO ($\mathrm{ITAE }= 0.2452$), DE ($\mathrm{ITAE }= 0.3391$), and FA ($\mathrm{ITAE }= 0.4714$). Additionally, the WCA-based PID has the smallest settling time for the frequency deviations of area 1 and area 2. Tie-line power deviations are presented in Table 2. Comparing our results and the results from the literature, the WCA had improved performance when dealing with LFC issues.

Table 2 Comparative analysis of different tuning methods-based PID controller under 10% SLP at area 1 for test system 1

4.1.2 Test system 1 with 10% SLP at area 1

Initially, the WCA based on the common fuzzy five MFs in the literature (WCA: FPID) was designed [15, 16, 27] to fairly compare between the WCA: FPID and the WCA based on the proposed fuzzy seven MFs (referred to as proposed FPID). This was employed to accomplish the more efficient operation of the AGC issues of test system 1. The optimal settings for all test system controller parameters are gathered in Table 3. The efficacy of the proposed FPID controller was compared to WCA: FPID, the COA into HS algorithm (HSCOA)-based FPID controller [15], foraging optimization algorithm (BFO)-based FPID controller [2], and the hybrid particle swarm optimization-pattern search (hPSO-PS) built fuzzy PI controller [25], as demonstrated in Table 4. These comparisons were made using the main indices; the objective functions like ITAE and ITSE, the settling time, and the peak undershoot. The proposed FPID controller had the lowest values of objective functions (ITAE = 0.0015, ITSE = 9.34 × 10⁻⁷) compared to WCA: FPID of five MFs, and the recently published strategies such as the HSCOA: FPID controller, the BFO: FPID controller, and the hPSO-PS: FPI controller. Also, the settling time and the peak undershoot were largely reduced in both frequency and tie-line power deviations. Figure 7 shows the dynamic response at 10% SLP in area 1. As mentioned before, the ITAE and ITSE minimally conflicted in settling time and in oscillation magnitude. However, the HSCOA has a good ITAE value compared to WCA: FPID, that results in less settling time and a higher ITSE value that leads to an increased oscillation magnitude. Based on the data (Fig. 7 and Table 4) the WCA: FPID has a similar performance to the HSCOA: FPID scheme. Therefore, there was no need to employ the WCA: FPID in further investigations. Direct comparison of the results can be done to the HSCOA: FPID and the other competitors.

Table 3 Optimal values of WCA-based proposed FPID controller for all test systems

Table 4 Comparative analysis of several tuning method-based FPID controller under 10% SLP at area 1 for test system 1

Fig. 7

Comparative dynamic responses under 10% puMW in area 1 of test system 1: a $\Delta F_{1}$, b $\Delta F_{2}$, and c $\Delta P_{{{\text{tie}}}}$

4.1.3 Sensitivity analysis of test system 1

Evaluating the power system dynamic behavior based on variations of loading conditions and system parameters are done to identify the robustness of the closed-loop system. All the system parameters increase and decrease by 25% and 50% under ΔP_L1 = 10% SLP at area 1 to document the stability of the system. Figure 8 shows the sensitivity analysis under variation of Tg. Table 5 displays the change in system parameters and many of the important indices like ITAE value, settling time, undershoot, and overshoot for the system transient responses, i.e., $\Delta F_{1} , \Delta F_{2} , \;\;{\text{and}}\;\; \Delta P_{{{\text{tie}}}}$. For example, the overshoots of $\Delta F_{2} \;\;{\text{and}} \;\;\Delta P_{{{\text{tie}}}}$ remain at zero in all changes. It is clear that the effect of fluctuations on the ITAE criterion, settling time, undershoot, and overshoot acquired by the proposed FPID controller under variation of system parameters was very small. These trivial fluctuations make the proposed FPID controller robust and perform well against with up to 50% variations in the parameters.

Fig. 8

Sensitivity analysis under variation of Tg: a $\Delta F_{1}$ and b $\Delta P_{{{\text{tie}}}}$

Table 5 Sensitivity analysis under varied conditions for test system 1

4.1.4 Test system 1 with GDB nonlinearity

The presence of the nonlinearity in the interconnected power system leads to larger oscillations and lower performance of the system response. To ensure the suitability of the proposed techniques in the presence of nonlinearity, the influence of GDB is studied in test system 1. The nominal parameters of test system 1 including GDB are available in “Appendix A.2”, [15]. The GDB nonlinearity is expressed as [15]

$$C_{g} = \frac{{0.8 - \frac{0.2}{\pi }S}}{{1 + T_{g} S}}$$

(17)

To check the proposed scheme performance under GDB, a 1% SLP is applied to area 1, the obtained cost functions ITAE and ITSE are compared to other reported strategy HSCOA: FPID. Table 6 shows that the value of ITAE is obtained using the proposed FPID (${\text{ITAE}} = 0.0030$) compared to HSCOA: FPID (${\text{ITAE}} = 0.0019$). Although, the obtained ITAE using the proposed technique is larger than HSCOA: FPID, but the ITSE for the proposed technique (ITSE = 2.747 × 10^–6) is smaller than the HSCOA: FPID (ITSE = 5.107 × 10^–6) indicating that the calculation of many cost function is preferable for fair comparison as seen in Fig. 9. The settling time of the system response and the undershoots value are also revealed in Table 6. To further show their difference, the transient responses of the considered regulators the proposed FPID and HSCOA: FPID are checked at 2%SLP and 5% SLP in each area are shown in Table 7. Figure 10 shows the dynamic response at 5% SLP. It is noticed that the proposed FPID works efficiently to the compared scheme HSCOA: FPID in the presence of GDB nonlinearity as a practical challenge to the concerned power system.

Table 6 Comparative analysis of tuning methods-based fuzzy PID controller for test system 1 with GDB under 1% SLP at area 1

Fig. 9

Comparative dynamic responses of test system 1 with GDB under 1% puMW in area 1: a $\Delta F_{1}$, b $\Delta F_{2}$, and c $\Delta P_{{{\text{tie}}}}$

Table 7 Comparative analysis of tuning methods based fuzzy PID controller for test system 1 with GDB under different SLP

Fig. 10

Comparative dynamic responses of test system 1 with GDB under 5% puMW in area 1 and 5% in area 2: a $\Delta F_{1}$ and b $\Delta P_{{{\text{tie}}}}$

4.2 Test system 2

4.2.1 Test system 2 with AC tie-lines

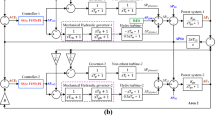
In order to add a more realistic and complex power system, the investigation was extended to a multi-source power system, as shown in Fig. 11a, [14, 15, 26, 56]. Additionally, The SIMULINK file incorporating the parameter values is demonstrated in Fig. 11b. To investigate the multi-source power systems dynamic performance with AC tie-lines only, a 1% SLP was subjected to area 1. The gains of the proposed FPID controller utilized by WCA are depicted in Table 3, and the optimized parameters of WCA were ${N}_{\mathrm{pop}}=100,\,\, {d}_{Max}={10}^{-8},\,\, \mathrm{and}\,\, {N}_{Sr}=5$. The transient response in terms of settling time and undershoot are represented in Table 8, and the dynamic responses are shown in Fig. 12. The most ideal values of the objective functions obtained by the proposed regulator demonstrate the suitability of the proposed approach compared to recently published approaches, such as HSCOA: FPID [15], LUS-TLBO: FPI [26], DE: FPI [26], and DE: PID [56].

Fig. 11

a Transfer function model of test system 2 with HVDC link. b Transfer function of test system 2 with HVDC link

Table 8 Comparative performance of ITAE value and settling time for test system 2 with just AC

Fig. 12

Comparative the dynamic responses of test system 2 after 1% puMW in area 1 with just AC tie-line: a $\Delta F_{1}$, and b $\Delta P_{{{\text{tie}}}}$

To improve the investigation and differentiate between the regulators, different SLPs were applied in area 1 and area 2. The studied objective functions for this scenario are summarized in Table 9. The ITAE and ITSE values are slightly increased, which is confirmed in Figs. 13 and 14. From the above results, the proposed technique has been well done at high load perturbations, where the oscillation magnitude successfully reduced, and the transient response rapidly settled.

Table 9 Comparative analysis of tuning methods-based FPID for test system 2 just AC under different SLP

Fig. 13

Transient responses of test system 2 under (1% SLP in area 1 and 2% SLP in area 2) with just AC: a $\Delta F_{1}$, b $\Delta F_{2}$, and c $\Delta P_{{{\text{tie}}}}$

Fig. 14

Comparative dynamic responses of test system 2 after 3% puMW in area 1 with just AC: a $\Delta F_{1}$, b $\Delta F_{2}$, and c $\Delta P_{{{\text{tie}}}}$

4.2.2 Test system 2 with AC–DC tie-lines

An extra study was supported by including the HVDC link in the test system 2, as shown in Fig. 11 [26, 56]. The finest scaling factors obtained with WCA-based ITAE criterion for reheat thermal, hydro, and gas units are shown in Table 3. Table 10 demonstrates the time-domain analysis in terms of ITAE, ITSE, undershoot, and settling time. The deviations of frequency and tie-line power are shown in Fig. 15. The finest values of the objective functions for the proposed regulator at 1% SLP in area 1 were (ITAE = 0.0023, ITSE = 1.89 × 10⁻⁷), which proves the effectiveness of the proposed FPID compared to the HSCOA: FPID [15].

Table 10 Comparative performance of ITAE value, settling time, and undershoot for test system 2 with HVDC link

Fig. 15

Transient responses of test system 2 after 1% puMW in area 1 with HVDC link: a $\Delta F_{1}$, b $\Delta F_{2}$, and c $\Delta P_{{{\text{tie}}}}$

Also, different SLPs were investigated, similar in AC tie-line as shown in Table 11. The deviations of frequency and tie-line power for 3% SLP in area 1 are shown in Fig. 16. From the above scenarios, it can be concluded that the main indices of the transient responses confirm the superiority of the proposed FPID scheme in all terms at different SLPs compared to recently published schemes. Also, the AC–DC link enhances the transient responses compared to AC only tie-lines.

Table 11 Comparative analysis of tuning methods-based FPID for test system 2 under different SLP

Fig. 16

Comparative dynamic responses of test system 2 under 3% puMW in area 1 with HVDC link: a $\Delta F_{1}$, b $\Delta F_{2}$, and c $\Delta P_{{{\text{tie}}}}$

5 Conclusions

In this study, an optimally tuned FPID controller with seven MFs using an ITAE criterion was calculated and its corresponding ITSE value using an optimized algorithm in a WCA power system was employed. Two models were selected, a two-area two-unit, and a two-area six-unit model to test the performance of our analysis. To have a more realistic LFC study and to demonstrate the suitability of the proposed FPID controller, the dynamic LFC response profiles of the studied test systems are compared to recently published schemes. A common system, test system 1, was initially investigated. The dynamic responses showed that the results obtained by the proposed FPID were superior to recently published schemes and the uncertainty of the system parameters was improved with the proposed FPID. Also, to authenticate the competence of the proposed FPID, the study was extended to a two-area six-unit power system with/without an HVDC link. The time-domain investigation shows the superior performance of the proposed FPID controller because it had smaller magnitudes of oscillation and less settling time in all investigated scenarios. The proposed FPID with a seven-MF controller showed superior performance for the LFC test systems and readaption was not needed in a wide range of deviations from the nominal conditions. In conclusion, the WAC based on the proposed FPID controller makes the LFC framework more robust and shows a more stable and better outcome in a wide variation of loadings and conditions.

In the future, prior to establishing its robustness, the suggested approach will be tested on complex real-world applications such as LFC with integrated electric cars, wind, and PV systems with time delay nonlinearity.

Appendices

Appendix A.1: Two-area two-unit power plant [7, 11, 15]

$P_{R} = 2000\,{\text{MW}};$ $P_{L} = 1000\,{\text{ MW}};$ $f = 60{\text{ H}}_{{\text{Z}}} ;$ $B_{1} = B_{2} = 0.425 {\text{ p}}.{\text{u}}.{\text{ MW}}/{\text{H}}_{{\text{Z}}}$; $R_{1} = R_{2} = 2.4{\text{ H}}_{Z} /{\text{p}}.{\text{u}}.$; $T_{g1} = T_{g2} = 0.08{\text{ s}}$; $T_{t1} = T_{t2} = 0.3 s$; $K_{PS1} = K_\text{PS2} = 120{\text{ H}}_{Z} /{\text{p}}.{\text{u}}.$; $T_{PS1} = T_\text{PS2} = 20 {\text{ s}}$; $2* \pi *T_{12} = 0.545 \,{\text{p}}.{\text{u}}.;{ }a_{12} = - 1.$

Appendix A.2: Two-area two-unit with governor dead band [15, 57]

$B_{1} = B_{2} = 0.425{\text{ p}}.{\text{u}}.{\text{ MW}}/{\text{H}}_{{\text{Z}}}$; $R_{1} = R_{2} = 2.4{\text{ H}}_{Z} /{\text{p}}.{\text{u}}.$; $T_{g1} = T_{g2} = 0.2{\text{ s}}$; $T_{t1} = T_{t2} = 0.3{ }s$;

$K_{PS1} = K_\text{PS2} = 120{\text{ H}}_{Z} /{\text{p}}.{\text{u}}$; $T_{PS1} = T_\text{PS2} = 20{\text{ s}}$; $T_{12} = 0.0707\,{\text{ p}}.{\text{u}}.;{ }a_{12} = - 1.$

Appendix B: Two-area six-unit power plant [15, 56]

$B_{1} = B_{2} = 0.4312\;{\text{ p}}.{\text{u}}.{\text{ MW}}/{\text{H}}_{{\text{Z}}}$; $R_{1} = R_{2} = R_{3} = 2.4{ }\;{\text{H}}_{Z} /{\text{p}}.{\text{u}}.$; $T_\text{sg1} = T_\text{sg2} = 0.08{\text{ s}}$; $T_{t1} = T_{t2} = 0.3{ }s$;

$K_{r1} = K_{r2} = 0.3;$ $T_{r1} = T_{r2} = 10{ }s;$ $K_{{{\text{PS}}1}} = K_{{{\text{PS}}2}} = 68.9566{\text{ H}}_{Z} /{\text{p}}.{\text{u}}$; $T_{PS1} = T_\text{PS2} = 11.49{\text{ s}}$;

$T_{12} = 0.0433{\text{ p}}.{\text{u}}.;{ }a_{12} = - 1;$ $T_{w1} = T_{w2} = 1{\text{ s}};$ $T_\text{RS1} = T_\text{RS2} = 5{\text{ s}}$; $T_\text{RH1} = T_\text{RH2} = 78.75{\text{ s}}$;

$T_\text{GH1} = T_\text{GH2} = 0.2{\text{ s}}$; $X_{C} = 0.6{ }s$; $Y_{C} = 1{\text{ s}};$ $c_{g} = 1{ }s;$ $b_{g} = 0.05{ }s;$ $T_{F1} = T_{F2} = 0.23{\text{ s}}$; $T_\text{CD1} = T_\text{CD2} = 0.2{\text{ s}}$;

$T_\text{CR1} = T_\text{CR2} = 0.01{\text{ s}}$; $K_{T} = 0.543478$; $K_{H} = 0.326084$; $K_{G} = 0.130438$; $K_\text{DC} = 1$; $T_{DC} = 0.2{ }s$.