1 Introduction

Exocytosis and endocytosis are the main mechanisms of cellular communication [1]. For the discovery of this vesicle-based transport mechanism in cells, James E. Rothman, Randy W. Schekman and Thomas C. Südhof were awarded the Nobel Prize in Physiology or Medicine in 2013. In both processes, chemical messengers are wrapped inside a vesicle which travels outside the cell in case of exocytosis or inside the cell in case of endocytosis. During exocytosis, at the moment of impact with a cell membrane, a pore is created, which enables the release of a chemical messenger outside the cell. This messenger is later recollected by another cell through endocytosis. There are two discovered types of exocytosis: a full fusion and a kiss-and-run fusion [2]. In the first type a vesicle releases all of its contents outside the cell. In the second type only some of its contents get released and such a leftover vesicle is then consumed in the process of endocytosis by the same cell. There is evidence that there might be a third mode of exocytosis, an open-closed fusion. It is partially similar to the kiss-and-run fusion [2].

Endocytosis and exocytosis work closely together. There is evidence that certain endocytosis-based cell nutrition patterns are associated with precancerous conditions in cells [3]. On the other hand, exocytosis is the main mechanism in cancer metastases [4]. Nowadays, monitoring of exocytosis opens new possibilities for early diagnoses of many diseases. Examples include Alzheimer’s disease [5], cholestasis [6], hypoxia [7], inflammation and thrombosis [8], tetanus [9], among others. The current research also makes it possible to model the course of some diseases by deliberately disrupting exocytosis. Synaptic disruption and altered neurotransmitter release in NDDs (NeuroDegenerative Diseases), e.g. impairing the stress fight-or-flight response is an example of such a disease [10]. It is even possible to stimulate the exocytosis process to treat rare diseases. An example of such an approach is the deliberate induction of lysosomal exocytosis by increasing the level of two transcription factors: TFEB and TFE3 in the therapy of Pompe disease [11]. Considering the above areas of application of exocytosis-based imaging, in this article we focused on the effective processing of amperometric signals analyzing the movement of vesicles in exocytosis in order to provide mechanisms for early diagnosis.

In amperometric AFE (Analog Front-End) systems, monitoring of vesicle movement is performed using sensors built from Carbon NanoTube (CNT) electrodes. They provide current measurements directly from the cell membrane in which the vesicle fusion occurs [12]. For the purpose of collecting data from tissues, specialized matrices of sensors are used [13]. The biochemical sensor production technology based on carbon nanotube arrays is the subject of a NASA patent [14]. The potential areas of application of this technology include medical and bio-medical treatments, environmental monitoring, Point-of-Care, implantable sensors and early disease diagnosis [15]. The measurement technique used to monitor exocytosis using nanoelectrodes is amperometry [16]. Three nanoelectrodes are used in the measurement: a reference electrode, an anode and a cathode. The reference electrode provides a reference potential. The anode and the cathode oxidize vesicle cargo causing current flow, which can be monitored [17]. Its values are of pA range. This kind of data forms a time waveform with a relatively high level of noise.

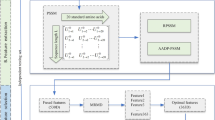
The basic stage of preprocessing data in the diagnostic process is the fusion classification. The analysis of patterns in noisy time waveforms is often performed using advanced models of recursive neural networks such as LSTM (Long Short-Term Memory), which guarantees high processing precision [18]. The task of detecting vesicle fusions, however, requires data analysis—not from one sensor—but from a huge matrix of sensors. A hardware implementation of such processing requires, on one hand, real-time calculations performed on massive data, and on the other, ensuring accuracy sufficient to accurately classify patterns in exocytosis. For this reason, the authors proposed an approach based on a large matrix of simple perceptron networks. The structure of a mobile system sufficient for continuous monitoring of exocytosis in a patient’s tissue is shown in Fig. 1.

Fig. 1
figure 1

System for continuous monitoring of exocytosis

Full size image

Analog exocytosis currents are collected by the CNT array of electrodes, which can be directly applied to the tissue in which vital processes take place. The conversion of analog currents into their digital form requires using CMOS Analog-Digital Converter (ADC) matrices dedicated to the analysis of currents of sub-nA values. Circuits based on \(\varSigma \varDelta\) modulators operating in weak-inversion mode can act as such converters [19]. The role of the classifier of digital representations of fusion signals is played by a GPU (Graphics Processing Unit) system, on which a matrix of classifiers based on neural networks (NN-C) was implemented. Registers are responsible for preparing digital data for the GPU. Figure 1 also shows the power distribution tree. The matrix of CNT sensors requires proper polarization of operating electrodes using a voltage of 650–700 mV versus an Ag/AgCl reference electrodes, while the matrix of ADC circuits requires a power supply of 0.2–0.4 V, depending on the used CMOS technology. Providing low bias voltage is the basis for using power techniques in a mobile AFE system based on obtaining human heat energy [20]. Keeping CMOS supply voltages low is in turn possible thanks to using dedicated moderate and weak inversion modes [21]. Additionally, thanks to using GPU-based processing as shown in Fig. 1, it is possible to constantly monitor life processes and changes in tissues using mobile devices. This work focuses on effective real-time analysis of data from tens of thousands of CNT sensors in AFE amperometric system. The paper is organized as follows. Chapter two describes the preparation of the neural network array. Chapter three dives deeper into the hardware architecture of the GPU-based system. Chapter four presents performance results and chapter five provides summary and final thoughts.

2 Vesicle fusion analysis using a perceptron network

Current vesicle fusion signals obtained using amperometry are in the form of time waveforms. This type of data is often available in scientific literature (e.g. [22, 23]). However, in order to train a neural network, a large quantity of data is needed. For this purpose a Python script was created. It approximates the vesicle fusion time waveform using a polynomial interpolation. These polynomials are based on manually selected border points, which separate characteristic parts of both fusion plots. Other transformations included additions to x or y coordinates of border points and an artificial noise addition. Both techniques use random values from manually selected ranges specific for each case. As a result—time waveform data is generated in large quantity, which exhibits little variations across the dataset. Figures 2 and 3 present such examples. Figure 2 depicts a full vesicle fusion. During this process a pore opens in a cell membrane starting a chemical messenger release, which is marked by a pre-spike foot in the plot. After that the pore grows bigger to the point in which the full vesicle content can be released. This moment is marked by the spike. Figure 3 depicts a kiss-and-run vesicle fusion, during which a pore opens slightly, enabling only a partial release of vesicle contents. This section is marked by the stand-alone foot in the plot. Drops in current during the foot are caused by the vesicle repeatedly coming in contact with the cell membrane before it is finally recycled by the cell through endocytosis.

Fig. 2
figure 2

Example of the generated full fusion plot. The A character marks the pre-spike foot and the B character marks the spike

Full size image
Fig. 3
figure 3

Example of the generated kiss-and-run fusion plot. The B character marks the stand alone foot

Full size image

As mentioned in the introduction, a simple perceptron network plays the role of the single classifier (NN-C) in the system. The main reason for choosing a perceptron, instead of e.g. a recurrent architecture, was performance. The goal of neural network preparation was to prepare the network with as little memory and computation time requirements as possible, while maintaining a minimal baseline accuracy. This baseline value was chosen to be \(99\%\). Furthermore, typical time waveforms of full and kiss-and-run fusions last 170–180 ms. For this reason, we assumed the duration of a single pattern equal to 180 ms. We checked that for the above-described patterns of both fusion types, the number of points obtained from the patterns making it possible to classify them using the assumed baseline accuracy equals 18. The relatively small size of the input data vector makes it possible to use a perceptron network with an architecture dedicated to the classification of time waveforms [24]. This also determines the size of the input layer equal to 18 neurons and the sampling frequency of the current signals equal to 100 Hz. The second layer of the network consists of 10 neurons with ReLU activation functions. ReLU was chosen due to its ability to avoid occurrences of the vanishing gradient. The third layer has 2 neurons with sigmoid activation functions. Usually, for the task of multi-class classification, the Softmax activation is used. However, in this case sigmoid makes it possible to use one less neuron for inference between three classes: full fusion, kiss-and-run fusion and no fusion. It results in a performance gain. The output of the neural network forms a vector of size two, consisting of probabilities for full and kiss-and-run fusions. It represents a double-binary classification task. Due to this fact, probabilities for the third class, which represent no fusion, were determined by calculating an average of probabilities of the other two classes and subtracting these values from one, resulting in artificial values for no fusion class probabilities. Figure 4 presents a perceptron network structure.

Fig. 4
figure 4

The chosen perceptron network structure

Full size image

Each layer’s output can be summarized with a following equation: \(a_{n} = \sigma (Wa_{n-1}+b)\), where n is current layer’s index starting from the beginning of the network, \(a_{n}\) is an output vector, \(a_{n-1}\) is an input vector, \(\sigma\) is an activation function, W is a matrix of weights and b is a vector of biases for each neuron in current layer. Activation functions matching layer’s sequence are as follows:

  1. 1.

    Identity: \(\sigma = x\)

  2. 2.

    ReLU: \(\sigma = max(0, x)\)

  3. 3.

    Sigmoid: \(\sigma = \frac{1}{1 + e^{-x}}\)

Network training was carried out using a set of 1600 fusion time waveforms generated using the aforementioned python script. The generated data retained the complexity of the original. The validation set and the test set both consisted of 400 waveforms. Each set was divided into full and kiss-and-run fusion examples so that both get \(50\%\) of all samples. In each class there were only \(20\%\) of positive examples and \(80\%\) of negative examples. The data was prepared so that the fusions are recognized only in particular area of the time waveform and further translations result in a negative prediction. This was done to make it possible to later define the number of fusions which occur per each type. Any deviation in the translation ranging from \(-\,10\) to \(+\,10\) ms was treated as a negative sample.

The training was performed using the TensorFlow Keras framework. The stopping rule was as follows: if the validation accuracy does not improve in 60 epochs, stop training and restore best weights for that purpose. The minimal accuracy gain to count as an improvement was 0.005. The optimal accuracy was reached at epoch 79. Accuracy with the test set equalled \(99\%\). Loss across epochs is presented in Fig. 5, whereas accuracy across epochs is presented in Fig. 6. In both figures blue curves concern validation, while orange curves concern training.

Fig. 5
figure 5

Loss changes over training epochs for training and validation

Full size image
Fig. 6
figure 6

Accuracy changes over training epochs for training and validation

Full size image
Table 1 Confusion matrix
Full size table
Table 2 classifier parameters
Full size table

The confusion matrix is presented in Table 1. F stands for Full fusion, K stands for Kiss-and-run and N represents No fusion. Based on the confusion matrix it is possible to calculate precision, sensitivity, specificity, the F1 Score and the AUC score for all classes. The parameters are listed in Table 2. These parameters were calculated using a Python script. The AUC Score was calculated using a roc_auc_score function of the scikit-learn Python module.

Fig. 7
figure 7

Histograms of weight distributions in the first layer across epochs

Full size image
Fig. 8
figure 8

Histograms of weight distributions in the second layer across epochs

Full size image
Fig. 9
figure 9

Histograms of weight distributions in the third layer across epochs

Full size image

Histograms in Figs. 7, 8 and 9 present weight distributions across all 3 layers. In each layer a bias is used and its distribution is represented by histograms on the left. Histograms on the right represent the weight distribution of neurons. Using Keras in the TensorFlow framework, each layer starts with a uniform distribution (unless specified otherwise).

3 Hardware architecture

The chosen network architecture offers a relatively low computational complexity. There is no need to remember previous states, as in the case of using recurrent neural networks. Therefore, this perceptron neural network can be run with multiple instances on a GPU, handling multiple sensors in real time. However, in terms of parallel processing, there are alternatives to GPU platforms, which require consideration. They mostly include FPGAs and SoM (System on Module) platforms with various AI accelerators.

FPGAs (Field-Programmable Gate Arrays) offer flexible functionality. Through the process of an HDL (Hardware Description Language) synthesis, an integrated circuit can be reconfigured to completely change its mode of operation. Furthermore, if the reconfigured circuit contains programmable logic, it can be reprogrammed after the synthesis. A reconfigured specialized integrated circuit is then called a SoC (System on Chip). With these platforms the only limitations are hardware resources present on the given chip. It is also their biggest disadvantage. Massive parallelization is inferior to GPU-based systems due to the lack of multiplication blocks present in FPGA chips in great quantity. Apart from that, they also require expert knowledge and the amount of time needed to create and deploy a system is considerably longer than using normal, software-driven platforms. Some FPGAs also contain an additional CPU to make up for this particular disadvantage. Examples of FPGAs include Arty and Zynq device families from Xilinx and the Cyclone family from Intel.

At platforms with AI accelerators, using software is the only way of creating and deploying solutions. Because of this the time to create and deploy is considerably shorter than using FPGAs. AI accelerators are usually designed in the form of coprocessors. These coprocessors are usually specialized to handle only certain types of neural networks or other machine learning algorithms. This is their main downside. It also causes issues with the compatibility of some ML (Machine Learning) frameworks. Examples include the Google Coral development board and the Intel Movidius USB stick.

In terms of ML frameworks, GPU-based platforms offer the widest compatibility. Also, due to the fact that they are software-driven, the time to design and deploy solutions is short. For our task we chose the Nvidia Jetson. It is a family of embedded GPU-based devices, which combine high computing power and low costs. As the main processing platform, we chose Jetson TX2. It consists of a Dual-Core Nvidia Denver CPU, a Quad-core ARM Cortex-A57 MPCore CPU and a 256-Core Nvidia Pascal GPU. The primary memory is 8 GB of LPDDR4 RAM (Random Access Memory), which is shared between CPUs and the GPU. This fact eliminates a common bottleneck, which is low data transfer rate from the CPU memory space to the GPU memory space. The memory bandwidth is 59.7 GB/s. As the operating system we chose Ubuntu Linux 18.04. Its kernel was modified, though. In order to minimize system latency, a patch called Preempt RT was applied, making it a soft real-time operating system.

As swhon in Fig. 10 the system structure is divided into three parts: a sensor matrix, a preprocessor and a Jetson TX2 as the main processing platform. The current signal is assumed to be sampled using a frequency of 100 Hz in the analog form (voltage level), periodically. The preprocessor converts this data into a digital format, scales it, stores it and sends it to the processing platform. The main processing algorithm consists of N number of FIFO (queue) data structures and N instances of a perceptron neural network. N is the size of amperometric sensor matrix which the system can handle within a time span of 10 ms in real time. Each new sample is placed at the end of the queue effectively pushing the oldest sample out. The queue size is 18 due to the sampling rate equaling 10 ms and the perceptron input layer width equaling 18 neurons. The system starts inference as soon as the whole queue is populated (a minimum number of samples is provided). As mentioned earlier, any translation for fusions which is less than \(-\,10\) ms or more than 10 ms results in a negative prediction. This, in combination with the FIFO-based algorithm, results in one fusion occurrence detected exactly three times. We made an assumption that the latency from the sensor matrix and the preprocessor is close to 0. The main processing algorithm was implemented using Jetson TX2. The sensor matrix and the preprocessor were chosen to be emulated using a PC.

Fig. 10
figure 10

System structure

Full size image
figure a
figure b

Algorithm 1 presents steps included in the preprocessor. It begins with a for loop iterating NumberOfSamples times, which is the total number of current measurements performed by the sensor matrix and processed by other elements in the system. Each current measurement is performed for the whole sensor matrix. In the body of a for loop we probe currents in the analog format with a frequency of 100 Hz (SampleCurrents100Hz()), convert them to digital format using ADC (ConvertCurrentsToDigitalFormat()), scale them to the appropriate range (ScaleCurrents()) and send them to the main processing platform (SendData()).

Algorithm 2 presents steps included in the main processing platform. It also starts with the same for loop as before because these two elements of the system are synchronized. In the body of the for loop we wait for the data from preprocessor (WaitForData()), then we shift values in FIFO queues (ShiftValuesInQueues()) and write data to them (WriteDataToQueues()). For each iteration data is in the form of a vector with size equal to the size of sensor matrix (N). It is also equal to the number of FIFO queues held in memory and to the batch size of the neural network. As soon as 18 samples are collected (queues are populated) inference starts. Neural network performs inference on all of the queues (RunInferenceOnQueues()) for the remaining iterations and results are stored in memory for further analysis (StoreInferenceResults()).

The software used was Python3, NumPy, TensorFlow and TensorRT. Python3 was used as a wrapper language for other components implemented in lower level languages (e.g. C, C++, CUDA). A NumPy package was used to implement an array of FIFO data structures. It is implemented in C, so it provides optimal performance. TensorFlow was used for training and deployment of the neural network. The network graph optimization was achieved using TensorRT. It is dedicated to Nvidia GPUs and is fully compatible with TensorFlow. It was also one of the reasons why we chose Jetson TX2 as the main processing platform. This optimizer performs a platform-specific optimization, eliminates useless operations and combines similar operations (e.g. bias and ReLU) into one. The result of this process is one or more TensorRT engines which replace a number of operations inside the neural network graph.

4 System performance

To find the maximum performance setup we prepared a benchmarking script in Python3. It was designed to mimic a real use case of the system.

The first important thing to mention is the format of the used model. TensorFlow offers three formats of neural network models: a Keras HDF5 model, a saved model and a frozen graph. The first two can be retrained, while the third one can’t. The frozen graph is also the lightest of all three in terms of memory, and is the fastest in terms of performance. Our training script produced a Keras HDF5 model. It was then converted to the TensorFlow saved model. After that we performed the TensorRT optimization. In a real use case scenario, as well as in the benchmark, the TensorRT model is loaded from the saved model format and is then converted in memory to the frozen graph for maximum performance.

Another crucial thing to mention is the storage data type of neural network parameters, such as weights, input and output tensors. The Jetson TX2’s architecture provides a 16-bit floating-point precision. It greatly reduces the computing time and provides enough accuracy for the model to perform its task well, compared to the regular 32-bit floating-point precision. During training via the TensorFlow Keras framework a float16 data type was specified for the whole model. Another commonly used data type is the 8-bit integer type. It provides the biggest performance gains but brings some accuracy loss. This type is also different from others because it cannot be used for training. Afterwards, the whole model needs to be quantized to 8-bit integers in order to use it. This mode is unavailable for Jetson TX2 due to the GPU architecture.

Lastly, before describing the benchmarking algorithm, we need to describe TensorRT more thoroughly. It was mentioned that it combines multiple operations into one. The TensorFlow framework offers dedicated CUDA kernels for all operations supported by the GPU. What TensorRT does is that it takes some of these operations/kernels and combines them into one, called the TRT inference engine. In our case, before optimization, the TensorFlow graph contained 33 nodes and 57 edges. Nodes are separate mathematical operations and edges are data tensors used by the graph. The optimization produced one TRT inference engine, which replaced 17 nodes. The optimized graph consisted of 14 nodes and 15 edges. Another thing to mention about TensorRT is that its engines need to be built for every new batch size which enters the model. There are two ways to build them: static and dynamic. In the static mode, engines are built for a chosen batch size before deployment and are saved along with the model. In the dynamic mode engines are built at the time of deployment, when the data with a new batch size enters the model. The first inference is delayed by the time it takes to build engines. After that there is no delay and the inference runs normally. For benchmarking purposes, we chose the second mode.

The benchmark script used NumPy to prepare the data. In a real use case scenario an array of sizes [batch size] x [number of samples] needs to be stored in the primary memory. The batch size is equal to the number of sensors which the system can handle within the time span of 10 ms and the number of samples is 18 due to the time waveform lasting 180 ms. Each new batch of data from sensors pushes the oldest samples out of the array. It mimics the queue data structure behavior. In order to find the maximum batch size we needed to implement queue operations for an array of data. For this task we chose numpy.take(). It does not move the data in memory like numpy.roll() does, but it changes the array indexing, resulting in a faster compute time. This way the only thing we needed to do was to overwrite data in the last column and change indexing using numpy.take() so that the last column is considered first again and other indexes are moved by 1 (indexes of columns range from 0 to 17). The model inference is done for the whole array.

For the time measurement we chose the Python’s timeit module. The biggest advantage over the time module is that it excludes garbage collection from the measurement. The Python’s garbage collector checks for the allocated memory that is no longer useful and deallocates it, slowing the execution of the program. This module needs a function to run and a number of iterations to run it. For this task we chose 100,000 iterations and prepared a benchmarking function. It included four steps:

  1. 1.

    Replace the oldest batch of samples with the newest batch

  2. 2.

    Shift indexes in the array

  3. 3.

    Create a tensor using the array

  4. 4.

    Run an inference for the given tensor

We calculated an average based on measurements of 100,000 runs. The benchmarking script was run with various batch sizes to find the most optimal one. Eventually we achieved the result of 140,000 perceptron neural networks which this system can run inference with in parallel with frequency of 100 Hz. This number is also equal to the size of the sensor matrix probed within the mentioned frequency. To discover the exact number of sensors which Jetson TX2 can handle, benchmarking needs to be rewritten to C or the C++ language. Thanks to using a custom real-time patched linux kernel, the operating system latency was reduced almost to 0. We also tested the results using a TensorFlow model without optimization. The TensorRT model achieved an average of 9.84 ms of compute time, while the TensorFlow model achieved 12.12 ms. This drew us to conclusion that the performance gain from the TensorRT optimization is roughly \(19\%\) in our case. It is quite substantial, even though the model is relatively small and even though we changed data type to 16-bit floating-point before optimization. If we hadn’t done that TensorRT would have converted our model to float16 and the performance gain would have been much bigger.

Apart from performing the benchmark for the chosen use case, a number of general purpose analyses were performed. The main goal of these analyses was to reveal the relation between the batch size and various other factors. These factors included:

  1. 1.

    Total number of neurons

  2. 2.

    Total number of connections between neurons

  3. 3.

    Input pattern size (number of neurons in the perceptron input layer)

  4. 4.

    Sampling period

Constant sampling rate of 100 Hz and a constant ratio of neurons between the input and the hidden layer were maintained during the first three types of analyses. All neural networks used during the studies were optimized using the previously described methods.

The first three relations are presented in Figs. 11, 12 and 13. All of them present similar shapes of the plot curves. It is due to the fact that all three parameters: the number of neurons, the number of connections between neurons and the pattern size depend on each other and change in similar manner when the classifier architecture changes. In general the batch size decreases with the increase of any of the aforementioned parameters.

Fig. 11
figure 11

Batch size changes over number of neurons

Full size image
Fig. 12
figure 12

Batch size changes over number of connections between neurons

Full size image
Fig. 13
figure 13

Batch size changes over pattern sizes

Full size image

The study of dependency between the batch size and the sampling period was conducted differently. Neural network optimizations were performed but this time the sampling period was variable and the perceptron architecture was constant. The analysis was performed for the following architectures:

  1. 1.

    18-10-2

  2. 2.

    30-17-2

  3. 3.

    42-23-2

  4. 4.

    54-30-2

We chose logarithmically-related sampling periods. The following periods were used:

  1. 1.

    2 ms

  2. 2.

    3.838 ms

  3. 3.

    7.365122 ms

  4. 4.

    14.13366912 ms

  5. 5.

    27.12251104 ms

  6. 6.

    52.04809868 ms

  7. 7.

    99.88030137 ms

The relations are presented in Figs. 14, 15, 16 and 17. Unsurprisingly, as the sampling period increases, the batch size also increases. However, during the analyses, two significant system limitations were found.

An attempt to run the classifier inference with a sampling period below 2 ms was impossible for all architectures, due to the latency of the Python programming language. As the network size increased, the lower inference time limit also increased, though insignificantly. It is also possible that some latency was the result of using TensorFlow. In order to precisely find out what caused it, the analyses would need to be performed in the C++ programming language, instead of Python.

The second limitation is due to the fact that only 8 GB of RAM are available using the Jetson TX2 platform. As the analyses were run for all architectures and batch sizes increased, at some point, varying on architecture, the inference time jumped above 200 ms. It was caused by the Jetson TX2 platform running out of primary memory and starting the swapping process, which includes temporarily storing some data using mass storage. Write and read times of the mass memory are significantly longer than the ones for the primary memory. In the presented figures this behavior is shown by the mild plateauing of the curves.

Fig. 14
figure 14

Batch size changes over sampling period for the 18-10-2 perceptron architecture

Full size image
Fig. 15
figure 15

Batch size changes over sampling period for the 30-17-2 perceptron architecture

Full size image
Fig. 16
figure 16

Batch size changes over sampling period for the 42-23-2 perceptron architecture

Full size image
Fig. 17
figure 17

Batch size changes over sampling period for the 54-30-2 perceptron architecture

Full size image

5 Related works

Finally, let us compare the effectiveness of the approach described in this paper with other methods of fusion classification. Approaches to automatic detection of full and partial vesicle fusion described in literature are based primarily on the analysis of images obtained in Total Internal Reflection Fluorescence Microscopy [25]. This method is based on a relatively old technique of inducing fluorescence in the region of cell contact with the substrate [26]. Due to the need to monitor the fluorescence phenomenon, the detection of a single fusion requires an analysis of the sequence of several or a dozen or so images, and thus using more complex neural networks. In order to ensure a high degree of classification precision, Convolutional Neural Networks are used [27]. In this case the precision for the full fusion classification equals 95% and for the partial fusion: 96.7%. Simpler methods based on the Single Gaussian Model [28] make it possible to obtain the precision level of 54.9% for the full fusion and 64.6% for the partial fusion. In turn methods based on the Gaussian Mixture Model [29] feature a level of precision of 77.0% for the full fusion and 75.5% for the partial fusion. Using the Gaussian Mixture Model together with the Hierarchical Convolutional Neural Network (HCNN) allows the precision to be improved, which in this case based on [30] is: 95.2% for full fusion and 96.1% for partial fusion. In our approach described in this paper, we used data analysis using modern nanoscale sensors. It allowed us to use simpler classifiers. This way the approach makes it possible to detect many thousands of fusions in real time using a mobile platform. Moreover, the precision of classification of amperometric waveforms of the full fusion equals 98.0%, of the partial fusion: 100% and of negative waveforms: 99%. Additionally, monitoring exocytosis processes using the proposed method and a mobile computing platform does not limit the patient’s freedom of movement. The comparison of precision with the examples from the literature is presented in Table 3.

Table 3 Accuracy comparison with other implementations
Full size table

6 Conclusion

We designed a mobile GPU-based system for monitoring life processes in tissues. The main processing algorithm was implemented using Jetson TX2, while the preprocessor and the sensor matrix were emulated using a PC. It was proven that the system can handle a sensor matrix of an approximate size equal to 140,000 in real time, using a sensor sampling frequency of 100 Hz and an accuracy of 99\(\%\). We additionally conducted an analysis of the system performance with varying network sizes, input data sizes and sampling periods. In the future similar systems might be used to aid biologists or medics who study cancer cells. A possible future direction of this work is to gather amperometric measurements from precancerous cells and normal cells, and to train a neural network classifier which could find a difference between these two types based on the vesicle fusion type and the frequency.