An algorithm to compute the strength of competing interactions in the Bering Sea based on pythagorean fuzzy hypergraphs

Abstract

The networks of various problems have competing constituents, and there is a concern to compute the strength of competition among these entities. Competition hypergraphs capture all groups of predators that are competing in a community through their hyperedges. This paper reintroduces competition hypergraphs in the context of Pythagorean fuzzy set theory, thereby producing Pythagorean fuzzy competition hypergraphs. The data of real-world ecological systems posses uncertainty, and the proposed hypergraphs can efficiently deal with such information to model wide range of competing interactions. We suggest several extensions of Pythagorean fuzzy competition hypergraphs, including Pythagorean fuzzy economic competition hypergraphs, Pythagorean fuzzy row as well as column hypergraphs, Pythagorean fuzzy k-competition hypergraphs, m-step Pythagorean fuzzy competition hypergraphs and Pythagorean fuzzy neighborhood hypergraphs. The proposed graphical structures are good tools to measure the strength of direct and indirect competing and non-competing interactions. Their aptness is illustrated through examples, and results support their intrinsic interest. We propose algorithms that help to compose some of the presented graphical structures. We consider predator-prey interactions among organisms of the Bering Sea as an application: Pythagorean fuzzy competition hypergraphs encapsulate the competing relationships among its inhabitants. Specifically, the algorithm which constructs the Pythagorean fuzzy competition hypergraphs can also compute the strength of competing and non-competing relations of this scenario.

1 Introduction

Graph theory gradually emerged as an autonomous subject after the publication of Euler’s work on the problem of the Seven Bridges of Knigsberg in 1736. This subject has turned out to be an efficient tool for the interpretation of combinatorial problems of various areas like algebra, topology, geometry and operations research. Later on, combinatorics of graph theory was generalized to hypergraph theory where a hypergraph H on a non-empty set U is a family of subsets of U. Each member of this family is called hyperedge which connects multiple vertices (rather than only two vertices as in case of graphs). These discrete mathematical structures were broadly analyzed by Berge [8, 9]. Hypergraph theory can be successfully implemented to find the solutions of location problems, scheduling problems, as well as integer optimization problems. Therefore it has noteworthy applications in the fields of transportation engineering, computer science, database theory, etc.

Particularly interesting are the competition graphs presented by Cohen [14]. They are very effective to represent the competition occurring in the networks of predator-prey relationships, economic market structures, politics, cell metabolism and in various forms of ecosystems. Cohen put forth this idea while studying an ecological food web as an acyclic digraph such that two species ${\mathfrak {u}}_{1}$ and ${\mathfrak {u}}_{2}$ compete for an organism ${\mathfrak {u}}$ if ${\mathfrak {u}}$ is a common prey of both ${\mathfrak {u}}_{1}$ and ${\mathfrak {u}}_{2}$ (that is, if the digraph contains the arcs $({\mathfrak {u}}_{1},{\mathfrak {u}})$ and $({\mathfrak {u}}_{2},{\mathfrak {u}})$). Various forms of competition graphs introduced afterwards include open neighborhood graphs [1, 10], competition common-enemy graph (or double competition graph) [25], niche graphs [12], tolerance competition graphs [11], p-competition graphs [22] and m-step competition graphs [13]. All these forms are effective to encapsulate the visual representation of different types of competitions taking place in various fields.

Competition graphs were generalized to competition hypergraphs by Sonntag and Teichert [41] who declared that the latter provide clear description of competition taking place in ecological interactions, an improvement as compared to the former. In terms of predator-prey narrative, an edge in competition hypergraph captures all those species competing for a specific prey, while that of a competition graph merely demonstrates that the connected species have certain common prey. Many subclasses of competition hypergraphs have also been explored. These include the open neighborhood hypergraph [20], double competition hypergraphs [35], niche hypergraphs [17] and competition cluster hypergraphs [38]. Some properties of competition hypergraphs are discussed in [42, 43].

But crisp models are not always adequate to describe real interactions. The presence of fuzziness in linguistic communication cannot be denied. Zadeh [47] was the pioneer of fuzzy set (FS) theory that handles the uncertainty of actual-world problems. A FS assigns truth-membership grade from the unit closed interval to each of its elements, that describe the degrees to which its members partake in. In order to improve its representation ability, Atanassov [7] put forward a non-standard FS, the intuitionistic fuzzy set (IFS), that incorporates an independent falsity-membership grade to illustrate the extent to which the elements do not contribute to that set; a natural restriction is presumed, namely, that for each element, the sum of its truth-membership and falsity-membership values should be at most one. Yager [46] introduced the Pythagorean fuzzy set (PFS) that allows the Pythagorean membership values thus providing more flexibility in the assignment of membership and non-membership values as compared to IFS. It permits all those membership and non-membership values for which the addition of their squares never exceeds one. Different authors described applications of IFSs and PFSs in decision-making [3, 6, 15, 26]. For further studies, the readers are referred to [5, 16, 23, 29, 32].

The concept of graph was soon studied in FS theory and related extensions. The notion of fuzzy graph was introduced by Kaufmann [21], and its operations were determined by Moderson and Nair [28]. Paravathi and Karunambigai [33] developed the intuitionistic fuzzy generalizations of various notions of fuzzy graphs and revealed that the proposed graphs have applications in network analysis. Naz et al. [31] presented a more generalized model of Pythagorean fuzzy graphs (PFGs) together with properties and several applications to decision-making problems. Goetschel [18] found that any finite collection of fuzzy subsets over a finite crisp set gives rise to the notion of fuzzy hypergraphs, and he applied this technique on Hebbian structures. Similarly, Paravathi et al. [34] presented intuitionistic as well as dual intuitionistic fuzzy hypergraphs. Akram and Dudek [2] also discussed intuitionistic fuzzy hypergraphs and implemented these structures on scheduling and telecommunication problems. Luqman et al. [24] put forth q-rung orthopair fuzzy hypergraphs with some applications to decision-making. The proposed hypergraphs correspond to Pythagorean fuzzy hypergraphs (PFHs) for $q=2$. Akram and Luqman [4] deeply discussed the fuzzy hypergraphs and its distinct variations.

Likewise, the idea of competition graphs was also extended to represent notions from several theories of uncertain knowledge. Fuzzy competition graphs were defined by Samanta and Pal [39], which not only describe the competing entities of a system, but also compute the strength of competition. Samanta et al. [37] investigated m-step fuzzy competition graphs. Similarly, intuitionistic fuzzy competition graphs [36], q-rung orthopair fuzzy competition graphs [19] and fuzzy soft competition graphs [30] are also found in literature. Fuzzy competition hypergraphs with several applications were presented by Sarwar et al. [40].

Given these antecedents, the motivation behind this article is as follows:

• 1. PFHs can effectively deliver visual representation of multinary relations, in such way that one can study the strength of these connections with the help of Pythagorean membership grades. For that reason, representing competing interactions in the framework of PFHs is a constructive exercise.

• 2. The introduction of Pythagorean fuzzy competition hypergraphs (PFCH) has potential advantages over existing models, as it inherits the properties of both PFS and competition hypergraphs.

• 3. The reason why different forms of PFCHs are useful is that it is always interesting to find competition at distinct levels and steps. At a practical level, the relationship of species with their neighbors is also helpful in the study of different ecological systems.

Bearing in mind these evidences, this research contributes to the specialized literature with the following achievements.

• 1. It defines and illustrates PFCHs, Pythagorean fuzzy economic competition hypergraphs (PFECHs), Pythagorean fuzzy row hypergraph ($\hbox {PFR}_{{w}}$H), Pythagorean fuzzy column hypergraph ($\hbox {PFC}_{{l}}$H), m-step Pythagorean fuzzy hypergraphs ($\hbox {PFC}_{{m}}$Hs) and Pythagorean fuzzy neighborhood hypergraphs of both open and closed types.

• 2. This study also presents various results regarding the strength of competition at different levels and steps.

• 3. It provides some algorithms which help in the understanding of related concepts.

• 4. It considers an interesting ecosystem of the Bering Sea and describes the competition among its organisms with the help of PFCH. Further, it computes both the competing and non-competing strengths of predators corresponding to each prey.

This article has many new features that make it excel over the existing literature. Primarily, competition is the focal point of this work and it is discussed in the background of PFHs. PFHs have been studied extensively for the solution of problems in discrete mathematics and decision-making. The suggested PFCHs are better suited for representing real data as the ecological networks of different biological communities are also assembled in terms of directed graphs. Likewise, PFCHs are constructed using PFDs and not from PF directed hypergraphs. In addition to this, competition hypergraphs [41] are able to exhibit who eats whom, but they do not convey any information about how much the predators of a community compete for an organism. However, the consumers of an ecosystem do not crave alike for their preys. This imprecision and uncertainty is fully demonstrated by PFCHs.

This article is organized as follows. In the next section, we give some preliminary concepts which will be used in the following parts. Section 3 includes the concepts of $\hbox {PFR}_{{w}}$H, $\hbox {PFC}_{{l}}$H, PFCH and PFECH. In Sect. 4, we introduce the concept of $\hbox {PFC}_{{m}}$H which helps to compute the strength of preys in indirect competitions of various ecological systems. Then in Sect. 5, the ideas of Pythagorean fuzzy neighborhood graphs of both open and closed types are presented. An application representing the predator-prey relationship is considered in Sect. 6 to present the pertinence of PFCHs. The Bering Sea is well known due to the diversity of its bionetwork as it contains numerous species of mammals and fish. This characteristic of Bering Sea urged us to study mutual competition among its organisms with the proposed model of PFCHs. Section 7 provides the comparative analysis, and the last section summarizes the main findings of the paper.

2 Preliminaries

Throughout the paper, U denotes a universal set. In addition, unless otherwise stated, all Pythagorean fuzzy digraphs (PFDs) and PFHs considered may have isolated vertices but they are void of loops as well as multiple arcs and hyperedges, respectively.

Definition 1

[46] A PFS $\alpha$ over the universal set U is defined as an object $\alpha =({\mathfrak {t}}_\alpha , {\mathfrak {f}}_\alpha ):U \rightarrow [0,1]\times [0,1]$ such that the characteristic functions ${\mathfrak {t}}_\alpha :U\rightarrow [0,1]$ and ${\mathfrak {f}}_\alpha :U\rightarrow [0,1]$ represent the truth-membership and falsity-membership functions, respectively, and for each ${\mathfrak {u}}_{i}\in U$, $0\le {\mathfrak {t}}^2_\alpha ({\mathfrak {u}}_{i})+ {\mathfrak {f}}^2_\alpha ({\mathfrak {u}}_{i})\le 1$ holds. Moreover, ${\mathfrak {i}}_\alpha ({\mathfrak {u}}_{i})=\sqrt{1- ({\mathfrak {t}}^2_\alpha ({\mathfrak {u}}_{i})+ {\mathfrak {f}}^2_\alpha ({\mathfrak {u}}_{i}))}$ is the PF index or indeterminacy value of the element ${\mathfrak {u}}_{i}$ to the set $\alpha$.

Next we define some notions that help to lay the foundations of PFSs:

Definition 2

[19] The height $h(\alpha )$ of a PFS $\alpha$ is defined as $h(\alpha )=(h_{{\mathfrak {t}}}(\alpha ),h_{{\mathfrak {f}}}(\alpha ))$, where $h_{{\mathfrak {t}}}(\alpha )=\max _{{\mathfrak {u}}_{i}\in U}{{\mathfrak {t}}}_{\alpha }({\mathfrak {u}}_{i})$ and $h_{{\mathfrak {f}}}(\alpha )=\min _{{\mathfrak {u}}_{i}\in U}{{\mathfrak {f}}}_{\alpha }({\mathfrak {u}}_{i}))$.

Definition 3

[19] The cardinality $C(\alpha )$ of a PFS $\alpha$ is defined as $C(\alpha )=(|\alpha |_{{\mathfrak {t}}},|\alpha |_{{\mathfrak {f}}})$, where $|\alpha |_{{\mathfrak {t}}}=\sum _{{\mathfrak {u}}_{i}\in U}{{\mathfrak {t}}}_{\alpha }({\mathfrak {u}}_{i})$ and $|\alpha |_{{\mathfrak {f}}}=\sum _{{\mathfrak {u}}_{i}\in U}{{\mathfrak {f}}}_{\alpha }({\mathfrak {u}}_{i})$.

Definition 4

[19] The support $Supp(\alpha )$ of a PFS $\alpha$ is defined as $Supp(\alpha )=(Supp_{{\mathfrak {t}}}(\alpha )\cup Supp_{{\mathfrak {f}}}(\alpha ))$, where $Supp_{{\mathfrak {t}}}(\alpha )=\{{\mathfrak {u}}_{i}\in U\mid {\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{i})>0\}$ and $Supp_{{\mathfrak {f}}}(\alpha )=\{{\mathfrak {u}}_{i}\in U\mid {\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{i})<1\}$.

We can now introduce Pythagorean fuzzy digraphs (and related concepts) as follows:

Definition 5

[31] A PFD $\overrightarrow{G}$ on universe U is a pair $\overrightarrow{G}=(\alpha , \overrightarrow{\xi })$, where $\alpha =({\mathfrak {t}}_{\alpha }, {\mathfrak {f}}_{\alpha })$ is a PFS over U with $0\le {\mathfrak {t}}^2_{\alpha }({\mathfrak {u}}_{i}) +{\mathfrak {f}}^2_{\alpha }({\mathfrak {u}}_{i}) \le 1$ for all ${\mathfrak {u}}_{i}\in U$ and $\overrightarrow{\xi }=({\mathfrak {t}}_{\overrightarrow{\xi }}, {\mathfrak {f}}_{\overrightarrow{\xi }})$ is a PF relation (not symmetric) over $\alpha$ such that $\forall {\mathfrak {u}}_{i}{\mathfrak {u}}_{j}\in U\times U$,

$$\begin{aligned}&{\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})\le \min \{{\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{i}), {\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{j})\};\\&{\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})\le \max \{{\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{i}), {\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{j})\}, \end{aligned}$$

with $0\le {\mathfrak {t}}^2_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})+{\mathfrak {f}}^2_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})\le 1$. Note that $\alpha$ is the PFS of vertices and $\overrightarrow{\xi }$ is a PFS of directed edges for the PFD $\overrightarrow{G}=(\alpha , \overrightarrow{\xi })$. Also, in PFD, generally ${\mathfrak {u}}_{i}{\mathfrak {u}}_{j}\ne {\mathfrak {u}}_{j}{\mathfrak {u}}_{i}$.

Definition 6

[19] A PF out-neighborhood $N^{+}({\mathfrak {u}}_{i})$ of a vertex ${\mathfrak {u}}_{i}$ of a PFD $\overrightarrow{G}=(\alpha , \overrightarrow{\xi })$ is defined as $N^{+}({\mathfrak {u}}_{i})=\{\langle {\mathfrak {u}}_{j}, ({\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j}), {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j}))\rangle \mid {\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})>0\, { or }\, {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})>0\}$.

Definition 7

[19] A PF in-neighborhood $N^{-}({\mathfrak {u}}_{i})$ of a vertex ${\mathfrak {u}}_{i}$ of a PFD $\overrightarrow{G}=(\alpha , \overrightarrow{\xi })$ is defined as $N^{-}({\mathfrak {u}}_{i})=\{\langle {\mathfrak {u}}_{j}, ({\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j}{\mathfrak {u}}_{i}), {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j}{\mathfrak {u}}_{i}))\rangle \mid {\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j}{\mathfrak {u}}_{i})>0 \,{ or }\, {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j}{\mathfrak {u}}_{i})>0\}$.

Pythagorean fuzzy graphs are defined in the following terms:

Definition 8

[31] A PFG G on universe U is a pair ${G}=(\alpha ,{\xi })$, where $\alpha =({\mathfrak {t}}_{\alpha }, {\mathfrak {f}}_{\alpha })$ is a PFS over U with $0\le {\mathfrak {t}}^2_{\alpha }({\mathfrak {u}}_{i}) +{\mathfrak {f}}^2_{\alpha }({\mathfrak {u}}_{i}) \le 1$ for all ${\mathfrak {u}}_{i}\in U$ and ${\xi }=({\mathfrak {t}}_{{\xi }}, {\mathfrak {f}}_{{\xi }})$ is a PF symmetric relation over $\alpha$ such that $\forall ({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})\in U\times U$,

$$\begin{aligned}&{\mathfrak {t}}_{{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})\le \min \{{\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{i}), {\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{j})\}; \\&{\mathfrak {f}}_{{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})\le \max \{{\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{i}), {\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{j})\}, \end{aligned}$$

with $0\le {\mathfrak {t}}^2_{{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})+{\mathfrak {f}}^2_{{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})\le 1$. Note that $\alpha$ is the PFS of vertices and ${\xi }$ is a PFS of edges for the PFG ${G}=(\alpha ,{\xi })$.

Definition 9

A PF open neighborhood $N({\mathfrak {u}}_{i})$ of a vertex ${\mathfrak {u}}_{i}$ of PFG $G=(\alpha ,\xi )$ is defined as $N({\mathfrak {u}}_{i})=\{\langle {\mathfrak {u}}_{j},({\mathfrak {t}}_{\xi }({\mathfrak {u}}_{i}{\mathfrak {u}}_{j}),{\mathfrak {f}}_{\xi }({\mathfrak {u}}_{i}{\mathfrak {u}}_{j}))\rangle \mid {\mathfrak {t}}_{\xi }({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})>0\, or\, {\mathfrak {f}}_{\xi }({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})>0\}$.

Definition 10

A PF closed neighborhood $N[{\mathfrak {u}}_{i}]$ of a vertex ${\mathfrak {u}}_{i}$ of PFG $G=(\alpha ,\xi )$ is defined as $N[{\mathfrak {u}}_{i}]=N({\mathfrak {u}}_{i})\cup \{\langle {\mathfrak {u}}_{i},({\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{i}),{\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{i}))\rangle \}$.

Definition 11

[19] The underlying PFG ${\mathcal {U}}(\overrightarrow{G})$ of a PFD $\overrightarrow{G}$ over U has the same PFS of vertices as that of $\overrightarrow{G}$, and there exists a PF edge between ${\mathfrak {u}}_{i},{\mathfrak {u}}_{j}\in U$ if

$$\begin{aligned} {\mathfrak {t}}_{\xi }({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})= {\left\{ \begin{array}{ll} \begin{array}{ll} {\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})\wedge {\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j}{\mathfrak {u}}_{i}), &{}\quad \hbox {if}\quad {\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})>0, {\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j}{\mathfrak {u}}_{i})>0,\\ {\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j}), &{} \quad \hbox {if}\quad {\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})>0, {\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j}{\mathfrak {u}}_{i})\ngtr 0,\\ {\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j}{\mathfrak {u}}_{i}), &{}\quad \hbox {if}\quad {\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})\ngtr 0, {\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j}{\mathfrak {u}}_{i})>0, \end{array} \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} {\mathfrak {f}}_{\xi }({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})= {\left\{ \begin{array}{ll} \begin{array}{ll} {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})\vee {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j}{\mathfrak {u}}_{i}), &{}\quad \hbox {if}\quad {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})>0, {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j}{\mathfrak {u}}_{i})>0,\\ {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j}), &{} \quad \hbox {if}\quad {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})>0, {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j}{\mathfrak {u}}_{i})\ngtr 0,\\ {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j}{\mathfrak {u}}_{i}), &{}\quad \hbox {if}\quad {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})\ngtr 0, {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j}{\mathfrak {u}}_{i})>0. \end{array} \end{array}\right. } \end{aligned}$$

Pythagorean fuzzy hypergraphs are next defined:

Definition 12

[24] A PFH ${\mathbb {H}}$ over U is a pair ${\mathbb {H}}=(\alpha ,\beta )$, where

• 1. $\alpha =\{\langle {\mathfrak {u}}_{i},({\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i}),{\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i}))\rangle | {\mathfrak {u}}_{i}\in U, 1\le i \le n\}$ is a finite PFS of vertices over U, and

• 2. $\beta$ is a PFS $\beta =\{\langle E_{j}, ({\mathfrak {t}}_\beta ({E}_{j}),{\mathfrak {f}}_\beta ({E}_{j}))\rangle | E_{j}\subseteq U, 1\le j\le m\}$ of PF hyperedges $E_{j}$ of ${\mathbb {H}}$, such that $\bigcup _{j} Supp(E_{j})=U$. Additionally, the truth-membership and falsity-membership values of the PF hyperedge $E_{j}$ with vertices ${\mathfrak {u}}_{1}, {\mathfrak {u}}_{2},\ldots ,{\mathfrak {u}}_{3}$ can be computed by the relations

  $$\begin{aligned} {\mathfrak {t}}_{\beta }(E_{j})\le & {} \text {min}\{{\mathfrak {t}}_\alpha ({\mathfrak {u}}_{1}), {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{2}),\ldots , {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{s})\},\\ {\mathfrak {f}}_{\beta }(E_{j})\le & {} \text {max}\{{\mathfrak {f}}_\alpha ({\mathfrak {u}}_{1}), {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{2}),\ldots , {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{s})\},\quad \quad \quad s\le n \end{aligned}$$

  respectively, such that $0\le {\mathfrak {t}}^2_{\beta }(E_{j})+ {\mathfrak {f}}^2_{\beta }(E_{j})\le 1$.

To facilitate their study, the next concept is especially useful:

Definition 13

A PF hyperedge $E_{j}=\{{\mathfrak {u}}_{1},{\mathfrak {u}}_{2},\ldots ,{\mathfrak {u}}_{s}\}$ is called independent strong in the PFH ${\mathbb {H}}=(\alpha ,\beta )$ if the inequalities

$$\begin{aligned}&{\mathfrak {t}}_{\beta }(E_{j})\ge \frac{1}{2}({\mathfrak {u}}_{1}\wedge {\mathfrak {u}}_{2}\wedge \ldots \wedge {\mathfrak {u}}_{s});\\&{\mathfrak {f}}_{\beta }(E_{j})\le \frac{1}{2}({\mathfrak {u}}_{1}\vee {\mathfrak {u}}_{2}\vee \ldots \vee {\mathfrak {u}}_{s}), \end{aligned}$$

hold true, otherwise it is called weak. The strength $\mathrm {Str}(E_{j})$ of a PF hyperedge $E_{j}$ is defined as $\mathrm {Str}(E_{j})=(\mathrm {Str}(E_{j})_{{\mathfrak {t}}}, \mathrm {Str}(E_{j})_{{\mathfrak {f}}})$, where

$$\begin{aligned}&\mathrm {Str}(E_{j})_{{\mathfrak {t}}}=\frac{{\mathfrak {t}}_{\beta }(E_{j})}{{\mathfrak {u}}_{1}\wedge {\mathfrak {u}}_{2}\wedge \ldots \wedge {\mathfrak {u}}_{s}};\\&\mathrm {Str}(E_{j})_{{\mathfrak {f}}}=\frac{{\mathfrak {f}}_{\beta }(E_{j})}{{\mathfrak {u}}_{1}\vee {\mathfrak {u}}_{2}\vee \ldots \vee {\mathfrak {u}}_{s}}. \end{aligned}$$

3 Pythagorean fuzzy competition hypergraphs

Pythagorean fuzzy row and column hypergraphs are designed in the next definitions:

Definition 14

Let $\overrightarrow{G}=(\alpha , \overrightarrow{\xi })$ be a PFD over U. The $\hbox {PFR}_{{w}}$H ${\mathbb {R}}o{\mathbb {H}}(\overrightarrow{G})$ of $\overrightarrow{G}$, denoted by ${\mathbb {R}}o{\mathbb {H}}(\overrightarrow{G})=(\alpha ,\xi _{r})$, is a PF hypergraph whose PFS of vertices is same as for $\overrightarrow{G}$ and the PF hyperedges can be constructed as follows: for all $1\le j\le n,$

$$\begin{aligned} E_{j}&= \{{\mathfrak {u}}_{i_{1}},{\mathfrak {u}}_{i_{2}},\ldots ,{\mathfrak {u}}_{i_{s}}\mid s\ge 2, {\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})>0\quad \text \,{ or }\, \quad\\&\quad {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})>0; i\in \{i_{1}, i_{2},\ldots ,i_{s}\}\}, \end{aligned}$$

whose Pythagorean membership grades are computed as

$$\begin{aligned} {\mathfrak {t}}_{\xi _{r}}(E_{j})&= [\mathrm {\min }\{{\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i})\}]\\&\quad \times [\mathrm {\min }\{{\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i},{\mathfrak {u}}_{j})\}],\\ {\mathfrak {f}}_{\xi _{r}}(E_{j})&= [\mathrm {\max }\{{\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i})\}]\\&\quad \times [\mathrm {\max }\{{\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i},{\mathfrak {u}}_{j})\}], \end{aligned}$$

where $i\in \{i_{1}, i_{2},\ldots ,i_{s}\}$.

Definition 15

Let $\overrightarrow{G}=(\alpha , \overrightarrow{\xi })$ be a PFD over U. The $\hbox {PFC}_{{l}}$H ${\mathbb {C}}o{\mathbb {H}}(\overrightarrow{G})$ of $\overrightarrow{G}$, denoted by ${\mathbb {C}}o{\mathbb {H}}(\overrightarrow{G})=(\alpha ,\xi _{c})$, is a PF hypergraph whose PFS of vertices is same as for $\overrightarrow{G}$ and the PF hyperedges can be constructed as follows: for all $1\le i\le n,$

$$\begin{aligned} E_{i}&= \{{\mathfrak {u}}_{j_{1}},{\mathfrak {u}}_{j_{2}},\ldots ,{\mathfrak {u}}_{j_{s}}\mid s\ge 2, {\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})\\&\quad >0 or {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})>0; j\in \{j_{1}, j_{2},\ldots ,j_{s}\}\}, \end{aligned}$$

whose Pythagorean membership grades are computed as

$$\begin{aligned} {\mathfrak {t}}_{\xi _{c}}(E_{i})&= [\mathrm {\min }\{{\mathfrak {t}}_\alpha ({\mathfrak {u}}_{j})\}]\\&\quad \times [\mathrm {\min }\{{\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i},{\mathfrak {u}}_{j})\}], \\ {\mathfrak {f}}_{\xi _{c}}(E_{i})&= [\mathrm {\max }\{{\mathfrak {f}}_\alpha ({\mathfrak {u}}_{j})\}]\\&\quad \times [\mathrm {\max }\{{\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i},{\mathfrak {u}}_{j})\}], \end{aligned}$$

where $j\in \{j_{1}, j_{2},\ldots ,j_{s}\}$.

Algorithms 1 and 2, respectively, give the detailed steps for the construction of $\hbox {PFR}_{{w}}$H and $\hbox {PFC}_{{w}}$H as defined above.

The next example illustrates the application of Algorithms 1 and 2.

Example 1

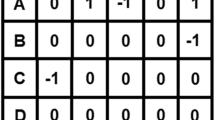
Consider a PFD $\overrightarrow{G}=(\alpha , \overrightarrow{\xi })$, where

$$\begin{aligned} \alpha &= \bigg \langle \bigg (\frac{{\mathfrak {u}}_{1}}{0.59},\frac{{\mathfrak {u}}_{2}}{0.82},\frac{{\mathfrak {u}}_{3}}{0.86},\frac{{\mathfrak {u}}_{4}}{0.68}, \frac{{\mathfrak {u}}_{5}}{0.63},\frac{{\mathfrak {u}}_{6}}{0.74},\frac{{\mathfrak {u}}_{7}}{0.95},\frac{{\mathfrak {u}}_{8}}{0.43}\bigg ),\\&\bigg (\frac{{\mathfrak {u}}_{1}}{0.65}, \frac{{\mathfrak {u}}_{2}}{0.36},\frac{{\mathfrak {u}}_{3}}{0.33},\frac{{\mathfrak {u}}_{4}}{0.58},\frac{{\mathfrak {u}}_{5}}{0.57},\frac{{\mathfrak {u}}_{6}}{0.42}, \frac{{\mathfrak {u}}_{7}}{0.18},\frac{{\mathfrak {u}}_{8}}{0.62}\bigg ) \bigg \rangle \quad \hbox{and} \\ \overrightarrow{\xi }&= \bigg \langle \bigg (\frac{{\mathfrak {u}}_{2}{\mathfrak {u}}_{1}}{0.37},\frac{{\mathfrak {u}}_{3}{\mathfrak {u}}_{2}}{0.77}, \frac{{\mathfrak {u}}_{4}{\mathfrak {u}}_{2}}{0.66},\frac{{\mathfrak {u}}_{5}{\mathfrak {u}}_{1}}{0.55},\frac{{\mathfrak {u}}_{5}{\mathfrak {u}}_{2}}{0.56}, \frac{{\mathfrak {u}}_{5}{\mathfrak {u}}_{3}}{0.62},\frac{{\mathfrak {u}}_{6}{\mathfrak {u}}_{1}}{0.52},\frac{{\mathfrak {u}}_{6}{\mathfrak {u}}_{2}}{0.73},\\&\frac{{\mathfrak {u}}_{6}{\mathfrak {u}}_{4}}{0.70},\frac{{\mathfrak {u}}_{7}{\mathfrak {u}}_{3}}{0.84}, \frac{{\mathfrak {u}}_{7}{\mathfrak {u}}_{4}}{0.67},\frac{{\mathfrak {u}}_{7}{\mathfrak {u}}_{5}}{0.61}, \frac{{\mathfrak {u}}_{7}{\mathfrak {u}}_{6}}{0.72}, \frac{{\mathfrak {u}}_{8}{\mathfrak {u}}_{3}}{0.36}, \frac{{\mathfrak {u}}_{8}{\mathfrak {u}}_{4}}{0.41}, \frac{{\mathfrak {u}}_{8}{\mathfrak {u}}_{7}}{0.39}\bigg ),\\&\bigg (\frac{{\mathfrak {u}}_{2}{\mathfrak {u}}_{1}}{0.48},\frac{{\mathfrak {u}}_{3}{\mathfrak {u}}_{2}}{0.35}, \frac{{\mathfrak {u}}_{4}{\mathfrak {u}}_{2}}{0.58},\frac{{\mathfrak {u}}_{5}{\mathfrak {u}}_{1}}{0.64},\frac{{\mathfrak {u}}_{5}{\mathfrak {u}}_{2}}{0.55}, \frac{{\mathfrak {u}}_{5}{\mathfrak {u}}_{3}}{0.54},\frac{{\mathfrak {u}}_{6}{\mathfrak {u}}_{1}}{0.45},\frac{{\mathfrak {u}}_{6}{\mathfrak {u}}_{2}}{0.38},\\&\frac{{\mathfrak {u}}_{6}{\mathfrak {u}}_{4}}{0.56}, \frac{{\mathfrak {u}}_{7}{\mathfrak {u}}_{3}}{0.32}, \frac{{\mathfrak {u}}_{7}{\mathfrak {u}}_{4}}{0.49},\frac{{\mathfrak {u}}_{7}{\mathfrak {u}}_{5}}{0.50}, \frac{{\mathfrak {u}}_{7}{\mathfrak {u}}_{6}}{0.40}, \frac{{\mathfrak {u}}_{8}{\mathfrak {u}}_{3}}{0.44}, \frac{{\mathfrak {u}}_{8}{\mathfrak {u}}_{4}}{0.57}, \frac{{\mathfrak {u}}_{8}{\mathfrak {u}}_{7}}{0.58}\bigg )\bigg \rangle . \end{aligned}$$

It is presented graphically in Fig. 1. The adjacency matrix of $\overrightarrow{G}$ is given in Table 1. Note that the vertices are labeled in such a way that the corresponding adjacency matrix is strictly lower triangular. By following Algorithm 1, we can construct the $\hbox {PFR}_{{w}}$H of $\overrightarrow{G}$. It comprises four hyperedges $E_{1}=\{{\mathfrak {u}}_{2},{\mathfrak {u}}_{5},{\mathfrak {u}}_{6}\}$, $E_{2}=\{{\mathfrak {u}}_{3},{\mathfrak {u}}_{4}, {\mathfrak {u}}_{5},{\mathfrak {u}}_{6}\}$, $E_{3}=\{{\mathfrak {u}}_{5},{\mathfrak {u}}_{7}, {\mathfrak {u}}_{8}\}$ and $E_{4}=\{{\mathfrak {u}}_{6},{\mathfrak {u}}_{7}, {\mathfrak {u}}_{8}\}$, whose truth-membership and falsity-membership values are computed as

$$\begin{aligned} {\mathfrak {t}}_{\xi _r}(E_{1})&= [{\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{2})\wedge {\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{5})\wedge {\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{6})]\\&\quad \times [{\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{2}{u}_{1})\wedge {\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{5}{u}_{1})\wedge {\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{6}{u}_{1})]\\&=0.63\times 0.37=0.2331,\\ {\mathfrak {f}}_{\xi _r}(E_{1})&= [{\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{2})\vee {\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{5})\vee {\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{6})]\\&\quad \times [{\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{2}{u}_{1})\vee {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{5}{u}_{1})\vee {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{6}{u}_{1})]\\&=0.57\times 0.64=0.3648. \end{aligned}$$

Fig. 1

A PFD $\overrightarrow{G}$

Table 1 Adjacency matrix

Similarly, we have ${\mathfrak {t}}_{\xi _r}(E_{2})=0.3528$, ${\mathfrak {f}}_{\xi _r}(E_{2})=0.3364$, ${\mathfrak {t}}_{\xi _r}(E_{3})=0.1548$, ${\mathfrak {f}}_{\xi _r}(E_{3})=0.3348$, ${\mathfrak {t}}_{\xi _r}(E_{4})=0.1763$ and ${\mathfrak {f}}_{\xi _r}(E_{4})=0.3534$. The obtained $\hbox {PFR}_{{w}}$H is shown in Fig. 2.

Fig. 2

A $\hbox {PFR}_{{w}}$H ${\mathbb {R}}o{{\mathbb {H}}}(\overrightarrow{G})$

Likewise, we can construct the $\hbox {PFC}_{{l}}$H of $\overrightarrow{G}$ by following Algorithm 2. The hyperedges of $\hbox {PFC}_{{l}}$H are $E_{5}=\{{\mathfrak {u}}_{1},{\mathfrak {u}}_{2},{\mathfrak {u}}_{3}\}$, $E_{6}=\{{\mathfrak {u}}_{1},{\mathfrak {u}}_{2}, {\mathfrak {u}}_{4}\}$, $E_{7}=\{{\mathfrak {u}}_{3},{\mathfrak {u}}_{4},{\mathfrak {u}}_{5}, {\mathfrak {u}}_{6}\}$ and $E_{8}=\{{\mathfrak {u}}_{3},{\mathfrak {u}}_{4}, {\mathfrak {u}}_{7}\}$, whose truth-membership and falsity-membership values can be calculated as

$$\begin{aligned} {\mathfrak {t}}_{\xi _c}(E_{5})&= [{\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{1})\wedge {\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{2})\wedge {\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{3})]\\&\quad \times [{\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{5}{\mathfrak {u}}_{1})\\&\wedge {\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{5}{\mathfrak {u}}_{2})\wedge {\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{5}{\mathfrak {u}}_{3})]=0.59\times 0.55=0.3245,\\ {\mathfrak {f}}_{\xi _c}(E_{5})&= [{\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{1})\vee {\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{2})\vee {\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{3})]\\&\quad \times [{\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{5}{\mathfrak {u}}_{1})\vee {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{5}{\mathfrak {u}}_{2})\\&\vee {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{5}{\mathfrak {u}}_{3})]=0.65\times 0.64=0.4160. \end{aligned}$$

Similarly, we have ${\mathfrak {t}}_{\xi _c}(E_{6})=0.3068$, ${\mathfrak {f}}_{\xi _c}(E_{6})=0.3640$, ${\mathfrak {t}}_{\xi _c}(E_{7})=0.3843$, ${\mathfrak {f}}_{\xi _c}(E_{7})=0.290$, ${\mathfrak {t}}_{\xi _c}(E_{8})=0.2448$ and ${\mathfrak {f}}_{\xi _c}(E_{8})=0.3364$. Its graphical representation is given in Fig. 3. Notice that any arrangement of rows and columns in A preserves the $\hbox {PFR}_{{w}}$H and the $\hbox {PFC}_{{l}}$H (up to isomorphism).

Fig. 3

A $\hbox {PFC}_{{l}}$H ${\mathbb {C}}o{{\mathbb {H}}}(\overrightarrow{G})$

Pythagorean fuzzy competition hypergraphs have the following structure:

Definition 16

A PFCH ${\mathbb {C}}_{{\mathbb {H}}}(\overrightarrow{G})=(\alpha , \xi _{{\mathbb {C}}})$ of a PFD $\overrightarrow{G}=(\alpha , \overrightarrow{\xi })$ has the same PF vertex set as of $\overrightarrow{G}$ and $E_{j}\subseteq U$ is a PF hyperedge of ${\mathbb {C}}_{{\mathbb {H}}}(\overrightarrow{G})$ if and only if $|E_{j}|\ge 2$ and there exists a vertex ${\mathfrak {u}}_{j}\in U$ such that $E_{j}=\{{\mathfrak {u}}_{i_{1}},{\mathfrak {u}}_{i_{2}}, \ldots , {\mathfrak {u}}_{i_{s}} \mid {\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})>0 \quad \, \hbox{or}\, \quad {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})>0;\quad i\in \{i_{1}, i_{2},\ldots , i_{s}\}\}$, that is, $N^{+}({\mathfrak {u}}_{i_{1}})\cap N^{+}({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{i_{s}})$ is a non-empty set due to ${\mathfrak {u}}_{j}$. The Pythagorean membership grades of $E_{j}$ can be computed as

$$\begin{aligned} {\mathfrak {t}}_{\xi _{{\mathbb {C}}}}(E_{j})&= [{\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{1}})\wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{2}})\wedge \ldots \wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{s}})]\\&\times h_{{\mathfrak {t}}}(N^{+}({\mathfrak {u}}_{i_{1}})\cap N^{+}({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{i_{s}})),\\ {\mathfrak {f}}_{\xi _{{\mathbb {C}}}}(E_{j})&= [{\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{1}})\vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{2}})\vee \ldots \vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{s}})]\\&\quad \times h_{{\mathfrak {f}}}(N^{+}({\mathfrak {u}}_{i_{1}})\cap N^{+}({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{i_{s}})). \end{aligned}$$

Remark 1

In the above definition, the factor $h_{{\mathfrak {t}}}(N^{+}({\mathfrak {u}}_{i_{1}})\cap N^{+}({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{i_{s}}))=\mathrm {\min }_{i}\{{\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})\mid i\in \{i_{1}, i_{2}, \ldots ,i_{s}\}\}$ and $h_{{\mathfrak {f}}}(N^{+}({\mathfrak {u}}_{i_{1}})\cap N^{+}({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{i_{s}}))=\mathrm {\max }_{i}\{{\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})\mid i\in \{i_{1}, i_{2}, \ldots ,i_{s}\}\}$ for some fixed j, because multiple hyperedges are ruled out in PFCHs. This representation yields the following immediate result, which explains that the concepts defined in this section are related.

Lemma 1

For a PFD $\overrightarrow{G}$, its associated PFCH ${\mathbb {C}}_{{\mathbb {H}}}(\overrightarrow{G})$ and $\hbox {PFR}_{{w}}$H ${\mathbb {R}}o{{\mathbb {H}}}(\overrightarrow{G})$ coincide.

Let us now introduce Pythagorean fuzzy economic competition hypergraphs:

Definition 17

A PFECH ${{\mathbb {E}}}{{\mathbb {C}}}_{{\mathbb {H}}}(\overrightarrow{G})=(\alpha , \xi _{{\mathbb {E}}})$ of a PFD $\overrightarrow{G}=(\alpha , \overrightarrow{\xi })$ has the same PF vertex set as of $\overrightarrow{G}$ and $E_{i}\subseteq U$ is a PF hyperedge of ${{\mathbb {E}}}{{\mathbb {C}}}_{{\mathbb {H}}}(\overrightarrow{G})$ if and only if $|E_{i}|\ge 2$ and there exists a vertex ${\mathfrak {u}}_{i}\in U$ such that $E_{i}=\{{\mathfrak {u}}_{j_{1}},{\mathfrak {u}}_{j_{2}}, \ldots , {\mathfrak {u}}_{j_{s}} \mid {\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})>0 or {\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})>0; j\in \{j_{1}, j_{2},\ldots , j_{s}\}\}$, that is, $N^{-}({\mathfrak {u}}_{j_{1}})\cap N^{-}({\mathfrak {u}}_{j_{2}})\cap \ldots \cap N^{-}({\mathfrak {u}}_{j_{s}})$ is a non-empty set due to ${\mathfrak {u}}_{i}$. The Pythagorean membership grades of $E_{i}$ can be computed as

$$\begin{aligned} {\mathfrak {t}}_{\xi _{{\mathbb {E}}}}(E_{i})&= [{\mathfrak {t}}_\alpha ({\mathfrak {u}}_{j_{1}})\wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{j_{2}})\wedge \ldots \wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{j_{s}})]\\&\quad \times h_{{\mathfrak {t}}}(N^{-}({\mathfrak {u}}_{j_{1}})\cap N^{-}({\mathfrak {u}}_{j_{2}})\cap \ldots \cap N^{-}({\mathfrak {u}}_{j_{s}})),\\ {\mathfrak {f}}_{\xi _{{\mathbb {E}}}}(E_{i})&= [{\mathfrak {f}}_\alpha ({\mathfrak {u}}_{j_{1}})\vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{j_{2}})\vee \ldots \vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{j_{s}})]\\&\quad \times h_{{\mathfrak {f}}}(N^{-}({\mathfrak {u}}_{j_{1}})\cap N^{-}({\mathfrak {u}}_{j_{2}})\cap \ldots \cap N^{-}({\mathfrak {u}}_{j_{s}})). \end{aligned}$$

A result that parallels Lemma 1 for this concept ensues:

Lemma 2

For a PFD $\overrightarrow{G}$, its associated PFECH ${{\mathbb {E}}}{{\mathbb {C}}}_{{\mathbb {H}}}(\overrightarrow{G})$ and $\hbox {PFC}_{{l}}$H ${\mathbb {C}}o{{\mathbb {H}}}(\overrightarrow{G})$ coincide.

The next theorem characterizes PF hyperedges of Pythagorean fuzzy competition hypergraphs and Pythagorean fuzzy economic competition hypergraphs that are independent strong:

Theorem 1

Let $\overrightarrow{{G}}=(\alpha ,\overrightarrow{\xi })$ be a PFD on U.

• 1. If ${Supp}(N^{+}({\mathfrak {u}}_{1})\cap N^{+}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{{s}}))$ is a singleton subset of U, then the PF hyperedge $E_{j}=\{{\mathfrak {u}}_{{1}},{\mathfrak {u}}_{{2}},\ldots ,{\mathfrak {u}}_{{s}}\}$ of ${\mathbb {C}}_{{\mathbb {H}}}(\overrightarrow{G})$ is independent strong if and only if $|N^{+}({\mathfrak {u}}_{1})\cap N^{+}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{{s}})|_{{\mathfrak {t}}}>\frac{1}{2}$ and $|N^{+}({\mathfrak {u}}_{1})\cap N^{+}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{{s}})|_{{\mathfrak {f}}}<\frac{1}{2}$.

• 2. If ${Supp}(N^{-}({\mathfrak {u}}_{1})\cap N^{-}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{-}({\mathfrak {u}}_{{s}}))$ is a singleton subset of U, then the PF hyperedge $E_{i}=\{{\mathfrak {u}}_{{1}},{\mathfrak {u}}_{{2}},\ldots ,{\mathfrak {u}}_{{s}}\}$ of ${{\mathbb {E}}}{{\mathbb {C}}}_{{\mathbb {H}}}(\overrightarrow{G})$ is independent strong if and only if $|N^{-}({\mathfrak {u}}_{1})\cap N^{-}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{-}({\mathfrak {u}}_{{s}})|_{{\mathfrak {t}}}>0.5$ and $|N^{-}({\mathfrak {u}}_{1})\cap N^{-}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{-}({\mathfrak {u}}_{{s}})|_{{\mathfrak {f}}}<0.5$.

Proof. Let $\overrightarrow{{\mathcal {G}}}=(\alpha ,\overrightarrow{\xi })$ be a PFD. Suppose that ${\mathfrak {u}}$ is the only element with truth-membership value ${\mathfrak {t}}({\mathfrak {u}})$ and falsity-membership value ${\mathfrak {f}}({\mathfrak {u}})$ such that $N^{+}({\mathfrak {u}}_{1})\cap N^{+}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{{s}})=\{\langle {\mathfrak {u}},({\mathfrak {t}}(u),{\mathfrak {f}}(u))\rangle \}$. Clearly ${Supp}(N^{+}({\mathfrak {u}}_{1})\cap N^{+}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{{s}}))=\{{\mathfrak {u}}\}$. Note that $|N^{+}({\mathfrak {u}}_{1})\cap N^{+}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{{s}})|_{{\mathfrak {t}}}={\mathfrak {t}}({\mathfrak {u}})=h_{{\mathfrak {t}}}(N^{+}({\mathfrak {u}}_{1})\cap N^{+}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{{s}}))$ and $|N^{+}({\mathfrak {u}}_{1})\cap N^{+}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{{s}})|_{{\mathfrak {f}}}={\mathfrak {f}}({\mathfrak {u}})=h_{{\mathfrak {f}}}(N^{+}({\mathfrak {u}}_{1})\cap N^{+}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{{s}}))$. Let ${\mathbb {C}}_{{\mathbb {H}}}(\overrightarrow{G})=(\alpha ,\xi _{{\mathbb {C}}})$ be the PFCH of $\overrightarrow{{G}}$. Then ${\mathfrak {t}}_{\xi _{{\mathbb {C}}}}(E_{j})=({\mathfrak {u}}_{{1}}\wedge {\mathfrak {u}}_{{2}}\wedge \ldots \wedge {\mathfrak {u}}_{{s}}) \times {\mathfrak {t}}({\mathfrak {u}})$ and ${\mathfrak {f}}_{\xi _{{\mathbb {C}}}}(E_{j})=({\mathfrak {u}}_{{1}}\vee {\mathfrak {u}}_{{2}}\vee \ldots \vee {\mathfrak {u}}_{{s}})\times {\mathfrak {f}}({\mathfrak {u}})$ yields the truth-membership and falsity-membership values of PF hyperedge $E_{j}$. The outcome is $\frac{{\mathfrak {t}}_{\xi _{{\mathbb {C}}}}(E_{j})}{{\mathfrak {u}}_{{1}}\wedge {\mathfrak {u}}_{{2}}\wedge \ldots \wedge {\mathfrak {u}}_{{s}}} ={\mathfrak {t}}({\mathfrak {u}})$ and $\frac{{\mathfrak {f}}_{\xi _{{\mathbb {C}}}}(E_{j})}{{\mathfrak {u}}_{{1}}\vee {\mathfrak {u}}_{{2}}\vee \ldots \vee {\mathfrak {u}}_{{s}}} ={\mathfrak {f}}({\mathfrak {u}})$.

Suppose that $E_{j}$ is independent strong, that is, ${\mathfrak {t}}_{\xi _{{\mathbb {C}}}}(E_{j})>\frac{1}{2}({\mathfrak {u}}_{{1}}\wedge {\mathfrak {u}}_{{2}}\wedge \ldots \wedge {\mathfrak {u}}_{{s}})$ and ${\mathfrak {f}}_{\xi _{{\mathbb {C}}}}(E_{j})<\frac{1}{2}({\mathfrak {u}}_{{1}}\vee {\mathfrak {u}}_{{2}}\vee \ldots \vee {\mathfrak {u}}_{{s}})$ or $\frac{{\mathfrak {t}}_{\xi _{{\mathbb {C}}}}(E_{j})}{{\mathfrak {u}}_{{1}}\wedge {\mathfrak {u}}_{{2}}\wedge \ldots \wedge {\mathfrak {u}}_{{s}}} >\frac{1}{2}$ and $\frac{{\mathfrak {f}}_{\xi _{{\mathbb {C}}}}(E_{j})}{{\mathfrak {u}}_{{1}}\vee {\mathfrak {u}}_{{2}}\vee \ldots \vee {\mathfrak {u}}_{{s}}} <\frac{1}{2}$. Combining these results gives ${\mathfrak {t}}({\mathfrak {u}})>\frac{1}{2}$ and ${\mathfrak {f}}({\mathfrak {u}})<\frac{1}{2}$. Consequently, $|N^{+}({\mathfrak {u}}_{1})\cap N^{+}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{{s}})|_{{\mathfrak {t}}}>\frac{1}{2}$ and $|N^{+}({\mathfrak {u}}_{1})\cap N^{+}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{{s}})|_{{\mathfrak {f}}}<\frac{1}{2}$.

For the converse part, let $|N^{+}({\mathfrak {u}}_{1})\cap N^{+}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{{s}})|_{{\mathfrak {t}}}>\frac{1}{2}$ and $|N^{+}({\mathfrak {u}}_{1})\cap N^{+}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{{s}})|_{{\mathfrak {f}}}<\frac{1}{2}$ which shows that ${\mathfrak {t}}({\mathfrak {u}})>\frac{1}{2}$ and ${\mathfrak {f}}({\mathfrak {u}})<\frac{1}{2}$, respectively. These expressions combine to produce $\frac{{\mathfrak {t}}_{\xi _{{\mathbb {C}}}}(E_{j})}{{\mathfrak {u}}_{{1}}\wedge {\mathfrak {u}}_{{2}}\wedge \ldots \wedge {\mathfrak {u}}_{{s}}} >\frac{1}{2}$ and $\frac{{\mathfrak {f}}_{\xi _{{\mathbb {C}}}}(E_{j})}{{\mathfrak {u}}_{{1}}\vee {\mathfrak {u}}_{{2}}\vee \ldots \vee {\mathfrak {u}}_{{s}}} <\frac{1}{2}$. So the PF hyperedge $E_{j}$ of ${\mathbb {C}}_{{\mathbb {H}}}(\overrightarrow{G})$ is independent strong.

The strategy for the proof of (2) is similar.

Pythagorean fuzzy k-(economic)competition hypergraphs capture the following concepts:

Definition 18

Let k be a non-negative real number. The Pythagorean fuzzy k-competition hypergraph ($\hbox {PFC}_{{k}}$H) ${\mathbb {C}}^{k}_{{\mathbb {H}}}(\overrightarrow{{G}})=(\alpha , \xi _{k{\mathbb {C}}})$ of a PFD $\overrightarrow{{G}}=(\alpha ,\overrightarrow{{\xi }})$ has the same PF vertex set as of $\overrightarrow{{G}}$ and $E_{j}\subseteq U$ is a PF hyperedge of ${\mathbb {C}}^{k}_{{\mathbb {H}}}(\overrightarrow{{G}})$ if and only if $|E_{j}|\ge 2$ and $|N^{+}({\mathfrak {u}}_{i_{1}})\cap N^{+}({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{i_{s}})|_{{\mathfrak {t}}}>k$ and $|N^{+}({\mathfrak {u}}_{i_{1}})\cap N^{+}({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{i_{s}})|_{{\mathfrak {f}}}>k$. The Pythagorean membership grades of $E_{j}$ can be computed as

$$\begin{aligned} {\mathfrak {t}}_{\xi _{k{\mathbb {C}}}}(E_{j})&= \frac{k_{1}-k}{k_{1}}({\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{1}})\wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{2}})\wedge \ldots \wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{s}}))\\&\quad \times h_{{\mathfrak {t}}}(N^{+}({\mathfrak {u}}_{i_{1}})\cap N^{+}({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{i_{s}})), \\ {\mathfrak {f}}_{\xi _{k{\mathbb {C}}}}(E_{j})&= \frac{k_{2}-k}{k_{2}}({\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{1}})\vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{2}})\vee \ldots \vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{s}}))\\&\quad \times h_{{\mathfrak {f}}}(N^{+}({\mathfrak {u}}_{i_{1}})\cap N^{+}({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{i_{s}})), \end{aligned}$$

where $k_{1}=|N^{+}({\mathfrak {u}}_{i_{1}})\cap N^{+}({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{i_{s}})|_{{\mathfrak {t}}}$ and $k_{2}=|N^{+}({\mathfrak {u}}_{i_{1}})\cap N^{+}({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N^{+}({\mathfrak {u}}_{i_{s}})|_{{\mathfrak {f}}}$.

Definition 19

Let k be a non-negative real number. The Pythagorean fuzzy k-economic competition hypergraph ($\hbox {PFEC}_{{k}}$H) ${{\mathbb {E}}}{{\mathbb {C}}}^{k}_{{\mathbb {H}}}({\overrightarrow{G}})=(\alpha , \xi _{k{\mathbb {E}}})$ of a PFD $\overrightarrow{{G}}=(\alpha ,\overrightarrow{{\xi }})$ has the same PF vertex set as of $\overrightarrow{{G}}$ and $E_{i}\subseteq U$ is a PF hyperedge of ${{\mathbb {E}}}{{\mathbb {C}}}^{k}_{{\mathbb {H}}}(\overrightarrow{{G}})$ if and only if $|E_{i}|\ge 2$ and $|N^{-}({\mathfrak {u}}_{j_{1}})\cap N^{-}({\mathfrak {u}}_{j_{2}})\cap \ldots \cap N^{-}({\mathfrak {u}}_{j_{s}})|_{{\mathfrak {t}}}>k$ and $|N^{-}({\mathfrak {u}}_{j_{1}})\cap N^{-}({\mathfrak {u}}_{j_{2}})\cap \ldots \cap N^{-}({\mathfrak {u}}_{j_{s}})|_{{\mathfrak {f}}}>k$. The Pythagorean membership grades of $E_{i}$ can be computed as

$$\begin{aligned} {\mathfrak {t}}_{\xi _{k{\mathbb {E}}}}(E_{i})&= \frac{k_{1}-k}{k_{1}}({\mathfrak {t}}_\alpha ({\mathfrak {u}}_{j_{1}})\wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{j_{2}})\wedge \ldots \wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{j_{s}}))\\&\quad \times h_{{\mathfrak {t}}}(N^{-}({\mathfrak {u}}_{j_{1}})\cap N^{-}({\mathfrak {u}}_{j_{2}})\cap \ldots \cap N^{-}({\mathfrak {u}}_{j_{s}})), \\ {\mathfrak {f}}_{\xi _{k{\mathbb {E}}}}(E_{i})&= \frac{k_{2}-k}{k_{2}}({\mathfrak {f}}_\alpha ({\mathfrak {u}}_{j_{1}})\vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{j_{2}})\vee \ldots \vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{j_{s}}))\\&\quad \times h_{{\mathfrak {f}}}(N^{-}({\mathfrak {u}}_{j_{1}})\cap N^{-}({\mathfrak {u}}_{j_{2}})\cap \ldots \cap N^{-}({\mathfrak {u}}_{j_{s}})), \end{aligned}$$

where $k_{1}=|N^{-}({\mathfrak {u}}_{j_{1}})\cap N^{-}({\mathfrak {u}}_{j_{2}})\cap \ldots \cap N^{-}({\mathfrak {u}}_{j_{s}})|_{{\mathfrak {t}}}$ and $k_{2}=|N^{-}({\mathfrak {u}}_{j_{1}})\cap N^{-}({\mathfrak {u}}_{j_{2}})\cap \ldots \cap N^{-}({\mathfrak {u}}_{j_{s}})|_{{\mathfrak {f}}}$.

A result that parallels Theorem 1 for these concepts ensues:

Theorem 2

Let $\overrightarrow{{G}}=(\alpha ,\overrightarrow{\xi })$ be a PFD on U.

• 1. If $h_{{\mathfrak {t}}}({N}^{+}({\mathfrak {u}}_{1})\cap {N}^{+}({\mathfrak {u}}_{2})\cap \ldots \cap {N}^{+}({\mathfrak {u}}_{s}))=1=h_{{\mathfrak {f}}}({N}^{+}({\mathfrak {u}}_{1})\cap {N}^{+}({\mathfrak {u}}_{2})\cap \ldots \cap {N}^{+}({\mathfrak {u}}_{s}))$, $|{N}^{+}({\mathfrak {u}}_{1})\cap {N}^{+}({\mathfrak {u}}_{2})\cap \ldots \cap {N}^{+}({\mathfrak {u}}_{s})|_{\mathfrak {t}}>2k$ and $|{N}^{+}({\mathfrak {u}}_{1})\cap {N}^{+}({\mathfrak {u}}_{2})\cap \ldots \cap {N}^{+}({\mathfrak {u}}_{s})|_{{\mathfrak {f}}}<2k$, then the PF hyperedge $E_{j}=\{{\mathfrak {u}}_{1},{\mathfrak {u}}_{2},\ldots ,\mathfrak {u_{s}}\}$ of ${\mathbb {C}}^{k}_{{\mathbb {H}}}(\overrightarrow{{G}})$ is independent strong.

• 2. If $h_{{\mathfrak {t}}}({N}^{-}({\mathfrak {u}}_{1})\cap {N}^{-}({\mathfrak {u}}_{2})\cap \ldots \cap {N}^{-}({\mathfrak {u}}_{s}))=1=h_{{\mathfrak {f}}}({N}^{-}({\mathfrak {u}}_{1})\cap {N}^{-}({\mathfrak {u}}_{2})\cap \ldots \cap {N}^{-}({\mathfrak {u}}_{s}))$, $|{N}^{-}({\mathfrak {u}}_{1})\cap {N}^{-}({\mathfrak {u}}_{2})\cap \ldots \cap {N}^{-}({\mathfrak {u}}_{s})|_{\mathfrak {t}}>2k$ and $|{N}^{-}({\mathfrak {u}}_{1})\cap {N}^{-}({\mathfrak {u}}_{2})\cap \ldots \cap {N}^{-}({\mathfrak {u}}_{s})|_{{\mathfrak {f}}}<2k$, then the PF hyperedge $E_{i}=\{{\mathfrak {u}}_{1},{\mathfrak {u}}_{2},\ldots ,\mathfrak {u_{s}}\}$ of ${{\mathbb {E}}}{{\mathbb {C}}}^{k}_{{\mathbb {H}}}(\overrightarrow{{G}})$ is independent strong.

Proof. Let $\overrightarrow{{G}}=(\alpha ,\overrightarrow{\xi })$ be a PFD and let ${{\mathbb {E}}}{{\mathbb {C}}}^{k}_{{\mathbb {H}}}({\overrightarrow{G}})=(\alpha , \xi _{k{\mathbb {E}}})$ be the corresponding $\hbox {PFEC}_{{k}}$ H. Given that $h_{{\mathfrak {t}}}({N}^{-}({\mathfrak {u}}_{1})\cap {N}^{-}({\mathfrak {u}}_{2})\cap \ldots \cap {N}^{-}({\mathfrak {u}}_{s}))=1$ and $k_{1}=|{N}^{-}({\mathfrak {u}}_{1})\cap {N}^{-}({\mathfrak {u}}_{2})\cap \ldots \cap {N}^{-}({\mathfrak {u}}_{s})|_{{\mathfrak {t}}}>2k$. Inserting these expressions to the definition of ${\mathfrak {t}}_{\xi _{k{\mathbb {E}}}}(E_{i})$, we have ${\mathfrak {t}}_{\xi _{k{\mathbb {E}}}}(E_{i})=\frac{k_{1}-k}{k_{1}}({\mathfrak {t}}_\alpha ({\mathfrak {u}}_{j_{1}})\wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{j_{2}})\wedge \ldots \wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{j_{s}}))$. Consequently, $\frac{{\mathfrak {t}}_{\xi _{k{\mathbb {E}}}}(E_{i})}{{\mathfrak {t}}_\alpha ({\mathfrak {u}}_{j_{1}})\wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{j_{2}})\wedge \ldots \wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{j_{s}})}=\frac{k_{1}-k}{k_{1}}>\frac{k_{1}-\frac{k_{1}}{2}}{k_{1}}=\frac{1}{2}$. Similarly, $\frac{{\mathfrak {f}}_{\xi _{k{\mathbb {E}}}}(E_{i})}{{\mathfrak {f}}_\alpha ({\mathfrak {u}}_{j_{1}})\vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{j_{2}})\vee \ldots \vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{j_{s}})}=\frac{k_{2}-k}{k_{2}}<\frac{k_{2}-\frac{k_{2}}{2}}{k_{2}}=\frac{1}{2}$ which shows that the PF hyperedge $E_{i}$ is independent strong in ${{\mathbb {E}}}{{\mathbb {C}}}^{k}_{{\mathbb {H}}}(\overrightarrow{{G}})$.

The proof of statement (1) is similar to above.

Example 2

Consider again the PFD $\overrightarrow{{G}}=(\alpha ,\overrightarrow{\xi })$ whose graphical representation is given in Fig. 1. The PF out-neighborhoods as well as in-neighborhoods of vertices of $\overrightarrow{G}$ are given in Tables 2 and 3, respectively. In order to construct PFCH of $\overrightarrow{G}$, consider the vertex ${\mathfrak {u}}_{1}$ to make $E_1$ in ${\mathbb {C}}_{{\mathbb {H}}}(\overrightarrow{G})$. Note that ${\mathfrak {u}}_{1}$ is the common PF out-neighbor of ${\mathfrak {u}}_{2}$, ${\mathfrak {u}}_{5}$ and ${\mathfrak {u}}_{6}$, i.e., either ${\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{1})$ or ${\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{i}{\mathfrak {u}}_{1})$ is nonzero for $i\in \{2,5,6\}$. Therefore, $E_{1}=\{{\mathfrak {u}}_{2}, {\mathfrak {u}}_{5},{\mathfrak {u}}_{6}\}$ whose Pythagorean membership values are computed as

$$\begin{aligned}&N^{+}({\mathfrak {u}}_{2})\cap N^{+}({\mathfrak {u}}_{5})\cap N^{+}({\mathfrak {u}}_{6})\\&\quad =\{\langle {\mathfrak {u}}_{1}, (0.37,0.64)\rangle \},\quad \Rightarrow \quad h(N^{+}({\mathfrak {u}}_{2})\cap N^{+}({\mathfrak {u}}_{5})\cap N^{+}({\mathfrak {u}}_{6}))=(0.37,0.64),\\&{\mathfrak {t}}_{\xi _{{\mathbb {C}}}}(E_{1})\\&\quad =[{\mathfrak {t}}_\alpha ({\mathfrak {u}}_{2})\wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{5})\wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{6})]\\&\quad \times \, h_{{\mathfrak {t}}}(N^{+}({\mathfrak {u}}_{2})\cap N^{+}({\mathfrak {u}}_{5})\cap N^{+}({\mathfrak {u}}_{6}))=(0.63)(0.37)=0.2331,\\&{\mathfrak {f}}_{\xi _{{\mathbb {C}}}}(E_{1})\\&\quad =\,[{\mathfrak {f}}_\alpha ({\mathfrak {u}}_{2})\vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{5})\vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{6})]\\&\quad \times \, h_{{\mathfrak {f}}}(N^{+}({\mathfrak {u}}_{2})\cap N^{+}({\mathfrak {u}}_{5})\cap N^{+}({\mathfrak {u}}_{6}))=(0.57)(0.64)=0.3648. \end{aligned}$$

Similarly, $E_{2}=\{{\mathfrak {u}}_{3},{\mathfrak {u}}_{4},{\mathfrak {u}}_{5},{\mathfrak {u}}_{6}\}$, $E_{3}=\{{\mathfrak {u}}_{5},{\mathfrak {u}}_{7},{\mathfrak {u}}_{8}\}$ and $E_{4}=\{{\mathfrak {u}}_{6},{\mathfrak {u}}_{7},{\mathfrak {u}}_{8}\}$ are hyperedges in ${\mathbb {C}}_{{\mathbb {H}}}(\overrightarrow{G})$ with truth-membership and falsity-membership grades as ${\mathfrak {t}}_{\xi _{\mathbb {C}}}(E_{2})=0.3528$, ${\mathfrak {f}}_{\xi _{\mathbb {C}}}(E_{2})=0.3364$, ${\mathfrak {t}}_{\xi _{\mathbb {C}}}(E_{3})=0.1548$, ${\mathfrak {f}}_{\xi _{\mathbb {C}}}(E_{3})=0.3348$, ${\mathfrak {t}}_{\xi _{\mathbb {C}}}(E_{4})=0.1736$ and ${\mathfrak {f}}_{\xi _{\mathbb {C}}}(E_{4})=0.3534$. The obtained PFCH ${\mathbb {C}}_{{\mathbb {H}}}(\overrightarrow{G})$ is shown in Fig. 4.

Table 2 PF out-neighborhoods of vertices of $\overrightarrow{G}$

Fig. 4

A PFCH ${\mathbb {C}}_{{\mathbb {H}}}(\overrightarrow{G})$

Likewise, the PFECH for considered PFD $\overrightarrow{G}$ has the hyperedges $E_{5}=\{{\mathfrak {u}}_{1},{\mathfrak {u}}_{2},{\mathfrak {u}}_{3}\}$, $E_{6}=\{{\mathfrak {u}}_{1},{\mathfrak {u}}_{2},{\mathfrak {u}}_{4}\}$, $E_{7}=\{{\mathfrak {u}}_{3},{\mathfrak {u}}_{4},{\mathfrak {u}}_{5}, {\mathfrak {u}}_{6}\}$ and $E_{8}=\{{\mathfrak {u}}_{3},{\mathfrak {u}}_{4},{\mathfrak {u}}_{7}\}$ with truth-membership and falsity-membership grades as ${\mathfrak {t}}_{\xi _{\mathbb {E}}}(E_{5})=0.3245$, ${\mathfrak {f}}_{\xi _{\mathbb {E}}}(E_{5})=0.5504$, ${\mathfrak {t}}_{\xi _{\mathbb {E}}}(E_{6})=0.3068$, ${\mathfrak {f}}_{\xi _{\mathbb {E}}}(E_{6})=0.3640$, ${\mathfrak {t}}_{\xi _{\mathbb {E}}}(E_{7})=0.3843$, ${\mathfrak {f}}_{\xi _{\mathbb {E}}}(E_{7})=0.290$, ${\mathfrak {t}}_{\xi _{\mathbb {E}}}(E_{8})=0.2448$ and ${\mathfrak {f}}_{\xi _{\mathbb {E}}}(E_{8})=0.3364$. The acquired PFECH is shown in Fig. 5.

Table 3 PF in-neighborhoods of vertices of $\overrightarrow{G}$

Fig. 5

A PFECH ${{\mathbb {E}}}{{\mathbb {C}}}_{{\mathbb {H}}}(\overrightarrow{G})$

The $\hbox {PFC}_{0.4}$H ${\mathbb {C}}^{0.4}_{{\mathbb {H}}}(\overrightarrow{G})$ and $\hbox {PFEC}_{0.5}$H ${{\mathbb {E}}}{{\mathbb {C}}}^{0.5}_{{\mathbb {H}}}(\overrightarrow{G})$ of $\overrightarrow{G}$ are given in Figs. 6 and 7, respectively.

Fig. 6

A $\hbox {PFC}_{0.4}$H ${\mathbb {C}}^{0.4}_{{\mathbb {H}}}(\overrightarrow{G})$

Fig. 7

A $\hbox {PFEC}_{0.5}$H ${{\mathbb {E}}}{{\mathbb {C}}}^{0.5}_{{\mathbb {H}}}(\overrightarrow{G})$

4 m-Step pythagorean fuzzy competition hypergraphs

In order to study $\hbox {PFC}_{{m}}$H, we revise some basic concepts:

Definition 20

[19] An m-step PFD $\overrightarrow{G}_{m}$ of a PFD $\overrightarrow{G}$, denoted by $\overrightarrow{G}_{m}=(\alpha , \overrightarrow{\xi }_{m})$, is a PFD that has same PFS of vertices as that of $\overrightarrow{G}$ and has a PF arc from ${\mathfrak {u}}_{i}$ to ${\mathfrak {u}}_{j}$ if there exists a PF directed path $\overrightarrow{P}^m_{({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})}$ of length m from ${\mathfrak {u}}_{i}$ to ${\mathfrak {u}}_{j}$. The Pythagorean membership values of PF arc ${\mathfrak {u}}_{i}{\mathfrak {u}}_{j}$ can be computed as

$$\begin{aligned} {\mathfrak {t}}_{\overrightarrow{\xi }_{m}}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})&= \mathrm {min}\{{\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}{\mathfrak {u}}')\mid {\mathfrak {u}}{\mathfrak {u}}' { is\,\, an\, arc\, of\, } \overrightarrow{P}^m_{({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})}\},\\ {\mathfrak {f}}_{\overrightarrow{\xi }_{m}}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})&= \mathrm {max}\{{\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}{\mathfrak {u}}')\mid {\mathfrak {u}}{\mathfrak {u}}' {\, is\, an\, arc\, of\, } \overrightarrow{P}^m_{({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})}\}. \end{aligned}$$

Definition 21

[19] An m-step PF out-neighborhood $N_{m}^{+}({\mathfrak {u}}_{i})$ of a vertex ${\mathfrak {u}}_{i}$ of a PFD $\overrightarrow{G}=(\alpha , \overrightarrow{\xi })$ is defined as $N_{m}^{+}({\mathfrak {u}}_{i})=\{\langle {\mathfrak {u}}_{j}, ({\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j}),$ ${\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j}))\rangle \mid {\overrightarrow{P}^{m}}_{({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})} { exists }\}$, where ${\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j})=\min \{{\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}{\mathfrak {u}}')\mid {\mathfrak {u}}\mathfrak {u'}\, { is\, an\, arc\, of }\, {\overrightarrow{P}^{m}}_{({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})}\}$ and ${\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j})=\max \{{\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}{\mathfrak {u}}')\mid {\mathfrak {u}}\mathfrak {u'} \, { is\, an\, arc\, of }\, {\overrightarrow{P}^{m}}_{({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})}\}$.

Definition 22

[19] An m-step PF in-neighborhood $N_{m}^{-}({\mathfrak {u}}_{i})$ of a vertex ${\mathfrak {u}}_{i}$ of a PFD $\overrightarrow{G}=(\alpha , \overrightarrow{\xi })$ is defined as $N_{m}^{-}({\mathfrak {u}}_{i})=\{\langle {\mathfrak {u}}_{j}, ({\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j}),$ ${\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j}))\rangle \mid {\overrightarrow{P}^{m}}_{({\mathfrak {u}}_{j}{\mathfrak {u}}_{i})} { exists }\}$, where ${\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j})=\min \{{\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}{\mathfrak {u}}')\mid {\mathfrak {u}}\mathfrak {u'} \, { is\, an\, arc\, of }\, {\overrightarrow{P}^{m}}_{({\mathfrak {u}}_{j}{\mathfrak {u}}_{i})}\}$ and ${\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}_{j})=\max \{{\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}{\mathfrak {u}}')\mid {\mathfrak {u}}\mathfrak {u'} \, { is\, an\, arc\, of }\, {\overrightarrow{P}^{m}}_{({\mathfrak {u}}_{j}{\mathfrak {u}}_{i})}\}$.

The $\hbox {PFC}_{{m}}$Hs are helpful to compute the strength of indirect competing and non-competing relationships at m-steps. These are defined below:

Definition 23

An $\hbox {PFC}_{{m}}$H ${\mathbb {C}}^{m}_{{\mathbb {H}}}(\overrightarrow{G})=(\alpha , \xi _{m{\mathbb {C}}})$ of a PFD $\overrightarrow{G}=(\alpha , \overrightarrow{\xi })$ has the same PF vertex set as of $\overrightarrow{G}$ and $E_{j}\subseteq U$ is a PF hyperedge of ${\mathbb {C}}^{m}_{{\mathbb {H}}}(\overrightarrow{G})$ if and only if $|E_{j}|\ge 2$ and there exists a vertex ${\mathfrak {u}}_{j}\in U$ such that $N^{+}_{m}({\mathfrak {u}}_{i_{1}})\cap N^{+}_{m}({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N^{+}_{m}({\mathfrak {u}}_{i_{s}})$ is a non-empty set due to ${\mathfrak {u}}_{j}$. The Pythagorean membership grades of $E_{j}$ can be computed as

$$\begin{aligned} {\mathfrak {t}}_{\xi _{m{\mathbb {C}}}}(E_{j})&= [{\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{1}})\wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{2}})\wedge \ldots \wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{s}})]\\&\quad \times h_{{\mathfrak {t}}}(N^{+}_{m}({\mathfrak {u}}_{i_{1}})\cap N^{+}_{m}({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N^{+}_{m}({\mathfrak {u}}_{i_{s}})),\\ {\mathfrak {f}}_{\xi _{m{\mathbb {C}}}}(E_{j})&= [{\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{1}})\vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{2}})\vee \ldots \vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{s}})]\\&\quad \times h_{{\mathfrak {f}}}(N^{+}_{m}({\mathfrak {u}}_{i_{1}})\cap N^{+}_{m}({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N^{+}_{m}({\mathfrak {u}}_{i_{s}})). \end{aligned}$$

Definition 24

An m-step Pythagorean fuzzy economic competition hypergraph ($\hbox {PFEC}_{{m}}$H) ${{\mathbb {E}}}{{\mathbb {C}}}^{m}_{{\mathbb {H}}}(\overrightarrow{G})=(\alpha , \xi _{m{\mathbb {E}}})$ of a PFD $\overrightarrow{G}=(\alpha , \overrightarrow{\xi })$ has the same PF vertex set as of $\overrightarrow{G}$ and $E_{i}\subseteq U$ is a PF hyperedge of ${{\mathbb {E}}}{{\mathbb {C}}}^{m}_{{\mathbb {H}}}(\overrightarrow{G})$ if and only if $|E_{i}|\ge 2$ and there exists a vertex ${\mathfrak {u}}_{i}\in U$ such that $N^{-}_{m}({\mathfrak {u}}_{j_{1}})\cap N^{-}_{m}({\mathfrak {u}}_{j_{2}})\cap \ldots \cap N^{-}_{m}({\mathfrak {u}}_{j_{s}})$ is a non-empty set due to ${\mathfrak {u}}_{i}$. The Pythagorean membership grades of $E_{i}$ can be computed as

$$\begin{aligned} {\mathfrak {t}}_{\xi _{m{\mathbb {E}}}}(E_{i})&= [{\mathfrak {t}}_\alpha ({\mathfrak {u}}_{j_{1}})\wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{j_{2}})\wedge \ldots \wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{j_{s}})]\\&\quad \times {h_{{\mathfrak {t}}}(N^{-}_{m}({\mathfrak {u}}_{j_{1}})\cap N^{-}_{m}({\mathfrak {u}}_{j_{2}})\cap \ldots \cap N^{-}_{m}({\mathfrak {u}}_{j_{s}}))},\\ {\mathfrak {f}}_{\xi _{m{\mathbb {E}}}}(E_{i})&= [{\mathfrak {f}}_\alpha ({\mathfrak {u}}_{j_{1}})\vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{j_{2}})\vee \ldots \vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{j_{s}})]\\&\quad \times {h_{{\mathfrak {f}}}(N^{-}_{m}({\mathfrak {u}}_{j_{1}})\cap N^{-}_{m}({\mathfrak {u}}_{j_{2}})\cap \ldots \cap N^{-}_{m}({\mathfrak {u}}_{j_{s}}))}. \end{aligned}$$

Example 3

Consider a PFD $\overrightarrow{G}=(\alpha ,\overrightarrow{\xi })$, where

$$\begin{aligned} \alpha&= \bigg \langle \bigg (\frac{{\mathfrak {u}}_{1}}{0.83},\frac{{\mathfrak {u}}_{2}}{0.48},\frac{{\mathfrak {u}}_{3}}{0.79},\frac{{\mathfrak {u}}_{4}}{0.98}, \frac{{\mathfrak {u}}_{5}}{0.92},\frac{{\mathfrak {u}}_{6}}{0.63},\frac{{\mathfrak {u}}_{7}}{0.59}\bigg ),\\&\bigg (\frac{{\mathfrak {u}}_{1}}{0.46}, \frac{{\mathfrak {u}}_{2}}{0.69},\frac{{\mathfrak {u}}_{3}}{0.46},\frac{{\mathfrak {u}}_{4}}{0.11},\frac{{\mathfrak {u}}_{5}}{0.21},\frac{{\mathfrak {u}}_{6}}{0.55}, \frac{{\mathfrak {u}}_{7}}{0.71}\bigg ) \bigg \rangle and \\ \overrightarrow{\xi }&= \bigg \langle \bigg (\frac{{\mathfrak {u}}_{2}{\mathfrak {u}}_{1}}{0.46},\frac{{\mathfrak {u}}_{3}{\mathfrak {u}}_{2}}{0.41}, \frac{{\mathfrak {u}}_{4}{\mathfrak {u}}_{1}}{0.82},\frac{{\mathfrak {u}}_{4}{\mathfrak {u}}_{3}}{0.76},\frac{{\mathfrak {u}}_{5}{\mathfrak {u}}_{4}}{0.91}, \frac{{\mathfrak {u}}_{6}{\mathfrak {u}}_{2}}{0.48},\frac{{\mathfrak {u}}_{6}{\mathfrak {u}}_{3}}{0.61},\\&\frac{{\mathfrak {u}}_{6}{\mathfrak {u}}_{5}}{0.63}, \frac{{\mathfrak {u}}_{7}{\mathfrak {u}}_{1}}{0.57},\frac{{\mathfrak {u}}_{7}{\mathfrak {u}}_{2}}{0.36}, \frac{{\mathfrak {u}}_{7}{\mathfrak {u}}_{5}}{0.53},\frac{{\mathfrak {u}}_{7}{\mathfrak {u}}_{6}}{0.55}\bigg ),\\&\bigg (\frac{{\mathfrak {u}}_{2}{\mathfrak {u}}_{1}}{0.53}, \frac{{\mathfrak {u}}_{3}{\mathfrak {u}}_{2}}{0.65}, \frac{{\mathfrak {u}}_{4}{\mathfrak {u}}_{1}}{0.39},\frac{{\mathfrak {u}}_{4}{\mathfrak {u}}_{3}}{0.43},\frac{{\mathfrak {u}}_{5}{\mathfrak {u}}_{4}}{0.19}, \frac{{\mathfrak {u}}_{6}{\mathfrak {u}}_{2}}{0.67},\frac{{\mathfrak {u}}_{6}{\mathfrak {u}}_{3}}{0.38},\\&\frac{{\mathfrak {u}}_{6}{\mathfrak {u}}_{5}}{0.48}, \frac{{\mathfrak {u}}_{7}{\mathfrak {u}}_{1}}{0.64},\frac{{\mathfrak {u}}_{7}{\mathfrak {u}}_{2}}{0.65}, \frac{{\mathfrak {u}}_{7}{\mathfrak {u}}_{5}}{0.42},\frac{{\mathfrak {u}}_{7}{\mathfrak {u}}_{6}}{0.66}\bigg )\bigg \rangle . \end{aligned}$$

The graphical representation and adjacency matrix of $\overrightarrow{G}$ are given in Fig. 8 and Table 4, respectively. By following Definition 20, we have constructed the 2-step PFD $\overrightarrow{G}_{2}$ displayed in Fig. 9.

Fig. 8

A PFD $\overrightarrow{G}$

Table 4 Adjacency matrix of PFD $\overrightarrow{G}$

Fig. 9

A 2-step PFD $\overrightarrow{G}_{2}$

The 2-step PF out-neighborhoods as well as in-neighborhoods of vertices of $\overrightarrow{G}$ are given in Tables 5 and 6, respectively. The $\hbox {PFC}_{{2}}$H ${\mathbb {C}}^2_{{\mathbb {H}}}(\overrightarrow{G})$ of the considered PFD $\overrightarrow{G}$ has same PFS of vertices and its PF hyperedges are $E_{1}=\{{\mathfrak {u}}_3,{\mathfrak {u}}_5,{\mathfrak {u}}_6,{\mathfrak {u}}_7\}$, $E_{2}=\{{\mathfrak {u}}_{4},{\mathfrak {u}}_{6},{\mathfrak {u}}_{7}\}$, $E_{3}=\{{\mathfrak {u}}_{5},{\mathfrak {u}}_{7}\}$ and $E_{4}=\{{\mathfrak {u}}_{6},{\mathfrak {u}}_{7}\}$ with truth-membership and falsity-membership grades as ${\mathfrak {t}}_{\xi _{2{\mathbb {C}}}}(E_{1})=0.2124$, ${\mathfrak {f}}_{\xi _{2{\mathbb {C}}}}(E_{1})=0.4757$, ${\mathfrak {t}}_{\xi _{2{\mathbb {C}}}}(E_{2})=0.2419$, ${\mathfrak {f}}_{\xi _{2{\mathbb {C}}}}(E_{2})=0.4757$, ${\mathfrak {t}}_{\xi _{2{\mathbb {C}}}}(E_{3})=0.3245$, ${\mathfrak {f}}_{\xi _{2{\mathbb {C}}}}(E_{3})=0.4686$, ${\mathfrak {t}}_{\xi _{2{\mathbb {C}}}}(E_{4})=0.3127$ and ${\mathfrak {f}}_{\xi _{2{\mathbb {C}}}}(E_{4})=0.3408$. The obtained $\hbox {PFC}_{{2}}$H ${\mathbb {C}}^2_{{\mathbb {H}}}(\overrightarrow{G})$ is shown in Fig. 10.

Table 5 2-step PF out-neighborhoods of vertices of $\overrightarrow{G}$

Table 6 2-step PF in-neighborhoods of vertices of $\overrightarrow{G}$

Fig. 10

A $\hbox {PFC}_{{2}}$H ${\mathbb {C}}^2_{{\mathbb {H}}}(\overrightarrow{G})$

Likewise, the $\hbox {PFEC}_{{2}}$H ${{\mathbb {E}}}{{\mathbb {C}}}^2_{{\mathbb {H}}}(\overrightarrow{G})$ for considered PFD $\overrightarrow{G}$ has PF hyperedges $E_{5}=\{{\mathfrak {u}}_{1},{\mathfrak {u}}_{3}\}$, $E_{6}=\{{\mathfrak {u}}_{1},{\mathfrak {u}}_{2},{\mathfrak {u}}_{4}\}$ and $E_{7}=\{{\mathfrak {u}}_{1},{\mathfrak {u}}_{2},{\mathfrak {u}}_{3},{\mathfrak {u}}_{4},{\mathfrak {u}}_{5}\}$ with truth-membership and falsity-membership grades as ${\mathfrak {t}}_{\xi _{2{\mathbb {E}}}}(E_{5})=0.6004$, ${\mathfrak {f}}_{\xi _{2{\mathbb {E}}}}(E_{5})=0.1978$, ${\mathfrak {t}}_{\xi _{2{\mathbb {E}}}}(E_{6})=0.1968$, ${\mathfrak {f}}_{\xi _{2{\mathbb {E}}}}(E_{6})=0.4623$, ${\mathfrak {t}}_{\xi _{2{\mathbb {E}}}}(E_{7})=0.1728$ and ${\mathfrak {f}}_{\xi _{2{\mathbb {E}}}}(E_{7})=0.4623$. The acquired $\hbox {PFEC}_{{2}}$H is shown in Fig. 11.

Fig. 11

A $\hbox {PFEC}_{{2}}$H ${{\mathbb {E}}}{{\mathbb {C}}}^2_{{\mathbb {H}}}(\overrightarrow{G})$

Theorem 3

If $\overrightarrow{G}$ is a PFD and $\overrightarrow{G}_{m}$ is its m-step PFD, then

• 1. ${\mathbb {C}}_{\mathbb {H}}(\overrightarrow{G}_{m})={\mathbb {C}}^{m}_{\mathbb {H}}(\overrightarrow{G})$,

• 2. ${{\mathbb {E}}}{{\mathbb {C}}}_{\mathbb {H}}(\overrightarrow{G}_{m})={{\mathbb {E}}}{{\mathbb {C}}}^{m}_{\mathbb {H}}(\overrightarrow{G})$.

Proof

Let $\overrightarrow{G}=(\alpha , \overrightarrow{\xi })$ be a PFD, $\overrightarrow{G}_{m}=(\alpha , \overrightarrow{\xi }_{m})$ be the m-step PFD of $\overrightarrow{G}$, ${\mathbb {C}}_{\mathbb {H}}(\overrightarrow{G}_{m})=(\alpha , \xi _{{\mathbb {C}}})$ be the PFCH of $\overrightarrow{G}_{m}$ and ${\mathbb {C}}^{m}_{\mathbb {H}}(\overrightarrow{G})=(\alpha , \xi _{m})$ be the $\hbox {PFC}_{{m}}$H of $\overrightarrow{G}$. It is evident that the PF vertex sets of these graphs as well as hypergraphs are equal. Let $E_{j}=\{{\mathfrak {u}}_{1}, {\mathfrak {u}}_{2},\ldots , {\mathfrak {u}}_{s}\}$ be a PF hyperedge in ${\mathbb {C}}_{\mathbb {H}}(\overrightarrow{G}_{m})$. Consequently, there exist PF arcs ${\mathfrak {u}}_{1} {\mathfrak {u}}_{j}, {\mathfrak {u}}_{2} {\mathfrak {u}}_{j},\ldots ,{\mathfrak {u}}_{s} {\mathfrak {u}}_{j}$ for some ${\mathfrak {u}}_{j}$ in $\overrightarrow{G}_{m}$. So in $\overrightarrow{G}_{m}$, we have $N^{+}({\mathfrak {u}}_{1})\cap N^{+}({\mathfrak {u}}_{2})\cap \ldots \cap N^{+}({\mathfrak {u}}_{s})=\{\langle {\mathfrak {u}}_{j},(z_{{\mathfrak {t}}}, z_{{\mathfrak {f}}})\rangle \}$, where $z_{{\mathfrak {t}}}={\mathfrak {t}}_{\overrightarrow{\xi }_{m}}({\mathfrak {u}}_{1} {\mathfrak {u}}_{j})\wedge {\mathfrak {t}}_{\overrightarrow{\xi }_{m}}({\mathfrak {u}}_{2} {\mathfrak {u}}_{j})\wedge \ldots \wedge {\mathfrak {t}}_{\overrightarrow{\xi }_{m}}({\mathfrak {u}}_{s} {\mathfrak {u}}_{j})$ and $z_{{\mathfrak {f}}}={\mathfrak {f}}_{\overrightarrow{\xi }_{m}}({\mathfrak {u}}_{1} {\mathfrak {u}}_{j})\vee {\mathfrak {f}}_{\overrightarrow{\xi }_{m}}({\mathfrak {u}}_{2} {\mathfrak {u}}_{j})\vee \ldots \vee {\mathfrak {f}}_{\overrightarrow{\xi }_{m}}({\mathfrak {u}}_{s} {\mathfrak {u}}_{j})$. Thus, ${\mathfrak {t}}_{\xi _{{\mathbb {C}}}}(E_{j})=({\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{1})\wedge {\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{2})\wedge \ldots \wedge {\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{s}))\times h_{{\mathfrak {t}}}( N^{+}({\mathfrak {u}}_{1})\cap N^{+}({\mathfrak {u}}_{2})\cap \ldots \cap N^{+}({\mathfrak {u}}_{s}))=({\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{1})\wedge {\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{2})\wedge \ldots \wedge {\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{s}))\times z_{{\mathfrak {t}}}$. Similarly, ${\mathfrak {f}}_{\xi _{{\mathbb {C}}}}(E_{j})=({\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{1})\vee {\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{2})\vee \ldots \vee {\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{s}))\times h_{{\mathfrak {f}}}( N^{+}({\mathfrak {u}}_{1})\cap N^{+}({\mathfrak {u}}_{2})\cap \ldots \cap N^{+}({\mathfrak {u}}_{s}))=({\mathfrak {f}}_{\alpha } ({\mathfrak {u}}_{1})\vee {\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{2})\vee \ldots \vee {\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{s}))\times z_{{\mathfrak {f}}}$. An arc ${\mathfrak {u}}_{1}{\mathfrak {u}}_{j}$ in $\overrightarrow{G}_{m}$ implies the existence of a PF directed path ${\overrightarrow{P}^{m}}_{({\mathfrak {u}}_{1}{\mathfrak {u}}_{j})}$ of length m from ${\mathfrak {u}}_{1}$ to ${\mathfrak {u}}_{j}$ in $\overrightarrow{G}$. As a result, ${\mathfrak {t}}_{{\overrightarrow{\xi }}_{m}}({\mathfrak {u}}_{1}{\mathfrak {u}}_{j})=\min \{{\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}{\mathfrak {u}}')\mid {\mathfrak {u}}{\mathfrak {u}}' is an arc in {\overrightarrow{P}^{m}}_{({\mathfrak {u}}_{1}{\mathfrak {u}}_{j})}\}$ and ${\mathfrak {f}}_{{\overrightarrow{\xi }}_{m}}({\mathfrak {u}}_{1}{\mathfrak {u}}_{j})=\max \{{\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}{\mathfrak {u}}')\mid {\mathfrak {u}}{\mathfrak {u}}' is an arc in {\overrightarrow{P}^{m}}_{({\mathfrak {u}}_{1}{\mathfrak {u}}_{j})}\}$. Thus the PF hyperedge $E_{j}$ is contained in ${\mathbb {C}}^{m}_{\mathbb {H}}(\overrightarrow{G})$ also. Finally, ${\mathfrak {t}}_{\xi _{m}}(E_{j})=({\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{1})\wedge {\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{2})\wedge \ldots \wedge {\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{s}))\times h_{{\mathfrak {t}}}( N_{m}^{+}({\mathfrak {u}}_{1})\cap N_{m}^{+}({\mathfrak {u}}_{2})\cap \ldots \cap N_{m}^{+}({\mathfrak {u}}_{s}))=({\mathfrak {t}} _{\alpha }({\mathfrak {u}}_{1})\wedge {\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{2})\wedge \ldots \wedge {\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{s}))\times z_{{\mathfrak {t}}}$ and ${\mathfrak {f}}_{\xi _{m}}(E_{j})=({\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{1})\vee {\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{2})\vee \ldots \vee {\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{s}))\times h_{{\mathfrak {f}}}( N_{m}^{+}({\mathfrak {u}}_{1})\cap N_{m}^{+}({\mathfrak {u}}_{2})\cap \ldots \cap N_{m}^{+}({\mathfrak {u}}_{s}))=({\mathfrak {f}} _{\alpha }({\mathfrak {u}}_{1})\vee {\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{2})\vee \ldots \vee {\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{s}))\times z_{{\mathfrak {f}}}$. This verifies the existence of a PF hyperedge in ${\mathbb {C}}^{m}_{\mathbb {H}}(\overrightarrow{G})$ corresponding to each PF hyperedge in ${\mathbb {C}}_{\mathbb {H}}(\overrightarrow{G}_{m})$ and vice versa. This proves ${\mathbb {C}}_{\mathbb {H}}(\overrightarrow{G}_{m})={\mathbb {C}}^{m}_{\mathbb {H}}(\overrightarrow{G})$. $\square$

Theorem 4

Let $\overrightarrow{G}$ be a PFD. If $m>|U|$, then the corresponding $\hbox {PFC}_{{m}}$H ${\mathbb {C}}^{m}_{\mathbb {H}}(\overrightarrow{G})$ and $\hbox {PFEC}_{{m}}$H ${{\mathbb {E}}}{{\mathbb {C}}}^{m}_{\mathbb {H}}(\overrightarrow{G})$ are void of PF hyperedges.

Proof

Let $\overrightarrow{G}=(\alpha , \overrightarrow{\xi })$ and ${\mathbb {C}}^{m}_{\mathbb {H}}(\overrightarrow{G})=(\alpha , \xi _{m})$. Then ${\mathfrak {t}}_{\xi _{m}}(E_{j})=({\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{1})\wedge {\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{2})\wedge \ldots \wedge {\mathfrak {t}}_{\alpha }({\mathfrak {u}}_{s}))\times h_{{\mathfrak {t}}}( N_{m}^{+}({\mathfrak {u}}_{1})\cap N_{m}^{+}({\mathfrak {u}}_{2})\cap \ldots \cap N_{m}^{+}({\mathfrak {u}}_{s}))$ and ${\mathfrak {f}}_{\xi _{m}}(E_{j})=({\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{1})\vee {\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{2})\vee \ldots \vee {\mathfrak {f}}_{\alpha }({\mathfrak {u}}_{s}))\times h_{{\mathfrak {f}}}( N_{m}^{+}({\mathfrak {u}}_{1})\cap N_{m}^{+}({\mathfrak {u}}_{2})\cap \ldots \cap N_{m}^{+}({\mathfrak {u}}_{s}))$. If $m>|U|$, there does not exist any directed path of length m in $\overrightarrow{G}$. So, $N_{m}^{+}({\mathfrak {u}}_{1})\cap N_{m}^{+}({\mathfrak {u}}_{2})\cap \ldots \cap N_{m}^{+}({\mathfrak {u}}_{s})=\{\}$. As a result, ${\mathbb {C}}^{m}_{\mathbb {H}}(\overrightarrow{G})$ is void of PF hyperedges. This completes the proof. $\square$

The proof for $\hbox {PFEC}_{{m}}$ H is similar to the argument above.

Definition 25

[19] Let $\overrightarrow{{G}}=(\alpha ,\overrightarrow{\xi })$ be a PFD over U. Let ${\mathfrak {u}}$ be a common PF prey of m-step PF out-neighborhoods of vertices ${\mathfrak {u}}_{1}$, ${\mathfrak {u}}_{2}$,...,${\mathfrak {u}}_{s}$ in $\overrightarrow{{G}}$ such that ${\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}'_{1}{\mathfrak {u}}''_{1})$, ${\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}'_{2}{\mathfrak {u}}''_{2})$,...,${\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}'_{s}{\mathfrak {u}}''_{s})$ be the minimum truth-membership degree and ${\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}'_{1}{\mathfrak {u}}''_{1})$, ${\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}'_{2}{\mathfrak {u}}''_{2})$,...,${\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}'_{s}{\mathfrak {u}}''_{s})$ be the maximum falsity-membership degree of directed edges in PF directed paths $\overrightarrow{P}^{m}_{({\mathfrak {u}}_{1},{\mathfrak {u}})}$, $\overrightarrow{P}^{m}_{({\mathfrak {u}}_{2},{\mathfrak {u}})}$,...,$\overrightarrow{P}^{m}_{({\mathfrak {u}}_{s},{\mathfrak {u}})}$, respectively. The m-step PF prey ${\mathfrak {u}}$ is said to be independent strong if for all $1\le k \le s$, ${\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}'_{k}{\mathfrak {u}}''_{k})>0.5$ and ${\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}'_{k}{\mathfrak {u}}''_{k})<0.5$.

The strength of a PF prey ${\mathfrak {u}}$ is denoted by $\mathrm {Str}({\mathfrak {u}})=(\mathrm {Str}({\mathfrak {u}})_{{\mathfrak {t}}},\mathrm {Str}({\mathfrak {u}})_{{\mathfrak {f}}})$, where the mappings $\mathrm {Str}({\mathfrak {u}})_{{\mathfrak {t}}}: U\rightarrow [0,1]$ and $\mathrm {Str}({\mathfrak {u}})_{{\mathfrak {f}}}: U\rightarrow [0,1]$ are defined as

$$\begin{aligned} {{\mathrm {Str}({\mathfrak {u}})_{{\mathfrak {t}}}=\dfrac{\sum _{k=1}^{s}{\mathfrak {t}}_{\overrightarrow{\xi }}({\mathfrak {u}}'_{k}{\mathfrak {u}}''_{k})}{s},} \quad {\mathrm {Str}({\mathfrak {u}})_{{\mathfrak {f}}}=\dfrac{\sum _{k=1}^{s}{\mathfrak {f}}_{\overrightarrow{\xi }}({\mathfrak {u}}'_{k}{\mathfrak {u}}''_{k})}{s}.}} \end{aligned}$$

Below we give a relationship of m-step PF preys and PF hyperedges of $\hbox {PFC}_{{m}}$H.

Theorem 5

If all m-step PF preys of PFD $\overrightarrow{G}$ are strong, then all PF hyperedges of $\hbox {PFC}_{{m}}$H ${\mathbb {C}}^{m}_{\mathbb {H}}(\overrightarrow{G})$ are independent strong.

Proof

Let $\overrightarrow{G}=(\alpha , \overrightarrow{\xi })$ be a PFD and suppose that all m-step PF preys of $\overrightarrow{G}$ are strong. Further, consider the $\hbox {PFC}_{{m}}$H ${\mathbb {C}}^{m}_{\mathbb {H}}(\overrightarrow{G})=(\alpha , \overrightarrow{\xi }_{m{\mathbb {C}}})$ in which the Pythagorean membership grades of an arbitrary hyperedge $E_{j}=\{{\mathfrak {u}}_{1}, {\mathfrak {u}}_{2},\ldots , {\mathfrak {u}}_{s}\}$ are computed as ${\mathfrak {t}}_{\xi _{m{\mathbb {C}}}}(E_{j})=[{\mathfrak {t}}_\alpha ({\mathfrak {u}}_{{1}})\wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{{2}})\wedge \ldots \wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{{s}})]\times h_{{\mathfrak {t}}}(N^{+}_{m}({\mathfrak {u}}_{{1}})\cap N^{+}_{m}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{+}_{m}({\mathfrak {u}}_{{s}}))$ and ${\mathfrak {f}}_{\xi _{m{\mathbb {C}}}}(E_{j})=[{\mathfrak {f}}_\alpha ({\mathfrak {u}}_{{1}})\vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{{2}})\vee \ldots \vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{{s}})]\times h_{{\mathfrak {f}}}(N^{+}_{m}({\mathfrak {u}}_{{1}})\cap N^{+}_{m}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{+}_{m}({\mathfrak {u}}_{{s}}))$. There arise two cases. $\square$

Case I: Let $N^{+}_{m}({\mathfrak {u}}_{{1}})\cap N^{+}_{m}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{+}_{m}({\mathfrak {u}}_{{s}})=\{\}$. Then there is no hyperedge $E_{j}=\{{\mathfrak {u}}_{1}, {\mathfrak {u}}_{2},\ldots , {\mathfrak {u}}_{s}\}$ in ${\mathbb {C}}^{m}_{\mathbb {H}}(\overrightarrow{G})$.

Case-II: Let $N^{+}_{m}({\mathfrak {u}}_{{1}})\cap N^{+}_{m}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{+}_{m}({\mathfrak {u}}_{{s}})$ intersect at ${\mathfrak {u}}_{j}$. Since all m-step PF preys are strong therefore, $h_{{\mathfrak {t}}}(N^{+}_{m}({\mathfrak {u}}_{{1}})\cap N^{+}_{m}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{+}_{m}({\mathfrak {u}}_{{s}}))>0.5$ and $h_{{\mathfrak {f}}}(N^{+}_{m}({\mathfrak {u}}_{{1}})\cap N^{+}_{m}({\mathfrak {u}}_{{2}})\cap \ldots \cap N^{+}_{m}({\mathfrak {u}}_{{s}}))<0.5$. Thus, the PF hyperedge $E_{j}=\{{\mathfrak {u}}_{1}, {\mathfrak {u}}_{2},\ldots , {\mathfrak {u}}_{s}\}$ in ${\mathbb {C}}^{m}_{\mathbb {H}}(\overrightarrow{G})$ have the membership values ${\mathfrak {t}}_{\xi _{m{\mathbb {C}}}}(E_{j})\ge \frac{1}{2}[{\mathfrak {t}}_\alpha ({\mathfrak {u}}_{{1}})\wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{{2}})\wedge \ldots \wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{{s}})]$ and ${\mathfrak {f}}_{\xi _{m{\mathbb {C}}}}(E_{j})\le \frac{1}{2}[{\mathfrak {f}}_\alpha ({\mathfrak {u}}_{{1}})\vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{{2}})\vee \ldots \vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{{s}})]$. As $E_{j}$ is arbitrary, all PF hyperedges of ${\mathbb {C}}^{m}_{\mathbb {H}}(\overrightarrow{G})$ are independent strong.

Corollary 1

Consider an m-step PFD $\overrightarrow{G}_{m}$ of a PFD $\overrightarrow{G}$. If the Pythagorean membership grades of all arcs ${\mathfrak {u}}_{i}{\mathfrak {u}}_{j}$ of $\overrightarrow{G}_{m}$ satisfy ${\mathfrak {t}}_{\overrightarrow{\xi }_{m}}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})>0.5$ and ${\mathfrak {f}}_{\overrightarrow{\xi }_{m}}({\mathfrak {u}}_{i}{\mathfrak {u}}_{j})<0.5$, then all PF hyperedges of $\hbox {PFC}_{{m}}$H ${\mathbb {C}}^{m}_{\mathbb {H}}(\overrightarrow{G})$ are independent strong.

5 Pythagorean fuzzy neighborhood hypergraphs of open and closed types

The PF hyperedges of Pythagorean fuzzy open neighborhood hypergraph (PFONH) and Pythagorean fuzzy closed neighborhood hypergraph (PFCNH), respectively, represent the relationship among neighbors of a species and how a species interact with its neighbors. Mathematically, these are defined as follows:

Definition 26

A PFONH ${\mathbb {N}}_{{\mathbb {H}}}({G})=(\alpha , \xi _{({{\mathbb {N}}})})$ of a PFG ${G}=(\alpha ,{\xi })$ has the same PF vertex set as of G and $E_{j}\subseteq U$ is a PF hyperedge of ${\mathbb {N}}_{{\mathbb {H}}}({G})$ if and only if $|E_{j}|\ge 2$ and $E_{j}=Supp(N({\mathfrak {u}}_{j}))$, that is, $N({\mathfrak {u}}_{i_{1}})\cap N({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N({\mathfrak {u}}_{i_{s}})$ is a non-empty set due to ${\mathfrak {u}}_{j}$. The Pythagorean membership grades of $E_{j}$ can be computed as

$$\begin{aligned} {\mathfrak {t}}_{\xi _{({{\mathbb {N}}})}}(E_{j})&= [{\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{1}})\wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{2}})\wedge \ldots \wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{s}})]\\&\quad \times h_{{\mathfrak {t}}}(N({\mathfrak {u}}_{i_{1}})\cap N({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N({\mathfrak {u}}_{i_{s}})), \\ {\mathfrak {f}}_{\xi _{({{\mathbb {N}}})}}(E_{j})&= [{\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{1}})\vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{2}})\vee \ldots \vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{s}})]\\&\quad \times h_{{\mathfrak {f}}}(N({\mathfrak {u}}_{i_{1}})\cap N({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N({\mathfrak {u}}_{i_{s}})). \end{aligned}$$

Proposition 1

The PFONH ${\mathbb {N}}_{{\mathbb {H}}}({G})$ of PFG G has n PF hyperedges if and only if $\forall i\ne j$, $N({\mathfrak {u}}_{i})\ne N({\mathfrak {u}}_{j})$ and $|Supp(N({\mathfrak {u}}_{j}))|\ge 2$; $1\le i,j\le n$.

Definition 27

A PFCNH ${\mathbb {N}}_{{\mathbb {H}}}[{G}]=(\alpha , \xi _{[{{\mathbb {N}}}]})$ of a PFG ${G}=(\alpha ,{\xi })$ has the same PF vertex set as of G and $E_{j}\subseteq U$ is a PF hyperedge of ${\mathbb {N}}_{{\mathbb {H}}}[{G}]$ if and only if $|E_{j}|\ge 2$ and $E_{j}=Supp(N[{\mathfrak {u}}_{i}])$, that is, $N[{\mathfrak {u}}_{i_{1}}]\cap N[{\mathfrak {u}}_{i_{2}}]\cap \ldots \cap N[{\mathfrak {u}}_{i_{s}}]$ is a non-empty set due to ${\mathfrak {u}}_{j}$. The Pythagorean membership grades of $E_{j}$ can be computed as

$$\begin{aligned} {\mathfrak {t}}_{\xi _{[{{\mathbb {N}}}]}}(E_{j})&= [{\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{1}})\wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{2}})\wedge \ldots \wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{s}})]\\&\quad \times h_{{\mathfrak {t}}}(N[{\mathfrak {u}}_{i_{1}}]\cap N[{\mathfrak {u}}_{i_{2}}]\cap \ldots \cap N[{\mathfrak {u}}_{i_{s}}]), \\ {\mathfrak {f}}_{\xi _{[{{\mathbb {N}}}]}}(E_{j})&= [{\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{1}})\vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{2}})\vee \ldots \vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{s}})]\\&\quad \times h_{{\mathfrak {f}}}(N[{\mathfrak {u}}_{i_{1}}]\cap N[{\mathfrak {u}}_{i_{2}}]\cap \ldots \cap N[{\mathfrak {u}}_{i_{s}}]). \end{aligned}$$

Proposition 2

The PFCNH ${\mathbb {N}}_{{\mathbb {H}}}[{G}]$ of PFG G has n PF hyperedges if and only if $\forall i\ne j$, $N[{\mathfrak {u}}_{i}]\ne N[{\mathfrak {u}}_{j}]$ and $|Supp(N[{\mathfrak {u}}_{j}])|\ge 2$; $1\le i,j\le n$.

Definition 28

Let k be a non-negative real number. The Pythagorean fuzzy (k)-neighborhood hypergraph (read as open Pythagorean fuzzy k-neighborhood hypergraph $\hbox {PFON}_{{k}}$H) ${\mathbb {N}}^{k}_{{\mathbb {H}}}({G})=(\alpha , \xi _{(k)})$ of a PFG ${G}=(\alpha ,{\xi })$ has the same PF vertex set as of G and $E_{j}\subseteq U$ is a PF hyperedge of ${\mathbb {N}}^{k}_{{\mathbb {H}}}({G})$ if and only if $|E_{j}|\ge 2$ and $|N({\mathfrak {u}}_{i_{1}})\cap N({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N({\mathfrak {u}}_{i_{s}})|_{{\mathfrak {t}}}>k$ and $|N({\mathfrak {u}}_{i_{1}})\cap N({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N({\mathfrak {u}}_{i_{s}})|_{{\mathfrak {f}}}>k$. The Pythagorean membership grades of $E_{j}$ can be computed as

$$\begin{aligned} {\mathfrak {t}}_{\xi _{(k)}}(E_{j})&= \frac{k_{1}-k}{k_{1}}({\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{1}})\wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{2}})\wedge \ldots \wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{s}}))\\&\quad \times h_{{\mathfrak {t}}}(N({\mathfrak {u}}_{i_{1}})\cap N({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N({\mathfrak {u}}_{i_{s}})), \\ {\mathfrak {f}}_{\xi _{(k)}}(E_{j})&= \frac{k_{2}-k}{k_{2}}({\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{1}})\vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{2}})\vee \ldots \vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{s}}))\\&\quad \times h_{{\mathfrak {f}}}(N({\mathfrak {u}}_{i_{1}})\cap N({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N({\mathfrak {u}}_{i_{s}})), \end{aligned}$$

where $k_{1}=|N({\mathfrak {u}}_{i_{1}})\cap N({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N({\mathfrak {u}}_{i_{s}})|_{{\mathfrak {t}}}$ and $k_{2}=|N({\mathfrak {u}}_{i_{1}})\cap N({\mathfrak {u}}_{i_{2}})\cap \ldots \cap N({\mathfrak {u}}_{i_{s}})|_{{\mathfrak {f}}}$.

Definition 29

Let k be a non-negative real number. The Pythagorean fuzzy [k]-neighborhood hypergraph (read as closed Pythagorean fuzzy k-neighborhood hypergraph $\hbox {PFCN}_{{k}}$H) ${\mathbb {N}}^{k}_{{\mathbb {H}}}[{G}]=(\alpha , \xi _{[k]})$ of a PFG ${G}=(\alpha ,{\xi })$ has the same PF vertex set as of G and $E_{j}\subseteq U$ is a PF hyperedge of ${\mathbb {N}}^{k}_{{\mathbb {H}}}[{G}]$ if and only if $|E_{j}|\ge 2$ and $|N[{\mathfrak {u}}_{i_{1}}]\cap N[{\mathfrak {u}}_{i_{2}}]\cap \ldots \cap N[{\mathfrak {u}}_{i_{s}}]|_{{\mathfrak {t}}}>k$ and $|N[{\mathfrak {u}}_{i_{1}}]\cap N[{\mathfrak {u}}_{i_{2}}]\cap \ldots \cap N[{\mathfrak {u}}_{i_{s}}]|_{{\mathfrak {f}}}>k$. The Pythagorean membership grades of $E_{j}$ can be computed as

$$\begin{aligned} {\mathfrak {t}}_{\xi _{[k]}}(E_{j})&= \frac{k_{1}-k}{k_{1}}({\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{1}})\wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{2}})\wedge \ldots \wedge {\mathfrak {t}}_\alpha ({\mathfrak {u}}_{i_{s}}))\\&\quad \times h_{{\mathfrak {t}}}(N[{\mathfrak {u}}_{i_{1}}]\cap N[{\mathfrak {u}}_{i_{2}}]\cap \ldots \cap N[{\mathfrak {u}}_{i_{s}}]), \\ {\mathfrak {f}}_{\xi _{[k]}}(E_{j}) &= \frac{k_{2}-k}{k_{2}}({\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{1}})\vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{2}})\vee \ldots \vee {\mathfrak {f}}_\alpha ({\mathfrak {u}}_{i_{s}}))\\&\quad \times h_{{\mathfrak {f}}}(N[{\mathfrak {u}}_{i_{1}}]\cap N[{\mathfrak {u}}_{i_{2}}]\cap \ldots \cap N[{\mathfrak {u}}_{i_{s}}]), \end{aligned}$$

where $k_{1}=|N[{\mathfrak {u}}_{i_{1}}]\cap N[{\mathfrak {u}}_{i_{2}}]\cap \ldots \cap N[{\mathfrak {u}}_{i_{s}}]|_{{\mathfrak {t}}}$ and $k_{2}=|N[{\mathfrak {u}}_{i_{1}}]\cap N[{\mathfrak {u}}_{i_{2}}]\cap \ldots \cap N[{\mathfrak {u}}_{i_{s}}]|_{{\mathfrak {f}}}$.

The above mentioned concepts are useful when the concern is to compute the neighboring relations at different levels. The following example demonstrates them clearly.

Example 4

Consider a PFG $G=(\alpha ,\xi )$, where

$$\begin{aligned} \alpha&= \bigg \langle \bigg (\frac{{\mathfrak {u}}_{1}}{0.69},\frac{{\mathfrak {u}}_{2}}{0.58},\frac{{\mathfrak {u}}_{3}}{0.94},\frac{{\mathfrak {u}}_{4}}{0.89}, \frac{{\mathfrak {u}}_{5}}{0.63},\frac{{\mathfrak {u}}_{6}}{0.78}\bigg ),\\&\bigg (\frac{{\mathfrak {u}}_{1}}{0.43}, \frac{{\mathfrak {u}}_{2}}{0.72},\frac{{\mathfrak {u}}_{3}}{0.18},\frac{{\mathfrak {u}}_{4}}{0.27},\frac{{\mathfrak {u}}_{5}}{0.55},\frac{{\mathfrak {u}}_{6}}{0.46}\bigg ) \bigg \rangle and \\ {\xi }&= \bigg \langle \bigg (\frac{{\mathfrak {u}}_{1}{\mathfrak {u}}_{2}}{0.52},\frac{{\mathfrak {u}}_{1}{\mathfrak {u}}_{3}}{0.62}, \frac{{\mathfrak {u}}_{1}{\mathfrak {u}}_{6}}{0.66},\frac{{\mathfrak {u}}_{2}{\mathfrak {u}}_{3}}{0.58},\frac{{\mathfrak {u}}_{2}{\mathfrak {u}}_{4}}{0.50}, \frac{{\mathfrak {u}}_{3}{\mathfrak {u}}_{5}}{0.56},\frac{{\mathfrak {u}}_{4}{\mathfrak {u}}_{5}}{0.62},\frac{{\mathfrak {u}}_{4}{\mathfrak {u}}_{6}}{0.74},\\&\frac{{\mathfrak {u}}_{5}{\mathfrak {u}}_{6}}{0.57}\bigg ),\bigg (\frac{{\mathfrak {u}}_{1}{\mathfrak {u}}_{2}}{0.70},\frac{{\mathfrak {u}}_{1}{\mathfrak {u}}_{3}}{0.41}, \frac{{\mathfrak {u}}_{1}{\mathfrak {u}}_{6}}{0.40},\frac{{\mathfrak {u}}_{2}{\mathfrak {u}}_{3}}{0.28},\frac{{\mathfrak {u}}_{2}{\mathfrak {u}}_{4}}{0.68}, \frac{{\mathfrak {u}}_{3}{\mathfrak {u}}_{5}}{0.47},\frac{{\mathfrak {u}}_{4}{\mathfrak {u}}_{5}}{0.55},\\&\frac{{\mathfrak {u}}_{4}{\mathfrak {u}}_{6}}{0.38}. \frac{{\mathfrak {u}}_{5}{\mathfrak {u}}_{6}}{0.48}\bigg )\bigg \rangle , \end{aligned}$$

It is graphically presented in Fig. 12. The PF open neighborhoods of vertices of G are given in Table 7.

Fig. 12

A PFG G

Table 7 PF open neighborhoods of vertices of G

The PFONH of the considered PFG consists of hyperedges $E_{1}=\{{\mathfrak {u}}_{2},{\mathfrak {u}}_{3},{\mathfrak {u}}_{6}\}$, $E_{2}=\{{\mathfrak {u}}_{1},{\mathfrak {u}}_{3}, {\mathfrak {u}}_{4}\}$, $E_{3}=\{{\mathfrak {u}}_{1},{\mathfrak {u}}_{2}, {\mathfrak {u}}_{5}\}$, $E_{4}=\{{\mathfrak {u}}_{2},{\mathfrak {u}}_{5},{\mathfrak {u}}_{6}\}$, $E_{5}=\{{\mathfrak {u}}_{3},{\mathfrak {u}}_{4},{\mathfrak {u}}_{6}\}$ and $E_{6}=\{{\mathfrak {u}}_{1},{\mathfrak {u}}_{4},{\mathfrak {u}}_{5}\}$. The Pythagorean membership values of these hyperedges are ${\mathfrak {t}}_{\xi _{({{\mathbb {N}}})}}(E_{1})=0.3016$, ${\mathfrak {f}}_{\xi _{({{\mathbb {N}}})}}(E_{1})=0.5040$, ${\mathfrak {t}}_{\xi _{({{\mathbb {N}}})}}(E_{2})=0.3450$, ${\mathfrak {f}}_{\xi _{({{\mathbb {N}}})}}(E_{2})=0.3010$, ${\mathfrak {t}}_{\xi _{({{\mathbb {N}}})}}(E_{3})=0.3132$, ${\mathfrak {f}}_{\xi _{({{\mathbb {N}}})}}(E_{3})=0.3384$, ${\mathfrak {t}}_{\xi _{({{\mathbb {N}}})}}(E_{4})=0.290$, ${\mathfrak {f}}_{\xi _{({{\mathbb {N}}})}}(E_{4})=0.4896$, ${\mathfrak {t}}_{\xi _{({{\mathbb {N}}})}}(E_{5})=0.4368$, ${\mathfrak {f}}_{\xi _{({{\mathbb {N}}})}}(E_{5})=0.2530$, ${\mathfrak {t}}_{\xi _{({{\mathbb {N}}})}}(E_{6})=0.3591$ and ${\mathfrak {f}}_{\xi _{({{\mathbb {N}}})}}(E_{6})=0.2064$. The graphical representation of PFONH is shown in Fig. 13.

Fig. 13

A PFONH ${\mathbb {N}}_{{\mathbb {H}}}(G)$

Table 8 PF closed neighborhoods of vertices of G

The PF closed neighborhoods of all vertices of G are given in Table 8. The PFCNH of the considered PFG consists of hyperedges $E_{1}=\{{\mathfrak {u}}_{1}, {\mathfrak {u}}_{2},{\mathfrak {u}}_{3},{\mathfrak {u}}_{6}\}$, $E_{2}=\{{\mathfrak {u}}_{1},{\mathfrak {u}}_{2}, {\mathfrak {u}}_{3}, {\mathfrak {u}}_{4}\}$, $E_{3}=\{{\mathfrak {u}}_{1},{\mathfrak {u}}_{2},{\mathfrak {u}}_{3}, {\mathfrak {u}}_{5}\}$, $E_{4}=\{{\mathfrak {u}}_{2},{\mathfrak {u}}_{4},{\mathfrak {u}}_{5},{\mathfrak {u}}_{6}\}$, $E_{5}=\{{\mathfrak {u}}_{3},{\mathfrak {u}}_{4},{\mathfrak {u}}_{5},{\mathfrak {u}}_{6}\}$ and $E_{6}=\{{\mathfrak {u}}_{1},{\mathfrak {u}}_{4},{\mathfrak {u}}_{5},{\mathfrak {u}}_{6}\}$. The Pythagorean membership grades of these hyperedges are ${\mathfrak {t}}_{\xi _{[{{\mathbb {N}}}]}}(E_{1})=0.3016$, ${\mathfrak {f}}_{\xi _{[{{\mathbb {N}}}]}}(E_{1})=0.5040$, ${\mathfrak {t}}_{\xi _{[{{\mathbb {N}}}]}}(E_{2})=0.290$, ${\mathfrak {f}}_{\xi _{[{{\mathbb {N}}}]}}(E_{2})=0.5184$,${\mathfrak {t}}_{\xi _{[{{\mathbb {N}}}]}}(E_{3})=0.3132$, ${\mathfrak {f}}_{\xi _{[{{\mathbb {N}}}]}}(E_{3})=0.3384$, ${\mathfrak {t}}_{\xi _{[{{\mathbb {N}}}]}}(E_{4})=0.290$, ${\mathfrak {f}}_{\xi _{[{{\mathbb {N}}}]}}(E_{4})=0.4896$, ${\mathfrak {t}}_{\xi _{[{{\mathbb {N}}}]}}(E_{5})=0.3528$, ${\mathfrak {f}}_{\xi _{[{{\mathbb {N}}}]}}(E_{5})=0.3025$, ${\mathfrak {t}}_{\xi _{[{{\mathbb {N}}}]}}(E_{6})=0.3591$ and ${\mathfrak {f}}_{\xi _{[{{\mathbb {N}}}]}}(E_{6})=0.2208$. The graphical representation of PFCNH is shown in Fig. 14.

Fig. 14

A PFCNH ${\mathbb {N}}_{{\mathbb {H}}}[G]$

The $\hbox {PFON}_{0.5}$H ${\mathbb {N}}^{0.5}_{{\mathbb {H}}}(G)$ and $\hbox {PFCN}_{0.5}$H ${\mathbb {N}}^{0.5}_{{\mathbb {H}}}[G]$ are shown in Figs. 15 and 16, respectively.

Fig. 15

A $\hbox {PFON}_{0.5}$H ${\mathbb {N}}^{0.5}_{{\mathbb {H}}}(G)$

Fig. 16

A $\hbox {PFCN}_{0.5}$H ${\mathbb {N}}^{0.5}_{{\mathbb {H}}}[G]$

Theorem 6

Let ${\mathcal {U}}(\overrightarrow{G})$ be the underlying PFG of PFD $\overrightarrow{G}$. If $\overrightarrow{G}$ is a symmetric loop less PFD, then ${\mathbb {C}}^{k}_{{\mathbb {H}}}(\overrightarrow{G})={{\mathbb {E}}}{{\mathbb {C}}}^{k}_{{\mathbb {H}}}(\overrightarrow{G})={\mathbb {N}}^{k}_{{\mathbb {H}}}({\mathcal {U}}(\overrightarrow{G}))$, where k is a non-negative real number.

Proof

Suppose that $\overrightarrow{G}=(\alpha ,\overrightarrow{\xi })$, ${\mathcal {U}}(\overrightarrow{G})=(\alpha ,{\xi })$, ${\mathbb {C}}^{k}_{{\mathbb {H}}}(\overrightarrow{G})=(\alpha , \xi _{k{\mathbb {C}}})$, ${{\mathbb {E}}}{{\mathbb {C}}}^{k}_{{\mathbb {H}}}(\overrightarrow{G})=(\alpha , \xi _{k{\mathbb {E}}})$ and ${\mathbb {N}}^{k}_{{\mathbb {H}}}({\mathcal {U}}(\overrightarrow{G}))=(\alpha ,\xi _{(k)})$ represent PFD, underlying PFG, $\hbox {PFC}_{{k}}$H, $\hbox {PFEC}_{{k}}$H of $\overrightarrow{G}$ and $\hbox {PFON}_{{k}}$H of ${\mathcal {U}}(\overrightarrow{G})$, respectively. It is clear that the PFS of vertices are same for the above mentioned PFHs. We only need to show that $\xi _{k{\mathbb {C}}}=\xi _{k{\mathbb {E}}}=\xi _{(k)}$. There arise two cases:

Case I: When for some ${\mathfrak {u}}_{1},{\mathfrak {u}}_{2},\ldots ,{\mathfrak {u}}_{s}\in U$, ${\mathfrak {t}}_{\xi _{k{\mathbb {C}}}}({\mathfrak {u}}_{1},{\mathfrak {u}}_{2},\ldots ,{\mathfrak {u}}_{s})=0={\mathfrak {f}}_{\xi _{k{\mathbb {C}}}}({\mathfrak {u}}_{1},{\mathfrak {u}}_{2},\ldots , {\mathfrak {u}}_{s})$ then, $|N^+({\mathfrak {u}}_{1})\cap N^+({\mathfrak {u}}_{2})\cap \ldots \cap N^+({\mathfrak {u}}_{s})|_{{\mathfrak {t}}}\le k$ and $|N^+({\mathfrak {u}}_{1})\cap N^+({\mathfrak {u}}_{2})\cap \ldots \cap N^+({\mathfrak {u}}_{s})|_{{\mathfrak {f}}}\le k$. As $\overrightarrow{G}$ is symmetric, $|N^-({\mathfrak {u}}_{1})\cap N^-({\mathfrak {u}}_{2})\cap \ldots \cap N^-({\mathfrak {u}}_{s})|_{{\mathfrak {t}}}\le k$ and $|N^-({\mathfrak {u}}_{1})\cap N^-({\mathfrak {u}}_{2})\cap \ldots \cap N^-({\mathfrak {u}}_{s})|_{{\mathfrak {f}}}\le k$ as well as $|N({\mathfrak {u}}_{1})\cap N({\mathfrak {u}}_{2})\cap \ldots \cap N({\mathfrak {u}}_{s})|_{{\mathfrak {t}}}\le k$ and $|N({\mathfrak {u}}_{1})\cap N({\mathfrak {u}}_{2})\cap \ldots \cap N({\mathfrak {u}}_{s})|_{{\mathfrak {f}}}\le k$ in $\overrightarrow{G}$ and ${\mathcal {U}}(\overrightarrow{G})$, respectively. As a consequence, ${\mathfrak {t}}_{\xi _{k{\mathbb {E}}}}({\mathfrak {u}}_{1},{\mathfrak {u}}_{2},\ldots ,{\mathfrak {u}}_{s})=0={\mathfrak {f}}_{\xi _{k{\mathbb {E}}}}({\mathfrak {u}}_{1},{\mathfrak {u}}_{2},\ldots , {\mathfrak {u}}_{s})$ and ${\mathfrak {t}}_{\xi _{(k)}}({\mathfrak {u}}_{1},{\mathfrak {u}}_{2},\ldots ,{\mathfrak {u}}_{s})=0={\mathfrak {f}}_{\xi _{(k)}}({\mathfrak {u}}_{1},{\mathfrak {u}}_{2},\ldots , {\mathfrak {u}}_{s})$.

Case II: When for some ${\mathfrak {u}}_{1},{\mathfrak {u}}_{2},\ldots ,{\mathfrak {u}}_{s}\in U$, ${\mathfrak {t}}_{\xi _{k{\mathbb {C}}}}({\mathfrak {u}}_{1},{\mathfrak {u}}_{2},\ldots ,{\mathfrak {u}}_{s})\ne 0$ and ${\mathfrak {f}}_{\xi _{k{\mathbb {C}}}}({\mathfrak {u}}_{1},{\mathfrak {u}}_{2},\ldots , {\mathfrak {u}}_{s})\ne 0$ then, $|N^+({\mathfrak {u}}_{1})\cap N^+({\mathfrak {u}}_{2})\cap \ldots \cap N^+({\mathfrak {u}}_{s})|_{{\mathfrak {t}}}> k$ and $|N^+({\mathfrak {u}}_{1})\cap N^+({\mathfrak {u}}_{2})\cap \ldots \cap N^+({\mathfrak {u}}_{s})|_{{\mathfrak {f}}}> k$. As $\overrightarrow{G}$ is symmetric, $|N^-({\mathfrak {u}}_{1})\cap N^-({\mathfrak {u}}_{2})\cap \ldots \cap N^-({\mathfrak {u}}_{s})|_{{\mathfrak {t}}}> k$ and $|N^-({\mathfrak {u}}_{1})\cap N^-({\mathfrak {u}}_{2})\cap \ldots \cap N^-({\mathfrak {u}}_{s})|_{{\mathfrak {f}}}> k$ as well as $|N({\mathfrak {u}}_{1})\cap N({\mathfrak {u}}_{2})\cap \ldots \cap N({\mathfrak {u}}_{s})|_{{\mathfrak {t}}}> k$ and $|N({\mathfrak {u}}_{1})\cap N({\mathfrak {u}}_{2})\cap \ldots \cap N({\mathfrak {u}}_{s})|_{{\mathfrak {f}}}> k$ in $\overrightarrow{G}$ and ${\mathcal {U}}(\overrightarrow{G})$, respectively. As a consequence, ${\mathfrak {t}}_{\xi _{k{\mathbb {C}}}}({\mathfrak {u}}_{1},{\mathfrak {u}}_{2},\ldots ,{\mathfrak {u}}_{s})={\mathfrak {t}}_{\xi _{k{\mathbb {E}}}}({\mathfrak {u}}_{1},{\mathfrak {u}}_{2},\ldots ,{\mathfrak {u}}_{s})={\mathfrak {t}}_{\xi _{k{\mathbb {E}}}}({\mathfrak {u}}_{1},{\mathfrak {u}}_{2},\ldots , {\mathfrak {u}}_{s})$ and ${\mathfrak {f}}_{\xi _{k{\mathbb {C}}}}({\mathfrak {u}}_{1},{\mathfrak {u}}_{2},\ldots , {\mathfrak {u}}_{s})={\mathfrak {t}}_{\xi _{(k)}}({\mathfrak {u}}_{1},{\mathfrak {u}}_{2},\ldots ,{\mathfrak {u}}_{s})={\mathfrak {f}}_{\xi _{(k)}}({\mathfrak {u}}_{1},{\mathfrak {u}}_{2},\ldots , {\mathfrak {u}}_{s})$. Hence, the PFS of hyperedges are also same, i.e., $\xi _{k{\mathbb {C}}}=\xi _{k{\mathbb {E}}}=\xi _{(k)}$. This completes the proof. $\square$

6 Application

Marine ecosystems are characterized by a community of living organisms and their interactions in this environment. Here, an organism that preys one species is preyed upon by some other species. The predator-prey interactions of these organisms configure their behaviors, strategies, morphologies and physiologies. Predators in marine ecosystems adapt to acquire special abilities like breath-holding, diving, dentition, hearing and vision to capture their prey. Similarly, preys also develop strategies to enhance their chances of survival. Some species take refuge deep down in the sea during daytime and swim upward in the night to feed themselves. Other techniques are cryptic countershading in which organisms blend themselves to confuse their predators when viewed from top and bottom, schooling wherein a group of species quickly disperse creating difficulty for the predator to select one of them as prey, fleeing, scattering etc. [45] Note that as the number of species in a community increases, so does the number of preys that are consumed by a predator. In marine ecosystems, the average length of a food chain in food web is $2-5$ linkages. Additionally, no matter how many species a predator can eat, it usually consumes only a few species in an environment. The organisms that have a common prey in a community compete with one another for that specie [44].

The Bering Sea has great diversity in its ecosystem. It is located between Siberia and Alaska, and is linked with the Arctic Ocean through the Bering Strait. We have considered its simplified food web [27] and inverted its arrowheads to represent the predator-prey relationships (rather than the flow of energy) in order to examine competition among predators for their preys. Due to the binary nature of an ordinary predator-prey interaction model (i.e., either a connection between two species exists or not), the linkages are ambiguous without mentioning the proportion of consumption of preys. This proportion can be computed by analyzing the stomach contents, fatty acid signatures, faecal remains, stable isotopes, etc. of the organisms.

The predator-prey interactions of the Bering Sea are shown by a PFD $\overrightarrow{G}$ in Fig. 17. The vertices and arcs in $\overrightarrow{G}$ represent organisms of the Bering Sea and who eats whom, i.e., the arc is drawn from predator to prey, respectively. The truth-membership and falsity-membership of its vertices depict the biomass (total mass of living matter in that area) of the corresponding species present and absent in the Bering Sea; and directed edges imply the proportion in which the biomass of prey is consumed by the predator. The Pythagorean membership grades of vertices and arcs of $\overrightarrow{G}$ are given in Tables 9 and 10. The primary productivity of the considered ecosystem is due to ice algae and phytoplankton. These organisms live in the upper few meters of sea and are consumed by herbivores. Those which are not used settle down in sea, get mixed into detritus and become a part of saprotrophic chain. Species like clams, basket stars, worms and sand dollars consume bacteria that feed upon detritus, and these deposit feeders are preyed upon by crabs, marine mammals and ground fish and the cycle goes on.

Fig. 17

A PFD $\overrightarrow{G}$ representing the predator-prey interactions in the Bering Sea: ${\mathfrak {u}}_{1}$, ice algae; ${\mathfrak {u}}_{2}$, phytoplankton; ${\mathfrak {u}}_{3}$, copepods; ${\mathfrak {u}}_{4}$, mysids and euphausiids; ${\mathfrak {u}}_{5}$, medusae; ${\mathfrak {u}}_{6}$, hyperid amphipods; ${\mathfrak {u}}_{7}$, seabirds; ${\mathfrak {u}}_{8}$, pelagic fishes; ${\mathfrak {u}}_{9}$, pelagic fishes; ${\mathfrak {u}}_{10}$, walrus; ${\mathfrak {u}}_{11}$, seals; ${\mathfrak {u}}_{12}$, basket stars; ${\mathfrak {u}}_{13}$, ascidians; ${\mathfrak {u}}_{14}$, shrimps; ${\mathfrak {u}}_{15}$, filter-feeding bivalves; ${\mathfrak {u}}_{16}$, sand dollars; ${\mathfrak {u}}_{17}$, sea stars; ${\mathfrak {u}}_{18}$, crabs; ${\mathfrak {u}}_{19}$, bottom feeding fishes; ${\mathfrak {u}}_{20}$, polychaetes; ${\mathfrak {u}}_{21}$, predatory gastropods; ${\mathfrak {u}}_{22}$, deposit feeding bivalves [27]

Table 9 PFS of vertices of $\overrightarrow{G}$

Table 10 PFS of directed edges of $\overrightarrow{G}$

The PFCH ${\mathbb {C}}_{{\mathbb {H}}}(\overrightarrow{G})$ of the considered model is shown in Fig. 18. The hyperedges of ${\mathbb {C}}_{{\mathbb {H}}}(\overrightarrow{G})$ are $E_{1}=\{{\mathfrak {u}}_{3},{\mathfrak {u}}_{4},{\mathfrak {u}}_{13},{\mathfrak {u}}_{14},{\mathfrak {u}}_{15},{\mathfrak {u}}_{16},{\mathfrak {u}}_{20},{\mathfrak {u}}_{22}\}$, $E_{2}=\{{\mathfrak {u}}_{3},{\mathfrak {u}}_{4},{\mathfrak {u}}_{12},{\mathfrak {u}}_{13},{\mathfrak {u}}_{14},{\mathfrak {u}}_{15},{\mathfrak {u}}_{16},{\mathfrak {u}}_{20},{\mathfrak {u}}_{22}\}$, $E_{3}=\{{\mathfrak {u}}_{4},{\mathfrak {u}}_{5},{\mathfrak {u}}_{6}, {\mathfrak {u}}_{8},{\mathfrak {u}}_{9},{\mathfrak {u}}_{12},{\mathfrak {u}}_{13},{\mathfrak {u}}_{14},$ ${\mathfrak {u}}_{15}, {\mathfrak {u}}_{19}\}$, $E_{4}=\{{\mathfrak {u}}_{5},{\mathfrak {u}}_{6},{\mathfrak {u}}_{7},{\mathfrak {u}}_{8},{\mathfrak {u}}_{9},{\mathfrak {u}}_{19}\}$, $E_{6}=\{{\mathfrak {u}}_{7},{\mathfrak {u}}_{9},{\mathfrak {u}}_{19}\}$, $E_{8}=\{{\mathfrak {u}}_{5},{\mathfrak {u}}_{7},{\mathfrak {u}}_{11},{\mathfrak {u}}_{19}\}$, $E_{9}=\{{\mathfrak {u}}_{7},{\mathfrak {u}}_{11},{\mathfrak {u}}_{19}\}$, $E_{15}=\{{\mathfrak {u}}_{10},{\mathfrak {u}}_{17},{\mathfrak {u}}_{18},{\mathfrak {u}}_{19},{\mathfrak {u}}_{21}\}$, $E_{19}=\{{\mathfrak {u}}_{11},{\mathfrak {u}}_{18}\}$, $E_{20}=\{{\mathfrak {u}}_{17},{\mathfrak {u}}_{19}\}$ and $E_{22}=\{{\mathfrak {u}}_{10},{\mathfrak {u}}_{17},{\mathfrak {u}}_{18},{\mathfrak {u}}_{21}\}$. The hyperedge $E_{1}$ represents all those predators that are competing for ice algae and their competing and non-competing strength is given by the Pythagorean membership grades (0.1053, 0.57) of the PF hyperedge $E_{1}$. The competing and non-competing strength of predators corresponding to each organism is given in Table 11.

Table 11 PFS of hyperedges of obtained PFCH

Fig. 18

A PFCH of the considered network

Algorithm 3 explains the method to produce PFCH for a considered PFD representing the predator-prey relationships among organisms of the Bering Sea. Primarily, it finds the PF out-neighborhoods of all organisms and then utilize them to construct the PF hyperedges of the PFCH which demonstrates that which species compete for a specific organism. Finally, it computes the strength of competing and non-competing interactions of organisms.

7 Comparative analysis and discussion

PFSs proposed by Yager [46] possess better traits than IFSs. An IFS permits the expression of truth-membership ${\mathfrak {t}}$ as well as falsity-membership ${\mathfrak {f}}$, and it imposes the constraint that $0\le {\mathfrak {t}}+{\mathfrak {f}}\le 1$ throughout, whereas the PFS provides more space to nominate the grades as the limitation relaxes to $0\le {\mathfrak {t}}^2+{\mathfrak {f}}^2\le 1$. Thus any PFS-based theory allows for a wider range of applications than the corresponding IFS-based, or FS-based, theories.

The competition hypergraphs defined and explained by Sonntag and Teichert [43] consist of hyperedges, each of which illustrates the competing constituents of a system for a specific entity. As competition hypergraphs merely deliver binary data, they only enable us to model cases where either the components of a system fully compete or the competing interaction is absent for some entity. This scarce information about who competes for whom is not always realistic enough. Due to the existence of fuzziness in many real-life problems, the fuzzy competition hypergraphs suggested by Sarwar et al. [40] resolved the issue as the proposed fuzzy competition hypergraphs include the explanation of strength of competition for each set of competing elements. But information about non-competition is still missing in fuzzy competition hypergraphs.

The motivation supporting the introduction of PFCH (instead of intuitionistic fuzzy competition hypergraph) is to add the knowledge about non-competing interaction together with the strength of competition among the constituents of a system. Additionally, it also facilitates to analyze the data when the decision-makers and researchers assign the Pythagorean membership grades to elements. This study investigates the most common yet significant problem of competition among the organisms at the Bering Sea. The food chain of the Bering Sea presents predator-prey interactions. Since one organism is preyed upon by many other organisms, the existence of a prey is a cause of competition among its predators. This set of predators is represented by a hyperedge of PFCH, and the truth-membership and falsity-membership values of this hyperedge suggest the strength of competing and non-competing interactions.

8 Concluding remarks

The PFS model, as a non-standard stance towards enhanced FS theories, is effective to represent uncertain information by pairs of disjoint sets known as orthopairs. This theory has been implemented on hypergraphs and its significance lies in the fact that many researchers have discussed problems modeled within the framework of PFHs. The competition hypergraphs proposed earlier are unable to handle certain types of real-world data. The ability of PFHs to display the interactions among more than two components of a system motivated us to discuss the idea of competition with PFHs, and to start exploring its practical applications.

Thus in this paper we have investigated the concepts of $\hbox {PFR}_{{w}}$H, $\hbox {PFC}_{{l}}$H, PFCH and PFECH. Similarly, the notion of $\hbox {PFC}_{{m}}$H has also been introduced so that one can study the indirect m-step competing interactions for any positive integral value of m. We have also discussed the Pythagorean fuzzy neighborhood hypergraphs of open and closed types. All these concepts have been elaborated with examples, and theorems have shown the main facts about them. Most of the results describe different ways of finding the strength of competing relationships in the proposed graphical structures. The significance of these structures lies in the fact that they can find the straightforward and mediate competing and neighboring relations of an ecological system.

The idea of PFCHs has been elaborated by an application in which the predator-prey interactions of organisms of the Bering Sea is addressed. Since each organism is generally consumed by more than two organisms (predators), the PF hyperedges of PFCH can effectively exhibit competition among consumers. We have designed three algorithms in this article, which are, respectively, designed for the construction of $\hbox {PFR}_{{w}}$H, $\hbox {PFC}_{{l}}$H and PFCH. The latter one can be used to compute the strength of competing interactions of the Bering Sea. One can study general ecological networks to understand competition taking place among their constituents with the help of these graphical structures, thus helping the development of biological communities.

In the future this theory can be extended to study the following topics among others: (1) Multi attribute group decision making based on PFHs, (2) Group decision making based on complex spherical fuzzy soft hypergraphs, and (3) Group decision making with neutrosophic soft hypergraphs.