Abstract
Parkinson’s disease (PD) genes identification plays an important role in improving the diagnosis and treatment of the disease. A number of machine learning methods have been proposed to identify disease-related genes, but only few of these methods are adopted for PD. This work puts forth a novel neural network-based ensemble (n-semble) method to identify Parkinson’s disease genes. The artificial neural network is trained in a unique way to ensemble the multiple model predictions. The proposed n-semble method is composed of four parts: (1) protein sequences are used to construct feature vectors using physicochemical properties of amino acid; (2) dimensionality reduction is achieved using the t-Distributed Stochastic Neighbor Embedding (t-SNE) method, (3) the Jaccard method is applied to find likely negative samples from unknown (candidate) genes, and (4) gene prediction is performed with n-semble method. The proposed n-semble method has been compared with Smalter’s, ProDiGe, PUDI and EPU methods using various evaluation metrics. It has been concluded that the proposed n-semble method outperforms the existing gene identification methods over the other methods and achieves significantly higher precision, recall and F Score of 88.9%, 90.9% and 89.8%, respectively. The obtained results confirm the effectiveness and validity of the proposed framework.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Parkinson’s disease (PD) was first described by Dr. James Parkinson as a “shaking palsy” in 1817 [1]. It is the second most common disease after Alzheimer’s, most prevalent among the elderly. PD is a chronic, progressive neurodegenerative disease associated with the central nervous system. PD is affected by continuous degeneration of dopamine-producing neurons in the pars compacta of the substantia nigra. Dopamine is a chemical messenger acting as a connector that sends messages from the body to the brain. PD mainly affects neurons, thereby reducing the level of dopamine; as a result, the abnormal brain movements that promote the onset of Parkinson's enable movement control [2]. Healthy people have higher dopamine levels than people with PD. Figure 1 illustrates the dopamine level of normal and Parkinson-affected neurons. The PD genes identification method helps to detect underlying molecular mechanisms and diagnose the disease efficiently. It is a time-consuming and expensive task to identify PD-related genes from a large number of unknown genes with experimental methods. Therefore, there is a need to identify genes with computational methods which have been used to discover similar features between disease genes and unknown genes.
We have introduced a novel n-semble method to identify Parkinson’s disease genes. Geary autocorrelation (GA), Moran autocorrelation (MA) and normalized Moreau–Broto autocorrelation (NA) representation methods on the basis of physicochemical properties of amino acids are applied to translate corresponding protein sequences into a feature vector. The t-Distributed Stochastic Neighbor Embedding (t-SNE) feature extraction technique is adopted to reduce high-dimensional features. In the absence of information about negative data, Jaccard similarity measure is employed to extract a reliable negative gene set from an unknown gene set. Finally, various ML methods such as Support Vector Machine (SVM), Random Forest (F), Adaboost, Decision Tree (DT), Xgboost, Neural network and Gradient Descent are used to identify genes responsible for PD.
1.1 Contribution
Several machine learning models have been used for identification of PD genes. However, these models were not able to obtain the results of a best classifier. Therefore, this paper proposes an n-semble model to build an efficient classifier with significant enhancement over existing methods. The major contributions of this paper are as follows:
-
1.
Collection and statistical analysis of Parkinson’s and non-Parkinson protein sequences (genes) from NCBI, Ensembl and Uniprot databases were performed.
-
2.
Twelve physicochemical properties of amino acids were applied to generate features with Geary autocorrelation, normalized Moreau–Broto autocorrelation and Moran autocorrelation representation methods.
-
3.
The t-Distributed Stochastic Neighbor Embedding (t-SNE) feature reduction method was used to extract relevant features from high-dimensional feature vectors.
-
4.
Six machine learning methods were evaluated for gene identification to find the best model based on performance measures and a neural network-based ensemble model was put forth.
-
5.
The performance of the proposed n-semble method was analysed using parameters like precision, recall and F Score, and the comparative study was conducted to show the effectiveness of the proposed model.
1.2 Organization
The paper is organized as follows. Section 2 gives a brief overview of related work in the field of gene identification. The methodology adopted in this work along with proposed n-semble method is described in Sect. 3. Section 4 discusses about results and the comparison of proposed method with existing works to demonstrate its effectiveness for PD gene identification, and finally Sect. 5 concludes the paper.
2 Related work
In recent years, several Machine Learning (ML) methods have been proposed to identify the similarity between disease and candidate genes.
Xu and Li [14] applied K-nearest neighbor (KNN) with PPI topological features to identify disease- related genes. Smalter et al. [9] employed PPI-topological properties to generate features and the Support Vector Machine (SVM) classifier to identify Parkinson’s disease genes. Radivojac et al. [10] used three types of feature vectors such as PPI properties, protein sequences, and protein-functional information to propose a method by building three individual Support Vector Machine (SVM) classifiers to predict disease genes. All the above methods consider a two-class classification problem with disease data as a positive set and unknown genes data as a negative set. As the negative set may consist of several disease genes, the negative set may be noisy and leads to reduction in accuracy.
Mordelet et al. [12] developed an algorithm to prioritize disease genes using positive and unlabelled samples named ProDiGe. They had selected a random subset (RS) from Unknown genes (U). Also, they integrated various sources of information related to genes which can be divided into features including protein sequences, protein functional information, and PPI data. Then, they used SVM to train various classifiers to distinguish positive genes from the subset RS. The final result was obtained by combining all of the prediction results. Its performance is superior to traditional binary classification methods that used unknown genes as a negative set but still suffer from noise as the negative set is separated randomly from the unknown set, thereby deteriorating performance. Yang et al. [15] developed a method named PUDI that used the PPI network, gene ontology and protein domains biological networks. According to the similarity between both positive and negative genes, the unlabelled set (U) was separated into numerous subsets, which are called reliable negative, likely negative, likely positive and weak negative respectively. Finally, they applied multi-layer weighted SVM for disease gene prioritization. Yang et al. [16] expanded their prior work and proposed an overall positive unlabelled learning method (EPU) for disease gene identification. They integrated other data sources such as phenotype similarity networks and gene expression data along with previous data sources. However, they used PPI topological properties, the protein domain and gene ontology data to generate feature vectors which contain more than 4,000 features. For neurological diseases, EPU method achieved F Score of 78.6%. Experimental results have confirmed that the classifier built with high-dimensional features may not be an efficient in terms of detection of PD. Hwang [17] proposed a SRF (Stepwise Random Forests) approach for disease gene identification on biological data sources used by Yang. He had enhanced his method by considering only important features with filter-based feature selection method for classification. Further, it was analysed that he may not be able to achieve better classification results by using all the 4004 features. However, his method considered only 23 features and performed significantly better than the existing methods.
Yousef et al. [11] introduced a sequence-based one-class classification method to identify disease genes. The Support Vector Data Description (SVDD) method is used by them to train the model and selected the significant features with PCA. These methods select a few numbers of unknown genes as the negative set since the unknown genes set usually contains certain disease genes, which reduces the confusion in the classification process. However, these methods are not reliable or robust because the negative results obtained from unlabelled genes are plagued by noisy data.
Miao et al. [18] proposed an Alzheimer’s disease gene identification method based on multiple classifier integration with microarray data. They had adopted the ReliefF feature selection method to extract relevant features and then produced a two-stage cascading classifier to identify genes. Results from SVM, RF and Extreme Learning Machine (ELM) were merged through majority voting for classification. Peng et al. [19] developed a N2A-SVM method for PD gene prediction. They had used the node2vec method for feature extraction and reduced the features using the deep neural network (auto encoder) and finally SVM to predict the genes. Malhi et al. [20] put forth an ensemble method with five best machine learning methods out of 25 regression models on publically available datasets of voice measures of PD patients. Guruler et al. [21] introduced a hybrid method with k-means clustering-based feature weighting and a complex valued Artificial Neural Network (KMCFW) method on speech and sound signals to diagnose PD. The dataset consisted of only 31 people with 8 healthy and 23 PD patients. Senturk [22] used CART, SVM and ANN classifiers to classify Parkinson’s patients. They developed a feature selection-based system using voice signals features.
Some of the methods aim to prioritize disease genes using protein–protein interaction (PPI) [3] data, gene expression profiles [4] and gene ontology [5]. Unfortunately, all the above-mentioned methods depend on the knowledge of proteins attained from PPI data, protein domains and gene ontology. Therefore, these methods cannot be able to implement properly because the information is expensive, time consuming and suffers from a multitude of missing values. Protein sequences are the only data that can be used for proteins and contribute significantly to resolving issues such as protein–protein interactions [6, 7], predicting subcellular locations [8], and functional classes. The key difference between the computational methods is in the type of data used to generate feature vectors and the type of algorithm used to train the model. Some other methods considered the unknown proteins (genes) as a negative set and known disease proteins (genes) as a positive set [9, 10], while other considered this as one class classification method by training only positive data [11]. Since the unknown proteins usually contain certain disease proteins, some of the methods aim to reduce this problem in classification process by extracting the most reliable proteins as a negative protein set [12, 13].
From the above-mentioned methods, we concluded that the research conducted in the field of gene prediction is mainly restricted to the SVM classifier. Also, the existing methods are trained for multiple disease genes data, but not limited to Parkinson’s disease only. However, some of the methods used only six physicochemical properties of amino acids and recommended adding more to achieve better classification performance. Therefore, we have employed twelve physicochemical properties of amino acids to represent the features. Hence, using more physicochemical properties will allow us to provide more information about the interactions. Since there is no information about negative data, we have also selected reliably negative genes from unknown genes using the Jaccard distance metric. Then we have applied various classification methods to yield the final prediction results.
3 Proposed method
To identify Parkinson’s disease genes, sequence representation methods with physicochemical properties of amino acids are chosen to improve the efficiency of existing machine learning classifiers. In this paper, we have employed twelve physicochemical properties of amino acids to represent the amino acid features. Therefore, relying on more physicochemical properties will allow us to discover more information about the interactions. However, the increased characteristics lead to generate more features for each protein, which is why we have normalized the output feature vector, instead of concatenating the feature vector of two proteins. A novel n-semble method is proposed to develop an efficient disease gene identification method.
Mathematically, a problem statement is defined as follows: to classify G = {PD, nPD} for a protein sequence S where S = {a1, a2, a3…, an}and ai represents the amino acid in a sequence. Our task is to evaluate the best machine learning classifier with efficient features to calculate high efficiency in our proposed method.
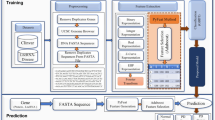
The proposed n-semble method for identifying PD genes has been described in this section. The proposed approach consists of four steps: (1) adopting twelve physicochemical properties to transform corresponding protein sequences into feature vectors; (2) t-Distributed Stochastic Neighbor embedding (t-SNE) applied to reduce dimensionality (3) differentiating negative samples from unknown genes; (4) modelling features using n-semble method. The proposed method architecture is depicted in Fig. 2.
3.1 Extracting features from protein sequences
Extracting features for both disease and unknown genes constitutes one of the most significant tasks in identifying disease genes. This paper applies protein sequences to characterize genes and used three representation methods to extract information encoded in proteins, such as normalized Moreau–Broto autocorrelation (NA) [23], Moran autocorrelation (MA) [24] and Geary autocorrelation (GA) [25]. These methods represent adjacent influences between amino acids that have a specific ratio of amino acids apart in the sequence using their particular physicochemical property. Similarly, it is possible to find patterns throughout the sequence. We used these representation methods to avoid missing significant information regarding the protein sequences. Moreover, the selected methods are being used in several other works [11] also and have an advantage over other methods.
We used twelve physicochemical properties of amino acid to attain more information regarding the amino acid sequence. The physicochemical properties include polarity [26], residue-accessible surface area (RAS) in tripeptide [27], hydrophilicity [28], polarizability [29], solvation-free energy [30], entropy of formation [31], partition coefficient [32], amino acid composition (AAC) [33], hydrophobicity [34], transfer-free energy [35], correlation coefficient (CC) in regression analysis [36], and graph shape index [37]. Further, the min–max normalization method is considered to normalize the original values of the physicochemical properties. These normalized values are shown in Table 1.
3.2 t-Distributed stochastic neighbor embedding (t-SNE)
We applied the t-SNE dimensionality reduction method to find the most important and useful features from high-dimensional data. t-SNE is a nonlinear dimensionality reduction approach that can identify observed clusters created on similarity of data points with multiple features, thereby detecting patterns in data. It is better suited for converting high-dimensional data into a space of low-dimensional data in such a way that similar instances are modelled by closed instances and dissimilar instances are modelled by distant instances. It helps to calculate the probability similarity of points in both high and low-dimensional space. Therefore, it is used to find similar features that retain most of the information and remove redundant information. T-SNE minimizes the KL (KullbackLiebler) divergence between the two distributions with respect to location of instances in a map.
The existing features in the dataset may have some irrelevant features from the high dimensional data (360 features), which may decrease the performance of classifiers and results in poor accuracy. Thus a proper feature extraction technique for pre-processing of input data is required. The t-SNE extracted features have less correlation and less redundancy among the features, which consequently increases the internal representation of a dataset. These modified data representations improve the performance of classifiers. Table 2 shows the number of t-SNE extracted features with sequence-represented methods.
3.3 Extracting negative samples
After extracting relevant features with the above feature reduction method, it becomes a requirement to develop a classifier for PD genes identification. For this, reliable negative genes need to be extracted from unknown genes to construct a method together with positive and reliable negative genes. We propose an algorithm (Algorithm1) for selecting negative genes from unknown samples (US). The algorithm comprises of six steps. First, initialize the negative set as an empty set. Second, compute the positive set (PS) of all positive proteins for each of MA, GA and NA representation methods, respectively. Third, compute the unknown set and assign any one value of the representation method. Fourth, compute the similarity between an unknown sample (US) and positive mean (Pm). The Jaccard similarity metric has been evaluated to calculate distance between each protein and positive mean. Fifth, find the reliable (r) negative genes from US by selecting the sample farthest from the positive mean vector for each feature vector. Finally, the resulted genes acquired by means of intersection of selected negative genes are considered a reliable negative set.
Table 3 shows the comparison of three different distance measures to compute the negative samples. Yang et al. [16] applied Euclidean distance to find the negative set from unknown samples. Euclidean distance gives better results only if positive data show identity covariance. Therefore, the distance measure directly affects the cogency of the extracted negative set. According to the results shown in Table 3, the Jaccard matric yields better results when compared with the other two methods.

3.4 n-semble
The proposed n-semble model helps to improve the classifiers performance. The motivation behind the proposed method is to analyse the interdependence between base learners. Two levels are proposed to perform the experiment as discussed below.
Level 1 Three machine learning models are selected based on accuracy to train the neural network.
Level 2 A neural network is trained using the prediction results of the top three selected models and actual values of these predictions.
The architecture of the proposed n-semble model is depicted in Fig. 3. It is comprised of 3 parts: (1) data partition, (2) data classification, training and testing of selected models, and (3) training and testing of a neural network. Three feature representation methods (GA, MA and NA) are used to represent features from collected protein sequences. The features retrieved from the feature extraction phase are fed to various classification algorithms. The data obtained are split 75% into training and 25% into testing phase. In the second phase, various classification algorithms are applied such as Random Forest (RF), Support Vector Machine (SVM), Adaboost, Decision Tree (DT), Xgboost and Gradient Descent to identify genes. The models are selected based on their prediction accuracy. The top three models on the basis of accuracy are then integrated to form an ensemble method to achieve high efficiency.
In the last phase, the predictions of the selected model are used as training data, and the actual predicted values are taken as target values. The predicted actual data set is applied to train the neural network, the size of which is 20% of the data set. Adaboost, Random Forest and Xgboost are selected as top three models based on highest F Score among other methods. The training data create the relationship between the actual model and the predicted values of the top three models by calculating the weights required for the predictions assigned to each model. Each network has a hidden layer containing ten hidden units. The size of the input layer is the same as the number of attributes in training data and sigmoid activation function is adopted for the output layer.
4 Results and discussion
The performance of the proposed n-semble method on the imbalanced data set is evaluated in this section. First, we investigated the impact of three sequence representation methods such as GA, MA and NA on the performance of n-semble method. Additionally, an optimal number of features retrieved through the t-SNE method has been reviewed and optimized. Then, the effect of several machine learning methods has been evaluated, and on the predictions of top three models, a neural network is trained to develop an ensemble method. Finally, our method and another disease gene identification method were compared to confirm the method effectiveness. The ML methods applied in this work are Support Vector Machine (SVM), Random Forest (F), Adaboost, Decision Tree (DT), Xgboost, Neural network and Gradient Descent. Table 3 shows the values of various performance measures, i.e. Precision, Recall, and F Score for comparative analysis of the ML models experimented with. The top three models, random forest, adaboost and xgboost were selected on the basis of the highest F Score used to generate an ensemble method. The prediction values evaluated by means of each selected model are used as training data for the neural network, and the actual prediction values are used as target data. As shown in Table 3, the proposed ensemble method outperforms other methods with Precision (88.9%), Recall (90.9%) and F-Sore (89.8%). It was observed that the proposed method outperforms the Adaboost by 2.8%, Xgboost by 4.5% and Random Forest by 5.4%. To evaluate the predictive performance of all methods, the ROC (Receiver Operating Characteristic) curve is plotted. The performance of True Positive Rate (TPR) versus False Positive Rate (FPR) at various thresholds for the selected methods is shown in Fig. 4. Random Forest outperforms other methods with the area of 83.6% under ROC.
4.1 Validation of proposed method
We have performed k-fold cross-validation due to its simplicity and randomness property to validate the robustness of the proposed ensemble model. The process cross-validated different samples of equal size, k times [38]. We have considered the k value as 5, i.e. the model is trained and tested 5 times. Use random data samples of the same size to train and test the model each time, and then compare the results. Figure 5 shows the k-fold values of the top three, selected models. Figure 5a shows the results of precision on selected and n-semble methods. From the graph, we can infer that the n-semble method curve lies on top of other models. It indicates that the proposed model is robust as the plot shows a straight line. This means that the accuracy of the model has nothing to do with the given data sample and remain unchanged for a fixed data set. Figure 5b shows the results of recall values on other selected and n-semble methods. Figure 5c demonstrates the results of F Score values on other selected and n-semble methods. The curve of the n-semble method is above the selected methods, which proves that the gain in F Score is robust, that is, independent of the samples obtained from the dataset.
4.2 Comparison with state-of-the-art techniques
In this section, the n-semble method is compared with five state-of-the-art methods, such as SFM, [13], Smalter’s [9], ProDiGe [12], PUDI [15] and EPU [16]. The comparison between the proposed method and other existing methods is shown in Table 5. The F Score of proposed approach averages 5.4%, 6.4%, 10.1%, 16.9%, 22.8% and 23.4% higher than with Yousef’s method, SFM, PUDI, ProDiGe, and Smalter’s method, respectively, for imbalanced datasets. The key difference between these other methods and the proposed one is the previous information used to generate features. The protein sequences were realized as the important information to generate features in this paper, and in previous methods, prior information was affected by noise. The second issue centres on the extraction of negative samples from unknown genes. Smalter’s method considered unknown or candidate genes as negative samples, while ProDiGe randomly used multiple negative samples of unknown genes. The PUDI method applied the Euclidean metric to find distance between each gene features and a positive vector. However, the feature vector generated by PUDI consists of noisy data. Yousef’s method applied only positive data to train a model, which is an ineffective approach. In this paper, we find the Jaccard distance metric the most reliable method for selective negative genes from unknown samples.
5 Conclusion
The main objective of this paper is to identify genes associated with Parkinson’s disease with the best known classification methods. To specify the conditions under which a classification method outperforms other classifiers is a key question in machine learning. This paper, introduced various methods, including Support Vector Machine (SVM), Random Forest (RF), Adaboost, Decision Tree (DT), Xgboost and Gradient Descent for genes identification. After evaluating and analysing the classification methods, more emphasis is placed on exploiting the strengths of a model to complement the weaknesses of another. Therefore, an n-semble method was proposed which trained a neural network in a special way and integrated three classification methods based on their F Score to ensemble the predictions and to achieve more accurate predictive analysis. On the basis of various performance measures, results from the proposed n-semble method show enhanced performance compared to state-of-the-art works. We have adopted protein sequences based on previous knowledge to extract features. GA, MA AND NA representation methods with twelve physicochemical properties of the amino acids are adopted to convert protein sequences into numerical feature vectors. Consequently, t-SNE is applied to extract relevant features. We found that physicochemical properties of amino acids would be highly beneficial in extracting features. Compared with the previous methods on unbalanced datasets, the proposed n-semble method improves the F Score.
In this paper, we have shown that the GA representation method is characterized by a higher success rate than other representation methods. Therefore, in the future, we will consider using a single GA feature vector to combine multiple different classifiers to improve classification. We will also use this method in the prediction of other related diseases.
References
Langston JW (2002) Parkinson’s disease: current and future challenges. Neurotoxicology 23(4):443–450
Hanson DG, Gerratt BR, Ward PH (1984) Cinegraphic observations of laryngeal function in parkinson’s disease. Laryngoscope 94(3):348–353
Zhang W, Sun F, Jiang R (2011) Integrating multiple protein-protein interaction networks to prioritize disease genes: a Bayesian regression approach. BMC Bioinformatics 12(1):1
Ala U, Piro RM, Grassi E, Damasco C, Silengo L, Oti M, Provero P, Di Cunto F (2008) Prediction of human disease genes by human-mouse conserved coexpression analysis. PLoS Comput Biol 4(3):e1000043
Freudenberg J, Propping P (2002) A similarity-based method for genome-wide prediction of disease-relevant human genes. Bioinformatics 18(suppl_2):S110–S115
Yu CY, Chou LC, Chang DT (2010) Predicting protein-protein interactions in unbalanced data using the primary structure of proteins. BMC Bioinform 11(1):167
Yousef A, Charkari NM (2013) A novel method based on new adaptive LVQ neural network for predicting protein–protein interactions from protein sequences. J Theor Biol 336:231–239
Fukasawa Y, Leung RK, Tsui SK, Horton P (2014) Plus ça change–evolutionary sequence divergence predicts protein subcellular localization signals. BMC Genomics 15(1):46
Smalter A, Lei SF and Chen X (2007) Human disease-gene classification with integrative sequence-based and topological features of protein–protein interaction networks. In: Proceedings of the IEEE international conference on bioinformatics and biomedicine, pp 209–216
Radivojac P, Peng K, Clark WT, Peters BJ, Mohan A, Boyle SM, Mooney SD (2008) An integrated approach to inferring gene–disease associations in humans. Proteins Struct Funct Bioinform 72(3):1030–1037
Yousef A, Charkari NM (2015) A novel method based on physicochemical properties of amino acids and one class classification algorithm for disease gene identification. J Biomed Inform 56:300–306
Mordelet F, Vert JP (2011) ProDiGe: Prioritization of Disease Genes with multitask machine learning from positive and unlabeled examples. BMC Bioinformatics 12(1):389
Yousef A, Charkari NM (2015) SFM: a novel sequence-based fusion method for disease genes identification and prioritization. J Theor Biol 383:12–19
Xu J, Li Y (2006) Discovering disease-genes by topological features in human protein–protein interaction network. Bioinformatics 22:2800–2805
Yang P, Li XL, Mei JP, Kwoh CK, Ng SK (2012) Positive-unlabeled learning for disease gene identification. Bioinformatics 28(20):2640–2647
Yang P, Li X, Chua HN, Kwoh CK, Ng SK (2014) Ensemble positive unlabeled learning for disease gene identification. PLoS ONE 9(5):e97079
Hwang WY (2017) Biological feature selection and disease gene identification using new stepwise random forests. Ind Eng Manag Syst 16(1):64–79
Miao Y, Jiang H, Liu H, Yao YD (2017) An Alzheimers disease related genes identification method based on multiple classifier integration. Comput Methods Programs Biomed 150:107–115
Peng J, Guan J, Shang X (2019) Predicting Parkinson’s disease genes based on node2vec and autoencoder. Front Genet 10:226
Kaur H, Malhi AK and Pannu HS (2020) Machine learning ensemble for neurological disorders. Neural Comput Appl 1–18
Gürüler H (2017) A novel diagnosis system for Parkinson’s disease using complex-valued artificial neural network with k-means clustering feature weighting method. Neural Comput Appl 28:1657–1666
Senturk ZK (2020) Early diagnosis of Parkinson’s disease using machine learning algorithms. Med Hypotheses 138:109603
Feng ZP, Zhang CT (2000) Prediction of membrane protein types based on the hydrophobic index of amino acids. J Protein Chem 19(4):269–275
Xia JF, Han K, Huang DS (2010) Sequence-based prediction of protein–protein interactions by means of rotation forest and autocorrelation descriptor. Protein Pept Lett 17(1):137–145
Sokal RR, Thomson BA (2006) Population structure inferred by local spatial autocorrelation: an example from an Amerindian tribal population. Am J Phys Anthropol 129(1):121–131
Grantham R (1974) Amino acid difference formula to help explain protein evolution. Science 185(4154):862–864
Chothia C (1976) The nature of the accessible and buried surfaces in proteins. J Mol Biol 105(1):1–12
Hopp TP, Woods KR (1981) Prediction of protein antigenic determinants from amino acid sequences. Proc Natl Acad Sci USA 78(6):3824–3828
Charton M, Charton BI (1982) The structural dependence of amino acid hydrophobicity parameters. J Theor Biol 99:629–644
Eisenberg D, McLachlan AD (1986) Solvation energy in protein folding and binding. Nature 319:199–203
Chothia C (1992) Proteins. One thousand families for the molecular biologist. Nature 357:543–544
Quinlan JR (1996) Improved use of continuous attributes in C4.5, arXiv preprintcs/ 9603103
Grantham R (1974) Amino acid difference formula to help explain protein evolution. Science 185:862–864
Sweet RM, Eisenberg D (1983) Correlation of sequence hydrophobicities measures similarity in three-dimensional protein structure. J Mol Biol 171:479–488
Janin J (1979) Surface and inside volumes in globular proteins. Nature 277:491–492
Prabhakaran M, Ponnuswamy PK (1982) Shape and surface features of globular proteins. Macromolecules 15:314–320
Fauchere JL (1988) Amino acid side chain parameters for correlation studies in biology and pharmacology. Int J Pept Protein Res 32:269–278
Rayal R, Khanna D, Sandhu JK, Hooda N, Rana PS (2019) N-semble: neural network based ensemble approach. Int J Mach Learn Cybern 10(2):337–345
Funding
Open access funding provided by Aalto University.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Arora, P., Mishra, A. & Malhi, A. N-semble-based method for identifying Parkinson’s disease genes. Neural Comput & Applic 35, 23829–23839 (2023). https://doi.org/10.1007/s00521-021-05974-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-021-05974-z