Passive concept drift handling via variations of learning vector quantization

Abstract

Concept drift is a change of the underlying data distribution which occurs especially with streaming data. Besides other challenges in the field of streaming data classification, concept drift has to be addressed to obtain reliable predictions. Robust Soft Learning Vector Quantization as well as Generalized Learning Vector Quantization has already shown good performance in traditional settings and is modified in this work to handle streaming data. Further, momentum-based stochastic gradient descent techniques are applied to tackle concept drift passively due to increased learning capabilities. The proposed work is tested against common benchmark algorithms and streaming data in the field and achieved promising results.

1 Introduction

A key concept in machine learning is to separate the training step of the model and the evaluation phase. However, this is not applicable in the domain of stream classification. In this field, it is assumed that data arrive continuously, making the storage of data in memory unfeasible. Further, not all training data are available at training time, raising the need for constantly updating the model, e.g., online or incremental. Stream classification algorithms [1] tackle these requirements.

However, stream classifiers are prone to concept drift of streaming data, which is a change of underlying distribution and could lead to a collapse in prediction performance. There are various types of concept drift, i.e., incremental, abrupt, gradual and reoccurring, and as a consequence, a variety of approaches addressing these issues have been proposed [13]. In general, these strategies are separated into active and passive [22]. Active adaptation changes a model noticeable. The passive ones use no explicit detection strategy, but are continually updating the model, without awareness of concept drift.

The family of prototype-based classification algorithms, the Learning Vector Quantization (LVQ) [19], receives much attention as a potential stream classification algorithm due to its online learning capabilities [30]. In [30], it was also shown that the usage of weight decay has the potential to improve the generalization error of the LVQ in non-stationary environments. Other LVQ variants have not been considered as stream classifiers yet, except from our adaptive Robust Soft Learning Vector Quantization (RSLVQ) in [16]. Therefore, we propose adaptive versions of RSLVQ and Generalized Learning Vector Quantization (GLVQ) which maximize the objective function with momentum-based gradient descent/ascent in Sect. 4.1. This is applied to increase learning speed and rapid adaptation to occurring concept drifts. As we show in the experiments, the LVQ variants with constant learning rate perform considerably worse than with weight decay or momentum-based gradient descent.

In summary, we provide the following contributions in this article:

• 1. we apply momentum-based gradient techniques known from deep learning to prototype-based stream learning

• 2. we provide two adaptive RSLVQ versions using Adadelta and Adamax

• 3. we provide two adaptive GLVQ versions using Adadelta and Adamax

• 4. we provide experiments comparing our proposed methods against state-of-the-art classifiers without hyperparameter optimization to get a realistic comparison in non-stationary environments

The paper is structured as follows: Sect. 2 presents related work on stream classification and adaptive gradient optimization. In Sect. 3, the fundamentals and particularities of streaming data and concept drift are shown. In Sect. 4, we modify RSLVQ and GLVQ by replacing the gradient optimization technique by adaptive optimization algorithms. The comparison of our proposed methods to baseline RSLVQ/GLVQ and standard algorithms on common data streams in the field is presented in Sect. 5. Section 6 summarizes up the results of this work.

2 Related work

In the field of streaming data, different kinds of algorithms successfully apply passive drift handling to evolving data streams, which is often done by using a fixed size window of recent samples.

In [22], a modern approach of a self-adjusting memory version of the K-Nearest Neighbor (KNN) which is called SAM–KNN is proposed. SAM–KNN is developed to handle various types of concept drift, using biologically inspired memory models and their coordination. The basic idea is to store dedicated models for current and former concepts, used according to the demands of the given situation [22].

The Adaptive Windowing algorithm (ADWIN) [2] is a drift detector and works by keeping updated statistics of a variable sized window, such that changes can be detected. It performs cuts in its window to better adapt to the learning algorithms. Kolmogorv–Smirnov Windowing (KSWIN) [25] follows a similar concept, but uses a more sensitive statistical test.

For evolving data stream, classification tree-based algorithms, like the famous Hoeffding Tree (HT) [9], are common [6]. To address the problem of concept drift, an adaptive HT with ADWIN as drift detector was published in [3] and showed better prediction performance on evolving data streams as the classical HT.

Also, ensemble models are used to combine multiple classifiers [14] in the streaming domain. The OzaBagging (OB) [23] algorithm is an online ensemble model that uses different base classifiers. For the use of concept drift detection, this ensemble model can be again combined with the ADWIN algorithm to the OzaBagging ADWIN (OBA) algorithm. For a comprehensive data stream description, see [21].

Also, LVQ algorithms first introduced by [19] have received attention as potential stream classification algorithms [30]. The Robust Soft Learning Vector Quantization (RSLVQ) [29] is a promising probabilistic classifier, which assumes class distributions as Gaussian mixture models learned via Stochastic Gradient Ascent (SGA) and has only been evaluated as a stream classifier in a previous version of this article [16] so far. Also, Generalized Learning Vector Quantization has not been considered as a stream classifier yet.

In the advent of deep learning, variations in SGD algorithms receive more and more attention. A comparison is given in [27]. It has been shown that momentum-based gradient descent algorithms like Adadelta [34] and RMSprop [33] converge faster to better optimums as traditional approaches. Both of these algorithms are extensions of the Adagrad [10] algorithm. Note that momentum-based gradient descents have been applied to a prototype-based learner for stationary environments in [20], showing Adam gradient update technique as well working algorithm. Furthermore, there is a proposed extension of Adam which is called AdaMax [18], which has not been considered as update technique of a LVQ algorithm yet.

In this work, we reformulate Adadelta and AdaMax as SGA optimizer and apply it to RSLVQ and to GLVQ as a gradient descent optimizer.

3 Streaming data and concept drift

3.1 Streaming data

In the context of supervised learning, a data stream is given as a sequence $S=\{s_1,\dots ,s_t,\dots \}$ of tuples $s_i=\{\mathbf {x}_i,y_i\}$, with potentially infinite length. A tuple $s_i=\{\mathbf {x}_i,y_i\}$ contains the data point $\mathbf {x}_i \in {\mathbb {R}}^d$ and the respective label $y_i=\{1,\dots ,C\}$ whereby $s_t$ arrives at time t. A classifier predicts labels $\hat{y}_t$ of unseen data $\mathbf {x}_t \in {\mathbb {R}}$ employing a prior model $h_{t-1}$, i.e., $\hat{y}_t=h_{t-1}(\mathbf {x}_t)$. The prior model and $s_t$ are subsequently included into the new model $h_{t}=learn(h_{t-1},s_t)$. This behavior is called immediate or test-then-train evaluation. It also means that the learning algorithm trains for an infinite time and that at time t the classifier is (re-)trained on the just arrived tuple.

3.2 Concept drift

Concept drift is the change of joint distributions of a set of samples $\mathbf {X}$ and corresponding labels $\mathbf {y}$ between two points in time:

$$\begin{aligned} \exists \mathbf {X} : p(\mathbf {X},\mathbf {y})_{t} \ne p(\mathbf {X},\mathbf {y})_{t-1} \end{aligned}$$

(1)

The term virtual drift refers to a change in distribution $p(\mathbf {X})$ for two points in time, without affecting $p(\mathbf {y}|\mathbf {X})$. Note that we can rewrite Eq.(1) to

$$\begin{aligned} \exists \mathbf {X} : p(\mathbf {X})_t p(\mathbf {y}|\mathbf {X})_t \ne p(\mathbf {X})_{t-1} p(\mathbf {y}|\mathbf {X})_{t-1}, \end{aligned}$$

(2)

A virtual concept drift may appear in conjunction with a real concept drift.

Fig. 1

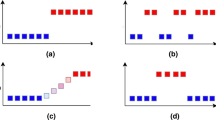
Different types of drifts, one per sub-figure and illustrated as data mean. The colors mark the dominant concept at a given time step. The vertical axis shows the data mean and the transition from one to another concept. Given the time axis, the speed of the transition is given. The figures are inspired by [13]

Figure 1 shows the four common drift types. For a comprehensive study of these concept drift types, see [13]. The stability–plasticity dilemma [13] defines the trade-off between incorporating new knowledge into models (plasticity) and preserves prior knowledge (stability). This prevents stable performance over time because on the edge of a drift, significant efforts go into learning and testing against new distributions.

4 Adaptive learning vector quantization

4.1 Robust Soft Learning Vector Quantization

The Robust Soft Learning Vector Quantization (RSLVQ) [29] is a probabilistic prototype-based classification algorithm. Given a labeled dataset $\mathbf {X} = \{ ( \mathbf {x}_i,y_i) \in {\mathbb {R}}^d \times \{1,\dots ,C\}\}_{i=1}^n$, with data points $\mathbf {x_i}$, labels $y_i$, C as the number of classes, d the number of features and n as the number of samples, the RSLVQ algorithm trains a prototype model such that the error on the classification task is minimized. The RSLVQ model consists of a set of m prototypes $\Theta = \{ (\varvec{\theta }_j,y_j) \in {\mathbb {R}}^d \times \{1,\dots ,C\}\}_{j=1}^m$. Each prototype represents a multi-variate Gaussian model, i.e., $\mathcal {N}(\varvec{\theta }_j,\sigma )$, approximating an assumed class dependent Gaussian mixture of $\mathbf {X}$. The goal of RSLVQ algorithms is to learn prototypes, representing the class dependent distribution, i.e., corresponding class samples $\mathbf {x}_i$ should be mapped to the correct class or Gaussian mixture based on the highest probability. The RSLVQ algorithms maximize the maximum likelihood ratio as objective function:

$$\begin{aligned} E(\mathbf {X},\mathbf {y}|\Theta )_R = \sum \limits _{i=1}^n \frac{p(\mathbf {x}_i, y_k|\Theta )}{p(\mathbf {x}_i|\Theta )} \end{aligned}$$

(3)

where $p(\mathbf {x}_i, y_k|\Theta )$ is the probability density function that $\mathbf {x}$ is generated by the mixture model of the same class and $p(\mathbf {x}_i|\Theta )$ is the overall probability density function of $\mathbf {x}$ given $\Theta$. Equation (3) will be optimized with SGA, i.e.,

$$\begin{aligned} \varvec{\theta }_l(t+1) = \varvec{\theta }_l(t ) - \alpha ^* {\left\{ \begin{array}{ll} (P_y(l|\mathbf {x}) - P(l|\mathbf {x})) (\mathbf {x} - \varvec{\theta }_l), & c_l = y,\\ -P(l|\mathbf {x})(\mathbf {x}-\varvec{\theta }_l), & c_l \ne y. \end{array}\right. } \end{aligned}$$

(4)

where $P_y(l|\mathbf {x})$ is the assignment probability that $\mathbf {x}$ is assigned to the component l of the mixture model of same class prototype $\varvec{\theta }_y$ and $P(l|\mathbf {x})$ is the probability that $\mathbf {x}$ is assigned to the component l of the mixture using all classes. The parameter $\alpha ^* = \frac{\alpha }{\sigma ^2}$ is the learning rate. For a more comprehensive derivation, see [29].

4.2 Generalized Learning Vector Quantization

GLVQ is a prototype-based classifier and has many things in common with RSLVQ. However, in GLVQ prototypes are not representing a Gaussian model and prototypes are updated using the winner-takes-all rule. Assume $\varvec{\theta }_+$ represents the nearest prototype of the same class as $\mathbf {x}$ and $\varvec{\theta }_-$ represents the nearest prototype belonging to a different class than $\mathbf {x}$. Consider the relative distance difference:

$$\begin{aligned} \mu (\mathbf{x} )=\frac{d_+ - d_-}{d_+ + d_-}, \end{aligned}$$

(5)

where $d_+$ is the distance between $\varvec{\theta }_+$ and $\mathbf {x}$ and $d_-$ is the distance between $\varvec{\theta }_-$ and $\mathbf {x}$. $\mu (\mathbf {x})$ is in $[-1; +1]$, and if $\mu$ is negative, $\mathbf {x}$ is classified correct, else it is classified incorrect. To reduce error rates, $\mu (\mathbf {x})$ should be minimized for all input vectors. Hence, the goal is to minimize a cost function S:

$$\begin{aligned} S = \sum ^{n}_{i=1} f(\mu (\mathbf {x})), \end{aligned}$$

(6)

where n is the number of input vectors for training and $f(\mu )$ is a monotonically increasing function [28]. To minimize the cost function, the prototypes $\varvec{\theta }_+$ and $\varvec{\theta }_-$ are updated by gradient descent, using a learning rate $\alpha$:

$$\begin{aligned} \varvec{\theta }_l(t+1) = \varvec{\theta }_l(t) - \alpha \frac{\partial S}{\partial \varvec{\theta }_l}, l \in \{+, -\} \end{aligned}$$

(7)

Using squared euclidean distance $d_l = \Vert \mathbf {x} - \varvec{\theta }_l\Vert ^2$, we can obtain the following learning rule

[28]:

$$\begin{aligned} \varvec{\theta }_l(t+1) = \varvec{\theta }_l(t ) + {\left\{ \begin{array}{ll} \alpha \frac{\partial f}{\partial \mu } \frac{d_-}{(d_+ d_-)^2}(\mathbf {x - \varvec{\theta }_+)}, & l = +,\\ - \alpha \frac{\partial f}{\partial \mu } \frac{d_+}{(d_+ + d_-)^2}(\mathbf {x} - \varvec{\theta }_-), &{}l = -. \end{array}\right. } \end{aligned}$$

(8)

$\frac{\partial f}{\partial \mu }$ is a kind of update weight depending on $\mathbf {x}$. To decrease the error rate, it is effective to update the prototypes mainly by the input vectors near the class boundaries, so that decision boundaries are shifted toward Bayes limits. Hence, $f(\mu )$ should be a nonlinear monotonically increasing function and it is considered that the classification ability depends on the definition of $f(\mu )$. We choose $\frac{\partial f}{\partial \mu } = f(\mu , t)(1 - f(\mu , t))$, where t is the time step and $f(\mu , t)$ is a sigmoid function with $\frac{1}{1 + e^{-\mu t}}$ as proposed in [28].

4.3 Momentum-based optimization

One of the most common algorithms to optimize error functions is the gradient descent/ascent algorithm, and in particular the stochastic formulations SGD and SGA [27]. In the field of Deep Learning, the classic SGA has been further modified to reduce common problems, like sensitivity to steep imbalanced valleys, i.e., areas where the cost surface curves are much more steep in one dimension than in another [32], which are common around local optima.

Momentum [24] is a method that helps accelerate SGA in the relevant direction and dampens oscillations. It does this by adding a fraction $\gamma$ of the update vector $\mathbf {v}$ of the previous time step to the current update vector:

$$\begin{aligned} \begin{aligned} \mathbf {v}_t&= \gamma \mathbf {v}_{t-1} + \eta \nabla _{\theta }J(\varvec{\theta })\\ \varvec{\theta }&= \varvec{\theta } - \mathbf {v}_t \end{aligned} \end{aligned}$$

(9)

The momentum term $\gamma$ is usually set to 0.9 or a similar value [18, 27, 33] but can be seen as a hyperparameter which can be optimized, e.g., via grid search. A common range for optimizing $\gamma$ is [0.9, 0.99] [34], while lower decay rates like $\gamma = 0.5$ are appropriate when having larger gradients, e.g., at the first iterations of optimization [33].

Effective momentum-based techniques are Adagrad, Adadelta, Adam, AdaMax, and RMSprop [27]. While Adagrad was the first publication of these three algorithms, RMSprop and Adadelta are further developments of Adagrad, which both try to reduce its aggressive, monotonically decreasing learning rate [34]. These momentum-based algorithms diverge to a local optima much faster and sometimes reach better optima than SGA [27].

Due to the fact that momentum-based algorithms make larger steps per iteration, it should adapt faster to new concepts. Thus, we implemented this idea into the RSLVQ and GLVQ and replaced the gradient update rule by Adadelta and AdaMax.

4.4 Adadelta

Instead of accumulating all past squared gradients, like in the Adagrads momentum approach, Adadelta restricts the window of accumulated past gradients to some fixed size w.

While it could inefficiently store all w squared gradients, the sum of gradients is recursively defined as a decaying average of all past squared gradients instead. The running average $E[\mathbf {g}^2]_t$ at time step t of the squared gradient $\mathbf {g}^2$ then depends (as a fraction $\gamma$ similarly to the Momentum term) only on the previous average and the current gradient:

$$\begin{aligned} E[\mathbf {g}^2]_t = \gamma E[\mathbf {g}^2]_{t - 1} + (1 - \gamma ) \mathbf {g}_t^2 \end{aligned}$$

(10)

The decay rate $\gamma$ should be set to a value of around 0.9 [10].

Hence, in [10] another exponentially decaying average is introduced, this time not of squared gradients but squared parameter updates:

$$\begin{aligned} E[\Delta \varvec{\theta }^2]_t = \gamma E[\Delta \varvec{\theta }^2]_{t-1} + (1 - \gamma ) \Delta \varvec{\theta }_t^2 \end{aligned}$$

(11)

Thus, the update of the root mean squared (RMS) error of parameters is:

$$\begin{aligned} RMS[\Delta \varvec{\theta }]_t = \sqrt{E[\Delta \varvec{\theta }^2]_t + \epsilon } \end{aligned}$$

(12)

Because of the reason that $RMS[\Delta \varvec{\theta }]_t$ is not known, it is approximated by the RMS of parameter updates until the previous time step $RMS[\Delta \varvec{\varvec{\theta }}]_{t-1}$. Finally, the learning rate $\eta$ of the previous update rule is replaced with $RMS[\Delta \varvec{\theta }]_{t-1}$, and we receive the following equation for updating Adadelta:

$$\begin{aligned} \begin{aligned} \Delta \varvec{\theta }_t&= - \frac{RMS[\Delta \varvec{\theta }]_{t-1}}{RMS[\mathbf {g}]_t} \mathbf {g}_t\\ \varvec{\theta }_{t+1}&= \varvec{\theta }_t + \Delta \varvec{\theta }_t \end{aligned} \end{aligned}$$

(13)

Due to the fact that the learning rate $\eta$ has been eliminated, it does not have to be optimized when using Adadelta, which keeps the number of hyperparameters small [27].

4.4.1 Robust Soft Learning Vector Quantization

To exchange the SGA learning of the RSLVQ with the Adedelta algorithm, the learning rule of the RSLVQ is replaced by the update rule provided in Eq. (13).

The prior and posterior probabilities are calculated the same way as in the RSLVQ$_{SGA}$. Based on the posterior and prior, the gradient is calculated over the objective function of the RSLVQ:

$$\begin{aligned} \mathbf {g}_t = {\left\{ \begin{array}{ll} P_y(l|\mathbf {x}) - P(l|\mathbf {x})) (\mathbf {x} - \varvec{\theta }_l), &{}c_l = y,\\ -P(l|\mathbf {x})(\mathbf {x} - \varvec{\theta }_l), &{}c_l \ne y. \end{array}\right. } \end{aligned}$$

(14)

In the next step, the running average of past squared gradients $E[\mathbf {g}^2]$ is updated by Eq. (10). Now the gradient update at time step t can be calculated:

$$\begin{aligned} \Delta \varvec{\theta }_t = - \frac{\sqrt{E[\Delta \varvec{\theta }^2]_{t-1} + \epsilon }}{\sqrt{E[\mathbf {g}^2]_t + \epsilon }}\mathbf {g}_t \end{aligned}$$

(15)

Afterward, the prototype update $\Delta \varvec{\theta }_t$ has to be applied as gradient ascent:

$$\begin{aligned} \varvec{\theta }_{t+1} = \varvec{\theta }_t - \Delta \varvec{\theta }_t \end{aligned}$$

(16)

Finally, the squared parameter updates $E[\Delta \varvec{\theta }^2]$ are stored by Eq. (11).

4.4.2 Generalized Learning Vector Quantization

Exchanging the gradient descent technique of GLVQ is done by replacing the update of Eq. (8) by a gradient calculation:

$$\begin{aligned} \mathbf {g}_t = {\left\{ \begin{array}{ll} \alpha \frac{\partial f}{\partial \mu } \frac{d_-}{(d_+ d_-)^2}(\mathbf {x - \varvec{\theta }_+)}, &{}l = +,\\ - \alpha \frac{\partial f}{\partial \mu } \frac{d_+}{(d_+ + d_-)^2}(\mathbf {x} - \varvec{\theta }_-), &{}l = -. \end{array}\right. } \end{aligned}$$

(17)

The other steps are the same as for introducing Adadelta into RSLVQ. Only Eq. (14) is replaced by Eq. (17) and the prototype update is a gradient descent instead of ascent:

$$\begin{aligned} \varvec{\theta }_{t+1} = \varvec{\theta }_t + \Delta \varvec{\theta }_t \end{aligned}$$

(18)

4.5 AdaMax

AdaMax is an extension of Adam algorithm [18]; thus, we will introduce Adam first. Adam stores an exponentially decaying average of past squared gradients $\mathbf {v}_t$ like Adadelta. Additionally, it keeps an exponentially decaying average of past gradients $\mathbf {m}_t$. It also has two separate decay factors: $\beta _1$ decays $\mathbf {m}_t$ and $\beta _2$ decays $\mathbf {v}_t$. The decaying average of past gradients is computed as follows:

$$\begin{aligned} \mathbf {m}_t = \beta _1 \mathbf {m}_{t - 1} + (1 - \beta _1) \mathbf {g}_t \end{aligned}$$

(19)

The corresponding decaying average of past squared gradients:

$$\begin{aligned} \mathbf {v}_t = \beta _2 \mathbf {v}_{t - 1} + (1 - \beta _2) \mathbf {g}^2_t \end{aligned}$$

(20)

As $\mathbf {m}_t$ and $\mathbf {v}_t$ are initialized as vectors of zeros, Adam is biased to 0, especially during the initial time steps and especially when the decay rates are small (i.e. $\beta _1$ and $\beta _2$ are close to 1).

Thus, the authors of [18] introduce a bias correction for the first and second moment estimates:

$$\begin{aligned} \begin{aligned} {\hat{\mathbf{m}}}_t&= \frac{\mathbf {m}_t}{1 - \beta ^t_1}\\ {\hat{\mathbf{v}}}_t&= \frac{\mathbf {v}_t}{1 - \beta ^t_2} \end{aligned} \end{aligned}$$

(21)

Finally, these parameters are used to update $\varvec{\theta }$:

$$\begin{aligned} \varvec{\theta }_{t + 1} = \varvec{\theta }_t - \frac{\eta }{\sqrt{\hat{\mathbf{v}}_t} + \epsilon }{\hat{\mathbf{m}}}_t \end{aligned}$$

(22)

Here $\eta$ is a learning rate like in vanilla gradient descent. Recommended default values for Adam, as well as AdaMax, are $\beta _1 = 0.9$, $\beta _2 = 0.999$ and $\epsilon = 10^{-8}$.

In Adam, $\mathbf {v}_t$ scales the gradient inversely proportional to the $L_2$ norm of the past gradients and current gradients $\Vert \mathbf {g}_t\Vert ^2$:

$$\begin{aligned} \mathbf {v}_t = \beta _2 \mathbf {v}_{t - 1} + (1 - \beta _2)\Vert \mathbf {g}_t\Vert ^2 \end{aligned}$$

(23)

This update can be generalized to the $L_p$ norm:

$$\begin{aligned} \mathbf {v}_t = \beta _2 \mathbf {v}_{t - 1} + (1 - \beta _2)\Vert \mathbf {g}_t\Vert ^p \end{aligned}$$

(24)

Norms for large p values become numerically unstable; thus, $L_1$ and L2 norm are most common in practice. However, $L_\infty$ also exhibits stable behavior [27]. Hence, in [18] AdaMax is proposed and shown that $\mathbf {v}_t$ with $L_\infty$ converges to the following more stable value. We denote the infinity constrained $\mathbf {v}_t$ of Adam as $\mathbf {u}_t$:

$$\begin{aligned} \begin{aligned} \mathbf {u}_t =\, \beta _2^\infty \mathbf {u}_{t - 1} + (1 - \beta _2^\infty )\Vert \mathbf {g}_t\Vert ^\infty \\ =\, max(\beta _2 \mathbf {u}_{t - 1}, \Vert \mathbf {g}_t\Vert ) \end{aligned} \end{aligned}$$

(25)

Now Eq. (22) is transformed into:

$$\begin{aligned} \varvec{\theta }_{t + 1} = \varvec{\theta }_t - \frac{\eta }{\mathbf {u}_t} {\hat{\mathbf{m}}}_t \end{aligned}$$

(26)

Due to the fact that $\mathbf {u}_t$ relies on a max operation, it is not suggestible to bias toward zero as in Adam. Hence, a bias correction for $\mathbf {u}_t$ is not necessary. In this paper, we use a learning rate $\eta$ of 0.001.

4.5.1 Robust Soft Learning Vector Quantization

To transform the update rule of RSLVQ to AdaMax, we start by calculating $\mathbf {g}_t$ by Eq. (14). Then, $\mathbf {m}_t$ is calculated via Eq. (19). We then do the bias correction of $\mathbf {m}_t$, following Eq. (21) to obtain ${\mathbf{\hat{m}}} _t$. Afterward, we obtain $\mathbf {u}_t$ by using Eq. (25) and calculating the prototype update by an ascending version of Eq. (26):

$$\begin{aligned} \varvec{\theta }_{t + 1} = \varvec{\theta }_t + \frac{\eta }{\mathbf {u}_t} {\hat{\mathbf{m}}}_t \end{aligned}$$

(27)

Note that $\mathbf {u}_0$ and $\mathbf {m}_0$ are vectors of zeros.

4.5.2 Generalized Learning Vector Quantization

To change the gradient descent technique of GLVQ to AdaMax, we also start by calculating $\mathbf {g}_t$ via Eq. (14). Furthermore, we can again calculate $\mathbf {m}_t$ by Eq. (19) and its bias corrected version $\hat{\mathbf{m}}_t$ via Eq. (21). Afterward, we obtain $\mathbf {u}_t$ via Eq. (25) and perform the final prototype update by Eq. (26). As we can see, it is the same procedure for exchanging prototypes for both LVQ versions expect for the gradient calculation and final update calculation.

Note that we can now address the stability plasticity dilemma [13] of all presented algorithms by our decay factors $\gamma , \beta _1, \beta _2$.

5 Experiments

5.1 Setup

We compared our classifiers against other state-of-the-art stream classifiers. Evaluation is done using the test-then-train method as described in Sect. 3. Since accuracy can be misleading on datasets with class imbalances, we also report Kappa statistics $\kappa$. Kappa is a statistic for imbalanced classes, which compares the classifiers performance with those of a chance classifier. If the classifier is always correct, then $\kappa = 1$. If its predictions coincide with the correct ones as often as those of a chance classifier, then $\kappa = 0$ [4].

To test if there are significant differences between the performance of the algorithms, the Friedman [11] test with a 95 % significance level is performed followed by the Bonferroni–Dunn [8] post hoc test.

Nine synthetic and three real data streams are used in the experiments. The synthetic data streams include abrupt, gradual, incremental drifts and one stationary data stream. The real-world data streams have been thoroughly used in the literature [15, 22] to evaluate the classification performance of data stream classifiers and exhibit multi-class, temporal dependencies and imbalanced data streams with different drift characteristics. Note that the gradual and abrupt drifts are generated by a concept drift generator which switches the class data generator functions as described below.

LED The LED data set simulates both abrupt and gradual drifts based on the used generator. The generator was first introduced in [7]. This data set yields instances with 24 Boolean features, 17 of which are irrelevant. The remaining 7 features correspond to each segment of a seven-segment LED display. The goal is to predict the digit displayed on the LED display, where each feature has a 10 % chance of being inverted. To simulate drifts in this data set, the relevant features are swapped with irrelevant features. The gradual drift, as well as the abrupt drift, happens at the 250,000th instance of the stream. The first drift swaps three features and is replaced with a drift that swaps seven features. ${\mathrm {LED}}_g$ simulates one gradual drift, while ${\mathrm {LED}}_a$ simulates three abrupt drifts.

SEA The SEA generator is an implementation of the data stream with abrupt concept drift, first described by Street and Kim in [31]. It produces data streams with three continuous attributes $(f_1, f_2, f_3 )$. The range of values that each attribute can assume lies between 0 and 10. Only the first two attributes $(f_1, f_2)$ are relevant, i.e., $f_3$ does not influence the class value determination. New instances are obtained through randomly setting a point in a two-dimensional space, such that these dimensions correspond to $f_1$ and $f_2$. This two-dimensional space is split into four blocks, each of which corresponds to one of the four different functions. In each block, a point belongs to class 1 if $f_1 + f_2 \le \theta$ and to class 0 otherwise. The threshold $\theta$ is used to split instances between class 0 and 1, assumes values 8 (block 1), 9 (block 2), 7 (block 3), and 9.5 (block 4). Two important features are the possibility to balance classes, which means the class distribution will tend to a uniform one, and the possibility to add noise, which will, according to some probability, change the chosen label for an instance. In this experiment, the SEA generator is used with 10 % noise in the data stream. ${\mathrm {SEA}}_g$ simulates one gradual drift, while ${\mathrm {SEA}}_a$ simulates an abrupt drift. Both drifts happen at the 250,000th instance. Figure 2 shows the sliding mean per class of one run of the ${\mathrm {SEA}}_a$ generator.

Fig. 2

Sliding mean per class of the last 10,000 samples on data generated by one run of ${\mathrm {SEA}}_a$. Abrupt drift is introduced at time step 250,000

RBF This generator produces data sets utilizing the Radial Basis Function (RBF). This generator creates several centroids, having a random central position and associates them with a standard deviation value, a weight, and a class label. To create new instances, one centroid is selected at random, where centroids with higher weights have more chances to be selected. The new instance input values are set according to a random direction chosen to offset the centroid. The extent of the displacement is randomly drawn from a Gaussian distribution according to the standard deviation associated with the given centroid. Incremental drift is introduced by moving centroids at a continuous rate, effectively causing new instances that ought to belong to one centroid to another with (maybe) a different class. Both ${\mathrm {RBF}}_m$ and ${\mathrm {RBF}}_f$ were parametrized with 50 centroids, and all of them drift. ${\mathrm {RBF}}_m$ simulates a moderate incremental drift (speed of change set to 0.0001) while ${\mathrm {RBF}}_f$ simulates a faster incremental drift (speed of change set to 0.001).

Sine The Sine generator [12] creates 4 numerical attributes that vary from 0 to 1, where only 2 of them are relevant to the classification task. A classification function is chosen among four possible ones:

• 1. SINE1: Abrupt concept drift, noise-free examples. It has two relevant attributes. Each of the attributes values is uniformly distributed in [0; 1]. In the first context, all points below the curve $y = \sin (x)$ are classified as positive.

• 2. SINE2: Consisting of the same attributes as SINE1. The classification function is given by $y < 0.5 + 0.3 \sin (3 \pi x)$.

• 3. Reversed classification of SINE1.

• 4. Reversed classification of SINE2.

The abrupt drift is generated by changing the classification function, thus changing the threshold. In our experiments, we switch the classification function between SINE1 and SINE2.

HYPER The HYPER data set simulates an incremental drift and it was generated based on the hyperplane generator [17]. A hyperplane is a flat, $n - 1$-dimensional subset of that space that divides it into two disconnected parts. It is possible to change a hyperplane orientation and position by slightly changing its relative size of the weights $w_i$. This generator can be used to simulate time-changing concepts, by varying the values of its weights as the stream progresses [4]. HYPER was parametrized with ten attributes and a magnitude of change of 0.001. Also, 10 % noise was added.

GMSC The Give Me Some Credit (GMSC) data set¹ is a credit scoring data set where the objective is to decide whether a loan should be allowed or not. This decision is important for banks since erroneous loans lead to the risk of default and unnecessary expenses on future lawsuits. The data set contains historical data on 150,000 borrowers, each described by ten attributes.

Electricity The Electricity data set² was collected from the Australian New South Wales Electricity Market, where prices are not fixed. These prices are affected by the demand and supply of the market itself and set every five minutes. The Electricity data set contains 45, 312 instances, where class labels identify the changes in the price (2 possible classes: up or down) relative to a moving average of the last 24 hours. An important aspect of this data set is that it exhibits temporal dependencies [12].

Poker Hand The Poker Hand data set consists of 1,000,000 instances and eleven attributes. Each record of the Poker Hand data set is an example of a hand consisting of five playing cards drawn from a standard deck of 52. Each card is described using two attributes (suit and rank), for a total of ten predictive attributes. There is one class attribute that describes the “Poker Hand” .

This data set has no drift in its original form since the poker hand definitions do not change and the instances are randomly generated. Thus, the version presented in [5] is used, in which virtual drift is introduced via sorting the instances by rank and suit. Duplicate hands were also removed.

For comparison purposes, the configuration of synthetic stream generators is taken from [15]. In most real-world stream scenarios, we only have limited information about our data at the beginning. Thus, hyperparameter optimization cannot be done before creating the model. Hence, we do not optimize hyperparameters in our experiments. Note that in [16] hyperparameters of all classifiers were tuned, which lead to different results.

As a rule of thumb, we use 2 prototypes per class for RSLVQ classifiers; we use the default decay values for Adadelta [34] and Adamax [18]. For HAT, OBA, and SAMKNN, we used the default parameters as provided by the scikit-multiflow framework.

Table 1 presents the data streams which are used in our experiment, as well as their configuration by the drift types. For a detailed description of the used data streams, see [15] and [21]. The tests of RSLVQ and GLVQ are performed with two prototypes per class.

Table 1 Configuration of the data streams (A: Abrupt Drift, G: Gradual Drift, ${\mathrm {I}}_m$: Moderate Incremental Drift, ${\mathrm {I}}_f$: Fast Incremental Drift and N: No Drift)

5.2 Results

In the following, we present the experimental results. Please note that in all tables, the values are represented in percent, which means a Kappa score of 1 equals 100 % in the table. At the beginning, we only compare different LVQ versions against each other, to see which performs best.

Table 2 Accuracy of the LVQ algorithms on synthetic and real-world streams

Table 2 shows the performance of the LVQ variants based on their accuracy. Based on the overall average, RSLVQ$_{Adamax}$ performs best. Also, the Adadelta version of RSLVQ performs significantly better than the vanilla version. The improvements are statistically significant based on a Friedman and Bonferroni–Dunn test. The better performance does not seem to be related to a specific drift type and can be seen on nearly every stream. However, the vanilla RSLVQ performs better than the adaptive versions on ELEC and POKR. Note that this was not the case when hyperparameters were tuned as in [16]. The results for GLVQ are very similar—the Adamax version is superior to Adadelta and vanilla GLVQ. However, the improvements are not significant here.

Table 3 Kappa statistic of the algorithms on synthetic and real-world streams

Table 3 shows the results of the LVQ variants according to Kappa statistics. Again, RSLVQ$_{Adamax}$ performs best overall and on the synthetic streams. On the real-world streams, the vanilla RSLVQ has superior results to every other LVQ version and also to all other tested classifiers (Table 5). This is due to its good performance on ELEC and POKR, while the performance on the very imbalanced GMSC dataset is near 0. In summary, RSLVQ$_{Adamax}$ performed statistically significant better than the vanilla RSLVQ. Once again, the GLVQ behaves very similar, which means overall the adaptive versions achieve a better Kappa score, while being worse than its vanilla version on ELEC and POKR. Also, the improvements between GLVQ$_{Adamax}$ and GLVQ are not significant here.

Both tables show that the adaptive versions lack accuracy and Kappa on ELEC and POKR streams. This is probably caused by the fact that the decay does not make sense on a dataset which is not time dependent and thus not change over time like the cards of POKR. On all other datasets, the adaptive versions are superior; in particular, Adamax leads to remarkable improvements compared to the both vanilla LVQ variants.

In the next experiment, we compare our LVQ versions to other state-of-the-art streaming classifiers. We only use GLVQ and RSLVQ based on Adamax, due to its performance in the previous experiment. As non-LVQ classifiers, we use OzaBaggingAdwin (OBA), Hoeffding Adaptive Tree (HAT), and Self-Adjusting Memory K-Nearest Neighbor (SAMKNN), which are common stream classifiers [13, 14].

Table 4 Accuracy of the algorithms on synthetic and real-world streams

Table 4 shows the results comparing our LVQ variants against state-of-the-art classifiers. SAMKNN is the best performing classifier, followed by OBA and GLVQ$_{Adamax}$. On the synthetic data, RSLVQ$_{Adamax}$ is close above HAT but still behind OBA and SAMKNN. However, overall HAT and RSLVQ$_{Adamax}$ are very similar according to their accuracy. Also, GLVQ$_{Adamax}$ is only close behind its RSLVQ implementation. Note that while the results tend to give the impression that SAMKNN and OBA are superior to the LVQ variants, there are several advantages of the LVQ techniques. The experiments of [26] gives detailed comparison of the time and memory complexity of stream classifiers, clearly showing that RSLVQ is superior regarding time and memory complexity to SAMKNN and OBA. This makes the LVQ techniques more interesting for the real-time analysis of higher-dimensional data and analysis with less powerful devices like single-board computers.

Table 5 Kappa statistic of the algorithms on synthetic and real-world streams

Finally, Table 5 shows the performance of the classifiers w.r.t. Kappa statistics. The results are as we would expect them from the accuracy. SAMKNN is the leading classifier with an overall Kappa of 0.76, followed by OBA and RSLVQ$_{Adamax}$. The GLVQ variant stays $\sim 7$ % behind the RSLVQ$_{Adamax}$. Again HAT is only close behind our adaptive RSLVQ and nearly achieved a nearly similar Kappa score.

6 Conclusion

In summary, the integration of Adadelta and Adamax into RSLVQ and GLVQ leads to improvements in prediction performance over their vanilla versions. In particular, RSLVQ$_{Adamax}$ performed best of all LVQ variants and is statistically significant better than RSLVQ. RSLVQ$_{Adamax}$ achieved a better performance than HAT, which is a very widely used stream classifier. Furthermore, the complexity of the RSLVQ variants is much lower than those of HAT. Hence, our adaptive RSLVQ variant is a suitable stream classifier which can be easily interpreted by its prototype-based characteristic. In further work, the performance is verified by using an ensemble of RSLVQ$_{Adamax}$ and a concept drift detector like done by other famous stream classifiers (e.g., Hoeffding Adaptive Tree). Additionally, momentum-based gradient descent should handle different drift types more explicitly, which should be addressed in subsequent work.