Multimodal medical image fusion algorithm in the era of big data

Abstract

In image-based medical decision-making, different modalities of medical images of a given organ of a patient are captured. Each of these images will represent a modality that will render the examined organ differently, leading to different observations of a given phenomenon (such as stroke). The accurate analysis of each of these modalities promotes the detection of more appropriate medical decisions. Multimodal medical imaging is a research field that consists in the development of robust algorithms that can enable the fusion of image information acquired by different sets of modalities. In this paper, a novel multimodal medical image fusion algorithm is proposed for a wide range of medical diagnostic problems. It is based on the application of a boundary measured pulse-coupled neural network fusion strategy and an energy attribute fusion strategy in a non-subsampled shearlet transform domain. Our algorithm was validated in dataset with modalities of several diseases, namely glioma, Alzheimer’s, and metastatic bronchogenic carcinoma, which contain more than 100 image pairs. Qualitative and quantitative evaluation verifies that the proposed algorithm outperforms most of the current algorithms, providing important ideas for medical diagnosis.

1 Introduction

Multimodal medical imaging is a research field that has been getting increasing attention in the scientific community in the last few years, specially due to its significance in medical diagnosis, computer vision, and internet of things [3, 5, 15, 20, 28, 31, 32, 35]. Defined as the simultaneous production of signals belonging to different medical imaging techniques, one of the biggest challenges in this research field is how to combine (or fuse) in an effective and optimal way multimodal medical imaging sensors, such as positron emission tomography (PET), single-photon emission computed tomography (SPECT), and magnetic resonance imaging (MRI). This image fusion process comprises many techniques and research areas, ranging from image processing techniques, computer vision to pattern recognition, with the goal of promoting more accurate medical diagnosis and more effective medical decision-making [8, 10, 18, 26, 45].

1.1 Current challenges in multimodal image fusion

Image fusion can usually be divided into three levels: pixel-level, feature-level, and decision level [21, 31, 42,43,44, 47]. Since the aim is to fuse pixel information from source images, medical image fusion belongs to the pixel-level.

Multi-scale transform (MST) method is one of the most famous categories [40]. Commonly, the MST fusion methods consist of three steps. First, the source images are transformed into MST domain. Then, the parameters in different scales merged in light of a specific fusion strategy. Finally, the fused image is reconstructed through the corresponding inverse transform. The MST methods mainly contain the Laplacian pyramid (LP) [6], the wavelet transform (WT) [27, 34], the non-subsampled contourlet transform (NSCT) [49], and the non-subsampled shearlet transform (NSST) [4, 23, 38]. However, if the MST method performs without other fusion measures, some unexpected block effect may appear [39].

To overcome this disadvantage, some fusion measures are applied in the MST method. For instance, spatial frequency (SF), local variance (LV), the energy of image gradient (EIG) and sum-modified-Laplacian (SML) are commonly used as fusion measures [17, 41]. However, most of these measures are acquired in the spatial domain or low-order gradient domain, which means the fusion map may not be always precise. This imprecision may lead to blocking artefacts.

Except for traditional MST methods, the edge-preserving filtering (EPF)-based MST decomposition method are also commonly used. In the EPF-MST methods, Gaussian filtering and EPF are used to decompose the input image into two scale-layers and one base layer. Then, three layers are fused based on suitable fusion strategies. Finally, the fused image is reproduced by a reconstruction algorithm. The EPF-MST methods contain bilateral filtering (BF)-based [51], curvature filtering (CF)-based [40], and co-occurrence filtering (CoF)-based [37] methods.

1.2 A pulse-coupled neural network model for medical image fusion

To overcome this challenge, a method called pulse-coupled neural network (PCNN) has been proposed in the literature [46]. This method was initially proposed to emulate the underlying mechanisms of a cat’s visual cortex and became later an essential method in image processing [29]. Kong et al. presented an SF modulated PCNN fusion strategy in NSST domain with the solution of infrared and visible image fusion [19]. Inspired by this kind of fusion measure modulated by the PCNN model, one interesting research path would be a solution to a new measure to modulate PCNN in the medical image fusion field.

To further improve the fusion quality of medical images, we propose a medical image fusion method based on boundary measure modulated by a pulse-coupled neural network in the non-subsampled shearlet domain. Firstly, the source images are transformed into the NSST domain with low-frequency bands and high-frequency bands. Then, the low-frequency bands are merged through an energy attribute-based fusion strategy, and the high-frequency bands are merged through a boundary measure modulated PCNN strategy. Finally, the fused image is reconstructed by combining the inverse NSST. We evaluate the proposed algorithm by comparing its performance with several existing methods using both a quantitative and qualitative evaluation. Experimental results demonstrate that the proposed method performs better than most of the existing fusion methods.

1.3 Contribution

The main contributions of the proposed research article are the following:

• 1. A medical image fusion framework based on boundary measured PCNN in NSST domain, which can complete the fusion task effectively;

• 2. The application of a boundary measured PCNN model for high-frequency bands. In this method, the gradient information of the image can be easily extracted, and the size of the structure can be changed to adapt to the scale of structure;

• 3. The application of an energy attribute-based fusion strategy to low-frequency bands.

Experiments conducted in this research paper suggest that the proposed boundary measured PCNN-NSST achieves the best performance in most cases in qualitative and quantitative when compared to other state-of-the-art image fusion techniques.

1.4 Organization

The rest of this paper is organized as follows. In Sect. 2, it is presented the most significant works in the image fusion domain. In Sect. 3, the proposed fusion method BM-PCNN-NSST is described. In Sect. 4, it is presented the set of experiments that were performed to evaluate the proposed algorithm. Finally, in Sect. 5, the main conclusions of this research work are presented.

2 Related work

In this section, we present an overview of the most significant image fusion algorithms in the literature, namely the non-subsampled shearlet transform (Sect. 2.1), the multi-scale morphological gradient (Sect.  2.2), and the pulse-coupled neural network (Sect. 2.3).

2.1 Non-subsampled shearlet transform

The non-sampled shearlet transform is an image fusion method, originally proposed by Easley [13]. It consists in combining the non-subsampled pyramid transform with different shearing filters, and it has the characteristics of multi-scale and multi-directionality. The non-subsampled pyramid transform makes it invariant, which is superior than the LP, and WT methods. Additionally, since the size of the shearing filter is smaller than the directional filter, NSST can represent smaller scales, which makes it better than NSCT.

Given the superiority of its underlying functions, NSST performs better than most commonly used MST. It is therefore widely used in the field of image denoising [36] and image fusion [22].

The NSST model can be described as follows. For the case, n = 2, the shearlet function is satisfied

$$ \varOmega_{AB} \left( \psi \right) = \left\{ {\psi_{i,j,k} \left( x \right) = \left| {\det A} \right|^{j/2} \psi \left( {B^{l} A^{j} x - k} \right);j,l \in Z^{2} } \right\} $$

(1)

where ψ ∊ L²(R²), both A and B are invertible matrices with size 2 × 2, and $\left| {\det B} \right| = 1$. For instance, A and B can be represented as

$$ A = \left[ {\begin{array}{*{20}c} 4 & 0 \\ 0 & 2 \\ \end{array} } \right],\quad B = \left[ {\begin{array}{*{20}c} 1& 1\\ 0 & 1\\ \end{array} } \right] $$

(2)

In this situation, the tiling of the frequency plane of NSST is shown in Fig. 1 It can be seen that (a) represents the decomposition, and (b) represents the size of the frequency support of the shearlet element $\psi_{i,l,k}$.

Fig. 1

The structure of the frequency tiling

For convenience, two related functions are used to represent the NSST and the inverse NSST

$$ \left\{{{L}_{n}},{{H}_{n}} \right\}={\text{nsst}}\_{\text{de}}\left({{I}_{\text{in}}} \right) $$

(3)

$$ I_{\text{re}} = {\text{nsst\_re}}\left( {L_{n} ,H_{n} } \right) $$

(4)

where ${\text{nsst\_de}}\left( \cdot \right)$ represents the NSST decomposition function for the input image $I_{\text{in}}$, and ${\text{nsst\_re}}\left( \cdot \right)$ represents the NSST reconstruction steps for the reconstructed image $I_{\text{re}}$. The parameters $L_{n}$ and $H_{n}$ represent low-frequency sub-bands and high-frequency sub-bands, respectively.

2.2 Multi-scale morphological gradient

Multi-scale morphological gradient (MSMG) is an effective operator which extracts gradient information from an image in order to indicate the contrast intensity in the close neighborhood of a pixel in the image. For this reason, MSMG is a method that is highly efficient and used in edge detection and image segmentation. In image fusion, MSMG has been used as a type of focus measure in multi-focus image fusion [50]. The specific details of MSMG are as follows.

A multi-scale structuring element is defined as

$$ {\text{SE}}_{j} = \underbrace {{{\text{SE}}_{1} \oplus {\text{SE}}_{1} \oplus \cdots \oplus {\text{SE}}_{1} }}_{j},\quad \, j \in \left\{ {1,2, \ldots ,N} \right\} $$

(5)

where ${\text{SE}}_{1}$ denotes a basic structure element, and t represents the number of scales.

The gradient feature $G_{t}$ can be represented by the morphological gradient operators from the image f.

$$ {{G}_{t}}\left(x,y \right)=f\left(x,y \right)\oplus {{\text{SE}}_{t}}-f\left(x,y \right)\odot {{\text{SE}}_{t}} $$

(6)

where $\oplus$ and $\odot$ denote the morphological dilation and erosion operators, respectively. $\left( {x,y} \right)$ denotes the pixel coordinate.

From the multi-scale structuring element and the gradient feature, then one can obtain the MSMG by computing the weighted sum of gradients over all scales.

$$ M\left( {x,y} \right) = \sum\limits_{t = 1}^{N} {w_{t} \cdot G_{t} \left( {x,y} \right)} $$

(7)

where $w_{t}$ represents the weight of gradient in t-th scale, and it can be represented as

$$ w_{t} = \frac{1}{2t + 1} $$

(8)

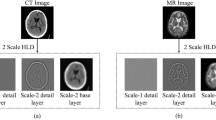
Figure 2 shows an example of MSMG. One can see that the boundary information of the images has been well extracted, which demonstrates the effectiveness of the boundary measure.

Fig. 2

An example of MSMG

2.3 Pulse-coupled neural network

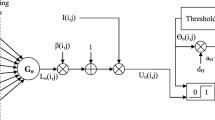
As the third-generation artificial neural network, PCNN has achieved great success in the image fusion field. A PCNN model often contains three parts: the receptive field, the modulation field and the pulse generator. The expressions of a simplified dual-channel PCNN model can be defined as

$$ F_{ij}^{1} \left( k \right) = S_{ij}^{1} \left( k \right) $$

(9)

$$ F_{ij}^{2} \left( k \right) = S_{ij}^{2} \left( k \right) $$

(10)

$$ L_{ij} \left( k \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if }}\sum\limits_{r,t \in S} {Y_{rt} \left( {k - 1} \right) > 0} } \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$

(11)

$$ U_{ij} \left( k \right) = \hbox{max} \left\{ {F_{ij}^{1} \left( k \right)\left( {1 + \beta_{ij}^{1} L_{ij} \left( k \right)} \right),F_{ij}^{2} \left( k \right)\left( {1 + \beta_{ij}^{2} L_{ij} \left( k \right)} \right)} \right\} $$

(12)

$$ Y_{ij} \left( k \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if }}\;\;U_{ij} \left( k \right) \ge \theta_{ij} \left( {k - 1} \right)} \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$

(13)

$$ \theta_{ij} \left( k \right) = \theta_{ij} \left( {k - 1} \right) - \Delta + V_{\theta } Y_{ij} \left( k \right) $$

(14)

$$ T_{ij} = \left\{ {\begin{array}{*{20}l} {k,} \hfill & {{\text{ if}}\;\;U_{ij} \left( k \right) \ge \theta_{ij} \left( {k - 1} \right)} \hfill \\ {T_{ij} \left( {k - 1} \right),} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$

(15)

As is shown in Fig. 3, $S_{ij}^{1}$ and $S_{ij}^{2}$ denote the pixel value of two input images at point $\left( {i,j} \right)$ in the neural network; $L_{ij}$ represents the linking parameter; $\beta_{ij}^{1}$ and $\beta_{ij}^{2}$ denote the linking strength; $F_{ij}^{1}$ and $F_{ij}^{2}$ represent the feedback of inputs. $U_{ij}$ is the output of the dual-channel. $\theta_{ij}$ is the threshold of step function, $d_{e}$ is the declining extent of the threshold, $V_{\theta }$ decides the threshold of the active neurons, and $T_{ij}$ is the parameter to determine the number of iterations. $Y_{ij} \left( k \right)$ is the k-th output of PCNN.

Fig. 3

Classical PCNN model

3 A Bounded measured PCNN in NSST domain algorithm

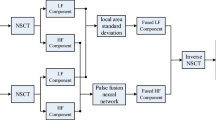
In this section, we present the proposed algorithm for multimodal medical image fusion: a bounded measured PCNN approach in the NSST domain (BM-PCNN-NSST). The framework of the proposed algorithm is illustrated in Fig. 4. The fusion algorithm consists in four parts: the NSST decomposition, the low-frequency fusion, the high-frequency fusion, and the NSST reconstruction.

Fig. 4

Framework of the proposed algorithm

The algorithm starts with a pseudocolor image source A which contains three-bands (PET/SPECT image). The first step is to apply an intensity-hue-saturation (IHS) transform in A, which will result in a pair containing the intensity image $I_{A}$ and a source image B. After performing the fusion of this image pair, an inverse IHS transform is applied in order to obtain the final fused image.

3.1 NSST decomposition

An N-level NSST decomposition is performed on images $I_{A}$ and B to acquire the decomposition bands $L_{A}$, $H_{A}^{l,k}$ and $L_{B}$, $H_{B}^{l,k}$ based on Eq (3), where L denotes low-frequency sub-bands and $H^{l,k}$ represents high-frequency sub-bands at level l with direction k.

$$ \left\{ {L_{A} ,H_{A}^{l,k} } \right\} = {\text{nsst\_de}}\left( A \right) $$

(16)

$$ \left\{ {L_{B} ,H_{B}^{l,k} } \right\} = {\text{nsst\_de}}\left( B \right) $$

(17)

3.2 Low-frequency fusion

The low-frequency sub-band contains most information of the source images (texture structure and background). In this paper, an energy attribute (EA) fusion strategy is presented in the low-frequency fusion. This EA fusion strategy is divided into three steps:

• 1. The intrinsic property values of the low-frequency sub-band are computed as

  $$ IP_{A} = \mu_{A} + Me_{A} $$

  (18)
  $$ IP_{B} = \mu_{B} + Me_{B} $$

  (19)

  where μ and Me represent the mean value and the median value of $L_{A}$ and $L_{B}$, respectively.

• 2. The EA function $E_{A}$ and $E_{B}$ are calculated by

  $$ E_{A} \left( {x,y} \right) = \exp \left( {\alpha \left| {L_{A} \left( {x,y} \right) - IP_{A} } \right|} \right) $$

  (20)
  $$ E_{B} \left( {x,y} \right) = \exp \left( {\alpha \left| {L_{B} \left( {x,y} \right) - IP_{B} } \right|} \right) $$

  (21)

  where $\exp \left( {\alpha \left| {L_{A} \left( {x,y - IP_{A} } \right)} \right|} \right)$ represents the exponential operator, and α denotes the modulation parameter.

• 2. The fused low-frequency sub-band is obtained by a weighted mean

  $$ L_{F} \left( {x,y} \right) = \frac{{E_{A} \left( {x,y} \right) \times L_{A} \left( {x,y} \right) + E_{B} \left( {x,y} \right) \times L_{B} \left( {x,y} \right)}}{{E_{A} \left( {x,y} \right) + E_{B} \left( {x,y} \right)}} $$

  (22)

3.3 High-frequency fusion

While low-frequency sub-band contains most information about the source images (such as background and texture), high-frequency sub-bands contain more information about details in images (for example, pixel-level information). Since in the PCNN model one pixel corresponds to one neuron, it is suitable to use PCNN in high-frequency sub-bands. In addition, modulating PCNN with MSMG can increase the spatial correlation in the image. Therefore, the MSMG operator can be used to adjust the linking strength between $\beta_{ij}^{1}$ and $\beta_{ij}^{2}$

$$ \beta_{ij}^{A} = M_{A} $$

(23)

$$ \beta_{ij}^{B} = M_{B} $$

(24)

where $M_{A}$ and $M_{B}$ are computed by Eq. (7).

The high-frequency sub-bands are merged based on this MSMG-PCNN model until all neurons are activated (equal to 1). The fused high-frequency sub-bands can be obtained by

$$ H_{F}^{l,k} \left( {x,y} \right) = \left\{ {\begin{array}{*{20}l} {H_{A}^{l,k} \left( {x,y} \right),} \hfill & { \, \quad {\text{if }}\;\;T_{xy,A} \ge T_{xy,B} ;} \hfill \\ {H_{B}^{l,k} \left( {x,y} \right), \, } \hfill & {\quad {\text{otherwise}} .} \hfill \\ \end{array} } \right. $$

(25)

where $T_{xy,A}$ and $T_{xy,B}$ can be computed using Eq (15).

3.4 NSST reconstruction

The fused image F is reconstructed by $L_{F}$ and $H_{F}^{l,k}$ through the inverse NSST according to Eq (4)

$$ F = nsst\_re\left( {L_{F} ,H_{F}^{l,k} } \right) $$

(26)

4 Experiments

To validate the proposed algorithm, a set of experiments was made using three datasets representing different diseases: (1) glioma, (2) mild Alzheimer’s, and (3) hypertensive encephalopathy. The proposed algorithm was compared with seven state-of-the-art image fusion methods. Qualitative and quantitative analyses were made to assess its performance. The code of the paper is made available.¹

4.1 Datasets

To verify the proposed algorithm, more than 100 pairs of multimodal medical images were used, including 30 image pairs of MRI-PET and 13 image pairs of MRI-SPECT of glioma disease, 10 image pairs of MRI-PET of mild Alzheimer’s disease, 11 image pairs of MRI-SPECT of Metastatic bronchogenic carcinoma, 10 image pairs of MRI-SPECT of hypertensive encephalopathy, 11 image pairs of MRI-SPECT of motor neuron disease, and 16 image pairs of MRI-SPECT of normal aging. All the image pairs can be downloaded from the Whole Brain Atlas dataset [1]. All the pairs have been perfectly registered, and the size of all images is 256 × 256.

4.2 Comparison methods

The proposed BM-PCNN-NSST algorithm is compared with seven state-of-the-art fusion methods. There methods are the convolutional neural network (CNN) [ [24], [53] ], the convolutional sparsity-based morphological component analysis (CSMCA) [25], the information of interest in local Laplacian filtering domain (LLF-IOI) [11], the neuro-fuzzy approach (NFA) [9], the parameter-adaptive PCNN in NSST domain (NSST-PAPCNN) [48], the phase congruency and local Laplacian energy in NSCT domain (PC-LLE-NSCT) [52], and the parallel saliency features (PSF) [12]. These methods are recently proposed fusion methods. The parameters that we used in our experiments are the same as in their papers.

4.3 Parameter settings

In the proposed BM-PCNN-NSST algorithm, the following parameters were used:

• the NSST decomposition level N is set to 4;

• the number of directions in each level is set to 16,16,8,8;

• the modulation parameter is set to 4;

• the scales number of MSMG operator t is set to 3.

4.4 Evaluation metrics

To analyze the performance of the proposed algorithm in a quantitative way, we evaluate the different fusion methods using five metrics: entropy (EN), standard deviation (SD), normalized mutual information (NMI) [14], Piella’s structure similarity (SS) [33], and visual information fidelity (VIF) [16]. In general, both SD and EN can measure the amount of information of the fused image. NMI evaluates the amount of information transferred from the source images to fused image. SS mainly evaluates the structure similarity between source images and fused image. VIF evaluates the visual information fidelity between the source images and fused image. More detailed information about these evaluation metrics can be found on the references related to each fusion method.

4.5 Experimental results

The results of medical image fusion cannot be completely dependent on visual effects evaluation. As long as the feature information is not lost, the medical diagnosis will not be misjudged because of this, and the visual effect will be acceptable. Therefore, in this paper, each disease demonstrates a set of experimental results, which is shown in Figs. 5, 6, 7, 8, 9, 10, and 11. Different methods have different visual effects, but the feature information does not seem to be lost. Therefore, objective evaluation indicators are needed for a further quantitative evaluation.

Fig. 5

One set of glioma disease MRI and PET image fusion results. a MRI; b PET; c CNN; d CSMCA; e LLF-IOI; f NFA; g NSST-PAPCNN; h PC-LLE-NSCT; i PSF; j Proposed

Fig. 6

One set of glioma disease MRI and SPECT image fusion results. a MRI; b SPECT; c CNN; d CSMCA; e LLF-IOI; f NFA; g NSST-PAPCNN; h PC-LLE-NSCT; i PSF; j Proposed

Fig. 7

One set of mild Alzheimer’s disease MRI and PET image fusion results. a MRI; b PET; c CNN; d CSMCA; e LLF-IOI; f NFA; g NSST-PAPCNN; h PC-LLE-NSCT; i PSF; j Proposed

Fig. 8

One set of metastatic bronchogenic carcinoma MRI and SPECT image fusion results. a MRI; b SPECT; c CNN; d CSMCA; e LLF-IOI; (f) NFA; g NSST-PAPCNN; h PC-LLE-NSCT; i PSF; j Proposed

Fig. 9

One set of hypertensive encephalopathy MRI and SPECT image fusion results. a MRI; b SPECT; c CNN; d CSMCA; e LLF-IOI; f NFA; g NSST-PAPCNN; h PC-LLE-NSCT; i PSF; j Proposed

Fig. 10

One set of motor neuron disease MRI and SPECT image fusion results. a MRI; b SPECT; c CNN; d CSMCA; e LLF-IOI; f NFA; g NSST-PAPCNN; h PC-LLE-NSCT; i PSF; j Proposed

Fig. 11

One set of normal aging MRI and SPECT image fusion results. a MRI; b SPECT; c CNN; d CSMCA; e LLF-IOI; (f) NFA; g NSST-PAPCNN; h PC-LLE-NSCT; i PSF; j Proposed

The mean value of each metrics of different fusion methods is listed in Tables 1, 2, 3, 4, 5, 6 and 7. Each column represents the same metrics for different methods. The highest value is shown in bold, while the second highest in italic. It can be seen that the proposed method performs the best in half of the cases. Even if it is not the highest value in one column, it is still the second highest value, except in the NMI of the normal aging case.

Table 1 Mean quality of glioma disease (30 image pairs of MRI-PET)

Table 2 Mean quality of glioma disease (13 image pairs of MRI-SPECT)

Table 3 Mean quality of mild Alzheimer’s disease (10 image pairs of MRI-PET)

Table 4 Mean quality of metastatic bronchogenic carcinoma (11 image pairs of MRI-SPECT)

Table 5 Mean quality of hypertensive encephalopathy (10 image pairs of MRI-SPECT)

Table 6 Mean quality of motor neuron disease (11 image pairs of MRI-SPECT)

Table 7 Mean quality of normal aging (16 image pairs of MRI-SPECT)

5 Conclusion

In this paper, a multimodal medical image fusion algorithm is proposed based on boundary measured PCNN and EA fusion strategies in NSST domain. The main advantage of the proposed algorithm is that the two fusion strategies are suitable for different scales. Decomposing images into different scales with NSST can give full play to the advantages of the two fusion strategies. Meanwhile, as an excellent decomposition method, NSST can well blend the differences of multimodal medical images. The performance of the proposed algorithm has been verified in public datasets, which represents it has reached state-of-the-art level. One of the important outcomes of this paper is reported in “Appendix,” which showed the experimental performance of different values of α and t. One can see that when α = 4 and t = 3 the performance is the best in most cases. Since the deep learning technology has been widely used, in the future research, we will focus on the deep learning method in multimodal medical image fusion [2, 7, 30].

Appendix

Figures 12, 13, 14, 15, 16, 17, and 18 show the experimental performance of different α and t. One can see that when α = 4, t = 3, the performance is the best in most cases.

Fig. 12

Glioma disease (MRI-PET). a t–EN; b t–SD; c t–NMI; d t–SS; e t–VIF

Fig. 13

Glioma disease (MRI-SPECT). a t–EN; b t–SD; c t–NMI; d t–SS; e t–VIF

Fig. 14

Mild Alzheimer’s disease (MRI-PET). a t–EN; b t–SD; c t–NMI; d t–SS; e t–VIF

Fig. 15

Metastatic bronchogenic carcinoma (MRI-SPECT). a t–EN; b t–SD; c t–NMI; d t–SS; (e) t–VIF

Fig. 16

Hypertensive encephalopathy (MRI-SPECT). a t–EN; b t–SD; c t–NMI; d t–SS; e t–VIF

Fig. 17

Motor neuron disease (MRI-SPECT). a t–EN; b t–SD; c t–NMI; d t–SS; e t–VIF

Fig. 18

Normal aging (MRI-SPECT). a t–EN; b t–SD; c t–NMI; d t–SS; e t–VIF