1 Introduction

Class-imbalance classification is a long withstanding problem in the literature [1,2,3,4,5] where a binary dataset contains a disproportionately larger amount of samples of the majority class (i.e., negative class) [6]. Such datasets are common in many domains including life sciences [7], protein classification [8], DNA sequence recognition [9], financial sector [10], Medical domain [11], Medicine rating and recommendations [12], engineering drawings analysis [13,14,15] and others. An example of a binary classification problem is shown in Eq. 1. In a classification task, the aim is to learn a function \(\textit{h(x)}\) that maps an instance \(\mathbf{x} _{i} \in X\) to a class \(\mathbf{y} _{i}\), where \(y_i \in Y=\{C_N,C_P\}\), denoting negative and positive class, respectively. In an imbalanced dataset, the positive class \(C_P\) (class of interest) is often underrepresented in the dataset, causing a learning algorithm to be biased toward the majority class instances \(C_N\).

$$\begin{aligned} X = \begin{bmatrix} x_{11} &{} x_{12} &{} \dots &{} x_{1n} \\ x_{21} &{} x_{22} &{} \dots &{} x_{2n} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ x_{m1} &{} \vdots &{} \dots &{} x_{mn} \\ \end{bmatrix} ,\quad Y=\begin{bmatrix} y_{1} \\ y_{i} \\ \vdots \\ y_{m} \\ \end{bmatrix} \end{aligned}$$
(1)

Consider the banking sector, a dataset for handling fraudulent transactions. Most transactions are legitimate (i.e., 90–99%, \(x_i \in C_N\)), and few are fraud (class \(C_P\) in Eq. 1). In such scenario, an accuracy more than 90% can be easily obtained. However, it is easy to miss-classify the class of interest (i.e., \(x_i \in C_P\)), and hence, the need for different solutions accounts for the data distribution. Solutions for handling such a problem can be broadly categorized as data-based, algorithmic-based or cost-sensitive [2]. Data-based solutions are commonly used to compact class-imbalanced datasets. These methods are focused on either undersampling the data to reduce the dominance of the majority class instances, oversample the minority class, or a hybrid approach that combines both methods. Algorithmic-based solutions tend to modify the learning algorithms. Such algorithms include C4.5, k nearest neighbors (k-NN), support vector machine (SVM) and others.

Unlike most learning models which assign the same cost for all misclassifications in the learning process, cost-sensitive methods are based on the actual class and aiming at minimizing the total cost [16]. These methods emphasize the class of interest (positive class) by assigning higher costs for misclassifying it.

In this paper, we propose a new method for handling the class-imbalance problem based on class decomposition (CD) of the majority class and synthetic oversampling of the minority class. For short, we will refer to the proposed method as CDSMOTE. Our method is designed to first find the similarities within the majority class instances and group them accordingly. This results in reducing the dominance of the majority class without causing information loss, as it is the case with other undersampling techniques. To ensure a balanced distribution of the data, we then apply an oversampling method to improve the representation of the minority class. Extensive experiments were carried out, and the results show the superiority of the proposed method in improving different metrics when compared with the common and state-of-the-art methods.

The rest of the paper is organized as follows. Section 2 provides the necessary background and relevant literature. In Sect. 3, we present our method. Section 4 details the experiments with thorough evaluation and discussion of the results. Finally, Sect. 5 concludes the work and discusses possible future directions.

2 Related work

Handling the class-imbalance is most commonly achieved using ether data-based [17, 18] or algorithmic-based solutions [19]. Because of the purpose and scope of this paper, we will focus on data-based methods. For those interested in algorithmic-based solutions, we refer the reader to a recent survey [20] for more details. Data resampling is one of the standard methods for handling class-imbalanced datasets classification. These methods include undersampling, which aims at reducing the dominance of the majority class instances, oversampling, aiming at increasing the visibility of the minority class instances or hybrid approaches (combining both methods).

Random sampling is one of the most basic methods used to handle the class-imbalance problem. It can be applied as random undersampling (RUS), with the aim of rebalancing a dataset by randomly sampling a subset of the majority class instances, or as random oversampling (ROS), to multiply the instances of the minority class. This approach is simple, and thus, it is almost certain that it will result in losing data or overfitting. Therefore, these methods are rarely used alone. For example, in [21] a hybrid approach of RUS and a boosting algorithm (RUSBoost) was implemented to improve the classification results.

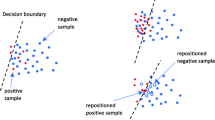
Other methods are focused on undersampling data from the overlapping region aiming at minimizing the overlap between positive and negative instances. Figure 1a shows a typical example of a hugely imbalanced dataset with the overlapping region highlighted in Fig. 1b, while Fig. 1c shows a possible solution where undersampling is carried out within that region. Several techniques are available to facilitate undersampling from the overlapping region. Among these, Tomek Link (T-Link) [22] which is a popular concept is originally proposed to edit the nearest neighbor rule which is used to remove instances in an overlapping region. The main idea is simple, given a dataset Z, two samples (a from the majority class and b from the minority class) and a distance function d between them, a T-Link is obtained if there is an example \(z\in Z\) such that:

$$\begin{aligned} \text{dist}(z,a)>\text{dist}(a,b) \wedge \text{dist}(z,b)>\text{dist}(a,b) \end{aligned}$$
(2)
Fig. 1
figure 1

Undersampling imbalanced datasets. a Imbalanced dataset, b overlapping region and c undersampling from overlapping region

Full size image

The basic idea then is to discard sample a from the dataset whenever a T-link is obtained. This method is proved to be useful in handling class-imbalance and provided a better alternative to random sampling. For example, Kubat and Matwin [23] proposed an undersampling method by shrinking the overlapping region using T-Link [22]. This was achieved by selectively removing redundant majority class instances close to the class boundary. Better performance was reported based on real datasets. Devi et al. [24] proposed a more recent method based on T-Link which also aimed at removing noise and redundant negative instances from the overlapping region. Other similar approaches include neighboring cleaning rule (NCL) for small sets [25] and the majority undersampling technique (MUTE) [26]. Removing negative class instances selectively (i.e., from the overlapping region) often yields to better results. However, this does not prevent data loss which might affect the overall accuracy. Therefore, in some scenarios or application domains where the overall accuracy matters, alternatives should be considered to minimize the risk of losing information [2]. A recent work presented in [6] by Vuttipittayamongkol and Elyan followed a similar approach to selectively remove the negative instances from the overlapping region by using fuzzy C-Means and reported the comparable results with the state of the art. More recently, the authors extended their work by proposing new methods for handling class-imbalance where unlike other common resampling methods, they introduced a novel way to detect and remove negative instances from the overlapping region using neighborhood searching techniques and reported the comparable results with state-of-the-art methods [27].

Oversampling methods aiming at improving the presence of the minority class instances are also common practice. Synthetic minority oversampling technique (SMOTE) proposed by Chawla et al. [28] is still widely used in this domain. SMOTE is based on generating synthetic data points using a neighborhood-based technique (i.e., k-NN). Several extensions of SMOTE have been proposed since its introduction, including SMOTEBoost [29], Borderline-SMOTE [17], DBSMOTE [30], MWMOTE [31] and others. ADASYN [32] is another common oversampling method that is widely used. This method is based on assigning a higher weight to harder-to-learn samples (samples in the overlapping region) using k-NN.

Clustering-based methods are common practice across different domains [33] and widely used for undersampling data. A clustering method such as k-means or fuzzy C-means (FC-means) [34] is applied to cluster the majority class instances into k clusters. Data are then sampled from each cluster aiming at having a smaller and yet representative sample. As a result, a more balanced dataset is obtained. Bunkhumpornpat et al. [35] proposed a majority class undersampling technique based on density-based spatial clustering algorithm (DBMUTE). DBMUTE was designed to eliminate negative instances from the overlapping region. Lin et al. [36] presented another clustering-based undersampling method where the negative instances were first clustered with the number of clusters set to equal the number of data points in the minority class. The undersampling was then carried out using cluster centers and clusters nearest neighbors, respectively. An experiment using 44 public datasets showed the competitive results.

Clustering-based methods were also used to handle minority classes in the dataset. For example, Yong et al. [37] used k-means to divide the minority class into smaller clusters, and genetic algorithm was then used to generate new samples based on those clusters. This technique, however, will not be applicable when the number of minority class instances is minimal. Similarly, Seoane Santos et al. [38] handled patients data by clustering the minority class instances and then rebalanced the data using SMOTE. Puntumapon et al. [39] proposed a new method called TRIM, as a preprocessing stage before applying oversampling methods such as SMOTE or one of its extensions. Lim et al. [40] implemented an evolutionary ensemble learning framework by clustering the minority class instances using mini-batch k-means and hierarchical agglomerative clustering before generating synthetic samples.

Overall, it can be said that undersampling minority class instances contributed to improving the results before applying oversampling; however, such methods require enough samples from the minority class instances before they can be applied. More recently, Generative Adversarial Neural Networks (GAns) have been applied successfully to handle class-imbalance, by synthesizing new samples of the minority class’s instances to handle the imbalance problem. A typical example was presented in [14, 41, 42] where a new data augmentation approach using variants of GANs to handle the class-imbalance problem was presented. Using image-based datasets, the methods showed favorable performance over other traditional sampling techniques.

3 Methods

The method presented in this paper is designed to first reduce the dominance of the majority class instances in the dataset by applying unsupervised learning algorithm to group it into subclasses. An oversampling technique is then used to improve the presence of the minority class instances in the dataset. Algorithm 1 provides a schematic overview of the proposed method, where for any dataset A, first, it is transformed into a decomposed dataset \(A_c\) (Sect. 3.1), followed by oversampling of the minority class instances (oversample) subject to reassessing the decomposed dataset \(A_c\) (Sect. 3.2). If oversampling is then applied, then a dataset \(A_{cm}\) is created which is a result of class decomposition and oversampling combined. Finally, a learning algorithm is applied to the resulting dataset dataset.

figure a

3.1 Class decomposition

Class decomposition is achieved by applying a clustering algorithm to a training set and aims at minimizing the bias-variance trade-off [43] by creating more local boundaries within the dataset. The method was presented by Vilalta et al. [44], where experiments using 20 datasets showed an improvement in performance in Naive Bayes and SVM. In [45], Polaka used hierarchical and k-means clustering to decompose the majority class instances and reported an improvement in RF performance. More recently in [7], Elyan and Gaber extended this approach by applying class decomposition to all classes in the dataset. The results showed significant improvement. The K value (number of clusters) was set experimentally in this work. Later on, the authors [46] showed that RF performance via decomposition could be optimized using genetic algorithm. More recently, CD was applied to a set of engineering symbols extracted from engineering drawings, and it proved that the performance of SVM, RF and convolutional neural networks (CNN) was improved significantly [15].

In this paper, we follow a similar approach to [7, 46] by applying k-means clustering algorithm to the majority class instances. By decomposing the majority class into k subclasses, we aim to achieve two goals. First, reduce the dominance of the majority class instances and also avoid the loss of information which often results from applying other undersampling methods. This is illustrated in Fig. 2.

Fig. 2
figure 2

Class decomposition applied to an imbalanced binary dataset

Full size image

Figure 2 (left) shows the original dataset with the minority class instances (P), while the right side shows the dataset after applying class decomposition, which resulted in the same dataset but with different subclasses (clusters) representing the majority class instances (N) as \(N\_C1, N\_C2, \ldots \). Notice that with such an approach, we transform the dataset into different distributions and at the same time preserve all information. Consider the binary classification task in Eq. 3, where we want to learn h(x) that maps each instance \(x_i\) to a class \(y_i \in \{C_N,C_P\}\).

$$\begin{aligned} h(X):X \rightarrow Y \end{aligned}$$
(3)

Notice that in a classification task such as in Eq. 5, we aim to minimize the number of misclassification as shown in Eq. 4

$$\begin{aligned} \min \left( \sum _{i=1}^{m} (y_{i} \ne {\hat{y}}_{i})\right) \end{aligned}$$
(4)

where \(y_i\) is the actual class label, \({\hat{y}}_{i}\) is the predicted class label and m is the number of instances in the dataset. When we apply class decomposition to the dataset X in Eq. 3, we get a new classification task (Eq. 5).

$$\begin{aligned} h^{\prime }(X):X \rightarrow Y^{\prime } \end{aligned}$$
(5)

Here, we want to learn a function \(h^{\prime }(x)\) that maps each instance \(x_i\) to the corresponding label \(y^{\prime }_i \in \{C_{N1},C_{N2},\ldots C_{NK},C_P\}\), where K denotes the number of clusters. Notice that with such approach, we transform a binary classification problem into a multiclass classification problem. Here, transforming the data will not only reduce the dominance of the negative class \(C_N\) by clustering it into K subclasses, but will also allow training of the learning algorithm at a fine-grained level. The same objective function in Eq. 4 holds but with a minor change, such that each prediction is considered correct as far as it is within the main class of labels. In other words for any negative instance \(x_i \rightarrow C_N\), a predicted label \({\hat{y}}_i\) is considered correct, if and only if \({\hat{y}}_i \in \{C_{N1},C_{N2},\ldots C_{NK}\}\).

3.2 Minority class oversampling

Applying CD to a dataset will result in different data distribution. In other words, new minority/majority-class instances may appear (from within the clusters of the majority class instances). So, first, we check whether the number of samples in the minority class is close to the average number of samples of the majority subclasses. For instance, in Fig. 2, it is shown that the minority class is below the average number of samples of the five subclasses after class decomposition. (The horizontal line represents the average in red color in Fig. 2.) In this case, an oversampling is applied to the minority class. To oversample, we chose SMOTE [28] due to its efficiency and popularity as one of the most common oversampling methods. SMOTE requires two classes as input (a minority and a majority) to perform the oversampling of the minority class using the majority class samples as a reference for the synthetic sample generation. In this paper, we use the majority subclass with the number of samples closest to the mean as the majority class input to SMOTE. In Fig. 2, this would be \(N\_C3\). In cases where a tie takes place (i.e., more than one majority class to chose), one is selected at random. It has to be noted that these simple heuristics were chosen empirically when implementing CDSMOTE to handle class-imbalance classification. In other words, it was found that oversampling the minority class when it falls below the average number of subclasses yields better results overall.

4 Experiments

A large-scale experiment has been carried out aiming at comparing CDSMOTE with other common undersampling methods for handling class-imbalance data classification. In this experiment, CDSMOTE is compared against SMOTE [28] and ADASYN [32]. These were chosen as they are among the most common undersampling methods in the literature. Moreover, CDSMOTE is compared against class decomposition [7] and with recent and state-of-the-art methods including [36, 47, 48]. The following subsections describe the experiment in details.

4.1 Datasets

A collection of 60 datasets was used in this experiment, and these are publicly available and commonly used in class-imbalance data classification (i.e., [36, 47, 48], ...). The datasets were obtained from the KEEL repository.Footnote 1 As can be seen in Table 1, these datasets are binary classification datasets with different imbalance ratios, different numbers of instances and a varied number of features.

Table 1 Datasets
Full size table

4.2 Settings and implementation details

All datasets were partitioned into training and testing sets with a ratio of 80%, 20%, respectively, and fivefold cross-validation training. In all experiments, SVM with linear kernel was used as the learning algorithm. Other learning algorithms could have been considered, for example RF which showed the favorable results over other state-of-the-art methods [49] such as boosting and SVM. However, RF had shown already the favorable results concerning accuracy when class-decomposition was applied to the dataset as discussed in [7, 46]. In this work, we have chosen SVM with a linear kernel and default settings to establish the impact of class decomposition on class-imbalanced dataset classification.

Table 2 shows that each dataset was processed using SMOTE, ADASYN, CD, CDSMOTE and finally the baseline where no undersampling or oversampling. Regarding SMOTE and ADASYN, the number of nearest neighbors was set to equal 4 (\(k=4\)), and for class decomposition, we used k-means with \(k=2\). It is worth pointing out that we held these parameters fixed throughout, and no-parameter tuning was carried out to ensure a fair comparison between methods and to assess the impact of CDSMOTE on learning from imbalanced datasets using the three different evaluation metrics. First, we evaluate the results using Area Under the Curve (AUC) of the receiving operating characteristic (ROC) curve, which is a plot of the sensitivity or true positive rate (TPR) as a function of the false positive rate (FPR). The second evaluation metric we used is geometric mean (Gmean), which measures the balance between the TPR and the true negative rate (TNR) and is defined as \(\sqrt{\mathrm{TPR} \times \mathrm{TNR}}\). Finally, we used \(F_1\) Score between the TPR and the FPR [35] and is defined as \(F_1\) Score = \(\beta \times \frac{\mathrm{TPR} \times \mathrm{FPR}}{\mathrm{TPR} + \mathrm{FPR}}\), with \(\beta \) value = 2.

The experiments were implemented using Python 3.6 and were carried out on a Windows 10 machine with 16 GB RAM and a 2.7 GHz processor.

Table 2 CDSMOTE outperforming SMOTE, ADASYN and CD
Full size table

4.3 Results

As can be seen in Table 2, CDSMOTE outperformed all methods across one or more evaluation metric in 39 datasets. Moreover, it was observed that across the 60 datasets, CDSMOTE outperformed at least one method in one or more comparison. The comparison against CD was made to establish the need for applying oversampling after reducing the dominance of the majority class instances.

A closer look at Table 2, and comparing the performance of CDSMOTE against all other methods using Gmean, \(F_1\) Score and AUC, we can see an improvement gained by applying CDSMOTE. Statistical significance of the results was measured using the paired t test. With 95% confidence, the p-values for paired t-tests between CDSMOTE and all other methods across the three evaluation metrics are shown in Table 3, which clearly show a statistically significant improvement in performance using CDSMOTE.

Table 3 CDSMOTE versus other methods using Gmean, \(F_1\) score and AUC (t test)
Full size table

It was also observed from the results that the best improvement across the three evaluation metrics was achieved using \(F_1\) Score. This suggests that CDSMOTE improves the presence of the minority-class instances and reduces the dominance of the majority-class cases. The results show also that CDSMOTE did not lose in any dataset against the three different methods (ADASYN, SMOTE and CD) combined. It was, however, observed that a similar performance (tie) was recorded in six different datasets and across the three evaluation metrics. These include Iris0, New-thyroid1, New-thyroid2, Shuttle0_vs_4, Shuttle2_vs_4 and Dermatology6. These are the datasets where 100% accuracy was recorded (i.e., \(F_1\) Score = 1).

For further evaluation, we compared our method with recent state-of-the-art techniques using the most recent results and reported the same experiment settings and datasets. First, we consider Cleofas-Sanchez et al. [47], who attempted class-imbalance classification using 31 of the datasets through a hybrid associative classifier with translation (HACT) based on SMOTE and used Gmean for evaluating the results. Table 4 lists the performance of CDSMOTE against this method. Then, we considered Lin et al. [36] who presented a clustering-based undersampling method on 44 datasets and reported performance using AUC. An Ensemble Adaboost C4.5 classifier was used for classification. The results in comparison with CDSMOTE is shown in Table 5. Finally, Zhu et al. [48] used 31 of the datasets used in this paper, and the authors adopted an algorithmic-based approach by designing their own classifier: Boundary-Eliminated Pseudoinverse Linear Discriminant (BEPILD). Table 6 compares CDSMOTE performance against BEPILD using the two metrics reported by the authors (AUC and Gmean).

Table 4 compares CDSMOTE with [47] in terms of Gmean. Notice that CDSMOTE obtains the better results in 20 out of 31 datasets. Using a paired t test on the 20 datasets where CDSMOTE wins shows a statistically significant difference with p value equal to 0.000506.

Table 4 CDSMOTE against SMOTE+HACT [47] using Gmean
Full size table

Table 5 compares CDSMOTE and [36] across AUC, where it is shown that CDSMOTE outperformed [36] in 37 out of 44 datasets. A paired t test shows significant statistical improvement with a p value of \(2.633 \times 10^{-7}\).

Table 5 CDSMOTE against Clust+\(C4.5_{Ab}\) [36] using AUC
Full size table

Table 6 shows the comparison of CDSMOTE against the BEPILD method presented in [48] for Gmean and AUC. In terms of Gmean, CDSMOTE obtains the better results in 13 out of 31 datasets. The difference in performance in these datasets is not statistically significant (using t test resulted in a p value = 0.0695); however, for some application domains, such as health, life science and security, such improvement in performance could be crucial. Considering only the 13 winning datasets in Table 6, we found out a statistically significant improvement using CDSMOTE using a paired t test resulting in a p value of 0.006054. When measuring performance using AUC Table 6, our proposed method proved to be superior across almost all datasets. Out of 31 datasets, CDSMOTE outperformed BEPILD in 30 datasets. Using a t test, a p value of \(2.821 \times 10^{-10}\) was obtained.

Table 6 CDSMOTE against BEPILD [48] using Gmean and AUC
Full size table

4.4 Discussion

To summarize, out of 60 datasets, CDSMOTE proved to be superior to the most common and established methods used in handling class-imbalanced datasets classification. These methods include SMOTE [28] and ADASYN [32] and CD [46]. The improvement across three common evaluation metrics (Gmean, \(F_1\) Score and AUC) was statistically significant as shown in Tables 3. These results suggest that applying class decomposition to a majority class instances in a binary dataset does not only reduce the dominance of the majority class but also such decomposition provides a more linearly separable space within the local class boundaries.

The proposed method also showed superior performance over recent and state-of-the-art methods presented in the literature such as Cleofas-Sanchez et al. [36, 47], and [48], as can be seen in Tables 4, 5 and 6. An improvement over these methods was statistically significant. The results also showed that the best trade-off between AUC and Gmean, the two classically used metrics for imbalanced datasets, was obtained by CDSMOTE. Overall, the proposed method obtains the better results in terms of AUC than other methods. CDSMOTE maximizes the \(F_1\) Score results, meaning that it effectively offers the best trade-off between the precision and recall for the minority class. Therefore, CDSMOTE can provide an alternative to handle the class-imbalance problem in specific scenarios. It has to be pointed out that there is a large room for improving these results. This includes hyper-parameters tuning and optimization (optimize the k value), further experiments with different learning algorithms (i.e., ensemble-based methods), using alternative clustering methods (i.e., soft clustering techniques, density-based and others) or using different oversampling methods such as GANs.

5 Conclusions and future work

In this paper, we have presented a new approach for handling class-imbalance problem by means of class decomposition. Unlike most common undersampling methods, our method suffers no data loss and preserves all majority class instances. A large-scale experiment showed that CDSMOTE produces the comparable results with state-of-the-art methods, while significantly outperforming some of the most established methods across metrics such as AUC, Gmean and \(F_1\) Score. The number of datasets used in this experiment with different sizes, dimensions and imbalance ratios suggests that the proposed methods can generalize and scalable across larger and more diverse datasets. It has to be noted that these results were obtained using default parameters settings and with one classifier, namely SVM with a linear kernel, meaning that further improvement can be made at the data level as well as the algorithmic level. At the data level, the method presented in this paper can benefit from better clustering and grouping of the majority class instances. This might include isolating the instances within the overlapping region. At the algorithmic level, we intend to examine other learning algorithms, in particular, ensemble-based classification methods such as RF, which has proved to outperform other learning methods. Also, the use of other clustering methods can be explored for further improvement in the results. This might include considering density-based clustering methods instead of using k-means, which is often sensitive to noise. Finally, the results can be further improved by applying some parameter tuning techniques, to ensure that the best parameter setting is chosen.