Skip to main content
SpringerLink
Log in

Modeling and optimization of a reliable blood supply chain network in crisis considering blood compatibility using MOGWO

  • Real-world Optimization Problems and Meta-heuristics
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

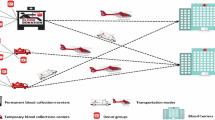
Due to the prominent role of blood in human life, designing an efficient blood supply chain in case of an emergency situation is essential especially considering blood compatibility. This research proposes a multi-objective model for emergency blood supply chain management considering blood compatibility, routing, and location–allocation decisions. The blood supply chain network consists of donors, collection facilities, laboratories, blood centers, and hospitals. The mathematical model aims to minimize total supply chain cost and time while maximizing minimum reliability of established routes by making decisions regarding location–allocation, blood flow, inventory levels, and optimal routes. In order to solve the problem, a novel algorithm called Multi-Objective Grey Wolf Optimizer is used and compared to two classical algorithms Multi-Objective Particle Swarm Optimization and Non-dominated Sorting Genetic Algorithm-II. Performance of the algorithms is evaluated in various test problems using powerful measures. Also, the application of the proposed model is investigated in a case study in Iran’s capital, Tehran. Based on the results, important managerial insights are derived and optimal locations for facilities, inventory levels, routes and blood flow between facilities are determined.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Arqub OA, Abo-Hammour Z (2014) Numerical solution of systems of second-order boundary value problems using continuous genetic algorithm. Inf Sci 279:396–415

    MathSciNet  MATH  Google Scholar 

  2. Arqub OA, Mohammed AS, Momani S, Hayat T (2016) Numerical solutions of fuzzy differential equations using reproducing kernel Hilbert space method. Soft Comput 20(8):3283–3302

    MATH  Google Scholar 

  3. Arqub OA, Al-Smadi M, Momani S, Hayat T (2017) Application of reproducing kernel algorithm for solving second-order, two-point fuzzy boundary value problems. Soft Comput 21(23):7191–7206

    MATH  Google Scholar 

  4. Arqub OA (2017) Adaptation of reproducing kernel algorithm for solving fuzzy Fredholm-Volterra integrodifferential equations. Neural Comput Appl 28(7):1591–1610

    Google Scholar 

  5. Arvan M, Tavakkoli-Moghaddam R, Abdollahi M (2015) Designing a bi-objective and multi-product supply chain network for the supply of blood. Uncertain Supply Chain Manag 3(1):57–68

    Google Scholar 

  6. Bakeshlu EA, Sadeghi J, Poorbagheri T, Taghizadeh M (2014) Optimizing a bi-objective inventory model for a two-echelon supply chain management using a tuned meta-heuristic algorithm. Prod Manuf Res 2(1):156–166

    Google Scholar 

  7. Fahimnia B, Jabbarzadeh A, Ghavamifar A, Bell M (2017) Supply chain design for efficient and effective blood supply in disasters. Int J Prod Econ 183:700–709

    Google Scholar 

  8. Fazli-Khalaf M, Khalilpourazari S, Mohammadi M (2017) Mixed robust possibilistic flexible chance constraint optimization model for emergency blood supply chain network design. Ann Oper Res 259:1–31

    MathSciNet  Google Scholar 

  9. Habibi-Kouchaksaraei M, Paydar MM, Asadi-Gangraj E (2018) Designing a bi-objective multi-echelon robust blood supply chain in a disaster. Appl Math Model 55:583–599

    MathSciNet  MATH  Google Scholar 

  10. Hamza F, Abderazek H, Lakhdar S, Ferhat D, Yıldız AR (2018) Optimum design of cam-roller follower mechanism using a new evolutionary algorithm. Int J Adv Manuf Technol 99(5–8):1267–1282

    Google Scholar 

  11. Jabbarzadeh A, Fahimnia B, Seuring S (2014) Dynamic supply chain network design for the supply of blood in disasters: a robust model with real world application. Transp Res Part E Logist Transp Rev 70:225–244

    Google Scholar 

  12. Kaasgari MA, Imani DM, Mahmoodjanloo M (2017) Optimizing a vendor managed inventory (VMI) supply chain for perishable products by considering discount: Two calibrated meta-heuristic algorithms. Comput Ind Eng 103:227–241

    Google Scholar 

  13. Karagöz S, Yıldız AR (2017) A comparison of recent metaheuristic algorithms for crashworthiness optimisation of vehicle thin-walled tubes considering sheet metal forming effects. Int J Veh Des 73(1–3):179–188

    Google Scholar 

  14. Khalilpourazari S, Khamseh AA (2017) Bi-objective emergency blood supply chain network design in earthquake considering earthquake magnitude: a comprehensive study with real world application. Ann Oper Res 255:1–39

    MathSciNet  Google Scholar 

  15. Khalilpourazari S, Khalilpourazary S (2018) Optimization of production time in the multi-pass milling process via a Robust Grey Wolf Optimizer. Neural Comput Appl 29(12):1321–1336

    Google Scholar 

  16. Khalilpourazari S, Pasandideh SHR (2018) Multi-objective optimization of multi-item EOQ model with partial backordering and defective batches and stochastic constraints using MOWCA and MOGWO. Oper Res 262:1–33

    Google Scholar 

  17. Khalilpourazari S, Pasandideh SHR, Niaki STA (2016) Optimization of multi-product economic production quantity model with partial backordering and physical constraints: SQP, SFS, SA, and WCA. Appl Soft Comput 49:770–791

    Google Scholar 

  18. Khalilpourazari S, Pasandideh SHR (2017) Multi-item EOQ model with nonlinear unit holding cost and partial backordering: moth-flame optimization algorithm. J Ind Prod Eng 34(1):42–51

    Google Scholar 

  19. Khalilpourazari S, Khalilpourazary S (2019) An efficient hybrid algorithm based on Water Cycle and Moth-Flame Optimization algorithms for solving numerical and constrained engineering optimization problems. Soft Comput 22:1699–1722

    Google Scholar 

  20. Khalilpourazari S, Khalilpourazary S (2018) A Robust Stochastic Fractal Search approach for optimization of the surface grinding process. Swarm Evolut Comput 38:173–186

    Google Scholar 

  21. Khalilpourazari S, Pasandideh SHR (2016) Bi-objective optimization of multi-product EPQ model with backorders, rework process and random defective rate. In: 2016 12th international conference on industrial engineering (ICIE). IEEE, pp 36–40

  22. Khalilpourazari S, Khalilpourazary S (2017) A lexicographic weighted Tchebycheff approach for multi-constrained multi-objective optimization of the surface grinding process. Eng Optim 49(5):878–895

    MathSciNet  Google Scholar 

  23. Khalilpourazari S, Pasandideh SHR, Ghodratnama A (2018) Robust possibilistic programming for multi-item EOQ model with defective supply batches: Whale Optimization and Water Cycle Algorithms. Neural Comput Appl 30:1–28

    Google Scholar 

  24. Khalilpourazari S, Khalilpourazary S (2018) SCWOA: an efficient hybrid algorithm for parameter optimization of multi-pass milling process. J Ind Prod Eng 35(3):135–147

    Google Scholar 

  25. Khalilpourazari S, Khalilpourazary S (2018) Optimization of time, cost and surface roughness in grinding process using a robust multi-objective dragonfly algorithm. Neural Comput Appl 30:1–12

    Google Scholar 

  26. Khalilpourazari S, Pasandideh SHR (2019) Modeling and optimization of multi-item multi-constrained EOQ model for growing items. Knowl Based Syst 164:150–162

    Google Scholar 

  27. Khalilpourazari S, Pasandideh SHR, Niaki STA (2019) Optimizing a multi-item economic order quantity problem with imperfect items, inspection errors, and backorders. Soft Comput 23:1–28

    Google Scholar 

  28. Kohneh JN, Teymoury E, Pishvaee MS (2016) Blood products supply chain design considering disaster circumstances (Case study: earthquake disaster in Tehran). J Ind Syst Eng 9:51–72

    Google Scholar 

  29. Mirjalili S, Mirjalili SM, Lewis A (2014) Grey wolf optimizer. Adv Eng Softw 69:46–61

    Google Scholar 

  30. Mirjalili S, Saremi S, Mirjalili SM, Coelho LDS (2016) Multi-objective grey wolf optimizer: a novel algorithm for multi-criterion optimization. Expert Syst Appl 47:106–119

    Google Scholar 

  31. Mirjalili S (2016) Dragonfly algorithm: a new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput Appl 27(4):1053–1073

    Google Scholar 

  32. Mirjalili S, Jangir P, Saremi S (2017) Multi-objective ant lion optimizer: a multi-objective optimization algorithm for solving engineering problems. Appl Intell 46(1):79–95

    Google Scholar 

  33. Mirjalili SZ, Mirjalili S, Saremi S, Faris H, Aljarah I (2018) Grasshopper optimization algorithm for multi-objective optimization problems. Appl Intell 48(4):805–820

    Google Scholar 

  34. Mohammadi M, Khalilpourazari S (2017) Minimizing makespan in a single machine scheduling problem with deteriorating jobs and learning effects. In Proceedings of the 6th international conference on software and computer applications. ACM, pp 310–315

  35. Nagurney A, Masoumi AH, Yu M (2012) Supply chain network operations management of a blood banking system with cost and risk minimization. CMS 9(2):205–231

    MathSciNet  MATH  Google Scholar 

  36. Nia AR, Far MH, Niaki STA (2014) A fuzzy vendor managed inventory of multi-item economic order quantity model under shortage: an ant colony optimization algorithm. Int J Prod Econ 155:259–271

    Google Scholar 

  37. Pasandideh SHR, Khalilpourazari S (2018). Sine Cosine Crow Search Algorithm: a powerful hybrid meta heuristic for global optimization. arXiv preprint arXiv:1801.08485

  38. Patel VK, Savsani VJ (2016) A multi-objective improved teaching–learning based optimization algorithm (MO-ITLBO). Inf Sci 357:182–200

    Google Scholar 

  39. Pholdee N, Bureerat S, Yıldız AR (2017) Hybrid real-code population-based incremental learning and differential evolution for many-objective optimisation of an automotive floor-frame. Int J Veh Des 73(1–3):20–53

    Google Scholar 

  40. Rahmani D (2018) Designing a robust and dynamic network for the emergency blood supply chain with the risk of disruptions. Ann Oper Res 266:1–29

    MathSciNet  Google Scholar 

  41. Ramezanian R, Behboodi Z (2017) Blood supply chain network design under uncertainties in supply and demand considering social aspects. Transp Res Part E Logist Transp Rev 104:69–82

    Google Scholar 

  42. Sadeghi J, Mousavi SM, Niaki STA, Sadeghi S (2013) Optimizing a multi-vendor multi-retailer vendor managed inventory problem: two tuned meta-heuristic algorithms. Knowl Based Syst 50:159–170

    Google Scholar 

  43. Şahin G, Süral H, Meral S (2007) Locational analysis for regionalization of Turkish Red Crescent blood services. Comput Oper Res 34(3):692–704

    MATH  Google Scholar 

  44. Salehi F, Mahootchi M, Husseini SMM (2017) Developing a robust stochastic model for designing a blood supply chain network in a crisis: a possible earthquake in Tehran. Ann Oper Res 252:1–25

    MathSciNet  Google Scholar 

  45. Sha Y, Huang J (2012) The multi-period location-allocation problem of engineering emergency blood supply systems. Syst Eng Procedia 5:21–28

    Google Scholar 

  46. Yıldız BS, Yıldız AR (2018) Comparison of grey wolf, whale, water cycle, ant lion and sine-cosine algorithms for the optimization of a vehicle engine connecting rod. Mater Test 60(3):311–315

    Google Scholar 

  47. Yıldız BS, Yıldız AR (2017) Moth-flame optimization algorithm to determine optimal machining parameters in manufacturing processes. Mater Test 59(5):425–429

    Google Scholar 

  48. Yildiz AR, Solanki KN (2012) Multi-objective optimization of vehicle crashworthiness using a new particle swarm based approach. Int J Adv Manuf Technol 59(1–4):367–376

    Google Scholar 

  49. Yıldız AR, Kurtuluş E, Demirci E, Yıldız BS, Karagöz S (2016) Optimization of thin-wall structures using hybrid gravitational search and Nelder-Mead algorithm. Mater Test 58(1):75–78

    Google Scholar 

  50. Yildiz AR (2013) A new hybrid artificial bee colony algorithm for robust optimal design and manufacturing. Appl Soft Comput 13(5):2906–2912

    Google Scholar 

  51. Yıldız BS (2017) A comparative investigation of eight recent population-based optimisation algorithms for mechanical and structural design problems. Int J Veh Des 73(1–3):208–218

    Google Scholar 

  52. Zahiri B, Pishvaee MS (2017) Blood supply chain network design considering blood group compatibility under uncertainty. Int J Prod Res 55(7):2013–2033

    Google Scholar 

  53. Zahiri B, Torabi SA, Mohammadi M, Aghabegloo M (2018) A multi-stage stochastic programming approach for blood supply chain planning. Comput Ind Eng 122:1–14

    Google Scholar 

  54. Zitzler E, Thiele L (1999) Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach. IEEE Trans Evol Comput 3(4):257–271

    Google Scholar 

  55. Zitzler E, Thiele L (1998) Multiobjective optimization using evolutionary algorithms—a comparative case study. In: International conference on parallel problem solving from nature. Springer, Berlin, pp 292–301

Download references

Author information

Authors and Affiliations

  1. Department of Industrial Engineering, Faculty of Engineering, Payame Noor University, Tehran, Iran

    Seyed Behzad Ghorashi, Maryam Hamedi & Ramin Sadeghian

Authors
  1. Seyed Behzad Ghorashi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Maryam Hamedi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ramin Sadeghian
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Maryam Hamedi.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

The city is located on 13 active faults. In recent year, many mid-magnitude earthquakes have occurred around the city which is warning to IBTO and related organizations to prepare for an emergency situation after a destructive earthquake. Note that based on recent researches, it is revealed that every 150 years a high-magnitude earthquake is expected in the city; however, it is 200 years that such event has not occurred around the city.

The city has 22 districts, for each district, the geographical coordination of each donor group is presented in Table 14.

Table 14 Geographical coordinates of donor groups
Full size table

For each donor groups, maximum blood supply of all blood types is approximated based on 13% deferral rate which is shown in Table 15 [11, 14, 44].

Table 15 Blood supply of donor groups from each blood type [44]
Full size table

A schematic view of the location of donors is provided in Fig. 12.

Fig. 12
figure 12

Location of the donor groups. [14]

Full size image

Each district is considered as a potential location for the establishment of a permanent or temporary blood collection center. Establishment cost of permanent blood collection center is considered to be $1518.23. Also, operational costs related to the collection of blood from donors is considered to be $0.069 per donated blood. Cost of moving temporary blood collection centers between sites is presented in Table 16.

Table 16 Cost of moving a temporary blood collection facility between sites ($) [14].]
Full size table

The capacity of permanent and mobile blood collection facilities are considered to be 300 and 100 donated blood units, respectively. In addition, the coverage radius of the blood collection centers is considered as 12 km. Table 17 presents geographical coordination of laboratories and blood centers. Note that these data are obtained using Google Earth software. To calculate the distances, the following formula is used which is presented by Khalilpourazari and Khamseh [14] as follows.

$$r_{ij} = {\text{Arccos}}\left( {\sin \left( {{\text{Lat}}_{i} } \right) \times \sin \left( {{\text{Lat}}_{j} } \right) + \cos \left( {{\text{Lat}}_{i} } \right) \times \cos \left( {{\text{Lat}}_{j} } \right) \times { \cos }\left( {{\text{Long}}_{j} - {\text{Long}}_{i} } \right)} \right) \times 6371.1$$
(38)

where 6371.1 is the earth’s radius and latitude and longitude are the geographic coordinates of the facilities multiplied by \(\pi /180\).

Table 17 Geographical coordinates of laboratories, blood centers, and hospitals
Full size table

Cost of transportation of each blood unit from collection centers to laboratories is presented in Table 18.

Table 18 Transportation cost of unit donated blood from blood collection centers to laboratories [8]
Full size table

Also, transportation costs from laboratories to blood centers and from blood centers to hospitals are reported in Tables 19, 20 and 21.

Table 19 Transportation cost from laboratories to blood centers [8]
Full size table
Table 20 Transportation cost from blood centers to hospitals
Full size table
Table 21 Transportation cost between hospitals
Full size table

Blood demand at hospitals is approximated based on real data provided by Salehi et al. [44]. Table 22 presents the demand for each hospital at each period.

Table 22 Blood demand in hospitals from each blood type at the first and second periods
Full size table

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ghorashi, S.B., Hamedi, M. & Sadeghian, R. Modeling and optimization of a reliable blood supply chain network in crisis considering blood compatibility using MOGWO. Neural Comput & Applic 32, 12173–12200 (2020). https://doi.org/10.1007/s00521-019-04343-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-019-04343-1

Keywords

Search

Navigation