Heat and mass transport phenomena of nanoparticles on time-dependent flow of Williamson fluid towards heated surface

Abstract

An enhancement in the thermal conductivity of conventional base fluids has been a topic of great concern in recent years. An effective way to improve the heat transfer rate of conventional base fluids is the suspension of solid nanoparticles. In this framework, a theoretical study is performed to analyse the heat and mass transfer performance in the time-dependent flow of non-Newtonian Williamson nanofluid towards a stretching surface. There exist several studies focusing on the flow of Williamson fluid by assuming zero infinite shear rate viscosity. Nonetheless, there is a lack of knowledge regarding mathematical formulation for two-dimensional flow of the Williamson fluid by taking into account the impacts of infinite shear rate viscosity. In the current review, the Buongiorno model for nanofluids associated with Brownian motion and thermophoretic diffusion is employed to describe the heat transfer performance of nanofluids. The thermal system is composed of flow velocity, temperature, and nanoparticles concentration fields, respectively. The governing dimensionless equations are solved numerically by Runge–Kutta Fehlberg integration method. The numerical results are compared with published results and are found to have an excellent agreement. Effects of numerous dimensionless parameters on velocity, temperature, and nanoparticle concentration field together with the skin friction coefficient and rates of heat and mass transfer are presented with the assistance of graphical and tabular illustrations. With this analysis, we reached that the thermal boundary layer thickness as well as the nanofluids temperature has higher values with increase in thermophoresis and Brownian motion. It is further observed that the rate of heat transfer is significantly raised with an increment in Prandtl number and unsteadiness parameter.

1 Introduction

At present, the world is confronting a noteworthy problem of low heat transfer rate of base fluids, which limits the effectiveness of heat transfer performance in heat exchangers. The most regular working liquids are water, ethanol and ethylene–glycol blend. To cope up this problem, recently, engineers and scientists have shown their great concern in improving the thermal properties of energy transmission fluids and their heat transfer performance for industrial applications. This innovation aims at enhancing the thermal conductivities and the convective heat transfer of fluids through suspensions of ultrafine nanoparticles in the base fluids. This mixture is known as “nanofluid,” which was first employed by Choi [1]. Nanofluids are the fluids that possess 100 nm or less size of nanoparticles such as metals, oxides and nitrides together with usual base fluids like water, engine oil and toluene. Considering higher thermal conductivity of nanoparticles contrasted with base liquids, nanofluids have tremendous applications in almost every field of science, technology and biomedicine, viz. better coolants in PCs and nuclear reactors, cancer therapy, wire drawing and quenching in metal foundries, lubricants, heat exchangers. It is experimentally verified that the nanoparticles may be of the shape like spherical, rod-like, tubular. It was an amusing start by Choi [1] to ponder experimentally and uncover to the society about the improvement in thermal conductivity of liquids with nanoparticle. In this work, he utilized the nanoparticles for the first time to improve the thermal conductivity of working fluids. He explained numerous experimental and numerical studies in the literature to know how the thermal conductivity is improved.

Many engineering and technological applications of nanofluids have motivated and encouraged many researchers in early decades of twentieth century to investigate the several aspects of flow and heat transfer of nanofluids over various surfaces. In 1993, Masuda et al. [2] presented the work to enhance the thermal conductivity of fluid particles. Later on, Eastman et al. [3] have exposed that the thermal conductivity-improved ethylene glycol-based nanofluid has raised up to 60% when CuO nanoparticles of volume fraction 5% are added to base fluid. The most important and widely used mechanisms in industrial applications are the thermophoresis and Brownian movement phenomena. Therefore, Buongiorno [4] exhibited that the homogeneous models tend to predict the nanofluid heat transfer coefficient, while the distribution impact is totally negligible because of the nanoparticle size. Thus, Buongiorno developed an alternative model to clarify the unusual convective heat transfer improvement in nanofluids and thus wipe out the weaknesses of the homogeneous and dispersion models. On the basics of his findings, he proposed a two-component four-equation non-homogeneous equilibrium model for convective transport in nanofluids. The effects of heat transfer on the flow of nanofluids in a two-sided lid-driven heated square cavity have been scrutinized by Tiwari and Das [5]. Experimental study [6] has described that the nanofluid requires 5% volumetric portion for a compelling warmth exchange upgrades. The Buongiorno’s model has been utilized by Kuznetsov and Nield [7] to investigate the effects of thermophoresis and Brownian movement on the natural convection flow in the presence of nanoparticles over a vertical plate. Khan and Pop [8] inspected the heat and mass transfer features in free convection flows of nanofluid over a porous stretched surface. Transient hydromagnetic rotating flow of a nanofluid with free convection was analysed by Hamad and Pop [9]. The three-dimensional flow of an electrically conducting nanofluid along with heat transfer in a rotating system has been examined by Sheikholeslami [10]. He utilized the well-known fourth-order Runge–Kutta numerical scheme to solve the governing problem. After that, loads of articles have been reported on improvement in heat transfer rate in flow of nanofluids over different geometries, like Dhanai et al. [11], Hashim and Khan [12], Aman et al. [13], Khan et al. [14] and Dogonchi and Ganji [15].

After reviewing the pertinent literature, we see that the existing literature does not provide enough scope to study the flow of non-Newtonian Williamson fluid along with heat and mass transfer in the presence of suspended nanoparticles. Considering such deficiency, the novelty of this work focuses on the following key factors:

• 1. Mathematical modelling for two-dimensional time-dependent flow of non-Newtonian Williamson fluid.

• 2. The impacts of nonzero infinite shear rate viscosity in constitutive relation of Williamson fluid are taken.

• 3. The influence of suspended nanoparticles on the thermal conductivity enhancement during the flow of Williamson fluid with heat transfer are studied in this article.

• 4. The numerical simulations of the governing equations for Williamson nanofluid flow have been conducted by employing the Runge–Kutta Fehlberg technique which has been proved for its accuracy over the years.

In view of above-stated points, a comprehensive analysis is presented to examine the time-dependent flow of Williamson nanofluids caused by a stretching surface. With the assistance of boundary layer approximations, the conservation equations for the two-dimensional flow of Williamson liquid have been modelled. Numerical simulations of the governing momentum and energy along with concentration equations are made via Runge–Kutta Fehlberg scheme along with shooting technique. Finally, the influence of diverse physical parameters such as unsteadiness parameter, ratio of viscosities, mass transfer parameter, Brownian motion parameter, thermophoresis parameter, Weissenberg number and Prandtl number on the flow, heat and mass transfer has been explored.

2 Modelling of the physical problem

2.1 Problem statement and governing equations

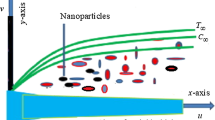
A time-dependent flow of incompressible Williamson fluid along with heat transfer characteristics in the presence of nanoparticles is examined. Besides, the present study focused on the mathematical modelling for two-dimensional boundary layer flow caused by a moving surface by including nonzero infinite shear rate viscosity. The schematic representation of the physical model is delineated in Fig. 1. The $x$-direction is taken along the stretching surface and $y$-direction normal to this axis. The motion of nanofluid extends to the region $y \ge 0$. We have incorporated Buongiorno model [4] in the current analysis because of unusual improvement of thermal conductivity of nanofluids that is due to the presence of two major velocity-slip effects, such as the Brownian motion and thermophoretic diffusion of nanoparticles. The value of temperature and nanoparticle concentration at the surface are $T_{w}$ and $C_{w}$ which are measured to be higher than that of ambient temperature and concentration $T_{\infty }$ and $C_{\infty }$, respectively.

Fig. 1

Schematic of the physical model

The governing equations for the flow regime by using Boussinesq approximations for the current problem are expressed as:

Mass:

$$\frac{{{\mathbf{\partial }}u}}{{{\mathbf{\partial }}x}} + \frac{{{\mathbf{\partial }}v}}{{{\mathbf{\partial }}y}} = 0,$$

(1)

Momentum:

$$\frac{\partial u}{\partial t} + u\frac{{{\mathbf{\partial }}u}}{{{\mathbf{\partial }}x}} + v\frac{{{\mathbf{\partial }}u}}{{{\mathbf{\partial }}y}} = \nu \frac{{\partial^{2} u}}{{\partial y^{2} }}\left[ {\beta^{ * } + (1 - \beta^{ * } )\left( {1 - \varGamma \frac{{{\mathbf{\partial }}u}}{{{\mathbf{\partial }}y}}} \right)^{ - 1} } \right]\quad + \nu \varGamma \left( {\frac{\partial u}{\partial y}} \right)\,\left( {\frac{{\partial^{2} u}}{{\partial y^{2} }}} \right)\left[ {\beta^{ * } + (1 - \beta^{ * } )\left( {1 - \varGamma \frac{{{\mathbf{\partial }}u}}{{{\mathbf{\partial }}y}}} \right)^{ - 2} } \right],$$

(2)

Energy:

$$\frac{\partial T}{\partial t} + u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha_{m} \frac{{\partial^{2} T}}{{\partial y^{2} }} + \tau \left[ {D_{B} \frac{\partial C}{\partial y}\frac{\partial T}{\partial y} + \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial y}} \right)^{2} } \right],$$

(3)

Nanoparticle concentration:

$$\frac{\partial C}{\partial t} + u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{B} \frac{{\partial^{2} C}}{{\partial y^{2} }} + \frac{{D_{T} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial y^{2} }}.$$

(4)

In Eqs. (1–4), $u$ and $v$ denote the velocity components in $x$- and $y$-directions, $\nu$ the kinematic viscosity, $\beta^{ * } = \tfrac{{\mu_{\infty } }}{{\mu_{0} }}$ the ratio of viscosities, $\varGamma$ the material parameter, $T$ the fluid temperature, $\;\alpha_{m} = \tfrac{k}{{\rho C_{p} }}$ the effective thermal diffusivity, $\tau = \left( {\rho c} \right)_{p} /\left( {\rho c} \right)_{f}$ the ratio of effective heat capacity of nanoparticles and effective heat capacity of the base fluid, $D_{\text{T}}$ the thermophoresis diffusion coefficient, $D_{\text{B}}$ the Brownian diffusion coefficient and $C$ the nanoparticle concentration.

2.2 Physical boundary conditions

The corresponding boundary conditions at the surface and far from the stretching surface are written below:

$$u = U_{w} (x,t),\quad v = 0,\quad T = T_{w} (x,t),\quad C = C_{w} (x,t)\quad {\text{at}}\;y = 0,$$

(5)

$$u \to 0, \, T \to T_{\infty ,} \, C \to C_{\infty } \, as \, y \to \infty .$$

(6)

The stretching velocity $U_{w} (x,t)$ of the surface in axial direction is taken as

$$U_{w} (x,\,t) = \frac{ax}{1 - ct},\, \,$$

(7)

where $a$ (stretching rate) and $c$ are positive constants with dimension $\left( {\text{time}} \right)^{ - 1}$ with $ct < 1,\;c \ge 0.$ Moreover, the stretching rate $\frac{a}{1 - ct}$ shows an increasing behaviour with time because $a > 0.$

In this study, we assume that both the temperature $T_{w} (x,\,t)$ and the nanoparticles concentration at the wall $C_{w} (x,\,t)$ vary along the sheet and with time, which are given by [16,17,18]

$$T_{w} (x,\,t) = T_{\infty } + T_{0} \left[ {\frac{{ax^{2} }}{2\nu }} \right](1 - ct)^{ - 3/2} ,\, \, C_{w} (x,\,t) = C_{\infty } + C_{0} \left[ {\frac{{ax^{2} }}{2\nu }} \right](1 - ct)^{ - 3/2} ,$$

(8)

where $T_{0}$ and $C_{0}$ are the positive reference temperature and nanoparticle concentration, respectively, such that $0 \le T_{0} \le T_{w}$ and $0 \le C_{0} \le C_{w} .$ It is important to note that the above Eq. $\left( 8 \right)$ is physically possible for time $t < c^{ - 1} .$

2.3 Non-dimensional problem

Let us introduce the following relations for $u,\;v$, $\theta$ and $\phi$ as

$$u = \tfrac{\partial \psi }{\partial y},\quad v = - \tfrac{\partial \psi }{\partial x},\quad and\quad \theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\quad \phi (\eta ) = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }},$$

(9)

in which $\psi$ is the Stokes stream function. Therefore, the governing Eqs. (1–4) are transformed into non-dimensional ones by defining the following variables:

$$\begin{aligned} \eta & = y\sqrt {\frac{a}{{\nu \left( {1 - ct} \right)}}} ,\quad \psi (x,y,t) = \sqrt {\frac{a\nu }{{\left( {1 - ct} \right)}}} xf(\eta ), \\ T & = T_{\infty } + T_{0} \left[ {\frac{{ax^{2} }}{2\nu }} \right](1 - ct)^{ - 3/2} \theta \left( \eta \right), \, C = C_{\infty } + C_{0} \left[ {\frac{{ax^{2} }}{2\nu }} \right](1 - ct)^{ - 3/2} \phi \left( \eta \right). \\ \end{aligned}$$

(10)

In the light of above non-dimensional transformations, the governing equations reduced to the subsequent nonlinear system

$$\left[ {\beta^{ * } + (1 - \beta^{ * } )\left( {1 - Wef^{\prime\prime}} \right)^{ - 2} } \right]\,f^{\prime\prime\prime} + ff^{\prime\prime} - (f^{\prime})^{2} - A\left[ {f^{\prime} + \frac{\eta }{2}f^{\prime\prime}} \right] = 0,$$

(11)

$$\theta^{\prime\prime} + \mathop {\Pr }\limits \left( {f\theta^{\prime} - 2f^{\prime}\theta } \right) - \mathop {\Pr }\limits A\left( {\frac{\eta }{2}\theta^{\prime} + \frac{3}{2}\theta } \right) + \mathop {\Pr }\limits Nb\theta^{{^{\prime } }} \varphi^{{^{\prime } }} + \mathop {\Pr }\limits Nt\left( {\theta^{{^{\prime } }} } \right)^{2} = 0,$$

(12)

$$\varphi^{\prime\prime} + \mathop {Le }\limits \left( {f\varphi^{\prime} - 2f^{\prime}\varphi } \right) - \mathop ALe\left( {\frac{\eta }{2}\varphi^{\prime} + \frac{3}{2}\varphi } \right) + \frac{Nt}{Nb}\theta^{{^{\prime \prime } }} = 0.$$

(13)

Also, the non-dimensional boundary conditions are

$$f(0) = 0,\,\;\;\;\;\;\;f^{\prime}(0) = 1,\,\;\;\;\;\;\;\theta (0) = 1,\, \, \varphi (0) = 1,$$

(14)

$$f^{\prime}(\infty ) \to 0,\, \, \theta (\infty ) \to 0,\, \, \varphi (\infty ) \to 0,$$

(15)

where primes indicate differentiation with respect to $\eta$.

In above equations, the dimensionless physical emerging variables are: the local Weissenberg number, the Prandtl number, the unsteadiness parameter, the viscosity ratio parameter, the thermophoresis parameter, the Brownian motion parameter and Lewis number. These are defined as:

$$\begin{array}{*{20}l} {We = \sqrt {\frac{{a^{3} \varGamma^{2} x^{2} }}{{\nu (1 - ct)^{3} }}} ,\quad \mathop {\Pr }\limits = \frac{\nu }{\alpha_{m} },\quad A = \frac{c}{a},\;\beta^{ * } = \tfrac{{\mu_{\infty } }}{{\mu_{0} }},} \hfill \\ {Le = \frac{\nu }{{D_{B} }},\quad Nt = \frac{{\tau D_{T} \left( {T_{w} - T_{\infty } } \right)}}{{\nu T_{\infty } }},\quad Nb = \frac{{\tau D_{B} \left( {C_{w} - C_{\infty } } \right)}}{\nu }.} \hfill \\ \end{array}$$

2.4 Engineering coefficients

The other important feature of this study from practical point of view is to evaluate the skin friction, Nusselt number and Sherwood number along the stretching wall. Therefore, the equations for the surface drag force, heat and mass transfer rates are given by:

$$C_{fx} = \frac{{\tau_{w} }}{{\rho U_{w}^{2} }},\, \, Nu_{x} = \frac{{xq_{w} }}{{k(T_{w} - T_{\infty } )}},\, \, Sh_{x} = \frac{{xq_{m} }}{{D_{B} (C_{w} - C_{\infty } )}},$$

(16)

with

$$\tau_{w} = \mu_{0} \frac{\partial u}{\partial y}\left[ {\beta^{ * } + (1 - \beta^{ * } )\left( {1 - \varGamma \frac{\partial u}{\partial y}} \right)^{ - 1} } \right],\;q_{w} = \left. { - k\left( {\frac{\partial T}{\partial y}} \right)} \right|_{y = 0} ,\;q_{m} = \left. { - D_{B} \left( {\frac{\partial C}{\partial y}} \right)} \right|_{y = 0} .$$

(17)

The application of above-defined dimensionless transformations (10) changes Eqs. (16–17) into the following expressions:

$$\begin{aligned} Re_{x}^{1/2} C_{fx} & = f^{{\prime \prime }} (0)[\beta^{ * } + (1 - \beta^{ * } )\left\{ {1 - Wef^{{\prime \prime }} (0)} \right\}^{ - 1} ], \\ Re_{x}^{ - 1/2} Nu_{x} & = - \theta^{{\prime }} (0),\;Re_{x}^{ - 1/2} Sh_{x} = - \varphi^{{\prime }} (0). \\ \end{aligned}$$

(18)

Here, $Re_{x} = \frac{{U_{w} x}}{\nu }$ depicts the local Reynolds number.

3 Implementation of numerical method

The set of nonlinear coupled ODEs (11–13) subject to the boundary conditions (14) and (15) are solved by using an effective numerical technique known as Runge–Kutta Fehlberg integration procedure. To do this, we convert the current governing problem to a set of first-order equations. Here, we denote

$$f = U_{1} ,\; \, f^{{\prime }} = U_{2} ,\; \, f^{{\prime \prime }} = U_{3} ,\;\theta = U_{4} ,\;\theta^{{\prime }} = U_{5} ,\;\phi = U_{6} ,\;\phi^{{\prime }} = U_{7} .$$

(19)

Hence, the system of first-order equations becomes

$$U_{1}^{\prime } = U_{2} ,\;U_{2}^{\prime } = U_{3} ,\;U_{3}^{\prime } = \frac{{U_{2}^{2} + A(U_{2} + \tfrac{\eta }{2}U_{3} ) - U_{1} U_{3} }}{{\left[ {\beta^{ * } + (1 - \beta^{ * } )\left( {1 - WeU_{3} } \right)^{ - 2} } \right]}},$$

(20)

$$U_{4}^{\prime } = U_{5} ,\;U_{5}^{\prime } = - \;Pr\left( {U_{1} U_{5} - 2U_{2} U_{4} } \right) + Pr\frac{A}{2}\left( {\eta U_{5} + 3U_{4} } \right) + PrNbU_{5} U_{7} - PrNtU_{5}^{2} ,$$

(21)

$$U_{6}^{\prime } = U_{7} ,\;U_{7}^{\prime } = - Pr(U_{1} U_{7} - 2U_{2} U_{6} ) + Pr\frac{A}{2}\left( {\eta U_{7} + 3U_{6} } \right) - \frac{Nt}{Nb}U_{5}^{\prime } ,$$

(22)

with the associated initial conditions as

$$U_{1} \left( 0 \right) = 0,\;U_{2} \left( 0 \right) = 1,\;U_{4} \left( 0 \right) = 1,\;U_{6} \left( 0 \right) = 1,$$

(23)

$$U_{2} \left( \infty \right) = 0,\;U_{4} \left( \infty \right) = 0,\;U_{6} \left( \infty \right) = 0.$$

(24)

In this study, we must consider the range of numerical integration to be finite dimensions (such as $\eta_{\hbox{max} } = 10)$. The computation procedure is continued up to the convergence criterion $10^{ - 6}$ is accomplished.

3.1 Validation of numerical computations

In this section, the accuracy of the developed model and the implemented numerical scheme are validated by presenting a comparison between the current work and several previous numerical studies [19,20,21,22,23,24] found in the literature. These comparisons are presented in Tables 1 and 2. In Table 1, the computed values of skin friction for varying values of unsteadiness parameter $A$ are compared with those of Mukhopadhyay and Gorla [19], Sharidan et al. [20] and Chamkha et al. [21]. In fact, these results show a good consistency, as given in Table 1. In another comparison, the results of heat transfer rate of Williamson nanofluid flow are compared with those of Sharma [22], Grubka and Bobba [23] and Chen [24] as depicted in Table 2. As can be seen from these tables, there is good agreement between the results of this work and the previous works, indicating the accuracy of the present model.

Table 1 Comparison for the numerical values of $- f^{\prime\prime}(0)$ when $We = \beta^{ * } = 0.$

Table 2 Comparison for the numerical values of $- \;\theta^{\prime}(0)$ when $We = \beta^{ * } = Nt = Nb = A = 0$

4 Discussion of graphical results

In the current problem, the numerical solution for nanofluid velocity, temperature and concentration is derived to describe the flow behaviour of Williamson fluid towards a stretching surface. For this aim, we discuss the numerical results in terms of non-dimensional velocity, temperature and nanoparticles concentration for different model parameters, like, unsteadiness parameter, viscosity ratio parameter, Weissenberg number, Brownian motion parameter, thermophoresis parameter and Lewis number.

4.1 Impacts of unsteadiness parameter

The influence of unsteadiness parameter on the non-dimensional velocity, temperature and nanoparticles concentration profiles is depicted in Fig. 2a–c. As can be seen in Fig. 2a, non-dimensional velocity $f^{\prime}\left( \eta \right)$ along the wall reduces with an increase in unsteadiness parameter $A.$ Moreover, it is imperative to notice that both the temperature $\theta \left( \eta \right)$ and nanoparticle concentration $\phi \left( \eta \right)$ profiles show a decreasing behaviour with higher unsteadiness parameter. Hence, an enhancement in the unsteadiness parameter yields a significant reduction in associated boundary layer thicknesses. From physical point of view, when the unsteadiness increases, the stretching wall loses more heat and mass transfer due to which temperature and volume fraction concentration decrease. Further, it can be observed that with a rise in $A,$ the distance of two adjacent profiles rises remarkably.

Fig. 2

Velocity, temperature and concentration profiles with variation in unsteadiness parameter

4.2 Impacts of Weissenberg number

The variation of non-dimensional velocity $f^{\prime}\left( \eta \right)$, temperature $\theta (\eta )$ and nanoparticle concentration $\phi \left( \eta \right)$ profiles for several values of Weissenberg number $We$ is presented in Fig. 3a–c. It is seen from Fig. 3a that a significant deviation in velocity profiles is observed for varying values of Weissenberg number. All of the curves show that a larger $We$ parameter causes a substantial decrease in velocity of the fluid as well as the corresponding boundary layer thickness.

Fig. 3

Velocity, temperature and concentration profiles with variation in Weissenberg number

The Weissenberg number plays a vital role on the profiles of non-dimensional temperature, as shown in Fig. 3b. It is known from the graphs that, as the Weissenberg number increases, the fluid temperature is found to rise significantly. This is due to that the increase in the Weissenberg number means the rise in relaxation time, which, in turn, results in the increase in non-dimensional fluid temperature. The variation of nanoparticle concentration profile for growing values of Weissenberg number is portrayed in Fig. 3c. One can easily observe that, for larger values of $We$, the nanoparticle concentration and associated boundary layer thickness increases.

4.3 Impacts of Brownian motion parameter

Figure 4a, b shows the influence of Brownian motion parameter $Nb$ on the profiles of temperature $\theta (\eta )$ and nanoparticle volume fraction $\phi \left( \eta \right)$, respectively. It is evident that uplifting the values of Brownian motion parameter will increase the non-dimensional temperature profiles and an inverse behaviour is noted for the nanoparticle volume fraction. Basically, a rise in the nanofluid temperature is attributed to nanoparticle interaction linked to growing Brownian motion. It is noticed that concentration profile and concentration boundary layer thickness reduce due to low Brownian diffusivity. Physically, it can be noted that the different nanoparticles have different Brownian motion $Nb$ and, increasing the Brownian motion parameter, the strength of this chaotic motion enriches the kinetic energy of the nanoparticles, and this leads to enhancement of the thermal and concentration boundary layer thickness. Mostly, an escalation in the Brownian motion tends to heat the fluid near the boundary layer, and at the same time, it exacerbates particle deposition away from the fluid region, on behalf of this perceived that declines in the nanoparticle volume fraction.

Fig. 4

Temperature and concentration profiles with variation in thermophoresis parameter

4.4 Impacts of thermophoresis parameter

The impacts of thermophoresis parameter $Nt$ on dimensionless temperature and concentration profiles are demonstrated in Fig. 5a, b. It is clearly shown in these figures that the thermophoresis parameter $Nt$ has a significant effect on both temperature and concentration profiles. It is most important to note that with the growing values of $Nt$ the temperature as well as the nanoparticles concentration profiles enhances gradually. However, the effects are much pronounced in case of nanoparticles concentration. The physics behind this fact is that the thermophoretic force is generated by the gradient of temperature and it produces a very high-speed flow far from the stretching surface. In this regard, the fluid is more heated and away from the stretching sheet and consequentially, as the $Nt$ rises, the thermal and nanoparticle concentration boundary layer thickness uplifted. Further, the temperature as well as concentration gradient at the surface reduces as $Nt$ increases. Moreover, developing the values of thermophoresis parameter produces a force which moves the nanoparticles from the hotter to colder region which results in the rate of heat and mass transfer.

Fig. 5

Temperature and concentration profiles with variation in Brownian motion parameter

4.5 Impacts of Prandtl number

The behaviour of the Prandtl number $Pr$ on the temperature profiles $\theta (\eta )$ is exhibited in Fig. 6. We noticed that heat transfer behaviour obviously depends on the values of the Prandtl number. As the values of Prandtl number increase, the rate of heat transfer also increases. Therefore, it reduces the nanofluid temperature and thickness of the thermal boundary layer. In view of physical aspect, the Prandtl number is the ratio of momentum to thermal diffusivity and higher $Pr$ corresponds to weaker thermal diffusivity which yields a reduction in the thermal boundary layer thickness. Fluids with lower Prandtl number will have thicker thermal boundary layer structure and higher thermal conductivity. Therefore, for larger $Pr$, heat diffuses quickly from the surface to the fluid. Subsequently Prandtl number can be utilized to expand the rate of cooling in conducting flows.

Fig. 6

Temperature profiles with variation in Prandtl number

4.6 Impacts of Lewis number

Figure 7 exposes the effect of the Lewis number $Le$ on nanoparticle concentration profile keeping another physical parameter constant. By increasing the values of $Le$ the concentration field and concentration boundary layer thickness depreciates. The reason is because the mass transfer rate enriches as the $Le$ enlarges. For a base fluid of certain momentum diffusivity, a larger Lewis number causes low Brownian diffusion coefficient which must result in a shorter penetration depth for the concentration boundary layer thickness.

Fig. 7

Concentration profiles with variation in Lewis number

Table 3 depicts the influence of unsteadiness parameter $A$, viscosity ratio parameter $\beta^{*}$ and local Weissenberg number $We$ on the skin-friction coefficient. The friction coefficient enhances by higher values of unsteadiness parameter $A$ and viscosity ratio parameter $\beta^{*}$, whereas it decreases for higher values of Weissenberg number $We$. Table 4 exhibited the impact of pertinent parameters $A$, $\beta^{*}$, $Pr$, $Nt$, $Nb$ and $Le$ on the local Nusselt number $Re_{x}^{ - 1/2} Nu_{x}$ and Sherwood number $Re_{x}^{ - 1/2} Sh_{x}$ when $We = 2.0$. On the evident of Table 4, the local Nusselt number enhances by uplifting the values of unsteadiness parameter $A$ and Prandtl number $Pr$. It is also shown that the rate of heat transfer is a declining function of the $Nt$, $Nb$ and $Le.$ Table 4 also gives an example of our numerical results of the dimensionless Sherwood number $- \varphi^{\prime}(0).$ It is cleared from this table for augmented values of Prandtl number $Pr$, unsteadiness parameter $A,$ Lewis number $Le$ and Brownian motion parameter $Nb$ the local Sherwood number $Re_{x}^{ - 1/2} Sh_{x}$ increases. Further, growth in thermophoresis parameter $Nt$ diminishes the mass transfer rate. Physically, a parametric report is shown, and the desired approximate values are revealed with the aid of graphical illustrations.

Table 3 Numerical values of $Re_{x}^{1/2} C_{fx}$ for distinct values of $A,$$\beta^{ * }$ and $We$

Table 4 Numerical values of $Re_{x}^{ - 1/2} Nu_{x}$ and $Re_{x}^{ - 1/2} Sh_{x}$ for distinct values of $A$, $\beta^{ * }$$Pr$, $Nt$, $Nb\;$ and $Le$ when $We = 2.0$

5 Conclusions

Keeping in view the basic applications of heat transfer enhancement due to the addition of nanoparticles in base fluid, the main aim of this article is to numerically investigate the time-dependent flow and heat transfer mechanism for Williamson fluid with suspended nanoparticle. The flow was caused by a stretching surface. Numerical simulations for governing differential equations have been conducted by employing Runge–Kutta integration method coupled with Newton’s iterative scheme. The physical characteristics of several sets of values of the governing flow parameters on non-dimensional velocity, temperature and nanoparticles concentration were presented graphically, analysed and discussed in detail. According to the achieved results, some interesting observations from present analysis are as follow:

• The most practical outcome of this study was that the fluid velocity was significantly enhanced by higher viscosity ratio parameter.

• Temperature of the nanofluids was considerably promoted by the thermophoresis phenomenon.

• Heat transfer rate was elevated by higher values of Lewis number.

• Velocity, temperature, and concentration profiles were depressed by increasing the unsteadiness parameter.

• Larger values of Brownian motion parameter created an enhancement in temperature profile due to higher thermal conductivity of the liquid.