Learning vector quantization and relevances in complex coefficient space

Abstract

In this contribution, we consider the classification of time series and similar functional data which can be represented in complex Fourier and wavelet coefficient space. We apply versions of learning vector quantization (LVQ) which are suitable for complex-valued data, based on the so-called Wirtinger calculus. It allows for the formulation of gradient-based update rules in the framework of cost-function-based generalized matrix relevance LVQ (GMLVQ). Alternatively, we consider the concatenation of real and imaginary parts of Fourier coefficients in a real-valued feature vector and the classification of time-domain representations by means of conventional GMLVQ. In addition, we consider the application of the method in combination with wavelet-space features to heartbeat classification.

1 Introduction

Time series constitute an important example of functional data [1]: Their time-domain-discretized vector representations comprise components which reflect the temporal order and are often highly correlated over characteristic times. This is in contrast to more general datasets, where the feature vectors are concatenations of more or less independent quantities and without any meaningful interpretation of their order.

The machine learning analysis of time series data, e.g., for the purpose of classification, should take into account their functional nature. Recently, prototype-based systems have been put forward, which employ the representation of data and prototypes in terms of suitable basis functions [2, 3]. In addition, corresponding adaptive distance measures can be defined and trained in the space of expansion coefficients [4,5,6]. Hence, the functional nature of data is taken advantage of, explicitly. At the same time, it is possible to compress high-dimensional data by functional approximations, thus reducing computational effort and—potentially—the risk of over-fitting.

Examples of the basic approach include the application of wavelet representations of mass spectra [7] or hyperspectral images [8], and also polynomial expansions of smooth functional data [2, 3].

In the context of signal processing, the discrete Fourier transform (DFT) to the frequency domain is a popular tool which can be applied to time series or more general, sequential data. In the following, the discussion is presented mostly in terms of actual time series, but it is understood that methods and results would carry over to suitable sequential data from other contexts.

The standard formulation of the DFT resorts to the determination of complex coefficients, conveniently. Hence, we suggest and study the combination of DFT functional representations with the extension of generalized matrix relevance learning vector quantization (GMLVQ) [9, 10] to complex feature space [11].

We present furthermore the formalism to back-transform the resulting prototypes and relevance matrix to the time domain, thus retaining the intuitive interpretability of the LVQ approach.

We apply the suggested framework to a number of benchmark datasets [12] and study, among other aspects, the dependence of the performance on the approximation quality, i.e., the number of coefficients considered.

In addition, we compare performance with an approach that resorts to the concatenation of the imaginary and real parts of coefficients in a real-valued feature vector. The application of conventional GMLVQ classification in the time domain serves as an important and intuitive baseline for comparison of performances and for the interpretation of the obtained relevance matrices.

Some of our results have been presented at the Workshop on Self-Organizing Maps and Learning Vector Quantization (WSOM+ 2017) [13]. Here we extend the scope of the work significantly by considering wavelet representations of time series, which provide local features of the signal, in contrast to the standard DFT. We study the usefulness of the combination of wavelet representations with the extension of GMLVQ to complex feature space for heart beat classification in ECG data. We apply the method to the well-known MIT-BIH dataset [14]. We study the performance of general learning and patient-specific learning, for both full-wavelet representations and truncated representations. We interpret the classifiers in wavelet space, and we also discuss the back transformation of prototypes, for retaining time-domain interpretability.

2 The mathematical framework

In this section, we present the mathematical framework that underlies the method. This consists of the discrete Fourier transform (DFT), the dual-tree complex wavelet transform (DTCWT), the adaptation of the machine learning algorithm GMLVQ to complex-valued feature space using Wirtinger calculus [15] and the back transformation of the classifiers that retains interpretability in the original time domain of the data.

2.1 Discrete Fourier transform

Sampling a continuous process f(t) with sampling interval $\varDelta T$ results in a potentially high-dimensional feature vector $\varvec{x} \in {{\mathbb {R}}}^N$ containing the values of f(t) at the sampling times, $f(i\varDelta T), i=0,1,\ldots ,N-1$. The time-domain vector $\varvec{x} \in {{\mathbb {R}}}^N$ can be written as a linear combination of sampled complex sinusoids:

$$\begin{aligned} \varvec{x}[t] = \sum _{k=0}^{N-1} \varvec{x}_f[\omega _k] \hbox {e}^{-j2\pi tk/N},\quad t=0,1,2,\ldots ,N-1, \end{aligned}$$

(1)

where the coefficients $\varvec{x}_f[\omega _k] \in {\mathbb {C}}$ can be calculated efficiently by the DFT [16]:

$$\begin{aligned} \varvec{x}_f[\omega _k] = \sum _{t=0}^{N-1} \varvec{x}[t] \hbox {e}^{-j2\pi kt/N},\quad k=0,1,2,\ldots ,N-1. \end{aligned}$$

(2)

As in Eqs. (1) and (2) and the rest of the discussion, the subscript f is used to denote a vector or matrix in the Fourier domain. As can be observed in Eq. (2), the transformed feature vectors consist of N coefficients. It should be noted that the coefficients of $\varvec{x}_f[\omega _k]$ are conjugate symmetric and therefore all the information is contained in the first $\lfloor N/2 \rfloor + 1$ coefficients: $\varvec{x}_f[\omega _k], k=0,1,\ldots ,\lfloor N/2 \rfloor$. By restricting the number of coefficients to a number $n < \lfloor N/2 \rfloor + 1$ in Eq. (1), an approximation $\hat{\varvec{x}}[t]$ of the original time-domain vector $\varvec{x}[t]$ is obtained. Note that for the purpose of classification, in some datasets the discriminative information may be contained in the higher band of frequencies as well. However, in this contribution, we consider smooth versions of the time series which are obtained by cutting off high frequencies.

Note that according to Eq. (2), the computation of a single coefficient $\varvec{x}_f[\omega _k] \in {\mathbb {C}}$ for the kth frequency is defined as the dot product between the time-domain vector $\varvec{x}[t]$ and the sampled complex sinusoid of the kth frequency, $g_k[t] = \hbox {e}^{-j2\pi k t/N}$. We could therefore equivalently write the transformation in Eq. (2) as a matrix equation:

$$\begin{aligned} \varvec{x}_f[\omega ] = \varvec{F} \varvec{x}, \end{aligned}$$

(3)

where $\varvec{x}_f[\omega ] \in {\mathbb {C}}^{n}$ is the complex Fourier approximation of $\varvec{x} \in {{\mathbb {R}}}^N$ truncated at n frequency coefficients and $\varvec{F} \in {\mathbb {C}}^{{n}\times {N}}$ is the transformation matrix where the sampled complex sinusoids appear on the rows. The multiplication with $\varvec{F}$ in Eq. (3) could be done using the FFT, which reduces computational cost to ${\mathcal {O}}(N \log N)$, as compared to computing the DFT directly as it is defined in Eq. (3) which has a cost of ${\mathcal {O}}(N^2)$ in case of a DFT that considers all the N frequencies.

2.2 Dual-Tree Complex Wavelet Transform

In contrast to the DFT, the wavelet transform also provides local information. The one-dimensional continuous wavelet transform is defined as [17]:

$$\begin{aligned} W(\tau , s)^\psi _x = {\mathbf {\varPsi }}^\psi _x(\tau , s) = \frac{1}{\sqrt{|s|}} \int x(t) \psi ^* \left( \frac{t - \tau }{s} \right) \hbox {d}t, \end{aligned}$$

(4)

where $s \in {{\mathbb {R}}}^+$ is the scale of the wavelet, $\tau \in {{\mathbb {R}}}$ is the translation or shift of the wavelet and ${\mathbf {\varPsi }}$ is the so-called mother wavelet, which has a finite activation. The mother wavelet ${\mathbf {\varPsi }}$ is the main function from which the specific scaled and translated basis functions $\psi ^*$ are derived.

For increasing s, more compressed functions are obtained and decreasing s results in more dilated functions. Obviously, the more compressed wavelets provide more resolution in time. The $\tau$ parameter shifts the wavelet with finite activation along the signal.

The discrete wavelet transform (DWT) is efficiently implemented as a repeated filtering process referred to as sub-band coding: A high- and low-pass filter h and g are applied to the sampled signal $\varvec{x}[t]$ in each level of the decomposition up to the highest level j [18]. This yields detail coefficients $d_i$ and approximation coefficients $a_i$ for each level $1 \le i \le j$, obtained from the high- and low-pass filter, respectively:

$$\begin{aligned} d_i[k] = \sum _t x[t] \cdot h[2k - t]. \end{aligned}$$

(5)

For $i=1$, we obtain $d_1$ following Eq. 5 and $a_1$ by an application of the low-pass filter g:

$$\begin{aligned} a_i[k] = \sum _t x[t] \cdot g[2k - t]. \end{aligned}$$

(6)

In the next level $i=2$, h and g are applied on $a_1$, reducing the analyzed frequency window by a factor two in each step. The output of the DWT is the concatenation of all detail coefficients $d_i$ for $1 \le i \le j$ and the approximation coefficients of the last level $a_j$:

$$\begin{aligned} \varvec{x}_w = [d_i, a_j] \in {\mathbb {R}}^N. \end{aligned}$$

(7)

In the following, the subscript w is used to denote a vector or matrix in wavelet space, as in Eq. (7).

The original discrete wavelet transform is not shift-invariant. In [19], a version of the discrete wavelet transform was proposed which attains approximate shift invariance: the dual-tree complex wavelet transform (DTCWT). This transform uses two filter-trees, in contrast to the normal DWT in which only a single filter tree is used. One tree produces the real parts and the other tree produces the imaginary parts of the complex wavelet transform. When applying the DTCWT, we therefore obtain vectors $\varvec{x}_w = [d_i, a_j] \in {\mathbb {C}}^N$. We will use the DTCWT mainly in order to exploit its approximate shift invariance property.

2.3 GMLVQ with Wirtinger calculus

Having transformed the data to Fourier or wavelet space as described in the previous sections, we consider a classification setup in which GMLVQ works directly on complex-valued data, following the prescription outlined in [6]. In our case, the complex-valued data vectors are representations of the time series in terms of the basis functions of the used transform, either obtained by the DFT or the DTCWT. For illustration purposes, we consider Fourier representations, and therefore, we use the f subscript for the vectors in this section. Let the dataset consist of labeled feature vectors $(\varvec{x}_f,y) \in {\mathbb {C}}^{n} \times \{1,\ldots ,C\}$, i.e., each feature vector $\varvec{x}_f \in {\mathbb {C}}^{n}$ being a member of one of the C distinct classes in the dataset. During the GMLVQ training process, complex-valued prototypes $\varvec{w}_f \in {\mathbb {C}}^{n}$ representing the classes in the dataset are learned and a quadratic distance measure $d_{\varvec{\varLambda }}[\varvec{x}_f,\varvec{w}_f]$ parameterized by a matrix $\varvec{\varLambda } = \varvec{\varOmega }^H \varvec{\varOmega }$ is adapted according to the relevance of the features in the space of the transform. In the end, we obtain a classifier defined in terms of distance measure $d_{\varvec{\varLambda }}[\varvec{x}_f,\varvec{w}_f]$ and the set of prototypes $\varvec{W} = \{\varvec{w}_f^1,\varvec{w}_f^2,\ldots ,\varvec{w}_f^K \}$, where in the case of multiple prototypes per class $K>C$. A novel data point $\varvec{x}_f^\mu$ is then assigned the class label of the nearest prototype according to the learned distance measure $d_{\varvec{\varLambda }}[\varvec{x}_f^\mu ,\varvec{w}_f]$.

Given an example $(\varvec{x}_f^\mu , c = j)$ of class j, the closest prototype of the same class $(\varvec{w}_f^+, c = j)$ and the closest prototype of a different class $(\varvec{w}_f^-, c \not = j)$, the cost for example $\varvec{x}_f^\mu$ in cost-function-based GMLVQ is defined as:

$$\begin{aligned} \hbox {e}^\mu = \frac{d_{\varvec{\varLambda }}[\varvec{x}_f^\mu , \varvec{w}_f^+] -d_{\varvec{\varLambda }}[\varvec{x}_f^\mu , \varvec{w}_f^-]}{d_{\varvec{\varLambda }}[\varvec{x}_f^\mu , \varvec{w}_f^+] +d_{\varvec{\varLambda }}[\varvec{x}_f^\mu , \varvec{w}_f^-]} \in [-\,1, 1]. \end{aligned}$$

(8)

The total cost is then the sum of the individual cost contributions of all data points:

$$\begin{aligned} E = \sum _{\mu } \hbox {e}^\mu . \end{aligned}$$

(9)

Note that, for simplicity, we refrain from introducing a nonlinear function $\varPhi (\hbox {e}^\mu )$ in the sum, as originally suggested in [20].

Upon presentation of vector $\varvec{x}_f^\mu$, the prototypes $\varvec{w}_f^+$, $\varvec{w}_f^-$ and the matrix $\varvec{\varOmega }$ are adapted according to steepest descent of the cost function:

$$\begin{aligned}&\varvec{w}_f^+ := \varvec{w}_f^+ -\eta \nabla _{\varvec{w}_f^+} \hbox {e}^\mu , \end{aligned}$$

(10)

$$\begin{aligned}&\varvec{w}_f^- := \varvec{w}_f^- -\eta \nabla _{\varvec{w}_f^-} \hbox {e}^\mu , \end{aligned}$$

(11)

$$\begin{aligned}&\varvec{\varOmega } := \varvec{\varOmega } - \eta \nabla _{\varvec{\varOmega }} \hbox {e}^\mu . \end{aligned}$$

(12)

Derivations of the gradients with respect to complex-valued $\varvec{w}_f^+$, $\varvec{w}_f^-$ and $\varvec{\varOmega }$ as appear in the above equations can be found in [11, 21]. In [11] the learning rules for updating the prototypes $\varvec{w}_f^+$ and $\varvec{w}_f^-$ and adaptive distance matrix $\varvec{\varLambda }$ used in cost-function-based GMLVQ are formulated for complex-valued data, relying on the mathematical formalism of Wirtinger calculus [15] for the computation of the gradients which yields intuitive adaptation rules. Note that $\nabla _{\varvec{w}_f^+} \hbox {e}^\mu = \frac{\partial e^\mu }{\partial d_{\varvec{\varLambda }}} \frac{\partial d_{\varvec{\varLambda }}}{\partial \varvec{w}_f^+}$, and therefore only the inner gradient is taken with respect to complex variables, for which Wirtinger calculus is used. The distance between a data vector $\varvec{x}_f \in {\mathbb {C}}^{n}$ and a prototype $\varvec{w}_f \in {\mathbb {C}}^{n}$ is defined as:

$$\begin{aligned} d_{\varvec{\varLambda }}[\varvec{x}_f,\varvec{w}_f] = (\varvec{x}_f-\varvec{w}_f)^H \varvec{\varOmega }^H \varvec{\varOmega } (\varvec{x}_f-\varvec{w}_f), \end{aligned}$$

(13)

where $\varvec{A}^H$ denotes the Hermitian transpose of a matrix, which is obtained by the transpose operation on $\varvec{A}$ and the complex conjugation of each element $A_{ij}$.

The gradient of $d_{\varvec{\varLambda }}$ with respect to complex prototype $\varvec{w}_f \in {\mathbb {C}}^{n}$ is then, using the Wirtinger gradient, intuitively formulated as:

$$\begin{aligned} \nabla _{\varvec{w}_f^*} d_{\varvec{\varLambda }}[\varvec{x}_f,\varvec{w}_f] =-\varvec{\varOmega }^H \varvec{\varOmega }(\varvec{x}_f - \varvec{w}_f). \end{aligned}$$

(14)

The gradient of $d_{\varvec{\varLambda }}$ w.r.t. matrix $\varvec{\varOmega }$ is defined as:

$$\begin{aligned} \nabla _{\varvec{\varvec{\varOmega }}^*} d_{\varvec{\varLambda }}[\varvec{x}_f,\varvec{w}_f] =\varvec{\varOmega }(\varvec{x}_f - \varvec{w}_f)(\varvec{x}_f - \varvec{w}_f)^H. \end{aligned}$$

(15)

A comparison of the above gradients for complex-valued data with the gradients for real-valued GMLVQ [9, 10] reveals that the two are formally very similar, and therefore naturally, by substitution of the gradients of the complex variables into Eqs. (10)–(12), the learning rules for prototypes $\varvec{w}_f^+$ and $\varvec{w}_f^-$ and relevance matrix $\varvec{\varLambda }$ in the complex case are formally similar to the learning rules in the real case.

2.4 Back transformation

Training on the data in coefficient space as described in the previous section yields complex-valued prototypes and relevance matrix, i.e., the classifier is defined by the employed transformation. In this section, we formulate back transformations to retain time-domain interpretability.

2.4.1 Fourier space

The result of training in Fourier space as described in the previous section yields complex-valued prototypes $\varvec{w}_f \in {\mathbb {C}}^{n}$ and relevance matrix $\varvec{\varLambda }_f \in {\mathbb {C}}^{n\times n}$. The prototypes $\varvec{w}_f$ can be interpreted as typical Fourier space representations of the different classes and relevance matrix $\varvec{\varLambda }_f \in {\mathbb {C}}^{n\times n}$ indicate the relevance of the Fourier basis functions in the classification problem. A transformation of the prototypes to the time domain using the inverse discrete Fourier transform (iDFT) retains the time-domain intuitiveness of the prototypes [16]:

$$\begin{aligned} \varvec{w}[t] = \frac{1}{N} \sum _{k=0}^{N-1} \varvec{w}_f[k] \hbox {e}^{j2\pi tk/N}, \quad t=0,1,2,\ldots ,N-1. \end{aligned}$$

(16)

We further note that the distance measure in Fourier space can be written in terms of the Fourier transformation matrix $\varvec{F}$:

$$\begin{aligned} d[\varvec{x}_f,\varvec{w}_f] = (\varvec{x} - \varvec{w})^H \varvec{F}^H \varvec{\varLambda }_f \varvec{F} (\varvec{x} - \varvec{w}), \end{aligned}$$

(17)

where $\varvec{x} \in {\mathbb {R}}^N$ and $\varvec{w} \in {\mathbb {R}}^N$ are vectors in the time domain. By Eq. (17), the matrix $\varvec{\varLambda } = \varvec{F}^H \varvec{\varLambda }_f \varvec{F}$ yields a time-domain interpretation of the feature relevances.

2.4.2 Wavelet space

After training, each prototype $\varvec{w}_w \in {\mathbb {C}}^n$ can be interpreted as a typical wavelet-space representation of the class which it represents. The diagonal $\text {diag}(\varvec{\varLambda }_w) \in {\mathbb {R}}^{n}$ of the relevance matrix $\varvec{\varLambda }_w \in {\mathbb {C}}^{n\times n}$, which is real-valued since the matrix is always Hermitian, will reflect the importance of the wavelet coefficients on the various scales in the classification problem. The off-diagonal elements, which can be complex-valued, reflect the relevance of correlations between wavelet-space coefficients.

It is also possible to interpret the wavelet-space prototypes in the original time domain, by back-transforming the prototypes to the time domain using the inverse wavelet transform. The inverse transform starts with the detail- and approximation coefficients at the highest level j and works its way backwards by repeated upsampling and application of reconstruction high-pass and low-pass filters on the analysis coefficients until the time-domain signal after the reversal of the first level is obtained. The reconstruction filters are simply the reverse of the analysis filters used in the forward transform.

The back transformation of the relevance matrix could be performed in a similar way: Working its way backward by repeated upsampling and application of the reconstruction filters starting from the highest level. After the reversal of the first level, we obtain a matrix of relevance values in the time domain. However, we will not back-transform wavelet-space relevances here, as wavelets already provide time-domain interpretability.

3 Experiments learning in Fourier space

In this section, we describe the setup of the experiments for studying the usefulness of the method in combination with Fourier space representations.

3.1 Workflows

For our investigation into the usefulness and performance of the proposed method, we compare and study the results for the scenarios listed here. In order to evaluate the performance of classifiers, we compute the accuracies achieved in training and test set. We also present the temporal evolution of the cost function, Eqs. (8) and (9) and its counterpart computed as the analogous sum over the test set, referred to as ‘validation costs’ in the following.

• 1. Train a GMLVQ system using the feature vectors $\varvec{x} \in {\mathbb {R}}^N$ in the original time domain and evaluate the system on the test data. This serves as the baseline performance. Note that it is required that $\lfloor N/2 \rfloor + 1 \ge n_{max}$ (see Sect. 3.3).

• 2. Transform the feature vectors to complex Fourier space truncated at different numbers of Fourier coefficients $n=[6,11,\ldots ,51]$ yielding feature vectors $\varvec{x}_f \in {\mathbb {C}}^{n}$. On each of these representations, a GMLVQ system is trained. The training results in a classifier defined by prototypes $\varvec{w}_f \in {\mathbb {C}}^{n}$ and complex relevance matrix $\varvec{\varLambda }_f \in {\mathbb {C}}^{n\times n}$, which is evaluated on the corresponding test set.

• 3. As in Scenario 2, transform the data to complex Fourier space truncated at $n=[6,11,\ldots ,51]$ coefficients obtaining vectors $\varvec{x}_f \in {\mathbb {C}}^{n}$, but here we consider the representation that concatenates the real and imaginary parts forming real-valued feature vectors $\varvec{x}_f = \left[ \begin{array}{c} {\mathfrak {R}}{(\varvec{x}_f)} \\ {\mathfrak {I}}{(\varvec{x}_f)} \end{array}\right] \in {\mathbb {R}}^{2n}$. We train a GMLVQ system on each of these representations resulting in a classifier defined by prototypes $\varvec{w}_f \in {\mathbb {R}}^{2n}$ and a real-valued relevance matrix $\varvec{\varLambda }_f \in {\mathbb {R}}^{2n\times 2n}$, which is evaluated on the corresponding test set.

• 4. Transform the feature vectors $\varvec{x} \in {\mathbb {R}}^N$ to Fourier space for the same numbers $n=[6,11,\ldots ,51]$ of coefficients as in scenarios 2 and 3, after which the data is transformed back to the original space yielding feature vectors $\hat{\varvec{x}} \in {\mathbb {R}}^N$, which are smoothed versions of the original feature vectors. The GMLVQ systems are now trained and evaluated on these smoothed feature vectors in the time domain. The comparison of the obtained performance with the performance of scenarios B and C allows an estimate of the performance gain that results from the noise reduction caused by the truncation of high frequencies.

3.2 Training settings and parameter values

Prior to training, the training data is transformed such that all dimensions have zero mean and unit variance. The test data is transformed correspondingly using the mean and standard deviation of the features in the training set. This normalization is useful for the intuitive interpretation of the relevance matrix, since the relevance matrix does not have to account for the different scales of the features. The relevance values will therefore be directly comparable. All systems used one prototype per class, which was initialized to a small random deviation from the corresponding class-conditional mean. The relevance matrix was initialized proportional to the identity matrix. Furthermore, a batch gradient descent along the lines of [22] was applied as the optimization procedure using the default parameters from [23]. All classification results are obtained from the model as it is trained after a fixed number of training epochs, namely 300. Please note, that the goal of the experiments is to gain insights into the properties and highlight potential advantages of the proposed method. The presented classification accuracies may be further improved through the implementation of early stopping strategies or regularization methods.

Fig. 1

Example time series of each dataset. For the Plane, Symbols and MALLAT datasets, one example is shown from the first three classes in the dataset. For the FacesUCR dataset, one example is shown for the first two classes in the dataset

3.3 Example datasets

The suggested approach was applied to four time series datasets from the UCR Time Series Repository [12]. The names of the datasets and their properties are given in Table 1. All of the selected datasets contain time series with more or less periodic behavior. The repository does not provide any further details nor annotations about the origin and interpretation of the datasets. As shown in Fig. 1 depicts examples for each of the datasets and allows the evaluation of the intrinsic complexity of each dataset. Note that it is required that $\lfloor N/2 \rfloor + 1 \ge n_{\max }$, where $n_{\max }=51$, the maximum number of coefficients we consider in the experiments (see Scenario 2). As mentioned in Sect. 2.1, all information is contained in $\lfloor N/2 \rfloor + 1$ coefficients which is therefore the upper-bound for the number of approximation coefficients n. As shown in Table 1, all the considered datasets satisfy $\lfloor N/2 \rfloor + 1 \ge 51$.

Table 1 Time series datasets

These benchmark datasets have been widely studied in previous work. For example, in [3], a classification accuracy of approximately 95% is achieved on the PLANE dataset in the original space, and a similar or higher classification accuracy is achieved in the space of Chebyshev approximation coefficients. For the FacesUCR dataset, a classification accuracy of around 80% is reported in [24] using a nearest neighbor method with an adapted DTW similarity measure. In [25], a deep neural network architecture is used with which an accuracy of approximately 95% is achieved for the MALLAT dataset and an accuracy of 97% for the Symbols dataset. Nevertheless, we want to state explicitly that the scope of this study is not the achievement of higher classification accuracy. The datasets serve as an illustration for the properties of the proposed approach.

3.4 Performance evaluation

The performance for the different scenarios is evaluated by the classification accuracy, i.e., the percentage of correctly classified feature vectors on the validation set as indicated in Table 1. For Scenario 1 this is one baseline classification accuracy. For the functional approximation scenarios, 2, 3 and 4, each level of approximation n yields a classification accuracy, which will then be compared and discussed.

Fig. 2

Fraction of correctly classified vectors in the test sets for each dataset. The solid line represents the classification result in the original time domain of the data. Filled circles show the classification accuracy in the n-coefficient complex Fourier space of the data. Empty squares show the classification accuracy in the n-coefficient Fourier space where the real and imaginary parts of the complex features are concatenated yielding real feature vectors. Crosses show the classification accuracy on the smooth data in the original space that was obtained by an inverse transform of the Fourier representation. For each dataset the number of dimensions N of the original feature vectors is indicated

4 Results and discussion

The results displayed in Fig. 2 suggest that, in general, the classification results of functional data using a Fourier representation are comparable to or better than the baseline performance in the original time domain of the data.

The results on the PLANE dataset in Fig. 2a show that for all numbers of complex Fourier coefficients $n > 5$ the classification accuracy is at least as good as the accuracy in the original 144-dimensional feature space. The obtained accuracies are robust with respect to n, as there are no large fluctuations in performance. For this particular dataset, a functional approximation with 15 or 20 complex Fourier coefficients already seems sufficient to accurately distinguish between the classes. The representation with concatenated Fourier coefficients of Scenario 3 achieves a similar accuracy as the complex representation.

In the results of the method on the FACESUCR dataset as shown in Fig. 2b, the best performance is achieved for 20 Fourier coefficients. For $n \ge 15$, the performance of the two Fourier representations is similar. The performance in Fourier space is better than the performance in original space in the $n=20$ region, but the classification becomes less accurate the more higher frequency components are added. This indicates the presence of higher frequency noise in the original signals that negatively affects the classification accuracy.

Fig. 3

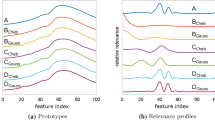
a The resulting class prototypes of the PLANE dataset are shown for training in the original 144-dimensional space. For clarity, only three of the seven prototypes are shown. The corresponding feature relevances, which are the diagonal elements of the resulting relevance matrix for the PLANE dataset, are shown in c. b The back-transformed prototypes obtained from training in 20-coefficient Fourier space are shown. d The corresponding feature relevances, obtained from back-transforming the complex relevance matrix as discussed in Sect. 2.4

Fig. 4

Training and validation error for the MALLAT dataset in the course of training. The solid line shows the error development in the original space of the data. The dashed line is the error development in 20-coefficient complex Fourier space. The dotted line shows the error development in 20-coefficient concatenated Fourier space

On the SYMBOLS dataset, the functional Fourier representations structurally achieve a better performance than the baseline performance in the original 398-dimensional space, even with a number of coefficients as low as $n=15$, as displayed in Fig. 2c. The accuracies of the complex representation and the concatenated real representation are similar. On the other hand, the accuracies achieved on the smoothed time series of Scenario 4 are systematically lower than the accuracies in Fourier space. Therefore, the observed improvement achieved from the transformation of the feature vectors to Fourier space cannot only be explained by the smoothing that the functional approximation brings about.

For further investigation of the performance of the method for even higher-dimensional functional data, the dataset MALLAT is considered consisting of feature vectors with dimensions $N=1024$. Figure 2d shows that the results in complex and concatenated Fourier space do not deviate significantly from the achieved accuracy in the original space. A functional Fourier approximation with 20 coefficients provides the same classification accuracy as in the original space, i.e., the system was able to achieve a similar accuracy on the 20-coefficient Fourier space representation compared to using all 1024 available original features. Despite the result on this dataset showing no improvement in accuracy, the dimensionality in the classification problem was reduced by $99.6\%$ without loss of classification accuracy, yielding a large computational advantage in the training and classification stage.

The prototypes that arise in the training process in complex Fourier coefficient space can be interpreted as class-specific contributions of the complex sinusoidal components of different frequencies in the corresponding classes. In Fig. 3b, the back transformation of the prototypes as formulated in Sect. 2.4 has been applied to the resulting complex prototypes of the PLANE dataset in 21-coefficient Fourier space, $\varvec{w}_f \in {\mathbb {C}}^{21}$, yielding a representation of the prototypes in the original time domain. A comparison with the prototypes resulting from training in the original time domain (Fig. 3a) reveals that the back-transformed prototypes are smoother, but resemble the prototypes from training in the full original space closely. Correspondingly, Fig. 3d shows the back-transformed relevance values. A comparison with the relevance values obtained in the original time domain shown in Fig. 3c reveals that the general relevance profiles are similar.

Figure 4 shows the error development on the training- and validation set of the MALLAT dataset. The three methods all achieve zero training error before 50 training epochs. After 50 epochs, the increased error in the original space on the validation set indicates an over-fitting effect. Both Fourier representations, complex and concatenated real- and imaginary parts, are less affected by over-fitting here, as the error on the validation set for these representations does not increase significantly. This confirms the conjecture that training in reduced Fourier coefficient space may help to alleviate over-fitting effects that arise in the original space. On this dataset, the complex Fourier representation eventually achieves the lowest error, followed by the concatenated Fourier representation.

Besides the potential to improve performance with a transformation to Fourier space, we must note that the difference in accuracy between the complex Fourier representation of Scenario 2 and the concatenated representation of Scenario 3 is small. However, training on the complex-valued data directly with GMLVQ using learning rules derived with Wirtinger calculus has the advantage of treating the complex dimensions as such and is therefore mathematically well formulated.

The dimensionality reduction results in less computational effort. The observed training times in a generic desktop PC environment for the MALLAT and SYMBOLS dataset are listed in Table 2. Both datasets have a high number of sampling points (cf. Table 1) in their original feature domain, so the approximation of the data with 20 Fourier coefficients renders a drastic reduction of input dimensions of 98.1% for the MALLAT dataset and 95% for the SYMBOLS dataset. The computational effort—as represented by the time spent during the training process—is also reduced significantly, though not as drastically as the number of input dimensions.

Table 2 Relations between absolute training time and dimensionality reduction

5 Learning in wavelet space

In this section, we study the usefulness of the complex-valued extension of GMLVQ in combination with wavelet-space representations for the classification of heartbeats extracted from ECG data. This section will describe the dataset, data preparation, feature extraction, and the general training settings for the experiments.

5.1 Dataset and training setup

The data on which we apply the method comes from the MIT-BIH Arrhythmia dataset [14]. The data was obtained from 4000 long-term Holter recordings [26]. In total, 48 recordings selected from this set are available in the MIT-BIH database. Twenty-three of those were chosen randomly from the total set of 4000, and the other 25 recordings were selected to include a variety of rare phenomena occurring in the heart rhythm. The signals were band-pass-filtered using a passband from 0.1 to 100 Hz and then digitized with a sampling rate of 360 Hz. For each record, slightly over 30 min of ECG signal is selected. In principal, two leads are available for each recording. Usually the main lead is MLII, which is a modified limb lead that is obtained by placing the electrodes on the chest.

In the literature, different learning scenarios are described. For example in [27], high classification accuracies of approximately 98% are achieved using a feed-forward neural network and DTCWT features, but the authors appear to select beats randomly. These classifiers may show degraded performance when applied to a new patient. It is common to learn patient-specific classifiers, as is done for example in [28].

It should be stated that in contrast to the above papers, we do not include additional temporal features that have the ability to further improve classification accuracy. The current paper aims to reveal potential benefits of the basic method as outlined above. Using the method along with other features to improve classification accuracy could be of interest in future research.

5.1.1 Annotations

After the records had been selected and digitized, a simple QRS detector was applied on the signals [26]: The R-point is the central peak of the heartbeat, the Q-point is the valley before the peak, and the S-point the valley directly after the peak. This wave is often referred to as the QRS-complex. After the simple QRS detector was applied, two cardiologists independently annotated the abnormal beats and beats that were missed by the detector. Additionally, annotations for heart rhythm, signal quality, and comments are also available.

The heartbeat classes are denoted by symbols. The mapping from symbols to specific types of heart beats is found on [29]. There are 17 different classes in the dataset.

5.2 Data preparation and feature extraction

Using the beat annotations, we extract the beats from the recorded electrocardiograms: For each annotated R-peak sample, 128 samples are extracted toward the left and 127 samples toward the right. Including the R-peak sample itself, this gives segments of $256=2^8$ samples in length. This length segments the full QRS-complex including the P and T waves and we have chosen a power of 2 deliberately for direct compatibility with the DTCWT. With a sampling rate of 360 Hz, the segments are approximately 0.711 s.

From the segmented time-domain heart beat vectors $\varvec{x} \in {\mathbb {R}}^{256}$, we extract wavelet features using the DTCWT up till level $j=5$. For the first level, this gives $2^{8-1} = 2^7$ complex-valued detail coefficients, representing higher frequency wavelet correlations in the signal. The second level reduces the frequency window by a factor two and yields $2^6$ complex-valued detail coefficients. This continues up till the highest level j, which yields $2^3$ complex-valued detail coefficients and also $2^3$ complex-valued approximation coefficients. The approximation coefficients were obtained from the application of the low-pass filter at the highest level and therefore correspond to the lowest level frequencies in the signal. In summary, the procedure which transforms the time-domain beat $\varvec{x} \in {\mathbb {R}}^{256}$ to wavelet space, yields $2^7+2^6+2^5+2^4+2^3+2^3 = 256$ complex-valued coefficients in the feature vector $\varvec{x}_w \in {\mathbb {C}}^{256}$; the time-domain vector and the wavelet-space vector have the same length.

5.3 Training settings and parameter values

In each experiment, we consider the wavelet-space feature vectors $\varvec{x}_w \in {\mathbb {C}}^{256}$, which are obtained by applying a 5-level DTCWT on each of the segmented time-domain beat vectors $\varvec{x} \in {\mathbb {R}}^{256}$. We will also consider truncated versions of the wavelet-space feature vectors, and hence we will refer to the wavelet-space vectors in the general discussion as $\varvec{x}_w \in {\mathbb {C}}^n$, where $n \le 256$. In the general experiment setup, we standardize the wavelet-space feature vectors, and on the resulting vectors, we apply GMLVQ learning with one prototype for each beat type. The prototypes $\varvec{w}_w \in {\mathbb {C}}^{n}$ are initialized to a small random deviation from the class-conditional mean. The relevance matrix $\varvec{\varLambda }_w \in {\mathbb {C}}^{n\times n}$ is initialized as a proportion of the identity matrix, (1 / n)I, satisfying $\sum _{i=1}^n \varLambda _{ii} = 1$ and $\varLambda _{ii} = \varLambda _{jj}$ for all pairs i, j.

We use batch gradient descent along the lines of [22] in order to optimize the GMLVQ cost function given in Eq. (8), using the default parameters from [23].

6 Experiments learning in wavelet space

This section describes the specific experiment scenarios for studying the usefulness of the extension of GMLVQ in combination with wavelet representations for classifying heart beats.

6.1 General classifier

In the first experiment, we consider the classes normal beat (N), left bundle branch block beat (L), right bundle branch block beat (R), premature ventricular contraction (V) and paced beat (/), segmented from all available MIT-BIH records. We perform a 5-level DTCWT on the labeled time-domain beats and obtain labeled wavelet-space feature vectors $(\varvec{x}_w \in {\mathbb {C}}^{256}, y)$, where y is a label from the set $C=\{N, L, R, V, /\}$. Next, we randomly select 100 examples from each of the classes in C to be used as training data in GMLVQ learning. One hundred and fifty other examples from each class in C are randomly selected for validation during the GMLVQ learning epochs. We perform sufficient training epochs in order to let the GMLVQ cost-function converge on the validation set.

In the first experiment, we also consider truncated wavelet-space vectors $\varvec{x}_w \in {\mathbb {C}}^{32}$ that consist of the coefficients of the fourth- and fifth-level decomposition and compare the validation performance to the validation performance when the full-wavelet space representation is used. Note that as the number of parameters in GMLVQ increases quadratically with the number of input features, training on only the fourth- and fifth-level coefficients results in considerably less adaptive parameters. The training- and validation sets consist of the same examples as are chosen for the experiment in which full-wavelet space feature vectors are used.

6.2 Patient-specific classifiers

In the second experiment, we consider patient-specific classification. We follow a similar approach as in [30]: We select a common training set from the MIT-BIH records 100 till 124 and perform the patient-specific classification on the records 200 till 234. For each record in the latter group, the first 5 min of the record serves as additional training data to the common beats and the beats occurring in the remaining 25 min, which the classifier has not seen during learning, will be used for assessing the performance of the classifier.

In the first patient-specific experiment, we train on the full-wavelet space vectors $\varvec{x}_w \in {\mathbb {C}}^{256}$. Then we perform the same patient-specific experiment using vectors containing only the fourth- and the fifth-level wavelet coefficients, $\varvec{x}_w \in {\mathbb {C}}^{32}$.

7 Results and discussion

Fig. 5

GMLVQ learning results of beat classification in experiment 1

7.1 General classifier

The results obtained from the first experiment are shown in Fig. 5: Panels a and b display the performance of the classifier throughout the learning process while panels c and d show the interpretation of the final classifier, after batch step number 300. In Fig. 5a, the value of the cost function computed on the training data and computed on the validation data is shown for each learning step. The training set cost shows a stable converge toward a value of approximately $-\,0.87$. At the same time, the development of the cost on the validation set shows signs of over-fitting, after its initial decrease. After batch step 300, the value of the validation cost is approximately $-\,0.57$, but the lowest value seen during training is at batch step 38 where the validation cost has a value of $-\,0.62$. As expected, the classification error curves in Fig. 5b are quite correlated with the cost-function curves. The classification error on the training set converges to approximately 0.4%. The lowest achieved validation error is 8.9% after batch step 38, where also the validation cost was lowest. Due to the over-fitting, the validation error increases after batch step 38 toward a value of 11.7% after batch step 300.

Concerning the interpretation of the resulting classifier, Fig. 5c shows the relevance value of each wavelet coefficient in the classification problem. The highest values correspond to the most distinctive coefficients while low values correspond to features with which the classifier can not adequately discriminate between the classes. The dashed vertical lines mark the transition between different scales of the wavelet decomposition. Hence, the first dashed line appears at feature 128, indicating the border between the first-level detail coefficients and the second-level detail coefficients. Inside each wavelet-scale window, the horizontal axis indicates the translation $\tau$ of the wavelet. The wavelet transform makes the relevance values interpretable both in frequency/scale and in time. As an example of this, in most scales, the highest relevance is around the center, indicating a higher relevance of correlations with wavelets that are active in the QRS-complex region, while at the same time it can be inferred that one of the most discriminative wavelets is a second-level wavelet. It is also evident that coefficients corresponding to the fourth- and fifth-level decomposition are highly discriminative.

In Fig. 5d, three time-domain prototypes are displayed, as back-transformed from wavelet space. This allows for the time-domain interpretation of what the classifier has learned as typical examples of the different beats in the classification problem. The figure shows the time-domain prototypes for the beat classes Normal beat (N), Left Bundle Branch Block Beat (LBBB) and Premature Ventricular Contraction (PVC).

Fig. 6

GMLVQ learning results of beat classification in experiment 1 where only the wavelet decomposition of the fourth- and fifth levels is considered

In Fig. 6, the results of GMLVQ learning on truncated wavelet-space feature vectors is shown. It can be seen in Fig. 6a that there are no over-fitting effects anymore in this case. For this reason, the final validation set cost ($-\,0.66$), which is also the minimum cost achieved throughout training, is lower than the final validation cost ($-\,0.57$) achieved when using all wavelet-space coefficients. The validation set cost is also lower than the minimum achieved validation cost for GMLVQ learning on the full-wavelet space vectors.

In Fig. 6b, the relevance of the fourth- and fifth-level wavelet space coefficients is shown. The most discriminative coefficient is an approximation coefficient. Higher values are obtained for wavelets with an activation corresponding to the center of the signal: A peak occurs around the center of the fourth- and fifth-level detail coefficients, indicating a relevance of wavelets active in the QRS-complex region on different scales. After training, the classification error on the validation set is 10.1%.

Table 3 Per-class prediction accuracy for truncated- and the full-wavelet coefficient vectors

Table 3 shows that GMLVQ learning on the truncated wavelet-space vectors achieves a high accuracy on all beat classes except for the PVC class. Although learning on the full-wavelet space vectors results in a lower average validation accuracy, the classification of the PVC class is slightly more accurate in this case. Although the GMLVQ classifier trained on the full-wavelet space feature vectors has the advantage of full-wavelet space interpretation and time-domain prototype interpretation, the fourth- and fifth-level wavelet coefficients already seem to provide enough information to adequately discriminate between the classes. Training on the truncated wavelet-space coefficients has the additional advantage of requiring considerably less training effort and alleviating over-fitting.

Fig. 7

GMLVQ learning results in patient-specific classification

7.2 Patient-specific classifiers

Patient-specific learning was applied on the last 25 records in the database. In Fig. 7a, the average validation cost over the 25 patient-specific learning curves is shown for GMLVQ learning on the full-wavelet space vectors and on the truncated vectors. In this case as well, learning on the full-wavelet space vectors results in over-fitting, whereas over-fitting does not occur for learning on the truncated wavelet-space vectors. The cost after batch step 100 is − 0.83 for learning on the truncated vectors. Not surprisingly, patient-specific classifiers are on average more accurate than more general classifiers. The average error per batch step on the validation set is shown in Fig. 7b. In both scenarios, the training quickly results in an error below 5%. For the truncated scenario, the final error is approximately 3.6%, whereas for the full-wavelet space scenario, the final error is 3.7%.

Table 4 The per-class prediction accuracy in patient-specific learning for truncated- and the full-wavelet coefficient vectors

Figure 7c, d shows the interpretation of the resulting patient-specific classifier for record 217, a patient that mainly has normal beats, premature ventricular contractions and paced beats. The relevance profile in Fig. 7c displays peaks around the center of each scale, indicating that correlations of the signal with wavelets that are activated around the center of the signal are most discriminative, on multiple scales. Figure 7d shows the time-domain representation of the prototypes which were learned in wavelet space for the three main beat types that occur in this record.

In Table 4, the classification accuracy of all 25 patient-specific classifiers taken together is shown per class for the two scenarios. On average, GMLVQ patient-specific learning is slightly more accurate. The GMLVQ learning on the full-wavelet space vectors is more accurate in classifying premature ventricular contractions (V).

8 Summary and outlook

In this contribution, we have shown and discussed the benefits to the classification of transforming smooth time series to the complex Fourier domain, for reasonably periodic data, and to wavelet space for ECG data. In the Fourier experiments, the classification accuracy for even a reasonably small number of coefficients ($n=20$) was similar and frequently better than the classification accuracy on the corresponding dataset in the original time domain. Besides the potential of improving classification accuracy, this suggests that the method can be used to reduce the number of dimensions of the feature vectors to a large extent. A similar observation was made for heartbeat classification using wavelet features, where we have obtained a better classification performance when training was applied on only the fourth- and fifth-level coefficients, as compared to training on the full-wavelet space representation. For either transform and subsequent truncation, we have observed a reduction of over-fitting effects. As the number of parameters in GMLVQ scales quadratically with the number of features, the truncation also reduces the computational effort in the training phase considerably.

The optimal number of coefficients is dependent on the properties of the dataset. For future study, an automatic method could be devised that suggests a number of coefficients based on the available training data according to a criterion of optimality, which seeks the best balance between accuracy and the number of coefficients.

Concerning interpretability of the classifier, we have shown by means of back transformation of the benefits of obtaining interpretability in both spaces: The space of the transform and the original space. It allows to inspect prototypes in the space of the transform and in the time domain, while still maintaining all benefits of training in coefficient space. The relevance profile gives useful insight into the most discriminative components of the transform. Especially in the case of Fourier, we have seen that back-transforming the relevance matrix yields plausible time-domain interpretability of relevances, which lacks by default when training in Fourier space. The relevance profile in wavelet space is interpretable in time and scale by default, as we have seen verified in the experiments, hence it is less essential to back-transform the wavelet-space relevances.

We have chosen heartbeat classification for our study into the usefulness of the method in combination with the wavelet transform. However, when classification performance is the main priority, additional important ECG features should be included in the wavelet-space vectors. Increasing the classification performance by using the proposed approach and adding other important features could be interesting for future study.

In summary, our work demonstrates that the combination of dimension-reducing transformations with, e.g., GMLVQ constitutes a versatile framework which offers the potential to improve performance and reduce computational workload significantly while retaining the interpretability and white-box character of prototype-based relevance learning.