An adaptive twin support vector regression machine based on rough and fuzzy set theories

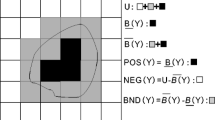
Abstract

It is known that the existing $\nu$-twin support vector regression ($\nu$-TWSVR) has the ability to optimize $\varepsilon _1$ and $\varepsilon _2$ automatically through the proper selections of the parameters $\nu _1$ and $\nu _2$. However, since only the points near the lower-bound and upper-bound regressors are considered, it often results in overfitting problems. Furthermore, the equal penalties are applied to all samples that normally have different effects on the regressor function. In this paper, we propose an adaptive twin support vector regression (ATWSVR) machine to reduce the negative impacts of the possible outliers in $\nu$-twin support vector regression ($\nu$-TWSVR) by incorporating the fuzzy and rough set theories. First, two optimization models are constructed to obtain the lower and upper-bound regressors involving the use of the tools in rough and fuzzy set theories. Consequently, Theorems 1 and 2 are derived, through the application of KKT conditions and duality theory, to provide the connections between the dual optimal values and the location regions of the data points. Then, the definitions of different types of support vectors and their fuzzy proportions are given and Theorems 3 and 4 are proved to provide the bounds for the fuzzy proportions of these support vectors. Finally, the training data points located in different regions are assigned different fuzzy membership values by using iterative methods. Moreover, this approach can achieve the structural risk minimization and automatically control the fuzzy proportions of support vectors. The proposed ATWSVR is more robust for the data sets with outliers, as evidenced by the experimental results on both simulated examples as well as the benchmark real-world data sets. These results also confirm the claims made in the theorems mentioned above.