Calculations of the heat source parameters on the basis of temperature fields with the use of ANN

Abstract

In the paper, a method of automatic choice of the boundary conditions is presented. This method allows the initial estimation the value of the boundary conditions during the heating operation for the welding process. The solutions described in this paper can successfully support the work of the specialists performing numerical simulations. They also significantly reduce the time required to estimate the boundary conditions parameters consistent with the actual experiment. The accuracy of the solution in the presented method is not dependent on the empirical models of boundary conditions for the heating process. It is also much more universal. Artificial neural networks after the learning process can be used to perform a reverse analysis for the heat treatment process, for example, to determine the parameters of welding process in the production process of steel elements.

1 Introduction

The modeling of mechanical phenomena, which occur in the welding process, is very complicated, especially by the number of phenomena in this process and the coupling among them. Determination of the value of important parameters of the analyzed process in the industrial conditions causes significant calculation errors. It is due to the lack of appropriate data available from the measurements and the empirical function of environmental variables defined in the laboratory conditions to approximate of process parameters. Calculating the stress state in the welding joint is the last stage of the numerical calculations. It is preceded by analysis of thermal phenomena and the phase transitions between the solid and liquid states. It means that the estimation errors of the parameters of the thermal phenomena can cause inaccuracy (beyond an acceptable level) of the calculations of the stress state. Assuming that all elements in the numerical model that significantly influence the obtained results are taken into account, the correct value of boundary and initial conditions must be also assumed.

In the paper, the method of calibration of the parameters of the heat source, used in the modeling of thermal phenomena in the welding process of the steel element with a constant profile, is presented (typical inverse problem) [8]. The parameters of the heat source are determined by the artificial neural network (ANN) on the basis of data from the control nodes from the welded element [11,12,13]. The input data for the ANN can be the values of the temperature fields, phase composition, shape of the heat-affected zone or the value of hardness. In the paper, the set of the input values of the multilayer perceptron is restricted to the values of the temperature profile in the plane perpendicular to the path of the heat source. To the learning process of the ANN, the significant number of learning and testing data is required. Therefore, due to economic reasons, the data from the numerical calculations are used. Two thousand numerical simulations for the different combination of the parameters of the heat source are performed. The computations for the constant welding rate are made. It is assumed that the heat source is modeled by the sum of the Neumann boundary condition and the volumetric heat source with Gaussian distributions. The learning and testing sets are calculated using the copyright software which solves the heat transfer equation with a convective term based on the finite element method in the Petrov–Galerkin formulation (task in 3D).

A literature survey shows that in many cases on the basis of the output data, the input data are determined. In the case of welding, the determination of the process parameter or parameters of the computational model is rarely considered.

Chokkalingham et al. [4] used an artificial neural network to estimate the weld bead width and depth of penetration from the infrared thermal image of the weld pool during A-TIG welding. An artificial neural network (ANN) model has been applied to the prediction of key weld geometries produced while using gas metal arc welding with alternating shielding gases [3]. The model can predict the penetration, leg length and effective throat thickness for a given set of weld parameters and alternating shielding gas frequency. Dhas and Somasundaram [5] applied ANN to modeling and prediction of dimensions of the heat-affected zone for the submerged arc welding process. Welding current, arc voltage, arc efficiency and heat flux have been used as the learning file for the ANN model. Khalaj et al. [7] used ANN to predict the ferrite fraction of microalloyed steels during continuous cooling. Fourteen parameters affecting the ferrite fraction were considered as inputs, including the cooling rate, initial austenite grain size and different chemical compositions. Modeling of laser welding of a stainless sheet butt joint has also been made using a backpropagation-trained neural network [2]. A neural network has been used to analyze the effects of input parameters, namely beam power, welding speed and beam angle on the output parameters depth of penetration and bead width. Ahmadzadeh et al. [1] developed the backpropagation neural network model for the prediction of maximum residual stresses produced in gas metal arc welding process. The thickness of the plate, electrode size, welding speed, current/voltage intensity have been considered as the input parameters and the maximum residual stresses due to welding as output parameters in the development of the model.

2 Determining of the parameters of the heat source for the numerical model of a welded steel plate

The calibration of the parameters of boundary and initial conditions for the numerical model can be performed in many ways. One possibility is searching for the required values through multiple numerical simulations. It is also possible to calibrate the parameters by using an inverse method. Such a method can be solved by using artificial intelligence, in particular artificial neural networks. In the presented model, the parameters of the heat source which should be used in the considered process are achieved by basing them on data from the plane perpendicular to the path of the heat source. The information in the section plane may relate to: the temperature profile, the profile of hardness or the obtained metallographic structure. The input data can also be the range of the melted area or the heat-affected zone area. The set of input data for the multilayer perceptron herein is limited to the value of temperature in the plane perpendicular to the path of the heat source.

Fig. 1

The hybrid model of the heat source: a superficial source, b volumetric source, c sum of the sources, [K]

In the model of thermal phenomena, in order to simulate the welding process, the hybrid model of a source is included. This model allows for including nonlinear distribution of the heat source on the depth of penetration. Depending on the used technology (induction heating, laser, flame heating, TIG welding), the volumetric and surface factor will have equal weight. Therefore, for practical applications, this model needs to be calibrated for a specific technology. This hybrid model is a combination of superficial and volumetric sources (Fig. 1c)

$$\begin{aligned} q=q_{\mathrm{N}}+q_{\mathrm{V}} \end{aligned}$$

(1)

The superficial source (Fig. 1a) is determined by the function [14]

$$\begin{aligned} q_{\mathrm{N}}\left( x,z\right) =\frac{Q_{\mathrm{N}}}{2 \pi R_{\mathrm{N}}^2}\exp \left( -\frac{\left( x-x_0\right) ^2+\left( z-z_0\right) ^2}{2R_{\mathrm{N}}^2}\right) \end{aligned}$$

(2)

The volumetric source (Fig. 1b)—function [14]

$$\begin{aligned} q_{\mathrm{V}}\left( x,z\right) =\frac{Q_{\mathrm{V}}}{2 \pi R_{\mathrm{V}}^2h}\exp \left( -\frac{\left( x-x_0\right) ^2+\left( z-z_0\right) ^2}{2R_{\mathrm{V}}^2}\right) \end{aligned}$$

(3)

In the presented model, the radius of the superficial $(R_{\mathrm{N}})$ and volumetric $(R_{\mathrm{V}})$ sources and their power $(Q_{\mathrm{N}}, Q_{\mathrm{V}})$ are searched [8]. There are many technologies where the size of a heat source (its radius) can be easily controlled. The selection of the radius of the heat source can be made once for the whole process (laser heating, induction heating) or can be changed dynamically during the process. This is possible, for example, for TIG welding where the size of the heat source depends on the distance of the electrode from the surface. In this paper, only the constant value of the radius of the heat source for the whole process was analyzed. The heating process for the considered geometry (Fig. 2) does not require dynamic changes of the radius. All calculations were performed on the copyrighted software implemented in C$++$ language.

Fig. 2

Graphical interpretation of the described example

It was established that a steel sheet of the geometry shown in Fig. 2 would be heated. Based on the data on technological processes, limit values for the parameters of the heat source were determined. It was assumed that the parameters of the heat source would change randomly within the appropriate ranges: $R_{\mathrm{N}} \in [0.0015,0.024]$ [m], $Q_{\mathrm{N}} \in [1000,8000]$ [W], $R_{\mathrm{V}} \in [0.001,0.016]$ [m], $Q_{\mathrm{V}} \in [5\cdot 10^3,5\cdot 10^4]$ [W]. Based on these randomly selected parameters, and assuming that the maximal temperature in the area should be in the range of 1500–4000 K, 2000 numerical simulations were performed. These additional temperature limits affected the reduction in the range of parameters of the heat source (Figs. 3, 4). The data from the simulations were split in two halves and assigned to the learning and testing sets (one thousand for each). The number of parameters of the heat source (specified randomly) for the learning and testing that sets are presented below (Figs. 3, 4). The number of elements was determined for unit intervals, respectively, equal to $R_{\mathrm{N}}=0.0005$ m, $Q_{\mathrm{N}} =266.67$ W, $R_{\mathrm{V}}=0.0005233$ m, $Q_{\mathrm{V}}=166{,}633$ W. As can be seen, the distribution of the analyzed sources is similar to Gaussian, while the distribution of power is rather linear.

Fig. 3

The histogram of parameters of the boundary condition in a learning set: a the radius of superficial and volumetric sources, b the power of superficial and volumetric sources

Fig. 4

The histogram of parameters of the boundary condition in a testing set: a the radius of superficial and volumetric sources, b the power of superficial and volumetric sources

The parameters of the heat source for the welding simulation were obtained according to the following scheme:

Step 1: Solution of the steady-state task. Determination of the learning and testing of n-element sets

In the first step, which allows the implementation of the inverse analysis of the presented problem, the learning and testing data are determined. These data have been calculated by using a numerical model to solve the heat conductivity equation with the convection term by using the finite element method in a Petrov–Galerkin formulation [8]. The adoption of the above assumptions (radius and powers of the heat source) for the presented task enables the determination of the temperature profiles for the moving heat source and for different boundary and initial conditions. The numerical simulation of the welding process was performed for the plate made from C45 steel (Fig. 2). Only part of half of the steel element, due to the symmetry (plane of the symmetry $\varGamma _{\mathrm{S}}$) of the technological process, was considered. The steel element with dimensions: $l_x=0.05$ m, $l_y=0.01$ m and $l_z=0.025$ m were divided equally into 50, 10, 25 nodes in the (x, y, z) directions, respectively. The use of steady-state tasks significantly shortens the time of the calculations, because the temperature profile is obtained by solving, at most, a few iterations (taking into account the heat of melting and solidification of the weld pool).

To model the thermal phenomena, the differential equation which describes a steady-state heat transfer is used, with a convective term (Euler coordinates)

$$\begin{aligned} \nabla \cdot \left( \lambda \nabla T\right) -\rho C\nabla T \cdot V=-q_v \end{aligned}$$

(4)

Equation 4 is supplemented with appropriate boundary conditions and physical properties (see Fig. 2):

• the drift velocity $V_x = 0.025$ m/s,

• on boundary $\varGamma _{\mathrm{F}}$ (front plane) Dirichlet boundary condition $T = 293$ K,

• on boundary $\varGamma _{\mathrm{S}}$ (plane of symmetry) Neumann boundary condition with $q=0$ W/m$^2$,

• on boundaries $\varGamma _{\mathrm{T}}$ (upper plane) and $\varGamma _{\mathrm{D}}$ (lower plane) Newton boundary condition with $T_{\mathrm{air}} = 293$ K (outside the area of heat source), the heat transfer coefficient of air $(\alpha _{\mathrm{air}})$ was assumed as in the paper of Li [10],

• on boundary $\varGamma _{\mathrm{B}}$ (back plane) the continuation of element is assumed (the remaining part of the element in direction x was considered),

• the material properties: thermal conductivity coefficient $\lambda =35$ [W/m K], thermal capacity $C= 644$ [J/kg K] and density $\rho =7760$ [kg/m$^3$].

Assuming constant material properties and a constant velocity of heat source, as well as the number of required simulations, the use of a steady-state task instead of a non-steady-state one does not introduce any significant errors, but significantly shortens the calculation time. The use of the convection term in the Euler coordinates well approximates the moving heat source. In the case of small values of the volumes of moving heat sources, the influence of the latent heat on the obtained results is insignificant.

In the presented example, the Pécleta number is equal to $Pe=1.82$; therefore, the method of stabilization model due to drift velocity has been used. The task was solved by using the finite element method in the Petrov–Galerkin formulation [16]

$$\begin{aligned} \left( K_{ij}+B_{ij}^{\mathrm{NR}}\right) T_j=B_{ij}^{\mathrm{NR}}T_J^\infty -B_{ij}^{Q}q_j^*+Q_{ij}q_j^V \end{aligned}$$

(5)

The matrices appearing in Eq. (5) are determined by the following integrals

$$\begin{aligned} \begin{aligned} K_{ij}^{*e}&= \int \limits _{\varOmega ^e}\lambda w_i,_\alpha \varPhi _j,_\alpha {\mathrm{d}}\varOmega \\ V_{ij}^{e}&= \rho C\int \limits _{\varOmega ^e} w_i\varPhi _j,_\alpha V_{k\alpha } \varPhi _k {\mathrm{d}}\varOmega \\ K_{ij}^{e}&= K_{ij}^{*e} + V_{ij}^{e}\\ B_{ij}^{e}&= \int \limits _{\varGamma ^{e(Q)}}w_i\varPhi _j{\mathrm{d}}\varGamma +\int \limits _{\varGamma ^{e(\mathrm{NR})}}\alpha ^\infty w_i\varPhi _j{\mathrm{d}}\varGamma = B_{ij}^Q+B_{ij}^{\mathrm{NR}}\\ Q_{ij}^e&= \int \limits _{\varOmega ^e}w_i\varPhi _j{\mathrm{d}}\varOmega \end{aligned} \end{aligned}$$

(6)

The system of equations was solved on the basis of the MKL library and the PARADISO function.

The weighting functions are combinations of trilinear approximation functions and functions with moving integration points (upwind function) [9, 15]

$$\begin{aligned} w_i\left( \xi ,\eta ,\zeta \right) =\left( \varPhi _i\left( \xi \right) +w_i^*\left( \xi \right) \right) \left( \varPhi _i\left( \eta \right) +w_i^*\left( \eta \right) \right) \left( \varPhi _i\left( \zeta \right) +w_i^*\left( \zeta \right) \right) \end{aligned}$$

(7)

where $w_i^*\left( \xi \right)$, $w_i^*\left( \eta \right)$, $w_i^*\left( \zeta \right)$ are the stabilizing members that take the following form

$$\begin{aligned} \begin{aligned} w_i^*\left( \xi \right)&= \xi _i\alpha _ik\left( 1-\xi ^2\right) \\ w_i^*\left( \eta \right)&= \eta _i\beta _ik\left( 1-\eta ^2\right) \\ w_i^*\left( \zeta \right)&= \xi _i\theta _ik\left( 1-\zeta ^2\right) \\ \end{aligned} \end{aligned}$$

(8)

The factors of moving the integration points $\alpha _i$, $\beta _i$, $\theta _i$ are

$$\begin{aligned} \begin{aligned} \alpha _i&= \mathrm{coth}\left( \gamma _i^x\right) -\frac{1}{\gamma _i^x},\quad \gamma _i^x=\frac{\rho C}{\lambda }h_iv_x\\ \beta _i&= \mathrm{coth}\left( \gamma _i^y\right) -\frac{1}{\gamma _i^y},\quad \gamma _i^y=\frac{\rho C}{\lambda }h_iv_y\\ \theta _i&= \mathrm{coth}\left( \gamma _i^z\right) -\frac{1}{\gamma _i^z},\quad \gamma _i^z=\frac{\rho C}{\lambda }h_iv_z\\ \end{aligned} \end{aligned}$$

(9)

In the first step, the profile of temperature (input data of artificial neural network) for the assumed parameters of the heat source (output data of artificial neural network) has been obtained. In the task, it is assumed that for each of the two thousand numerical simulations, the values of temperature are obtained from 250 control nodes. The number of control points is determined by the number of grid nodes in the cross section to element. This number can be optimized due to the small variability of temperature in some nodes. The location of the control nodes, the selection of the appropriate cross section, was made on the basis of the maximum temperature in the grid nodes (Fig. 5). The parameters of the hybrid model of the heat source, the radius of superficial and volumetric sources and their power are analyzed.

Fig. 5

The temperature profile—location of control nodes

Step 2: Neural network modeling

On the basis of the obtained input and output data, the numbers of neurons in the hidden layer were determined by using a geometrical pyramid rule. The artificial neural network was built with one-way multilayer perceptron with sigmoidal neurons.

The input signal of the neurons is added together by using the appropriate weights of neuron including bias. The sum is then activated by a nonlinear activation function to get output signal $y_i^k$. The output signal of ith neuron in kth layer $(i=1,\ldots , N_k, k=1,\ldots ,L)$ is described by equation [12, 13]

$$\begin{aligned} y_i^k=f\left( s_i^k\left( t\right) \right) =f\left( \mathop {\sum }\limits _{i=1}^{N_k}w_{ij}^k\left( t\right) x_j^k\left( t\right) +w_0\right) \end{aligned}$$

(10)

To solve the task, the hyperbolic tangent activation function $f(s_i^k\left( t\right) )={\mathrm{tanh}}(s_i^k\left( t\right) )$ has been used [6]. The hyperbolic tangent activation function is perhaps the most common activation function used for neural networks. This function allows the continuous transition between the maximum and minimum value, and its derivative is easy to calculate.

The input and output data, due to their wide range of values before the learning process has been subjected to normalization. To calculate the normalized values, the min–max normalization has been used [11]

$$\begin{aligned} x_i^\prime =\frac{x_i-x_i^{\mathrm{MIN}}}{x_i^{\mathrm{MAX}}-x_i^{\mathrm{MIN}}} \end{aligned}$$

(11)

Fig. 6

The diagram of the applied multilayer network

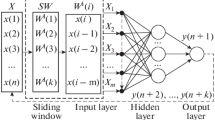
Figure 6 shows a graphical representation of the applied artificial neural network. In the input of the network (first layer, $k=1$), the value of temperature from 250 control nodes is given. The outputs of the last layer ($k=L$) are the radius of the superficial and volumetric sources and their power. It was assumed that the two hidden layers, made, respectively, from N1 and N2 neurons, are needed because the number of inputs is significant compared to the number of outputs. To examine of the influence of the different structure of the neural network model, the RMSE errors and the percentage errors of the learning and testing sets were determined. In order to determine the optimal structure of ANN, the networks with two hidden layers and a constant number of inputs—250 and outputs—4 were considered. In the first hidden layer, the number of neurons was in the ranged from 30 to 120 (6 cases), while in the second layer 10–30 (3 cases). All errors were in the range from 1.5 to 2% (Table 1). The two neural networks with different numbers of neurons in the hidden layers have been taken into account. The first neural network consisted of $N1=100$, $N2=30$ neurons in the hidden layers (Analysis No. 1). The second neural network was built with $N1=50$, $N2=30$ neurons in the hidden layers (Analysis No. 2).

Step 3: Learning of a neural network

To train the network, the backpropagation algorithm has been used [12, 13]. The aim of the algorithm is to minimize layer errors defined patterns (learning sequence), which are the set of corresponding values of the inputs and outputs of the neural network. The error at network output is calculated by formula [12, 13]

$$\begin{aligned} Q\left( t\right) =\mathop {\sum }\limits _{i=1}^{N_L}\left( \varepsilon _i^L\right) ^2\left( t\right) =\mathop {\sum }\limits _{i=1}^{N_L}\left( d_i^L \left( t\right) -y_i^L\left( t\right) \right) ^2 \end{aligned}$$

(12)

The network error is minimized by the steepest descent rule for the learning process. To increase the speed of the learning neural network, the backpropagation with momentum (MBP) has been applied. This method depends on the use of an additional coefficient $\left( \alpha \right)$ in the equation called momentum. This coefficient makes the value of weight in the next step $\left( t+1\right)$ dependent not only on its value in the current step (as in the classic backpropagation method) but also on the previous step $\left( t-1\right)$ [13]

$$\begin{aligned} w_{ij}^k\left( t+1\right) =w_{ij}^k\left( t\right) +2\eta \varepsilon _i^k\left( t\right) f'\left( s_i^k\left( t\right) \right) x_j^k+\alpha \left( w_{ij}^k\left( t\right) -w_{ij}^k\left( t-1\right) \right) \end{aligned}$$

(13)

An evaluation of the quality of the applied artificial neural network in the learning process based on a root-mean-square error (RMSE) has been performed (RMSE)

$$\begin{aligned} {\mathrm{RMSE}}=\sqrt{\frac{\mathop {\sum }\nolimits _{i=1}^{N_L}\left( d_i^L\left( t\right) -y_i^L\left( t\right) \right) ^2}{N_L}} \end{aligned}$$

(14)

An analysis of a network error due to the adopted momentum coefficient and learning coefficient (Fig. 7) has been carried out. It was assumed that the values of the coefficients for the presented task are, respectively, equal $\alpha = 0.86$, $\eta = 0.03$.

Fig. 7

RMSE error dependency on the value of learning and momentum coefficient

Table 1 Summary of neural network with different structures and their learning and testing error

During the learning process, the influence of network construction on the accuracy of the results has been determined. The values of error depending on a number of elements of the learning set using a percentage and RSME error have been presented (Fig. 8). It was assumed that the number of unique elements in the learning and testing sets is n equal to 1000 for each set. The learning process has been implemented through the execution of n epochs. In the presented considerations, the number n takes values from the set of $\{100, 200, 250, 400, 500, 1000\}$.

Fig. 8

The percentage and RMSE error dependency on the number of elements in the learning set and number of epochs: a analysis No. 1, b analysis No. 2

The results in Fig. 8 show the average error values determined on the basis of 10 series of calculations.

Step 4: Testing of a neural network

To verify the algorithm, a numerical test has been performed. On the basis of the parameters of the heat source determined by the artificial neural network, the numerical simulation has been performed to obtain the temperature profile. The error between the values of the temperature obtained from the numerical simulation and the temperature values determined by the artificial neural network have been estimated. On the basis of the obtained results, the maximum error for each individual simulation has been determined. From among these values of errors, the maximum and minimum percentage error value for the testing set was determined as well as the average, standard deviation and median, separately and independently for the two neural networks with different structures (Table 2).

Table 2 The value of error for the two neural networks

The values of parameters of the heat source obtained from numerical simulations and the values determined by the artificial neural network have been compared. The mean percentage value of the difference between each of parameters during the testing process, is presented in Fig. 9. The value of the test error was determined by using a testing set consisting of 1000 cases.

Fig. 9

The mean percentage error dependency on the number of elements in the testing set and number of epochs: a analysis No. 1, b analysis No. 2

The results in Table 2 and in Fig. 9 show the average error values determined on the basis of 10 series of calculations.

3 Conclusion

In the paper, the use of a model based on artificial neural networks in order to determine the parameters of the heat source to the simulation of welding process has been presented. During the learning operation, it was determined how the structures of the network and the number of elements of the learning set affect the value of RMSE and the percentage error (Fig. 8). The use of a different number of neurons in the first hidden layer does not significantly affect the value of the error. To obtain a value of an estimated error less than 10% for the output value, the minimum size of the learning set must amount to 1000 elements and 400 epochs.

A trained neural network allows for solving the inverse task with a small value of error in the various parameters of the heat source (Fig. 9). The percentage error for the value of maximum, minimum as well as median, average and standard deviation for the two neural networks with different structures has been presented in Table 2. The values of error have been calculated for the testing data, which have not been subjected to a learning process. It was observed that in the case of a second network, the error decreases faster when the number of learning data is increased. This follows from the better match which the number of neurons in the hidden layer for the present example. The value of standard deviation in relation to the mean is significant (more than 50%). This means a large variation in the value of error but on an acceptable level. The maximum error values in comparison with the average and standard deviation point to the occurrence of a few cases where the matching error of the value is large. The average indicates the accuracy of the applied artificial neural networks for solving inverse tasks.

Taking into account the required number of elements in the learning and testing sets, it is not possible to obtain such data from experimental research. For manufacturing processes, it is necessary to use the large number of data in the sets obtained from numerical models. This number is a basic element affecting the accuracy of the network performance. Using the data from a numerical model is especially associated with cost-effective experimental research. Performing the experiment for various type of the materials and the type of the heat source is associated with high costs of research. The obtained results, which determine well the characteristics of the heat source, can be used to correctly determine the device that generates a given type of heat source. The authors could not use the results from experimental research due to the amount of data required to train the network and the cost of their receipt. Only the accuracy of calculations obtained using the artificial neural network—steady-state tasks with non-steady-state tasks were compared. Well-verified numerical models allow for the construction of neural networks for solving inverse tasks or may be an additional element in the control process.