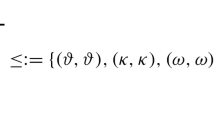Characterizations of ordered semigroups in terms of (∈, ∈ ∨ q)-fuzzy interior ideals

Abstract

In this paper, we give characterizations of ordered semigroups in terms of (∈, ∈ ∨q)-fuzzy interior ideals. We characterize different classes regular (resp. intra-regular, simple and semisimple) ordered semigroups in terms of (∈, ∈ ∨q)-fuzzy interior ideals (resp. (∈, ∈ ∨q)-fuzzy ideals). In this regard, we prove that in regular (resp. intra-regular and semisimple) ordered semigroups the concept of (∈, ∈ ∨q)-fuzzy ideals and (∈, ∈ ∨q)-fuzzy interior ideals coincide. We prove that an ordered semigroup S is simple if and only if it is (∈, ∈ ∨q)-fuzzy simple. We characterize intra-regular (resp. semisimple) ordered semigroups in terms of (∈, ∈ ∨q)-fuzzy ideals (resp. (∈, ∈ ∨q)-fuzzy interior ideals). Finally, we consider the concept of implication-based fuzzy interior ideals in an ordered semigroup, in particular, the implication operators in Lukasiewicz system of continuous-valued logic are discussed.

1 Introduction

In mathematics, an ordered semigroup is a semigroup together with a partial order that is compatible with the semigroup operation. Ordered semigroups have many applications in the theory of sequential machines, formal languages, computer arithmetics, and error-correcting codes. A theory of fuzzy sets on ordered semigroups can be developed. Using the idea of a quasi-coincidence of a fuzzy point with a fuzzy set, the concept of an (α, β)-fuzzy interior ideal in an ordered semigroup can be developed. The idea of a quasi-coincidence of a fuzzy point with a fuzzy set, which is mentioned in [4], played a vital role to generate some different types of fuzzy subgroups. It is worth pointing out that Bhakat and Das [4] gave the concepts of (α, β)-fuzzy subgroups by using the “belongs to” relation (∈) and “quasi-coincident with” relation (q) between a fuzzy point and a fuzzy subgroup, and introduced the concept of an (∈, ∈ ∨q)-fuzzy subgroup. In particular, (∈, ∈ ∨q)-fuzzy subgroup is an important and useful generalization of Rosenfeld’s fuzzy subgroup. It is now natural to investigate similar type of generalizations of the existing fuzzy subsystems of other algebraic structures. With this objective in view, Davvaz [7] introduced the concept of (∈, ∈ ∨q)-fuzzy sub-near-rings (R-subgroups, ideals) of a near-ring and investigated some of their interesting properties. Jun and Song [12] discussed general forms of fuzzy interior ideals in semigroups. Kazanci and Yamak introduced the concept of a generalized fuzzy bi-ideal in semigroups [15] and gave some properties of fuzzy bi-ideals in terms of (∈, ∈ ∨q)-fuzzy bi-ideals. Jun et al. [14] gave the concept of a generalized fuzzy bi-ideal in ordered semigroups and characterized regular ordered semigroups in terms of this notion. Many other researchers used the idea of generalized fuzzy sets and gave several characterizations results in different branches of algebra, for example (see [13, 18, 20, 27, 29]).

This paper is divided in the following sections, in Sect. 2, we give some basic definitions and preliminaries lemmas of interior ideals and fuzzy interior ideals of ordered semigroups. In Sect. 3, we give the characterizations of interior ideals in terms of (∈, ∈ ∨q)-fuzzy interior ideals and prove that in regular (resp. intra-regular and semisimple) ordered semigroups the concepts of (∈, ∈ ∨q)-fuzzy interior ideals and (∈, ∈ ∨q)-fuzzy ideals coincide. In Sect. 4, we introduce the concept of (∈, ∈ ∨q)-fuzzy simple ordered semigroups, we also characterize semisimple ordered semigroups in terms of (∈, ∈ ∨q)-fuzzy interior ideals. In the last of this paper, we consider the concept of implication-based fuzzy interior ideals in an ordered semigroup, in particular, the implication operators in Lukasiewicz system of continuous-valued logic are discussed.

2 Preliminaries

By an ordered semigroup (or po-semigroup), we mean a structure (S, ·,  ≤) in which the following are satisfied:

• (OS1) (S, ·) is a semigroup;

• (OS2) (S,  ≤) is a poset;

• (OS3) $a\leq b\longrightarrow ax\leq bx$ and xa ≤ xb for all a, b, x ∈ S.

For $A\,{\subseteq}\,S$, we denote (A] := {t ∈ S|t ≤ h for some h ∈ A}. If A = {a}, then we write (a] instead of ({a}]. For $A,B\,{\subseteq}\,S$, we denote,

$$ AB:=\{ab|a\in A,b\in B\}. $$

Ordered semigroups arise by considering different numerical semigroups, semigroups of functions and binary relations, semigroups of subsets (or subsystems of different algebraic systems, for example ideals in rings and semigroups), etc. Every ordered semigroup is isomorphic to a certain semigroup of binary relations, considered as an ordered semigroup, where the order is set-theoretic inclusion. The classical example of a lattice-ordered semigroup is the semigroup of all binary relations on an arbitrary set.

Let (S, ·,  ≤) be an ordered semigroup. A nonempty subset A of S is called an interior ideal of S if

• (1) If $S\,{\ni}\,b{\leq}a\,{\in}\,A$ then b ∈ A;

• (2) $A^{2}\,{\subseteq}\,A;$

• (3) $SAS\,{\subseteq}\,A.$

Let (S, ·,  ≤) be an ordered semigroup. A nonempty subset A of S is called a left (resp. right) ideal of S if

• (1) If $S\,{\ni}\,b{\leq}a\,{\in}\,A$ then b ∈ A;

• (2) $SA\,{\subseteq}\,A\,\, (\hbox{resp.} \,\,AS\,{\subseteq}\,A).$

A nonempty subset A of S is called an ideal if it is both a left and a right ideal of S.

Obviously, every ideal of an ordered semigroup S is an interior ideal of S. We denote by $I(a)=(a\cup Sa\cup aS\cup SaS]$ the ideal of S generated by a (a ∈ S).

An ordered semigroup (S, ·,  ≤) is called regular if for each a ∈ S there exists x ∈ S such that a ≤ axa. Equivalent Definitions: (1) $A\,{\subseteq}\,(ASA]$ for each $A\subseteq S$. (2) a ∈ (aSa] for each a ∈ S (see [26]). An ordered semigroup (S, ·,  ≤) is called intra-regular if for each a ∈ S there exist x, y ∈ S such that a ≤ xa ² y. Equivalent Definitions: (1) $A\,{\subseteq}\,(SA^{2}S]$ for each $A\,{\subseteq}\,S$. (2) a ∈ (Sa ² S] for each a ∈ S [26]. An ordered semigroup (S, ·,  ≤) is called semisimple if for each a ∈ S, there exist x, y, z ∈ S such that a ≤ xayaz. Equivalent Definition: (1) $A\,{\subseteq}\,(SASAS]$ for each $A\subseteq S$. (2) a ∈ (SaSaS] for each a ∈ S [26]. An ordered semigroup S is called simple (see [16, 17]) if it does not contain proper ideals, that is, for any ideal A of S, we have A = S.

In regular (resp. intra-regular and semisimple ordered semigroups) the concepts of an ideal and interior ideal coincide.

A fuzzy subset F from a universe X is a function from X into unit closed interval [0, 1] of real numbers, i.e., $F:X\longrightarrow \lbrack 0,1]$.

For any two fuzzy subsets F and G of $S, F\preceq G$ means that F(x) ≤ G(x), for all x ∈ S. The symbols $F\wedge G$ and F ∨ G will mean the following fuzzy subsets:

$$ \begin{aligned} (\forall x \in S)(F\wedge G:S&\longrightarrow \lbrack 0,1],x\longmapsto (F\wedge G)(x) =\hbox{min}\{F(x),G(x)\});\\ (\forall x \in S)(F\vee G:S&\longrightarrow \lbrack 0,1],x\longmapsto (F\vee G)(x)=\hbox{max}\{F(x),G(x)\}). \end{aligned} $$

Let a ∈ S and $\emptyset \neq A\subseteq S$, we denote A _a by

$$ A_{a}=\{(y,z)\in S\times S|a\leq yz\}. $$

Let F and G be any two fuzzy subsets of an ordered semigroup S, the product $F\circ G$ of F and G is defined by:

$$ F\circ G:S\longrightarrow \lbrack 0,1],a\longmapsto (F\circ G)(a)=\left \{ \begin{array}{ll} \mathop \bigvee\nolimits_{(y,z)\in A_{a}}\hbox{min}\{F(y),G(z)\} \hbox{ if } A_{a}\neq \emptyset\\ 0\qquad \qquad \qquad \qquad \quad \hbox{ if } A_{a}=\emptyset\\ \end{array}\right. $$

Definition 2.1

A fuzzy subset F of S is called a fuzzy interior ideal of S if

• (1) $({\forall}x,y\,{\in}\,S)(x{\leq}y\,{\longrightarrow}\,F(x){\geq}F(y));$

• (2) (∀x, y ∈ S)(F(xy) ≥ min{F(x), F(y)});

• (3) (∀x, a, y ∈ S)(F(xay) ≥ F(a)).

Definition 2.2

A fuzzy subset F of S is called a fuzzy left (resp. right) ideal of S if

• (1) $({\forall}x,y\,{\in}\,S)(x{\leq}y\,{\longrightarrow}\,F(x){\geq}F(y))$ and

• (2) (∀x, y ∈ S)(F(xy) ≥ F(y) (resp. F(xy) ≥ F(x)).

In regular (resp. intra-regular and semisimple ordered semigroups) the concepts of a fuzzy ideal and fuzzy interior ideal coincide.

Let S be an ordered semigroup and F a fuzzy subset of S, then for all t ∈ (0,1], the set

$$ U(F;t):=\{x\in S|F(x)\geq t\}, $$

is called a level set of F.

In the following, we characterize fuzzy interior ideals of ordered semigroups in terms level interior ideals.

Theorem 2.3

A fuzzy subset F of an ordered semigroup S is a fuzzy interior ideal of S if and only if for all t ∈ (0,1], the set $U(F;t)(\neq \emptyset )$ is an interior ideal of S.

Let (S, ·,  ≤) be an ordered semigroup and $\emptyset \neq A\subseteq S$. Then the characteristic function F _A of A is defined by

$$ F_{A}:S\longrightarrow \left[ 0,1\right],x\longmapsto F_{A}(x):=\left \{ \begin{array}{l} 1\quad\hbox{ if }x\in A,\\ 0\quad\hbox{ if }x \notin A \\ \end{array}\right. $$

Clearly, a nonempty subset A of S is an interior ideal of S if and only if the characteristic function F _A of A is a fuzzy interior ideal of S.

3 (α, β)-fuzzy interior ideals

From now on S is an ordered semigroup and α, β  ∈ {∈, q,  ∈ ∨q,  ∈ ∧ q} unless otherwise specified. Fixed any t ∈ (0,1] and x ∈ S, a fuzzy subset F of the form

$$ F:S\longrightarrow \left[ 0,1\right],y\longmapsto F(y)=\left \{ \begin{array}{ll} t\quad\hbox{ if }y=x,\\ 0\quad\hbox{ otherwise}\\ \end{array}\right. $$

is called a fuzzy point with support x and value t and is denoted by [x; t]. Consider a fuzzy point [x; t], a fuzzy subset F and α, β ∈ {∈, q,  ∈ ∨q,  ∈ ∧q} we define [x; t]αF as follows:

• (a) [x; t] ∈ F (resp. [x; t]q F) means that F(x) ≥ t (resp. F(x) + t > 1) and in this case we say that [x; t] belongs to (resp. quasi-coincident with) fuzzy subset F.

• (b) [x; t] ∈ ∨q F (resp. $\left[x;t\right]\,{\in}\,{\wedge}$ q F) means that [x; t] ∈ F or [x; t]q F (resp. [x; t] ∈ F and [x; t]q F).

By $\left[x;t\right]\overline{\alpha}F$, we mean that [x; t]αF does not hold.

Note that if F is a fuzzy subset S, defined by F(x) ≤ 0.5 for all x ∈ S, then the set $\{\left[x;t\right]|[x;t]\in \wedge qF\}$ is empty.

Definition 3.1

A fuzzy subset F of S is called an (α, β)-fuzzy left (resp. right) ideal of S, where $\alpha\,\neq\, \in \wedge\, q$, if

• (1) $(\forall x,y \in S)(\forall t\in (0,1])(x\leq y,[y;t]\alpha F\longrightarrow \lbrack x;t]\beta F);$

• (2) $(\forall x \in S)(\forall t\in (0,1])([y;t]\alpha F,x\in S\longrightarrow \lbrack xy;t]\beta F(\hbox{resp. }[yx;t]\beta F).$ A fuzzy subset F of S is called an (α, β)-fuzzy ideal of S if it is both an (α, β)-fuzzy right and an (α, β)-fuzzy left ideal of S.

Definition 3.2

A fuzzy subset F of S is called an (α, β)-fuzzy interior ideal of S, where $\alpha \neq \in \wedge$q, if

• (1) $(\forall x,y \in S)(\forall t\in (0,1])(x\leq y,[y;t]\alpha F\longrightarrow \lbrack x;t]\beta F);$

• (2) $(\forall x,y \in S)(\forall t,r\in (0,1])([x;t]\alpha F,[y;r]\alpha F\longrightarrow \lbrack xy; \hbox{min}\{t,r\}]\beta F);$

• (3) $(\forall x,a,y \in S)(\forall t\in (0,1])([a;t]\alpha F\longrightarrow \lbrack xay;t]\beta F).$

In the theory of (α, β)-fuzzy interior ideals, the central role is played by (α,  ∈ ∨q)-fuzzy interior ideals, where α ∈ {∈, q,  ∈ ∨q}, especially (∈, ∈ ∨q)-fuzzy interior ideals.

Theorem 3.3 (cf. [18])

Let F be a fuzzy subset of S. Then F is a fuzzy interior ideal if and only if

• (1) $(\forall x,y \in S)(\forall t\in (0,1])(x\leq y,[y;t]\in F\longrightarrow \lbrack x;t]\in F).$

• (2) $(\forall x,y \in S)(\forall t,r\in (0,1])([x;t]\in F,[y;t]\in F\longrightarrow \lbrack xay;t]\in F).$

• (3) $(\forall x,a,y \in S)(\forall t\in (0,1])([a;t]\in F\longrightarrow \lbrack xay;t]\in F).$

Clearly, a fuzzy subset F is an (∈, ∈)-fuzzy interior ideal if and only if for all t ∈ (0,1], the set $U(F;t)(\neq\emptyset )$ is an interior ideal of S.

Theorem 3.4 (cf. [18])

If F is a nonzero (α, β)-fuzzy interior ideal of S, then the set F ₀ = {x ∈ S|F(x) > 0} is an interior ideal of S.

4 (∈, ∈ ∨q)-fuzzy interior ideals

In this section, we prove that the concepts of an (∈, ∈ ∨q)-fuzzy ideal and (∈, ∈ ∨q)-fuzzy interior ideal in a regular (resp. intra-regular and semisimple) ordered semigroup coincide.

Lemma 4.1 (cf. [18])

A fuzzy subset F is an (∈, ∈ ∨q)-fuzzy interior ideal of S if and only if

• (1) $({\forall}x,y\,{\in}\,S)(x{\leq}y{\longrightarrow}F(x)\geq \hbox{min}\{F(y),0.5\});$

• (2) $(\forall x,y\in S)(F(xy)\geq \hbox{min}\{F(x),F(y),0.5\});$

• (3) $(\forall x,a,y\in S)(F(xay)\geq \hbox{min}\{F(a),0.5\}).$

Lemma 4.2 (cf. [18])

A fuzzy subset F is an (∈, ∈ ∨q)-fuzzy left (resp. right or two-sided) ideal of S if and only if

• (1) $({\forall}x,y\,{\in}\,S)(x{\leq}y{\longrightarrow}F(x)\geq \hbox{min}\{F(y),0.5\}).$

• (2) (∀x, a, y ∈ S)(F(xay) ≥ min{F(y), 0.5} (resp. F(xy) ≥ min {F(x), 0.5}).

Lemma 4.3 (cf. [18])

The characteristic function F _A of A is an (∈, ∈ ∨q)-fuzzy interior ideal of S if and only if A is an interior ideal of S.

Proposition 4.4

Every (∈, ∈ ∨q)-fuzzy ideal of S is an (∈, ∈ ∨q)-fuzzy interior ideal of S.

Proof

The proof is straightforward. $\square$

The converse of Proposition 4.4 is not true, in general.

Example 4.5

Consider the ordered semigroup S = {0, 1, 2, 3} with the following multiplication table and order relation

$$ \leq :=\{(0,0),(1,1),(2,2),(3,3),(0,1)\} $$

Let $F:S\longrightarrow \lbrack 0,1]$ be a fuzzy subset defined by:

$$ F(0)=0.7,\qquad F(1)=0.4,\qquad F(2)=0.6,\qquad F(3)=0 $$

Then F is an (∈, ∈ ∨q)-fuzzy interior ideal of S, but F is not an (∈, ∈ ∨q)-fuzzy ideal of S. Because $F(xyz)=F(0)=0.7>0.5 \geq F(y)\wedge 0.5.$ Also if xy = 0, then $F(xy)=F(0)=0.7>0.5\geq F(x)\wedge F(y)\wedge 0.5$. If xy = 1, then $F(xy)=F(1)=0.4>0=F(x)\wedge F(y)\wedge 0.5$ and if xy = 2, then $F(xy)=F(2)=0.6>0=F(x)\wedge F(y)\wedge 0.5$ for every x, y, z ∈ S. Obviously for every x, y ∈ S, such that x ≤ y we have $F(x)\geq F(y)\wedge 0.5$. But $F(2.3)=F(1)=0.4<0.5=F(2) \wedge 0.5$. Hence F is not an (∈, ∈ ∨q)-fuzzy right ideal. Thus F is not an (∈, ∈ ∨q)-fuzzy ideal of S.

Proposition 4.6

Let S be a regular ordered semigroup, then every (∈, ∈ ∨q)-fuzzy interior ideal is an (∈, ∈ ∨q)-fuzzy ideal of S.

Proof

Let F be an (∈, ∈ ∨q)-fuzzy interior ideal and a, b ∈ S. Then there exists x ∈ S such that a ≤ axa, hence we have

$$ \begin{aligned} F(ab) &\geq F((axa)b)\wedge 0.5\hbox{ (because }F\hbox{ is an }(\in ,\in \vee q\hbox{)-fuzzy interior ideal)}\\ &=F((ax)ab)\wedge 0.5\\ &\geq(F(a)\wedge 0.5)\wedge 0.5 (\hbox{because }F\hbox{ is an }(\in ,\in \vee q\hbox{)-fuzzy interior ideal)}\\ &=F(a)\wedge 0.5 \\ \end{aligned} $$

Similarly, we can show that $F(ab)\geq F(b)\wedge 0.5$ for every a, b ∈ S. Thus F is an (∈, ∈ ∨q)-fuzzy ideal of S. $\square$

From Propositions 4.4 and 4.6, we have the following Corollary:

Corollary 4.7

In regular ordered semigroups, the concepts of an (∈, ∈ ∨q)-fuzzy ideals and (∈, ∈ ∨q)-fuzzy interior ideals coincide.

Proposition 4.8

Let S be a is semisimple ordered semigroup, then every (∈, ∈ ∨q)-fuzzy interior ideal is an (∈, ∈ ∨q)-fuzzy ideal of S.

Proof

Let F be an (∈, ∈ ∨q)-fuzzy interior ideal and a, b ∈ S. There exist x, y, z ∈ S such that a ≤ xayaaz. Then

$$ \begin{aligned} F(ab) &\geq F((xayaz)b)\wedge 0.5\quad (\hbox{because }F\hbox{ is an } (\in ,\in \vee q\hbox{)-fuzzy interior ideal)} \\ &=F((xay)a(zb))\wedge 0.5 \\ &\geq (F(a)\wedge 0.5)\wedge 0.5\\ &=F(a)\wedge 0.5 \\ \end{aligned} $$

Similarly, we can show that $F(ab)\geq F(b)\wedge 0.5$ for every a, b ∈ S. Thus F is an (∈, ∈ ∨q)-fuzzy ideal of S. $\square$

From Propositions 4.4 and 4.8, we have the following Corollary:

Corollary 4.9

In semisimple ordered semigroups, the concepts of an (∈, ∈ ∨q)-fuzzy interior and an (∈, ∈ ∨q)-fuzzy ideal coincide.

If (S, ·,  ≤) is an ordered semigroup and a ∈ S, and F a fuzzy subset of S, we denote by I _a the subset of S defined as follows:

$$ I_{a}:=\{b\in S|F(b)\geq F(a)\wedge 0.5\}. $$

Proposition 4.10

Let S be an ordered semigroup and F an (∈, ∈ ∨q)-fuzzy right ideal of S. Then I _a is a right ideal of S for every a ∈ S.

Proof

Let F be an (∈, ∈ ∨q)-fuzzy right ideal of S and a ∈ S. Then $I_{a}\neq \emptyset ,$ because a ∈ I _a for every a ∈ S. Let b ∈ I _a and x ∈ S. We have to prove that bx ∈ I _a . Since F is an (∈, ∈ ∨q)-fuzzy right ideal of S, we have $F(bx)\geq F(b)\wedge 0.5.$ Since b ∈ I _a , we have $F(b)\geq F(a)\wedge 0.5$ and $F(b)\wedge 0.5\geq F(a)\wedge 0.5\wedge 0.5=F(a)\wedge 0.5.$ Thus $F(bx)\geq F(b)\wedge 0.5\geq F(a)\wedge 0.5,$ hence bx ∈ I _a .

Let b ∈ I _a and $S\,{\ni}\,x{\leq}b$. Then x ∈ I _a . Indeed, since F is an (∈, ∈ ∨q)-fuzzy right ideal of S, and $S\,{\ni}\,x{\leq}b$, we have $F(x)\geq F(b)\wedge 0.5.$ Thus I _a is a right ideal of S. $\square$

In a similar way we can prove that:

Proposition 4.11

Let S be an ordered semigroup and F an (∈, ∈ ∨q)-fuzzy left ideal of S. Then I _a is a left ideal of S for every a ∈ S.

Combining Propositions 4.10 and 4.11 we have the following:

Proposition 4.12

Let S be an ordered semigroup and F an (∈, ∈ ∨q)-fuzzy ideal of S. Then I _a is an ideal of S for every a ∈ S.

5 Upper and lower parts of (∈, ∈ ∨ q)-fuzzy interior ideals

Definition 5.1

Let S be an ordered semigroup and F a fuzzy subset of S. We define the upper part F ⁺ and the lower part F ⁻ of F as follows:

$$ \begin{aligned} F^{+} :&\;S\longrightarrow \lbrack 0,1],x\longmapsto F^{+}(x)=F(x)\vee 0.5 \hbox{ and }\\ F^{-} :&\;S\longrightarrow \lbrack 0,1],x\longmapsto F^{-}(x)=F(x)\wedge 0.5 \hbox{ for all }x\in S\hbox{.}\\ \end{aligned} $$

Lemma 5.2 [11, 25]

Let F and G be fuzzy subsets of an ordered semigroup. Then the following hold:

• (1) $(F\wedge G)^{-}=(F^{-}\wedge G^{-}).$

• (2) (F ∨ G)⁻ = (F ⁻ ∨ G ⁻).

• (3) $(F\circ G)^{-}=(F^{-}\circ G^{-}).$

Lemma 5.3 [11, 25]

Let F and G be fuzzy subsets of an ordered semigroup S. Then the following hold:

• (1) $(F\wedge G)^{+}=(F^{+}\wedge G^{+}).$

• (2) (F ∨ G)⁺ = (F ⁺ ∨ G ⁺).

• (3) $(F\circ G)^{+}\geq (F^{+}\circ G^{+}).$

(If $A_{a}\neq \emptyset$ then $(F\circ G)^{+}= (F^{+}\circ G^{+})).$

Definition 5.4

Let A be a nonempty subset of an ordered semigroup. Then the upper part $F_{A}^{+}$ and the lower part $F_{A}^{-}$ of the characteristic function F _A of A are defined by

$$ F_{A}^{-}:S\longrightarrow \lbrack 0,1],x\longmapsto F_{A}^{-}(x):=\left \{ \begin{array}{ll} 0.5 & \quad \hbox{ if }x\in A,\\ 0 & \quad \hbox{ if }x\notin A \\ \end{array}\right. $$

and

$$ F_{A}^{+}:S\longrightarrow \lbrack 0,1],x\longmapsto F_{A}^{+}(x):=\left \{ \begin{array}{ll} 1&\qquad\hbox{if }x\in A,\\ 0.5&\quad\hbox{ if }x\notin A\\ \end{array} \right. $$

Lemma 5.5 [11]

If A and B be nonempty subsets of an ordered semigroup. Then the following hold:

• (1) $(F_{A}\wedge F_{B})^{-}=F_{A\cap B}^{-}.$

• (2) $(F_{A}\vee F_{B})^{-}=F_{A\cup B}^{-}.$

• (3) $(F_{A}\circ F_{B})^{-}=F_{(AB]}^{-}.$

Lemma 5.6

The lower part of the characteristic function $F_{I}^{-}$ is an (∈, ∈ ∨q)-fuzzy interior ideal of S if and only if I is an interior ideal of S.

Proof

The proof follows from Lemma 4.3. $\square$

From Theorem 3.3, we know that every fuzzy interior ideal of an ordered semigroup S is an (∈, ∈)-fuzzy interior ideal of S. Obviously every (∈, ∈)-fuzzy interior ideal of S is an (∈, ∈ ∨q)-fuzzy interior ideal of S.

In the following we show that if F is an (∈, ∈ ∨q)-fuzzy interior ideal of S then F ⁻ is a fuzzy interior ideal of S.

Proposition 5.7

Let F be an (∈, ∈ ∨q)-fuzzy interior ideal of S, then F ⁻ is a fuzzy interior ideal of S.

Proof

Let F be an (∈, ∈ ∨q)-fuzzy interior ideal of S, then for all x, y ∈ S, we have $F(xy)\geq (F(x)\wedge F(y)\wedge 0.5).$ Then $F(xy)\wedge 0.5\geq (F(x)\wedge F(y)\wedge 0.5)=((F(x)\wedge 0.5)\wedge (F(y)\wedge 0.5)).$ Hence $F^{-}(xy)\geq (F^{-}(x)\wedge F^{-}(y))$ and

$F(xay)\geq (F(a)\wedge 0.5).$ Then $F(xay)\wedge 0.5\geq (F(a)\wedge 0.5)=(F(a)\wedge 0.5).$ Hence F ⁻(xay) ≥ F ⁻(a). Let x, y ∈ S, x ≤ y, then by hypothesis, $F(x)\geq (F(y)\wedge 0.5)$, and we have $F(x)\wedge 0.5\geq (F(y)\wedge 0.5)\wedge0.5=F(y)\wedge 0.5,$ then $F(x)\wedge 0.5\geq F(y)\wedge 0.5$ and we have F ⁻(x) ≥ F ⁻(y). Thus F ⁻ is a fuzzy interior ideal of S. $\square$

Lemma 5.8

The lower part of the characteristic function $F_{I}^{-}$ is an (∈, ∈ ∨q)-fuzzy left ideal of S if and only if I is a left ideal of S.

Proof

Let I be a left ideal of S. Then $F_{I}^{-}$ is a fuzzy left ideal and so an (∈, ∈ ∨q)-fuzzy left ideal of S. Conversely, assume that $F_{I}^{-}$ is an (∈, ∈ ∨q)-fuzzy left ideal of S. Let x ∈ S, and y ∈ I, then $F_{I}^{-}(y)=0.5.$ Since $F_{I}^{-}$ is an (∈, ∈ ∨q)-fuzzy left ideal and $[y;0.5]\in F_{I}^{-},$ by hypothesis, $[xy;0.5]\in \vee qF_{I}^{-}.$ Which implies that $[xy;0.5]\in F_{I}^{-}$ or $[xy;0.5]qF_{I}^{-}.$ Hence $F_{I}^{-}(xy)\geq 0.5$ or $F_{I}^{-}(xy)+0.5>1.$ The case $F_{I}^{-}(xy)+0.5>1$ is not possible, because then $F_{I}^{-}(xy)\leq 0.5$ for all x, y ∈ S which is not allowed. Thus $F_{I}^{-}(xy)\geq 0.5,$ and so $xy\in I\Longrightarrow SI\subseteq I.$ Let x, y ∈ S, such that x ≤ y, if y ∈ I, then $F_{I}^{-}(y)=0.5.$ Since x ≤ y, by hypothesis, we have $F_{I}^{-}(x)\geq F_{I}^{-}(y)=0.5,$ then $F_{I}^{-}(x)\geq 0.5,$ and so x ∈ I. Therefore I is a left ideal of S. $\square$

Similarly, we have the following Lemma:

Lemma 5.9

The lower part of the characteristic function $F_{I}^{-}$ is an (∈, ∈ ∨q)-fuzzy right ideal of S if and only if I is a right ideal of S.

Combining Lemmas 5.8 and 5.9, we have the following:

Lemma 5.10

The lower part of the characteristic function $F_{I}^{-}$ is an (∈, ∈ ∨q)-fuzzy ideal of S if and only if I is an ideal of S.

Definition 5.11

An ordered semigroup S is called (∈, ∈ ∨q)-fuzzy left (resp. (∈, ∈ ∨q)-fuzzy right) simple if every (∈, ∈ ∨q)-fuzzy left (resp. (∈, ∈ ∨q)-fuzzy right) ideal is constant, that is, for every a, b ∈ S, we have, F ⁻(a) = F ⁻(b), for every (∈, ∈ ∨q)-fuzzy left (right) ideal F of S. An ordered semigroup S is called (∈, ∈ ∨q)-fuzzy simple if it is both (∈, ∈ ∨q)-fuzzy left and right simple.

Theorem 5.12

An ordered semigroup (S, ·,  ≤) is simple if and only if it is (∈, ∈ ∨q)-fuzzy simple.

Proof

$\Longrightarrow.$ Let F be an (∈, ∈ ∨q)-fuzzy ideal of S and a, b ∈ S. Using Proposition 4.12, I _a is an ideal of S. Since S is simple, it follows that I _a  = S so that b ∈ I _a . Thus $F(b)\geq F(a)\wedge 0.5,$ and so

$$ F^{-}(b)=F(b)\wedge 0.5\geq F(a)\wedge 0.5=F^{-}(a). $$

Similarly, we get F ⁻(b) ≤ F ⁻(a). Hence F ⁻(a) = F ⁻(b), and thus S is (∈, ∈ ∨q)-fuzzy simple.

$\Longleftarrow.$ Suppose that S contains proper ideals and let I be an ideal of S such that I ≠ S. Using Lemma 5.10, $F_{I}^{-}$ is an (∈, ∈ ∨q)-fuzzy ideal of S. Let x ∈ S. Since S is (∈, ∈ ∨q)-fuzzy simple, $F_{I}^{-}$ is a constant function, that is, $F_{I}^{-}(x)=F_{I}^{-}(b)$ for every b ∈ S. Thus, for any a ∈ I, we have $F_{I}^{-}(x)=F_{I}^{-}(a)=0.5$ and so x ∈ I. Therefore S = I, a contradiction. Consequently, S is simple. $\square$

Lemma 5.13 (cf. [25])

An ordered semigroup S is simple if and only if for every a ∈ S, we have S = (SaS].

Theorem 5.14

An ordered semigroup (S, ·,  ≤) is simple if and only if for every (∈, ∈ ∨q)-fuzzy ideal F of S, we have F ⁻(a) = F ⁻(b) for every a, b ∈ S.

Proof

$\Longrightarrow .$ Suppose that F is an (∈, ∈ ∨q)-fuzzy interior ideal of S and a, b ∈ S. Since S is simple and b ∈ S, by Lemma 5.13, we have S = (SaS]. Since a ∈ S, we have a ∈ (SbS]. Then a ≤ xby for some x, y ∈ S. Since F is an (∈, ∈ ∨q)-fuzzy interior ideal of S, we have

$$ \begin{aligned} F(a) &\geq F(xby)\wedge 0.5\\ &=F(x(by))\wedge 0.5\\ &\geq (F(b)\wedge 0.5)\wedge 0.5 (\hbox{since }F\hbox{ is an }(\in ,\in \vee q\hbox{)-fuzzy interior ideal)}\\ &=F(b)\wedge 0.5,\\ \end{aligned} $$

hence $F(a)\geq F(b)\wedge 0.5$ and $F(a)\wedge 0.5\geq (F(b)\wedge 0.5)\wedge 0.5=F(b)\wedge 0.5.$ Thus F ⁻(a) ≥ F ⁻(b). By a similar way, we can find that F ⁻(b) ≥ F ⁻(a). Therefore F ⁻(a) = F ⁻(b) for every a, b ∈ S.

$\Longleftarrow .$ Assume that F is an (∈, ∈ ∨q)-fuzzy interior ideal of S, then by Proposition 4.8, F is an (∈, ∈ ∨q)-fuzzy ideal of S. By hypothesis, F ⁻(a) = F ⁻(b) for every a, b ∈ S. Thus S is an (∈, ∈ ∨q)-fuzzy simple and by Theorem 5.12, S is simple. $\square$

Theorem 5.15

An ordered semigroup S is intra-regular if and only if for every (∈, ∈ ∨q)-fuzzy ideal F of S, we have

$$ F^{-}(a)=F^{-}(a^{2})\hbox{ for all }a\in S. $$

Proof

$\Longrightarrow .$ Let F be an (∈, ∈ ∨q)-fuzzy ideal of S and let a ∈ S. Then there exist x, y ∈ S such that a ≤ xa ² y and

$$ \begin{aligned} F(a) &\geq F(xa^{2}y)\wedge 0.5\\ &=F(x(a^{2}y))\wedge 0.5\\ &\geq (F(a^{2}y)\wedge 0.5)\wedge 0.5\\ &=F(a^{2}y)\wedge 0.5\geq (F(a^{2})\wedge 0.5)\wedge 0.5\\ &=F(a^{2})\wedge 0.5=F^{-}(a^{2})\\ \end{aligned} $$

On the other hand, $F^{-}(a^{2})=F(a^{2})\wedge 0.5\geq (F(a)\wedge 0.5)\wedge 0.5=F(a)\wedge 0.5=F^{-}(a).$ Hence F ⁻(a) = F ⁻(a ²).

Conversely, consider the ideal I(a ²) = (a ²∪Sa ²∪ a ² S∪ Sa ² S], generated by a ². Then by Lemma 5.10, $F_{I(a^{2})}^{-}$ is an (∈, ∈ ∨q)-fuzzy ideal of S and by hypothesis $F_{I(a^{2})}^{-}(a)=F_{I(a^{2})}^{-}(a^{2})=1,$ hence a ∈ I(a ²) = (a ²∪Sa ²∪a ² S∪Sa ² S]. Thus a ≤ a ² or a ≤ xa ² or a ≤ a ² x or a ≤ xa ² y for some x, y ∈ S. If a ≤ a ² = aa ≤ a ² a ² = aa ² a ∈ Sa ² S and a ∈ (Sa ² S]. Similarly, for other cases we have a ≤ ua ² v for some u, v ∈ S. Thus S is intra-regular. $\square$

Theorem 5.16

Let S be an intra-regular ordered semigroup and F is an (∈, ∈ ∨q)-fuzzy ideal of S. Then for every a, b ∈ S, we have

$$ F^{-}(ab)=F^{-}(ba). $$

Proof

Let a, b ∈ S. Then by Theorem 5.15, we have

$$ \begin{aligned} F^{-}(ab) &=F^{-}((ab)^{2})=F^{-}((ab)(ab))=F^{-}(a(ba)b)\\ &\geq F^{-}(ba).\\ \end{aligned} $$

By symmetry we have F ⁻(ba) ≥ F ⁻(ab). Thus F ⁻(ab) = F ⁻(ba) for every a, b ∈ S. $\square$

In [26], semisimple ordered semigroups are characterized by the properties of their fuzzy interior ideals. Next we are characterizing the semisimple ordered semigroups by the properties of lower parts of (∈, ∈ ∨q)-fuzzy interior ideals.

Proposition 5.17

If S is semisimple ordered semigroup and F, G are (∈, ∈ ∨q) -fuzzy interior ideals. Then $(F\circ G)^{-}\preceq (F\wedge G)^{-}$.

Proof

Let S be a semisimple and F an (∈, ∈ ∨q) -fuzzy interior ideal of S. If $A_{a}={\emptyset}$, then $(F\circ G)^{-}(a)=(F\circ G)(a)\wedge 0.5=0\wedge 0.5=0\leq (F\wedge G)(a)\wedge 0.5=(F\wedge G)^{-}(a).$ Let $A_{a}\neq \emptyset ,$ then

$$ \begin{aligned} (F\circ G)^{-}(a) &=(F\circ G)(a)\wedge 0.5\\ &=\left[\bigvee \limits_{(y,z)\in A_{a}}(F(y)\wedge G(z))\right] \wedge 0.5\\ &=\bigvee \limits_{(y,z)\in A_{a}}(F(y)\wedge G(z)\wedge 0.5)\\ &=\bigvee \limits_{(y,z)\in A_{a}}((F(y)\wedge 0.5)\wedge (G(z)\wedge 0.5)\wedge 0.5).\\ \end{aligned} $$

Since S is semisimple and F and G (∈, ∈ ∨q)-fuzzy interior ideals, so by Proposition 4.8, F and G are (∈, ∈ ∨q)-fuzzy ideal of S. Since a ≤ yz, we have $F(a)\geq F(yz)\wedge 0.5\geq F(y)\wedge 0.5$ and $G(a)\geq G(yz)\wedge 0.5\geq G(z)\wedge 0.5.$

Thus

$$ \begin{aligned} \bigvee \limits_{(y,z)\in A_{a}}((F(y)\wedge 0.5)\wedge (G(z)\wedge 0.5)\wedge 0.5) &\leq \bigvee \limits_{(y,z)\in A_{a}}(F(a)\wedge G(a)\wedge 0.5)\\ &=\bigvee \limits_{(y,z)\in A_{a}}(F(a)\wedge G(a)\wedge 0.5)\\ &=(F\wedge G)(a)\wedge 0.5=(F\wedge G)^{-}(a).\\ \end{aligned} $$

Therefore $(F\circ G)^{-}(a)\leq (F\wedge G)^{-}(a).$

Remark 5.18

If S is semisimple and F an (∈, ∈ ∨q)-fuzzy interior ideal of S. Then $(F\circ F)^{-}\preceq F^{-}.$

Theorem 5.19

An ordered semigroup S is semisimple if and only if for every (∈, ∈ ∨q)-fuzzy interior ideal F and G of S, we have $(F\circ G)^{-}=(F\wedge G)^{-}$.

Proof

Let S be a semisimple ordered semigroup and F, G are (∈, ∈ ∨q)-fuzzy interior ideals of S. Since S is semisimple so for each a ∈ S , there exist x, y, z ∈ S such that a ≤ axayaz ≤ ax(axayaz)yaz = ((ax)a(xay)(azy)a(z)), then ((ax)a(xay), (azy)a(z)) ∈ A _a and $A_{a}\neq \emptyset$. Thus

$$ \begin{aligned} (F\circ G)^{-}(a) &=(F\circ G)(a)\wedge 0.5\\ &=\left[\bigvee \limits_{(y,z)\in A_{a}}(F(y)\wedge G(z))\right] \wedge 0.5\\ &=\bigvee \limits_{(y,z)\in A_{a}}(F(y)\wedge G(z)\wedge 0.5)\\ &\geq (F((ax)a(xay))\wedge G((azy)a(z))\wedge 0.5)\\ &\geq (F(a)\wedge 0.5)\wedge (G(a)\wedge 0.5)\wedge 0.5\\ &=(F(a)\wedge G(a)\wedge 0.5)=(F\wedge G)(a)\wedge 0.5\\ &=(F\wedge G)^{-}(a). \end{aligned} $$

This implies that $(F\wedge G)^{-}\preceq (F\circ G)^{-}.$ On the other hand, by Proposition 5.17, we have $(F\circ G)^{-}\preceq (F\wedge G)^{-}$ and so $(F\circ G)^{-}=(F\wedge G)^{-}$.

Conversely, assume that $(F\circ G)^{-}=(F\wedge G)^{-}$ for every (∈, ∈ ∨q)-fuzzy interior ideal F and G of S. Let I be an interior ideal of S, then I is an ideal of S and by Lemma 5.6, the characteristic function $F_{I}^{-}$ of I is an (∈, ∈ ∨q)-fuzzy interior ideal of S. By hypothesis and Lemma 5.5 (3), we have

$$ F_{I}^{-}=F_{I}^{-}\wedge F_{I}^{-}=F_{I}^{-}\circ F_{I}^{-}=F_{(I^{2}]}^{-}. $$

Using Lemma 5.5 again we have I = (I ²]. Thus S is semisimple. $\square$

By Remark 5.18 and Theorem 5.19, we have the following Theorem:

Theorem 5.20

An ordered semigroup S is semisimple if and only if for every (∈, ∈ ∨q)-fuzzy interior ideal F of S, we have ${(F\circ F)^{-}}= F^{-}.$

6 Implication-based fuzzy interior ideals

Fuzzy logic is an extension of set theoretic variables in terms of the linguistic variable truth. Some of the operators, like $\wedge ,\vee ,\lnot ,\longrightarrow$ in fuzzy logic can also be defined by using the truth tables. Also, the extension principle can be used to derive definitions of the implicative operators.

In the fuzzy logic, we denote the truth value of fuzzy proposition P by [P]. In the following, we display the fuzzy logical and corresponding set-theoretical notions:

$$ \begin{aligned} &[x\in F]=F(x);\\ &[x\notin F]=1-F(x);\\ &[P\wedge Q]=\hbox{min}\{[P],[Q]\};\\ &[P\vee Q]=\hbox{max}\{[P],[Q]\};\\ &[P\longrightarrow Q]=\hbox{min}\{1,1-[P]+[Q]\};\\ &[\forall xP(x)]=\hbox{inf}[P(x)];\\ &\models P \hbox{ if and only if }[P]=1 \hbox{ for all valuations}. \end{aligned} $$

Various implication operators can similarly be defined. We only show a selection of them in the following table, where α denotes the degree of truth (or the degree of membership) of the premise and β denotes the respective values for the consequence, and I the resulting degree of truth for the implication:

Name	Definition of implication operator
Luckaseiwickz	I α(α, β) = min{1, 1 − α + β}
Standard Star (Godel)	$I_{g}(\alpha ,\beta )=\left \{ \begin{array}{l} 1\quad\hbox{ if }\alpha \leq \beta\\ \beta \quad \hbox{ if }\alpha >\beta \\ \end{array}\right.$
Gaines-Rescher	$I_{gr}(\alpha ,\beta )=\left\{ \begin{array}{l} 1\quad \hbox{ if }\alpha \leq \beta\\ 0 \quad \hbox{ if }\alpha >\beta\\ \end{array}\right.$

The “quality” of these implication operators could be evaluated either by empirically or by axiomatically methods.

In the following definition, we consider the implication operators in the Lukasiewicz system of continuous-valued logic.

Definition 6.1

Suppose that the fuzzy subset F of S satisfies the following conditions:

• (1) for any $x,y\in S, \models \left[ \left[ y\in F\right]\longrightarrow \left[ x\in F\right],x\leq y\right];$

• (2) for any $x,y\in S, \models \left[ \hbox{min}\{\left[x\in F\right],\left[y\in F\right]\} \longrightarrow \left[ xy\in F\right]\right];$

• (3) for any $x,a,y\in S, \models \left[ \left[ a\in F\right]\longrightarrow \left[ xay\in F\right]\right].$

Then F is called a fuzzifying interior ideal of S.

Clearly, Definition 2.1 is equivalent to 6.1. Therefore a fuzzifying interior ideal is an ordinary fuzzy interior ideal.

Now, we introduce the concept of t-tautology, i.e.,

$\models_{t}P$ if and only if [P] ≥ t, for all valuations.

Now, we can extend the concept of implication-based fuzzy interior ideals in the following way:

Definition 6.2

Let F be a fuzzy subset of S and t ∈ (0,1] is a fixed number. If the following conditions hold:

• (1) for any $x,y\in S, \models _{t}\left[\left[y\in F\right]\longrightarrow \left[ x\in F\right],x\leq y\right];$

• (2) for any $x,y\in S, \models _{t}\left[\hbox{min} \{\left[x\in F\right],\left[y\in F\right]\} \longrightarrow \left[ xy\in F\right]\right];$

• (3) for any $x,a,y\in S, \models_{t}\left[\left[a\in F\right]\longrightarrow\left[ xay\in F\right]\right].$

Then F is called a t-implication-based fuzzy interior ideal of S.

Now, if I is an implication operator then we have the following corollary:

Corollary 6.3

A fuzzy subset F of S is a t -implication-based fuzzy interior ideal of S if and only if it satisfies the following conditions:

• (1) for any x, y ∈ S, I(F(y), F(x)) ≥ t with x ≤ y,

• (2) for any x, y ∈ S, I(min{F(x), F(y)}, F(xy)) ≥ t,

• (3) for any x, a, y ∈ S, I(F(a), F(xay)) ≥ t.

Let F be a fuzzy subset of S. Then we have the following theorem:

Theorem 6.4

• (1) Let I = I _gr . Then F is an 0.5-implication-based fuzzy interior ideal of S if and only if F is a fuzzy interior ideal with thresholds (α = 0, β = 1] of S.

• (2) I = I _g . Then 0.5-implication-based fuzzy interior ideal of S if and only if F is a fuzzy interior ideal with thresholds (α = 0, β = 0.5] of S.